TD-DFT spin-adiabats with analytic nonadiabatic derivative couplings

Abstract

We present an algorithm for efficient calculation of analytic nonadiabatic derivative couplings between spin-adiabatic, time-dependent density functional theory states within the Tamm-Dancoff approximation. Our derivation is based on the direct differentiation of the Kohn-Sham pseudowavefunction using the framework of Ou et al. Our implementation is limited to the case of a system with an even number of electrons in a closed shell ground state, and we validate our algorithm against finite difference at an S₁/T₂ crossing of benzaldehyde. Through the introduction of a magnetic field spin-coupling operator, we break time-reversal symmetry to generate complex valued nonadiabatic derivative couplings. Although the nonadiabatic derivative couplings are complex valued, we find that a phase rotation can generate an almost entirely real-valued derivative coupling vector for the case of benzaldehyde.

I. INTRODUCTION

After a molecular system is photoexcited, it can undergo two types of nonradiative transitions between electronic states. An internal conversion (IC) is a transition between electronic states of the same spin multiplicity (e.g., singlet to singlet or triplet to triplet), while an intersystem crossing (ISC) is a transition between electronic states of different spin multiplicities (e.g., singlet to triplet or conversely). ISCs are forbidden in spin-free quantum mechanics but can be mediated by spin-orbit coupling (SOC). SOC tends to be small for systems without heavy metals, which historically led many to believe that ISC would be slow compared with IC rates, but recent work has shown that ISC can occur at short times, even in small molecules,¹ and may compete with IC in some systems.² Moreover, even though most photoexcited systems start in a singlet state, excited state triplets are usually lower in energy than excited state singlets due to antisymmetry and exchange; thus, ISC is usually possible thermodynamically.³ Thus, whether an ISC event occurs is dictated by dynamics and not by thermodynamics.

A popular tool for elucidating nonradiative relaxation dynamics is Tully’s fewest switches surface hopping (FSSH) algorithm, an intuitive and computationally efficient approach.⁴ According to FSSH, the total nuclear plus electronic wavefunction of a system is simulated by a swarm of trajectories. The inputs to the FSSH calculation are adiabatic energies, adiabatic gradients, and the nonadiabatic derivative couplings (NADC),

$$d_{IJ}^{\left[x\right]}=⟨{\Psi }_I\left|{\Psi }_J^{\left[x\right]}\right.⟩.$$

Propagation is along the adiabatic potential energy surfaces (hence the need for adiabatic nuclear gradients), with stochastic hops between adiabats. Even though the NADCs are not required to integrate the electronic Schrödinger equation,^5–8 they are needed to determine the direction of momentum rescaling when a hop occurs.^9–12 Thus, the goal of this manuscript is to provide the necessary electronic structure matrix elements (especially NADCs) for ISC processes so that one can model ISC dynamics with FSSH.^13–19

Now, the standard electronic structure software usually generates eigenstates of the spin-free electronic Hamiltonian, which we will also sometimes refer to as the “usual” electronic Hamiltonian. Without SOC, these eigenstates do not mix spin, and so we will call them spin-diabats. Obviously, the standard FSSH dynamics along these surfaces will never capture an ISC event, as there will always be zero probability to hop between the spin-diabats. Therefore, in order to capture ISC, we must first include some spin-coupling. With this obvious fact in mind, the most straightforward and computationally efficient approach would be to run dynamics on the spin-diabats (singlet, triplet, etc.) and switch surfaces with a rate determined by both diabatic spin orbit coupling and nonadiabatic derivative coupling. Indeed, this approach has previously been followed by Gonzalez and co-workers^17,20 as well as by Cui and Thiel.¹⁴ More generally, however, this approach carries risk: the diabatic couplings are usually delocalized (which is suboptimal for surface hopping). Furthermore, surface hopping can only be derived approximately in an adiabatic representation^21,22 which must make one question the validity of spin-diabatic surface hopping. In addition, practical questions arise: for instance, if the SOC is large, what direction should we choose for momentum rescaling with spin-diabatic FSSH? Last, as shown by Granucci et al.¹³ for spin-diabatic FSSH, one must take great care to enforce rotational invariance of the hopping rate. And in particular, if the SOC matrix elements change sign, it may be almost fruitless to work with a spin-diabatic representation.

For all the reasons mentioned above, it is now commonly accepted²³ that even when running ISC dynamics, it is preferable to use a spin-adiabatic basis. In other words, one should calculate spin-electronic eigenfunctions of the entire (usual + SOC) Hamiltonian and then generate adiabatic gradients and NADCs for FSSH. With such a spin-adiabatic approach, one will not only avoid the many pitfalls discussed above but also be guaranteed to enjoy the usual benefits of FSSH dynamics: low energy barrier crossings will be possible (which is important in the case of large SOC), detailed balance will be enforced approximately,²⁴ etc.

Of course, the downside to working with spin-adiabatic wavefunctions is the extra computational cost. Nevertheless, recently, we presented a computationally efficient algorithm (with an additional roughly two-fold computational cost) for the generation of spin-adiabat energies and gradients by including SOC within configuration interaction singles (CIS).²⁵ In this work, we will now extend the algorithm in Ref. 25 to time-dependent density functional theory (TD-DFT) within the Tamm-Dancoff approximation (TDA), which corrects the orbital energies relative to Hartree-Fock and CIS and yields better excitation energies while retaining the same structure as the CIS.²⁶ Moreover, we will also calculate CIS and TDA NADCs, extending the previous work with semiempirical²⁷ or MR-CISD wavefunctions²⁸ into the realm of modern TD-DFT calculations (where calculating NADCs has been a hot topic in the recent years^29–34 given the formal absence of a TD-DFT wavefunction). In principle, our algorithm should also be extendable to spin-flip methods.^35–37 Note that we are far from the first to consider SOC effects in the context of TD-DFT/TDA calculations (e.g., see Ref. 38), but we believe our focus on generating matrix elements for nonadiabatic nuclear dynamics in the context of SOC TD-DFT calculations is new. Importantly, we have also chosen to add the effect of a magnetic field B through B · S coupling. Without the magnetic field, the Hamiltonian for a system with an even number of electrons will obey time-reversal symmetry and so can be transformed into a basis in which all its elements are real-valued.^39,40 Thus, for a system with an even number of electrons, one should never recover a complex NADC; the hypothetical appearance of any such complex NADC would only imply an artificial introduction of the imaginary number i to the spin-electronic basis. That being said, by introducing a magnetic field, we allow the new spin-coupled Hamiltonian to break time-reversal symmetry, and so we will need to generate complex-valued NADCs—which can introduce some rich new physics.⁴¹

A few more words are now appropriate regarding complex electronic Hamiltonians. The original FSSH algorithm was clearly designed around real-valued electronic structure. For example, a real Hamiltonian ensures that the NADCs are real and the momentum rescaling direction is well defined. Nevertheless, one must presume that semiclassical mechanics are possible with complex NADCs, and a recent work has explored various ansätze for the extension of FSSH with complex-valued NADCs.⁴² Since the overall phases of the adiabats are not well defined, the total phase of the derivative coupling is not well-defined, and choosing a direction of momentum rescaling is not obvious. Previous work in Ref. 42 has suggested that one possible choice for momentum rescaling is the direction of the NADC between the participating states, as rotated to have the maximum norm in the real-valued component; and yet, (unpublished) data suggest that this ansatz may not be completely general. To date, the optimal direction for rescaling momenta likely remains unknown. Nevertheless, such a direction must lie within the two-dimensional space spanned by $\text{Re}\left[{\mathbf{d}}_{IJ}\right]$ and $\text{Im}\left[{\mathbf{d}}_{IJ}\right]$. Moreover, for the case of a real-valued NADC, there is ample evidence that rescaling in the wrong direction can lead to erroneous results,⁴³ especially for upward hops where velocity reversal is important,^6,44–48 and so calculating the derivative coupling will be absolutely essential for any and all versions of FSSH dynamics.

With this background in mind, in the present paper, we will derive and implement a computationally efficient algorithm to compute the complex-valued NADC of TDA spin-adiabats in the presence of a magnetic field. For the analytic gradient, see Appendix C. We will use the framework developed in Ref. 34, deriving the NADCs for TDA states by treating the TDA Kohn-Sham wavefunction as a true wavefunction. Our derivation will not be completely self-contained; we will rely on some derivations from Refs. 25 and 49. As a simple application, we will explore the complex nature of the NADC in the context of benzaldehyde at an S₁/T₂ crossing.

A. Notation

Before we dive into the theory, it will be helpful to define our notation. Lowercase Greek letters {μ, ν, λ, γ, ω} index atomic orbitals, and the two-electron integrals will be written in physics notation:⁵⁰ ${\mathrm{\Pi }}_{\mu \nu \lambda \sigma }=\int d{r}_1\int d{r}_2{\chi }_{\mu }\left(r_1\right){\chi }_{\nu }\left(r_2\right)\frac{1}{\left|r_1-r_2\right|}{\chi }_{\lambda }\left(r_1\right){\chi }_{\sigma }\left(r_2\right)$. Lowercase Roman letters {p, q, r, s} index general molecular orbitals from a restricted, closed-shell ground state, $\left|{\Phi }_{gs}\right.⟩$. Lowercase {a, b, c, d} index specifically virtual orbitals, and {i, j, k, l, m} index specifically occupied orbitals. The Greek letters {σ, τ, υ} will index spin, with up spin denoted by α and down by β. Spin orbitals are represented by bold type as p or μ, or when explicitness is required, with a subscript as p_σ or μ_σ. A singly excited determinant is defined by $\left|{\mathrm{\Phi }}_{\mathbf{i}}^{\mathbf{a}}\right.⟩\equiv a_{\mathbf{a}}^{†}{a}_{\mathbf{i}}\left|{\Phi }_{gs}\right.⟩$. The singlet spin-diabat is indexed by (s) and triplet spin-diabats (t) are indexed by m_s = −1, 0, +1. The four spin-diabats (one singlet and three triplets) will be indexed by $ϵ\in \left\{s,t^{\left(m_s=0\right)},t^{\left(m_s=1\right)},t^{\left(m_s=-1\right)}\right\}$. A superscript [x] implies the derivative with respect to x. A vector quantity in three dimensional space will be indicated by an arrow, $\left(\overrightarrow{v}\right)$. Finally, note that some quantities below will be complex; an asterisk (*) will denote the complex conjugate.

II. THEORY: ANALYTIC NONADIABATIC DERIVATIVE COUPLINGS FOR TDA SPIN-ADIABATS

A. Coupling spin

Below, we will include the effects of two spin operators, the spin-orbit coupling V_so and an external magnetic field V_m:

$$\mathbf{V}={\mathbf{V}}_{so}+{\mathbf{V}}_m.$$ (1)

To model spin-orbit coupling, a one-electron (usually mean field) operator has been shown to capture many effects of the full SOC coupling operator (both the one- and two-electron terms).^36,51 For the present paper, our spin-orbit coupling operator will be the one-electron component of the Breit-Pauli spin-orbit coupling,⁵²

$${\mathbf{V}}_{so}=-\frac{{\alpha }_0^2}{2}\sum _{j,A}\frac{Z_A}{|{\overrightarrow{r}}_{jA}{|}^3}\left({\overrightarrow{r}}_{jA}\times {\overrightarrow{p}}_j\right)\cdot {\overrightarrow{s}}_j.$$ (2)

Here, α₀ is the fine structure constant and j and A index the electrons and nuclei, respectively. Z_A is the charge of nucleus A, ${\overrightarrow{s}}_j$ is the spin operator of the j electron, ${\overrightarrow{r}}_{jA}$ is the distance between electron j and nucleus A, and ${\overrightarrow{p}}_j$ is the momentum of electron j. We will include the effects of a magnetic field through B · S coupling with the standard assumption of a gyromagnetic coupling equal to 2,

$${\mathbf{V}}_m=-\frac{e}{m_e}\sum _j\overrightarrow{B}\cdot {\overrightarrow{s}}_j.$$ (3)

Here, e is the charge of an electron, m_e is the mass of an electron, and $\overrightarrow{B}$ is the magnetic field, $\overrightarrow{B}=\left[B_x,B_y,B_z\right]$.

The components of V are expressed in second quantization notation as

$${\mathbf{V}}_x=\sum _{pq}\left(\frac{2{\mu }_B}{\hslash }{B}_x{\delta }_{pq}-\frac{{\alpha }_0^2}{2}{\tilde{L}}_{x_{pq}}\right)\cdot \frac{\hslash }{2}\left(a_{p_{\alpha }}^{†}{a}_{q_{\beta }}+a_{p_{\beta }}^{†}{a}_{q_{\alpha }}\right),$$ (4a)

$${\mathbf{V}}_y=\sum _{pq}\left(\frac{2{\mu }_B}{\hslash }{B}_y{\delta }_{pq}-\frac{{\alpha }_0^2}{2}{\tilde{L}}_{y_{pq}}\right)\cdot \frac{\hslash }{2i}\left(a_{p_{\alpha }}^{†}{a}_{q_{\beta }}-a_{p_{\beta }}^{†}{a}_{q_{\alpha }}\right),$$ (4b)

$${\mathbf{V}}_z=\sum _{pq}\left(\frac{2{\mu }_B}{\hslash }{B}_z{\delta }_{pq}-\frac{{\alpha }_0^2}{2}{\tilde{L}}_{z_{pq}}\right)\cdot \frac{\hslash }{2}\left(a_{p_{\alpha }}^{†}{a}_{q_{\alpha }}-a_{p_{\beta }}^{†}{a}_{q_{\beta }}\right).$$ (4c)

Here, μ_B is the Bohr magneton μ_B = eℏ/2m_e and $\tilde{\mathbf{L}}$ is a completely imaginary and antisymmetric matrix that captures the angular momentum of an electron moving around all different nuclei A with positions ${\overrightarrow{r}}_A$,²⁵ e.g.,

$${\tilde{L}}_{z_{pq}}=\sum _A{Z}_A⟨p\left|\frac{{\left[\left(\overrightarrow{r}-{\overrightarrow{r}}_A\right)\times \overrightarrow{p}\right]}_z}{|\overrightarrow{r}-{\overrightarrow{r}}_A{|}^3}\right|q⟩.$$ (5)

It will be useful to express V in the molecular spin orbital basis,

$$V_{p_{\alpha }{q}_{\alpha }}=\left({\mu }_B{B}_z{\delta }_{pq}-\frac{\hslash {\alpha }_0^2}{4}{\tilde{L}}_{z_{pq}}\right),$$ (6a)

$$V_{p_{\beta }{q}_{\beta }}=-\left({\mu }_B{B}_z{\delta }_{pq}-\frac{\hslash {\alpha }_0^2}{4}{\tilde{L}}_{z_{pq}}\right),$$ (6b)

$$V_{p_{\alpha }{q}_{\beta }}=\left({\mu }_B{B}_x{\delta }_{pq}-\frac{\hslash {\alpha }_0^2}{4}{\tilde{L}}_{x_{pq}}\right)+\frac{1}{i}\left({\mu }_B{B}_y{\delta }_{pq}-\frac{\hslash {\alpha }_0^2}{4}{\tilde{L}}_{y_{pq}}\right),$$ (6c)

$$V_{p_{\beta }{q}_{\alpha }}=\left({\mu }_B{B}_x{\delta }_{pq}-\frac{\hslash {\alpha }_0^2}{4}{\tilde{L}}_{x_{pq}}\right)-\frac{1}{i}\left({\mu }_B{B}_y{\delta }_{pq}-\frac{\hslash {\alpha }_0^2}{4}{\tilde{L}}_{y_{pq}}\right),$$ (6d)

where ${\tilde{L}}_{x_{pq}}={\sum }_{\mu \nu }{C}_{\mu p}{\tilde{L}}_{x_{\mu \nu }}{C}_{\nu q}$, etc.

Due to our choice of a spatially constant magnetic field, the gradient of the total spin-coupling operator will include only a contribution from the spin-orbit coupling,

$$V_{\mathbf{pq}}^{\left[x\right]}=-\frac{\hslash {\alpha }_0^2}{4}{\tilde{L}}_{\mathbf{pq}}^{\left[x\right]}.$$ (7)

Nevertheless, the derivation outlined below will be general, as applicable to nonuniform magnetic fields.

B. Spin-adiabats within TD-DFT/TDA

Our total Hamiltonian is the sum of the usual electronic Hamiltonian and a perturbation that mixes in spin (H_tot = H_el + V). Within the TDA, we diagonalize a modified Kohn-Sham linear response tensor A to solve the following eigenequation:

$$\mathbf{A}{\mathbf{X}}^J={\omega }_J{\mathbf{X}}^J,$$ (8)

where ω_J is the total energy (ground plus excited) of state J.

The TDA excited states are linear combinations of singly excited determinants that differ from the ground state by an excitation from an occupied spin orbital i to a virtual spin orbital a. Because we mix spin states, a TDA state $\left|{\Psi }_J\right.⟩$ will contain contributions from all possible spin combinations,

$$\left|{\Psi }_J\right.⟩=\sum _{\mathbf{ai}}{X}_{\mathbf{a}\mathbf{i}}^J\left|{\Phi }_{\mathbf{i}}^{\mathbf{a}}\right.⟩=\sum _{ai}\sum _{\sigma \tau }{X}_{a_{\sigma }{i}_{\tau }}^J\left|{\Phi }_{i_{\tau }}^{a_{\sigma }}\right.⟩.$$ (9a)

It will be useful to define the spin-diabat basis. The four spin-diabats include one singlet (s) and three triplets ($t^{\left(m_s=-\mathrm{1,0,1}\right)}$), and the wavefunction can be expressed in this basis as

$$\begin{array}{ccc}\hfill \left|{\Psi }_J\right.⟩& =\hfill & \frac{1}{\sqrt{2}}\sum _{ai}{s}_{ai}^J\left(\left|{\Phi }_{i_{\alpha }}^{a_{\alpha }}\right.⟩+\left|{\Phi }_{i_{\beta }}^{a_{\beta }}\right.⟩\right)\hfill \\ \hfill & \hfill & +\frac{1}{\sqrt{2}}\sum _{ai}{t}_{ai}^{J\left(m_s=0\right)}\left(\left|{\Phi }_{i_{\alpha }}^{a_{\alpha }}\right.⟩-\left|{\Phi }_{i_{\beta }}^{a_{\beta }}\right.⟩\right)\hfill \\ \hfill & \hfill & +\sum _{ai}{t}_{ai}^{J\left(m_s=+1\right)}\left|{\Phi }_{i_{\beta }}^{a_{\alpha }}\right.⟩+\sum _{ai}{t}_{ai}^{J\left(m_s=-1\right)}\left|{\Phi }_{i_{\alpha }}^{a_{\beta }}\right.⟩\hfill \end{array}$$ (9b)

$$=\sum _{ϵ}\sum _{ai}{X}_{ai}^{J\left(ϵ\right)}\left|{\Phi }_i^{a\left(ϵ\right)}\right.⟩.$$ (9c)

Here,

$$\left|{\Phi }_i^{a\left(ϵ\right)}\right.⟩\equiv \left\{\begin{array}{cc}\frac{1}{\sqrt{2}}\left(|{\Phi }_{i_{\alpha }}^{a_{\alpha }}⟩+|{\Phi }_{i_{\beta }}^{a_{\beta }}⟩\right),\hfill & \mathrm{i}\mathrm{f}ϵ=s\hfill \\ \frac{1}{\sqrt{2}}\left(|{\Phi }_{i_{\alpha }}^{a_{\alpha }}⟩-|{\Phi }_{i_{\beta }}^{a_{\beta }}⟩\right),\hfill & \mathrm{i}\mathrm{f}ϵ=t^{\left(m_s=0\right)}\hfill \\ |{\Phi }_{i_{\beta }}^{a_{\alpha }}⟩,\hfill & \mathrm{i}\mathrm{f}ϵ=t^{\left(m_s=+1\right)}\hfill \\ |{\Phi }_{i_{\alpha }}^{a_{\beta }}⟩,\hfill & \mathrm{i}\mathrm{f}ϵ=t^{\left(m_s=-1\right)}.\hfill \end{array}\right.$$

The relationship between the matrix X and the s and ${\mathbf{t}}^{\left(m_s=-\mathrm{1,0,1}\right)}$ amplitudes is

$$s_{ai}^J=X_{ai}^{J\left(s\right)}=\frac{1}{\sqrt{2}}\left(X_{a_{\alpha }{i}_{\alpha }}^J+X_{a_{\beta }{i}_{\beta }}^J\right),$$ (10a)

$$t_{ai}^{J\left(m_s=0\right)}=X_{ai}^{J\left(t^{\left(m_s=0\right)}\right)}=\frac{1}{\sqrt{2}}\left(X_{a_{\alpha }{i}_{\alpha }}^J-X_{a_{\beta }{i}_{\beta }}^J\right),$$ (10b)

$$t_{ai}^{J\left(m_s=+1\right)}=X_{ai}^{J\left(t^{\left(m_s=+1\right)}\right)}=X_{a_{\alpha }{i}_{\beta }}^J,$$ (10c)

$$t_{ai}^{J\left(m_s=-1\right)}=X_{ai}^{J\left(t^{\left(m_s=-1\right)}\right)}=X_{a_{\beta }{i}_{\alpha }}^J.$$ (10d)

Our linear response tensor A can be expressed as the total Hamiltonian projected into the space of all single excitations $\left|{\Phi }_{\mathbf{i}}^{\mathbf{a}}\right.⟩$,

$$\begin{array}{ccc}\hfill A_{\mathbf{aibj}}& =\hfill & ⟨{\Phi }_{\mathbf{i}}^{\mathbf{a}}\left|\right.{\mathbf{H}}_{tot}\left|{\Phi }_{\mathbf{j}}^{\mathbf{b}}\right.⟩\hfill \\ \hfill & =\hfill & ⟨{\Phi }_{\mathbf{i}}^{\mathbf{a}}\left|\right.{\mathbf{H}}_{el}\left|{\Phi }_{\mathbf{j}}^{\mathbf{b}}\right.⟩+⟨{\Phi }_{\mathbf{i}}^{\mathbf{a}}\left|\right.\mathbf{V}\left|{\Phi }_{\mathbf{j}}^{\mathbf{b}}\right.⟩\hfill \\ \hfill & =\hfill & F_{\mathbf{ab}}{\delta }_{\mathbf{ij}}-F_{\mathbf{ji}}{\delta }_{\mathbf{ab}}+{\mathrm{\Pi }}_{\mathbf{ajib}}+{\mathrm{\Omega }}_{\mathbf{aibj}}+E_{gs}{\delta }_{\mathbf{ab}}{\delta }_{\mathbf{ij}}+V_{\mathbf{ab}}{\delta }_{\mathbf{ij}}-V_{\mathbf{ji}}{\delta }_{\mathbf{ab}}.\hfill \\ \hfill & \hfill & \hfill \end{array}$$ (11)

Here, F is the Fock matrix, which is diagonal in the molecular orbital basis,

$$F_{\mathbf{pq}}=h_{\mathbf{pq}}+g_{\mathbf{pq}}+\sum _{\mathbf{m}}{\mathrm{\Pi }}_{\mathbf{pmqm}}={\epsilon }_{\mathbf{p}}{\delta }_{\mathbf{pq}}.$$ (12)

The Fock matrix includes (i) the kinetic energy and external potential h, (ii) the DFT exchange-correlation matrix g [Eq. (A4)], and (iii) the Coulomb and fraction of Hartree-Fock exchange Π,

$${\mathrm{\Pi }}_{\mathbf{pqsr}}=⟨\mathbf{p}\mathbf{q}\left|\mathbf{s}\mathbf{r}\right.⟩-c_{\text{HF}}⟨\mathbf{p}\mathbf{q}\left|\mathbf{r}\mathbf{s}\right.⟩.$$ (13)

Here, c_HF represents the fraction of exact exchange present according to the DFT functional of choice; for CIS, c_HF = 1. Note that the set {Π_pqsr} are not matrix elements for the full two-electron repulsion operator but rather screened matrix elements; obviously, these matrix elements are not fully antisymmetric. As such, one should not consider $\widehat{\mathrm{\Pi }}$ in Eq. (11) to be a second quantized operator but a first quantized operator in the space of all single excitations (${\mathrm{\Pi }}_{\mathbf{ajib}}=⟨{\Phi }_{\mathbf{i}}^{\mathbf{a}}\left|\right.\widehat{\mathrm{\Pi }}\left|{\Phi }_{\mathbf{j}}^{\mathbf{b}}\right.⟩$).

Let us now be more explicit. An essential aspect of the spin-diabatic basis is that the two-electron tensors are block diagonal. Using the fact that the nonzero matrix elements of Π in Eq. (13) are

$$⟨{\Phi }_{i_{\alpha }}^{a_{\alpha }}\left|\right.\widehat{\mathrm{\Pi }}\left|{\Phi }_{j_{\alpha }}^{b_{\alpha }}\right.⟩=⟨{\Phi }_{i_{\beta }}^{a_{\beta }}\left|\right.\widehat{\mathrm{\Pi }}\left|{\Phi }_{j_{\beta }}^{b_{\beta }}\right.⟩=⟨aj\left|ib\right.⟩-c_{\text{HF}}⟨aj\left|bi\right.⟩,$$ (14a)

$$⟨{\Phi }_{i_{\alpha }}^{a_{\alpha }}\left|\right.\widehat{\mathrm{\Pi }}\left|{\Phi }_{j_{\beta }}^{b_{\beta }}\right.⟩=⟨{\Phi }_{i_{\beta }}^{a_{\beta }}\left|\right.\widehat{\mathrm{\Pi }}\left|{\Phi }_{j_{\alpha }}^{b_{\alpha }}\right.⟩=⟨aj\left|ib\right.⟩,$$ (14b)

$$⟨{\Phi }_{i_{\beta }}^{a_{\alpha }}\left|\right.\widehat{\mathrm{\Pi }}\left|{\Phi }_{j_{\beta }}^{b_{\alpha }}\right.⟩=⟨{\Phi }_{i_{\alpha }}^{a_{\beta }}\left|\right.\widehat{\mathrm{\Pi }}\left|{\Phi }_{j_{\alpha }}^{b_{\beta }}\right.⟩=-c_{\text{HF}}⟨aj\left|bi\right.⟩,$$ (14c)

it follows that we can define a simplified block-diagonal notation for $\mathbf{\Pi }$ as follows:

$$\begin{array}{ccc}\hfill {\mathrm{\Pi }}_{pqsr}^{\left(ϵ\right)}\equiv \left\{\begin{array}{c}2⟨pq\left|sr\right.⟩-c_{\text{HF}}⟨pq\left|rs\right.⟩,\mathrm{i}\mathrm{f}ϵ=s\hfill \\ -c_{\text{HF}}⟨pq\left|rs\right.⟩,\mathrm{i}\mathrm{f}ϵ\in \left\{t^{\left(m_s=0\right)},t^{\left(m_s=1\right)},t^{\left(m_s=-1\right)}\right\}.\hfill \end{array}\right.& \hfill & \hfill \\ \hfill & \hfill & \hfill \end{array}$$ (15)

With this definition, we can say that the operator $\widehat{\mathrm{\Pi }}$ in Eq. (11) satisfies

$$⟨\left.{\Psi }_I^{\left(ϵ\right)}\right|\widehat{\mathrm{\Pi }}\left|{\Psi }_J^{\left({ϵ}^{\prime }\right)}\right.⟩={\delta }_{ϵ{ϵ}^{\prime }}\sum _{aijb}{X}_{ai}^{I\left(ϵ\right)*}{X}_{jb}^{J\left({ϵ}^{\prime }\right)}{\mathrm{\Pi }}_{ajib}^{\left(ϵ\right)}.$$ (16)

Note that in Eq. (12), if p and q have spin α, then

$$\begin{array}{ccc}\hfill \sum _{\mathbf{m}}{\mathrm{\Pi }}_{\mathbf{pmqm}}& =\hfill & \sum _m\sum _{\sigma }{\mathrm{\Pi }}_{p_{\alpha }{m}_{\sigma }{q}_{\alpha }{m}_{\sigma }}\hfill \\ \hfill & =\hfill & \sum _m\left(\right.2⟨p_{\alpha }{m}_{\alpha }\left|q_{\alpha }{m}_{\alpha }\right.⟩-c_{\text{HF}}⟨p_{\alpha }{m}_{\alpha }\left|m_{\alpha }{q}_{\alpha }\right.⟩\left)\right.\hfill \\ \hfill & =\hfill & \sum _m{\mathrm{\Pi }}_{pmqm}^{\left(s\right)}.\hfill \end{array}$$

Of course, the same holds true when p and q have spin β. Thus, when dealing with the closed shell ground state, the correct screened interaction tensor is ${\mathbf{\Pi }}^{\left(s\right)}$.

Last, the DFT contributions in Eqs. (11) and (12) are discussed in detail in Appendix A. The exchange-correlation response functional, $\widehat{\mathrm{\Omega }}$, is the second derivative of the DFT exchange-correlation energy [Eq. (A5)]. As above, we can define a similar spin-diabatic notation for the linear response tensor. Using the fact that the nonzero matrix elements of Ω in Eq. (11) are

$$⟨\left.{\Phi }_{i_{\alpha }}^{a_{\alpha }}\right|\widehat{\mathrm{\Omega }}\left|{\Phi }_{j_{\alpha }}^{b_{\alpha }}\right.⟩=⟨\left.{\Phi }_{i_{\beta }}^{a_{\beta }}\right|\widehat{\mathrm{\Omega }}\left|{\Phi }_{j_{\beta }}^{b_{\beta }}\right.⟩={\mathrm{\Omega }}_{a_{\alpha }{i}_{\alpha }{b}_{\alpha }{j}_{\alpha }}$$ (17a)

and

$$⟨\left.{\Phi }_{i_{\alpha }}^{a_{\alpha }}\right|\widehat{\mathrm{\Omega }}\left|{\Phi }_{j_{\beta }}^{b_{\beta }}\right.⟩=⟨\left.{\Phi }_{i_{\beta }}^{a_{\beta }}\right|\widehat{\mathrm{\Omega }}\left|{\Phi }_{j_{\alpha }}^{b_{\alpha }}\right.⟩={\mathrm{\Omega }}_{a_{\alpha }{i}_{\alpha }{b}_{\beta }{j}_{\beta }},$$ (17b)

we can define a block diagonal notation for Ω as follows:

$$\begin{array}{ccc}\hfill {\mathrm{\Omega }}_{pqsr}^{\left(ϵ\right)}\equiv \left\{\begin{array}{c}{\mathrm{\Omega }}_{p_{\alpha }{q}_{\alpha }{s}_{\alpha }{r}_{\alpha }}+{\mathrm{\Omega }}_{p_{\alpha }{q}_{\alpha }{s}_{\beta }{r}_{\beta }},\mathrm{i}\mathrm{f}ϵ=s\hfill \\ {\mathrm{\Omega }}_{p_{\alpha }{q}_{\alpha }{s}_{\alpha }{r}_{\alpha }}-{\mathrm{\Omega }}_{p_{\alpha }{q}_{\alpha }{s}_{\beta }{r}_{\beta }},\mathrm{i}\mathrm{f}ϵ\in \left\{t^{\left(m_s=0\right)},t^{\left(m_s=1\right)},t^{\left(m_s=-1\right)}\right\}.\hfill \end{array}\right.& \hfill & \hfill \\ \hfill & \hfill & \hfill \end{array}$$ (18)

Now, given the definition of Ω in Eq. (A5), it should be clear that Ω_pqsr must formally be zero if orbitals p and q are of different spin value. In other words, we should set ${\mathrm{\Omega }}_{pqsr}^{t^{\left(m_s=-1\right)}}={\mathrm{\Omega }}_{pqsr}^{t^{\left(m_s=+1\right)}}=0$. Nonetheless, we will enforce Eq. (18) as a means of insisting that we preserve the degeneracy of the pure triplets. In practice, DFT functionals have almost always been parameterized and benchmarked for the m_s = 0 triplet and should be most accurate with this choice of Ω tensor. Alternatively, one could work with noncollinear exchange-correlation functions, for which there is a large history going back to Liu and co-workers,^53,54 Wang and Ziegler,^55–57 and Vahtras⁵⁸ and explored by Krylov, Casida, and co-workers;^59,60 nevertheless, below, we will keep the standard collinear approximations in TD-DFT, and we will write

$$⟨\left.{\Psi }_I^{\left(ϵ\right)}\right|\widehat{\mathrm{\Omega }}\left|{\Psi }_J^{\left({ϵ}^{\prime }\right)}\right.⟩\equiv {\delta }_{ϵ{ϵ}^{\prime }}\sum _{aijb}{X}_{ai}^{I\left(ϵ\right)*}{X}_{jb}^{J\left({ϵ}^{\prime }\right)}{\mathrm{\Omega }}_{aibj}^{\left(ϵ\right)}.$$ (19)

All remaining terms on the right-hand side of Eq. (11) are the result of the one-electron spin-coupling term, V.

In general, for computational efficiency, we find it optimal to first calculate the spin-diabats with a standard TDA calculation and then use the resulting TDA spin-diabats as initial guesses for the larger calculation in Eq. (8) to find the TDA spin-adiabats. Let us now address the derivative coupling. For the savvy reader already familiar with analytic gradient theory, the final answer can be found in Sec. II F.

C. Derivation by direct differentiation

There are two methods to obtain an analytic form for the nonadiabatic derivative couplings: (i) the nuclear derivative of the wavefunction can be evaluated directly³⁴ or (ii) one can apply the Hellmann-Feynman theory.⁴⁹ Both methods will generate the same expression after extensive algebra. In this section, we will follow the more straightforward approach in Ref. 34, direct differentiation, followed by conversion to the atomic orbital basis. However, beyond the limits of Ref. 34, we will also need to add a step to integrate over many of the spin degrees of freedom as well as keep track of the conjugation of the complex-valued amplitudes and coupling terms. Note that we do not allow SOC coupling between the ground state and excited states, which will make the mathematics a bit simpler. Future work will necessarily include this contribution, following the rigorous response approach of Send and Furche.²⁹

To begin the derivation, one directly applies the nuclear derivative to the wavefunction, as in Eqs. (21)–(24) in Ref. 34,

$$⟨{\Psi }_I\left|{\Psi }_J^{\left[x\right]}\right.⟩=\sum _{\mathbf{ijab}}{X}_{\mathbf{a}\mathbf{i}}^{I*}\left.⟨{\Phi }_{\mathbf{i}}^{\mathbf{a}}\right|{\left(X_{\mathbf{b}\mathbf{j}}^J\left|{\Phi }_{\mathbf{j}}^{\mathbf{b}}\right.⟩\right)}^{\left[x\right]}$$ (20a)

$$\begin{array}{ccc}\hfill & =\hfill & \frac{1}{\mathrm{\Delta }{\omega }_{JI}}\sum _{\mathbf{abij}}{X}_{\mathbf{a}\mathbf{i}}^{I*}{A}_{\mathbf{aibj}}^{\left[x\right]}{X}_{\mathbf{b}\mathbf{j}}^J\hfill \\ \hfill & \hfill & -\sum _{\mathbf{iab}}{X}_{\mathbf{a}\mathbf{i}}^{I*}{X}_{\mathbf{b}\mathbf{i}}^J{O}_{\mathbf{ba}}^{R\left[x\right]}-\sum _{\mathbf{ija}}{X}_{\mathbf{a}\mathbf{i}}^{I*}{X}_{\mathbf{a}\mathbf{j}}^J{O}_{\mathbf{ji}}^{R\left[x\right]}.\hfill \end{array}$$ (20b)

The two terms of the derivative coupling are the off-diagonal force matrix term⁶¹ and the right derivative of the molecular orbital overlap, $O_{\mathbf{pq}}^{R\left[x\right]}\equiv ⟨\mathbf{p}|{\mathbf{q}}^{\left[x\right]}⟩$. We denote the energy difference between states J and I as Δω_JI ≡ ω_J − ω_I. The derivative of the response tensor can be broken up into the derivatives of all of the tensor’s components,

$$\begin{array}{ccc}\hfill A_{\mathbf{aibj}}^{\left[x\right]}& =\hfill & F_{\mathbf{ab}}^{\left[x\right]}{\delta }_{\mathbf{ij}}-F_{\mathbf{ji}}^{\left[x\right]}{\delta }_{\mathbf{ab}}+{\mathrm{\Pi }}_{\mathbf{ajib}}^{\left[x\right]}+{\mathrm{\Omega }}_{\mathbf{aibj}}^{\left[x\right]}\hfill \\ \hfill & \hfill & +V_{\mathbf{ab}}^{\left[x\right]}{\delta }_{\mathbf{ij}}-V_{\mathbf{ji}}^{\left[x\right]}{\delta }_{\mathbf{ab}}+E_{gs}^{\left[x\right]}{\delta }_{\mathbf{ab}}{\delta }_{\mathbf{ij}}.\hfill \end{array}$$ (21)

Plugging Eq. (21) into Eq. (20a), we have all of the terms for the derivative coupling in the molecular orbital basis,

$$\begin{array}{ccc}\hfill ⟨{\Psi }_I\left|{\Psi }_J^{\left[x\right]}\right.⟩& =\hfill & \frac{1}{\mathrm{\Delta }{\omega }_{JI}}\left[\right.\sum _{\mathbf{abij}}{X}_{\mathbf{a}\mathbf{i}}^{I*}\left({\mathrm{\Pi }}_{\mathbf{ajib}}^{\left[x\right]}+{\mathrm{\Omega }}_{\mathbf{aibj}}^{\left[x\right]}\right)X_{\mathbf{b}\mathbf{j}}^J\hfill \\ \hfill & \hfill & +\sum _{\mathbf{iab}}{X}_{\mathbf{a}\mathbf{i}}^{I*}{X}_{\mathbf{b}\mathbf{i}}^J\left(F_{\mathbf{ab}}^{\left[x\right]}+V_{\mathbf{ab}}^{\left[x\right]}\right)\hfill \\ \hfill & \hfill & -\sum _{\mathbf{ija}}{X}_{\mathbf{a}\mathbf{i}}^{I*}{X}_{\mathbf{a}\mathbf{j}}^J\left(F_{\mathbf{ji}}^{\left[x\right]}+V_{\mathbf{ji}}^{\left[x\right]}\right)\left]\right.\hfill \\ \hfill & \hfill & -\sum _{\mathbf{iab}}{X}_{\mathbf{a}\mathbf{i}}^{I*}{X}_{\mathbf{b}\mathbf{i}}^J{O}_{\mathbf{ba}}^{R\left[x\right]}-\sum _{\mathbf{ija}}{X}_{\mathbf{a}\mathbf{i}}^{I*}{X}_{\mathbf{a}\mathbf{j}}^J{O}_{\mathbf{ji}}^{R\left[x\right]}.\hfill \end{array}$$ (22)

Most quantum chemistry software is written in the atomic orbital basis to take advantage of Gaussian-type orbitals with analytic integral formulas for the two-electron terms. Therefore, it is necessary to convert Eq. (22) into the atomic orbital basis.

D. The atomic orbital basis

1. Preliminary definitions

Before conversion to the atomic orbital basis, there are several important matrices that must be defined. First, we look at the terms resulting from the nature of the molecular orbitals. The molecular orbitals are linear combinations of atomic orbitals with coefficients C,

$$\left|\mathbf{p}\right.⟩=\sum _{\mu }{C}_{\mathit{\mu }\mathbf{p}}\left|\mathit{\mu }\right.⟩,$$ (23)

and the molecular orbital coefficients diagonalize the atomic orbital overlap, S_μν = ⟨μ|ν⟩,

$$O_{\mathbf{pq}}=⟨\mathbf{p}|\mathbf{q}⟩=\sum _{\mathit{\mu }\mathit{\nu }}{C}_{\mathit{\mu }\mathbf{p}}{S}_{\mathit{\mu }\mathit{\nu }}{C}_{\mathit{\nu }\mathbf{q}}={\delta }_{\mathbf{pq}}.$$ (24)

The ground state density matrix is

$$P_{\mathit{\mu }\mathit{\nu }}=\sum _{\mathbf{i}}{C}_{\mathit{\mu }\mathbf{i}}{C}_{\mathit{\nu }\mathbf{i}},$$ (25)

and the formal inverse of S is

$${\tilde{P}}_{\mathit{\mu }\mathit{\nu }}=\sum _{\mathbf{p}}{C}_{\mathit{\mu }\mathbf{p}}{C}_{\mathit{\nu }\mathbf{p}}=P_{\mathit{\mu }\mathit{\nu }}+\sum _{\mathbf{a}}{C}_{\mathit{\mu }\mathbf{a}}{C}_{\mathit{\nu }\mathbf{a}}.$$ (26)

The molecular orbital coefficients depend on both the atomic overlap matrix and the occupied-virtual rotation matrix Θ_bi. Therefore, the coefficient derivative includes contributions from each of their derivatives,

$$C_{\mathit{\mu }\mathbf{p}}^{\left[x\right]}=-\frac{1}{2}\sum _{\mathit{\gamma }\mathit{\lambda }}{\tilde{P}}_{\mathit{\mu }\mathit{\gamma }}{S}_{\mathit{\gamma }\mathit{\lambda }}^{\left[x\right]}{C}_{\mathit{\lambda }\mathbf{p}}+\sum _{\mathbf{ck}}\left(C_{\mathit{\mu }\mathbf{k}}{\delta }_{\mathbf{cp}}-C_{\mathit{\mu }\mathbf{c}}{\delta }_{\mathbf{kp}}\right){\mathrm{\Theta }}_{\mathbf{ck}}^{\left[x\right]}.$$ (27)

See Eqs. (63a)–(63b) in Ref. 49. Using Eq. (27) and following the steps outlined in Eqs. (64)–(69) in Ref. 49, we have an expression for the right derivative of the overlap in the atomic orbital basis,

$$O_{\mathbf{\text{pq}}}^{R\left[x\right]}=⟨\mathbf{\text{p}}|{\mathbf{\text{q}}}^{\left[x\right]}⟩=\sum _{\mathit{\mu }\mathit{\nu }}{C}_{\mathit{\mu }\mathbf{p}}{S}_{\mathit{\mu }\mathit{\nu }}^{A\left[x\right]}{C}_{\mathit{\nu }\mathbf{q}}-\sum _{\mathbf{ck}}\left({\delta }_{\mathbf{cp}}{\delta }_{\mathbf{kq}}-{\delta }_{\mathbf{kp}}{\delta }_{\mathbf{cq}}\right){\mathrm{\Theta }}_{\mathbf{ck}}^{\left[x\right]}.$$ (28)

Equation (28) breaks the right derivative into two contributions, the orbital response term ${\mathrm{\Theta }}_{bi}^{\left[x\right]}$ and the antisymmetrized right derivative of the atomic orbital overlap matrix, S^A[x],

$$S_{\mathit{\mu }\mathit{\nu }}^{A\left[x\right]}\equiv \frac{1}{2}\left(⟨\mathit{\mu }\left|{\mathit{\nu }}^{\left[x\right]}\right.⟩-⟨\mathit{\nu }\left|{\mathit{\mu }}^{\left[x\right]}\right.⟩\right)=⟨\mathit{\mu }\left|{\mathit{\nu }}^{\left[x\right]}\right.⟩-\frac{1}{2}{S}_{\mathit{\nu }\mathit{\mu }}^{\left[x\right]}.$$ (29)

Second, all other derivatives of the contributions to the linear response tensor in Eq. (21) (F^[x], Ω^[x], V^[x], Π^[x]) can be expressed in the atomic orbital basis using the derivations in Eqs. (32)–(37) in Ref. 25. As an example, since V is expressed in the atomic orbital basis as V_pq = ∑_μνV_μνC_μpC_νq, we find using Eq. (27)

$$\begin{array}{ccc}\hfill V_{\mathbf{pq}}^{\left[x\right]}& =\hfill & \sum _{\mathit{\mu }\mathit{\nu }}{V}_{\mathit{\mu }\mathit{\nu }}^{\left[x\right]}{C}_{\mathit{\mu }\mathbf{p}}{C}_{\mathit{\nu }\mathbf{q}}-\frac{1}{2}\sum _{\mathit{\mu }\mathit{\nu }\mathit{\gamma }\mathit{\lambda }}{S}_{\mathit{\gamma }\mathit{\lambda }}^{\left[x\right]}{V}_{\mathit{\mu }\mathit{\nu }}\left(C_{\mathit{\lambda }\mathbf{p}}{C}_{\mathit{\nu }\mathbf{q}}{\tilde{P}}_{\mathit{\gamma }\mathit{\mu }}+C_{\mathit{\gamma }\mathbf{q}}{C}_{\mathit{\mu }\mathbf{p}}{\tilde{P}}_{\mathit{\nu }\mathit{\lambda }}\right)\hfill \\ \hfill & \hfill & +\sum _{\mathit{\mu }\mathit{\nu }\mathbf{c}\mathbf{k}}{\mathrm{\Theta }}_{\mathbf{ck}}^{\left[x\right]}{V}_{\mathit{\mu }\mathit{\nu }}\left(\right.\left(C_{\mathit{\mu }\mathbf{k}}{\delta }_{\mathbf{cp}}-C_{\mathit{\mu }\mathbf{c}}{\delta }_{\mathbf{kp}}\right)C_{\mathit{\nu }\mathbf{q}}+C_{\mathit{\mu }\mathbf{p}}\left(C_{\mathit{\nu }\mathbf{k}}{\delta }_{\mathbf{cq}}-C_{\mathit{\nu }\mathbf{c}}{\delta }_{\mathbf{kq}}\right)\left)\right..\hfill \\ \hfill & \hfill & \hfill \end{array}$$ (30)

The three contributions in Eq. (30) are as follows: (i) the derivative of the V matrix elements, (ii) the overlap derivative S^[x], and (iii) the orbital response ${\mathbf{\Theta }}^{\left[x\right]}$.

Third, it will be helpful to transform the TDA coefficients into the atomic orbital basis and thus recover the standard transition density matrix,

$$R_{\mathit{\mu }\mathit{\nu }}^J=\sum _{\mathbf{ia}}{C}_{\mathit{\mu }\mathbf{a}}{X}_{\mathbf{a}\mathbf{i}}^J{C}_{\mathit{\nu }\mathbf{i}},$$ (31)

and a modified difference density matrix,

$$B_{\mathit{\mu }\mathit{\nu }}^{IJ}=\sum _{\mathbf{iab}}{C}_{\mathit{\mu }\mathbf{a}}{X}_{\mathbf{a}\mathbf{i}}^{I*}{X}_{\mathbf{b}\mathbf{i}}^J{C}_{\mathit{\nu }\mathbf{b}}-\sum _{\mathbf{ija}}{C}_{\mathit{\nu }\mathbf{i}}{X}_{\mathbf{a}\mathbf{i}}^{I*}{X}_{\mathbf{a}\mathbf{j}}^J{C}_{\mathit{\mu }\mathbf{j}}.$$ (32)

The second term in Eq. (32) is the transpose of the more traditional difference density matrix.^25,49,62 See, for example, Eq. (59b) in Ref. ^?49.

We can now state (skipping most of the algebra) the remaining derivatives for the quantities in Eq. (21). To begin with, the Fock matrix can be expanded in the same way as the spin-coupling in Eq. (30), using F_pq = ∑_μνF_μνC_μpC_νq,

$$\begin{array}{ccc}\hfill F_{\mathbf{pq}}^{\left[x\right]}& =\hfill & \sum _{\mathit{\mu }\mathit{\nu }}{F}_{\mathit{\mu }\mathit{\nu }}^{\left[x\right]}{C}_{\mathit{\mu }\mathbf{p}}{C}_{\mathit{\nu }\mathbf{q}}-\frac{1}{2}\sum _{\mathit{\mu }\mathit{\nu }\mathit{\gamma }\mathit{\lambda }}{S}_{\mathit{\gamma }\mathit{\lambda }}^{\left[x\right]}{F}_{\mathit{\mu }\mathit{\nu }}\left(C_{\mathit{\lambda }\mathbf{p}}{C}_{\mathit{\nu }\mathbf{q}}{\tilde{P}}_{\mathit{\gamma }\mathit{\mu }}+C_{\mathit{\gamma }\mathbf{q}}{C}_{\mathit{\mu }\mathbf{p}}{\tilde{P}}_{\mathit{\nu }\mathit{\lambda }}\right)\hfill \\ \hfill & \hfill & +\sum _{\mathit{\mu }\mathit{\nu }\mathbf{c}\mathbf{k}}{\mathrm{\Theta }}_{\mathbf{ck}}^{\left[x\right]}{F}_{\mathit{\mu }\mathit{\nu }}\left(\right.\left(C_{\mathit{\mu }\mathbf{k}}{\delta }_{\mathbf{cp}}-C_{\mathit{\mu }\mathbf{c}}{\delta }_{\mathbf{kp}}\right)C_{\mathit{\nu }\mathbf{q}}+C_{\mathit{\mu }\mathbf{p}}\left(C_{\mathit{\nu }\mathbf{k}}{\delta }_{\mathbf{cq}}-C_{\mathit{\nu }\mathbf{c}}{\delta }_{\mathbf{kq}}\right)\left)\right..\hfill \\ \hfill & \hfill & \hfill \end{array}$$ (33)

Unlike the spin-coupling in the atomic orbital basis, the Fock matrix in the atomic orbital basis is dependent on the molecular orbital coefficients. Therefore, it is necessary to further expand the first term on the right-hand side of Eq. (33), using $F_{\mu \nu }=h_{\mu \nu }+g_{\mu \nu }+\sum _{\gamma \lambda }{P}_{\gamma \lambda }{\mathrm{\Pi }}_{\mu \gamma \nu \lambda }$ and Eqs. (A6) and (A8):

$$\begin{array}{ccc}\hfill \sum _{\mathit{\mu }\mathit{\nu }}{F}_{\mathit{\mu }\mathit{\nu }}^{\left[x\right]}{C}_{\mathit{\mu }\mathbf{p}}{C}_{\mathit{\nu }\mathbf{q}}& =\hfill & \sum _{\mathit{\mu }\mathit{\nu }}\left(h_{\mathit{\mu }\mathit{\nu }}^{\left[x\right]}+g_{\mathit{\mu }\mathit{\nu }}^{0\left[x\right]}\right)C_{\mathit{\mu }\mathbf{p}}{C}_{\mathit{\nu }\mathbf{q}}+\sum _{\mathit{\mu }\mathit{\nu }\mathit{\gamma }\mathit{\lambda }}{\mathrm{\Pi }}_{\mathit{\mu }\mathit{\gamma }\mathit{\nu }\mathit{\lambda }}^{\left[x\right]}{C}_{\mathit{\mu }\mathbf{p}}{C}_{\mathit{\nu }\mathbf{q}}{P}_{\mathit{\gamma }\mathit{\lambda }}-\frac{1}{2}\sum _{\mathit{\mu }\mathit{\nu }\mathit{\gamma }\mathit{\lambda }\mathit{\delta }\mathit{\kappa }}{S}_{\mathit{\kappa }\mathit{\delta }}^{\left[x\right]}\left({\tilde{P}}_{\mathit{\gamma }\mathit{\kappa }}{P}_{\mathit{\lambda }\mathit{\delta }}+P_{\mathit{\gamma }\mathit{\kappa }}{\tilde{P}}_{\mathit{\lambda }\mathit{\delta }}\right)\left({\mathrm{\Pi }}_{\mathit{\mu }\mathit{\gamma }\mathit{\nu }\mathit{\lambda }}+{\mathrm{\Omega }}_{\mathit{\mu }\mathit{\nu }\mathit{\gamma }\mathit{\lambda }}\right)C_{\mathit{\mu }\mathbf{p}}{C}_{\mathit{\nu }\mathbf{q}}\hfill \\ \hfill & \hfill & -\sum _{\mathit{\mu }\mathit{\nu }\mathit{\gamma }\mathit{\lambda }\mathbf{c}\mathbf{k}}{\mathrm{\Theta }}_{\mathbf{ck}}^{\left[x\right]}\left(C_{\mathit{\gamma }\mathbf{c}}{C}_{\mathit{\lambda }\mathbf{k}}+C_{\mathit{\gamma }\mathbf{k}}{C}_{\mathit{\lambda }\mathbf{c}}\right)\left({\mathrm{\Pi }}_{\mathit{\mu }\mathit{\gamma }\mathit{\nu }\mathit{\lambda }}+{\mathrm{\Omega }}_{\mathit{\mu }\mathit{\nu }\mathit{\gamma }\mathit{\lambda }}\right)C_{\mathit{\mu }\mathbf{p}}{C}_{\mathit{\nu }\mathbf{q}}.\hfill \end{array}$$ (34)

Next, the derivative of the two-electron tensors can be expressed similarly as

$$\begin{array}{ccc}\hfill {\mathrm{\Pi }}_{\mathbf{ajib}}^{\left[x\right]}& =\hfill & \sum _{\mathit{\mu }\mathit{\lambda }\mathit{\nu }\mathit{\gamma }}{C}_{\mathit{\mu }\mathbf{a}}{C}_{\mathit{\lambda }\mathbf{j}}{\mathrm{\Pi }}_{\mathit{\mu }\mathit{\lambda }\mathit{\nu }\mathit{\gamma }}^{\left[x\right]}{C}_{\mathit{\nu }\mathbf{i}}{C}_{\mathit{\gamma }\mathbf{b}}-\frac{1}{2}\sum _{\mathit{\mu }\mathit{\lambda }\mathit{\nu }\mathit{\gamma }\mathit{\delta }\mathit{\kappa }}{S}_{\mathit{\delta }\mathit{\kappa }}^{\left[x\right]}\left({\tilde{P}}_{\mathit{\mu }\mathit{\delta }}{C}_{\mathit{\kappa }\mathbf{a}}{C}_{\mathit{\lambda }\mathbf{j}}+C_{\mathit{\mu }\mathbf{a}}{\tilde{P}}_{\mathit{\lambda }\mathit{\delta }}{C}_{\mathit{\kappa }\mathbf{j}}\right){\mathrm{\Pi }}_{\mathit{\mu }\mathit{\lambda }\mathit{\nu }\mathit{\gamma }}{C}_{\mathit{\nu }\mathbf{i}}{C}_{\mathit{\gamma }\mathbf{b}}\hfill \\ \hfill & \hfill & -\frac{1}{2}\sum _{\mathit{\mu }\mathit{\lambda }\mathit{\nu }\mathit{\gamma }\mathit{\delta }\mathit{\kappa }}{S}_{\mathit{\delta }\mathit{\kappa }}^{\left[x\right]}{C}_{\mathit{\mu }\mathbf{a}}{C}_{\mathit{\lambda }\mathbf{j}}{\mathrm{\Pi }}_{\mathit{\mu }\mathit{\lambda }\mathit{\nu }\mathit{\gamma }}\left({\tilde{P}}_{\mathit{\gamma }\mathit{\delta }}{C}_{\mathit{\nu }\mathbf{i}}{C}_{\mathit{\kappa }\mathbf{b}}+{\tilde{P}}_{\mathit{\nu }\mathit{\delta }}{C}_{\mathit{\kappa }\mathbf{i}}{C}_{\mathit{\gamma }\mathbf{b}}\right)+\sum _{\mathit{\mu }\mathit{\lambda }\mathit{\nu }\mathit{\gamma }}\left(\sum _{\mathbf{k}}{\mathrm{\Theta }}_{\mathbf{ak}}^{\left[x\right]}{C}_{\mathit{\mu }\mathbf{k}}{C}_{\mathit{\lambda }\mathbf{j}}-\sum _{\mathbf{c}}{\mathrm{\Theta }}_{\mathbf{cj}}^{\left[x\right]}{C}_{\mathit{\mu }\mathbf{a}}{C}_{\mathit{\lambda }\mathbf{c}}\right){\mathrm{\Pi }}_{\mathit{\mu }\mathit{\lambda }\mathit{\nu }\mathit{\gamma }}{C}_{\mathit{\nu }\mathbf{i}}{C}_{\mathit{\gamma }\mathbf{b}}\hfill \\ \hfill & \hfill & +\sum _{\mathit{\mu }\mathit{\lambda }\mathit{\nu }\mathit{\gamma }}{C}_{\mathit{\mu }\mathbf{a}}{C}_{\mathit{\lambda }\mathbf{j}}{\mathrm{\Pi }}_{\mathit{\mu }\mathit{\lambda }\mathit{\nu }\mathit{\gamma }}\left(\sum _{\mathbf{k}}{\mathrm{\Theta }}_{\mathbf{bk}}^{\left[x\right]}{C}_{\mathit{\nu }\mathbf{i}}{C}_{\mathit{\gamma }\mathbf{k}}-\sum _{\mathbf{c}}{\mathrm{\Theta }}_{\mathbf{ci}}^{\left[x\right]}{C}_{\mathit{\gamma }\mathbf{b}}{C}_{\mathit{\nu }\mathbf{c}}\right),\hfill \end{array}$$ (35)

$$\begin{array}{ccc}\hfill {\mathrm{\Omega }}_{\mathbf{aibj}}^{\left[x\right]}& =\hfill & \sum _{\mathit{\mu }\mathit{\lambda }\mathit{\nu }\mathit{\gamma }}{C}_{\mathit{\mu }\mathbf{a}}{C}_{\mathit{\nu }\mathbf{i}}\left({\mathrm{\Omega }}_{\mathit{\mu }\mathit{\nu }\mathit{\gamma }\mathit{\lambda }}^{0\left[x\right]}+{\mathrm{\Omega }}_{\mathit{\mu }\mathit{\nu }\mathit{\gamma }\mathit{\lambda }}^{Y\left[x\right]}\right)C_{\mathit{\gamma }\mathbf{b}}{C}_{\mathit{\lambda }\mathbf{j}}-\frac{1}{2}\sum _{\mathit{\mu }\mathit{\lambda }\mathit{\nu }\mathit{\gamma }\mathit{\delta }\mathit{\kappa }}{S}_{\mathit{\delta }\mathit{\kappa }}^{\left[x\right]}\left({\tilde{P}}_{\mathit{\mu }\mathit{\delta }}{C}_{\mathit{\kappa }\mathbf{a}}{C}_{\mathit{\nu }\mathbf{i}}+{\tilde{P}}_{\mathit{\nu }\mathit{\delta }}{C}_{\mathit{\mu }\mathbf{a}}{C}_{\mathit{\kappa }\mathbf{i}}\right){\mathrm{\Omega }}_{\mathit{\mu }\mathit{\nu }\mathit{\gamma }\mathit{\lambda }}{C}_{\mathit{\gamma }\mathbf{b}}{C}_{\mathit{\lambda }\mathbf{j}}\hfill \\ \hfill & \hfill & -\frac{1}{2}\sum _{\mathit{\mu }\mathit{\lambda }\mathit{\nu }\mathit{\gamma }\mathit{\delta }\mathit{\kappa }}{S}_{\mathit{\delta }\mathit{\kappa }}^{\left[x\right]}{C}_{\mathit{\mu }\mathbf{a}}{C}_{\mathit{\nu }\mathbf{i}}{\mathrm{\Omega }}_{\mathit{\mu }\mathit{\nu }\mathit{\gamma }\mathit{\lambda }}\left({\tilde{P}}_{\mathit{\gamma }\mathit{\delta }}{C}_{\mathit{\kappa }\mathbf{b}}{C}_{\mathit{\lambda }\mathbf{j}}+{\tilde{P}}_{\mathit{\lambda }\mathit{\delta }}{C}_{\mathit{\gamma }\mathbf{b}}{C}_{\mathit{\kappa }\mathbf{j}}\right)+\sum _{\mathit{\mu }\mathit{\lambda }\mathit{\nu }\mathit{\gamma }}\left(\sum _{\mathbf{k}}{\mathrm{\Theta }}_{\mathbf{ak}}^{\left[x\right]}{C}_{\mathit{\mu }\mathbf{k}}{C}_{\mathit{\nu }\mathbf{i}}-\sum _{\mathbf{c}}{\mathrm{\Theta }}_{\mathbf{ci}}^{\left[x\right]}{C}_{\mathit{\mu }\mathbf{a}}{C}_{\mathit{\nu }\mathbf{c}}\right){\mathrm{\Omega }}_{\mathit{\mu }\mathit{\nu }\mathit{\gamma }\mathit{\lambda }}{C}_{\mathit{\gamma }\mathbf{b}}{C}_{\mathit{\lambda }\mathbf{j}}\hfill \\ \hfill & \hfill & +\sum _{\mathit{\mu }\mathit{\lambda }\mathit{\nu }\mathit{\gamma }}{C}_{\mathit{\mu }\mathbf{a}}{C}_{\mathit{\nu }\mathbf{i}}{\mathrm{\Omega }}_{\mathit{\mu }\mathit{\nu }\mathit{\gamma }\mathit{\lambda }}\left(\sum _{\mathbf{k}}{\mathrm{\Theta }}_{\mathbf{bk}}^{\left[x\right]}{C}_{\mathit{\gamma }\mathbf{k}}{C}_{\mathit{\lambda }\mathbf{j}}-\sum _{\mathbf{c}}{\mathrm{\Theta }}_{\mathbf{cj}}^{\left[x\right]}{C}_{\mathit{\gamma }\mathbf{b}}{C}_{\mathit{\lambda }\mathbf{c}}\right),\hfill \end{array}$$ (36)

Equation (36) is similar to Eq. (35), with the $\mathbf{\Pi }$ replaced with $\mathbf{\Omega }$ and some indices relabeled. The only difference is that we split ${\mathbf{\Omega }}^{\left[x\right]}$ in the atomic orbital basis into two contributions, the response (${\mathrm{\Omega }}^{Y\left[x\right]}$) and nonresponse (${\mathrm{\Omega }}^{0\left[x\right]}$) terms, as seen in Eq. (A9).

2. The nonadiabatic derivative coupling in the atomic orbital basis

Finally, we can use the terms defined above in Eqs. (23)–(32) as well as the formal derivatives in Eqs. (33)–(36) to express Eq. (22) in the atomic orbital basis. It is helpful to break the final formula into three pieces,

$$⟨{\Psi }_I\left|{\Psi }_J^{\left[x\right]}\right.⟩=\frac{1}{\mathrm{\Delta }{\omega }_{JI}}{\mathrm{\Gamma }}_{IJ}^{\left[x\right]}-\frac{1}{\mathrm{\Delta }{\omega }_{JI}}\sum _{\mathbf{bi}}{\mathrm{\Theta }}_{\mathbf{bi}}^{\left[x\right]}{Y}_{\mathbf{bi}}+\sum _{\mathit{\mu }\mathit{\nu }}{B}_{\mathit{\mu }\mathit{\nu }}^{IJ}{S}_{\mathit{\nu }\mathit{\mu }}^{A\left[x\right]}.$$ (37)

The first term contains the nonresponse components to the gradient,

$$\begin{array}{ccc}\hfill {\mathrm{\Gamma }}_{IJ}^{\left[x\right]}& =\hfill & \sum _{\mathit{\mu }\mathit{\nu }}{B}_{\mathit{\mu }\mathit{\nu }}^{IJ}\left(h_{\mathit{\mu }\mathit{\nu }}^{\left[x\right]}+g_{\mathit{\mu }\mathit{\nu }}^{0\left[x\right]}\right)+\sum _{\mathit{\mu }\mathit{\nu }}{V}_{\mathit{\mu }\mathit{\nu }}^{\left[x\right]}{B}_{\mathit{\mu }\mathit{\nu }}^{IJ}+\sum _{\mathit{\mu }\mathit{\lambda }\mathit{\nu }\mathit{\gamma }}{R}_{\mathit{\mu }\mathit{\nu }}^{I*}{R}_{\mathit{\gamma }\mathit{\lambda }}^J\left({\mathrm{\Pi }}_{\mathit{\mu }\mathit{\lambda }\mathit{\nu }\mathit{\gamma }}^{\left[x\right]}+{\mathrm{\Omega }}_{\mathit{\mu }\mathit{\nu }\mathit{\gamma }\mathit{\lambda }}^{0\left[x\right]}\right)+\sum _{\mathit{\mu }\mathit{\lambda }\mathit{\nu }\mathit{\gamma }}{B}_{\mathit{\mu }\mathit{\nu }}^{IJ}{P}_{\mathit{\lambda }\mathit{\gamma }}{\mathrm{\Pi }}_{\mathit{\mu }\mathit{\lambda }\mathit{\nu }\mathit{\gamma }}^{\left[x\right]}\hfill \\ \hfill & \hfill & -\frac{1}{2}\sum _{\mathit{\mu }\mathit{\nu }\mathit{\gamma }\mathit{\lambda }}{S}_{\mathit{\gamma }\mathit{\lambda }}^{\left[x\right]}{\tilde{P}}_{\mathit{\mu }\mathit{\gamma }}\left(B_{\mathit{\lambda }\mathit{\nu }}^{IJ}+B_{\mathit{\nu }\mathit{\lambda }}^{IJ}\right)F_{\mathit{\mu }\mathit{\nu }}-\frac{1}{2}\sum _{\mathit{\mu }\mathit{\nu }\mathit{\gamma }\mathit{\lambda }}{S}_{\mathit{\gamma }\mathit{\lambda }}^{\left[x\right]}{V}_{\mathit{\mu }\mathit{\nu }}\left(B_{\mathit{\lambda }\mathit{\nu }}^{IJ}{\tilde{P}}_{\mathit{\gamma }\mathit{\mu }}+B_{\mathit{\mu }\mathit{\lambda }}^{IJ}{\tilde{P}}_{\mathit{\nu }\mathit{\gamma }}\right)\hfill \\ \hfill & \hfill & -\frac{1}{2}\sum _{\mathit{\lambda }\mathit{\gamma }\mathit{\eta }\mathit{\delta }}{S}_{\mathit{\eta }\mathit{\delta }}^{\left[x\right]}{\tilde{P}}_{\mathit{\lambda }\mathit{\eta }}{P}_{\mathit{\delta }\mathit{\gamma }}\left(B_{\mathit{\mu }\mathit{\nu }}^{IJ}+B_{\mathit{\nu }\mathit{\mu }}^{IJ}\right)\left({\mathrm{\Pi }}_{\mathit{\mu }\mathit{\lambda }\mathit{\nu }\mathit{\gamma }}+{\mathrm{\Omega }}_{\mathit{\mu }\mathit{\nu }\mathit{\gamma }\mathit{\lambda }}\right)-\frac{1}{2}\sum _{\mathit{\mu }\mathit{\lambda }\mathit{\nu }\mathit{\gamma }\mathit{\omega }\mathit{\delta }}{\tilde{P}}_{\mathit{\mu }\mathit{\omega }}{S}_{\mathit{\omega }\mathit{\delta }}^{\left[x\right]}\left(R_{\mathit{\delta }\mathit{\nu }}^{I*}{R}_{\mathit{\gamma }\mathit{\lambda }}^J+R_{\mathit{\nu }\mathit{\delta }}^{I*}{R}_{\mathit{\lambda }\mathit{\gamma }}^J\right)\left({\mathrm{\Pi }}_{\mathit{\mu }\mathit{\lambda }\mathit{\nu }\mathit{\gamma }}+{\mathrm{\Omega }}_{\mathit{\mu }\mathit{\nu }\mathit{\gamma }\mathit{\lambda }}\right)\hfill \\ \hfill & \hfill & -\frac{1}{2}\sum _{\mathit{\mu }\mathit{\lambda }\mathit{\nu }\mathit{\gamma }\mathit{\omega }\mathit{\delta }}{\tilde{P}}_{\mathit{\lambda }\mathit{\omega }}{S}_{\mathit{\omega }\mathit{\delta }}^{\left[x\right]}\left(R_{\mathit{\mu }\mathit{\nu }}^{I*}{R}_{\mathit{\gamma }\mathit{\delta }}^J+R_{\mathit{\nu }\mathit{\mu }}^{I*}{R}_{\mathit{\delta }\mathit{\gamma }}^J\right)\left({\mathrm{\Pi }}_{\mathit{\mu }\mathit{\lambda }\mathit{\nu }\mathit{\gamma }}+{\mathrm{\Omega }}_{\mathit{\mu }\mathit{\nu }\mathit{\gamma }\mathit{\lambda }}\right)-\frac{1}{2}\sum _{\mathit{\delta }\mathit{\kappa }\mathit{\zeta }\mathit{\eta }}\sum _{\mathit{\mu }\mathit{\lambda }\mathit{\nu }\mathit{\gamma }}{S}_{\mathit{\zeta }\mathit{\eta }}^{\left[x\right]}\left({\tilde{P}}_{\mathit{\delta }\mathit{\zeta }}{P}_{\mathit{\eta }\mathit{\kappa }}+P_{\mathit{\delta }\mathit{\zeta }}{\tilde{P}}_{\mathit{\eta }\mathit{\kappa }}\right)R_{\mathit{\mu }\mathit{\nu }}^{I*}{R}_{\mathit{\gamma }\mathit{\lambda }}^J{\mathrm{\Xi }}_{\mathit{\mu }\mathit{\nu }\mathit{\gamma }\mathit{\lambda }\mathit{\delta }\mathit{\kappa }}.\hfill \end{array}$$ (38)

The quantities $g_{\mathit{\mu }\mathit{\nu }}^{0\left[x\right]}$ and ${\mathrm{\Omega }}_{\mathit{\mu }\mathit{\nu }\mathit{\gamma }\mathit{\lambda }}^{0\left[x\right]}$ are defined in Appendix A.

The second term includes all response contributions,

$$\begin{array}{ccc}\hfill Y_{\mathbf{bi}}& =\hfill & \sum _{\mathbf{ak}}\sum _{\mathit{\mu }\mathit{\nu }}{X}_{\mathbf{b}\mathbf{k}}^{I*}{X}_{\mathbf{a}\mathbf{k}}^J{C}_{\mathit{\nu }\mathbf{a}}{V}_{\mathit{\mu }\mathit{\nu }}{C}_{\mathit{\mu }\mathbf{i}}+\sum _{\mathbf{ak}}\sum _{\mathit{\mu }\mathit{\nu }}{X}_{\mathbf{b}\mathbf{k}}^J{X}_{\mathbf{a}\mathbf{k}}^{I*}{C}_{\mathit{\mu }\mathbf{a}}{V}_{\mathit{\mu }\mathit{\nu }}{C}_{\mathit{\nu }\mathbf{i}}+\sum _{\mathbf{ak}}\sum _{\mathit{\mu }\mathit{\nu }}{C}_{\mathit{\mu }\mathbf{b}}{V}_{\mathit{\mu }\mathit{\nu }}{C}_{\mathit{\nu }\mathbf{k}}{X}_{\mathbf{a}\mathbf{k}}^{I*}{X}_{\mathbf{a}\mathbf{i}}^J+\sum _{\mathbf{ak}}\sum _{\mathit{\mu }\mathit{\nu }}{C}_{\mathit{\nu }\mathbf{b}}{V}_{\mathit{\mu }\mathit{\nu }}{C}_{\mathit{\mu }\mathbf{k}}{X}_{\mathbf{a}\mathbf{k}}^J{X}_{\mathbf{a}\mathbf{i}}^{I*}\hfill \\ \hfill & \hfill & +\sum _{\mathbf{a}}\sum _{\mathit{\mu }\mathit{\lambda }\mathit{\nu }\mathit{\gamma }}{C}_{\mathit{\nu }\mathbf{b}}{C}_{\mathit{\mu }\mathbf{a}}\left(X_{\mathbf{a}\mathbf{i}}^{I*}{R}_{\mathit{\gamma }\mathit{\lambda }}^J+R_{\mathit{\gamma }\mathit{\lambda }}^{I*}{X}_{\mathbf{a}\mathbf{i}}^J\right)\left({\mathrm{\Pi }}_{\mathit{\mu }\mathit{\lambda }\mathit{\nu }\mathit{\gamma }}+{\mathrm{\Omega }}_{\mathit{\mu }\mathit{\nu }\mathit{\gamma }\mathit{\lambda }}\right)+\sum _{\mathit{\mu }\mathit{\nu }\mathit{\lambda }\mathit{\gamma }}{C}_{\mathit{\lambda }\mathbf{b}}{C}_{\mathit{\gamma }\mathbf{i}}\left(B_{\mathit{\mu }\mathit{\nu }}^{IJ}+B_{\mathit{\nu }\mathit{\mu }}^{IJ}\right)\left({\mathrm{\Pi }}_{\mathit{\mu }\mathit{\lambda }\mathit{\nu }\mathit{\gamma }}+{\mathrm{\Omega }}_{\mathit{\mu }\mathit{\nu }\mathit{\gamma }\mathit{\lambda }}\right)\hfill \\ \hfill & \hfill & -\sum _{\mathbf{j}}\sum _{\mathit{\mu }\mathit{\lambda }\mathit{\nu }\mathit{\gamma }}{C}_{\mathit{\mu }\mathbf{i}}{C}_{\mathit{\nu }\mathbf{j}}\left(X_{\mathbf{b}\mathbf{j}}^{I*}{R}_{\mathit{\gamma }\mathit{\lambda }}^J+R_{\mathit{\gamma }\mathit{\lambda }}^{I*}{X}_{\mathbf{b}\mathbf{j}}^J\right)\left({\mathrm{\Pi }}_{\mathit{\mu }\mathit{\lambda }\mathit{\nu }\mathit{\gamma }}+{\mathrm{\Omega }}_{\mathit{\mu }\mathit{\nu }\mathit{\gamma }\mathit{\lambda }}\right)+\sum _{\mathit{\mu }\mathit{\lambda }\mathit{\nu }\mathit{\gamma }}\sum _{\mathit{\delta }\mathit{\kappa }}\left(C_{\mathit{\delta }\mathbf{b}}{C}_{\mathit{\kappa }\mathbf{i}}+C_{\mathit{\delta }\mathbf{i}}{C}_{\mathit{\kappa }\mathbf{b}}\right)R_{\mathit{\mu }\mathit{\nu }}^{I*}{R}_{\mathit{\gamma }\mathit{\lambda }}^J{\mathrm{\Xi }}_{\mathit{\mu }\mathit{\nu }\mathit{\gamma }\mathit{\lambda }\mathit{\delta }\mathit{\kappa }}.\hfill \end{array}$$ (39)

The third term $\left(\sum _{\mathit{\mu }\mathit{\nu }}{B}_{\mathit{\mu }\mathit{\nu }}^{IJ}{S}_{\mathit{\nu }\mathit{\mu }}^{A\left[x\right]}\right)$ includes the antisymmetric overlap matrix derivative S^A[x], which breaks translational invariance such that ${\sum }_x⟨{\Psi }_I\left|{\Psi }_J^{\left[x\right]}\right.⟩\ne 0$. Terms of this form are well known in the theory of derivative couplings^63–65 and are always of the form “density matrix times antisymmetric overlap derivative.” In general, it is well established that this term arises because when computing the derivative coupling, we ignore the momentum of the electron as imparted by the nucleus moving; however, this term will disappear when missing electron translation factors are included.^49,66,67 Furthermore, in the explicit context of CIS/TD-DFT derivative couplings, one can show that this spurious third term arises from the “Pulay terms” associated with the non-Hellman-Feynman component of the derivative coupling.³⁵ In other words, this third term is associated with neither the Hellman-Feynman terms nor the orbital response, and for surface hopping calculations, one should ignore such a term. Nevertheless, this problematic term must be included when debugging any ab initio derivative coupling code if one wants to match finite difference simulations.

Most components of Eqs. (37)–(39) are available directly in quantum chemistry codes, except the derivative of $\mathbf{\Theta }$. To calculate ${\mathbf{\Theta }}^{\left[x\right]}$ directly, one must solve the coupled-perturbed Hartree-Fock (CPHF) equation [Eq. (B2)] for each nuclear coordinate. Instead of solving the CPHF equation 3N times, we will use the standard Handy and Schaefer “z-vector” approach to replace the response term with a mixed derivative term,

$$-\sum _{bi}\sum _{\sigma }{Y}_{b_{\sigma }{i}_{\sigma }}{\mathrm{\Theta }}_{b_{\sigma }{i}_{\sigma }}^{\left[x\right]}=\sum _{aj}{z}_{aj}{M}_{aj}^{\left[x\right]}.$$ (40)

Here, M^[x] is a mixed derivative [Eq. (B3)]. The construction of the z-vector requires solving the CPHF equation only once. The details of the z-vector approach are presented in Appendix B.

At this point, one could naively calculate the NADC by summing Eq. (37) over all possible spin combinations, and yet, such a process would be computationally expensive and unnecessary. Instead, we can use symmetries in the spin degrees of freedom to further simplify the solution and reduce the nontrivial spin indices.

E. Spin symmetries

To further simplify the form of the NADCs, we take advantage of three aspects of our choice of spin-adiabats to integrate out many of the spin degrees of freedom: the fact that we have a restricted molecular orbital basis (so that orbitals are either spin α or spin β), the fact that our ground state determinant is a closed-shell singlet (so that α and β molecular orbitals are spatially identical) and the fact that the two-electron tensor is block diagonal in the spin-diabatic basis.

Since we are using a restricted, closed-shell molecular orbital basis, many of the matrices defined so far will not mix spin and will be equivalent for either up or down spin. Therefore, we can actually write these spin orbital matrices as matrices in the spatial orbital basis times a delta function for spin indices. In other words,

$$C_{{\mu }_{\sigma }{p}_{\tau }}=C_{\mu p}{\delta }_{\sigma \tau }.$$ (41)

The matrices S, Θ, F, O, P, and $\tilde{\mathbf{P}}$ can be expressed similarly, and these same-spin relationships will simplify all summations below.

In general, the only contributions that will contain mixed spin terms are the two-electron tensors (Π and Ω), the spin-coupling (V), and the TDA amplitudes (X). That being said, the modified two-electron tensor Π and exchange-correlation matrix Ω within the usual electronic Hamiltonian are block diagonal in the spin-diabatic basis, so we can in fact separate all terms originating from the usual electronic Hamiltonian. In other words, for Π and Ω, we can avoid explicit summation over a set of 4 spin orbitals (with independent spins) and instead express all Π and Ω matrix elements in the spin-diabatic basis so as to minimize the number of expensive matrix multiplication subroutine calls, which are invoked when dotting Π or Ω into any other spin tensor. To that end, we will express the spin-diabatic components of the transition density matrix as

$$R_{\mu \nu }^{J\left(ϵ\right)}=\sum _{ia}{C}_{\mu a}{X}_{ai}^{J\left(ϵ\right)}{C}_{\nu i}.$$ (42)

We will also define a total difference density matrix as the sum of the spin-diabatic components of the modified difference density matrix,

$${\overline{B}}_{\mu \nu }^{IJ}\equiv \sum _{ϵ}\sum _{iab}{C}_{\mu a}{X}_{ai}^{I\left(ϵ\right)*}{X}_{bi}^{J\left(ϵ\right)}{C}_{\nu b}-\sum _{ϵ}\sum _{ija}{C}_{\nu i}{X}_{ai}^{I\left(ϵ\right)*}{X}_{aj}^{J\left(ϵ\right)}{C}_{\mu j}.$$ (43)

Note the bar over the ($\overline{B}$) in Eq. (43).

F. Calculating the NADC of TDA spin-adiabats

Now that we have the necessary tools, we can explicitly write the steps to calculate the NADC.

First, the total response vector Y in Eq. (39) is constructed by breaking it into its usual electronic Hamiltonian contribution, summed over the spin-diabats, Y^E, and spin-coupling contribution, Y^V, summed over the nontrivial spin indices,

$$\sum _{\sigma }{Y}_{b_{\sigma }{i}_{\sigma }}=Y_{bi}^E+Y_{bi}^V,$$ (44a)

$$\begin{array}{ccc}\hfill Y_{bi}^E& =\hfill & \sum _{\mu \nu \lambda \gamma }{C}_{\lambda b}{C}_{\gamma i}\left({\overline{B}}_{\mu \nu }^{IJ}+{\overline{B}}_{\nu \mu }^{IJ}\right)\left({\mathrm{\Pi }}_{\mu \lambda \nu \gamma }^{\left(s\right)}+{\mathrm{\Omega }}_{\mu \nu \gamma \lambda }^{\left(s\right)}\right)\hfill \\ \hfill & \hfill & +\sum _{ϵ}\sum _{a\mu \lambda \nu \gamma }{C}_{\nu b}{C}_{\mu a}\left(X_{ai}^{I\left(ϵ\right)*}{R}_{\gamma \lambda }^{J\left(ϵ\right)}+R_{\gamma \lambda }^{I\left(ϵ\right)*}{X}_{ai}^{J\left(ϵ\right)}\right)\hfill \\ \hfill & \hfill & \times \left({\mathrm{\Pi }}_{\mu \lambda \nu \gamma }^{\left(ϵ\right)}+{\mathrm{\Omega }}_{\mu \nu \gamma \lambda }^{\left(ϵ\right)}\right)-\sum _{ϵ}\sum _{j\mu \lambda \nu \gamma }{C}_{\mu i}{C}_{\nu j}\hfill \\ \hfill & \hfill & \times \left(X_{bj}^{I\left(ϵ\right)*}{R}_{\gamma \lambda }^{J\left(ϵ\right)}+R_{\gamma \lambda }^{I\left(ϵ\right)*}{X}_{bj}^{J\left(ϵ\right)}\right)\left({\mathrm{\Pi }}_{\mu \lambda \nu \gamma }^{\left(ϵ\right)}+{\mathrm{\Omega }}_{\mu \nu \gamma \lambda }^{\left(ϵ\right)}\right)\hfill \\ \hfill & \hfill & +\sum _{ϵ}\sum _{\mu \lambda \nu \gamma \delta \kappa }{C}_{\delta b}{C}_{\kappa i}\left(R_{\mu \nu }^{I\left(ϵ\right)*}{R}_{\lambda \gamma }^{J\left(ϵ\right)}+R_{\lambda \gamma }^{I\left(ϵ\right)*}{R}_{\mu \nu }^{J\left(ϵ\right)}\right){\mathrm{\Xi }}_{\mu \nu \gamma \lambda \delta \kappa }^{\left(ϵ\right)},\hfill \\ \hfill & \hfill & \hfill \end{array}$$ (44b)

$$\begin{array}{ccc}\hfill Y_{bi}^V& =\hfill & \sum _{\sigma \tau \upsilon }\sum _{ak\mu \nu }{X}_{b_{\sigma }{k}_{\tau }}^{I*}{X}_{a_{\upsilon }{k}_{\tau }}^J{C}_{\nu a}{V}_{{\mu }_{\sigma }{\nu }_{\upsilon }}{C}_{\mu i}\hfill \\ \hfill & \hfill & +\sum _{\sigma \tau \upsilon }\sum _{ak\mu \nu }{X}_{b_{\sigma }{k}_{\tau }}^J{X}_{a_{\upsilon }{k}_{\tau }}^{I*}{C}_{\mu a}{V}_{{\mu }_{\upsilon }{\nu }_{\sigma }}{C}_{\nu i}\hfill \\ \hfill & \hfill & +\sum _{\sigma \tau \upsilon }\sum _{ak\mu \nu }{C}_{\mu b}{V}_{{\mu }_{\upsilon }{\nu }_{\sigma }}{C}_{\nu k}{X}_{a_{\tau }{k}_{\sigma }}^{I*}{X}_{a_{\tau }{i}_{\upsilon }}^J\hfill \\ \hfill & \hfill & +\sum _{\sigma \tau \upsilon }\sum _{ak\mu \nu }{C}_{\nu b}{V}_{{\mu }_{\sigma }{\nu }_{\upsilon }}{C}_{\mu k}{X}_{a_{\tau }{k}_{\sigma }}^J{X}_{a_{\tau }{i}_{\upsilon }}^{I*}.\hfill \end{array}$$ (44c)

Second, to indirectly evaluate the ${\mathrm{\Theta }}_{\mathbf{bi}}^{\left[x\right]}$ term from Eq. (37), we solve the CPHF equation [Eq. (B2)] to solve for the z-vector in Eq. (40). Therefore, as is common, one constructs the modified relaxed difference density matrix,

$$D_{\mu \nu }^{IJ}\equiv {\overline{B}}_{\mu \nu }^{IJ}-\sum _{aj}{z}_{aj}\left(C_{\mu a}{C}_{\nu j}+C_{\nu a}{C}_{\mu j}\right).$$ (45)

Third, again looking at Eq. (37), we combine Γ [Eq. (38)] and the mixed derivative terms [Eq. (B6a)] and break the sum into three terms: Γ^D[x] includes the terms that depend on the relaxed difference density, Γ^R[x] includes the terms that depend on the transition density matrices resulting from the usual electronic Hamiltonian and summed over the spin-diabats, and Γ^V[x] includes the terms that come from the spin-coupling, summed over two nontrivial spin indices,

$${\mathrm{\Gamma }}_{IJ}^{\left[x\right]}-\sum _{\mathbf{bi}}{Y}_{\mathbf{bi}}{\mathrm{\Theta }}_{\mathbf{bi}}^{\left[x\right]}={\mathrm{\Gamma }}_{IJ}^{\left[x\right]}+\sum _{aj}{z}_{aj}{M}_{aj}^{\left[x\right]}\equiv {\mathrm{\Gamma }}_{IJ}^{D\left[x\right]}+{\mathrm{\Gamma }}_{IJ}^{R\left[x\right]}+{\mathrm{\Gamma }}_{IJ}^{V\left[x\right]}.$$ (46a)

Here,

$$\begin{array}{ccc}\hfill {\mathrm{\Gamma }}_{IJ}^{D\left[x\right]}& =\hfill & \sum _{\mu \nu }{D}_{\mu \nu }^{IJ}\left(h_{\mu \nu }^{\left[x\right]}+g_{\mu \nu }^{0\left[x\right]}\right)+\sum _{\mu \nu \lambda \gamma }{D}_{\mu \nu }^{IJ}{P}_{\lambda \gamma }{\mathrm{\Pi }}_{\mu \lambda \nu \gamma }^{\left(s\right)\left[x\right]}\hfill \\ \hfill & \hfill & -\frac{1}{2}\sum _{\mu \nu \lambda \gamma }{\tilde{P}}_{\mu \gamma }{S}_{\gamma \lambda }^{\left[x\right]}\left(D_{\lambda \nu }^{IJ}+D_{\nu \lambda }^{IJ}\right)F_{\mu \nu }\hfill \\ \hfill & \hfill & -\frac{1}{2}\sum _{\mu \nu \lambda \gamma \delta \omega }{\tilde{P}}_{\lambda \omega }{S}_{\omega \delta }^{\left[x\right]}{P}_{\delta \gamma }\left(D_{\mu \nu }^{IJ}+D_{\nu \mu }^{IJ}\right)\left({\mathrm{\Pi }}_{\mu \lambda \nu \gamma }^{\left(s\right)}+{\mathrm{\Omega }}_{\mu \nu \gamma \lambda }^{\left(s\right)}\right),\hfill \end{array}$$ (46b)

$$\begin{array}{ccc}\hfill {\mathrm{\Gamma }}_{IJ}^{R\left[x\right]}& =\hfill & \sum _{ϵ}\sum _{\mu \nu \lambda \gamma }{R}_{\mu \nu }^{I\left(ϵ\right)*}{R}_{\gamma \lambda }^{J\left(ϵ\right)}\left({\mathrm{\Pi }}_{\mu \lambda \nu \gamma }^{\left(ϵ\right)\left[x\right]}+{\mathrm{\Omega }}_{\mu \nu \gamma \lambda }^{0\left(ϵ\right)\left[x\right]}\right)\hfill \\ \hfill & \hfill & -\frac{1}{2}\sum _{ϵ}\sum _{\mu \nu \lambda \gamma \delta \omega }{\tilde{P}}_{\lambda \omega }{S}_{\omega \delta }^{\left[x\right]}\left(R_{\delta \gamma }^{I\left(ϵ\right)*}{R}_{\nu \mu }^{J\left(ϵ\right)}+R_{\gamma \delta }^{I\left(ϵ\right)*}{R}_{\mu \nu }^{J\left(ϵ\right)}\right)\hfill \\ \hfill & \hfill & \times \left({\mathrm{\Pi }}_{\mu \lambda \nu \gamma }^{\left(ϵ\right)}+{\mathrm{\Omega }}_{\mu \nu \gamma \lambda }^{\left(ϵ\right)}\right)-\frac{1}{2}\sum _{ϵ}\sum _{\mu \nu \lambda \gamma \delta \omega }{\tilde{P}}_{\lambda \omega }{S}_{\omega \delta }^{\left[x\right]}\hfill \\ \hfill & \hfill & \times \left(R_{\mu \nu }^{I\left(ϵ\right)*}{R}_{\gamma \delta }^{J\left(ϵ\right)}+R_{\nu \mu }^{I\left(ϵ\right)*}{R}_{\delta \gamma }^{J\left(ϵ\right)}\right)\left({\mathrm{\Pi }}_{\mu \lambda \nu \gamma }^{\left(ϵ\right)}+{\mathrm{\Omega }}_{\mu \nu \gamma \lambda }^{\left(ϵ\right)}\right)\hfill \\ \hfill & \hfill & -\frac{1}{2}\sum _{ϵ}\sum _{\mu \nu \lambda \gamma \delta \omega \zeta \eta }{\tilde{P}}_{\lambda \omega }{S}_{\omega \delta }^{\left[x\right]}{P}_{\delta \gamma }\hfill \\ \hfill & \hfill & \times \left(R_{\mu \nu }^{I\left(ϵ\right)*}{R}_{\zeta \eta }^{J\left(ϵ\right)}+R_{\eta \zeta }^{I\left(ϵ\right)*}{R}_{\nu \mu }^{J\left(ϵ\right)}\right){\mathrm{\Xi }}_{\mu \nu \zeta \eta \lambda \gamma }^{\left(ϵ\right)},\hfill \end{array}$$ (46c)

$$\begin{array}{ccc}\hfill {\mathrm{\Gamma }}_{IJ}^{V\left[x\right]}& =\hfill & \sum _{\sigma \tau }\sum _{\mu \nu }{V}_{{\mu }_{\sigma }{\nu }_{\tau }}^{\left[x\right]}{B}_{{\mu }_{\sigma }{\nu }_{\tau }}^{IJ}-\frac{1}{2}\sum _{\sigma \tau }\sum _{\mu \nu \gamma \lambda }{S}_{\gamma \lambda }^{\left[x\right]}{V}_{{\mu }_{\sigma }{\nu }_{\tau }}\left(B_{{\lambda }_{\sigma }{\nu }_{\tau }}^{IJ}{\tilde{P}}_{{\gamma }_{\sigma }{\mu }_{\sigma }}+B_{{\mu }_{\sigma }{\lambda }_{\tau }}^{IJ}{\tilde{P}}_{{\nu }_{\tau }{\gamma }_{\tau }}\right).\hfill \\ \hfill & \hfill & \hfill \end{array}$$ (46d)

The last step is to put all these terms together, divide by the energy difference, and add the electronic translational invariance term,⁶⁸ recovering the final answer,

$$⟨{\Psi }_I\left|{\Psi }_J^{\left[x\right]}\right.⟩=\frac{1}{\mathrm{\Delta }{\omega }_{JI}}\left(\right.{\mathrm{\Gamma }}_{IJ}^{D\left[x\right]}+{\mathrm{\Gamma }}_{IJ}^{R\left[x\right]}+{\mathrm{\Gamma }}_{IJ}^{V\left[x\right]}\left)\right.+\sum _{\mu \nu }{\overline{B}}_{\mu \nu }^{IJ}{S}_{\nu \mu }^{A\left[x\right]}.$$ (47)

Equations (44a)–(47) provide a complete framework to calculate the NADCs between TDA spin-adiabats with the minimum number of calls to the two electron tensor derivatives (Π^[x] and Ω^[x]).

III. RESULTS

We have implemented Eqs. (44a)–(47) in a development version of the Q-Chem software package.⁶⁹ We will now validate our analytic NADC against finite difference and then use the algorithm to explore the S₁/T₂ crossing in benzaldehyde. Benzaldehyde has been widely studied because it is the smallest aromatic carbonyl, and understanding benzaldehyde’s electronic relaxation is essential for a broader understanding of the relaxation of other organic phosphorescent molecules.⁷⁰ When benzaldehyde is excited to the S₁ state, it quickly undergoes ISC. Previous work suggests that the transition between S₁ and T₂ is favorable due to large SOC and low energy barriers between the states.^70,71

A. Comparison with finite difference

Finite difference is used to verify our equations and implementation of the analytic NADC. A five-point stencil is used to approximate the derivative of the ket,

$$\begin{array}{ccc}\hfill ⟨{\Psi }_I\left|{\Psi }_J^{\left[x\right]}\right.⟩& =\hfill & \frac{1}{12\mathrm{\Delta }}⟨{\Psi }_I\left(x\right)\left|{\Psi }_J\left(x-2\mathrm{\Delta }\right)\right.⟩-\frac{2}{3\mathrm{\Delta }}⟨{\Psi }_I\left(x\right)\left|{\Psi }_J\left(x-\mathrm{\Delta }\right)\right.⟩\hfill \\ \hfill & \hfill & +\frac{2}{3\mathrm{\Delta }}⟨{\Psi }_I\left(x\right)\left|{\Psi }_J\left(x+\mathrm{\Delta }\right)\right.⟩-\frac{1}{12\mathrm{\Delta }}⟨{\Psi }_I\left(x\right)\left|{\Psi }_J\left(x+2\mathrm{\Delta }\right)\right.⟩.\hfill \\ \hfill & \hfill & \hfill \end{array}$$ (48)

Here, the overlap between two nuclear geometries x₁ and x₂ can be computed using

$$\begin{array}{ccc}\hfill ⟨{\Psi }_I\left(x_1\right)\left|{\Psi }_J\left(x_2\right)\right.⟩& =\hfill & \sum _{ϵ}\sum _{abij}{X}_{ai}^{I\left(ϵ\right)*}\left(x_1\right)\hfill \\ \hfill & \hfill & \times ⟨{\Phi }_i^a\left(x_1\right)\left|{\Phi }_j^b\left(x_2\right)\right.⟩X_{bj}^{J\left(ϵ\right)}\left(x_2\right)e^{-i{\theta }_J}.\hfill \end{array}$$ (49)

The overlap will not mix different spin states, so it is useful to use the spin-diabatic basis to decrease the number of determinants we are calculating. The factor $e^{-i{\theta }_J}$ is a rotation of the ket invoked to line up the phases of the adiabats, so they vary smoothly as a function of geometry. For small changes to the geometry, the overlap of a state with itself at two different geometries should be close to 1, real-valued, and positive, which uniquely defines θ ∈ [0, 2π).

Table I presents a comparison of the finite difference results with that of our analytic formula for the largest components of the NADC between the 4th and 7th spin-adiabats. Tables S2 and S3 present the full results for the real and imaginary components, respectively. Here, we have chosen a small basis set (STO-3G) to limit the computational cost of calculating the finite difference terms. The terms are calculated at an S₁/T₂ crossing with a magnetic field of B_y = 5 T and Δ = 10⁻⁴Å. At this value of Δ, the error of the finite difference is on the order of $10^{-4}{a}_0^{-1}$.

TABLE I.

NADC between TDA spin-adiabats 4th and 7th using ωB97X/STO-3G. These spin-adiabats are primarily composed of the S₁ and T₂ spin-diabats. Note that the analytic results agree with finite difference up to $10^{-4}{a}_0^{-1}$. The full finite difference results can be found in Tables S2 and S3.

	Finite difference			Analytic NADC
Atom	x	y	z	x	y	z
	Real-valued component ($a_0^{-1}$)
C	69.0507	−0.0261	32.7396	69.0507	−0.0261	32.7396
H	7.9082	−0.0012	4.4373	7.9082	−0.0012	4.4373
O	−81.1334	0.0269	−41.5192	−81.1333	0.0268	−41.5192
	Imaginary-valued component($a_0^{-1}$)
C	−0.0535	0.0190	−0.0253	−0.0533	0.0190	−0.0253
H	−0.0061	−0.0033	−0.0034	−0.0061	−0.0033	−0.0034
O	0.0630	−0.0125	0.0321	0.0626	−0.0125	0.0321

B. Benzaldehyde: Effects of a magnetic field on spin-adiabatic PESs and NADCs

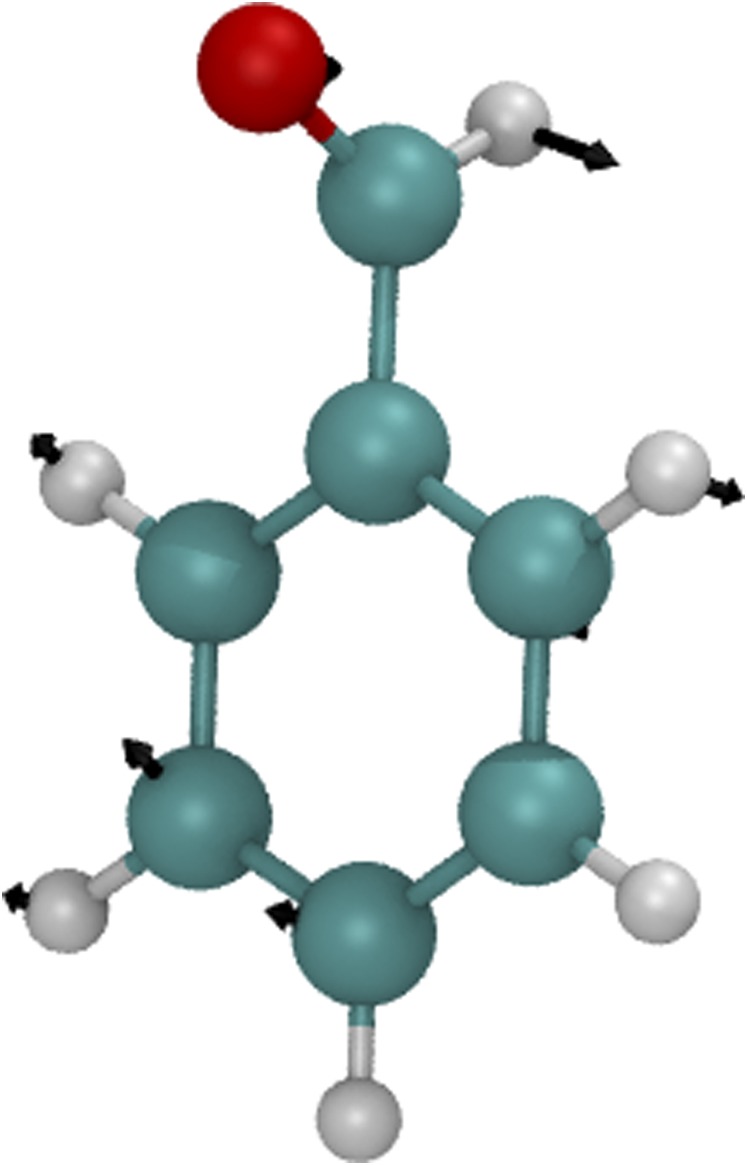
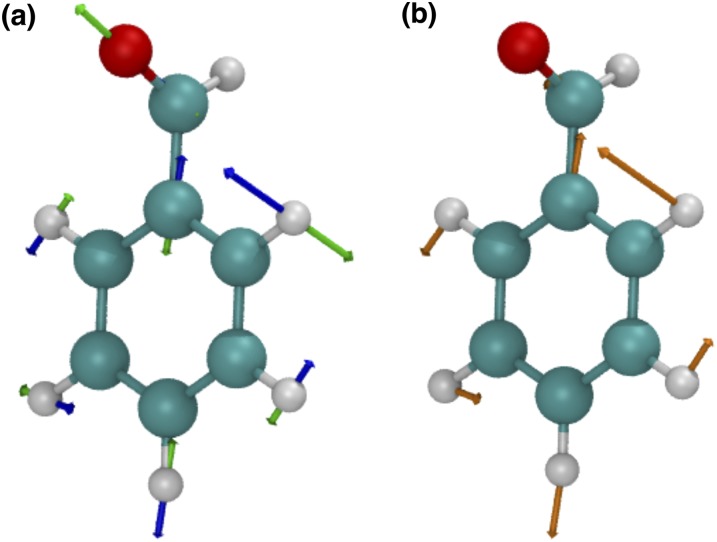
We will now explore how an S₁/T₂ crossing of benzaldehyde (with a SOC less than 10 cm⁻¹) changes as a function of magnetic field B. The coordinates of the nuclear geometry are presented in Table S4 and shown in Fig. 1.

FIG. 1.

Benzaldehyde at an S₁/T₂ crossing of benzaldehyde using ωB97X/6-31G^**, with black vectors depicting the direction of the reaction coordinate plotted in Fig. 2.

At this geometry, the size of the (Zeeman) coupling to the external magnetic field is roughly the same magnitude as the SOC. Figure 1 shows the direction of the reaction coordinate, which lies along the line from the S₁ minimum to the crossing point.

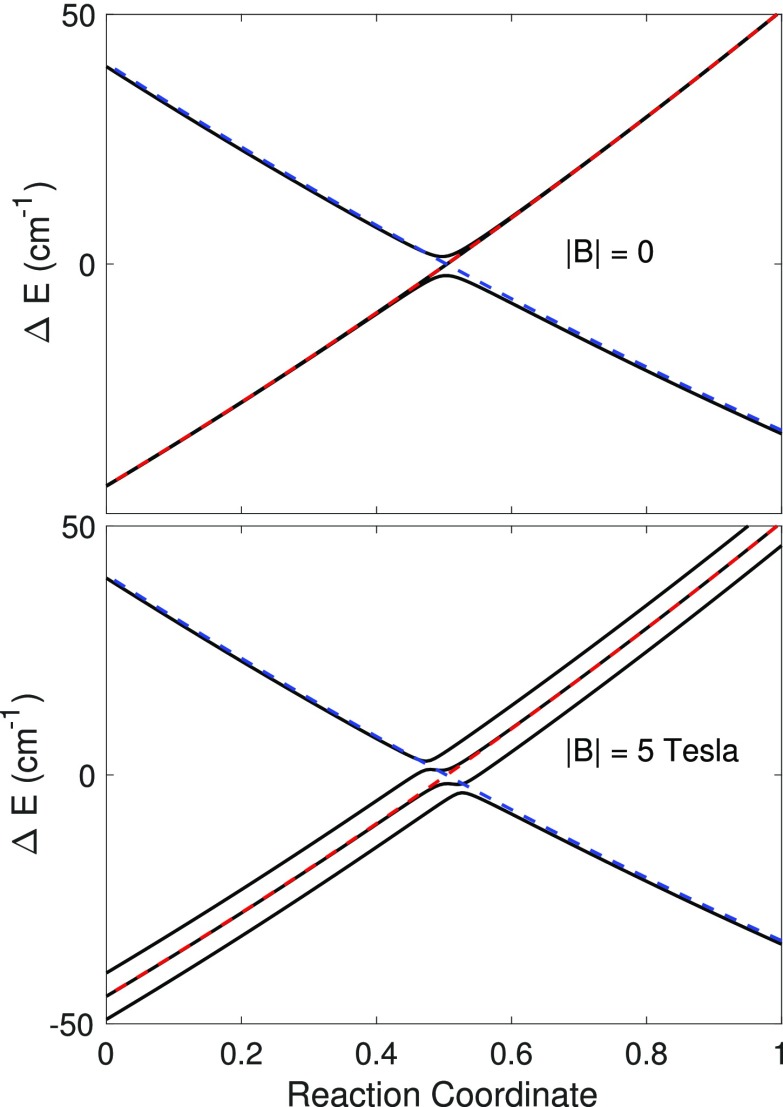
Note that as demonstrated in Fig. 2, the presence of the magnetic field splits the degeneracy of the triplet states. In the upper panel, the spin-diabats and spin-adiabats are shown without the magnetic field. The triplets are nearly degenerate away from the crossing. In the lower panel, once the magnetic field is applied, the triplets split into three nearly parallel surfaces.

FIG. 2.

The TDA spin-diabats and spin-adiabats at an S₁/T₂ crossing of benzaldehyde using ωB97X/6-31G^** along a reaction coordinate. The potential energy surfaces are plotted relative to the energy of the crossing point of the TDA spin-diabats ($\tilde{E}$ = −345.317 096 74 E_h). The blue (red) dashed line represents the singlet (triplet) TDA spin-diabat. The black lines are our TDA spin-adiabats (states 4–7). (Top) The crossing point is shown without a magnetic field. This crossing point was chosen for its small spin-orbit coupling (less than 10 cm⁻¹). (Bottom) When the magnetic field is applied (B_y = 5 T), the triplet degeneracy is broken.

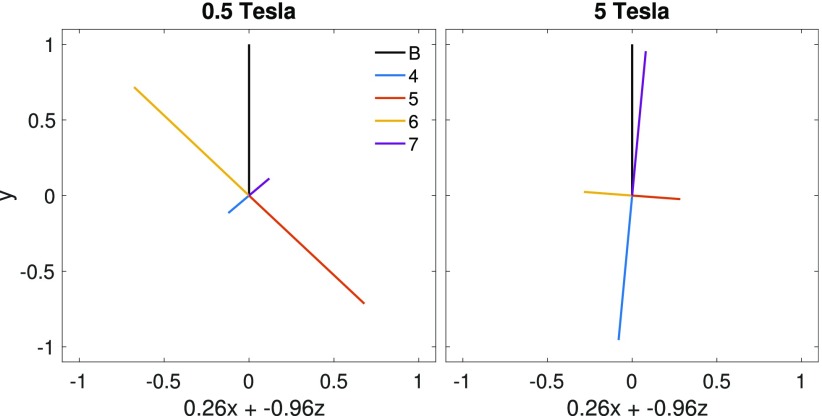
Let us now consider the resulting spin of each spin-adiabatic state at the crossing and assess the direction of each spin state relative to the magnetic field. On the one hand, if there is no magnetic field and just SOC, each spin-adiabatic state would have zero total spin ($⟨\overrightarrow{S}⟩=0$). On the other hand, if one applies a magnetic field but does not include SOC, the singlet and one triplet would still have zero total spin, but two triplets would have their spin aligned with the magnetic field in equal and opposite amounts. When these two effects are put together, the resulting spin vectors are coplanar with the magnetic field, but as can be seen in Fig. 3, the spin vectors of our spin-adiabats at the crossing point in Fig. 2 are not collinear with the magnetic field.

FIG. 3.

The spin expectation values ($⟨\overrightarrow{S}⟩$) for spin-adiabats 4–7 at the crossing point in Fig. 2 for two field strengths (B_y = 0.5T and B_y = 5T) in the two-dimensional space created by the expectation values. At the crossing point, the spin vectors form collinear pairs that lie in plane with the direction of the magnetic field (shown in black). As the magnetic field strength is increased, the 4th and 7th spin-adiabats mix less with other states and the corresponding spin vectors align with the magnetic field.

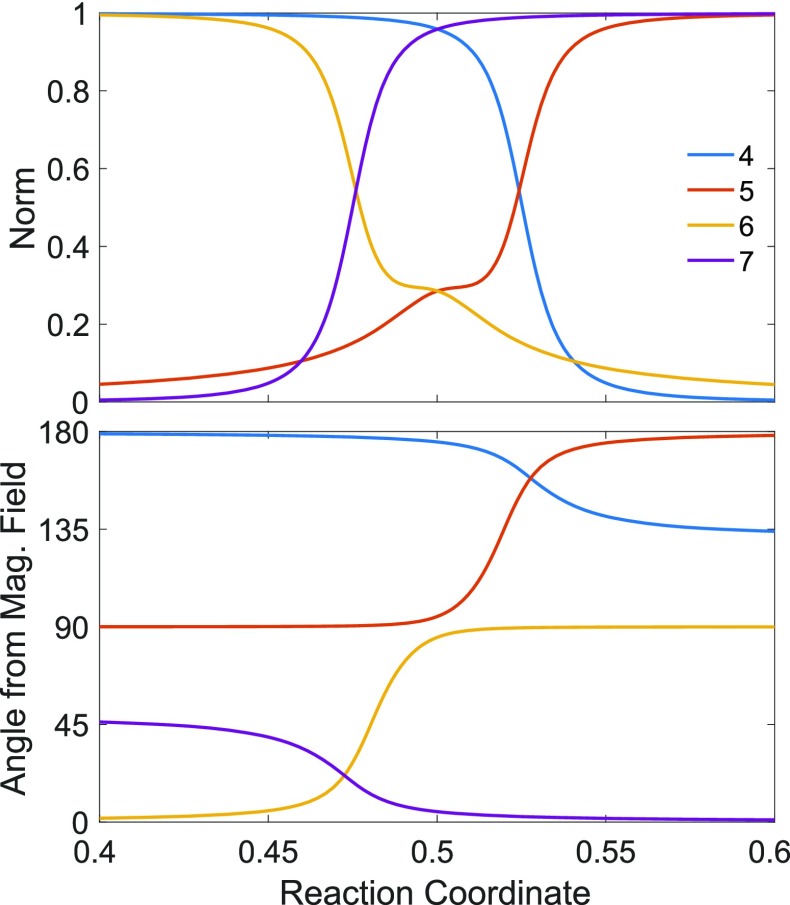
At the crossing point, where the spin-diabats are degenerate, Fig. 3 shows that the four spin-adiabatic spin vectors form a planar orthogonal set. Figure 4 shows how the norm and relative angles of the spin vectors change along the reaction coordinate in Fig. 2; note that when the system is away from a crossing, the triplets are in line with the magnetic field. Future work will need to address (1) how the four spin vectors form a plane, (2) how the direction of that plane can best be characterized as a function of the external magnetic field, $\overrightarrow{B}$, and (3) how the magnitudes of the different components depend on the particular molecule.

FIG. 4.

Comparison of the spin expectation values for the spin-adiabats near the crossing in Fig. 2 for a strong magnetic field (B_y = 5 T). (Top) The norm of the spin for our TDA spin-adiabats (states 4–7), e.g., $N_4={⟨S_{44}^x⟩}^2+{⟨S_{44}^y⟩}^2+{⟨S_{44}^z⟩}^2$. (Bottom) The relative angle of the spin vectors with the magnetic field direction ($\overrightarrow{y}$).

IV. DISCUSSION

In this paper, we have presented a complete approach for calculating gradients and NADCs between TDA spin-adiabatic states, which should be very helpful for running FSSH ISC dynamics. Future work in our research group will explore systems with large SOCs where using these NADCs and gradients for spin-adiabatic FSSH dynamics should yield different results than running FSSH along spin-diabats. Future work will also no doubt explore the introduction of SOC between the ground and excited states²⁹ such that one will be able to treat the final step of nonadiabatic, radiationless transitions.

Now, one interesting aspect of this project is the introduction of complex-valued NADCs. Recent dynamical work has suggested that the imaginary component of NADCs can yield very rich new physical behaviors.⁴² In particular, whenever the derivative coupling d is complex, such complexity automatically introduces nontrivial Berry phase effects,^72,73 whereby a given trajectory moving on adiabat J with momentum $\overrightarrow{p}$ should feel a force,^42,74

$$F_J^{Berry}=2\hslash \sum _{K\ne J}\text{Im}\left[d_{JK}\left(\frac{\overrightarrow{p}}{m}\cdot d_{KJ}\right)\right].$$ (50)

Thus, whether a derivative coupling is nontrivially complex is absolutely essential as far as understanding the nonadiabatic dynamics. If d has both a real and imaginary part, the resulting physics will be different from the standard Tully FSSH prescription.

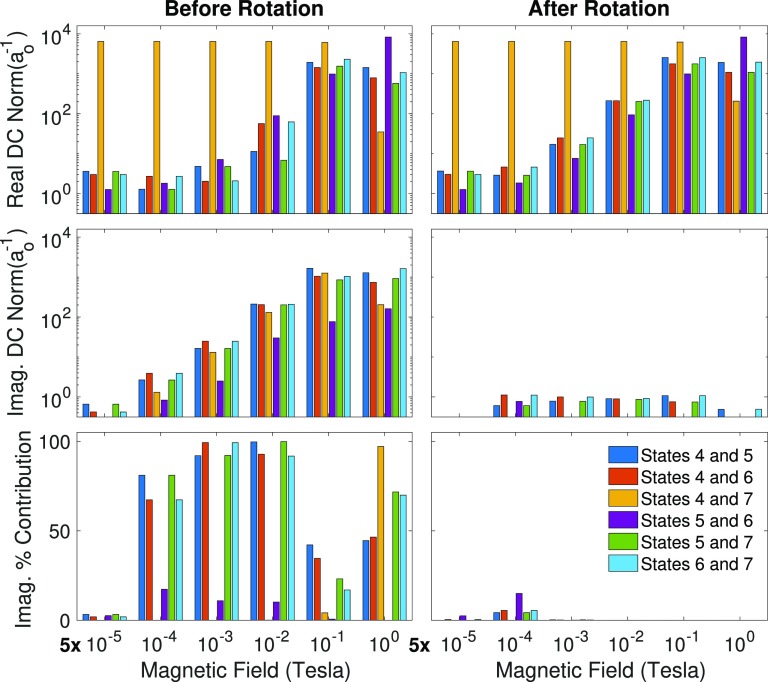
Unfortunately, in practice, analyzing the phases of NADCs is complicated since each electronic state’s phase can be picked arbitrarily at any given geometry. With that in mind, in Fig. 5, we investigate the crossing point geometry of Fig. 2 and apply six different magnetic fields from 5 · 10⁻⁵ T to 5 T. The upper panels present the norm of the real-valued component of the NADCs between our states of interest (4–7) on a logarithmic scale, while the middle panels presents the imaginary-valued components. The lower panels presents the percent contribution of the imaginary component as a fraction of the total NADC norm squared. On the left, we analyze the couplings in terms of the (fixed but arbitrary) phases that Q-Chem chooses for each adiabatic state. On the right, we follow the prescription of Ref. 42 and maximize the norm of the real component of each NADC individually (one at a time). This implies that we give each adiabatic wavefunction a different phase depending on which NADC we are looking at. As discussed above, we are interested inthe real/imaginary nature of the NADC because if the NADC is truly imaginary, we should find interesting Berry phase physics.^42,74 However, it is clear (disappointingly) that in practice, for the case of benzaldehyde, after rotation there are little to no remaining imaginary components, and the NADCs can be rotated into an almost entirely real-valued vector; thus, no Berry phase effects will be strong here, using the formula in Eq. (50). This statement is quantified in Fig. 6. On the left, we plot (again using the fixed but arbitrary phases chosen by Q-Chem) the real-valued component (blue) and the imaginary-valued component (green) of the NADC between states 4 and 5 with a magnetic field B_y = 0.5 T. On the right, we plot the final real-valued NADC as found after adjusting the phases of states 4 and 5 (orange). The imaginary component is too small to display. Future work will need to explore conditions for which these NADCs cannot be rotated into a single real vector.

FIG. 5.

The norm of the NADCs between our TDA spin-adiabats (states 4–7) at an S₁/T₂ crossing of benzaldehyde using ωB97X/6-31G^** as the magnetic field is increased in the y direction. All coordinates are given in Table S4. (Top) The norm of the real-valued component of the NADCs before and after rotation. (Middle) The norm of the imaginary components of the NADCs before and after rotation. (Bottom) The percent contribution of the imaginary component to the total norm squared of the derivative coupling. Note that before rotation (left), the phase of each adiabat is assigned randomly (but in a fixed fashion) by the Q-Chem electronic structure program for each adiabatic state; however, after rotation (right), the imaginary component is nearly zero.

FIG. 6.

The NADC between spin-adiabats 4 and 5 of benzaldehyde (from Fig. 5) before and after rotation by η with a magnetic field of 0.5 T. (a) Using the (fixed but arbitrary) phases that are found by Q-Chem, we plot the real (imaginary) component of the NADC, shown as vectors in blue (green). The total NADC is normalized. (b) After rotation, the real component of the NADC is shown in orange. The imaginary component is too small to be displayed.

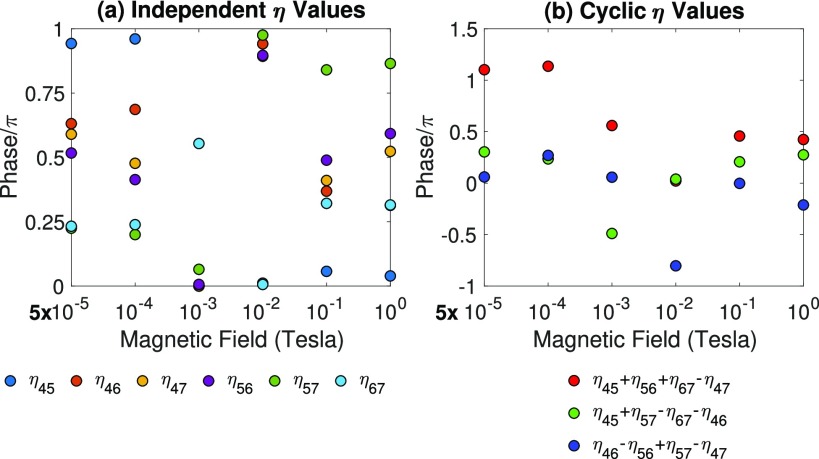
At this point, one can ask: since the NADCs in Fig. 5 can each be independently rotated into a real-valued vector, can these NADCs perhaps be codependently rotated into real-valued vectors? In other words, can we choose the N phases for the N adiabatic wave functions such that the derivative coupling matrix is always real and imaginary numbers are not actually necessary? To answer this question, note that there are N − 1 degrees of freedom for the relative phases of adiabatic states, but there are N(N − 1)/2 relative phases. With that in mind, we can perform the following experiment. Starting from a set of fixed but arbitrary phases for the adiabatic wavefunctions, we find the necessary phases {η₄₅,…, η₆₇} that make the matrix of derivative couplings as real as possible through the equation

$${\tilde{d}}_{JK}=d_{JK}{e}^{i{\eta }_{JK}}.$$ (51)

These η quantities are plotted in Fig. 7 on the left.

FIG. 7.

Values of η for each NADC in Fig. 5; see Eq. (51) for the definition of η. (a) η values as a function of magnetic field for the different NADCs. Note that in general, for the correct η parameter one can rotate each NADC for benzaldehyde into an almost completely real-valued vector. (b) If it were possible to choose phases for each adiabatic state such that all NADCs were real, then the sum of any cyclic choice of phases η_JK would necessarily need to be 0 or π. The fact that such a choice is not possible implies that the complex nature of the Hamiltonian cannot be rigorously removed.

Then, if it were possible to find a consistent set of phases to make the derivative coupling real, we must have

$${\eta }_{45}+{\eta }_{56}+{\eta }_{67}+{\eta }_{74}=0\mathrm{o}\mathrm{r}\pi$$

as well as a host of similar identities. In short, for any arrangement of phases that is cyclic, ${\eta }_{i_1{i}_2}+{\eta }_{i_2{i}_3}+{\eta }_{i_3{i}_4}+\cdots +{\eta }_{i_N-1i_N}+{\eta }_{i_N{i}_1}$ must equal 0 or π. In Fig. 7, on the right, we plot several such sums; note that none of them are zero or π. Thus, one clearly cannot choose the phases of the adiabats such that the derivative coupling matrix is entirely real.

What are the implications of this last statement and the presence of complex nonadiabatic couplings? According to the FSSH, one requires the derivative coupling only insofar as it is needed to rescale velocities, and so if one hops between states I and J and d_IJ is real, one presumably would not care about the total phase of the derivative coupling d_IJ. Furthermore, if d_IJ is real, there should not be a Berry force according to Eq. (50). Thus, it is safe to assume that according to the FSSH algorithm, the fact that not all derivative couplings can simultaneously be real would likely have no important consequences. Nevertheless, FSSH is not exact dynamics, and at this point, it is not clear to the authors what would be the implications for the exact Schrödinger equation when a set of derivative couplings is presented which cannot be made real-valued simultaneously. Clearly, such a situation can arise only with three or more electronic states, i.e., when the number of derivative couplings between electronic states is larger than the number of electronic states themselves. This statement is a reminder that when there are more than 2 states, nonadiabatic problems become more complex⁷⁵ and semiclassical approaches become more complicated.⁷⁶

V. CONCLUSION

In this paper, we have presented a method for constructing TDA spin-adiabats and their NADCs in the presence of a magnetic field using a pseudowavefunction ansatz.³⁴ The magnetic field breaks time reversal symmetry, and thus, the resulting derivative couplings should be formally complex valued, even for a system with an even number of electrons.⁷⁷ We have verified our algorithm for the gradients and derivative couplings by benchmarking against finite difference with a small basis set at an S₁/T₂ crossing. This algorithm should be very useful for running nonadiabatic dynamics (in the future) with spin-orbit coupling and complex Hamiltonians.

There are many important questions that will need to be addressed in the future. First, for the case of benzaldehyde, preliminary calculations suggest that (disappointingly) each of our NADCs can be rotated by a phase to a vector that is nearly real for all magnetic field strengths, such that Berry forces will not obviously appear. Will this be consistently true with small organic molecules? Or will the imaginary component be larger for other systems? Many other questions also remain regarding the effect of the relative phases of the NADCs for dynamics: even though relative phases may not be important for FSSH, what are their consequences with exact dynamics? Second, more work will need to be done to understand the nature of spin-adiabatic states and one must necessarily investigate all underlying symmetries; at present, we cannot predict the overall spin expectation values a priori. Third and finally, the most obvious remaining questions are the following: what will be the practical effect of including an odd number of electrons, where the V_so cannot ever be made into a real operator? Are the derivative couplings nontrivially complex? Is there a great deal of new nonadiabatic dynamics to be discovered? This is a very interesting time to be studying ISC and SOC dynamics.

SUPPLEMENTARY MATERIAL

See the supplementary material for the full geometries and NADCs results for benzaldehyde, including both the real and imaginary components and different magnetic field directions.

APPENDIX A: SPIN DETAILS OF TD-DFT WITHIN TDA

In this section, we present the important details for the inclusion of density functional theory into our gradient and derivative coupling derivation. The real space spin density ρ_σ(r) is

$${\rho }_{\sigma }\left(\mathbf{r}\right)=\sum _{\mu \nu }{P}_{{\mu }_{\sigma }{\nu }_{\sigma }}{\varphi }_{{\mu }_{\sigma }}\left(\mathbf{r}\right){\varphi }_{{\nu }_{\sigma }}\left(\mathbf{r}\right).$$ (A1)

Here, ϕ refers to real space, spin atomic orbitals. The exchange-correlation energy is an integral over all space,

$$E_{xc}\left[\rho \right]=\int f_{xc}\left(\mathbf{r}\right)d\mathbf{r}.$$ (A2)

The exchange-correlation functional f_xc can depend on many variables but is usually a local operator of some kind or another, so that we can write

$$E_{xc}\left[\rho \right]=\int f_{xc}\left(\right.{\rho }_{\sigma }\left(\mathbf{r}\right),\nabla {\rho }_{\sigma }\left(\mathbf{r}\right),{\nabla }^2{\rho }_{\sigma }\left(\mathbf{r}\right),\dots \left)\right.d\mathbf{r}.$$ (A3)

Here, the spin-density is ρ_σ(r), the electronic gradient of the spin-density is ∇ρ_σ(r), and one can move up Jacob’s ladder of DFT with higher derivatives.⁷⁸ We will adopt the notation in Ref. 79, denoting these variables as ξ ∈ {ρ_σ(r), ∇ρ_σ(r), …}. Note that each ξ depends linearly on the density matrix, P. See Eq. (A1) for the case ξ = ρ_σ(r); for the case ξ = ∇ρ_σ(r), note that $\nabla {\rho }_{\sigma }\left(\mathbf{r}\right)={\sum }_{\mu \nu }{P}_{{\mu }_{\sigma }{\nu }_{\sigma }}\left(\nabla {\varphi }_{{\mu }_{\sigma }}\left(\mathbf{r}\right){\varphi }_{{\nu }_{\sigma }}\left(\mathbf{r}\right)+{\varphi }_{{\mu }_{\sigma }}\left(\mathbf{r}\right)\nabla {\varphi }_{{\nu }_{\sigma }}\left(\mathbf{r}\right)\right)$.⁸⁰

The exchange-correlation matrix g⁸¹ can be written as the first derivative of the energy E_xc with respect to the density matrix,

$$g_{{\mu }_{\sigma }{\nu }_{\sigma }}=\frac{\partial E_{xc}}{\partial P_{{\mu }_{\sigma }{\nu }_{\sigma }}},$$ (A4a)

$$=\sum _{\xi }\int \frac{\partial f_{xc}}{\partial \xi }\frac{\partial \xi }{\partial P_{{\mu }_{\sigma }{\nu }_{\sigma }}}d\mathbf{r}.$$ (A4b)

We note that g is zero if μ and ν have different spins. Similarly, the TD-DFT/TDA response tensor Ω can be expressed as the derivative of g with respect to the density matrix,

$${\mathrm{\Omega }}_{{\mu }_{\sigma }{\nu }_{\sigma }{\delta }_{\tau }{\gamma }_{\tau }}=\frac{\partial g_{{\mu }_{\sigma }{\nu }_{\sigma }}}{\partial P_{{\delta }_{\tau }{\gamma }_{\tau }}}$$ (A5a)

$$=\sum _{\xi {\xi }^{\prime }}\int \frac{{\partial }^2{f}_{xc}}{\partial \xi \partial {\xi }^{\prime }}\frac{\partial \xi }{\partial P_{{\mu }_{\sigma }{\nu }_{\sigma }}}\frac{\partial {\xi }^{\prime }}{\partial P_{{\delta }_{\tau }{\gamma }_{\tau }}}d\mathbf{r}.$$ (A5b)

Here, we note that Ω is formally zero if μ and ν or δ and γ have different spins.

In Secs. II C–II F, we have presented the derivation of the NADC for our spin-adiabats, culminating in Eqs. (44a)–(47). Within these equations, we need the nuclear gradients of the elements of the exchange-correlation matrix and the response tensor.

To that end, it is helpful to break the nuclear gradient of the exchange-correlation matrix [see Eq. (A4)] into two terms,

$$g_{{\mu }_{\sigma }{\nu }_{\sigma }}^{\left[x\right]}=g_{{\mu }_{\sigma }{\nu }_{\sigma }}^{0\left[x\right]}+g_{{\mu }_{\sigma }{\nu }_{\sigma }}^{Y\left[x\right]},$$ (A6a)

$$\begin{array}{ccc}\hfill g_{{\mu }_{\sigma }{\nu }_{\sigma }}^{0\left[x\right]}& =\hfill & \sum _{\xi }{\int }^{\left[x\right]}\frac{\partial f_{xc}}{\partial \xi }\frac{\partial \xi }{\partial P_{{\mu }_{\sigma }{\nu }_{\sigma }}}d\mathbf{r}+\sum _{\xi }\int \frac{\partial f_{xc}}{\partial \xi }{\left(\frac{\partial \xi }{\partial P_{{\mu }_{\sigma }{\nu }_{\sigma }}}\right)}^{\left[x\right]}d\mathbf{r}\hfill \\ \hfill & \hfill & +\sum _{\xi {\xi }^{\prime }}\int \frac{{\partial }^2{f}_{xc}}{\partial \xi \partial {\xi }^{\prime }}\frac{\partial \xi }{\partial P_{{\mu }_{\sigma }{\nu }_{\sigma }}}{\xi }^{\prime \left[x\right]}d\mathbf{r},\hfill \end{array}$$ (A6b)

$$g_{{\mu }_{\sigma }{\nu }_{\sigma }}^{Y\left[x\right]}=\sum _{\gamma \lambda }\sum _{\tau }{\mathrm{\Omega }}_{{\mu }_{\sigma }{\nu }_{\sigma }{\gamma }_{\tau }{\lambda }_{\tau }}{P}_{{\gamma }_{\tau }{\lambda }_{\tau }}^{\left[x\right]}.$$ (A6c)

Here, all nonresponse changes in $g_{{\mu }_{\sigma }{\nu }_{\sigma }}$ are grouped together in the quantity g^0[x]; these are terms that depend directly on the nuclear displacement. For instance, the term ${\sum }_{\xi }{\int }^{\left[x\right]}\frac{\partial f_{xc}}{\partial \xi }\frac{\partial \xi }{\partial P_{{\mu }_{\sigma }{\nu }_{\sigma }}}d\mathbf{r}$ reflects how the electronic grid (for integrating the exchange-correlation function) induces changes in $g_{{\mu }_{\sigma }{\nu }_{\sigma }}$ as the nuclear positions are changed. Vice versa, we define g^Y[x] to include all indirect changes in $g_{{\mu }_{\sigma }{\nu }_{\sigma }}$ as induced by the response of the Kohn-Sham orbitals (or equivalently the density matrix $P_{{\mu }_{\sigma }{\nu }_{\sigma }}$) to nuclear displacement.

Although it is slightly confusing, in Eq. (A6b) given above, we have followed standard convention and defined ξ^[x] to be that portion of the full derivative $\frac{\partial \xi }{\partial x}$ that does not depend on P^[x]. As an example, consider the case $\xi ={\rho }_{\sigma }\left(\mathbf{r}\right)={\sum }_{\mu \nu }{P}_{{\mu }_{\sigma }{\nu }_{\sigma }}{\varphi }_{{\mu }_{\sigma }}\left(\mathbf{r}\right){\varphi }_{{\nu }_{\sigma }}\left(\mathbf{r}\right)$. Here, obviously

$$\begin{array}{ccc}\hfill \frac{\partial \xi }{\partial x}& =\hfill & \sum _{\mu \nu }{P}_{{\mu }_{\sigma }{\nu }_{\sigma }}^{\left[x\right]}{\varphi }_{{\mu }_{\sigma }}\left(\mathbf{r}\right){\varphi }_{{\nu }_{\sigma }}\left(\mathbf{r}\right)+P_{{\mu }_{\sigma }{\nu }_{\sigma }}{\left({\varphi }_{{\mu }_{\sigma }}\left(\mathbf{r}\right){\varphi }_{{\nu }_{\sigma }}\left(\mathbf{r}\right)\right)}^{\left[x\right]}\hfill \\ \hfill & \equiv \hfill & \sum _{\mu \nu }{P}_{{\mu }_{\sigma }{\nu }_{\sigma }}^{\left[x\right]}{\varphi }_{{\mu }_{\sigma }}\left(\mathbf{r}\right){\varphi }_{{\nu }_{\sigma }}\left(\mathbf{r}\right)+{\xi }^{\left[x\right]}.\hfill \end{array}$$ (A7)

Both terms on the right-hand side of Eq. (A7) can be found in Eq. (A6). Finally, we can use Eqs. (25) and (27) to expand P^[x],

$$\begin{array}{ccc}\hfill g_{{\mu }_{\sigma }{\nu }_{\sigma }}^{Y\left[x\right]}& =\hfill & -\frac{1}{2}\sum _{\gamma \lambda \delta \eta }\sum _{\tau }{S}_{{\lambda }_{\tau }{\eta }_{\tau }}^{\left[x\right]}\left({\tilde{P}}_{{\delta }_{\tau }{\lambda }_{\tau }}{P}_{{\eta }_{\tau }{\gamma }_{\tau }}+P_{{\delta }_{\tau }{\lambda }_{\tau }}{\tilde{P}}_{{\eta }_{\tau }{\gamma }_{\tau }}\right){\mathrm{\Omega }}_{{\mu }_{\sigma }{\nu }_{\sigma }{\delta }_{\tau }{\gamma }_{\tau }}\hfill \\ \hfill & \hfill & -\sum _{\delta \gamma }\sum _{\tau }\sum _{bi}{\mathrm{\Theta }}_{b_{\tau }{i}_{\tau }}^{\left[x\right]}\left(C_{{\delta }_{\tau }{b}_{\tau }}{C}_{{\gamma }_{\tau }{i}_{\tau }}+C_{{\delta }_{\tau }{i}_{\tau }}{C}_{{\gamma }_{\tau }{b}_{\tau }}\right){\mathrm{\Omega }}_{{\mu }_{\sigma }{\nu }_{\sigma }{\delta }_{\tau }{\gamma }_{\tau }}.\hfill \end{array}$$ (A8)

We also need the nuclear gradient of the response term for the TDA gradient. We again have a response term and a nonresponse term,

$${\mathrm{\Omega }}_{{\mu }_{\sigma }{\nu }_{\sigma }{\delta }_{\tau }{\gamma }_{\tau }}^{\left[x\right]}={\mathrm{\Omega }}_{{\mu }_{\sigma }{\nu }_{\sigma }{\delta }_{\tau }{\gamma }_{\tau }}^{0\left[x\right]}+{\mathrm{\Omega }}_{{\mu }_{\sigma }{\nu }_{\sigma }{\delta }_{\tau }{\gamma }_{\tau }}^{Y\left[x\right]},$$ (A9a)

$$\begin{array}{ccc}\hfill {\mathrm{\Omega }}_{{\mu }_{\sigma }{\nu }_{\sigma }{\delta }_{\tau }{\gamma }_{\tau }}^{0\left[x\right]}& =\hfill & \sum _{\xi {\xi }^{\prime }}{\int }^{\left[x\right]}\frac{{\partial }^2{f}_{xc}}{\partial \xi \partial {\xi }^{\prime }}\frac{\partial \xi }{\partial P_{{\mu }_{\sigma }{\nu }_{\sigma }}}\frac{\partial {\xi }^{\prime }}{\partial P_{{\delta }_{\tau }{\gamma }_{\tau }}}d\mathbf{r}\hfill \\ \hfill & \hfill & +\sum _{\xi {\xi }^{\prime }}\int \frac{{\partial }^2{f}_{xc}}{\partial \xi \partial {\xi }^{\prime }}{\left(\frac{\partial \xi }{\partial P_{{\mu }_{\sigma }{\nu }_{\sigma }}}\right)}^{\left[x\right]}\frac{\partial {\xi }^{\prime }}{\partial P_{{\delta }_{\tau }{\gamma }_{\tau }}}d\mathbf{r}\hfill \\ \hfill & \hfill & +\sum _{\xi {\xi }^{\prime }}\int \frac{{\partial }^2{f}_{xc}}{\partial \xi \partial {\xi }^{\prime }}\frac{\partial \xi }{\partial P_{{\mu }_{\sigma }{\nu }_{\sigma }}}{\left(\frac{\partial {\xi }^{\prime }}{\partial P_{{\delta }_{\tau }{\gamma }_{\tau }}}\right)}^{\left[x\right]}d\mathbf{r}\hfill \\ \hfill & \hfill & +\sum _{\xi {\xi }^{\prime }{\xi }^{″}}\int \frac{{\partial }^3{f}_{xc}}{\partial \xi \partial {\xi }^{\prime }\partial {\xi }^{″}}\frac{\partial \xi }{\partial P_{{\mu }_{\sigma }{\nu }_{\sigma }}}\frac{\partial {\xi }^{\prime }}{\partial P_{{\delta }_{\tau }{\gamma }_{\tau }}}{\xi }^{\prime \prime \left[x\right]}d\mathbf{r},\hfill \end{array}$$ (A9b)

$${\mathrm{\Omega }}_{{\mu }_{\sigma }{\nu }_{\sigma }{\delta }_{\tau }{\gamma }_{\tau }}^{Y\left[x\right]}=\sum _{\lambda \kappa }\sum _{\upsilon }{\mathrm{\Xi }}_{{\mu }_{\sigma }{\nu }_{\sigma }{\delta }_{\tau }{\gamma }_{\tau }{\lambda }_{\upsilon }{\kappa }_{\upsilon }}{P}_{{\lambda }_{\upsilon }{\kappa }_{\upsilon }}^{\left[x\right]}.$$ (A9c)

Here, Ξ is the derivative of Ω with respect to the density matrix,

$${\mathrm{\Xi }}_{{\mu }_{\sigma }{\nu }_{\sigma }{\delta }_{\tau }{\gamma }_{\tau }{\lambda }_{\upsilon }{\kappa }_{\upsilon }}=\frac{\partial {\mathrm{\Omega }}_{{\mu }_{\sigma }{\nu }_{\sigma }{\delta }_{\tau }{\gamma }_{\tau }}}{\partial P_{{\lambda }_{\upsilon }{\kappa }_{\upsilon }}}$$ (A10a)

$$=\sum _{\xi {\xi }^{\prime }{\xi }^{″}}\int \frac{{\partial }^3{f}_{xc}}{\partial \xi \partial {\xi }^{\prime }\partial {\xi }^{″}}\frac{\partial \xi }{\partial P_{{\mu }_{\sigma }{\nu }_{\sigma }}}\frac{\partial {\xi }^{\prime }}{\partial P_{{\delta }_{\tau }{\gamma }_{\tau }}}\frac{\partial {\xi }^{″}}{\partial P_{{\lambda }_{\upsilon }{\kappa }_{\upsilon }}}d\mathbf{r}.$$ (A10b)

We again expand the response term using Eqs. (25) and (27),

$$\begin{array}{ccc}\hfill {\mathrm{\Omega }}_{{\mu }_{\sigma }{\nu }_{\sigma }{\delta }_{\tau }{\gamma }_{\tau }}^{Y\left[x\right]}& =\hfill & -\frac{1}{2}\sum _{\lambda \kappa \zeta \eta }\sum _{\upsilon }{S}_{{\zeta }_{\upsilon }{\eta }_{\upsilon }}^{\left[x\right]}\left({\tilde{P}}_{{\lambda }_{\upsilon }{\zeta }_{\upsilon }}{P}_{{\eta }_{\upsilon }{\kappa }_{\upsilon }}+P_{{\lambda }_{\upsilon }{\zeta }_{\upsilon }}{\tilde{P}}_{{\eta }_{\upsilon }{\kappa }_{\upsilon }}\right){\mathrm{\Xi }}_{{\mu }_{\sigma }{\nu }_{\sigma }{\delta }_{\tau }{\gamma }_{\tau }{\lambda }_{\upsilon }{\kappa }_{\upsilon }}\hfill \\ \hfill & \hfill & -\sum _{\lambda \kappa }\sum _{\upsilon }\sum _{bi}{\mathrm{\Theta }}_{b_{\upsilon }{i}_{\upsilon }}^{\left[x\right]}\left(C_{{\lambda }_{\upsilon }{b}_{\upsilon }}{C}_{{\kappa }_{\upsilon }{i}_{\upsilon }}+C_{{\lambda }_{\upsilon }{i}_{\upsilon }}{C}_{{\kappa }_{\upsilon }{b}_{\upsilon }}\right){\mathrm{\Xi }}_{{\mu }_{\sigma }{\nu }_{\sigma }{\delta }_{\tau }{\gamma }_{\tau }{\lambda }_{\upsilon }{\kappa }_{\upsilon }}.\hfill \\ \hfill & \hfill & \hfill \end{array}$$ (A11)

APPENDIX B: THE RESPONSE TERMS: THE “z-VECTOR” APPROACH

To construct the derivative of Θ, it is standard in quantum chemistry software to solve the coupled-perturbed Hartree-Fock (CPHF) equation, $F_{aj}^{\left[x\right]}=0$, or more explicitly using the chain rule,

$$\begin{array}{ll}\hfill & \sum _{bi}\frac{{\partial }^2{E}_{gs}}{\partial {\mathrm{\Theta }}_{aj}\partial {\mathrm{\Theta }}_{bi}}{\mathrm{\Theta }}_{bi}^{\left[x\right]}+\sum _{\mu \nu }\frac{{\partial }^2{E}_{gs}}{\partial {\mathrm{\Theta }}_{aj}\partial S_{\mu \nu }}{S}_{\mu \nu }^{\left[x\right]}+\sum _{\mu \nu }\frac{{\partial }^2{E}_{gs}}{\partial {\mathrm{\Theta }}_{aj}\partial h_{\mu \nu }}\hfill \\ \hfill & \times \left(h_{\mu \nu }^{\left[x\right]}+g_{\mu \nu }^{0\left[x\right]}\right)+\sum _{\mu \nu \gamma \delta }\frac{{\partial }^2{E}_{gs}}{\partial {\mathrm{\Theta }}_{aj}\partial {\mathrm{\Pi }}_{\mu \nu \gamma \delta }}{\mathrm{\Pi }}_{\mu \nu \gamma \delta }^{\left(s\right)\left[x\right]}=0.\hfill \end{array}$$ (B1)

By inversion, one can solve for ${\mathrm{\Theta }}_{bi}^{\left[x\right]}$ as follows:

$${\mathrm{\Theta }}_{bi}^{\left[x\right]}=-\sum _{aj}{\left(\frac{{\partial }^2{E}_{gs}}{\partial {\mathrm{\Theta }}_{aj}\partial {\mathrm{\Theta }}_{bi}}\right)}^{-1}{M}_{aj}^{\left[x\right]},$$ (B2)

where $M_{aj}^{\left[x\right]}$ is the mixed-derivative term,

$$\begin{array}{ccc}\hfill M_{aj}^{\left[x\right]}& =\hfill & \sum _{\mu \nu }\frac{{\partial }^2{E}_{gs}}{\partial {\mathrm{\Theta }}_{aj}\partial S_{\mu \nu }}{S}_{\mu \nu }^{\left[x\right]}+\sum _{\mu \nu }\frac{{\partial }^2{E}_{gs}}{\partial {\mathrm{\Theta }}_{aj}\partial h_{\mu \nu }}\left(h_{\mu \nu }^{\left[x\right]}+g_{\mu \nu }^{0\left[x\right]}\right)\hfill \\ \hfill & \hfill & +\sum _{\mu \nu \gamma \delta }\frac{{\partial }^2{E}_{gs}}{\partial {\mathrm{\Theta }}_{aj}\partial {\mathrm{\Pi }}_{\mu \nu \gamma \delta }}{\mathrm{\Pi }}_{\mu \nu \gamma \delta }^{\left(s\right)\left[x\right]}.\hfill \end{array}$$ (B3)

As Eq. (B2) requires a large matrix inversion, it becomes computationally expensive to calculate the response functions $\left\{{\mathrm{\Theta }}_{bi}^{\left[x\right]}\right\}$ for each nuclear coordinate [x]. The “z-vector” approach of Handy and Schaefer⁸² significantly decreases this cost by exploiting the fact that we only consider the product of Y^tot and Θ^[x],

$$\begin{array}{ccc}\hfill -\sum _{bi}{Y}_{bi}^{tot}{\mathrm{\Theta }}_{bi}^{\left[x\right]}& =\hfill & \sum _{abij}{Y}_{bi}^{tot}{\left(\frac{{\partial }^2{E}_{gs}}{\partial {\mathrm{\Theta }}_{aj}\partial {\mathrm{\Theta }}_{bi}}\right)}^{-1}{M}_{aj}^{\left[x\right]}\hfill \\ \hfill & =\hfill & \sum _{aj}{\left[\sum _{bi}{Y}_{bi}^{tot}{\left(\frac{{\partial }^2{E}_{gs}}{\partial {\mathrm{\Theta }}_{bi}\partial {\mathrm{\Theta }}_{aj}}\right)}^{-1}\right]}_{aj}{M}_{aj}^{\left[x\right]}.\hfill \end{array}$$ (B4)

The z-vector is defined as

$$z_{aj}\equiv \sum _{bi}{Y}_{bi}^{tot}{\left(\frac{{\partial }^2{E}_{gs}}{\partial {\mathrm{\Theta }}_{bi}\partial {\mathrm{\Theta }}_{aj}}\right)}^{-1}.$$ (B5)

This approach allows us to invert the double angle derivative only once for all atomic coordinates [x] as we have also integrated over the spin degrees of freedom (which is allowed because the molecular orbitals are pure spin and restricted). The three contributions to the sum in Eq. (B4) can be expressed in terms of z_μν = ∑_ajC_μaz_ajC_νj,

$$\begin{array}{ccc}\hfill & \hfill & \sum _{ja\mu \nu }{z}_{aj}\frac{{\partial }^{2}E}{\partial {\mathrm{\Theta }}_{aj}\partial h_{\mu \nu }}\left(h_{\mu \nu }^{\left[x\right]}+g_{\mu \nu }^{0\left[x\right]}\right)=-\sum _{\mu \nu }\left(z_{\mu \nu }+z_{\nu \mu }\right)\left(h_{\mu \nu }^{\left[x\right]}+g_{\mu \nu }^{0\left[x\right]}\right),\hfill \\ \hfill & \hfill & \hfill \end{array}$$ (B6a)

$$\begin{array}{ccc}\hfill & \hfill & \sum _{ja\mu \nu }{z}_{aj}\frac{{\partial }^{2}E}{\partial {\mathrm{\Theta }}_{aj}\partial S_{\mu \nu }}{S}_{\mu \nu }^{\left[x\right]}=\sum _{\delta \omega \mu \nu }{\tilde{P}}_{\delta \mu }{F}_{\delta \omega }\left(z_{\nu \omega }+z_{\omega \nu }\right)S_{\mu \nu }^{\left[x\right]}\hfill \\ \hfill & \hfill & +\frac{1}{2}\sum _{\delta \omega \lambda \sigma \mu \nu }\left({\tilde{P}}_{\lambda \mu }{P}_{\sigma \nu }+P_{\lambda \nu }{\tilde{P}}_{\sigma \mu }\right)\hfill \\ \hfill & \hfill & \times \left(z_{\delta \omega }+z_{\omega \delta }\right)\left({\mathrm{\Pi }}_{\delta \lambda \omega \sigma }+{\mathrm{\Omega }}_{\delta \omega \lambda \sigma }\right)S_{\mu \nu }^{\left[x\right]},\hfill \end{array}$$ (B6b)

$$\sum _{ja\mu \nu \gamma \delta }{z}_{aj}\frac{{\partial }^{2}E}{\partial {\mathrm{\Theta }}_{aj}\partial {\mathrm{\Pi }}_{\mu \nu \gamma \delta }}{\mathrm{\Pi }}_{\mu \nu \gamma \delta }^{\left(s\right)\left[x\right]}=-\sum _{\mu \nu \gamma \delta }\left(z_{\mu \gamma }+z_{\gamma \mu }\right)P_{\delta \nu }{\mathrm{\Pi }}_{\mu \nu \gamma \delta }^{\left(s\right)\left[x\right]}.$$ (B6c)

APPENDIX C: THE GRADIENT OF THE TDA SPIN-ADIABATS

For completeness, we will now outline the steps for calculating the TDA spin-adiabatic gradient. These terms are derived following the same procedure as for the NADC starting from,

$${\omega }_J^{\left[x\right]}=\sum _{\mathbf{abij}}{X}_{\mathbf{a}\mathbf{i}}^{J*}{A}_{\mathbf{iajb}}^{\left[x\right]}{X}_{\mathbf{b}\mathbf{j}}^J$$ (C1)

$$={\mathrm{\Gamma }}_{JJ}^{\left[x\right]}-\sum _{\mathbf{bi}}{\mathrm{\Theta }}_{\mathbf{bi}}^{\left[x\right]}{Y}_{\mathbf{bi}}.$$ (C2)

In the same spirit as in Sec. II F, we can explicitly write the steps to calculate the gradient. Here, we will denote the real-valued component of a complex quantity as $\text{Re}\left[-\right]$. As the gradient is real-valued, we can quickly decrease our terms using this symmetry.

First, the gradient response vector Y is constructed using Eq. (39), with I = J. We again break Y into its usual electronic Hamiltonian contribution, summed over the spin-diabats, Y^E, and spin-coupling contribution, Y^V, summed over the nontrivial spin indices,

$$\sum _{\sigma }{Y}_{b_{\sigma }{i}_{\sigma }}=Y_{bi}^E+Y_{bi}^V,$$ (C3a)

$$\begin{array}{ccc}\hfill Y_{bi}^E& =\hfill & 2\sum _{\mu \nu \lambda \gamma }{C}_{\lambda b}{C}_{\gamma i}\text{Re}\left[{\overline{B}}_{\mu \nu }^{JJ}\right]\left({\mathrm{\Pi }}_{\mu \lambda \nu \gamma }^{\left(s\right)}+{\mathrm{\Omega }}_{\mu \nu \gamma \lambda }^{\left(s\right)}\right)\hfill \\ \hfill & \hfill & +2\sum _{ϵ}\sum _{a\mu \lambda \nu \gamma }{C}_{\nu b}{C}_{\mu a}\text{Re}\left[X_{ai}^{J\left(ϵ\right)*}{R}_{\gamma \lambda }^{J\left(ϵ\right)}\right]\left({\mathrm{\Pi }}_{\mu \lambda \nu \gamma }^{\left(ϵ\right)}+{\mathrm{\Omega }}_{\mu \nu \gamma \lambda }^{\left(ϵ\right)}\right)\hfill \\ \hfill & \hfill & -2\sum _{ϵ}\sum _{j\mu \lambda \nu \gamma }{C}_{\mu i}{C}_{\nu j}\text{Re}\left[X_{bj}^{J\left(ϵ\right)*}{R}_{\gamma \lambda }^{J\left(ϵ\right)}\right]\left({\mathrm{\Pi }}_{\mu \lambda \nu \gamma }^{\left(ϵ\right)}+{\mathrm{\Omega }}_{\mu \nu \gamma \lambda }^{\left(ϵ\right)}\right)\hfill \\ \hfill & \hfill & +2\sum _{ϵ}\sum _{\mu \lambda \nu \gamma \delta \kappa }{C}_{\delta b}{C}_{\kappa i}\text{Re}\left[R_{\mu \nu }^{J\left(ϵ\right)*}{R}_{\lambda \gamma }^{J\left(ϵ\right)}\right]{\mathrm{\Xi }}_{\mu \nu \gamma \lambda \delta \kappa }^{\left(ϵ\right)},\hfill \end{array}$$ (C3b)

$$\begin{array}{ll}\hfill Y_{bi}^V=& 2\text{Re}\left[\sum _{\sigma \tau \upsilon }\sum _{ak\mu \nu }{X}_{b_{\sigma }{k}_{\tau }}^{J*}{X}_{a_{\upsilon }{k}_{\tau }}^J{C}_{\nu a}{V}_{{\mu }_{\sigma }{\nu }_{\upsilon }}{C}_{\mu i}\right]\hfill \\ \hfill & +2\text{Re}\left[\sum _{\sigma \tau \upsilon }\sum _{ak\mu \nu }{C}_{\mu b}{V}_{{\mu }_{\upsilon }{\nu }_{\sigma }}{C}_{\nu k}{X}_{a_{\tau }{k}_{\sigma }}^{J*}{X}_{a_{\tau }{i}_{\upsilon }}^J\right].\hfill \end{array}$$ (C3c)

Second, to indirectly (but efficiently) evaluate the ${\mathrm{\Theta }}_{\mathbf{bi}}^{\left[x\right]}$ term from Eq. (C2), we solve the CPHF equation [Eq. (B2)] to solve for the z-vector in Eq. (40). Therefore, as is common, one constructs the modified relaxed difference density matrix,

$$D_{\mu \nu }^{JJ}\equiv {\overline{B}}_{\mu \nu }^{JJ}-\sum _{aj}{z}_{aj}\left(C_{\mu a}{C}_{\nu j}+C_{\nu a}{C}_{\mu j}\right).$$ (C4)

Third, looking at Eq. (37), we combine Γ [Eq. (38)] and the mixed derivative terms [Eq. (B6a)] and break the sum into three terms: Γ^D[x] includes the terms that depend on the relaxed difference density, Γ^R[x] includes the terms that depend on the transition density matrices resulting from the usual electronic Hamiltonian and summed over the spin-diabats, and Γ^V[x] includes the terms that come from the spin-coupling, summed over two nontrivial spin indices,

$${\mathrm{\Gamma }}_{JJ}^{\left[x\right]}-\sum _{\mathbf{bi}}{Y}_{\mathbf{bi}}{\mathrm{\Theta }}_{\mathbf{bi}}^{\left[x\right]}={\mathrm{\Gamma }}_{JJ}^{\left[x\right]}+\sum _{aj}{z}_{aj}{M}_{aj}^{\left[x\right]}\equiv {\mathrm{\Gamma }}_{JJ}^{D\left[x\right]}+{\mathrm{\Gamma }}_{JJ}^{R\left[x\right]}+{\mathrm{\Gamma }}_{JJ}^{V\left[x\right]}.$$ (C5a)

Here,

$$\begin{array}{ccc}\hfill {\mathrm{\Gamma }}_{JJ}^{D\left[x\right]}& =\hfill & \sum _{\mu \nu }\text{Re}\left[D_{\mu \nu }^{JJ}\right]\left(h_{\mu \nu }^{\left[x\right]}+g_{\mu \nu }^{0\left[x\right]}\right)+\sum _{\mu \nu \lambda \gamma }\text{Re}\left[D_{\mu \nu }^{IJ}\right]P_{\lambda \gamma }{\mathrm{\Pi }}_{\mu \lambda \nu \gamma }^{\left(s\right)\left[x\right]}\hfill \\ \hfill & \hfill & -\sum _{\mu \nu \lambda \gamma }{\tilde{P}}_{\mu \gamma }{S}_{\gamma \lambda }^{\left[x\right]}\text{Re}\left[D_{\lambda \nu }^{JJ}\right]F_{\mu \nu }\hfill \\ \hfill & \hfill & -\sum _{\mu \nu \lambda \gamma \delta \omega }{\tilde{P}}_{\lambda \omega }{S}_{\omega \delta }^{\left[x\right]}{P}_{\delta \gamma }\text{Re}\left[D_{\mu \nu }^{JJ}\right]\left({\mathrm{\Pi }}_{\mu \lambda \nu \gamma }^{\left(s\right)}+{\mathrm{\Omega }}_{\mu \nu \gamma \lambda }^{\left(s\right)}\right),\hfill \end{array}$$ (C5b)

$$\begin{array}{ccc}\hfill {\mathrm{\Gamma }}_{JJ}^{R\left[x\right]}& =\hfill & \sum _{ϵ}\sum _{\mu \nu \lambda \gamma }\text{Re}\left[R_{\mu \nu }^{J\left(ϵ\right)*}{R}_{\gamma \lambda }^{J\left(ϵ\right)}\right]\left({\mathrm{\Pi }}_{\mu \lambda \nu \gamma }^{\left(ϵ\right)\left[x\right]}+{\mathrm{\Omega }}_{\mu \nu \gamma \lambda }^{0\left(ϵ\right)\left[x\right]}\right)\hfill \\ \hfill & \hfill & -\sum _{ϵ}\sum _{\mu \nu \lambda \gamma \delta \omega }{\tilde{P}}_{\lambda \omega }{S}_{\omega \delta }^{\left[x\right]}\text{Re}\left[R_{\delta \gamma }^{J\left(ϵ\right)*}{R}_{\nu \mu }^{J\left(ϵ\right)}+R_{\mu \nu }^{J\left(ϵ\right)*}{R}_{\gamma \delta }^{J\left(ϵ\right)}\right]\left({\mathrm{\Pi }}_{\mu \lambda \nu \gamma }^{\left(ϵ\right)}+{\mathrm{\Omega }}_{\mu \nu \gamma \lambda }^{\left(ϵ\right)}\right)\hfill \\ \hfill & \hfill & -\sum _{ϵ}\sum _{\mu \nu \lambda \gamma \delta \omega \zeta \eta }{\tilde{P}}_{\lambda \omega }{S}_{\omega \delta }^{\left[x\right]}{P}_{\delta \gamma }\text{Re}\left[R_{\mu \nu }^{J\left(ϵ\right)*}{R}_{\zeta \eta }^{J\left(ϵ\right)}\right]{\mathrm{\Xi }}_{\mu \nu \zeta \eta \lambda \gamma }^{\left(ϵ\right)},\hfill \end{array}$$ (C5c)

$${\mathrm{\Gamma }}_{JJ}^{V\left[x\right]}=\sum _{\sigma \tau }\sum _{\mu \nu }{V}_{{\mu }_{\sigma }{\nu }_{\tau }}^{\left[x\right]}{B}_{{\mu }_{\sigma }{\nu }_{\tau }}^{JJ}-\sum _{\sigma \tau }\sum _{\mu \nu \gamma \lambda }{S}_{\gamma \lambda }^{\left[x\right]}\text{Re}\left[V_{{\mu }_{\sigma }{\nu }_{\tau }}{B}_{{\lambda }_{\sigma }{\nu }_{\tau }}^{JJ}\right]{\tilde{P}}_{\mu \gamma }.$$ (C5d)

The last step is to put all these terms together recovering the final answer,

$${\omega }_J^{\left[x\right]}={\mathrm{\Gamma }}_{IJ}^{D\left[x\right]}+{\mathrm{\Gamma }}_{IJ}^{R\left[x\right]}+{\mathrm{\Gamma }}_{IJ}^{V\left[x\right]}.$$ (C6)

Equations (C3a)–(C6) provide a complete framework to calculate the gradients of TDA spin-adiabats with the minimum number of calls to the two electron tensor derivatives (Π^[x] and Ω^[x]).