Abstract
We describe surface wave propagation in soft elastic media at speeds exceeding the bulk shear wave speed. By linking these waves to the elastodynamic Green's function, we derive a simple relationship to quantify the elasticity of a soft medium from the speed of this supershear evanescent wave (SEW). We experimentally probe SEW propagation in tissue-mimicking phantoms, human cornea ex vivo, and skin in vivo using a high-speed optical coherence elastography system. Measurements confirm the predicted relationship between SEW and bulk shear wave speeds, agreeing well with both theoretical and numerical models. These results suggest that SEW measurements may be a robust method to quantify elasticity in soft media, particularly in complex, bounded materials where dispersive Rayleigh-Lamb modes complicate measurements.
Optical coherence elastography (OCE) is a rapidly growing field to evaluate tissue biomechanical properties at high spatial resolution. Leveraging previous work in ultrasound-1–4 and magnetic resonance-based5–7 elastography, systems have been developed using optical coherence tomography (OCT) for three-dimensional imaging of propagating mechanical waves in subsurface regions of soft tissues, such as the eye and skin. As for all pulsed imaging methods, OCE spatial resolution is defined by the bandwidth of generated mechanical waves. Consequently, methods to excite broadband mechanical waves, especially noncontact approaches, are critical for OCE. Recently, we reported a noncontact, acoustic microtapping (AμT) method to launch compact (submillimeter) mechanical pulses propagating along the air-tissue interface that could be tracked in real-time with phase sensitive (PhS) OCT.8,9 This technology may enable practical, high-resolution OCE for many important biomedical applications, especially for those in the eye and skin.
Although initial OCE studies on eyes and skin are promising, true elasticity quantification has been severely limited by the bounded and layered nature of these tissues. In bounded media, mechanical waves traveling along the surface are no longer a simple Rayleigh mode but contain multiple highly dispersive Rayleigh-Lamb modes. Extracting the Young's modulus from complex modes is not simple, especially when the field of view is limited, as in the cornea. Furthermore, biological tissues such as the skin and cornea have complex geometries with variable material thickness over the propagation path. This complicates dispersion analysis and makes it difficult to obtain quantitative estimates of the true elastic properties with finite mechanical wave bandwidths.
In this paper, we demonstrate that supershear evanescent waves (SEWs), traveling along the surface of an elastic solid faster than the bulk shear wave speed (i.e., break the “surface wave speed limit”), can be experimentally measured in soft tissues. In addition, they can be efficiently generated with AμT and yield simple, direct, and very accurate estimates of the Young's modulus even in bounded media. In our study, we analyze the Green's function for a pulsed excitation to define SEW propagation speed and produce complementary numerical simulations and experiments in tissue-mimicking phantoms closely matching theoretical predictions. We also provide evidence of SEW propagation in ex vivo human cornea and in vivo human skin.
It has been shown theoretically that the SEW corresponds to a complex root of the Rayleigh equation (in addition to the real Rayleigh-wave root; see the supplementary S1) and represents a physical solution to certain elastodynamic problems, such as line source excitation.10,11 However, this root was almost forgotten and barely explored in the literature. Though the literature is sparse, the SEW has at various times been called a pseudo-P wave,10 leaky Rayleigh wave,12 nongeometric PS wave,13 leaky surface wave,11,14 and supershear Rayleigh wave.15 We use the term supershear evanescent wave (SEW) to emphasize its leaky behavior and supershear propagation speed, while still differentiating it from similar terms used to describe waves at a liquid-solid interface.16,17 The SEW is distinct from the “head wave,” also called a “lateral” wave. Head waves are plane waves originating from P-wave interactions with the free surface, rather than from the complex roots of the Rayleigh equation.11,18,19 A few studies14,15 concluded that SEW speed is roughly twice that of the bulk shear wave, but the analysis is complicated by conventional Rayleigh (or SAW) waves. SEWs may not separate until propagating some distance from their source, at which point their evanescent nature may make measurement difficult. A possible solution is to derive a dispersion relation for a mixed model of SAWs and SEWs.14 This approach can be difficult to interpret, as it combines the nondispersive SAW, the dispersive SEW, and near-field effects from the bulk shear wave.
We developed a finite element model of elastic wave propagation using OnScale (Onscale, Redwood City, CA, formerly PZFlex) to study SAW and SEW propagation in soft media and examine the effects of different excitation parameters (see the supplementary S2 for details). Briefly, we solve the two-dimensional (plane strain) elastic wave equations in a rectangular domain with a free surface on one side and absorbing boundaries on the other sides. The material is a nearly incompressible, linear elastic solid with shear wave speed and longitudinal wave speed . A pressure load is applied to the free surface with a Gaussian spatial distribution (full-width-at-half-maximum, = 500 μm) and super-Gaussian temporal distribution (varying full-width-at-half-maximum, ) chosen to approximate OCE experimental AμT parameters.8,9 In a separate set of simulations, we investigated SEW behavior in a bounded geometry by setting a small domain thickness and replacing the bottom absorbing boundary with a fluid layer.
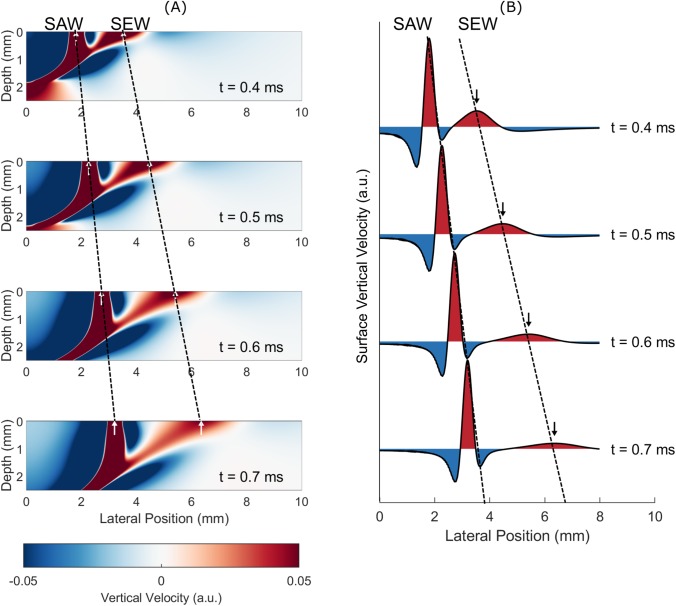
Figure 1(a) shows wave fields obtained from the finite element model at various times ( = 5 m/s). Both SEW and SAW are visible and clearly separate after 0.4 ms. The SAW propagates at a constant speed (as seen in Fig. 1), but the SEW signal local maximum also propagates with a constant speed, roughly twice as fast as the shear wave, and attenuates quickly due to leakage into the bulk. One-dimensional surface waveforms [Fig. 1(b)] better display this behavior. A full video of SEW and SAW propagation can be found in supplementary video 1. By tracking the SEW local maximum for different bulk shear wave speeds and excitation parameters, we confirmed that it propagates at a constant speed, approximately 1.954 .
FIG. 1.
(a) Simulated wave fields at various times show surface acoustic wave (SAW) and supershear evanescent wave (SEW) propagation. Simulation parameters are = 5 m/s, = 10 μs, and = 500 μm. The dynamic range has been adjusted to emphasize the SEW. (b) Surface waveforms at the same times show faster propagation and decaying amplitude of the SEW compared to those of the SAW.
To obtain the exact value of SEW propagation speed, the Green's function for a line force (infinite in the y-direction) impulsively applied normal to the surface of an isotropic, elastic half space (z ≥ 0) is derived using the Cagniard-de Hoop method.20,21 For lateral location , the SEW resides in the time interval between the arrival of the longitudinal wave and that of the shear wave . For , the vertical velocity component of the Green's function in this interval simplifies to (see supplementary S3)
| (1) |
where is the amplitude of the pressure load applied to the surface, is the material shear modulus, and .
Although the SEW is a dispersive nonstationary wave leaking energy inside the material, it has a constant propagation speed for both its minimum and maximum given by Eqs. (2) and (3), respectively (see the full derivation in supplementary S3)
| (2) |
| (3) |
This property, namely, the propagation speed of SEW local extrema, has not been addressed in the literature and has important practical implications. Indeed, we propose a simple method to quantify elasticity even in bounded media using this effect.
Thus, for an impulsive line source excitation on the surface of an elastic half space, a local maximum of the vertical velocity arrives at a given surface location before the arrival of the SAW. It propagates with a supershear velocity of approximately 1.9554 , extremely close to that obtained in the simulations.
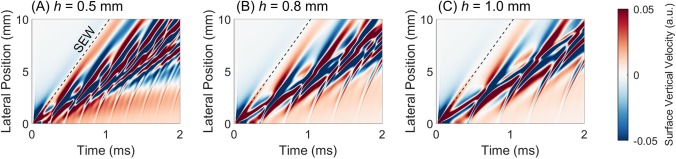
We also observed SEWs in simulations of bounded materials with thickness , provided the thickness was larger than the push width . In this case, the SEW appears as a near-field effect, and its speed can be estimated to give an estimate of the shear wave speed. For a push width of = 0.5 mm, we simulated guided wave propagation in bounded media with thicknesses = 0.5, 0.8, and 1.0 mm and estimated the SEW speed to be (1.95 ± 0.01), (1.98 ± 0.01), and (1.97 ± 0.01), respectively (Fig. 2). The bounded geometry seems to introduce a small amount of variability to the SEW speed but remains close to the theoretical value for semi-infinite media, 1.9554 .
FIG. 2.
Simulated guided wave XT plots for bounded media of various thicknesses = 0.5, 0.8, and 1.0 mm. The SEW (dashed line) is visible in the near-field, and its behavior closely matches the SEW in semi-infinite media.
We performed experimental studies of SEWs in semi-infinite and thin-layered tissue-mimicking phantoms, ex vivo human cornea, and in vivo human forearm skin. Phantoms were constructed using polyvinyl alcohol (PVA) cryogels with controllable mechanical and optical properties.22–24 Large phantoms (10 cm × 10 cm × 10 cm) approximated a semi-infinite medium. Thin-layered (0.5 mm thickness) ones approximated a medium bounded on one side by water and the other by air, such as the cornea. We varied PVA concentration (4, 8, or 12 wt. %) to control the stiffness and, therefore, the shear wave speed. A more detailed description is in supplementary S.4.
Broadband elastic waves were generated using AμT.8,9 The system utilizes a 1 MHz cylindrically focused, air-coupled ultrasound transducer to mechanically “push” the phantom surface without contact. The transducer produces a pseudoline source with a lateral width of approximately 0.5 mm and an elevational height of 9 mm (normal to the propagation plane). The lateral profile was nearly Gaussian. The AμT push lasted for = 100 or 200 μs. We tracked elastic waves with high-speed phase-sensitive OCT (PhS-OCT) operating in M-B mode.25–27 More system details are provided in supplementary S5.
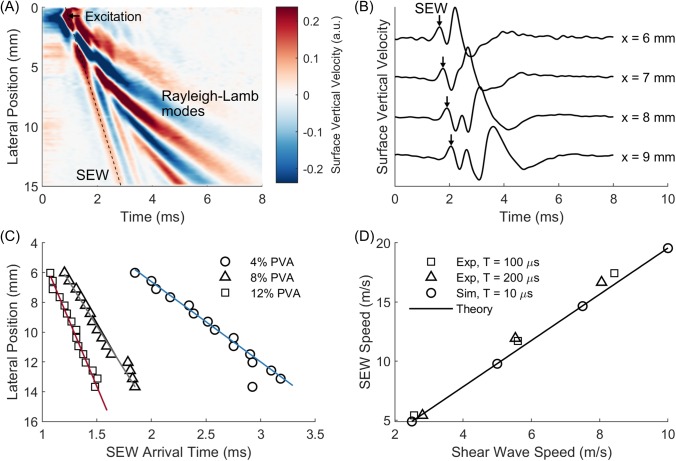
The same trends were observed in both bulk and thin-layered phantom experiments. For example, Fig. 3(a) shows surface velocity data for a 0.5 mm thick phantom ( = 3.8 m/s). Near the excitation, it is difficult to distinguish different modes. At 5–6 mm from this point, modes begin to separate, and the SEW can be distinguished from dispersive Rayleigh-Lamb modes. Past this point, the SEW clearly arrives before Rayleigh-Lamb modes, with amplitude decaying with the propagation distance. Extracting surface signals at discrete locations [Fig. 3(b)], the local SEW maximum can be identified and tracked across lateral positions to estimate its speed.
FIG. 3.
(a) Surface vertical velocity XT plot showing SEW arrival preceding Rayleigh-Lamb mode arrivals in a 0.5 mm thick PVA phantom ( = 3.8 m/s). The dynamic range has been adjusted to better visualize the SEW. (b) Corresponding surface vertical velocity waveforms at various lateral positions. (c) Linear fits of lateral position vs SEW arrival time in different bulk (semi-infinite) phantoms give SEW speeds for PVA concentrations of 4% (blue, circles, = 2.7 m/s, = 5.4 m/s), 8% (gray, triangles, = 5.6 m/s, = 11.7 m/s), and 12% (red, squares, = 8.2 m/s, = 17.4 m/s). (D) Simulation, experimental, and theoretical estimates of SEW speed in bulk media closely agree.
The repeating SEW-like reverberations following the arrival of the SEW may correspond to a separate type of supershear surface wave. As the SEW propagates along the surface, it leaks energy into plane shear waves in the bulk. For bounded media, these plane shear waves will reflect from the bottom boundary and propagate back toward the surface, where they can re-couple into a surface wave (see supplementary S6). This behavior was theoretically predicted by Schröder and Scott,11 though they did not propose a physical scenario in which it might occur.
For semi-infinite media, Rayleigh-Lamb modes do not develop, and a SAW propagates along the surface at speed slightly slower than the shear wave speed . For nearly incompressible materials, the ratio of these two wave speeds is ≈ 0.9553.25,28 By measuring the Rayleigh-wave group velocity in thick (approximately semi-infinite) phantoms, we obtained shear wave speeds of 2.69 ± 0.12 m/s, 5.57 ± 0.04 m/s, and 8.24 ± 0.19 m/s for PVA concentrations of 4%, 8%, and 12%, respectively [Figs. 3(c) and 3(d)].
As before, we identified and tracked the SEW local maximum, applying a linear fit to determine the propagation speed [Fig. 3(c)]. The results are summarized in Table I. SAW speed does not depend on the frequency in a linear elastic medium, but we note that the SEW's local maximum also propagates at a constant speed. Furthermore, its speed is very close to that provided by Eq. (3) for very different excitation conditions and material properties. Indeed, by applying the theoretical conversion of = 1.955 , we obtained shear wave speeds accurate to within 10% of the true value (see Table I). For higher accuracy, we quantified the effect of different excitation durations ( = 100 μs, 200 μs) on the SEW speed using our numerical model. For a 100 μs duration, the SEW propagated at 2.016 , while for a 200 μs excitation, it propagated at 2.051 . Applying these corrections, we obtained SEW speed estimates accurate to within 5% of the true bulk shear wave speed.
TABLE I.
Summary of measured shear wave speeds, SEW speeds, and SEW-based estimates of shear wave speed, with and without corrections for the excitation duration.
| %PVA | (m/s) | = 100 μs | = 200 μs | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (m/s) | %Error | %Error | (m/s) | %Error | %Error | ||||||
| 4 | 2.69 | 5.39 | 2.76 | 2.47 | 2.67 | 0.61 | 5.40 | 2.76 | 2.66 | 2.63 | 2.12 |
| 8 | 5.57 | 11.70 | 5.98 | 7.42 | 5.80 | 4.19 | 11.91 | 6.09 | 9.35 | 5.81 | 4.25 |
| 12 | 8.24 | 17.44 | 8.92 | 8.24 | 8.65 | 4.99 | 16.65 | 8.51 | 3.34 | 8.12 | 1.48 |
To explore SEW propagation in soft tissue, we performed OCE experiments in human cornea ex vivo and in human skin in vivo. A human cornea sample (26 year-old male) was secured via the Utah Lion's Eye Bank in Murray, UT, and kept in Optisol (Chiron Ophthalmics, Irvine, California, USA) solution for 4 days post mortem prior to imaging. It was mounted to an artificial anterior chamber filled to physiological pressure with balanced saline solution (BSS, Alcon, Johns Creek, GA). For human forearm skin measurements, a healthy 30 year-old volunteer was recruited using the human subject protocol provided in supplementary S7.
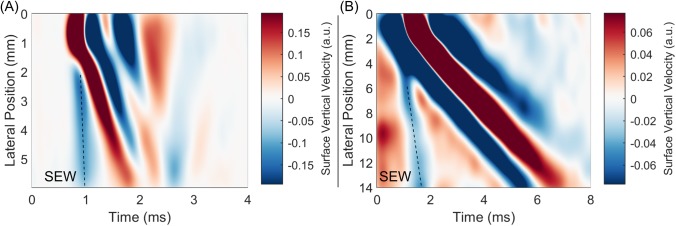
We observed SEWs in both ex vivo human cornea [Fig. 4(a)] and in vivo human forearm skin [Fig. 4(b)]. Here, the SEW's main energy is contained in a local minimum instead of a local maximum. We believe these changes are induced by anisotropy in these tissues. Because of the complex mode structure in anisotropic media, the correct relationship between SEW and bulk shear wave speeds is not entirely clear. We will examine this further in future studies. Nevertheless, it appears that the SEW exists in anisotropic, layered media as well and also travels many times faster than the bulk shear wave.
FIG. 4.
Surface vertical velocity XT plots showing SEW propagation in (a) ex vivo human cornea and (b) human forearm skin in vivo. The dynamic range has been adjusted independently to better visualize the SEW in each case.
Here, we observed supershear evanescent waves (SEWs) propagating along the surface of nearly incompressible materials – specifically, PVA phantoms, human cornea, and human skin. The relationship between the measured SEW and shear wave speeds in both numerical simulations and OCE experiments closely matched theoretical predictions in isotropic phantoms based on the Green's function. Consequently, the measured SEW speed can be used to accurately estimate the bulk shear wave speed and finally to calculate Young's modulus
| (4) |
We propose SEW tracking as a robust method to estimate the elasticity of nearly incompressible materials such as biological tissue. In certain applications, SEW speed measurements may provide more reliable estimates of shear wave speed than commonly used methods such as group velocity estimation.9,25,29–36 For example, in bounded media, Rayleigh-Lamb modes yield group velocity estimates far from bulk shear wave speeds.37,38 Dispersion analysis is required to estimate the true shear wave speed. This carries its own limitations, as both the elastic wave bandwidth and imaging field-of-view affect the accuracy of shear wave speed estimates.39 Additionally, biological tissues such as the skin and cornea have complex geometries with a variable material thickness over the propagation path. This complicates dispersion analysis and makes it difficult to obtain quantitative estimates of true elastic properties with finite mechanical wave bandwidths. In contrast, if the OCE system has sufficient bandwidth to detect the SEW, then the elastic modulus can be quantitatively estimated independent of geometric complications such as variable material thickness. This is a significant advantage for quantitative elastography.
One potential concern of SEW-based estimates of tissue elasticity is the exact relationship between the shear and SEW waves for different biological tissues. In the experiments presented here in human tissues, we observed very fast propagating SEWs in both cornea and skin, which may be driven by the anisotropic elastic properties of these tissues.40–42 Thus, we do not provide here quantitative estimates of Young's modulus in the cornea and skin using SEW speed estimates. We are currently investigating SEW behavior in anisotropic media and will extend this study to such media in near-future publications.
See the supplementary material for derivations for the supershear evanescent wave (SEW) properties based on plane wave expansions and the elastodynamic Green's function, details on the finite element models described in this letter, and details on the tissue-mimicking phantoms, optical coherence elastography system, and human study protocols used to experimentally investigate SEW propagation. Also included are video files showing the simulated propagation of the SAW and SEW in a semi-infinite medium and simulated propagation of guided modes and re-coupling of SEWs to surface waves in a bounded medium.
Acknowledgments
The authors wish to thank Antoine Ramier for helpful discussions. This work was supported, in part, by NIH Nos. R01EY026532, R01EY024158, R01EB016034, R01CA170734, and R01HL093140, Life Sciences Discovery Fund 3292512, the Coulter Translational Research Partnership Program, an unrestricted grant from the Research to Prevent Blindness, Inc., New York, New York, and the Department of Bioengineering at the University of Washington. M. Kirby was supported by NSF graduate fellowship (No. DGE-1256082). This material was based upon the work supported by the National Science Foundation Graduate Research Fellowship Program under Grant No. DGE-1256082. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the funders.
References
- 1. Sarvazyan A. P., Rudenko O. V., Swanson S. D., Fowlkes J. B., and Emelianov S. Y., “ Shear wave elasticity imaging: a new ultrasonic technology of medical diagnostics,” Ultra. Med. Biol. 24(9), 1419–1435 (1998). 10.1016/S0301-5629(98)00110-0 [DOI] [PubMed] [Google Scholar]
- 2. Sandrin L., Tanter M., Catheline S., and Fink M., “ Shear modulus imaging with 2-D transient elastography,” IEEE Trans. UFFC 49(4), 426–435 (2002). 10.1109/58.996560 [DOI] [PubMed] [Google Scholar]
- 3. Nightingale K., McAleavey S., and Trahey G., “ Shear-wave generation using acoustic radiation force: in vivo and ex vivo results,” Ultra. Med. Biol. 29(12), 1715–1723 (2003). 10.1016/j.ultrasmedbio.2003.08.008 [DOI] [PubMed] [Google Scholar]
- 4. Bercoff J., Tanter M., and Fink M., “ Supersonic shear imaging: a new technique for soft tissue elasticity mapping,” IEEE Trans. UFFC 51(4), 396–409 (2004). 10.1109/TUFFC.2004.1295425 [DOI] [PubMed] [Google Scholar]
- 5. Muthupillai R., Lomas D. J., Rossman P. J., Greenleaf J. F., Manduca A., and Ehman R. L., “ Magnetic resonance elastography by direct visualization of propagating acoustic strain waves,” Science 269(5232), 1854–1857 (1995). 10.1126/science.7569924 [DOI] [PubMed] [Google Scholar]
- 6. Manduca A., Oliphant T. E., Dresner M. A., Mahowald J. L., Kruse S. A., Amromin E., Felmlee J. P., Greenleaf J. F., and Ehman R. L., “ Magnetic resonance elastography: non-invasive mapping of tissue elasticity,” Med. Image Anal. 5, 237–254 (2001). 10.1016/S1361-8415(00)00039-6 [DOI] [PubMed] [Google Scholar]
- 7. Mariappan Y. K., Glaser K. J., and Ehman R. L., “ Magnetic resonance elastography: a review,” Clinic. Anat. 23, 497–511 (2010). 10.1002/ca.21006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Ambroziński L., Pelivanov I., Song S., Yoon S. J., Li D., Gao L., Shen T. T., Wang R. K., and O'Donnell M., “ Air-coupled acoustic radiation force for non-contact generation of broadband mechanical waves in soft media,” Appl. Phys. Lett. 109, 043701 (2016). 10.1063/1.4959827 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Ambroziński L., Song S., Yoon S. J., Pelivanov I., Li D., Gao L., Shen T. T., Wang R. K., and O'Donnell M., “ Acoustic micro-tapping for non-contact 4D imaging of tissue elasticity,” Sci. Rep. 6, 38967 (2016). 10.1038/srep38967 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Phinney R. A., “ Propagation of leaking interface waves,” Bull. Seismol. Soc. Am. 51(4), 527–555 (1961). [Google Scholar]
- 11. Schröder C. T. and W. R. Scott, Jr. “ On the complex conjugate roots of the Rayleigh equation: The leaky surface wave,” J. Acoust. Soc. Am. 110(6), 2867–2877 (2001). 10.1121/1.1419085 [DOI] [PubMed] [Google Scholar]
- 12. Gusev V., Desmet C., Lauriks W., Glorieux C., and Thoen J., “ Theory of Scholte, leaky Rayleigh, and lateral wave excitation via the laser-induced thermoelastic effect,” J. Acoust. Soc. Am. 100(3), 1514–1528 (1996). 10.1121/1.416021 [DOI] [Google Scholar]
- 13. Roth M. and Holliger K., “ The non-geometric PS wave in high-resolution seismic data: observations and modelling,” Geophys. J. Int. 140, F5–F11 (2000). 10.1046/j.1365-246x.2000.00030.x [DOI] [Google Scholar]
- 14. Benech N., Brum J., Grinspan G., Aguiar S., and Negreira C. A., “ Analysis of the transient surface wave propagation in soft-solid elastic plates,” J. Acoust. Soc. Am. 142, 2919–2932 (2017). 10.1121/1.4993633 [DOI] [PubMed] [Google Scholar]
- 15. Le Goff A., Cobelli P., and Lagubeau G., “ Supershear Rayleigh waves at a soft interface,” Phys. Rev. Let. 110, 236101 (2013). 10.1103/PhysRevLett.110.236101 [DOI] [PubMed] [Google Scholar]
- 16. Scruby C. B. and Drain L. E., Laser Ultrasonics, Techniques and Applications ( Taylor & Francis Group, New York, 1990). [Google Scholar]
- 17. Rose J. L., Ultrasonic Waves in Solid Media ( Cambridge University Press, New York, 1999). [Google Scholar]
- 18. Graff K. F., Wave Motion in Elastic Solids ( Dover Publications, New York, 1991). [Google Scholar]
- 19. Sherwood J. W. C., “ Elastic wave propagation in a semi-infinite solid medium,” Proc. Phys. Soc. 71, 207–219 (1958). 10.1088/0370-1328/71/2/308 [DOI] [Google Scholar]
- 20. de Hoop A. T., “ The surface line source problem in elastodynamics,” De Ingenieur, Electronica en Telecommunicatie, ET19-ET21, 1970.
- 21. Kausel E., Fundamental Solutions in Elastodynamics, a Compendium ( Cambridge University Press, New York, 2006). [Google Scholar]
- 22. Hyon S. H., Cha W. I., and Ikada Y., “ Preparation of transparent poly(vinyl alcohol) hydrogel,” Polym. Bull. 22(2), 119–122 (1989). 10.1007/BF00255200 [DOI] [Google Scholar]
- 23. Kirby M. A., Zhou K., Gao L., Pelivanov I. M., Li C., Huang Z., Shen T. T., Wang R. K., and O'Donnell M., “ Lateral mechanical resolution in dynamic optical coherence elastography (OCE),” presented at SPIE Photonics West BIOS, San Francisco, CA, 1–6 February 2019.
- 24. Kirby M. A., Zhou K., J. J. Pitre, Jr. , Gao L., Li D., Pelivanov I., Song S., Li C., Huang Z., Shen T., Wang R., and O'Donnell M., “ Spatial resolution in dynamic coherence elastography” (unpublished). [DOI] [PMC free article] [PubMed]
- 25. Kirby M. A., Pelivanov I., Song S., Ambrozinski L., Yoon S. J., Gao L., Li D., Shen T. T., Wang R. K., and O'Donnell M., “ Optical coherence elastography in ophthalmology,” J. Biomed. Opt. 22(12), 121720 (2017). 10.1117/1.JBO.22.12.121720 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Wang R. K. and Nuttall A. L., “ Phase-sensitive optical coherence tomography imaging of the tissue motion with in the organ of Corti at a subnanometer scale: A preliminary study,” J. Biomed. Opt. 15, 056005 (2010). 10.1117/1.3486543 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Song S., Huang Z., and Wang R. K., “ Tracking mechanical wave propagation within tissue using phase-sensitive optical coherence tomography: motion artifact and its compensation,” J. Biomed. Opt. 18(12), 121505 (2013). 10.1117/1.JBO.18.12.121505 [DOI] [PubMed] [Google Scholar]
- 28. Viktorov I. A., Rayleigh and Lamb Waves: Physical Theory and Applications ( Springer, New York, 1967). [Google Scholar]
- 29. Wang S. and Larin K. V., “ Optical coherence elastography for tissue characterization: A review,” J. Biophotonics 8, 279–302 (2015). 10.1002/jbio.201400108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Song S., Huang Z., Nguyen T. M., Wong E. Y., Arnal B., O'Donnell M., and Wang R. K., “ Shear modulus imaging by direct visualization of propagating shear waves with phase-sensitive optical coherence tomography,” J. Biomed. Opt. 18, 121509 (2013). 10.1117/1.JBO.18.12.121509 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Larin K. V. and Sampson D., “ Optical coherence elastography—OCT at work in tissue biomechanics,” Biomed. Opt. Express. 8, 1172–1202 (2017). 10.1364/BOE.8.001172 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Han Z., Li J., Singh M., Wu C., Liu C. H., Wang S., Idugboe R., Raghunathan R., Sudheendran N., Aglyamov S. R., Twa M. D., and Larin K. V., “ Quantitative methods for reconstructing tissue biomechanical properties in optical coherence elastography: a comparison study,” Phys. Med. Biol. 60, 3531–3547 (2015). 10.1088/0031-9155/60/9/3531 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Li C. H., Guan G., Cheng X., Huang Z., and Wang R. K., “ Quantitative elastography provided by surface acoustic waves measured by phase-sensitive optical coherence tomography,” Opt. Lett. 37, 722–724 (2012). 10.1364/OL.37.000722 [DOI] [PubMed] [Google Scholar]
- 34. Wang S., Lopez A. L. III, Morikawa Y., Tao G., Li J., Larina I. V., Martin J. F., and Larin K. V., “ Noncontact quantitative biomechanical characterization of cardiac muscle using shear wave imaging optical coherence tomography,” Biomed. Opt. Express. 5, 1980–1992 (2014). 10.1364/BOE.5.001980 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Zhu J., Qi L., Miao Y., Ma T., Dai C., Qu Y., He Y., Gao Y., Zhou Q., and Chen Z., “ 3D mapping of elastic modulus using shear wave optical micro-elastography,” Sci. Rep. 6, 35499 (2016). 10.1038/srep35499 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Zhu J., Miao Y., Qi L., Qu Y., He Y., Yang Q., and Chen Z., “ Longitudinal shear wave imaging for elasticity mapping using optical coherence elastography,” Appl. Phys. Lett. 110, 201101 (2017). 10.1063/1.4983292 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Pelivanov I., Gao L., J. J. Pitre, Jr. , Kirby M. A., Song S., Li D., Shen T., Wang R., and O'Donnell M., “ Does group velocity always reflect elastic modulus in shear wave elastography?,” J. Biomed. Opt. 24(7), 076003 (2019). 10.1117/1.JBO.24.7.076003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Gao L., Kirby M. A., Song S., Pelivanov I. M., Shen T. T., Wang R. K., and O'Donnell M., “ Evaluation of tissue elasticity using spectral characteristics of AμT generated mechanical waves,” presented at SPIE Photonics West BIOS, San Francisco, CA, 1–6 February 2019.
- 39. Gao L., Kirby M. A., Ambroziński L., Song S., Li D., Pelivanov I., Wang R., and O'Donnell M., “ Dispersion analysis of guided waves in bounded media induced by acoustic micro-tapping,” in Proceeding of the IEEE International Ultrasound Symposium October 2018. Kobe, Japan. Conference Presentation. [Google Scholar]
- 40. Benoit A., Latour G., Schanne-Klein M.-C., and Allain J.-M., “ Simultaneous microstructural and mechanical characterization of human corneas at increasing pressure,” J. Mech. Behavior Biomed. Mater. 60, 93–105 (2016). 10.1016/j.jmbbm.2015.12.031 [DOI] [PubMed] [Google Scholar]
- 41. Nguyen T.-M., Aubry J.-F., Fink M., Bercoff J., and Tanter M., “ In vivo evidence of porcine cornea anisotropy using supersonic shear wave imaging,” Invest. Ophthalmol. Vis. Sci. 55, 7545–7552 (2014). 10.1167/iovs.14-15127 [DOI] [PubMed] [Google Scholar]
- 42. Joodaki H. and Panzer M. B., “ Skin mechanical properties and modeling: a review,” Proc. Inst. Mech. Eng., Part H 232(4), 323–343 (2018). 10.1177/0954411918759801 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
See the supplementary material for derivations for the supershear evanescent wave (SEW) properties based on plane wave expansions and the elastodynamic Green's function, details on the finite element models described in this letter, and details on the tissue-mimicking phantoms, optical coherence elastography system, and human study protocols used to experimentally investigate SEW propagation. Also included are video files showing the simulated propagation of the SAW and SEW in a semi-infinite medium and simulated propagation of guided modes and re-coupling of SEWs to surface waves in a bounded medium.