Abstract
Use of the auditory brainstem response (ABR) in research has increased in the search for physiological correlates of noise-induced damage to the cochlea. The extraction of data from the ABR has traditionally relied on visual determination of peaks and troughs to calculate metrics such as wave amplitude. Visual determination can be reliable when evaluated by trained, experienced personnel, but noisy waveforms and overlapping waves produce uncertain data. The present study proposes and validates a method of fitting summed Gaussian functions to the summating potential and wave I of the ABR. This method could be useful to the research community studying these potentials by providing more accurate measures of wave amplitude than by visual determination.
I. INTRODUCTION
The auditory brainstem response (ABR) represents electrical activity generated by the peripheral auditory nerve and auditory brainstem. The ABR can be recorded reliably from far field electrodes on the face and scalp, making it a useful tool for both clinical and research purposes. The ABR consists of a series of waves within 10 ms following an acoustic stimulus, the most prominent of which in humans are waves I, III, and V (Boston and Møller, 1985). Latencies and amplitudes of these waves have been correlated with several pathologies such as decreased auditory sensitivity and tumors on the auditory nerve and brainstem. Wave I is of particular interest, as it represents the peripheral auditory nerve (Britt and Rossi, 1980). Interest in wave I has surged recently as a measure of synaptopathy, the decoupling of the auditory nerve from the sensory hair cells. Incidentally, hair cell electrical activity can also be recorded proximal to wave I latencies, typically used in the diagnosis of auditory neuropathy (Stuermer et al., 2015) and Meniere's disease (Ferraro, 2010). Both alternating current (AC) and direct current (DC) components of hair cell membrane potentials coincide with wave I, which may be relevant in the diagnosis of synaptopathy. For example, the reflection of current flow through hair cells, called the cochlear microphonic (CM), is an AC response that follows the stimulus frequency and duration. A summed DC component, known as the summating potential (SP), also manifests in ABR recordings. Liberman et al. (2016) observed changes in the relationship between the SP and wave I in young adults with a history of noise exposure.
Extraction of data from auditory evoked potentials such as the ABR has typically relied on visual determination of peaks and troughs in the waveform. This allows for the calculation of wave amplitude and peak latencies but inherently injects human error into ABR evaluations. To mitigate this error, most studies employ multiple experts to identify wave features. However, disagreements between experts are common, leading to uncertainty in the data (Arnold, 1985).
A number of methods have been proposed to automate this process. The majority of these applications focus on detecting a response (e.g., Bogaerts et al., 2009; Bradley and Wilson, 2004; Cabana-Pérez et al., 2017; Kostorz et al., 2013; Pratt et al., 1989; Rushaidin et al., 2009; Rushaidin et al., 2012). While response detection is useful for measuring hearing sensitivity, most of these methods do not estimate wave amplitude. Some algorithms have been developed to find local maxima within predetermined latency constraints for peaks and either minima in the waveforms or time derivatives of the waveforms for troughs. Such algorithms can calculate amplitude but can be less reliable than visual determination in noisy waveforms (Arnold, 1985) or when evoked potentials overlap in time, such as the SP and wave I, or waves V and VI of the ABR. Modeling waveform morphology is a lesser-used approach (Elberling, 1979) but one that could provide more information than algorithms that mimic the visual-determination process or that merely detect the presence of a response. Chertoff (2004) developed an equation modeling the morphology of the compound action potential (also wave I of the ABR) by summing the post-stimulus time histograms of single auditory nerve fibers. Temporary hearing loss in humans could be modeled by altering components of the equation, providing insight into the pathophysiology underlying temporary noise-induced hearing loss (Lichtenhan and Chertoff, 2008).
Two Gaussian-like models have been proposed to fit peaks of the ABR. Valderrama et al. (2014) used a Mexican hat wavelet, the second derivative of the Gaussian function, to fit waves III and V of the ABR in eight normal hearing subjects. Latencies and amplitudes estimated by the model were comparable to metrics estimated by visual-determination, suggesting the usefulness of a Gaussian-like model in the extraction of ABR data. Similarly, Morawski et al. (2019) proposed summing two Gaussian functions to estimate metrics of the SP and action potential (analogous to wave I) of the electrocochleogram (ECochG) in order to calculate the amplitude and area ratios for the diagnosis of Meniere's disease.
In this study, we assess the use of a summed-Gaussian model for estimating the morphology and parameters of the SP and wave I of the ABR. The first experiment focuses on the feasibility of the model by testing it on ABR data recorded from adult humans. Metrics of latency and amplitude of the SP and wave I estimated by the model were compared to metrics determined visually by two experienced audiologists. The second experiment focuses on the validity of the model using a parameter-recovery experiment on simulated ABR data.
II. MODEL
The ABR waveform amplitude as a function of time was modeled by summing two Gaussian functions
where the first function models the SP and the second models wave I. t is post-stimulus time (ms), A is the peak-to-peak amplitude of the SP (subscript 1) and wave I (subscript 2), L is peak latency (ms), and W is the width (ms). A nonlinear regression analysis estimated six parameters. Initial values and boundary conditions (Table I) were set for the parameters to speed estimation and convergence of the algorithm and ensure accurate wave identification. Boundary conditions for latency (L) were chosen based on the latency ranges found in the literature and instructions given to human observers in typical clinical paradigms for choosing response peaks (Ferraro and Durrant, 1994).
TABLE I.
Bound constraints. A: estimates peak-to-trough or peak-to-baseline amplitude; L: estimates peak latency; W: estimates peak width.
| Initial | Lower | Upper | |
|---|---|---|---|
| Value | Bound | Bound | |
| A1 (μV) | 0.75 | 0 | ∞ |
| L1 (ms) | 1.5 | 0 | 2 |
| W1 (ms) | 0.3 | 0 | 0.7 |
| A2 (μV) | 1 | 0 | ∞ |
| L2 (ms) | 2.75 | 2 | 3.5 |
| W2 (ms) | 0.2 | 0 | 0.7 |
III. EXPERIMENT 1: PROOF OF CONCEPT
A. Methods
The model was tested on ABR data from 32 adults, previously published by Ridley et al. (2018). Twelve participants [6 female; mean age = 31, standard deviation (SD) = 8.5, range = 23–48 years] had normal hearing. Twenty participants (10 female; mean age = 49, SD = 7, range = 35–64 years) had sensorineural hearing loss. All participants were assessed using standard audiometric procedures and tympanometry, as described in Ridley et al. (2018). All procedures were approved by the Institutional Review Board of the Boys Town National Research Hospital. All participants provided informed consent. Participants were paid for their participation.
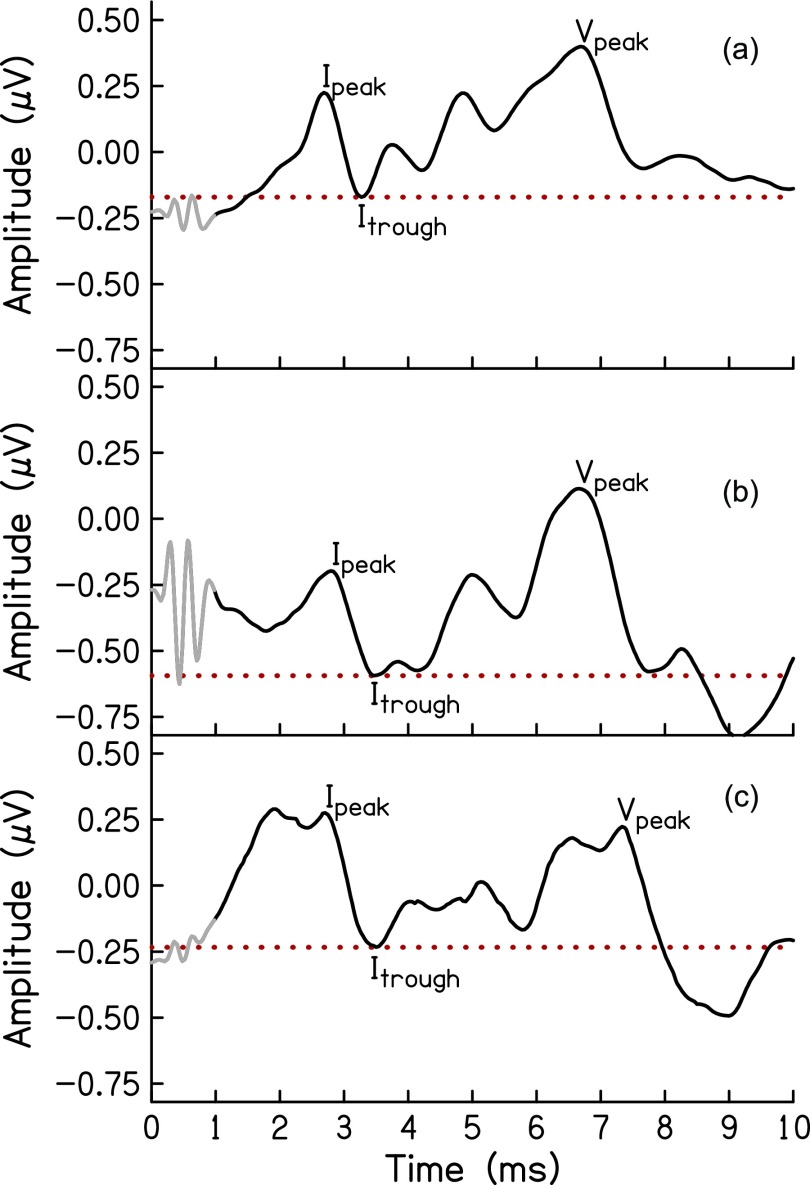
ABR was recorded using custom-designed software [Cochlear Response (CResp) version 1.0; Boys Town National Research Hospital, Omaha, NE] on a computer equipped with a 24-bit soundcard (Babyface; RME, Germany). Electroencephalographic (EEG) responses were acquired using surface electrodes placed at the forehead (Fpz, ground), vertex (Cz, noninverting active), and an inverting reference electrode placed in the ear canal (ER3–26A gold foil tiptrodes). The stimulus was a 1-ms, Blackman-gated pure-tone at 4 kHz presented in alternating polarity monaurally at a rate of 27/s to an ER-3A insert earphone (Etymotic Research, Elk Grove, IL) connected to the soundcard. The stimulus level was 100 dB peak-equivalent sound pressure level (peSPL). Calibration of the stimulus levels was done using a sound level meter (System 824 and SoundTrack LxT1; Larson Davis, Provo, UT) with the ER-3A connected to the sound level meter via a 2 cc coupler (G.R.A.S. 60 126, Denmark). Electrode impedances were ≤5 kΩ in all cases. The EEG signal was amplified (gain = 100 000), filtered (from 0.1 to 1.5 kHz; Opti-Amp 8001; Intelligent Hearing Systems, Miami, FL), filtered for line interference using a 60 Hz notch filter and directed to the computer via the soundcard for averaging. Responses were separated by even and odd recordings and stored in two buffers, which were averaged for the final waveform (total averages = 8000 artifact-free responses). Two examiners independently identified peaks and troughs of the SP and wave I of the response. The software allowed for a resolution of 0.02 μV for amplitude and 0.02 ms for latency. Wave I amplitude was calculated as the difference between the positive peak and the following trough. The amplitude of the SP was calculated from the baseline—or midpoint of the alternating current signal resulting from stimulus artifact or cochlear microphonic (Chertoff et al., 2012)—to the peak or shoulder preceding wave I. Latencies were used to clarify disagreements between examiners. The processing delay of the soundcard was taken into account when analyzing the data for latency. Disagreements >0.02 ms were resolved by a third expert examiner. Figure 1 presents example ABR waveforms from one participant with normal hearing [Fig. 1(a)] and two participants with hearing loss [Figs. 1(c) and 1(d)].
FIG. 1.
ABR waveforms of three participants. Stimulus artifact (grey) is present in the waveform until approximately1 ms post-stimulus time. To model wave I of the ABR, amplitudes were centered around the wave I trough (red dotted line), then the resulting waveform was time-windowed from 1 to 3.5 ms.
B. Statistical analyses
We took two approaches to assess the performance of the model. The first was to measure the model fit to the data in the time-domain. The ABR was windowed from 1 to 3.5 ms post-stimulus time (PST) to exclude the stimulus artifact (Fig. 1, gray) and later-latency waves. The data were then centered around the amplitude of the wave I trough (Fig. 1, dotted line). This resulted in a waveform with a positive average amplitude and reduced the need to include a constant variable in the model. Absolute agreement between the estimated Gaussian model and data for each participant are reported as intraclass correlation coefficients (ICC). The strength of the agreement of each measure was categorized such that ICC values 0.9 ≤ ICC < 1.0 were considered in excellent agreement; 0.75 ≤ ICC < 0.9 were considered good; 0.5 ≤ ICC < 0.75 were considered moderate; and 0 ≤ ICC < 0.5 were considered in poor agreement (Koo and Li, 2016). An additional measure of model fit in the time-domain is the root-mean-square error of the residuals normalized to the maximum amplitude of the waveform (nRMSE).
The second approach to assess model performance compared the model-estimated metrics with metrics visually-determined by expert audiologists and reported in Ridley et al. (2018). ICC was used again as a measure of criterion-referenced reliability between the model-estimation and visual-estimation. Small between-subject variance can cause ICC to take on a negative value, even if there is small within-subject variance. Negative ICC values are theoretically impossible (Giraudeau, 1996), thus negative values were changed to zero and the only interpretation was that the two methods of estimation were not in agreement.
C. Results
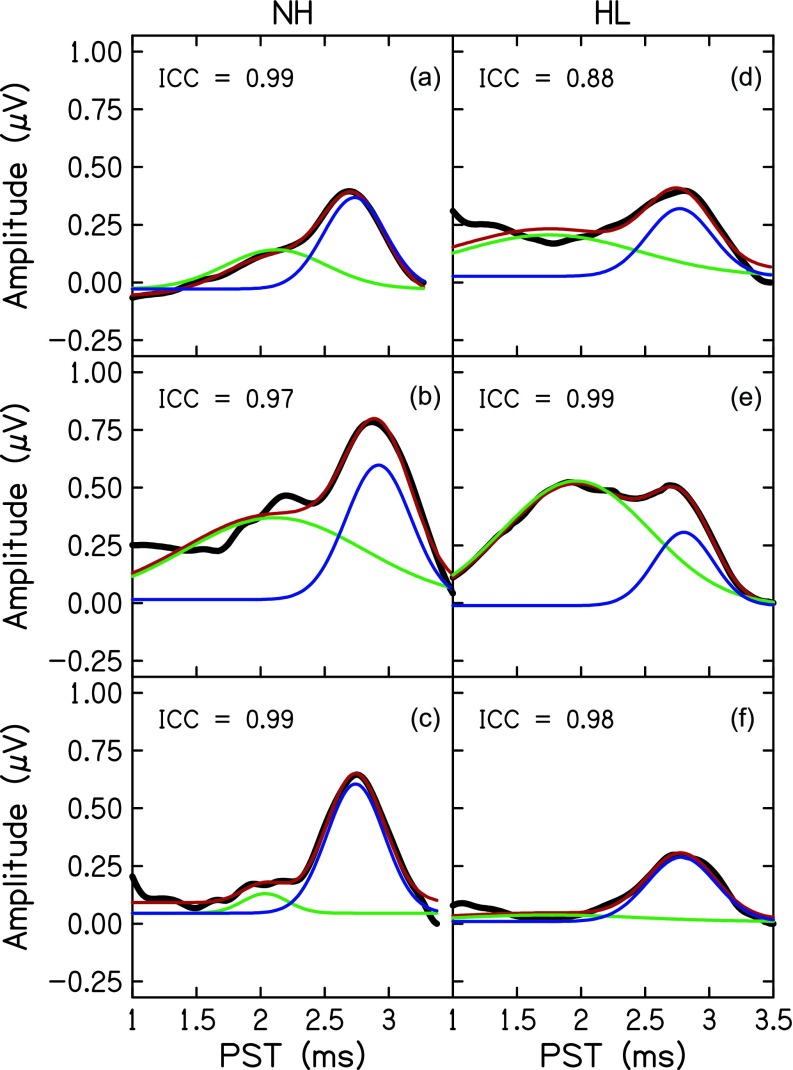
Figure 2 plots the ABR wave I of six of the 32 participants (black) and the estimated Gaussian model (red). The range of intraclass correlations between the modeled waveform and participant data was ICC = 0.88 [Fig. 2(d)] to ICC = 0.99 [Figs. 2(a) and 2(f)], with a mean of ICC = 0.97 (n = 32) and SD of 0.03. The range of nRMSE was 0.012–0.112 μV with a mean nRMSE = 0.055 μV and SD of 0.025 μV.
FIG. 2.
ABR waveforms of six participants (black) with normal audiometric thresholds (a)–(c) and hearing loss (d)–(f). The Gaussian model (red) is comprised of an SP (green) and wave I (blue).
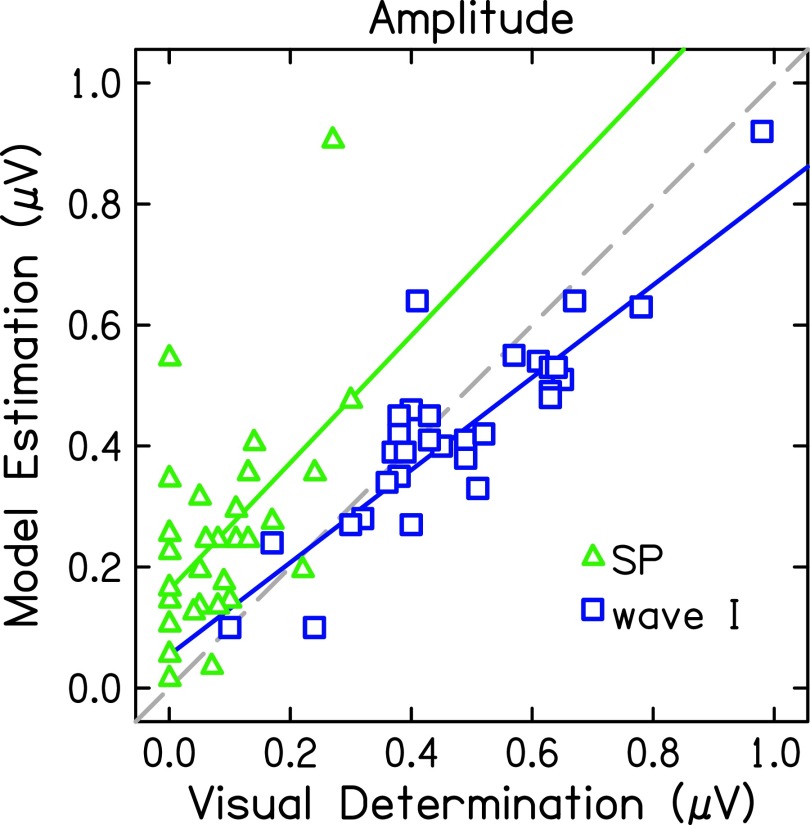
Agreement between the model and visual-determination was different for estimated SP and wave I metrics (Table II). The agreement was excellent for wave I latency (ICC = 0.97, p < 0.001), suggesting that the experts and model chose the same peak. Consequently, wave I amplitude was also in good agreement (ICC = 0.88, p < 0.001). SP latency data from the Ridley et al. (2018) study was not available but modeled and visually-determined SP amplitudes were in poor agreement (ICC = 0.24, p = 0.104). Amplitudes determined visually and by the model for each participant's data are plotted in Fig. 3. There were ten (of 32) ABR waveforms for which the experts did not visually identify an SP, plotted as 0 μV on the x-axis. Conversely, the Gaussian model assumes an SP exists and will fit a function to the waveform. Therefore, the Gaussian model estimated positive SP amplitude values in all 32 participants, though two SP values were 0.01 [Fig. 2(f)] and 0.06 μV. Interestingly, if these ten data points are removed, the ICC only increases to 0.30 (p = 0.093), which is still considered in poor agreement. The slopes of the correlations between the model and visually-determined amplitudes (Fig. 3, solid lines) indicate that the model consistently estimated larger SP amplitudes and smaller wave I amplitudes than the experts.
TABLE II.
Absolute agreement between model and expert determination.
| 95% CI | F Test | |||||||
|---|---|---|---|---|---|---|---|---|
| ICC | Lower | Upper | Value | df1 | df2 | p | ||
| SP | Amplitude | 0.24 | 0 | 0.56 | 2.64 | 31 | 6.40 | 0.104 |
| Amp. if > 0 | 0.30 | 0 | 0.64 | 3.01 | 21 | 5.76 | 0.093 | |
| wave I | Amplitude | 0.88 | 0.70 | 0.94 | 19.14 | 31 | 14.11 | <0.001 |
| Latency | 0.97 | 0.93 | 0.98 | 58.58 | 31 | 31.89 | <0.001 | |
FIG. 3.
Amplitudes determined by visual estimation of peaks and troughs compared to amplitudes determined by nonlinear estimation of Gaussian functions for SP (green triangles) and wave I (blue squares). The dashed line indicates a unit slope.
IV. EXPERIMENT 2: VALIDITY
The results of Experiment 1 indicated agreement between the model and visual-determination was excellent for wave I amplitudes, but poor for SP amplitudes. Disagreement typically occurred on waveforms that were noisy or otherwise difficult to visually determine peaks. Since the actual values of SP amplitude are unknown in these waveforms, it is impossible to determine whether the model or expert is truly correct. Therefore, we assessed the validity of the model and experts using a parameter-recovery experiment in which ABR wave I data were simulated and presented to the model and expert for determination of metrics.
A. Methods
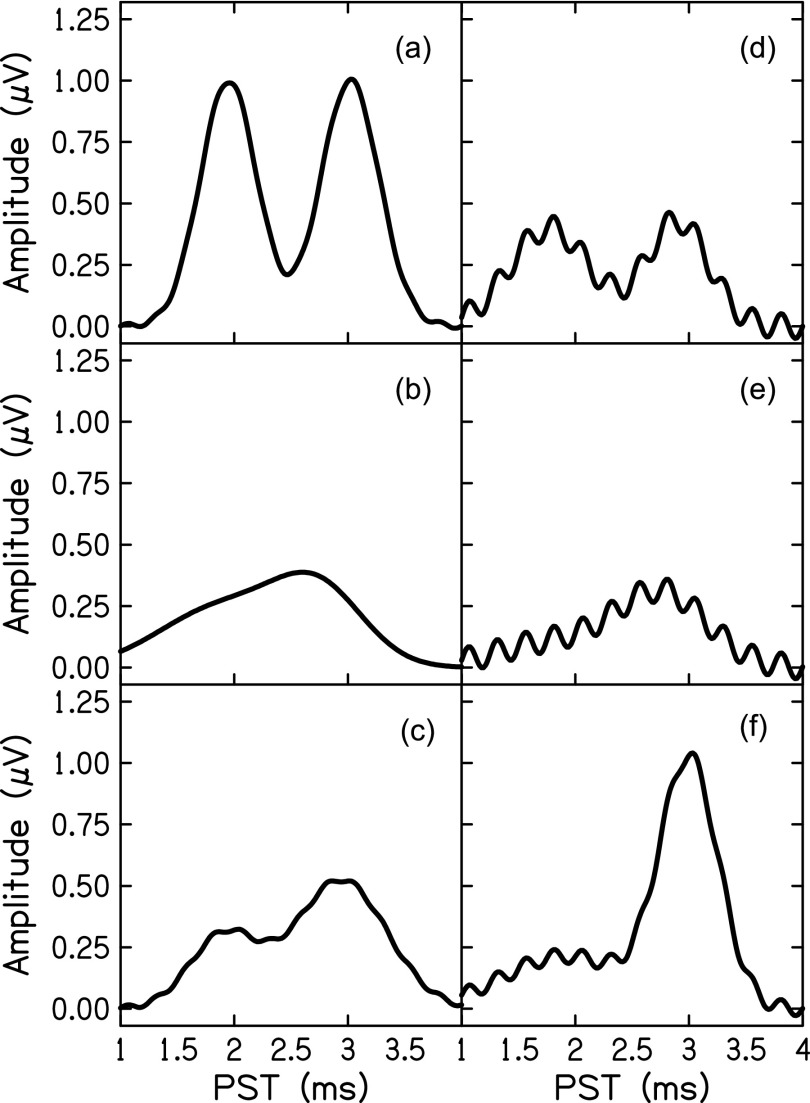
Thirty-two ABR waveforms were simulated using a summed-Gaussian model and inputting pseudorandom values for each parameter. Parameter values were determined, independently, by randomly sampling from the distribution of values estimated by the model in Experiment 1. To mimic residual traces of cochlear microphonic or stimulus artifact typically found in real data, a sinusoid at the frequency of the stimulus (4 kHz) was added to the SP and wave I components. The amount of 4 kHz noise was determined at random but not to exceed 0.05 μV. Figure 4 presents several examples of simulated ABR wave I data. These waveforms were provided to the model and to two experts who independently identified troughs and peaks in the same manner as the real ABR waveform data described above. SP amplitude was calculated as the difference in amplitude between the baseline (time = 1 ms) to the SP peak. Wave I amplitude was calculated as the difference between the identified wave I peak and the following trough. The two experts were given the latency boundaries used for the simulated data as guidelines to identify SP and wave I peaks. For ease of visual-determination, each figure with a waveform was scalable to the experts' preferences, as was the case for Experiment 1.
FIG. 4.
Examples of six simulated ABR waveforms.
ICC was used again as a measure of agreement between the true parameters, i.e., those supplied to the simulation, and the metrics estimated by the model and visual determination.
B. Results
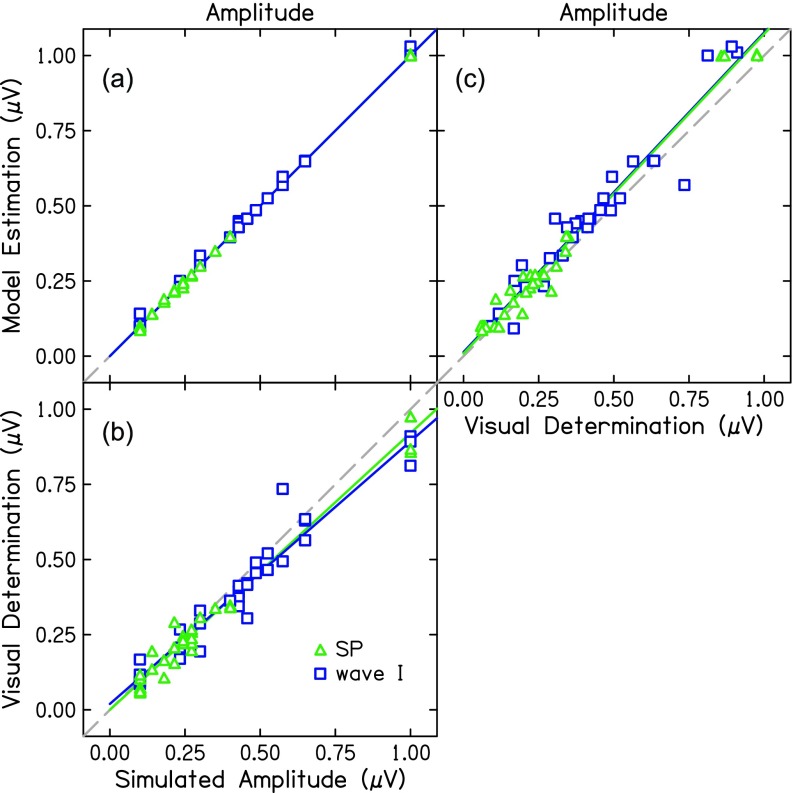
The model recovered the wave I metrics of amplitude, latency, and width near-perfectly [ICC = 0.99, p < 0.001; Fig. 5(a); Table III]. SP amplitude was also recovered [ICC = 0.99, p < 0.001; Fig. 5(a); Table III]. Estimated SP width was in good agreement with the simulated peak width (ICC = 0.83, p < 0.001) and SP latency was in moderate agreement (ICC = 0.58, p < 0.001).
FIG. 5.
(a) Simulated amplitudes compared to amplitudes determined by visual estimation of peaks and troughs for SP (green triangles) and wave I (blue squares). (b) Simulated amplitudes compared to amplitudes determined by nonlinear estimation of Gaussian functions. (c) Visual estimation compared to model estimation. The dashed line indicates a unit slope.
TABLE III.
Absolute agreement between simulated metrics, model, and expert determination.
| 95% CI | F Test | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| ICC | Lower | Upper | Value | df1 | df2 | p | |||
| SP | Amplitude | Model | 0.99 | 0.99 | 0.99 | 14,808 | 31 | 31.14 | <0.001 |
| Expert 1 | 0.99 | 0.97 | 0.99 | 186 | 31 | 25.55 | <0.001 | ||
| Expert 2 | 0.98 | 0.94 | 0.99 | 150 | 31 | 9.76 | <0.001 | ||
| Latency | Model | 0.58 | 0.27 | 0.77 | 4.26 | 31 | 22.22 | <0.001 | |
| Expert 1 | 0.21 | 0 | 0.50 | 1.96 | 31 | 13.97 | 0.091 | ||
| Expert 2 | 0.26 | 0 | 0.54 | 1.77 | 31 | 31.55 | 0.057 | ||
| Width | Model | 0.83 | 0.64 | 0.92 | 12.82 | 31 | 17.81 | <0.001 | |
| Experts | - | - | - | - | - | - | - | ||
| wave I | Amplitude | Model | 0.99 | 0.99 | 0.99 | 1,556 | 31 | 17.37 | <0.001 |
| Expert 1 | 0.94 | 0.60 | 0.98 | 66.11 | 31 | 3.73 | <0.001 | ||
| Expert 2 | 0.95 | 0.88 | 0.98 | 53.96 | 31 | 13.99 | <0.001 | ||
| Latency | Model | 0.99 | 0.97 | 0.99 | 150 | 31 | 30.71 | <0.001 | |
| Expert 1 | 0.86 | 0.72 | 0.93 | 14.15 | 31 | 27.02 | <0.001 | ||
| Expert 2 | 0.75 | 0.51 | 0.88 | 8.12 | 31 | 20.65 | <0.001 | ||
| Width | Model | 0.99 | 0.98 | 0.99 | 200 | 31 | 29.28 | <0.001 | |
| Experts | - | - | - | - | - | - | - | ||
Metrics were also calculated from the visual-determination of peaks and troughs. Two experienced research audiologists performed similarly on latency and amplitude metrics for both the SP and wave I (Table III). Overall, the model performed better than visual-determination at recovering parameters of the simulated data; however, visual determination also performed highly [Fig. 5(b)].
V. DISCUSSION
The purpose of the study was to assess the use of a Gaussian model of wave I to extract metrics of latency and amplitude of the SP and wave I from the ABR waveform, which is typically done by visual determination of peaks and troughs and subject to error. The results of Experiment 1 indicate good agreement between the model and visual-determination of wave I metrics, though the model estimated smaller wave I amplitudes on average, compared to the traditional method of visual-determination. There was poor agreement between methods for SP amplitude, with the model estimating larger SP amplitudes than visual determination. Additionally, the model estimated SP amplitudes in all 32 waveforms while the experts could only determine SP amplitudes for 22 of 32 waveforms. For example, in three participants with hearing loss in Figs. 2(d), 2(e), and 2(f), experts failed to identify an SP. For Figs. 2(d) and 2(f), the experts noted that although an SP might be present, it could not be distinguished with confidence from the surrounding noise and was therefore not identified. For the participant in Fig. 2(e), the large peak preceding wave I was not identified as the SP again because of the low-frequency noise present in the ABR waveform. This is exemplified by Fig. 1(c), which shows the full ABR waveform of the participant in Fig. 2(e). Conversely, the model identified an SP in all waveforms. In Experiment 2, early ABR waves were simulated and the model and experts were given the same instructions, in terms of latency bounds, and tasked with recovering the amplitude and latency parameters that generated each waveform. Both the model and visual-determination performed well in recovering both SP and wave I metrics, with the model performing slightly better than visual-determination.
The results of Experiment 1 mirror that of the results found by the use of a Mexican hat wavelet (Valderrama et al., 2014) in that wave I latencies and amplitudes estimated by the model and visual determination were highly correlated but not entirely in absolute agreement. Interestingly, both the Mexican hat wavelet and Gaussian model estimated smaller wave amplitudes than visual determination. Valderrama et al. (2014) attributed this difference to the overestimation of amplitudes by visual determination as a consequence of local noise surrounding peaks and troughs. This likely accounts for a portion of the differences seen in the present data, but we also argue that in the case of wave I, overestimation of wave I amplitude is due to the overlapping nature of the SP and wave I. For example, in Fig. 2(e) a large SP could cause the adjacent wave I to appear larger in the waveform (black) than the uncoupled action potential (dark blue). The Gaussian model examined in this study and Mexican hat wavelet proposed by Valderrama et al. are comparable in fitting a single wave. The advantage of the Gaussian function is its simplicity, especially when fitting in series to several waves of the ABR.
Noise in the data played a significant role in the performance of visual-determination, but not the model. Noise due to electromagnetic artifact or muscle movement can be controlled by physically removing sources of noise, artifact rejection, and averaging over repeated responses (Don and Elberling, 1994). Even with such measures, there is often noise early in the ABR due to stimulus artifact and cochlear microphonic. These sources of noise are most often controlled by alternating the polarity of the stimulus; however, small amounts of cochlear microphonic may remain superimposed on the SP making a visual determination of an SP peak difficult. In Experiment 1, the visual determination of the SP was difficult in the presence of noise, hence the undetermined SP amplitudes in 10 of the 32 waveforms. The Gaussian model, on the other hand, estimated SP amplitudes in eight of these ten visually-undetermined amplitudes. Of course, it is impossible to definitively conclude the presence of SP in these waveforms, but we observe in this sample that the visually-indeterminate SPs occurred in particularly noisy waveforms. This is reiterated in Experiment 2, where noise was purposefully added to waveforms to increase the difficulty of visual-determination. Indeed, visual-determination performed best for waveforms with little to no noise added [Figs. 4(a) and 4(c)], but performed poorly in noisy waveforms [Figs. 4(d) and 4(e)]. Overlap in the SP-wave I waves also affected performance. Visual-determination performed highly when SP and wave I were clearly distinct [Figs. 4(a) and 4(c)], but performed poorly in waveforms in which SP and wave I overlap [Figs. 4(b) and 4(e)]. On the contrary, the Gaussian model performed consistently on both noisy and clean waveforms.
Though noisy waveforms resulted in erroneous visual-determination of peaks and troughs, visual-determination more closely approximated model estimation of simulated data from Experiment 2 [Fig. 5(c)] than the real data presented in Experiment 1 (Fig. 3). Simulated SP waves were easier to identify and measure than the real SP waves. Since ABR waves in Experiment 2 were simulated pseudo-randomly, some uncommon SP-wave I combinations were presented, such as Fig. 4(a). Another difference in Experiment 2 was that experts were instructed to always find an SP peak regardless of their confidence that one was present. This is different than the instructions given to the experts in Experiment 1, who only chose an SP peak if they were confident one was present.
Another potential advantage of a model over visual-determination is the estimation of metrics difficult to determine with the naked eye, especially when peaks overlap in time. One such metric is wave width. In Experiment 2, the Gaussian model recovered wave I width with an absolute agreement of 0.99. Evidence from computational modeling and empirical studies suggest wave width could be useful in characterizing synaptopathy and other auditory nerve disorders. For example, loss of auditory nerve fibers due to noise exposure may narrow wave I (Harris et al., 2018; Lichtenhan and Chertoff, 2008).
Finally, a more obvious advantage of a model approach over visual-determination is task time. The manual labeling of ABR waveforms is a tedious, time-consuming task that requires training and experience. For clinicians, an automated approach would reduce task time and aid in decision making for diagnoses. For researchers, this would reduce training and expertise requirements and improve the reliability of the data.
A. Limitations and future directions
A summed-Gaussian model of ABR morphology is a promising method of extracting data from the ABR and other auditory evoked potentials. Further development and applications of the model will be pursued in future studies. Some conceivable issues in the model application need to be addressed. First, a Gaussian function fit the SP well in this particular dataset. These ABR data were recorded to a short-duration (1 ms) tone-burst and high-pass filtered at 100 Hz. The SP is a DC response but when elicited by a transient sound and high-pass filtered, it looks like a wave (Durrant and Ferraro, 1991). SP morphology is highly dependent on stimulus and recording parameters and will differ vastly across datasets. The use of a Gaussian model should be re-examined with ABR data collected with lower filter cutoff frequencies and with a longer stimulus duration. A second limitation of the present study is the simulation of the data used to validate the Gaussian model in Experiment 2. The data were generated using a Gaussian model, therefore, a good model fit was expected. The fact that visual determination was also accurate in Experiment 2 supports the fitting validation by suggesting that the simulation had ecological validity. The addition of noise to the simulations increased the complexity of the parameter recovery for the model. However, the difference in correlation between the model and visual-determination in Experiments 1 and 2 [Fig. 3 compared to Fig. 5(c)] was possibly due to an inability of the Gaussian model to accurately simulate realistic ABR waveforms.
Additional studies include the optimization of the model for use on other ABR waves. The advantage of a summed Gaussian model over fitting individual functions is the ability to account for overlapping waves. A summed-Gaussian function could easily be expanded to include later-latency waves such as waves IV, V, and VI which tend to overlap in time and are difficult to visually estimate true amplitudes. Further studies on physiological correlates of wave width and latency are also of interest for the application of this model.
VI. CONCLUSIONS
-
(1)
A summed-Gaussian model successfully fit the SP and wave I of the ABR recorded in adults with a range of auditory thresholds.
-
(2)
A summed-Gaussian model out-performed visual-determination in estimating amplitude and latency in noisy, simulated waveforms and when the SP and wave I overlapped in time.
-
(3)
Accurate recovery of SP and wave I metrics from simulated waveforms supports the use of the summed-Gaussian model for fitting ABR waveforms.
ACKNOWLEDGMENTS
We would like to thank the experienced audiologists and researchers who determined ABR metrics for the Ridley et al. (2018) study: Judy Kopun M.S., Michael Gorga Ph.D., and Courtney Ridley Au.D., and the simulated data: Judy Kopun M.S. and Sara Fultz Au.D. This research was funded by NIH 5R01DC016348-02 and T32DC000013.
References
- 1. Arnold, S. A. (1985). “ Objective versus visual detection of the auditory brain stem response,” Ear Hear. 6(3), 144–150. 10.1097/00003446-198505000-00004 [DOI] [PubMed] [Google Scholar]
- 2. Bogaerts, S. , Clements, J. D. , Sullivan, J. M. , and Oleskevich, S. (2009). “ Automated threshold detection for auditory brainstem responses: Comparison with visual estimation in a stem cell transplantation study,” BMC Neurosci. 10, 104. 10.1186/1471-2202-10-104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Boston, J. R. , and Møller, A. R. (1985). “ Brainstem auditory-evoked potentials,” Crit. Rev. Biomed. Eng. 13(2), 97–123. [PubMed] [Google Scholar]
- 4. Bradley, A. P. , and Wilson, W. J. (2004). “ Automated analysis of the auditory brainstem response,” in Proceedings of the 2004 Intelligent Sensors, Sensor Networks and Information Processing Conference, ISSNIP '04, December 14–17, Melbourne, Australia, pp. 541–545. [Google Scholar]
- 5. Britt, R. H. , and Rossi, G. T. (1980). “ Neural generators of brainstem auditory-evoked responses,” J. Acoust. Soc. Am. 67(S1), S89–S90. 10.1121/1.2018464 [DOI] [Google Scholar]
- 6. Cabana-Pérez, I. M. , Velarde-Reyes, E. , Torres-Fortuny, A. , Eimil-Suarez, E. , and García-Giró, A. (2017). “ Automatic ABR detection at near-threshold intensities combining template-based approach and energy analysis,” in IFMBE Proceedings, Vol. 60 ( Springer, New York: ), pp. 122–125. [Google Scholar]
- 7. Chertoff, M. E. (2004). “ Analytic treatment of the compound action potential: Estimating the summed post-stimulus time histogram and unit response,” J. Acoust. Soc. Am. 116(5), 3022–3030. 10.1121/1.1791911 [DOI] [PubMed] [Google Scholar]
- 8. Chertoff, M. E. , Earl, B. R. , Diaz, F. J. , and Sorensen, J. L. (2012). “ Analysis of the cochlear microphonic to a low-frequency tone embedded in filtered noise,” J. Acoust. Soc. Am. 132(5), 3351–3362. 10.1121/1.4757746 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Don, M. , and Elberling, C. (1994). “ Evaluating residual background noise in human auditory brain-stem responses,” J. Acoust. Soc. Am. 96(5), 2746–2757. 10.1121/1.411281 [DOI] [PubMed] [Google Scholar]
- 10. Durrant, J. D. , and Ferraro, J. A. (1991). “ Analog model of human click-elicited SP and effects of high-pass filtering,” Ear Hear. 12(2), 144–148. 10.1097/00003446-199104000-00011 [DOI] [PubMed] [Google Scholar]
- 11. Elberling, C. (1979). “ Auditory electrophysiology: The use of templates and cross correlation functions in the analysis of brain stem potentials,” Scand. Audiol. 8(3), 187–190. 10.3109/01050397909076320 [DOI] [PubMed] [Google Scholar]
- 12. Ferraro, J. A. (2010). “ Electrocochleography: A review of recording approaches, clinical applications, and new findings in adults and children,” J. Am. Acad. Audiol. 21(3), 145–152. 10.3766/jaaa.21.3.2 [DOI] [PubMed] [Google Scholar]
- 13. Ferraro, J. , and Durrant, J. D. (1994). “ Auditory evoked potentials,” in Handbook of Clinical Audiology, 5th ed., edited by Katz J. ( Williams & Wilkins, Baltimore, MD: ), pp. 317–338. [Google Scholar]
- 14. Giraudeau, B. (1996). “ Negative values of the intraclass correlation coefficient are not theoretically possible,” J. Clin. Epidemiol. 49(10), 1205–1206. 10.1016/0895-4356(96)00053-4 [DOI] [PubMed] [Google Scholar]
- 15. Harris, K. C. , Vaden, K. I. , McClaskey, C. M. , Dias, J. W. , and Dubno, J. R. (2018). “ Complementary metrics of human auditory nerve function derived from compound action potentials: Measures of human auditory nerve function,” J. Neurophysiol. 119(3), 1019–1028. 10.1152/jn.00638.2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Koo, T. K. , and Li, M. Y. (2016). “ A guideline of selecting and reporting intraclass correlation coefficients for reliability research,” J. Chiropr. Med. 15(2), 155–163. 10.1016/j.jcm.2016.02.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Kostorz, I. , Kowalski, W. , Ludwig, Z. , and Zając, J. (2013). “ Detection of waves of auditory brainstem responses using IPAN99 algorithm,” J. Med. Inform. Technol. 22, 219–225. [Google Scholar]
- 18. Liberman, M. C. , Epstein, M. J. , Cleveland, S. S. , Wang, H. , and Maison, S. F. (2016). “ Toward a differential diagnosis of hidden hearing loss in humans,” PLoS ONE 11(9), 1–15. 10.1371/journal.pone.0162726 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Lichtenhan, J. T. , and Chertoff, M. E. (2008). “ Temporary hearing loss influences post-stimulus time histogram and single neuron action potential estimates from human compound action potentials,” J. Acoust. Soc. Am. 123(4), 2200–2212. 10.1121/1.2885748 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Morawski, K. F. , Pierchala, K. , and Delgado, R. (2019). “ TT-ECochG-morphology analysis by the nonlinear approximation of the Gauss function,” presented at the Meeting of the American Auditory Society, February 28-March 2, Scottsdale, AZ.
- 21. Pratt, H. , Urbach, D. , and Bleich, N. (1989). “ Auditory brainstem evoked potentials peak identification by finite impulse response digital filters,” Int. J. Audiol. 28(5), 272–283. 10.3109/00206098909081634 [DOI] [PubMed] [Google Scholar]
- 22. Ridley, C. L. , Kopun, J. G. , Neely, S. T. , Gorga, M. P. , and Rasetshwane, D. M. (2018). “ Using thresholds in noise to identify hidden hearing loss in humans,” Ear Hear. 39, 829–844. 10.1097/AUD.0000000000000543 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Rushaidin, M. M. , Salleh, S.-H. , Swee, T. T. , Najeb, J. M. , and Arooj, A. (2009). “ Wave V detection using instantaneous energy of auditory brainstem response signal,” Am. J. Appl. Sci. 6(9), 1669–1674. 10.3844/ajassp.2009.1669.1674 [DOI] [Google Scholar]
- 24. Rushaidin, M. M. , Salleh, S. H. , Hafizi, O. , Mahyar, H. , Ting, C. M. , and Ariff, A. K. (2012). “ Wave V detection using continuous wavelet transform of auditory brainstem response signal,” in Progress in Electromagnetics Research Symposium, March 27–30, Malaysia, pp. 1889–1893. [Google Scholar]
- 25. Stuermer, K. J. , Beutner, D. , Foerst, A. , Hahn, M. , Lang-Roth, R. , and Walger, M. (2015). “ Electrocochleography in children with auditory synaptopathy/neuropathy: Diagnostic findings and characteristic parameters,” Int. J. Pediatr. Otorhinolaryngol. 79(2), 139–145. 10.1016/j.ijporl.2014.11.025 [DOI] [PubMed] [Google Scholar]
- 26. Valderrama, J. T. , De la Torre, A. , Alvarez, I. , Segura, J. C. , Thornton, A. R. D. , Sainz, M. , and Vargas, J. L. (2014). “ Automatic quality assessment and peak identification of auditory brainstem responses with fitted parametric peaks,” Comput. Methods Progr. Biomed. 114(3), 262–275. 10.1016/j.cmpb.2014.02.015 [DOI] [PubMed] [Google Scholar]