Abstract
This paper proposes a modular architecture for articulatory synthesis from a gestural specification comprising relatively simple models for the vocal tract, the glottis, aero-acoustics, and articulatory control. The vocal tract module combines a midsagittal statistical analysis articulatory model, derived by factor analysis of air-tissue boundaries in real-time magnetic resonance imaging data, with an model for converting midsagittal section to area function specifications. The aero-acoustics and glottis models were based on a software implementation of classic work by Maeda. The articulatory control module uses dynamical systems, which implement articulatory gestures, to animate the statistical articulatory model, inspired by the task dynamics model. Results on synthesizing vowel-consonant-vowel sequences with plosive consonants, using models that were built on data from, and simulate the behavior of, two different speakers are presented.
I. INTRODUCTION
Articulatory synthesis can be defined as the automatic generation of acoustic speech signals from linguistic specifications by mimicking the human speech production process (Kröger and Birkholz, 2009; Scully, 1990; Shadle and Damper, 2001). A successful system for synthesis of continuous, co-articulated speech can be an indispensable tool for research into fundamental aspects of human speech communication (Cooper et al., 1952; Vaissiere, 2007). Such a system would integrate elaborate and realistic models of the vocal tract (Badin et al., 2002; Dang and Honda, 2004; Engwall, 2003; Maeda, 1990; Mermelstein, 1973), the vocal folds (Erath et al., 2011; Ishizaka and Flanagan, 1972; Moisik and Esling, 2014), aero-acoustics (Birkholz et al., 2007; Elie and Laprie, 2016; Maeda, 1982; Mokhtari et al., 2008; Story, 2013), and articulatory control (Birkholz, 2013; Byrd and Saltzman, 2003; Kröger, 1993; Öhman, 1966; Saltzman and Munhall, 1989).
Historically, the lack of adequate data on vocal tract shaping has been argued to be a factor that hindered progress in articulatory synthesis (Shadle, 1985). Recent advances in real-time magnetic resonance imaging (rtMRI) have enabled the acquisition of high-speed imaging data from the entire midsagittal slice of the vocal tract in unprecedented volumes (Lingala et al., 2016; Narayanan et al., 2004; Toutios and Narayanan, 2016). The present paper presents initial steps toward a modular system, or architecture, for articulatory synthesis informed by rtMRI data.
rtMRI data, combined with automatic air-tissue segmentation and factor analysis of air-tissue boundaries, have enabled the development of speaker specific, statistical articulatory models (Toutios and Narayanan, 2015). These midsagittal models, combined with a classic model of the relationship between the midsagittal section and the area function (Maeda, 1979, 1990; Perrier et al., 1992; Soquet et al., 2002) constitute the vocal tract module of the proposed architecture. The vocal fold and aero-acoustics modules are based on the articulatory synthesizer proposed by Maeda (Maeda, 1982), of which we provide a new matlab software implementation. The use of matlab leads to greater flexibility in adapting the model for individual use, compared with previous implementations of the synthesizer written in c.
The articulatory control module is based on a recent implementation of articulatory gestures as dynamical systems, informed by the theory of articulatory phonology (Browman and Goldstein, 1992) and task dynamics (Saltzman and Munhall, 1989). More specifically, by way of the articulatory model, a speaker's midsagittal vocal tract configuration is represented by the time-course of a small number of control parameters. The articulatory model generates this time-course through the temporal activation of articulatory gestures. Each gesture is a critically damped oscillator that is characterized by a target and a stiffness. In the transitions from vowel to consonant, the gestural target is defined as a distance (constriction degree) between an active and passive articulator. In the transitions towards vowels, the target is the complete midsagittal shape, as represented by an array of control parameters. The midsagittal vocal tract dynamics generated by these processes are then converted to area function dynamics via a commonplace -model, using specifications provided by Maeda (1979, 1990).
Glottal control parameters consist of a fast-varying and slow-varying glottal opening component and a fundamental frequency of vibration. The time-course of these parameters is also generated by a set of dynamical systems, the timings of which are derived from the durations of each articulatory gesture using empirical rules. Area function dynamics and glottal specifications are input to an aero-acoustic simulation. This is a matlab implementation of the method proposed by Maeda to solve in the time domain a time-varying lumped electrical network, whose elements are functions of the dynamically changing cross-sectional dimensions of the vocal tract, including the glottis (Maeda, 1982, 1996). The adequacy of Maeda's method for realistic copy synthesis of connected speech from known articulatory dynamics has been previously demonstrated using electromagnetic articulography (Toutios and Narayanan, 2013) and x-ray (Laprie et al., 2013) data. The novel implementation is available online with synthesis results (ownCloud, 2019). Our proposed architecture provides a framework for generating speech acoustics given a set of target vocal tract configurations and timings for each articulatory gesture. In the present paper we consider synthesis of vowel-consonant-vowel (VCV) sequences with plosive consonants, but our methods can be extended to other classes of speech sounds.
II. METHODS
A. Dynamic vocal tract imaging data
The present paper uses real-time vocal tract MRI data from two native American English speakers: a 29-year old female born in Brawley, CA; and a 36-year old male born in Medina, OH. Acquisition of these data was performed on a 1.5 T GE Signa Excite scanner at the Los Angeles County Hospital. A custom receiver coil specifically designed for upper-airway imaging was used, with eight coil elements, that provides superior sensitivity to all upper airway regions of interest, including tongue, lips, and also deep structures such as velum, epiglottis, and glottis (Lingala et al., 2017). Audio was recorded concurrently with MRI acquisition inside the MRI scanner, using a fiberoptic microphone (Optoacoustics Ltd., Moshav Mazor, Israel) and custom recording and synchronization setup (Bresch et al., 2006). Speech in the recorded audio was then enhanced, using a customized de-noising method (Vaz et al., 2018), in order to reduce the effect of loud scanner noise.
MR images were acquired using a multi-shot short spiral readout spoiled gradient echo pulse sequence with the following parameters: flip angle 15°; slice thickness 6 mm; readout time 2.5 ms; repetition time (TR) 6.004 ms; spatial resolution 2.4 mm2. Even though online reconstruction was available with a temporal resolution of 78 ms/frame (each image formed from 13 consecutive spirals), a SENSE constrained acquisition algorithm was implemented to enable improved temporal resolution (Lingala et al., 2017). In sum, the final speech production videos had 83.33 (true time resolution of 12 ms/frame) frames per second, each frame having 84 by 84 pixels with 2.4 by 2.4 mm per pixel.
The speech material included two repetitions of a large set of symmetric vowel-consonant-vowel-sequences (aCa, uCu, iCi for several consonants) and other scripted and spontaneous speech material, for a total of approximately 30 min per speaker (Lingala et al., 2016).
B. Articulatory model
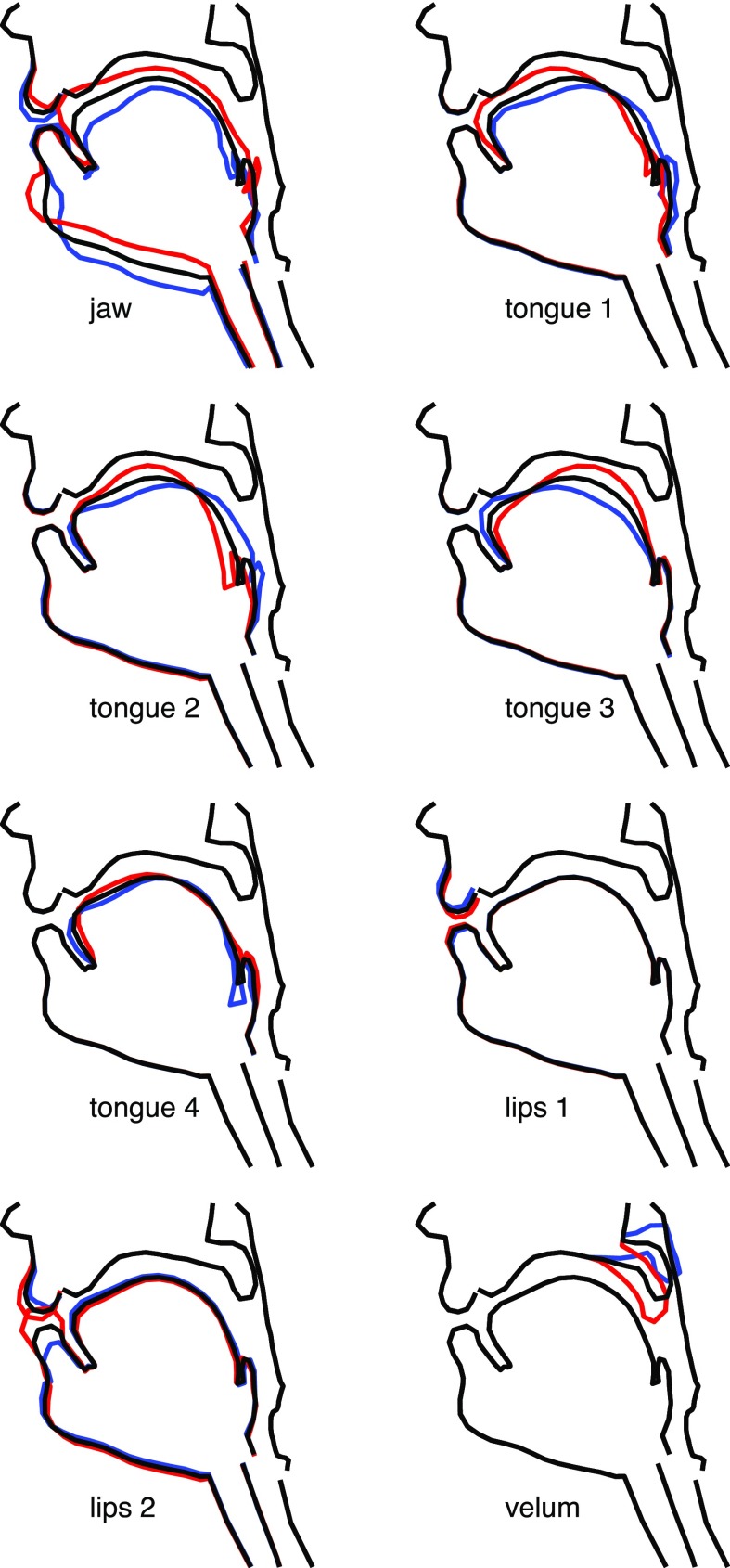
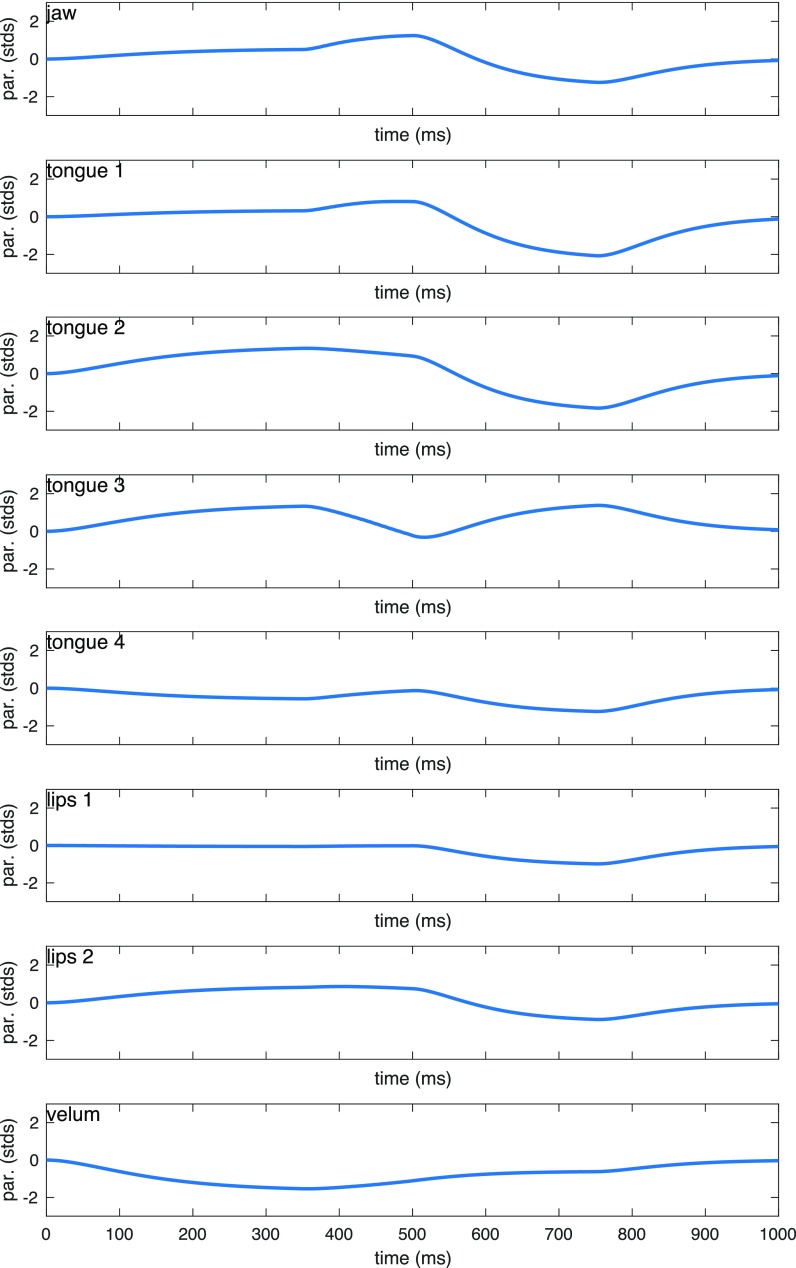
Images of the midsagittal slice from these data were processed using an automatic segmentation algorithm (Bresch and Narayanan, 2009) to obtain a vocal tract outline of 184 points on the midsagittal plane that described 15 anatomical features. A factor analysis (Sorensen et al., 2019; Toutios and Narayanan, 2015) was applied to the coordinates of these points to determine a set of constant factors that correspond to speaker-specific linguistically meaningful articulatory components (Fig. 1). Specifically, there is one factor for the jaw movement, four additional degrees of freedom for the tongue and two for the lips (after removal of the jaw contribution), and an independent velum factor. Each vocal tract configuration is thus represented by a vector of eight weights (or, control parameters of the articulatory model) that correspond to the degree of deformation of each factor, and can be used to accurately reconstruct the midsagittal vocal tract.
FIG. 1.
(Color online) Factors of the articulatory model. Line segments denote mean and ±2 standard deviations.
C. Tract variables
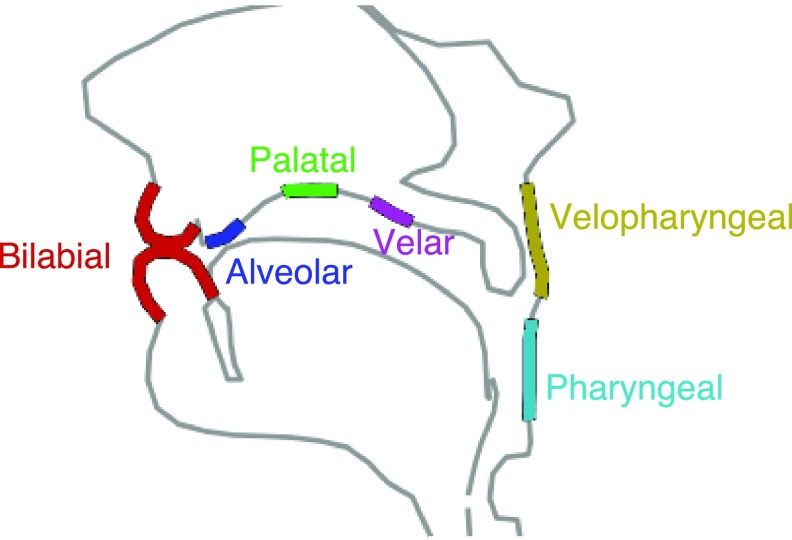
Constriction degrees were defined in previous work (Sorensen et al., 2016, 2019) to determine the distance between surfaces of active and passive articulators at the places of articulation specified in Fig. 2. For each vocal tract configuration, six such constriction degrees, or tract variables, were computed as the minimum distances between opposing surfaces at each place of constriction.
FIG. 2.
(Color online) Locations of constrictions considered in this study. (Bilabial, alveolar, palatal, velar, pharyngeal, and velopharyngeal.)
Tract variables were related to the articulatory parameters at each frame of the rtMRI video using a locally linear map defined by a hierarchical clustering procedure (Sorensen et al., 2016). This clustering algorithm estimates the forward map (Lammert et al., 2013; Ouni and Laprie, 2005) , from articulatory parameters to tract variables. The algorithm computes a tree whose root node is the set of all observed articulatory parameter vectors in the dataset. A k-means subroutine starts at the root and iteratively breaks nodes in two (i.e., k = 2). Children in this tree are disjoint subsets of the parent and the union of siblings is the parent. Nodes stop breaking either when a child would contain fewer than nine articulatory parameter vectors (to prevent rank-deficiency in least squares estimation of G) or when G maps the articulatory parameters of that node to tract variables in approximately linearly [i.e., when estimates z with a mean absolute error of less than λ mm, where λ is a free parameter chosen to be 0.24 mm]. Within each terminal node, the algorithm uses least squares to estimate G, the Jacobian J of G, and the time derivative of the Jacobian. By change of variables , articulatory parameters could be converted to tract variables and vice versa, allowing for inputs and outputs from the dynamical system to be used as vocal tract dynamics for articulatory synthesis.
The forward map G allows us to describe vowel configurations with articulatory parameters (weight vectors) and to describe the consonant configurations with tract variables (i.e., a target constriction degree at one of the places of articulation in Fig. 2). The linear map allows these two representations to interface in the dynamical system.
D. Dynamical system model
Change in the vector z of tract variables over time can be described with the second order differential equation , where is a vector of six tract variable targets and K and B are 6 × 6 diagonal matrices of stiffness and damping coefficients, respectively (Saltzman and Munhall, 1989). In the present work we consider that targets are only specified for one tract variable at a time; thus, K and B are non-zero at exactly one value along their diagonals, corresponding to the index of the place of articulation. We also consider that our dynamical systems correspond to critically damped oscillators. Thus, stiffness and damping are simple functions of a frequency ω0. For example, the stiffness and damping coefficients for a velar constriction (index 5) would be configured as below:
| (1) |
| (2) |
Using the forward map determined above, the differential equation over z can be converted to one over w, as
This follows from the change of variables and from the pseudoinverse of J. In practice, following Saltzman and Munhall (1989), we introduce on the right hand side the additional term
where and are parameters of the neutral attractor which we set empirically as and
| (3) |
where if articulatory parameter j (order: jaw, tongue1, tongue2, tongue3, tongue4, lips1, lips2, velum) is critically involved in the production of constriction i (order: bilabial, velopharyngeal, alveolar, palatal, velar, pharyngeal), and 0 otherwise. We refer to the equations specifying changes over tract variables as a type 1 dynamical system.
Trajectories of articulatory parameters can also be described with a similar equation , where specifies eight articulatory parameters instead of tract variables, and K and B are 8 × 8 matrices. The targets of these systems are specified in the articulatory parameter space, which best describes the configuration of the vocal tract when producing a vowel or transitioning in and out of the articulatory setting, here operationalized as a neutral vocal tract shape approximately corresponding to the production of a schwa. In this case, targets are specified for each of the 8 articulatory parameters, so stiffness and damping coefficients are specified in all 8 values along the diagonal. This type 2 dynamical system is used in the transition from the specified articulatory setting to the first vowel (), the consonant to the second vowel (), and from the second vowel to the articulatory setting (),
| (4) |
| (5) |
By solving consecutive dynamical systems of either type, using the target articulatory configuration and final velocity of initial systems as the starting position and velocity of subsequent ones, we can animate the articulatory model to accurately produce VCV sequences in both the articulatory parameter and tract variable spaces, while also modeling carryover coarticulation (anticipatory coarticulation is not modeled by the framework as described). Each dynamical system represents a vocal tract gesture and requires the specification of a target vocal tract configuration, either in the control parameter space for vowels or the tract variable space for consonants, and an appropriately selected frequency ω0, that is used to generate the matrices K and B. The concatenation of four such gestures animates a vowel-consonant-vowel sequence that begins and ends at the articulatory setting.
The first system in the sequence () begins with a vocal tract configuration for the articulatory setting, copied from the observed vocal tract configuration in the rtMRI data at the beginning of speech, and represented by an eight-dimensional vector of articulatory parameters. A type 2 dynamical system operating in the articulatory parameter space deforms that configuration to reach the parameter weights for a target vowel V1, which are measured from real-time data of the speaker producing the target VCV. This vowel configuration is then converted, using the locally linear mapping, from its representation in articulatory parameters to that of tract variables, which are used as the initial configuration to the second dynamical system along with the final velocity of the first system. This second system (), a type 1 equation operating on tract variables, deforms the vocal tract to achieve a specified constriction for the consonant C, which is chosen from bilabial (for /p/, /b/), alveolar (/t/, /d/), palatal (/k/, /g/ followed by /i/), or velar (/k/, /g/ followed by /a/, /u/). For stop consonants, this constriction is defined as a distance between the relevant articulators of a small negative value. The final consonantal configuration is then converted back to its representation in articulatory parameters, again using the forward map, which are used as input to the third dynamical system (). The third system, using the type 2 equation, deforms the parameters into the configuration for the vowel V2 (again determined from real-time data and operating on articulatory parameters rather than tract variables). Finally, the fourth dynamical system (), also of type 2, deforms the vocal tract from the vowel V2 back to the articulatory setting, again measured from real data in the space of articulatory parameters.
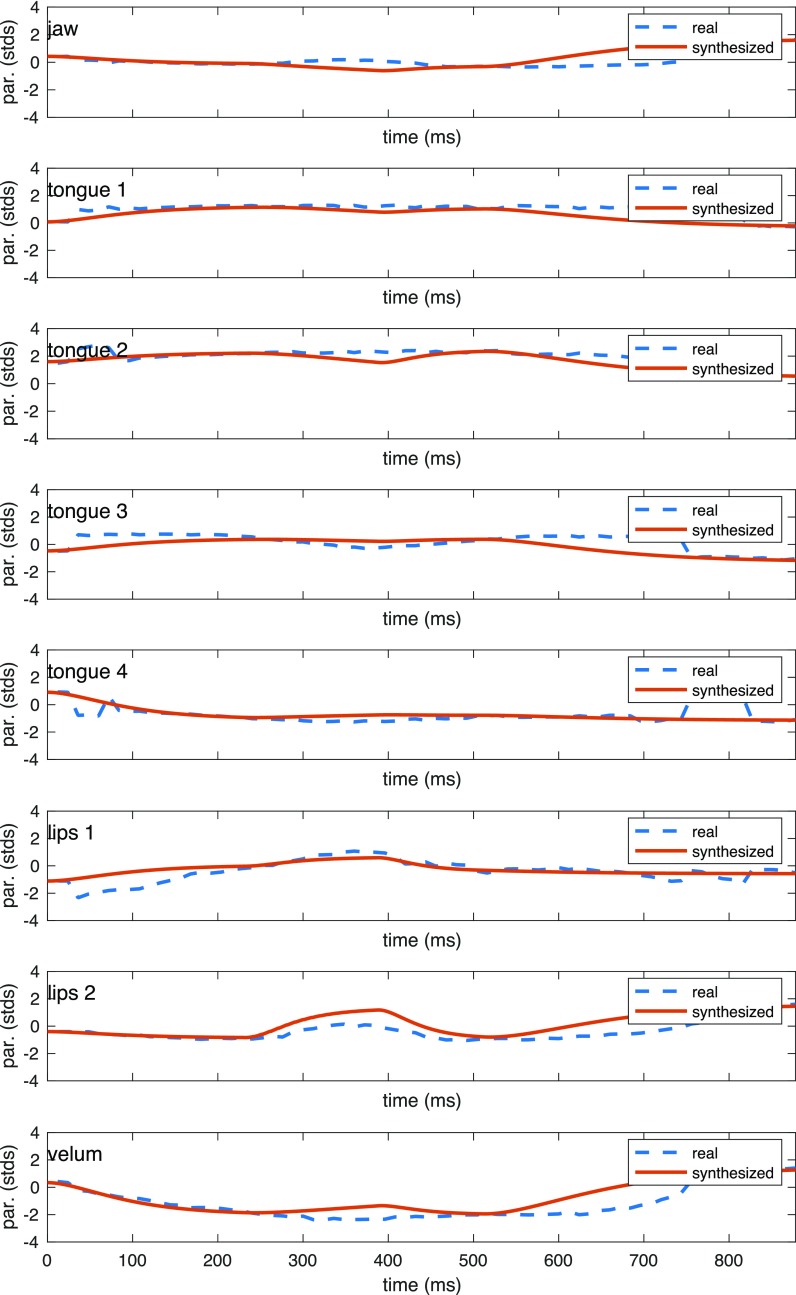
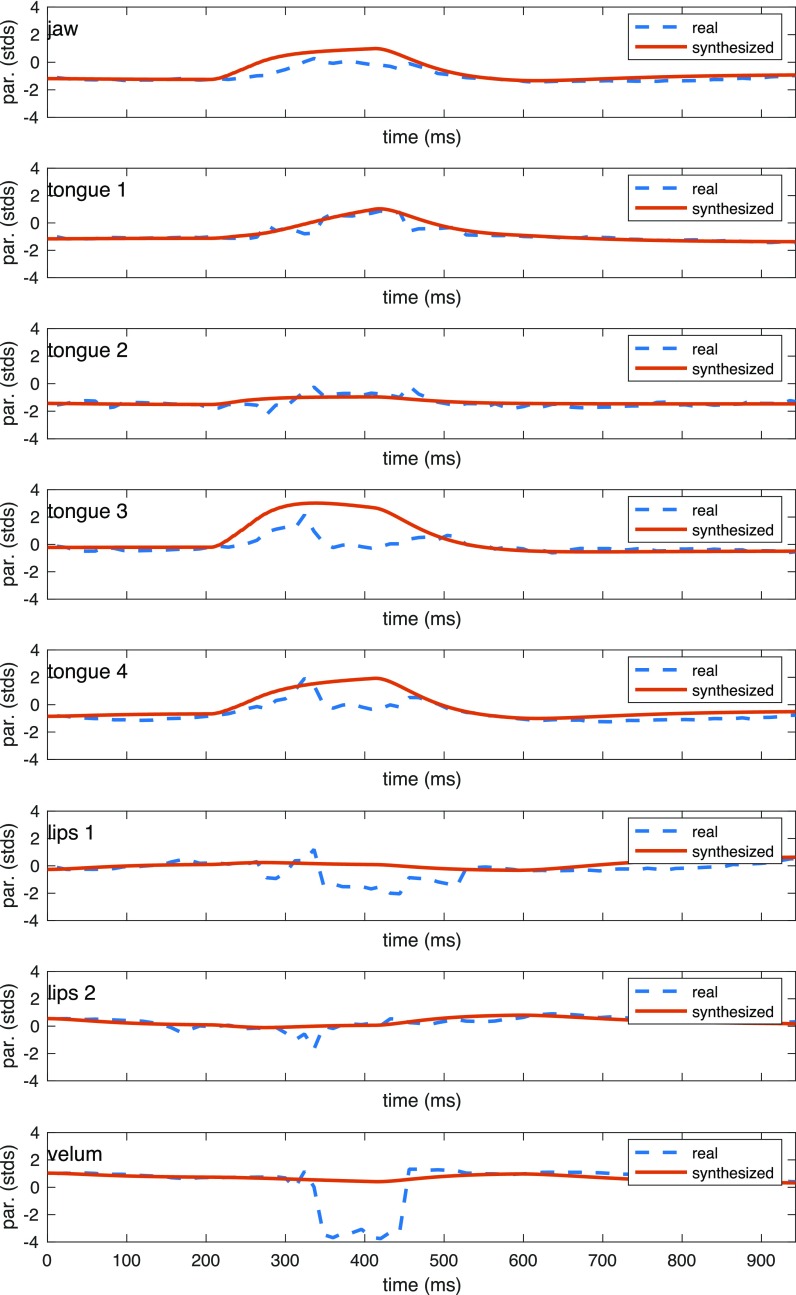
The transitions to and from the articulatory setting at the beginning and end of each sequence allow us to more accurately reproduce the articulatory trajectories measured from the data, as each VCV sequence has been recorded in isolation rather than in connected speech. The durations of the dynamical systems (gestural durations) are set to reproduce the length of the transitions between the beginning, first vowel, consonant, second vowel, and end of the corresponding recorded utterance. Stiffness and damping coefficients K and B, respectively, are calculated based on the duration t0 of each dynamical system as shown in Eqs. (1) and (2), or (4) and (5) depending on the type of dynamical system used, with . Figures 3 and 4 illustrate the comparison between the original recorded articulatory parameter trajectories, and the synthesized ones generated with dynamical systems for each speaker. Using the forward map, we can also convert the parameters to tract variables and compare the original recorded constriction degrees with the synthesized ones, as shown in Figs. 5 and 6. One source of differences between original and synthesized trajectories could be the fact that multiple configuration of articulatory parameters can create similar constrictions in the vocal tract (Sorensen et al., 2019). We note that in in optimizing synthesis results, our focus was primarily on distinguishing voicing and closure types, as well as appropriateness of formant transitions, rather than exact replication of parameters.
FIG. 3.
(Color online) Recorded and synthesized parameters of the articulatory model for sequence /ibi/ produced by the female speaker.
FIG. 4.
(Color online) Recorded and synthesized parameters of the articulatory model for sequence /aka/ produced by the male speaker.
FIG. 5.
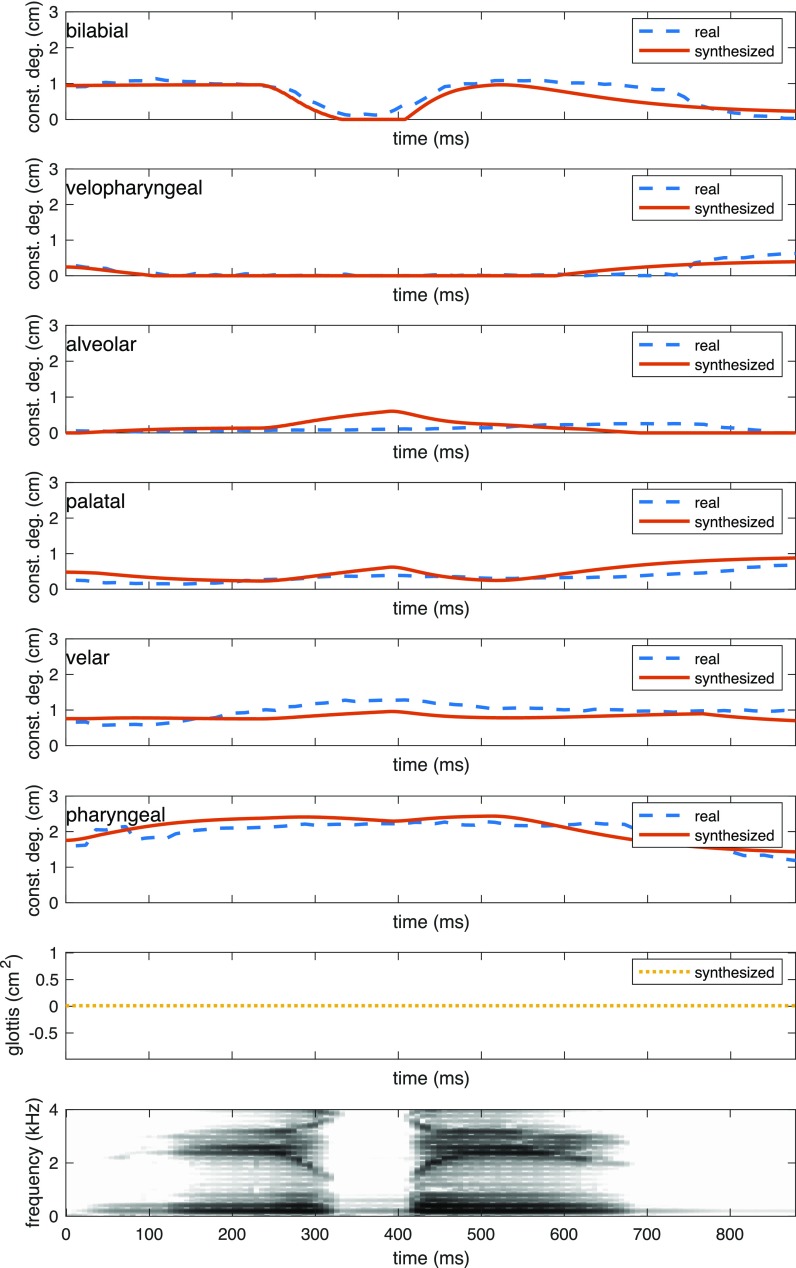
(Color online) Recorded and synthesized tract variables (degrees of constriction), synthesized slow-varying glottal opening component Ag0, and spectrogram of synthesized audio for sequence /ibi/ produced by the female speaker.
FIG. 6.
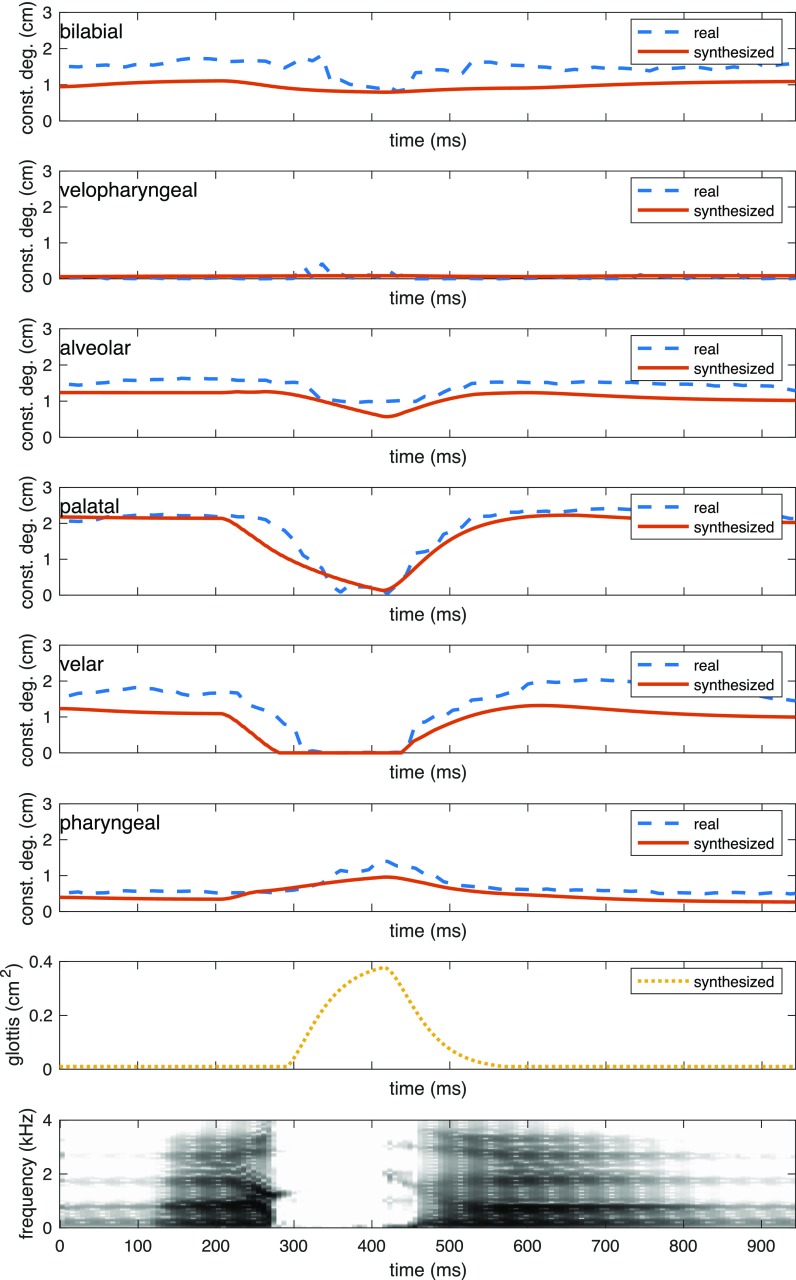
(Color online) Recorded and synthesized tract variables (degrees of constriction), synthesized slow-varying glottal opening component Ag0, and spectrogram of synthesized audio for sequence /aka/ produced by the male speaker.
E. Area functions, glottis control, and speech acoustics
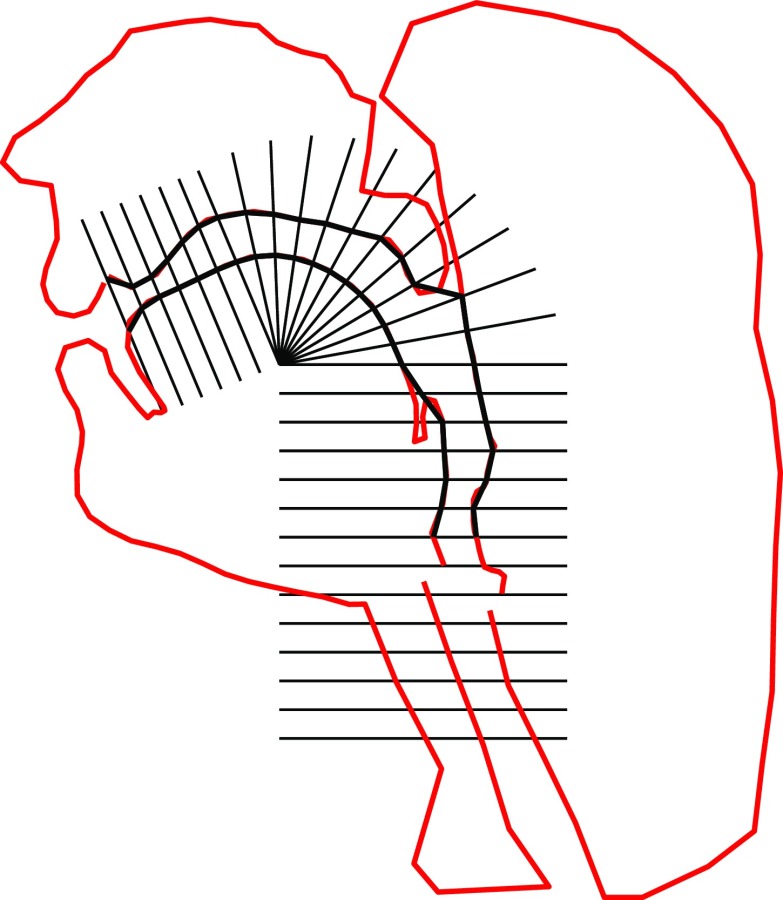
The concatenated output of the four sequential dynamical systems is a matrix of articulatory weights (columns) over time (rows). The dynamic vocal tract shape is recreated from these articulatory parameter specifications and converted to a dynamic area function by superimposing gridlines on the reconstructed midsagittal slice which segment the vocal tract into 27 sections characterized by a cross-sectional area A and a length d. The length d is calculated from the geometry of the grid, using points of intersection between gridlines and vocal tract walls, and the cross-sectional area for a specified value of α and β (Maeda, 1979, 1990; Perrier et al., 1992; Soquet et al., 2002). For each section, the area of a trapezoid is defined by two consecutive gridlines and the upper and lower vocal tract contours as in Fig. 7 and used to calculate the volume V of a three-dimensional polygon. Dimensions of a cylinder are calculated for each section with distance d and equivalent volume V, and the cross-sectional areas of these cylinders, along with their lengths, are returned as 27-dimensional arrays for A and d that describe area functions of the vocal tract throughout the VCV sequence.
FIG. 7.
(Color online) Semi-polar articulatory grid superposed on a mid-sagittal slice. Intersections of the grid with the slice, supplemented by minimal lip opening information, define the internal and external tract walls (thicker lines).
Controls describing the glottal opening are generated with a sequence of six dynamical systems operating on a single parameter. The set of parameters describing the glottis consists of a slow-varying, non-vibrating component added to a fast-varying triangular glottal pulse with fundamental frequency F0 and amplitude Ap (Fant, 1979; Maeda, 1996). Changes in each parameter are specified by the equation , where g0 is Ap or Ag0, and K and B determine stiffness and damping, similar to the systems used to describe changes in the shape of the vocal tract. F0 is held constant throughout the sequence at 200 Hz for the female speaker and 130 Hz for the male speaker.
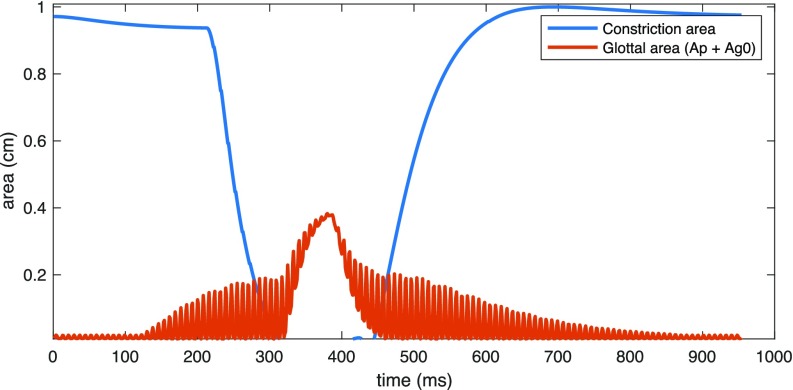
The durations of each transition for Ap and Ag0 are derived from the articulatory trajectories of the VCV using a set of empirical rules determined by examining the relationship between the rtMRI articulatory and acoustic data. For all VCVs, voicing amplitude Ap of the first vowel reaches its maximum value 100 ms after the sequence begins, and voicing of the second vowel begins to decrease 100 ms before the sequence ends. For a VCV with a voiceless consonant, the trajectory of the slow-varying component Ag0, which controls the glottal opening, is determined based on feedback from the synthesized vocal tract sequence. We measure the time point at which the vocal tract first achieves a full closure, specified as a constriction distance less than 0.08 cm2 at the relevant place of articulation, and the last time point at which the vocal tract is fully closed before articulating the second vowel. The component Ag0 is then manipulated to begin increasing 100 ms after the moment of first closure and return to a value of 0 cm2 200 ms after the burst of the consonant, reaching its maximum value halfway between both time points. Figures 6 and 10 illustrate the relationship between the timing of the glottal opening and the target vocal tract constriction for a voiceless consonant.
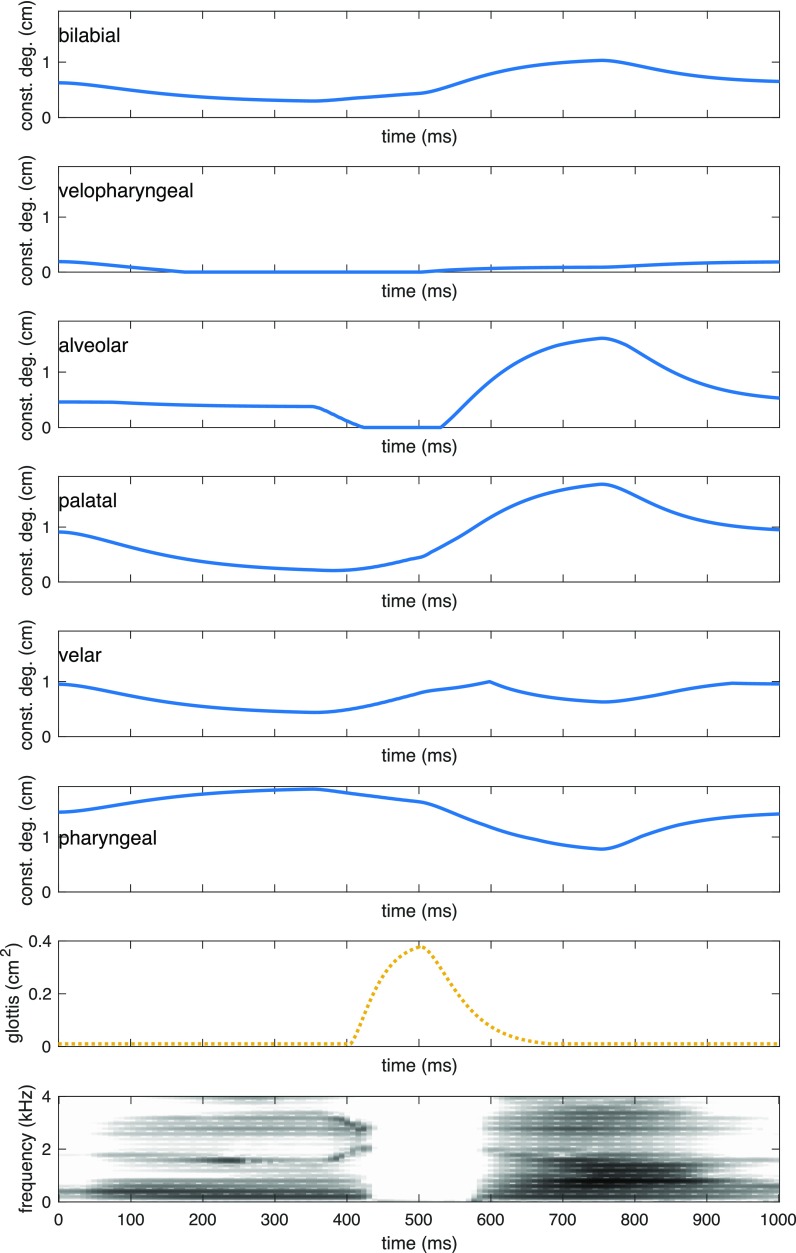
FIG. 10.
(Color online) Synthesized tract variables (degrees of constriction), synthesized slow-varying glottal opening component Ag0, and spectrogram of synthesized audio for sequence /uta/ produced by a female speaker.
Values of the glottal parameters are specified as follows: for voiced consonants, Ap is held constant at 0.2 cm2, with a smooth transition to and from 0 at the beginning and end of the sequence. Likewise, Ag0 is held constant at 0 cm2. For unvoiced consonants, dynamical systems are used to transition Ap from 0 cm2 at the beginning of the utterance to 0.2 cm2 at the peak of the first vowel, then to 0 cm2 at the consonant, to 0.2 cm2 at the peak of the second vowel, and back to 0 cm2 at the completion of the sequence, using the durations described previously. The trajectory of Ag0 is timed identically but transitions from 0 cm2 at the peak of the first vowel to 0.4 cm2 for the duration of the consonant, then returns to 0 cm2 at the peak of the second vowel. Figure 8 illustrates the temporal relationship between the consonantal closure and the glottal variables.
FIG. 8.
(Color online) Targeted constriction degree and synthesized glottal component Ag.
The glottal specifications and area functions are input to a matlab implementation of Maeda's synthesizer, which calculates the propagation of sound in a time-varying lumped electrical transmission-line network specified by the given area function dynamics (Maeda, 1982). The acoustic equations through which the glottal signal is passed simulate a system which can be solved at any point in space and time with a backward substitution and elimination procedure, calculating the pressure and volume velocity at each section of the vocal tract. The volume velocity at the lips is differentiated with respect to time to provide the final speech signal.
III. RESULTS
A. VCVs from articulatory measurements
18 symmetric VCV sequences with combinations of 3 vowels (/a/, /i/, /u/) and 6 consonants, 3 voiced and 3 unvoiced (/b/, /d, /g/, /k/, /p/, /t/) were synthesized by directly replicating the articulatory trajectories and glottal controls from rtMRI data for each of the two speakers. All the synthesis results described in this section are available online (ownCloud, 2019). Each sequence required the measurement of articulatory parameter vectors from recorded data of the speaker producing the target VCV at four time points: the articulatory setting at the beginning of the sequence, the peak of the first vowel, the peak of the second vowel, and the articulatory setting at the conclusion of the sequence. Peaks were defined as the points in time during the production of each vowel where the amplitude of the recorded sound wave was at a maximum. These articulatory parameter weights were used as inputs and targets of the four dynamical systems controlling the vocal tract, while the durations of each dynamical system were measured from the time intervals between the four specified time points and a fifth point measured at the burst of the consonant. The stiffness and damping coefficients for each dynamical system are calculated based on duration so that the target vocal tract shape is reached asymptotically at the end of the transition.
The same articulatory parameter trajectories are used for VCVs that differ only in voicing of the consonant (e.g., /aba/ and /apa/), with a 200 ms increase in the duration of the consonant for the voiceless sequence. The duration of the transition from V1 to the consonant is also decreased, further increasing the duration of the voiceless consonant.
Each example produced a VCV with a distinct vowel and full consonantal closure, with audible distinctions between voiced and unvoiced examples. The articulatory parameter trajectories of the synthesized sequences approximate the trajectories of the recorded utterances, as do the trajectories of each tract variable, for all combinations of vowels, consonants, voicing, and speakers; examples are provided above for the sequences /ibi/ and /aka/ in Figs. 3 and 4. While the critical constriction is directly controlled in the dynamical systems and therefore closely approximates the recorded constriction distance at the target place of articulation, the other five synthesized tract variables follow a similar trajectory to their equivalents in the data despite not being explicitly manipulated.
B. VCVs from articulatory prototypes
We used a second method to synthesize VCVs which required fewer articulatory measurements and enabled the synthesis of examples beyond those found in the data. Given a speaker-specific articulatory model, it is also possible to develop a prototypical representation for each vowel present in the speaker's data as a set of articulatory parameter weights corresponding to a vocal tract configuration that produces the intended vowel. These parameters can either be measured from one recorded utterance of the vowel or calculated as an average of all utterances of the vowel in the dataset, and can then be used as inputs to the four dynamical systems that generate a VCV sequence. In this study, we chose a single recorded utterance of each vowel to serve as a prototypical representation for synthesis. The articulatory setting was simulated by setting the weights for all articulatory parameters to zero rather than measuring them directly from data, as zero values represent the average normalized positions of each articulator, corresponding to a neutral vocal tract configuration.
Using prototypical vowels rather than directly replicating a VCV sequence helps to reduce some of the noise that may be present in the rtMRI data, leading in some cases to clearer articulation of the vowel. Given the inevitable variability across different utterances of the same vowel or VCV, an archetypal representation eliminates the need to adjust the timing of the sequence of dynamical systems in order to account for these minor differences. Instead, the timing of each transition is set empirically and is the same for each VCV: 350 ms from the articulatory setting to the first vowel, 150 ms from the first vowel to the consonant, 250 ms from the consonant to the second vowel, and 250 ms from the second vowel to the articulatory setting. This could be refined in the future to be set according to the specific target sequence. Similarly, the duration of each transition for the glottal parameters is set empirically based on the articulatory trajectory durations, but could be refined further.
In addition, generating a set of prototypical vowel representations for a speaker enables the simulation and synthesis of VCVs not explicitly recorded by that speaker by allowing us to mix and match combinations of an initial vowel, consonant, and final vowel to create a VCV independently of whether the full sequence appears in the rtMRI data. In contrast to the examples described in Sec. III A, VCVs produced this way do not use four articulatory measurements per utterance, but instead require only one set of measurements per vowel. The synthesized examples that use articulatory measurements enable us to compare our results to real data, while the prototypical examples allow us to expand our potential set of VCVs.
We simulated the same 18 symmetric sequences for each speaker using prototypical vowels and timings as described above, with results comparable to the original sequences. In addition, we synthesized 36 asymmetric VCV sequences for each speaker with unique combinations of the same vowels and consonants again using the prototypical method, without requiring a corresponding example to be present in the data.
C. Evaluation
Figure 9 illustrates synthesized articulatory parameters for an asymmetrical VCV sequence, /uta/, which was achieved by specifying a prototypical vocal tract shape for the vowels /u/ and /a/ and using its representation in articulatory parameters as inputs and targets to the dynamical systems, with an alveolar closure specified for the consonant. Figure 10 displays the equivalent sequence in terms of tract variables.
FIG. 9.
(Color online) Synthesized parameters of the articulatory model for sequence /uta/ produced by a female speaker.
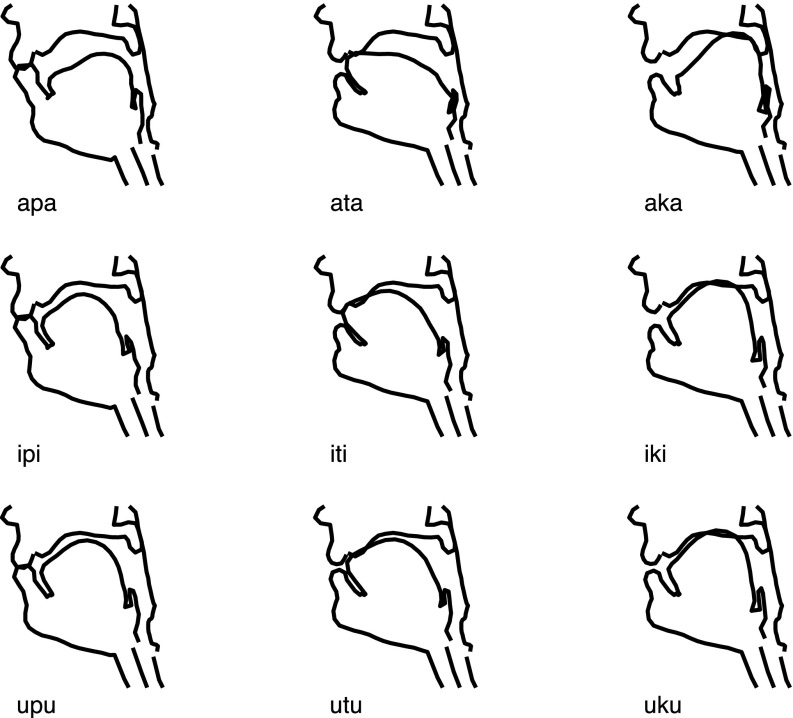
Figure 11 illustrates the effects of coarticulation on the synthesized vocal tract shapes. Constrictions at each of the three places of articulation targeted in this experiment (bilabial, alveolar, and velar) are articulated differently in each of the three vowel contexts aCa, iCi, and uCu. The sequence of dynamical systems links gestures together by coordinating the inputs and outputs of each consecutive system, modeling coarticulation by achieving each consonantal constriction in the most likely manner given an initial vocal tract configuration and its target. Because only one target constriction degree is specified, the other tract variables and articulatory parameters are free to move in a natural fashion: for example, the tongue remains in a low back position when achieving a bilabial constriction in the sequence /apa/, but takes a high front position when articulating /ipi/ because this allows the vocal tract to achieve the VC and CV transitions efficiently.
FIG. 11.
Vocal tract shapes at the point of consonantal closure with carryover coarticulation, produced by a female speaker.
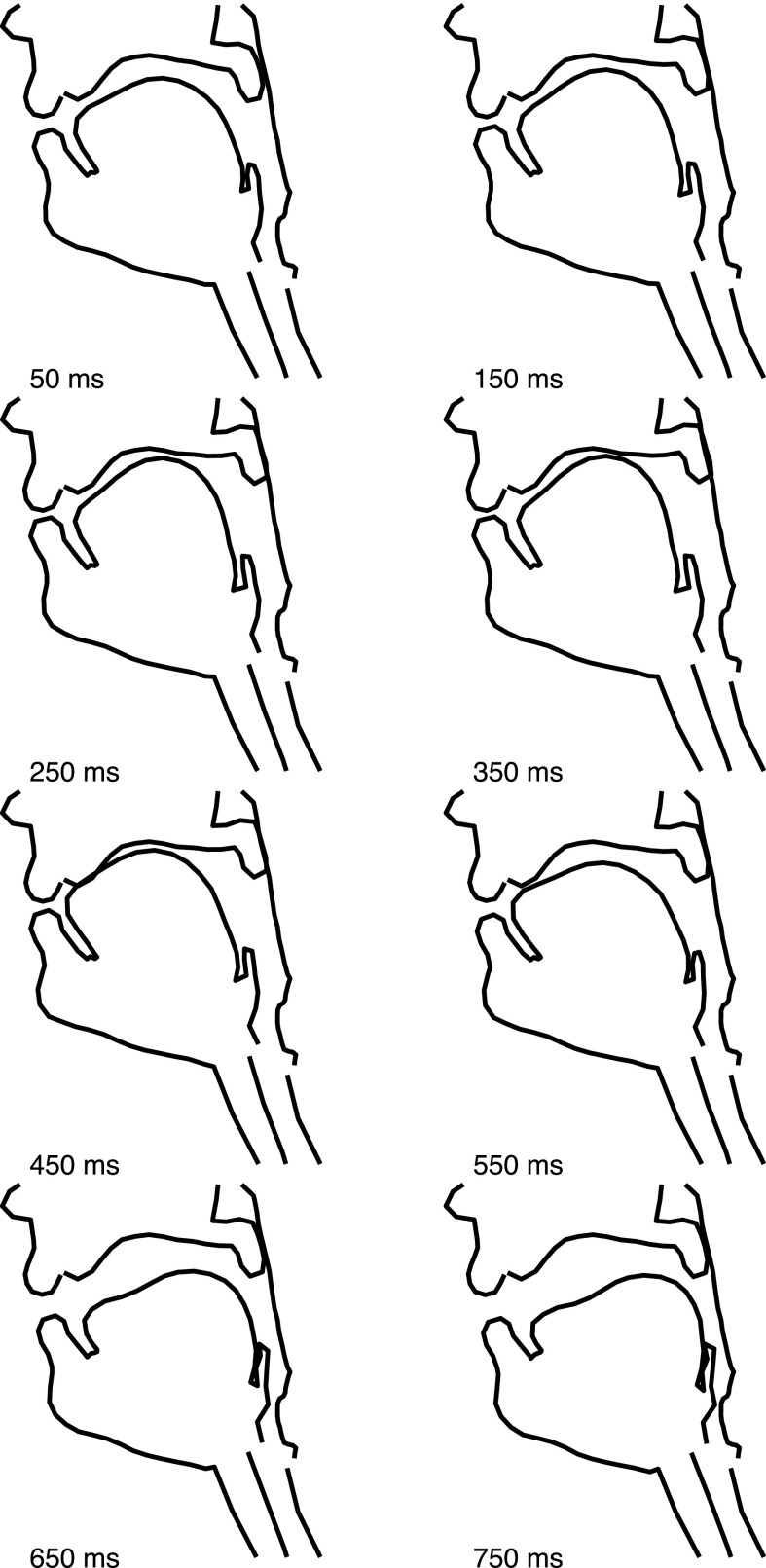
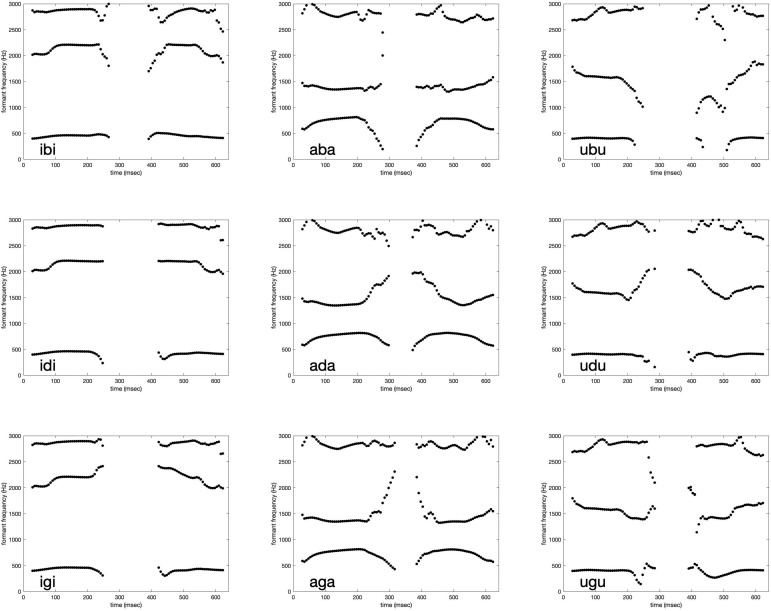
The constrictions achieved through the sequence of dynamical systems provide inputs to the synthesizer that successfully produce audible stops, with the area of the vocal tract reaching 0 cm2 at the appropriate place of articulation. As an illustrative example, for the VCV /uta/, the constriction degree of the alveolar tract variable reached 0 cm (Fig. 10) for about 150 ms, corresponding to a voiced alveolar closure. As expected, the other tract variables displayed no significant closures. The generated result from the synthesizer is displayed in the spectrogram in Fig. 10, which illustrates the expected voicing and fundamental frequency trajectories for the sequence /uta/. Figure 9 shows the deformation of the articulatory components used to create this sequence, represented by trajectories of articulatory weights that are converted from the appropriate tract variables, and illustrating that the tongue and jaw are the main factors in creating and releasing the alveolar closure. The dynamics of these components can be used to reconstruct and reanimate the midsagittal slice as it changes over the course of the VCV, as shown in Fig. 12. The vocal tract begins at the articulatory setting, achieves a high front unrounded vowel a third of the way through the sequence, brings the tongue tip to the alveolar ridge to fully close the vocal tract at 450 ms, and achieves a low back unrounded vowel at the end of the VCV before returning to the articulatory setting, as expected from the prescribed timings for this dynamical system. The combination of the modules described in this paper provide a framework for synthesizing vowel-consonant-vowel examples that is consistent throughout all steps of the architecture, from gestural specifications, to a dynamic vocal tract configuration, to the final synthesized audio. Formant transitions of the synthesized VCVs present a general agreement with perceptual considerations (Delattre et al., 1955)—see Fig. 13 for some examples. A comprehensive set of synthesized examples can be found online (ownCloud, 2019).
FIG. 12.
Temporal evolution of the midsagittal vocal tract shape for the sequence /uta/ produced by a female speaker.
FIG. 13.
First three formant trajectories for “prototypical” VCV's for the female speaker. Trajectories were extracted from praat (Boersma, 2001). Data points corresponding to the occlusion phase were hidden.
IV. CONCLUSION
We proposed a modular architecture for articulatory synthesis from a gestural specification that relies on relatively simple models for articulatory control, vocal tract, glottis, and aero-acoustic simulations. Our first results synthesizing VCV sequences with plosive consonants indicate that such a combination of simple models is promising for generating sufficiently intelligible speech. More elaborate models for any of the modules can also be considered; we believe that the modularity and open source availability of our system will enable such experimentation, potentially aiding research in articulatory synthesis at large.
An important step forward will be to move toward synthesis of more complex utterances. This will require expanding the inventory of speech sounds that the can be generated by the system. Synthesis of more vowels than the set /a/, /i/, /u/ is straightforward. Nasal consonants can be achieved given a specification of the nasal cavity shape and the temporal coordination between the articulation of the consonant and the opening of the velopharyngeal port; airflow through the nasal cavity is already implemented in our aero-acoustic simulation. Fricative consonants can be generated with an appropriately narrow constriction at the appropriate place of articulation; again, a mechanism for generating friction noise in the vicinity of such a constriction is already implemented. Expanding to the full set of English vowels and consonants is thus a matter of additional experimentation.
Our original motivation for developing an articulatory synthesis system was its potential as a tool for conducting analysis-by-synthesis experiments under precise control of articulatory dynamics and coordination, with a view to helping illuminate speech production-perception links. The proposed system could also serve as the basis of a future fully-fledged articulatory text-to-speech synthesis system. Such a system would also integrate a mechanism to generate gestural specifications from an intended linguistic, or even paralinguistic, message: this is, of course, a challenging open problem.
ACKNOWLEDGMENTS
This research was supported by NIH Grant No. R01DC007124 and NSF Grant No. 1514544. We thank Dani Byrd, Melissa Xu, Rachel Walker, Sarah Harper, and Samantha Gordon Danner for their help with the paper.
References
- 1. Badin, P. , Bailly, G. , Revéret, L. , Baciu, M. , Segebarth, C. , and Savariaux, C. (2002). “ Three-dimensional linear articulatory modeling of tongue, lips and face, based on MRI and video images,” J. Phon. 30(3), 533–553. 10.1006/jpho.2002.0166 [DOI] [Google Scholar]
- 2. Birkholz, P. (2013). “ Modeling consonant-vowel coarticulation for articulatory speech synthesis,” PloS One 8(4), e60603. 10.1371/journal.pone.0060603 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Birkholz, P. , Jackel, D. , and Kröger, B. J. (2007). “ Simulation of losses due to turbulence in the time-varying vocal system,” IEEE Trans. Audio Speech Lang. Process. 15(4), 1218–1226. 10.1109/TASL.2006.889731 [DOI] [Google Scholar]
- 4. Boersma, P. (2001). “ Praat, a system for doing phonetics by computer,” Glot Int. 5(9/10), 341–345. [Google Scholar]
- 5. Bresch, E. , and Narayanan, S. S. (2009). “ Region segmentation in the frequency domain applied to upper airway real-time magnetic resonance images,” IEEE Trans. Med. Imag. 28(3), 323–338. 10.1109/TMI.2008.928920 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Bresch, E. , Nielsen, J. , Nayak, K. S. , and Narayanan, S. S. (2006). “ Synchronized and noise-robust audio recordings during realtime magnetic resonance imaging scans,” J. Acoust. Soc. Am. 120(4), 1791–1794. 10.1121/1.2335423 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Browman, C. P. , and Goldstein, L. (1992). “ Articulatory phonology: An overview,” Phonetica 49, 155–180. 10.1159/000261913 [DOI] [PubMed] [Google Scholar]
- 8. Byrd, D. , and Saltzman, E. (2003). “ The elastic phrase: Modeling the dynamics of boundary-adjacent lengthening,” J. Phon. 31(2), 149–180. 10.1016/S0095-4470(02)00085-2 [DOI] [Google Scholar]
- 9. Cooper, F. S. , Delattre, P. C. , Liberman, A. M. , Borst, J. M. , and Gerstman, L. J. (1952). “ Some experiments on the perception of synthetic speech sounds,” J. Acoust. Soc. Am. 24(6), 597–606. 10.1121/1.1906940 [DOI] [Google Scholar]
- 10. Dang, J. , and Honda, K. (2004). “ Construction and control of a physiological articulatory model,” J. Acoust. Soc. Am. 115(2), 853–870. 10.1121/1.1639325 [DOI] [PubMed] [Google Scholar]
- 11. Delattre, P. , Liberman, A. , and Cooper, F. (1955). “ Acoustic loci and transitional cues for consonants,” J. Acoust. Soc. Am. 27(4), 769–773. 10.1121/1.1908024 [DOI] [Google Scholar]
- 12. Elie, B. , and Laprie, Y. (2016). “ Extension of the single-matrix formulation of the vocal tract: Consideration of bilateral channels and connection of self-oscillating models of the vocal folds with a glottal chink,” Speech Commun. 82, 85–96. 10.1016/j.specom.2016.06.002 [DOI] [Google Scholar]
- 13. Engwall, O. (2003). “ Combining MRI, EMA and EPG measurements in a three-dimensional tongue model,” Speech Commun. 41(2), 303–329. 10.1016/S0167-6393(02)00132-2 [DOI] [Google Scholar]
- 14. Erath, B. D. , Peterson, S. D. , Zañartu, M. , Wodicka, G. R. , and Plesniak, M. W. (2011). “ A theoretical model of the pressure field arising from asymmetric intraglottal flows applied to a two-mass model of the vocal folds,” J. Acoust. Soc. Am. 130(1), 389–403. 10.1121/1.3586785 [DOI] [PubMed] [Google Scholar]
- 15. Fant, G. (1979). “ Vocal source analysis—A progress report,” STL-QPSR (Speech Transmission Laboratory, KTH, Stockholm, Sweden) 20(3–4), 31–53. [Google Scholar]
- 16. Ishizaka, K. , and Flanagan, J. L. (1972). “ Synthesis of voiced sounds from a two-mass model of the vocal cords,” Bell Syst. Tech. J. 51(6), 1233–1268. 10.1002/j.1538-7305.1972.tb02651.x [DOI] [Google Scholar]
- 17. Kröger, B. J. (1993). “ A gestural production model and its application to reduction in German,” Phonetica 50(4), 213–233. 10.1159/000261943 [DOI] [PubMed] [Google Scholar]
- 18. Kröger, B. J. , and Birkholz, P. (2009). “ Articulatory synthesis of speech and singing: State of the art and suggestions for future research,” in Multimodal Signals: Cognitive and Algorithmic Issues, edited by Esposito A., Hussain A., Marinaro M., and Martone R. ( Springer, Berlin: ), Vol. 5398, pp. 306–319. [Google Scholar]
- 19. Lammert, A. , Goldstein, L. , Narayanan, S. , and Iskarous, K. (2013). “ Statistical methods for estimation of direct and differential kinematics of the vocal tract,” Speech Commun. 55(1), 147–161. 10.1016/j.specom.2012.08.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Laprie, Y. , Loosvelt, M. , Maeda, S. , Sock, R. , and Hirsch, F. (2013). “ Articulatory copy synthesis from cine X-ray films,” in Interspeech, Lyon, France, pp. 2024–2028. [Google Scholar]
- 21. Lingala, S. G. , Toutios, A. , Töger, J. , Lim, Y. , Zhu, Y. , Kim, Y.-C. , Vaz, C. , Narayanan, S. , and Nayak, K. (2016). “ State-of-the-art MRI protocol for comprehensive assessment of vocal tract structure and function,” in Interspeech, San Francisco, CA, pp. 475–479. [Google Scholar]
- 22. Lingala, S. G. , Zhu, Y. , Kim, Y.-C. , Toutios, A. , Narayanan, S. , and Nayak, K. S. (2017). “ A fast and flexible MRI system for the study of dynamic vocal tract shaping,” Magn. Reson. Med. 77(1), 112–125. 10.1002/mrm.26090 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Maeda, S. (1979). “ Un modèle articulatoire de la langue avec des composantes linéaires,” in Actes 10èmes Journées d'Étude sur la Parole, Grenoble, France, pp. 152–162. [Google Scholar]
- 24. Maeda, S. (1982). “ A digital simulation method of the vocal-tract system,” Speech Commun. 1(3-4), 199–229. 10.1016/0167-6393(82)90017-6 [DOI] [Google Scholar]
- 25. Maeda, S. (1990). “ Compensatory articulation during speech: Evidence from the analysis and synthesis of vocal tract shapes using an articulatory model,” in Speech Production and Speech Modelling, edited by Hardcastle W. and Marchal A. ( Kluwer Academic, Amsterdam: ), pp. 131–149. [Google Scholar]
- 26. Maeda, S. (1996). “ Phonemes as concatenable units: VCV synthesis using a vocal-tract synthesizer,” in Sound Patterns of Connected Speech: Description, Models and Explanation, edited by Simpson A. and Pätzold M., pp. 145–164. [Google Scholar]
- 27. Mermelstein, P. (1973). “ Articulatory model for the study of speech production,” J. Acoust. Soc. Am. 53(4), 1070–1082. 10.1121/1.1913427 [DOI] [PubMed] [Google Scholar]
- 28. Moisik, S. R. , and Esling, J. H. (2014). “ Modeling the biomechanical influence of epilaryngeal stricture on the vocal folds: A low-dimensional model of vocal–ventricular fold coupling,” J. Speech Lang. Hear. Res. 57(2), S687–S704. 10.1044/2014_JSLHR-S-12-0279 [DOI] [PubMed] [Google Scholar]
- 29. Mokhtari, P. , Takemoto, H. , and Kitamura, T. (2008). “ Single-matrix formulation of a time domain acoustic model of the vocal tract with side branches,” Speech Commun. 50(3), 179–190. 10.1016/j.specom.2007.08.001 [DOI] [Google Scholar]
- 30. Narayanan, S. , Nayak, K. , Lee, S. , Sethy, A. , and Byrd, D. (2004). “ An approach to real-time magnetic resonance imaging for speech production,” J. Acoust. Soc. Am. 115, 1771. 10.1121/1.1652588 [DOI] [PubMed] [Google Scholar]
- 31. Öhman, S. (1966). “ Coarticulation in VCV utterances: Spectrographic measurements,” J. Acoust. Soc. Am. 39(1), 151–168. 10.1121/1.1909864 [DOI] [PubMed] [Google Scholar]
- 32. Ouni, S. , and Laprie, Y. (2005). “ Modeling the articulatory space using a hypercube codebook for acoustic-to-articulatory inversion,” J. Acoust. Soc. Am. 118(1), 444–460. 10.1121/1.1921448 [DOI] [PubMed] [Google Scholar]
- 33.ownCloud (2019). http://sail.usc.edu/span/artsyn2019 (Last viewed 12/10/2019).
- 34. Perrier, P. , Boë, L.-J. , and Sock, R. (1992). “ Vocal tract area function estimation from midsagittal dimensions with CT scans and a vocal tract cast: Modeling the transition with two sets of coefficients,” J. Speech Lang. Hear. Res. 35(1), 53–67. 10.1044/jshr.3501.53 [DOI] [PubMed] [Google Scholar]
- 35. Saltzman, E. L. , and Munhall, K. G. (1989). “ A dynamical approach to gestural patterning in speech production,” Ecol. Psychol. 1(4), 333–382. 10.1207/s15326969eco0104_2 [DOI] [Google Scholar]
- 36. Scully, C. (1990). “ Articulatory Synthesis,” in Speech Production and Speech Modelling, edited by Hardcastle W. and Marchal A. ( Kluwer Academic, Amsterdam: ), pp. 151–186. [Google Scholar]
- 37. Shadle, C. (1985). “ The Acoustics of Fricative Consonants,” Ph.D. thesis, Massachusetts Institute of Technology, Cambridge, MA. [Google Scholar]
- 38. Shadle, C. H. , and Damper, R. I. (2001). “ Prospects for articulatory synthesis: A position paper,” in 4th ISCA Tutorial and Research Workshop on Speech Synthesis (SSW-4), Perthshire, Scotland. [Google Scholar]
- 39. Soquet, A. , Lecuit, V. , Metens, T. , and Demolin, D. (2002). “ Mid-sagittal cut to area function transformations: Direct measurements of mid-sagittal distance and area with MRI,” Speech Commun. 36(3), 169–180. 10.1016/S0167-6393(00)00084-4 [DOI] [Google Scholar]
- 40. Sorensen, T. , Toutios, A. , Goldstein, L. , and Narayanan, S. (2016). “ Characterizing vocal tract dynamics across speakers using real-time MRI,” in Interspeech, San Francisco, CA. [Google Scholar]
- 41. Sorensen, T. , Toutios, A. , Goldstein, L. , and Narayanan, S. (2019). “ Task-dependence of articulator synergies,” J. Acoust. Soc. Am. 145(3), 1504–1520. 10.1121/1.5093538 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Story, B. H. (2013). “ Phrase-level speech simulation with an airway modulation model of speech production,” Comput. Speech Lang. 27(4), 989–1010. 10.1016/j.csl.2012.10.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Toutios, A. , and Narayanan, S. (2016). “ Advances in real-time magnetic resonance imaging of the vocal tract for speech science and technology research,” APSIPA Trans. Sign. Inf. Process. 5, e6. 10.1017/ATSIP.2016.5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Toutios, A. , and Narayanan, S. S. (2013). “ Articulatory synthesis of French connected speech from EMA data,” in Interspeech, Lyon, France, pp. 2738–2742. [Google Scholar]
- 45. Toutios, A. , and Narayanan, S. S. (2015). “ Factor analysis of vocal-tract outlines derived from real-time magnetic resonance imaging data,” in International Congress of Phonetic Sciences (ICPhS), Glasgow, UK. [Google Scholar]
- 46. Vaissiere, J. (2007). “ Area functions and articulatory modeling as a tool for investigating the articulatory, acoustic and perceptual properties of sounds across languages,” in Experimental Approaches to Phonology, edited by Solé M., Beddor P., and Ohala M. ( Oxford University Press, Oxford: ), pp. 54–71. [Google Scholar]
- 47. Vaz, C. , Ramanarayanan, V. , and Narayanan, S. (2018). “ Acoustic denoising using dictionary learning with spectral and temporal regularization,” IEEE/ACM Trans. Audio Speech Lang. Process. 26(5), 967–980. 10.1109/TASLP.2018.2800280 [DOI] [PMC free article] [PubMed] [Google Scholar]