Biomechanical contribution of the sclera to dynamic corneal response in air-puff induced deformation in human donor eyes

Abstract

This study was conducted to evaluate the impact of varying scleral material properties on the biomechanical response of the cornea under air-puff induced deformation. Twenty pairs of human donor eyes were obtained for this study. One eye from each pair had its sclera stiffened using 4% glutaraldehyde, while the fellow eye served as control for uniaxial strip testing. The whole globes were mounted in a rigid holder and intraocular pressure (IOP) was set using a saline column. Dynamic corneal response parameters were measured before and after scleral stiffening using the CorVis ST, a dynamic Scheimpflug analyzer. IOP was set to 10, 20, 30, and 40 mmHg, with at least 3 examinations performed at each pressure step. Uniaxial tensile testing data were fit to a neo-Hookean model to estimate the Young’s modulus of treated and untreated sclera. Scleral Young’s modulus was found to be significantly correlated with several response parameters, including Highest Concavity Deformation Amplitude, Peak Distance, Highest Concavity Radius, and Stiffness Parameter-Highest Concavity (SP-HC). There were significant increases in SP-HC after scleral stiffening at multiple levels of IOP, while no significant difference was observed in the corneal Stiffness Parameter – Applanation 1 (SP-A1) at any level of IOP. Scleral mechanical properties significantly influenced the corneal deformation response to an air-puff. The stiffer the sclera, the greater the constraining effect on corneal deformation resulting in lower displaced amplitude. This may have important clinical implications and suggests that both corneal and scleral material properties contribute to the observed corneal response in air-puff induced deformation.

1. Introduction

Elevated intraocular pressure (IOP) is an important diagnostic marker in ocular diseases such as glaucoma (Weinreb and Khaw, 2004) and ocular hypertension (Copt et al., 1999). Understanding how the biomechanical behavior of ocular structures influence IOP measurement may assist in the diagnosis, management, and treatment of ocular diseases (Liu and Roberts, 2005; Elsheikh et al., 2009; Metzler et al., 2014; Girard et al., 2015; Tejwani et al., 2015; Ariza-Gracia et al., 2016; Roberts, 2016). IOP is estimated by either contact tonometry (such as Goldmann Applanation Tonometry) or noncontact tonometry (such as air-puff tonometers) which apply a load to the cornea and estimate the IOP based on assumptions about the structure and mechanical properties of the cornea (Liu and Roberts, 2005; Luce, 2005; Ruberti et al., 2011).

Previous studies have shown that the thickness and mechanical properties of the cornea can influence tonometric readings (Liu and Roberts, 2005; Tejwani et al., 2015; Broman et al., 2007), and neglecting patient-to-patient variability in the mechanical response of the cornea would lead to measurement error. Several devices utilize various algorithms to account for the contributions of corneal stiffness, thickness, and age (Joda et al., 2016; Ruberti et al., 2011). The limitation in these algorithms is the underlying assumption that the corneal response to a mechanical load is solely attributable to the cornea’s structural and material properties, without taking into account the contribution of the sclera.

It has been shown that the interactions between the cornea and other ocular tissues (Metzler et al., 2014; Elsheikh, 2010; Nguyen et al., 2018) will impact the corneal biomechanical response to an applied load. Substantially fewer studies have explored the impact of the sclera on clinical tonometry measurements as compared to the cornea, and to our knowledge, a method for clinical evaluation of scleral properties has yet to be developed. The purpose of this study was to explore the impact of varying scleral properties on the corneal biomechanical response under air-puff induced deformation in human donor eyes.

2. Materials and methods

2.1. Eye preparation

Human donor eyes (40 paired eyes from 20 donors) from the Central Ohio Lions Eye Bank were obtained within 24 h post-mortem, so experiments could be completed within 48 h. Mean donor age was 66.8 ± 9.4 years, with 13 male and 7 female donors. Exclusion criteria included gross defects on the corneal epithelium and corneal surgeries other than bilateral cataracts. 7 donor pairs contained bilateral intraocular lenses. On enucleation, the anterior chamber of each eye was injected via 22-gauge needle with 0.5–1.0 mL of 12.5–15% dextran (Sigma-Aldrich, St. Louis, Missouri, USA) dissolved in Dulbecco’s phosphate-buffered saline (DPBS; Sigma-Aldrich) prior to submersion in 35 mL of the same solution. Eyes were then refrigerated until the central corneal thickness was measured to be 550–600 μm by ultrasound pachymeter (generally 12–14 h).

2.2. Experimental setup

One eye from each matched pair was randomly selected to have its sclera stiffened by crosslinking treatment with glutaraldehyde, while the fellow eye served as a control for uniaxial testing. The globe was immersed for 30 min in 4% glutaraldehyde in DPBS just below the level of the limbus, such that the cornea remained untreated. Corneal hydration was maintained using a humidifier.

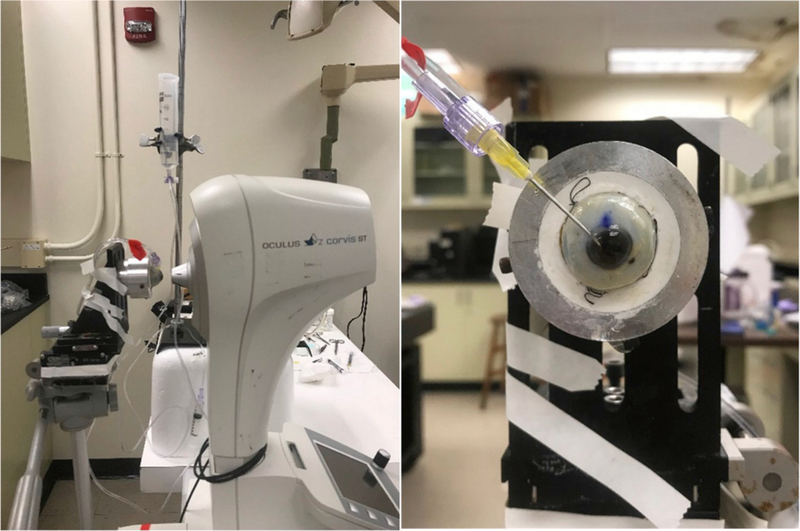
A dynamic Scheimpflug analyzer (CorVis ST with research software 1.3b1716; Oculus, Wetzlar, Germany) was used to load the eye and quantify the resulting corneal deformation response (Fig. 1). Each eye was secured in a custom whole-globe mount using shallow sutures in the sclera. A 22-gauge needle attached to a saline column was inserted into the anterior chamber of the eye to set and maintain the IOP. The saline column was set to specified heights to generate IOPs corresponding to 10, 20, 30, and 40 mmHg. At least 3 examinations were performed at each pressure step, and DPBS was dripped onto the cornea between examinations to maintain hydration and reflectivity. The order of eyes during testing was randomized, and measurements were taken before and after treatment with gluteraldehyde.

Fig. 1.

(Left) Experimental setup for ex vivo studies on human donor eyes, showing a whole globe in the purpose-designed mount in front of the CorVis ST. (Right) A view of the human donor eye showing the 22-gauge needle inserted into the anterior chamber, used to set and maintain IOP (Nguyen et al., 2018).

Simple uniaxial testing was performed to quantify the effect of the stiffening protocol on the mechanical properties of the sclera. Nasotemporal strips from the sclera were excised along the central meridian of the eye. Strip dimensions were measured using a digital caliper before the strips were mounted in the testing apparatus (Fig. 2; Rheometrics Systems Analyzer, RSA III; TA Instruments, New Castle, Delaware, USA). A humidified chamber was constructed around the testing apparatus to maintain tissue hydration.

Fig. 2.

(Left) Excised strip of sclera mounted in a (Right) commercial testing fixture. A humidified chamber, not pictured, surrounded the test fixture to maintain tissue hydration.

A strip testing protocol was adapted from a study by Metzler et al. (2016) and is described briefly herein. Tissues were preconditioned by manually cycling the load 5 times from 0.5 to 5 g-force (gf). The strip was then loaded to 2.0 gf for 1 min prior to sinusoidal tension with strain amplitude of 0.15% and frequency of 1.0 Hz. The tissue was unloaded to 0.5 gf for 5 min before applying a tensile ramp up to 6% strain at a strain rate of 0.1% per second. Tensile strains beyond 6% were not considered as 6% tensile strain already exceeds physiologically relevant deformation in the eye.

The tensile ramp data were fit with an incompressible, isotropic, neo-Hookean model to estimate the Young’s modulus E of the sclera. This formulation predicts a force-displacement relationship

$$F(u)=\frac{EA}{3}\left[1+\frac{u}{L}-\frac{1}{{\left(1+\frac{u}{L}\right)}^2}\right],$$

where A is the unloaded cross-sectional area, u is the change in sample length, and L is the original length of sample between clamps. E was estimated by fitting this model equation to the experimentally-measured data using a least-squares approach. While the nonlinear stress-strain response of the sclera under tensile strip testing is not fully characterized by any single value of Young’s modulus, a neo-Hookean model was adopted as a first approximation to an average stiffness over the entire load-deformation response.

2.3. Statistical analyses

Dynamic corneal response (DCR) parameters were exported by the CorVis ST analysis software for each exam. Paired t-tests compared the change in DCRs following either stiffening or control treatment, and multiple analysis of co-variance (MANCOVA) was performed for selected delta DCRs as dependent variables with log(IOP) and scleral Young’s modulus as independent co-variates. The log(IOP) was used in order to normalize the distribution of residuals. Because our study focuses on a small subset of planned comparisons, a correction for multiple t-tests was not applied in order to avoid type II error (Armstrong, 2014). Statistical significance was determined if p < 0.05. The Cohen effect size were calculated for each DCR parameter to evaluate the size of the effect of IOP, Scleral Modulus, or the interaction effect.

A subset of DCRs were selected for further statistical analysis: peak distance (PD), highest concavity (HC) deformation amplitude (DA), DA Ratio 2 mm, integrated inverse radius, and stiffness parameter-applanation 1 (SP-A1) and stiffness parameter-highest concavity (SP-HC). Peak distance refers to the distance between the two highest points of the cornea at highest concavity. Deformation amplitude ratio is the ratio of deformed amplitude of the corneal apex and the average deformation either 2 mm or 1 mm on either side of the apex, respectively. The integrated inverse radius, denoted as Integrated Radius in the export, is the integrated sum of inverse radius of curvature between first and second applanation. Finally, the stiffness parameters are calculated as a ratio of load to displacement. Displacement for SP-A1 is between the undeformed apex and the position of first applanation, and displacement for SP-HC is between the position of first applanation and highest concavity. SP-A1 and SP-HC were calculated using the equations developed and described by Roberts et al. (2017). These parameters are summarized in Table 1.

Table 1.

Select CorVis ST dynamic corneal response parameters and their description.

Parameter Name [unit]	Description
Peak Distance [mm]	Distance between corneal peaks at highest concavity
HC Deformation Amplitude [mm]	Deformation amplitude at highest concavity
Radius [mm]	Radius of curvature at highest concavity
DA Ratio Max (2 mm)	Deformation amplitude ratio at 2 mm from corneal apex
Integrated Inverse Radius [mm−1]	Integrated inverse radius of curvature
SP-A1	Stiffness parameter at first applanation
SP-HC	Stiffness parameter at highest concavity

3. Results

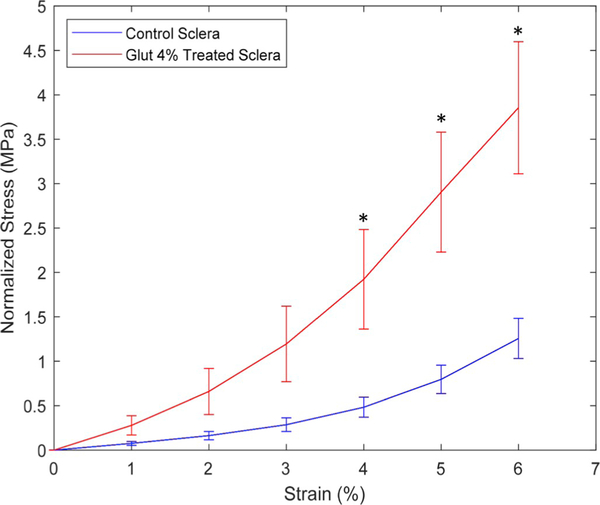
Tensile strip testing ramp data confirmed that the glutaraldehyde-treated sclera had a stiffer biomechanical behavior than the matched controls. The control and treated scleral Young’s modulus were found to be significantly different, and were determined to be 2.5 ± 2.4 MPa and 7.6 ± 8.4 MPa, respectively. Paired t-tests showed a statistically significant (p < 0.05) increase in scleral stiffness at 4, 5, and 6% strain (Fig. 3).

Fig. 3.

Average tensile stress-strain results for glutaraldehyde-treated and control sclera with error bars representing standard error of the mean. Statistically significant (p < 0.05) differences were observed at 4, 5, and 6% strain using paired t-test, denoted by *.

Paired t-tests showed statistically significant (p < 0.05) decreases after scleral stiffening in peak distance and HC deformation amplitude for all tested levels of IOP (Table 2). There were also significant decreases in Integrated Inverse Radius only at IOP of 10 mmHg. Of the two stiffness parameters, only SP-HC was affected. SP-HC was higher post-scleral-stiffening at all levels of IOP while there was no significant difference observed for SP-A1 at any level of IOP.

Table 2.

Paired t-test results for DCRs at each tested level of IOP. Statistical significance was determined if p < 0.05, denoted by †.

CorVis ST DCR	IOP 10
	Control	Glut 4 Sclera	Mean Δ
Peak Dist. [mm]	5.838 ± 0.283	5.398 ± 0.333	−0.527 ± 0.411†
HC Deformation Amp. [mm]	1.441 ± 0.184	1.182 ± 0.159	−0.317 ± 0.243†
Radius [mm]	5.974 ± 0.572	6.123 ± 0.735	0.380 ± 0.755†
DA Ratio Max (2 mm) Integrated Radius [mm−1]	4.491 ± 0.603 9.961 ± 1.196	4.236 ± 0.672 9.700 ± 1.236	−0.174 ± 0.702 −0.786 ± 1.438†
SP-A1	99.448 ± 17.385	102.039 ± 16.153	2.591 ± 15.993
SP-HC	9.709 ± 2.847	13.016 ± 3.982	3.306 ± 2.939†
CorVis ST DCR	IOP 20
	Control	Glut 4 Sclera	Mean Δ
Peak Dist. [mm]	4.965 ± 0.194	4.668 ± 0.295	−0.313 ± 0.394†
HC Deformation Amp. [mm]	0.982 ± 0.094	0.879 ± 0.091	−0.112 ± 0.134†
Radius [mm]	6.872 ± 0.759	6.588 ± 0.792	−0.076 ± 0.841
DA Ratio Max (2 mm)	3.853 ± 0.497	3.640 ± 0.439	−0.178 ± 0.513
Integrated Radius [mm−1]	7.752 ± 1.081	7.809 ± 1.191	−0.087 ± 0.838
SP-A1	127.609 ± 15.925	127.480 ± 19.689	−0.128 ± 16.558
SP-HC	19.847 ± 4.929	23.840 ± 4.568	3.993 ± 2.055†
CorVis ST DCR	IOP 30
	Control	Glut 4 Sclera	Mean Δ
Peak Dist. [mm]	4.126 ± 0.206	3.889 ± 0.276	−0.217 ± 0.366†
HC Deformation Amp. [mm]	0.712 ± 0.061	0.662 ± 0.065	−0.041 ± 0.084†
Radius [mm]	6.509 ± 0.758	6.297 ± 0.880	−0.176 ± 0.935
DA Ratio Max (2 mm)	3.434 ± 0.330	3.342 ± 0.371	−0.054 ± 0.439
Integrated Radius [mm−1]	6.492 ± 1.041	6.374 ± 1.280	−0.086 ± 0.986
SP-A1	142.966 ± 15.484	145.485 ± 25.129	2.519 ± 19.770
SP-HC	34.504 ± 7.488	38.985 ± 6.529	4.481 ± 7.182†
CorVis ST DCR	IOP 40
	Control	Glut 4 Sclera	Mean Δ
Peak Dist. [mm]	3.388 ± 0.196	3.175 ± 0.242	−0.185 ± 0.335†
HC Deformation Amp. [mm]	0.530 ± 0.050	0.492 ± 0.047	−0.030 ± 0.062†
Radius [mm]	6.908 ± 1.141	6.985 ± 1.292	0.222 ± 1.523
DA Ratio Max (2 mm)	3.033 ± 0.367	2.840 ± 0.396	−0.121 ± 0.487
Integrated Radius [mm−1]	4.799 ± 1.062	4.458 ± 1.218	−0.360 ± 1.225
SP-A1	141.683 ± 18.567	144.668 ± 25.093	2.985 ± 15.272
SP-HC	54.655 ± 14.970	62.889 ± 25.093	8.234 ± 16.024†

Several important relationships were elucidated via MANCOVA analyses (Table 3). It was shown that the HC deformation amplitude and SP-HC had a statically significant relationship with both IOP and scleral Young’s modulus. While SP-A1 did vary significantly with IOP, there was no significant relationship with scleral Young’s modulus. Peak distance and radius were significantly correlated with scleral Young’s modulus. While integrated inverse radius was found to significantly correlate with scleral modulus, this was driven by the response at 10 mmHg and there were no differences at all other levels of IOP. Additionally, while DA Ratio max (2 mm) was found to vary significantly with IOP, paired t-test analysis showed no differences between treated and control eyes at each tested level of IOP.

Table 3.

MANCOVA analysis for DCR parameters, with delta responses as the dependent variable, and with log(IOP) and Scleral Young’s modulus as independent covariates. Cohen effect sizes are shown, and statistical significance from MANCOVA was determined if p < 0.05 denoted by †.

CorVis ST DCR	log(IOP)	Scleral Modulus (E)	log(IOP)*Scl Mod (E)
Peak Dist. [mm]	0.6019	0.0386†	0.0949
HC Deformation Amp. [mm]	0.2542†	0.0680†	0.0335
Radius [mm]	2.7522	0.1690†	0.2479†
DA Ratio Max (2 mm)	0.9032†	0.0204	0.0755
Integrated Radius [mm−1]	0.1979	0.0307†	0.0308
SP-A1	2.909†	0.0019	0.112
SP-HC	3.7287†	0.0149†	0.0368

4. Discussion

The response of the cornea to a dynamic load such as the CorVis ST air-puff is the result of both corneal and scleral material properties, in addition to loading by IOP. The deformation response of the cornea is greatly impacted by the loading due to IOP, which generates tension in the collagen microstructure of both cornea and sclera. During air-puff induced deformation, the cornea deforms through applanation, then continues to deform and becomes concave. This concave state will result in displacement of fluid, i.e. aqueous humor, in the anterior chamber. The volume of fluid displacement will be limited by the scleral biomechanical properties, such that the greatest influence of the sclera on corneal deformation response is at highest concavity. With stiffer sclera, elastic stresses that are transmitted from the cornea to the limbus will experience additional stresses, and stress wave propagation through the sclera will dissipate less energy, potentially returning more stress in the sclera and other ocular tissues and resulting in increased resistance to corneal deformation (Esposito et al., 2015). This impact of ocular tissues on corneal response was demonstrated in a study by Roberts et al., (2014), where it was observed that hyperopic eyes exhibited stiffer corneal biomechanical response as compared to myopic eyes. Progression of myopia may be characterized by remodeling of the sclera, which would impact its biomechanical properties and response.

Decreases in HC DCRs at low IOP (peak distance, radius of curvature, and HC deformation amplitude) showed that after stiffening only the sclera, the cornea will behave as if it has a higher apparent stiffness under the same load. This is a result of the altered boundary condition at the limbus, where the stiffened sclera is less compliant and will have greater resistance to the displaced fluid in the anterior chamber (Nguyen et al., 2018). This may lead to misinterpretation of corneal response in ocular disease states or treatments that alter the sclera, such as progressive myopia or topical prostaglandin-analogs for glaucoma management.

At all levels of IOP, the highest concavity parameters of HC Deformation Amplitude, Peak Distance and SP-HC were significantly different with treatment, indicating a stiffer response despite only stiffening the sclera and leaving the cornea unaltered. In contrast, at all levels of IOP, there were no significant differences in DA Ratio Max (2 mm) or SP-A1 with scleral stiffening, indicating these parameters are primarily corneal parameters and are not influenced by scleral properties. Larger differences were expected and observed between eyes having stiffened and untreated sclerae at HC over those at A1, because at HC the cornea has reached its maximum deformation and therefore has induced aqueous displacement in the anterior chamber. At the same time, scleral resistance to corneal deformation is maximized. A1 occurs very early in the CorVis ST loading curve, where the corneal deformation is very small compared to HC, and the contribution of the sclera to limiting corneal motion is minimal due to the miniscule amount of displaced aqueous humor. Therefore parameters derived at A1 would be less sensitive to scleral properties and primarily indicative of corneal properties. As the corneae were left untreated, it was expected that there were no significant differences in A1 parameters, and indeed this was observed in the experimental results.

The two stiffness parameters SP-HC and SP-A1 are indicative of the stiffness of the cornea. SP-A1 is determined as the load on the cornea over the displacement to A1, where SP-HC is the same load over the deflection displacement beyond applanation to HC (difference of HC deformation amplitude and A1 deformation amplitude). SP-A1 only varied significantly with IOP and was independent of scleral stiffening in paired eyes. Since first applanation occurs very early and there is minimal contribution of the sclera to limiting corneal deformation, the SP-A1 results suggest that there were no differences in corneal properties. SP-A1 has been shown to be sensitive to changes in corneal properties (Roberts et al., 2017), and the findings of our study are consistent. SP-HC was shown to vary significantly with both IOP and estimated scleral stiffness, increasing at all levels of IOP. These results show that differences in scleral stiffness are detectable in observing the change in SP-HC parameter, which may be clinically useful as a diagnostic tool.

Only at 10 mmHg, the two parameters based on radius of curvature at highest concavity – radius and integrated inverse radius – were significantly different indicating a stiffer response. At all other levels of IOP, these two parameters were not different, indicating they are also primarily corneal parameters and not influenced by scleral properties unless the IOP is at the lower limit of what is considered physiologic. A limitation of this study was that other physiologic levels of IOP between 10 mmHg and 20 mmHg were not included. However, studies have shown that integrated inverse radius and radius are sensitive corneal parameters that can detect subtle differences in corneal response, such as the difference between standard surface ablation and an “extra” procedure where accelerated crosslinking was performed immediately after surface ablation (Lee et al., 2017).

The results of this study may have important clinical implications. The corneal biomechanical response evaluated by the Corvis ST is often attributed solely to the properties of the cornea. However, this study shows that the corneal deformation response under air-puff induced deformation is significantly impacted by varying the properties of the sclera and leaving the cornea untreated. Specifically, the stiffer the sclera, the greater will be the limitation on corneal deformation. It is important to consider, especially in vivo, that the biomechanical deformation response of the cornea is due to contributions from both the cornea and sclera, in addition to the effects of IOP. Some parameters have been shown to be more sensitive to scleral properties while others have been shown to be unaffected by scleral properties, which may be useful in clinical interpretation.

5. Conclusions

It has been shown that scleral properties influence corneal biomechanical deformation response to an air puff. Specifically, a stiffer sclera will limit corneal motion by resisting displacement of fluid when the cornea becomes concave, and thus the resulting response might be misinterpreted as a stiffer cornea. The study results suggest that there may be a need to account for scleral properties in the assessment of corneal biomechanical response and the estimation of IOP under air-puff loading. Through careful study, we may be able to evaluate the respective contributions of cornea, sclera, and IOP to the dynamic corneal deformation response to give a better understanding of the eye’s overall susceptibility to glaucoma and other ocular diseases.