Skip to main content
PMC home page
Genetics Research logoLink to Genetics Research
. 2014 May 16;96:e003. doi: 10.1017/S0016672314000068

Improving the inference of population genetic structure in the presence of related individuals

SILVIA T RODRÍGUEZ-RAMILO 1, MIGUEL A TORO 2, JINLIANG WANG 3, JESÚS FERNÁNDEZ 1,*
PMCID: PMC7044976  PMID: 25022872

Summary

It is well known that the presence of related individuals can affect the inference of population genetic structure from molecular data. This has been verified, for example, on the unsupervised Bayesian clustering algorithm implemented in the software STRUCTURE. This methodology assumes, among others, Hardy–Weinberg and linkage equilibrium within subpopulations. The existence of groups of close relatives, such as full-sib families, may prevent these assumptions to be fulfilled, causing the algorithm to work suboptimally. The purpose of this study was to evaluate the effect of the presence of related individuals on a different methodology (implemented in CLUSTER_DIST) for population genetic structure inference. This approach arranges individuals to maximize the genetic distance between groups and does not make Hardy–Weinberg and linkage equilibrium assumptions. We study the robustness of this approach to the presence of close relatives in a sample using simulated scenarios involving combinations of several factors, including the number of subpopulations, the level of differentiation between them, the number, size and type (full or half-sibs) of families in a sample, and the type and number of molecular markers available for clustering analysis. Results indicate that the methodology that maximizes the genetic distance between subpopulations is less influenced by the presence of related individuals than the program STRUCTURE. Therefore, the former can be used, in combination with the program STRUCTURE, to analyse population genetic structure when related individuals are suspected to be present in a sample.

1. Introduction

Several unsupervised Bayesian clustering approaches have been proposed to infer population genetic structure using exclusively molecular marker information obtained from sampled individuals. These methodologies can be used to determine the number of clusters (K) and to assign individuals to the inferred clusters (Pritchard et al., 2000; Dawson & Belkhir, 2001; Corander et al., 2004; Gao et al., 2007; Huelsenbeck & Andolfatto, 2007). Loosely speaking, such methods (e.g. the one implemented in the program STRUCTURE) are developed based on population genetics models and try to infer population genetic structure by minimizing Hardy–Weinberg and linkage disequilibrium within the different groups.

However, related individuals or members of the same family can be present in the same subpopulation. Such a situation can occur when individuals are sampled from small populations, from populations of high fecund species, or when sessile individuals are sampled. Consequently, the lack of Hardy–Weinberg and linkage equilibrium which may arise from this situation could lead to a reduction in the accuracy to detect population structure with the program STRUCTURE (Pritchard et al., 2009). To our knowledge, three studies (Guinand et al., 2006; Anderson & Dunham, 2008; Rodríguez-Ramilo & Wang, 2012) have investigated the effects of the presence of close relatives on the power of the software STRUCTURE (Pritchard et al., 2000; Falush et al., 2003) to estimate K. Using real and simulated data, these studies showed that the presence of close relatives led to the false detection of population genetic structure when it is absent or to the overestimation of the number of clusters. Rodríguez-Ramilo & Wang (2012) evaluated the improvement achieved by first identifying and removing all family members but one using a relatedness analysis (Wang, 2004; Wang & Santure, 2009) before conducting population structure analysis. This study found better performance of the clustering method implemented in the software STRUCTURE (i.e. higher accuracy in terms of estimated number of clusters) once the samples had been pruned.

Another approach to circumvent the problem of related individuals when inferring population genetic structure could be using clustering methodologies which do not make assumptions about Hardy–Weinberg and linkage equilibrium. Dupanloup et al. (2002) proposed a spatial procedure that uses a simulated annealing algorithm to find the arrangement that maximizes the proportion of total genetic variance due to differences between groups of populations. With a similar rationale, Rodríguez-Ramilo et al. (2009) developed an approach (implemented in the software CLUSTER_DIST; http://dl.dropbox.com/u/5714008/Fernandez.htm) based on the maximization of the mean genetic distance between inferred populations (also solved through a simulated annealing algorithm). This approach was developed based on the idea that highly differentiated populations show a large genetic distance between them. This distance can be calculated from the molecular marker information without assumptions on Hardy–Weinberg or linkage equilibrium. In Rodríguez-Ramilo et al. (2009) the actually implemented distance was the Nei minimum distance (Nei, 1987), which can be calculated from the pairwise molecular co-ancestry between individuals (Caballero & Toro, 2002) or directly from the allelic frequencies.

In the present study, the algorithm implemented in CLUSTER_DIST was evaluated in the presence of related individuals (i.e. full-sib and half-sib families). The performance of this method, in terms of the number of estimated clusters, is compared with the performance of the software STRUCTURE using simulated data.

2. Materials and methods

(i). Simulations

The simulated data were the same as in Rodríguez-Ramilo & Wang (2012). Briefly, the allele frequencies at a locus for the entire population, pi (i = 1, 2,…, L; where L is the number of genotyped loci), were drawn from a uniform Dirichlet distribution, with all parameters set to a value of 1. From these allele frequencies and the parameter FST, the particular allele frequencies of subpopulation j, pij (i = 1, 2,…, n; where n is the number of subpopulations), were then obtained also from a Dirichlet distribution with parameters pi (1−FST)⁄FST. Using the allele frequencies of each subpopulation, the genotypes of individuals from a given subpopulation were then randomly generated for each marker locus. A further generation was simulated to create families of individuals with a given relationship, with genotypes of each descendant obtained following the rules of Mendelian transmission independently for each locus. Individuals with a particular family structure (detailed below) were sampled from the 2nd generation of each subpopulation for clustering analysis.

The simulations considered scenarios involving 3 or 5 subpopulations (n) with 50 individuals per subpopulation and, thus, a total census size of 150 or 250 individuals (N); genetic differentiation level FST = 0·1 or 0·2; individuals genotyped for 10 (20) microsatellite-like markers with 20 alleles each or 100 (200) bi-allelic markers (mimicking single nucleotide polymorphisms (SNPs)); 0, 1 or 2 sib families (in the same subpopulation or in different subpopulations) comprising 4 or 16 siblings per family; and full-sib or half-sib (only simulated for 10 microsatellites) families simulated. The combination of all these factors resulted in a huge number of different scenarios.

(ii). Algorithms

STRUCTURE (Pritchard et al., 2000; Falush et al., 2003) was run with 5000 sweeps of burn-in and 10 000 sweeps of data collection in each replicated scenario, using the admixture and the correlated allele frequency models. All other settings were left with their default values. The range of possible K values evaluated was from two to the simulated number of subpopulations plus one (4 or 6). Note that, following Anderson and Dunham (2008) to reduce computation time, STRUCTURE was run only one time per replicated scenario, then the estimation of K could not be done using Evanno et al. (2005) criterion, because it needs several runs of STRUCTURE for each evaluated K.

However, other alternative criteria have been proposed to estimate K from the output of STRUCTURE. One of these alternative criteria (which does not need several runs of STRUCTURE) is to estimate K from the proportion of inferred ancestry (Q). For a given value of K, STRUCTURE provides the value 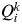Inline graphic, the proportion of the inferred ancestry of individual i (i = 1,…, N) being from cluster k (k = 1,…, K). For each individual i, the cluster that has the highest Q value is the cluster to which this individual belongs to (given a particular value of K). The average of the 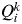Inline graphic for all individuals i belonging to cluster k is symbolized as 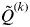Inline graphic. The smallest value of 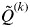Inline graphic across clusters is denoted as 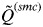Inline graphic, and this value indicates to what extent individuals are assigned unambiguously to the clusters or whether they show mixed ancestry.

Analyses of many simulated and real data sets indicated that 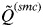Inline graphic decreases slowly as the number of K increases until the true number of subpopulations is reached (see Anderson & Dunham, 2008; Rodríguez-Ramilo & Wang, 2012 for more details). Thereafter, 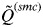Inline graphic decreases rapidly with an increasing value of K. According to this, the inferred number of clusters was determined to be the highest value of K that has 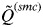Inline graphic > 0·8. This threshold value depends on the number and polymorphism of the evaluated molecular markers, and showed a high efficiency in the simulations considered in this study (Rodríguez-Ramilo & Wang, 2012).

CLUSTER_DIST (Rodríguez-Ramilo et al., 2009) is based on the idea that highly differentiated populations show a high genetic distance between them. This distance can be calculated from molecular markers without taking into account Hardy–Weinberg and linkage equilibrium assumptions. Several genetic distances have been proposed (Laval et al., 2002). Among those distances, the Nei minimum distance (Nei, 1987) has the advantage that it can be calculated through the pairwise molecular co-ancestry between individuals (Caballero & Toro, 2002).

Notwithstanding, a shortcoming of the method is that no measure of confidence is obtained for the final arrangement of clusters. This problem is circumvented in the actual implementation of CLUSTER_DIST by using an allele frequency approach. The considered configurations, instead of assigning each individual to a single cluster, are lists of vectors (one for each individual) carrying their probability to belong to each cluster. Consequently, the sum of positions (i.e. probabilities) for a particular individual equals one. In the final (optimal) configuration those individuals with a probability close to one of belonging to a particular cluster can be assigned with great confidence. Contrarily, assignment of individuals with lower probabilities will carry a higher uncertainty, possibly reflecting the presence of admixture or the insufficient amount of information to assign this individual to a single cluster. Realize that the algorithm does not explicitly allow for admixture, but tries to put individuals in completely separated groups.

The implementation of the method within CLUSTER_DIST uses a simulated annealing algorithm to find the partition that showed the maximal average genetic distance between subpopulations. Simulated annealing is an optimization procedure adequate to deal with many genetic problems (e.g. Fernáandez & Toro, 1999). Parameters used to run the CLUSTER_DIST software in this study included 10 000 alternative solutions generated per step, the maximum number of steps (temperatures) is set to 250, and an initial temperature (T) of 0·00001, which was reduced for each step by a factor of Z (cooling factor) equal to 0·9. CLUSTER_DIST was also run one time per replicated scenario. For each simulated scenario, the range of possible K values evaluated with CLUSTER_DIST ranged between two and six. The number of inferred clusters was estimated with an approach following the same rationale as Evanno et al. (2005), but adapted to genetic distances (please see Rodríguez-Ramilo et al., 2009 for more details).

(iii). Measurement of accuracy

Twenty replicates of each combination of the considered parameters were carried. Accordingly, the proportion of the 20 replicates, where the compared software identified the correct number of subpopulations (3 or 5), was used as the accuracy measure.

3. Results

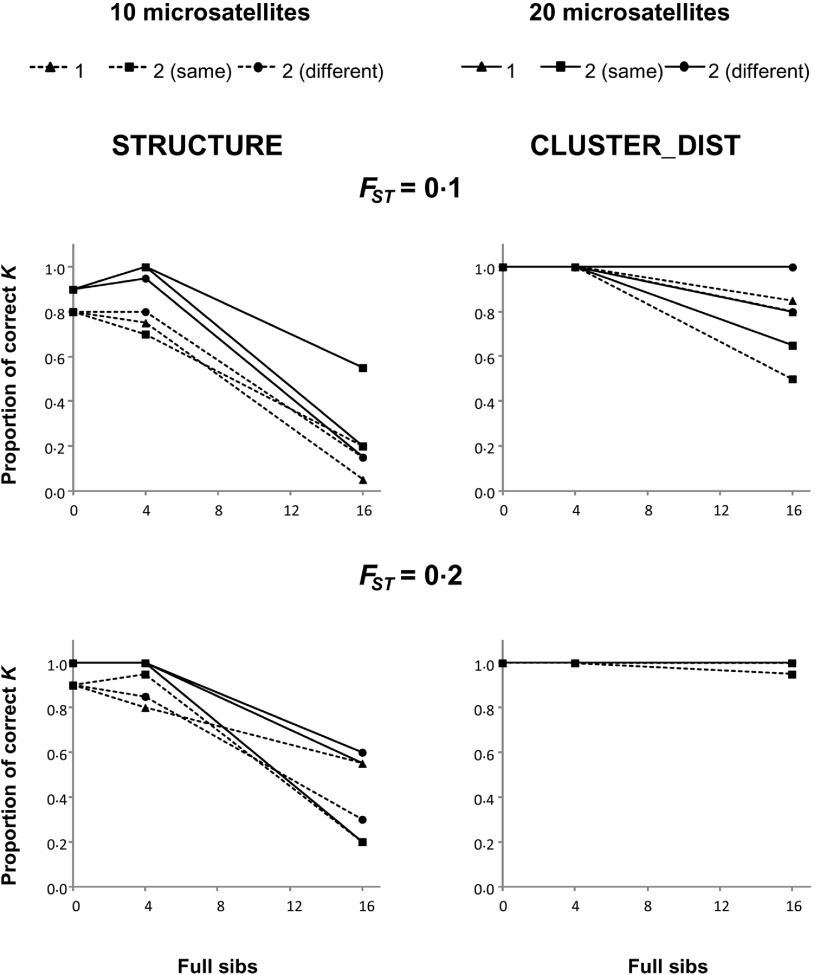
Figure 1 shows the proportion of replicates where the number of clusters was correctly inferred (i.e. estimate was K = 3) by STRUCTURE and CLUSTER_DIST when the real number of subpopulations was n = 3 in the presence of full-siblings. The figure presents results for the two differentiation levels among subpopulations (FST = 0·1 and 0·2) and the two sets of microsatellites-like markers (10 and 20).

Fig. 1.

Fig. 1.

Open in a new tab

Proportion of replicates where STRUCTURE (left panels) and CLUSTER_DIST (right panels) infer K = 3 when n = 3 in the presence of full-siblings. Dashed and solid lines indicate 10 and 20 microsatellites, respectively. Triangles represent one family, squares indicate two families in the same subpopulation, and circles represent two families in different subpopulations.

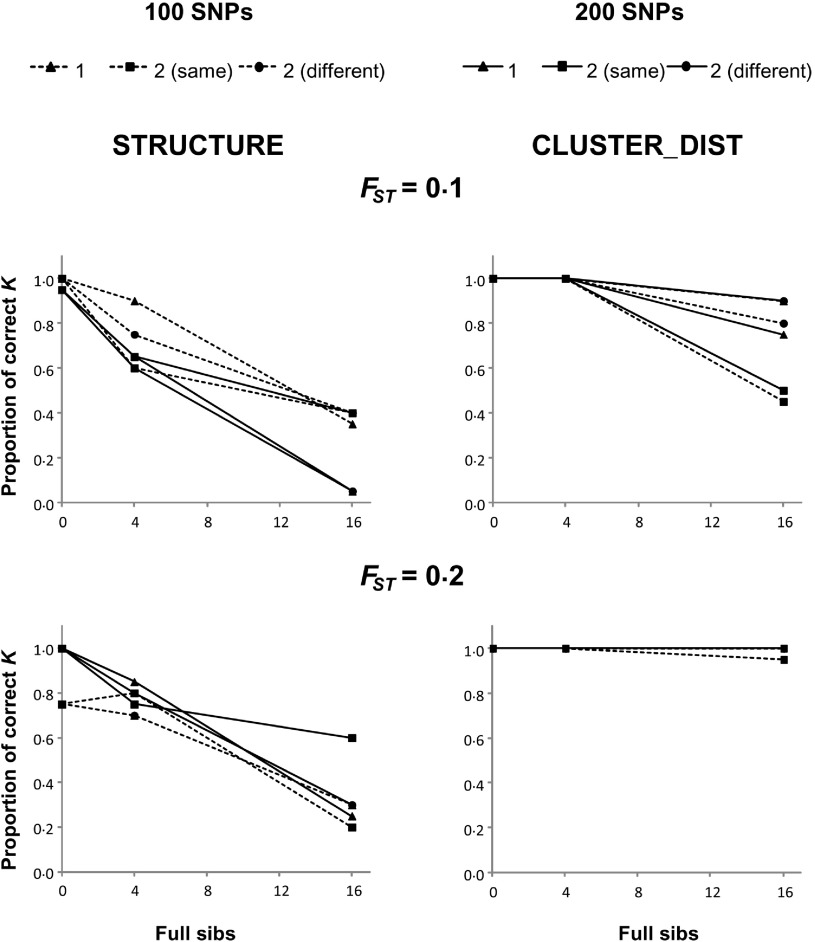
The accuracy of both STRUCTURE and CLUSTER_DIST decreases as the size of the families increases. In fact, both methodologies show a high accuracy when there are no siblings. However, the deterioration in performance with the presence of sib families is less pronounced in the case of CLUSTER_DIST (right panels), especially when the differentiation between subpopulations is high (FST = 0·2). Expectedly, the use of more markers results in a higher accuracy for both methodologies. There is not a clear effect of the number of families when the total number of full-siblings in a sample is fixed. Similar results to those observed for microsatellite loci were also obtained for full-siblings using 100 or 200 SNPs (Fig. 2).

Fig. 2.

Fig. 2.

Open in a new tab

Proportion of replicates where STRUCTURE (left panels) and CLUSTER_DIST (right panels) infer K = 3 when n = 3 in the presence of full-siblings. Dashed and solid lines indicate 100 and 200 SNPs, respectively. Triangles represent one family, squares indicate two families in the same subpopulation, and circles represent two families in different subpopulations.

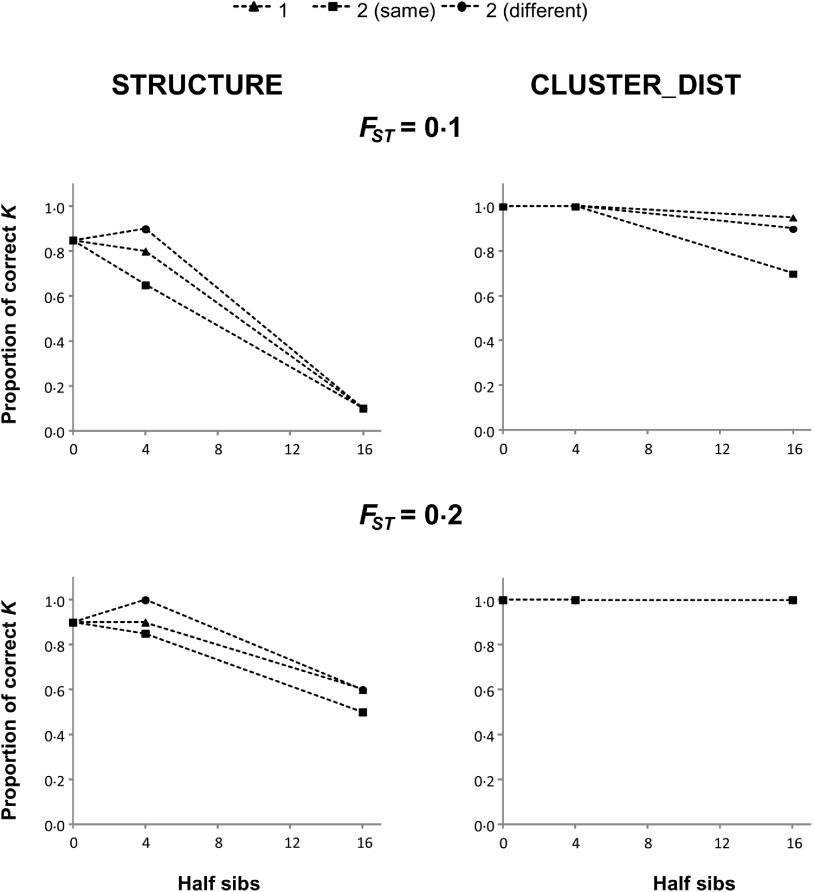
Figure 3 shows the proportion of replicates in which K is correctly inferred by STRUCTURE and CLUSTER_DIST when n = 3 in the presence of half-siblings and using 10 microsatellites. Results and conclusions obtained from them are in agreement with those of previous figures. However, for the same family size and number of families, full-sibs (Fig. 1) produced a greater reduction in accuracy than half-sibs (Fig. 3). In the half-sib scenario, it seems that a greater number of families do lead to a less accurate estimate of K.

Fig. 3.

Fig. 3.

Open in a new tab

Proportion of replicates where STRUCTURE (left panels) and CLUSTER_DIST (right panels) infer K = 3 when n = 3 in the presence of half-siblings, using 10 microsatellites. Triangles represent one family, squares indicate two families in the same subpopulation, and circles represent two families in different subpopulations.

Results obtained for n = 5 with microsatellites, SNPs and full- or half-siblings were very similar to those showed above for three subpopulations (Figs. S1, S2 and S3 in Supplementary Material).

4. Discussion

The existence of close relatives within a subpopulation may lead the program STRUCTURE to infer a wrong number of groups as the assumptions of Hardy–Weinberg and linkage equilibrium within subpopulations will not be met. This has been already shown by some authors (Guinand et al., 2006; Anderson & Dunham, 2008; Rodríguez-Ramilo & Wang, 2012). Families are really genetic structures, but are usually not the focus of most studies which are interested in knowing the organization at the population level. But depending on the final objective of the study, and the particular situation, families may become the relevant grouping, especially when differentiation levels (i.e. FST) are low between subpopulations.

To avoid the bias of clustering methods when relatives are present, Rodríguez-Ramilo & Wang (2012) proposed a simple 2-step alternative consisting of (1) detecting with the software COLONY (Wang, 2004; Wang & Santure, 2009) the confounding family structures from a sample and removing all but one of the members of each family and then (2) conducting a STRUCTURE (Pritchard et al., 2000; Falush et al., 2003) analysis with the reduced sample. The first stage of this 2-step procedure trims the data and makes them to better meet the assumptions of the specific clustering methodology, greatly improving the accuracy of a population structure analysis with the software STRUCTURE. But the final results will be influenced by the accuracy of the estimator of relationships and to what extent the assumptions of the chosen methodology are fulfilled by the data.

In this paper, we introduced another alternative to improve the population genetic structure analyses in the presence of close relatives. This is a one-step procedure that uses a clustering method that is insensitive to deviations from Hardy–Weinberg and linkage equilibrium. Using this approach, there is no need of pre-correcting the data and, therefore, we avoid the possible bias that could appear if the data do not fit the assumptions of the method used to detect the family structure. Accordingly, the results presented in this study indicate that this one-step methodology is less influenced than STRUCTURE when dealing with samples containing close relatives. For this reason, CLUSTER_DIST can be used, in combination with the program STRUCTURE, to infer population genetic structure when close relatives are supposed to be present in a sample.

Removing relatives prior to inferring genetic structure using the genetic distances approach has a negligible effect (data not shown). This is another evidence of the little influence of the presence of relatives within subpopulations on the power of this clustering strategy.

5. Supplementary material

For supplementary material accompanying this paper visit http://dx.doi.org/10.1017/S0016672314000068.

S0016672314000068sup001.pdf (295.1KB, pdf)

click here to view supplementary material

Supplementary Material

Supplementary information supplied by authors.

Acknowledgments

We are very grateful to one anonymous referee for helpful comments on the manuscript.

Financial support

This work was funded by the Spanish government project (Consolider Ingenio Aquagenomics: CSD200700002).

Statement of Interest

None.

References

  1. Anderson E. C. & Dunham K. K. (2008). The influence of family groups on inferences made with the program STRUCTURE. Molecular Ecology Resources 8, 1219–1229. [DOI] [PubMed] [Google Scholar]
  2. Caballero A. & Toro M. A. (2002). Analysis of genetic diversity for the management of conserved subdivided populations. Conservation Genetics 3, 289–299. [Google Scholar]
  3. Corander J., Waldmann P., Marttinen P. & Sillanpaa M. J. (2004). BAPS 2: enhanced possibilities for the analysis of genetic population structure. Bioinformatics 20, 2363–2369. [DOI] [PubMed] [Google Scholar]
  4. Dawson K. J. & Belkhir K. (2001). A Bayesian approach to the identification of panmictic populations and the assignment of individuals. Genetics Research 78, 59–77. [DOI] [PubMed] [Google Scholar]
  5. Dupanloup I., Schneider S. & Excoffier L. (2002). A simulated annealing approach to define the genetic structure of populations. Molecular Ecology 11, 2571–2581. [DOI] [PubMed] [Google Scholar]
  6. Evanno G., Regnaut S. & Goudet J. (2005). Detecting the number of clusters of individuals using the software STRUCTURE: a simulation study. Molecular Ecology 14, 2611–2620. [DOI] [PubMed] [Google Scholar]
  7. Falush D., Stephens M. & Pritchard J. K. (2003). Inference of population structure using multilocus genotype data: linked loci and correlated allele frequencies. Genetics 164, 1567–1587. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Fernández J. & Toro M. A. (1999). The use of mathematical programming to control inbreeding in selection schemes. Journal of Animal Breeding and Genetics 116, 447–466. [Google Scholar]
  9. Gao H., Williamson S. & Bustamante C. D. (2007). A Markov chain Monte Carlo approach for joint inference of population structure and inbreeding rates from multilocus genotype data. Genetics 176, 1635–1651. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Guinand B., Scribner K. T., Page K. S., Filcek K., Main L. & Burnham-Curtis M. K. (2006). Effects of coancestry on accuracy of individual assignments to populations of origin: examples using Great Lakes lake trout (Salvelinus namaycush). Genetica 127, 329–340. [DOI] [PubMed] [Google Scholar]
  11. Huelsenbeck J. P. & Andolfatto P. (2007). Inference of population structure under a Dirichlet process model. Genetics 175, 1787–1802. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Laval G., Sancristobal M. & Chevalet C. (2002) Measuring genetic distances between breeds: use of some distances in various short term evolution models. Genetics Selection Evolution 34, 481–507. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Nei M. (1987). Molecular Evolutionary Genetics. New York: Columbia University Press. [Google Scholar]
  14. Pritchard J. K., Stephens M. & Donnelly P. (2000). Inference of population structure using multilocus genotype data. Genetics 155, 945–959. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Pritchard J. K., Wen X. & Falush D. (2009). Documentation for STRUCTURE Software: Version 2.3. Technical Report. Department of Human Genetics, University of Chicago, Chicago, Illinois. [Google Scholar]
  16. Rodríguez-Ramilo S. T. & Wang J. (2012). The effect of close relatives on unsupervised Bayesian clustering algorithms in population genetic structure analysis. Molecular Ecology Resources 12, 873–884. [DOI] [PubMed] [Google Scholar]
  17. Rodríguez-Ramilo S. T., Toro M. A. & Fernández J. (2009). Assessing population genetic structure via the maximisation of genetic distance. Genetics Selection Evolution 41, 49. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Wang J. (2004). Sibship reconstruction from genetic data with typing errors. Genetics 166, 1963–1979. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Wang J. & Santure A. W. (2009). Parentage and sibship inference from multilocus genotype data under polygamy. Genetics 181, 1579–1594. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

For supplementary material accompanying this paper visit http://dx.doi.org/10.1017/S0016672314000068.

S0016672314000068sup001.pdf (295.1KB, pdf)

click here to view supplementary material

Supplementary Material

Supplementary information supplied by authors.

Articles from Genetics Research are provided here courtesy of Wiley

RESOURCES