Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2020 Feb 14;5(7):3571–3578. doi: 10.1021/acsomega.9b03911

Prediction of Nanofluid Temperature Inside the Cavity by Integration of Grid Partition Clustering Categorization of a Learning Structure with the Fuzzy System

Narjes Nabipour †, Meisam Babanezhad ‡, Ali Taghvaie Nakhjiri §, Saeed Shirazian ∥,⊥,*
PMCID: PMC7045517  PMID: 32118172

Abstract

graphic file with name ao9b03911_0010.jpg

In this study, a quadratic cavity is simulated using computational fluid dynamics (CFD). The simulated cavity includes nanofluids containing copper (Cu) nanoparticles. The L-shaped thermal element exists in this cavity to produce heat distribution along with the domain. Results such as fluid velocity distribution in two dimensions and the fluid temperature field were generated as CFD simulation results. These outputs were evaluated using an adaptive neuro-fuzzy inference system (ANFIS) for learning and then the prediction process. In the training process related to the ANFIS method, x coordinates, y coordinates, and fluid temperature are three inputs, and the fluid velocity in line with Y is the output. During the learning process, the data have been classified using a clustering method called grid clustering. In line with the attempt to rise ANFIS intelligence, the alterations in the number of input parameters and of membership structure have been analyzed. After reaching the highest level of intelligence, the fluid velocity nodes were predicted to be in line with y, especially cavity nodes, which were absent in CFD simulations. The simulation findings indicated that there is a good agreement between CFD and clustering approach, while the total simulation time for learning and prediction is shorter than the time needed for calculation using the CFD method.

1. Introduction

The past few decades have witnessed an increase in the attention of fluid flow in the industrial domain size in different engineering applications including lubrication technology, nuclear reactors, pharmaceuticals, cooling of electronic devices, processing foods, and membrane sequestration.1−7 A large number of research studies has been carried out to study the flow field and thermal distribution in different shapes of lid-driven cavities, while the main area of concern has been fluids with a thermal performance which is relatively low.8−11 Still, there is an increasing demand for cooling systems with high performance which require a specific agent with a high heat transfer rate. Choi12 introduced nanofluids as highly effective coolant fluids that outperformed standard pure fluids as to heat exchange performance. Given the highly sophisticated thermal and fluid behavior of nanofluids, different models have been introduced for estimating the specifications of nanofluids, including thermophysical properties.13−15 The design of the models is based on heat transfer, Brownian dynamics, and nanoparticle geometry along with the interaction of pure fluid and nanoparticles.15−20

There are recent reports about thermal distribution in lid-driven cavities which states that nanofluids can change the thermal behavior of fluid in the domain. Authors in ref (21) examined the thermal behavior of Cu-water nanofluids in the cavity by using the numerical method. The authors concluded that with increasing amounts of nanoparticles, the heat transfer rate increases. Moreover, they demonstrated that the direction of sliding walls and Richardson number were effective in the performance of the cavity in terms of heat transfer. In a similar study by Muthtamilselvan et al.,22 a lid-driven cavity filled with Cu-water nanofluids was examined in terms of the transport mechanism of mixed convection in a numerical way. The numerical results supported that adding pure water with Cu nanoparticles improved the thermal performance of the cavity. The laminar mixed convection flows were examined numerically by Talebi et al23 using the Cu-water nanofluid fed into a cavity. The results showed that when Reynolds numbers are fixed, the flow field and thermal distribution of the nanofluid are affected by the amount of solids in the fluid, particularly at very high Rayleigh numbers.24,25

It is notable that improving heat transfer using nanofluids is still a complicated problem. According to ref26 and,3 the augmentation or decrease in heat transfer was because of the changes in the models employed to find the properties of nanofluids. Therefore, there is a need for further studies on computational fluid dynamics (CFD) to model nanofluid properties in a more reliable manner. Such modeling, still, is time-consuming and needs more funding. The recent development in the field is more emphasized on the learning process with an artificial neural cell algorithm called the artificial neural network (ANN) and integration of this method with the fuzzy system27−30 for solving engineering problems with shorter computation time. Still, the application of these methods in studies on thermal energy distribution is highly limited.31,32 The adaptive neuro-fuzzy inference system (ANFIS) is known as a reliable method because it includes the ANN superior features and the neuro-fuzzy architectures.33−35

The ANFIS structure represents the ANN and fuzzy logic methodologies. A key feature of the ANFIS is its capability to train complex relationship using the pattern data.15,28,36,37 For nonlinear system modeling, the input space is divided by the ANFIS into several local regions. A simple local model is created for each local region using linear functions of adjustable coefficients. Therefore, ANFIS utilizes fuzzy membership functions (MFs) for dividing each input dimension.38 It is possible to activate many local regions at the same time to cover the input space by overlapping MFs. A critical role is played by the resolution of partitioning of the input space to determine ANFIS ability for approximation. This is carried out based on the MF count in the ANFIS and the number of layers.

It is critical to find an effective and comprehensive pattern set for training the ANFIS.39−41 In the case where an incomplete set (where not every possible condition is met) is chosen as the ANFIS training set, the network’s capability to deal with an unknown condition will be attenuated. To improve the capability, a learning set of the ANFIS must be as wide as possible over the whole space of the input–output data set. Here, the results of the CFD simulation are obtained as a part of the study for training the models. In this study, with the subtractive clustering method, the flow field and thermal field in the cavity domain are categorized. For better accuracy of the method, different function structures and input parameters are used during the learning process. After the learning process, the CFD results and the ANFIS method are compared with the standard deviation (StD) method, and then, the CFD and ANFIS flow field and thermal distribution are compared with each other. The multiphase flow modeling is used to show the behavior of the nanofluid in the matrix phase. This type of modeling enables us to analyze the hydrodynamics between nanoparticles and the primary fluid/phase. In this study, as a novelty, the interaction between phases is simulated with the CFD method. After modeling of nanofluids in the domain, a machine-learning method, such as the ANFIS method, is used to model nanofluids with a faster modeling algorithm. The machine-learning method is the interface modeling between CFD and the optimization process to reduce the time of optimization during process engineering.

2. Methodology

2.1. CFD Method

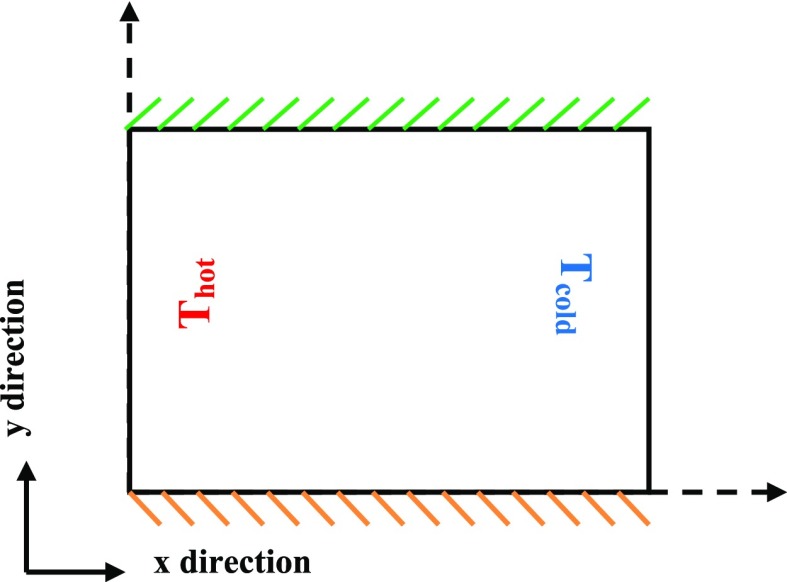
As shown in Figure 1, a vertical square enclosure with relevant physical parameters is provided. Constant temperature conditions are considered for the right and left vertical boundaries. The value of one is considered for their various dimensionless values between them.42,43 The temperature of the left boundary is higher than the right one and is considered to be a hot boundary.20 The solid boundaries are exposed to constant conditions, and adiabatic conditions are considered for the bottom and top boundaries. The interaction of nanoparticles with the matrix phase is simulated by the cubic-interpolated pseudo particle (CIP) method, and different nanoparticles are used during validation of the CFD study with the existing analytical solution. In the cavity, the shear flow can appear in the domain and the shear mechanism can be changed, and the break-up process during mixing can be defined and modeled. Therefore, we use simple geometry to define the heat source or shear mechanism for simulation of the mixing process. In this work, for the first time, the nanofluid contains Cu in water. CIP is employed for minimizing the numerical diffusion of a high-order Navier–Stokes equation for two-dimensional problems.

Figure 1.

Figure 1

Open in a new tab

Schematic and boundary condition of the cavity.

The equations of vorticity and energy have been obtained based on the dimensionless analysis16 in which the thermal diffusivity is calculated as follows20

2.1. 1

According to a reference temperature, the following relation is considered for the effective density of a fluid with suspended particles44

2.1. 2

where φ, ρf, and ρs stand for the volume fraction of suspended particles, pure fluid density, and particle density, respectively. The effective viscosity for a nanofluid is provided by Brinkman. This nanofluid includes pure water with viscosity μf. Brinkman also provided a dilute suspension of spherical, solid, and small particles45

2.1. 3

Wasp developed the effective stagnant thermal conductivity for the solid–liquid mixture as follows46

2.1. 4

The CIP model is applied for solving the advection term, which is necessary for solving vorticity, and further details can be found in ref (16). Several factors including the thermal conductivity as well as the heat capacity of both the ultrafine particles and the pure fluid, the nanofluid viscosity, the flow arrangement, and the volume fraction of solids particles are the key factors affecting the Nusselt number of the nanofluids. The nanofluid local Nusselt number is derived as follows44

2.1. 5

and

2.1. 6

The mean Nusselt number is defined as follows

2.1. 7

2.2. ANFIS Method

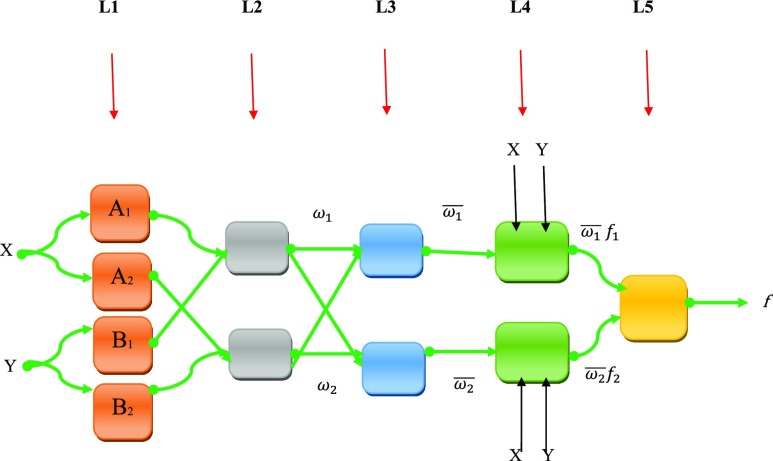
The ANFIS is an effective fuzzy system designed to predict how complicated nonlinear systems behave.47,48 The ANFIS method is a combination of neural network and fuzzy system.7,49,50 The learning part is the responsibility of neural cells because of the great ability of this method in learning different phenomena. After the learning process, the method transfers all information of learning to the fuzzy structure system, and the fuzzy system can predict the process behavior.20,32,51−53 There are three different fuzzy reasonings in which if-then rules were proposed by Takagi and Sugeno. These were used in the ANFIS structure.23Figure 2 illustrates the structure used by the ANFIS method to predict hydrodynamic specifications in the cavity. Here, X coordinate, Y coordinate, and nanofluid temperature were adopted to achieve nanofluid velocity (in Y coordinate) as the output. At the first layer, the inputs were divided into different numbers of MFs. Then, at the second layer, the input signals generated by the first layer were multiplied using AND rule and the node function. For example, the ith rule’s function is as follows

2.2. 8

where wi stands for the outcoming signal of the node at the second layer and μAi, μBi, and μCi represent the input signals generated from implemented MFs on inputs, X coordinate (X), Y coordinate (Y), and nanofluid temperature (T), to the node of the second layer, respectively. At the third layer, the relative value of the firing strength of each rule is obtained. The total size of all rules’ firing power is as follows

2.2. 9

where w̅i represents the called normalized firing strengths. The fourth layer uses the function of a consequence according to the if-then rule introduced in ref (54). Therefore, the node function is as follows

2.2. 10

where pi, qi, ri, and si (known as consequent parameters) stand for the if-then rules’ parameters.

Figure 2.

Figure 2

Open in a new tab

Schematic of the ANFIS structure.

3. Results and Discussion

In this article, the CFD method outputs were analyzed as inputs and outputs of learning processes of ANFIS methods in different requirements considering the number of inputs and MFs.

Some hypothesizes have been created in order to start the ANFIS method which are as follows:

  • In heat transfer, Grashof number (Gr) is dimensionless in which GR is 71,000.

  • In nanofluids, the value shows the nanoparticle percentage which is 20%.

  • The P-value conveys the data percentage in the ANFIS training process.

  • The Epoch frequency is 750.

  • Generalized bell-shop MF (gbellmf) is an MF and has been used in this study.

  • At the beginning of the learning process, the x coordinate is considered as the first input, while velocity in y is considered as the output, and the number of MFs equals to 2 in the training process.

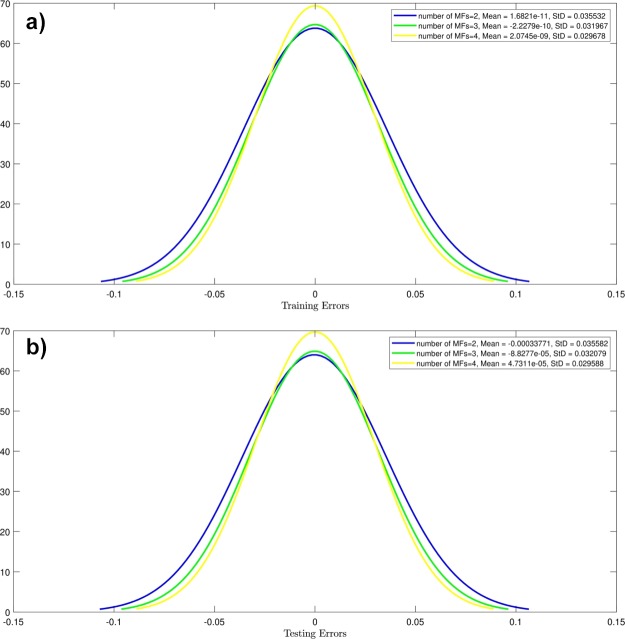
Figure 3a,b shows the StD error training and testing processes equal to 0.0355. Next, the learning process occurs with the increase in MFs from 2 to 3 and 4. In this process, the change in the StD value was low which demonstrates a slight increase in ANFIS intelligence. According to this failure in increasing MFs of the system intelligence, the number of inputs changed from 1 to 2, and also, the y coordinate was considered to be the second input.

Figure 3.

Figure 3

Open in a new tab

(a) Training process errors (one input), type of MFs is gbellmf, variety number of MFs, max iteration = 750. (b) Testing process errors (one input), type of MFs is gbellmf, variety number of MFs, max iteration = 750.

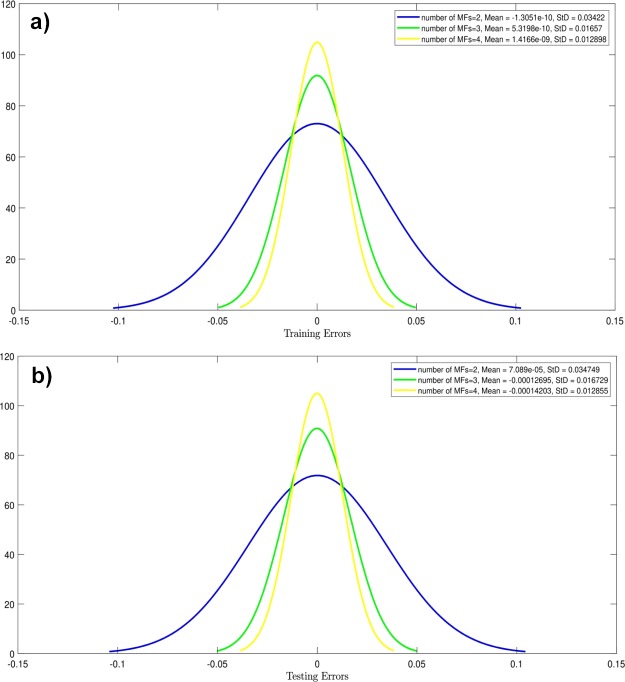
The learning process is fulfilled by fixing the number of MFs to 2. Considering Figure 4a for the training process and Figure 4b for the testing process, the StD value in training and testing processes equals to 0.03422 and 0.034749, respectively. Considering the previous condition, the StD value did not change a lot. Hence, the number of MFs increases from 2 to 3 and 4. Then, testing and training processes were performed once again. The results showed an appropriate change and increase in the StD value, where MFs equal to 4. An increase in the StD value for training and testing processes equals to 0.012898 and 0.012855, respectively. Then, in order to attain higher intelligence in the ANFIS method, the number of input effects from 2 to 3 was analyzed; also, the fluid temperature was considered to be the third input. The learning process was completed separately for number of MFs 2, 3, and 4. The results are shown in Figure 5a for the training process and in Figure 5b for the testing process.

Figure 4.

Figure 4

Open in a new tab

(a) Training process errors (two inputs), type of MFs is gbellmf, variety number of MFs, max iteration = 750. (b) Testing process errors (two inputs), type of MFs is gbellmf, variety number of MFs, max iteration = 750.

Figure 5.

Figure 5

Open in a new tab

(a) Training process errors (three inputs), type of MFs is gbellmf, variety number of MFs, max iteration = 750. (b) Testing process errors (three inputs), type of MFs is gbellmf, variety number of MFs, max iteration = 750.

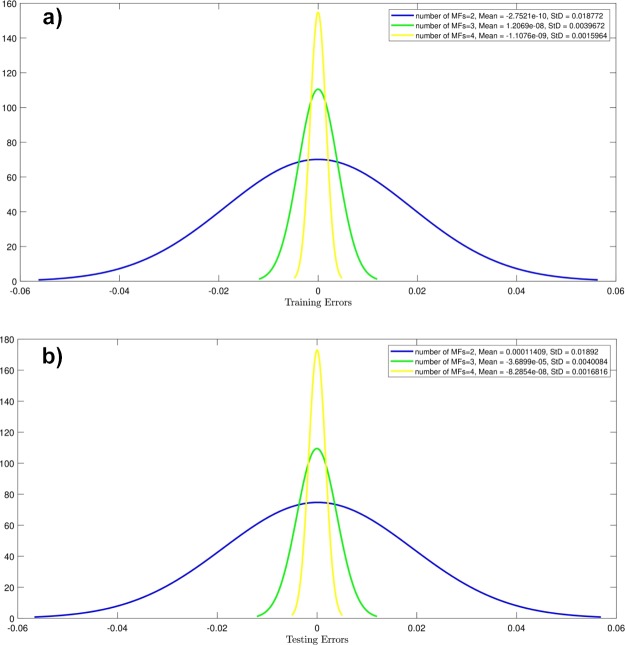
The input numbers increased from 2 to 3, while the number of MFs equaled to 2, but there was no significant difference when MFs equal to 4. However, there is an increase in StD. Now, if MFs change from 3 to 4, there is a significant increase in StD. Therefore, in the training and testing process, we have 0.015964 and 0.0016816, respectively. Considering these two numbers, the chances of error are less and we can see complete intelligence in the ANFIS method (see Figure 6).

Figure 6.

Figure 6

Open in a new tab

Learning process (three inputs), type of MFs is gbellmf, number of MFs = 4, max iteration = 750.

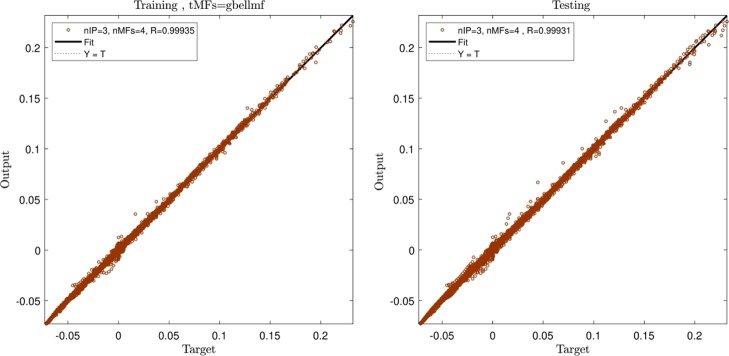
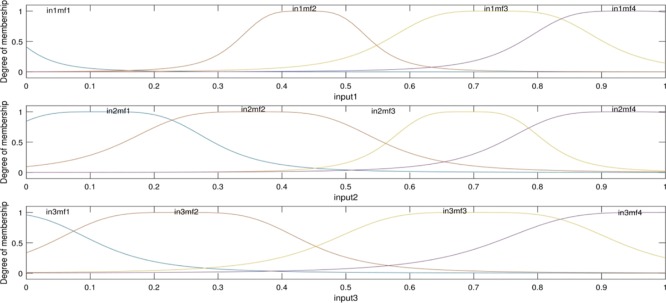
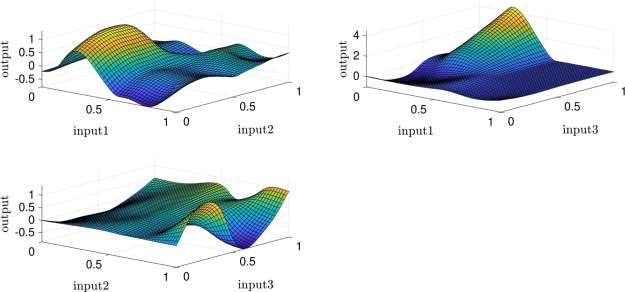
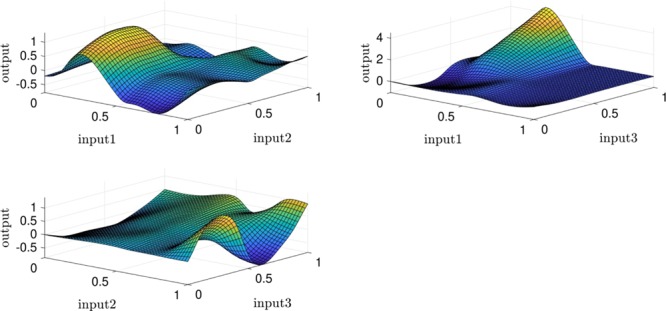
In Figure 7, the degree of membership can be seen. Using the appropriate intelligence in ANFIS, the absent points in ANFIS learning would be predicted and also compared with the CFD results, in which, the appropriate correspondence between the CFD output and ANFIS method can be illustrated (see Figure 8).

Figure 7.

Figure 7

Open in a new tab

Degree of membership (three inputs), grid partition clustering, gbellmf, number of MFs = 4, max iteration = 750.

Figure 8.

Figure 8

Open in a new tab

Validation process (three inputs), gbellmf, number of MFs = 4, max iteration = 750.

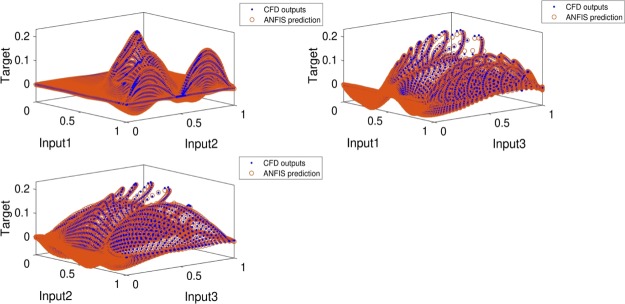
Another ability of the ANFIS is to predict points that are absent in the CFD simulation of fluid flow, and it can provoke appropriate ability in stopping complex CFD method calculations (see Figure 9).

Figure 9.

Figure 9

Open in a new tab

Prediction (three inputs), type of MFs is gbellmf, number of MFs = 4, max iteration = 750.

4. Conclusions

In this study, the ANFIS method has been employed to train the thermal and fluid field in the cavity calculated by the CFD method. The grid partition clustering method was used for clustering the fluid and thermal field in the domain. The flow and thermal distribution in the cavity were simulated with the clustering method and then compared with the CFD results. Additionally, the effects of changing parameters such as the number of inputs and MFs were analyzed in ANFIS intelligence. We have reached complete intelligence by changing ANFIS intelligence parameters. We finally predicted the velocity in the domain and compared the results with CFD outputs. The positive effect of combining ANFIS and CFD methods in nanofluid studies in a cavity shows that smart modeling can be a good alternative to predict the flow and thermal distribution in the industrial domains with inexpensive computational time.

The authors declare no competing financial interest.

References

  1. Koseff J. R.; Street R. L. The lid-driven cavity flow: a synthesis of qualitative and quantitative observations. J. Fluids Eng. 1984, 106, 390. 10.1115/1.3243136. [DOI] [Google Scholar]
  2. Morzynski M.; Popiel C. O. Laminar heat transfer in a two-dimensional cavity covered by a moving wall. Numer. Heat Transfer 1988, 13, 265–273. 10.1080/10407788808910004. [DOI] [Google Scholar]
  3. Abu-Nada E. Effects of variable viscosity and thermal conductivity of Al2O3-water nanofluid on heat transfer enhancement in natural convection. Int. J. Heat Fluid Flow 2009, 30, 679–690. 10.1016/j.ijheatfluidflow.2009.02.003. [DOI] [Google Scholar]
  4. Asadi A.; Pourfattah F.; Miklós Szilágyi I.; Afrand M.; Żyła G.; Seon Ahn H.; Wongwises S.; Minh Nguyen H.; Arabkoohsar A.; Mahian O. Effect of sonication characteristics on stability, thermophysical properties, and heat transfer of nanofluids: A comprehensive review. Ultrason. Sonochem. 2019, 58, 104701. 10.1016/j.ultsonch.2019.104701. [DOI] [PubMed] [Google Scholar]
  5. Nakhjiri A. T.; Heydarinasab A.; Bakhtiari O.; Mohammadi T. The effect of membrane pores wettability on CO2 removal from CO2/CH4 gaseous mixture using NaOH, MEA and TEA liquid absorbents in hollow fiber membrane contactor. Chin. J. Chem. Eng. 2018, 26, 1845–1861. 10.1016/j.cjche.2017.12.012. [DOI] [Google Scholar]
  6. Nakhjiri A. T.; Heydarinasab A. Computational simulation and theoretical modeling of CO2 separation using EDA, PZEA and PS absorbents inside the hollow fiber membrane contactor. J. Ind. Eng. Chem. 2019, 78, 106–115. 10.1016/j.jiec.2019.06.031. [DOI] [Google Scholar]
  7. Alarifi I. M.; Nguyen H. M.; Naderi Bakhtiyari A.; Asadi A. Feasibility of ANFIS-PSO and ANFIS-GA Models in Predicting Thermophysical Properties of Al2O3-MWCNT/Oil Hybrid Nanofluid. Materials 2019, 12, 3628. 10.3390/ma12213628. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Besagni G.; Guédon G. R.; Inzoli F. Computational fluid-dynamic modeling of the mono-dispersed homogeneous flow regime in bubble columns. Nucl. Eng. Des. 2018, 331, 222–237. 10.1016/j.nucengdes.2018.03.003. [DOI] [Google Scholar]
  9. Duan G.; Chen B.; Koshizuka S.; Xiang H. Stable multiphase moving particle semi-implicit method for incompressible interfacial flow. Comput. Methods Appl. Mech. Eng. 2017, 318, 636–666. 10.1016/j.cma.2017.01.002. [DOI] [Google Scholar]
  10. Shi Y.; Tang G. H.; Wang Y. Simulation of three-component fluid flows using the multiphase lattice Boltzmann flux solver. J. Comput. Phys. 2016, 314, 228–243. 10.1016/j.jcp.2016.03.011. [DOI] [Google Scholar]
  11. Li Q.; Luo K. H.; Kang Q. J.; He Y. L.; Chen Q.; Liu Q. Lattice Boltzmann methods for multiphase flow and phase-change heat transfer. Prog. Energy Combust. Sci. 2016, 52, 62–105. 10.1016/j.pecs.2015.10.001. [DOI] [Google Scholar]
  12. Choi S. U.; Eastman J. A.. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Argonne National Laboratory: IL (United States), 1995.
  13. Daungthongsuk W.; Wongwises S. A critical review of convective heat transfer of nanofluids. Renewable Sustainable Energy Rev. 2007, 11, 797–817. 10.1016/j.rser.2005.06.005. [DOI] [Google Scholar]
  14. Delavar M. A.; Farhadi M.; Sedighi K. Numerical simulation of direct methanol fuel cells using lattice Boltzmann method. Int. J. Hydrogen Energy 2010, 35, 9306–9317. 10.1016/j.ijhydene.2010.02.126. [DOI] [Google Scholar]
  15. Selimefendigil F.; Öztop H. F. Magnetic field effects on the forced convection of CuO-water nanofluid flow in a channel with circular cylinders and thermal predictions using ANFIS. Int. J. Mech. Sci. 2018, 146–147, 9–24. 10.1016/j.ijmecsci.2018.07.011. [DOI] [Google Scholar]
  16. Safdari A.; Dabir H.; Kim K. C. Cubic-Interpolated Pseudo-particle model to predict thermal behavior of a nanofluid. Comput. Fluids 2018, 164, 102–113. 10.1016/j.compfluid.2017.05.029. [DOI] [Google Scholar]
  17. Mohebbi R.; Rashidi M. M.; Izadi M.; Sidik N. A. C.; Xian H. W. Forced convection of nanofluids in an extended surfaces channel using lattice Boltzmann method. Int. J. Heat Mass Transfer 2018, 117, 1291–1303. 10.1016/j.ijheatmasstransfer.2017.10.063. [DOI] [Google Scholar]
  18. Asadi A.; Aberoumand S.; Moradikazerouni A.; Pourfattah F.; Żyła G.; Estelle P.; Mahian O.; Wongwises S.; Nguyen H. M.; Arabkoohsar A. Recent advances in preparation methods and thermophysical properties of oil-based nanofluids: A state-of-the-art review. Powder Technol 2019, 352, 209. 10.1016/j.powtec.2019.04.054. [DOI] [Google Scholar]
  19. Nakhjiri A. T.; Heydarinasab A.; Bakhtiari O.; Mohammadi T. Modeling and simulation of CO2 separation from CO2/CH4 gaseous mixture using potassium glycinate, potassium argininate and sodium hydroxide liquid absorbents in the hollow fiber membrane contactor. J. Environ. Chem. Eng. 2018, 6, 1500–1511. 10.1016/j.jece.2018.01.068. [DOI] [Google Scholar]
  20. Xu P.; Babanezhad M.; Yarmand H.; Marjani A. Flow visualization and analysis of thermal distribution for the nanofluid by the integration of fuzzy c-means clustering ANFIS structure and CFD methods. J. Visualization 2019, 1–14. 10.1007/s12650-019-00614-0. [DOI] [Google Scholar]
  21. Tiwari R. K.; Das M. K. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int. J. Heat Mass Transfer 2007, 50, 2002–2018. 10.1016/j.ijheatmasstransfer.2006.09.034. [DOI] [Google Scholar]
  22. Muthtamilselvan M.; Kandaswamy P.; Lee J. Heat transfer enhancement of copper-water nanofluids in a lid-driven enclosure. Commun. Nonlinear Sci. Numer. Simulat. 2010, 15, 1501–1510. 10.1016/j.cnsns.2009.06.015. [DOI] [Google Scholar]
  23. Talebi F.; Mahmoudi A. H.; Shahi M. Numerical study of mixed convection flows in a square lid-driven cavity utilizing nanofluid. Int. Commun. Heat Mass Transfer 2010, 37, 79–90. 10.1016/j.icheatmasstransfer.2009.08.013. [DOI] [Google Scholar]
  24. Lai F.-H.; Yang Y.-T. Lattice Boltzmann simulation of natural convection heat transfer of Al2O3/water nanofluids in a square enclosure. Int. J. Therm. Sci. 2011, 50, 1930–1941. 10.1016/j.ijthermalsci.2011.04.015. [DOI] [Google Scholar]
  25. Mahmoodi M. Numerical simulation of free convection of a nanofluid in L-shaped cavities. Int. J. Therm. Sci. 2011, 50, 1731–1740. 10.1016/j.ijthermalsci.2011.04.009. [DOI] [Google Scholar]
  26. Ho C. J.; Chen M. W.; Li Z. W. Numerical simulation of natural convection of nanofluid in a square enclosure: effects due to uncertainties of viscosity and thermal conductivity. Int. J. Heat Mass Transfer 2008, 51, 4506–4516. 10.1016/j.ijheatmasstransfer.2007.12.019. [DOI] [Google Scholar]
  27. Varol Y.; Avci E.; Koca A.; Oztop H. F. Prediction of flow fields and temperature distributions due to natural convection in a triangular enclosure using Adaptive-Network-Based Fuzzy Inference System (ANFIS) and Artificial Neural Network (ANN). Int. Commun. Heat Mass Transfer 2007, 34, 887–896. 10.1016/j.icheatmasstransfer.2007.03.004. [DOI] [Google Scholar]
  28. Varol Y.; Koca A.; Oztop H. F.; Avci E. Analysis of adaptive-network-based fuzzy inference system (ANFIS) to estimate buoyancy-induced flow field in partially heated triangular enclosures. Expert Syst. Appl. 2008, 35, 1989–1997. 10.1016/j.eswa.2007.08.073. [DOI] [Google Scholar]
  29. Gültekin Çitil H.; Altınışık N. On the eigenvalues and the eigenfunctions of the Sturm-Liouville fuzzy boundary value problem. J. Math. Comput. Sci. 2017, 7, 786–805. [Google Scholar]
  30. Gültekin H.; Altinişik N. On solution of two-point fuzzy boundary value problems. Bull. Soc. Math. Serv. Stand. 2014, 11, 31–39. 10.18052/www.scipress.com/bsmass.11.31. [DOI] [Google Scholar]
  31. Babanezhad M.; Rezakazemi M.; Hajilary N.; Shirazian S. Liquid-phase chemical reactors: Development of 3D hybrid model based on CFD-adaptive network-based fuzzy inference system. Can. J. Chem. Eng. 2019, 97, 1676–1684. 10.1002/cjce.23378. [DOI] [Google Scholar]
  32. Shamshirband S.; Babanezhad M.; Mosavi A.. Prediction of Flow Characteristics in the Bubble Column Reactor by the Artificial Pheromone-Based Communication of Biological Ants. 2019, arXiv:2001.04276. [Google Scholar]
  33. Çitil H. G. The relationship between the solutions according to the noniterative method and the generalized differentiability of the fuzzy boundary value problem. Malaya J. Matematik 2018, 06, 781–787. 10.26637/mjm0604/0012. [DOI] [Google Scholar]
  34. Citil H. G. On the exact and the approximate solutions of second-order fuzzy initial value problems with constant coefficients. Malaya J. Matematik 2018, 06, 61–68. 10.26637/mjm0601/0009. [DOI] [Google Scholar]
  35. Citil H. G. Comparison results of linear differential equations with fuzzy boundary values. J. Sci. Arts 2018, 18, 33–48. [Google Scholar]
  36. Pourtousi M.; Sahu J. N.; Ganesan P.; Shamshirband S.; Redzwan G. A combination of computational fluid dynamics (CFD) and adaptive neuro-fuzzy system (ANFIS) for prediction of the bubble column hydrodynamics. Powder Technol. 2015, 274, 466–481. 10.1016/j.powtec.2015.01.038. [DOI] [Google Scholar]
  37. Nakhjiri A. T.; Heydarinasab A.; Bakhtiari O.; Mohammadi T. Experimental investigation and mathematical modeling of CO2 sequestration from CO2/CH4 gaseous mixture using MEA and TEA aqueous absorbents through polypropylene hollow fiber membrane contactor. J. Membr. Sci. 2018, 565, 1–13. 10.1016/j.memsci.2018.07.095. [DOI] [Google Scholar]
  38. Pourtousi M.; Zeinali M.; Ganesan P.; Sahu J. N. Prediction of multiphase flow pattern inside a 3D bubble column reactor using a combination of CFD and ANFIS. RSC Adv. 2015, 5, 85652–85672. 10.1039/c5ra11583c. [DOI] [Google Scholar]
  39. Panella M.; Gallo A. S. An input-output clustering approach to the synthesis of ANFIS networks. IEEE Trans. Fuzzy Syst. 2005, 13, 69–81. 10.1109/tfuzz.2004.839659. [DOI] [Google Scholar]
  40. Pashaie P.; Jafari M.; Baseri H.; Farhadi M. Nusselt number estimation along a wavy wall in an inclined lid-driven cavity using adaptive neuro-fuzzy inference system (anfis). Int. J. Eng., Trans. A 2013, 26, 383. 10.5829/idosi.ije.2013.26.04a.07. [DOI] [Google Scholar]
  41. Pourfattah F.; Abbasian Arani A. A.; Babaie M. R.; Nguyen H. M.; Asadi A. On the thermal characteristics of a manifold microchannel heat sink subjected to nanofluid using two-phase flow simulation. Int. J. Heat Mass Transfer 2019, 143, 118518. 10.1016/j.ijheatmasstransfer.2019.118518. [DOI] [Google Scholar]
  42. Doran P. M.Bioprocess Engineering Principles; Elsevier, 1995. [Google Scholar]
  43. Takewaki H.; Yabe T. The cubic-interpolated pseudo particle (CIP) method: application to nonlinear and multi-dimensional hyperbolic equations. J. Comput. Phys. 1987, 70, 355–372. 10.1016/0021-9991(87)90187-2. [DOI] [Google Scholar]
  44. Yan Y.; Safdari A.; Kim K. C. Visualization of nanofluid flow field by adaptive-network-based fuzzy inference system (ANFIS) with cubic interpolation particle approach. J. Visualization 2020, 1–9. 10.1007/s12650-019-00623-z. [DOI] [Google Scholar]
  45. Brinkman H. C. The viscosity of Concentrated Suspensions and Solutions. J. Chem. Phys. 1952, 20, 571. 10.1063/1.1700493. [DOI] [Google Scholar]
  46. Wasp F. J.Solid-liquid slurry pipeline transportation. Trans. Tech. Berlin 1977. [Google Scholar]
  47. Khodadadi J. M.; Hosseinizadeh S. F. Nanoparticle-enhanced phase change materials (NEPCM) with great potential for improved thermal energy storage. Int. Commun. Heat Mass Transfer 2007, 34, 534–543. 10.1016/j.icheatmasstransfer.2007.02.005. [DOI] [Google Scholar]
  48. Kefayati G. H. R.; Hosseinizadeh S. F.; Gorji M.; Sajjadi H. Lattice Boltzmann simulation of natural convection in an open enclosure subjugated to water/copper nanofluid. Int. J. Therm. Sci. 2012, 52, 91–101. 10.1016/j.ijthermalsci.2011.09.005. [DOI] [Google Scholar]
  49. Çitil H. G.; Altinişik N. The Examination of Eigenvalues and Eigenfunctions of the Sturm-Liouville Fuzzy Problem According to Boundary Conditions. Int. J. Math. Comb. 2018, 1, 51–60. 10.6084/m9.figshare.7098518.v1. [DOI] [Google Scholar]
  50. Citil H. G.; Altinisik N. The eigenvalues and the eigenfunctions of the sturm-liouville fuzzy problem with fuzzy coefficient boundary conditions. J. Sci. Arts 2018, 18, 947–958. [Google Scholar]
  51. Tian E.; Babanezhad M.; Rezakazemi M.; Shirazian S. Simulation of a Bubble-Column Reactor by Three-Dimensional CFD: Multidimension- and Function-Adaptive Network-Based Fuzzy Inference System. Int. J. Fuzzy Syst. 2019, 10.1007/s40815-019-00741-8. [DOI] [Google Scholar]
  52. Cao Y.; Babanezhad M.; Rezakazemi M.; Shirazian S. Prediction of fluid pattern in a shear flow on intelligent neural nodes using ANFIS and LBM. Neural Comput. Appl. 2019, 10.1007/s00521-019-04677-w. [DOI] [Google Scholar]
  53. Alhajri I. H.; Alarifi I. M.; Asadi A.; Nguyen H. M.; Moayedi H. A general model for prediction of BaSO4 and SrSO4 solubility in aqueous electrolyte solutions over a wide range of temperatures and pressures. J. Mol. Liq. 2019, 299, 112142. 10.1016/j.molliq.2019.112142. [DOI] [Google Scholar]
  54. Takagi T.; Sugeno M. Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. Syst. Man Cybern. B Cybern. 1985, SMC-15, 116–132. 10.1109/tsmc.1985.6313399. [DOI] [Google Scholar]

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES