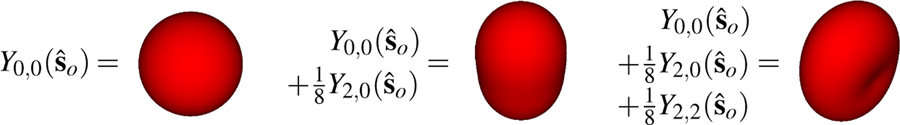Spatio-angular fluorescence microscopy I. Basic theory

Abstract

We introduce the basic elements of a spatio-angular theory of fluorescence microscopy, providing a unified framework for analyzing systems that image single fluorescent dipoles and ensembles of overlapping dipoles that label biological molecules. We model an aplanatic microscope imaging an ensemble of fluorescent dipoles as a linear Hilbert-space operator, and we show that the operator takes a particularly convenient form when expressed in a basis of complex exponentials and spherical harmonics—a form we call the dipole spatio-angular transfer function. We discuss the implications of our analysis for all quantitative fluorescence microscopy studies and lay out a path towards a complete theory.

1. Introduction

Fluorescence microscopes are widely used in the biological sciences for imaging fluorescent molecules that label specific proteins and biologically important molecules. While most fluorescence microscopy experiments are designed to measure only the spatial distribution of fluorophores, a growing number of experiments seek to measure both the spatial and angular distributions of fluorophores by the use of polarizers [1–5] or point spread function engineering [6,7].

Meanwhile, single-molecule localization microscopy (SMLM) experiments use spatially sparse fluorescent samples to localize single molecules with precision that surpasses the diffraction limit. Noise limits the precision of this localization [8,9], and several studies have shown that model mismatch (e.g. ignoring the effects of vector optics, dipole orientation [10], and dipole rotation [11]) can introduce localization bias as well. Therefore, the most precise and accurate SMLM experiments must use an appropriate model and jointly estimate both the position and orientation of each fluorophore. Several studies have successfully used vector optics and dipole models to estimate the position and orientation of single molecules [12–16], and there is growing interest in designing optical systems for measuring the position, orientation, and rotational dynamics of single molecules [6,7,17–19].

While many studies have focused on improving imaging models for spatially sparse fluorescent samples, we consider the more general case and aim to improve imaging models for arbitrary samples including those containing ensembles of fluorophores within a resolvable volume. In particular, we examine the effects of two widely used approximations in fluorescence microscopy—the monopole approximation and the scalar approximation.

We use the term monopole to refer to a model of a fluorescent object that treats it as an isotropic absorber/emitter. Although the term monopole approximation is not in widespread use, we think it accurately describes the way many models of fluorescence microscopy treat fluorescent objects, and we use the term to distinguish the monopole model from more realistic dipole and higher-order models. Despite their use in models, electromagnetic monopole absorber/emitters do not exist in nature. All physical fluorescent objects absorb and emit radiation with dipole or higher-order moments, and these moments are always oriented in space. For a classical mental model of fluorescent objects we imagine each dipole as a small oriented antenna where electrons are constrained to move along a single direction.

All fluorescence microscopy models that use an optical point spread function or an optical transfer function to describe the propagation of light through the microscope implicitly make the monopole approximation. The optical point spread function is the irradiance response of an optical system to an isotropic point source, so it cannot model the response due to an anisotropic dipole radiator. In this work we define monopole and dipole transfer functions that describe the mapping between fluorescent emissions and the measured irradiance. Although optical systems are an essential part of microscopes, fluorescence microscopists are interested in measuring the properties of fluorophores (not optics), so the monopole and dipole transfer functions are more directly useful than the optical transfer function for the problems that fluorescence microscopists are interested in solving.

While the monopole approximation applies to the fluorescent object, the scalar approximation applies to the fields that propagate through the microscope. Modeling the electric fields in a region requires a three-dimensional vector field, but if the electric fields are random or completely parallel to one another, a scalar field is sufficient, and we can replace the vector-valued electric field, E, with a scalar-valued field, U.

The scalar approximation is often made together with the monopole approximation. For example, the Born-Wolf model [20] and the Gibson-Lanni model [21] make both the monopole and scalar approximations when applied to fluorescence microscopes. However, some models make the monopole approximation but not the scalar approximation. For example, the Richards-Wolf model [22] considers the role of vector-valued fields in the optical system, but it is implicitly an optical model so when it is applied to fluorescence microscopes the monopole approximation is assumed.

This work lies at the intersection of three subfields of fluorescence microscopy: (1) spatial ensemble imaging where each resolvable volume contains many fluorophores and the goal is to find the concentration of fluorophores as a function of position in the sample, (2) spatio-angular ensemble imaging where each resolvable volume contains many fluorophores and the goal is to find the concentration and average orientation of fluorophores as a function of position in the sample, and (3) SMLM imaging where fluorophores are sparse in the sample and the goal is to find the position and orientation of each fluorophore. We briefly review how these three subfields use the monopole and scalar approximations.

The large majority of fluorescence microscopes are used to image ensembles of fluorophores, and most existing modeling techniques make use of the monopole approximation, the scalar approximation, or both. As discussed above, the Gibson-Lanni model, the Born-Wolf model, and the Richards-Wolf model are approximate when applied to fluorescence microscopy data because they only model monopole emitters. Deconvolution algorithms that use these models may make biased estimates of fluorophore concentrations since they ignore the dipole excitation and emission of fluorophores.

A small but growing group of microscopists is interested in measuring the orientation and position of ensembles of fluorophores [1–5]. These techniques typically use polarizers to make multiple measurements of the same object with different polarizer orientations, then they use a model of the dipole excitation and emission processes [23] to recover the orientation of fluorophores using pixel-wise arithmetic. Although these studies do not adopt the scalar or monopole approximations for the angular part of the problem, they adopt both approximations when they consider the spatial part of the problem. Existing works either ignore the spatial reconstruction problem [1–4] or assume that the spatial and angular reconstruction problems can be solved sequentially [5].

The most precise experiments in SMLM imaging do not adopt the scalar or monopole approximations. Many works have applied dipole models with vector optics, and several works have considered the effects of rotational and spatial diffusion on the images of single molecules [7, 24–27]. We will see that the dipole transfer functions are useful tools for incorporating angular and spatial diffusion into SMLM simulations and reconstructions.

In the present work we begin to place these three subfields on a common theoretical footing. First, in section 2, we consider arbitrary fluorescence imaging models and lay out a plan for developing a model for spatio-angular imaging. In section 3 we review the familiar monopole imaging model, and in section 4 we extend the model to dipoles. Finally, in section 5 we discuss the results and their broader implications.

In this paper we focus on modeling a single-view fluorescence microscope with neither polarized excitation nor detection. In future papers of this series we will extend our models to include polarized excitation, polarized detection, and multi-view microscopes. Additionally, we have restricted this paper to the forward problem—the mapping between a known object and the data. In future papers we will consider the inverse problem, and the singular value decomposition (SVD) will play a central role.

2. Theory

We begin our analysis with the abstract Hilbert space formalism of Barrett and Myers [28, ch. 1.3]. Our first task is to formulate the imaging process as a mapping between two Hilbert spaces $\mathcal{H}:\mathbb{U}\to \mathbb{V}$, where $\mathbb{U}$ is a set that contains all possible objects, $\mathbb{V}$ is a set that contains all (possibly noise-corrupted) datasets, and $\mathcal{H}$ is a model of the instrument that maps between these two spaces. We denote (possibly infinite-dimensional) Hilbert-space vectors in $\mathbb{U}$ with f, Hilbert-space vectors in $\mathbb{V}$ with g, and the mapping between the spaces with

$$\mathbf{\text{g}}=\mathcal{H}\mathbf{\text{f}}.$$ (1)

Throughout this work we will use the letters g, h, and f with varying fonts, capitalizations, and arguments to represent the data, the instrument, and the object, respectively.

Once we have identified the spaces $\mathbb{U}$ and $\mathbb{V}$, we can start expressing the mapping between the spaces in a specific object-space and data-space basis. In most cases the easiest mapping to find uses a delta-function basis—we expand object and data space into delta functions, then express the mapping as an integral transform. After finding this mapping we can start to investigate the same mapping in different bases.

The above discussion is quite abstract, but it is a powerful point of view that will enable us to unify the analysis of spatio-angular fluorescence imaging. In section 3 we will demonstrate the formalism by examining a familiar monopole imaging model, and we will demonstrate the mapping between object and data space in two different bases. In section 4 we will extend the monopole imaging model to dipoles and examine the mapping in four different bases.

3. Monopole imaging

We start by modeling the imaging process for a field of dynamic fluorescent monopoles. We have split our model into two pieces: (1) the dynamics of excitation, decay, and diffusion processes, and (2) the emission and detection processes. This section treads familiar ground, but it serves to establish the concepts and notation that will be necessary when we extend to the dipole case.

3.1. Monopole dynamics

We begin by considering a spatial distribution of monopoles that can occupy just two states—a ground state and an excited state. We use $f^{\left(\text{gr}\right)}\left({\mathfrak{r}}_o,t\right)$ to represent the number of monopoles in the ground state at position ${\mathfrak{r}}_o$ per unit volume at time t per unit time. Similarly, we use $f^{\left(\text{ex}\right)}\left({\mathfrak{r}}_o,t\right)$ to represent the number of monopoles in the excited state.

Next, we describe all of the transitions between states. If we excite the monopoles with an illumination pattern that is uniform in space and time, then the rate of excitation will be the product of an excitation constant κ^(ex) with the number of monopoles in the ground state. Similarly, the rate of molecules decaying from the excited state to the ground state will be the product of a decay constant κ^(d) with the number of monopoles in the excited state (assuming that stimulated emission is negligible).

Finally, we describe the effect of diffusion within each state. If the diffusion is homogeneous (independent of position) and isotropic (independent of direction) then the rate of change of the spatial distribution will be proportional to a diffusion constant D_R multiplied by the Laplacian operator ${\mathrm{\Delta }}_{{ℝ}^3}=\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}+\frac{{\partial }^2}{\partial z^2}$ acting on the spatial distribution of monopoles at that point.

Bringing the effects of excitation, decay, and diffusion together yields a pair of coupled partial differential equations

$$\frac{\partial f^{\left(gr\right)}\left({\mathfrak{r}}_o,t\right)}{\partial t}=-{\kappa }^{\left(ex\right)}{f}^{\left(gr\right)}\left({\mathfrak{r}}_o,t\right)+{\kappa }^{\left(d\right)}{f}^{\left(ex\right)}\left({\mathfrak{r}}_o,t\right)+D_R{\mathrm{\Delta }}_{{ℝ}^3}{f}^{\left(gr\right)}\left({\mathfrak{r}}_o,t\right),$$ (2)

$$\frac{\partial f^{\left(\text{ex}\right)}\left({\mathfrak{r}}_o,t\right)}{\partial t}=-{\kappa }^{\left(\text{ex}\right)}{f}^{\left(\text{gr}\right)}\left({\mathfrak{r}}_o,t\right)-{\kappa }^{\left(\text{d}\right)}{f}^{\left(\text{ex}\right)}\left({\mathfrak{r}}_o,t\right)+D_R{\mathrm{\Delta }}_{{ℝ}^3}{f}^{\left(\text{ex}\right)}\left({\mathfrak{r}}_o,t\right).$$ (3)

Eqs. (2) and (3) serve as a minimal model of monopole dynamics, and these equations can be generalized to model a broad class of fluorescence imaging techniques. For example, space-and time-varying excitation patterns ${\kappa }^{\left(\text{ex}\right)}\left({\mathfrak{r}}_o,t\right)$ are useful for modeling structured illumination microscopes (SIM); space- and time-varying decay constants ${\kappa }^{\left(\text{d}\right)}\left({\mathfrak{r}}_o,t\right)$ are of interest in fluorescence lifetime imaging microscopy (FLIM); space-, time-, and direction-varying (tensor-valued) diffusion coefficients are of interest in diffusion imaging; and extra states and transitions can be added to model single-molecule techniques, stimulated emission and depletion (STED) techniques, Forster resonance energy transfer (FRET), and photobleaching.

3.2. Monopole detection

Next, we model the monopole emission and detection processes independent of the underlying dynamics. In our simple two-state model we can only measure the photons radiated during transitions from the excited state to the ground state, which occur at a rate ${\kappa }^{\left(\text{d}\right)}{f}^{\left(\text{ex}\right)}\left({\mathfrak{r}}_o,t\right)$. If we expose a detector for a period t_e, then the most we can hope to recover from our data without knowing more about the dynamics of the system is the quantity

$$f\left({\mathfrak{r}}_o\right)={\int }_0^{t_{\text{e}}}dt\hspace{0.17em}{\kappa }^{\left(\text{d}\right)}{f}^{\left(\text{ex}\right)}\left({\mathfrak{r}}_o,t\right).$$ (4)

The function $f\left({\mathfrak{r}}_o\right)$ represents the number of monopole emissions during the exposure time from position ${\mathfrak{r}}_o$ per unit volume. A complete name for $f\left({\mathfrak{r}}_o\right)$ would be the time-integrated monopole emission density rate, but for brevity we will refer to it as the monopole emission density.

We identify the set of all possible monopole emission densities as our object space $\mathbb{U}={\mathbb{L}}_2\left({ℝ}^3\right)$— the set of square-integrable functions in three-dimensional space. If we measure the irradiance on a two-dimensional detector then data space is $\mathbb{V}={\mathbb{L}}_2\left({ℝ}^2\right)$ and the data can be represented by a function $g^{\prime }\left({\text{r}}_d^{\text{'}}\right)$ called the irradiance—the power received by a surface per unit area at position ${\text{r}}_d^{\text{'}}$. Note that we have adopted a slightly unusual convention of using primes to denote unscaled coordinates. Later in this section we will introduce unprimed scaled coordinates that we will use throughout the rest of the paper.

A reasonable starting point is to assume that the relationship between the object and the data is linear—this is true in many fluorescence microscopes because fluorophores emit incoherently, so a scaled sum of emissions result in a scaled sum of the irradiance patterns created by the individual emissions.

If the mapping is linear, we can write the irradiance as a weighted integral over the monopole emission density

$$g^{\prime }\left({\text{r}}_d^{\text{'}}\right)={\int }_{{ℝ}^3}d{\mathfrak{r}}_o\hspace{0.17em}{h}^{\prime }\left({\text{r}}_d^{\text{'}},{\mathfrak{r}}_o\right)f\left({\mathfrak{r}}_o\right),$$ (5)

where $h^{\prime }\left({\text{r}}_d^{\text{'}},{\mathfrak{r}}_o\right)$ is the irradiance at two-dimensional position ${\text{r}}_d^{\text{'}}$ (roman font) created by a point source at three-dimensional position ${\mathfrak{r}}_o$ (gothic font).

Next, we assume that the optical system is aplanatic—Abbe’s sine condition is satisfied and on-axis points are imaged without aberration. Abbe’s sine condition guarantees that off-axis points are imaged without spherical aberration or coma [29, ch. 1], so the imaging system can be modeled within the field of view of the optical system as a transverse magnifier with shift-invariant blur. We split the three-dimensional object coordinate ${\mathfrak{r}}_o$ into a two-dimensional transverse coordinate ${\text{r}}_o^{\perp }$ and a one-dimensional axial coordinate $r_o^{\parallel }$ to write the forward model as

$$g^{\prime }\left({\text{r}}_d^{\text{'}}\right)={\int }_{ℝ}d{r}_o^{\parallel }{\int }_{{ℝ}^2}d{\text{r}}_o^{\perp }{h}^{\prime }\left({\text{r}}_d^{\text{'}}-m{\text{r}}_o^{\perp },r_o^{\parallel }\right)f\left({\text{r}}_o^{\perp },r_o^{\parallel }\right),$$ (6)

where m is a transverse magnification factor. Note that non-paraxial imaging systems that satisfy Abbe’s sine condition cannot simultaneously satisfy the Herschel condition when m ≠ 1 [30, 31], so non-paraxial magnifying imaging systems cannot be shift-invariant in three dimensions. For paraxial imaging systems the Abbe sine and Herschel conditions are approximately the same, and the imaging system can be described as approximately shift invariant in three dimensions.

We can simplify our analysis by changing coordinates and writing Eq. (6) as a transverse convolution [28, ch. 7.2.7]. We define a demagnified detector coordinate ${\text{r}}_d={\text{r}}_d^{\text{'}}/m$ and a normalization factor that corresponds to the total power incident on the detector plane due to an in-focus point source $P_{\text{mono}}={\int }_{{ℝ}^2}d\text{r}\hspace{0.17em}{h}^{\prime }\left(m\text{r},0\right)$ where $\text{r}={\text{r}}_d-{\text{r}}_o^{\perp }$. We use these scaling factors to define the monopole point spread function as

$$h\left({\text{r}}_d-{\text{r}}_o^{\perp },r_o^{\parallel }\right)=\frac{h^{\prime }\left(m\left[{\text{r}}_d-{\text{r}}_o^{\perp }\right],r_o^{\parallel }\right)}{P_{\text{mono}}},$$ (7)

and the scaled irradiance as

$$g\left({\text{r}}_d\right)=\frac{g^{\prime }\left(m{\text{r}}_d\right)}{P_{\text{mono}}}.$$ (8)

With these definitions we can express the mapping between the object and the data as a familiar transverse convolution

$$g\left({\text{r}}_d\right)={\int }_{ℝ}d{r}_o^{\parallel }{\int }_{{ℝ}^2}d{\text{r}}_o^{\perp }h\left({\text{r}}_d-{\text{r}}_o^{\perp },r_o^{\parallel }\right)f\left({\text{r}}_o^{\perp },r_o^{\parallel }\right).$$ (9)

We have chosen to normalize the monopole point spread function so that

$${\int }_{{ℝ}^2}d\text{r}\hspace{0.17em}h\left(\text{r},0\right)=1.$$ (10)

The monopole point spread function corresponds to a measurable irradiance, so it is always real and positive.

The mapping between the object and the data in a linear shift-invariant imaging system takes a particularly simple form in a complex exponential (i.e. Fourier) basis. If we apply the Fourier convolution theorem to Eq. (9) we find that

$$G\left(\mathit{\nu }\right)={\int }_{ℝ}d{r}_o^{\parallel }H\left(\mathit{\nu },r_o^{\parallel }\right)F\left(\mathit{\nu },r_o^{\parallel }\right),$$ (11)

where we define the scaled irradiance spectrum as

$$G\left(\mathit{\nu }\right)={\int }_{{ℝ}^2}d\text{r}\hspace{0.17em}g\left(\text{r}\right)\exp \left(-2\pi i\text{r}\cdot \mathit{\nu }\right),$$ (12)

the monopole transfer function as

$$H\left(\mathit{\nu },r_o^{\parallel }\right)={\int }_{{ℝ}^2}d\text{r}\hspace{0.17em}h\left(\text{r},r_o^{\parallel }\right)\exp \left(-2\pi i\text{r}\cdot \mathit{\nu }\right),$$ (13)

and the monopole spectrum as

$$F\left(\mathit{\nu },r_o^{\parallel }\right)={\int }_{{ℝ}^2}d\text{r}\hspace{0.17em}f\left(\text{r},r_o^{\parallel }\right)\exp \left(-2\pi i\text{r}\cdot \mathit{\nu }\right).$$ (14)

The monopole point spread function is normalized and real, so we know that the monopole transfer function is normalized, H(0, 0) = 1, and conjugate symmetric, H(−ν, 0) = H^*(ν, 0), where z* denotes the complex conjugate of z.

Notice that Eqs. (9) and (11) are expressions of the same mapping between object and data space in different bases. Figure 1 summarizes the relationship between object and data space in both bases.

Fig. 1.

The mapping between the object and data space of a monopole fluorescence microscope can be computed in two different bases—a delta function basis and a complex exponential basis. The change of basis can be computed with a two-dimensional Fourier transform denoted ${\mathcal{F}}_{{ℝ}^2}$. Gray highlighting indicates which part of each expression is being named.

We have been careful to use the term monopole transfer function instead of the commonly-used term optical transfer function. We reserve the term optical transfer function for optical systems—the optical transfer function maps between an input irradiance spectrum and an output irradiance spectrum in an optical system. We can use optical transfer functions to model the propagation of light through a microscope, but ultimately we are always interested in the object, not the light emitted by the object. We will find the distinction between the optical transfer function and the object transfer function to be especially valuable when we consider dipoles in section 4.

3.3. Monopole coherent transfer functions

Although the Fourier transform can be used to calculate the monopole transfer function directly from the monopole point spread function, there is a well-known alternative that exploits coherent transfer functions. The key idea is that the monopole point spread function can always be written as the absolute square of a scalar-valued monopole coherent spread function, $c\left({\text{r}}_d-{\text{r}}_o^{\perp },r_o^{\parallel }\right)$, defined by

$${\left|c\left({\text{r}}_d-{\text{r}}_o^{\perp },r_o^{\parallel }\right)\right|}^2=h\left({\text{r}}_d-{\text{r}}_o^{\perp },r_o^{\parallel }\right).$$ (15)

Physically, the monopole coherent spread function corresponds to the scalar-valued electromagnetic field on the detector with appropriate scaling.

We can plug Eq. (15) into Eq. (13) and use the autocorrelation theorem to rewrite the monopole transfer function as

$$H\left(\mathit{\nu },r_o^{\parallel }\right)={\int }_{{ℝ}^2}d\mathbf{\tau }\hspace{0.17em}C\left(\mathbf{\tau },r_o^{\parallel }\right)C^{\ast }\left(\mathbf{\tau }-\mathit{\nu },r_o^{\parallel }\right),$$ (16)

where we have introduced the monopole coherent transfer function as the two-dimensional Fourier transform of the monopole coherent spread function:

$$C\left(\mathbf{\tau },r_o^{\parallel }\right)={\int }_{{ℝ}^2}d\text{r}\hspace{0.17em}c\left(\text{r},r_o^{\parallel }\right)\exp \left[-2\pi i\text{r}\cdot \mathbf{\tau }\right].$$ (17)

Physically, the monopole coherent transfer function corresponds to the scalar-valued field in a Fourier plane of the detector with appropriate scaling.

The coherent transfer function provides a valuable shortcut for analyzing microscopes since it is often straightforward to calculate the field in a Fourier plane of the detector. A typical approach for calculating the transfer functions is to (1) calculate the field in a Fourier plane of the detector, (2) scale the field to find the monopole coherent transfer function, then (3) use the relationships in Fig. 2 to calculate the other transfer functions.

Fig. 2.

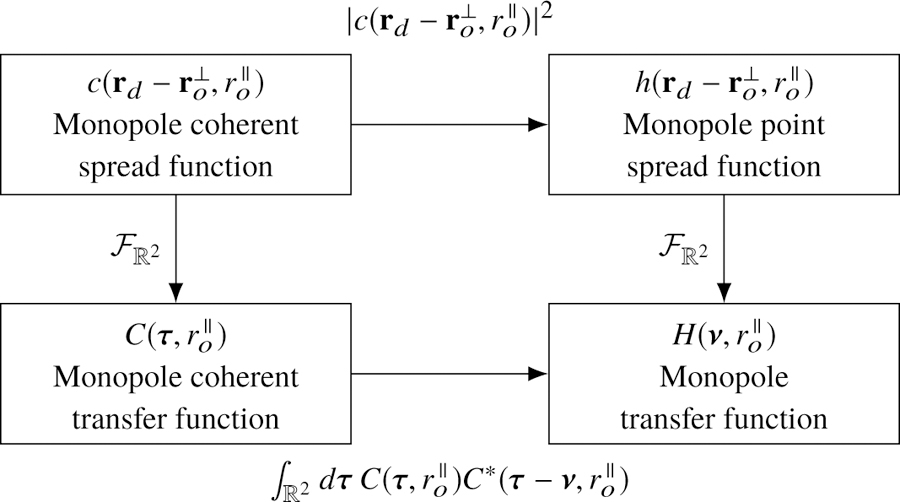
The monopole transfer functions are related by a two-dimensional Fourier transform (right column). The coherent monopole transfer functions (left column) can be used to simplify the calculation of the remaining transfer functions.

4. Dipole imaging

Now we consider a microscope imaging a field of dipoles by recording the irradiance on a two-dimensional detector. Similar to the monopole case, we split our model in two pieces: a dynamics model and an imaging model.

4.1. Dipole dynamics

We consider a distribution of dipoles that can occupy a ground state and an excited state. A function that assigns a real number to each point in space ${\mathfrak{r}}_o$ and time t is not enough to specify a dynamic field of dipoles because the dipoles can have different orientations. Therefore, we introduce an orientation coordinate ${\widehat{\mathbf{\text{s}}}}_o$ and use the function $f^{\left(\text{gr}\right)}\left({\mathfrak{r}}_o,{\widehat{\mathbf{\text{s}}}}_o,t\right)$ to represent the number of dipoles in the ground state at position ${\mathfrak{r}}_o$ per unit volume oriented along ${\widehat{\mathbf{\text{s}}}}_o$ per steradian at time t per unit time. Similarly, we use $f^{\left(\text{ex}\right)}\left({\mathfrak{r}}_o,{\widehat{\mathbf{\text{s}}}}_o,t\right)$ to represent the number of dipoles in the excited state.

We can model the transitions between states in the same way that we did with monopoles. If we excite the dipoles with an illumination pattern that is uniform in space, orientation, and time, then the rate of excitation will be ${\kappa }^{\left(\text{ex}\right)}{f}^{\left(\text{gr}\right)}\left({\mathfrak{r}}_o,{\widehat{\mathbf{\text{s}}}}_o,t\right)$. Similarly, the rate of decay from the excited state to the ground state will be ${\kappa }^{\left(\text{d}\right)}{f}^{\left(\text{ex}\right)}\left({\mathfrak{r}}_o,{\widehat{\mathbf{\text{s}}}}_o,t\right)$ (assuming that stimulated emission is negligible).

We can model homogeneous and isotropic spatial diffusion in the same way that we did for monopoles—the rate of change of the spatial distribution will be the product of a spatial diffusion coefficient D_R multiplied by the Laplacian ${\mathrm{\Delta }}_{{ℝ}^3}$ acting on the dipole distribution at that point. Similarly, if angular diffusion is homogeneous (independent of orientation ${\widehat{\mathbf{\text{s}}}}_o$) and isotropic (independent of angular diffusion direction) then the rate of the change of angular distribution will be the product of an angular diffusion coefficient D_S multiplied by the spherical Laplacian ${\mathrm{\Delta }}_{{\mathbb{S}}^2}$ acting on the dipole distribution at that orientation. If we choose a set of spherical coordinates ${\widehat{\mathbf{\text{s}}}}_o=\left(\theta ,\varphi \right)$ where θ is the inclination angle and ϕ is the azimuthal angle, then the spherical Laplacian takes the form ${\mathrm{\Delta }}_{{\mathbb{S}}^2}=\frac{1}{{\sin }^2\theta }\frac{{\partial }^2}{\partial {\varphi }^2}+\frac{1}{\sin \theta }\frac{\partial }{\partial \theta }\left(\sin \theta \frac{\partial }{\partial \theta }\right)$.

Bringing everything together yields a pair of coupled partial differential equations

$$\begin{gathered} \frac{\partial f^{\left(\text{gr}\right)}\left({\mathfrak{r}}_o,{\widehat{\mathbf{\text{s}}}}_o,t\right)}{\partial t}=-{\kappa }^{\left(\text{ex}\right)}{f}^{\left(\text{gr}\right)}\left({\mathfrak{r}}_o,{\widehat{\mathbf{\text{s}}}}_o,t\right)+{\kappa }^{\left(\text{d}\right)}{f}^{\left(\text{ex}\right)}\left({\mathfrak{r}}_o,{\widehat{\mathbf{\text{s}}}}_o,t\right)+D_R{\mathrm{\Delta }}_{{ℝ}^3}{f}^{\left(\text{gr}\right)}\left({\mathfrak{r}}_o,{\widehat{\mathbf{\text{s}}}}_o,t\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+D_S{\mathrm{\Delta }}_{{\mathbb{S}}^2}{f}^{\left(\text{gr}\right)}\left({\mathfrak{r}}_o,{\widehat{\mathbf{\text{s}}}}_o,t\right), \end{gathered}$$ (18)

$$\begin{gathered} \frac{\partial f^{\left(\text{ex}\right)}\left({\mathfrak{r}}_o,{\widehat{\mathbf{\text{s}}}}_o,t\right)}{\partial t}={\kappa }^{\left(\text{ex}\right)}{f}^{\left(\text{gr}\right)}\left({\mathfrak{r}}_o,{\widehat{\mathbf{\text{s}}}}_o,t\right)-{\kappa }^{\left(\text{d}\right)}{f}^{\left(\text{ex}\right)}\left({\mathfrak{r}}_o,{\widehat{\mathbf{\text{s}}}}_o,t\right)+D_R{\mathrm{\Delta }}_{{ℝ}^3}{f}^{\left(\text{ex}\right)}\left({\mathfrak{r}}_o,{\widehat{\mathbf{\text{s}}}}_o,t\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}+D_S{\mathrm{\Delta }}_{{\mathbb{S}}^2}{f}^{\left(\text{ex}\right)}\left({\mathfrak{r}}_o,{\widehat{\mathbf{\text{s}}}}_o,t\right). \end{gathered}$$ (19)

Variants of Eqs. (18) and (19) can be used to model a wide range of more realistic dynamics. For example, a space-, orientation-, and time-varying excitation pattern ${\kappa }^{\left(\text{ex}\right)}\left({\mathfrak{r}}_o,{\widehat{\mathbf{\text{s}}}}_o,t\right)$ can be used to model spatio-angular structured illumination patterns. Specifically, an orientation-dependent excitation pattern can be used to model selective excitation with polarized light. There is also the possibility of modeling space-, orientation-, and time-varying decay constants and diffusion constants.

Finally, we note that many fluorescent molecules have excitation and emission dipole moments that are not collinear. We can model these types of molecules by choosing the orientation coordinate ${\widehat{\mathbf{\text{s}}}}_o$ to be along the emission dipole moment, then accounting for the excitation moment in the excitation rate function ${\kappa }^{\left(\text{ex}\right)}\left({\mathfrak{r}}_o,{\widehat{\mathbf{\text{s}}}}_o,t\right)$.

4.2. Dipole detection

Next, we model the dipole emission and detection processes independent of the underlying dynamics. We can only measure photons radiated during transitions from the excited state to the ground state, which occur at rate ${\kappa }^{\left(\text{d}\right)}{f}^{\left(\text{ex}\right)}\left({\mathfrak{r}}_o,{\widehat{\mathbf{\text{s}}}}_o,t\right)$. If we expose a detector for a period t_e then the most we can hope to recover from our data without knowing more about the underlying dynamics is the quantity

$$f\left({\mathfrak{r}}_o,{\widehat{\mathbf{\text{s}}}}_o\right)={\int }_0^{t_{\text{det}}}dt\hspace{0.17em}{\kappa }^{\left(\text{d}\right)}{f}^{\left(\text{ex}\right)}\left({\mathfrak{r}}_o,{\widehat{\mathbf{\text{s}}}}_o,t\right).$$ (20)

The function $f\left({\mathfrak{r}}_o,{\widehat{\mathbf{\text{s}}}}_o\right)$ represents the number of dipole emissions during the exposure time from position ${\mathfrak{r}}_o$ per unit volume and orientation ${\widehat{\mathbf{\text{s}}}}_o$ per unit steradian. A complete name for $f\left({\mathfrak{r}}_o,{\widehat{\mathbf{\text{s}}}}_o\right)$ would be the time-integrated dipole emission density rate, but for brevity we will refer to it as the dipole emission density. We identify the set of all possible dipole emission densities as our object space $\mathbb{U}={\mathbb{L}}_2\left({ℝ}^3\times {\mathbb{S}}^2\right)$—the set of square-integrable functions on the product space of a volume and a two-dimensional spherical surface (the usual spherical surface embedded in ${ℝ}^3$). To visualize functions in object space we imagine a sphere at every point in a three-dimensional volume with a scalar value assigned to every surface point on each sphere.

Predicting the dipole emission density for a specific experiment requires (1) a model of the underlying dynamics (a variant of Eqs. (18) and (19)), (2) a set of initial/boundary conditions, (3) a solution of the coupled partial differential equations $f^{\left(\text{ex}\right)}\left({\mathfrak{r}}_o,{\widehat{\mathbf{\text{s}}}}_o,t\right)$ (either an analytic or a numerical solution), then (4) the computation of the dipole emission density using Eq. (20). In Appendix B we demonstrate this procedure for an experiment with an instantaneous excitation pulse.

Similar to the monopole case, we model the mapping between the object and the irradiance as an integral transform

$$g^{\prime }\left({\text{r}}_d^{\text{'}}\right)={\int }_{{\mathbb{S}}^2}d{\widehat{\mathbf{\text{s}}}}_o{\int }_{{ℝ}^3}d{\mathfrak{r}}_o\hspace{0.17em}{h}^{\prime }\left({\text{r}}_d^{\text{'}},{\mathfrak{r}}_o,{\widehat{\mathbf{\text{s}}}}_o\right)f\left({\mathfrak{r}}_o,{\widehat{\mathbf{\text{s}}}}_o\right),$$ (21)

where $h^{\prime }\left({\text{r}}_d^{\text{'}},{\mathfrak{r}}_o,{\widehat{\mathbf{\text{s}}}}_o\right)$ is the irradiance at position ${\text{r}}_d^{\text{'}}$ created by a point source at ${\mathfrak{r}}_o$ with orientation ${\widehat{\mathbf{\text{s}}}}_o$. Notice that we have considered all possible orientations ${\widehat{\mathbf{\text{s}}}}_o$ and integrated over the sphere ${\mathbb{S}}^2$. The dipole emission density is always symmetric under angular inversion, $f\left({\mathfrak{r}}_o,{\widehat{\mathbf{\text{s}}}}_o\right)=f\left({\mathfrak{r}}_o,-{\widehat{\mathbf{\text{s}}}}_o\right)$, so we could have chosen to integrate over a hemisphere and adjusted the definition of the dipole emission density by a factor of two. For convenience we will continue to integrate over the complete sphere. We note that all functions in this work with ${\widehat{\mathbf{\text{s}}}}_o$ as an independent variable are symmetric under angular inversion,${\widehat{\mathbf{\text{s}}}}_o\to -{\widehat{\mathbf{\text{s}}}}_o$.

If the optical system is aplanatic, then we can split the three-dimensional object coordinate ${\mathfrak{r}}_o$ into a transverse coordinate ${\text{r}}_o^{\perp }$ and an axial coordinate $r_o^{\parallel }$ and write the forward model as

$$g^{\prime }\left({\text{r}}_d^{\text{'}}\right)={\int }_{{\mathbb{S}}^2}d{\widehat{\mathbf{\text{s}}}}_o{\int }_{ℝ}d{r}_o^{\parallel }{\int }_{{ℝ}^2}d{\text{r}}_o^{\perp }\hspace{0.17em}{h}^{\prime }\left({\text{r}}_d^{\text{'}}-m{\mathfrak{r}}_o{\text{r}}_o^{\perp },r_o^{\parallel },{\widehat{\mathbf{\text{s}}}}_o\right)f\left({\text{r}}_o^{\perp },r_o^{\parallel },{\widehat{\mathbf{\text{s}}}}_o\right).$$ (22)

We define the same demagnified detector coordinate ${\text{r}}_d={\text{r}}_d^{\text{'}}/m$ and a new normalization factor that corresponds to the total power incident on the detector due to an in-focus spatial point source with an angularly uniform distribution of dipoles $P_{\text{dip}}={\int }_{{\mathbb{S}}^2}d{\widehat{\mathbf{\text{s}}}}_o{\int }_{{ℝ}^2}d\text{r}\hspace{0.17em}{h}^{\prime }\left(m\text{r},0,{\widehat{\mathbf{\text{s}}}}_o\right)$. We use these scaling factors to define the dipole point spread function as

$$h\left({\text{r}}_d-{\text{r}}_o^{\perp },r_o^{\parallel },{\widehat{\mathbf{\text{s}}}}_o\right)=\frac{h^{\prime }\left(m\left[{\text{r}}_d-{\text{r}}_o^{\perp }\right],r_o^{\parallel },{\widehat{\mathbf{\text{s}}}}_o\right)}{P_{\text{dip}}},$$ (23)

and the scaled irradiance as

$$g\left({\text{r}}_d\right)=\frac{g^{\prime }\left(m{\text{r}}_d\right)}{P_{\text{dip}}}.$$ (24)

With these definitions we can express the mapping between the object and the data as

$$g\left({\text{r}}_d\right)={\int }_{{\mathbb{S}}^2}d{\widehat{\mathbf{\text{s}}}}_o{\int }_{ℝ}d{r}_o^{\parallel }{\int }_{{ℝ}^2}d{\text{r}}_o^{\perp }\hspace{0.17em}h\left({\text{r}}_d-{\text{r}}_o^{\perp },r_o^{\parallel },{\widehat{\mathbf{\text{s}}}}_o\right)f\left({\text{r}}_o^{\perp },r_o^{\parallel },{\widehat{\mathbf{\text{s}}}}_o\right).$$ (25)

Equation (25) is a key result because it represents the mapping between object space and data space in a delta function basis. The integrals in Eq. (25) would be extremely expensive to compute for an arbitrary object, but the integrals simplify to an efficient sum if the object is spatially and angularly sparse. For example, Eq. (25) would reduce to a superposition of dipole point spread functions if the object consisted of immobile dipole emitters.

Similar to the monopole case, we have chosen to normalize the dipole point spread function so that

$${\int }_{{\mathbb{S}}^2}d{\widehat{\mathbf{\text{s}}}}_o{\int }_{{ℝ}^2}d\text{r}\hspace{0.17em}h\left(\text{r},0,{\widehat{\mathbf{\text{s}}}}_o\right)=1.$$ (26)

The dipole point spread function is a measurable irradiance, so it is real and positive.

4.3. Dipole spatial transfer function

We can make our first change of basis by applying the Fourier-convolution theorem to Eq. (25), which yields

$$G\left(\mathit{\nu },r_o^{\parallel }\right)={\int }_{{\mathbb{S}}^2}d{\widehat{\mathbf{\text{s}}}}_o{\int }_{ℝ}d{r}_o^{\parallel }H\left(\mathit{\nu },r_o^{\parallel },{\widehat{\mathbf{\text{s}}}}_o\right)F\left(\mathit{\nu },r_o^{\parallel },{\widehat{\mathbf{\text{s}}}}_o\right),$$ (27)

where we define the dipole spatial transfer function as

$$H\left(\mathit{\nu },r_o^{\parallel },{\widehat{\mathbf{\text{s}}}}_o\right)={\int }_{{ℝ}^2}d\text{r}\hspace{0.17em}h\left(\text{r},r_o^{\parallel },{\widehat{\mathbf{\text{s}}}}_o\right)\exp \left(-2\pi i\text{r}\cdot \mathit{\nu }\right),$$ (28)

and the dipole spatial spectrum as

$$F\left(\mathit{\nu },r_o^{\parallel },{\widehat{\mathbf{\text{s}}}}_o\right)={\int }_{{ℝ}^2}d\text{r}\hspace{0.17em}f\left(\text{r},r_o^{\parallel },{\widehat{\mathbf{\text{s}}}}_o\right)\exp \left(-2\pi i\text{r}\cdot \mathit{\nu }\right).$$ (29)

Since the dipole point spread function is normalized and real, we know that the dipole spatial transfer function is normalized, ${\int }_{{\mathbb{S}}^2}d\widehat{\mathbf{\text{s}}}\hspace{0.17em}H\left(\mathbf{\text{0}},0,{\widehat{\mathbf{\text{s}}}}_o\right)=1$, and conjugate symmetric,$H\left(-\mathit{\nu },0,{\widehat{\mathbf{\text{s}}}}_o\right)=H^{\ast }\left(\mathit{\nu },0,{\widehat{\mathbf{\text{s}}}}_o\right)$.

This basis is efficient for simulating and analyzing objects that are angularly sparse and spatially dense; e.g. rod-like structures that contain fluorophores in a fixed orientation, or rotationally fixed fluorophores that are undergoing spatial diffusion.

4.4. Dipole angular transfer function

The spherical harmonics are another set of convenient basis functions that play the same role as complex exponentials in spatial transfer functions—see Appendix A for an introduction to the spherical harmonics. We can change basis from spherical delta functions to spherical harmonics by applying the generalized Plancherel theorem for spherical functions

$${\int }_{{\mathbb{S}}^2}d\widehat{\mathbf{\text{s}}}\hspace{0.17em}p\left(\widehat{\mathbf{\text{s}}}\right)q^{\ast }\left(\widehat{\mathbf{\text{s}}}\right)=\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }{P}_{\ell }^m{Q}_{\ell }^{m\ast },$$ (30)

where $p\left(\widehat{\mathbf{\text{s}}}\right)$ and $q\left(\widehat{\mathbf{\text{s}}}\right)$ are arbitrary functions on the sphere, $P_{\ell }^m$ and $Q_{\ell }^m$ are their spherical Fourier transforms defined by

$$P_{\ell }^m={\int }_{{\mathbb{S}}^2}d\widehat{\mathbf{\text{s}}}\hspace{0.17em}p\left(\widehat{\mathbf{\text{s}}}\right)Y_{\ell }^{m\ast }\left(\widehat{\mathbf{\text{s}}}\right),$$ (31)

and $Y_{\ell }^m\left(\widehat{\mathbf{\text{s}}}\right)$ are the spherical harmonic functions defined in Appendix A. Equation (30) expresses the fact that scalar products are invariant under a change of basis [28, Eq. 3.78]. The left-hand side of Eq. (30) is the scalar product of ${\mathbb{L}}_2\left({\mathbb{S}}^2\right)$ functions in a delta function basis and the right-hand side is the scalar product of ${\mathbb{L}}_2\left({\mathbb{S}}^2\right)$ functions in a spherical harmonic function basis. Applying Eq. (30) to Eq. (25) yields

$$g\left({\text{r}}_d\right)=\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }{\int }_{ℝ}d{r}_o^{\parallel }{\int }_{{ℝ}^2}d{\text{r}}_o^{\perp }{H}_{\ell }^m\left({\text{r}}_d-{\text{r}}_o^{\perp },r_o^{\parallel }\right)F_{\ell }^m\left({\text{r}}_o^{\perp },r_o^{\parallel }\right),$$ (32)

where we have defined the dipole angular transfer function as

$$H_{\ell }^m\left({\text{r}}_d-{\text{r}}_o^{\perp },r_o^{\parallel }\right)={\int }_{{\mathbb{S}}^2}d{\widehat{\mathbf{\text{s}}}}_o\hspace{0.17em}h\left({\text{r}}_d-{\text{r}}_o^{\perp },r_o^{\parallel },{\widehat{\mathbf{\text{s}}}}_o\right)Y_{\ell }^{m\ast }\left({\widehat{\mathbf{\text{s}}}}_o\right),$$ (33)

and the dipole angular spectrum as

$$F_{\ell }^m\left({\text{r}}_o^{\perp },r_o^{\parallel }\right)={\int }_{{\mathbb{S}}^2}d{\widehat{\mathbf{\text{s}}}}_o\hspace{0.17em}f\left({\text{r}}_o^{\perp },r_o^{\parallel },{\widehat{\mathbf{\text{s}}}}_o\right)Y_{\ell }^{m\ast }\left({\widehat{\mathbf{\text{s}}}}_o\right).$$ (34)

Since the dipole point spread function is normalized and real, we know that the dipole angular transfer function is normalized, ${\int }_{{ℝ}^2}d\text{r}\hspace{0.17em}{H}_0^0\left(\text{r},0\right)=1$, and conjugate symmetric,$H_{\ell }^{-m}\left(\text{r},0\right)={\left(-1\right)}^m{H}_{\ell }^{m\ast }\left(\text{r},0\right)$.

This basis is efficient for simulating and analyzing objects that are spatially sparse and angularly dense; e.g. single fluorophores that are undergoing angular diffusion, or many fluorophores that are within a resolvable volume with varying orientations.

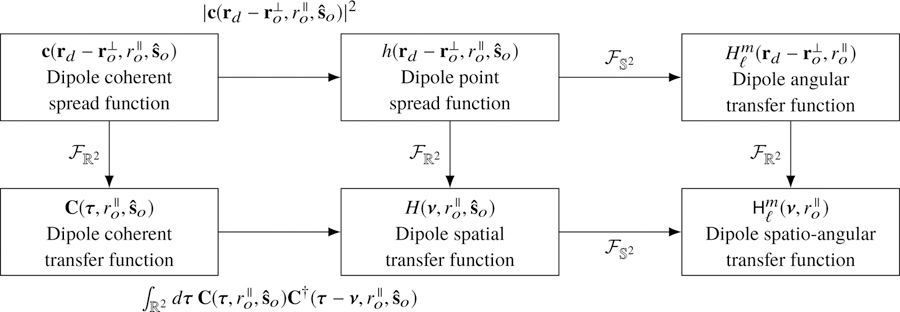
4.5. Spatio-angular dipole transfer function

We can arrive at our final basis in two ways: by applying the generalized Plancherel theorem for spherical functions to Eq. (27) or by applying the Fourier convolution theorem to Eq. (32). We follow the first path and find that

$$G\left(\mathit{\nu },r_o^{\parallel }\right)=\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }{\int }_{ℝ}d{r}_o^{\parallel }{\text{H}}_{\ell }^m\left(\mathit{\nu },r_o^{\parallel }\right){\text{F}}_{\ell }^m\left(\mathit{\nu },r_o^{\parallel }\right),$$ (35)

where we have defined the dipole spatio-angular transfer function as

$${\text{H}}_{\ell }^m\left(\mathit{\nu },r_o^{\parallel }\right)={\int }_{{\mathbb{S}}^2}d{\widehat{\mathbf{\text{s}}}}_o\hspace{0.17em}H\left(\mathit{\nu },r_o^{\parallel },{\widehat{\mathbf{\text{s}}}}_o\right)Y_{\ell }^{m\ast }\left({\widehat{\mathbf{\text{s}}}}_o\right),$$ (36)

and the dipole spatio-angular spectrum as

$${\text{F}}_{\ell }^m\left(\mathit{\nu },r_o^{\parallel }\right)={\int }_{{\mathbb{S}}^2}d{\widehat{\mathbf{\text{s}}}}_o\hspace{0.17em}F\left(\mathit{\nu },r_o^{\parallel },{\widehat{\mathbf{\text{s}}}}_o\right)Y_{\ell }^{m\ast }\left({\widehat{\mathbf{\text{s}}}}_o\right).$$ (37)

Since the dipole point spread function is normalized and real, we know that the dipole spatio-angular transfer function is normalized, ${\text{H}}_0^0\left(\mathbf{\text{0}},0\right)=1$, and conjugate symmetric,${\text{H}}_{\ell }^{-m}\left(-\mathit{\nu },0\right)={\left(-1\right)}^m{\text{H}}_{\ell }^{m\ast }\left(\mathit{\nu },0\right)$.

This basis is efficient for simulating and analyzing arbitrary samples because it exploits the band limit of the imaging system. We note that most single molecule imaging experiments are efficiently described in this basis because of the effects of spatial and rotational diffusion—see Appendix B for an example.

Figure 3 summarizes the relationships between the four bases that we can use to compute the image of a field of dipoles. We reiterate that all four bases may be useful depending on the sample.

Fig. 3.

The mapping between the object space and data space of a dipole imaging system can be computed in four different bases—a delta function basis, a complex-exponential/angular-delta basis, a spatial-delta/spherical-harmonic basis, and a complex-exponential/spherical-harmonic basis. The changes of basis can be computed with the two-dimensional Fourier transform denoted ${\mathcal{F}}_{{ℝ}^2}$, and the spherical Fourier transform denoted ${\mathcal{F}}_{{\mathbb{S}}^2}$. Gray highlighting indicates which part of each expression is being named.

4.6. Dipole coherent transfer functions

Similar to the monopole case, there is an efficient way to calculate the transfer functions using coherent transfer functions. The dipole point spread function can always be written as the absolute square of a vector-valued function, $\text{c}\left({\text{r}}_d-{\text{r}}_o^{\perp },r_o^{\parallel },{\widehat{\mathbf{\text{s}}}}_o\right)$, called the dipole coherent spread function:

$${\left|\text{c}\left({\text{r}}_d-{\text{r}}_o^{\perp },r_o^{\parallel },{\widehat{\mathbf{\text{s}}}}_o\right)\right|}^2=h\left({\text{r}}_d-{\text{r}}_o^{\perp },r_o^{\parallel },{\widehat{\mathbf{\text{s}}}}_o\right).$$ (38)

Physically, the dipole coherent spread function corresponds to the vector-valued electric field on the detector with appropriate scaling. We need a vector-valued coherent transfer function since the polarization of the field plays a significant role in dipole imaging, so the dipole point spread function cannot be written as an absolute square of a scalar-valued function.

We can plug Eq. (38) into Eq. (28) and use the autocorrelation theorem to rewrite the dipole spatial transfer function as

$$H\left(\mathit{\nu },r_o^{\parallel },{\widehat{\mathbf{\text{s}}}}_o\right)={\int }_{{ℝ}^2}d\mathbf{\tau }\hspace{0.17em}\text{C}\left(\mathbf{\tau },r_o^{\parallel },{\widehat{\mathbf{\text{s}}}}_o\right){\text{C}}^{†}\left(\mathbf{\tau }-\mathit{\nu },r_o^{\parallel },{\widehat{\mathbf{\text{s}}}}_o\right),$$ (39)

where we have introduced the dipole coherent transfer function $\text{C}\left(\mathbf{\tau },r_o^{\parallel },{\widehat{\mathbf{\text{s}}}}_o\right)$ as the two-dimensional Fourier transform of the dipole coherent spread function:

$$\text{C}\left(\mathbf{\tau },r_o^{\parallel },{\widehat{\mathbf{\text{s}}}}_o\right)={\int }_{{ℝ}^2}d\text{r}\hspace{0.17em}\text{c}\left(\text{r},r_o^{\parallel },{\widehat{\mathbf{\text{s}}}}_o\right)\exp \left[-2\pi i\text{r}\cdot \mathbf{\tau }\right].$$ (40)

Physically, the dipole coherent transfer function corresponds to the vector-valued electric field created by a dipole oriented along ${\widehat{\mathbf{\text{s}}}}_o$ in a Fourier plane of the detector with appropriate scaling. Similar to the monopole case, we can calculate the dipole-orientation-dependent fields in a Fourier plane of the detector, scale appropriately to find the dipole coherent transfer function, then use the relationships in Fig. 4 to calculate the other transfer functions. Finally, we note that the dipole coherent transfer function is identical (up to scaling factors) to what Agrawal et al. call the Green’s tensor [6] and Novotny and Hecht’s dyadic point spread function multiplied by the dipole moment vector [32].

Fig. 4.

There is one transfer function for each set of object-space basis functions, and these transfer functions are related by two-dimensional and spherical Fourier transforms—see center and right columns. There is an additional pair of coherent transfer functions that are useful for calculating the transfer functions—see left column.

5. Discussion

5.1. When are alternative bases useful?

Describing a sample f, an imaging system $\mathcal{H}$, or data g in a basis other than a delta function basis is useful when the signal is sparse or band-limited in the new basis. Expressing a signal in a sparser basis is particularly useful for improving intuition about the signal and for reducing computation time.

Throughout this work we have emphasized examples of samples that are sparse in alternative bases. For example, dipoles that are undergoing spatial and angular diffusion give rise to dipole emission densities that are sparse in a basis of complex exponentials and spherical harmonics. In the second of this pair of papers we describe how a common imaging system—a single-view aplanatic microscope—can be described sparsely in the same basis, and this will lead us to a natural definition of the angular band-limit of the imaging system that augments the widely known spatial band-limit.

5.2. Alternatives to the spherical harmonics

Throughout this work we have used the spherical harmonic functions as a basis for functions on the sphere, but there are other basis functions that can be advantageous in some cases. Several works [7, 15, 17, 19, 27, 33] have used the second moments of the Cartesian unit vectors in orientation space (or second moments for brevity) as basis functions for the sphere because they arise naturally when computing the dipole point spread function. These works use an alternative to the dipole angular transfer function that uses the second moments as basis functions so the forward model can be written as

$$g\left(r_d\right)=\sum _{j=1}^6{\int }_{ℝ}d{r}_o^{\parallel }{\int }_{{ℝ}^2}d{r}_o^{\perp }{H}_j\left(r_d-r_o^{\perp },r_o^{\parallel }\right)F_j\left(r_o^{\perp },r_o^{\parallel }\right),$$ (41)

where

$$H_j\left({\text{r}}_d-{\text{r}}_o^{\perp },r_o^{\parallel }\right)={\int }_{{\mathbb{S}}^2}d{\widehat{\mathbf{\text{s}}}}_o\hspace{0.17em}h\left({\text{r}}_d-{\text{r}}_o^{\perp },r_o^{\parallel },{\widehat{\mathbf{\text{s}}}}_o\right)Z_j\left({\widehat{\mathbf{\text{s}}}}_o\right),$$ (42)

$$\hspace{1em}\hspace{1em}{F}_j\left({\text{r}}_o^{\perp },r_o^{\parallel }\right)={\int }_{{\mathbb{S}}^2}d{\widehat{\mathbf{\text{s}}}}_o\hspace{0.17em}f\left({\text{r}}_o^{\perp },r_o^{\parallel },{\widehat{\mathbf{\text{s}}}}_o\right)Z_j\left({\widehat{\mathbf{\text{s}}}}_o\right),$$ (43)

and $Z_j\left(\widehat{\mathbf{\text{s}}}\right)=\left\{s_x^2,s_y^2,s_z^2,s_x{s}_y,s_y{s}_z,s_x{s}_z\right\}$ are the second moments. This formulation is convenient because it can exploit the spatial sparsity of the sample, the angular sparsity of diffusing samples in the basis of second moments, and the angular band-limit of common imaging systems. Additionally, the second moments approach does not require an expansion of the dipole point spread function onto spherical harmonics.

The spherical harmonics provide the same conveniences as the second moments: samples undergoing angular diffusion can be efficiently described using the spherical harmonics, and common imaging systems have an angular band-limit. Additionally, the spherical harmonics provide several potential advantages over the second moments. First, the spherical harmonics form a complete basis for functions on the sphere, while the second moments span a much smaller function space. Descoteaux et al. show that the even order spherical harmonics up to order ℓ and the degree-ℓ homogeneous polynomials restricted to the sphere span the same $\frac{1}{2}\left(\ell +1\right)\left(\ell +2\right)$-dimensional function space [34]. Therefore, the spherical harmonic basis can be extended by adding an extra order of spherical harmonics to the existing set of spherical harmonics. Meanwhile, extending the basis of homogeneous polynomials without redundant basis vectors requires a completely new set of functions. Second, the spherical harmonics are orthogonal, which will allow us to deploy invaluable tools from linear algebra—linear subspaces, rank, SVD, etc.— to analyze and compare microscope designs. Finally, using the spherical harmonics provides access to a set of fast algorithms. The naive expansion of an arbitrary discretized N point spherical function onto spherical harmonics (or second moments) requires a $\mathcal{O}\left(N^2\right)$ matrix multiplication, while pioneering work by Driscoll and Healy [35] showed that the forward discrete fast spherical harmonic transform can be computed with a $\mathcal{O}\left(N{\left(\log N\right)}^2\right)$ algorithm and its inverse can be computed with a $\mathcal{O}\left(N^{3/2}\right)$ algorithm. To our knowledge no similarly fast algorithms exist for expansion onto the higher-order moments.

Zhang et al. [7] have used the second moments to optimize a phase mask that creates a tri-spot point spread function. The authors formulate a system model as a 6×6 matrix that maps the six second moments that describe a rotating single molecule to the six intensity measurements from each lobe and polarization of the tri-spot point spread function. They show that the measurement matrices for existing phase mask designs are rank 4 or 5, and they implement a new rank 6 design that can measure all six second moments. The spherical harmonics can be used to similar effect in this problem by rewriting the system matrix in a basis of spherical harmonics instead of second moments. Additionally, the spherical harmonics form an orthogonal basis, so optimizing the system will be slightly easier (for example, the Fisher information matrix will be diagonal in a spherical harmonic basis).

Backer et al. [36] have used the transverse second moments $\left\{s_x^2,s_y^2,s_x{s}_y\right\}$ to design a polarized-excitation imaging system and reconstruction algorithm that can recover the transverse distribution of fluorescent molecules. Similarly, Zhanghao et al. [5] have used the circular harmonics to design a polarized structured illumination imaging system and reconstruction scheme that can recover the transverse distribution of fluorescent molecules. The transverse second moments and the circular harmonics share the same relationship as the three-dimensional second moments and the spherical harmonics—each pair spans the same function space but only the circular/spherical harmonics are orthogonal. The transverse second moments and the circular harmonics are useful design tools for restricting the number of parameters to estimate, but these approaches artificially restrict the reconstructed dipole distributions to the transverse plane. Finally, we note that the relationship between 2D and 3D estimation problems is slightly simpler in a second moment basis than a spherical/circular harmonic basis. In a second moment basis the six second moments that describe the 3D problem can be truncated to the three second moments that describe the 2D problem. Meanwhile, the spherical harmonics that describe the 3D problem require a matrix multiplication (not a truncation) to map to the circular harmonics.

The diffusion magnetic resonance imaging community uses both the second moments (or second-order tensor) basis functions [37] and the spherical harmonic basis functions [38]. Descoteaux et al. have provided an explicit invertible transformation matrix to convert between the second moments and the zeroth- and second-order spherical harmonics [34]. Since the transformation between these two bases is invertible, functions on the sphere can be described with equal accuracy in either basis.

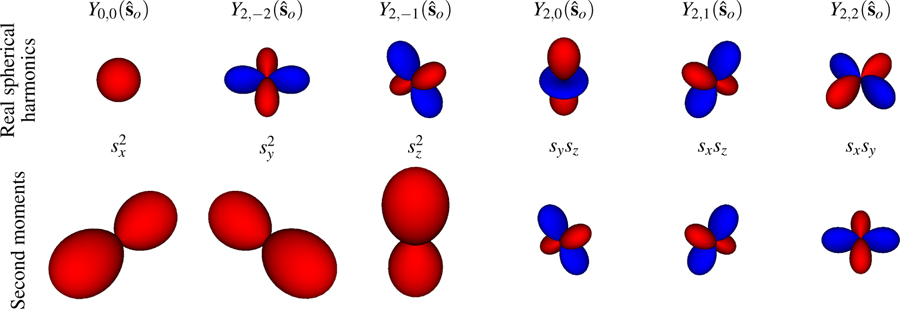
Another difference between the spherical harmonics and the second moments is that the spherical harmonics are complex-valued functions while the second moments are real-valued. Complex-valued spherical harmonics are convenient for mathematical manipulations, but we can also work with real-valued spherical harmonics for cheaper numerical manipulations or for improving our intuition. One possible definition of real-valued spherical harmonics is

$$Y_{\ell ,m}\left({\widehat{\mathbf{\text{s}}}}_o\right)=\{\begin{array}{ll}\sqrt{2}{\left(-1\right)}^m\mathrm{Im}\left[Y_{\ell }^{\left|m\right|}\left({\widehat{\mathbf{\text{s}}}}_o\right)\right]\hfill & \text{if }m<0,\hfill \\ Y_{\ell }^0\left({\widehat{\mathbf{\text{s}}}}_o\right)\hfill & \text{if }m=0,\hfill \\ \sqrt{2}{\left(-1\right)}^m\mathrm{Re}\left[Y_{\ell }^m\left({\widehat{\mathbf{\text{s}}}}_o\right)\right]\hfill & \text{if }m>0,\hfill \end{array}$$ (44)

where the pair of lower indices imply that these are real-valued spherical harmonic functions. In Fig. 5 we directly compare the real-valued spherical harmonic functions to the second moment functions.

Fig. 5.

Top row: Real spherical harmonic basis functions for ℓ = 0 and ℓ = 2. Bottom row: Second moments of the Cartesian unit vectors in orientation space. The radius of each glyph indicates the value of the function along that direction. Red surfaces indicate positive values and blue surfaces indicate negative values. The two sets of basis functions span the same function space, but only the real spherical harmonics form an orthogonal basis.

5.3. Towards spatio-angular reconstructions

We have focused on modeling the mapping between the object and the data in this paper, but ultimately we are interested in reconstructing the object from the data. Considering in-focus objects and applying the monopole approximation simplifies the reconstruction problem because both object and data space are ${\mathbb{L}}_2\left({ℝ}^2\right)$, so we can directly apply regularized inverse filters and maximum likelihood methods. The complete three-dimensional dipole model expands object space to ${\mathbb{L}}_2\left({ℝ}^3\times {\mathbb{S}}^2\right)$, so the inverse problem becomes much more challenging. In future work we will use the singular value decomposition to find inverse filters, and we will consider using polarizers and multiple views to increase the size of data space.

6. Conclusions

Many models of fluorescence microscopes use the monopole and scalar approximations, but complete models need to consider dipole and vector optics effects. In this work we have introduced several transfer functions that simplify the mapping between the dipole emission density and the irradiance pattern on the detector. In future papers of this series we will calculate these transfer functions for specific instruments and use the results to simulate and analyze data collected by these instruments. Also, we note that polarized excitation and/or polarization analysis of the fluorescence emission plays an extremely important role in measuring/imaging the orientation distributions of dipoles. Although we have not included the effects of polarizers in this paper, we plan to extend our work in this direction in upcoming papers of this series.

A. Spherical harmonics and the spherical Fourier transform

The spherical harmonic function of degree ℓ and order −ℓ ≤ m ≤ ℓ is defined as [39]

$$Y_{\ell }^m\left(\vartheta ,\phi \right)=\sqrt{\frac{2\ell +1}{4\pi }}\sqrt{\frac{\left(\ell -\left|m\right|\right)!}{\left(\ell +\left|m\right|\right)!}}{P}_{\ell }^m\left(\cos \vartheta \right)\exp \left(im\phi \right),$$ (45)

where $P_{\ell }^m\left(\cos \vartheta \right)$ are the associated Legendre polynomials with the Condon-Shortley phase

$$P_{\ell }^m\left(x\right)={\left(-1\right)}^m{\left(1-x^2\right)}^{\left|m\right|/2}\frac{d\left|m\right|}{dx\left|m\right|}{P}_{\ell }\left(x\right),$$ (46)

and P_ℓ(x) are the Legendre polynomials defined by the recurrence

$$P_0\left(x\right)=1,$$ (47)

$$P_1\left(x\right)=x,$$ (48)

$$\ell P_{\ell }\left(x\right)=\left(2\ell -1\right)x{P}_{\ell -1}\left(x\right)-\left(\ell -1\right)P_{\ell -2}\left(x\right).$$ (49)

The spherical harmonics are orthonormal, which means that

$${\int }_{{\mathbb{S}}^2}d\widehat{\mathbf{\text{s}}}\hspace{0.17em}{Y}_{\ell }^m\left(\widehat{\mathbf{\text{s}}}\right)Y_{\ell \prime }^{m\prime \ast }\left(\widehat{\mathbf{\text{s}}}\right)={\delta }_{\ell {\ell }^{\prime }}{\delta }_{m{m}^{\prime }},$$ (50)

where ${\delta }_{\ell {\ell }^{\prime }}$ denotes the Kronecker delta. The spherical harmonics form a complete basis for ${\mathbb{L}}_2\left({\mathbb{S}}^2\right)$, so an arbitrary square-integrable function on the sphere $f\left(\widehat{\mathbf{\text{s}}}\right)$ can be expanded into a sum of weighted spherical harmonic functions

$$f\left(\widehat{\mathbf{\text{s}}}\right)=\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^l{F}_{\ell }^m{Y}_{\ell }^m\left(\widehat{\mathbf{\text{s}}}\right).$$ (51)

We can find the spherical harmonic coefficients $F_{\ell }^m$ for a given function using Fourier’s trick— multiply both sides by $Y_{\ell }^{m\ast }\left(\widehat{\mathbf{\text{s}}}\right)$, integrate over the sphere, and exploit orthogonality to find that

$$F_{\ell }^m={\int }_{{\mathbb{S}}^2}d\widehat{\mathbf{\text{s}}}\hspace{0.17em}f\left(\widehat{\mathbf{\text{s}}}\right)Y_{\ell }^{m\ast }\left(\widehat{\mathbf{\text{s}}}\right).$$ (52)

The coefficients $F_{\ell }^m$ are called the spherical Fourier transform of a spherical function.

We can build an intuition for the spherical harmonics by building several spherical functions from their spherical harmonic components—see Fig. 6. We can build a constant function on the sphere with the ℓ = 0, m = 0 spherical harmonic $Y_{0,0}\left(\vartheta ,\phi \right)=\sqrt{1/4\pi }$. The ℓ = 2, m = 0 spherical harmonic $Y_{2,0}\left(\vartheta ,\phi \right)=\sqrt{5/16\pi }\left(3{\cos }^2\vartheta -1\right)$ is independent of the azimuthal angle φ, so the function is rotationally symmetric about the ϑ = 0 axis (see the fourth column of the top row of Fig. 5). Y_2,0(ϑ, φ) is negative for 55° < ϑ < 125°, zero for ϑ = 55°, 125°, and positive otherwise. The weighted sum of these two spherical harmonics $Y_{0,0}\left(\vartheta ,\phi \right)+\frac{1}{8}{Y}_{2,0}\left(\vartheta ,\phi \right)$ results in a rotationally symmetric function that is relatively large near the ϑ = 0 axis (the poles) and relatively small near $\vartheta =\pi /2$ (the equator). The real-valued ℓ = 2, m = 2 spherical harmonic $Y_{2,2}\left(\vartheta ,\phi \right)=\sqrt{15/16\pi }{\sin }^2\vartheta \cos \left(2\phi \right)$ (see Eq. (44)) depends on both the polar angle ϑ and the azimuthal angle φ, so it is not a rotationally symmetric function (see the sixth column of the top row of Fig. 5). The weighted sum of these three spherical harmonics $Y_{0,0}\left(\vartheta ,\phi \right)+\frac{1}{8}{Y}_{2,0}\left(\vartheta ,\phi \right)+\frac{1}{8}{Y}_{2,2}\left(\vartheta ,\phi \right)$ results in a non-rotationally symmetric function that is relatively large near the ϑ = 0 axis (the poles) and the $\left(\vartheta ,\phi \right)=\left(\pi /2,0\right)$ axis, and relatively small near the $\left(\vartheta ,\phi \right)=\left(\pi /2,\pi /2\right)$ axis. By adding spherical harmonics with suitable prefactors, arbitrary square-integrable spherical functions can be built using the spherical harmonics (see Eq. (51)).

Fig. 6.

Square-integrable functions on the sphere can be written as a weighted sum of spherical harmonics. The ℓ = 0, m = 0 spherical harmonic can represent a constant function (left), m = 0 spherical harmonics can represent rotationally symmetric functions (center), and m ≠ 0 spherical harmonics can represent non-rotationally symmetric functions (right).

B. Spatio-angular dynamics

In this appendix we will demonstrate the calculation of the dipole emission density from a simple underlying dynamic model. Our analysis is related to Stallinga’s [18], but here we consider an ensemble of dipoles diffusing both spatially and rotationally with homogeneous and isotropic diffusion coefficients. We start by considering a sample with all of its fluorescent molecules in the ground state. At t = 0 an instantaneous pulse excites a spatio-angular distribution of dipoles so that the initial condition is given by a known function $f^{\left(\text{ex}\right)}\left({\mathfrak{r}}_o,{\widehat{\mathbf{\text{s}}}}_o,t=0\right)$. As time evolves, we assume the fluorescent molecules decay at a constant rate κ^(d), diffuse spatially with a constant coefficient D_R, and diffuse angularly with a constant coefficient D_S so that the dynamics are governed by the partial differential equation

$$\frac{\partial f^{\left(\text{ex}\right)}\left({\mathfrak{r}}_o,{\widehat{\mathbf{\text{s}}}}_o,t\right)}{\partial t}=\left[-{\kappa }^{\left(\text{d}\right)}+D_R{\mathrm{\Delta }}_{{ℝ}^3}+D_S{\mathrm{\Delta }}_{{\mathbb{S}}^2}\right]f^{\left(\text{ex}\right)}\left({\mathfrak{r}}_o,{\widehat{\mathbf{\text{s}}}}_o,t\right).$$ (53)

As written this equation is difficult to solve, but in a basis of complex exponentials and spherical harmonics this equation reduces to an ordinary differential equation. We start by expanding $f^{\left(\text{ex}\right)}\left({\mathfrak{r}}_o,{\widehat{\mathbf{\text{s}}}}_o,t\right)$ into its frequency components using

$$f^{\left(\text{ex}\right)}\left({\mathfrak{r}}_o,{\widehat{\mathbf{\text{s}}}}_o,t\right)=\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }{\int }_{{ℝ}^3}d\mathfrak{v}\hspace{0.17em}{F}_{\ell }^{\left(\text{ex}\right),m}\left(\mathfrak{v},t\right)\exp \left[i2\pi \mathfrak{v}\cdot {\mathfrak{r}}_o\right]Y_{\ell }^m\left({\widehat{\mathbf{\text{s}}}}_o\right).$$ (54)

Plugging this expansion into Eq. (53) we find that

$$\begin{gathered} \sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }{\int }_{{ℝ}^3}d\mathfrak{v}\frac{\partial F_{\ell }^{\left(\text{ex}\right),m}\left(\mathfrak{v},t\right)}{\partial t}\exp \left[i2\pi \mathfrak{v}\cdot {\mathfrak{r}}_o\right]Y_{\ell }^m\left({\widehat{\mathbf{\text{s}}}}_o\right)= \\ \left[-{\kappa }^{\left(\text{d}\right)}+D_R{\mathrm{\Delta }}_{{ℝ}^3}+D_S{\mathrm{\Delta }}_{{\mathbb{S}}^2}\right]\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }{\int }_{{ℝ}^3}d\mathfrak{v}\hspace{0.17em}{F}_{\ell }^{\left(\text{ex}\right),m}\left(\mathfrak{v},t\right)\exp \left[i2\pi \mathfrak{v}\cdot {\mathfrak{r}}_o\right]Y_{\ell }^m\left({\widehat{\mathbf{\text{s}}}}_o\right). \end{gathered}$$ (55)

We can simplify this equation using the eigenvectors and eigenvalues of the spatial and spherical Laplacian operators

$${\mathrm{\Delta }}_{{ℝ}^3}\exp \left[2\pi i\mathfrak{v}\cdot {\mathfrak{r}}_o\right]=-{\left(2\pi \left|\mathfrak{v}\right|\right)}^3\exp \left[2\pi i\mathfrak{v}\cdot {\mathfrak{r}}_o\right],$$ (56)

$$\hspace{1em}\hspace{1em}{\mathrm{\Delta }}_{{\mathbb{S}}^2}{Y}_{\ell }^m\left({\widehat{\mathbf{\text{s}}}}_o\right)=-\ell \left(\ell +1\right)Y_{\ell }^m\left({\widehat{\mathbf{\text{s}}}}_o\right),$$ (57)

to find that

$$\begin{gathered} \sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }{\int }_{{ℝ}^3}d\mathfrak{v}\frac{\partial F_{\ell }^{\left(\text{ex}\right),m}\left(\mathfrak{v},t\right)}{\partial t}\exp \left[i2\pi \mathfrak{v}\cdot {\mathfrak{r}}_o\right]Y_{\ell }^m\left({\widehat{\mathbf{\text{s}}}}_o\right)= \\ \sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }{\int }_{{ℝ}^3}d\mathfrak{v}\left[-{\kappa }^{\left(\text{d}\right)}-D_R{\left(2\pi \left|\mathfrak{v}\right|\right)}^3-D_S\ell \left(\ell +1\right)\right]F_{\ell }^{\left(\text{ex}\right),m}\left(\mathfrak{v},t\right)\exp \left[i2\pi \mathfrak{v}\cdot {\mathfrak{r}}_o\right]Y_{\ell }^m\left({\widehat{\mathbf{\text{s}}}}_o\right). \end{gathered}$$ (58)

Comparing both sides we find that

$$\frac{\partial F_{\ell }^{\left(\text{ex}\right),m}\left(\mathfrak{v},t\right)}{\partial t}=\left[-{\kappa }^{\left(\text{d}\right)}-D_R{\left(2\pi \left|\mathfrak{v}\right|\right)}^3-D_S\ell \left(\ell +1\right)\right]F_{\ell }^{\left(\text{ex}\right),m}\left(\mathfrak{v},t\right).$$ (59)

The solution of this equation is given by

$$F_{\ell }^{\left(\text{ex}\right),m}\left(\mathfrak{v},t\right)=F_{\ell }^{\left(\text{ex}\right),m}\left(\mathfrak{v},0\right)\exp \left[\alpha t\right],$$ (60)

where $\alpha =-{\kappa }^{\left(\text{d}\right)}-D_R{\left(2\pi \left|\mathfrak{v}\right|\right)}^3-D_S\ell \left(\ell +1\right)$.

Eq. (60) shows that as time evolves the initial spectrum $F_{\ell }^{\left(\text{ex}\right),m}\left(\mathfrak{v},0\right)$ decays to the ground state while undergoing an effective decay of the high spatial- and angular-frequency components. In other words, we can interpret diffusion as a filtering operation applied to the spatio-angular spectrum.

$F_{\ell }^{\left(\text{ex}\right),m}\left(\mathfrak{v},t\right)$ is the excited state spectrum, but we can only detect photons emitted as molecules decay to the ground state during the exposure time t_e. In other words, we can only measure the quantity

$$F_{\ell }^m\left(\mathfrak{v}\right)={\int }_0^{t_e}dt\hspace{0.17em}{\kappa }^{\left(\text{d}\right)}{F}_{\ell }^{\left(\text{ex}\right),m}\left(\mathfrak{v},t\right)=F_{\ell }^{\left(\text{ex}\right),m}\left(\mathfrak{v},0\right)\frac{{\kappa }^{\left(\text{d}\right)}}{\alpha }\left\{\exp \left[\alpha t_e\right]-1\right\}.$$ (61)

The main conclusion of this section is that spatial and angular diffusion can be efficiently described in a basis of complex exponentials and spherical harmonics. Although we have only considered homogeneous and isotropic diffusion with constant diffusion coefficients, the complex exponentials and spherical harmonics can be used to simplify the analysis of inhomogeneous and anisotropic diffusion as well. Stallinga has used the spherical harmonics to model angular diffusion in rotationally symmetric potentials [18], and his approach can be generalized to arbitrary spatial and angular diffusion potentials.