Insights into the passive mechanical behavior of left ventricular myocardium using a robust constitutive model based on full 3D kinematics

Abstract

Myocardium possesses a hierarchical structure that results in complex three-dimensional (3D) mechanical behavior, forming a critical component of ventricular function in health and disease. A wide range of constitutive model forms have been proposed for myocardium since the first planar biaxial studies were performed by Demer and Yin (J. Physiol. 339 (1), 1983). While there have been extensive studies since, none have been based on full 3D kinematic data, nor have they utilized optimal experimental design to estimate constitutive parameters, which may limit their predictive capability. Herein we have applied our novel 3D numerical-experimental methodology (Avazmohammadi et al., Biomechanics Model. Mechanobiol., 2018) to explore the applicability of an orthotropic constitutive model for passive ventricular myocardium (Holzapfel and Ogden, Philos. Trans. R. Soc. Lond.: Math. Phys. Eng. Sci. 367, 2009) by integrating 3D optimal loading paths, spatially varying material structure, and inverse modeling techniques. Our findings indicated that the initial model form was not successful in reproducing all optimal loading paths, due to previously unreported coupling behaviors via shearing of myofibers and extracellular collagen fibers in the myocardium. This observation necessitated extension of the constitutive model by adding two additional terms based on the I₈(C) pseudo-invariant in the fiber-normal and sheet-normal directions. The modified model accurately reproduced all optimal loading paths and exhibited improved predictive capabilities. These unique results suggest that more complete constitutive models are required to fully capture the full 3D biomechanical response of left ventricular myocardium. The present approach is thus crucial for improved understanding and performance in cardiac modeling in healthy, diseased, and treatment scenarios.

1. Introduction

Ventricular myocardium is a biocomposite of myocytes, extracellular matrix, and blood vessels, possessing an intricate structural hierarchy and exhibiting complex behaviors at multiple length scales. Cardiomyocytes are structured as long interconnected myofibers [1] reinforced by a collagen weave and perfused by capillaries, assembled to contract synchronously. The orientation of myofibers changes between longitudinal (from base to apex) and circumferential directions throughout the heart. Networks of collagen fibers run roughly parallel to them and bundle neighboring myofibers with weave-like and sheet connections [2, 3]. Bundles of locally parallel myofibers are in turn layered in sheets called laminae [4], stacked along the transmural (or radial) direction of the heart wall from endocardium to epicardium [5].

An accurate understanding of the mechanical behavior of myocardium is indispensable for the treatment of cardiac pathologies. The mechanical behavior of myocardium is unsurprisingly highly nonlinear and anisotropic. From the above considerations, focusing on the scale of ~1–3 mm (at the tissue or meso-scale level), the structure of myocardium can be described as locally orthotropic, wherein the material axes are not generally aligned with the anatomical (longitudinal, circumferential, and radial) directions of the heart [6–9]. Previous experimental studies on the behavior of myocardium have shown how this fiber ensemble structure influences its anisotropic properties in mechanical measurements acquired from samples of left ventricular myocardium. Planar biaxial mechanical testing conducted on sheets of ventricular myocardium [10–12] have detailed the difference between the fiber and cross-fiber directions. The later three-dimensional (3D) shearing experiments performed by Dokos et al. have highlighted its orthotropic properties [13]. Combined triaxial shear and biaxial extension data have recently been collected for human ventricular myocardium and elucidated its viscoelastic, history dependent response [14–17]. In-vivo functional measurements of ventricular pressure, volume, and strain have formed the basis for estimation of constitutive parameters using clinically obtained data [18].

The development of mathematical models of myocardial mechanical behavior has been the focus of research for several decades [6, 19–23]. Ideally, minimally covariant estimation of parameters in a given material model should rely on complete 3D kinematic data. Nevertheless, these approaches are still based upon limited datasets that do not capture the entire kinematic space or may not be mathematically or computationally tractable [9, 24]. Moreover, few studies have substantially assessed the ability of fitted models to accurately predict behavior in generalized or even non-physiological states, such as those associated with disease and the treatment thereof. For a predictive model, the dataset used in fitting must be selected based on some notion of optimality. With respect to practical experimental applications, optimal experimental design (OED) also informs a mechanical testing approach that both maximizes the information obtained as well as minimizes the total time of tests to ensure maintenance of tissue viability. To the best of the authors’ knowledge, Lanir et al. [25] were the first to utilize optimality criteria in soft tissue mechanics in the context of 2D planar biaxial behavior. It should also be noted that OED should not be confused with traditional approaches that determine the form of the model, such as the works of Rivlin and Saunders [26] and Humphrey et al. [27, 28]. We have recently applied OED methods with full 3D kinematics to infarcted myocardium, including both tension and compression modes [29]. The impact of OED has been highlighted through yielding constitutive parameters that are more resistant to experimental noise and have more accurate predictive capability compared to parameters estimated from alternative datasets [29, 30].

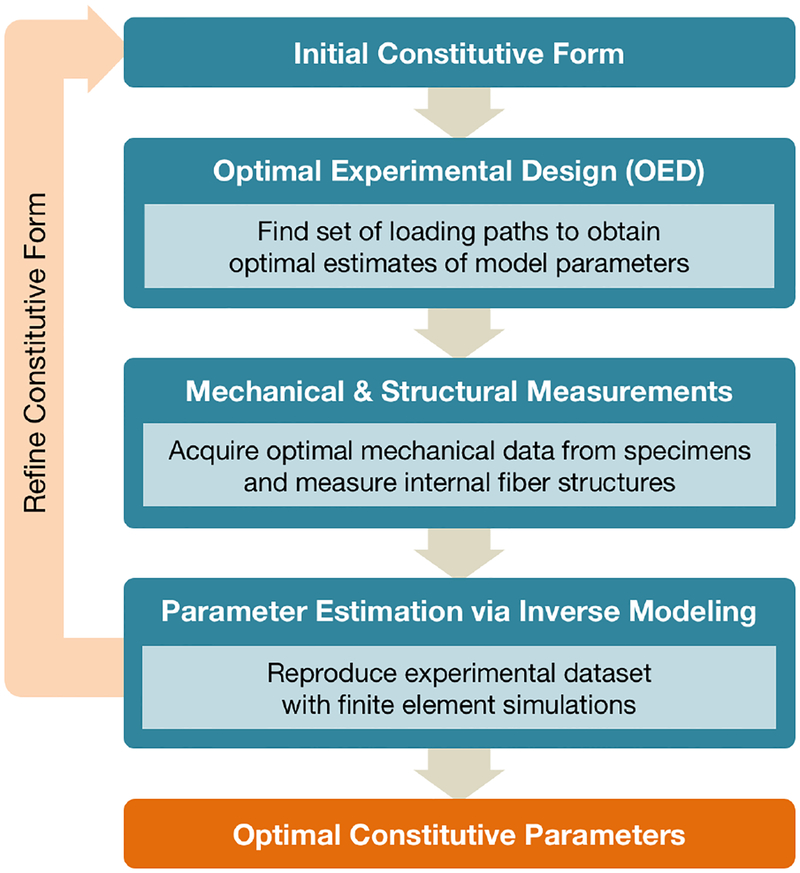
To this end, we have utilized our numerical-experimental methodology to optimally determine the parameters of a given form of the strain energy function for passive ventricular myocardium. Our framework consists of (i) choosing an initial constitutive form to model the mechanical response, (ii) using OED within the full 3D kinematic space to determine the optimal loading paths for robust parameter estimation, (iii) acquiring all necessary mechanical and structural measurements from cuboidal tissue specimens, and (iv) performing inverse modeling with finite element simulations to estimate material parameters. The results of this process can then be used to further refine the constitutive form as necessary (Figure 1). Applying this analysis to healthy ventricular myocardium, we gain deeper insight into possible mechanisms driving the 3D behavior of myocardium, which we employ to develop a novel constitutive model.

Figure 1:

Pipeline of numerical-experimental inverse modeling framework for tissue characterization. The inverse modeling analysis incorporates experimental measurements into finite element simulations in order to estimate constitutive parameters and can be used to refine the optimal constitutive form.

2. Methods

2.1. Optimal experimental design

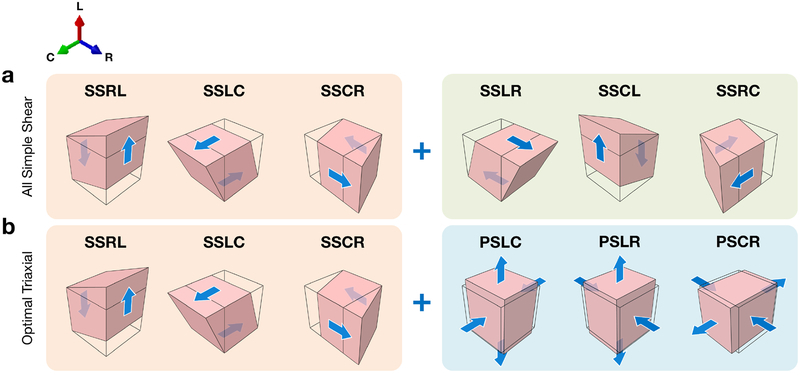
The fundamental objective of optimal experimental design (OED) is to determine a set of loading paths that minimizes the covariance between the estimated model parameters and maximizes the information content of the data for optimal parameter estimation [31–33]. We previously used OED for infarcted myocardium with a modified orthotropic Fungtype constitutive model [7, 34], assuming fiber directions varying linearly from the endo- to epicardium [29]. In the present work, we applied this method to cuboidal specimens whose edges are aligned with the left ventricle anatomical directions: longitudinal (from base to apex), circumferential, and radial (from endo- to epicardium). We also used an alternative invariant-based constitutive form (detailed in Section 2.3 [9]). We determined that, based on A-, D-, and E-optimality metrics [33, 35], the optimal set of six loading paths for the constitutive model consisted of a combination of one-axis simple shear and two-axis pure shear deformations (here named the “Optimal Triaxial” set), compared to the original set of simple shear paths considered in [13] (here named the “All Simple Shear” set) (Figure 2). Data from both loading path sets were collected in triaxial mechanical testing, and constitutive parameters were estimated with both sets within the inverse model.

Figure 2:

Diagrams of loading paths applied to a cuboidal myocardium specimen with edges aligned to the anatomical directions of the heart (see Figure 3a), with the undeformed geometry shown by the black outline. (a) The “All Simple Shear” loading paths emulating the experiments performed by Dokos et al. [13]. (b) “Optimal Triaxial” loading paths that minimize the covariance in parameter estimation. Note that the first three simple shear paths (orange) are common to both sets; in the “Optimal Triaxial” set, fewer simple shear paths are included compared to “All Simple Shear,” (green), and pure shear deformations are introduced (blue). Abbreviations: longitudinal (L), circumferential (C), radial (R).

2.2. Mechanical-structural measurements of passive ventricular myocardium

2.2.1. Tissue harvest and preparation

All animals in this study were used in compliance with the National Institute of Health’s guidelines for care of laboratory animals (NIH Publication 85–23, revised 1996), with approval by the Institutional Animal Care and Use Committee at the University of Pennsylvania (805038) and the University of Texas at Austin (AUP-2017–00204). Specimens of healthy myocardium were harvested from a cohort of adult Dorset sheep (n=5) at the Gorman Cardiovascular Research Group at the University of Pennsylvania. Euthanasia was performed with rapid injection of potassium chloride. Sections were cut out from the left ventricle (LV) and immediately placed in cardioplegic solution (Plegisol) with 20 mM 2,3-butanedione monoxime (BDM) in order to prevent hypercontraction due to cutting. After the tissue sections relaxed into a stress-free state, they were trimmed into 1 × 1 × 1-cm cuboids aligned with the anatomical directions of the heart (Figure 3a).

Figure 3:

(a) Tissue specimen alignment with respect to the anatomical directions of the heart. (b) Close-up of triaxial mechanical testing device, featuring (i) minimally restrictive attachment systems, containing (ii) force-torque cells measuring load in real time, within (iii) heated fluid bath. (c) Myocardium specimen mounted with anatomical directions aligned to device axes. Abbreviations: left ventricle (LV).

2.2.2. Triaxial mechanical testing

Mechanical testing was performed using our triaxial testing device (Figure 3b), capable of applying fully generalized multiaxial deformations on a single cuboidal tissue specimen, as detailed in [29]. Load cells within the minimally restrictive attachment systems were used to measure the 3D force response of the tissue in real time as cyclic deformations are applied to the specimen, controlled with a custom LabVIEW virtual instrument (National Instruments, TX, USA). Each of the specimens was mounted using cyanoacrylate adhesive (Loctite, Düsseldorf, Germany), with the anatomical directions aligned to the device axes (Figure 3c), and subjected to a comprehensive set of cyclic pure shear (tensile-compressive), and simple shear deformations determined from optimal design of experiments. All tests were conducted with the specimen immersed in cardioplegic solution with BDM maintained at 37°C. Additionally, we evaluated the viability of cuboidal myocardium specimens before and after testing using modified MTT assays [36]. For each specimen, a viability index was computed by scaling the difference in measured absorbance at 570 and 690 nm by the mass of the tissue sample, once immediately after harvest and once upon completion of mechanical testing.

2.2.3. Fiber structure measurements

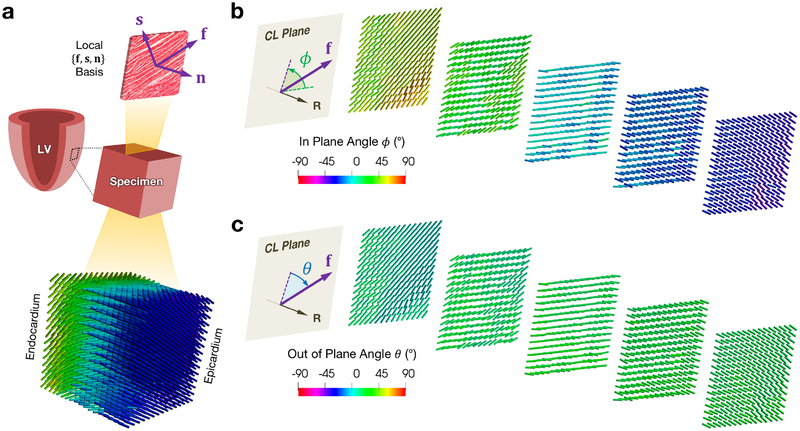
As discussed above, myocardium exhibits a “fiber-sheet-normal” organization at the meso scale, where “fiber” (f) indicates the myofiber orientation, “sheet” (s) indicates the cross-fiber direction within the laminar sheet, and “normal” (n) indicates the direction normal to the sheet (Figure 4a). We utilized diffusion tensor imaging (DTI), a non-destructive fully 3D method that has become standard for quantifying tissue fiber structure [37], especially ventricular myocardium, where the local diffusivity is represented by a second rank tensor D [38–40]. The major eigenvector of D corresponds to the myofiber direction, and the second and third eigenvectors correspond to the local sheet and normal directions, respectively [41].

Figure 4:

(a) Schematic of a tissue specimen with a representative laminar sheet isolated, showing the local fiber-sheet-normal basis, and representative fiber directions from processed DTI, with fiber angle ϕ computed with respect to the circumferential direction. (b–c) Selected circumferential-longitudinal planes along the radial direction showing the (b) in plane angle ϕ and (c) out of plane angle θ of the fiber direction. Abbreviations: fiber (f), sheet (s), normal (n), circumferential-longitudinal (CL). All DTI was visualized using ParaView [42].

Following mechanical testing, each specimen underwent DTI at the University of Utah. Each specimen was placed in a custom probe containing susceptibility matching fluid (Fomblin, Solvay Solexis, NJ, USA) and scanned in a 7.0-T horizontal bore scanner (Bruker BioSpin, Ettlingen, Germany) with magnetic field gradients of 600 mT/m. Encoding was performed along 48 directions with 500/19 TR/TE with a B-value of 800 s/mm², yielding a 40×33×38 matrix with voxel resolution of 400 μm [43]. The fiber architecture of the specimens (Figure 4a) was determined by computing and sorting the eigenvectors of the tensors in each voxel of the image using a custom MATLAB analysis routine (MathWorks, MA, USA). Measuring the fiber directions in this manner allowed for quantification of both the “in (circumferential-longitudinal) plane” helical angle ϕ (Figure 4b) as well as the “out of (circumferential-longitudinal) plane” angle θ (Figure 4c). When modeling the triaxial tests in finite element simulations (see Subsection 2.4), we filtered the small-scale in-plane variations of the DTI and assigned plane-averaged vectors for f, s, and n that were constant throughout the plane at each transmural depth (refer to Appendix A for more detail on the sensitivity of the inverse model to variations in tissue structure).

2.3. 3D constitutive model

To formulate a constitutive model that captures the full anisotropic mechanical response, the myocardium is assumed to behave as a hyperelastic incompressible solid. The deformation applied to the cuboidal specimen is represented with the deformation gradient F = Grad x. The right Cauchy-Green tensor is then given by C = F^TF. In the present work, the strain energy density function ψ, representing the stored elastic energy per unit volume of tissue, is expressed as a function of invariants of the right Cauchy-Green tensor C. The invariants of C are defined as

$$I_1=\text{tr }C,I_2=\frac{1}{2}\left[I_1^2-\text{tr}\left(C^2\right)\right],I_3=\text{det }C,$$ (1)

where I₃ = J² = 1 for an incompressible material. The Cauchy stress of the material T is given by

$$T=F\frac{\partial \psi }{\partial F}-pI=F\frac{\partial \psi }{\partial E}{F}^{\text{T}}-pI,$$ (2)

which can be expanded as

$$T=F\sum _{i=1,i\ne 3}^N{\psi }_i\frac{\partial I_i}{\partial F}-pI,$$ (3)

where pI is a Lagrange multiplier to enforce incompressibility, I is the identity tensor, and ψ_i = ∂ψ/∂I_i (i = 1, 2, …, N), noting that i = 3 is omitted for incompressible materials. Lastly, the Cauchy stress (3) is converted into the first Piola-Kirchhoff stress P by the relation P = JTF^T, which is in turn used to define the traction vector p = Pn, where n is the surface normal (in this case, different from the sheet normal direction).

The initial form of ψ(C) was chosen from the approach proposed by Holzapfel and Ogden [9], which was developed to fit the simple shear dataset of Dokos et al. [13] (Figure 2a) as well as the biaxial dataset of Yin et al. [11]. This approach models the myocardium as an orthotropic material with material axes oriented in the f₀, s₀, and n₀, which are the fiber, sheet, and normal directions in the reference configuration, respectively. It consists of an isotropic exponentially stiffening extracellular matrix (ECM) that is reinforced by exponentially stiffening fiber families in the f₀ and s₀ directions, interacting with one another via relative stretching and shearing. Based on this description, two additional pseudo-invariants are considered,

$$I_{4\text{f}}=f_0\cdot \left(C{f}_0\right)\text{ and }{I}_{4\text{s}}=s_0\cdot \left(C{s}_0\right),$$ (4)

which represent the square of the stretch in each fiber direction λ_i, (i = f, s), along with a coupling pseudo-invariant I_8fs [44], given by

$$I_{8\text{fs}}=f_0\cdot \left(C{s}_0\right)=s_0\cdot \left(C{f}_0\right).$$ (5)

The form of ψ ≡ ψ_HO(I₁, I_4f, I_4s, I_8fs), which will be referred to as the Holzapfel-Ogden (HO) model [9], is thus expressed as

$${\psi }_{\text{HO}}=\frac{a}{2b}\left\{\text{exp}\left[b\left(I_1-3\right)\right]-1\right\}+\sum _{i=\text{f},\text{s}}\frac{a_i}{2b_i}\left\{\text{exp}\left[b_i{\left(I_{4i}-1\right)}^2\right]-1\right\}+\frac{a_{\text{fs}}}{2b_{\text{fs}}}\left[\text{exp}\left(b_{\text{fs}}{I}_{8\text{fs}}^2\right)-1\right],$$ (6)

where {a, …, b_fs} are the eight model parameters.

2.4. Parameter estimation

The HO model (6) parameters were estimated using a custom inverse modeling script in MATLAB and ABAQUS (Dassault Systèmes, RI, USA) that uses finite element (FE) simulations to reproduce the experimental loading paths (for further details, the reader is referred to Appendix B and [9]). In light of the attachments (boundary conditions) associated with the triaxial testing (Figure 3c), we simulated a tetrahedral mesh with subsets of surface nodes that emulated the experimental attachments (Figure 5a). The mesh elements were assigned spatially varying material directions based on the proximity of each element centroid to the corresponding voxel position in the DTI. Each loading path in the set was prescribed as Dirichlet boundary conditions to the node subsets (Figure 5b), and the modeled stress was computed for a given set of material parameters α = {a, b, …, a_fs, b_fs} as the deformation was applied incrementally. The objective function Φ was expressed as

$$\mathrm{\Phi }(\alpha )=\sum _{m=1}^{\text{Paths}}\sum _{n=1}^{\text{Faces}}\sum _{q=1}^{\text{Data}}\Vert \widehat{p}-p(\alpha ){\Vert }_{m,n,q},$$ (7)

where ‖·‖ is the L² norm and $\widehat{p}$ and p(α) are the experimentally measured and simulation-derived stress vectors, respectively. The residual was calculated for each data point from each of the relevant faces of the specimen across all optimal loading paths. An optimal set of parameters α* was sought to minimize Φ:

$${\alpha }^{*}:=\text{arg }\underset{\alpha }{\text{min }}\mathrm{\Phi }(\alpha ).$$ (8)

Figure 5:

(a) Tetrahedral FE mesh (red) with node and element subsets emulating the triaxial loading configuration (yellow). (b) Representative FE simulations of simple shear and pure shear loading paths, with the undeformed geometry shown by the black outline.

We fitted the HO model to the (i) “All Simple Shear” set (Figure 2a), to verify that our approach could accurately reproduce previously measured types of shear behavior, and the (ii) “Optimal Triaxial” set (Figure 2b), which was determined based on ψ_HO. Nonlinear least squares regression was performed using a trust-region-reflective algorithm with a numerically approximated Jacobian in MATLAB [45, 46].

3. Results

3.1. Optimality comparison of simple shear and optimal loading paths

Comparing the values of the A-, D-, and E-optimality criteria for the “All Simple Shear” and “Optimal Triaxial” loading path sets, we determined that the optimal set improved in all metrics (Table 1). This substantial relative gain is consistent with that observed when performing OED on the strain-based model of Costa et al. [7, 29], which supported the enhanced identifiability and robustness of the parameters of the HO model when estimated with the “Optimal Triaxial” dataset.

Table 1:

Comparison of the A-, D-, and E-optimality of the “All Simple Shear” (Figure 2a) and “Optimal Triaxial” (Figure 2b) loading path sets using spatially varying fiber structure and a set of material parameters, computed for a common set of constitutive parameters and fiber structure.

Loading Path Set	ΔA	ΔD	ΔE
All Simple Shear	0.0056	2.90e09	0.0083
Optimal Triaxial	0.2683	2.39e18	0.6241

3.2. Fitting mechanical-structural measurements of healthy myocardium

As seen in previous studies, the specimens exhibited nonlinear mechanical behavior with moderate hysteresis in triaxial testing. Simple shear deformations showed “J” shapes while pure shear deformations showed moderate “S” shapes, and the stresses measured in pure shear modes were greater in general compared to simple shear modes. The maximum stresses measured in triaxial testing varied among specimens, particularly in the pure shear modes (representative data is shown in Figure 7). Evaluating the viability index of the myocardium before and after triaxial testing indicated no statistically significant difference between the two time points. From the DTI, the fiber angle ϕ was observed to decrease from the endoto epicardial sides of the specimens, with an average of roughly 70° of change (Figure 6a).

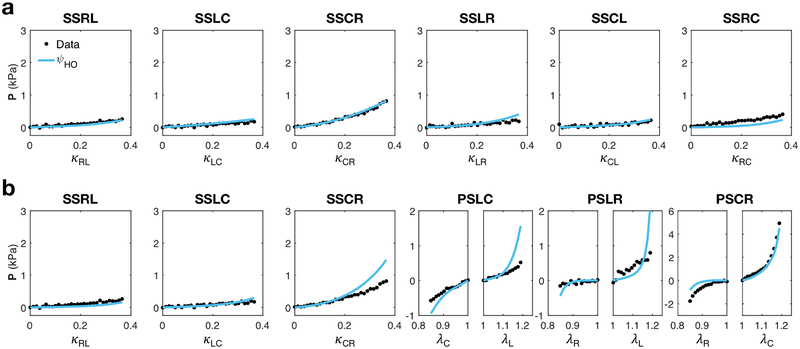
Figure 7:

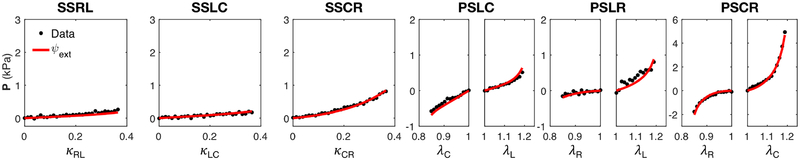
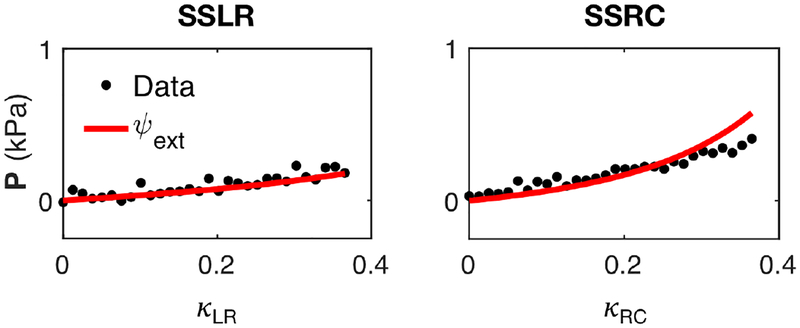
Fit of the HO model (6) (blue line) to the triaxial data (black dots) for the (a) “All Simple Shear” and (b) “Optimal Triaxial” datasets. Results are shown for the relevant components of the first Piola-Kirchhoff stress tensor P as functions of the corresponding shear deformations.

Figure 6:

(a) Circumferential (in plane) angle ϕ of each specimen (S1-S5). (b) Out of plane angle θ for each specimen. Angles computed from DTI eigenvectors corresponding to the f direction.

Interestingly, the fiber directions all showed a persistent out of plane angle θ of up to ±30° (Figure 6b). The heterogeneity of the fiber orientation within a 1-cm dimensional scale necessitated the incorporation of the transmurally varying 3D material directions in the finite element model. It must also be noted that there was significant inter-specimen variation in the endo- and epicardial angles, despite the harvest from roughly the same region of the LV free wall.

The HO model was able to achieve a good fit to the “All Simple Shear” dataset (Figure 7a, Table 2), even when incorporating more heterogeneous specimen structure and loading configurations compared to those in [13]. However, the HO model could not account for the mechanical anisotropy in the “Optimal Triaxial” dataset; although the fitted model captured the high stress of the circumferential-radial pure shear path, this resulted in overestimation of other paths. Despite this, the HO model did fit some simple shear paths well (Figure 7b).

Table 2:

Material parameters for HO model (6) fitted to the “All Simple Shear” and “Optimal Triaxial” loading path sets (Figure 7).

	a (Pa)	b	af (Pa)	bf	as (Pa)	bs	afs (Pa)	bfs
All Simple Shear	126.6	13.1	4099	0.0354	994.8	6.441	35.1	0.911
Optimal Triaxial	152.4	13.2	6665	0.88	84.6	0.08	39.0	1.51

3.3. Stiffening in multiaxial pure shear deformation modes

Closer examination of the “Optimal Triaxial” dataset results, particularly the pure shear modes, revealed substantial stiffening in the tissue under (i) tension in the circumferential and longitudinal directions and (ii) compression in the radial direction, which generally corresponded to tension along the fiber direction and compression along the normal direction. This phenomenon can be illustrated by idealizing the myocardium as bundles of locally parallel sheets of myofibers embedded within extracellular matrix (Figure 8a), placed under tension along the fiber direction. When coupled with compression along the normal direction (Figure 8b), the effective mechanical response was observed to be several times stiffer compared to coupling with compression along the sheet direction (Figure 8b,d).

Figure 8:

(a) Schematic of a representative element of myocardium containing locally parallel myofibers, organized in laminar sheets and embedded within extracellular matrix. (b) Pure shear modes indicating tension along the fiber direction with compression along the sheet direction (orange) and tension along the fiber direction with compression along the normal direction (blue), (c) corresponding to increased stress in both fiber and normal directions.

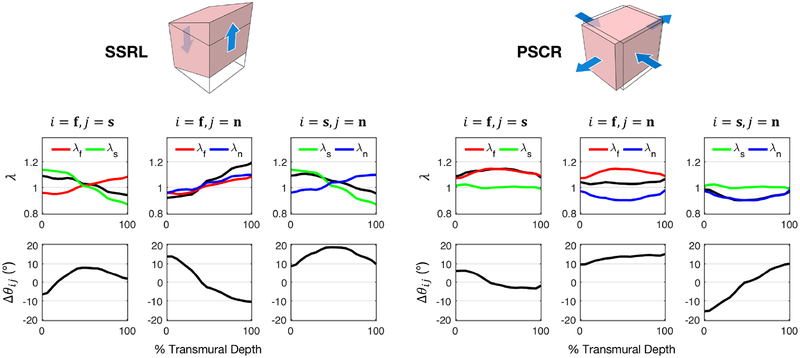
Incorporating the spatially varying fiber structure of the myocardium, the “Optimal Triaxial” deformation modes were examined at maximum strain to determine the transmural distribution of the stretch of each fiber family as well as relative shearing between fiber families in the tissue. The stretches λ, their product λ_iλ_j, and the change in initial angle Δθ_ij were evaluated at each transmural level (Figure 9). In particular, the distributions of these quantities within radial-longitudinal simple shear (SSRL) and circumferential-radial pure shear (PSCR) loading paths offers deeper insight into the relevant kinematic mechanisms in each path. In both modes, there is a relatively small angle change between the fiber and sheet directions as the deformation is applied (less than ±10°), which drastically limits its contribution in the fitted model. Consequently, because of the high fiber stretch contribution necessitated to fit the PSCR mode, the HO model overestimates the stress of other pure shear modes (Figure 7b).

Figure 9:

(Top) Stretches of fiber families (λ) as a function of percent transmural depth at maximum deformation for SSRL and PSCR loading paths: fiber stretch λ_f (red); sheet stretch λ_s (green); normal stretch λ_n (blue); and λ_iλ_j (black). (Bottom) Change in initial angle (Δθ_ij) between fiber families. Shearing of the sheet and normal directions dominates the response in SSRL, seen in the large value of Δθ_sn, whereas shearing of the fiber and normal directions dominates in PSCR, seen in the large value of Δθ_fn, which is distinguished in the extended model (11). i, j = f, s, n.

3.4. Extension of the HO model

Hypothesizing that the myocardium exhibits further modes of coupling related to the relative stretches and shears induced by the optimal deformations, we determined that additional coupling terms were required. Based on the above findings (Figure 9), the remaining I_8ij coupling pseudo-invariants were added, given by

$$I_{8\text{fn}}=f_0\cdot \left(C{n}_0\right)=n_0\cdot \left(C{f}_0\right)\text{ and }{I}_{8\text{sn}}=s_0\cdot \left(C{n}_0\right)=n_0\cdot \left(C{s}_0\right).$$ (9)

These were appealing candidates for extension of the HO model in light of the fact that the I_8ij invariants can be decomposed with the expression [30]

$$I_{8ij}={\lambda }_i{\lambda }_j\text{cos}{\theta }_{ij},i,j=\text{f},\text{s},\text{n},$$ (10)

where λ_i and λ_j are the stretches along fiber families i and j, respectively, and θ_ij is their mutual angle in the deformed configuration (recalling that I_8ij = 0 in the reference configuration). Based on this decomposition, alongside the shearing considerations from the kinematic analysis of the “Optimal Triaxial” dataset (Figure 9), additional terms based on I_8fn and I_8sn were added to ψ_HO. After incorporating these terms, the extended constitutive model ψ_ext resulted in the form

$${\psi }_{\text{ext}}=\frac{a}{2b}\left\{\text{exp}\left[b\left(I_1-3\right)\right]-1\right\}+\sum _{i=\text{f},\text{s}}\frac{a_i}{2b_i}\left\{\text{exp}\left[b_i{\left(I_{4i}-1\right)}^2\right]-1\right\}+\sum _{i,j=\text{f},\text{s},\text{n}}\frac{a_{ij}}{2b_{ij}}\left[\text{exp}\left(b_{ij}{I}_{8ij}^2\right)-1\right].$$ (11)

It is worth noting that these additional terms were originally proposed by Holzapfel and Ogden [9] but were ultimately excluded in fitting the “All Simple Shear” dataset.

The extended model was able reproduce the “Optimal Triaxial” dataset (Figure 10) more accurately compared to the original HO model (Figure 7b). We used the model to successfully fit the optimal datasets for each specimen with r² ≈ 0.80–0.99, the best-fit parameters for which are reported in Table 3. We also demonstrated that the extended model was capable of predicting the response of other paths outside of the Optimal set (Figure 11).

Figure 10:

Fits for the extended model ψ_ext (11) (red line) to the triaxial data from the “Optimal Triaxial” dataset (black dots) of a representative specimen. Results are shown for the relevant components of the first Piola-Kirchhoff stress tensor P as functions of the corresponding stretch and shear deformations.

Table 3:

Parameters of ψ_ext (11) fitted to the “Optimal Triaxial” set of each specimen.

	a (Pa)	b	af (Pa)	bf	as (Pa)	bs	afs (Pa)	bfs	afn (Pa)	bfn	asn (Pa)	bsn
S1	4.81	5.05	1175	0.276	1665	6.93	135.5	0.024	3440	2.01	3278	20.4
S2	0.100	0.346	2936	0.045	989.1	0.190	548.6	0.0020	384.0	1.47	6397	0.004
S3	6.07	4.90	2892	0.0300	178.2	0.0500	1553	0.78	4174	40.3	1791	44.6
S4	1.05	12.0	2964	3.10	496.0	0.0870	369.0	0.011	1712	68.8	547.7	1.17
S5	8.23	1.18	44.36	0.0002	3513	42.7	3591	0.019	1991	0.0017	1274	149

Figure 11:

Model prediction (red line) of radial-circumferential and longitudinal-radial simple shear data (black dots) that were not included in the “Optimal Triaxial” set, using the extended model ψ_ext with parameters obtained from fitting the optimal set (r² = 0.80).

4. Discussion

In this study, we determined optimal constitutive parameters for healthy left ventricular myocardium utilizing a full 3D kinematic approach with optimal loading paths and incorporating the specimen-specific transmurally varying 3D material axes mapped to a finite element mesh. Through the numerical-experimental inverse modeling approach, we extended an existing constitutive model to more fully account for the 3D behavior of the myocardium. This has led to the determination of material parameters for healthy myocardium in a cohort of multiple specimens. To the best of our knowledge, this work is the first estimation of material parameters for healthy myocardium with a full 3D mechanical-structural dataset.

4.1. The importance of optimal 3D datasets and constitutive forms

We initially used the Holzapfel-Ogden model to fit the “All Simple Shear” dataset and were able to reproduce the shearing behavior of the myocardium, which served as validation for the use of our triaxial approach. While the exact parameter values were not obtained due to the differences in specimen size, type, and structure, as well as the difference in shear deformation applied by the triaxial attachments (Figure 5), the same trends were observed in relative parameter values, even when incorporating transmurally varying 3D material structure (Table 2 and Table 1 in [9]). However, these parameters were found to be insufficient in predicting the behavior of the myocardium in multiaxial loading paths like pure shear. Moreover, the mechanical anisotropy of the “Optimal Triaxial” paths could not be captured with the HO model when performing a direct fit.

Considering the orthotropic structure of myocardium, these initial results seemed to indicate possible interactions between fiber families oriented perpendicularly to the myofibers — both within the laminar sheet and normal to it — that were not included in the HO model. This type of behavior could only be observed as a result of performing optimal experiments. Such mechanisms are not accounted for the HO model, due to the fact that the “All Simple Shear” kinematic space over which the model was developed neither caused compression of fiber families nor necessitated coupling interactions between the fiber and normal directions. While the extended model’s increased number of terms does offer an advantage in an overall fitting sense, we believe that the optimal set’s inclusion of new kinematics like tension-compression in pure shear, as well as its predictive performance, provides a more comprehensive look at the generalized behavior of myocardium through use of this model.

4.2. Towards mechanistic constitutive modeling of generalized myocardial behavior

Being that ψ_HO (6) and ψ_ext (11) were formulated as a linear combination of subfunctions of single invariants (ψ(I₁), …, ψ(I_8sn)), the total strain energy can be decomposed with respect to each invariant in the HO and extended models. The decomposition revealed that the ψ(I₁) and ψ(I_4f) terms of the HO model made up the largest portion of the total strain energy, with limited contribution from ψ(I_4s). The contribution due to fiber-sheet interaction (ψ(I_8fs)) was the smallest fraction, which agrees well with the results of Holzapfel and Ogden [9]. The distribution of strain energy subfunction values shifted substantially in the extended model, where proportionally more of the strain energy was due to the additional interaction terms (ψ(I_8fn) and ψ(I_8sn)), particularly in coupling in the fiber and normal directions.

The shearing behavior included in the extended constitutive model suggests that the reorientation of the fiber, sheet, and normal as deformation is applied, captured by the I_8ij invariants (10), could be a possible paradigm for understanding the behavior of myocardium in multiaxial deformation modes. Potential mechanisms such as interactions between myofibers and the surrounding collagen matrix, illustrated in other studies on the microstructural arrangement of myocardium, might be able to produce this behavior. Further studies are clearly required to better explore these potential mechanisms and their role in cardiac function.

Additionally, because of its incorporation of the compression behavior of myocardium in the context of multiaxial deformation, the extended constitutive model has particular relevance in the simulation of myocardium in surgical interventions in which the heart wall is placed under non-physiological conditions. For example, injection of biomaterials into the heart wall has been shown to compact the myocardium around the periphery of the injection mass, as well as cause substantial distortions to the myofiber arrangement local to the material [47], both of which must be taken into account in modeling the injected myocardium.

5. Limitations

The approach described in this work provides deeper understanding of the mechanical contributions of tissue constituents like matrix, fiber, and fiber-fiber interactions. However, without the ability to perform constant invariant experiments (such as those conducted by Humphrey et al. [27, 28]) in full 3D, as a consequence of the spatially variable fiber structure, developing an optimal invariant-based constitutive form remains practically infeasible.

The deformation prescribed in triaxial testing is also limited in that it is an approximation of the actual deformation undergone by the specimen. Despite this, previous work has demonstrated that despite some stress concentrations and heterogeneity at the specimen boundaries, majority of the specimen volume is nevertheless a reasonable representation of the deformation [29]. Additionally, as with related studies, we take a pseudoelastic approach. It has been shown that some hysteresis exists in the loading and unloading responses of myocardium, indicating the presence of viscoelastic effects [17]. Hence, both the loading and unloading measurements obtained in triaxial testing will be need to be explored to fully model the history dependent properties of myocardium.

Although the use of pseudo-invariant coupling terms (ψ(I_8ij)) was an intuitive option with which to extend the constitutive model, the decomposition of the I_8ij term (10) also indicates that the model is unable to sufficiently separate individual kinematic components of the optimal deformation modes within the model. While detailed fiber structure from DTI is used in our methodology, the fine structural details of myocardium are not explicitly modeled, as has been done in [48, 49]. Rather, the focus of this work is on the “effective tissue level” that is critical for accurate organ-level simulations [23].

Finally, the approach detailed here was focused on developing a novel constitutive form for passive myocardial properties, whereas the myocardium exhibits distinct (likely coupled) active and passive behaviors in-vivo. Other types of myocardium (e.g., infarcted and treated) remain to be characterized with this method when developing an organ-level computational modeling platform for the myocardium.

6. Summary

The present study is a crucial first step towards more robust constitutive modeling of healthy myocardium over the complete contraction cycle, which serves as a foundation for more complex models of the heart. We have applied a fully 3D experimental/modeling/simulation methodology to the characterization of the passive properties of ventricular myocardium. Through utilization of optimally designed experiments based on full 3D kinematics, we observed novel coupling modes under tensile-compressive pure shear deformations not found in previous studies of myocardial mechanical properties. Capturing the unique anisotropy exhibited by myocardium in the data, in conjunction with spatially varying fiber orientations, required the extension of an existing constitutive model to include all three I₈ coupling pseudo-invariants. Subsequent analysis of these responses offered insight on the importance of shearing of fiber constituents in the myocardium. We demonstrated that this extended model accurately captures a more comprehensive range of 3D deformations and is enriched by the integrated approach to yield material parameters that have increased predictive capability in generalized modes. We also note that it was the methodology that allowed us to delineate new behaviors not previously observed. While we performed DTI to obtain the local 3D fiber architecture, the length scale of this study was at the tissue level. Thus, detailed micro-structural mechanisms underlying our observations remain to be characterized in further studies that are currently being conducted. The ultimate goal of our line of study is to build toward calibrating a novel model and empower its predictability in the full kinematic space so that it accurately captures myocardial behavior in complex 3D deformations like those experienced in-vivo or in surgical interventions [20, 41, 50]. Ultimately, development of more robust and generalizable models will make such computational tools more suitable for clinical evaluation to facilitate improved patient outcomes.

Table 4:

Labels used to describe the triaxial loading paths and loading path sets. Diagrams of the loading paths are shown in Figure 2.

	Label	Description
Anatomical Direction	L	Longitudinal
	C	Circumferential
	R	Radial
Loading Path	SS	One-Axis Simple Shear
	PS	Two-Axis Pure Shear
All Simple Shear	SSRL	Radial-Longitudinal Simple Shear
	SSLC	Longitudinal-Circumferential Simple Shear
	SSCR	Circumferential-Radial Simple Shear
	SSLR	Longitudinal-Radial Simple Shear
	SSCL	Circumferential-Longitudinal Simple Shear
	SSRC	Radial-Circumferential Simple Shear
Optimal Triaxial	SSRL	Radial-Longitudinal Simple Shear
	SSLC	Longitudinal-Circumferential Simple Shear
	SSCR	Circumferential-Radial Simple Shear
	PSLC	Longitudinal-Circumferential Pure Shear
	PSLR	Longitudinal-Radial Pure Shear
	PSCR	Circumferential-Radial Pure Shear

Appendix A. Variation in fiber structure detail

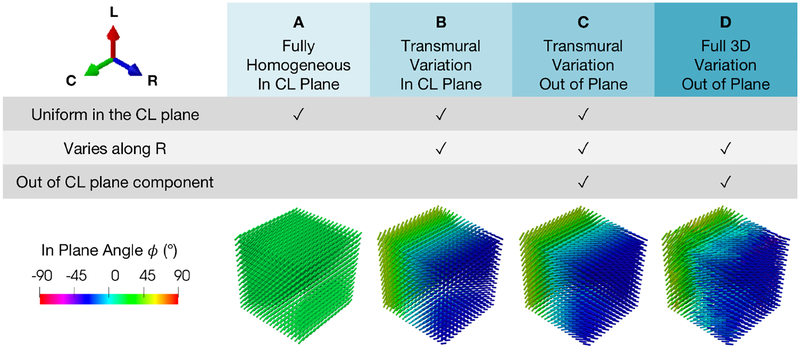
The degree to which the spatial (in particular, transmural) variation in fiber orientation influences fitted model parameters at the meso scale has only been explored in a few works [29], despite evidence that this effect may generate non-negligible out-of-plane stresses in the tissue [24]. With the information available through DTI, the influence of structural heterogeneity in the mapped DTI fiber structure on the goodness of fit and the predictive capability of estimated parameters must be assessed. The influence of 3D material directions — in particular, the “out of plane” component — on best-fit parameters of ψ_ext (11) was explored by constraining the DTI to the circumferential-longitudinal (CL) plane or allowing variation along the radial direction, with (i) one homogeneous CL fiber direction throughout the entire mesh (A), (ii) transmural variation but constant at a given depth, restricting the fiber direction to the CL plane (B), (iii) transmural variation but constant at a given depth, including the out of plane component (C), and (iv) full 3D spatial variation with the out-of-plane component (D) (Figure A.1). The resulting fits from each fiber structure were compared in terms of goodness of fit, parameter values, and capability to predict the mechanical behavior of other (non-optimal) triaxial loading paths not used in parameter estimation.

Figure A.1:

Four levels of increasing detail applied to DTI processing for a representative specimen. A: homogeneous constrained to CL plane. B: transmural variation constrained to CL plane. C: transmural variation with out of (CL) plane component. D: full 3D spatial variation within a given CL plane with out of plane component.

Each mesh was fit to the “Optimal Triaxial” dataset of a representative specimen, and the resulting best-fit parameters were used to predict the stresses of other simple shear paths (not overlapping with the “Optimal Triaxial” set) with a forward simulation. While each level of detail was fitted to the “Optimal Triaxial” dataset with a relatively high goodness of fit (r² ≈ 0.93–0.99), both the A and B fiber structures fell short in fitting the data, as seen in the overestimations in paths and underestimations in compression in PS paths (Figure A.2), and they were not considered when predicting the simple shear response. There was a small level variation in the predictive capability of the fitted models in the C and D cases when predicting alternative simple shear paths. The transmural variation out of plane (C) fiber structure was the only structure that provided a robust fit to the optimal data while also achieving the best prediction compared to other structures for the simple shear paths (Figure A.3), proving to contain a sufficient level of detail to accurately describe the mechanical anisotropy in the optimal data. Fitted parameters are reported in Table A.1.

Figure A.2:

Fit of each level of fiber structure detail (lines) to “Optimal Triaxial” dataset (black dots).

Figure A.3:

Predictions (lines) of the remaining simple shear data (black dots) outside of the “Optimal Triaxial” dataset using the best-fit parameters fit to the optimal data. A and B are not considered in the prediction due to their poor fit in Figure A.2.

Table A.1:

Material parameters of ψ_ext fitted to the “Optimal Triaxial” set for each fiber structure.

	a (Pa)	b	af (Pa)	bf	as (Pa)	bs	afs (Pa)	bfs	afn (Pa)	bfn	asn (Pa)	bsn
A	9.60	8.65	2569	1.37	1108	2.23	136.7	0.0100	1119	55.1	347.4	5.00
B	579	0.00	2176	6.46	173.3	0.00	0.0200	8.98	2206	29.5	0.210	0.00
C	1.05	12.0	2963.6	3.097	496.02	0.087	368.95	0.011	1712.4	68.774	547.74	1.165
D	0.35	17.2	3153	2.71	454.3	0.00100	155.0	0.00100	2790	44.4	572.2	0.696

Appendix B. Model parameter constraints

As described in [9], convexity is enforced by placing constraints on the coefficients within terms that are functions of one invariant. Given the linear combination of terms within the model, convexity can be assessed on an individual term-by-term basis. We assess convexity of the functions $\mathcal{F}\left(I_1\right)$, $\mathcal{G}\left(I_{4\text{f}}\right)$, and $\mathcal{H}\left(I_{\text{8fs}}\right)$ to provide parameter constraints for the overall model. The convexity requirements on $\mathcal{F}\left(I_1\right)$ are that for a given function

$$\mathcal{F}\left(I_1\right)=\frac{a}{2b}\left\{\text{exp}\left[b\left(I_1-3\right)\right]-1\right\},$$ (B.1)

and for all second-rank tensors A,

$$\frac{{\partial }^2\mathcal{F}\left(I_1\right)}{\partial C\partial C}[A,A]\equiv {\mathcal{F}}^{″}\left(I_1\right){(\text{tr }A)}^2\ge 0,$$ (B.2)

leading to the constraint ab ≥ 0, or a > 0 and b > 0. Similarly, for $\mathcal{G}\left(I_{4\text{f}}\right)$ it follows that for the function

$$\mathcal{G}\left(I_{4\text{f}}\right)=\frac{a_{\text{f}}}{2b_{\text{f}}}\left\{\text{exp}\left[b_{\text{f}}{\left(I_{4\text{f}}-1\right)}^2\right]-1\right\},$$ (B.3)

$$\frac{{\partial }^2\mathcal{G}\left(I_{4\text{f}}\right)}{\partial C\partial C}[A,A]\equiv {\mathcal{G}}^{″}\left(I_{4\text{f}}\right){\left[\left(A{f}_0\right)\cdot f_0\right]}^2\ge 0.$$ (B.4)

From this relation, a_f > 0 and b_f > 0.

Lastly, for $\mathcal{H}\left(I_{\text{8fs}}\right)$,

$$\mathcal{H}\left(I_{\text{8fs}}\right)=\frac{a_{\text{fs}}}{2b_{\text{fs}}}\left[\text{exp}\left(b_{\text{fs}}{I}_{\text{8fs}}^2\right)-1\right],$$ (B.5)

$$\frac{{\partial }^2\mathcal{H}\left(I_{8\text{fs}}\right)}{\partial C\partial C}[A,A]\equiv {\mathcal{H}}^{″}\left(I_{\text{8fs}}\right){\left[\left(A{f}_0\right)\cdot s_0\right]}^2\ge 0,$$ (B.6)

leading to the constraints a_fs > 0 and b_fs > 0.