Systems biology: perspectives on multiscale modeling in research on endocrine-related cancers

Abstract

Drawing on concepts from experimental biology, computer science, informatics, mathematics and statistics, systems biologists integrate data across diverse platforms and scales of time and space to create computational and mathematical models of the integrative, holistic functions of living systems. Endocrine-related cancers are well suited to study from a systems perspective because of the signaling complexities arising from the roles of growth factors, hormones and their receptors as critical regulators of cancer cell biology and from the interactions among cancer cells, normal cells and signaling molecules in the tumor microenvironment. Moreover, growth factors, hormones and their receptors are often effective targets for therapeutic intervention, such as estrogen biosynthesis, estrogen receptors or HER2 in breast cancer and androgen receptors in prostate cancer. Given the complexity underlying the molecular control networks in these cancers, a simple, intuitive understanding of how endocrine-related cancers respond to therapeutic protocols has proved incomplete and unsatisfactory. Systems biology offers an alternative paradigm for understanding these cancers and their treatment. To correctly interpret the results of systems-based studies requires some knowledge of how in silico models are built, and how they are used to describe a system and to predict the effects of perturbations on system function. In this review, we provide a general perspective on the field of cancer systems biology, and we explore some of the advantages, limitations and pitfalls associated with using predictive multiscale modeling to study endocrine-related cancers.

Introduction

Over the past few decades, many advances in endocrine-related cancers have come from the experimental fields of cellular and molecular biology and from their translation into clinical applications. Generally speaking, cellular and molecular studies have taken a mostly reductionist approach, focusing on mechanistic studies of specific genes and proteins, linear signaling pathways, and particular anticancer drugs and other interventions. A systems-based approach builds on this important work by providing a more holistic account of the complex networks of interacting genes, proteins and metabolites that determine how a cancer cell survives and thrives within the tumor microenvironment and how the host responds to the tumor. From this viewpoint, molecular networks and the subcellular processes they regulate are seen to interact with activities occurring within the tumor cell, its microenvironment and the cancer-bearing organism. A holistic view, where interactions can have both local and distant effects, is nothing new for endocrinologists and experts in some other fields. However, in what is now often referred to as the ‘post-genomic era’, the tools and technologies available to effectively study any cancer as a systems-disease have changed dramatically. In concert with these advances has come greater insight into the remarkable complexity of signaling, its integration and the coordination evident in controlling and executing cellular functions.

In this review article, we hope to introduce a broad readership to the potentials and limitations of a systems approach to improve our understanding and treatment of endocrine-related cancers. The scope of endocrine-related cancer systems biology is large and complex, and we acknowledge that some issues in this field are addressed here at a relatively simplistic level. Nonetheless, we believe that a systems approach, including computational and mathematical modeling of new data streams, is essential to transform data into actionable knowledge that leads to fundamental improvements in human health. An overview of the organization of this review is provided in Fig. 1. We begin with a section on why models are needed, how modelers generally approach building their models, and some considerations regarding the specific goals of modeling. Next, we describe how models may be based on a modular structure, and how modularity can lead to emergent behaviors, as consequences of the dynamical properties of signaling networks. We discuss deterministic, stochastic and Bayesian models, and how their parameters are estimated from data and provided with error bounds. We then discuss model performance, potential sources of error, the importance of independently validating model predictions and modeling drug interactions. Subsequent sections discuss examples of a knowledge-guided computational tool for building networks, a mathematical model of the estrogen receptor landscape and some insights into interpreting models.

Figure 1.

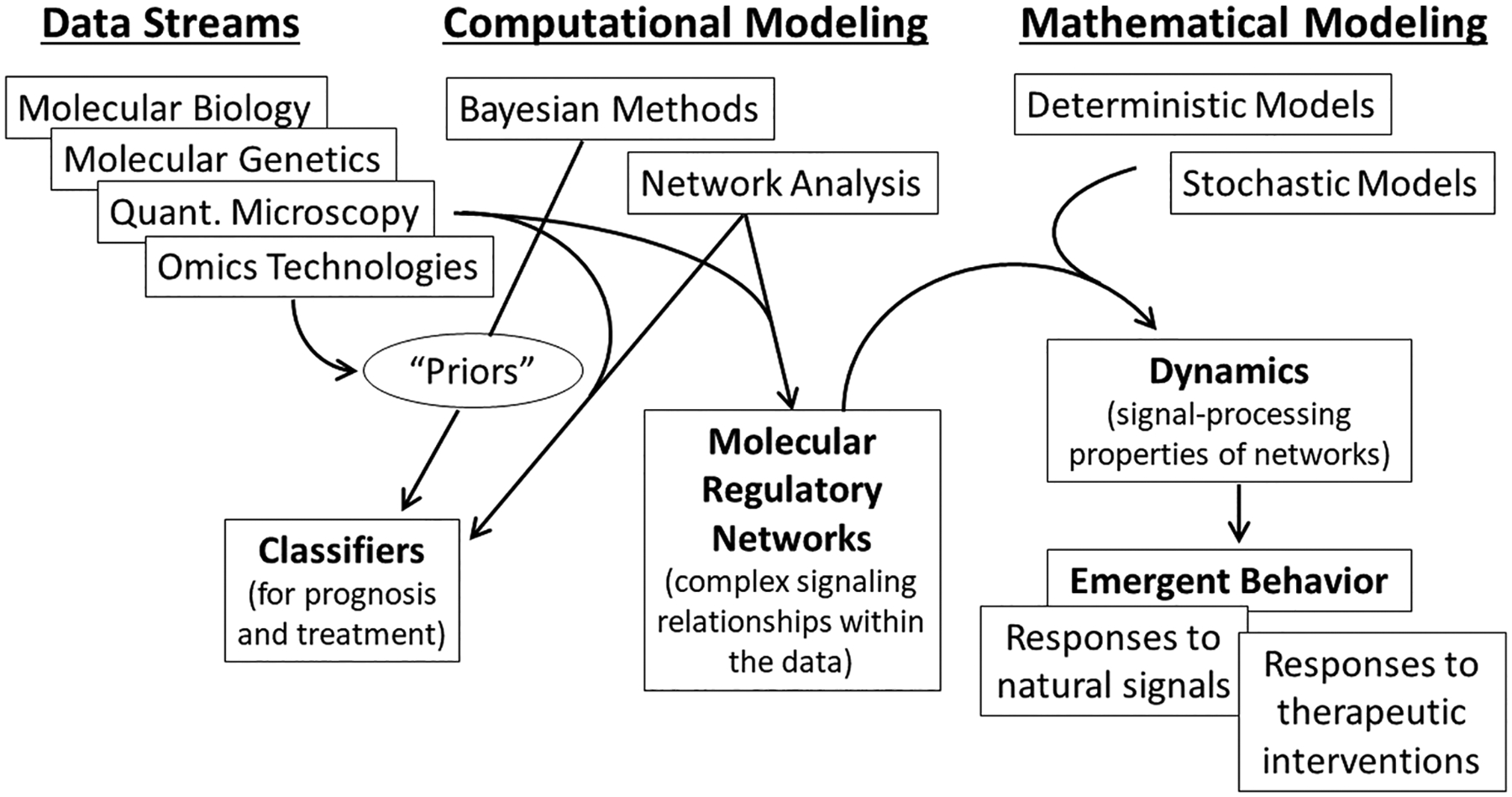
Representation of data streams and how these relate to computational and mathematical modeling in the context of systems biology. The four primary sections of this review contain specific insights into different aspects of modeling that reflect how modeling uses data streams to build multiscale models. We first describe why models are needed in ‘Why build models’. The second section ‘Multiscale modeling’ introduces several critical aspects of modeling, from some basic goals of modeling, then describing how models can use a modular structure that can explain the emergent properties of biological systems. Deterministic, stochastic, and Bayesian models are then presented, as is the critical feature for cancer therapies of strategies to model drug interactions. These subsections are followed by a discussion of types of error in modes, assessing model performance, and validating model predictions. The final two subsections within the section on multiscale modeling provide specific examples of tools or approaches to modeling: a knowledge-guided computational tool for building networks, and a mathematical model of the estrogen receptor landscape. The penultimate section ‘Interpreting models’ provides some insights into the challenges and pitfalls of interpreting model solutions. The final section ‘Future directions’ offers some brief insights into where the authors see the field going in the next few years.

For our purposes in this review, a system is a collection of interacting components that produces a defined biological output in response to specific inputs. To be useful, such input–output models must adequately capture the complexity of the system. Complexity does not necessarily mean ‘big’ (many nodes and edges). Relatively small networks can exhibit non-intuitive signal-processing capabilities due to inherent feedforward and feedback loops and non-linear kinetic rate laws, for which small changes in input produce disproportionately large changes in output.

Most biological systems are open, complex, dynamic and adaptive. While these fundamental properties may be missed in work that adopts a solely reductionist perspective, there would be little for systems biologists to model without the data and insights obtained from reductionist studies. Systems biologists acknowledge both the complexity of biological systems and the fact that much of what must be modeled and interpreted is still poorly understood. Computational and mathematical models are often used to analyze and integrate data from multiple technological platforms into new representations of system function. These new representations can expand our understanding of complex regulatory systems (Lavrik & Zhivotovsky 2014, Wang & Deisboeck 2014, Altrock et al. 2015, Peng et al. 2016, Janes et al. 2017, Ji et al. 2017). Ultimately, systems-based insights into the biology of endocrine-related cancers may lead to better treatments and outcomes for patients (Werner et al. 2014, Jinawath et al. 2016, Ji et al. 2017).

While the idea of generating mathematical models of signal flow in a biological system is not new (Le 2007, Ji et al. 2017), the sources and magnitude of data for multiscale modeling, and many of the computational/mathematical tools available, have changed dramatically in recent years. Many of the newer technologies fall into the rapidly developing fields of omics (genomics, transcriptomics, proteomics, metabolomics), an increasing number of sub-omic technologies and quantitative microscopy including gene expression in single cells (Sandberg 2014, Buettner et al. 2015, Kanter & Kalisky 2015). Central to our ability to analyze and integrate these new data streams and to build new mathematical models and computational representations of the data, are the analytical approaches and software tools that continue to be developed by computer scientists, mathematicians and statisticians. Rather than being identified with any of these particular specializations, systems biology sits uniquely at their nexus.

We will focus our discussion on the use of computational and mathematical approaches to model system function in the context of endocrine-related cancer biology. For the purposes of this review, we consider a ‘mathematical model’ as using differential equations and stochastic algorithms to create dynamic, semi-mechanistic models of control networks of limited scope (dozens of genes and their products). Of course, such dynamical models must ultimately be simulated on a digital computer, but we consider a ‘computational model’ as something different: as using machine-learning tools to explore high-dimensional data (hundreds or thousands of genes and/or proteins).

Mathematical models may be deterministic or stochastic in nature, depending on the role of random events in the system being modeled. In either case, all models ultimately entail a statistical evaluation of how well the model’s output fits the available experimental data. Both stochastic and deterministic models can be useful when used appropriately (Twycross et al. 2010). At present, deterministic models are usually the initial approach taken to provide a description of molecular events in cellular control systems. However, considering the paucity of informative data within the flood of omics results, the unavoidable noise in biological measurements, and our ignorance of latent variables in regulatory networks, stochastic (Wilkinson 2009) or hybrid models (Twycross et al. 2010) are being applied more widely. Some of the general limitations in modeling have been discussed elsewhere (Di et al. 2006, Wilkinson 2009, Twycross et al. 2010) and will not be reiterated here.

From a clinical perspective, useful in silico models will have to be multiscale. For example, drug action at the molecular scale must be linked to clinical outcomes at the tissue or organism scale. Multiscale models use many different data types from multiple sources, spanning scales from DNA to RNA to protein, from metabolites to cells to tissues, from tissues to organisms and even to interacting populations. Modeling based only on genome and/or transcriptome data can be limited because approximately 50% of changes found in the transcriptome may not be present in the proteome (Vogel & Marcotte 2012); an even smaller percentage of changes in the genome may filter through to the proteome. Hence, spanning scales (provided necessary data are available) may improve the models and provide new insights into cancer physiology (Deisboeck et al. 2011).

In this review, we explore some of the basic concepts and challenges in applying computational and mathematical modeling to endocrine-related cancer research. Rather than providing detailed descriptions of tools-of-the-trade, we discuss a variety of computational and mathematical approaches that are often applied, the advantages and limitations of each, and the specific challenges for using them correctly and usefully. Since we will not discuss specific experimental designs here, readers interested in exploring the many tools, workflows and frameworks and emerging standards for systems-based research may find the following sources useful (Brazma et al. 2006, Swertz & Jansen 2007, Gehlenborg et al. 2010, Ghosh et al. 2011, Wu & Stein 2012, Hofree et al. 2013, Sedgewick et al. 2013, Wen et al. 2013, Cheng et al. 2014a,b, Hoadley et al. 2014, Creixell et al. 2015, Leiserson et al. 2015, Dimitrova et al. 2017, Nam 2017, Keenan et al. 2018, Miryala et al. 2018). Similarly, there are many sources of cancer omics data in the public domain that are too numerous to capture here. However, we provide examples of some widely used large omics datasets that include data from breast and other endocrine-related cancers in Table 1.

Table 1.

Examples of the most commonly used endocrine-related breast cancer public omic datasets.

Database	URL	Data spaces
CPTAC	https://proteomics.cancer.gov/data-portal	Proteome
EGA	https://ega-archive.org/datasets	Genome, Transcriptome
EMBL-EBI	https://www.ebi.ac.uk/services/all	Genome, Transcriptome, Proteome, Metabolome
GNPS/Massive	https://gnps.ucsd.edu/ProteoSAFe/static/gnps-splash.jsp	Metabolome
ICGC	https://dcc.icgc.org/	Genome, Transcriptome
MassIVE	https://massive.ucsd.edu/ProteoSAFe/static/massive.jsp	Proteome
Metabolomics	https://www.metabolomicsworkbench.org/	Metabolome
Workbench
NCBI-GEO	https://www.ncbi.nlm.nih.gov/gds	Genome, Transcriptome
ONCOMINE	https://www.oncomine.org/resource/login.html	Genome, Transcriptome
ProteomeXchange (PX) Consortium	http://www.proteomexchange.org/	Proteome
ProteomicsDB	https://www.proteomicsdb.org/	Proteome
TCGA	https://portal.gdc.cancer.gov/	Genome, Transcriptome

Primary data and metadata quality vary across and within these sites. For example, clinical metadata for human subjects are often limited. The platform used for data collection in each omics space also can vary across and within these sites. While most provide access to the raw (unprocessed) data, ONCOMINE primarily exposes only processed data; the method of data processing can vary across individual studies.

Given clear evidence of a significant lack of reproducibility in biomedical research (Begley 2013, Mobley et al. 2013, Hatzis et al. 2014) and the potential for systems approaches to both reduce and exacerbate this problem, an appreciation of some of the key challenges – for which there may or may not be adequate current solutions – is timely. While we cannot address all the major issues in such an interdisciplinary subject, we hope that our perspective will be pertinent to using systems biology to attain a better understanding of endocrine-related cancers.

Why build quantitative models of biological systems?

‘The statistician knows, for example, that in nature there never was a normal distribution, there never was a straight line, yet with normal and linear assumptions, known to be false, he can often derive results which match, to a useful approximation, those found in the real world.’

George E P Box (1919–2013)

To extract new insights and build integrated, predictive models, particularly from experiments that generate ‘big data’, requires some form of in silico analysis to deal with the complexity of the data. For biological systems, complexity can arise from dimensionality (many genes and their interactions) and from general properties of the system that reflect its topology (feedforward and feedback loops), adaptability (redundancy, degeneracy), multimodality (concurrent performance of multiple integrated and coordinated tasks) and dynamism (changes in time and space) (Clarke et al. 2008, Tyson et al. 2011). Complexity can also arise at the cellular level. A notable feature of several endocrine-related cancers is their cellular heterogeneity, which creates a dynamic microenvironment of many cell types in addition to the cancer cell component and can also affect a tumor’s response to treatment (Junttila & de Sauvage 2013, Meacham & Morrison 2013, Martelotto et al. 2014). Often, models are built with transcriptome data that reflect averaged expression values, since tissue microdissection prior to collecting omic data remains relatively uncommon. When applying computational and mathematical modeling to study cell type/tissue type in data from complex tissue samples, data deconvolution using either supervised or unsupervised approaches is a prerequisite. Supervised data deconvolution can be performed by integrating tissue-specific gene or protein expression profiles (Newman et al. 2015) from the Gene-Tissue Expression program (GTex Consortium 2015) and The Human Protein Atlas (Ponten et al. 2011). Alternatively, in the more challenging case of intra-tumor heterogeneity where subclone-specific markers are often unknown, an unsupervised data deconvolution approach such as Convex Analysis of Mixtures can be exploited to uncover the hidden subclone specificity (Wang et al. 2015, 2016, Herrington et al. 2018). While tools for supervised (Zuckerman et al. 2013, Hart et al. 2015) and unsupervised deconvolution of averaged data from heterogeneous tissues (Chen et al. 2011, Wang et al. 2016) can be used as a data processing step prior to modeling – this preprocessing step remains uncommon.

The properties of high-dimensional data, particularly data from omics technologies, present unique challenges (Clarke et al. 2008) that are often inadequately addressed or fully appreciated. Nonetheless, the purpose of in silico analysis is to apply tools to extract meaningful results from high-dimensional data for the purposes of generating and testing biological hypotheses (Tyson et al. 2011). For instance, we may wish to understand and predict under what conditions a cancer cell will begin to proliferate in situ or migrate to a new location. Extracting such knowledge from large datasets by intuitive reasoning alone can be difficult or impossible and is often associated with a high risk of operator bias and/or error. Thus, new tools and approaches continue to emerge to deal with the challenges of working in high-dimensional data spaces and to enable integrating the spatial, temporal and cell context-specific nature of regulatory networks (Hoadley et al. 2014, Leiserson et al. 2015, Masoudi-Nejad et al. 2015, Tape 2016, Barberis & Verbruggen 2017, Dimitrova et al. 2017). New concepts, such as ‘master regulator proteins’ that may determine the transcriptional state of a cancer cell, also continue to arise (Califano & Alvarez 2017).

Computational modeling can provide unbiased results from large data sets, allowing us to visualize complex signaling relationships within the data (Gehlenborg et al. 2010). Some of the more useful approaches in this area come from applications of graph theory. Graphs are mathematical structures that represent pairwise relationships between nodes. Each gene/protein is a node (or vertex) and each connection with another gene/protein is an edge. Graphical representations of molecular signaling are readily available on the web. For example, signal transduction pathways may be found at the community-based Kyoto Encyclopedia of Genes and Genomes (KEGG; http://www.genome.jp/kegg) or the commercially supported Biocarta Pathways Project (http://www.biocarta.com/genes/index.asp). These graphical representations are mostly assembled intuitively from the literature to provide a static reflection of the topological features of mostly canonical signaling networks.

Static maps are widely used to represent complex signaling networks and to guide largely intuitive interpretations of signaling, but they are of limited use for predicting signal flows through edges of the network in a living cell responding to signals received from its environment. Limited dynamic information may be evident in the directionality of signal flow (such as, protein A upregulates the production of protein B), but the consequences of many such interactions in a complex, interconnected network are challenging to predict by intuitive reasoning alone. Appropriate computational models can help to uncover complex associations hidden in the data and often may provide a statistical assessment of the strength of any predicted association. For example, gene set enrichment analysis can rapidly probe a large database of genes and their hierarchically annotated functions to suggest signaling pathways closely affiliated with a list of differentially expressed genes (Subramanian et al. 2005); for example, see http://software.broadinstitute.org/gsea/index.jsp. A pathways database and a search tool is also provided by the Gene Ontology Consortium (see http://geneontology.org/page/go-enrichment-analysis).

Given adequate data, both computational and mathematical models can make quantitative predictions of the biological state under investigation. One of the primary uses of quantitative models is to perform in silico experiments where the values of specific nodes or edges are changed and the model is used to predict how the change affects other nodes in the network. It is possible to run hundreds or thousands of such simulations to explore both model performance and how specified changes in node/edge values affect the distribution of predicted outcomes. For example, in silico modeling can be used to compare multiple drug combinations including the effects of scheduling and dosing that would be very difficult in animal models or even in some cell culture models (Tang & Aittokallio 2014, Ryall & Tan 2015, Ledzewicz & Schaettler 2016). Appropriate quantitative models, when effectively applied to sufficient, high-quality data, can enable investigators to explore questions in ways that would otherwise not be possible. Visualization of the outputs from computational analysis of high-dimensional data can be an indispensable aid in interpreting the biological significance of the data (Gehlenborg et al. 2010, Cirillo et al. 2017, Pavlopoulos et al. 2017, Robinson et al. 2017). Thus, multiscale modeling enables investigators to explore complex datasets and signaling in new ways that are both tractable and productive.

Multiscale modeling

‘Numquam ponenda est pluralitas sine necessitate’ (Plurality should not be proposed unnecessarily)

William of Occam (c. 1287–1347)

‘Since all models are wrong the scientist cannot obtain a ‘correct’ one by excessive elaboration. On the contrary following William of Occam he should seek an economical description of natural phenomena.’

George E P Box (1919–2013)

All models are abstract representations of the system they are built to portray. The types of models we consider here are not intended to explain all of cancer biology. Rather, we use models to learn something new about how a specific function may operate, be controlled and interact with other cellular functions to affect a specific biological outcome. For example, we may wish to understand how estrogens affect the decision of some breast cancer cells to enter and complete a turn of the cell cycle. Understanding this function could then lead to addressing larger goals, such as developing new therapeutic interventions to block cell cycling or predicting which patients would receive the greatest benefit from blocking this action of estrogens. Thus, the primary goals of modeling are to give insights into how a control system works at the molecular level and to make robust, reliable predictions about how the system responds to a variety of natural situations and medical interventions.

For molecular signaling studies, the latter goal can be achieved by changing the values of parameters in the model and experimentally validating the predicted outcomes. Given a perturbation or rewiring of a control network, the output of a model is a prediction of the changed state of the cell (for example, alive or dead; proliferating or growth arrested). When simulations of a model under a variety of realistic conditions inadequately reflect what is already known to occur in cells, the model must be modified or extended. For example, a model may predict that reducing the expression of one gene should increase the expression of another, but the observed result of this experiment (perhaps using an RNAi approach) is the opposite. By considering how to resolve this discrepancy between model and experiment, new insights may be gained into how the control system works, and new predictions will be generated that can be used to test the modified assumptions.

A suitable framework to guide the modeling effort is a key starting point. The framework describes, at a high level, what is generally known about the system in the context of integrated modules that perform specific cellular functions. Thus, a modular function, such as cell death, may be explained by a model of the signaling that controls and executes one or more forms of cell death, such as apoptosis. Where there is sufficient knowledge of an individual module, a reasonably detailed influence diagram of known or predicted signaling relationships can be created to guide construction of the mathematical equations. This knowledge can be gained from specific experimental data available in the laboratory, from the literature, or perhaps based on a static canonical model as might be obtained from KEGG or Biocarta. Where a canonical model does not exist (or there is good reason to believe that canonical signaling is inadequate), computational modeling can be used to formulate new hypotheses about the topology of a control module from high-dimensional data (Clarke et al. 2011). Where there is sufficient knowledge of the components and interactions of a control system, the interaction diagram can be translated into a set of mathematical equations that quantitatively represent dynamical fluxes through the network (readers interested in exploring specific in silico models can find examples in several databases including JWS Online, available at http://jjj.biochem.sun.ac.za/index.html, and the Biomodels Database http://www.ebi.ac.uk/biomodels-main/). An example of such a framework can be seen in our roadmap for systems modeling of endocrine responsiveness in breast cancer (Tyson et al. 2011).

At some level, useful models need to address the open, complex, dynamic and adaptive nature of biological systems. While we do not intend to provide a detailed description of the concepts and methods of model building, we can mention some general, widely applicable principles. First of all, we must keep our end-goal in mind (what aspect of cancer cell physiology are we trying to understand) as well as our starting point (what is our working hypothesis about the underlying control system). Then, ideally, we would like to get from the working hypothesis to accurate predictions of cell behavior with a model that is as simple as possible, but not so simple as to leave out crucial features of the molecular biology or cell physiology. Of course, these are vague and often antithetical requirements (what is simple? what is crucial?), but it is the job of the modeler to make informed decisions about how much detail can and should be included in the mathematical model. Often these uncertainties can be addressed by an iterative approach, involving knowledge-guided trial-and-error or the use of multiple feature selection tools (as an example see the Feature Selection functions by MathWorks, http://www.mathworks.com/help/stats/feature-selection.html).

To highlight issues that may be useful for the non-expert wishing to evaluate published models and/or to collaborate with modelers, we next address the utility and methodology of mathematical and computational modeling. In our studies, we use computational tools to extract small, robust and information-rich topological features from high-dimensional data sets. These features can then be tested and validated experimentally, and at this stage, a simple mathematical model may be useful in capturing this knowledge, working out its implications, and making predictions to guide further laboratory experiments (Clarke et al. 2011). This iterative approach requires a modeling framework (a network diagram), some relevant experimental data, and a basic understanding of how components of the network may interact to produce observed physiological responses of cells. The network diagram guides the construction of the mathematical model, which can be used to compute the expected behavior of the simulated cells. To carry out simulations, we must first estimate the values of the parameters (such as rate constants and binding constants) in the mathematical model. Parameter estimation is a difficult problem, but it can (and must) be carried out in light of existing experimental data (Tyson et al. 2011). There would be no rationale to include a parameter without some data or direct evidence of its involvement in reactions, and these data can provide bounds on parameter values in the mathematical model. Once an initial model adequately accounts for the existing data, it can be used to predict specific outcomes of new experiments that can be run to confirm, extend or adjust the model. Thus, iterative modeling with the addition of new data allows both testing and refining of the model, which leads to new biological insights (Clarke et al. 2011).

Examples of modeling goals

Cancer systems biology studies tend to focus either on classification, where the goal is to predict a phenotype or outcome based on data, or on mechanistic modeling, where the goal is to learn something new about how the system (a tumor, a cancer cell or a signaling network within the cell) functions (Clarke et al. 2011).

An example of the classification task would be the use of gene expression data from a patient’s tumor to predict the patient’s prognosis and/or to determine the best choice of treatment. Among the simplest examples is the heuristic guide for the treatment of breast cancer patients based on a three-gene classification scheme: estrogen receptor alpha (ER), progesterone receptor (PGR) and HER2. Knowledge of the expression of these three genes defines three molecular subgroups: ER and/or PGR-positive (can be treated with an endocrine therapy), HER2-positive (can be treated with an anti-HER2 therapy, approximately half of these also express ER and/or PR and may also receive an endocrine therapy) and absence of expression of all three – often referred to as triple-negative breast cancer (TNBC) – which is usually treated with cytotoxic chemotherapy. A similar goal is exemplified by using a panel of clinical/pathological measures to predict prognosis in breast cancer; an example being the semi-quantitative assessment that produces the Nottingham Prognostic Index (Galea et al. 1992). Classifiers based on omics data are also available and in common clinical use, including the 70-gene signature that comprises the MammaPrint prognostic predictor (Bedard et al. 2009) and the prognostic PAM50 gene signature (Parker et al. 2009). Signatures that have not yet become adopted widely in the clinic continue to emerge (Wu & Stein 2012, Cheng et al. 2013). The output from these types of models is a prediction of the future behavior of the cancer – a clinical outcome such as an estimate of patient survival (prognosis) – often within a defined time period.

Omics-based classifiers (most frequently transcriptomic) are usually built using a supervised approach, where a training set of data from samples with known outcomes is used and the predictive model is subsequently validated in independent datasets. Classification models often rely primarily on the statistical properties of each measurement/input variable and do not require that these properties derive specifically from any biological function of the system (Clarke et al. 2008). The literature contains many different attempts to build classification schemes in breast cancer but often with varying results and robustness, even for some of the most widely used tools (Mackay et al. 2011, Venet et al. 2011). While some schemes produce comparable outcomes on a common dataset, the features selected for classification by each scheme often have little overlap (Imamov et al. 2005). Given the complexities in molecular signaling and the selection of genes based on their statistical properties to support classifier performance, it is not clear whether this observation reflects different genes representing similar underlying processes (Imamov et al. 2005) or a lack of robustness in feature selection unrelated to biology.

Network-based classification can also be performed on individual patient data (Creixell et al. 2012). The key is to develop a quantitative metric based on the topology of a learned network that can be applied to new observations to determine if the new observation is likely to share the same topology. For example, once phenotype-specific networks are learned, a model-based likelihood measure can be calculated to determine which topological hypothesis is more likely generating the new observation, where the learned variance of network topology is used to support such likelihood-based hypothesis testing.

The second goal of a systems analysis of data is to generate new insights into mechanistic aspects of the cancer phenotype. For example, the model may be used to understand why patients respond differently to a specific therapy or how molecular signaling regulates or executes a specific phenotype. Hence, the analysis may be structured to test if a series of proposed features might be true (hypothesis testing) or to discover new features that might explain mechanism (hypothesis generation). While these models also frequently use the statistical properties of the measurements to find signaling features of interest, there is an explicit assumption that the measurements, and any changes in their values across phenotypes, are derived from relevant biological properties of the system.

Among the more common approaches for mechanistic studies is the use of transcriptome data to build gene regulatory networks, as exemplified by a network of transcription factors (TFs) and the target genes that they are known, or predicted, to regulate. Insights from models built primarily from transcriptome data can be limited by the often low frequency with which transcriptome changes translate into similar expression changes in the proteome (Vogel & Marcotte 2012). The target genes for TFs are identified either in silico (predicted using DNA sequence data; see MotifDb at (http://www.bioconductor.org/packages/release/bioc/html/MotifDb.html) as an example of a tool for performing this function) or experimentally (chromosome immunoprecipitation-based methods; ChIP). These studies often produce small and mostly unidirectional maps (TF→target) and they can be noisy. For example, in silico predictions of targets based only on promoter sequences do not account for DNA structure/accessibility and are often incomplete. Experimentally measured promoter occupancy (such as by ChIP) does not always reflect functional regulation of the adjacent gene. Correlations of measured (ChIP/ChIPseq) or predicted promoter sequence binding with differential mRNA regulation in microarray data are often used to validate these signatures. Studies with RNAi or cDNA overexpression, mostly done using cell lines growing in vitro, may also be used to further establish the influence of gene expression on target gene regulation.

These approaches may not account fully for the complexity of a given target gene’s transcriptional regulation, such as whether factors other than the protein complex that is detected as being bound to a specific promoter element are driving the measured differential expression of the target gene. For example, TF1→Target Gene could still be driven through a latent variable(s), since the same experimental outcomes could be seen if TF1 was knocked down and the true relationship was TF1→TF2→Target Gene or even TF1⊣TF2⊣Target Gene. Hence, both false-positive and false-negative regulatory events may be obtained in addition to true events. For in silico modeling, including data on TF2 may or may not affect model function. Where it does not, the measurements of TF2 are superfluous and, in the interests of parsimony, can be eliminated from the model. Alternatively, there may be technical reasons that make the measurements of TF2 more reproducible than those of TF1. In this case, when TF1 and TF2 capture the same information, the model may perform better with TF2 measurements than using those for TF1.

Modules and emergent behavior

System models can be constructed as a network of integrated and interacting modules that perform the system’s component operations in a coordinated manner (Tyson et al. 2011). The topology of signaling for a module can be extracted de novo from the data, with functions being implied from any known activities of their member nodes (Wu & Stein 2012). However, for modeling known functions where there is significant data and prior knowledge, modules can be viewed more discretely as integrated network components that regulate and/or execute a specific function (Tyson et al. 2011). For example, apoptosis could be considered as a module that performs a cell death function; apoptosis can then be modeled as a discrete process, perhaps as a closed, input–output device. Cells have other modules that perform similar functions, including autophagy (which can produce prodeath or prosurvival outcomes). These modules represent biological redundancy because if an irreversible cell fate decision is made in favor of death, one of several differently constituted modules can execute that decision. Some genes may play key, but not necessarily similar, functions in more than one of these modules. For example, BCL2 can regulate the activation of the autophagy module through its ability to sequester BECN1, while also affecting execution of the apoptosis module through its effects on mitochondrial membrane permeability (Clarke et al. 2012). Cell fate may depend on the amount of BCL2 present and its subcellular location. For example, BCL2 bound to BECN1 may be unable to protect the mitochondria, with BCL2:BECN1 complexes effectively preventing the initiation of prosurvival autophagy (BECN1) and concurrently not preventing apoptosis (BCL2). Since other prosurvival BCL2 family members can also bind to BECN1, the balance of prosurvival-to-prodeath BCL2 family members (there is potentially significant signaling degeneracy within apoptosis), the concentration of free BECN1 remaining available to activate autophagy, and their respective subcellular localization(s) may all contribute to the final cell fate decision. The potential for cell context-specific wiring (and rewiring in response to stress) is evident.

A clear understanding of these interactions in ER+ breast cancer cells requires both significant insight and quantitative data from wet laboratory studies. Predicting cell fate outcomes robustly in the presence of various endocrine stressors (estrogen withdrawal, exposure to SERMs/SERDs) is unlikely to be successful without adequate in silico modeling. An effective dynamic model of these relationships could also be used to predict optimal drug dosing and scheduling to drive maximal cell death and potentially limit the emergence of drug resistance (Tang & Aittokallio 2014, Ryall & Tan 2015).

Integration of modular functions allows a cancer cell to coordinate and execute the activities it needs to proliferate, survive, move and invade locally, respond to stress and manage its metabolism to support these actions. Modules can be combined differentially in time and space, creating some of the phenotypic diversity that is characteristic of breast cancer cells. When modules interact in complex feedback and feedforward loops, they can exhibit redundancy (different modules performing similar functions), degeneracy (different signaling routes allowing a module to perform the same function in different ways) and novelty (the ability to perform new functions or old functions in new ways). This plasticity of the response characteristics of modular networks is the origin of their ‘emergent’ properties (Bhalla & Iyengar 1999). For example, an apoptosis module may be blocked in a cell but the cell death decision may now be executed by an autophagy module. The ability to recombine signaling features in complex regulatory networks in response to specific stresses is likely the emergent property that drives both the phenotypic plasticity often attributed to cancer cells and the development of resistance to anticancer drugs. From an intuitive point-of-view, emergent properties are challenging because they are difficult to deduce from a knowledge of the individual components of the system, and the relationships between the emergent property and its component parts may be non-linear and dynamic (changing over time). To deal reliably with these complexities requires comprehensive and accurate mathematical models to guide our thinking and predictions.

Emergence may underlie many novel behaviors of cancer cells that cannot easily be foreseen from knowledge of the system’s individual components. In evolutionary biology, emergence can reflect the development of larger or more complex functions or behaviors derived from the interactions among, but not shared with, individual smaller or less complex features (Okasha 2012, Gho & Lee 2017). New behaviors in tumors likely arise through changes that affect interactions within and among modules. For example, changes in signaling from within the tumor microenvironment (adaptive) or the acquisition of a genetic/epigenetic change (such as activating or inactivating mutations) could alter the level of expression, function or subcellular location of a molecule or the activity of a pathway in a network. Consequently, this pathway may now connect different modules that perform a new cellular function or continue to perform an existing function in a different manner. Where these new emergent properties confer a biological advantage, they are expected to experience positive selection (in a Darwinian sense) (Enriquez-Navas et al. 2015). Acquired drug resistance may be an example of a new emergent property that is not evident in the initial cell population. Such resistance could be mutational (ER mutations that confer resistance to aromatase inhibitors in breast cancer) or adaptive (activation and integration of the unfolded protein response module with a prosurvival autophagy module that act together to confer resistance to antiestrogens) (Clarke et al. 2011, 2012).

The emergent properties of cells in a system like an ER+ breast tumor likely explain, in part, the phenotypic heterogeneity of some breast tumors and also the diversity of responses that confer drug resistance (Clarke et al. 2012). The property of emergence with respect to acquired multiple drug resistance (a function that is likely subject to positive selection), and the potential that some complex functions may never stabilize (the rate of appearance of new metastatic foci may continue to increase throughout the disease process), may underlie the high prevalence of distant recurrences that are poorly responsive to available systemic therapies, and so are generally fatal.

Dynamics

One of the major strengths of quantitative mathematical modeling is the ability to capture the dynamic nature of a system (Aldridge et al. 2006, Anderson & Quaranta 2008, Toettcher et al. 2009, Spencer & Sorger 2011, Molinelli et al. 2013). In particular, models of endocrine-related cancers have provided new insights into the temporal development of invasive, metastatic cells (Quaranta et al. 2008, Gallaher et al. 2014), drug-treatment responses and drug-resistant states (Chen et al. 2013, 2014, Parmar et al. 2013, McKenna et al. 2017) and the origins of network plasticity (Tavassoly et al. 2015, Picco et al. 2017). Examples of some of the methods used in mathematical modeling are provided in Table 2 (Tyson et al. 2019).

Table 2.

Methods of mathematical modeling.

Method	Dynamic variables	Time	Example
Boolean networks	X(t) = 0 or 1 Y(t) = 0 or 1	t = integer (0, 1, 2, …)	X inhibits synthesis of Y and Y inhibits synthesis of X X (t + 1)=¬Y (t) Y (t + 1)=¬X (t)
Ordinary differential equations	X(t) = positive real number Y(t)= positive real number	t= real number (t ≥ 0)	X inhibits synthesis of Y and Y inhibits synthesis of X $\frac{dX}{dt}=\frac{k_{\text{sx}}}{1+Y^p}-k_{\text{dx}}X$ $\frac{dY}{dt}=\frac{k_{\text{sy}}}{1+X^q}-k_{\text{dy}}Y$
Stochastic models	M(t) = positive integer	t= real number (t ≥ 0)	Propensity of mRNA synthesis = ksm Propensity of mRNA degradation = kdmM Probability density function for number of mRNA molecules in the cell is $P(M)=e^{-\lambda }\frac{{\lambda }^M}{M!}$, where $\lambda =\frac{k_{\text{sm}}}{k_{\text{dm}}}$
Hybrid deterministic-stochastic models	M(t) = positive integer P(t) = positive real number	t = real number (t ≥ 0)	Genetic regulatory network: Simulate mRNA fluctuations, M(t), with a stochastic model and protein dynamics, P(t), with ordinary differential equations

Despite their evident utility, dynamic models in molecular cell biology must be interpreted cautiously. Model predictions can be very accurate when restricted to conditions close to the experimental conditions on which the model was built, but less reliable when extrapolated far beyond the range for which they have been verified. Nonetheless, like weather prediction, mathematical models of cellular regulatory systems can be very useful for short-term forecasting of local activity without being reliable predictors of long-term ‘weather’ patterns on a ‘global’ scale.

Parameters

To simulate a mathematical model, we must first estimate the values of all kinetic parameters from experimental observations. Examples of parameters include reaction rate constants (such as protein synthesis and degradation, or phosphorylation and dephosphorylation) and binding or dissociation constants (for example, Michaelis constants for enzyme-catalyzed reactions). Estimation of these parameter values is often the most difficult aspect of building a useful mathematical model (Liepe et al. 2014, Kimura et al. 2015). The goal of parameter estimation is often not to find the ‘optimal’ set of parameter values for fitting a selection of experimental results but rather to find a representative collection of parameter sets that all provide an ‘acceptable’ fit to the data (Tavassoly et al. 2015).

When faced with the dimensionality of data from an omics platform, a mathematical model with thousands of variables would be difficult to formulate and almost impossible to parametrize. Currently, high-dimensional data are more effectively explored using computational modeling where the assumptions of the model are higher level and less demanding of detailed kinetic information. For example, machine-learning techniques can learn the features of molecular networks and their relationships from the data. Bayesian approaches are common in this regard and are discussed below.

Deterministic and stochastic models

Deterministic models, defined usually by differential equations, produce specific outcomes for a given set of parameter values and initial conditions, without any evidence of randomness. In contrast, stochastic models evolve in time with significant random fluctuations (Singhania et al. 2011, Barik et al. 2016). For example, a gene regulatory network, where TFs regulate specific targets, could be modeled deterministically or stochastically. In a deterministic model, the rate of gene transcription would have a definite value determined by the activity of the transcription factor. In a stochastic model, the activity of the TF would determine only the propensity (probability per unit time) of transcribing the gene into an mRNA molecule. In this case, a stochastic model represents more accurately the noisy process of gene transcription in individual cells, but a deterministic model may capture adequately the average rate of expression of the gene over a population of cells responding to an external stimulus that is activating the TF. If we have data on the noise associated with gene transcription in individual cells, then a stochastic model may be warranted and needed. Stochastic models have been useful for exploring the dynamic responses of endocrine-related cancers (Jain et al. 2011, Chen et al. 2014, Morken et al. 2014). A deterministic model is simpler and more appropriate if we have only gross transcriptome data on populations of cells under constant conditions.

Bayesian models

A general objective of computational tools is to find patterns (correlation structures) within data. For example, with transcriptomic data an algorithm may look for patterns of changes in gene expression that are correlated with each other and with the phenotype(s) or function(s) of interest (Dutta et al. 2016, Anafi et al. 2017, Califano & Alvarez 2017). Some measure of the statistical strength of these correlations, using either a Bayesian (conditional probabilistic) or frequentist (parametric or non-parametric probabilistic) approach, is usually applied to help identify the associations most likely to be correct. Whichever approach is selected, statistical models (Bayesian or frequentist) have assumptions that can be violated and parameters (even non-parametric probabilistic tools have parameters; these are not fixed in advance but obtained from the data) that can be affected by the data structure and that can influence performance. While it is not always evident which statistical model is most appropriate for the data being analyzed, understanding what the model outputs represent is important for correctly inferring biological meanings or appreciating the uses and limitations of the output.

An increasingly common approach for computational modeling is to build models that incorporate prior knowledge of the system (Tian et al. 2014b, 2015). Prior knowledge can be as simple as looking at the expression levels of genes already known to contribute to the phenotype, at known interactions among molecules such as protein–protein or protein–DNA interactions (PPIs or PDIs) or at relationships reported in canonical signaling pathway representations. Incorporation of prior knowledge, depending on the quality of the knowledge, can greatly improve the performance of algorithms to build Bayesian networks. Indeed, a major challenge in constructing Bayesian networks is the selection of appropriate prior probability distributions (priors) for the variables in the model. How these parameters are estimated for a Bayesian approach affect its outcomes (Lampinen & Vehtari 2001). Poorly estimated priors (relative to ground truth – which is often unknown) may provide fits to the data that are statistically acceptable and intuitively logical, but solutions that are, nonetheless, noisy and lead to incorrect biological interpretations. Influence of the prior can be reduced using Bayesian hierarchical models and robust priors (Berger 2010).

In Bayesian networks, the edges are directed but the sign is not specified. Consequently, whether the edge is positive (such as driving) or negative (such as inhibiting) must be inferred from sources external to the model and/or established experimentally. A further limitation is that edges cannot be interpreted as necessarily reflecting direct interactions. While some interactions may well be direct, latent variables can also create direct edges in the model solution where none exist in the biological system. For example, the predicted edge of A→B in the model may really be A→C→B (see also the discussion of modules and emergent behavior, above). Inferring feedback loops can also be difficult, such as A→C→B→A.

For gene network modeling, the quality of the knowledge and its incorporation into the selection of priors will improve the predictions. Two implications follow from this observation. Firstly, a team with better biological understanding of a system may build a Bayesian-based algorithm that outperforms others on the analysis of this specific system (because the model’s priors are more correctly defined by the team’s existing knowledge) but produces less robust/accurate predictions than other algorithms when it is applied to related systems. Secondly, detailed prior knowledge of a system limits what new knowledge can be discovered. The more that is understood about the system ahead of time, the better the model will perform. However, the model will be making predictions in a shrinking space where there is less new knowledge to be discovered. In reasonably well understood systems, these latter models may have most utility in building our confidence that what we believe to be true may indeed be true. In systems that are inadequately known, the new knowledge space can be large and the predictions noisy; the extent to which something is now believed to be true may require careful evaluation. Overall, the primary advantages of modeling include the ability to integrate significant amounts of knowledge, to help researchers to understand confounding events seen in the data and to answer questions of combinatorial complexity for which experimentation within the wet laboratory is prohibitive.

Error, performance and validation

Some workflows may include the output of one algorithm as a means to guide parameter estimation for another. For example, in building a gene regulatory network from expression data, an investigator could take the output predictions from a tool that predicts a TF and its targets as a means to define the priors for a Bayesian network modeling analysis of how these molecules are related in the data from a gene expression study. Intuitively, even if the TF output is statistically noisy, it might be expected to outperform a model with uninformed priors where equal probabilities are assigned to each outcome. Nonetheless, some of the predictions will be wrong and represent errors in the prior that may be worse than uninformative; these types of errors will be propagated from the output of one tool to the output of the next. Since the variables and their relationships (as captured in their priors) were thought to be intuitively correct, if these incorrect variables persist as key features of the Bayesian model solution, they could create the trap of self-fulfilling prophecy (Clarke et al. 2008). Predictions from one tool will also be associated with a level of error (variability), and this type of error will also propagate when the outputs are used as input variables for another tool in a workflow. Here, error propagation represents the effects of the variability in the input variables on their respective model functions and on model output (Mangado et al. 2016). Estimating (and reporting) uncertainty propagation and its implications is an important consideration in assessing model calibration and interpretation (Vanlier et al. 2012). Methods to estimate uncertainty propagation continue to be developed and applied (Ades & Lu 2003, Welton & Ades 2005, Dubois 2010, Moseley 2013, Mangado et al. 2016). In his discussion of error propagation in metabolomics studies, Moseley notes that both derived and propagated uncertainty should be reported along with the results (Moseley 2013).

Measurement errors, as they apply to the relationship between a measured variable and its covariate, are additive (Eckert et al. 1997). Integrative analyses across workflows in multiscale modeling, as may occur when combining data from DNA sequence, RNA sequence/abundance and/or PPI studies, include many relationships between the measured variables (such as mRNA and protein expression levels) and covariates (such as a clinical outcome or changes in phenotype). Such analyses may be prone to error propagation and to error additivity or even amplification. For example, agglomerative techniques (such as some hierarchical clustering), growing decision trees (such as some random forest methods) or the network propagation algorithms that have begun to attract increased attention (Cowen et al. 2017) may be sensitive to error propagation. Once an error (node-edge connection) is made during the graph build, it may remain and affect the accuracy of subsequent local connections and of the overall model solution. A build error that remains can lead to a model solution that reaches convergence and appears ‘globally correct’ but contains features that are ‘locally wrong’. The challenge here is that it is the local connections that are used to guide individual wet laboratory experiments.

Studies that apply bioinformatic/biostatistic tools to solve problems in large data spaces are likely to be at greatest risk of experiencing the various types of errors described above. The ‘hairball’ models often produced are rarely robustly tested for local error, especially when the global model fit provides an apparently miniscule P value. For example, independent datasets showing the same topologies are often not shown, frequently because the data are not available to do independent validation. The internal topology of individual cliques is rarely tested, even using a simple n-fold cross-validation. Global solutions are also rarely tested by an analogous n-fold cross-validation, such as removing entire cliques at random. Since the overall topology of the solution is likely to be influenced by the relationships among discrete discovered features, without testing the effects of removing features on the remaining structures, there are few ways to determine topological robustness. While these ‘hairballs’ will likely have met the statistical requirements for global algorithmic convergence, how many of the local structures are correct, either internally within each feature or externally within the global solution, is often left to human intuition and the risks therein (Clarke et al. 2008).

Appropriate assessments of model robustness and validation are critical to the successful use of a systems biology approach (Steyerberg et al. 2001). There are many tools to assess model performance and validation and a detailed technical discussion is beyond our scope. Here, we use performance to denote assessments of the robustness or reproducibility of model predictions. For performance, biostatistical assessments of model fit are usually incorporated into the workflow. Examples of approaches to assess performance include use of a receiver operating characteristic analysis and estimates of the positive predictive value and negative predictive value. An internal n-fold cross-validation is commonly used, particularly when data are limited (Waljee et al. 2014). A random portion of the data is withheld at each interaction as a ‘validation set’, and the remaining data are used as a ‘training set’ for running the model. Multiple iterations are run and the performance for each iteration is compared to assess the overall model performance. A model can be tuned by adjusting its parameters until the predictions from the training and internal validation sets become sufficiently comparable. Since this approach can lead to model overfitting, the most informative assessment of model performance is obtained from the use of independent datasets not used in model building and any internal performance analyses. A robust model is expected to produce broadly similar predictions in all comparable data sets. For classification studies using human tumors, the use of independent datasets may also be the only tractable option for validating model predictions.

For models that are used to predict system function in a biological context, mechanistic or functional validation of a prediction is almost always required. Here, validation refers to experimental validation in the form of appropriate wet laboratory studies. These validation studies are often done in cell lines and/or animal models and can include applying perturbations to the experimental system and then measuring whether the changes predicted by the model occur. A common approach is to knockdown a target gene in cells where it is overexpressed, overexpress the gene in cells where its expression is low and then determine if the biological function(s) is altered as the model predicts. Knockdown is commonly achieved by an RNAi method such as siRNA or shRNA transfection. A gene may also be eliminated using CRISPR (Yin et al. 2019). How often a cell totally loses a gene or its expression likely requires careful consideration. Total loss of a protein’s expression, as would usually occur with CRISPR, could alter a signaling feature in a manner that does not occur when expression is lowered but not eliminated in the phenotype(s) of interest. While CRISPR is often preferred over RNAi, for genes where downregulation rather than total loss is the primary biological observation, RNAi may offer a more physiologically relevant validation approach. A similar caveat applies to the use of cDNA transfection to produce overexpression of a gene. The level of overexpression may be outside the range seen in the phenotype(s) under study, and so also produce changes in network features that are not physiologically relevant. These types of events could lead to misinterpretations of the validation experiments. For example, the phenotype predicted by the in silico model is not observed or further studies to determine the effects of the manipulation of a gene on signaling identifies new relationships that are signaling artifacts from a physiological relevance perspective.

As an example of a biological validation strategy, consider a prediction by an in silico model that an antiestrogen should induce autophagy through altering expression of BECN1 in ER+ breast cancer cells. One approach to mechanistic validation of this prediction could be to apply the drug and its vehicle control to ER+ and ER− cells (negative control), measure changes in BECN1 and autophagy and then use a molecular approach to study if BECN1 knockdown or overexpression altered the regulatory effects of the antiestrogen on autophagy. An underappreciated challenge with these types of studies is that the experimental validation may be frustrated by a high proportion of intuitively rational, statistically significant, but biologically incorrect in silico model predictions (the wet lab validation experiments show the predictions to be invalid).

Modeling drug interactions

Another area of significant potential for a systems approach is the search for drug combinations for treating a specific cancer in the context of a multicomponent signaling network within the cancer cells (Tang & Aittokallio 2014, Ryall & Tan 2015). Effective combination therapy, which is a hallmark of current cancer treatment, requires an adequate understanding of signal complexity. Developing and evaluating drug combinations is difficult because the complexity of the problem increases combinatorially with the number of constituent drugs proposed to address an integrated driver pathway of the cancer. When the possibility of sequencing drugs at different times relative to one another is added to the mix, complexity again increases dramatically. Progress has been made using a systems biology approach. For example, the joint effects of multidrug combinations can be evaluated based on the mechanisms of action of the drugs (Fitzgerald et al. 2006). If the constituent drugs in a combination therapy exert their effects through known mechanisms that feed into common pathways, the joint effect of the combination may be assessed by the ‘Loewe additivity’. If the drugs act non-exclusively on multiple targets, the effect may be assessed by the ‘Bliss additivity’ (Baeder et al. 2016). Knowledge of the biological system can be used for experimental design and data analysis. Thus, drugs with different mechanisms of action, as revealed by systems biology modeling, may exhibit different shapes of their dose–response relationships. Such information can be augmented by experimental data on a single drug to optimally design the experiments on the joint effect of the drug combinations.

Because the complexity of the problem increases rapidly with the number of constituent drugs, even the development of systems-based methods for the design and analysis of three-drug combinations has been only recent (Fang et al. 2017). The case of three-drug combinations is fundamentally more difficult than two-drug combinations. Finding doses of the combination, number of combinations and replicates needed to detect departures from additivity depend on the dose–response shapes of each of the constituent drugs. Thus, different classes of drugs with different dose–response shapes must be treated as separate cases. We designed and analyzed a combination study of three anticancer drugs (PD184, HA14–1 and CEP3891) that inhibit the H929 myeloma cell line. The three-drug combinations study used the original 4D dose–response surface formed by the dose ranges of the three drugs (Fang et al. 2017).

Methods for screening large numbers of drug combinations are being developed to reduce the problem to one that is more experimentally manageable by using the experimental data from dose–response studies of single drugs and from a few combinations along with a systems analysis of pathway/network information to obtain an estimate of the signaling network model parameters and the functional structure of the dose–response relationship (Fang et al. 2016). This model comprises a Hill equation for signals arriving at each receptor, a generic enzymatic rate equation to describe the transmission of signals among connecting genes, and a logistic equation to represent the cumulative effect of genes implicated in the onset of the cell death machinery. These statistical models generate a global drug sensitivity index based on the joint dose–response characteristics. Only the few terms with large global-sensitivity indices, much like principal components, are kept and subject to further experimental validation. Recently, the experimental design required for such subsequent experimentation has also been worked out (Fang et al. 2016, Huang et al. 2018).

An example of computational modeling: KDDN

Cancers are often characterized by dysregulation of molecular signaling (Barabasi et al. 2011, Tyson et al. 2011, Creixell et al. 2012). Significant rewiring of molecular networks can drive key phenotypic transitions that can occur in both a tumor and its microenvironment (Califano 2011, Roy et al. 2011, Ideker & Krogan 2012). The impact of a treatment can spread through the network and alter the activity of functionally relevant gene products (Roy et al. 2011, Creixell et al. 2012). Most molecular components exert their functions through interactions with other molecular components (Li et al. 2008, Gong & Miller 2013). How cancer cells differ from each other in their responses to environments or treatments is intrinsically context specific (Mitra et al. 2013) and identifying such differences may represent a ‘wicked’ problem for the research community (Rittle & Webber 1973, Courtney 2001, Clarke et al. 2011). Changes in molecular interdependencies across cancer phenotypes may reveal novel hub genes and pathways, which may be suitable targets for drug development. Instead of asking ‘which genes are differentially expressed?’ the question here is ‘which genes are differentially connected?’ (Hudson et al. 2009). Studies on network-attacking events will shed new light on whether network rewiring is a general principle of cancer cell responses, as most molecular therapies target proteins and their networks but not genes (Califano 2011). Novel hypotheses inferred from the rewired TFs and their distal enhancers or partners can be proposed and examined (Creixell et al. 2012, Mitra et al. 2013).

While multiscale omics data and the prior knowledge that provide insight into complex interactions are increasingly available, models and analysis methods to functionally integrate this information are still sorely needed. In particular, systematic efforts to characterize selectively activated regulatory components and mechanisms must effectively distinguish significant network rewiring from random background fluctuations. Most published biological network inferences were obtained from molecular datasets acquired under a single condition, for which the statistically significant network rewiring across different conditions is unknown or unreported (Mitra et al. 2013). The inability to identify significant rewiring in biological networks represents a major limitation on the use of these results for molecular signaling studies. The Knowledge-fused Differential Dependency Network (KDDN) method has been developed to infer significant rewiring of complex biological dependency networks, via sparse modeling and data-knowledge integration (Zhang et al. 2009, 2011, Tian et al. 2013, 2014a,b, 2015). Specifically, KDDN formulates the inference of differential dependency networks (Zhang et al. 2009, 2011, Tian et al. 2014a) that incorporate both conditional data and prior knowledge as a convex optimization problem (Zhang & Wang 2010, Tian et al. 2011) and uses an efficient learning algorithm to jointly infer the conserved biological network and significant rewiring across different conditions (Tian et al. 2014b, 2015). KDDN uses a minimax strategy to maximize the benefit of prior knowledge while confining its negative impact under the worst-case scenario. Furthermore, KDDN matches the values of model parameters to the expected false-positive rates on network edges at a specified significance level and assesses edge-specific P values on each of the differential connections.

Tests on synthetic data have shown that KDDN produces biologically plausible results (Zhang et al. 2009, 2016, Herrington et al. 2018) and can reveal statistically significant rewiring in biological networks. The utility of KDDN is evident following its application to a variety of real gene and protein expression datasets including yeast cell lines (Tian et al. 2014b), breast cancer (Tian et al. 2014b), ovarian cancer (Zhang et al. 2016) and medulloblastoma (Tian et al. 2014a). The method efficiently leverages data-driven evidence and existing biological knowledge while remaining robust to false-positive edges in the prior knowledge. The network rewiring events identified by KDDN reflect previous studies in the literature and provide new mechanistic insight into the biological system(s) that extends beyond this earlier work.

To study how gene networks may rewire during the transition from normal to neoplastic breast cells, we have focused on understanding how ER+ breast cancer cells adapt to the stresses of endocrine-based therapies. Our central hypothesis invokes a gene network that coordinately regulates those functions of a cell module that determine and execute the cell’s fate decision. Using the KDDN tool, we identified three small topological features and then overlaid these onto the canonical apoptosis pathway from KEGG (Fig. 2). The largest of the three features reflected much of our prior knowledge, despite not explicitly incorporating this knowledge into the models (Zhang et al. 2009). Following the predictions of this topology, we uncovered some fundamentally new insights into molecular signaling; for example, the direct regulation of BCL2 by XBP1 and the requirement of NFκB for XBP1 signaling to regulate the prosurvival cell fate outcome in the context of antiestrogen treatment and resistance (Clarke et al. 2011, Tyson et al. 2011, Hu et al. 2015). In applying KDDN to data from a rodent model, we found that exposure to estrogens in utero induces a rewired network in the mammary glands of the offspring that predicts for resistance to endocrine therapies in tumors that arise in these glands during adulthood. Subsequent studies showing that tumors in these mammary glands are less responsive to tamoxifen (TAM) provided the first direct demonstration of why many ER+ breast cancers may be pre-programmed to fail to respond to TAM treatment or respond and later recur (Hilakivi-Clarke et al. 2017).

Figure 2.

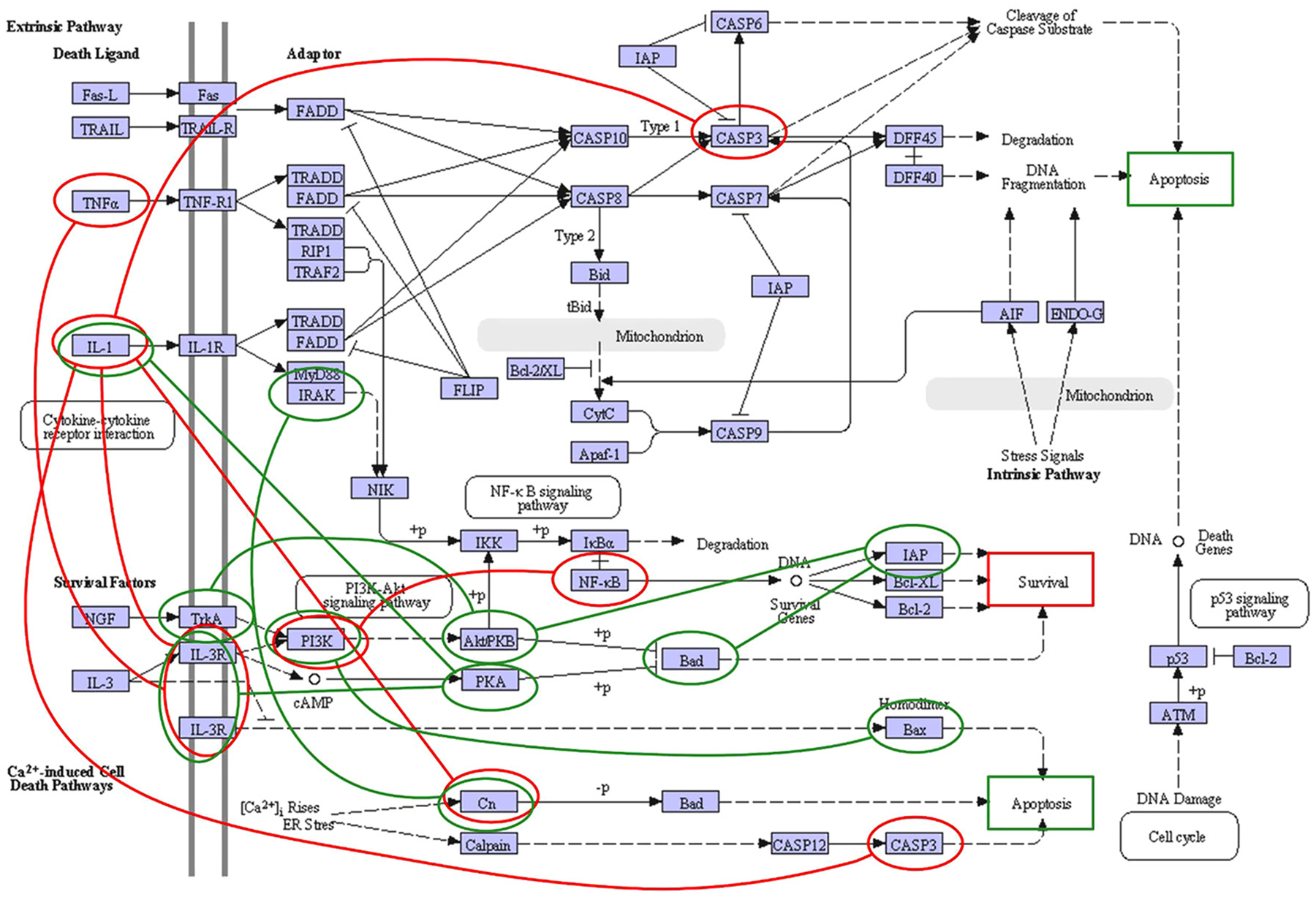
Differential dependency network focused on the KEGG apoptosis pathway (Kanehisa & Goto 2000). Recurrent breast cancers (uniquely featured by red edges) showed the imbalance between apoptosis and survival with only one route into the cell through IL1B-induced inhibition of proapoptotic CASP3. Non-recurrent breast cancer (uniquely featured by green edges) had a cascade of signaling pathways inside the cell that provides the balance between apoptosis and survival. Copyright Kanehisa Laboratories. Reproduced with permission from KEGG.

We further pursued the functional evidence of the hidden dependencies/crosstalk inferred by KDDN. For example, KDDN analysis of global protein expression data from 122 TCGA ovarian cancer samples (selected based on homologous recombination deficiency, HRD, a phenotype with distinct prognosis and response to therapies) resulted in a number of phenotype-dependent modules of co-expressed proteins. Several of the member proteins in the modules were known to be involved in histone modification. With the additional evidence of HRD status-dependent acetylation or deacetylation of histone proteins in the same samples, we were able, using patient population data, to support what has been shown in cells (Gong & Miller 2013, Tang et al. 2013) that histone protein acetylation affects the choice of DNA double-strand break repair pathways (between homologous recombination and non-homologous end-joining) (Zhang et al. 2016).

An example of mathematical modeling: ER landscape

Dynamic mathematical models track a system as it evolves in time. A key use of such models is to optimize therapeutic protocols. For example, instead of applying a given drug or combination of drugs continuously for a specified overall duration, the drug(s) can be applied for fixed durations with rest intervals in between. Alternatively, several drugs can be applied in a repeating sequence for fixed durations. Optimizing the durations and dosing of drugs is a combinatorial problem that is difficult to solve experimentally, but relatively simple to solve via computer simulation, assuming an accurate dynamical model is available. Impressive results have been obtained in prostate cancer and glioblastoma using two-compartment models that simulate the temporal development of the sensitive and drug-resistant populations of cancer cells (Jain et al. 2011, Leder et al. 2014, Morken et al. 2014).

In the case of ER+ breast cancer and antiestrogens, the resistance character of the cells changes with time in response to the drugs. Hence, it is necessary first to model the dynamics of development of drug resistance in individual cells, then to model the dynamics of a population of treated cells by linking the cellular scale to the population scale, and finally to consider strategies for optimizing drug therapy. A proof of concept of this idea considered estrogen deprivation therapy (Chen et al. 2014). ER+ cells were presumed to exist in three different states: an estrogen-sensitive state (growth driven by the estrogen receptor bound to estrogen), an estrogen-hypersensitive state (growth driven by membrane-associated estrogen receptor (ERM) bound to estrogen) and an estrogen-independent state (growth driven by growth factor receptors (GFRs)). Transitions between the states were governed by the estrogen level (high, low, trace) in which the cells were grown. If cells were growing in a high (physiological) concentration of estrogen, most cells would transition to the estrogen-sensitive state. If the estrogen concentration dropped to a low level, sensitive cells would begin to die, but some would transition to a hypersensitive state and continue growing.

To model the transitions among these states, we developed a stochastic differential equation model of an individual cell. States were characterized in the model by ERM activity (high or low) and GFR activity (high or low). The model qualitatively matched observations in the literature concerning sensitivity transitions in breast cancer cells as the estrogen level was varied. The fact that resistance to estrogen deprivation was reversible if resistant cells were transferred back to estrogen-rich medium for a sufficiently long time was also captured. Using techniques from statistical physics, it is possible to visualize this model as a landscape upon which the system makes spontaneous transitions among three low-lying basins (Fig. 3A), which represent the three states of estrogen sensitivity. Random fluctuations in the cells can occasionally cause transitions from one basin to another, representing the natural heterogeneity seen in a cell population. However, the system typically resides in the lowest basin, as determined by the estrogen level.

Figure 3.

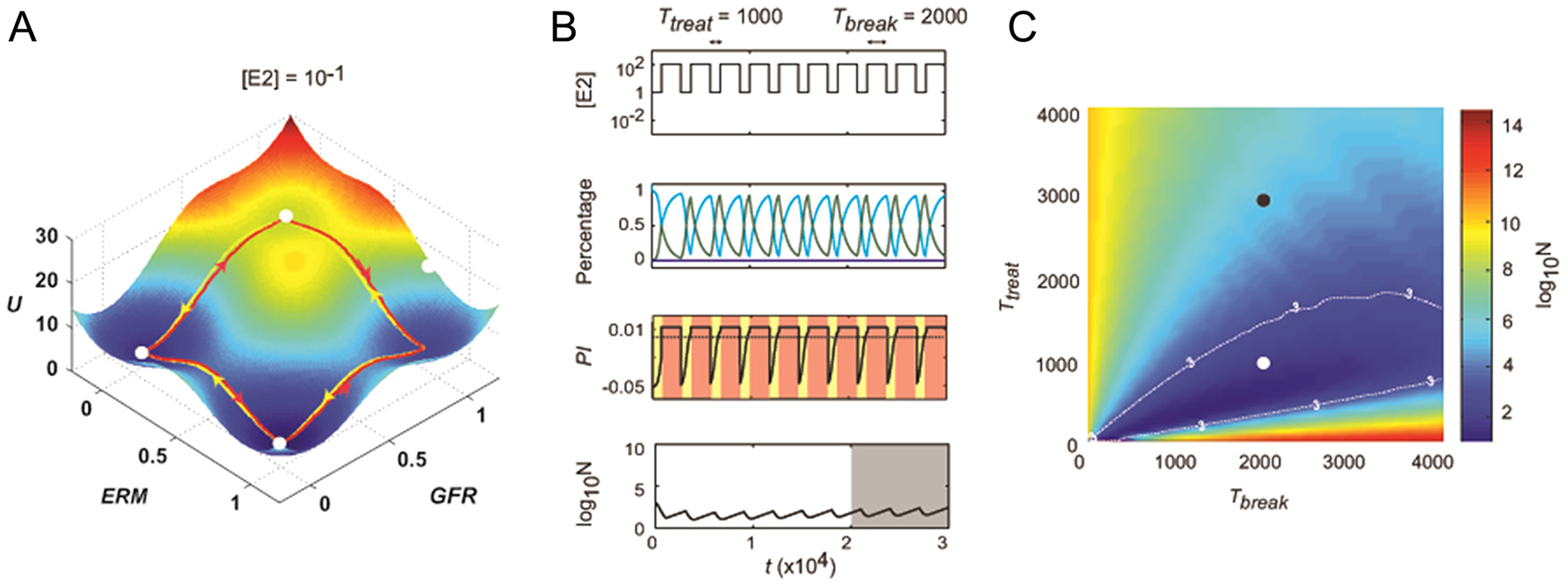
(A) The estrogen-response landscape for a particular level of estrogen stimulation. There are four basins of attraction for the cell state corresponding to sensitive (ERM−/GFR−), hypersensitive (ERM+/GFR−) and independent (GFR+). (B) A sample intermittent treatment regimen (top panel) produces varying proportion of cells in different states (second panel; cyan = sensitive, green = hypersensitive, blue = independent), a varying proliferation index of the overall cell population (third panel; yellow indicates death and red indicates growth). The overall population level, starting from 1000 cells, is shown in the bottom panel. (C) Plot of the average value of cell number <log₁₀ N> over the interval t ϵ (2 × 10⁴, 3 × 10⁴) as a function of T_treat and T_break. The white dot indicates the case in (B). Any combination of T_treat and T_break that puts the system within the log₁₀N = 3 contour will suppress cancer growth. This figure is adapted, with permission, from Fig. 3 and 6 of Chen et al. (2014).

It is not efficient to simulate large numbers of these ‘model cells’ for long periods of time in order to compute how a population would evolve in response to changes in estrogen dose. To circumvent this problem, a cell-level model was used to compute the transition probabilities among states as a function of estrogen concentration. These probabilities were then used to create a population model that efficiently tracked the number of cells in each state. A treatment regimen consisting of cycles of estrogen deprivation followed by a drug holiday was considered, and the deprivation and break durations were optimized to drive the cancer cell population as low as possible. Results are shown in Fig. 3B and C for the situation where the cancer population is initially 1000 cells. For the parameters in the model, the cancer cannot be eradicated. However, over a suitable range of therapeutic parameters, the disease can be kept in check (similar to increasing duration of the recurrence-free survival period).

This example provides a possible roadmap for how modeling a molecular understanding of the response of a cancer cell to a drug can be transitioned to a tissue-level model and used for therapy optimization. While the situation in patients is certainly more complicated than the model systems described here, the success of simple compartment models to guide therapy in simulated tumors provides hope that more complicated, molecularly-based, multiscale models will ultimately be useful in guiding therapy in the clinic.

Interpreting models: caveat lector

‘A little learning is a dang’rous thing; drink deep, or taste not the Pierian spring: there shallow draughts intoxicate the brain, and drinking largely sobers us again.’

Alexander Pope (1688–1744)

The qualitative and quantitative models that we have described above produce results that can be difficult to interpret correctly and usefully. Correct interpretation is important, of course, because no one wants to spend time and precious experimental resources failing to validate an incorrect understanding of the results of a computational and/or mathematical analysis of a cellular control network. For example, gene set enrichment is a powerful tool to explore high-dimensional data sets (Subramanian et al. 2005), but how its results are interpreted and used requires a thorough understanding of what the results do and do not imply. In this case, gene set enrichment analysis provides a static representation of canonical signaling pathways, which are highly idealized views of the most frequently observed events in a signal transduction pathway. However, once an event is identified and reported, it is more likely to be studied further and eventually to be considered as being canonical. Moreover, these canonical signaling maps (examples include KEGG and Biocarta) are often assembled from a variety of sources (cell types, tissues, and species). Consequently, these graphical representations may be relevant only in part to the signaling processes under consideration in the specific cell context that a researcher is studying experimentally and trying to model computationally.

Researchers are often limited to applying reductionist wet laboratory technologies to validate the predictions of models that attempt to explain some or all of the complexity in the biological system under investigation. Often, the cost in time and resources needed to validate experimentally the predictions of multiscale models can be prohibitive, making the ability to select among multiple solutions a necessity. Most algorithms, given input variables in the correct format, will produce outputs/predictions, but these often include false positives and false negatives that are not easily identified. While model outputs are usually associated with probability estimations, the results of any significance tests generally provide an evaluation only of how well the model fits the available data. This statistical evaluation is not necessarily an estimate of how well the predictions reflect biological truth. Moreover, when sorting through multiple apparently statistically significant predictions, an investigator can be left relying on subjective intuition, perhaps guided by an incomplete, inadequate, or incorrect understanding of the system. Since model predictions should generally be consistent with the experimental data and/or the (sometimes) limited knowledge of the system currently available, the trap of self-fulfilling prophesy becomes almost unavoidable (Clarke et al. 2008).

A gene set enrichment algorithm may produce several predicted pathways and functions associated with a single set of differentially expressed genes. While some genes can certainly participate in more than one pathway or regulate more than one cellular function, the investigator must determine which output(s) (which pathway, module, or function) is most likely to represent the truth. A statistical assessment, usually a P value, accompanies each model prediction, and understanding what these assessments represent is important in evaluating the results. It is not unusual for a model to provide many predictions for which the P values are small (highly statistically significant), but how easily or appropriately these statistical estimates can be used to guide biological interpretation is not always clear. Primarily, P values reflect how well each model output fits the data input, subject to the parameters and assumptions in the statistical model used. Thus, the use of different statistical tools with the same input gene list and the same database may give different outputs, or the same outputs with different P values, because the parameters and assumptions in each statistical model are different. Also, if some pathways in the database are larger, better annotated, or more fully (and correctly) understood than others, the P values associated with these pathways could be smaller (implying a more statistically significant fit) than less well represented pathways that may be a better reflection of the underlying biological truth.

When the decision as to which is likely to be the correct solution is left entirely to intuition, it is not surprising that the solution that best supports the current hypothesis, or that is most easily explained by the operator’s existing knowledge, is often selected over other statistically significant outputs that are not easily understood or may even refute the hypothesis. In such cases, the investigator is likely to fall into the trap of self-fulfilling prophesy (Clarke et al. 2008). To be able to interpret model outputs appropriately, it is often critical to understand both what the data represent and some of the basic principles of how the model works. This prior knowledge is particularly important when the correct interpretation is counterintuitive or inconsistent with the hopes or expectations of the study designers.

Cell context, by which we mean the unique patterns of genes, proteins, and metabolites that are expressed in a cell and that interact to influence the physiology of that cell (Clarke & Brünner 1996), is one of the central determinants of how signaling and function are related in biological systems. Context is clearly related to the cell/tissue type, local microenvironment, status of the host, and other external and internal influences. Some aspects of cellular context may be highly conserved, as can be seen from the DNA sequence of some genes through to the basic signaling topology of some highly conserved functions. Nonetheless, there can also be substantial diversity, even within closely related species, tissues, or cells. For cancer research, the differences between the normal and neoplastic state in the same tissue or cell type is where we look most often for molecular targets that can be diagnostic, prognostic, and/or therapeutic. Here, even small changes in cell context can have substantial implications for the ability to address a specific hypothesis. Despite the often fundamental importance of cellular context, it is frequently ignored.

Some modeling approaches are of limited utility either scientifically or clinically and need to be re-addressed. The complex hairball models often generated by some computational tools may (or may not) contain valid insights into regulatory biology. However, their complexity can be so high and the noise sufficiently extensive and the errors undefined that these models cannot be tested meaningfully or interpreted reliably. Employment of a razor to shave away those components that do not add to the utility, robustness, or accuracy of a model may be desirable, but only if its application is tractable and it is evident what ‘whiskers’ can be removed without a significant loss of predictive power. Proactively incorporating feature elimination tools during modeling (for example, applying a support vector machine with recursive feature elimination for classification; Guyon et al. 2003) may help to address this concern by attempting to arrive at the smallest model that meets predetermined requirements of convergence and statistical significance. Nonetheless, the need for human intuition to interpret outcomes remains central to many study designs, and, consequently, the risk of falling into the trap of self-fulfilling prophesy must be carefully avoided (Clarke et al. 2008).

Future directions

The properties of high-dimensional data spaces, and the challenges and opportunities these provide (Clarke et al. 2008), remain central to the performance of many computational modeling approaches and bioinformatic tools and workflows. Tools designed to manage these properties explicitly, such as support vector machines, and workflows to address high dimensionality, such as including dimensionality reduction as a preprocessing step in data analysis, are likely to remain in use. New and more powerful tools and workflows are likely to continue to emerge, increasing the power and accuracy of predictive models, the quality and accuracy of data interpretation, and the utility of the new knowledge gained. Deep learning, a subset of approaches within the broader field of machine learning that generally applies neural network-based modeling, has gained recent attention as a potentially powerful approach to extracting new features from high-dimensional data spaces (Hosny et al. 2018, Zou et al. 2019). It is likely that deep-learning approaches will be more commonly applied in the near future to guide knowledge discovery within the framework of cancer systems biology.

Another area that has attracted renewed interest is the heterogeneity arising from the presence of multiple cell types and the consequent complexity of interactions within tumor microenvironments. For molecular signaling, a key issue in this context is whether the events identified as being associated with a biological outcome or phenotype are intrinsic or extrinsic to the cancer cells and/or other cells within the microenvironment. While most therapeutic interventions attempt to induce cell death programs that are executed within the cancer cell (intrinsic), many of the signals that initiate this intrinsic activity are generated by activities originating in stromal or immune cells (extrinsic). Single-cell RNAseq can address some of these issues, but this is not always feasible and the technology has its own limitations (Cheng et al. 2014a, Saliba et al. 2014). Moreover, many public omics datasets are populated with data representing averaged signals from multiple cell types, as might be expected from a study that used tumor biopsies as the primary material. Some form of data deconvolution is then required. Tools to achieve deconvolution continue to emerge but for many of these datasets the tools must be effective when applied in an unsupervised manner because data that could supervise the analysis is often absent. Tools that can accurately and robustly perform unsupervised data deconvolution are likely to become more widely used in the near future.

The application of systems biology approaches to critical questions in endocrine-related and other cancers may provide new insights into cancer biology and lead to new treatments. Many signaling networks and the biological processes that they regulate often prove to be too complex for biostatistics, bioinformatics or mathematical biology alone to unravel. However, the integrated use of these approaches can support the building of predictive multiscale models from a systems perspective. The virtuous cycle of in silico model prediction, validation in appropriate wet laboratory experiments, with validated results feeding back to improve model predictions, can then drive new discovery of complex systems in a manner that often outstrips intuitive reasoning. In those cancers where hormone and growth factor receptors and their signaling play a major role, systems approaches may offer the best means to address the complexity and dynamic nature of signaling and how it responds to therapeutic interventions that affect the cancer cells and their interactions within their microenvironments.