Anion Distribution, Structural Distortion, and Symmetry-Driven Optical Band Gap Bowing in Mixed Halide Cs₂SnX₆ Vacancy Ordered Double Perovskites

Abstract

Mixed anion compounds in the Fm3̅m vacancy ordered perovskite structure were synthesized and characterized experimentally and computationally with a focus on compounds where A = Cs⁺. Pure anion Cs₂SnX₆ compounds were formed with X = Cl, Br, and I using a room temperature solution phase method. Mixed anion compounds were formed as solid solutions of Cs₂SnCl₆ and Cs₂SnBr₆ and a second series from Cs₂SnBr₆ and Cs₂SnI₆. Single phase structures formed across the entirety of both composition series with no evidence of long-range anion ordering observed by diffraction. A distortion of the cubic A₂BX₆ structure was identified in which the spacing of the BX₆ octahedra changes to accommodate the A site cation without reduction of overall symmetry. Optical band gap values varied with anion composition between 4.89 eV in Cs₂SnCl₆ to 1.35 eV in Cs₂SnI₆ but proved highly nonlinear with changes in composition. In mixed halide compounds, it was found that lower energy optical transitions appeared that were not present in the pure halide compounds, and this was attributed to lowering of the local symmetry within the tin halide octahedra. The electronic structure was characterized by photoemission spectroscopy, and Raman spectroscopy revealed vibrational modes in the mixed halide compounds that could be assigned to particular mixed halide octahedra. This analysis was used to determine the distribution of octahedra types in mixed anion compounds, which was found to be consistent with a near-random distribution of halide anions throughout the structure, although some deviations from random halide distribution were noted in mixed iodide–bromide compounds, where the larger iodide anions preferentially adopted trans configurations.

Introduction

The hybrid halide perovskites have attracted great interest as solar absorber materials, exhibiting a number of exceptional properties.^1,2 The discovery of these properties as well as the apparent drawbacks of instability and toxicity^3,4 have led to an intense search for materials with similar composition and structure to the hybrid halide perovskites, in the hope that the drawbacks may be overcome while the beneficial properties are maintained.

The Fm3̅m A₂BX₆ structure, formed by ordered removal of half of the B site cations from the cubic ABX₃ perovskite structure, has been known for some time as the K₂PtCl₆ structure⁵ and more recently has become referred to as the defect perovskite⁶ or vacancy-ordered double perovskite⁷ structure. Aside from three reports on oxy-halide compounds in the literature,⁸⁻¹⁰ all other known compounds in the K₂PtCl₆ structure have exclusively halide ions on the X site, an A site ion with a formal oxidation state of +1, and a B site cation with a formal oxidation state of +4. The K₂PtCl₆ structure is very similar to, and shares a space group with, the elpasolite structure (also known as the ordered double perovskite structure), and there are a great many oxide and halide elpasolites known; in these structures, there are two B site metals present in equal proportions which are ordered in a fcc arrangement,^11,12 just as the B site and vacancies are ordered in the K₂PtCl₆ structure. There is some controversy over the recent adoption of the word “perovskite” in naming materials with the K₂PtCl₆ structure due to the lack of corner sharing connectivity of the BX₆ sublattice¹³ (although this is also absent in the hexagonal perovskites which have been so named for over 50 years¹⁴). We choose here to describe the A₂BX₆ compounds as vacancy ordered double perovskites to emphasize their link to the double perovskite structure.

Considering the relationship between the halide ABX₃ perovskites and the vacancy ordered double perovskites discussed here, the removal of half of the B site cations naturally requires the doubling of the formal oxidation state of the remaining half. Thus, if the B site metal is selected from group 4 of the periodic table (e.g. Ge, Sn, Pb), the perovskite ABX₃ compound will contain the B metal in its formal lone pair oxidation state, with electronic configuration ns,² whereas in the A₂BX₆ analogue the metal will adopt its formal group oxidation state, with configuration ns⁰. The simple picture of formal oxidation states for these compounds has been critiqued recently, with calculations showing that the orbital occupancy of the Sn 5s states in Cs₂SnI₆ greater than zero.¹⁵⁻¹⁷ Clearly, however, moving from ABX₃ to A₂BX₆ will have important implications for the orbital makeup of the valence and conduction band extrema, which will impart differences in the charge transport properties.¹⁸ Unlike in the cubic perovskite, the BX₆ octahedra in A₂BX₆ do not share vertices and can be referred to as zero dimensional. Thus, the 3D network of the B–X sublattice, one of the key features of the cubic perovskite structure usually considered vital for the function of charge carrier separation, is absent in the A₂BX₆ structure.

Despite these differences, the A₂BX₆ structure is beginning to be seriously explored for use in photovoltaic devices¹⁹ as a replacement or companion for methylammonium lead iodide (MAPI) and related compounds²⁰⁻²⁵ or as a hole transport layer.^6,26,27 One reason for this is that the A₂BX₆ compounds tend to be much more air and moisture stable than their ABX₃ analogues, a property usually attributed to the increased stability of the B(IV) formal oxidation state.^21,28 Another reason is the good solution processability of the A₂BX₆.^22,29,30 Third, while the scope for chemical manipulation of the halide ABX₃ structure is rather limited (only a few halide perovskites can form and these have already been extensively explored³¹), in contrast, there seems to be a much greater composition space in which cubic A₂BX₆ structure will form, offering possibilities for chemical modification and optimization of properties. Despite expectations that the isolated nature of the BX₆ octahedra in A₂BX₆ structures would be a major hindrance to charge transport, compounds such as Cs₂SnI₆ have been found to have comparable electron mobility to corresponding perovskites.²⁶

Deployment of A₂BX₆ compounds in photovoltaic or other demanding optoelectronic applications will require a detailed understanding of their crystal chemistry and electronic structure. As with the hybrid halide perovskites, it is known that mixed halide compounds can form in the vacancy ordered double perovskite structure and that this is an important way to tune the band gap and other properties.^22,32 Here, we present a study on A₂SnX₆ mixed halide compounds. We focus on the A = Cs series, which adopts the Fm3̅m space group across the entire halide range from X = Cl to X = I. This proves to be a useful set of compounds to study compositional influences on electronic structure and optical properties.

We find that, like the ABX₃ perovskites, the A₂BX₆ structure distorts when the ionic radii of its constituents are not optimal, but unlike in the analogous ABX₃ compounds, this distortion can occur without reduction of long-range symmetry. We also probe the local structure of these materials using vibrational spectroscopy, which given the presence of isolated BX₆ octahedra is a simple and powerful method for semiquantitative study of local bonding environments. Our results on the optical properties show that mixed halide compounds show considerably smaller optical band gap than expected from interpolation from the pure halide compounds due to breaking of the octahedral symmetry of the B site cation, which allows electronic transitions that would be symmetry forbidden for pure halides. The important differences that we highlight here in optical, structural and electronic behavior of mixed halide A₂SnX₆ compounds compared with ABX₃ equivalents may have implications for design of functional materials in photovoltaic and related fields.

Experimental Section

All chemicals were obtained from Sigma-Aldrich. Aqueous HI is commonly found to contain I₃^– present through oxidation of iodide ions, giving a dark red color. Prior to use, I₃^– was removed by washing with a solution of 10% v/v tributyl phosphate in chloroform until a colorless aqueous solution of HI was obtained, which was then used immediately. All other chemicals were used as received.

Cs₂SnX₆ (X = Cl, Br, I) with a single halide anion was prepared as follows. The required cesium halide (CsCl, CsBr, CsI) was dissolved in the corresponding hydrohalic acid (either 6 M HCl, 3 M HBr, or 2 M HI). Separately, SnCl₄·5H₂O, SnBr₄, or SnI₄ was dissolved in ethanol. The two separate solutions were then mixed at room temperature such that the Cs:Sn molar ratio was 2:1, upon which a precipitate immediately formed. This was filtered, washed with ethanol, and dried in air. For example, to synthesize Cs₂SnI₆, 4 g of 2 M HI was added to CsI (0.45 g, 1.74 mmol) to afford a clear colorless solution of CsI. In a separate beaker, SnI₄ (0.547 g, 0.873 mmol) was dissolved in absolute ethanol (20.0 g) to afford a clear orange solution. The two solutions were then mixed, leading to rapid precipitation of the product as a fine black powder, which was isolated by filtration, washed with ethanol, and stored in air.

To produce mixed halide Cs₂SnX₆ compounds, i.e. the series Cs₂Sn(Br_nCl_1–n)₆ and Cs₂Sn(I_nBr_1–n)₆, the appropriate cesium halides were dissolved in their respective hydrohalic acids at the concentrations given above, and the solutions combined in the desired halide mole ratio. Likewise, the SnX₄ precursors were dissolved together in the desired halide mole ratio in ethanol. The acidic and ethanolic solutions were then combined with rapid stirring to yield the mixed halide product which precipitated immediately.

X-ray diffraction (XRD) was measured using a STOE Stadi P diffractometer (with STOE Dectris Mythen 1K detector), that operates with Mo Kα radiation (λ = 0.70930 nm) in transmission mode.

UV–vis spectra were recorded in diffuse reflectance mode using a PerkinElmer Lambda-950 spectrometer. Samples were ground and fixed to carbon tape on a glass slide. Diffuse reflectance spectra were recorded from 200 to 2000 nm. The reflecting reference used was a barium sulfate pellet. Reflectivity (R) data were converted using the Kubelka–Munk relationship: F(R) = (1 – R)²/2R.

X-ray photoelectron spectroscopy (XPS) was carried out in a Thermo K-alpha spectrometer. The instrument utilized a 72W monochromated Al Kalpha X-ray source (E = 1486.6 eV) focused to a spot of 400 μm diameter at the sample surface. Charging was compensated for by use of a dual beam (electron and Ar⁺ ion) flood gun. The electron energy analyzer consisted of a double focusing 180° hemisphere with mean radius 125 mm, operated in constant analyzer energy (CAE) mode, and a 128 channel position sensitive detector. The pass energy was set to 200 eV for survey scans and 50 eV for high resolution regions. The binding energy scale of the instrument is regularly calibrated using a three point energy reference (Ag, Au, Cu). Spectra were analyzed using the Thermo Avantage software. Powder samples were immobilized on conductive carbon tape for analysis. Stability was assessed by time-resolved measurements of the core lines; no changes were observed indicating that beam damage was not detectable on the time scale of these experiments. Spectra were charge corrected to adventitious C 1s at 285.0 eV.

X-ray fluorescence (XRF) spectroscopy was carried using a Panalytical Epsilon 4 spectrometer to quantify the halide composition of mixed halide samples. Samples were analyzed under helium gas. Calibration was carried out by using physical mixtures of the pure halide compounds in known proportions.

Raman spectra were acquired using a Renishaw inVia Raman microscope with a 50× objective in a back scattering configuration calibrated using the silicon Raman band at 520.5 cm^–1. The excitation wavelength was 785 nm (130 mW, 10%) and the acquisition time 20s. The laser spot size was around 1 μm².

Calculation Methodology

Density functional theory calculations were performed using the Vienna ab initio Simulation Package (VASP).³³⁻³⁶ A plane-wave basis set was employed with the interactions between core and valence electrons described using the projector-augmented wave (PAW) method.³⁷ For all systems studied, a Γ-centered 4 × 4 × 4 k-point mesh and plane-wave cutoff of 350 eV were found to converge the total energy to 1 meV/atom. Structural relaxations were performed using a larger plane-wave cutoff of 455 eV to avoid errors arising from Pulay stress.³⁸ Structures were deemed converged when the force on each atom totalled less than 0.01 eVÅ^–1.

This work utilized two exchange–correlation functionals: PBEsol,³⁹ a version of the Perdew, Burke, and Ernzerhof (PBE) functional revised for solids,⁴⁰ and the hybrid functional HSE06,^41,42 which combines 75% exchange and 100% of the correlation energies from PBE together with 25% exact Hartree–Fock (HF) exchange at short ranges. For accurate calculation of band gaps and optical properties, the structures were first relaxed using HSE06, with the final optoelectronic properties calculated using HSE06 with the addition of spin–orbit coupling (SOC) effects. This combination of HSE06+SOC has previously been employed for the vacancy-ordered double perovskites^43,44 and has been shown to provide an accurate description of the electronic structure in many metal–halide semiconductors containing heavy elements.^45,46 Optical properties were calculated within the PAW formalism through the manner described by Gajdos̆ et al.⁴⁷ and plotted using the sumo package.⁴⁸ Interband transitions were determined as optically active if the square of the transition matrix elements, |M|², was greater than 10^–3 eV^–2 Å^–2.^7,49

Simulated Raman spectra were obtained using the methodology detailed by Porezag et al.⁵⁰ In this approach, the Raman intensity for a mode is computed using the derivative of the electronic susceptibility, χ, where

and ε_r is the dielectric constant. The frequencies and atomic displacements of the phonon modes at the Γ point were calculated using density functional perturbation theory (DFPT). The derivate of the electronic susceptibility for a mode was obtained via finite difference by displacing the structure along the phonon eigenvector and recalculating the dielectric constant using DFPT. Further details of this methodology are described in detail elsewhere in the literature⁵⁰ with many studies reporting excellent agreement with experimental Raman intensities.^51,52 The computational expense of performing simulated Raman calculations precluded the use of the hybrid HSE06 functional. We instead employed the PBEsol functional which has previously been shown to give good agreement to experiment for the structural and vibrational properties of related metal–halide systems.^53,54 To increase accuracy when calculating atomic forces and phonon frequencies, the structures were first relaxed using a tighter ionic force criterion of 0.0001 eVÅ^–1. Raman intensities were calculated using the vasp_raman Python package.⁵⁵

For the bulk compounds (namely Cs₂SnX₆, where X = Cl, Br, I), the experimentally determined structures were used as the starting point for structural relaxations. We additionally calculated the optoelectronic and Raman properties of a series of alloy structures. As the primitive cell for the bulk compounds possesses six halide sites, the alloy structures were generated by substituting an increasing number of halide sites in the primitive structure. After reducing the number of substitutional configurations by only considering those that were symmetry inequivalent, a total of eight alloy structures for each series were identified. For the chloride–bromide series, these are SnCl₅Br, trans-SnCl₄Br₂, cis-SnCl₄Br₂, fac-SnCl₃Br₃, mer-SnCl₃Br₃, trans-SnCl₂Br₄, cis-SnCl₂Br₄, and SnClBr₅.

Results

Composition and Structure

XPS and XRF were used to determine the amount of each halide present in the mixed compounds of Cs₂Sn(Br_nCl_1–n)₆ and Cs₂Sn(I_nBr_1–n)₆. The sampling depth of XPS utilizing Al Kα radiation is approximately 10 nm, while XRF the sampling depth is much larger making this a bulk composition measurement. The XPS and XRF halide compositions, shown in Tables S3 and S4 (Supporting Information), match closely, suggesting that there is little difference between the surface and bulk halide composition in these materials. Therefore, we take the average of the XPS and XRF compositions as the experimental halide composition. This experimental composition differed significantly from the nominal composition, this being the ratio of halide ions present in the reagents in solution. For both series, the experimental composition, n, is lower than the nominal value, i.e. the samples are richer in the lighter halide than expected. This may be due to greater stability of the heavier halide salts in acid/ethanol solution versus in the solid state. Due to the differences between nominal and measured composition, henceforth references to composition mean experimentally derived composition as defined above.

X-ray diffraction patterns from each Cs₂SnX₆ sample were consistent with a single phase Fm3̅m vacancy ordered double perovskite structure. No additional diffraction peaks were observed in any sample, indicating that XRD is can detect neither secondary phases nor anion ordering in these samples, in contrast to some predictions from calculations on mixed anion compounds.⁵⁶ Rietveld refinement was carried out using the GSAS and EXPGUI software packages.^57,58 The cubic lattice parameter, occupancy of the halide site and the (x,0,0) crystallographic coordinate of the halide anion were refined. From the refined occupancy of the halide site, the anion composition can be derived. Varying the anion occupancy of our model from Cl to Br to I had profound effects on the calculated intensity ratios of the powder diffraction peaks, as can be seen in the Supporting Information, Figure S9. The refined anion occupancy was close to the measured experimental composition from XRF and XPS (Tables S1 and S2), which gives support to our structural model.

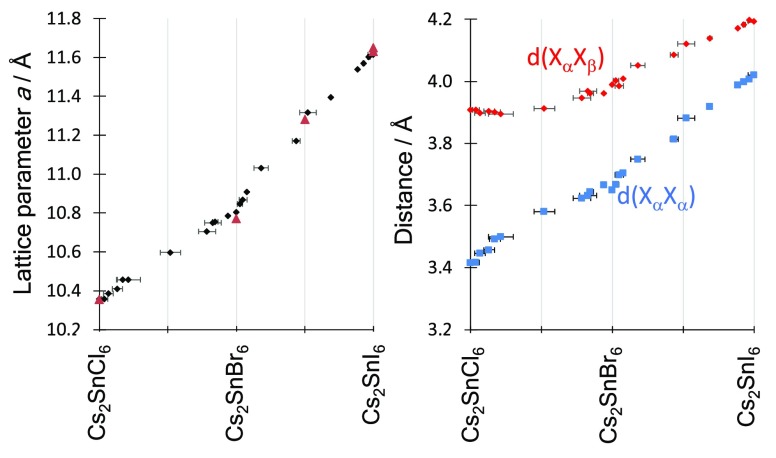
Figure 1 shows the lattice parameter variation with halide composition. For mixed halide samples in both series of compounds (chloride–bromide and bromide–iodide), we observe a slight positive deviation of the lattice parameter from a linear interpolation between the end members, showing that the introduction of the larger halide causes a slightly greater expansion of the lattice than expected based on Vegard’s Law. This is expected for disordered mixing of different size ions.⁵⁹ The pure halide compounds, Cs₂SnCl₆ and Cs₂SnBr₆, have been previously reported with experimentally determined lattice parameters of 10.3552(2) and 10.77(5) Å, respectively.^7,60−63 Cs₂SnI₆ has been studied by several groups, and the cubic lattice parameter has been reported between 11.65272(4) and 11.6276(9) Å.^7,30,63,64 Additionally, one mixed halide compound, Cs₂SnBr₃I₃, has been crystallographically characterized and found to have a lattice parameter of a = 11.2819(3) Å.⁶⁵ These literature measurements, also shown graphically in Figure 1, fit well with our measurements. The fact that single phase samples can be produced across the full composition range of both series shows that Cs₂SnCl₆ and Cs₂SnBr₆ are fully soluble in each other; likewise, so are Cs₂SnBr₆ and Cs₂SnI₆. The absence of any additional Bragg reflections compared with the pure halide structures shows that there is no long-range ordering of the anions or reduction in symmetry that is detectable by the XRD methodology used here.

Figure 1.

Left, variation in lattice parameter with composition in the mixed halide Cs₂SnX₆ series. Black points are samples from this work; red triangles refer to literature values.^6,7,30,64 Right, variation in interhalide distances with composition in the Cs₂SnX₆ series: d(X_αX_α), blue squares, is the shortest distance between two halides coordinated to the same Sn ion, while d(X_αX_β), red diamonds, is the shortest distance between two halides coordinated to different Sn ions.

The crystallographic (x,0,0) coordinate of the halide was also refined, and results shown in Tables S1 and S2 in the Supporting Information. Variation of x in the structural model causes large relative changes in the calculated intensities of some diffraction peaks, meaning that x is able to be determined with good reliability from lab powder XRD data (see Figure S8 in Supporting Information). The x coordinate is seen to increase from Cs₂SnCl₆ to Cs₂SnBr₆ to Cs₂SnI₆, taking values of 0.2331(3), 0.2388(4), and 0.2447(1) respectively, very close to values previously reported for the pure compounds.⁶ The average Sn–X bond distance is calculated from the crystallographic (x,0,0) parameter and the cubic lattice parameter and for both series increases with increasing average mass of the halide as expected due to the increasing halide ion radius. In the Cs₂Sn(Br_nCl_1–n)₆ series, the end members (n = 0, 1) have Sn–X bond distances of 2.4146(4) and 2.5806(8) Å, respectively. The intermediate compounds all have a slightly longer Sn–X distance than expected from a linear extrapolation between the end members.

We have previously shown that the sum of the Shannon radii overestimates the metal–halide bond distance in a related series of compounds, the ABX₃ halide perovskites, due to the increasingly covalent nature of the bonds.³¹ In the CsSnX₃ halide perovskites, the Sn cation formally takes a 2+ charge, in contrast to the 4+ charge of the Sn in Cs₂SnX₆. For Cs₂SnX₆ compounds with mixed halides, we calculated the Shannon bond length by summing the Sn(IV) six-cooridnate ionic radius and the composition weighted mean of the Shannon radii for the appropriate halide. The experimentally observed Sn–X bond length is consistently around 2% shorter than the Shannon bond length. The discrepancy is approximately constant across the composition range, and this suggests that, unlike the CsSnX₃ halide perovskites, the degree of covalency does not significantly increase when moving to the heavier halides. For comparison, for Sn(II) ABX₃ compounds, Sn–I bonds are found to be approximately 6% shorter than predicted by the sum of Shannon radii.³¹ The smaller discrepancy observed in the Sn(IV) compounds is likely due to the higher charge on the cation leading to a lower degree of covalency in the metal halide bonding.

The cubic A₂BX₆ vacancy ordered double perovskite structure consists of isolated [SnX₆]^2– octahedra in which a particular halide ion belongs uniquely to one octahedron. Two important interhalogen (X–X) distances can be defined: first the shortest distance between halide anions coordinated to the same Sn ion, which we denote d(X_αX_α) and second the shortest interhalogen separation between halide anions on neighboring octahedra (coordinated to different Sn ions) labeled d(X_αX_β). These are shown pictorially in Figure S1 (Supporting Information). In the Fm3̅m structure, there is only one crystallographic site for the X anion, so it should be noted that the relationship between these two distances depends only on the x crystallographic coordinate of the halide. For x = 0.25, d(X_αX_α) = d(X_αX_β), and in this case the X site sublattice (and indeed the A site sublattice) would be identical to that found in a Pm3̅m ABX₃ perovskite. For x < 0.25, which is the case for all compounds studied here (and to our knowledge all A₂BX₆ compounds in the Fm3̅m space group), d(X_αX_α) is shorter than d(X_αX_β). Figure 1 shows these two interhalogen distances as they vary with composition across both the chloride–bromide and bromide–iodide series. As expected, the Sn–X bond length, and hence, d(X_αX_α) increases with the composition parameter, n, for both Cs₂Sn(Br_nCl_1–n)₆ and Cs₂Sn(I_nBr_1–n)₆ series. Likewise, the octahedral separation, measured by d(X_αX_β), also increases with halide mass for the bromide–iodide series. However, for the Cs₂Sn(Br_nCl_1–n)₆ series, for samples where n < 0.5, i.e. the Cl-rich half of the series, d(X_αX_β) is roughly constant: the [SnX₆]^2– octahedra remain the same distance apart despite the octahedra themselves increasing in size with increasing bromide content. Figure 1 shows that, had the linear trend seen in the rest of the series been followed, d(X_αX_β) for Cs₂SnCl₆ would be less than 3.8 Å, whereas the measured value is 3.91 Å.

This behavior highlights an important difference between the A₂BX₆ vacancy ordered double perovskites and the ABX₃ cubic perovskites or the A₂BB′X₆ double perovskites. In the latter two structures, the corner sharing connectivity of the BX₃ (or BB′X₆) framework fixes the size of the A site cavity for a given B–X bond length; it is this restriction that gives rise to Goldschmidt’s tolerance factor equation. In the vacancy ordered perovskites, the fact that the BX₆ octahedra are not connected means that the separation between them, and thus the size of the A site cavity, can change independently of the size of the octahedra themselves. As seen in the Cs₂Sn(Br_nCl_1–n)₆ series studied here, the octahedral separation can in fact remain constant over a wide range of halide compositions, which is clearly impossible for corner sharing octahedra found in ABX₃ perovskites. It is useful to discuss why the [SnX₆]^2– octahedra in the chloride-rich half of our chloride–bromide series will tolerate greater separation than would be expected based on their size alone. In 1964, Brown considered the size of the A site cavity in the A₂BX₆ vacancy ordered double perovskite structure, and proposed that the ratio of the cavity size to the A site ionic radius could determine the formability of a particular A₂BX₆ structure, just as the tolerance factor can determine the formability of ABX₃ structures.⁶⁶ We adapt Brown’s equation and propose the following radius ratio to apply to A₂BX₆ compounds. As determined by Brown, the distance between the centers of A site ion and the surrounding halide ions, d(AX), is defined by the surrounding halide coordination sphere as follows:

1

i.e., the mean of the two interhalogen distances defined above. Thus, if the A site cation is to perfectly fit into the cavity provided by the surrounding halide ions, the following relation must hold:

2

where r_A and r_X are the ionic radii of the A site and halide ions, respectively. For compounds where two halides are mixed on the X site, we take r_X to be the compositionally weighted average of the two relevant halide ionic radii. We can express the deviation from the above equation, i.e. deviation from a perfectly fitting structure by calculating a ratio, R:

3

If R > 1, then the A site cation is too large to fit into the cavity. Note that, as discussed above, if the crystallographic x parameter for the halide ion in this Fm3̅m structure is equal to 0.25, then halide sublattice is identical to that found in the cubic perovskite. In this case, d(X_αX_α) = d(X_αX_β), and it can be shown (see Supporting Information) that eq 3 is then reduced to the well-known Goldschmidt tolerance factor equation.⁶⁷ Thus, it can be said that the Goldschmidt tolerance factor equation is a special case of the more general eq 3.

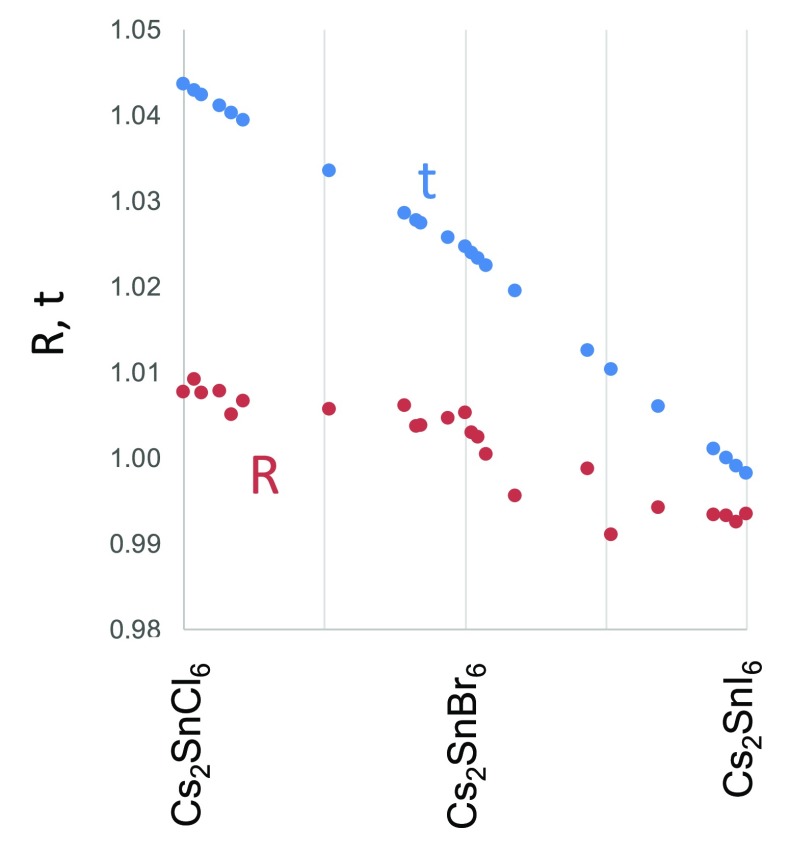
Figure 2 shows the calculated R values for the Cs₂SnX₆ mixed halide compounds. It is striking that the R value of all Cs₂SnX₆ compounds considered here falls in the range 0.989 < R < 1.008. In contrast, if the Goldschmidt tolerance factor, t, is calculated for this series, it values would fall in the range 0.999 < t < 1.04, a considerably greater range (see Figure 2). There is a clear contrast between the bromide–iodide series, where the R value falls with increasing halide mass, and the chloride–bromide series where the R value is almost constant at values between 1.00 and 1.01. This suggests that in the chloride–bromide series, the Cs⁺ cation is at the upper size limit of what can be tolerated within the structure. In fact, as discussed above, we observe that, upon moving from Cs₂SnBr₃Cl₃ to Cs₂SnCl₆, the [SnX₆]^2– octahedra do not move closer together as expected; instead, d(X_αX_β) remains almost constant. This can be interpreted as a distortion of the structure to accommodate the Cs⁺ cation: the [SnX₆]^2– are held further apart by the large Cs⁺ ion within their cavity than would otherwise be expected. Eq 3 thus illustrates the structural flexibility of the vacancy ordered double perovskite structure, as the d(X_αX_β) value can change to maintain the R value at very close to unity over a wide range of compositions.

Figure 2.

Goldschmidt tolerance factor, t (blue points), and the ratio R defined by eq 3 (red points), plotted against composition in the Cs₂SnX₆ series.

It might be said that the underlying cause of the variation of the interhalogen spacing across the composition series as shown in Figure 1 is the maintenance of the correct cavity size for the A site cation to fit within the BX₆ framework,¹⁸ or in other words, the maintenance of the ratio R in eq 3 as close to one as possible. We propose that this is analogous to the way that perovskites and double perovskites undergo octahedral tilting to accommodate A site cations that do not fit perfectly into the cavity formed by the B site octahedra.^11,68−70 In halide ABX₃ perovskites, as in the oxides, the cause of the tilting has been determined as optimizing the coordination environment of an A site cation that is too small to fit into the cubic lattice. However, while the magnitude of the tilting is around the same as that seen in the oxides, in the halide perovskites, a different characteristic pattern of tilts is observed.⁷⁰ It is notable that the vacancy ordered perovskite structure can also exhibit octahedral tilting.^44,71 Imposition of one tilt reduces the symmetry to either P4/mmc or I4/m, for example both of these structures are adopted by the composition Rb₂TeI₆, and indeed Cs₂SnI₆ adopts the I4/m structure at pressures above 10.9 GPa.⁷² Tilting is rather common in the ABX₃ perovskite structure: an analysis of the ICSD shows that only around 30% of crystallographically characterized ABX₃ perovskites are in the undistorted Pm3̅m space group. In contrast, our analysis of the ICSD shows that 80% of reported of vacancy ordered perovskite structures show no long-range cooperative octahedral tilting (i.e., are crystallographically cubic), although localized tiling in a compound with the A₂BX₆ structure has been detected via total X-ray scattering techniques.⁴³ As demonstrated above, in the A₂BX₆ structure, the size of the octahedra can change independently of their separation to accommodate the A site cation size, and so a driving force for tilting is removed. This may have important implications for materials design, as it is known that the angle of octahedra relative to each other can impact conductivity in perovskites.⁷³ It may also make the vacancy ordered double perovskites an interesting testing ground to study the underlying causes of octahedral tilts, as in these compounds, the steric impetus for tilting is removed, yet some compounds still experience tilting. This is beyond the scope of the current manuscript.

Raman Spectroscopy

Raman spectra were recorded from selected members of the Cs₂SnX₆ mixed halide series, which were representative of the complete compositional range. The spectra are shown in Figure S3 in the Supporting Information. The vibrational spectroscopy of A₂BX₆ compounds has been well studied, as these are useful model compounds for study of isolated [BX₆]^2– octahedra. The Raman spectra from Cs₂SnCl₆, Cs₂SnBr₆, and Cs₂SnI₆ consist of three peaks with Raman shift above 50 cm^–1 and can be explained by considering only Sn–X vibrations in octahedral symmetry.^6,74−76 On the other hand, vibrational spectra of mixed halide A₂BX₆ compounds have received significantly less attention. Kaltzoglou et al. presented a Raman spectrum of Cs₂SnBr₃I₃ which showed a complex series of peaks which the authors interpreted as being caused by a variety of different [SnX₆] octahedra with variable halide composition.⁶⁵ Very recently, Yuan et al. have reported Raman spectra of mixed Cs₂SnX₆ compounds with mixed Br and I anions. They too concluded that the complex Raman spectra characteristic of the mixed halides resulted from a degree of anion ordering.⁷⁷ We expand on these ideas below.

As seen in Figure S3, the mixed halide compounds studied here show Raman spectra that are significantly different to those of pure halide compounds. For samples with compositions close to one of the pure halides, small extra peaks are seen in addition to those characteristic of the pure halide. For compounds with compositions in the middle of each series, close to Cs₂SnCl₃Br₃ and Cs₂SnBr₃I₃, the spectra are very considerably different from either of the end members.

Because the pure halide compounds Cs₂SnCl₆, Cs₂SnBr₆, and Cs₂SnI₆ have Raman spectra that can be understood by considering only the vibrations of isolated [SnX₆]^2– octahedra,⁷⁵ we approach the Raman spectra of the mixed halide series with the same assumption. Within a mixed halide sample, there are likely to exist different mixed halide octahedra, i.e. a distribution of local Sn environments. The XRD results presented above rule out the existence of long-range halide order in Cs₂SnX₆ compounds, but local structural variations are still possible, and in fact, for compositions where 6n is not an integer, there must necessarily be multiple Sn environments present, as the overall stoichiometry cannot be reached using only one kind of octahedron. It is known that Raman spectra of physical mixtures of compounds can be decomposed using principle component analysis to the spectra of their components.⁷⁸ Assuming no vibrational interaction between SnX₆ octahedra, the observed Raman spectra would likewise be a combination of individual spectra from each different octahedron present, and we propose that it is possible to extract information about the distribution of Sn environments in mixed halide compounds from the Raman spectra. To achieve this, we calculated the Raman active vibrational frequencies and their expected intensities from each possible tin halide octahedron using DFPT computations with the PBEsol functional, following the methodology detailed by Porezag.⁵⁰ Spectra were simulated by applying a 50:50 Gaussian:Lorentzian peak with full width at half-maximum (fwhm) of between 3 and 5 cm^–1, the fwhm chosen to best fit the experimental spectra as described below. For the chloride–bromide series, we calculated the Raman spectrum from the 10 possible octahedron types, viz: SnCl₆, SnCl₅Br, trans-SnCl₄Br₂, cis-SnCl₄Br₂, fac-SnCl₃Br₃, mer-SnCl₃Br₃, trans-SnCl₂Br₄, cis-SnCl₂Br₄, SnClBr₅, and SnBr₆. The same approach was used for the bromide–iodide series. The resulting spectra are shown the Supporting Information, Figure S3.

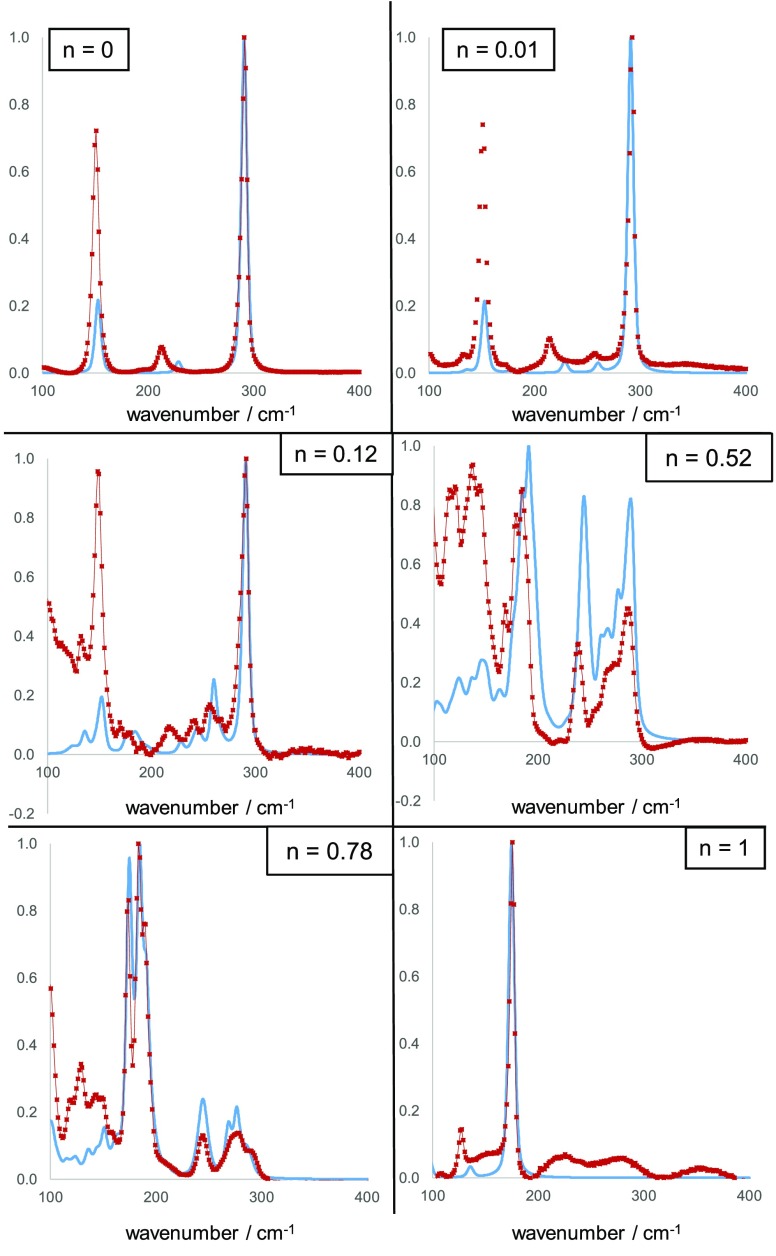
For Cs₂SnCl₆ (Figure 3), we measured three Raman active modes at 308, 232, and 168 cm^–1. These are assigned as vibrations of the [SnCl₆]^2– octahedron: the A_1g, E_g, and F_2g vibrations of the O_h point group.⁷⁴ Our calculated frequencies for these vibrations are 290, 229, and 154 cm^–1, respectively. The discrepancy between calculated and experimental vibrational frequencies is likely due to the lack of finite temperature effects included in our calculations. Specifically, while our calculations were nominally performed in the absence of temperature, the experimental results, recorded at room temperature, will be shifted due to the effects of crystal expansion.^79,80 We applied a shift to all calculated frequencies to correct for this, the size of the shift chosen for each sample to yield the best fit of the theoretical to the experimental data. Across all samples, the shifts applied were in the range 8–18 cm^–1. After temperature correction, in the Cs₂SnCl₆ spectrum, the calculated frequency of the E_g vibration is most at variance with the experimental spectrum. The most intense peak in the calculated Raman spectrum is the A_1g peak, in agreement with the experimental spectrum. Both experimental and calculated spectra were normalized to the A_1g peak. It is apparent that the calculated intensity of the E_g peak matches well with experiment, but the intensity of the calculated F_2g peak is much lower than that observed experimentally. These discrepancies with experiment may result from use of the PBEsol functional which can sometimes result in anomalous delocalization of electron charge. While use of a hybrid functional such as HSE06 might result in improved agreement, the computational cost of simulated Raman calculations precluded their use in this work.

Figure 3.

Comparison between experimental Raman spectra (red points) and calculated spectra (blue lines) for mixed halide compounds in the series Cs₂Sn(Br_nCl_1–n)₆. Intensity is normalized in each case.

The experimental Raman spectra of the mixed halide compounds are clearly not a simple sum of the end members, and several new peaks appear that are not present in either of the pure anion end members. This suggests a reduction in symmetry around at least some Sn cations due to the mixed halide coordination sphere. We calculated the distribution of octahedral types expected based on an assumption that the halide anions were distributed randomly throughout the structure. In this model, the probability of an anion site being occupied by a particular halide was determined only by the overall halide composition, and was independent of any other factors. We proceeded to calculate, for a given halide composition, and assuming random placement of halide ions, the proportion of each octahedron type that the sample would contain (see Supporting Information for full details). The DFT Raman spectra of each octahedral type were then summed in these proportions, and the results are compared with the experimental spectra in Figure 3. To reiterate, these calculated spectra represent what we expect to result from a random distribution of halides throughout the structure with no influence of the thermodynamic stability of the resulting distribution of SnX₆ octahedra. In general, the calculated DFT spectra provides a good match to the shape of the experimental Raman spectra for the chloride–bromide series. For the sample in the chloride–bromide series with n = 0.01, i.e. Cs₂SnCl_5.94Br_0.06, the DFT calculated Raman spectrum correctly predicts the appearance of small peaks close to 260 and 140 cm^–1 in addition to the peaks observed for Cs₂SnCl₆. These two additional peaks arise from vibrations of the [SnCl₅Br]^2– octahedron, which would make up 5.7% of the SnX₆ octahedra given our random distribution model. The next most abundant octahedron type for this composition is [cis-SnCl₄Br₂]^2–, which makes up 0.11% of octahedra. Given that the scattering intensities of the different octahedral types in the chloride–bromide series are calculated to be within an order of magnitude of each other, the [cis-SnCl₄Br₂]^2– and other octahedral types that appear in very low abundance will make almost no measurable contribution to the experimental Raman spectrum.

Figure 3 shows a comparison of the experimental and calculated Raman spectra for the compound with n = 0.12, i.e. Cs₂SnCl_5.28Br_0.72. Our statistical model for this composition indicates that this sample would consist of 46% [SnCl₆]^2– octahedra, 38% [SnCl₅Br]^2– octahedra, 10.4% [cis-SnCl₄Br₂]^2–, 2.6% [trans-SnCl₄Br₂]^2–, and 1.1% each of [mer-SnCl₃Br₂]^2– and [fac-SnCl₃Br₃]^2– with less than 1% of all other octahedral types combined. The calculated spectrum shows three additional maxima compared with the pure chloride compound in the region 200–275 cm^–1, and these are matched in approximate shape and intensity by the experimental spectra, but with a shift of ca. 10 cm^–1 for the lowest frequency of the three peaks. The shape of the peaks between 100 and 200 cm^–1 is also reproduced well by our model, but the intensities are predicted to be far lower than actually observed, as was found in the case of the Raman peaks in this region for the Cs₂SnCl₆ compound.

For the chloride–bromide compound with n = 0.52, i.e. Cs₂SnCl_2.88Br_3.12, and n = 0.78, i.e. Cs₂SnCl_1.32Br_4.68, the calculated Raman spectra again explain the complex shapes of the experimental Raman features well but with inaccuracies in intensities. To illustrate the impact on the calculated spectra of a nonrandom distribution of halides, we show in the Supporting Information Figure S5 a calculated spectrum for Cs₂SnCl_1.32Br_4.68 where no cis-octahedra are included, all SnX₂Y₄ octahedra are trans. It can be seen that there is a significant difference between the “trans only” model and the experimental data, and the random distribution model fits the experimentally observed shape to a better degree.

In summary, for the chloride–bromide series, the Raman spectra observed are consistent with calculated spectra assuming a random distribution of halides throughout the structure. Significant deviations from the random distribution model, that might be caused by greater thermodynamic stability of certain octahedra types, cause significant changes to the calculated spectrum and these do not fit with the experimental spectra.

We now move to the bromide–iodide series. The same approach was used to understand the Raman spectra as set out above, by modeling with a random distribution model. However, a challenge in this series is that the Raman scattering intensities calculated for different [SnI_6(1–n)Br_6n] octahedra types varied over several orders of magnitude. This is in contrast to the chloride–bromide series discussed above, where calculations showed that all octahedra scattered with approximate equal intensity. The consequence is that some bromide–iodide octahedron types can dominate the calculated Raman spectra even when present in very small amounts, and this means that calculated spectra vary considerably with very small changes in overall composition. Despite this, good agreement was found between the random distribution model and the experimental Raman spectra. However, unlike the chloride–bromide series, it was found that improvements to the fit could be made by slightly altering the halide distributions from the initially tried random distributions, as set out below.

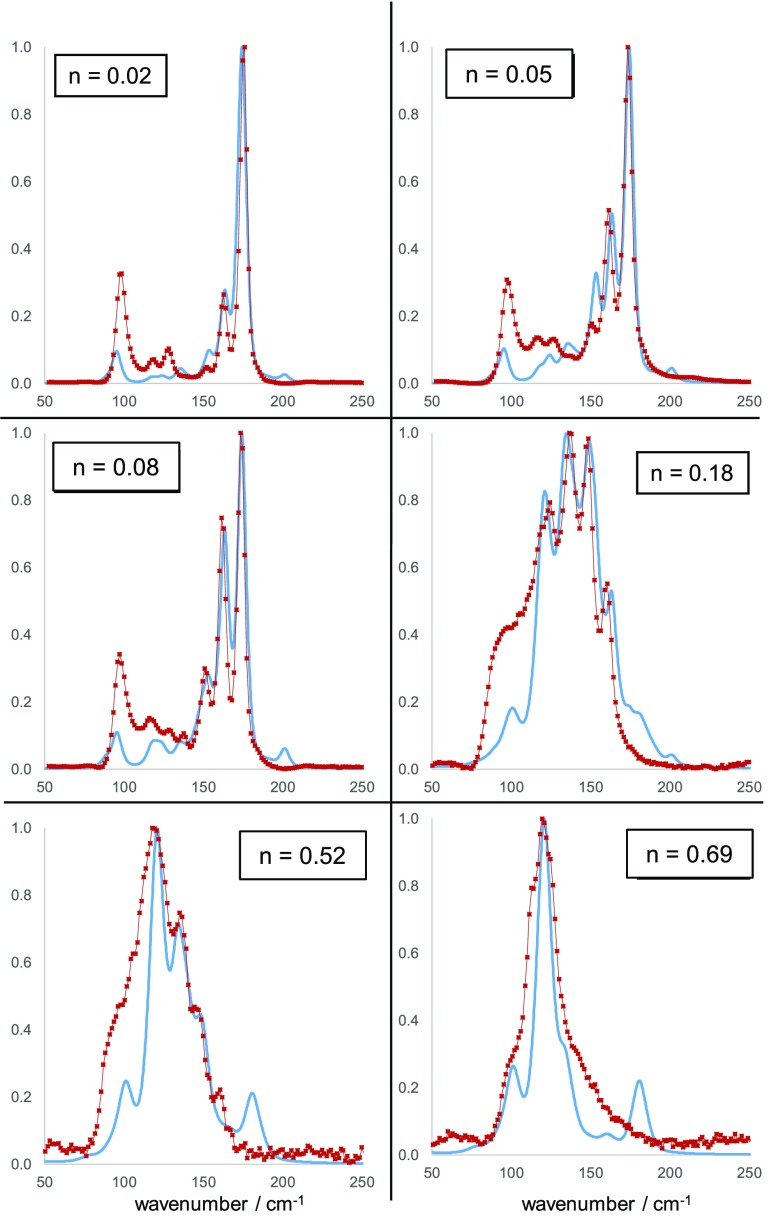
The comparison of experimental and calculated Raman spectra from the bromide–iodide series can be seen in Figure 4. Given a random halide distribution, the sample with composition n = 0.02, i.e. Cs₂SnBr_5.88I_0.12, is calculated to have 88% of the octahedra as [SnBr₆] with 11% as [SnBr₅I] and 0.4% from cis-[SnBr₄I₂] and <0.5% of the remaining types of octahedra. The experimental Raman spectral shape is reproduced well by this model in the region 150–200 cm^–1, where the appearance of two additional peaks that are not present in the Cs₂SnBr₆ spectrum, due to vibrations of [SnBr₅I] and cis-[SnBr₄I₂] are correctly predicted. The E_g peak of the [SnBr₆] octahedron is still calculated at a higher frequency than observed, but the appearance in the calculated spectrum of a new peak at 121 cm^–1, arising from cis-[SnBr₄I₂] vibration is also seen in experiment.

Figure 4.

Comparison between experimental Raman spectra (red points) and calculated spectra (blue lines) for mixed halide compounds in the series Cs₂Sn(I_nBr_1–n)₆. Intensity is normalized in each case.

Moving to higher iodide contents, it was found that altering the model to reduce the cis-[SnBr₄I₂] concentration to 25% of its expected value based on a random distribution of halides, and reassigning these octahedra as trans-[SnBr₄I₂], resulted in a significantly better match with experiment. The Raman spectra from samples with compositions n = 0.048 and n = 0.077 were matched well by the model with the enhanced trans-[SnBr₄I₂] content: the three peaks in both spectra between 150 and 180 cm^–1 are matched well in shape and intensity by the model. If the concentration of trans-[SnBr₄I₂] is not enhanced as described above, there is significant discrepancy between experiment and model in this wavenumber region, see Figure S6 in the Supporting Information.

The bromide–iodide sample with n = 0.18, i.e. Cs₂SnBr_4.92I_1.08, required another alteration of the random model to achieve a good fit. Although in this sample the octahedral type [SnBrI₅] represents only 2 in 10⁶ SnX₆ octahedra based on a random distribution model, the vibrations of this octahedron are calculated to have a very high Raman scattering coefficient, and is responsible for the Raman peak at ca. 125 cm^–1 seen in the spectrum for Cs₂SnBr_4.92I_1.08 and those samples with higher concentration of iodide. To achieve a good fit we had to multiply the expected concentration of [SnBrI₅] by a factor of 4. Our resulting model fits the experimental shape of the four maxima in the region 110–160 cm^–1 well, although at low wavenumber, our model fails to reproduce a broad scattering feature seen in experiment. The samples with the highest concentration of I: n = 0.52 and n = 0.69 have spectra that resemble closely those reported by Kaltzoglou et al. on Cs₂SnBr₃I₃.⁶⁵ Our model predicts these spectra are dominated by vibrations of [SnBrI₅] octahedra, although our model predicts a peak from this octahedron at 180 cm^–1 which is not seen in experiment. Despite this, for both of these compounds the general spectral shape is fitted well with our model with only minor changes to the concentration of [SnBrI₅] octahedra needed.

We acknowledge that the method of comparing experimental and calculated spectra could be improved by use of a quantitative goodness of fit parameter, and this is the subject of ongoing work. While our models reproduce the main features of the experimental spectra, the fits are not perfect, and this may be for a number of possible reasons: first, if the calculated spectra are a poor representation of the real spectra; second, if it is inaccurate to treat each octahedron as an independent Raman scatterer, or last, if Raman active impurities are present in the sample. We have no evidence for the latter option, but the former two may contribute.

However, even the qualitative comparisons we are able to make here strongly suggest that a halide distribution close to random is present in our chloride–bromide samples and that a slight deviation from a random distribution, i.e. the favoring of trans-[SnBr₄I₂] over cis-[SnBr₄I₂], occurs in the bromide–iodide series, which makes sense on steric grounds. It is notable that the halide distribution may well be altered by different synthetic conditions. With our room temperature synthetic method, it is perhaps unsurprising that any thermodynamic differences between different octahedral types is not expressed, or perhaps only expressed for the largest anions (iodide) where the steric effects will be greatest. It is likely that the distribution of halide octahedron types will have a strong impact on properties; it may be that different synthetic techniques offer the possibility to produce a different distribution of octahedra and hence compounds with the same overall composition but with modified optical and electronic properties compared with what we observe here. This is the subject of further studies but is beyond the scope of this report. Furthermore, it is important to note that, because the Raman spectra seem to give information only on the individual octahedral environments, while we may conclude that the overall concentration of octahedral types is close to that expected for a random distribution of halide ions, we cannot comment on the spatial distribution of the octahedra themselves. As a purely illustrative example, it may be that a mer-[SnBr₃I₃] octahedron is found preferentially adjacent another specific type of octahedron; using our method here it is impossible to tell, although we can rule out order that would give rise to long-range reduction in symmetry from our PXRD results.

X-ray Photoelectron Spectroscopy

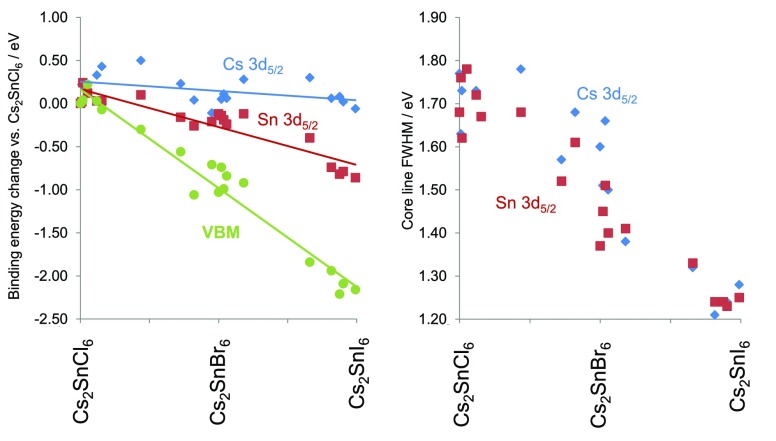
The electronic structure of the Cs₂SnX₆ materials was studied using XPS, which was used to measure both the core lines and valence band spectra. The principal core lines of Sn, Cs, and the halide(s) in each sample were found to display symmetrical peaks, suggestive of a single chemical environment. In our samples, the Sn 3d_5/2 core line showed a significant fall in binding energy with increasing halide mass, moving from a binding energy of 487.7 eV for Cs₂SnCl₆ to 486.8 eV for Cs₂SnI_6.These values match well with reported peaks in Sn containing compounds: SnCl₄(py)₂ was found with a Sn 3d_5/2 binding energy of 487.5 eV, and compounds of Sn with iodine were found to have Sn 3d_5/2 peaks at binding energies of 486.5 eV.⁸¹ Cs₂SnI₆, Cs₂SnBr₆, and Cs₂SnCl₆ have been studied by XPS previously. For Cs₂SnCl₆, the Sn 3d core line was reported at exactly the binding energy we observe here.⁸² One sample of Cs₂SnI₆ previously studied was highly oxidized, so unambiguous Sn binding energies could not be obtained,⁸³ but in another, oxidation was not evident, and Sn 3d peaks were reported with binding energy of 486.5 eV, 0.3 eV different from our measurement.⁸⁴ Han et al. also reported that in Cs₂SnBr₆, the Sn 3d_5/2 peak is at higher energy than in Cs₂SnI₆, although a precise binding energy is not given.⁸⁴ In the related compound MA₂SnI₆, the XPS binding energy of Sn 3d_5/2 has been reported as 487.6 eV, 0.8 eV higher than we report for Cs₂SnI₆.⁸⁵ Across both of our mixed halide series, we found that the Sn 3d_5/2 peak decreased in binding energy with increasing halide mass following an approximately linear trend with halide composition, with a total decrease in binding energy of 0.88 eV moving from Cs₂SnCl₆ to Cs₂SnI₆. In compounds containing Br, the Br 3d peak showed a 0.42 eV decrease from the most chloride-rich to the most iodide-rich compound (naturally no measurement of Br 3d could be made on Cs₂SnCl₆ and Cs₂SnI₆). The Cs 3d_5/2 peak binding energy showed a smaller total variation of only 0.60 eV, but this was not a linear decrease as with the other core lines discussed. In fact the Cs 3d_5/2 binding energy appears to increase toward the middle of each composition series before falling again. The variation in binding energy of the Sn and Cs principal core lines in Figure 5, where the shift in core lines relative to their binding energies in the compound Cs₂SnCl₆ is plotted. As shown by Raman measurements above, the distribution of SnX₆ octahedral types is widest at the center of each composition series, and thus, it appears the Cs 3d_5/2 binding energy correlates with the multiplicity of SnX₆ octahedral environments with a greater Cs 3d_5/2 binding energy corresponding to a greater range of environments present, although why this correlation should exist is not clear to these authors. This is shown in the Supporting Information, Figure S7.

Figure 5.

Left, binding energy shifts of Cs 3d_5/2, Sn 3d_5/2 core lines, and the VBM with composition across the Cs₂SnX₆ series. All shifts are calculated relative to the binding energies observed in Cs₂SnCl₆. Right, the variation in fwhm of the core lines Sn 3d_5/2 (red points) and Cs 3d_5/2 (blue points) with composition.

The valence band and shallow core lines of selected compounds in the bromide–iodide series are shown in Figure 6. The position of the low binding energy valence band edge, the valence band maximum (VBM), was determined here by fitting a Heaviside step function to the low binding energy valence band edge, with boundaries at −5 eV binding energy, representing the instrumental background, and the spectral maximum of each valence band. The position of the VBM was then defined as the point of intersection between the tangent to the step function and the horizontal portion of the step function. This method was chosen to achieve a consistent way to determine of the VBM across the composition range studied here and is not based any physcial modeling of the density of states at the top of the VB. In Cs₂SnCl₆, the VBM binding energy was 3.4 eV, while for Cs₂SnBr₆ it was 2.5 eV, and for Cs₂SnI₆ it was 1.2 eV. Thus, moving from Cs₂SnCl₆ to Cs₂SnI₆ causes a 2.2 eV decrease in the VBM position relative to the Fermi level (Figure 5). That this is considerably more than the shift seen in the core lines is perhaps unsurprising as the orbital makeup of the VB changes with composition whereas that of the core lines does not.

Figure 6.

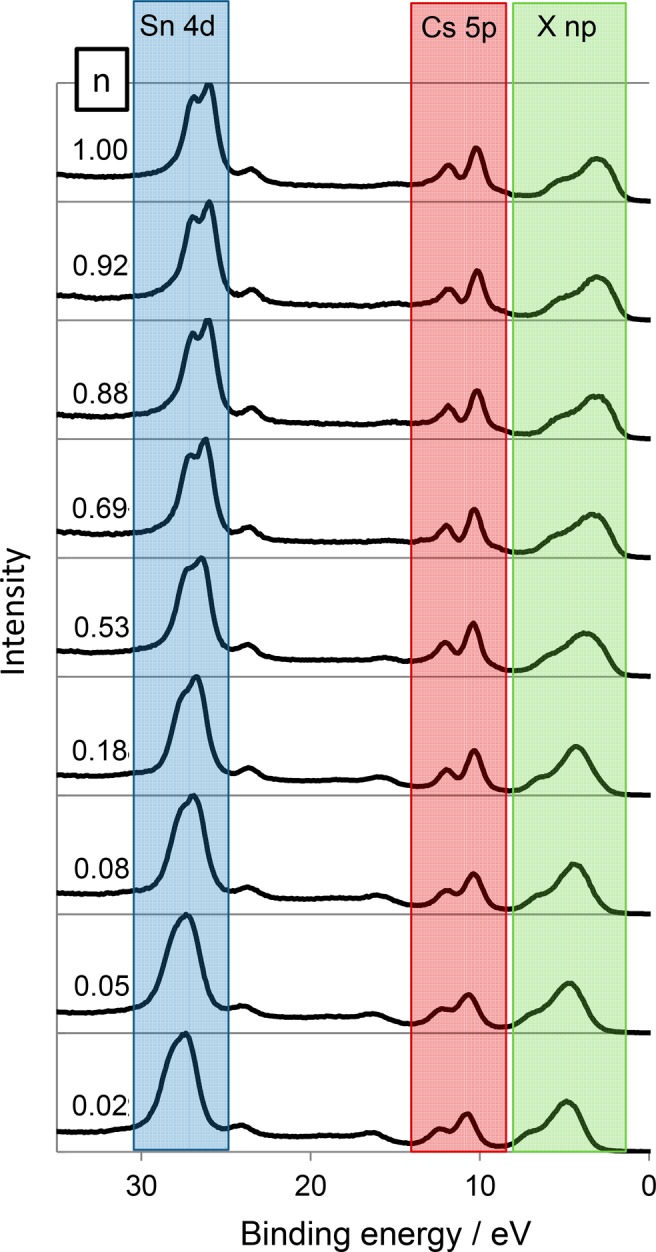
Offset valence band spectra of Cs2Sn(I_nBr_1–n)₆. The zero point on the binding energy scale corresponds to the Fermi Level. The main contributions from different orbitals are indicated: X np represents the valence p orbitals of the halide ions. It can be seen that the Sn 4d peaks decrease in binding energy with increasing n, whereas the Cs 5p binding energies are almost constant.

Because binding energies are referenced to the Fermi Level, changes in the binding energy of XPS peaks can be a convolution of Fermi energy change and chemical shift.⁸⁶ It is known from the binary halides CsCl, CsBr, and CsI that the Cs 3d_5/2 binding energy shows almost no variation as the halide is changed,⁸⁷ which are results we replicated on the spectrometer used here. This suggests that the chemical shift of the Cs 3d peaks when bound to different halides is minimal or that Fermi level changes and chemical shifts cancel out. It may be then that the variation we see in Cs 3d_5/2 binding energy (Figure S7), that correlates with the multiplicity of SnX₆ octahedral environments present, is indicative of a Fermi level change. This effect is small and requires further study for a definitive conclusion. The decreasing binding energy of the Sn orbitals with increasing halide mass could suggest a reduction in the positive charge on the Sn ion and hence reduction of the polarity of the Sn–X bonds with increasing mass of X, which would agree with recent computational and Mossbauer spectroscopy results.¹⁵

The fwhm of the core lines was measured as a function of composition. The fwhm of the Sn and Cs core lines decreased significantly with increasing halide mass, with the largest fwhm being observed for Cs₂SnCl₆ and chloride-rich members of the chloride–bromide series (Figure 5). This change can also be seen in the shallow core lines in Figure 6. Changes in fwhm in XPS core lines may be due to the presence of multiple chemical environments, phonon broadening, or presence of certain electron energy loss mechanisms such as plasma absorption of free carriers.^88,89 Raman analysis suggests that in the mixed halide samples, a range of different Sn environments exist with different halide coordination. As concluded by the Raman spectroscopic study, at the middle of each composition series the multitude of Sn environments is greatest, so it is interesting to note that the fwhm of the Sn core lines does not show a maximum at the middle of each series and instead decreases steadily from Cs₂SnCl₆ to Cs₂SnI₆, a trend mirrored in the Cs 3d core line. This shows that the Sn core line width is not primarily determined by the range of Sn coordination environments present, at least for these samples. It could be that the binding energy of a particular Sn⁴⁺ ion core line is influenced by more than the first coordination sphere, or it could be that Sn⁴⁺ shows little XPS chemical shift when coordinated with different halides, although this latter interpretation is in contrast with conventional interpretation of Sn 3d peaks, discussed above. A third possibility is that the Sn environments near the surface (probed by XPS) are not similar to those in the bulk (probed by Raman), although it seems likely that given the compositions measured, that there must be some distribution of Sn environments at the surface. Vibrational broadening in XPS peaks is increases roughly linearly with bond vibration frequency for stretching vibrations,^88,90,91 and therefore it would be expected that the contribution of the vibrational motion of the ions to the XPS core line fwhm would decrease moving from lighter to heavier halides, as is observed here. Thus, it appears the line widths we observe are dominated by phonon broadening rather than the multiplicity of chemical environments present.^91,92

Optical Absorption

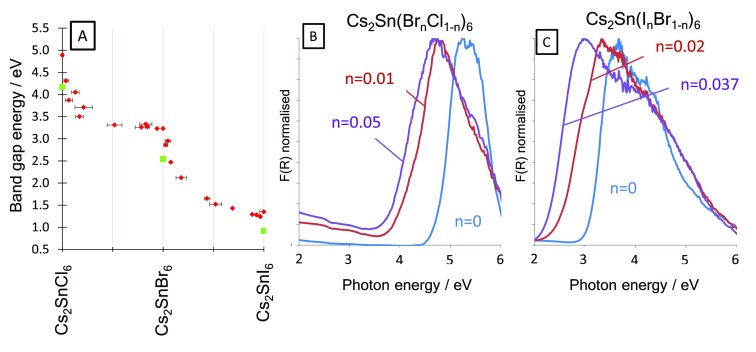
The optical absorption of the compounds was studied by diffuse reflectance spectroscopy. Each sample showed a band edge, and the direct optical band gap, E_opt, was calculated using the Tauc method. The optical band gaps of the pure halide compounds Cs₂SnCl₆, Cs₂SnBr₆ and Cs₂SnI₆ were found to be 4.89 eV, 3.23 and 1.35 eV respectively, spanning from the ultraviolet (UV) to the infrared (IR). Previous reports place E_opt of Cs₂SnI₆ close to 1.3 eV, consistent with our measurement,^22,26 although larger band gaps for quantum confined particles have been reported.²⁵ Cs₂SnI₆ films grown by vapor deposition, however, showed somewhat different optical and electronic properties compared with our powder samples.³⁰ Saparov et al. reported Cs₂SnI₆ thin films with E_opt = 1.68 eV. Previous reports have placed the Cs₂SnBr₆ optical band gap at 2.9–3.0 eV.^15,22 The Cs₂SnCl₆ optical band gap has been reported as 3.9 to 4.66 eV,^15,22,63,93 the lowest to these is around 1 eV different from our measured value. Regarding the previous measurement of the band gap of Cs₂SnCl₆ as 3.9 eV, we note that this was carried out on a film of the material on glass,²² which itself has a strong absorption edge at 4.0 eV. As described below, we measured several mixed halide compounds close in composition to Cs₂SnCl₆ as powders, and as all showed a band gap well above 4 eV (see Figure 7), we conclude that the true optical band gap of Cs₂SnCl₆ is considerably larger than 3.9 eV.

Figure 7.

(A) Optical band gaps (red points) and our calculated fundamental band gaps for pure halide compounds obtained from DFT (green squares). Diffuse reflectance spectra treated by the Kubelka–Munk function for Cs₂SnCl₆ and lightly Br doped Cs₂SnCl₆ (B) and Cs₂SnBr₆ and lightly I doped Cs₂SnBr₆ (C). A considerable band gap narrowing was observed upon small additions of the heavier halide in both cases.

In the mixed phase compounds, the optical band gaps are considerably lower than expected from a linear extrapolation between the pure halide compounds (Figure 7). Band gap bowing is known in mixed halide perovskites such as MAPb(Br_xI_1–x)₃,⁹⁴⁻⁹⁶ and in perovskites with mixed cations,⁹⁷ but is seen to a much greater degree in the Cs₂SnX₆ compounds studied here, where addition of a small amount of Br to Cs₂SnCl₆ and a small amount of I to Cs₂SnBr₆ led to a large reduction in E_opt. For example, the compound Cs₂SnCl_5.6Br_0.4 has an E_opt = 3.87 eV, a decrease of over 1 eV compared with Cs₂SnCl₆. In the Cs₂Sn(Br_nCl_1–n)₆ series, the optical band gaps of the mixed halide compounds all fall between those of the end members. However, in the Cs₂Sn(I_nBr_1–n)₆ series for iodide-rich samples with n = 0.88, 0.93, and 0.96, the band edge is at a lower energy than Cs₂SnI₆ with optical band gaps of 1.29, 1.28, and 1.24 eV, respectively, slightly lower than our pure iodide compound with an optical band gap of 1.35 eV (Figure S11, Supporting Information). We also note that in the mixed phase compounds there is greater optical absorption below the band edge. The nature of the optical measurements we carried out on these powders does not allow quantitative measurement of the absorption coefficient, so it cannot be stated definitively that the sub band gap optical absorption is greater in the mixed anion samples. But, if this is the case, it may be due to disorder tailing which is well-known in hybrid perovskite systems.⁹⁸ In any case, we believe the optical band edge is clear in each sample we report, so the influence of this sub band gap absorption need not affect our conclusions on the optical band gap trends.

The very large deviation from linearity of E_opt with composition may be explained by considering the nature of the band gap in the series, and we return to our computational results to help understand this. The Fm3̅m pure halide compounds possess a center of inversion at the Sn metal. While we index our diffraction patterns from the mixed halide in the Fm3̅m structure by assuming a mixture of halides on the anion site, many of the Sn coordination environments revealed by Raman spectroscopy lack a center of inversion. For each of the pure halide compounds, we calculate that the VBM to CBM transition is symmetry disallowed due to the inversion symmetry, and the optical band gap in fact arises from transitions five bands below the VBM (VBM-5) to the CBM. We calculate the fundamental (VBM to CBM) band gap of Cs₂SnI₆ to be 0.92 eV (this has been calculated by others as 0.88 eV using GW0 calculations)⁶ and the optical absorption (VBM-5 to CBM) to be 1.26 eV, matching well with our experimental value of 1.35 eV.

We now turn to the calculations on mixed halide compounds, and emphasize that the calculations were not intended to simulate the actual halide distribution found in the synthesized samples, but to study the effect of changing coordination of the Sn metal ions. Thus, our simulation of Cs₂SnBr₅I₁ contains only [SnBr₅I₁]^2– octahedra, rather than the distribution of octahedra that would be found in a real sample of that composition. We calculated the fundamental and optical band gaps of the pure halide compounds and those where one halide has been replaced, i.e. Cs₂SnCl₅Br, Cs₂SnClBr₅, Cs₂SnBr₅I, and Cs₂SnBrI₅; the results are shown in Table S5 (Supporting Information) and summarized here. Our calculations show that substituting one halide in the coordination sphere with a heavier or lighter halide causes the fundamental band gap (VBM-CBM) to become optically allowed due to reduction in symmetry around the Sn ion. In the case of Cs₂SnBr₅I₁, the optical band gap is calculated as 1.93 eV, almost 1 eV below that calculated for Cs₂SnBr₆ (2.85 eV). Similarly, Cs₂SnCl₅Br₁ has an optical band gap of 3.82 eV compared with 4.50 eV in Cs₂SnCl₆. These results match with our experimental observation of large band gap decreases upon incorporation of a small amount of a heavier halide. A similar situation occurs with Cs₂SnBr₁I₅ and Cs₂SnCl₁Br₅; in both cases, the calculated optical bandgap is smaller in the mixed halide compared to the closest pure halide compound. As well as the symmetry effects we describe, other contributions to the band gap bowing are possible; Prasanna et al. observed band gap bowing upon cation substitutions into MAPbI₃, where substitution of Cs on the A site led to band gap bowing with a total variation of 0.5 eV. This was explained by the influence of the A site cation on orbital overlap of the halide anions and the octahedral tilting.⁹⁷ We do not observe octahedral tilting by XRD, but it may occur locally. However, it is notable for the chloride–bromide series, as Br is substituted into Cs₂SnCl₆, the separation of octahedra does not increase despite the octahedra themselves increasing in size, at least up to ca. 50% Br (Figure 1). Thus, it might be expected that the overlap between anion orbitals on neighboring octahedra increases with increasing Br content more than would otherwise be expected, which might also contribute to the large band gap decreases observed in lightly Br doped Cs₂SnCl₆.

Lastly, we comment on the position of the Fermi level relative to band edges in these compounds. The calculated defect energies for Cs₂SnI₆ were found to favor donor V_I and Sn_i defects, suggesting that the pure iodide compound at least may be n-type with a Fermi level close to the conduction band minimum.⁹⁹ A measure of E_VBM relative to the Fermi level can be obtained from XPS; as shown above in Figure 5, the binding energy of the VBM decreases approximately linearly with composition across both chloride–bromide and bromide–iodide Cs₂SnX₆ series. If it were the case that all of these compounds similarly had a Fermi level close to the conduction band minimum, then the E_VBM derived from XPS would be a good approximation of the fundamental band gap. If however the E_VBM was significantly below the fundamental band gap, this would imply that the Fermi level in that material was within the bandgap further from the CBM, i.e. that the material is less strongly n-type. In accordance with previous defect energy calculations, we find that the E_VBM for Cs₂SnI₆ is 1.15 eV, close to the calculated fundamental band gap 0.92 eV, suggesting that the material as produced here is n-type. The E_VBM for Cs₂SnBr₆ is 2.45 eV, slightly below the calculated fundamental band gap of 2.85 eV. Lastly, the E_VBM of Cs₂SnCl₆ is 3.37 eV, and the fundamental band gap is 4.17 eV. Thus, moving from Cs₂SnI₆ to Cs₂SnBr₆ to Cs₂SnCl₆, the Fermi level as measured by XPS moves away from the CBM toward the center of the band gap, which can be interpreted as the material becoming less n-type with decreasing halide mass.

Conclusions

We have studied the structural, optical, and electronic properties of mixed halide A₂SnX₆ compounds, which are important emerging photovoltaic materials. We identify and quantify a new distortion mode in these compounds that does not result in loss of cubic symmetry but nonetheless alleviates size mismatch among constituent ions. We use a Raman spectroscopy method to quantify the concentrations of the various Sn coordination environments in the mixed halide compounds. To a first approximation, we find that these match well with the distribution expected if the halide ions were randomly distributed. In the Cs₂Sn(I_nBr_(1–n))₆ series there is some evidence of a preference for iodide ions being trans to each other, probably driven by the large ionic radius of iodide. A large degree of optical band gap bowing is observed in both Cs₂SnX₆ series studied, despite the fact that the variation in valence band maximum energy is roughly linear with composition. Hybrid density functional theory calculations reveal this is due to local symmetry breaking that causes the dipole disallowed fundamental band gap to become optically active.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.chemmater.9b03267.

• Tables of crystallographic data, further discussion of the geometric aspects of A₂BX₆ structure, further discussion of calculation of halide distribution based on a probabilistic model, discussion of generation of computationally derived Raman spectra for mixed halide compounds, and tabulations of optical spectra and comparison with computational band gaps (PDF)

The authors declare no competing financial interest.