Information-Limiting Correlations in Large Neural Populations

Understanding the neural code requires understanding how populations of neurons code information. Theoretical models predict that information may be limited by correlated noise in large neural populations. Nevertheless, analyses based on tens of neurons have failed to find evidence of saturation. Moreover, some studies have shown that noise correlations can be very small, and therefore may not affect information coding.

Abstract

Understanding the neural code requires understanding how populations of neurons code information. Theoretical models predict that information may be limited by correlated noise in large neural populations. Nevertheless, analyses based on tens of neurons have failed to find evidence of saturation. Moreover, some studies have shown that noise correlations can be very small, and therefore may not affect information coding. To determine whether information-limiting correlations exist, we implanted eight Utah arrays in prefrontal cortex (PFC; area 46) of two male macaque monkeys, recording >500 neurons simultaneously. We estimated information in PFC about saccades as a function of ensemble size. Noise correlations were, on average, small (∼10⁻³). However, information scaled strongly sublinearly with ensemble size. After shuffling trials, destroying noise correlations, information was a linear function of ensemble size. Thus, we provide evidence for the existence of information-limiting noise correlations in large populations of PFC neurons.

SIGNIFICANCE STATEMENT Recent theoretical work has shown that even small correlations can limit information if they are “differential correlations,” which are difficult to measure directly. However, they can be detected through decoding analyses on recordings from a large number of neurons over a large number of trials. We have achieved both by collecting neural activity in dorsal-lateral prefrontal cortex of macaques using eight microelectrode arrays (768 electrodes), from which we were able to compute accurate information estimates. We show, for the first time, strong evidence for information-limiting correlations. Despite pairwise correlations being small (on the order of 10⁻³), they affect information coding in populations on the order of 100 s of neurons.

Introduction

Understanding information coding in the brain has long been one of the goals of systems neurophysiology (Adrian, 1928; Bullock, 1959; Perkel and Bullock, 1969; Rieke et al., 1997). Much of our knowledge about coding comes from single-neuron studies. However, it is clear that labeled line codes, feature detectors, and other properties of single cells cannot account for perception (Paradiso, 1988), decision making (Beck et al., 2008), or motor control (Sparks et al., 1976; Georgopoulos et al., 1986; Lee et al., 1988). Therefore, to understand the neural code we need to understand the population code.

Theoretical and experimental studies on population coding have often focused on correlations between neurons, specifically noise correlations (Gawne and Richmond, 1993), and their effects on information coding (Averbeck and Lee, 2004; Kohn and Smith, 2005; Averbeck et al., 2006a; Cohen and Kohn, 2011; Kohn et al., 2016). Some empirical studies have found correlation coefficients around 0.2 in visual cortex and theoretical studies have shown how these correlations can limit information in large populations of neurons (Zohary et al., 1994; Abbott and Dayan, 1999; Kohn and Smith, 2005). However, another line of research has shown that correlations in populations of cortical neurons, under some conditions, can be around 0.01 (Averbeck and Lee, 2003; Ecker et al., 2010) or even 0 (Renart et al., 2010). Correlations of this magnitude may be too small to have a substantial effect on information coding. However, theoretical work has shown that even small correlations can limit information in large populations (Moreno-Bote et al., 2014). Information-limiting correlations can be hard to measure, as they can be mixed within stronger, non-information-limiting correlations (Moreno-Bote et al., 2014). Therefore, it is unclear whether the small correlations measured in some systems limit information.

Measuring correlations alone does not show whether they impact information coding, because it is the relation between average population activity and the structure of the noise correlations that affects information. Noise correlations have been shown to increase (Romo et al., 2003; Zavitz et al., 2019), decrease (Chen et al., 2015; Graf and Andersen, 2015), or have minimal effect (Averbeck and Lee, 2003, 2006; Averbeck et al., 2003) on information coding. Across these studies, measured effects have been modest, and they were estimated in small ensembles of at most 10 s of neurons. Theoretical work has suggested that noise correlations can lead to information saturation in large populations (Zohary et al., 1994; Abbott and Dayan, 1999). Also, populations of 100 s of neurons would be required to see an effect of noise correlations on information coding (Sompolinsky et al., 2001; Shamir and Sompolinsky, 2004). They have also shown that the impact of correlated noise depends specifically on the presence of information-limiting correlations (Moreno-Bote et al., 2014; Kanitscheider et al., 2015a). For instance, in a population of completely independent, homogeneous neurons, information scales linearly with the number of neurons. However, the presence of information-limiting correlations limits the amount of information that the population can encode, because these correlations cannot be averaged out by any decoding mechanism, leading to sub-linear scaling with population size.

We implanted eight Utah arrays in area 46 of macaque prefrontal cortex (PFC), bilaterally. We were able to record from up to 828 neurons simultaneously, which allowed us to estimate information in the regime in which theoretical studies have suggested that correlations should impact information. Information was estimated using a simple binary task because accurate information estimates require a large number of trials per condition (Averbeck, 2009), and information metrics that assess the impact of noise correlations are only defined for binary decisions (Arndt, 2001), or locally in the case of Fisher information for a continuous variable (Kay, 1993). In addition, PFC neurons respond well to eye movements (Averbeck et al., 2006b; Seo et al., 2012) and it contains many neurons that have poly-synaptic oculomotor projections (Moschovakis et al., 2004). Therefore, a large fraction of neurons was active during the task.

Materials and Methods

Procedures.

All experimental procedures were performed in accordance with the ILAR Guide for the Care and Use of Laboratory Animals under a protocol approved by the NIMH Animal Care and Use Committee. Two male monkeys (Macaca mulatta; Monkey W: 6.7 kg, age 4.5 y; Monkey V: 7.3 kg, age 5 y) were used as subjects in this study. All analyses were performed using custom-made scripts for MATLAB (The MathWorks).

Task.

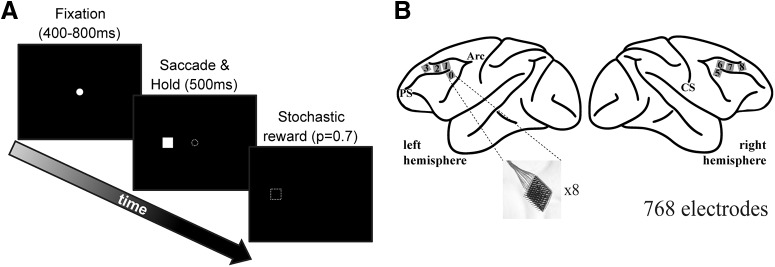
Monkeys were trained to perform left or right saccadic eye movements. The animals were comfortably seated in front of a computer screen. Each trial started with the presentation of a fixation dot on the center of the screen that the monkeys were required to fixate. After a variable time (400–800 ms) had elapsed, the fixation dot was toggled off and a target (white square, 2° × 2° side) was presented either to the left or right of the fixation point. The monkeys had to make a saccade toward the cue and hold for 500 ms. Seventy percent of the correctly performed trials were rewarded stochastically (see Fig. 1A) with a drop of juice (daily total 175–225 mL). Typically, monkeys performed >1000 correct trials in a recording session. All behavioral parameters were controlled using the open source MonkeyLogic software (http://www.brown.edu/Research/monkeylogic/).

Figure 1.

Task and recording sites. A, Schematic of the saccade task. The animals were required to fixate centrally and after a variable fixation time the fixation spot was toggled off at the same time a target was presented either to the left or right. The animals then made a saccade toward the target and were required to hold the target for 500 ms to successfully complete a trial. Stochastic reward (p = 0.7) was delivered for correct trials. B, Location of the 8 microelectrode arrays on the prefrontal cortex, surrounding the principal sulcus. Each array had 96 electrodes in a 10 × 10 arrangement. Numbers on the gray squares are an example of categorical distance, from the array located ventrolateral to the caudal end of the principal sulcus of the left hemisphere (labeled 0). PS, principal sulcus; Arc, arcuate sulcus; CS, central sulcus.

Data acquisition and preprocessing.

Microelectrode arrays (BlackRock Microsystems) were surgically implanted over the PFC surrounding the principal sulcus (see Fig. 1B). Four 96-electrode (10 × 10 layout) arrays were implanted on each hemisphere. Details of the surgery and implant design have been described previously (Mitz et al., 2017). Briefly, a single bone flap was temporarily removed from the skull to expose the PFC, and then the dura mater was cut open to insert the electrode arrays into the cortical parenchyma. The dura mater was then sutured, and the bone flap sewn back into place with absorbable suture, thus protecting the brain and the implanted arrays. In parallel, a custom-designed connector holder, 3D-printed using biocompatible material, was implanted onto the posterior portion of the skull.

Recordings were made using the Grapevine System (Ripple). Two neural interface processors (NIPs) made up the recording system, one NIP (384 channels each) was connected to the 4 multielectrode arrays of each hemisphere. Behavioral codes from MonkeyLogic and eye tracking signals were split and sent to each Ripple box. The raw extracellular signal was high-pass filtered (1 kHz cutoff) and digitized (30 kHz) to acquire single unit activity. Spikes were detected online and the waveforms (snippets) were stored using the Trellis package (Grapevine). Single units were manually sorted offline.

We collected data in four recording sessions (two sessions per animal). ANOVAs were applied to the single-unit data to assess task responsiveness (main effect of task epoch: fixation period vs saccade and hold period) and saccade direction selectivity (sliding window 300 ms, 20 ms steps, saccade and hold period, main effect saccade direction). Separately, spike-train vectors with a 1 ms resolution were built on a trial-by-trial basis for each sorted unit. Spike trains were aligned and trimmed to span from 0 to 600 ms after cue onset.

Comparison of covariance.

To compare two covariance matrices, we used S statistics (Garcia, 2012). Briefly, the S statistics index the overall difference (S1 = S2 + S3) between two covariance matrices (A and B) by estimating the difference in orientation (S2) and shape (S3) of the hyperellipses specified by the matrices. The estimates are based on the projection of the covariance matrix A onto the eigenvectors of the covariance matrix B, thus reflecting the amount of shared variance and the angle between corresponding eigenvectors. The index takes values ranging from 0, when the two samples have identical covariance, to 8 in the extreme case in which all the variance of both samples is explained by only one eigenvector, and the eigenvector sets of matrices A and B are orthogonal to each other.

Decoding analysis.

We used a support vector machine (SVM; Matlab statistics toolbox) to decode saccade direction from the neural data. We regularized the SVM by decreasing the value of the soft margin violation penalty coefficient, thus allowing more margin violations, until the decoding accuracy of a test set started to decrease, and then kept the previous value. For cross-validation, we split the data into three subsets of randomly selected trials: (1) A training set (90% of the trials) was used to train the SVM, (2) a testing subset (5% of the trials) was used for regularization, and (3) a reporting subset (5% of the trials) was used to make predictions and measure information (see below). We used 20 different splits for cross-validation.

We tested three different kernels: linear, quadratic polynomial, and radial basis function. We observed that the quadratic polynomial yielded slightly higher information values (see Fig. 4), which resulted in a significant increase (z-test, p < 0.001) of saturation values (Eq. 3). Hence, we report results obtained using a quadratic polynomial kernel.

Figure 4.

Comparison of different SVM kernels. Information measures obtained using three different kernels for the SVM classifier: linear and quadratic polynomials, and radial basis function (RBF). Decoding analyses for d² estimations as a function of ensemble size (number of neurons) were performed for each animal/session and using both unshuffled data and shuffled data. n = 500 ensembles of each size randomly drawn from the full recorded population.

Information measure.

We used the squared value of the discriminability index d′ as a measure of information. To calculate d², we generated distributions of the values of the SVM scores (distance to the boundary) separately for each saccade direction. Then, we fit a Gaussian function to each distribution (least squares). The estimated mean and SD of each Gaussian (μ, σ) were used to calculate, using the error function (erf in Matlab), the probability of decoding correctly any given trial (P). In other words, the fraction of the area under the curve on the same side as the μ parameter with respect to the decision boundary, averaged for the two directions. We then calculated d² using the following equation:

where erf⁻¹ is the inverse of the complementary error function (Averbeck and Lee, 2006). We also computed d² using the difference in the means of the two distributions, and a pooled estimate of their SD, with the following equation:

When we computed d² with a pooled estimate of the SD, information also saturated. However, the values of d² from Equation 1 were larger. In addition, it was frequently the case that the SDs of the two Gaussians were not the same. Therefore, we adopted the numerical technique as it was more accurate.

Projection of information to a population of infinite size.

We estimated the maximum amount of information in an ensemble of infinite size by using the d² values as a function of ensemble size to fit the saturating function (Zohary et al., 1994; Abbott and Dayan, 1999) as follows:

where S is the ensemble size, b is the asymptotic information, and a is the saturation rate. Furthermore, if λ is a fraction of the asymptotic information (λ = d(S)²/b), then, the ensemble size needed to encode a given λ is given by the following:

Results

Representation of saccade direction in area 46 neural activity

Previous studies of information scaling and correlated activity have been largely theoretical with few exceptions reporting recordings of small populations, the largest in the range of ∼50 neurons. To address how information scales with ensemble size and the impact of correlated activity in large populations of neurons, we trained 2 male macaques to perform a saccade direction task (Fig. 1A). The animals were required to acquire a fixation point at the center of the computer screen. After a variable time (400–800 ms) a target was presented either to the left or right of the fixation point. Then, they had to make a saccade toward the target and hold for 500 ms. While the monkeys performed this task, we recorded the extracellular activity of neural populations in the prefrontal cortex (PFC area 46). We were able to simultaneously record between 510 and 828 units using 8 microelectrode arrays (Fig. 1B). Across 4 sessions, two from each animal, we recorded from 902659 pairs of neurons. The choice of a simple task was important to ensure that we were extracting as much information as possible by collecting as many trials per condition as possible. The number of completed trials per recording session varied between 1187 and 2383. Saccade reaction times from cue onset had a mean of 212.95 ms and a SD of 34 ms. The lower, middle, and upper quartiles were 192, 207, and 225 ms, respectively.

Recorded neurons were evenly distributed across the left and right hemispheres (left: 50.70 ± 0.71% and right: 49.29 ± 0.71%, mean ± SD). We observed a broad diversity of activity profiles in single neurons, including differential responses to the saccade direction after cue onset. The latter included neurons responding preferentially to a given saccade direction, left or right, by either increasing or decreasing their firing rate (Fig. 2A). An ANOVA comparing the average firing rate before and after cue onset revealed that 78.8 ± 6.9% (mean ± SD) of the recorded neurons responded to the cue presentation. Furthermore, when an ANOVA on a sliding window of 300 ms (steps of 20 ms) was performed, we found a significant effect of saccade direction on the firing rate in at least one window after cue onset for 50.8 ± 6.9% (mean ± SD) of the recorded neurons (Fig. 2B–D). Despite a systematic increase in response latency across array locations (Fig. 2C,D), we observed that the largest difference in the response occurred within the first 500 ms after cue onset, which would include the saccade and the post-saccade hold period. Hence, we focused further analyses on this period since it contained most of the information about the saccade direction. To decode saccade direction from neural activity we used spike counts in bins of different sizes centered at different times within the 500 ms window.

Figure 2.

Neural responses. A, Raster plots of two example single cells with saccade direction selective activity. Each row of blue ticks represents the spikes during a trial. Red dots along each line represent trial start, cue onset, reward time and end of trial. Trials are aligned to cue onset and sorted by saccade direction. B, Venn diagrams illustrating the proportion of units responsive to the task. Blue circles represent neurons that significantly changed their activity between the fixation and the saccade and holding epochs of the task, tagged as “Task Responsive” (ANOVA, epoch wide firing rate, p < 0.05). Red circles represent units with a significant effect of saccade direction at any point during the saccade and hold epoch (ANOVA, 300 ms sliding window, p < 0.05). White circles indicate the total number of neurons recorded in each session (two sessions from each animal, Monkey W and Monkey V). C, Fraction of neurons responsive to saccade direction during trial execution at each array location. Spike counts from a 100 ms bin moving in 10 ms steps were used as dependent variable for an ANOVA with “direction” as factor. Results were pooled across hemispheres. Array numbers in legend correspond to those shown in Figure 1B. Plots show means ± SEM across the four sessions. D, Effect magnitude during trial execution measured as the negative logarithm of the p-value calculated from the ANOVAs. Same conventions as in C.

Neuronal responses show correlated variability

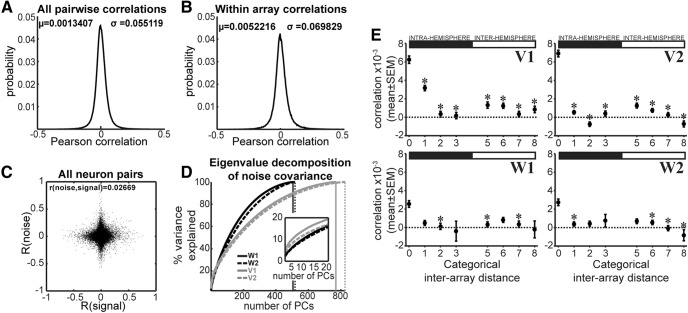
To determine whether neural correlations have an impact on the information encoded by an ensemble, we first assessed the correlations between pairs of neurons. Spikes were binned within 500 ms from cue onset and the Pearson correlation of trial-to-trial variability (noise) was estimated for all pairs of simultaneously recorded cells in each session. We found, across all data, that pairwise noise correlations were symmetrically distributed with a mean close to zero (Fig. 3A), and similar results were obtained restricting correlation measures to pairs within the same array (Fig. 3B).

Figure 3.

Noise correlations. A, Distribution of pairwise correlation coefficients. All possible pairs of simultaneously recorded neurons are included (n = 902659), and all recording sessions were pooled. B, Distribution of pairwise correlation coefficients including only same-array pairs of neurons (n = 125,552). All recording sessions were pooled. C, Noise correlations as a function of signal correlations. For individual sessions, the coefficient (mean ± SD) was 0.036 ± 0.017. Across all sessions, r = 0.02669 (p = 2.57 × 10⁻¹⁴¹). All correlations are Pearson coefficients. D, Scree plots from an eigenvalue decomposition of the noise covariance matrices illustrating the cumulative percentage of variance explained as a function of the number of principal components. The inset is a close up of the first 20 principal components. Vertical solid and dotted lines indicate the total number of components for each curve. E, Average correlation coefficient split by categorical-distance for each animal (V, W) and session (1, 2) separately. Categorical distance 0 indicates that the two units were recorded on the same multielectrode array, 1 indicates units were recorded in adjacent arrays, and so on. For interhemispheric distances, 5 indicates units recorded in location-matching arrays, 6 indicate units in adjacent to location-matching arrays, etc. (see example in Fig. 1B). Asterisks indicate a significant difference with respect to pairs recorded in the same array (U test, p < 0.05).

To rule out the possibility that noise correlations were decreased due to pooling neurons with different selectivity (i.e., stimulus responsive vs saccade responsive), we analyzed the noise correlation in 125 ms bins both starting at cue onset and at saccade start. These bins, when aligned to cue onset, do not cover the period of saccade execution. The correlation coefficients were similar between cue-aligned data (μ = 0.00056, σ = 0.033) and saccade-aligned data (μ = 0.00077, σ = 0.035). The decrease in the correlation values for the 125 ms bin aligned to cue onset, compared with those obtained for the cue-aligned 500 ms bin, is likely to be the result of using a shorter time bin (Cohen and Kohn, 2011).

Splitting the data by saccade direction resulted in similar correlation matrices for both left and right saccades. We compared the underlying covariance matrices using S statistics (Garcia, 2012) as described in the methods section. There was a small orientation difference between the left and right noise covariance matrices (S_rotation ± SD = 0.0046 ± 0.0011), while the difference in the shape of the hyper-ellipses defined by the covariance matrices was negligible (S_shape ± SD = 0.00005 ± 0.00001). The values of the S statistics imply that the main difference between the two covariance matrices is the angle between corresponding eigenvectors and that this difference is very small. Furthermore, we examined whether noise and signal correlations were related (Fig. 3C) and found that there was a significant correlation (r = 0.0267, p = 2.57 × 10⁻¹⁴¹). We further characterized the structure of the noise covariance by performing an eigenvalue decomposition (Fig. 3D) that included all the neurons recorded in each individual session (Fig. 2B).

Next, we split correlations according to the categorical distance between pairs of neurons. We assigned 0 to pairs recorded in the same multi-electrode array, 1 to pairs recorded in adjacent arrays, and so on. Likewise, a categorical distance of 5 was assigned to neurons recorded in location-matching arrays (as they were approximately symmetrically placed on the two hemispheres) but on opposite hemispheres, whereas a distance index of 6 meant that the neuron pair was recorded by an array adjacent to the location-matching array on the opposite hemisphere and so on (Fig. 1B). In agreement with previous reports (Smith and Kohn, 2008; Rosenbaum et al., 2017), we found that correlation decreased with increased distance (Fig. 3E). The lowest correlations were found for pairs of neurons located in different hemispheres. Overall, mean correlations were very small. However, such small correlations can have substantial impacts in large populations as shown below.

Correlated noise limits information encoded by neural ensembles

Next, we addressed the impact of noise correlations on information. To assess information scaling, we performed a decoding analysis on neural data from ensembles ranging from 10 to 700 neurons. We built each ensemble by taking a random subset out from the whole simultaneously recorded population and fitting an SVM classifier with a quadratic polynomial kernel to the subset. The quadratic kernel performed best (Fig. 4), consistent with the slight rotation of the covariance matrix across saccade directions. This procedure was repeated 1000 times for each ensemble size. We evaluated the decoding accuracy (proportion of correctly decoded trials) as a function of the number of neurons in the ensemble. The analysis was carried out on intact and trial-shuffled data. Shuffling trials destroys the noise correlations and provides an estimate of information in a non-simultaneously recorded population, as well as a reference against which the effects of correlations can be compared.

We found that the decoding accuracy increased rapidly with ensemble size (Fig. 5). Shuffling trials, such that noise correlations were eliminated but signal correlations remained intact, substantially increased the accuracy of the decoding, leading to almost perfect decoding with ensembles of size ∼200 or greater.

Figure 5.

Decoding accuracy. Shown is the percentage of correctly decoded test trials as a function of ensemble size. Ensembles of different sizes were built by drawing units randomly from the simultaneously recorded population (without replacement). An SVM decoder was fitted and tested on each ensemble. n = 1000 random samples for each ensemble size. Black lines depict results using normal spike data for decoding, while blue lines depict the results of repeating the analysis after shuffling the spike data across trials of the same type (left or right trials). Solid line is mean; shaded region is SD.

Decoding accuracy is bounded above by 1. However, information can continue to increase, even when perfect performance is achieved in a dataset with finite trials. To examine information scaling, we estimated the information in the population, as a function of ensemble size. To do this we computed the distribution of distances to the classification boundary (Fig. 6). We then fit Gaussians to these distributions. Next, we numerically calculated the fraction of the Gaussian that would have been correctly classified, and converted this estimate to information, d². When we examined scaling of information with population size (Fig. 7) we found linear scaling for the shuffled data, consistent with the fact that information adds in an uncorrelated population. Because we found approximately linear scaling in the trial-shuffled data, as theoretically predicted, we believe we had sufficient trials to estimate information in the data. We also found that information was sublinear in the original data that contained correlations. Similar results were obtained when we used both shuffled and unshuffled data aligned to the start of the saccades, counting spikes in a 500 ms bin that started 200 ms before saccade start (Fig. 7).

Figure 6.

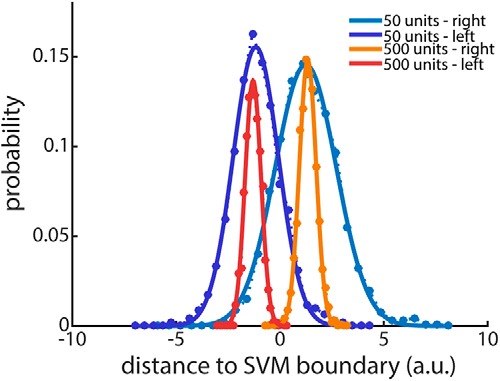
Example of the distribution of the distances to the SVM classification boundary. Data is split by trial type (left, right) and shown for two example ensemble sizes (50, 500 units). Solid lines are Gaussian fits, which were used to calculate the probability of correctly classifying any given trial. The average probability across trial types was used to calculate the discriminability index d² as a function of ensemble size (Eq. 1).

Figure 7.

Information saturation in the presence of correlated noise. Discriminability index (d²) as a function of ensemble size calculated from the response distributions (Fig. 6). All conventions are the same as in Figure 5. n = 1000 samples for each ensemble size. Solid line is mean; shaded line is SD across samples.

Information encoded by neural ensembles of infinite size is affected by bin width

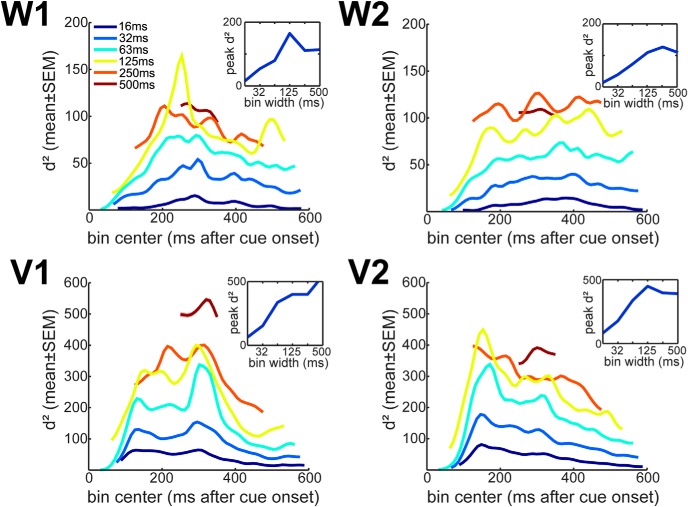
The previous analyses were based on a spike count bin of 500 ms. Therefore, in the next analyses we examined information scaling using smaller windows, and multiple latencies with respect to cue onset. Previous studies have shown that noise correlations increase with bin-size, because most correlated variability in the cortex is due to slow fluctuations (Bair et al., 2001; Averbeck and Lee, 2003) although it has also been shown that correlations decrease for short time bins due to an associated drop in spike counts (Cohen and Kohn, 2011). Consistent with this, we found that the mean correlation increased with bin size (Fig. 8A). To examine the effect of bin size on information, we fit the decoding model to ensembles of multiple sizes, at a series of bin widths, and at a series of times relative to cue onset. For each bin width and time relative to cue onset, this gave us an information scaling curve. Previous theoretical work (Zohary et al., 1994; Abbott and Dayan, 1999) has shown that information scales according to a simple function given by d² = $\frac{bS}{a+S}$, where S is ensemble size, b is the information that would be contained in an infinite population (S = ∞), and a is the scaling rate, or the rate at which information achieves asymptote. We fit this equation to the information scaling curves for each bin width and time. The equation gave excellent fits to these curves (Fig. 8B), which further supports the hypothesis that information saturates. We next examined the infinite population information estimates (i.e., b from Eq. 3), as a function of bin width and time relative to cue onset. When we did this, we found that information increased with bin width up to approximately 250 ms, and then began to decrease, except in one session (Fig. 9). Thus, integrating information over more than approximately 250 ms does not lead to additional information about saccades in prefrontal cortex. In addition, we can estimate the ensemble size that would contain a given fraction of the asymptotic information (see Eq. 4). We estimated that ensembles with ∼10⁵ neurons are required to code 99% of the available information (Fig. 10), the general trend is that population size decreases as bin width increases. However, the estimates of population size were surprisingly consistent across bin widths.

Figure 8.

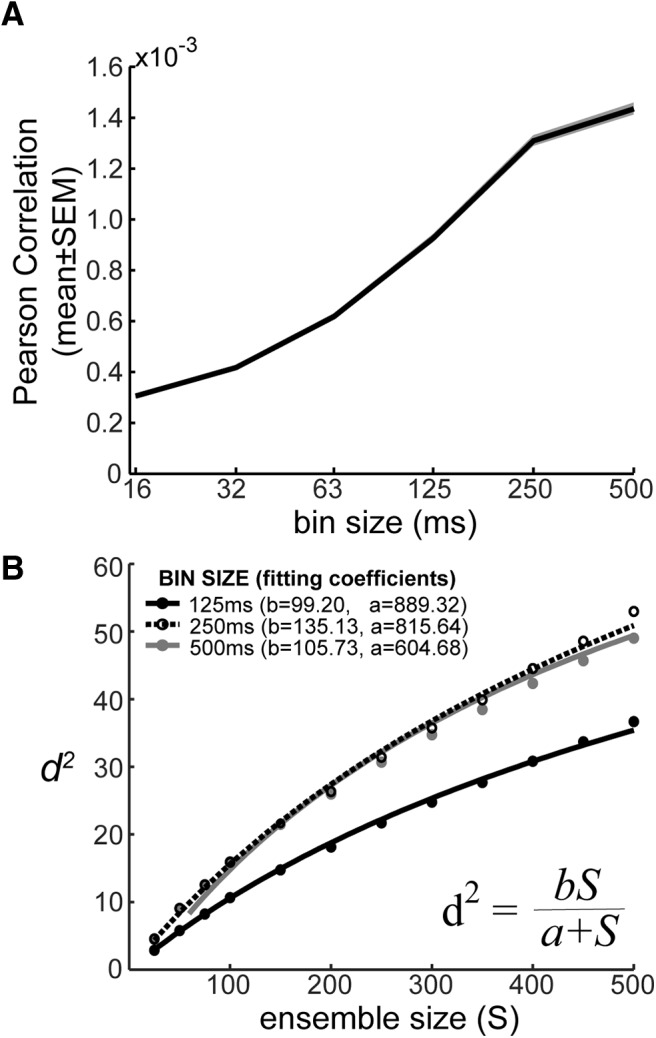
Effect of bin size. A, Effect of bin size on noise correlations. Correlations increase with bin width. B, Projection of information to ensembles of infinite size. Examples of nonlinear fittings to the measured d² values from unshuffled spike data to estimate the information value at the asymptotic level (coefficient b in the equation).

Figure 9.

Asymptotic information value. Information from infinite population is plotted as a function of the lag between the bin center and the time of cue onset, separately for different bin widths. Each panel shows results for an individual recording session. Insets in each panel show the peak of the asymptotic information estimates as a function of bin width. Values shown are means ± SEM across 500 individual fittings (see Fig. 8B).

Figure 10.

Estimated population size to encode 99% of the asymptotic information (S₉₉). Population sizes are plotted as a function of time after cue onset separately for different bin widths as indicated in the legend. All conventions are the same as in Figure 9.

Discussion

This study provides empirical evidence for information saturation in large neural populations. We recorded large ensembles of neurons in area 46 of prefrontal cortex while monkeys executed a visually guided left–right saccade task. We found sub-linear scaling of information as a function of ensemble size, suggesting information saturation. We computed estimates of infinite population information, by fitting a theoretically derived scaling function to our data. We also predicted the population size necessary to achieve 99% of the infinite population information and examined the results as a function of different timescales for binning spikes, at different times relative to target onset. Information increased up to a timescale of approximately 250 ms, and populations of around 10⁵ neurons, depending on the timescale, coded 99% of the information that would be contained in an infinite-size population. Thus, we show that information-limiting correlations are present in prefrontal cortex, and they decrease information relative to an uncorrelated population.

Information coding in neural populations is a complex topic, composed of at least three areas of study, including mixed selectivity/nonlinear basis function encoding (Poggio, 1990; Deneve et al., 2001; Rigotti et al., 2013), low-dimensional dynamics (Ganguli et al., 2008; Yu et al., 2009; Churchland et al., 2012; Mante et al., 2013; Kobak et al., 2016; Williamson et al., 2016), and the role of population activity patterns in information coding, which we study here (Averbeck and Lee, 2006; Averbeck et al., 2006a; Cohen and Kohn, 2011; Cohen and Maunsell, 2011). Theoretical work has made fundamental contributions, defining clear questions and analytical techniques to answer those questions. Early studies identified patterns of activity that differed across stimulus conditions in sensory areas (Gray and Singer, 1989; Dan et al., 1998). Subsequent development of information theory showed that while patterns of correlated activity were sometimes present, they did not add information to the neural code (Panzeri et al., 1999; Martignon et al., 2000; Nirenberg et al., 2001; Pola et al., 2003).

Theoretical work also suggests that correlations may limit information in neural populations (Zohary et al., 1994; Abbott and Dayan, 1999; Sompolinsky et al., 2001; Shamir and Sompolinsky, 2006). Even very small and difficult to measure noise correlations can lead to information saturation in large populations (Moreno-Bote et al., 2014; Kanitscheider et al., 2015a,b). Supporting this, we found small correlations (on the order of 10⁻³) and also found that information scales strongly sub-linearly with ensemble size. A simple model that was previously derived theoretically (Zohary et al., 1994; Abbott and Dayan, 1999) described scaling in our data. Thus, we provide evidence that linear information saturates in neural populations with correlated noise.

Information-limiting correlations have been called f-prime, or differential, noise correlations (Averbeck and Lee, 2006; Moreno-Bote et al., 2014). Linear information is conveyed by changes in the population response for different stimuli, decisions, or actions. A decoder, somewhere within the brain, must discriminate reliably between different patterns of activity. When the noise in the system has the same structure as the stimulus-induced changes, the decoder cannot differentiate between them. Since such noise cannot be eliminated by averaging over neurons, increasing the population size will not increase information.

Several lines of evidence suggest that information-limiting correlations exist in the brain. First, the data processing inequality shows that information cannot be increased by transforming representations (Averbeck et al., 2006a). Thus, the way information is represented can be modified and optimized for decoding at each processing stage (Yamins et al., 2014), but information cannot be increased over the amount present in the inputs. For example, ensembles of retinal ganglion cells shape noise correlations in a stimulus-dependent way, so that correlations do not harm decoding (Franke et al., 2016; Zylberberg et al., 2016). The retina, therefore, has at least as much information as any subsequent stage of visual processing, and relays it to upstream structures with optimized correlations. V1 uses more neurons to represent information than the LGN (i.e., has an expanded dimensionality) but it cannot have more information than the retina. In a motion-direction discrimination task, correlations increase as motion coherence (i.e., information) decreases (Chaplin et al., 2018). Considering this, if information-limiting correlations arise partially because information cannot be increased within the circuit, more complex stimuli or tasks requiring more information would lead to a slower saturation rate, and switch from information-limiting correlations (orthogonal to the decision boundary) to benign correlations (parallel to the decision boundary) (Montijn et al., 2016).

It is unclear how our findings generalize to other brain regions and tasks, given differences in local circuitry, the structure of shared inputs, and the dimensionality expansion seen in early sensory areas that can lead to correlated variability. Similar studies in different brain regions using different tasks are required to clarify this question. For example, classification performance saturates rapidly for our task due to its simplicity and the strength of saccade encoding in dlPFC. Perceptual tasks based on fine discrimination may lead to slower saturation. In addition, we see minimal differences at small population sizes. There are two caveats to this point, however. First, we have carried out our analyses by randomly sampling sub-populations, as we thought this would be the most conservative. In an analysis focused on populations that carried significant information, effects of correlations might emerge at smaller population sizes. Also, information scaling is sub-linear, therefore, assuming shuffled information provides an upper bound, there are differences in smaller populations even though they are not evident in pairwise comparisons.

Previous experiments have shown that noise is related to the underlying circuit organization of cortex (Tsodyks et al., 1999; Kenet et al., 2003; Fukushima et al., 2012; Leavitt et al., 2013). These studies show that spontaneous activity “looks like” stimulus driven activity (i.e., noise has the same shape as the signal). This has been interpreted in numerous ways. However, feedforward processing that increases the dimensionality, or recurrent connectivity that implements attractor computations (Seriès et al., 2004), both lead to noise with signal-like structure (Rosenbaum et al., 2017). Therefore, it is unclear how to implement a computational system that will not generate information-limiting correlations at some processing stage, because noise in a system that is transforming its inputs, when the inputs are stochastic, will reflect the nature of the computation.

Studies on attention have shown that attending to a visual cue decreases noise correlations in a way that increases information readability (Cohen and Maunsell, 2009, 2011; Ruff and Cohen, 2014). At a population level, these effects are much larger than changes in mean responses associated to attention. Therefore, manipulations that increase behavioral performance also decrease information-limiting noise correlations. Similar results have been seen following perceptual learning (Gu et al., 2011). And both learning and attention affect correlations (and performance) in a similar way (Ni et al., 2018). Furthermore, the representation of a saccadic target in the PFC seems to be dynamically enhanced before saccades, in association with selective changes in noise correlations (Dehaqani et al., 2018). Also, modest improvements in decoding accuracy have been observed after destroying noise correlations in ensembles of an average of 50 neurons (Tremblay et al., 2015).

Our analyses are based on ensembles built by randomly selecting units from the recorded population. Some studies have asked a different question (Leavitt et al., 2017). Specifically, how much information can be extracted from the most informative individual neurons recorded in a given experiment. While this is an interesting question, it may depend heavily on the exact ensemble recorded. It is unclear how well the brain can sift through a large population and find the few most informative neurons. Or whether such a strategy would be generally applicable. If the most informative neurons change from one context to the next, how would decoding be adapted? A better analysis would be to estimate the distribution of informativeness in a population, and then ask how many “very informative” neurons would be required for some task. The shape of these distributions, however, remains unclear.

Our results are limited by the simplicity of the task. We used a simple task so we could collect enough trials to accurately estimate information. More complex tasks/stimuli may reduce, but not eliminate, the saturation rate. Future work will be required to extend these results to more complex tasks and additional brain areas. Another caveat to keep in mind is that we are taking neurons randomly, without distinguishing between interneurons and projection neurons. The question of how the correlation pattern between different types of neurons affects information transmission between brain areas remains open for future research. Another important topic for future work, will be to unite work on information, which suggests that populations of 10⁵ neurons are required to represent sufficient information, with work on dynamics, that suggests that only a few 10 s of neurons are required to extract low-dimensional dynamics in cortex (Gao and Ganguli, 2015). Because noise will be affected by the dynamics that drive computation and mean responses, understanding low-dimensional dynamics will likely lead to a better understanding of information coding. A unified theory of information and dynamics will likely push forward our understanding.