Unique Spatial Integration in Mouse Primary Visual Cortex and Higher Visual Areas

Neurons in the visual system integrate over a wide range of spatial scales. This diversity is thought to enable both local and global computations. To understand how spatial information is encoded across the mouse visual system, we use two-photon imaging to measure receptive fields (RFs) and size-tuning in primary visual cortex (V1) and three downstream higher visual areas (HVAs: LM (lateromedial), AL (anterolateral), and PM (posteromedial)) in mice of both sexes.

Abstract

Neurons in the visual system integrate over a wide range of spatial scales. This diversity is thought to enable both local and global computations. To understand how spatial information is encoded across the mouse visual system, we use two-photon imaging to measure receptive fields (RFs) and size-tuning in primary visual cortex (V1) and three downstream higher visual areas (HVAs: LM (lateromedial), AL (anterolateral), and PM (posteromedial)) in mice of both sexes. Neurons in PM, compared with V1 or the other HVAs, have significantly larger RF sizes and less surround suppression, independent of stimulus eccentricity or contrast. To understand how this specialization of RFs arises in the HVAs, we measured the spatial properties of V1 inputs to each area. Spatial integration of V1 axons was remarkably similar across areas and significantly different from the tuning of neurons in their target HVAs. Thus, unlike other visual features studied in this system, specialization of spatial integration in PM cannot be explained by specific projections from V1 to the HVAs. Further, the differences in RF properties could not be explained by differences in convergence of V1 inputs to the HVAs. Instead, our data suggest that distinct inputs from other areas or connectivity within PM may support the area's unique ability to encode global features of the visual scene, whereas V1, LM, and AL may be more specialized for processing local features.

SIGNIFICANCE STATEMENT Surround suppression is a common feature of visual processing whereby large stimuli are less effective at driving neuronal responses than smaller stimuli. This is thought to enhance efficiency in the population code and enable higher-order processing of visual information, such as figure-ground segregation. However, this comes at the expense of global computations. Here we find that surround suppression is not equally represented across mouse visual areas: primary visual cortex has substantially more surround suppression than higher visual areas, and one higher area has significantly less suppression than two others examined, suggesting that these areas have distinct functional roles. Thus, we have identified a novel dimension of specialization in the mouse visual cortex that may enable both local and global computations.

Introduction

Hierarchical and parallel processing are two major organizing principles of sensory systems (Ungerleider and Mishkin, 1982; Felleman and Van Essen, 1991; Goodale and Milner, 1992; Nassi and Callaway, 2009). Together, these principles support an increase in both the specialization and generalization of receptive fields (RFs) along feedforward sensory processing pathways (Zeki, 1978; Kobatake and Tanaka, 1994). Specialization within an area both (1) enables better discrimination of selected features and (2) allows for a distinct set of computations to be performed across areas. In comparison, generalization is thought to allow for invariant representations of selected features amid variation in other parameters (e.g., position, size, or viewing angle; Riesenhuber and Poggio, 2002). Thus, the transformations that occur along the visual hierarchy mediate increases in both selectivity and tolerance of RFs to support higher-level perception (Rust et al., 2006; DiCarlo et al., 2012).

Our ultimate goal is to determine the circuit mechanisms that support such transformations of RFs across visual areas. The mouse is a useful model for studying such mechanisms, and as in humans and nonhuman primates, mice have an array of higher visual areas (HVAs) that each form their own representation of the visual field (Wang and Burkhalter, 2007; Garrett et al., 2014; Glickfeld and Olsen, 2017). Also like primates, the functional properties of the neurons in the HVAs are more specialized for encoding specific visual features than the population of neurons in primary visual cortex (V1; Andermann et al., 2011; Marshel et al., 2011; Roth et al., 2012). The differing tuning preferences of neurons in each of the HVAs, along with their unique patterns of connectivity with each other and downstream targets, suggest a division into ventral and dorsal streams (Wang et al., 2012; Smith et al., 2017; Han et al., 2018). However, as of yet, very little evidence for increasing generalization has been identified in the HVAs of the mouse (Juavinett and Callaway, 2015). Thus, in order for the mouse to be a useful model for understanding the diversity of mechanisms that underlie the transformations of RFs, we need a more complete understanding of the types of transformations that occur.

The scale of spatial integration is an important determinant of higher-order representations in the visual system. RF size typically increases along the visual hierarchy (Dräger, 1975; Wang and Burkhalter, 2007; Vermaercke et al., 2014). Larger RFs are thought to be necessary for the generation of position- and size-invariant responses (Rust and DiCarlo, 2010; Tafazoli et al., 2017). Yet, the responses of neurons to stimuli of different sizes is not simply defined by their RF size. Interactions in the extra-classical RF often drive suppression of responses to larger stimuli and generate size tuning (Hubel and Wiesel, 1968; DeAngelis et al., 1994; Angelucci et al., 2017). Suppression of responses by larger stimuli may support the generation of RFs specialized for local computations such as identification of boundaries or objects (Knierim and van Essen, 1992; Kapadia et al., 1995; Lamme, 1995; Nothdurft et al., 2000; Coen-Cagli et al., 2012). Conversely, integration across large spatial scales might enable generalization of feature representation across sizes. In addition, the weaker surround suppression in the dorsal stream of nonhuman primates has been proposed to support specialization of these areas for encoding global motion and optic flow (Tanaka et al., 1986; Born and Tootell, 1992). Thus, investigating how size is encoded across the HVAs may reveal transformations that could support both generalization and specialization of RFs in the visual system.

To investigate how size is encoded in the mouse visual system, we used two-photon (2P) calcium imaging to measure RF diameter and size tuning in populations of layer 2/3 neurons in V1 and three HVAs that receive the strongest direct input from V1: lateromedial (LM), anterolateral (AL), and posteromedial (PM). Similar to previous observations, we find that diameters of RFs in the HVAs are larger than in V1 and larger in PM than in AL or LM. Neurons in PM also had larger preferred sizes and much less surround suppression than was observed in the other three areas. These differences in preferred size and degree of suppression were conserved across stimulus contrasts and could not be explained by target-specific projections from V1. This suggests that there may be fundamental differences in connectivity and the recruitment of normalization mechanisms across the HVAs. Moreover, the unique encoding of size in PM, compared with LM and AL, demonstrates that it is poised to transform signals into increasingly general representations of the external world.

Materials and Methods

Animals.

All animal procedures conformed to standards set forth by the NIH, and were approved by the IACUC at Duke University. Seventeen mice (both sexes; 2–12 months old; singly and group housed (1–4 in a cage) under a regular 12 h light/dark cycle; primarily C57/B6J background (Jackson Laboratories, 000664) with up to 50% CBA/CaJ (Jackson Laboratories, 000654)) were used in this study. Ai93 [tm93.1(tetO-GCaMP6f)Hze; Jackson Laboratories, 024103; n = 4] and Ai94 [tm94.1(tetO-GCaMP6s)Hze; Jackson Laboratories, 024104; n = 8] were crossed to EMX1-IRES-Cre (Jackson Laboratories, 005628) and CaMK2a-tTA (Jackson Laboratories, 003010) to enable constitutive GCaMP6 expression for cell body imaging. To decrease the likelihood of seizures (Steinmetz et al., 2017), transgenic mice were fed a diet of doxycycline chow [200 mg/ml; from onset of pregnancy until postnatal day (P)45] to suppress calcium indicator expression during development.

Cranial window implant and viral injection surgeries.

Cranial window surgeries were performed on mice older than P45 (Goldey et al., 2014). Animals were administered dexamethasone (3.2 mg/kg, s.c.) and meloxicam (2.5 mg/kg, s.c.) 2–6 h before surgery, and anesthetized with ketamine (200 mg/kg, i.p.), xylazine (30 mg/kg, i.p.), and isoflurane (1.2–2% in 100% O₂) at the time of surgery. A custom titanium headpost was cemented to the skull with Metabond (Parkell) and a 5 mm craniotomy (coordinates from lambda: 3.10 mm lateral, 1.64 mm anterior) was fit with a custom-made glass window [an 8 mm coverslip bonded to two 5 mm coverslips (Warner, no. 1) with refractive index-matched adhesive (Norland, no. 71)] using Metabond. After surgery, animals were given buprenorphine (0.05 mg/kg) and cefazolin (50 mg/kg) for 48 h.

Mice were allowed to recover for at least 7 d postsurgery before beginning habituation to head restraint. Habituation to head restraint increased in duration from 15 min to >2 h over 1–2 weeks. After habituation and retinotopic mapping, wild-type mice used for axon imaging experiments (n = 5) were injected with virus to express GCaMP6s selectively in V1 neurons. Dexamethasone was administered at least 2 h before surgery and animals were anesthetized with isoflurane (1.2–2% in 100% O₂). The cranial window was removed and a glass micropipette was filled with virus (AAV1.Syn.GCaMP6s.WPRE.SV40, 6.18 × 10¹³; UPenn), mounted on a Hamilton syringe, and lowered into the brain. 100 nl of virus was injected at 250 and 450 μm below the pia (100 nl/min); the pipette was left in the brain for an additional 10 min to allow the virus to infuse into the tissue. Following injection, a new coverslip was sealed in place. Imaging experiments were conducted 6–24 weeks following injection to allow for sufficient expression.

Visual stimulation.

Visual stimuli were presented on a 144 Hz LCD monitor (Asus) calibrated with an i1 Display Pro (X-rite). The monitor was positioned 21 cm from the contralateral eye and at a 30° angle relative to the body axis and effort was made to position the mice at a similar angle and position relative to the monitor for all sessions. Presentation of rightward-drifting, vertical, sine-wave gratings alternated with periods of uniform mean luminance (60 cd/m²) and was controlled with MWorks software (http://mworks-project.org).

For wide-field imaging of retinotopy to identify V1 and the HVAs, 30° diameter sinusoidal Gabors [spatial frequency (SF): 0.1 cycles per degree (cpd); temporal frequency (TF): 2 cycles/s (Hz)] were presented in a 3 × 3 grid with 15–20° spacing (Fig. 1A) for 5 s with 5 s intertrial interval (ITI) for GCaMP imaging or 10 s with a 10 s ITI for autofluorescence imaging.

Figure 1.

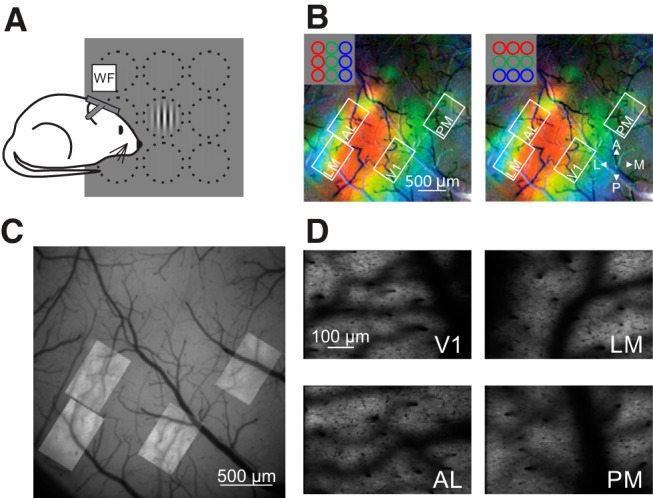
Targeting HVAs for 2P imaging. A, Schematic of rough retinotopic mapping experiments. Under wide-field fluorescence microscopy, mice were presented 30° diameter Gabor gratings at 1 of 9 positions in a 3 × 3 grid. B, Pseudocolored retinotopic maps showing changes in fluorescence (dF/F) in response to stimuli across three azimuths (left) or elevations (right) for an example mouse. White squares show FOVs acquired from V1, LM, AL, and PM during 2P imaging. Note that the FOVs target the green area that corresponds to a retinotopic location centered on the monitor. C, Alignment and overlay of average FOVs from 2P imaging sessions on vasculature map collected with single-photon fluorescence from the example mouse in B. D, Mean intensity images of FOVs from 2P imaging sessions.

For all 2P imaging experiments, the gratings were circularly-apertured and the SF and TF of the stimuli were tailored to the tuning of the neurons in that area: V1: 0.1 cpd and 2 Hz; LM and AL: 0.04 cpd and 6 Hz; PM: 0.16 cpd and 1 Hz (Andermann et al., 2011; Marshel et al., 2011). When imaging axons in the HVAs, V1 stimulus parameters were used independent of target area for more direct comparison with V1 cell bodies. When measuring the spatial RFs of neurons, we presented vertical drifting gratings in a 7 × 7 evenly spaced grid (Fig. 2A) and varied the diameter and spacing of the stimuli according to area: V1: 10° diameter, 5° spacing; LM, AL, and PM: 20° diameter, 10° spacing. We chose this stimulus-triggered method of measuring RFs for two reasons. First, in preliminary experiments we found that 10° stimuli did not reliably drive neurons in PM suggesting that noise-based methods for characterizing spatial RFs might not be efficient in the HVAs. Indeed, a recent study found that only 10% of neurons in PM were responsive to sparse noise stimuli (de Vries et al., 2020). Second, this protocol enabled rapid online analysis of the position that most effectively activated the imaged population to guide the choice of stimulus position used in the subsequent size-tuning and contrast-sensitivity imaging session. Notably, this method gave comparable results to the RF sizes for HVAs in the literature (Wang and Burkhalter, 2007).

Figure 2.

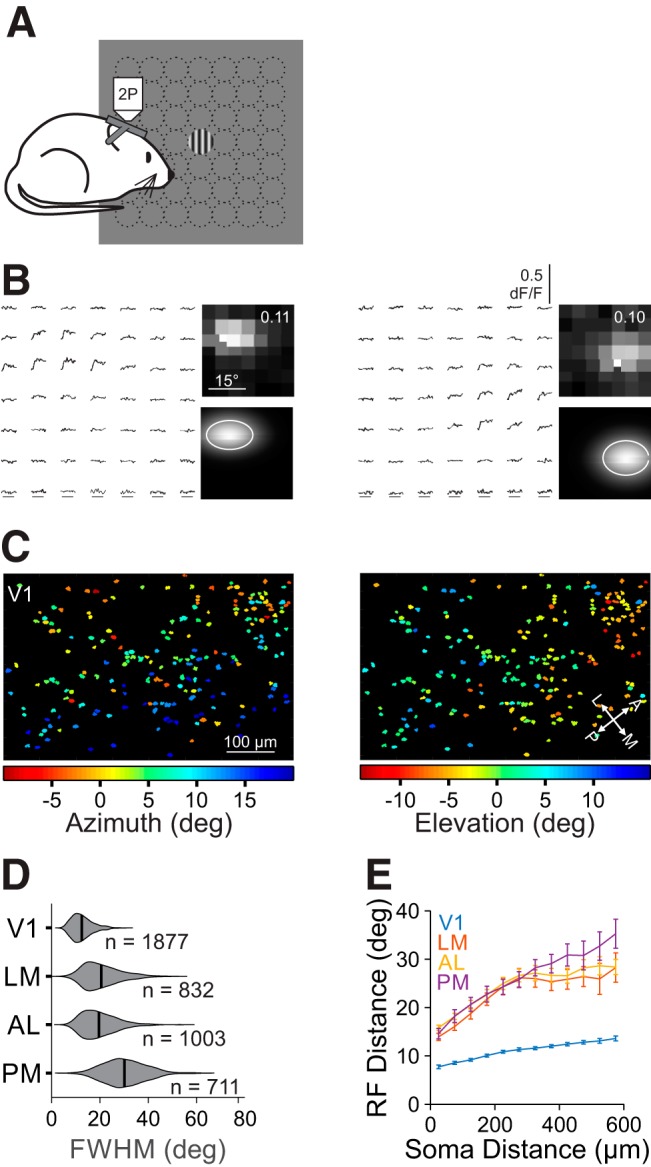
Retinotopic mapping of V1 and HVAs reveals differences in RF size across areas. A, Schematic of fine RF mapping experiments. Under 2P fluorescent microscopy, mice were presented circularly-apertured gratings at one of 49 positions in a 7 × 7 grid. B, Left, Average dF/F time courses for two example cells in response to stimuli in each of the 49 positions. Right Average responses (top; value is the maximum dF/F) and 2D Gaussian fits (bottom contour is 1 σ) for the cells above. C, RF center azimuth (left) and elevation (right) for all cells in an example V1 FOV. D, Summary of RF size (FWHM) for all neurons in each area. Violins are kernel density estimators; thick bars are mean. E, Summary of the average inter-RF distance for all pairs of well fit cells within each FOV as a function of distance in cortical space. Error bars indicate SEM across FOVs within each area.

Despite effort to have the RFs, and therefore the stimulus, centered on the monitor, in some cases, parts of the larger stimuli were cut off on the edges; however, there was no significant difference in the deviation of stimulus from the center of the monitor across areas (absolute distance from center, V1: 3.7 ± 3.7 °; LM: 6.2 ± 4.3°; AL: 4.9 ± 5.1°; PM: 4.7 ± 5.8°; Kruskal–Wallis test, p = 0.542), and thus the effective visual stimulus size should be comparable across areas. For most size-tuning experiments we examined eight sizes (5, 7.5, 11.25, 16.88, 23.31, 37.97, 56.95, and 85.43°) and 4 contrasts (0.1, 0.2, 0.4, and 0.8); in a subset of experiments (when imaging V1 axons in the HVAs and in the subset of experiments in PM in which we monitored eye position and locomotion) we used only the highest contrast (0.8). All stimuli during 2P imaging were presented for 1 s with a 3 s ITI, and all stimulus conditions were randomly interleaved and repeated at least 10 times.

Wide-field and 2P imaging.

Retinotopic maps of V1 and the HVAs (Fig. 1B) were generated using wide-field imaging of either intrinsic autofluorescence (in wild-type mice used for axon imaging) or GCaMP (in Ai93 or Ai94 mice) signals. The brain was illuminated with blue light [473 nm LED (Thorlabs) with a 462 ± 15 nm bandpass filter (Edmund Optics)], and emitted light was measured through a 500 nm long-pass (for autofluorescence) or a 520 ± 18 nm bandpass filter (for GCaMP). Images were collected using a CCD camera (Rolera EMC-2, QImaging) at 2 Hz through a 5× air immersion objective [0.14 numerical aperture (NA), Mitutoyo], using Micromanager acquisition software (NIH). Images were analyzed in ImageJ (NIH) to measure changes in fluorescence (dF/F; F is the average of all frames) in response to presentation of stimuli in each of nine positions. We then averaged across elevations to generate an azimuth map, and across azimuths to generate an elevation map (Fig. 1B) to identify locations of retinotopic reversals characteristic of V1 and the HVAs (Wang and Burkhalter, 2007; Andermann et al., 2011). Vasculature landmarks were then used to identify targeted sites for 2P imaging or viral injections (Fig. 1C,D). In particular, we aimed to target the part of the visual field within each area corresponding to the center of the monitor (in these pseudo-color maps we targeted locations labeled green for both azimuth and elevation). This enabled us to have very similar eccentricities of RFs across areas, and avoided imaging extremely nasal or peripheral visual field regions. In LM and AL, this corresponds to a central location far from the boundaries with neighboring areas, whereas in PM this corresponds to a more anterior position closer to the border with AM. However, because the visual stimulus is in the monocular zone, it is unlikely that cells in AM that were included in fields-of-view (FOVs) of PM were activated by the visual stimuli. Importantly, in control experiments using Fourier analysis and gradient inversion (in which we presented a 5° white bar moving at 9°/s in each of the four cardinal directions, and extracted the phase-modulated signal) we found a good match with our event-based approach for area-identification.

2P images of neurons and axons in the visual cortex were collected using a microscope controlled by Scanbox software (Neurolabware). Excitation light (920 nm) from a Mai Tai eHP DeepSee laser (Newport) was directed into a modulator (Conoptics) and raster scanned onto the brain with a resonant galvanometer (8 kHz, Cambridge Technology) through a 16× (0.8 NA, Nikon) water-immersion lens. Average power at the surface of the brain was 30–50 mW. Frames were collected at 15.5 Hz for a FOV of ∼605 × 340 μm for cell bodies and 500 × 300 μm for axons. Emitted photons were directed through a green filter (510 ± 42 nm band filter; Semrock) onto GaAsP photomultipliers (H10770B-40, Hamamatsu). For cell bodies, images were captured at a plane 250 ± 50 μm below the pia [range 200–300 μm; n = 9 mice, 52 FOV (V1: 18; LM: 9; AL: 10; PM: 15)]; for axons, images were 150 μm below the pia (LM: 4 mice, 4 FOV; AL: 3 mice, 3 FOV; PM: 4 mice, 7 FOV). Frame signals from the scan mirrors were used to trigger visual stimulus presentation for reliable alignment with collection.

Locomotion and pupil tracking.

During imaging sessions, mice were head restrained while allowed to freely run on a circular disc (InnoWheel, Bio-Serv). In a subset of sessions (n = 6 PM and 7 axon imaging sessions), locomotion was monitored with a digital encoder (US Digital, H5-32-NE-S) at 10 Hz. Pupil position was also monitored in a subset of sessions (n = 6 PM). Partially scattered infrared light from the 2P excitation was emitted from the pupil and either reflected with a hot-mirror (45° AOI, Edmund Optics), or directly collected with a Genie Nano CMOS (Teledyne DALSA) camera using a long-pass filter (695 nm) at the imaging frame rate.

Data analysis

All 2P imaging data were analyzed using custom code written in MATLAB (MathWorks).

Registration and segmentation.

Image stacks from each imaging session were registered for x–y motion to the same stable reference image selected out of several 500-frame-average images, using Fourier domain subpixel 2D rigid body registration. The same reference image was used for registration across multiple experiments in a single recording session.

Cell bodies were manually segmented from a filtered (3 × 3 pixel median filter) image of the average dF/F during the 1 s of stimulus presentation (where F is the average of the last 1 s of the ITI) for each stimulus presented during the fine RF mapping experiment. Fluorescence time courses were generated by averaging all pixels in a cell mask. Neuropil signals were removed by first selecting a shell around each neuron (excluding neighboring neurons), estimating the neuropil scaling factor (by maximizing the skew of the resulting subtraction), and removing this component from each cell's time course. Visually-evoked responses were measured as the average dF/F during a 1 s window around the peak response (window was selected separately for each experiment to account for variability in response latencies and indicator kinetics), where F is the average of the 1 s preceding the stimulus.

Axons were automatically segmented from the filtered, average dF/F images acquired during the fine RF mapping. Single pixels were identified as the center of an axonal bouton if they met the following criteria: (1) was the brightest pixel of the closest eight neighboring pixels, (2) had a dF/F of at least 0.05, and (3) was significantly responsive to at least two stimulus positions. Masks for each bouton included the single pixel plus the eight surrounding pixels. Neighboring boutons could be no less than 5 pixels from center to center, so that there were no pixels included in more than one bouton. The same approach as for cell bodies was used to extract time courses and measure single-trial responses, except no neuropil subtraction was performed on the boutons. In the case that there were one or two retrogradely labeled cell bodies in the HVAs, the area around the cell body was blanked for segmentation; in the case that there were more than two cell bodies, the experiment was discarded.

Following segmentation, the same analyses were performed on both cells and boutons unless otherwise stated. For both cells and boutons, the masks found in the retinotopy experiment were applied to the images collected during the size-tuning experiment.

Fitting spatial RFs.

The retinotopic organization of single cells and boutons was assessed by measuring the average dF/F response to each of 49 stimulus positions (7 × 7 grid). These data were fit by least-squares regression with a 2D Gaussian model:

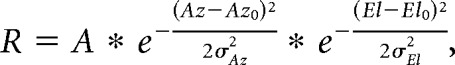where R is dF/F response, Az is stimulus azimuth, El is stimulus elevation, A is Gaussian amplitude, Az₀ is RF center in azimuth, El₀ is RF center in elevation, σ_Az is SD of RF in azimuth, σ_El is SD of RF in elevation. RF diameter was calculated as full-width at half-maximum (FWHM) of the geometric mean in each dimension of the Gaussian fit.

Quality and consistency of fit were assessed by resampling trials with replacement 500 times. Only cells with 95% of the RF center estimates within one step size in each dimension from the RF center fit using all of the data were included in further analysis. Additionally, cells for which the RF center estimates were within 1° of the edge of the grid were discarded. In the case that there were >2000 boutons in a FOV that were not on the edge, only boutons for which the r² of the original fit was >0.5 were assessed with the resampling analysis. For cell bodies, 1877/7107 in V1, 832/2745 in LM, 1003/2613 in AL, and 711/2902 in PM passed our criteria for inclusion; for V1 boutons: 3243/12,581 in LM, 3815/12,551 in AL, and 5083/19,349 in PM passed our criteria for inclusion.

The RFs of neurons imaged in PM were slightly more lateral than those in V1, LM, and AL (RF azimuth relative to the center of the monitor, V1: 4.5°±7.2°, n = 1877 cells; LM: 3.9°±14.5°, n = 832; AL: 3.7°±15.7°, n = 1003; PM: 8.1°±114.8°, n = 711; Kruskal–Wallis test, p < 0.001; with post hoc Tukey tests, V1-LM: p = 0.90; V1-AL: p = 0.11; LM-AL: p = 0.58; all comparisons with PM, p < 0.001). However, when comparing cells with similar eccentricity, we still identify a difference in RF size across areas (two-way ANOVA, with 10° bins for eccentricity, main effect of area: p < 0.001; n = 3792 cells).

Estimating cortical magnification.

For each FOV, a 2D linear polynomial surface was used to fit RF centroid positions of all well fit cells. For every fit, an F test was performed comparing the fits to a null model defined by the uniform mean of azimuth or elevation. Only FOVs with both azimuth and elevation fits having an F test of p < 0.05 were included to determine the mean magnification (in μm/°), defined as the inverse of the geometric mean of azimuth and elevation fit slopes.

Aggregate RF model.

Aggregate RFs were constructed by randomly seeding aggregation centers within the FOV. Boutons within a 150 μm radius from the seed were sampled randomly to simulate the spatial integration of a dendritic arbor (Marques et al., 2018). The aggregate RF was modeled by two methods. The first model is based on Marques et al. (2018), in which the aggregate was defined as the sum of the overlapping area of all selected bouton RFs, where the area for each bouton was an ellipse defining its FWHM. Because this method dramatically overestimated the RF size of neurons in the HVAs, we used a second summative model using the 2D Gaussian fits for each bouton RF, normalized to its respective maximum dF/F value, then summed across all chosen boutons with equal weights. The aggregate RF area was then defined as the total area in visual space with a response greater than one-half of the maximum value. Approximate RF diameter was defined as the square root of the aggregate RF area after dividing by π.

Fitting size-tuning curves.

Neurons that were well fit for spatial RF were subsequently fit for size. There are two major modes of responses to stimuli of increasing size that are typically observed in the visual cortex (Sceniak et al., 1999): one of a saturating response up to some size and remaining active at larger sizes (non-suppressed cell), and one of a peak response and declining response at larger sizes (suppressed cell). Thus, each cell was fit both with a saturating, single sigmoid (SS model):

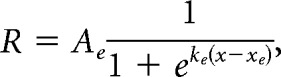and with a suppressed, difference of sigmoids (DOS model):

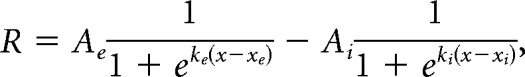where R is dF/F response, x is stimulus size, A_e is excitatory sigmoid amplitude, k_e is excitatory sigmoid steepness, x_e is excitatory sigmoid center, A_i is inhibitory sigmoid amplitude, k_i is inhibitory sigmoid steepness, and x_i is inhibitory sigmoid center. Some parameters were constrained when fitting these models. In both models, A_e > 0 and x_e > 0 ensured a positive excitatory response centered at a size above zero. In the DOS model, k_e > k_i and x_e < x_i ensured the second inhibitory sigmoid was less steep than and centered at a larger size than the excitatory sigmoid, to represent the larger size and spatial offset of the surround field. Initial guesses for sigmoid amplitudes and center were set based on the amplitude and size of the peak response across all sizes. The DOS model is highly similar to an integral of difference of Gaussian model (another commonly used model for fitting size-tuning curves), sharing a sigmoidal shape and the same number of free parameters, and was chosen to better fit the saturating curves seen in PM.

For each cell, size-tuning curves at each contrast condition were individually fit with both models using a least-squares regression method with an additional smoothness penalty to prevent overfitting of data. A sequential F test was used to assess whether the additional parameters of the DOS fit was significantly improved from the SS fit. If the fit passed the F test, the cell was designated suppressed (or DOS); otherwise, the cell was non-suppressed (or SS). For the SS model, preferred size was defined as the size at which 90% saturation is reached; for the DOS model, preferred size is the size that generates the peak response. In the SS model, suppression index (SI) is 0; in the DOS model, SI was defined as follows:

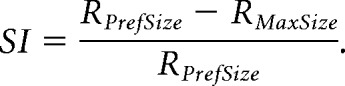Where R_MaxSize is the amplitude of the response to the largest stimulus, and R_PrefSize is the amplitude of the response at the preferred size.

Quality and consistency of fits were again assessed by bootstrapping over 500 shuffles in the highest contrast condition, examining that the preferred size estimates remain within 1 octave (ratio of 2) in either direction from the unshuffled fit, and that at least 50% of fits were designated by sequential F test as the same model as the unshuffled fit, otherwise discarding that cell from analysis. Additionally, boutons that were not significantly modulated across sizes (according to a one-way ANOVA) were discarded from analysis. For cell bodies: 1136/1877 in V1, 446/832 in LM, 486/1003 in AL, and 351/711 in PM passed our criteria for inclusion; for V1 boutons: 2244/3243 in LM, 1869/3815 in AL, and 1514/5083 in PM passed our criteria for inclusion.

Cells were also filtered from analysis based on the distance of the cell's RF center (as measured from the fit) to the center of the visual stimulus position used for the size-tuning experiment. Cutoffs for the maximum distance were chosen separately based on 50% of mean RF diameter in each area, rounding to the nearest degree: 6° for V1 (and V1 axons in HVAs), 10° for LM and AL, and 15° for PM. For cell bodies: 453/1136 in V1, 109/446 in LM, 147/486 in AL, and 169/351 in PM fell within the cutoff ranges; for V1 boutons: 1253/2244 in LM, 1389/1869 in AL, and 894/1514 in PM fell within the cutoff ranges. Additional comparisons were performed using a matched cutoff of 10° for cell bodies in all areas: 831/1136 in V1, 109/446 in LM, 147/486 in AL, and 82/351 in PM fell within the matched cutoff range.

For analyses of size-tuning parameters across all four contrast conditions, cell bodies were selected based of the goodness-of-fit at the lowest contrast condition to eliminate cells with noisy size-tuning curves at low contrasts. This was achieved by requiring r² of the designated size-tuning model fit at the lowest contrast to be >0.2. We note this requirement potentially introduces a bias for cells with lower C₅₀ than the larger population for which we measured contrast-response functions (see Fig. 4). For cell bodies: 140/453 in V1, 51/109 in LM, 49/147 in AL, and 82/169 in PM passed our criteria for inclusion for size-tuning across contrasts.

Figure 4.

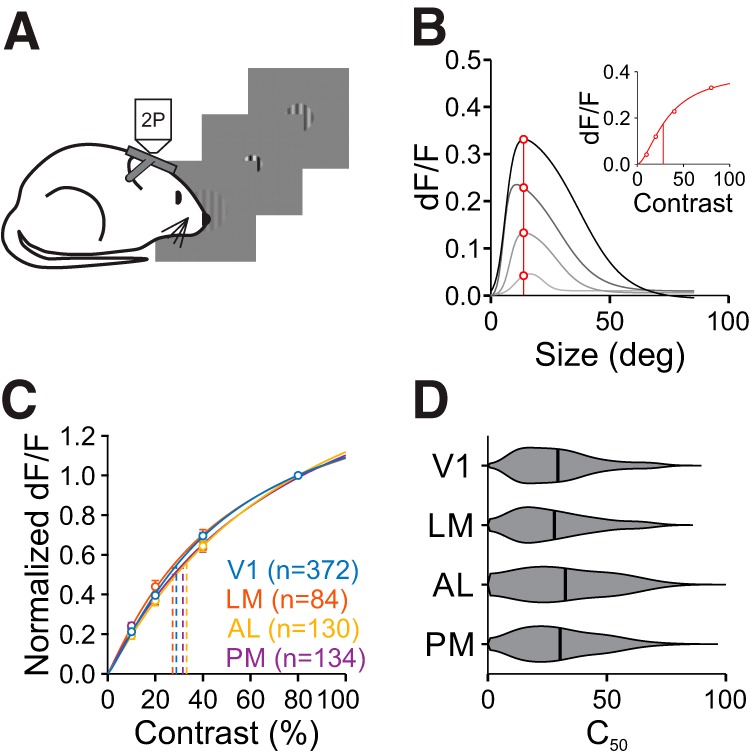
Contrast sensitivity is similar across areas. A, Schematic of size-by-contrast-tuning experiments. During 2P imaging, mice are presented circularly-apertured gratings of variable size and contrast at a fixed position. B, Contrast-response extraction in an example cell. Response values at the cell's preferred size (red line and circles, found at the highest contrast) were extracted from size-tuning curves across four contrasts (gray curves). Inset, Contrast response function for this cell fit with the Naka–Rushton equation. Vertical line is C₅₀. C, Summary of averaged normalized contrast response functions at the preferred size across areas. Error bars indicate ±SEM across cells. Fits are of average contrast response measures. D, Summary of C₅₀ for all cells in each area.

Fitting contrast response functions.

Contrast responses were extracted from the size-tuning curve fits in each contrast condition at the preferred size of the highest contrast condition. These data were fit with a Naka-Rushton hyperbolic function:

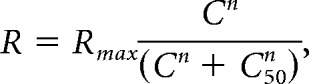where R is dF/F response, R_max is the saturating dF/F response, C is stimulus contrast, n is exponent of power function (constrained > 0), and C₅₀ is contrast of half-max response. We considered only cells with good fits by requiring r² of the contrast-response model fit to be >0.5. For cell bodies: 372/453 in V1, 84/109 in LM, 130/147 in AL, and 134/169 in PM passed our criteria for inclusion.

Locomotion.

Running trials were defined as having an average speed of at least 2 cm/s during the stimulus presentation. In the size tuning experiments, the mice ran on a minority of trials (5.0 ± 2.3%, range 0–25.5%, n = 13 sessions, 6 mice), and there was no significant relationship between the stimulus size and the likelihood of running (p = 0.82, one-way ANOVA).

Pupil tracking.

Pupil position was extracted from each frame using the native MATLAB function imfindcircles, and converted to degrees of visual angle with a 1:25 degrees to micrometer scale (Park et al., 2012). Average pupil position was quantified for each stimulus presentation during a subset of both the fine RF mapping and size tuning experiments when imaging area PM. The variability of eye position across trials was small (SD: 2.5 ± 0.87°, n = 6 sessions, 3 mice) and did not depend on stimulus size (p = 0.99, one-way ANOVA). Removing trials with large deviations in eye position (pupil >5° from mean, 23.9 ± 4.1% trials, range 18.0–29.8%; n = 6 sessions, 3 mice) did not significantly affect measures of RF diameter (FWHM, all trials: 33.5°±10.7°; trials <5° from median: 33.2°±10.6°; n = 184 cells, 3 mice; p = 0.085; paired t test, one-tailed), preferred size (all trials: 35.4°±17.5°; trials <5° from median: 37.4°±19.5°; n = 52 cells, 3 mice; p = 0.106; paired t test, one-tailed), or SI (all trials: 0.54 ± 0.41; trials <5° from median: 0.51 ± 0.43; n = 52 cells, 3 mice; p = 0.068; paired t test, one-tailed).

Experimental design and statistical analysis

Data were tested for normality using a Lilliefors test. None of the RF parameters were normally distributed; thus we used the Wilcoxon rank sum and Kruskal–Wallis tests (with post hoc Tukey tests) for two- and multiple-sample statistics, respectively. However, in the cases where we were interested in the relationship between two variables, we used a two-way ANOVA which has been shown to be robust to non-normality (Driscoll, 1996). All p values < 0.001 are reported as p < 0.001. Sample sizes were not predetermined by statistical methods, but our sample sizes of the neurons and animals are similar to other studies. The numbers of cells, animals or experiments are provided in the corresponding text, figures and figure legends. All error values in the text are SD unless otherwise specified. Data collection and analysis were not performed blind to experimental conditions, but all visual presentation conditions were randomized.

Data and code availability.

All relevant data and code will be made available upon reasonable request.

Results

Visual cortical areas have distinct RF sizes

To examine the representation of size in V1 and the HVAs, we first characterized the spatial RFs of neurons in these areas. Using wide-field calcium imaging in awake mice transgenically expressing the calcium indicator GCaMP6 in pyramidal cells (GCaMP6f: n = 7; GCaMP6s: n = 2), we generated retinotopic maps of visual cortex (Fig. 1A,B). V1 and the HVAs were designated based on previously established HVA maps (Wang and Burkhalter, 2007; Andermann et al., 2011). We then used these maps to target our 2P imaging experiments to a region corresponding to the center of the monitor in each area of interest, as well as to inform the approximate position of spatial RFs for those neurons (Fig. 1C,D).

Using cellular-resolution 2P imaging, we examined the spatial RF of pyramidal cells in layer 2/3 (L2/3) of V1 and three of its most densely innervated and best-characterized target cortical areas: LM, AL, and PM (Andermann et al., 2011; Marshel et al., 2011; Wang et al., 2011). To measure RFs, we presented small drifting gratings in a 7 × 7 grid (see Materials and Methods; Fig. 2A,B). Averaged responses to the 49 stimulus positions were fit with a 2D Gaussian function to model the cell's RF diameter and position in retinotopic space (Fig. 2B,C). These experiments revealed differences in RFs across V1 and the HVAs. Consistent with previous studies (Wang and Burkhalter, 2007), RF sizes in V1 were significantly smaller than in all of the other areas (FWHM, mean ± SD: 12.5°±4.3°, n = 1877 cells, 9 mice; Kruskal–Wallis test, p < 0.001; with post hoc Tukey tests: all comparisons with V1: p < 0.001; Fig. 2D). Of the HVAs, LM and AL were intermediate in RF size and were not significantly different from each other (LM: 20.5 ± 7.6°, n = 832 cells, 9 mice; AL: 19.6°±7.1°, n = 1003 cells, 9 mice; post hoc Tukey test, LM-AL: p = 0.14). Finally, the RFs of neurons in PM were significantly larger than those in both AL and LM (30.1°±8.5°, n = 711 cells, 9 mice; post hoc Tukey tests: all comparisons with PM: p < 0.001). Thus, we find a general increase in RF size from L2/3 of V1 to L2/3 of the HVAs, consistent with an increase in generalization in the HVAs. Further, we find a difference across areas, consistent with a specialization of the function of the HVAs.

The differences in RF size may be accounted for by differences in the amount of cortical territory in each area that is devoted to a given visual region of space. For instance, larger RFs might be needed if a smaller number of cells represent the same region of visual space. To assess the spatial distribution of RFs in each area, we measured the relationship between the RF distance and cortical distance for all pairs of neurons within each FOV. The RFs of neighboring cells are much closer in visual space in V1 than in the HVAs, consistent with a higher-magnification in V1 (two-way ANOVA: main effect of cortical distance: p < 0.001; main effect of area: p < 0.001; interaction: p < 0.001; Fig. 2E; Garrett et al., 2014). However, this relationship is remarkably similar across HVAs, although there is a small but significant interaction where cortically distant cells in PM have more distant RFs than those in LM or AL (two-way ANOVA on HVAs only; main effect of cortical distance: p < 0.001; main effect of area: p = 0.36; interaction: p < 0.01). To more directly estimate cortical magnification, we also fit a 2D plane to each FOV to determine the spatial gradient of RF azimuth or elevation. Again, we find a higher-magnification in V1 and no significant differences among HVAs (cortical magnification (μm/°); V1: 26.7 ± 2.9, n = 17 FOV; LM: 11.2 ± 4.0, n = 8; AL: 12.1 ± 3.3, n = 8; PM: 11.0 ± 1.7, n = 6; Kruskal–Wallis test, p < 0.001; with post hoc Tukey tests: all comparisons with V1: p < 0.005; LM-AL: p = 0.93; LM-PM: p = 0.98; AL-PM: p = 1.00). Thus, the increase in RF size in PM, relative to LM and AL, is not accompanied by a commensurate decrease in cortical magnification.

Visual cortical areas have distinct preferred sizes and surround suppression

To further investigate spatial integration in V1 and the HVAs, we measured single neuron responses to stimuli of varying diameter and contrast (Fig. 3A). We first addressed size tuning of neurons at the highest contrast used (0.8). Since size tuning is sensitive to how well the stimulus is centered on the RF, we only examined neurons with well fit RFs close to the center of the size-tuning stimulus (within 50% of the mean RF diameter in each area). Size-tuning curves lie along a continuum which can be described by either a SS, where responses are monotonically increasing or saturating, or a DOS, in which responses initially increase but then are suppressed at larger sizes (Sceniak et al., 1999). Thus, we fit all cells with both models and used a sequential F test to statistically determine whether the DOS model was significantly better than the SS model (Fig. 3B,C). This analysis revealed significant differences in the average size tuning curves of neurons across areas (two-way ANOVA, main effect of area: p < 0.001, interaction of area and size: p < 0.001; Fig. 3D).

Figure 3.

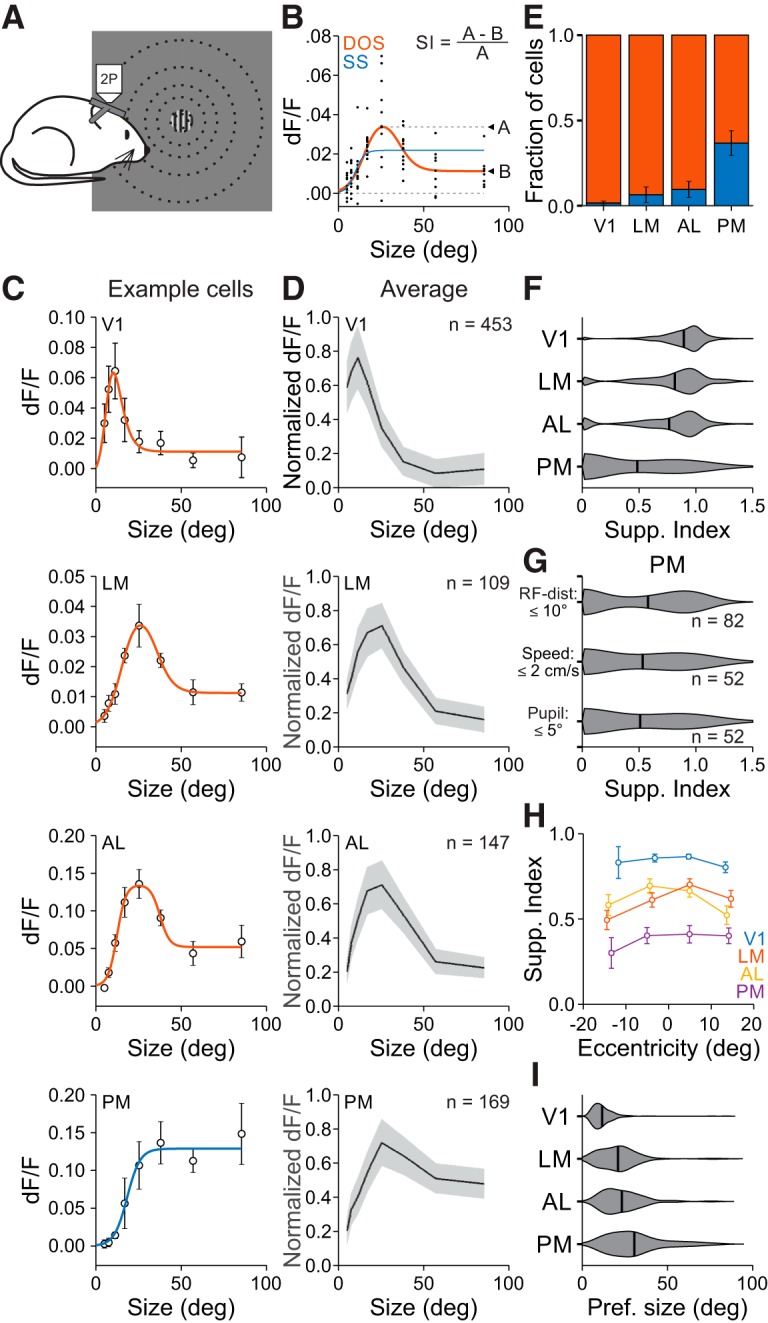
Size is encoded differently across visual cortical areas. A, Schematic of size-tuning experiments. During 2P imaging, gratings of varying size are presented at a fixed position. B, Single-trial responses (black dots) to stimuli of varying size fit with a SS (blue) and a DOS (red) for an example cell. If the SS is the better fit, then the SI is zero; if the DOS is the better fit, then the SI is equal to the ratio of the difference between the dF/F at the preferred size and the largest size to the dF/F at the preferred size. C, Average dF/F responses and best fit for an example cell in each area. Cell in LM is the cell in B. Error bars indicate ±SEM across trials. D, Average responses to each size stimulus across all well fit cells in each area within 50% of the FWHM for that area. Error bars indicate ±SD across cells. E, Proportion of cells best fit by an SS (blue) or DOS (red). Error is ±SEP across cells. F, Summary of SI by area. G, Summary of suppression index in PM when using the same criteria as in LM/AL for RF distance from the stimulus (top), trials in which the mouse was stationary (middle), and trials in which the pupil position was consistent (bottom). H, SI as a function of RF eccentricity for all areas. Error bars indicate ±SEM across cells. I, Summary of preferred size by area.

Differences in size tuning across visual areas were related to a number of tuning features of the population. First, the prevalence of suppressed cells was significantly different across areas. The highest fraction of suppressed cells was in V1, the lowest was in PM, and there was an intermediate fraction in LM and AL [fraction suppressed cells (mean ± SE of proportion (SEP); V1: 0.985 ± 0.006, n = 453 cells; LM: 0.936 ± 0.024, n = 109 cells; AL: 0.904 ± 0.024, n = 147 cells; PM: 0.633 ± 0.037, n = 169 cells; χ² test, p < 0.001; Fig. 3E]. Second, the amount of suppression, measured as the SI, was significantly different across areas. Neurons in V1 had the highest SI, PM had the lowest SI, and LM and AL were not statistically different from each other (SI; V1: 0.87 ± 0.18; LM: 0.79 ± 0.27; AL: 0.75 ± 0.30; PM: 0.48 ± 0.40; Kruskal–Wallis test, p < 0.001; with post hoc Tukey tests: all comparisons except V1-LM and LM-AL: p < 0.001; V1-LM: p < 0.05; LM-AL: p = 0.74; Fig. 3F). Thus, we find significant differences in spatial integration across HVAs.

The difference in spatial integration across visual areas could not be explained by features of our experiments or analysis. First, the difference in SI was not sensitive to our inclusion criteria: the differences observed above remained present if we used a constant RF-center cutoff in all areas (SI with 10° cutoff, V1: 0.85 ± 0.20, n = 831 cells; LM: 0.79 ± 0.27, n = 109; AL: 0.75 ± 0.30, n = 147; PM: 0.58 ± 0.40, n = 82; Kruskal–Wallis test, p < 0.001; with post hoc Tukey tests, V1-LM: p = 0.09; V1-AL: p < 0.001; V1-PM: p < 0.001; LM-AL: p = 0.72; LM-PM: p < 0.05; AL-PM: p = 0.09; Fig. 3G). Second, this difference could not be explained by effects of locomotion or eye movements. In a subset of sessions imaging PM, we included only trials where the mouse was stationary (a behavioral state that should maximize the degree of surround suppression; Ayaz et al., 2013) or the eye position was stable, and found that neurons in PM still had relatively little surround suppression (SI in PM, stationary: 0.53 ± 0.42; pupil <5° from mean: 0.51 ± 0.43; n = 52 cells, 3 mice; Fig. 3G). Third, differences in SI were not due to differences in the eccentricity of RF centers across experiments. PM still had a lower SI than V1, LM and AL when matching for RF eccentricity (two-way ANOVA with 10° bins for eccentricity, main effect of area: p < 0.001; Fig. 3H). Thus, differences in SI across areas are robust to our experimental and analysis conditions.

There were also significant differences across areas in the preferred size of neurons. The preferred size of neurons in V1 was significantly smaller than those in the HVAs (preferred size, V1: 11.7°±7.0°; Kruskal–Wallis test, p < 0.001; with post hoc Tukey tests: all comparisons with V1: p < 0.001; Fig. 3I). Within HVAs, the preferred size of neurons in LM and AL were not significantly different from each other, but were both significantly smaller than the neurons in PM (LM: 21.0 ± 11.9°; AL: 23.2° ± 12.1°; PM: 30.6° ±16.5°; post hoc Tukey tests, LM-AL: p = 0.40; LM-PM: p < 0.001; AL-PM: p < 0.05). Thus, these data suggest that PM has a unique representation of stimulus size compared with V1, LM, and AL, and therefore may be specialized for processing global features of the visual scene.

Contrast sensitivity of neurons is similar across areas

There is a strong relationship between surround suppression and stimulus contrast (DeAngelis et al., 1994; Levitt and Lund, 1997; Sengpiel et al., 1997; Sceniak et al., 1999). Thus, we next explored whether the differences in size tuning that we observed across areas could be explained by differences in contrast sensitivity. We identified cells that were well fit for size, and extrapolated contrast-response functions from the fits at the preferred size at the highest contrast (Fig. 4A,B). The average contrast response functions across areas were similar, with no significant differences in the effect of contrast across areas (two-way ANOVA, main effect of area: p = 0.08; interaction of area and contrast: p = 0.20; n = 720 cells; Fig. 4C). We then fit each cell's contrast response with the Naka-Rushton function to measure the contrast at 50% response (C₅₀). Again, the C₅₀ was similar across areas, with no significant differences between areas (C₅₀, V1: 0.29 ± 0.16, n = 372 cells; LM: 0.28 ± 0.16, n = 84; AL: 0.33 ± 0.18, n = 130; PM: 0.30 ± 0.16, n = 134; Kruskal–Wallis test, p = 0.26; Fig. 4D). When these contrast-response functions were constructed at the same size (20°) across neurons, instead of at each cell's preferred size, there were still no significant differences in the contrast response functions (two-way ANOVA, main effect of area: p = 0.06; interaction of area and contrast: p = 0.44; n = 559 cells) or C₅₀ (Kruskal–Wallis test, p = 0.07) across areas. Thus, we conclude that if there are differences in contrast sensitivity across areas, they are minimal and potentially dependent on the differences in size tuning across areas.

As expected, we observed a strong effect of contrast on visual responses (two-way ANOVA, main effect of contrast for all areas: p < 0.001; V1: n = 140 cells; LM: n = 49; AL: n = 51; PM: n = 82). However, we find a relatively weak, though significant, dependence of size-tuning on stimulus contrast (interaction of size and contrast for all areas: p < 0.001; Fig. 5A), demonstrating that there is minimal contrast dependence of size-tuning. There was a similar proportion of suppressed cells at high and low contrast (0.1 vs 0.8; χ² tests: V1: p = 0.62; LM: p = 0.46; AL: p = 0.11; PM: p = 0.43; Fig. 5B). We also find no significant contrast dependence of SI (two-way ANOVA, main effect of contrast: p = 0.84; interaction of contrast and area: p = 0.74; Fig. 5C), nor preferred size (two-way ANOVA, main effect of contrast: p = 0.54; interaction of contrast and area: p = 0.92; Fig. 5D). Importantly, however, the lowest-contrast data still reflected significant differences in size tuning across areas (fraction suppressed, χ² test, p < 0.001; SI, Kruskal–Wallis test, p < 0.001; with post hoc Tukey tests: all comparisons except V1-LM and LM-AL: p < 0.001; V1-LM: p < 0.05; LM-AL: p = 0.36; preferred size, Kruskal–Wallis test, p < 0.001; with post hoc Tukey tests: all comparisons except LM-AL and AL-PM: p < 0.001; LM-AL: p = 0.24; AL-PM: p = 0.13). Thus, neurons in V1 have narrower spatial integration and neurons in PM have broader integration, independent of stimulus contrast.

Figure 5.

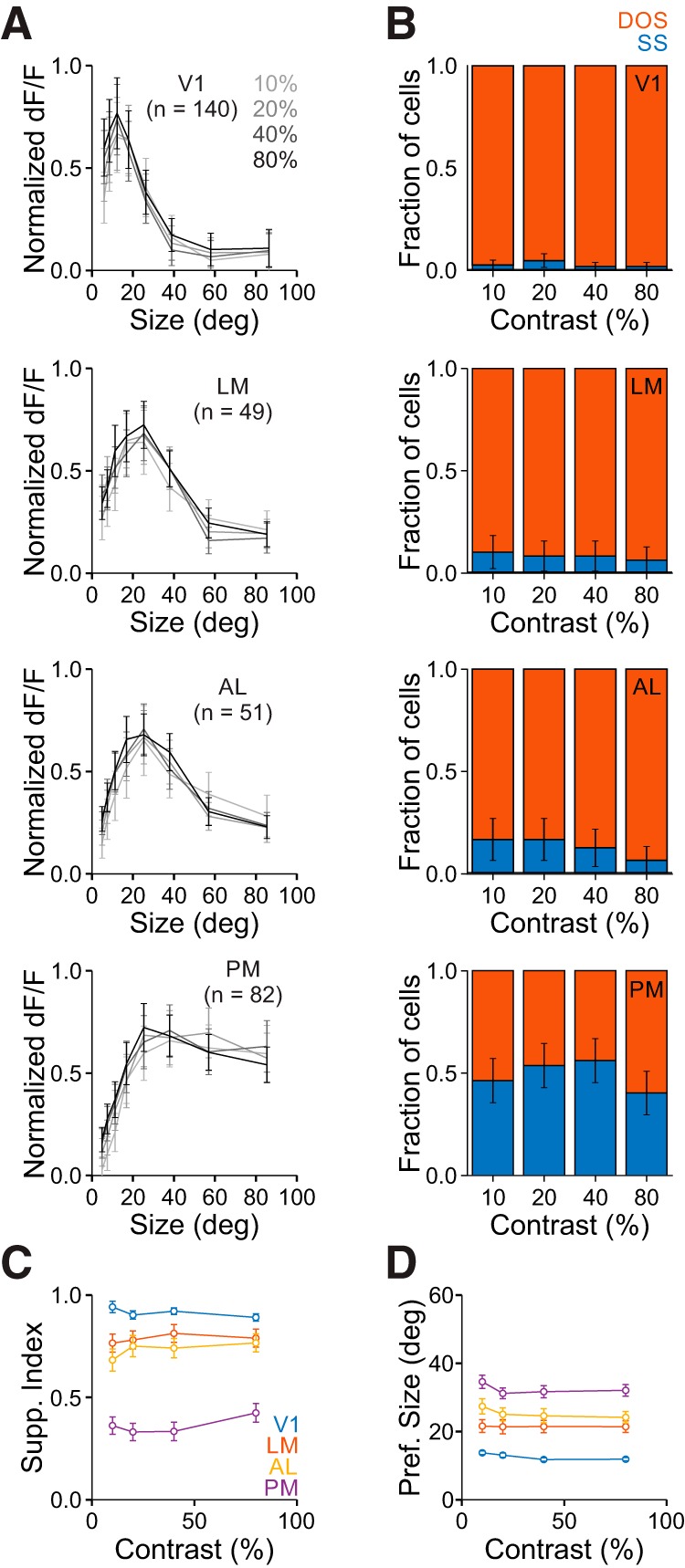
Differences in size tuning in V1 and the HVAs is conserved across contrasts. A, Average responses of all cells in each area to each size for all contrasts. Data are normalized to the maximum response for each cell at each contrast. Error bars indicate ±SEM across cells. B, Proportion of cells best fit by an SS (blue) or DOS (red) for each contrast in each area. Error bars indicate ±SEP across cells. Ten percent versus eighty percent contrast p > 0.05 for all areas. C, Summary of suppression index as a function of contrast in each area. Error bars indicate ±SEM across cells. D, Same as C, for preferred size.

Differences in spatial integration in the HVAs are not inherited from V1

Our experiments have revealed that neurons in the HVAs integrate over a much larger visual field than neurons in V1. In addition, we find that there is specialization among the HVAs where PM integrates more broadly than AL and LM. To test whether these differences can be explained by functionally specific projections to the HVAs, we virally expressed GCaMP6s in V1 neurons (Fig. 6A,B), and used 2P imaging to measure the functional properties of V1 inputs to LM, AL, and PM (Fig. 6C; Glickfeld et al., 2013). Because the viral expression labels neurons across all layers of V1, this also allows us to determine whether the HVAs receive inputs from weakly suppressed V1 neurons in any layer (including those that we did not image in our L2/3 cell body imaging experiments). For these experiments, we used a similar set of stimuli as when imaging cell bodies: first, using a dense presentation of stimuli in 49 different positions to measure RF size (Fig. 6D–F); and second, varying stimulus size (at a contrast of 0.8) to measure the preferred size and SI (Fig. 7).

Figure 6.

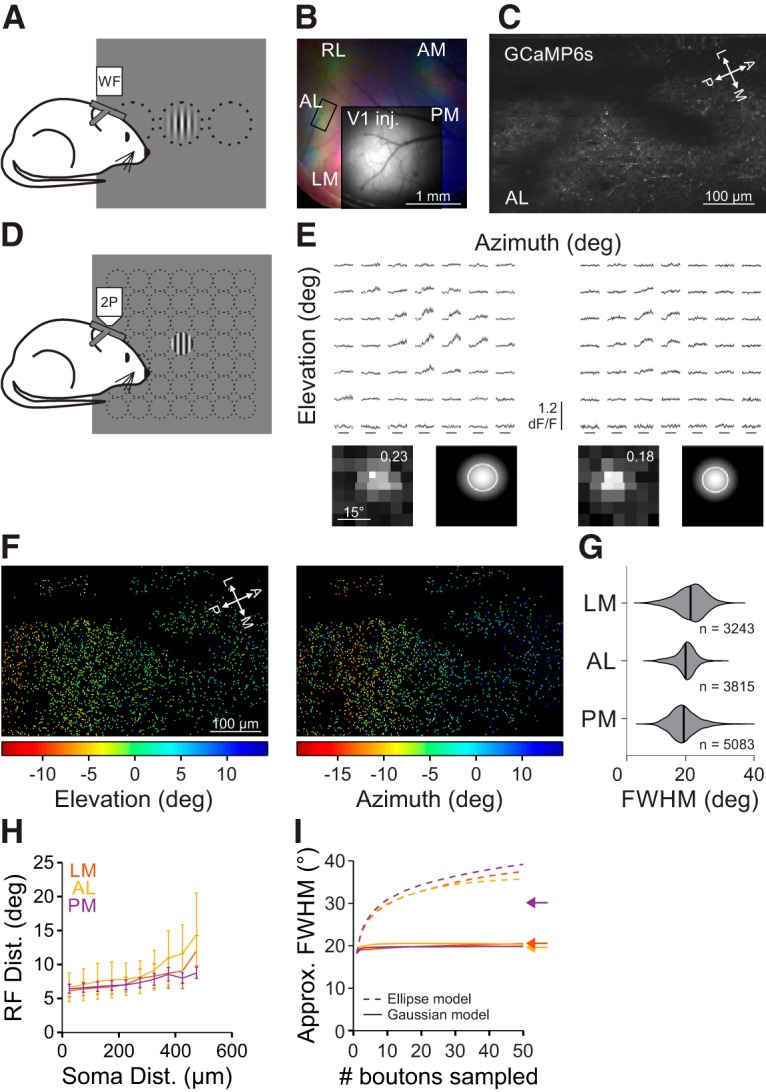
RF size of V1 inputs to the HVAs is similar across areas. A, Schematic of wide-field (WF) imaging stimulus and setup. B, Pseudo-color image of changes in fluorescence (dF/F) in axonal projections from V1 to the HVAs in response to stimuli of different azimuth (same conventions as Fig. 1B) for an example mouse. Inset, Raw fluorescence (F) image of the injection site in V1. C, Average fluorescence image of an example FOV from the region of interest in B (rectangle in AL). D, Schematic of fine RF mapping stimulus for 2P imaging. E, Average fluorescence (dF/F) traces (top) and RF with fit (bottom; same conventions as Fig. 2B) for two example cells from the FOV in C. F, RF center azimuth (left) and elevation (right) for all V1 boutons in the FOV in C. G, Summary of RF size for V1 boutons in each HVA. H, Summary of the average inter-RF distance for all pairs of well fit boutons within each FOV as a function of distance in cortical space. Error bars indicate SEM across FOVs within each area. I, Summary of the approximate FWHM of modeled aggregate RFs as a function of the number of boutons sampled, when summing either ellipses (dashed) or 2D Gaussians (solid) as a template for RF size. Arrows indicate the average FWHM of RFs within each HVA.

Figure 7.

Size tuning of V1 inputs to the HVAs is similar across areas. A, Schematic of stimulus protocol for size tuning experiments. B, Example single trial (black) responses to stimuli of varying size for a single cell (same conventions as in Fig. 3B). C, Average normalized dF/F for all well fit boutons in each area. Error bars indicate ±SD across cells. D, Proportion of boutons best fit by an SS (blue) or DOS (red) in each area. Error bars indicate ±SEP across cells. E, Summary of suppression index for all well fit boutons in each area. F, Same as E, for preferred size.

RFs of V1 axons in the HVAs were similarly sized, though significantly different, across areas (FWHM, LM: 20.0 ± 4.6°, n = 3243 boutons, 4 mice; AL: 18.5 ± 3.2°, n = 3815 boutons, 3 mice; PM: 17.9 ± 4.3°, n = 5083 boutons, 4 mice; Kruskal–Wallis test, p < 0.001; with post hoc Tukey tests: all comparisons, p < 0.001; Fig. 6G). The RF diameter of V1 axons in the HVAs was significantly larger than the RF size of neurons in L2/3 of V1 (Kruskal–Wallis test, p < 0.001; with post hoc Tukey tests: all comparisons with V1: p < 0.001), perhaps because of the inclusion of axons from deeper layers in V1 where neurons have larger RFs (Niell and Stryker, 2008). In fact, only in PM did the imaged neurons have significantly larger RFs than the V1 boutons coming into that area (one-tailed Wilcoxon rank sum tests, LM: p = 0.99; AL: p = 0.29; PM: p < 0.001). Together, this suggests that there is relatively little specificity for RF size in the projections to the HVAs. Moreover, the increase in RF size between L2/3 of V1 and LM and AL may partly be explained by computations within V1 (because these axons arise from all layers in V1), whereas the increase in RF size in PM requires the convergence of multiple V1 axons or local computations within PM.

To examine whether there may be differences in convergence of V1 axons in the HVAs, we measured the relationship between the distribution of V1 boutons in cortical space and their RF locations in the HVAs. If there were more convergence in an area, then we would expect that boutons close in cortical space might be farther apart in visual space. Whereas inter-bouton RF distances were indeed dependent on cortical distance (main effect of cortical distance: p < 0.001), we found no significant differences in either the RF distance across areas (main effect of area: p = 0.76) or the interaction between the cortical and RF distances across areas (interaction: p = 0.12; Fig. 6H). Thus, there do not seem to be any strong differences in convergence of V1 inputs to the HVAs.

To understand whether any differences in RF size or convergence of V1 inputs to the HVAs could account for the differences in RF size of neurons in the HVAs, we simulated the summation of V1 inputs across a dendritic arbor us to construct an aggregate RF for individual neurons in each HVA (Marques et al., 2018). We first used the approach of Marques et al. (2018), modeling aggregate RF as the union of the ellipses that define the FWHM of each bouton's RF. In particular, we aggregated groups of boutons within 300 μm of each other in the same FOV as these may potentially converge on the same dendritic arbor. Using this model, simulated HVA neurons were similar across areas (aggregate RF approximate diameter [FWHM] using 30 sampled boutons; 95% CI: [lower limit (LL), upper limit (UL)], LM: [27.6°, 42.5°]; AL: [25.3°, 41.7°]; PM: [26.3°, 47.2°]; Fig. 6I). However, this approach dramatically overestimated the size of the average measured RFs in all areas (Fig. 6I, arrows).

To better capture the nature of summation of V1 inputs in the HVAs, we modified this model to sum the 2D Gaussian fits for each bouton (instead of homogenous ellipses). We found that aggregate RFs were again similar across areas (aggregate RF approximate diameter [FWHM] using 30 sampled boutons; [95% CI: (LL, UL)]: LM: [15.8°, 24.1°]; AL: [18.5°, 24.0°]; PM: [16.4°, 24.3°]; Fig. 6I). Moreover, this model closely estimated the cell body RF sizes in LM and AL (i.e., the 95% CI includes the empirically observed mean RF area) yet underestimated that value in PM. This demonstrates that the same model of convergence of V1 inputs cannot account for the differences in RF sizes observed in LM, AL, and PM. Instead, these data suggest that there may be area-specific differences in other inputs or local circuitry, potentially related to the differences in size tuning we observe in PM.

To address whether the differences in surround suppression in the HVAs could be explained by specific projections to the HVAs, we again fit SS and DOS models to the responses of axons in the HVAs to stimuli of increasing size (Fig. 7A–C). Projections from V1 to the HVAs had relatively similar, although significantly different, fractions of suppressed boutons [LM: 0.994 ± 0.002 (mean ± SEP), n = 1253 boutons; AL: 0.993 ± 0.002, n = 1389 boutons; PM: 0.979 ± 0.005, n = 894 boutons; χ² test, p < 0.005; Fig. 7D], degree of surround suppression (SI, LM: 0.83 ± 0.14; AL: 0.78 ± 0.16; PM: 0.96 ± 0.23; Kruskal–Wallis test, p < 0.001; with post hoc Tukey tests: all comparisons: p < 0.001; Fig. 7E), and preferred size (LM: 10.3°±5.3°; AL: 11.2°±6.0°; PM: 9.4°±5.1°; Kruskal–Wallis test, p < 0.001; with post hoc Tukey tests: LM-AL: p = 0.28; all comparisons with PM: p < 0.001; Fig. 7F). The fraction of suppressed boutons in the HVAs was similar to the cell bodies imaged in V1 (χ² test, p = 0.339), and significantly higher than the cell bodies imaged in their respective areas (χ² tests for all areas, p < 0.001). Moreover, the preferred size was smaller and the degree of suppression was greater in V1 boutons than in the cell bodies in their target areas (one-tailed Wilcoxon rank sum tests: preferred size, all areas: p < 0.001; SI, LM: p = 0.067; AL: p < 0.005; PM: p < 0.001). Thus, we find that the inputs to the HVAs undergo a similar degree of surround suppression, and less surround suppression than the neurons in the target areas, suggesting that there may be distinct mechanisms of spatial integration within the HVAs, and especially in PM.

Discussion

Like primates, mice have multiple HVAs that likely serve specialized roles in visual processing (Glickfeld and Olsen, 2017). However, as yet, little is known about the specific features encoded in each area, and therefore what function each area might serve. Here, we used 2P calcium imaging to determine how stimulus size and contrast are encoded in neurons in V1 and three HVAs: LM, AL, and PM.

We observed a number of differences in the RF properties of neurons in V1 and the HVAs. For instance, we found that RF diameter was significantly larger in the HVAs than in V1, and larger in PM than in AL or LM. This is consistent with electrophysiological measurements made from these areas (Dräger, 1975; Wang and Burkhalter, 2007) and the increase in RF size along the visual hierarchy of nonhuman primates (Baker et al., 1981). The increase in RF size may be a consequence of the decrease in cortical magnification in the HVAs (Garrett et al., 2014), requiring increased convergence. However, although we see a decrease in cortical magnification from V1 to the HVAs, the magnification within the HVAs was very similar. Furthermore, there do not seem to be clear differences in convergence of V1 inputs in PM relative to LM and AL, and the model of aggregate RFs in the HVAs that best estimated the mean size in LM and AL, underestimated the size in PM. This suggests that differences in convergence and RF size of V1 inputs do not support the larger RF size in PM, and this instead may be because of differences in inputs from other areas (e.g., other higher-order cortical or thalamic areas) or local recurrent circuitry.

Consistent with differences in local and feedback circuits, we also observed major differences in how these areas encode size information. Neurons in V1 were much more likely to be suppressed by large stimuli than neurons in any of the three HVAs. Among HVAs, PM had significantly fewer suppressed cells than either LM or AL. Even at the highest contrast, ∼40% of cells in PM were better fit by a model that had no suppression at large sizes. Interestingly, there were very few non-suppressed inputs from V1 to any of the HVAs. This suggests that the differences in encoding of size cannot simply be inherited from V1. Furthermore, even if convergence could explain some of the increased RF size in PM, if surround mechanisms in PM were similar to those in V1, then one would still expect this to be countered by local suppression within PM at the largest sizes. Thus, the mechanism through which PM becomes sensitive to larger stimuli must also be mediated by differences in other sources of input or local connectivity.

In V1, somatostatin-expressing interneurons are thought to pool excitatory inputs over long ranges and thereby mediate surround suppression (Adesnik et al., 2012; Dipoppa et al., 2018). However, anatomical data suggest that there are actually fewer somatostatin cells in V1 than in PM, and similar densities in PM, LM, and AL (Kim et al., 2017), though these experiments did not resolve different subclasses of somatostatin cells that may be preferentially recruited by larger stimuli. It is also possible that there are differences in the strength and structure of local connectivity, or the cell types that support surround suppression, within these areas. Future experiments will be necessary to reveal whether surround suppression is the only form of normalization reduced in PM, or whether other forms of normalization, such as cross-orientation suppression, are also less pronounced.

In other species, surround suppression has been observed to persist or even increase along the visual hierarchy (Hubel and Wiesel, 1965; Schein and Desimone, 1990). Surround suppression has been suggested to be important for mediating computations involving salience, pop-out, or figure-ground segregation (Knierim and van Essen, 1992; Kapadia et al., 1995; Lamme, 1995; Nothdurft et al., 2000; Coen-Cagli et al., 2012). Although AL and LM undergo less surround suppression than V1, there is still substantial suppression in these areas. This is consistent with the proposed participation of LM in the ventral visual stream and object recognition (Wang et al., 2011) and may support a role for AL in local motion signals (Andermann et al., 2011; Tohmi et al., 2014).

In comparison, the weaker surround suppression in PM may support specialized encoding of global motion signals or responses to larger, looming stimuli. The weak surround suppression observed in PM is analogous to that seen in the nonhuman primate dorsal stream areas, MT and MST. These areas are responsible for encoding of optic flow and other global motion signals (Zeki, 1978; Duffy and Wurtz, 1991; Liu and Pack, 2017), which likely benefit from weaker surround suppression (Tanaka et al., 1986; Born and Tootell, 1992). Further, similar to what was observed in MT, ∼one-half of neurons in PM lack surround suppression. The diversity of spatial scales over which neurons in PM integrate visual input raises the interesting possibility that multiple functional subpopulations exist within this area. These populations could enable parallel processing of both local and global computations in through functionally segregated networks.

Together, our data reveal a novel dimension for specialization of function in the HVAs. All HVAs demonstrated an increase in surround suppression compared with V1, but this specialization cannot depend on specific connectivity between V1 and the HVAs, because V1 inputs are suppressed compared with cells in each HVA. Furthermore, PM appears to be unique in its representation of size among the three HVAs examined. The larger RFs and weaker surround suppression in PM may support an increase in generalization by allowing for position invariance of visual responses and integration of global motion signals. We propose the pattern of spatial integration in each HVA arises due to unique connectivity among local circuits and cell types. Revealing the circuit mechanisms underlying the decrease in surround suppression will not only support our understanding of hierarchical transformations but also clarify the mechanisms of cortical normalization by which surround suppression occurs.