Modeling the vibrational couplings of nucleobases

Abstract

Vibrational spectroscopy, in particular infrared spectroscopy, has been widely used to probe the three-dimensional structures and conformational dynamics of nucleic acids. As commonly used chromophores, the C=O and C=C stretch modes in the nucleobases exhibit distinct spectral features for different base pairing and stacking configurations. To elucidate the origin of their structural sensitivity, in this work, we develop transition charge coupling (TCC) models that allow one to efficiently calculate the interactions or couplings between the C=O and C=C chromophores based on the geometric arrangements of the nucleobases. To evaluate their performances, we apply the TCC models to DNA and RNA oligonucleotides with a variety of secondary and tertiary structures and demonstrate that the predicted couplings are in quantitative agreement with the reference values. We further elucidate how the interactions between the paired and stacked bases give rise to characteristic IR absorption peaks and show that the TCC models provide more reliable predictions of the coupling constants as compared to the transition dipole coupling scheme. The TCC models, together with our recently developed through-bond coupling constants and vibrational frequency maps, provide an effective theoretical strategy to model the vibrational Hamiltonian, and hence the vibrational spectra of nucleic acids in the base carbonyl stretch region directly from atomistic molecular simulations.

I. INTRODUCTION

Interactions between nucleobases play essential roles in maintaining the three-dimensional structures of nucleic acids and modulating their biological functions. Watson–Crick pairing of the purine and pyrimidine bases drives the association of complementary strands of DNA to form regular double helix structures. The alternative Hoogsteen hydrogen bonding arrangements allow nucleic acids to form triple helices and G-quadruplexes, which possibly regulate cellular pathways ranging from gene transcription to DNA replication and DNA–protein recognition.^1–4 As common building blocks of the RNA structure, wobble base pairs such as those between guanine and uracil are of fundamental importance to the translation of the genetic code.^5–7 These pairing schemes hold the nucleobases in planar configurations, which stack with one another through π–π interactions to construct a variety of functional structures of nucleic acids.

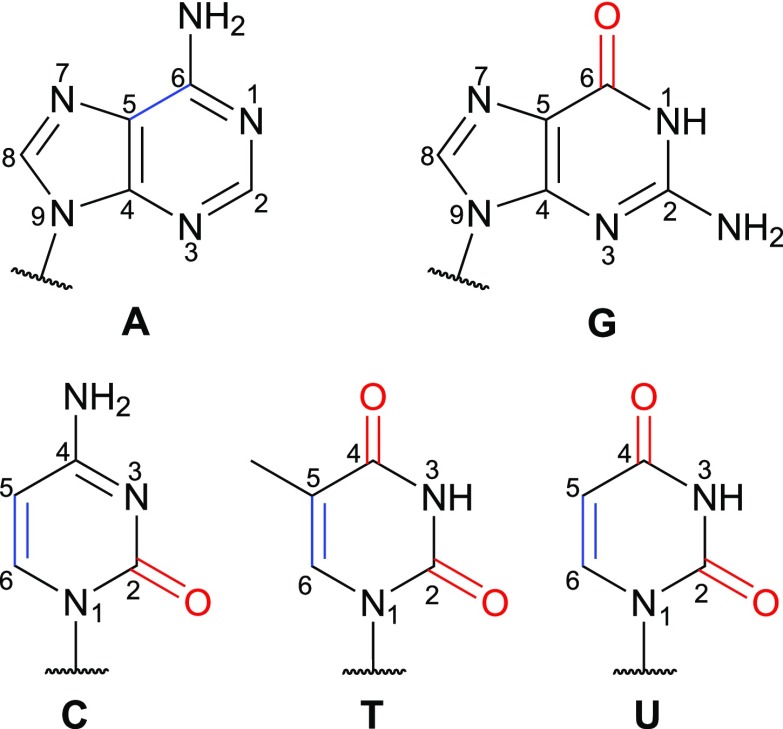
Vibrational spectroscopy, in particular infrared (IR) spectroscopy, provides a powerful tool to probe these interactions and unravel how they give rise to the characteristic structures and conformational dynamics of nucleic acids. These experiments often focus on the base carbonyl stretch modes, which absorb in the spectral region between 1600 cm⁻¹ and 1800 cm⁻¹, and are typically performed in D₂O to avoid the interference of the H₂O bending modes (∼1640 cm⁻¹). As illustrated in Fig. 1, except adenine, all the other nucleobases contain at least one carbonyl group and their spectral features are highly sensitive to the hydrogen bonding patterns and base stacking configurations. For example, guanosine 5′-monophosphate has a strong C=O stretch peak at 1663 cm⁻¹.⁸ Upon formation of Watson–Crick base pairs in double-stranded DNA, the absorption peak of guanine blue shifts to the 1678–1689 cm⁻¹ region.⁹ Instead, when guanine uses the O⁶ and N₇ atoms as hydrogen bonding sites to form Hoogsteen base pairs in DNA triple helices, its C=O stretch absorbs at a much higher frequency of 1715 cm⁻¹.⁹ Due to this structural sensitivity, IR spectroscopy in the base carbonyl stretch region has been utilized to distinguish between A-, B-, and Z-form DNA double helices, identify G-C⁺ and A-T Hoogsteen base pairs in duplex DNA, and track the fast denaturation kinetics of RNA tetraloops.^9–13

FIG. 1.

Chemical structures of the nucleobases with the C=O and C=C chromophores highlighted in red and blue, respectively. Atoms in the purine and pyrimidine rings are numbered.

Advancements in two-dimensional IR (2D IR) spectroscopy have significantly enhanced the spectral resolution and enabled the detection of nucleic acid dynamics over a broad range of time scales.^14–21 By spreading the IR absorption information over two frequency axes, 2D IR experiments directly probe the interactions, or couplings, between the vibrational modes. For example, in their pioneering studies, Zanni and co-workers applied 2D IR spectroscopy to A- and B-form DNA oligonucleotides, determined the intra- and interstrand couplings between the C=O groups in the guanine and cytosine bases, and elucidated the origin of the cross peaks in the spectra.^22,23 More recently, Tokmakoff and co-workers monitored the cross peaks that arised from the hydrogen bonding interactions between Watson–Crick base pairs and unraveled the thermal dehybridization mechanism of model DNA double helices with base-pair-specific resolution.¹⁶ In addition to the interactions between carbonyl groups, they also observed intense cross peaks between the C=O and C=C stretches in the 2D IR spectra of the pyrimidine bases, revealing their coupled motions.⁸ Using 2D IR spectroscopy, Hunt and co-workers uncovered that a ring mode of adenine mainly associated with the stretch of its C₅=C₆ group strongly interacts with the C=O groups in thymine in the A-T base pairs of DNA duplexes.^18,19,24

Given the importance of inter-base interactions, it is desirable to develop a theoretical scheme that efficiently predicts the coupling constants based on the structure of an oligonucleotide. To reduce the computational complexity, researchers often consider a vibrational subspace composed of all the chromophores of interest, in this case, the base C=O groups, and treat it quantum mechanically. We will also include the C₅=C₆ stretches in the vibrational subspace when dealing with the pyrimidine bases C, T, and U and the purine base A, considering their strong couplings with the C=O vibrations.^8,18,19,24 The chromophores in the nucleobases are highlighted in Fig. 1. Within this subspace, the vibrational Hamiltonian of a system containing N chromophores is a N × N matrix, in which the diagonal elements are the site frequencies of each C=O or C=C stretch and the off-diagonal elements are the couplings between them. By invoking the Hessian Matrix Reconstruction (HMR) method, Cho and co-workers effectively obtained the vibrational Hamiltonian of nucleobases and base pairs and used them to simulate the 2D IR spectra of model DNA double helices.^25–28 From the definition of the Hamiltonian elements, one can also calculate the coupling constants (in cm⁻¹) as

$${\beta }_{ij}=\frac{{\partial }^{2}V}{\partial x_i\partial x_j}.$$ (1)

Here, x_i and x_j are the vibrational displacements of chromophores i and j, respectively, and V is the interaction energy between them. Using electronic structure calculations, both the HMR and analytical differentiation approaches naturally incorporate the through-bond couplings, which arise from the charge flow between covalently linked chromophores, and through-space couplings such as those between hydrogen bonded nucleobases. However, the application of these methods is limited by the high computational costs for performing such calculations on large nucleic acids in the condensed phase.

In the modeling of proteins, it has been well established that the through-space couplings between the amide I vibrations, which are mainly the peptide bond C=O stretches, are dominated by electrostatic interactions.^29–33 Similarly, as two nucleobases in the same or complementary strands of nucleic acids approach each other, the electron densities of their C=O and C=C group interact electrostatically. When the distance between the chromophores is much larger than their sizes, the leading term in the interactions is between their transition dipole moments. This has led to the development of the transition dipole coupling (TDC) scheme,^29,34 a simple model that has been extensively used in the study of the protein amide I band.^31,35–39 When the TDC model is applied to the carbonyl groups in oligonucleotides, it underestimates the coupling constants between the hydrogen bonded G-C base pairs by about 50% as compared to those calculated from electronic structure methods or fitting to 2D IR experiments.²³ This is not surprising because the distance between the C=O groups in a standard Watson–Crick G-C pair, which is about 5 Å, is comparable to the C=O bond length of 1.2 Å. Hence, it is likely that the dipole approximation is not valid for the closely spaced base pairs, consistent with the well-known phenomenon that the TDC scheme is not adequate to describe the couplings between adjacent peptide groups.^31,36

To tackle this problem, a few approaches have been designed to incorporate higher-order multipoles in the expansion of Eq. (1). These include the transition density derivative distribution method and the transition charge coupling (TCC) scheme, which have been successfully applied to model the couplings between the protein amide I modes.^{31–33,38,39} In particular, the TCC method mimics the charge densities of the chromophores by assigning point charges and charge flows to individual atoms and provides an effective way to calculate the couplings directly from the distances and relative orientations of the chromophores.³³ In this work, we extend the TCC scheme to nucleobases and determine the parameters for the C=O and C=C vibrations from density functional theory (DFT) calculations. We then evaluate the performance of the TCC models by applying them to a series of model oligonucleotides with characteristic secondary and tertiary structures and elucidate the origin of the structural sensitivity of IR spectroscopy. We further show that in comparison with the TDC scheme, the TCC models are more reliable in predicting the interactions between nucleobases.

II. THEORETICAL AND COMPUTATIONAL METHODS

A. The TCC scheme

The electron density in the vicinity of an oscillator changes when it vibrates around the equilibrium geometry. If a quantum harmonic oscillator with a reduced mass of μ vibrates at a frequency of ω, the amplitude of its vibration is⁴⁰

$$A=\sqrt{\frac{\hslash }{2\mu \omega }},$$ (2)

where ℏ is the reduced Planck constant. One can displace an oscillator i by an amount of x_iA along its normal mode coordinate, where x_i is a dimensionless scalar, and the resulting charge density at position $\overrightarrow{r_i}$ is ${\rho }_i\left(x_i,\overrightarrow{r_i}\right)$. As two chromophores i and j move closer to each other, there is a strong electrostatic interaction between their charge densities ${\rho }_i\left(x_i,\overrightarrow{r_i}\right)$ and ${\rho }_j\left(x_j,\overrightarrow{r_j}\right)$. From Eq. (1), the vibrational coupling between chromophores i and j is^31,33

$${\beta }_{ij}=\frac{1}{4\pi {\epsilon }_0}{\left[\frac{{\partial }^2}{\partial x_i\partial x_j}\iint \frac{{\rho }_i\left(x_i,{\overrightarrow{r}}_i\right){\rho }_j\left(x_j,{\overrightarrow{r}}_j\right)}{\left|{\overrightarrow{r}}_i-{\overrightarrow{r}}_j\right|}\mathrm{d}{\overrightarrow{r}}_i\mathrm{d}{\overrightarrow{r}}_j\right]}_{x_i=0,x_j=0}.$$ (3)

In this equation, ε₀ is the vacuum permittivity, which takes the value of 8.854 × 10⁻²² F/Å, and the coupling constant β_ij is evaluated at the equilibrium geometry of the chromophores with x_i = x_j = 0. In a molecule, all the atoms involved in a normal mode move as the chromophore vibrates. As such, when a chromophore i is displaced by x_i, the Cartesian coordinates of atom n in the chromophore move by $x_i{\overrightarrow{\mathit{\text{v}}}}_{ni}$, where ${\overrightarrow{\mathit{\text{v}}}}_{ni}$ is the component for atom n in the normalized normal mode coordinates multiplied by A [Eq. (2)].

To simplify the evaluation of Eq. (3), one can approximate the charge density ${\rho }_i\left(x_i,{\overrightarrow{r}}_i\right)$ as the sum of the point charges q_n(x_i) on the atoms constituting the chromophore,³³

$${\rho }_i\left(x_i,{\overrightarrow{r}}_i\right)=\sum _n\delta \left(\overrightarrow{r_i}-{\overrightarrow{r}}_n\left(x_i\right)\right)q_n\left(x_i\right).$$ (4)

When chromophore i is in the equilibrium geometry, we assume that atom n is at the position of ${\overrightarrow{r}}_{n0}$ with a partial charge of q_n0. As the chromophore is displaced by x_i, the position of atom n in Eq. (4) becomes ${\overrightarrow{r}}_n\left(x_i\right)={\overrightarrow{r}}_{n0}+x_i{\overrightarrow{\mathit{\text{v}}}}_{ni}$. Its partial charge is taken as the first-order correction to the equilibrium value, $q_n\left(x_i\right)=q_{n0}+x_{i}d{q}_{ni}$, where dq_ni is the derivative of q_n with respect to the displacement x_i.³³ Note that both ${\overrightarrow{r}}_n$ and q_n are functions of x_i because it determines the position of each atom in the chromophore, which, in turn, determines the charge distribution in a normal mode vibration.

One can insert Eq. (4) in Eq. (3) and obtain the coupling constant in the TCC model,

$${\beta }_{ij}=\frac{1}{4\pi {\epsilon }_0}{\left[\frac{{\partial }^2}{\partial x_i\partial x_j}\sum _{n,m}\frac{q_n\left(x_i\right)q_m\left(x_j\right)}{\left|{\overrightarrow{r}}_n\left(x_i\right)-{\overrightarrow{r}}_m\left(x_j\right)\right|}\right]}_{x_i=0,x_j=0}.$$ (5)

Here, the summation is over all possible combinations of atom n in chromophore i and atom m in chromophore j. Using the expressions of ${\overrightarrow{r}}_n$ and q_n and taking the double derivative at x_i = 0 and x_j = 0, one can calculate β_ij analytically,³³

$$\begin{array}{ccc}\hfill {\beta }_{ij}& =\hfill & \frac{1}{4\pi {\epsilon }_0}\sum _{nm}\left[\frac{d{q}_{ni}d{q}_{mj}}{\left|{\overrightarrow{r}}_{nm}\right|}-\frac{3q_{n0}{q}_{m0}\left({\overrightarrow{\mathit{\text{v}}}}_{ni}\cdot {\overrightarrow{r}}_{nm}\right)\left({\overrightarrow{\mathit{\text{v}}}}_{mj}\cdot {\overrightarrow{r}}_{nm}\right)}{{\left|{\overrightarrow{r}}_{nm}\right|}^5}\right.\hfill \\ \hfill & \hfill & +\left.\frac{q_{m0}d{q}_{ni}{\overrightarrow{\mathit{\text{v}}}}_{mj}\cdot {\overrightarrow{r}}_{nm}-q_{n0}d{q}_{mj}{\overrightarrow{\mathit{\text{v}}}}_{ni}\cdot {\overrightarrow{r}}_{nm}+q_{n0}{q}_{m0}{\overrightarrow{\mathit{\text{v}}}}_{ni}\cdot {\overrightarrow{\mathit{\text{v}}}}_{mj}}{{\left|{\overrightarrow{r}}_{nm}\right|}^3}\right].\hfill \end{array}$$ (6)

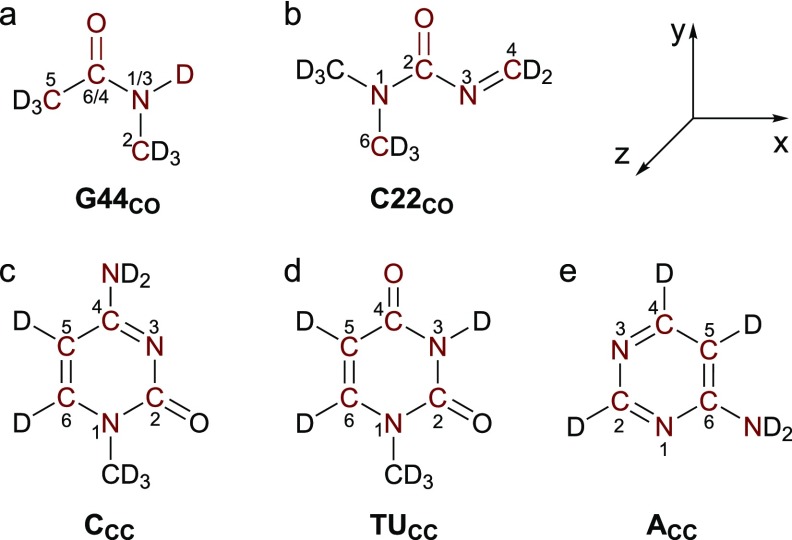
In Eq. (6), ${\overrightarrow{r}}_{nm}={\overrightarrow{r}}_{n0}-{\overrightarrow{r}}_{m0}$, which links atoms n and m when the chromophores are at their equilibrium geometries. Equation (6) can also be used in conjunction with molecular dynamics (MD) simulations to provide on-the-fly predictions of the coupling constants, and in this case, ${\overrightarrow{r}}_{nm}$ is taken as the displacement vector connecting atoms n and m in each snapshot of the simulation. Equation (6) provides an efficient way to compute the couplings between two chromophores based on their distances and relative orientations. To implement it, we need a parameter set of q₀, dq, and $\overrightarrow{\mathit{\text{v}}}$ for all the atoms in the chromophores. We determine these parameters from DFT calculations of model molecules, as shown in Fig. 2. The procedure to obtain the TCC parameters is described in Sec. III A.

FIG. 2.

Chemical structures of the model molecules with the atoms included in the TCC models highlighted. The internal coordinate system is also included. The numbers of the atoms are assigned according to their positions in the nucleobases G, C, T, U, and A. In the G44_CO model, the numbers before the slashes correspond to the atom numbering in guanine, and the ones after the slashes come from those in thymine and uracil.

B. Hessian matrix reconstruction

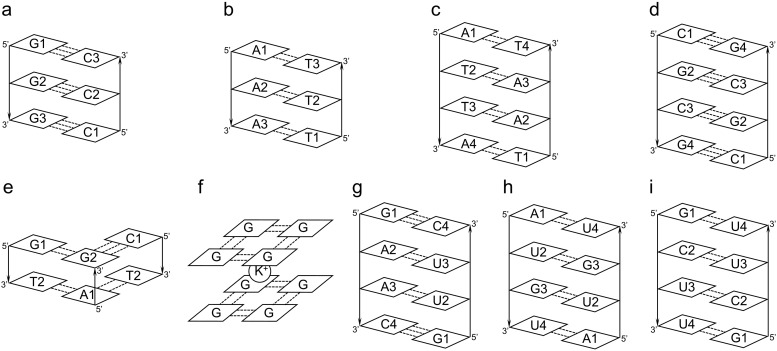
To validate the TCC models, we apply them to a series of oligonucleotides with different structures and hydrogen bonding patterns. These biological systems are schematically shown in Fig. 3. The predicted coupling constants from the TCC models are compared to the references values, as obtained from the HMR method.^41,42 As each of the purine bases contains only one chromophore, we consider the C₅=C₆ and C₆=O vibrations for adenine and guanine, respectively, in their vibrational subspaces. In contrast, we incorporate both C=O and C=C stretches in the vibrational subspaces for the pyrimidine bases since these vibrations are strongly coupled.^8,43 Specifically, we treat the C₂=O and C₅=C₆ groups as chromophores for cytosine, and the C₂=O, C₄=O, and C₅=C₆ groups for thymine and uracil (Fig. 1). For an oligonucleotide, the size of its vibrational subspace is determined by the number of purine and pyrimidine bases that it contains. For example, when we consider an oligonucleotide with two complementary strands of GAAC and GUUC, the vibrational subspace contains a total of 14 chromophores. This comes from one C=C vibration of each adenine, one C=O vibration of each guanine, two vibrations of each cytosine, and three vibrations of each uracil. As a result, the vibrational Hamiltonian, κ, is a 14 × 14 matrix.

FIG. 3.

Schematic representations of the oligonucleotides used to evaluate the performance of the TCC models. The bases in each strand are labeled, and strands 1 and 2 are numbered from left to right. The dotted lines and arrows represent hydrogen bonds and backbone directions, respectively.

Diagonalizing κ gives the normal mode frequency matrix, Ω, and the eigenvector matrix, U,

$$\mathrm{\Omega }=U^{-1}\kappa U.$$ (7)

The HMR method takes the reverse process to generate the vibrational Hamiltonian,^41,42

$$\kappa =U\mathrm{\Omega }{U}^{-1}.$$ (8)

Using DFT methods, we performed geometry optimization and frequency analysis of each system and collected all the normal mode frequencies to form Ω for the vibrational subspace. We then used the normal mode coordinates and the amplitude of the vibration, A [Eq. (2)], to obtain U. From its delocalized nature, each normal mode incorporates the contributions from multiple C=O or C=C chromophores. We assume that the eigenvector components are proportional to the changes of bond lengths in the normal mode,

$$U_{i\alpha }\propto r_{i\alpha }-r_i^0,$$ (9)

where U_iα is the matrix element of chromophore i in normal mode α. $r_i^0$ is the equilibrium length of a C=O or C=C bond in chromophore i, and r_iα is the disturbed length of this bond in normal mode α. After obtaining the values of U_iα, we used the Gram–Schmidt method⁴⁴ to make U orthonormal to ensure that κ from Eq. (8) was symmetric. In the reconstructed κ, the diagonal terms are the site frequencies of each chromophore and the off-diagonal elements are the coupling constants that we use as reference values in this work.

C. Model systems to validate the TCC parameters

We constructed a series of model oligonucleotides to validate the TCC models. First, we built double helical structures with the oligonucleotide sequences GGG, CCC, AAA, TTT, ATTA, and TAAT using the nucleic acid builder program⁴⁵ in the Amber 16 software.⁴⁶ Their structures are schematically shown in Figs. 3(a)–3(c). We then took segments of DNA and RNA oligonucleotides from the Protein Data Bank (PDB). Specifically, we chose residues 301–304 in chain C and residues 409–412 in chain D from a Z-DNA structure with the PDB ID 6AQV [Fig. 3(d)].⁴⁷ We included residues 3, 4, 11, 12, 17, and 18 in a model DNA triplex with the PDB ID 134D [Fig. 3(e)].⁴⁸ From a G-quadruplex structure (PDB ID 6FQ2), we chose residues 1, 4, 7, and 10 from both chains A and B and included the potassium ion between the two layers [Fig. 3(f)].⁴⁹ We also took residues 4–7 in chain A and residues 13–16 in chain B from an RNA double helix with PDB ID 6IA2 [Fig. 3(g)].⁵⁰ In addition, we took residues 3–6 in chain A and residues 11–14 in chain B from an RNA oligomer with G-U wobble pairs [PDB ID 315D, Fig. 3(h)].⁵¹ Finally, we considered an RNA duplex with the PDB ID 6N8F and chose residues 5–8 in chain A and residues 17–20 in chain B from the first structure of its PDB file [Fig. 3(i)].⁵² As some of the hydrogen atoms were missing in the crystal structures, we added them using the LEaP program in AMBER 2016.⁴⁶ For all model oligonucleotides, we replaced the backbone sugars and phosphates by methyl groups and used the resulting structures for the electronic structure evaluations.

D. DFT calculations

DFT calculations were first performed to determine the parameters q₀, dq, and $\overrightarrow{\mathit{\text{v}}}$ for the TCC models. In addition, they were used to calculate the reference couplings of the oligonucleotides. In all cases, the electronic structure was described using the B3LYP density functional,⁵³ the D3 dispersion correction,⁵⁴ and the 6-311G(d,p) basis set, as implemented in the Gaussian 16 program.⁵⁵ Considering that the experimental IR measurements of nucleic acids were performed in D₂O, we replaced the labile H’s that were covalently bonded to nitrogen atoms in all the structures with D. A correction factor of 0.9679 was applied to all the normal mode frequencies.⁵⁶

As described in Secs. II B and II C, we used the HMR method to obtain the reference couplings from DFT calculations. For each oligonucleotide (Fig. 3), we carried out geometry optimization and frequency analysis. The phosphate and sugar groups of the oligonucleotides were replaced with methyl groups to reduce the computational cost, as they have been shown to have minor influences on the vibrational properties of the C=O and C=C groups in the nucleobases.²⁵ To maintain the base pairing and stacking configurations of the model systems, we performed constrained geometry optimization where the positions of all the hydrogen bond donor and acceptor atoms as well as the atoms that were covalently bonded to the oligonucleotide backbone were fixed. For example, if an adenine formed a Watson–Crick pair with thymine, we would fix the position of its N₁, N⁶, and N₉ atoms (Fig. 1). If it formed both Watson–Crick and Hoogsteen base pairs with thymine in the triad T·AT, we would fix the positions of its N₁, N⁶, N₇, and N₉ atoms. From analyzing the vibrational normal modes, we confirmed that all the imaginary frequencies came from the inter-base movements and were not related to the stretching of the C=O and C=C bonds. All the DFT calculations were performed in vacuum. As the couplings between the chromophores are dominated by electrostatic interactions, we expect them to depend only on the geometry of the oligonucleotides and inclusion of solvent molecules will have minor influences on their values.

III. RESULTS AND DISCUSSION

A. The TCC models for nucleobase C=O and C=C stretches

From Fig. 1, the C=O groups in the nucleobases G, C, T, and U are in two distinct chemical environments. In the first case, C₆=O in guanine and C₄=O in thymine and uracil are bonded to only one amino group. To mimic their structures, we use deuterated cis-N-methylacetamide (cis-NMAD) as a model molecule [Fig. 2(a)] and refer to the resulting TCC model as G44_CO. In the second type, the C₂=O group in cytosine, thymine, and uracil is sandwiched between two N-containing functional groups. Accordingly, we use a deuterated compound 1,1-dimethyl-3-methyleneurea [Fig. 2(b)] to mimic the structures of these C=O chromophores and construct another TCC model, C22_CO. Using these molecules, we define an internal coordinate system as shown in Fig. 2. The y axis is along the $\overrightarrow{\mathrm{C}\mathrm{O}}$ bond direction, and the orthogonal x axis is in the molecular plane and points toward the N atom. In the C22_CO model, atom N₃ is used to determine the x axis. The z axis is placed to be perpendicular to the molecular plane.

From the vibrational analyses, we observe that the atoms highlighted in red in Figs. 2(a) and 2(b) contribute to over 90% of the carbonyl stretch normal modes. As such, we incorporate these atoms in the TCC models and determine their q, dq, and $\overrightarrow{\mathit{\text{v}}}$ from DFT calculations. For each molecule, we first carry out geometry optimization and compute the Mulliken charges^57,58 of the atoms as q₀. To keep the overall system neutral, we add the charges of the terminal atoms not included in the TCC model to the C or N atoms that are covalently bonded to them. With the DFT calculations, we obtain the reduced mass, vibrational frequency, and coordinates of the carbonyl stretch normal mode of each system, from which we compute the vibrational amplitude using Eq. (2). We then determine $\overrightarrow{\mathit{\text{v}}}$ as the product of the normal mode coordinates, normalized and rotated according to the internal coordinate system, and the vibrational amplitude. From the optimized geometry of a model molecule, we slightly displace the atoms involved in the normal mode by $x\overrightarrow{\mathit{\text{v}}}$, where x takes the values of ±0.005 and ±0.010, and conduct single-point energy calculations to acquire their partial charges q′. By plotting q′ (including q₀) against x, we obtain the charge flows dq using a linear regression algorithm. The resulting parameters for the G44_CO and C22_CO models are listed in Tables I and II, respectively.

TABLE I.

Parameters of the G44_CO model. The partial charges q₀ and charge flows dq are in atomic units. The displacements v_x, v_y, and v_z are in the unit of the vibrational amplitude, 0.028 34 Å. The atom numbers before the slashes correspond to those in guanine, and the numbers after the slashes correspond to those in thymine and uracil.

Atom	q0	dq	vx	vy	vz
C5	0.031 08	−0.015 50	−0.008	−0.057	0
C6/4	0.311 75	0.004 30	−0.011	0.815	−0.002
O	−0.359 79	0.028 80	−0.006	−0.497	0.001
N1/3	−0.405 27	−0.012 54	0.038	−0.114	0.007
D	0.226 57	−0.004 70	−0.135	0.150	−0.011
C2	0.195 66	−0.000 36	0.007	0.007	−0.006

TABLE II.

Parameters of the C22_CO model. The partial charges q₀ and charge flows dq are in atomic units. The displacements v_x, v_y, and v_z are in the unit of the vibrational amplitude, 0.02872 Å.

Atom	q0	dq	vx	vy	vz
N1	−0.186 35	−0.018 08	−0.090	−0.145	0
C2	0.482 62	0.000 56	0.119	0.788	0
O	−0.393 51	0.027 70	−0.007	−0.459	0
N3	−0.320 29	−0.002 26	−0.108	−0.117	0
C4	0.215 20	−0.006 50	0.097	0.070	0
C6	0.202 33	−0.001 42	0.011	0.010	0

From Table I, the C=O stretch of cis-NMAD accounts for 91.1% of its vibrational normal mode in the 1600–1800 cm⁻¹ region and the C_6/4–N_1/3–D bending motion also plays a role. As shown in Table II, the C=O stretch contributes to 84.5% of the corresponding normal mode in 1,1-dimethyl-3-methyleneurea. Due to the conjugation between the C=O and N₃=C₄ groups, this normal mode also involves the C₂–N₃ and N₃=C₄ stretches. For both molecules, the sum of $|\overrightarrow{\mathit{\text{v}}}{|}^2$ is less than 1 because the normal mode coordinates of a few terminal atoms are not included [Figs. 2(a) and 2(b)]. Note that in Tables I and II, the heavy atoms are numbered according to their positions in the nucleobases G, C, T, and U (Fig. 1). Considering that the purine base G and the pyrimidine bases T and U have different numbering for the amide groups, we include both notations in Table I.

From previous 2D IR experiments and DFT calculations, the C=O vibrations in cytosine, thymine, and uracil are strongly coupled to a ring mode mainly attributed to the C₅=C₆ stretches.^8,25,43 In addition, our calculations show that when adenine becomes part of the base pairs, its ring mode around 1600 cm⁻¹ also interacts with the chromophores in thymine or uracil. Therefore, we will develop TCC models for the C₅=C₆ stretches in C, T, U, and A to fully model the vibrational spectra of nucleobases in the 1600–1800 cm⁻¹ region.

Considering that the electrons are quantum mechanically delocalized over the C₅, C₆, and other atoms in the conjugated purine and pyrimidine rings, it is necessary to incorporate all the ring atoms in the development of their TCC models. Our DFT calculations further show that the partial charges and charge flows on these atoms are particularly sensitive to the electron-withdrawing groups covalently bonded to the rings. Accordingly, we use three model molecules to develop the parameters for the C₅=C₆ stretches and name the resulting TCC models as C_CC, TU_CC, and A_CC. As demonstrated in Figs. 2(c)–2(e), these include deuterated cytosine for the C_CC model, deuterated uracil for the C₅=C₆ group in both thymine and uracil (TU_CC), and deuterated 4-aminopyrimidine to mimic the ring structure of adenine (A_CC). The internal coordinate system for these molecules is defined such that the molecule is in the xy plane, with the y axis along the $\overrightarrow{{\text{C}}_6{\text{C}}_5}$ direction and the orthogonal x axis pointing toward N₁ in the C_CC and TU_CC models and toward N⁶ in A_CC. The z axis is perpendicular to the molecular plane. Following the same procedure as in the C=O stretch case, we determine the partial charges q₀, the charge flows dq, and the normal modes $\overrightarrow{\mathit{\text{v}}}$ for the three model molecules and list their parameters in Tables III–V. From these tables, we observe that the ring modes mainly concentrate in the xy plane and are delocalized over all the atoms. The C₅=C₆ stretch contributes to 43.3% of the normal mode in cytosine and 45.2% in 4-aminopyrimidine, whereas this ratio increases to 59.5% in uracil.

TABLE III.

Parameters of the C_CC model. The partial charges q₀ and charge flows dq are in atomic units. The displacements v_x, v_y, and v_z are in the unit of the vibrational amplitude, 0.032 28 Å.

Atom	q0	dq	vx	vy	vz
N1	−0.182 42	−0.012 26	0.136	−0.179	0
C2	0.060 84	0.002 32	0.139	0.045	0
N3	−0.391 50	−0.006 00	0.182	−0.219	0
C4	0.366 15	−0.004 06	−0.262	0.320	−0.001
N4	0.006 16	0.012 66	0.026	−0.070	0.007
C5	−0.176 28	0.003 34	−0.030	−0.388	0
C6	0.317 05	0.004 00	−0.215	0.485	0

TABLE IV.

Parameters of the TU_CC model. The partial charges q₀ and charge flows dq are in atomic units. The displacements v_x, v_y, and v_z are in the unit of the vibrational amplitude, 0.033 98 Å.

Atom	q0	dq	vx	vy	vz
N1	−0.174 56	−0.014 46	0.045	−0.212	0
C2	0.167 97	0.002 54	0.146	0.111	0
N3	−0.200 21	0.002 14	0.007	−0.076	0
C4	0.410 82	−0.001 90	−0.026	−0.062	0
O4	−0.342 61	0.000 12	0.027	0.110	0
C5	−0.175 35	0.000 56	−0.086	−0.473	0
C6	0.313 94	0.011 00	−0.164	0.581	0

TABLE V.

Parameters of the A_CC model. The partial charges q₀ and charge flows dq are in atomic units. The displacements v_x, v_y, and v_z are in the unit of the vibrational amplitude, 0.031 70 Å.

Atom	q0	dq	vx	vy	vz
N1	−0.349 67	−0.000 40	0.262	−0.134	−0.008
C2	0.240 50	0.000 88	−0.210	0.324	0.007
N3	−0.307 16	0.008 06	0.081	−0.133	−0.002
C4	0.184 78	0.000 50	−0.337	0.082	0.010
C5	−0.106 01	0.004 86	0.317	−0.384	−0.010
C6	0.343 62	0.000 90	−0.308	0.330	0.011
N6	−0.006 06	−0.014 80	0.094	−0.089	−0.013

B. Validation of the TCC models

To assess the performance of the TCC models, we apply them to a set of model oligonucleotides with well-defined pairing and stacking patterns, as schematically shown in Fig. 3. We start with DNA oligomers of the sequences GGG, AAA, and ATTA that form B- and A-type double helices with their complementary strands [Figs. 3(a)–3(c)]. We then consider a Z-DNA oligonucleotide from the PDB (PDB ID 6AQV), which contains a self-complementary sequence of CGCG and adopts the left-handed Z-form double helix structure [Fig. 3(d)].⁴⁷ As demonstrated in Figs. 3(e) and 3(f), we further consider a model DNA triplex that contains the hydrogen bonded G·GC and T·AT triples held together by both Watson–Crick and Hoogsteen base pairings (taken from PDB ID 134D)⁴⁸ and a two-layer G-quadruplex stabilized by an inter-layer K⁺ ion (from PDB ID 6FQ2).⁴⁹ Apart from the DNA oligomers, we incorporate 3 model RNA oligonucleotides. As shown in Figs. 3(g) and 3(h), these include a double-helical oligomer formed from complementary strands of sequences GAAC and GUUC (from PDB ID 6IA2)⁵⁰ and a duplex with self-complementary sequence of AUGU that contains both Watson–Crick and wobble base pairs (from PDB ID 315D).⁵¹ Finally, we consider an RNA internal loop 5′-GCUU/3′-UUCG that forms the non-canonical G-U and C–U base pairs (from PDB ID 6N8F).⁵²

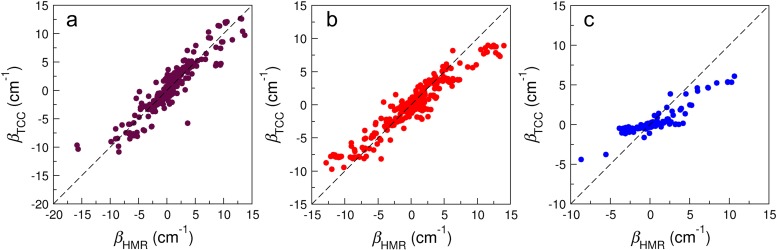
Each test case contains 8–18 C=O and C=C groups in the nucleobases. We calculate the coupling constants between each pair of the chromophores and compare the values predicted from the TCC models, β_TCC, with those from the HMR method, β_HMR. As demonstrated in Fig. 4, β_HMR spans a broad range between −16 cm⁻¹ and +14 cm⁻¹, with the negative and positive values corresponding to attractive and repulsive interactions between the vibrations of the chromophores, respectively. These couplings give rise to concerted vibrations in the normal modes of the oligonucleotides, and their signs determine the relative intensity of the IR absorption peaks.⁵⁹ The TCC models are capable of correctly reproducing the reference values in the full region. For example, when we consider the C=O/C=O interactions in Fig. 4(a), the average β_TCC is only 0.07 cm⁻¹ larger than that of β_HMR and the root-mean-square deviation (RMSD) is 1.55 cm⁻¹. From all the test cases, we find only one outlier with a β_TCC of −5.75 cm⁻¹ and a β_HMR of 3.65 cm⁻¹. This corresponds to the interaction between the C₂=O groups of U3 in Fig. 3(i), in which the two bases reside in strands 1 and 2 in the RNA internal loop and form a “shifted stacking” conformation. As these C=O groups are separated by a very short distance of 3.2 Å, we expect their electron densities to overlap strongly with each other and the TCC scheme to be inadequate to fully describe the interactions, resulting in this qualitatively incorrect prediction. To further examine the impact of the inter-chromophore distances, we consider the C₂=O groups between the U3 and U4 bases in chains 1 and 2 in Fig. 3(i) and find the distances between their midpoints to be 4.7 Å and 4.9 Å, respectively. Accordingly, their β_TCC are 3.87 cm⁻¹ and 3.98 cm⁻¹, respectively, in reasonable agreement with the β_HMR values of 1.84 cm⁻¹ and 1.71 cm⁻¹.

FIG. 4.

Correlation plots of β_TCC and β_HMR for the couplings between (a) the C=O groups, (b) the C=O and C=C groups, and (c) the C=C groups.

For the C=O/C=C couplings in Fig. 4(b), the average β_TCC is 0.16 cm⁻¹ smaller than that of β_HMR and the RMSD between them is 1.54 cm⁻¹. We notice that the TCC models slightly underestimate the C=O/C=C coupling constants when β_HMR is above +8 cm⁻¹ or below −8 cm⁻¹. Comparing the TCC parameters in Tables I–V, we find that the atomic charge flows dq accompanying the C=C vibrations are much smaller than those with the C=O vibrations. Therefore, factors other than electrostatics might have considerable contribute to the C=C vibrational modes, especially when they are in close proximity to other chromophores and the interactions are strong. This underestimation is even more prominent for the C=C/C=C couplings. As shown in Fig. 4(c), the correlation between β_TCC and β_HMR is much weaker compared to the C=O/C=O and C=O/C=C interactions. The absolute values of β_TCC are, in general, smaller than those of β_HMR, particularly when the couplings become larger. This phenomenon again indicates that non-electrostatic forces such as dispersion and polarization might play a role in determining how the C=C groups interact with each other. Despite this lack of agreement, we note that the C=C/C=C couplings are usually within 5 cm⁻¹ and the RMSD between β_TCC and β_HMR is 1.68 cm⁻¹, comparable to the other two cases. In addition, only 17% of all the inter-base interactions are between the C=C vibrations. Therefore, we will still implement the TCC model to describe the C=C/C=C interactions and their impact on the overall spectra in the 1600–1800 cm⁻¹ region is expected to be small.

In Tables I–V, we obtained the atomic charges and charge flows, q₀ and dq, from the Mulliken population analysis.^57,58 To further validate the TCC models, we repeat the parameterization using natural population analysis (NPA)⁶⁰ and apply the resulting models to compute the coupling constants in the model oligonucleotides, which we will refer to as ${\beta }_{\mathrm{T}\mathrm{C}\mathrm{C}}^{NPA}$. Taking the B-form double helix [Fig. 3(a)] as an example, we analyze 33 inter-base interactions that involve both the C=O and C=C chromophores and observe a maximal difference of 1.8 cm⁻¹ between the predicted β_TCC and ${\beta }_{\mathrm{T}\mathrm{C}\mathrm{C}}^{NPA}$ values. Compared to β_HMR, the RMSD is 1.53 cm⁻¹ for β_TCC and 1.65 cm⁻¹ for ${\beta }_{\mathrm{T}\mathrm{C}\mathrm{C}}^{NPA}$, demonstrating that the TCC parameterization does not have a strong dependence on the method for partial charge assignment.

C. Through-bond couplings in the pyrimidine bases

As demonstrated in Fig. 1, the pyrimidine bases C, T, and U contain multiple chromophores. In cytosine, the C₂=O and C₅=C₆ vibrations both absorb in the 1600–1800 cm⁻¹ region. Thymine and uracil further have the C₄=O stretch as a chromophore. These C=O and C=C groups are part of the conjugated rings and are linked by covalent bonds, leading to significant overlap between their electron densities. As such, the electrostatic TCC scheme is not sufficient to model the through-bond couplings between them, and methods that account for the full electronic quantum effects are required to provide the correct description.

Constrained by the pyrimidine ring structures, the C=O and C=C groups have relatively fixed positions and orientations with respect to each other throughout the MD simulations. Hence, it is reasonable to assume that these intra-base couplings take constant values. In a previous work, we used deoxycytidine, deoxythymidine, and uridine 5′-monophosphates (CMP, TMP, and UMP, respectively) as model molecules to calculate the through-bond coupling constants.⁴³ Specifically, we performed MD simulations of CMP, TMP, and UMP in water and extracted a total of 1200 solute–solvent clusters, for which we combined DFT calculations and the HMR method to obtain the off-diagonal elements of the vibrational Hamiltonian. The average values of these intramolecular couplings are listed in Table VI.⁴³ In the pyrimidine bases, stretching the C₂=O and C₅=C₆ groups simultaneously decreases their interaction energy, giving rise to negative coupling constants [Eq. (1)]. In contrast, vibrations of the other chromophores in thymine and uracil exhibit repulsive interactions and their corresponding coupling constants are positive.

TABLE VI.

Intramolecular coupling constants (in cm⁻¹) for the pyrimidine bases.⁴³

Nucleobase	C2=O/C4=O	C2=O/C5=C6	C4=O/C5=C6
C	…	−10.57	…
T	17.27	−8.16	6.26
U	18.55	−9.35	16.20

As a validation, we compute the intramolecular couplings in the oligonucleotide test cases (Fig. 3) and compare them to the values in Table VI. We first consider the C₂=O/C₄=O interactions in thymine and uracil and find the average β_HMR from the model oligonucleotides to be 14.40 cm⁻¹ and 16.45 cm⁻¹, respectively. These values are close to the coupling constants of 17.27 cm⁻¹ and 18.55 cm⁻¹ from the calculations of TMP and UMP, respectively, as shown in Table VI. Furthermore, β_HMR of the intramolecular C₂=O/C₄=O interactions sample a narrow range with a standard deviation of 0.63 cm⁻¹ for thymine and 1.27 cm⁻¹ for uracil, justifying our assumption that these couplings can be approximately treated as constants. Similarly, the average β_HMR of the C₂=O/C₅=C₆ and C₄=O/C₅=C₆ interactions in thymine and uracil are −9.26 cm⁻¹, 7.70 cm⁻¹, −10.15 cm⁻¹, and 16.32 cm⁻¹, respectively, and their standard deviations are all within 1.6 cm⁻¹. In all cases, the average β_HMR differ from the corresponding values in Table VI by less than 1.5 cm⁻¹, demonstrating that these interactions stay more or less constant in different environments around the nucleobases. For cytosine, the average β_HMR of the C₂=O/C₅=C₆ interaction is −9.66 cm⁻¹, very close to the value of −10.57 cm⁻¹ in Table VI. However, the standard deviation is 3.60 cm⁻¹, suggesting that the intra-base coupling in cytosine depends more on their chemical environment as compared to the other types of through-bond couplings.

D. Sensitivity of the coupling constants to the stacking and pairing of nucleobases

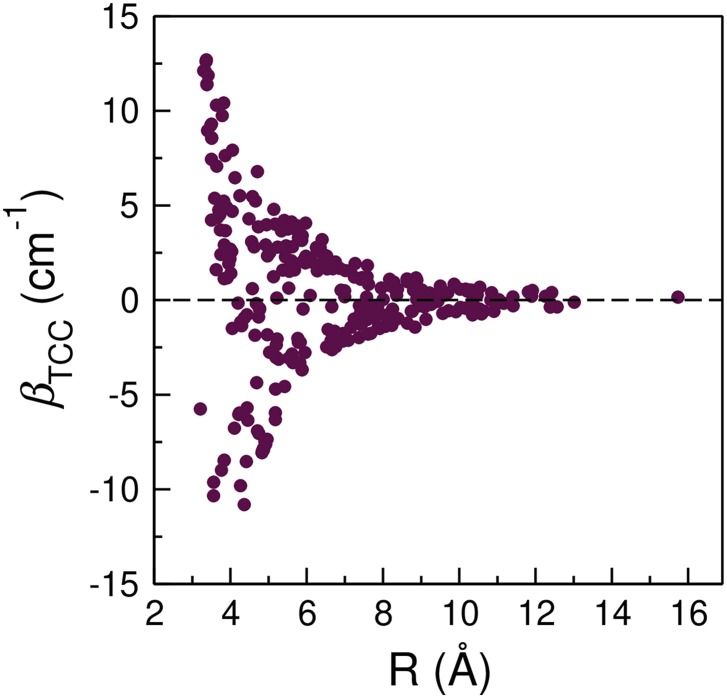
From Fig. 4, the vibrational couplings vary over a range of 30 cm⁻¹ depending on the three-dimensional arrangements of the nucleobases, and hence they provide a sensitive probe to the structures of nucleic acids. Among the factors that determine the coupling constants, the separation and relative angle between two chromophores, R and ϕ, are of particular interest. As an example, we plot β_TCC of the C=O/C=O interactions as a function of R, calculated as the distance between the midpoint of the C=O groups (Fig. 5). In general, the magnitude of the coupling constants follows an inverse relationship with R, in good agreement with the findings of previous DFT studies.^25,26 As R lengthens from 3.4 Å to 7 Å, the average coupling constants exhibit a 92% reduction in magnitude from 11.28 cm⁻¹ to −0.94 cm⁻¹. From Fig. 5, β_TCC sample different signs and magnitudes at a given R, which arises from the variation of ϕ in the model oligonucleotides. In the following, we will examine the systems in which R between the C=O groups are short to elucidate how the distance and angle between two chromophores influence their coupling constant.

FIG. 5.

Correlation between the C=O/C=O coupling constants and R. The coupling constants are predicted from the TCC models.

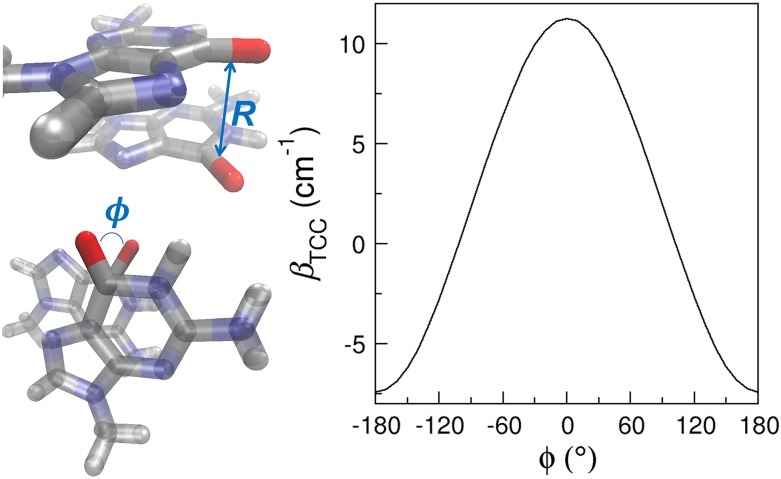
When R < 3.55 Å, the nucleobases are mostly in stacking configurations. Despite the short distances, there are considerable fluctuations in the C=O/C=O coupling constants, as shown in Fig. 5. For example, β_TCC is 12.69 cm⁻¹ for the stacked G1 and G2 in a model A-DNA with a R of 3.4 Å [Fig. 3(a)]. However, the coupling constant becomes 4.23 cm⁻¹ when the C₄=O groups in U3 and U4 of strand 1 in Fig. 3(i) have a distance of 3.5 Å. As the stacked bases are almost parallel to each other, this fluctuation in β_TCC mainly arises from the twist angle between their molecular planes. To elucidate its impact, we construct a model system consisted of two 9-methylguanine (mG) molecules stacked together, as depicted in Fig. 6. We place the two mG molecules in a parallel conformation so that the twist angle can be well represented by the angle between the two C=O groups, ϕ. We then fix R between the C=O groups at 3.5 Å and rotate one of the mG molecules about an axis perpendicular to its molecular plane. As shown in Fig. 6, the resulting β_TCC exhibit a strong variation with the angle and are symmetric about ϕ = 0. At a constant R of 3.5 Å, β_TCC reaches a maximum of 11.26 cm⁻¹ at ϕ = 0 and decreases to 6.58 cm⁻¹ when ϕ = 60°. As one further increases ϕ to over 100°, β_TCC becomes negative. Therefore, together with R, ϕ determines the sign and magnitude of the coupling constants. In the two cases described above, ϕ are 32° and 50° between the C=O groups in the stacked guanine [Fig. 3(a)] and uracil [Fig. 3(i)] bases, and hence their couplings are both positive and there is a 3-fold difference in their magnitude.

FIG. 6.

Model system containing two mG molecules in a stacking configuration and the dependence of its coupling constant on ϕ. In the mG dimer, silver, red, blue, and white represent C, O, N, and H, respectively.

One can use the mG dimer in Fig. 6 to elucidate how the stacking interactions influence the absorption peaks in the IR spectra. In a standard B-DNA, the twist angle is 36° ⁶¹ and it gives a β_TCC of 9.45 cm⁻¹. As the C=O stretch frequency of mG is 1746.14 cm⁻¹ from the DFT calculations in vacuum, the vibrational Hamiltonian of the mG dimer in a B-form double helix is

$${\kappa }_{\mathrm{G}\mathrm{G}}=\left(\begin{array}{cc}\hfill 1746.14\hfill & \hfill 9.45\hfill \\ \hfill 9.45\hfill & \hfill 1746.14\hfill \end{array}\right).$$

After diagonalizing κ_GG, one obtains the normal mode frequencies of 1736.69 cm⁻¹ and 1755.59 cm⁻¹. Therefore, at a R of 3.5 Å, the stacking of two mG bases gives rise to two absorption peaks separated by 2 × β_TCC = 18.90 cm⁻¹.

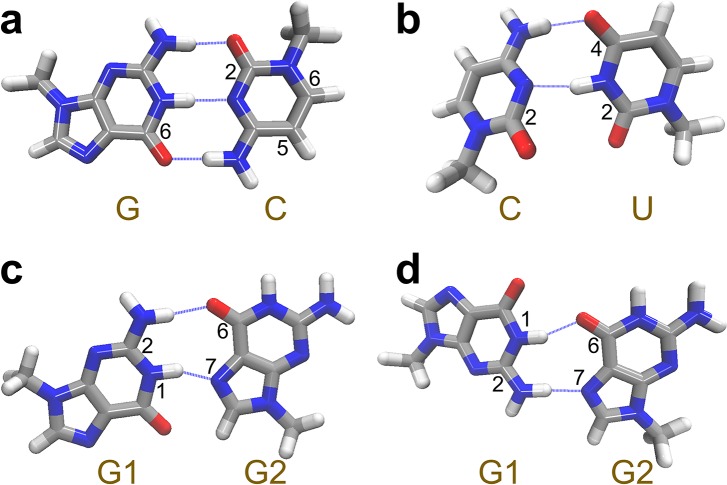
In addition to stacking, hydrogen bonding interactions bring the nucleobases together, resulting in R and ϕ between the C=O groups and characteristic coupling patterns. We will use the Watson–Crick G-C pair as an example [Fig. 7(a)]. From the model systems in Fig. 3, we find an average R of 4.9 Å between the C=O chromophores in the G-C pairs, giving an average β_TCC of −7.56 cm⁻¹, consistent with previous values obtained from DFT calculations and 2D IR experiments.^23,25 Here, the coupling constant is negative because the C=O groups have almost antiparallel alignment with an average ϕ of 171°. Similar arrangements of the C=O groups are observed in non-canonical hydrogen bonding patterns such as G-U wobble pairs and Hoogsteen pairs, producing large and negative coupling constants. For example, Fig. 7(b) demonstrates that the C–U base pair in an RNA internal loop [Fig. 3(i)] has an average R of 4.7 Å and ϕ of 145° between the C₂=O of cytosine and C₄=O of uracil, giving an average β_TCC of −6.98 cm⁻¹. In the model DNA triplex [Fig. 3(e)], the G·GC triple involves a Hoogsteen pair between the two guanine bases. As shown in Fig. 7(c), this base pair is held together by a hydrogen bond between the N²–H group of one guanine (G1) and the O⁶ atom of the other guanine (G2), and a second hydrogen bond between the N₁–H group of G1 and the N₇ atom of G2. The resulting R is 5.2 Å and ϕ is 169° between the C=O groups in G1 and G2, resulting in a β_TCC of −5.95 cm⁻¹.

FIG. 7.

Representative base pairing patterns that produce characteristic coupling constants. Silver, red, blue, and white represent C, O, N, and H, respectively.

While the C=O/C=O coupling constants in most of the base pairs are negative, they can also take positive values when the chromophores are arranged such that their ϕ are less than 100°. For example, compared to Figs. 7(c), G1 has a flipped configuration in the Hoogsteen base pairs of the G-quadruplex [Fig. 7(d)]. This leads to an average R of 3.9 Å and ϕ of 90° between the two C=O groups in the G-quadruplex, giving a β_TCC of +3.66 cm⁻¹. Furthermore, the average R and ϕ between the C₂=O groups in cytosine and uracil in the C–U base pair [Fig. 7(b)] are 3.8 Å and 62°, respectively. Due to their closer distance and more parallel orientation, the corresponding β_TCC of +10.08 cm⁻¹ is larger than that in the G-quadruplex. From these analyses, the vibrational couplings are strongly dependent on the base pairing geometries. They are sensitive to the hydrogen bonding patterns in Watson–Crick and C–U base pairs and have distinct values and signs for different types of Hoogsteen base pairs.

We now consider a Watson–Crick G-C pair, which is composed of mG and 1-methylcytosine (mC), to demonstrate the impact of hydrogen bonding on the IR absorption peaks. As shown in Fig. 7(a), this dimer system contains the C₆=O chromophore of mG and the C₂=O and C₅=C₆ chromophores of mC, and hence its vibrational Hamiltonian is a 3 × 3 matrix. To obtain the diagonal elements of the Hamiltonian, we replace C₆=O in mG and C₂=O in mC, one at a time, by the C=S group to remove their interactions while keeping the hydrogen bonding environment. After optimizing the mutated G-C dimers in vacuum and applying the HMR method, we find the site frequencies of the C₆=O stretch in mG and the C₂=O and C₅=C₆ stretches in mC to be 1675.55 cm⁻¹, 1652.62 cm⁻¹, and 1636.67 cm⁻¹, respectively. For the off-diagonal elements of the Hamiltonian, we acquire the intermolecular coupling constants from the TCC models and the intramolecular coupling constant in mC from Table VI. The resulting vibrational Hamiltonian of the G-C pair is

$${\kappa }_{\mathrm{G}\mathrm{C}}=\left(\begin{array}{ccc}\hfill 1675.55\hfill & \hfill -7.67\hfill & \hfill 8.83\hfill \\ \hfill -7.67\hfill & \hfill 1652.62\hfill & \hfill -10.57\hfill \\ \hfill 8.83\hfill & \hfill -10.57\hfill & \hfill 1636.67\hfill \end{array}\right).$$

By diagonalizing κ_GC, we obtain the eigenvalue matrix Ω_GC and the normal mode matrix U_GC,

$${\mathrm{\Omega }}_{\mathrm{G}\mathrm{C}}=\left(\begin{array}{ccc}\hfill 1681.00\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1652.93\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1630.91\hfill \end{array}\right),$$

$$U_{\mathrm{G}\mathrm{C}}=\left(\begin{array}{ccc}\hfill 0.90\hfill & \hfill 0.41\hfill & \hfill -0.11\hfill \\ \hfill -0.34\hfill & \hfill 0.85\hfill & \hfill 0.40\hfill \\ \hfill 0.26\hfill & \hfill -0.33\hfill & \hfill 0.91\hfill \end{array}\right).$$

Here, we observe three prominent influences of the hydrogen bonding interactions on the vibrational Hamiltonian, and hence the vibrational spectra of the G-C pair. First, they significantly reduce the site frequencies of the C=O groups. From DFT calculations of isolated mG and mC in the gas phase, the site frequencies of C₆=O in mG and C₂=O in mC are 1746.14 cm⁻¹ and 1710.21 cm⁻¹, respectively. This means that the formation of hydrogen bonds between the carbonyl and amino groups in guanine and cytosine red shifts their C=O frequencies by 70.59 cm⁻¹ and 57.59 cm⁻¹, respectively. In contrast, as the C₅=C₆ group does not participate in the base pairing interactions, its site frequency is almost unchanged as compared to the gas-phase value of 1635.65 cm⁻¹ in isolated mC. These observations are in good agreement with previous DFT calculations on paired bases.²⁶ Second, the hydrogen bonding interactions bring the C=O and C=C groups close together, leading to coupling constants that have the magnitude around 10 cm⁻¹. These large couplings further increase the separation of the normal mode frequencies, giving three absorption peaks at 1681.00 cm⁻¹, 1652.93 cm⁻¹, and 1630.91 cm⁻¹. Finally, due to the strong couplings, the vibrational normal modes of the G-C pair are delocalized over all 3 chromophores. For example, the peak at 1652.93 cm⁻¹ arises mostly (72%) from the C₂=O stretch of mC, while the contributions of C₆=O in mG and C₅=C₆ in mC are 17% and 11%, respectively. We note that the vibrational Hamiltonian is computed from the paired mG and mC in vacuum, and one can obtain more accurate predictions by incorporating the impact of the condensed phase environment and the structural fluctuations.

E. Comparison to the TDC scheme

In the TDC scheme, one assumes that the distances between two chromophores are sufficiently long that the interactions are mainly due to their transition dipole moments.^29,34 Within this scheme, the coupling between two chromophores i and j is^35,37

$${\beta }_{ij}=\frac{C}{\epsilon }\left[\frac{{\overrightarrow{m}}_i\cdot {\overrightarrow{m}}_j}{R^3}-3\frac{\left({\overrightarrow{m}}_i\cdot {\overrightarrow{r}}_{ij}\right)\left({\overrightarrow{m}}_j\cdot {\overrightarrow{r}}_{ij}\right)}{R^5}\right].$$ (10)

Here, ${\overrightarrow{m}}_i$ is the transition dipole of the ith C=O or C=C chromophore and ${\overrightarrow{r}}_{ij}$ is the vector connecting the two chromophores, which points from i to j. The transition dipoles are placed at the midpoint of the C=O or C=C bond. R is the distance between the chromophores, which is calculated as the magnitude of ${\overrightarrow{r}}_{ij}$ and has the unit of Å. ε is the dielectric constant of the medium and is taken to be 1. The conversion factor $C=84861.9/\sqrt{{\omega }_i{\omega }_j}$, which gives the coupling in cm⁻¹. Here, ω_i is the unperturbed frequency of chromophore i, and we take 1650³⁰ and 1627 cm⁻¹ for its value for the C=O and C=C vibrations, respectively. To compute β_ij using Eq. (10), one needs the direction and magnitude of the transition dipole of each chromophore. From our previous DFT calculations, we find that $\overrightarrow{m}$ of a C=O chromophore points from O toward the N atom that is covalently bonded to the carbonyl group with an angle of 3.65° from the $\overrightarrow{\mathrm{O}\mathrm{C}}$ direction. For the pyrimidine bases, the N₃ atom is used to define the direction of the transition dipoles. The magnitude of the carbonyl transition dipole is 2.57 D·Å⁻¹·u^−1/2,⁴³ where u represents the atomic mass unit, consistent with the values determined from previous DFT calculations and 2D IR experiments.^23,26 For a C=C group in cytosine, thymine, and uracil, $\overrightarrow{m}$ is along the chemical bond pointing from C₅ to C₆ with a magnitude of 1.44 D·Å⁻¹·u^−1/2.⁴³

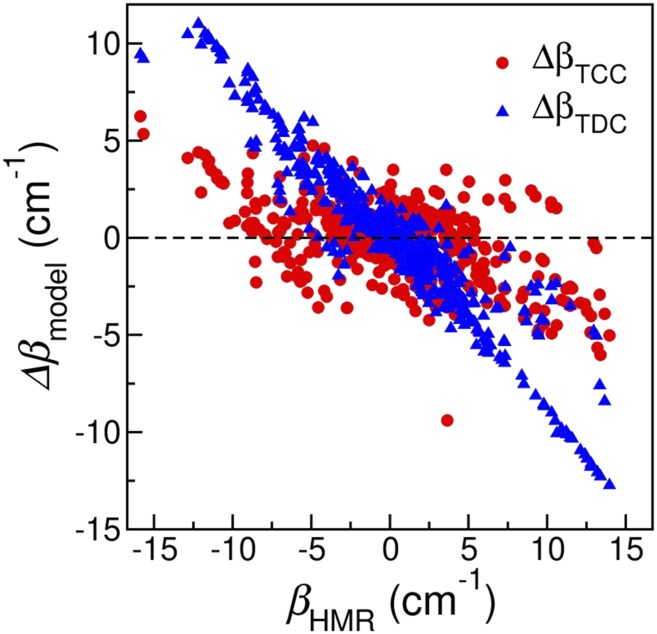
Using the TDC models, we repeat the calculations on the oligonucleotide test cases. We then use the coupling constants from the HMR method as reference values and calculate the error of the TCC and TDC models as Δβ_TCC = β_TCC − β_HMR and Δβ_TDC = β_TDC − β_HMR, respectively. As shown in Fig. 8, over the whole range of β_HMR, Δβ_TCC mostly fluctuate between −5 cm⁻¹ and +5 cm⁻¹ with an average of −0.06 cm⁻¹. There is one outlier with a Δβ_TCC of −9.40 cm⁻¹, which corresponds to the U3 base from both strands in Fig. 3(i). In contrast, the TDC model systematically underestimates the coupling constants predicted from the HMR method, with Δβ_TDC varying from −12.74 cm⁻¹ to +11.00 cm⁻¹. This underestimation is most prominent when the magnitude of β_HMR is larger than 10 cm⁻¹, which arises in 3 types of spatial arrangements of the nucleobases.

FIG. 8.

Error in the coupling constants predicted from the TCC (red) and TDC (blue) models as a function of β_HMR.

The first type is base pairing. For example, in a C–U base pair [Fig. 7(b)], β_HMR between the C₂=O groups of cytosine and uracil is +13.66 cm⁻¹. Compared to a Δβ_TCC of −3.91 cm⁻¹, the TDC model underestimates the coupling constant by 8.41 cm⁻¹. Similarly, in a G-U wobble pair with a β_HMR of −15.87 cm⁻¹, Δβ_TDC is as large as 9.44 cm⁻¹. These observations are further supported by the findings that the TDC method cannot quantitatively capture the C=O/C=O couplings between Watson–Crick base pairs.^23,25 In these cases, R between the C=O groups is below 3.8 Å. The underestimation indicates that the dipole approximation is not sufficient to capture the full interactions and high-order multipoles must be included to provide the correct description. We observe similar behavior for the C=O/C=C couplings in paired bases. As an example, the C–U base pair in Fig. 7(b) has a β_HMR of +13.39 cm⁻¹ between the C₅=C₆ group in cytosine and the C₄=O group in uracil, for which Δβ_TDC is −12.28 cm⁻¹. Likewise, in the B-form double helix formed from DNA sequences AAA and TTT [Fig. 3(b)], the average β_HMR between the C₅=C₆ group of adenine and the C₄=O group of thymine is −11.59 cm⁻¹, while the average Δβ_TDC is 10.41 cm⁻¹. Here, R between the C=O and C=C groups are 4.0–5.9 Å, slightly longer than those between the C=O groups. From Fig. 2, the atoms involved in the G44_CO and C22_CO models are around the C=O chromophore, whereas the atoms in the C=C models are distributed over the entire pyrimidine rings. For example, from DFT calculations of a Watson–Crick G-C pair in its optimized conformation, atoms N₃ and N⁴ in cytosine contribute to 83% of the C=O/C=C interactions. As a result, these C=O/C=C coupling constants remain large even when R between the C=O and C=C groups are long, which cannot be explained by the TDC model.

The second type is base stacking. For example, in an A-form double helix in Fig. 3(c), β_HMR between the C₅=C₆ group of A1 and the C₄=O group of T2 in strand 1 is −12.00 cm⁻¹, for which Δβ_TCC is 2.33 cm⁻¹ and Δβ_TDC is 9.94 cm⁻¹. In another model A-DNA as shown in Fig. 3(b), β_HMR of the C₅=C₆ vibrations of bases A2 and A3 is +10.29 cm⁻¹, and the TDC model underestimates it by 9.00 cm⁻¹. Apart from the first 2 types, we also observe a few cases of the shifted stacking configurations that result in large coupling constants. As shown in Fig. 3(d), C1 of strand 1 partially stack with C3 of strand 2, giving rise to a β_HMR of +11.48 cm⁻¹ between their C=O groups. For this case, Δβ_TCC is comparable to Δβ_TDC with values of −2.52 cm⁻¹ and −3.51 cm⁻¹, respectively. Similarly, in an A-form double helix [Fig. 3(c)], A4 of strand 1 and A2 of strand 2 form the shifted stacking geometry with a β_HMR of 10.61 cm⁻¹. For this system, Δβ_TDC is −10.07 cm⁻¹, much larger than the Δβ_TCC value of −4.50 cm⁻¹.

From Fig. 8, the TDC models can quantitatively predict the coupling constants only when the interactions of the chromophores are relatively weak. To further evaluate their applicability, we compute the average Δβ_TDC for a given β_HMR and assume that the TDC models are adequate if the average Δβ_TDC is less than 3 cm⁻¹. This gives β_HMR to be in a range of −5 to +5 cm⁻¹, which corresponds to R between 3.2 Å and 15.7 Å. When R is relatively short (<6 Å), configurations with these small coupling constants have an average ϕ of 82.6°. As R increases to above 8 Å, both the TCC and TDC models give quantitatively correct predictions. For example, for these long-range interactions between the C=O groups, the RMSD of β_TCC and β_TDC are 0.53 cm⁻¹ and 0.52 cm⁻¹, respectively, as compared to the reference β_HMR values. Likewise, the RMSD from the two models are 0.63 cm⁻¹ and 0.80 cm⁻¹, respectively, for the C=C/C=C interactions. Note that in our implementation of the TDC scheme, we placed the origin of the transition dipole moments at the midpoint of the C=O and C=C bonds and determined their magnitudes and directions from the DFT calculations of methylated guanine and thymine.⁴³ One can possibly improve the performance of the TDC method by optimizing the location, magnitude, and direction of the transition dipoles using a set of model oligonucleotides.

IV. CONCLUSIONS

In this work, we develop a set of TCC models to describe the interactions of the C=O and C=C groups between nucleobases. By applying them to oligonucleotides with well-defined base paring and stacking patterns, we demonstrate that the TCC models are capable of quantitatively capturing the coupling constants as compared to the results obtained from DFT calculations and the HMR method and provide an efficient way to obtain the inter-base interactions between the chromophores based on the structures of nucleic acids. As the TCC scheme is electrostatic in nature, it is not sufficient to describe the through-bond interactions between the chromophores in pyrimidine bases, and we provide these intra-base coupling constants by approximating them as constant values.⁴³ Combining the inter- and intra-base couplings, we demonstrate how the stacking and pairing of bases result in characteristic absorption peaks in the IR spectra. We further compare the TCC and TDC models and show that the dipole approximation is only valid when the β_HMR is between −5 cm⁻¹ and +5 cm⁻¹ and higher-order multipoles are required to capture stronger interactions between chromophores.

A widely used approach in spectroscopy modeling is the mixed quantum/classical approximation. For nucleobases in the 1600–1800 cm⁻¹ region, we treat the vibrational subspace constituted by the C=O and C=C chromophores quantum mechanically, ignore the higher-frequency modes, and treat all the other degrees of freedom as a classical bath. Within this approach, the Hamiltonian in the vibrational subspace is of central importance. In a previous work, we have developed vibrational frequency maps that effectively model the site frequencies of the C=O and C=C stretches from their local electrostatic environment, which provide the diagonal terms of the vibrational Hamiltonian.⁴³ The TCC models, in conjunction with the through-bond coupling constants, allow one to accurately and efficiently acquire the off-diagonal elements. These methods provide a theoretical framework to predict the vibrational Hamiltonian, and hence the vibrational spectra of nucleic acids directly from classical MD simulations. Hence, it bridges atomistic simulations and vibrational spectroscopy experiments and helps elucidate the structure and dynamics of nucleic acids that give rise to the observed spectral features at the molecular level.