Correlation of normal lung density changes with dose after stereotactic body radiotherapy (SBRT) for early stage lung cancer

Highlights

• •There is a strong positive correlation between HU changes in the peri-tumoral region and the grade of RP after SBRT for NSCLC.
• •V20, MLD, and gEUD are significantly correlated with RP grade.
• •Relative to model-based methods, PB algorithms overestimate mean peri-tumoral dose.
• •Relative to model-based methods, PB algorithms show a 10–15% volume displacement of the high-dose region.

Abstract

Background and Purpose

To investigate the correlation between normal lung CT density changes with dose accuracy and outcome after stereotactic body radiation therapy (SBRT) for patients with early stage non-small-cell lung cancer (NSCLC).

Materials and Methods

Thirty-one patients (with a total of 33 lesions) with non-small cell lung cancer were selected out of 270 patients treated with SBRT at a single institution between 2003 and 2009. Out of these 31 patients, 10 patients had developed radiation pneumonitis (RP). Dose distributions originally planned using a 1-D pencil beam-based dose algorithm were retrospectively recomputed using different algorithms. Prescription dose was 48 Gy in 4 fractions in most patients. Planning CT images were rigidly registered to follow-up CT datasets at 3–9 months after treatment. Corresponding dose distributions were mapped from planning to follow-up CT images. Hounsfield Unit (HU) changes in lung density in individual, 5 Gy, dose bins from 5 to 45 Gy were assessed in the peri-tumoral region. Correlations between HU changes in various normal lung regions, dose indices (V20, MLD, generalized equivalent uniform dose (gEUD)), and RP grade were investigated.

Results

Strong positive correlation was found between HU changes in the peri-tumoral region and RP grade (Spearman’s r = 0.760; p < 0.001). Positive correlation was also observed between RP and HU changes in the region covered by V20 for all algorithms (Spearman’s r ≥ 0.738; p < 0.001). Additionally, V20, MLD, and gEUD were significantly correlated with RP grade (p < 0.01). MLD in the peri-tumoral region computed with model-based algorithms was 5–7% lower than the PB-based methods.

Conclusion

Changes of lung density in the peri-tumoral lung and in the region covered by V20 were strongly associated with RP grade. Relative to model-based methods, PB algorithms over-estimated mean peri-tumoral dose and showed displacement of the high-dose region, which correlated with HU changes on follow-up CT scans.

1. Introduction

Stereotactic body radiation therapy (SBRT) is an excellent option for the treatment of stage I non-small cell lung cancer (NSCLC) in medically inoperable patients, with high local control rates (up to 94% at 3 years) comparable to those reported in surgical series [1], [2], [3], [4], [5], [6], [7], [8], [9]. A National Cancer Data Base Analysis has also supported the use of SBRT for the treatment of elderly patients with comorbid conditions [10], and a systematic review demonstrated that SBRT achieved comparable outcomes to surgical resection in patients with severe chronic obstructive pulmonary disease (COPD) [11]. In a recent trial by Navarro-Martin et al., lung toxicity with lung SBRT was found to be very minimal, even in patients with baseline poor lung function, with no significant changes at 36 months in forced expiratory vital capacity (FVC), forced expiratory volume in 1 s (FEV1), and diffusing lung capacity for carbon monoxide (DLCO) [4].

With the advent of modern highly conformal radiation treatment techniques, such as SBRT, and the increasing use of small field dosimetry, accuracy in treatment planning, including dose calculation and delivery, has become more important [12], [13]. Systems for immobilization, careful patient positioning and tracking of respiratory motion have allowed more accurate radiation dose delivery [14]. However, in heterogeneous patient tissues, such as the thoracic region, dose calculation can sometimes be challenging, and accurate dose algorithms are of paramount importance to determine actual dose received by the tumor and the surrounding normal structures. The Monte Carlo (MC) method has been shown to be very accurate in radiotherapy dose calculations for treatment planning, and is ideal for complex dose delivery scenarios in heterogeneous tissues [15], [16]. Retrospective calculation using MC-based algorithms in patients enrolled in Radiation Therapy Oncology Group (RTOG) 0915 for the treatment of peripheral NSCLC lesions indicated that only 25% actually met the RTOG dosimetric criteria, including conformity index and ratio of 50% isodose volume to PTV [17]. Literature on the correlation of MC–based dose distributions and outcome, in the context of SBRT for treatment of lung cancer, is limited [18].

One of the dose-limiting organs in SBRT for NSCLC is the lung parenchyma. Radiation pneumonitis (RP) is an interstitial lung inflammation, the acute or early-stage component of which can occur within 6 months after radiation therapy, while the chronic or late-stage fibrotic remodeling process can continue for up to two years after treatment [19], [20], [21], [22]. A systematic review on patient-related and treatment plan-related factors revealed that pulmonary function, dose-volume histogram parameters and plasma transforming growth factor beta 1 (TGF-β1) were significant predictors of RP development [23]. Multiple studies have consistently reported a significant association of specific dose-volume histogram (DVH) parameters or a combination of these parameters, such as NTCP, mean lung dose (MLD) and percentage of total lung volume that received a dose of at least 20 Gy (V20), with RP risk [24], [25], [26], [27], [28], [29], [30], [31]. A study by Ong et al. showed that in lung tumors >80 cm [3], acute RP was best predicted by the volume of contralateral lung receiving ≥5 Gy (V5) [32]. However, these studies are heterogeneous in that they used different RP scoring systems, cutoff values and endpoints. Also, NTCP, MLD, and V20 were shown not to have a high predictive power in a systematic review by Rodrigues et al.; thus the optimal DVH metric for RP risk stratification and prediction, either alone or in combination with other variables in a model, has not yet been clearly identified [33]. A better grasp of the correlation between dosimetric data and radiologically and/or clinically detectable normal lung tissue complication would allow for safer treatment delivery.

In 2010, Palma et al. reported a new method for quantification of radiation lung injury using normal lung computed tomography (CT) density changes [34]. This method was also shown to potentially allow for differentiation of SBRT-induced lung changes from tumor recurrence [35].

In this study, we sought to investigate the correlation of normal lung CT density changes with (1) dose accuracy and (2) radiation pneumonitis outcomes after SBRT for patients with early stage lung cancer.

2. Materials and methods

2.1. Patient selection and toxicity scoring

Thirty-one patients (with a total of 33 lesions) with non-small cell lung cancer were selected out of 270 patients treated with SBRT at our institution between 2003 and 2009. Radiation pneumonitis (RP) was graded using the National Cancer Institute’s Common Terminology Criteria for Adverse Events (CTCAE) version 4.03 [36], based on retrospective medical chart review by two radiation oncologists who were blinded to the HU changes in lung density. The CTCAE grading system incorporates patient symptoms (including cough, fever and dyspnea), radiological manifestations of lung injury, as well as patient requirements for steroids, oxygen or assisted ventilation.

Given the low incidence of RP (<4%) among early stage NSCLC patients treated with SBRT at our institution, patient selection was weighted to include all patients with RP, such that follow-up CT changes could be analyzed and correlated with outcome. Therefore, of the 31 patients selected, 6 and 4 were scored to have grades 1, and 2 RP, respectively, with 21 scored as grade 0 (no evidence of RP).

2.2. Treatment planning and analysis

Each patient underwent a four-dimensional computed tomography (4D-CT) simulation for management of respiratory-induced motion. The 4D-CT was sorted into four datasets corresponding to the inhale, mid-inhale, exhale, and mid-exhale positions. A physician contoured the gross tumor volume (GTV) on these datasets to form the internal target volume (ITV). The planning target volume (PTV) was generated by a 5 mm isotropic expansion of the ITV.

Dose distributions for lung tumors originally planned and treated using a 1-D pencil beam-based (PB-1D) dose algorithm (within the Brainscan/iPlan Treatment planning System (TPS), BrainLab, Feldkirchen, Germany) were retrospectively recomputed using the following algorithms: 3-D pencil beam (PB-3D, within the Eclipse TPS, Varian, Palo Alto, CA), and model-based methods: analytic anisotropic algorithm (AAA, Eclipse TPS), Acuros XB (AXB, Eclipse TPS), and a Monte Carlo (MC)-based algorithm (iPlan, BrainLab TPS). Commissioning was performed for these five algorithms in water, and solid-water slab-phantoms containing bone- and lung-equivalent materials [37].

The same beam configuration and monitor units (MUs) used in the PB-1D plan were used in the 4 other recalculated plans. Prescription dose was 12 Gy × 4 fractions (corresponding to a biologically effective dose (BED) of 105.6 Gy, assuming an alpha/beta ratio of 10). Dose was prescribed to the 95% isodose line covering the PTV. Doses to organs at risk were planned based on our standard normal tissue constraints for SBRT of NSCLC (4 fractions): V20 < 10% for both lungs minus ITV; D_max < 25 Gy for the esophagus; D_max < 20 Gy for the spinal canal and D_max < 35 Gy for the proximal bronchial tree. Intensity-modulated radiation therapy (IMRT) or three-dimensional conformal radiation therapy (3D-CRT) was selected to optimize both target coverage and normal tissue dose constraints.

Routine patient follow-up visits were typically performed at 3, 6 and 9 months, with diagnostic chest CT scans performed at these time points. Planning CT images were rigidly registered to the follow-up CT datasets at 5.2 ± 1.9 months (range: 3–9) months after treatment. The accuracy of the registration was assessed using landmarks such as vertebral bodies, sternal notch, ribs and bilateral lung apices. Corresponding dose distributions were mapped from the planning to follow-up CT images. Following the method of Palma et al. [34], [38], Hounsfield Unit (HU) changes in lung density in individual, 5 Gy, dose bins from 5 to 45 Gy (5–50 Gy for PB-1D and PB-3D) were assessed in the peri-tumoral region, defined as the normal lung tissue between the ITV and a 3 cm uniform expansion around the ITV [34]. The 0–5 Gy lung volume was used as a baseline correction of the density changes. We also studied the correlation between lung density changes in the region covered by V20 and RP grades. Associations between RP grade and dosimetric indices, MLD, V20, generalized equivalent uniform dose (gEUD) [39] were investigated.

A Spearman’s rank-order correlation was run to determine the relationship between CT lung density changes (HU) and RP grade. Finally, a multivariable logistic regression analysis including significant predictors of RP was conducted. Statistical analysis was performed using SPSS v16.0 (SPSS Inc. Released 2007. SPSS for Windows, Version 16.0. Chicago, SPSS Inc.). Statistical significance was set at p < 0.05 using a two-sided test.

3. Results

Table 1 illustrates patient characteristics. Median age in the “RP” and the “no RP” groups was 71 (range: 52–81) and 74 (range: 54–88), respectively. All 10 patients (100%) in the RP group had COPD at baseline evaluation, as opposed to 14 out of the 21 patients (66.7%) in the “no RP” group.

Table 1.

Patient Characteristics.

	Radiation Pneumonitis (n = 10)	No Radiation Pneumonitis (n = 21)	p-Value
Median age (Years)	71 (52–81)	74 (54–88)	0.051
Sex			0.088
Female	8 (80%)	10 (47.6%)
Male	2 (20%)	11 (52.4%)
Race			0.88
Caucasian	6 (60%)	12 (57%)
African American	4 (40%)	9 (43%)
Mean smoking index (pack-years)	48.3	53.9	0.59
Smoking status			0.077
Current smoker	1 (10%)	11 (52.4%)
Ex-smoker	8 (80%)	9 (43%)
Non-smoker	1 (10%)	1 (4.6%)
COPD at baseline	10 (100%)	14 (66.7%)	0.038
Pathology			0.025
Adenocarcinoma	3 (30%)	6 (28.6%)
Squamous cell carcinoma	2 (20%)	13 (61.9%)
No biopsy	5 (50%)	2 (9.5%)
Stage group			0.94
IA	7 (70%)	10 (47.6%)
IB	3 (30%)	5 (23.8%)
Recurrent	0 (0%)	6 (28.6%)
SBRT course			0.41
48 Gy (4 × 12 Gy)	9 (90%)	17 (81%)
36 (3 × 12 Gy)	1 (10%)	1 (4.8%)
Other	0 (0%)	3 (14.2%)
Living status at last F/U			0.97
Alive	1 (10%)	2 (9.5%)
Dead	9 (90%)	19 (90.5%)

Model-based dose algorithms (AAA, MC, AXB) predicted a 10–15% reduction in the 45 Gy isodose volume relative to PB algorithms, as observed in Fig. 1(a) for a patient with grade 2 RP, due to the electron transport of dose away from the tumor into normal lung tissue.

Fig. 1(a).

Dose coverage within dose bin 20–45 Gy using different algorithms for planning CT (left) and for follow-up CT (right) in a patient who developed grade 2 RP.

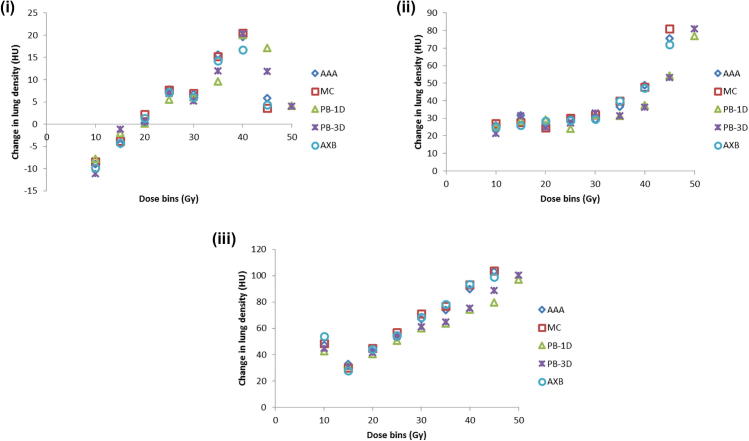
Fig. 1(b) shows the population average lung density change in the dose bins of 5–45 Gy (5–50 Gy for PB-1D and PB-3D) for the patients with radiation pneumonitis grades 0, 1, and 2, respectively. The density (HU) changes in the 45–50 Gy bin computed with PB-1D and PB-3D approximated those in the 40–45 Gy bins as computed with model-based algorithms (AAA, MC, AXB), due to the dose reduction noted in Fig. 1(a). Mean HU values and standard errors calculated for different algorithms are displayed in Table 2. For patients who did not develop RP, the mean change in CT lung density (HU) in the 45–50 Gy dose bin was 3.2 ± 8.0 for PB-based algorithms, and 3.8 ± 7.1 in the 40–45 Gy dose bin for model-based algorithms. For patients who developed RP, mean HU change in the 45–50 Gy dose bin was 66.4 ± 13.5 (Grade 1) and 104.0 ± 10.5 (Grade 2) for PB algorithms, versus 73.5 ± 10.3 (Grade 1) and 104.3 ± 8.4 (Grade 2) in the 40–45 Gy dose bin for model-based algorithms. The average HU change in the 20–25 Gy dose bin for PB-based algorithms were 5.1 ± 3.1 (Grade 0); 30.7 ± 4.4 (Grade 1); 57.7 ± 11.1 (Grade 2), and 6.2 ± 2.6 (Grade 0); 32.8 ± 3.9 (Grade 1); 64.9 ± 5.6 (Grade 2) for model-based algorithms.

Fig. 1(b).

Average change in lung density (HU) in the peri-tumoral region (3 cm ring) between planning and follow-up CT scans for all patients by grade of radiation pneumonitis (i) Patients with no radiation pneumonitis; (ii) Patients with Grade 1 RP; (iii) Patients with Grade 2 RP. (i) Grade 0 RP (N = 21). (ii) Grade 1 RP (N = 6). (iii) Grade 2 RP (N = 4). Abbreviations: CT: Computed Tomography; HU: Hounsfield Unit; AAA: Analytic anisotropic algorithm; MC: Monte Carlo-based algorithm; AXB: Acuros XB; PB-3D: 3-D pencil beam; PB-1D: 1-D pencil beam.

Table 2.

Change in CT lung density (HU, mean ± SE) for each algorithm in the different dose bins between planning and follow-up CT scans. Region evaluated consisted of normal lung tissue (both lungs minus internal target volume).

Algorithm	Dose bin (Gy)
	5–10	10–15	15–20	20–25	25–30	30–35	35–40	40–45	45–50
Grade 0 RP -ΔHU (follow-up CT–planning CT)
AAA	−8.6 ± 5.8	−1.8 ± 5.0	0.7 ± 4.5	6.6 ± 4.6	4.9 ± 6.1	14.1 ± 8.1	19.2 ± 9.2	5.0 ± 12.4
MC	−7.8 ± 6.8	−2.2 ± 5.1	2.3 ± 4.8	6.3 ± 4.7	4.8 ± 6.5	14.3 ± 8.5	19.7 ± 8.7	2.8 ± 12.6
AXB	−9.1 ± 6.1	−2.6 ± 4.6	1.7 ± 4.6	5.6 ± 4.9	4.0 ± 6.8	13.4 ± 8.3	15.6 ± 9.4	3.7 ± 12.4
PB-3D	−9.0 ± 7.3	0.93 ± 6.0	1.3 ± 5.0	5.6 ± 4.6	3.1 ± 5.6	10.2 ± 7.6	19.9 ± 7.8	10.7 ± 8.1	3.4 ± 12.4
PB-1D	−5.3 ± 4.7	0.68 ± 5.4	0.75 ± 5.2	4.5 ± 4.4	4.0 ± 5.9	7.6 ± 7.4	18.8 ± 8.0	16.4 ± 8.1	2.8 ± 10.7
Grade 1 RP - ΔHU (follow-up CT–planning CT)
AAA	21.1±17.5	20.3±16.8	29.1±9.6	31.8±7.1	34.3±9.3	42.6±8.2	56.0±12.6	73.8±18.6
MC	22.0±17.6	21.0±13.9	30.6±9.0	34.1±7.3	36.6±8.9	43.6±9.7	55.0±11.7	76.6±19.8
AXB	21.1±19.4	18.5±14.2	30.1±9.1	32.5±7.2	34.8±9.3	41.8±9.2	58.5±12.3	70.0±18.5
PB-3D	16.3±19.1	19.8±13.3	27.6±10.2	32.5±6.7	37.8±10.0	40.1±9.3	43.6±9.9	60.3±11.5	68.0±22.2
PB-1D	18.0±18.8	18.1±15.0	31.6±10.9	28.8±6.2	37.0±11.0	41.0±9.3	44.6±9.0	57.1±10.0	64.8±18.1
Grade 2 RP - ΔHU (follow-up CT–planning CT)
AAA	55.5±26.9	30.7±19.0	38.5±12.6	61.5±11.3	80.0±7.6	84.5±13.9	95.6±18.1	106.3±16.8
MC	55.0±24.0	27.0±13.8	40.2±15.8	64.2±9.3	85.0±4.1	86.5±14.3	103.6±23.2	105.8±10.4
AXB	62.5±31.8	25.7±15.6	41.0±15.1	62.5±11.0	82.5±6.3	91.7±10.9	97.0±21.5	101.3±15.6
PB-3D	47.7±22.3	31.7±20.5	37.0±15.6	59.5±14.3	69.5±12.1	70.0±12.2	83.6±19.7	90.3±12.9	104.2±17.6
PB-1D	44.3±18.0	29.7±16.5	32.5±13.1	56.0±19.1	68.2±12.2	68.0±9.8	82.3±19.7	83.6±15.7	103.7±14.6

Abbreviations: CT: Computed Tomography; SE: standard error; HU: Hounsfield Unit; CTCAE: Common Terminology Criteria for Adverse Events; RP: Radiation pneumonitis; AAA: Analytic anisotropic algorithm; MC: Monte Carlo-based algorithm; AXB: Acuros XB; PB-3D: 3-D pencil beam; PB-1D: 1-D pencil beam.

Fig. 2 illustrates strong, positive correlation between lung density change (HU) in the peri-tumoral region (3 cm ring) and RP grade (Spearman’s r = 0.760; p < 0.001). Patients who did not develop RP had a mean change in lung density in the 3 cm of ring of 1.6 ± 3.2HU (range: −1 to 5) compared with 37.3 ± 11.1 HU (range: 26–48 HU) and 72.5 ± 23.2 HU (range: 50–96 HU) in patients with grades 1 and 2 RP, respectively. The mean dose within 3 cm ring is also shown in Fig. 2 as a function of RP grade for all algorithms. As noted in Table 3(a), the mean dose computed in the 3 cm, peri-tumoral region, differed between PB and model-based algorithms. The PB-3D algorithm predicted between 2.3 ± 1.0% and 2.5 ± 1.3% lower peri-tumoral mean dose relative to the PB-1D method, for the different RP grade groups. Model-based methods (AAA, MC, AXB) computed lower mean peri-tumoral dose relative to the PB-1D algorithm as follows: 4.8 ± 3.0% (grade 0), 5.2 ± 2.6% (grade 1), and 5.3 ± 3.0% (grade 2). P values based on two-tailed student tests included in this table compare the differences between different algorithms, relative to the PB-1D algorithm, which has a P value of 1.0. No significant differences between the different algorithms were noted. Table 3(b) shows the association between tumor size, as computed by diameter of equivalent sphere, and RP grade. Spearman R value was 0.44 (medium correlation) but was statistically significant (p = 0.01).

Fig. 2.

Correlation between radiation pneumonitis grade and CT lung density changes (HU)/mean dose (Gy) for different algorithms in the peri-tumoral region (3 cm ring) (N = 21 for grade 0 RP, N = 6 for grade 1 RP, N = 4 for grade 2 RP). For lung density changes, mean values for each category are denoted by solid circle. Spearman’s correlation coefficient and significance are r = 0.76 and p < 0.01, respectively. The error bar represents one standard error. The mean dose using different algorithms is shown in Table 3(a). Abbreviations: HU: Hounsfield Unit; CTCAE: Common Terminology Criteria for Adverse Events. AAA: Analytic anisotropic algorithm; MC: Monte Carlo-based algorithm; AXB: Acuros XB; PB-3D: 3-D pencil beam; PB-1D: 1-D pencil beam.

Table 3a.

Quantification and correlation of mean dose within the 3-cm peri-tumoral ring with radiation pneumonitis grade for each algorithm. Values in parenthesis represent the ratio of the mean dose from each algorithm to the mean dose from PB-1D.

Mean dose ± SE within the 3 cm peri-tumoral ring
CTCAE RP grade	AAA	MC	AXB	PB-3D	PB-1D
0	18.15 ± 0.98 (0.96)	17.99 ± 1.00 (0.95)	18.22 ± 0.99 (0.96)	18.56 ± 1.01 (0.98)	18.99 ± 1.02 (1.00)
1	19.65 ± 1.49 (0.95)	19.43 ± 1.47 (0.94)	19.97 ± 1.53 (0.96)	20.25 ± 1.56 (0.98)	20.76 ± 1.54 (1.00)
2	20.55 ± 4.43 (0.95)	20.33 ± 4.66 (0.94)	20.93 ± 4.46 (0.96)	21.19 ± 4.69 (0.98)	21.69 ± 4.66 (1.00)
Coefficient r and p-value	r = 0.20 p = 0.32	r = 0.19 p = 0.33	r = 0.22 p = 0.26	r = 0.21 p = 0.29	r = 0.21 p = 0.28
Two-tailed student’s t test (Significance level at 0.05)	P = 0.48	P = 0.38	P = 0.56	P = 0.73	P = 1.00

Abbreviations: SE: standard error; CTCAE: Common Terminology Criteria for Adverse Events; AAA: Analytic anisotropic algorithm; MC: Monte Carlo-based algorithm; AXB: Acuros XB; PB-3D: 3-D pencil beam; PB-1D: 1-D pencil beam.

Table 3b.

Association between tumor size (equivalent diameter) with radiation pneumonitis grade. Population average equivalent sphere diameter was 3.43 ± 0.17 cm (range 1.9–5.7 cm).

CTCAE RP grade	Mean equivalent diameter ± SE (cm)
0	3.12 ± 0.18
1	3.86 ± 0.43
2	4.11 ± 0.35
Spearman’s coefficient r and p-value	r = 0.44, p = 0.01

In Table 4, we observe statistically significant correlations between changes in lung density in the region covered by V20 and RP grade, with r values > 0.70 and p < 0.01 for all algorithms. Statistically significant correlations were also noted between V20 and RP grade, with r values around 0.50 and p = 0.01 for all algorithms. These associations were not significantly different between model-based and pencil-based algorithms.

Table 4.

Quantification and correlation of CT lung density changes (HU) in the region covered by V20 and V20 with radiation pneumonitis grade for each algorithm.

	HU change in the region covered by V20 (mean ± SE)					V20 (mean ± SE)
CTCAE RP grade	AAA	MC	AXB	PB-3D	PB-1D	AAA	MC	AXB	PB-3D	PB-1D
0	5.2 ± 6.4	5.1 ± 6.1	5.1 ± 6.0	5.1 ± 6.1	5.1 ± 6.2	3.18 ± 0.44	3.15 ± 0.44	3.29 ± 0.45	3.40 ± 0.44	3.52 ± 0.46
1	42.0 ± 8.3	42.8 ± 8.5	42.2 ± 8.4	41.8 ± 8.1	41.5 ± 8.3	3.84 ± 0.86	3.67 ± 0.84	3.88 ± 0.86	4.03 ± 0.85	4.21 ± 0.83
2	78.3 ± 15.0	79.8 ± 14.3	78.5 ± 14.8	76.5 ± 15.1	76.0 ± 18.5	7.80 ± 2.67	7.82 ± 2.77	8.03 ± 2.31	8.03 ± 2.25	8.17 ± 2.80
Coefficient r and p-value	r = 0.74 p < 0.01	r = 0.75 p < 0.01	r = 0.75 p < 0.01	r = 0.73 p < 0.01	r = 0.72 p < 0.01	r = 0.50 p = 0.01	r = 0.49 p = 0.01	r = 0.49 p = 0.01	r = 0.49 p = 0.01	r = 0.49 p = 0.01
Two-tailed student’s t test	P = 0.96	P = 0.93	P = 0.96	P = 0.99	P = 1.00	P = 0.68	P = 0.63	P = 0.78	P = 0.87	P = 1.00

Abbreviations: HU: Hounsfield Unit; SE: standard error; V20: percent of total lung volume receiving a dose of at least 20 Gy; CTCAE: Common Terminology Criteria for Adverse Events; RP: Radiation pneumonitis; AAA: Analytic anisotropic algorithm; MC: Monte Carlo-based algorithm; AXB: Acuros XB; PB-3D: 3-D pencil beam; PB-1D: 1-D pencil beam.

Table 5(a) displays correlation between MLD and RP grade with Spearman’s r = 0.48 (p = 0.01) for both lungs and ipsilateral lung for PB-based algorithms, and Spearman’s r = 0.49 (p = 0.01) for both lungs and ipsilateral lung for model-based algorithms. Table 5(b) illustrates correlation between gEUD and RP grade with Spearman’s r = 0.44 (p = 0.02) for both lungs and ipsilateral lung for PB-based algorithms, and Spearman’s r = 0.46 (p = 0.02) for both lungs and ipsilateral lung for model-based algorithms. The value a = 2.44 from Tucker et al. [40] was used for the calculation of gEUD in this table. Similar correlations were obtained when ‘a’ values of 2.00 [41] and 1.41 [42] were used to compute gEUD.

Table 5a.

Quantification and correlation of the mean lung dose of both lungs minus ITV and radiation pneumonitis grade for each algorithm.

	MLD of both lungs minus ITV (mean ± SE)					MLD of ipsilateral lung minus ITV (mean ± SE)
CTCAE RP grade	AAA	MC	AXB	PB-3D	PB-1D	AAA	MC	AXB	PB-3D	PB-1D
0	2.74 ± 0.25	2.70 ± 0.25	2.77 ± 0.25	2.79 ± 0.26	2.87 ± 0.27	4.51 ± 0.39	4.41 ± 0.38	4.54 ± 0.39	4.52 ± 0.39	4.63 ± 0.40
1	3.05 ± 0.63	2.96 ± 0.62	3.07 ± 0.64	3.09 ± 0.63	3.20 ± 0.65	4.88 ± 0.86	4.72 ± 0.83	4.87 ± 0.84	4.91 ± 0.87	5.02 ± 0.87
2	5.16 ± 1.22	5.16 ± 1.25	5.34 ± 1.26	5.38 ± 1.32	5.45 ± 1.34	8.44 ± 2.22	8.46 ± 2.27	8.73 ± 2.28	8.75 ± 2.39	8.79 ± 2.36
Coefficient r and p-value	r = 0.49 p = 0.01	r = 0.49 p = 0.01	r = 0.49 p = 0.01	r = 0.48 p = 0.01	r = 0.48 p = 0.01	r = 0.49 p = 0.01	r = 0.50 p = 0.01	r = 0.49 p = 0.01	r = 0.48 p = 0.01	r = 0.48 p = 0.01
Two-tailed student’s t test	P = 0.74	P = 0.66	P = 0.83	P = 0.87	P = 1.00	P = 0.83	P = 0.73	P = 0.88	P = 0.91	P = 1.00

Abbreviations: MLD: the mean lung dose; SE: standard error; CTCAE: Common Terminology Criteria for Adverse Events; RP: Radiation pneumonitis; AAA: Analytic anisotropic algorithm; MC: Monte Carlo-based algorithm; AXB: Acuros XB; PB-3D: 3-D pencil beam; PB-1D: 1-D pencil beam.

Table 5b.

Quantification and correlation of the mean gEUD (a = 2.44) of both lungs minus ITV and ipsilateral lung minus ITV with radiation pneumonitis grade for each algorithm.

	gEUD of both lungs minus ITV (mean ± SE)					gEUD of ipsilateral lung minus ITV (mean ± SE)
CTCAE RP grade	AAA	MC	AXB	PB-3D	PB-1D	AAA	MC	AXB	PB-3D	PB-1D
0	8.53 ± 0.51	8.46 ± 0.52	8.46 ± 0.52	9.14 ± 0.53	9.43 ± 0.55	11.14 ± 0.62	11.04 ± 0.63	10.99 ± 0.63	11.87 ± 0.63	12.22 ± 0.64
1	9.14 ± 0.98	8.95 ± 0.98	9.16 ± 0.99	9.82 ± 1.01	10.16 ± 1.03	11.81 ± 1.18	11.56 ± 1.17	11.84 ± 1.20	12.70 ± 1.22	13.15 ± 1.27
2	12.29 ± 2.01	12.37 ± 2.12	12.52 ± 2.07	13.07 ± 2.16	13.36 ± 2.16	15.89 ± 2.74	15.99 ± 2.89	16.20 ± 2.82	16.87 ± 2.94	17.26 ± 2.95
Coefficient r and p-value	r = 0.45 p = 0.02	r = 0.47 p = 0.01	r = 0.45 p = 0.02	r = 0.44 p = 0.02	r = 0.44 p = 0.02	r = 0.46 p = 0.02	r = 0.47 p = 0.01	r = 0.46 p = 0.02	r = 0.45 p = 0.02	r = 0.44 p = 0.02
Two-tailed student’s t test	P = 0.22	P = 0.19	P = 0.23	P = 0.70	P = 1.00	P = 0.23	P = 0.20	P = 0.22	P = 0.71	P = 1.00

Abbreviations: gEUD: generalized Equivalent Uniform Dose; ITV: internal target volume; SE: standard error; CTCAE: Common Terminology Criteria for Adverse Events; RP: Radiation pneumonitis; AAA: Analytic anisotropic algorithm; MC: Monte Carlo-based algorithm; AXB: Acuros XB; PB-3D: 3-D pencil beam; PB-1D: 1-D pencil beam.

On multivariable logistic regression analysis, combining grade 1 and 2 RP events as “RP” versus “no RP” (categorical variable), MLD was found to be an independent predictor for the development of RP (p < 0.001) (independent of PTV).

4. Discussion

This study demonstrated that: (a) HU change is correlated to RP grade, and (b) although dose for this previous correlation has traditionally been based on the PB-1D algorithm, the use of model-based algorithms leads to better depiction of the reality.

Changes in CT densities, and correlations with dose-response, as computed with model-based algorithms, are in excellent agreement with the findings of Palma et al. in the setting of SBRT treatment of lung cancer [34], [38]. They also agree with other studies correlating CT density changes, radiation dose and pneumonitis symptoms after conventionally fractionated radiation therapy for lung cancer [43], [44]. In our series, we demonstrated a strong correlation between lung density changes and pneumonitis grade. We note that a HU change of >42 within the region covered by V20 (or >37 HU in the 3 cm peri-tumoral ring) from simulation to follow-up CT scans appears to be associated with the development of radiation pneumonitis.

V20, MLD, and gEUD were also significantly correlated with RP grades. In lung SBRT, it is generally the case that a small treatment volume receives a very high, targeted dose, with a large volume of lung receiving a low dose, by virtue of the sharp dose fall-off [45]. The hazard of irradiating large lung volumes with low doses in the context of SBRT is still unclear. We also noted a statistically significant correlation between RP grade and size (diameter) of the tumor, though only a medium correlation was found. Although this suggests a possible link between tumor size and the development of RP, one must note that the sample size here is quite small.

Aoki et al. found that the minimal dose associated with CT lung density changes ranged from 16 to 36 Gy (median dose of 24 Gy) [46]. Similarly, Palma et al., showed that changes in CT density became apparent in areas receiving >6 Gy, although they were more prominent in areas receiving >20 Gy [38]. Based on these findings, we chose to study the change in lung density in the region covered by V20, which was strongly correlated with RP grade. In contrast to the above-mentioned studies, Defraene et al. did not observe a significant correlation between lung density changes and dyspnea scores at 6 months in patients treated with SBRT [47]. In patients with NSCLC treated with conventionally fractionated radiation therapy, Bernchou et al. showed that two lung density change components are present during follow-up, a transient and a persistent phase, but these changes were not correlated with patient symptoms [48].

Of note, dose for all of the above-mentioned correlations were based on the PB-1D algorithm, and in our study, the dose in the various regions, 3 cm peritumoral ring and V20 region were shown to be different as a function of algorithm. Therefore, it is likely that the HU changes would have been different had the algorithm been based on model-based approaches. Although the correlation between CT density changes and different outcomes has been studied previously, data on the dependence of clinical outcome (and pneumonitis in particular) on accuracy of the dose calculation algorithm is sparse. Previous studies have shown that differences between prescribed and delivered doses vary based on TPS and algorithm and can significantly affect outcomes, in terms of local control [49], [50], and treatment side effects [45]. An important conclusion is that the PB-based dose distributions lead to inaccurate representation of the reality. The revised MC dose calculations performed in this study showed a 10–15% volume displacement of the high-dose region (40–45 Gy bin), which was in concordance with the HU changes seen on follow-up CT scans.

Multiple studies have evaluated differences in calculated dose distributions, as well as TCP and NTCP values between different algorithms in the setting of conventionally fractionated lung radiation therapy (RT) [51], [52], [53], [54], however literature about dose-effect relationships in the context of SBRT is sparse. Two reports on Monte Carlo dose recalculations for SBRT plans for pulmonary targets, showed that PB overestimated the minimum doses to the PTV by approximately 20% as compared to MC [55], [56]. This percent difference varied based on target volume and tumor location. These two groups did not analyze the impact of this calculated dose difference on outcomes. Similarly, in a study by Ding et al. reporting results from 10 NSCLC patients, the minimum doses to 95% and 99% of PTV calculated using the PB were overestimated by up to 40% and 36% of the prescribed dose, respectively, compared to that calculated by the AAA [57]. Another study compared two different algorithms (AAA and AXB) in lung SBRT plans, and showed that, as compared to AXB, AAA also overestimated the PTV dose with a difference in calculated TCP of up to 5.8% in lung SBRT. AAA and AXB had very similar NTCP regarding lung pneumonitis based on the Lyman-Kutcher-Burman (LKB) model [58]. In addition, Liu et al. [18] investigated clinical impact of dose overestimation by effective path length (EPL) calculation in stereotactic ablative radiation therapy of lung tumors. They found EPL overestimated dose compared with MC in all tumor DVH parameters in all plans. As a result, the magnitude of under-dosing based on EPL prescription translates to a concerning loss of TCP in a large proportion of patients. In summary, all of these studies demonstrated that PB algorithms result in overestimation of the PTV coverage in pulmonary SBRT, and this observation can be explained by the fact that these algorithms fail to properly account for electron transport in low-density tissues [59], [60].

Other studies reported on differences in LC outcomes in lung SBRT based on the choice of algorithm. In an analysis of 201 NSCLC cancer patients, with 116 patients treated with PB and 85 treated with collapsed cone convolution (CCC) dose calculation algorithms, a statistically significant difference in local recurrence rates was reported, with a hazard ratio of 3.4 (95% confidence interval, 1.18–9.83) in favor of CCC, possibly related to the under-dosing of tumors when using PB algorithms [61]. A recent retrospective study by Ohri et al. of 928 lung cancer patients treated with SBRT, showed that local control rates following treatments planned using a pencil beam algorithm were inferior to those observed following treatments planned using a Monte Carlo algorithm (89% vs. 96% at 2 years, log-rank p = 0.022) [62].

We believe that more studies related to correlation of dose with outcomes (both for tumor control and normal tissue complications) is important toward understanding the true impact of dose calculation algorithms in the clinical setting.

We recognize that our study has some limitations, one of which is its retrospective nature with all the inherent biases that accompany this study design, including missing information in patient charts. Also, we did not consider the temporal component of radiation pneumonitis/fibrosis, and only used follow-up CT scans up to 9 months after SBRT completion; a single follow-up CT scan was studied for each patient. Studies related to temporal dependency of RT-induced lung injury in an SBRT patient cohort are scant [54], [63] and will be confirmed in future work. We also acknowledge that many other risk factors for RP exist (such as pre-existing pulmonary disease), which could not be corrected for in a multivariable analysis due to the small number of RP events in this dataset. Additionally, we used rigid-body registration, and acknowledge that deformable registration techniques might have provided us with more accurate assessment of spatial dose-outcome relationships. However, it should be noted that it is quite challenging to perform deformable registration of the initial tumor volume on planning CT to a significantly different or even non-existent tumor volume on the follow-up CT. Observed differences in lung density were, in part, likely due to suboptimal co-registration of planning and follow-up CT scans, although rigid registration was shown to be a simpler, yet valid approach in a study by Gu et al. in the context of follow-up examinations for lung nodules [64].

5. Conclusion

We observed a 10–15% volume displacement of the high-dose region (40–45 Gy bin) with the use of model-based algorithms as compared with PB algorithms, which was in accordance with the HU changes seen on follow-up CT scans. Quantitative analysis of changes in lung density correlated strongly with radiation pneumonitis grades in the peri-tumoral region and the region covered by V20 irrespective of the algorithm used. V20, MLD, and gEUD were also significantly correlated with RP grades in this study. Prospective studies involving larger cohort of patients are needed to confirm these results.

Conflicts of interest

The Department of Radiation Oncology at Henry Ford Health System receives funding from Varian Medical Systems, Philips, and ViewRay.