Abstract
Methods to handle ordered-categorical indicators in latent variable interactions have been developed, yet they have not been widely applied. This article compares the performance of two popular latent variable interaction modeling approaches in handling ordered-categorical indicators: unconstrained product indicator (UPI) and latent moderated structural equations (LMS). We conducted a simulation study across sample sizes, indicators’ distributions and category conditions. We also studied four strategies to create sets of product indicators for UPI. Results supported using a parceling strategy to create product indicators in the UPI approach or using the LMS approach when the categorical indicators are symmetrically distributed. We applied these models to study the interaction effect between third- to fifth-grade students’ social skills improvement and teacher–student closeness on their state English language arts test scores.
Keywords: latent interaction, product indicator, categorical data, parceling
Interaction (moderation) effects, when the effects of predictors on outcomes are dependent on moderators, are commonly studied in educational and psychological research. For instance, West, Aiken, Cham, and Liu (2013) found that more than 60% of the published articles in two abnormal and clinical psychology journals have tested at least one interaction effect. Latent variable interaction modeling approaches have been developed when the predictor or moderator are best represented by confirmatory factor models. Among them, the unconstrained product indicator (UPI; Marsh, Wen, & Hau, 2004) and latent moderated structural equations (LMS; Klein & Moosbrugger, 2000; Schermelleh-Engel, Klein, & Moosbrugger, 1998) are popular most likely because of their availability in software packages. However, these approaches assume that the indicators of the predictor and the moderator are multivariate normally distributed and are measured on continuous scales. In practice, researchers often work with ordered-categorical variables measured on Likert-type scales (e.g., strongly disagree, disagree, agree, strongly agree) or binary responses (e.g., true/false) in psychological or educational measures. Although there are methods developed specifically to handle ordered-categorical variables in latent variable interaction modeling (e.g., Lee, Song, & Cai, 2010; Rizopoulos & Moustaki, 2008; Song & Lee, 2005), UPI and LMS still appear to be the most popular methods. According to Google Scholar, the original articles of the UPI (Marsh et al., 2004) and LMS (Klein & Moosbrugger, 2000) had 255 and 226 citations between January 1, 2017 and February 16, 2019, while the articles of methods that are developed to handle ordered-categorical variables had less than 35 citations each since their publication.
We conducted a literature review to further understand how applied researchers used UPI and LMS. We used Google Scholar to search for research articles which cited the original articles of the UPI (Marsh et al., 2004) and LMS (Klein & Moosbrugger, 2000) between 2018 and February, 2019, and reviewed those that we accessed the full versions of. Among these, 23 used UPI while 67 used LMS method. Twenty-three out of 28 articles that used UPI (82.1%), and 49 out of 67 articles that used LMS (73.1%) involved categorical variables. The majority of the articles did not report distributional properties of the indicators. These results show that (1) UPI and LMS are the most popular methods for estimating latent interaction effects, but (2) distributional assumptions of them are frequently violated in applied research. Thus, the primary goal of this study is to explore the extent to which the UPI and LMS approaches can handle nonnormal and/or ordered-categorical indicators through a simulation study, with a special focus on the role of different arrangements of the interaction term in the UPI approach.
Without loss of generality, we consider the latent variable interaction model in Equations (1) and (2) throughout the article:
| (1) |
| (2) |
Equation (1) is the structural model, in which the latent factors and interact with each other on the manifested outcome variable . is the disturbance and is assumed to have zero mean. is the intercept, and are the first-order effects, and is the interaction effect. Equation (2) is the factor model of and . We consider the situation where and have different numbers of X indicators (3 for and 12 for ). s are the intercepts. s are the factor loadings. s are the unique factors and are assumed to have zero means. In this model, we assume no cross-loadings of the indicators and that the unique factors are uncorrelated with each other.
Unconstrained Product Indicator
The UPI approach uses products of the X indicators to identify the interaction term as a factor model. Matching and parceling are two suggested strategies to create the product indicators.
Matching
In the matching strategy, the indicators of ( to ) are multiplied with those of ( to ) to form product indicators. In Equations (1) and (2), there are a total of (3 × 12) = 36 possible product indicators and numerous possible combinations to be used as a set. Among those possible combinations, the three-matched-pair strategy is studied the most and is recommended based on the simulation results (Cham, West, Ma, & Aiken, 2012; Coenders, Batista-Foguet, & Saris, 2008; Foldnes & Hagtvet, 2014; Jackman, Leite, & Cochrane, 2011; Marsh et al., 2004; Wu, Wen, Marsh, & Hau, 2013). In this strategy, we pair and multiply the three most reliable indicators of and according to their reliabilities and include these three product indicators in the factor model of .1 The reliability of an indicator (e.g., ) is
| (3) |
is the variance function. In Equation (2), if the three most reliable indicators of and are (, , ) and (, , ) in the descending order, we will have the product indicators , , and .
In addition to setting up the product indicators, a few extra model constraints are needed in the model specification. First, all the X indicators of and shall be mean-centered (i.e., raw scores are subtracted from mean) before creating the product indicators, in order to increase the model convergence rates and reduce model specification complexity (Algina & Moulder, 2001; Marsh et al., 2004). After centering, the factor model of , , and is the following:
| (4) |
All the intercepts of X indicators and product indicators are constrained to zero. The product indicators do not cross-load on and . When the X indicators can be assumed to be normal, the unique factors of the product indicators are uncorrelated among each other and with those of the X indicators. If not, an alternative specification is to let the unique factors of the product indicators correlate with those of the X indicators that form the product indicators. , , and are freely correlated. The means of and are set to zero while the mean of is constrained to be equal to the covariance between and (Bohrnstedt & Goldberger, 1969, equation 3). To identify the scales of , , and , we can fix the factor loadings of the most reliable indicators of and ( and ) and the corresponding product indicators ( to 1 (Jöreskog & Yang, 1996, equation 6).
Normal-theory maximum likelihood (NML) estimation, along with its standard error (SE) adjustment methods such as Satorra–Bentler (Satorra & Bentler, 1994) and Yuan–Bentler adjustments (Yuan & Bentler, 2000) are often used to estimate the UPI models. Theoretically, these estimators incorrectly assume that the product indicators are normally distributed and are linearly related to the X indicators (Bohrnstedt & Goldberger, 1969; Klein & Moosbrugger, 2000). On the other hand, simulation studies have supported using these estimators with the three-matched-pair strategy. The three-matched-pair strategy generally produces unbiased , , and estimates, unbiased standard errors of , and correct Type I error rates of the z test of across sample size (≥500), distributions of X indicators (skewness ≤2, kurtosis ≤6), and different numbers and reliabilities of X indicators (Cham et al., 2012; Coenders et al., 2008; Foldnes & Hagtvet, 2014; Jackman et al., 2011; Marsh et al., 2004; Wu et al., 2013).
Nevertheless, the three-matched-pair strategy is disadvantageous in ignoring the remaining indicators of in representing the interaction term, which results in lower statistical power of the z test of compared with other matching strategies that use more product indicators (Foldnes & Nagtvet, 2014; Marsh et al., 2004). These matching strategies are not suggested because the model specification regarding the unique factors is more complex. Parceling strategies is a promising alternative which uses all X indicators in the factor model of while reducing the model specification complexity.
Parceling
A parcel is the aggregation (e.g., average) of two or more indicators from the same construct and it often has no substantive meaning (Bandalos, 2008). In general applications in SEM, parcels can be used to replace the original indicators in the factor models. In UPI, one parceling strategy that is used to create the product indicators has been studied (Jackman et al., 2011; Wu et al., 2013). When and have unequal number of indicators, indicators from the construct that has more indicators are aggregated into parcels. The number of parcels is equal to the number of indicators of the construct that has fewer indicators. In Equation (2), we can compute three parcels from the 12 indicators of as there are three indicators of . We used the factorial algorithm (Rogers & Schmitt, 2004) to form parcels in this paper. In the factorial algorithm, the first parcel picks the indicators with the highest and lowest factor loadings. The second factor picks the indicators with second highest and second lowest factor loadings. The process repeats until all indicators are assigned to one and only one parcel. In our example, consider that the factor loadings of the 12 indicators of are in the descending order from to and all the X indicators are mean-centered. The first parcel () is equal to the average of (, , , ), the second parcel () is equal to the average of (, , , ), and the third parcel () is equal to the average of (, , ).2 After the parcels are computed, is matched with the most reliable indicator of to create the first product indicator , and so on.
The resulting factor model and model specification is the same as that in Equation (4) except for two matters. First, we use the product indicators , , and for the factor model of . Second, we need to use a different method to identify the scales of , , and . We can fix the variances of and to 1, and fix the variance of to (1 +), where is the covariance between and (Bohrnstedt & Goldberger, 1969, equation 5; Jackman et al., 2011). This identification constraint assumes that and are bivariate normally distributed. Wu et al. (2013) has evaluated the parceling strategy with NML estimation with Satorra–Bentler and Yuan–Bentler standard error adjustments. The parceling strategy generally produces unbiased estimates, unbiased standard errors of , and correct Type I error rates of the z test of across sample size (≥500) and different numbers and reliabilities of X indicators. As expected, the z test of has higher statistical power than the three-matched-pair strategy. However, when the indicators are nonnormal, the parceling strategy produces biased estimates because the identification constraint of assumes bivariate normality of and (Wu et al., 2013).
To overcome the violation of the normality assumption in the scaling constraints in the parceling strategy while having the potential advantages of parceling, in this article we propose another strategy to create product indicators that combines matching and parceling. In this new strategy, the most reliable indicators of and are matched to form the first product indicator(s). The remaining indicators of are then parceled and multiplied with the remaining indicator(s) of . The scales of , , and are defined by fixing the factor loadings of the most reliable indicators and the corresponding product indicator to 1, which does not assume bivariate normality of and . This strategy takes the advantage of the matching strategy in terms of the scaling identification and also the parceling strategy in terms of high statistical power to detect the interaction effect. We hypothesize that this strategy will produce unbiased estimates, and that the z test of will have correct Type I error rates and statistical power higher than that of the three-matched-pair strategy.
Latent Moderated Structural Equations
LMS (Klein & Moosbrugger, 2000; Schermelleh-Engel et al., 1998) is another popular latent interaction modeling approach. Unlike UPI, LMS estimates the interaction effect directly using maximum likelihood estimation, without having to specify a factor model for , and the factor model follows the typical confirmatory factor model such as that in Equation (2). LMS builds on the ideas that (1) the interaction effect is a conditioned linear effect on another variable and (2) a weighted combination of conditional normal distributions can be used to approximate the multivariate distributions of the observed indicators (Kelava et al., 2011). It uses Cholesky decomposition to decompose and to identify the conditioning variables (Equation 5):
| (5) |
The column vector of and () is decomposed into a lower triangular matrix and a column vector of values, which are standard normally distributed and orthogonal to each other. Further, LMS uses and by substituting them into Equation (1). To do so, Equation (1) is re-expressed as Equation (6):
| (6) |
is a row vector of regression coefficients of the first-order effects except the intercept. is a square matrix containing the interaction effect in the upper diagonal. Then, and are substituted into Equation (6):
| (7) |
Equation (7) shows that is linearly related to , but nonlinearly related to (Keleva et al., 2011). Assuming the X indicators are multivariate normal, Klein and Moosbrugger (2000) show that the joint distribution of the X indicators and outcome conditioned on is multivariate normal. Equivalently, the joint distribution is a mixture multivariate distribution across values of . Therefore, LMS estimates the latent interaction model by finding the maximum likelihood solution of the mixture distribution of the X indicators and using expectation–maximization (EM) algorithm (Dempster, Laird, & Rubin, 1977) with numerical integration (e.g., rectangular [trapezoid], Gauss–Hermite quadrature, and Monte Carlo).
Simulation studies have found that LMS is superior to the UPI in terms of yielding smaller bias of the interaction effect estimate and its standard error, and higher statistical power of the z test of the interaction effect when the X indicators are normally distributed (Cham et al., 2012; Jackman et al., 2011; Klein & Moosbrugger, 2000; Wu et al., 2013). However, when the distributions of X indicators deviate from normal, LMS produces biased interaction effect estimates (Cham et al., 2012; Wu et al., 2013).
Current Study
This current study explores how the UPI and LMS approaches perform when the X indicators are ordered-categorical. The literature in latent variables interactions has only considered when X indicators are measured on continuous scales, while the literature in factor analysis has well studied the appropriateness of treating ordered-categorical indicators as continuous. In factor analysis, NML can produce unbiased parameter estimates (≤10% bias) but negatively biased standard error estimates when the indicators have five or more categories and are moderately nonnormal (−.90 ≤ skewness ≤ 1.38, −1.19 ≤ kurtosis ≤−1.92; Babakus, Ferguson, & Jöreskog, 1987; B. Muthén & Kaplan, 1985; Rhemtulla, Brosseau-Liard, & Savalei, 2012). In addition, parcels are more continuous and are less nonnormal than the individual indicators (Bandalos, 2008; Little, Rhemtulla, Gibson, & Schoemann, 2013). Yang, Nay, and Hoyle (2010) found that parceling can reduce bias in parameter estimation when having categorical indicators.
Given these findings, we hypothesize that UPI and LMS will produce unbiased interaction effect estimates when the X indicators have five or more categories. LMS will produce unbiased interaction effect estimates when the X indicators are about symmetric and UPI using parceling will be more robust to nonnormal X indicators. We conducted a simulation study to test these hypotheses.
Simulation Study: Method
Population Model
The population model followed Equations (1) and (2). The predictors ( and ) were standardized with a medium effect size of correlation = .3 (Cohen, 1992), The intercept was arbitrarily set to .1. The first-order effects and were set to .3 and .1, respectively. Under the assumption that and are perfectly reliable, measured directly, and analyzed via multiple regression, the first-order effects are equivalent to a population = .3. We set two levels of the interaction effect in terms of increase = 0 (no effect) and .07 (small to medium effect; Cohen, 1992). The condition of increase = .07 was larger than those studied in the literature (e.g., .01 in Jackman et al., 2011; .02 in Kelava et al., 2011; .04 in Marsh et al., 2004). The disturbance variance was set according to the increase of the interaction effect. The factor loadings of the X indicators varied to represent realistic research settings. The unique factor variances were set such that the internal consistency of and equals .7, which is regarded as a benchmark for scale development (McDonald, 1999; Nunnally, 1978). Table 1 summarizes the parameters.
Table 1.
Population Parameters of Simulation Study.
| (A) Interaction model (Equation [1]) | |||||
|---|---|---|---|---|---|
| For all conditions | Increase of interaction effect = 0 | Increase of interaction effect = .07 | |||
| Parameter | Value | Parameter | Value | Parameter | Value |
| .10 | .00 | .159 | |||
| .30 | Disturbance variance | .275 | Disturbance variance | .248 | |
| .10 | |||||
Distributions of Indicators
We manipulated three conditions of the distributions of the indicators: symmetric, moderately skewed and kurtotic, and severely skewed and kurtotic. Here we describe the data generation procedures for the continuous indicators. In the symmetric condition, both and as well as the unique factors in the factor model were generated randomly from normal distribution. In the moderately skewed and kurtotic condition, and were generated randomly from distribution while unique factors were generated from distribution of different degrees of freedoms for each indicator (see Supplementary Material available online). In the severely skewed and kurtotic condition, and were generated randomly from gamma distribution with shape parameter = .34 and rate parameter = 3. Unique factors were generated from distribution of different degrees of freedoms for each indicator (see online supplementary materials). Table 2 shows the univariate skewness and kurtosis of the indicators by randomly generating one million observations for each condition.
Table 2.
Univariate Skewness and Kurtosis of the Indicators by Distribution and Category Conditions.
| Symmetric | Moderately skewed and kurtotic | Severely skewed and kurtotic | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Continuous | 5-category | 3-category | Continuous | 5-category | 3-category | Continuous | 5-category | 3-category | ||||||||||
| S | K | S | K | S | K | S | K | S | K | S | K | S | K | S | K | S | K | |
| .00 | .01 | .00 | −.41 | .00 | −.43 | 2.20 | 7.36 | 1.46 | .70 | 1.91 | 2.01 | 3.14 | 15.02 | 1.72 | 1.53 | 2.16 | 3.03 | |
| .00 | .00 | .00 | −.41 | .00 | −.44 | 1.53 | 3.58 | 1.28 | .21 | 1.74 | 1.40 | 2.88 | 12.57 | 1.65 | 1.30 | 2.10 | 2.77 | |
| .00 | .00 | .00 | −.43 | .00 | −.46 | 1.32 | 2.67 | 1.23 | .07 | 1.69 | 1.22 | 2.98 | 13.66 | 1.67 | 1.36 | 2.12 | 2.86 | |
| .00 | −.01 | .00 | −.44 | .00 | −.48 | 1.70 | 4.47 | 1.32 | .29 | 1.76 | 1.48 | 2.69 | 11.37 | 1.57 | 1.04 | 2.02 | 2.43 | |
| .00 | .00 | .00 | −.45 | .00 | −.50 | 1.50 | 3.44 | 1.26 | .13 | 1.70 | 1.26 | 2.53 | 9.84 | 1.53 | .90 | 1.97 | 2.25 | |
| .00 | −.01 | .00 | −.46 | .00 | −.53 | 1.77 | 4.89 | 1.32 | .29 | 1.76 | 1.46 | 2.04 | 6.46 | 1.39 | .48 | 1.83 | 1.70 | |
| .00 | −.01 | .00 | −.48 | .00 | −.55 | 1.91 | 5.70 | 1.35 | .37 | 1.78 | 1.54 | 3.03 | 14.52 | 1.63 | 1.23 | 2.07 | 2.65 | |
| .00 | .00 | .00 | −.50 | .00 | −.58 | 1.81 | 5.02 | 1.32 | .27 | 1.74 | 1.39 | 2.46 | 9.41 | 1.49 | .74 | 1.91 | 1.98 | |
| .00 | .01 | .00 | −.51 | .00 | −.61 | 1.66 | 4.18 | 1.28 | .15 | 1.69 | 1.21 | 2.85 | 12.82 | 1.57 | 1.02 | 2.00 | 2.33 | |
| .00 | .00 | .00 | −.53 | .00 | −.64 | 1.28 | 2.47 | 1.17 | −.11 | 1.59 | .88 | 2.77 | 12.15 | 1.55 | .91 | 1.96 | 2.17 | |
| .00 | .00 | .00 | −.63 | .00 | −.80 | 1.79 | 4.77 | 1.26 | .06 | 1.64 | .98 | 2.55 | 9.89 | 1.47 | .62 | 1.83 | 1.66 | |
| .00 | .00 | .00 | −.65 | .00 | −.82 | 1.38 | 3.21 | 1.15 | −.21 | 1.53 | .66 | 2.01 | 6.17 | 1.31 | .19 | 1.68 | 1.12 | |
| .00 | .00 | .00 | −.47 | .00 | −.53 | 1.68 | 4.24 | 1.30 | .23 | 1.74 | 1.37 | 1.98 | 6.01 | 1.37 | .42 | 1.80 | 1.58 | |
| .00 | .00 | .00 | −.52 | .00 | −.62 | 1.82 | 4.95 | 1.32 | .25 | 1.73 | 1.33 | 2.34 | 8.22 | 1.46 | .63 | 1.86 | 1.79 | |
| .00 | .00 | .00 | −.57 | .00 | −.70 | 1.44 | 3.56 | 1.20 | −.05 | 1.62 | .96 | 2.06 | 6.59 | 1.35 | .33 | 1.75 | 1.38 | |
Note. S = skewness, K = kurtosis. Normal distribution has skewness = 0 and kurtosis = 0. The results are based on randomly generating one million observations for each distribution and category condition.
Categories of Indicators
Under each distribution condition, the continuous indicators were standardized first, and then were categorized into five- and three-categories according to the thresholds used by Rhemtulla et al. (2012). In the symmetric condition, the thresholds were symmetrical around zero. The thresholds were set as (−1.5, −.5, .5, 1.5) for the five-category condition and (−.83, .83) for the three-category condition. In the moderately and severely skewed and kurtotic conditions, the thresholds were set as (.05, .44, .84, 1.34) for the five-category condition and (.58, 1.13) for the three-category condition. Table 2 shows the univariate skewness and kurtosis of the indicators by randomly generating one million observations for each condition.
Sample Size
We manipulated four levels of sample sizes (N) = 200, 500, 1,000, and 5,000. N = 200 is the median sample size used in regression analysis with interaction effects (Jaccard & Wan, 1995). N = 5,000 represents a large sample size at which the asymptotic properties of the estimators might be achieved.
Latent Variable Interaction Modeling Approaches
We studied the UPI and LMS approaches in the simulation. In UPI, we studied four strategies to form the product indicators: three-matched-pair (matching), parceling, two-matched-pair and one parcel (2M + P), and one-matched-pair and two parcels (M + 2P). In the 2M + P strategy, the two most reliable indicators of and were matched to create two product indicators and the least reliable indicator of was matched with the parcel of the remaining indicators of to create the third product indicator. In the M + 2P strategy, the most reliable indicators of and were matched to create a product indicator, and the remaining indicators of were matched with two parcels of to create two product indicators. As discussed, all the X indicators were mean-centered before creating product indicators. In the matching, 2M + P, and M + 2P strategies, we identified the factors by fixing the factor loadings of the most reliable indicators and the corresponding product indicator to 1. In parceling strategy, factors were identified by fixing the variances of and to 1 and fixing the variance of to (1 +). All the UPI models were estimated using NML estimation with robust standard errors (ESTIMATOR = MLR) via Mplus 7.2 (L. K. Muthén & Muthén, 1998-2014). In conditions where indicators were nonnormal, the unique factors of the product indicators and those of the X indicators that form the product indicators were allowed to correlate. Similarly, in these conditions, in models involving item parcels, unique factors of the item parcels and those of the X indicators that form them were also allowed to freely correlate. In the LMS models, factors were identified by fixing the latent intercepts and the factor loadings of the most reliable indicators of and to 0 and 1, respectively. The LMS models were estimated using the Gauss–Hermite quadrature integration algorithm with 16 integration points per dimension via Mplus 7.2 (Klein & Mossbrugger, 2000). Robust standard errors were calculated (ESTIMATOR = MLR).
Altogether, there were 72 simulation conditions (2 interaction effect sizes × 3 distributions of indicators × 3 categories of indicators × 4 sample sizes). For each condition, 1,100 datasets were generated using R (R Core Team, 2018). The gamma distributed variables were generated using R package copula 0.999-14 (Kojadinovic & Yan, 2010). All five latent interaction models were fit to the simulated data sets.
Results
The performances of the models in estimating the latent interaction effect () were summarized by six different dependent measures: model convergence rate, relative bias of parameter estimates, relative bias of estimated standard errors, Type I error rate, statistical power, and coverage rate. A full report of the results can be found in the Supplementary Material (available online).
Model Convergence Rate
Model convergence rate is the percentage of properly converged models across all replications for each condition. A model is considered as properly converged when there were no Mplus error messages and no negative variance estimates. Table S1 in the online supplementary materials shows the model converge rates. Across all conditions, the average model converge rate was 96.7% for the UPI models. As expected, when the sample sizes decreased and the indicators were more skewed and kurtotic and had fewer categories, model convergence rates decreased (lowest = 71% with 2M + P with three-category, severely skewed, and kurtotic indicators when N = 200). Matching, parceling, 2M + P, and M + 2P had similar average model converge rates (>95%). LMS had>99% convergence in all conditions and was superior than UPI in small (N = 200) sample sizes. The following analyses were conducted on properly converged replications.
Relative Bias of Interaction Effect Estimates
Relative bias of the parameter estimates is defined as
| (8) |
where represents the population parameter, represents the average of parameter estimates across the properly converged replications. Based on Hoogland and Boomsma (1998), relative bias of parameter estimates is considered acceptable if its absolute value is less than 5%. Relative biases of the interaction effect estimates are presented in Table 3. When the indicators were continuous, under symmetric condition, parceling strategy in UPI and LMS approach produced unbiased interaction estimates across all sample size conditions. The 2M + P, and M + 2P strategies produced unbiased interaction estimates when N≥500. On the other hand, matching required N≥1,000 to produce unbiased interaction estimates. Under skewed and kurtotic indicator conditions, however, parceling and LMS greatly overestimated interaction effects across all sample sizes (relative bias>30% for parceling,>28% for LMS). Under the moderately skewed and kurtotic condition, 2M + P, and M + 2P strategies produced unbiased interaction estimates across all sample sizes, while matching overestimated the effects when N = 200. Under severely skewed and kurtotic condition, 2M + P produced unbiased estimates across all sample sizes while matching and M + 2P produced unbiased interaction estimates when N≥1,000.
Table 3.
Relative Bias (%) of Interaction Effect Estimate.
| Indicators’ categories | Indicators’ distribution | N | Latent variable interaction modeling method | ||||
|---|---|---|---|---|---|---|---|
| Matching | Parceling | 2M + P | M + 2P | LMS | |||
| Continuous | Symmetric | 200 | 16.5 | 0.1 | 10.1 | 15.4 | −1.7 |
| 500 | 5.3 | 1.1 | 3.8 | 3.0 | −0.3 | ||
| 1,000 | 2.2 | 1.3 | 1.8 | 2.5 | 0.7 | ||
| 5,000 | 0.2 | −0.2 | 0.2 | 0.1 | −0.2 | ||
| Moderately skewed and kurtotic | 200 | 9.8 | 63.6 | 4.2 | 3.3 | 41.4 | |
| 500 | 2.7 | 78.2 | 1.1 | 1.2 | 45.5 | ||
| 1,000 | 2.1 | 82.3 | 0.7 | 0.1 | 47.8 | ||
| 5,000 | 0.8 | 87.5 | 0.4 | 0.2 | 49.0 | ||
| Severely skewed and kurtotic | 200 | 18.0 | 26.3 | 0.0 | 6.3 | 28.3 | |
| 500 | 7.0 | 30.4 | 4.3 | 7.2 | 33.9 | ||
| 1,000 | 4.8 | 31.9 | 2.4 | 3.3 | 35.3 | ||
| 5,000 | 0.4 | 31.7 | 0.1 | 0.0 | 37.1 | ||
| 5 Categories | Symmetric | 200 | 15.9 | 1.3 | 13.9 | 16.0 | −0.5 |
| 500 | 7.4 | 0.9 | 5.6 | 5.6 | 0.9 | ||
| 1,000 | 3.6 | 1.5 | 3.8 | 4.8 | 2.2 | ||
| 5,000 | 1.2 | −0.5 | 1.4 | 1.5 | 1.1 | ||
| Moderately skewed and kurtotic | 200 | 7.5 | 68.7 | 11.1 | 19.2 | 59.4 | |
| 500 | 3.2 | 76.7 | 17.5 | 23.6 | 69.4 | ||
| 1,000 | 3.1 | 78.4 | 17.7 | 22.8 | 72.9 | ||
| 5,000 | 0.7 | 78.9 | 16.5 | 22.6 | 75.2 | ||
| Severely skewed and kurtotic | 200 | −15.4 | 15.1 | −11.6 | −5.9 | 29.1 | |
| 500 | −18.4 | 16.0 | −12.7 | −8.6 | 37.1 | ||
| 1,000 | −19.5 | 16.6 | −15.0 | −11.7 | 39.2 | ||
| 5,000 | −21.4 | 15.5 | −16.2 | −13.7 | 41.2 | ||
| 3 Categories | Symmetric | 200 | 17.1 | −0.2 | 15.5 | 19.6 | −1.0 |
| 500 | 11.6 | 1.8 | 8.6 | 8.5 | 1.4 | ||
| 1,000 | 4.7 | 0.4 | 5.1 | 6.6 | 2.5 | ||
| 5,000 | 1.7 | −4.7 | 1.9 | 2.0 | 1.4 | ||
| Moderately skewed and kurtotic | 200 | −3.8 | 58.5 | −3.2 | 1.5 | 55.8 | |
| 500 | −7.5 | 69.2 | 2.9 | 9.7 | 67.2 | ||
| 1,000 | −10.1 | 69.9 | 3.1 | 8.2 | 70.5 | ||
| 5,000 | −12.8 | 71.0 | 1.9 | 7.7 | 73.2 | ||
| Severely skewed and kurtotic | 200 | −19.0 | 2.9 | −24.5 | −24.4 | 24.4 | |
| 500 | −24.2 | 4.7 | −23.3 | −18.1 | 34.3 | ||
| 1,000 | −26.1 | 8.1 | −23.5 | −19.7 | 37.9 | ||
| 5,000 | −30.9 | 6.8 | −26.4 | −23.8 | 40.0 | ||
Note. Boldfaced numbers indicate relative bias greater than the suggested value (>5% in value) by Hoogland and Boomsma (1998).
When the indicators had five categories, under symmetric condition, parceling and LMS produced unbiased interaction estimates across all sample sizes. Matching, 2M + P, and M + 2P strategies produced unbiased interaction estimates when N≥1,000. These three strategies overestimated the interaction effects when N≤ 500. Under moderately skewed and kurtotic condition, only the matching strategy produced unbiased interaction estimates when N≥500. Parceling and LMS greatly overestimated the interaction effects across all sample sizes (relative bias>68% for parceling,>59% for LMS). 2M + P, and M + 2P strategies overestimated the effects (>11% and>19%, respectively). Under severely skewed and kurtotic condition, none of the models produced unbiased interaction effect estimates. Models involving matched indicators (i.e., matching, 2M + P, M + 2P) tended to underestimate, while UPI parceling and LMS methods tended to overestimate the interaction effects.
When the indicators had three categories, under the symmetric condition, UPI parceling strategy and LMS produced unbiased interaction estimates across all sample sizes. Matching produced unbiased estimates when N≥1,000 while 2M + P and M + 2P strategies only produced unbiased estimates when N = 5,000. Under moderately skewed and kurtotic condition, 2M + P produced unbiased estimates across all sample size conditions, while matching and M + 2P produced unbiased estimates only when N = 200. Parceling (>58%), and LMS (>55%) overestimated the interaction effects across all sample sizes. Under the severely skewed and kurtotic condition, only the parceling strategy produced unbiased estimates with N≤ 500, while matching, 2M + P, and M + 2P strategies greatly underestimated (<−18%); and LMS greatly overestimated (>24%) the interaction effects across all sample sizes.
Relative Bias of Estimated Standard Errors of Interaction Effect
Relative bias of the estimated standard error is defined as
| (9) |
is the estimated standard error of the parameter estimate , and is the standard deviation of . Hoogland and Boomsma (1998) suggested that the acceptable relative bias of the estimated standard error is smaller than 10%. Table 4 shows the relative biases of the estimated standard errors of interaction effects. LMS, and 2M + P produced unbiased estimates with symmetric indicators, across all sample size and indicator type (i.e., continuous, five-category, three-category) conditions, while matching and M + 2P required N≥500. With moderately skewed and kurtotic continuous indicators, only LMS produced unbiased estimates across all sample size conditions while parceling, 2M + P, and M + 2P required N = 5,000 for unbiased estimates. With continuous and severely skewed and kurtotic indicators, all models except 2M + P required N = 5,000 for unbiased estimations while 2M + P performed well with N≥500. With categorical and skewed indicators, UPI models produced unbiased estimates in different sample size conditions while LMS underestimated the standard errors (<-23%)across all sample size conditions. Among the UPI models, matching tended to produce unbiased standard error estimates more frequently; however, it tended to overestimate the standard errors with N = 200 in these conditions (see Table 4).
Table 4.
Relative Bias (%) of Estimated Standard Error of Interaction Effect.
| Indicators’ categories | Indicators’ distribution | N | Latent variable interaction modeling method | ||||
|---|---|---|---|---|---|---|---|
| Matching | Parceling | 2M + P | M + 2P | LMS | |||
| Continuous | Symmetric | 200 | 16.7 | 6.7 | −6.8 | −17.9 | −5.0 |
| 500 | −2.0 | −0.7 | 0.3 | −3.4 | −2.8 | ||
| 1,000 | 0.5 | 0.1 | 2.9 | −1.7 | −1.3 | ||
| 5,000 | −3.2 | 0.2 | 2.2 | 0.8 | 0.1 | ||
| Moderately skewed and kurtotic | 200 | −5.1 | −15.4 | −16.2 | −29.2 | −7.2 | |
| 500 | −19.1 | −21.6 | −25.7 | −21.1 | −5.6 | ||
| 1,000 | −10.5 | −19.2 | −14.6 | −15.7 | −0.4 | ||
| 5,000 | −11.0 | −8.2 | −5.4 | −6.1 | −1.3 | ||
| Severely skewed and kurtotic | 200 | 94.6 | 14.1 | 35.1 | 20.8 | −15.1 | |
| 500 | −1.7 | 14.4 | −7.6 | −18.3 | −5.3 | ||
| 1,000 | −12.2 | −13.7 | −8.7 | −15.3 | −9.4 | ||
| 5,000 | −5.6 | −6.4 | −4.8 | −1.1 | −19.5 | ||
| 5 Categories | Symmetric | 200 | 5.5 | 10.7 | −9.7 | −6.9 | −6.6 |
| 500 | −1.3 | −0.1 | −0.9 | −0.1 | −2.9 | ||
| 1,000 | 2.7 | 1.2 | 6.0 | −1.9 | 0.9 | ||
| 5,000 | −1.3 | 0.3 | 3.8 | −0.5 | 0.4 | ||
| Moderately skewed and kurtotic | 200 | 11.8 | −9.8 | −4.8 | −1.4 | −25.8 | |
| 500 | −10.2 | −10.8 | −16.5 | −19.0 | −23.0 | ||
| 1,000 | −1.7 | −7.1 | −8.9 | −10.2 | −28.6 | ||
| 5,000 | −3.0 | 2.4 | −2.0 | −2.0 | −29.9 | ||
| Severely skewedand kurtotic | 200 | 48.6 | 10.6 | −6.4 | 80.1 | −24.0 | |
| 500 | −6.0 | −12.3 | −13.4 | –20.8 | –25.7 | ||
| 1,000 | −0.8 | −12.6 | −11.5 | −12.6 | −29.7 | ||
| 5,000 | 0.4 | −1.4 | −1.0 | −3.3 | −31.3 | ||
| 3 Categories | Symmetric | 200 | 28.7 | 14.0 | 9.1 | 16.4 | −8.0 |
| 500 | −1.2 | −5.7 | −3.3 | 1.7 | −5.3 | ||
| 1,000 | −3.3 | −14.0 | 3.9 | 1.1 | 1.3 | ||
| 5,000 | −2.8 | −68.5 | 2.1 | 2.2 | −0.7 | ||
| Moderately skewed and kurtotic | 200 | 46.9 | −3.2 | 0.5 | 10.0 | −28.3 | |
| 500 | −9.9 | −14.5 | −16.6 | −20.2 | −26.9 | ||
| 1,000 | −5.2 | −9.1 | −12.4 | −16.8 | −27.9 | ||
| 5,000 | −3.0 | −0.4 | −2.3 | −3.4 | −26.8 | ||
| Severely skewed and kurtotic | 200 | 94.3 | 39.8 | 19.4 | 148.4 | −34.9 | |
| 500 | 8.6 | −1.1 | 9.7 | 8.9 | −27.3 | ||
| 1,000 | −4.3 | −10.5 | −10.5 | −11.8 | −29.3 | ||
| 5,000 | −0.8 | −1.7 | 1.0 | −2.0 | −31.1 | ||
Note. Boldfaced numbers indicate relative bias greater than the suggested value (>10% in value) by Hoogland and Boomsma (1998).
Type I Error Rate of Interaction Effect
Type I error rate of the interaction effect is defined as the percentage of properly converged replications that wrongly reject the null hypothesis of no interaction effect (H0: ) when it is true in the population (setting = .05). The acceptable level of Type I error rate is within the 95% confidence interval of a binomial variable = [], where is the number of replications (Cham et al., 2012). Here, the interval is .037 to .063. Figure 1 shows Type I error rates of the interaction effects across conditions, with the gray color bands indicating the acceptable range (see Table S2 in the online supplementary materials for a full report). When the indicators were continuous, UPI parceling produced acceptable Type I error rates across all sample size and indicatory type conditions. Other UPI models had acceptable Type I error rates in most conditions, while LMS had acceptable Type I error rates in the symmetric condition and greatly inflated type I error rates (between .13 and 1.00) in the skewed and kurtotic conditions. Matching, 2M + P, and M + 2P had low Type I error rates under symmetric and N≤ 500 conditions.
Figure 1.
Type I error rate of interaction effect.
Note. The gray color bands indicate the acceptable range (.037 to .063). “S and K” means skewed and kurtotic.
When the indicators had five categories, under the symmetric condition, UPI matching, 2M + P, and M + 2P had low Type I error rates with N≤ 500, and LMS had low Type I error rates with N = 200, and high Type I error rates with N = 5,000. Under moderately skewed and kurtotic condition, parceling, 2M + P, and M + 2P produced acceptable Type I error rates except when N = 5,000, matching tended to have low, and LMS had very high (>.24) Type I error rates. Under severely skewed and kurtotic condition, all models had inflated Type I error rate when N = 5,000, while the rates were acceptable or low when N≤ 1,000 for UPI models. In this condition, LMS showed greatly inflated type I error rates (between .18 and .99).
When the indicators had three categories, parceling produced acceptable Type I error rates in all conditions except with severely skewed and kurtotic indicators when N≥1,000. Matching tended to produce low Type I error rates except with N = 5,000 where it produced acceptable (symmetric), or high (moderately and severely symmetric and kurtotic) Type I error rates. 2M + P and M + 2P produced low rates with N≤ 500 and acceptable rates with N≥1,000 with symmetric and moderately skewed and kurtotic indicators; and low rates with N = 200, and high rates with N = 5,000 with severely skewed and kurtotic indicators. LMS produced acceptable or slightly low rates with symmetrical indicators, while it produced highly elevated (between .13 and 1.00) rates with moderately and severely skewed and kurtotic indicators.
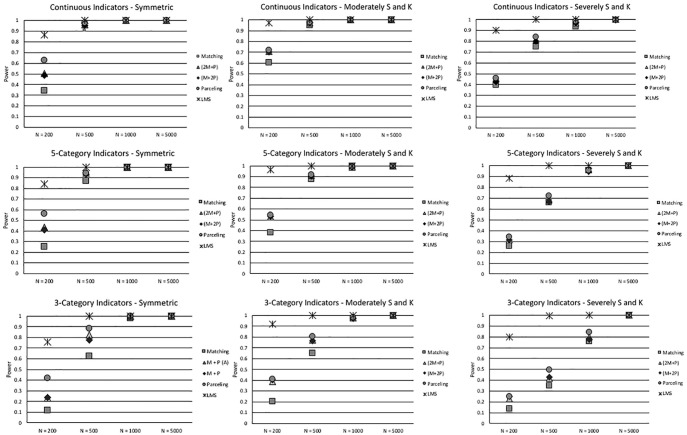
Statistical Power of Interaction Effect
Statistical power of the interaction effect is defined as the percentage of properly converged replications that correctly reject the null hypothesis of no interaction effect when it is false in the population (setting = .05). Figure 2 shows the statistical power results across conditions (see Table S3 in the online supplementary materials for a full report). Overall, LMS approach had the highest average statistical power (.97), followed by UPI parceling (.82), 2M + P (.80), M + 2P (.79), and matching (.75) strategies in descending order. As expected, when the indicators had fewer categories and sample size decreased, statistical power decreased. With continuous and five-category, symmetric and moderately skewed and kurtotic indicators, all models except UPI matching had 90% or greater power with N≥500. With continuous and five-categorical, severely skewed, and kurtotic indicators, N≥1,000 was needed for acceptable power levels in UPI models. With three-category symmetric and moderately skewed and kurtotic indicators N≥1,000 was needed for adequate power levels for UPI models while N = 5,000 was needed when the indicators were severely skewed and kurtotic.
Figure 2.
Statistical power of interaction effect.
Note. “S and K” means skewed and kurtotic.
Coverage Rate of Interaction Effect
Coverage rate of the interaction effect is defined as the percentage of replications that the 95% Wald confidence interval of the interaction effect estimates includes the population value. Coverage rate incorporates the information of both the bias of the parameter estimates and that of the estimated standard errors. Coverage rate of 90% and above is considered acceptable (Cham et al., 2012). Table 5 presents the coverage rates across conditions. When the indicators were symmetrically distributed, all models had acceptable coverage rates across all sample size and indicators’ category conditions. With continuous and skewed and kurtotic indicators, only M + 2P produced acceptable coverage rates across all sample size conditions while 2M + P required N≥500, and matching required N≥1,000. UPI parceling and LMS produced poor coverage rates in these conditions. With five-category and skewed and kurtotic indicators, UPI matching, and 2M + P, and LMS models consistently produced low coverage rates while UPI parceling and M + 2P produced acceptable coverage rates in some sample size conditions. With three-category and skewed and kurtotic conditions, UPI matching, 2M + P, and M + P produced very high (>99%) coverage rates, while UPI parceling and LMS models produced very low (<10%) coverage rates with moderately skewed and kurtotic indicators with N = 5,000, and lower than acceptable rates in other sample size conditions.
Table 5.
Coverage Rate (%) of Interaction Effect.
| Indicators’ categories | Indicators’ distribution | N | Latent variable interaction modeling method | ||||
|---|---|---|---|---|---|---|---|
| Matching | Parceling | 2M + P | M + 2P | LMS | |||
| Continuous | Symmetric | 200 | 94.8 | 95.5 | 96.6 | 97.4 | 96.5 |
| 500 | 96.2 | 94.4 | 97.6 | 97.2 | 96.6 | ||
| 1,000 | 96.2 | 94.0 | 98.2 | 98.3 | 97.7 | ||
| 5,000 | 95.5 | 95.0 | 98.7 | 98.3 | 97.7 | ||
| Moderately skewed and kurtotic | 200 | 87.7 | 87.8 | 89.8 | 91.8 | 88.1 | |
| 500 | 89.9 | 73.4 | 90.0 | 91.4 | 60.8 | ||
| 1,000 | 90.7 | 47.9 | 91.3 | 93.8 | 20.0 | ||
| 5,000 | 94.5 | 0.4 | 96.0 | 96.4 | 0.0 | ||
| Severely skewed and kurtotic | 200 | 84.3 | 92.2 | 88.2 | 90.7 | 88.3 | |
| 500 | 89.6 | 92.6 | 92.4 | 92.6 | 76.6 | ||
| 1,000 | 90.4 | 87.0 | 92.4 | 93.2 | 54.2 | ||
| 5,000 | 95.0 | 52.3 | 95.2 | 97.6 | 0.8 | ||
| 5 Categories | Symmetric | 200 | 95.9 | 96.2 | 97.6 | 98.6 | 97.6 |
| 500 | 97.5 | 94.8 | 98.8 | 99.3 | 98.2 | ||
| 1,000 | 97.8 | 95.5 | 99.3 | 99.4 | 98.9 | ||
| 5,000 | 97.6 | 95.5 | 99.3 | 99.3 | 99.1 | ||
| Moderately skewed and kurtotic | 200 | 77.4 | 90.6 | 81.9 | 89.1 | 56.6 | |
| 500 | 79.8 | 83.2 | 83.6 | 90.2 | 15.8 | ||
| 1,000 | 80.6 | 65.8 | 84.5 | 91.1 | 1.4 | ||
| 5,000 | 79.3 | 1.1 | 68.3 | 68.3 | 0.0 | ||
| Severely skewed and kurtotic | 200 | 67.0 | 90.4 | 70.0 | 79.2 | 64.9 | |
| 500 | 63.0 | 93.7 | 70.3 | 79.6 | 45.0 | ||
| 1,000 | 58.2 | 93.3 | 67.6 | 77.8 | 24.3 | ||
| 5,000 | 21.6 | 89.0 | 52.5 | 68.1 | 0.1 | ||
| 3 Categories | Symmetric | 200 | 100.0 | 95.6 | 100.0 | 100.0 | 100.0 |
| 500 | 100.0 | 94.6 | 100.0 | 100.0 | 100.0 | ||
| 1,000 | 100.0 | 95.4 | 100.0 | 100.0 | 100.0 | ||
| 5,000 | 100.0 | 93.4 | 100.0 | 100.0 | 100.0 | ||
| Moderately skewed and kurtotic | 200 | 99.0 | 92.0 | 99.9 | 99.9 | 98.8 | |
| 500 | 99.9 | 88.3 | 99.9 | 100.0 | 98.2 | ||
| 1,000 | 100.0 | 78.0 | 100.0 | 100.0 | 97.4 | ||
| 5,000 | 100.0 | 9.6 | 100.0 | 100.0 | 8.0 | ||
| Severely skewed and kurtotic | 200 | 98.4 | 89.7 | 99.5 | 99.6 | 99.5 | |
| 500 | 99.1 | 92.3 | 100.0 | 99.4 | 99.6 | ||
| 1,000 | 99.0 | 93.4 | 99.7 | 99.6 | 99.5 | ||
| 5,000 | 96.2 | 95.4 | 99.6 | 99.8 | 82.2 | ||
Note. Boldfaced numbers indicate coverage rate lower than the suggested value (<90% in value) by Cham et al. (2012).
Lower-Order Effects
We also studied the lower-order effects , , and in terms of the relative bias of the parameter estimates, standard error estimates, and coverage rates. The full report of these results is provided in the online supplementary material. In summary, all four UPI models produced unbiased estimates across all conditions, and unbiased and estimates across all conditions except with severely skewed and kurtotic categorical indicators. LMS produced negatively biased , and estimates when the indicators were skewed and kurtotic and produced mixed results with . All four UPI models produced acceptable or slightly high relative bias of the standard errors of the lower-order effects with N≥500, while LMS produced unbiased estimates in N = 200 condition as well. Across all conditions, coverage rates of the lower order effects were better with the UPI models, however, skewed and kurtotic categorical indicators caused lower coverage rates. LMS suffered from skewness and kurtosis more, resulting in coverage rates as low as .2 ( estimates with moderately skewed and kurtotic five-category items).
Summary and Discussion
The simulation study results partly supported our hypotheses. Drawing on previous findings suggesting it is appropriate to treat ordered-categorical indicators with five or more categories as continuous indicators in confirmatory factor analysis, we hypothesized that the UPI method with NML estimation with robust standard errors would perform well with five-category indicators and fail with three-category indicators. Our simulation study results only partly supported this hypothesis.
With continuous indicators, UPI matching approach produced unbiased estimates of interaction effect with correct Type I error rates with N≥1,000 while it underestimated standard errors when the indicators were nonsymmetrically distributed. With five-category indicators, it made unbiased interaction effect and standard error estimates with acceptable Type I error and power rates only when indicators were symmetric or moderately skewed and kurtotic with N≥1,000. When the indicators were severely skewed and kurtotic, it underestimated the interaction effect. With three-category indicators, it produced unbiased interaction and standard error estimates, acceptable Type I error, power, and coverage rates only when the indicators were symmetrically distributed and the sample sizes were large (N≥1,000).
UPI parceling approach produced unbiased estimates of the interaction effect with good coverage, and Type I error rates for all indicator type conditions (i.e., continuous, five-category, three-category) and across all sample sizes when the indicators were symmetrical. However, it required N≥500 for adequate power and needed N≥500 for unbiased standard error estimates with five-category indicators and produced biased SE estimates with three-category indicators. When the indicators were nonsymmetrical, UPI parceling models resulted in highly overestimated interaction effects, and low coverage rates with increased sample size (as low as 0.4%) in all conditions except with three-category severely skewed and kurtotic indicators.
LMS approach performed similar to the UPI parceling approach in that it produced unbiased interaction estimates with all indicator types as long as they were symmetrically distributed, but highly overestimated the interaction effects even with moderate levels of skewness and kurtosis. LMS also tended to underestimate the standard error of the interaction estimates, had extremely elevated Type I error rates and low coverage rates in these conditions.
We also considered a new strategy that involves both matching and parceling strategies to create product indicators (2M + P and M + 2P strategies) in the hope of retaining the advantages of both matching and parceling. However, the results did not fully meet our expectations. UPI 2M + P, and M + 2P strategies performed well under the symmetry condition with larger sample sizes (N≥500 in continuous, N≥1,000 in five-category, N = 5,000 in three-category indicators). When the indicators were moderately skewed and kurtotic and continuous, 2M + P, and M + 2P produced unbiased interaction effect estimates, correct Type I error rates, and high coverage rates in most conditions, and satisfactory power rates with N≥500. However, they tended to underestimate the standard errors. 2M + P showed similar patterns of results with three-category indicators as well, while M + 2P performed poorly in these conditions. When the indicators were five-category, 2M + P and M + 2P overestimated the interaction effects with low coverage rates. When the indicators were severely skewed and kurtotic, 2M + P and M + 2P produced unbiased interaction estimates only with continuous indicators (M + 2P required N≥1,000), with nominal or slightly inflated Type I errors and high power with N≥1,000.
Based on the simulation study results, we provide some guidelines for researchers in using these models when estimating latent variable interactions. Table 6 is a summary table that presents the models that produced unbiased interaction effect estimates in the indicator symmetry, number of categories of indicators, and sample size conditions. The models showed varying levels of performance based on other evaluation criteria depending on the study condition, as indicated by coded superscripts. This table can be used by applied researchers as a reference to choose a suitable model to use in their unique research scenario. Our main recommendations are:
Table 6.
Methods Producing Unbiased Interaction Effect Estimates.
| Indicators’ categories | Indicators’ distribution | N | |||
|---|---|---|---|---|---|
| 200 | 500 | 1,000 | 5,000 | ||
| Symmetric | Continuous | Parceling6 | Parceling | Matching | Matching |
| LMS6 | 2M + P4 | Parceling | Parceling | ||
| M + 2P4 | 2M + P | 2M + P | |||
| LMS | M + 2P | M + 2P | |||
| LMS | LMS | ||||
| 5 Categories | Parceling2, 6 | Parceling | Matching | Matching | |
| LMS4, 6 | LMS | Parceling | Parceling | ||
| 2M + P | 2M + P | ||||
| M + 2P | M + 2P | ||||
| LMS | LMS5 | ||||
| 3 Categories | Parceling2, 6 | Parceling6 | Matching4 | Matching | |
| LMS4, 6 | LMS | Parceling1 | Parceling1 | ||
| LMS | 2M + P | ||||
| M + 2P | |||||
| LMS | |||||
| Moderately skewed and kurtotic | Continuous | 2M + P1, 3, 6 | Matching1, 3 | Matching1 | Matching1 |
| M + 2P1, 6 | 2M + P1, 5 | 2M+P1 | 2M+P | ||
| M + 2P1, 5 | M+2P1 | M+2P | |||
| 5 Categories | Matching1, 3, 4, 6 | Matching3, 4 | Matching3 | ||
| 3 Categories | Matching2, 4, 6 | 2M + P1, 4, 6 | 2M + P1 | 2M + P | |
| 2M + P4, 6 | |||||
| M + 2P4, 6 | |||||
| Severely skewed and kurtotic | Continuous | 2M + P2, 3, 6 | 2M + P6 | Matching1 | Matching |
| 2M + P | 2M + P | ||||
| M + 2P1 | M + 2P | ||||
| 5 Categories | |||||
| 3 Categories | Parceling2, 3, 6 | Parceling6 | |||
Note. Superscript 1 = underestimated standard errors (relative bias < −10%); 2 = overestimated standard errors (relative bias > 10%); 3 = low coverage rate (<.9); 4 = low Type I error rate (<.037); 5 = inflated Type I error rate (>.063); 6 = low statistical power (<.9).
When the indicators are symmetric, choose the LMS approach, or UPI parceling strategy or other UPI strategies listed in the corresponding cells in Table 6. Models listed without superscripts (which indicates suboptimal performance in other evaluation criteria when present) should be of higher preference order. This recommendation applies to ordered-categorical indicators as well.
Do NOT use UPI parceling or LMS when the indicators are skewed or kurtotic.
Use UPI 2M + P for continuous skewed and kurtotic indicators with caution. It can produce suboptimal standard error estimates, Type I error rates, power, or coverage rates, depending on particular research conditions. UPI matching and M + 2P models can also produce unbiased estimates with continuous skewed and kurtotic indicators especially with large (N≥1,000) sample sizes, but 2M + P behaves more consistently. Or, try other methods that can handle nonsymmetrical indicators (see the General Discussion section for recommendations).
Do not use any of the studied UPI models or LMS approach for categorical skewed and kurtotic indicators. Although some of the models seemed to work relatively well in some simulation conditions, the patterns of results are not consistent to make a clear recommendation. Instead, try generalized methods that are developed to handle ordered-categorical and nonnormal indicators (see the General Discussion section for recommendations).
Have N≥500 to avoid low statistical power when estimating latent variable interactions using UPI or LMS approach.
Substantive Example
We applied the UPI approach (matching, parceling, 2M + P, and M + 2P) and the LMS approach in a substantive example of latent variable interaction with ordered-categorical indicators. Data are from a randomized controlled efficacy trial of the Cultivating Awareness and Resilience in Education program, a mindfulness-based teacher professional development program which has been shown to reduce teacher psychological distress, improve teacher adaptive emotion regulation and mindfulness, and improve the quality of classroom interactions (Jennings et al., 2017). In our example, we tested whether there is an interaction effect between third- and fifth-grade students’ social skills and student–teacher closeness on students’ proficiency rating on the New York State English Language Arts (ELA) test. It was expected that higher teacher–student closeness may confer a protective influence for children with low social skill regarding their academic achievement. Students’ social skills were measured by the teacher-reported Social Skills Improvement System Rating Scale (SSIS; Gresham & Elliott, 2008). Teachers responded to 10 items for which they rated the frequency with which a student exhibited various social skill–related behaviors over the past 2 months on a four-point scale (never, seldom, often, and almost always). Student–teacher closeness was measured by using the teacher-reported Closeness subscale of the Student–Teacher Relationship Scale–Short Form (Pianta, 2001). Teachers responded to seven items for which they rated the degree of closeness they experienced with a specific student on a 5-point scale (1 = definitely does not apply to 5 = definitely applies). Both measures had satisfactory internal consistencies (SSIS: McDonald’s ω = .95; Closeness: McDonald’s ω = .88). The outcome variable, ELA proficiency ratings, were provided by the New York State Department of Education. ELA proficiency ratings range between 1.0 and 4.5. To simplify the analysis for demonstration purpose, only the students with complete observations on all variables were used, resulting in 1,851 students. The data have a three-level clustered structure of students nested within teachers (median intraclass correlations across variables = .18, range = .11 to .40), and teachers within schools (median intraclass correlations across variables = .04, range = .02 to .11). To account for this clustered data structure, we used the TYPE=COMPLEX with the CLUSTER and STRATIFICATION options in Mplus to adjust the standard errors of the parameter estimates (e.g., Guo et al., 2016).
The skewness and kurtosis of the indicators of SSIS and closeness were similar in magnitude to the moderately skewed and kurtotic conditions of the simulation study (SSIS: median skewness = −.47, range = −.62 to −.02; median kurtosis = −.47, range = −.85 to −.17. Closeness: median skewness = −.64, range = −1.38 to −.52; median kurtosis = −.24, range = −.48 to 2.52). Based on the simulation results, the matching strategy would provide the interaction effect estimate with the least bias and acceptable Type I error rate. All four strategies in the UPI approach followed the procedures described previously and were estimated using NML estimation with robust standard errors (ESTIMATOR = MLR) via Mplus 7.2. For the LMS model, the default Gauss–Hermite integration algorithm with 16 integration points per dimension was used, and robust standard errors were calculated (ESTIMATOR = MLR). Table 7 shows the unstandardized parameter estimates, estimated standard errors, and the significance levels of the coefficients in the interaction model (, , , ). For the interaction effect estimate, the ascending order of its value produced by the five models was matching < 2M + P < LMS < M + 2P < parceling. The results of the UPI models were consistent with the simulation results that the ascending order of the biases of the interaction effect estimates was also matching <2M + P < M + 2P < parceling for the moderately skewed and kurtotic five-category indicators, while LMS behaved unexpectedly. All models produced similar lower-order effect estimates, which was also consistent with the simulation results.
Table 7.
Unstandardized Results of Substantive Example.
| Method | Intercept () | SSIS () | Closeness () | Interaction () | ||||
|---|---|---|---|---|---|---|---|---|
| Est. | SE | Est. | SE | Est. | SE | Est. | SE | |
| Matching | 2.333 | .026*** | .291 | .031*** | −.077 | .038* | −.067 | .035† |
| Parceling | 2.329 | .026*** | .204 | .022*** | −.052 | .028† | .030 | .021 |
| 2M + P | 2.327 | .027*** | .293 | .032*** | −.075 | .039† | −.031 | .033 |
| M + 2P | 2.325 | .026*** | .293 | .032*** | −.075 | .039† | −.025 | .031 |
| LMS | 2.327 | .027*** | .294 | .032*** | −.077 | .039* | −.030 | .033 |
Note. SE = Standard error. SSIS stands for Social Skills Improvement System Rating Scale.
p < .10. *p < .05. **p < .01. ***p < .001.
Based on the results of the suggested matching strategy, Figure 3 visualizes the interaction effect. On average, students’ social skills improvement was positively related to their English language arts test scores. When the students’ felt closer to their teachers, the relationship remained positive but decreased slightly. However, it should be noted that this interaction effect was only marginally significant (unstandardized coefficient = −.07, z = −1.94, p = .052) with a trivial increase (= .004).
Figure 3.

Interaction between Grade 3 and 5 students’ social skills improvement and teacher–student closeness on students’ English language arts test scores.
General Discussion
In this article, we studied the performance of the unconstrained product indicator approach in estimating latent variable interaction effects when the indicators of the predicting (exogenous) factors are ordered-categorical, in comparison with the LMS approach (Klein & Moosbrugger, 2000). We have studied four strategies to creating sets of product indicators for the latent interaction terms across various sample sizes, distributions, and categories of predictors. Based on the results, we have provided some guidelines for researchers encountering different research situations and then applied them in a substantive example. In this section, we further discuss some other related issues that were not investigated in this article.
The first issue is other estimators for categorical indicators. In UPI, one may consider other estimations that are tailored for ordered-categorical indicators, such as the limited-information unweighted least squares and diagonally weighted least squares estimations. These estimations assume that each ordered-categorical indicator is categorized by an underlying normally distributed continuous variable with different threshold parameters. However, these estimators might not be appropriate for handling the product indicators. For instance, when two five-category indicators are matched, the resulting product indicator will have 25 categories. This may introduce data sparseness and might result in imprecision in parameter estimation.
The second issue is when the indicators have missing values. Cham, Reshetnyak, Rosenfeld, and Breitbart (2017) found that UPI with NML produce unbiased parameter estimates only when the continuous indicators are missing completely at random and LMS produce unbiased parameter estimates when the continuous indicators are missing at random. Reshetnyak and Cham (2016) suggested imputing the missing values of the indicators by regression tree modeling for UPI when the continuous indicators are missing at random. Future research is needed to find out methods to handle incompletely observed ordered-categorical indicators in latent variable interactions.
The third issue concerns the data generation procedures in the simulation study. We used and gamma distributions to randomly generate , , and unique factors in the moderately and severely skewed and kurtotic conditions. Foldnes and Olsson (2016) found that, when using different methods to generate variables with the same levels of skewness and kurtosis in a simulation study, the dependent measures of the study would change. This is one potential reason for different results and conclusions for the five- and three-category indicators in the simulation study. Also, our simulation study did not consider negatively skewed and platykurtic indicators. Future research may further consider other distribution conditions.
To conclude, among the models that were included in this study, when the indicators are symmetrically distributed, UPI with parceling strategy or LMS approach are recommended with indicators with three or more ordered response categories. When continuous indicators are skewed and kurtotic, UPI models involving matching (matching, 2P + M, M + 2P) may be used with cautions. When the categorical indicators are skewed and kurtotic, models studied in this article are not recommended. Instead, researchers should opt for methods that have been specifically developed to handle ordered-categorical indicators, such as Rizopoulos and Moustaki (2008) which can be applied using the ltm package (Rizopoulos, 2006) in R (R Core Team, 2018), or use the categorical extension of the LMS approach, which can be implemented in MPlus (Version 6 or newer versions; L. K. Muthén & Muthén, 1998-2014). Future research shall continue to study the applicability of other latent variable interaction methods for nonnormal and ordered-categorical indicators.
Supplemental Material
Supplemental material, Online_supplement-R1 for Latent Variable Interactions With Ordered-Categorical Indicators: Comparisons of Unconstrained Product Indicator and Latent Moderated Structural Equations Approaches by Ezgi Aytürk, Heining Cham, Patricia A. Jennings and Joshua L. Brown in Educational and Psychological Measurement
Acknowledgments
We thank David Budescu for his comments on the article.
When or have only two indicators, it is suggested to pair the indicators of and according to their reliabilities and includes the two product indicators in the factor model of .
Unweighted averaging of the indicators assumes that the indicators are measured on the same scale. Little et al. (2013, footnote 2) suggest converting the indicators to a comparable scale when the indicators have different scales.
Footnotes
Declaration of Conflicting Interests: The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding: The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This research was supported by the National Center for Education Research at the Institute of Education Sciences (Grant No. R30 5A120180).
ORCID iD: Ezgi Aytürk  https://orcid.org/0000-0001-6509-4288
https://orcid.org/0000-0001-6509-4288
Supplemental Material: Supplemental material for this article is available online.
References
- Algina J., Moulder B. C. (2001). A note on estimating the Jöreskog-Yang model for latent variable interaction using LISREL 8.3. Structural Equation Modeling, 8, 40-52. doi: 10.1207/s15328007sem0801_3 [DOI] [Google Scholar]
- Babakus E., Ferguson C. E., Jr., Jöreskog K. G. (1987). The sensitivity of confirmatory maximum likelihood factor analysis to violations of measurement scale and distributional assumptions. Journal of Marketing Research, 24, 222-228. [Google Scholar]
- Bandalos D. L. (2008). Is parceling really necessary? A comparison of results from item parceling and categorical variable methodology. Structural Equation Modeling, 15, 211-240. doi: 10.1080/10705510801922340 [DOI] [Google Scholar]
- Bohrnstedt G. W., Goldberger A. S. (1969). On the exact covariance of products of random variables. Journal of the American Statistical Association, 64, 1439-1442. doi: 10.1080/01621459.1969.10501069 [DOI] [Google Scholar]
- Cham H., Reshetnyak E., Rosenfeld B., Breitbart W. (2017). Full information maximum likelihood estimation for latent variable interactions with incomplete indicators. Multivariate Behavioral Research, 51, 12-30. doi: 10.1080/00273171.2016.1245600 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cham H., West S. G., Ma Y., Aiken L. S. (2012). Estimating latent variable interactions with nonnormal observed data: A comparison of four strategies. Multivariate Behavioral Research, 47, 840-876. doi: 10.1080/00273171.2012.732901 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coenders G., Batista-Foguet J. M., Saris W. E. (2008). Simple, efficient and distribution-free approach to interaction effects in complex structural equation models. Quality and Quantity, 42, 369-396. doi: 10.1007/s11135-006-9050-6 [DOI] [Google Scholar]
- Cohen J. (1992). A power primer. Psychological Bulletin, 112, 155-159. doi: 10.1037/0033-2909.112.1.155 [DOI] [PubMed] [Google Scholar]
- Dempster A. P., Laird N. M., Rubin D. B. (1977). Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society, Series B, 39, 1-38. doi: 10.2307/2344877 [DOI] [Google Scholar]
- Foldnes N., Hagtvet K. A. (2014). The choice of PIs in latent variable interaction models: Post hoc analyses. Psychological Methods, 19, 444-457. doi: 10.1037/a0035728 [DOI] [PubMed] [Google Scholar]
- Foldnes N., Olsson U. H. (2016). A simple simulation technique for nonnormal data with prespecified skewness, kurtosis, and covariance matrix. Multivariate Behavioral Research, 51, 207-219. doi: 10.1080/00273171.2015.1133274 [DOI] [PubMed] [Google Scholar]
- Gresham F., Elliott S. N. (2008). Social Skills Improvement System (SSIS) rating scales. Bloomington, MN: Pearson Assessments. [Google Scholar]
- Guo J., Nagengast B., Marsh H. W., Kelava A., Gaspard H., Brandt H., . . .Brisson B. (2016). Probing the unique contributions of self-concept, task values, and their interactions using multiple value facets and multiple academic outcomes. AERA Open, 2(1). doi: 10.1177/2332858415626884 [DOI] [Google Scholar]
- Hoogland J. J., Boomsma A. (1998). Robustness studies in covariance structure modeling: An overview and a meta-analysis. Sociological Methods & Research, 26, 329-367. doi: 10.1177/0049124198026003003 [DOI] [Google Scholar]
- Jaccard J., Wan C. K. (1995). Measurement error in the analysis of interaction effects between continuous predictors using multiple regression: Multiple indicator and structural equation strategies. Psychological Bulletin, 117, 348-357. doi: 10.1037/0033-2909.117.2.348 [DOI] [Google Scholar]
- Jackman M. G.-A., Leite W. L., Cochrane D. (2011). Estimating latent variable interactions with the unconstrained approach: A comparison of methods to form PIs for large, unequal numbers of items. Structural Equation Modeling, 18, 274-288. doi: 10.1080/10705511.2011.557342 [DOI] [Google Scholar]
- Jennings P. A., Brown J. L., Frank J. L., Doyle S., Oh Y., Tanler R., Rasheed D., . . . Greenberg M. T. (2017). Impacts of the CARE for Teachers Program on teachers’ social and emotional competence and classroom interactions. Journal of Educational Psychology, 109, 1010-1028. doi: 10.1037/edu0000187 [DOI] [Google Scholar]
- Jöreskog K. G., Yang F. (1996). Nonlinear structural equation models: The Kenny-Judd model with interaction effects. In Marcoulides G. A., Schumacker R. E. (Eds.), Advanced structural equation modeling: Issues and techniques (pp. 57-88). Mahwah, NJ: Lawrence Erlbaum. [Google Scholar]
- Kelava A., Werner C. S., Schermelleh-Engel K., Moosbrugger H., Zapf D., Ma Y., . . .West S. G. (2011). Advanced nonlinear structural equation modeling: Distribution-analytic LMS and QML estimators of interaction and quadratic effects. Structural Equation Modeling, 18, 465-491. doi: 10.1080/10705511.2011.582408 [DOI] [Google Scholar]
- Klein A. G., Moosbrugger H. (2000). Maximum likelihood estimation of latent interaction effects with the LMS method. Psychometrika, 65, 457-474. doi: 10.1007/bf02296338 [DOI] [Google Scholar]
- Kojadinovic I., Yan J. (2010). Modeling multivariate distributions with continuous margins using the copula R package. Journal of Statistical Software, 34(9), 1-20. Retrieved from http://www.jstatsoft.org/v34/i09/ [Google Scholar]
- Lee S.-Y., Song X.-Y., Cai J.-H. (2010). A Bayesian approach for nonlinear structural equation models with dichotomous variables using logit and probit links. Structural Equation Modeling, 17, 280-302. doi: 10.1080/10705511003659425 [DOI] [Google Scholar]
- Little T. D., Rhemtulla M., Gibson K., Schoemann A. M. (2013). Why the items versus parcels controversy needn’t be one. Psychological Methods, 18, 285-300. doi: 10.1037/a0033266 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marsh H. W., Wen Z., Hau K.-T. (2004). Structural equation models of latent interactions: Evaluation of alternative estimation strategies and indicator construction. Psychological Methods, 9, 275-300. doi: 10.1037/1082-989x.9.3.275 [DOI] [PubMed] [Google Scholar]
- McDonald R. P. (1999). Test theory: A unified treatment. Mahwah, NJ: Lawrence Erlbaum. [Google Scholar]
- Muthén B., Kaplan D. (1985). A comparison of some methodologies for the factor analysis of non-normal Likert variables. British Journal of Mathematical and Statistical Psychology, 38, 171-189. doi: 10.1111/j.2044-8317.1985.tb00832.x [DOI] [Google Scholar]
- Muthén L. K., Muthén B. O. (1998-2014). Mplus user’s guide (7th ed.) Los Angeles, CA: Muthén & Muthén. [Google Scholar]
- Nunnally J. C. (1978). Psychometric theory (2nd ed.). New York, NY: McGraw-Hill. [Google Scholar]
- Pianta R. C. (2001). Student-Teacher Relationship Scale: Professional manual. Lutz, FL: Psychological Assessment Resources. [Google Scholar]
- R Core Team. (2018). R: A language and environment for statistical computing [Computer software]. Vienna, Austria: R Foundation for Statistical Computing; Retrieved from http://www.R-project.org [Google Scholar]
- Reshetnyak E., Cham H. (2016, May). Estimating latent variable interactions with incomplete exogenous indicators via CART in MICE using unconstrained product indicator approach. Paper presented at 2016 Modern Modeling Methods (M3) Conference, Storrs, CT. [Google Scholar]
- Rhemtulla M., Brosseau-Liard P., Savalei V. (2012). When can categorical variables be treated as continuous? A comparison of robust continuous and categorical SEM estimation methods under suboptimal conditions. Psychological Methods, 17, 354-373. doi: 10.1037/a0029315 [DOI] [PubMed] [Google Scholar]
- Rizopoulos D. (2006). ltm: An R package for latent variable modelling and item response theory analyses. Journal of Statistical Software, 17(5), 1-25. Retrieved from http://www.jstatsoft.org/v17/i05/ [Google Scholar]
- Rizopoulos D., Moustaki I. (2008). Generalized latent variable models with nonlinear effects. British Journal of Mathematical and Statistical Psychology, 61, 415-438. doi: 10.1348/000711007X213963 [DOI] [PubMed] [Google Scholar]
- Rogers W. M., Schmitt N. (2004). Parameter recovery and model fit using multidimensional composites: A comparison of four empirical parceling algorithms. Multivariate Behavioral Research, 39, 379-412. doi: 10.1207/s15327906mbr3903_1 [DOI] [Google Scholar]
- Satorra A., Bentler P. M. (1994). Corrections to test statistics and standard errors in covariance structure analysis. In von Eye A., Clogg C. C. (Eds.), Latent variables analysis: Applications for developmental research (pp. 399-419). Thousand Oaks, CA: Sage. [Google Scholar]
- Schermelleh-Engel K., Klein A. G., Moosbrugger H. (1998). Estimating nonlinear effects using a latent moderated structural equations approach. In Schumacker E., Marcoulides G. A. (Eds.), Interaction and nonlinear effects in structural equation modeling (pp. 203-238). Mahwah, NJ: Lawrence Erlbaum. [Google Scholar]
- Song X. Y., Lee S. Y. (2005). Maximum likelihood analysis of nonlinear structural equation models with dichotomous variables. Multivariate Behavioral Research, 40, 151-177. doi: 10.1207/s15327906mbr4002_1 [DOI] [PubMed] [Google Scholar]
- West S. G., Aiken L. S., Cham H., Liu Y. (2013). Multiple regression: The basics and beyond for clinical scientists. In Comer J. S., Kendall P. C. (Eds.), The Oxford handbook of research strategies for clinical psychology (pp. 227-252). New York, NY: Oxford University Press. [Google Scholar]
- Wu Y., Wen Z., Marsh H. W., Hau K.-T. (2013). A comparison of strategies for forming PIs for unequal numbers of items in structural equation models of latent interactions. Structural Equation Modeling, 20, 551-567. doi: 10.1080/10705511.2013.824772 [DOI] [Google Scholar]
- Yang C., Nay S., Hoyle R. H. (2010). Three strategies to using lengthy ordinal scales in structural equation models: Parceling, latent scoring, and shortening scales. Applied Psychological Measurement, 34, 122-142. doi: 10.1177/0146621609338592 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan K.-H., Bentler P. M. (2000). Three likelihood-based methods for mean and covariance structure analysis with nonnormal missing data. Sociological Methodology, 30, 165-200. doi: 10.1111/0081-1750.00078 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplemental material, Online_supplement-R1 for Latent Variable Interactions With Ordered-Categorical Indicators: Comparisons of Unconstrained Product Indicator and Latent Moderated Structural Equations Approaches by Ezgi Aytürk, Heining Cham, Patricia A. Jennings and Joshua L. Brown in Educational and Psychological Measurement