Unified Model for Photophysical and Electro-Optical Properties of Green Fluorescent Proteins

Abstract

Green fluorescent proteins (GFPs) have become indispensable imaging and optogenetic tools. Their absorption and emission properties can be optimized for specific applications. Currently, no unified framework exists to comprehensively describe these photophysical properties, namely the absorption maxima, emission maxima, Stokes shifts, vibronic progressions, extinction coefficients, Stark tuning rates, and spontaneous emission rates, especially one that includes the effects of the protein environment. In this work, we study the correlations among these properties from systematically tuned GFP environmental mutants and chromophore variants. Correlation plots reveal monotonic trends, suggesting that all these properties are governed by one underlying factor dependent on the chromophore’s environment. By treating the anionic GFP chromophore as a mixed-valence compound existing as a superposition of two resonance forms, we argue that this underlying factor is defined as the difference in energy between the two forms, or the driving force, which is tuned by the environment. We then introduce a Marcus–Hush model with the bond length alternation vibrational mode, treating the GFP absorption band as an intervalence charge transfer band. This model explains all of the observed strong correlations among photophysical properties; related subtopics are extensively discussed in the Supporting Information. Finally, we demonstrate the model’s predictive power by utilizing the additivity of the driving force. The model described here elucidates the role of the protein environment in modulating the photophysical properties of the chromophore, providing insights and limitations for designing new GFPs with desired phenotypes. We argue that this model should also be generally applicable to both biological and nonbiological polymethine dyes.

Graphical Abstract

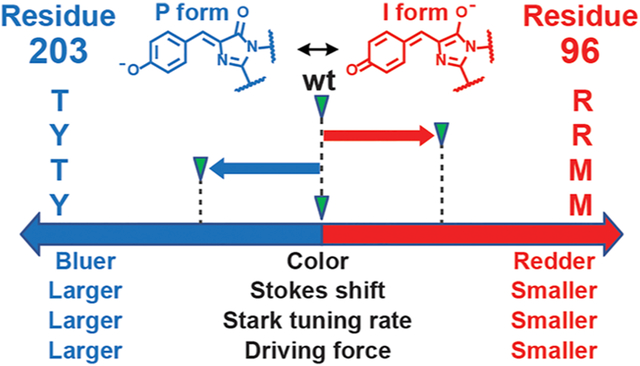
1. INTRODUCTION

Since its discovery from the jellyfish Aequorea victoria, green fluorescent protein (GFP) and its relatives have become the most widely used genetically encoded in vivo imaging and tracking tools for biological studies.^1,2 Their versatility and diverse photophysical properties (e.g., color, fluorescence quantum yield, and Stokes shift) have inspired numerous innovative applications beyond imaging, such as ionic- and voltage-dependent sensors,³ protein–protein interaction probes,⁴ and optical controls of proteins in cells,⁵ among others. Remarkably, all this functional diversity stems from the autocatalytically formed chromophores that share the same π-conjugated system, 4-hydroxybenzylideneimidazolinone (HBI) (Figure 1A), encapsulated in a structurally conserved β-barrel; only the protein environment in which the chromophore is embedded differs. Studies have shown that, through site-directed mutagenesis, GFPs can exhibit a palette of colors and wide range of fluorescence quantum yields⁶ and are thus excellent model systems for investigating how properties are influenced by the interaction between the chromophore and its environment, a question intimately linked to the general goal of designing proteins with properties of interest. A major challenge of protein design involves rationally devising a strategy to obtain a desired protein function on the basis of its structure. While the most fruitful approach to partially address this issue has relied on harnessing the power of evolution and ingenious screening,^7–11 rational design has had only sparse success with the aid of computation.^12,13

Figure 1.

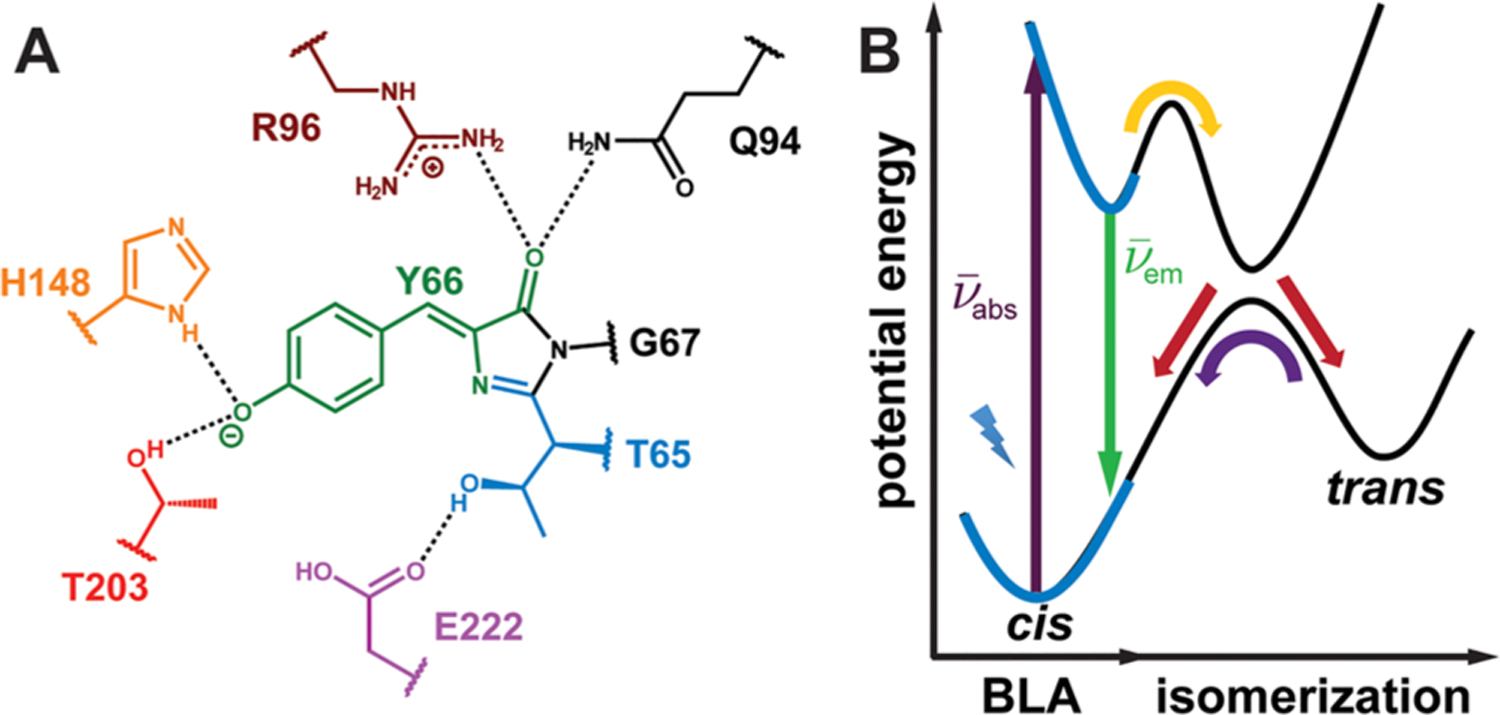
Structure and energetics of the GFP chromophore embedded in the protein environment. (A) The GFP chromophore, 4-hydroxybenzylideneimidazolinone (HBI), and surrounding residues within GFP. The colored residues represent those mutated in this work (Table 1). (B) Potential energy diagram of the ground and excited electronic states for the GFP chromophore.¹⁴ In this work, we focus on the region of the diagram highlighted by the blue boldface curves associated with absorption (${\overline{v}}_{\text{abs}}$) and emission (${\overline{v}}_{\text{em}}$). The nuclear motion relevant to this part of the potential energy diagram is the bond length alternation (BLA).

In a previous publication,¹⁴ we divided the difficult problem of linking structure to function into smaller conquerable pieces: namely, bridging those two entities with energetics through the understanding of potential energy surfaces (PESs, Figure 1B).^15,16 The relation between energetics and function was clearly elaborated, but the missing connection between structure and energetics remains elusive, especially since the electrostatic contribution is typically difficult to visualize from atomic coordinates.^17,18 Computational methods incorporating various levels of approximations, such as ab initio quantum and classical MD simulations, are the most popular and viable approaches so far because they aim to relate atomic positions to energy eigenstates. The most advanced and reliable methods require substantial computational knowledge and resources not available for most experimental groups; unfortunately, cheaper and more accessible computational methods tend to yield unreliable results.^13,19 In this manuscript we ask the following: is it possible to develop a simple and intuitive framework with the fewest possible parameters to shed light on design principles without relying on advanced computational methods?

Usually, endeavors to experimentally elucidate property tuning rely on pre-existing protein mutants that carry mutations at noncritical residues²⁰ or saturation mutagenesis at specific sites;^21,22 both approaches are limited to the 20 canonical amino acids. In this study, we perform systematic site-directed mutagenesis on several critical residues that directly interact with the GFP chromophore, highlighted in Figure 1A. We also take advantage of the semisynthetic split GFP technique previously developed in our laboratory to generate mutants that are inaccessible via other methods,^23,24 due to either impaired chromophore maturation efficiency²⁵ or the lack of aminoacyl-tRNA synthetases necessary to site-specifically incorporate certain noncanonical amino acids via amber suppression.²⁶ Through these methods, we can therefore achieve a wide range of values for any property of interest and systematically observe any correlation between structure and energetics. If strong correlations are observed among these photophysical properties, they are likely to be controlled by a common underlying factor tied to the variation in the protein environment. Therefore, examining correlations among properties from these mutants offers instructive information for proposing a minimal model.

In this study, we focus on the properties of the anionic chromophore related to the region of the PESs involving Franck–Condon excitation and emission (blue curves in Figure 1B). We show that the chromophore’s behavior within this PES region can be described via the Marcus–Hush theory for electron transfer^27,28 because a large extent of charge transfer is associated with the excitation process, and this can be probed through either electronic Stark spectroscopy²⁹ or chromophore modification.³⁰ We treat the chromophore as a mixed-valence compound and explicitly consider the vibronic coupling, building upon the works pioneered in the field of push–pull molecules using the mixing of chemically intuitive valence-bond structures.^31–35 The Marcus–Hush parameters, namely the electronic coupling and reorganization energy, are assumed to be intrinsic properties of the chromophore and thus are not easily tuned by the protein environment, which we justify later by comparing chromophores with similar conjugation lengths (section 2.4). The only parameter that distinguishes the differences among various mutants is the driving force, which describes the difference in electron affinity between the two chromophore rings in each environment. The role of the environment can therefore be thought to tune the energy difference between the valence-bond structures. In other words, the anionic GFP chromophore can be simply understood as a superposition of its two resonance forms, whose relative contributions can be modulated by interactions with the environment. This adapted Marcus–Hush theory quantitatively rationalizes the observed correlations among absorption maxima, Stokes shifts, electronic Stark tuning rates (degrees of charge transfer during excitation), vibronic structures, extinction coefficients, and other photophysical properties pertinent to the PES region under investigation. We finally argue that the GFP chromophore, as the simplest model system among all π-conjugated biochromophores (a methine bridge connected to two rigid rings), can serve as a stepping stone for elucidating design principles of other photosensory proteins, including photoactive yellow proteins (PYPs) and rhodopsins.^36,37

2. RESULTS AND DISCUSSION

2.1. Mutant and Variant Design.

Several residues that either directly interact with the chromophore or form part of the chromophore were chosen for site-specific mutation (Figure 1A). For convenience, we refer to GFP constructs that carry mutations at the former as “mutants” and the latter as “variants”; see Table 1 for a short list, with a full list given in Table S1 in the Supporting Information. Although the primary focus of this work is how the environment tunes the properties of the chromophore, we include data for chromophore variants from our recent study³⁰ to complement the results from environmental mutants.

Table 1.

GFP Mutation Sites Chosen for This Study^a

mutation sites	amino acids
Environmental Mutants
R96	R, E, M
H148	H, D
T203	T, V, H, F, Y, 4-F1F, F5F, 4-NH2F, 3-OCH3Y
E222	E, Q K
Chromophore Variants
S65	S, T, C
Y66	Y, 3-F1Y, 3-Cl1Y, 3-Br1Y, 3-I1Y, 2,3-F2Y, 3,5-F2Y, 3,5-Cl2Y, 2,3,5-F3Y, 3-CH3Y, 3-OCH3Y, 3-NO2Y

^aNoncanonical amino acids are abbreviated as follows: 4-fluorophenylalanine is 4-F₁F, 3-fluorotyrosine is 3-F₁Y, 2,3-difluorotyrosine is 2,3-F₂Y, 3,5-difluorotyrosine is 3,5-F₂Y, 2,3,5-trifluorotyrosine is 2,3,5-F₃Y, 2,3,4,5,6-pentafluorophenylalanine is F₅F, 3-chlorotyrosine is 3-Cl₁Y, 3,5-dichlorotyrosine is 3,5-Cl₂Y, 3-bromotyrosine is 3-Br₁Y, 3-iodotyrosine is 3-I₁Y, 3-methyltyrosine is 3-CH₃Y, 3-methoxytyrosine is 3-OCH₃Y (3-OMeY), 3-nitrotyrosine is 3-NO₂Y, and 4-aminophenylalanine is 4-NH₂F (see also Table S1).

First, we focus on residues in proximity to the chromophore. Two residues interact with the phenolate oxygen: threonine 203 and histidine 148 (Figure 1A). The former has been extensively studied, since mutating T203 is a common way to red-shift the absorption maximum without impairing the chromophore maturation efficiency.^38,39 We replaced T203 with various canonical and noncanonical amino acids to sample a wide range of interactions with the chromophore, including hydrogen-bonding (T), hydrophobic (V), and π–π stacking (H, F, 4-F₁F, F₅F, Y, 4-NH₂F and 3-OCH₃Y) interactions^40,41 (Figures 2 and 3A, see also Figure S20 in the Supporting Information for the T203(3-OMeY) structure). Notably, electron donating and withdrawing groups were introduced as variants of T203F in order to more finely modulate the π–π interaction. H148 has also been targeted for various reasons, especially the peculiar H148D mutation in which the aspartate carboxylate interacts with the protonated chromophore via a short hydrogen bond;^42,43 here we are interested in probing its influence on the chromophore’s anionic state.

Figure 2.

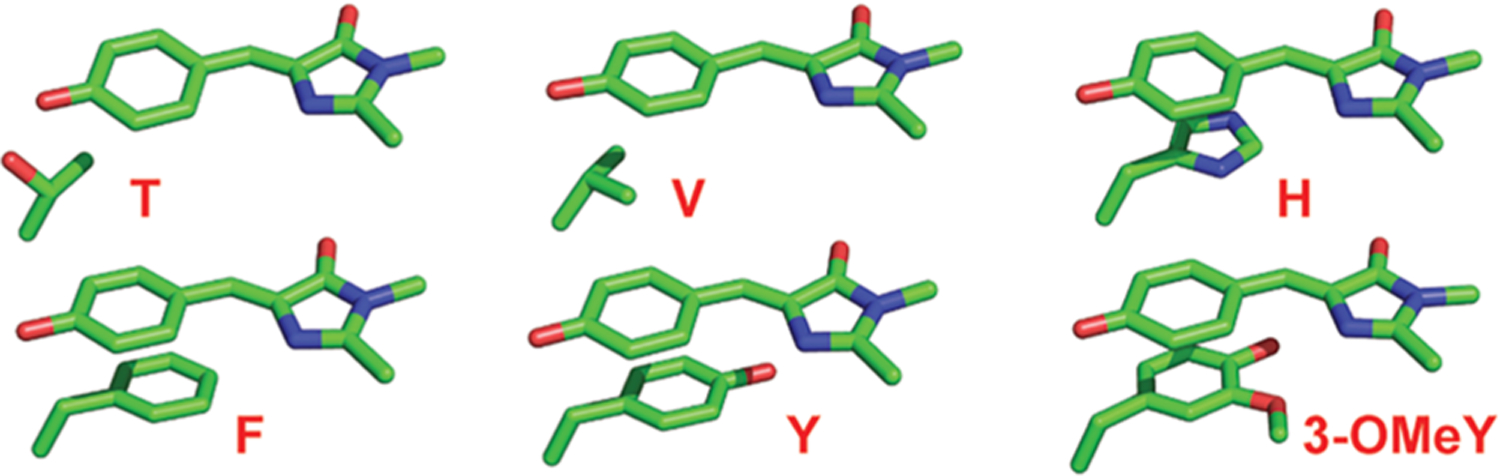
Structural comparison of the interactions between the chromophore’s phenolate ring and the different side chains of residue 203 in this work, sampling a range of effects including hydrogen-bonding (T), hydrophobic (V), and π–π stacking (H, F, Y, and 3-OMeY) interactions. The atomic coordinates for T203, T203V, T203H, T203F, T203Y, and T203(3-OMeY) are extracted from PDB entries 6OFK (this work), 4OGS,⁴⁸ 3GJ1,⁴⁹ 3V3D,⁵⁰ 1YFP,⁴⁰ and 6OFN (this work), respectively.

Figure 3.

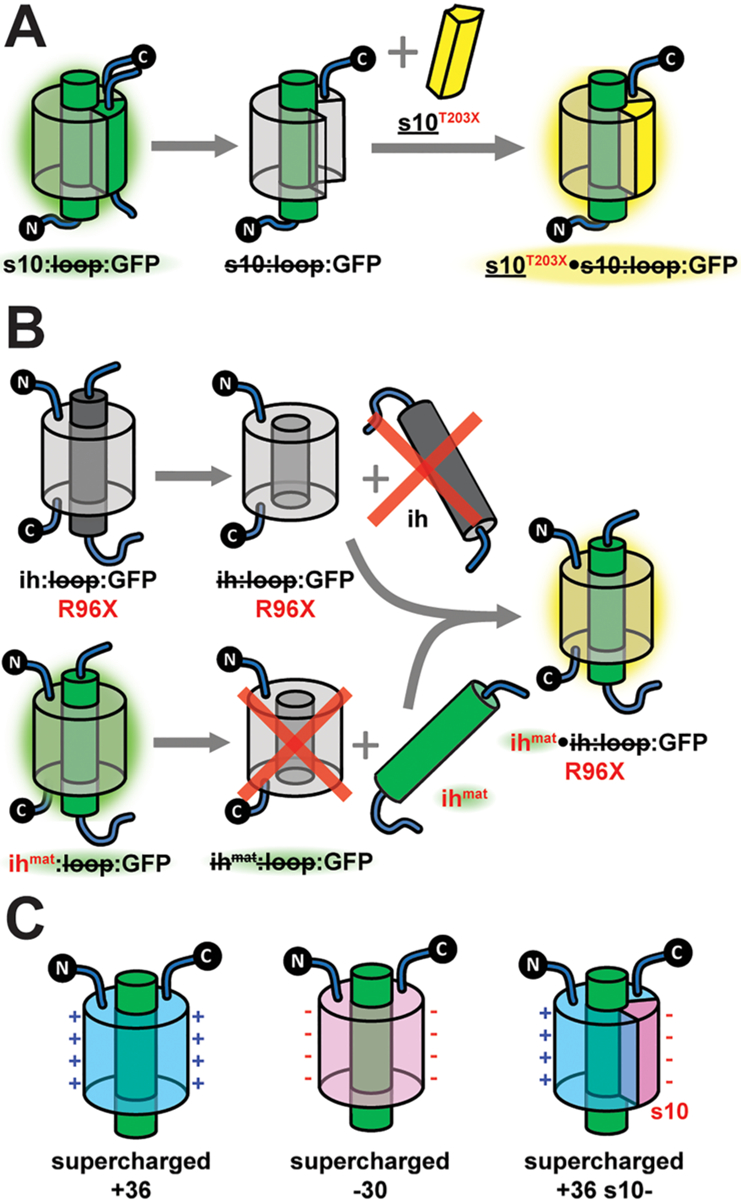
Preparation of split and supercharged GFP constructs in this study. (A) Cartoon illustration of the semisynthetic strategy to incorporate various mutations of T203 on β-strand 10 (s10). (B) Cartoon schematic depicting the insertion of a mature chromophore (mat) within the internal helix (ih) into an empty β-barrel containing the R96 mutations. This split GFP strategy enables the study of proteins for which chromophore maturation is hindered.⁴⁵ See section S1 in the Supporting Information or ref 14 for an explanation of the split GFP nomenclature, logic, and details of assembly. (C) Representation of the surface charge patterns of the supercharged GFP mutants in this work.

On the other side of the chromophore, arginine 96 and glutamine 94 interact with the imidazolinone oxygen (Figure 1A). These residues are rarely mutated due to their critical roles in chromophore maturation,^25,44 but we were able to fully incorporate the matured chromophore into the protein pockets of the R96 mutants with sufficient yields using the split GFP method illustrated in Figure 3B.^23,45 Because of the mismatch between the side-chain lengths of arginine and methionine, the R96M mutation causes a water molecule to insert between methionine and the imidazoline oxygen, presumably retaining the hydrogen bonding interaction.²⁵ Nevertheless, the environment has been substantially modified, since a positive charge has been eliminated. We assume that R96E would also impart a similar effect. Unfortunately, the yield of the Q94 mutant was insufficient for any characterization (section S1 in the Supporting Information). We also mutated glutamate 222 (Figure 1A), which is critical in both the ground and excited state proton transfer processes.^46,47 We incorporated E222Q mainly to bias S65 mutants into the anionic state to facilitate spectroscopic studies (section 2.2).⁴⁷

For chromophore variants, we can only target serine 65 and tyrosine 66, since glycine 67 is highly conserved^46,51 (Figure 1A). Virtually every mutation of S65 has been achieved,⁵² and here we chose a popular subset of mutants: S65 (in wild-type Aequorea victoria GFP, avGFP), S65T (in enhanced GFP⁵³), and S65C (in Dronpa from the Pectiniidae coral family,⁵⁴ Figure S21 in the Supporting Information). S65T mutants are especially favorable because most exhibit only the anionic state at basic pH and nearly single-site titration behavior.⁴⁷ Following our previous exploration on the photophysics of chromophore variants,³⁰ we introduce electron withdrawing and donating moieties directly to the chromophore by replacing Y66 with noncanonical tyrosine analogues using amber suppression.

Aside from all these mutations at critical residues, supercharged GFPs⁹ were investigated as controls to test whether residues with side chains exposed to solvent influence the chromophore’s photophysical properties, especially when positively or negatively charged (Figure 3C, see also Table S8 in the Supporting Information for the mutation site list). GFP model chromophore analogues parallel to the chromophore variants were also synthesized and studied in aqueous buffer or ethanol to enable comparisons between protein environments and solvents (Figure 4).

Figure 4.

Analogues of the GFP model chromophore, 4-hydroxybenzylidene-1,2-dimethylimidazolinone (HBDI), synthesized and characterized in this study. Note that the orientations of the substituents are not known for the singly substituted model chromophores.

2.2. 77 K Absorption Maximum and Vibronic Structure.

We measured absorption spectra of these GFP mutants and chromophore analogues at 77 K to obtain sharp and well-resolved absorption bands. Representative spectra are shown in Figure 5A. Similar to early low-temperature studies on fluorescent proteins,^30,55,56 the A and B bands associated with the protonated (neutral) and deprotonated (anionic) species, respectively, can be identified on the basis of their positions and conserved vibronic structures across mutants. Specifically, three prominent bluer peaks and two redder peaks can be assigned to the A and B bands, respectively (Figure S23 in the Supporting Information). The latter assignment is especially evident in mutants that only exhibit the anionic state, and theoretical studies suggest that the associated peaks correspond to 0–0 and 0–1 transitions.^57,58 The relative intensity between 0–0 and 0–1 peaks increases as the absorption maximum becomes redder. Second derivatives of the spectra reveal peak positions of these vibronic progressions (Figure S24 in the Supporting Information). Aside from HBDI in aqueous buffer, which could be complicated by the inhomogeneous solvation environment^59,60 or nonplanarity,⁶¹ nearly constant separations of approximately 1340 ± 40 cm⁻¹ were observed between the 0–0 and 0–1 energies within experimental errors (Figure 5B and Figure S24 and Table S11 in the Supporting Information), suggesting a conserved vibrational mode that is strongly coupled to the electronic transition. This mode is generally assigned as the bond length alternation (BLA),^57,58 which is also conserved across cyanine dyes.⁶² Since no other outstanding vibronic feature is seen for the anionic chromophore, we can treat this BLA mode as the primary source of the vibronic coupling. Further evidence comes from excited-state simulations, which demonstrate that relaxation along the BLA coordinate is required following Franck–Condon excitation of the chromophore.⁶³ We also notice that the assigned 0–0 peak is not necessarily the dominant one in the absorption spectra, especially for model chromophores (Figure 5A and Figure S26 in the Supporting Information).

Figure 5.

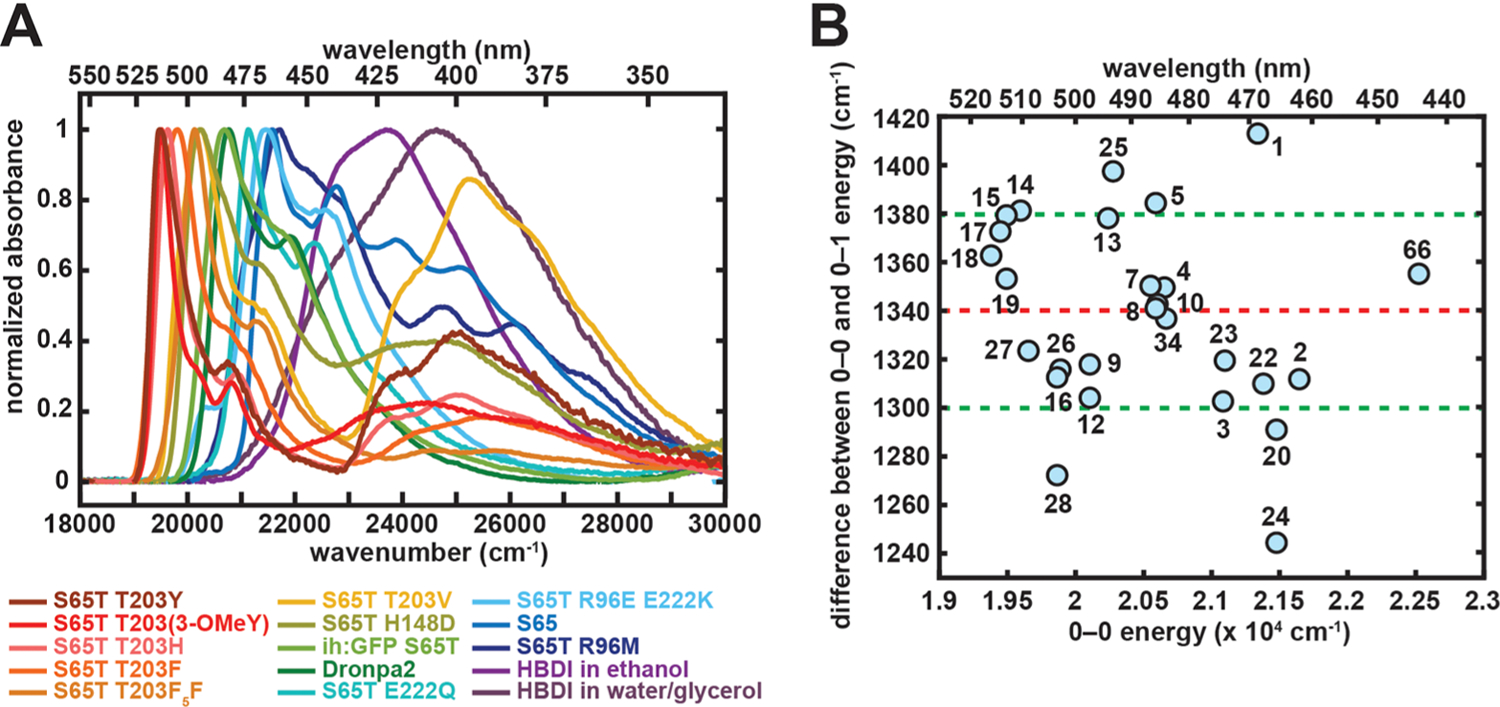
(A) Representative 77 K absorption spectra of GFP mutants, Dronpa2, and the model chromophore HBDI. Samples of T203Y, T203H, T203V, H148D, R96M, and HBDI in water/glycerol were at pH 10.0, and HBDI in ethanol contained 0.01 M NaOH to minimize A state absorption. The remaining samples were at pH 8.0. (B) Difference between the 0–0 and 0–1 energies plotted against 0–0 transition energy for GFP mutants, Dronpa2, and the model chromophore HBDI obtained from a second-derivative analysis (Figure S24 in the Supporting Information). The x–y coordinates and the numerical labels for the species are given in Table S11 in the Supporting Information. The value is nearly constant with an average of 1340 ± 40 cm⁻¹, which corresponds to the bond length alternation (BLA) mode. The red and green dashed lines correspond to the mean value and ±1σ, respectively. The point for HBDI in water/glycerol is excluded, as it is an extreme outlier (1932 cm⁻¹) from the rest of the data.

From these protein mutants and variants, we were able to sample a wide variation in absorption maxima ranging from 460 to 515 nm (Tables S11 and S12 in the Supporting Information). This implies the anionic GFP chromophore’s electronic distribution is highly tunable. Any attempt to destabilize the negative charge on the phenolate or imidazolinone by mutating T203 or R96 leads to a red or blue shift in absorption, respectively, supporting gas-phase studies on model systems.⁶⁴ The same color tuning effect can be achieved in Y66 variants through electron donating and withdrawing groups, because both mutational approaches result in modulation of the chromophore’s electron density.³⁰ The other chosen sites, such as H148 and residues exposed to the solvent (Table S8 in the Supporting Information), have a relatively minimal effect on the absorption maxima. The anionic model chromophore in water and ethanol shows broader and bluer B bands in comparison to those of the chromophore when it is within the protein environment (Figure 5A).⁶⁵ The model chromophore’s vibronic structure in water resembles that of the GFP A band, which will be explained in section 2.6. For the remainder of this work, we approximate 0–0 transition energies as the absorption maxima due to the small Stokes shifts of GFPs (section 2.4, see also Supplementary Text S5 in ref 30), unless the Huang–Rhys factor is larger than 1 as in the model chromophores (section 2.6, see also Figure S26 in the Supporting Information).

2.3. Formulation of the Marcus–Hush Theory.

Electronic Stark spectroscopy reveals that the photoexcitation process of the GFP chromophore is associated with a large degree of charge transfer, as implied from its large difference dipole moment or Stark tuning rate between the ground and excited states.²⁹ The directionality of negative charge transfer from the phenolate to imidazolinone rings was later inferred from the absorption maxima change across chromophore variants.³⁰ A similar phenomenon, namely the presence of an intervalence charge transfer (IVCT) absorption band,^66,67 has been discovered and thoroughly studied in mixed-valence compounds such as the Creutz–Taube ion (Figure 6A). These compounds usually possess two charge centers sharing the overall charge to various degrees. The two limiting structures with charge fully localized on one or the other center are coupled through an electronic coupling term. The electron transfer is accompanied by displacement in nuclear coordinate(s) either within the molecule (inner sphere) or from the surrounding environment (outer sphere). The associated theoretical construction is generally known as the Marcus–Hush theory for charge transfer processes⁶⁸ and is applicable to a wide variety of scenarios, including long-distance electron transfer,⁶⁹ IVCT,⁷⁰ organic reactions,⁷¹ and enzyme catalysis.^72,73

Figure 6.

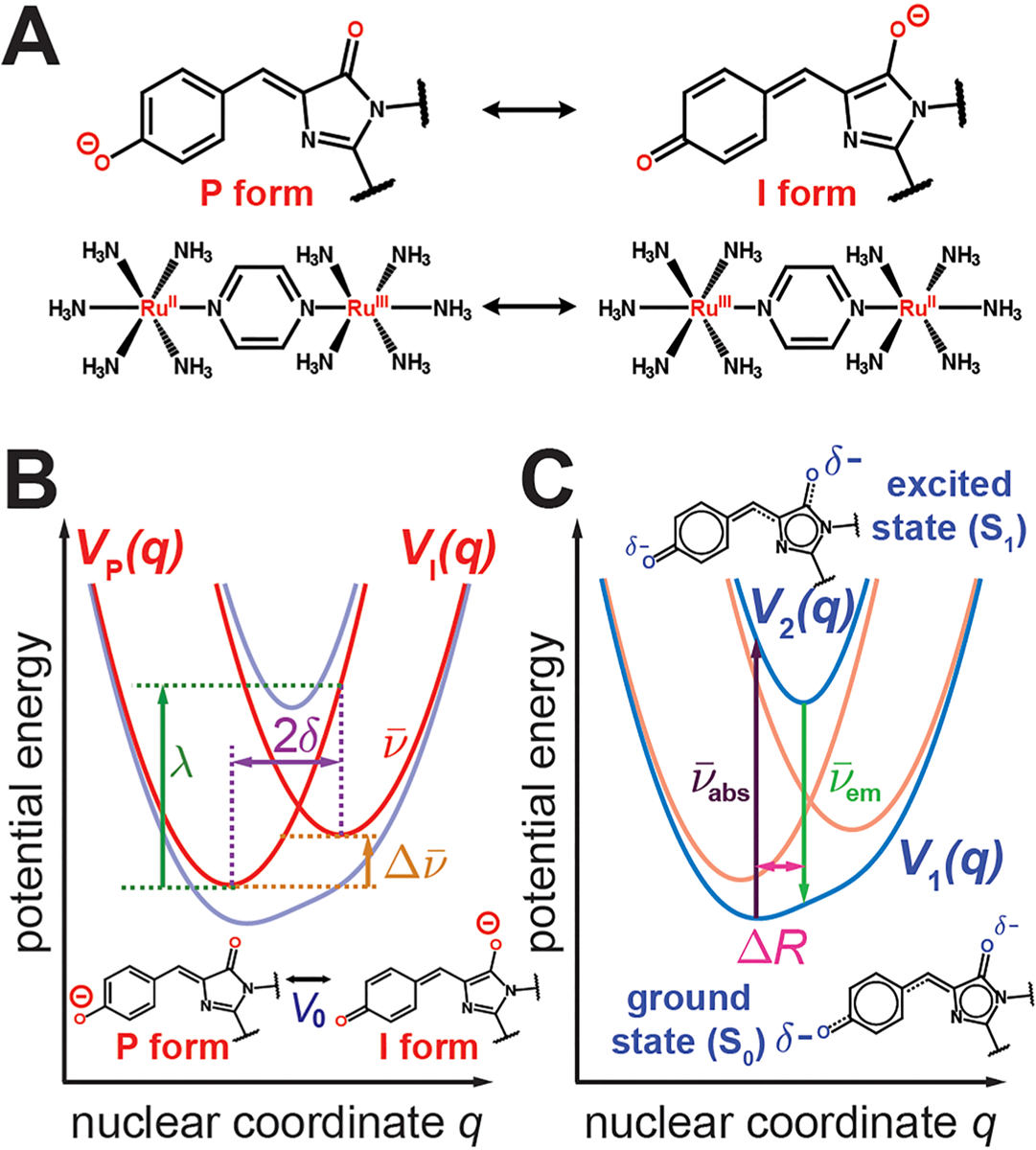
Marcus–Hush model for the anionic GFP chromophore. (A) Analogy between the resonance structures of the anionic GFP chromophore and the Creutz–Taube ion. For the anionic GFP chromophore, the charge localization centers are the two oxygen atoms on the phenolate ring (P form) or imidazolinone ring (I form), while in the Creutz–Taube ion they are the two ruthenium atoms. (B) Diabatic potential energy curves (red), V_P(q) and V_I(q), along the nuclear coordinate q coupled to charge transfer, for each resonance form of the GFP chromophore. The nuclear coordinate q is assigned to BLA, as evidenced by the resonance forms. V₀ represents the electronic coupling between the P and I forms, $\Delta \overline{v}$ is the driving force, $\overline{v}$ is the curvature, λ is the reorganization energy, and 2δ is the displacement between the two diabatic curve minima. (C) Adiabatic potential energy curves (blue), V₁(q) and V₂(q), representing the S₀ and S₁ electronic states, respectively. ${\overline{v}}_{\text{abs}}$ is the absorption energy, ${\overline{v}}_{\text{em}}$ is the emission energy, and ΔR relates to the vibronic coupling. In these adiabatic states, the negative charge is delocalized between the two rings, with the size of δ− reflecting the relative amount of electron density on each ring.

We suggest that the anionic GFP chromophore can be thought of in an analogous manner. The two charge centers are intuitively recognized as the highly electronegative oxygens at opposite ends of the structure, each of which carries a full negative charge in the anionic state in the two valence-bond structures referred to as diabatic states⁷⁴ (Figure 6A). The diabatic states are not energy eigenstates but rather are coupled through the electronic coupling V₀ (Figure 6B), which can be interpreted as chemical resonance.⁷⁵ The energy of each diabatic state depends on the coupled nuclear coordinates, and each state has a corresponding energy minimum at the most favorable nuclear configuration for that given charge distribution (Figure 6B). As stated before, the difference in these preferred nuclear configurations (denoted as 2δ in Figure 6B) can be primarily attributed to BLA displacement (q in Figure 6B), also suggested by the resonance structures (Figure 6A). We chose to neglect other nuclear degrees of freedom due to their relatively insignificant contribution to the absorption spectra (section 2.2), and thus we can successfully reduce the problem from an intractable number of degrees of freedom down to just one. Torsional angle variation between chromophores in different environments is neglected, justified by the general chromophore planarity observed from crystal structures (ref 76 and Table S10 in the Supporting Information). Furthermore, in accordance with the common practice of Marcus–Hush theory, we invoke the harmonic approximation, such that the diabatic state energy is quadratically dependent on q with the curvature corresponding to the BLA frequency $\overline{v}$, which was determined to be approximately 1340 cm⁻¹ across different environments (Figure 5B and Table S11 in the Supporting Information). This approximation is valid as long as the BLA displacement is small (see also section S10 in the Supporting Information). The energy dissipated from the BLA rearrangement during charge transfer between the two centers, known as the reorganization energy λ, is therefore $2\overline{v}{\delta }^2$. The full construction and explicit mathematical treatment are summarized in Figure 6B and section S4 in the Supporting Information. Note that the spectroscopic unit cm⁻¹ is used for various energies to facilitate direct comparisons among spectroscopic observables.

A critical parameter in Marcus–Hush theory is the minimum energy difference between the two charge-localized states, usually defined as the driving force $\Delta \overline{v}$ (Figure 6B). In the context of GFP, the driving force corresponds to the energy difference between the valence-bond structures (Figure 6A). Due to the differential electrostatic stabilization between these two structures interacting with the environment, it is straightforward to conclude that the driving force is strongly sensitive to the chromophore’s surroundings. In the following theoretical development using minimal parameters, we assume that the driving force is the only quantity that can be tuned by the environment, while the rest ($\overline{v}$, δ, λ, and V₀) are intrinsic properties of the chromophore. We will encounter cases in which this assumption is violated in section 2.4. In addition, we also assume that the nuclear positions of the chromophore’s immediate environment stay constant within the PES region of interest due to the fast excitation and emission timescale and small observed Stokes shifts (section 2.4).

With these considerations, our primary goal is to find correlations among spectroscopic observables, namely the absorption maxima, Stokes shifts, Stark tuning rates, transition dipole moments, and vibronic couplings, by varying the driving force of the GFP chromophore through the mutations discussed in section 2.1. To account for the quantities directly related to the charge distribution of the chromophore, which we refer to as the electro-optic properties,⁷⁷ the difference dipole moment between the diabatic states Δμ_CT is required and also assumed, as an initial approximation, to be an intrinsic property of the chromophore.⁷⁹ Note that, throughout this paper, all dipole moments are denoted without the vector notation to represent their magnitudes ($=|\Delta {\overrightarrow{\mu }}_{\text{CT}}|$), since no directional information can be obtained by only performing electronic Stark spectroscopy on isotropic immobilized samples⁷⁷ (section S4 in the Supporting Information). To obtain the relevant ground and excited state surfaces (adiabatic states, Figure 6C), one solves for the eigenvalues of the Marcus–Hush Hamiltonian as a function of BLA displacement q, which is explicitly derived in section S4 in the Supporting Information. For mixed-valence compounds, the Robin–Day classification scheme is widely adopted to qualitatively characterize the delocalization behavior of electrons over the two centers⁶⁶ (Figure 7A). In brief, class I compounds have electrons completely localized on one of the two centers, class III compounds exhibit complete electron delocalization, and class II compounds fall somewhere in between. These behaviors are determined by the relative magnitudes of 2V₀ and $\left|\Delta \overline{v}+\lambda \right|$.^27,67 Here we assert and later verify that the anionic GFP chromophore, just like benzene and other cyanine dyes,⁸⁰ belongs to class III (sections 2.4 and 2.5); hence, only one global minimum on the ground state can be found. Figure 7B shows the evolution of PESs by varying driving forces of a class III compound. Qualitatively, as the driving force increases, the absorption and fluorescence maxima blue-shift, the Stokes shift increases, the vibronic coupling (equilibrium displacement between S₀ and S₁) increases, the Stark tuning rate increases, and a more dominant 0–1 sideband is anticipated. We will confirm and elucidate these trends with quantitatively determined parameters below.

Figure 7.

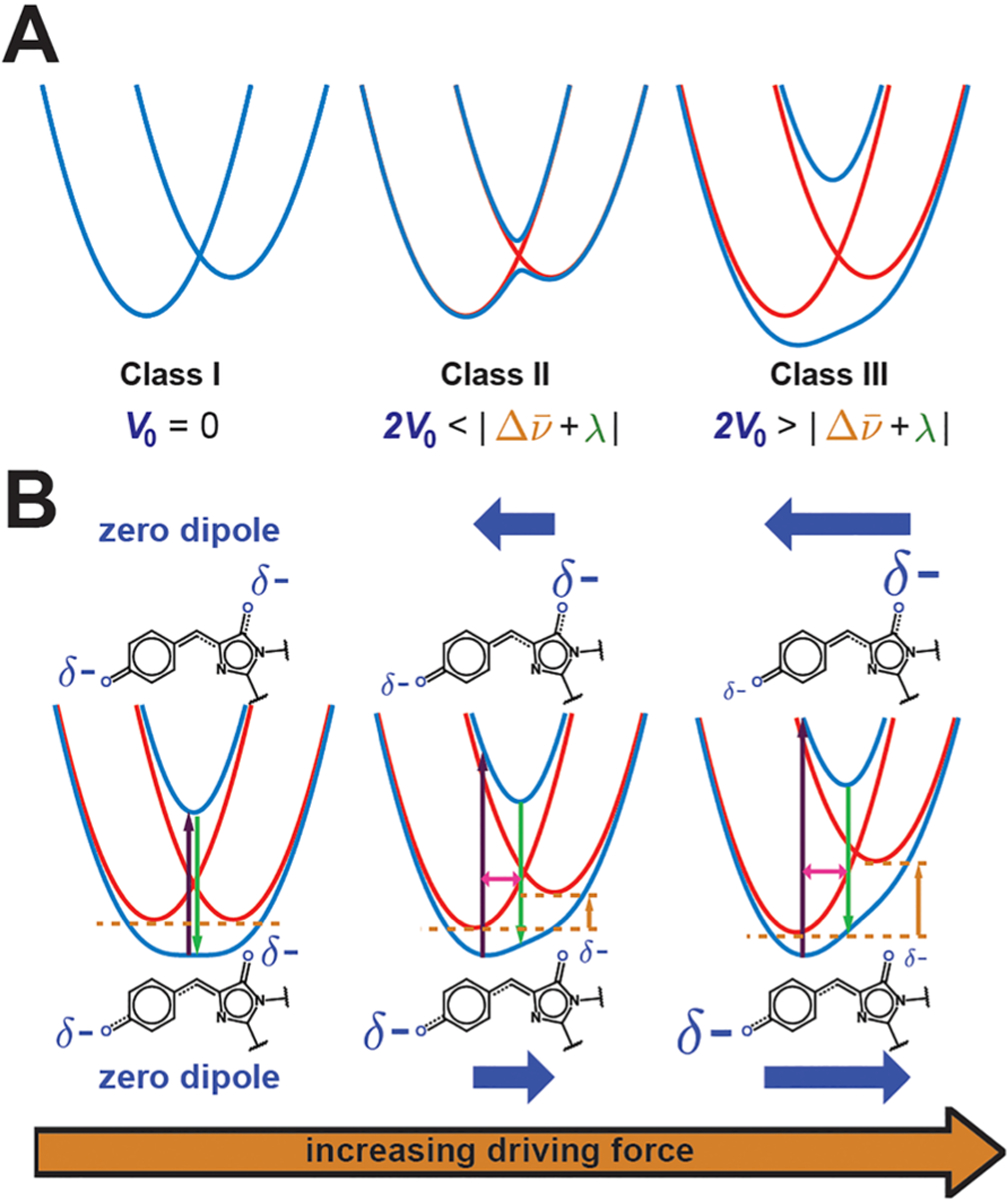
Evolution of potential energy curves with varying parameters. (A) Robin–Day classification scheme that separates mixed-valence compounds by the strength of the electronic coupling V₀. Blue and red depict the diabatic and adiabatic curves, respectively, showing that class II systems have a double-well potential in the ground state, while class III systems have a single well. (B) Influence of the driving force on the potential energy curves of the anionic GFP chromophore. As the driving force (orange arrow) increases, the absorption maximum (dark purple arrow) blue-shifts, the Stokes shift (difference between dark purple and green arrows) increases, the vibronic coupling (magenta arrow) increases, and the negative charge (size of δ−) is more localized, leading to a larger Stark tuning rate. The directions and magnitudes of the excited- and ground-state dipoles in each case are shown above and below the potential energy curves, respectively, as blue thick arrows. Note that, for the case on the left, while the schematic implies no dipole change upon excitation, the actual molecule may have a small nonzero dipole.

Historically, the use of resonance theory to understand dye colors can be traced back to Platt’s quantum mechanical explanation of Brooker’s empirical rules for cyanine dyes.^31,32 The driving force was formulated under the name “difference basicity” and shown to be transferrable and additive among dyes with different combinations of moieties. Ongoing interest in nonlinear optical properties^33,34,81 resulted in the resurrection of this valence-bond approach as opposed to the more widely practiced molecular orbital theory,⁸² culminating in a series of Olsen and McKenzie papers demonstrating that an effective two-state model indeed captures the essential physics of the cyanine dyes, confirmed by high-level computational methods.^83–85 This was later applied to numerous dyes,^85–87 particularly the GFP chromophore^{20,35,78,83,84} (see also ref 88). Note that this formalism is equivalent to Marcus–Hush theory without nuclear degrees of freedom considered, and thus properties related to nuclear rearrangement, such as Stokes shift and vibronic structure, cannot be accounted for. Because of the relatively small vibronic coupling (sections 2.4 and 2.6), quantities involving only the electronic degree of freedom are still well-approximated. There are several treatments of conjugated systems as organic mixed-valence compounds,^89,90 and it is very natural to consider the GFP chromophore as one example. Here we adapt Marcus–Hush theory to elucidate the role of the chromophore environment on the photophysical properties of GFPs and extract the physical principles pertaining to rational protein design, as opposed to previous studies that focused more on the change in the chemical identity of dyes. GFP serves as a superb system to study how a cyanine dye (or a mixed-valence compound) responds to its environment due to its amenability to a plethora of mutations,^9,44 with well-defined atomic positions of the chromophore and its environment readily determined by X-ray crystallography,⁵² and relatively large data sets available from the literature thanks to its widespread applications.⁹¹ Interestingly, another widely used vibronic model for polyacetylene developed by Su, Schrieffer, and Heeger⁹² can be shown to be equivalent to the Marcus–Hush model in the three-site limit (section S10 in the Supporting Information).

2.4. Stokes Shift and Absorption Maximum.

The anionic state of GFP is well-known to possess a small yet measurable Stokes shift.^55,56 In Figure 8, we show the correlation plot between Stokes shift and absorption maximum from environmental mutants with SYG (S65), TYG (S65T), and CYG (Dronpa) chromophores, from which a strong monotonic trend can be readily observed regardless of the identity of the chromophore. Bluer mutants have larger Stokes shifts that reach ~2000 cm⁻¹, while redder mutants can have nearly zero Stokes shift. The trend is also attested by an online database of various FPs with anionic GFP chromophores;⁹³ thus, the observation can be generalized to mutants not covered in this work. Marcus–Hush theory predicts the following correlation between Stokes shift ${\overline{v}}_{\text{stokes}}$ and absorption maximum ${\overline{v}}_{\text{abs}}$ (eq S17 in the Supporting Information):

$${\overline{\nu }}_{\text{Stokes }}=\frac{\lambda }{2V_0^2}\left[{\overline{\nu }}_{\text{abs}}^2-{\left(2V_0\right)}^2\right]$$ (1)

As seen in Figure 8, the fit to the data is excellent. The electronic coupling V₀ and reorganization energy λ can be extracted from the fit and are determined to be 9530 and 2910 cm⁻¹, respectively. Since the driving force is the only tunable parameter in the model, each mutant can be associated with a driving force (eq S13 and Table S13 in the Supporting Information). We can then deduce the critical driving force to be 2V₀ − λ ≈ 16000 cm⁻¹, beyond which the system transitions from class III to class II. All protein mutants are far from the borderline (driving forces <11000 cm⁻¹), verifying that the anionic chromophores can be treated as class III compounds. Notably, the reorganization energy λ is 15% of 2V₀, suggesting that small nuclear displacements are required to accommodate different electron distributions, thus resulting in small Stokes shifts. The point at which the Stokes shift vanishes corresponds to the reddest possible absorption for the GFP chromophore due to maximal electron delocalization (zero driving force, the cyanine limit) caused by changing its environment (Figure 7B). In other words, it is impossible to create a mutant harboring the planar GFP chromophore that has a redder absorption than 2V₀ = 19060 cm⁻¹ or 525 nm by virtue of the conjugation length, consistent with the FP database.⁹³

Figure 8.

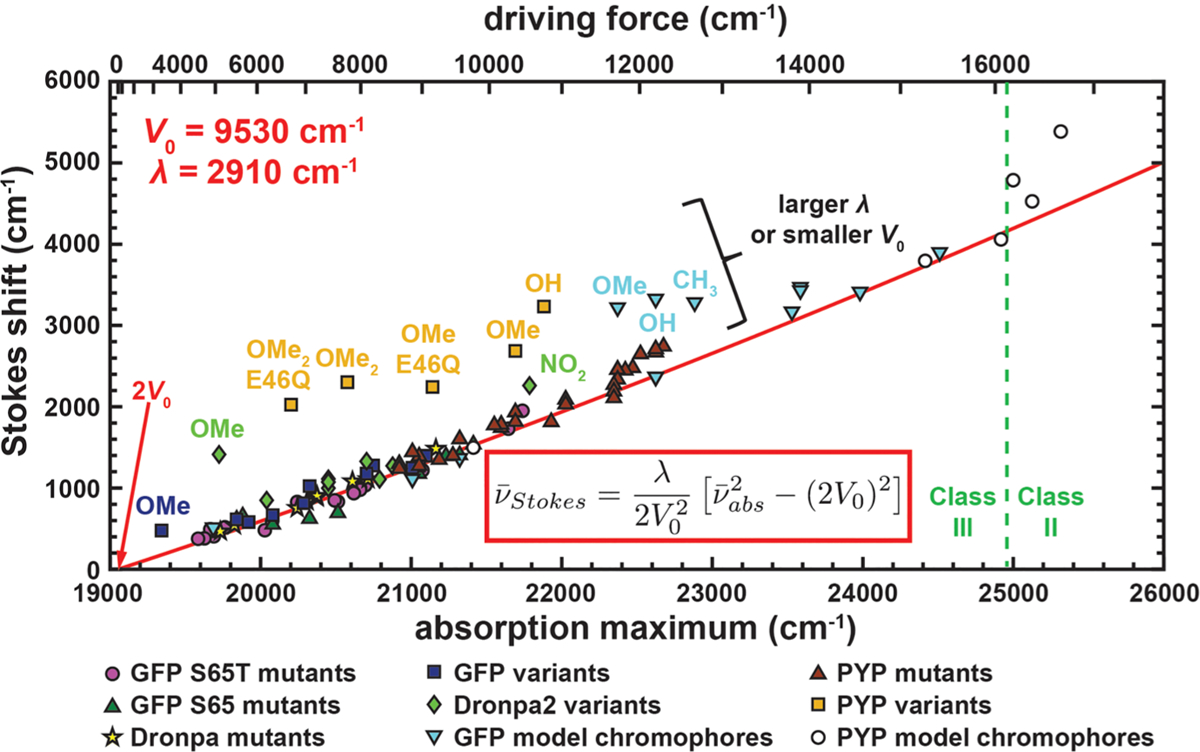
Correlation between Stokes shift and absorption maximum for all mutants, variants, and model chromophores of GFP, Dronpa, and PYP at room temperature (Table S12 in the Supporting Information). The Stokes shift is calculated as the difference between the room-temperature absorption and emission maxima. The latter are extracted from the corresponding room-temperature emission spectra, which are shown for a representative subset of mutants in Figure S27 in the Supporting Information. References for the data not measured in this study are also given in Table S12. The red curve comes from fitting the data for the GFP S65T mutants to eq 1. The outliers, corresponding to chromophores with strongly electron donating or withdrawing groups, are labeled with their corresponding substituents. The distinction between class II and class III systems is shown with a green dashed line. See Figure S30 in the Supporting Information for an identical figure reproduced with numerical labels defined in Table S12. The driving force is related to the absorption maximum by eq S13 in the Supporting Information.

When we perturb the chromophore via introduction of electron withdrawing or donating groups, in either the protein matrix or aqueous buffer, we find that the same V₀ and λ values which characterize the environmental mutants are still applicable, except for a few variants exhibiting apparent deviations (Figure 8). Aside from these anomalies, the general agreement between variants and mutants suggests that the same electronic structure perturbation to the chromophore can be achieved by either tuning the environment or modifying the chromophore itself, consistent with studies on polymethine dyes.³³

The correlation between Stokes shift and absorption maximum, or equivalently between absorption and emission maxima, has been extensively discussed in the context of photoactive yellow proteins (PYPs).²² The authors hypothesized three simple changes in PESs between S₀ and S₁ from mutant to mutant: namely, the change in difference equilibrium position, vertical energy, or relative curvatures. The trend of tighter and wider variation in fluorescence and absorption maxima, respectively, led to the conclusion that the change in relative curvature contributes the most. Since the structure of the PYP chromophore (thioester of p-coumaric acid, Figure S22 in the Supporting Information) resembles the GFP counterpart, we can extract the data from the PYP study and plot them with the correlation curve already obtained from GFP (Figure 8, brown triangles). Remarkably, the correlation for PYP mutants is quantitatively accounted for with the same values of V₀ and λ as the GFPs, suggesting that these two quantities are fundamentally intrinsic to the structures of the chromophores rather than the environment. It is well-known that the electronic coupling strength is governed by the distance between the two charge-localization centers.^94,95 The two oxygens are separated by eight bonds for both the GFP and PYP chromophores, and the chromophores’ electronic coupling is in amazing accordance with that obtained from a symmetric cyanine dye with the same conjugation length (≈27 kcal/mol = 9500 cm⁻¹).⁸⁰ The reorganization energy can thus be mostly assigned to inner-sphere reorganization, namely the BLA nuclear displacement, rather than solvation from the protein matrix. Moreover, Marcus–Hush theory can reproduce the ratio of ranges over which absorption and emission maxima vary for PYPs and GFPs, echoing the assertion that the major mechanism is the relative PES curvature change suggested by Philip et al.²¹ (see the context of eq S18 in Section S4 in the Supporting Information).

The GFP and PYP variants that deviate from the general trend observed in Figure 8 contain strongly π donating (e.g., −OMe) or withdrawing (e.g., −NO₂) groups. These substituents add to the conjugation length and the number of resonance contributors, resulting in even smaller effective electronic coupling, assuming inner sphere reorganization is minimally affected. The model chromophores deviate for a variety of potential reasons. For example, they approach the borderline between classes II and III and may have different reorganization energies due to solvation (outer-sphere reorganization). The former possibility is consistent with our observation of the intervalence Stark effect,²⁷ which is not seen with protein mutants or variants (section S11 in the Supporting Information).

2.5. Stark Tuning Rate and Absorption Maximum.

In an attempt to link the chromophore’s electronic distribution to its energetics, we analyzed the correlation between Stark tuning rate and absorption maximum in FPs (Figure 9), an approach pioneered by Drobizhev et al.^20,58 The Stark tuning rate is a measure of electron redistribution upon photoexcitation and can be obtained from the response of the visible absorption spectrum to an applied electric field, namely the electronic Stark effect (note that the Stark tuning rate will be scaled by a local field factor f, section S6 in the Supporting Information).⁷⁷ This is also a critical quantity for understanding how the absorption is tuned by the chromophore environment through electrostatics. Importantly, the Stark tuning rate of the GFP chromophore is not constant in different environments (Figure 9). This phenomenon results from the chromophore’s nontrivial difference polarizability between excited and ground states,²⁰ quite different from the situation for vibrational Stark effects of carbonyls and nitriles where the difference polarizability is very small.^96,97 Specifically, bluer mutants possess larger Stark tuning rates. This trend is also supported by semiempirical quantum mechanical calculations,²⁰ while less expensive ab initio methods tend to yield erratic results.¹⁹ As a control experiment, supercharged GFPs with multiple solvent-exposed charged residues were designed to study how the placement of charges affects electronic properties (section S7 in the Supporting Information). Intriguingly, nearly no change in color or Stark tuning rate is observed for these constructs even when nonuniform charge distribution is deliberately incorporated onto the β-barrel (Figure 3C). This suggests that the chromophore’s electronic distribution is only dictated by the immediate environment around the chromophore and any residues further away minimally influence its optical properties. As a side note and in contrast, the relative free energy between the protonated and deprotonated states of the chromophore reflected by its pK_a can be drastically perturbed by these outer residues, and thus any physical attempt to correlate chromophore pK_a with absorption/emission maxima can be misleading⁹⁸ (sections S7 and S8 in the Supporting Information).

Figure 9.

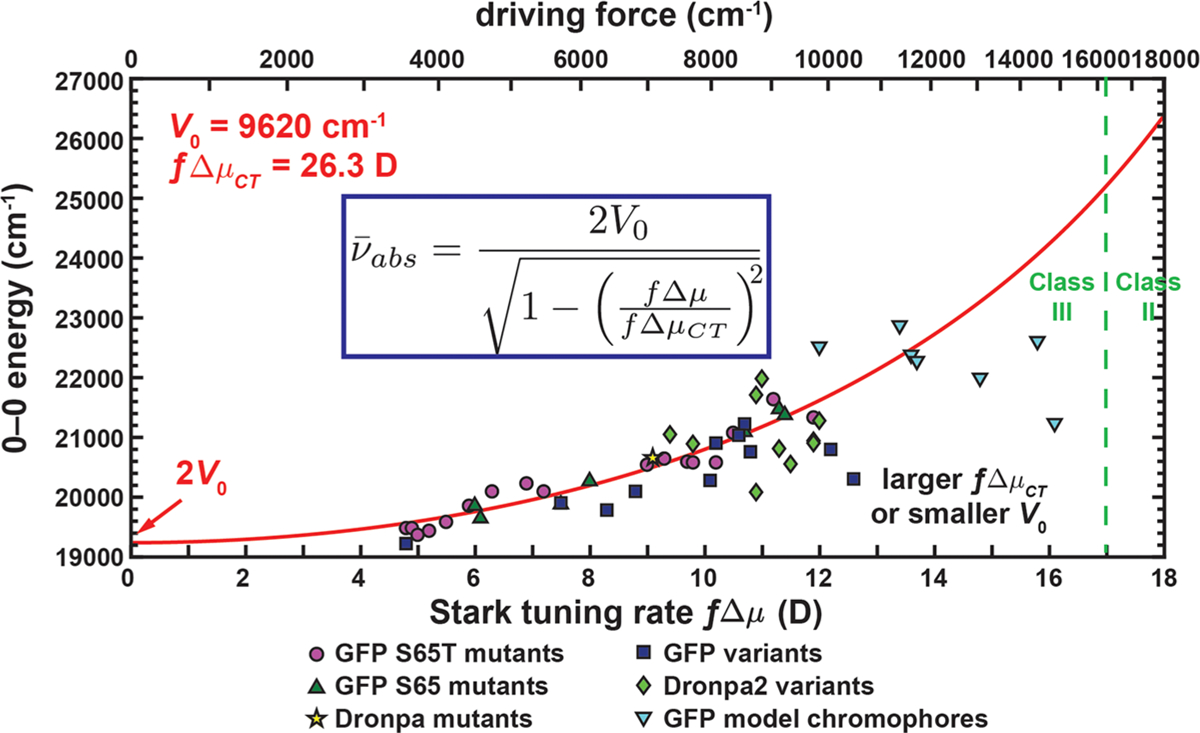
Correlation between Stark tuning rate and 0–0 transition energy for mutants, variants, and model chromophores of GFP and Dronpa at 77 K (Table S14 in the Supporting Information). The red curve comes from fitting the data for the S65T mutants to eq 2. The distinction between class II and class III systems is shown with a green dashed line. The local field factor f is required as a conversion factor between the observed and true Stark tuning rates (section S6 in the Supporting Information). Note that the Stark tuning rates of the model chromophores are obtained from the classical Stark analysis to be consistent with those of proteins, but their corresponding Stark spectra show nonclassical features (Figures S14 and S15 in the Supporting Information). See Figure S31 in the Supporting Information for an identical figure reproduced with numerical labels defined in Table S14. The driving force is related to the Stark tuning rate by eqs S13 and S21.

The correlation in Figure 9 can be quantitatively captured by the relation (eq S23 in the Supporting Information)

$${\overline{\nu }}_{\text{abs}}=\frac{2V_0}{\sqrt{1-{\left(\frac{f\Delta \mu }{f\Delta {\mu }_{\text{CT}}}\right)}^2}}$$ (2)

which has been derived by Olsen and McKenzie³⁵ and earlier by Blanchard-Desce in the context of push–pull compounds.³⁴ The local field factor f accounts for the difference between the applied field and the local field experienced by the chromophore (section S6 in the Supporting Information). The electronic coupling V₀ (=9620 cm⁻¹) obtained from the fit using eq 2 agrees well with that from the Stokes shift analysis (9530 cm⁻¹, Figure 8). The reddest possible absorption maximum, again at 2V₀, corresponds to a Stark tuning rate of zero due to maximal electron delocalization (Figure 7B). A simple model invoking the quadratic Stark effect with constant chromophore difference polarizability has been proposed by Drobizhev et al. to explain this trend with the notion of an effective electric field exerted by the protein environment.²⁰ We argue that this quadratic Stark effect model can also be justified using Marcus–Hush theory (section S5 in the Supporting Information), but with only two parameters: the electronic coupling V₀ and difference dipole moment Δμ_CT.

The diabatic difference dipole moment Δμ_CT of the chromophore is determined to be 26.3 D, corresponding to a full negative charge moving 5.5 Å, which is shorter than the direct O–O distance (~8.7 Å). The local field factor f (>1) further increases this difference in distance (sections S5 and S6 in the Supporting Information). Similar differences between the expected and observed distances, the latter derived from the observed Δμ_CT, have been found in class III compounds such as the special pair cation of bacterial photosynthetic reaction center mutants¹⁰⁰ and the Creutz–Taube ion;⁶⁷ thus, this phenomenon is ubiquitous in systems with delocalized charge and can be rationalized by the resonating valence-bond theory (section S9 in the Supporting Information). Data from GFP chromophore variants are plotted in Figure 9 and show a larger spread from the model, mostly toward the side of larger Δμ_CT or smaller V₀. Since we have seen from the Stokes shift plot (Figure 8) that V₀ for most variants can be treated as roughly identical with that of mutants, it is more likely that Δμ_CT is the parameter responsible for the deviations observed in Figure 9, presumably reflecting the ability for substituents to extend the range over which the electrons can delocalize through covalent modification. Apart from small deviations, the general trends in correlations of Stark tuning rate and absorption maximum from mutants and variants coincide, further strengthening the equivalence of perturbing the chromophore’s electronic structure by modifying the environment and the chromophore itself.^30,33 Stark effects of PYP mutants, which were observed to have abnormally large Stark tuning rates,¹⁰¹ involve perturbation from short hydrogen bonds and will be treated in future publications.

2.6. Absorption Band Shape.

As mentioned earlier, from normalized 77 K absorption spectra of mutants and variants shown in Figure 5A and ref 30, the relative intensity between 0–1 and 0–0 peaks from the deprotonated state increases as the absorption becomes bluer. This is expected since the vibronic coupling strength (or the Huang–Rhys factor) should be stronger as the driving force becomes larger (Figure 7B). Assuming minimal contribution to λ from outer-sphere reorganization, as justified by comparing GFP to PYP in section 2.4 and past studies on temperature-dependent emission spectra¹⁰² and dynamic Stokes shifts,⁵⁵ we can now predict the Huang–Rhys factor S and hence the 0–1 to 0–0 band intensity (proportional to the Franck–Condon factor FC) ratio from the following relation with V₀, λ, and the BLA frequency $\overline{v}$ (eq S29 in the Supporting Information):

$$\frac{{(\text{FC})}_{0\to 1}}{{(\text{FC})}_{0\to 0}}=S={\left(\frac{\Delta \overline{\nu }}{2V_0}\right)}^2\frac{\lambda }{\overline{\nu }}$$ (3)

Using the estimated driving forces (Table S13 in the Supporting Information) and parameters extracted from Figures 5B and 8, the intensity ratios for YFP (T203Y mutants), GFP, and the model chromophore in aqueous buffer are estimated to be 0.14, 0.37, and 1.2, respectively. The last value being greater than 1 suggests that the associated peak maximum is no longer 0–0 but rather 0–1, agreeing with the second-derivative analysis (Figure S24 in the Supporting Information) and explaining why the chromophore has different general band shapes in solution in comparison to the shapes when it is in the protein environment. The absorption features of the protonated chromophores (A bands) also resemble those of the model chromophores, implying a Huang–Rhys factor between 1 and 2 (Figure S23 in the Supporting Information).

Another trend that can be readily observed from Figure 5A is that the anionic band tends to be broader as the driving force increases. This phenomenon could be dominantly attributed to inhomogeneous broadening and explained by Drobizhev et al.:²⁰ the larger the Stark tuning rate, i.e. the larger the sensitivity of the transition to an electric field, the wider the absorption energy distribution becomes due to the distribution in the electric field exerted by the environment, under the assumption of constant electric field fluctuations across different proteins. Chromophores in the protein environment versus those in solution also exhibit appreciable differences in their spectral widths, which were similarly observed in vibrational absorption peaks of a carbonyl moiety bound to enzyme mutants and isolated in protic solvents.^103,104 Aside from the varying Stark tuning rates, this could indicate more sharply distributed electrostatic interactions from the proteins due to the relative rigidity in their atomic positions, as opposed to the freely solvating water molecules with broadly distributed dipole moment orientations surrounding the chromophore. Additionally, these absorption bands are asymmetric and tail toward the bluer edge, which could be due to the strong coupling between two harmonic diabatic states¹⁰⁵ and/or simply the vibronic progression from transitions involving higher vibrational excited states.¹⁰⁶

2.7. Extinction Coefficient, Transition Dipole Moment, and Spontaneous Emission Rate.

Absorption spectra normalized to extinction coefficients are plotted in Figure 10A, with redder mutants exhibiting higher extinction coefficients. Interestingly, absorption band broadness and extinction coefficients are inversely correlated, rendering the peak area nearly constant and thus the oscillator strength (eq S4 in the Supporting Information) unity across mutants (0.99 ± 0.02, Figure 10B). This curious observation stems from the insensitivity of the transition dipole moment to its environment (9.9 ± 0.2 D, Figure 10C). According to Marcus–Hush theory, the transition dipole moment m can be estimated from the following equation (eq S25 in the Supporting Information):

$$m=\frac{V_0}{{\overline{\nu }}_{\text{abs}}}\Delta {\mu }_{\text{CT}}$$ (4)

The relation suggests an insensitivity to the driving force, and the subsequent estimation of transition dipole moments is plotted in Figure 10D using V₀ and Δμ_CT determined from Figure 9. The transition dipole moments calculated from extinction coefficients are also shown in Figure 10C for comparison. The results from these two orthogonal approaches agree once a scaling factor is applied, owing to the differences in local field factors evaluated at different frequencies (see section S6 in the Supporting Information). This insensitivity of the transition dipole moment in comparison to the Stark tuning rate is profound, suggesting that spontaneous emission rates across mutants (inferred from the Strickler–Berg relation¹⁰⁷ for example) should be nearly constant due to the relatively narrow variation in fluorescence maxima, which explains the linear relation between fluorescence lifetimes and fluorescence quantum yields for PYP mutants,²² the slope of which is exactly the inverse of the spontaneous emission rate. Echoing our previous publication,¹⁴ this finding further supports the assertion that it is only possible to tune the fluorescence quantum yield of a chromophore by orders of magnitude by affecting a competing nonradiative decay pathway, such as isomerization or excited state electron transfer,¹⁰⁸ which can be manipulated through steric confinement or electrostatic tuning if large motions or charge redistribution, respectively, is involved.³⁰

Figure 10.

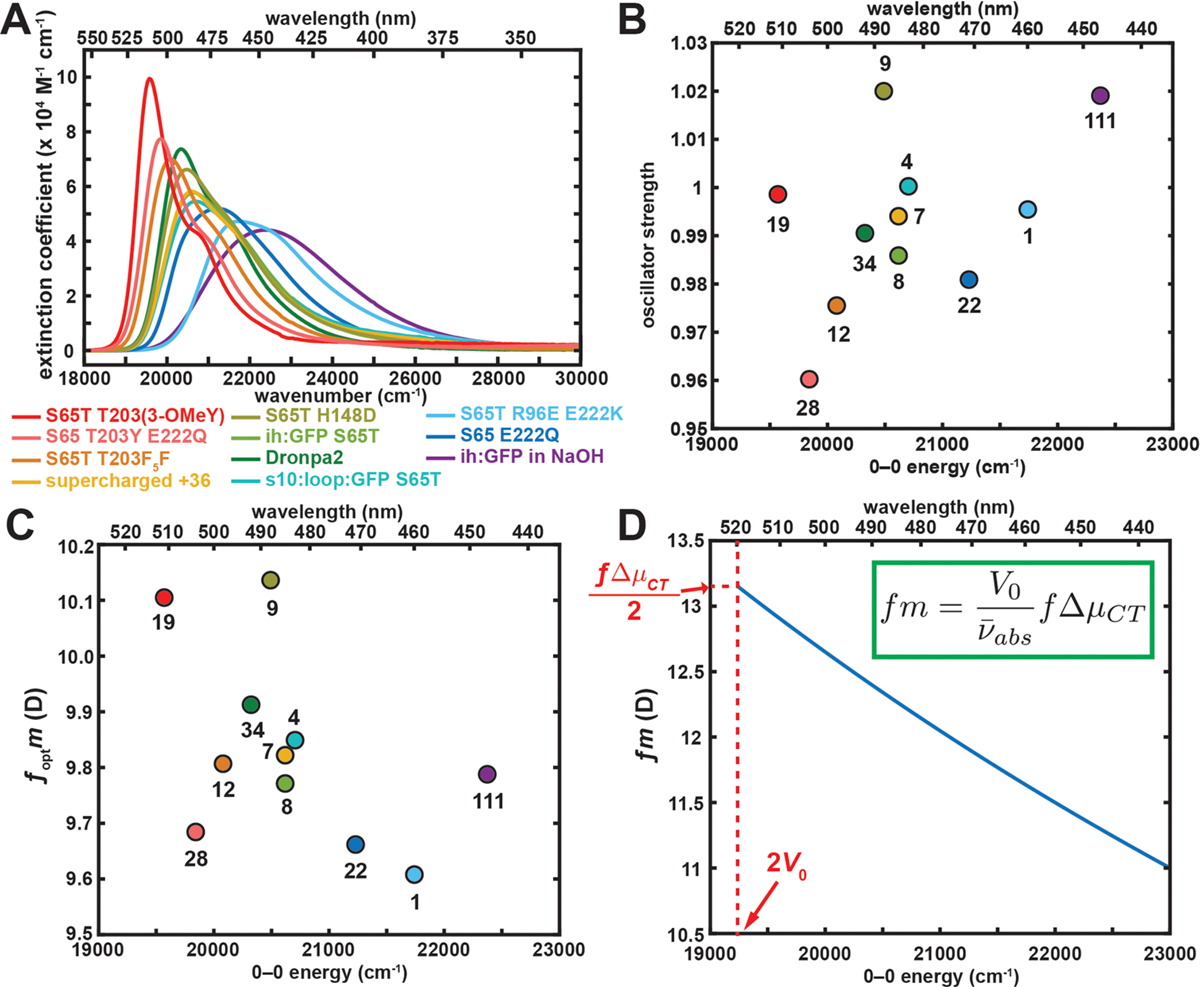
(A) Absorption spectra for GFP and Dronpa mutants that exhibit only anionic states normalized to extinction coefficient. (B) Oscillator strength and (C) transition dipole moment each calculated from the extinction coefficients in (A) plotted against 0–0 transition energy. The x–y coordinates and the numerical labels for the species are given in Table S15 in the Supporting Information. The color coding in (B) and (C) matches that in (A). (D) Transition dipole moment predicted from Figure 9 using eq 4. The difference in local field factor f between (C) and (D) arises from the different frequencies of the external field (visible light and the applied electric field, respectively; see section S6 in the Supporting Information).

2.8. Other Properties.

The correlation between two-photon absorption cross section and color in FPs has been extensively investigated by Drobizhev and Rebane,^58,109 in which they demonstrated a clear trend that bluer mutants possess larger two-photon cross sections. Ground-state vibrational frequencies from various stretching modes of the chromophore also exhibit a strong correlation with color,¹¹⁰ a phenomenon similarly observed in rhodopsins.^111,112 Since vibrational frequencies are probes for local electrostatics rather than photophysical properties of interest for protein design, we will reserve further discussion to a future publication.

2.9. Additivity of Driving Forces Enables Accurate Predictions of Properties.

So far, we have revealed how the variation in driving force, caused by the protein environment, dictates various properties of GFPs associated with absorption and emission. By assuming the driving force is the only tunable property, we can explain correlations among photophysical properties, facilitated by the invariability of the diabatic states and intrinsic parameters of the chromophore. The remaining missing link is how the driving force is governed by the specific environment of the chromophore. The definition of the driving force is the difference in negative charge stabilization between the imidazolinone and phenolate rings. Interactions with the surrounding residues preferentially (de)stabilize one diabatic state over another and thereby modulate the driving force and the resulting PESs (Figure 7B). Intuitively, from the series of mutants and variants, any attempt to destabilize the charge on the phenolate, such as removing its hydrogen bonding partner, π–π stacking, and attaching electron-donating groups, red-shifts the absorption maximum by more closely matching each ring’s affinity for the negative charge. On the other hand, destabilizing the charge on the imidazolinone or stabilizing the charge on the phenolate blue-shifts the absorption, since it increases the driving force (Table S13 in the Supporting Information). With the mutants and variants at hand, we never create a system in which the negative charge on the imidazolinone is more stable than that on the phenolate, or in other words, reverse the intrinsic asymmetry in electron distribution of the GFP chromophore, also evidenced by the consistent electron flow direction from the phenolate to imidazolinone ring observed in GFP variants³⁰ (Figure 7B). To achieve negative driving forces, we would have to introduce more donating groups to the phenolate and/or the aromatic ring it is π–π stacked with. For the model chromophore in an aqueous environment, the water molecules likely organize themselves in a way such that they stabilize the negative charge almost exclusively on the phenolate, causing a large driving force and consequent blue shift in absorption that is only observed in the GFP protein matrix when the positive charge of R96 proximal to the imidazolinone moiety is removed.

Using the driving force to characterize the protein environment can be powerful, since the effects from several point mutations should be reflected in a linearly additive manner (section S8 in the Supporting Information). Therefore, we should be able to predict properties of mutants carrying multiple mutations from the corresponding single mutants. To test this claim, we devised an unusual combination of mutations, R96M and T203Y, which are only accessible via the semisynthetic split GFP method.²³ These mutations are contrived to maximally destabilize the negative charge on both oxygens of the chromophore within the protein environment, leading to an absorption maximum not far from that of wild-type GFP. If the driving force is truly additive, we expect the anionic state of the double mutant to absorb at 492 nm on the basis of the driving forces evaluated from the individual mutations R96M and T203Y (Table 2). The predicted value is in good agreement with the experimental value of 494 nm (Figure 11), suggesting that the driving force can serve as a linear scale for property prediction. In contrast, the transition energy itself is not additive because it is a nonlinear function of the driving force (eq S13 in the Supporting Information) due to the nonzero difference polarizability of the chromophore. The naïve assumption of its additivity would instead lead to an absorption maximum for the double mutant of 485 nm, and thus the transition energy is not ideal for predicting color from mutations. Consequently, synergistic or (anti)cooperative effects from multiple mutations on certain properties (transition energy in this case) may simply arise from the nonlinear dependence of an additive scale, and thus it is important to identify the underlying linear parameter for better predictive power. From a theoretical perspective, we also promote the language of driving force rather than electric field from the protein environment^20,99 (see section S8 for further discussion).

Table 2.

Prediction of the Absorption Maximum of the GFP S65T R96M T203Y Mutant at Room Temperature, Comparing the Assumption That Either the Driving Force or the Transition Energy Is Additive^a

	driving force (cm−1)	transition energy (cm−1)
ihmat(65T)·ih:loop:GFP R96M	10270	21645
s10:loop:GFP S65T	8080	20695
s10:loop:GFP S65T T203Y	4870	19666
	ihmat(65T)·ih:loop:GFP R96M T203Y
assumption	driving force is additive	transition energy is additive
prediction	10270 − 8080 + 4870 = 7060	21645 – 20695 + 19666 = 20616
predicted transition energy (absorption maximum)	(70602 + 190602)1/2 = 20330 cm−1 (492 nm)	20616 cm−1 (485 nm)
observed transition energy (absorption maximum)	20240 cm−1 (494 nm)

^aTo account for the minor differences between absorption maxima of circular permutants, we use the ih circular permutant as the basal value. The driving forces and transition energies are extracted from Tables S13 and S12, respectively. The conversion between transition energy and driving force is performed via eq S13 using V₀ = 9530 cm⁻¹ (Figure 8).

Figure 11.

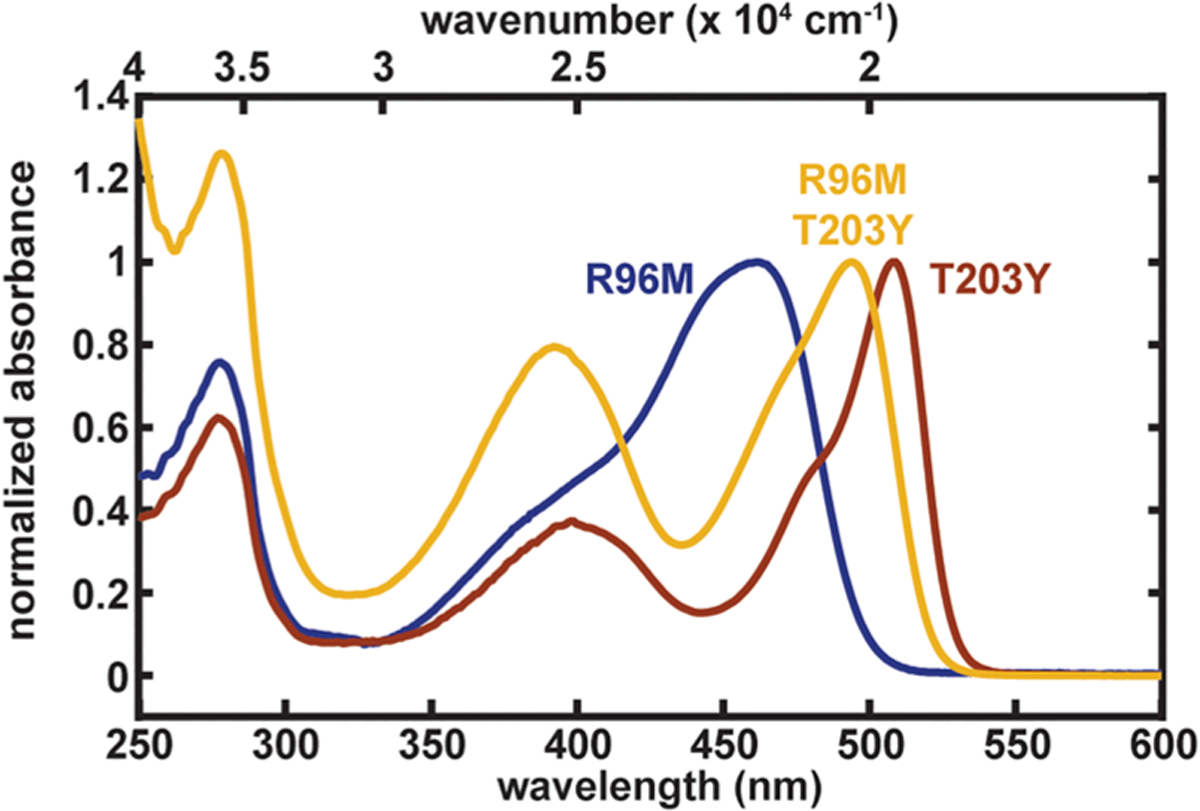
Normalized room-temperature absorption spectra of GFP S65T R96M, T203Y, and R96M T203Y at pH 8.0, 8.0, and 10.0, respectively. The observed peak maximum of 494 nm for the anionic state closely matches the predicted value of 492 nm, assuming the driving force is additive.

3. CONCLUSIONS AND OUTLOOK

Through this study of a large number of systematically tuned GFP mutants and variants, we are able to uncover the underlying factors governing the correlations between photophysical properties using a small number of parameters intrinsic to the chromophore. The intimate correlations among optical properties arise from the BLA mode coupling to the electronic redistribution that is adequately captured by Marcus–Hush theory for mixed-valence compounds. The protein environment plays a role in differentially stabilizing the negative charge on the two chromophore rings through electrostatic interactions, thus leading to different driving forces that can be used as a linear scale for characterizing each mutant and quantitatively predicting photophysical properties for new mutants. This simple and intuitive framework provides the missing link between structure and energetics and is critical for designing new GFPs. In particular, when one eliminates the hydrogen bond with the phenolate oxygen through mutating T203 in GFP, the driving force is reduced, leading to a redder absorption peak, a decreased Stokes shift, a decreased Stark tuning rate, a less prominent vibronic sideband, and a slightly decreased transition dipole moment. The converse is true when R96 in GFP is mutated to remove the hydrogen bond with the imidazolinone oxygen. Since all of these spectroscopic properties are dictated by the one-dimensional space of driving forces, physical principles set severe constraints on possible phenotypes.

It is not possible to tune these properties independently within the proposed color-tuning mechanism. For instance, a red-shifted mutant containing the anionic chromophore cannot have a large Stokes shift unless it violates the underlying assumptions of this model (e.g., by modifying the chromophore structure to increase conjugation^11,113 or changing the protonation state to utilize excited state proton transfer⁵⁵). In addition, searching for a GFP mutant that is redder than 525 nm is futile, provided the fixed conjugation length of the chromophore. Further, tuning the fluorescence quantum yield of GFPs can only be achieved through enhancing or suppressing the nonradiative decay pathway in the excited state, since their spontaneous emission rate is almost constant across different mutants. Understanding these underlying principles can help rule out phenotypes that are potentially contradictory or physically impossible and provide guidelines for how to modify the system to achieve those phenotypes through engineered interactions. One can imagine that this information can be more efficiently obtained through correlations from a wide range of mutants generated by extensive screening or directed evolution. However, mutants with unwanted properties tend to be discarded during the selection processes, which can bias the proteins published in the literature and databases.⁹³ Here we advocate that those mutants with user-defined poor performances are not useless. Rather, they can provide valuable data to help reveal the factors that influence properties of interest, which can ultimately lead to the rational design of mutants with superior functions.

Additionally, we demonstrated that the use of Marcus–Hush theory is not limited to GFP mutants and variants but can also be applicable to PYP mutants, surprisingly with the same set of parameters. This general framework allows us to understand and predict the properties of light-responsive proteins in a unified manner. Given the resemblance to charged cyanine dyes and polyenes, for which strong charge-transfer character upon excitation has been verified,^33,114 we believe that the photophysical behaviors of rhodopsins with protonated Schiff bases¹¹⁵ and phytochromes with bilins¹¹⁶ can be captured by Marcus–Hush style theory with different values of electronic coupling, reorganization energy, and diabatic difference dipole moment. This assertion is supported by similar color tuning strategies¹¹⁷ and extensive computational studies.^13,16 The approach proposed here may complement the decades-long efforts from computations and experiments to uncover and control the mechanism of opsin shifts.^{16,112,118–120}

This work also illustrates the difficulty of elucidating design principles for a general system, such as an optogenetic tool involving a chromophore or an enzyme that catalyzes a desired substrate reaction. One has to formulate a general theory for a certain type of molecular behavior such that it can be applicable to various protein environments, but the theory must be specific enough to retain intelligible insights, which are usually extracted from simple models but rarely from computations using sophisticated theoretical methods. For example, one can formulate the opsin shift of rhodopsins, color tuning of GFPs, or even redox tuning of pigments in photosynthetic complexes in terms of the most general Coulomb’s law,¹²¹ but no general conclusion can be drawn unless one calculates the corresponding electrostatic energy with known nuclear coordinates.^122–124 A certain degree of coarse-graining is useful to simplify the whole picture, but the model involved needs to be tailored to the characteristics of each molecule of interest. Specifically, the current proposed theory might be useful for general cyanine dyes, but not for chlorophyll-like or heme-like systems, in which the electrons can be thought of as delocalized over two dimensions rather than one. Nonetheless, this work can serve as a guide to biophysicists and chemists to pursue the general principles of protein design in a quantitative manner using comprehensible minimal models.