SUMMARY
Translation of mRNA into protein is a fundamental yet complex biological process with multiple factors that can potentially affect its efficiency. Here, we study a stochastic model describing the traffic flow of ribosomes along the mRNA, and identify the key parameters that govern the overall rate of protein synthesis, sensitivity to initiation rate changes, and efficiency of ribosome usage. By analyzing a continuum limit of the model, we obtain closed-form expressions for stationary currents and ribosomal densities, which agree well with Monte Carlo simulations. Furthermore, we completely characterize the phase transitions in the system, and by applying our theoretical results, we formulate design principles that detail how to tune the key parameters we identified to optimize translation efficiency. Using ribosome profiling data from S. cerevisiae, we shows that its translation system is generally consistent with these principles. Our theoretical results have implications for evolutionary biology, as well as synthetic biology.
INTRODUCTION
Being a major determinant of gene expression and protein abundance levels (Lu et al., 2007; Kristensen et al., 2013), translation of mRNA into polypeptides is one of the most fundamental biological processes underlying life. The extent to which this process is regulated and shaped by the sequence landscape has been widely studied over the past decades (Dever et al., 2016; Hanson and Coller, 2018; Quax et al., 2015), revealing many intricate mechanisms that may affect translation dynamics. From a more global perspective, however, it has been challenging to integrate these findings to elucidate the key factors that govern translation efficiency. Indeed, translation is a complex process that depends on many parameters, including the initiation rate, site-specific elongation rates (which can vary substantially along a given transcript), and the termination rate. How does the overall rate of protein synthesis depend on these parameters? To make the problem more concrete, suppose that the goal is to achieve the fastest rate of protein production while minimizing the cost. Would choosing the “fastest” synonymous codon at each site do the job? If the local elongation rate changes at a particular site, would it necessarily affect the overall rate of protein synthesis? If not, then which parameters actually matter? Aside from achieving a desired protein production rate, how does a translation system make efficient use of available resources, particularly the ribosomes? These are important questions in molecular and evolutionary biology, as well as synthetic biology, but challenging to answer because there are many parameters involved – for a transcript consisting of N codons, one has to analyze a model with about N parameters, which is seemingly intractable when N is large.
In this article, we develop a theoretical tool to answer the above questions. Our work hinges on analyzing a mathematical model that describes the traffic flow of ribosomes, which mediate translation by moving along the mRNA transcript. Beginning with MacDonald et al. (1968), most mechanistic studies of translation dynamics have been based on the so-called Totally Asymmetric Simple Exclusion Process (TASEP), a probabilistic model that explicitly describes the flow of particles along a lattice (Zia et al., 2011; Zur and Tuller, 2016). As a classical model of transport phenomena in non-equilibrium, the TASEP has attracted wide interest from mathematicians and physicists (Blythe and Evans, 2007). To describe translation realistically, however, a generalized version of the model needs to be employed, taking into account the extended size of the ribosome and the heterogeneity of the elongation rate along the transcript. Under such general conditions, critical questions have hitherto remained open; in particular, identifying the parameters most crucial to the current and particle density has proven elusive.
Here we carry out a theoretical analysis of a generalized version of the TASEP and obtain analytic results that provide practical insights into translation dynamics. Our approach is to study the process in a continuum limit called the hydrodynamic limit, which leads to a general PDE satisfied by the density of particles. Upon solving this PDE, we obtain exact closed-form expressions for stationary currents and particle densities that agree very well with Monte Carlo simulations of the original TASEP model. Furthermore, we provide a complete characterization of phase transitions in the system. These results allow us to identify the key parameters that govern translation dynamics, and to formulate a set of specific design principles for optimizing translation efficiency in terms of protein production rate and resource usage. Using experimental ribosome profiling data of S. cerevisiae, we show that the translation system of this organism is generally efficient according to the design principles we found.
RESULTS
We first present our theoretical results on a mathematical model of translation and identify the key parameters that govern its dynamics. We then apply our theoretical results to formulate four simple design principles that detail how to tune these parameters to optimize the overall rate of protein synthesis and efficiency of ribosome usage. We then analyze ribosome profiling data of S. cerevisiae and demonstrate that its translation system is generally efficient, consistent with the design principles we found.
Theoretical Results on a Stochastic Model of Translation
Model description of the inhomogeneous ℓ-TASEP
At a high level, translation of mRNA involves three types of movement of the ribosome, as illustrated in Figure 1A: 1) Initiation – a small ribosomal subunit enters the open reading frame so that its A-site is positioned at the second codon and then a large ribosomal subunit binds with the small subunit. 2) Elongation – the nascent peptide chain gets elongated by one amino acid and the ribosome moves forward by one codon. 3) Termination – the ribosome with its A-site at the stop codon unbinds from the transcript. An important point to note is that more than one ribosome can translate the same mRNA transcript simultaneously, so the movement of a ribosome can be obstructed by another ribosome in front, similar to what happens in a traffic flow on a one-lane road. Such interaction is what makes the dynamics difficult to analyze.
Figure 1. Illustration of the translation process, the inhomogeneous ℓ-TASEP with open boundaries, and its phase diagram.
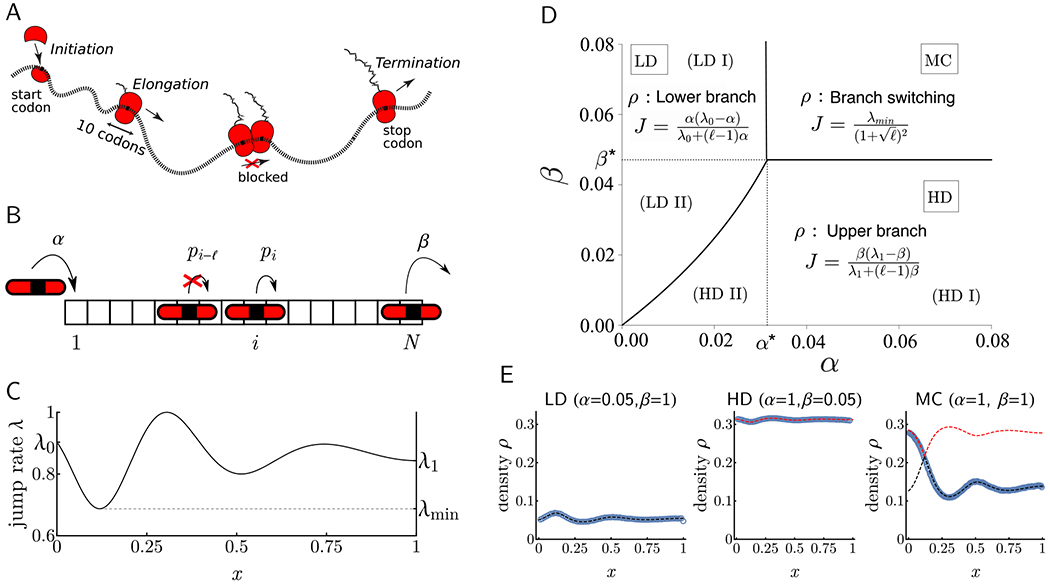
A: Ribosomes initiate translation at the mRNA 5′ end, elongate the polypeptide by decoding one codon at a time, and eventually terminate the process by detaching from the transcript. B: Particles (of size ℓ = 3 here) enter the lattice at rate α and a particle at position i (here defined by the position of the midpoint of the particle) moves one site to the right at rate pi, provided that the move is not blocked by another particle in front. C: Example rate function with key parameters shown. D: The phase diagram is completely determined by λ0, λ1, λmin and ℓ. In this example, (λ0, λ1, λmin, ℓ) = (0.9, 0.3, 0.1, 10). All phase transitions are continuous in J and, unless λmin coincides with λ0 or λ1, discontinuous in ρ. E: Simulated results for ℓ = 3, N = 800, and λ as in C are compared with theoretical predictions. Dashed black and red lines represent upper and lower branches of solutions to (1). Circles are averaged counts over 5 × 107 Monte-Carlo steps after 107 burn-in cycles.
We model the flow of ribosomes on mRNA using a generalized TASEP, called the inhomogeneous ℓ-TASEP, on a one-dimensional lattice with N sites (see Figure 1B). In this process, each particle (corresponding to a ribosome in mRNA translation) is of a fixed size and is assigned a common reference point (e.g., the midpoint in the example illustrated in Figure 1B). The position of a particle is defined as the location of its reference point on the lattice. A configuration of particles is denoted by the vector τ = (τ1, … , τN), where τi = 1 if the ith site is occupied by a particle reference point and τi = 0 otherwise. The jump rate at site i of the lattice is denoted by pi > 0. During every infinitesimal time interval dt, each particle located at position i ∈ {1, … , N − 1} has probability pidt of jumping exactly one site to the right, provided that the next ℓ sites are empty; particles at positions between N − ℓ + 1 and N, inclusive, never get obstructed. Additionally, a new particle enters site 1 with probability αdt if τi = 0 for all i = 1, … , ℓ. If τN = 1, the particle at site N exits the lattice with probability βdt. The parameter α is called the entrance (or initiation) rate, while β is called the exit (or termination) rate.
The hydrodynamic limit
The key quantities of interest are the stationary probability 〈τi〉 of any individual site i being occupied or not, and the current (or flux) J of particles in the system. In the corresponding translation process, these quantities reflect the local ribosomal density and the protein production rate, respectively.
In the special case of the homogeneous 1-TASEP (pi = p for all i and ℓ = 1), the stationary distribution of the process decomposes into matrix product states, which can be treated analytically (Derrida et al., 1993). Unfortunately, in the general case this approach is intractable, necessitating alternative methods such as the hydrodynamic limit. When ℓ > 1, deriving the hydrodynamic limit is not straightforward, however, as the process does not possess stationary product measures (Schönherr and Schütz, 2004). To tackle this problem, we mapped the ℓ-TASEP to another interacting particle system called the zero range process (ZRP, see The hydrodynamic limit of the inhomogeneous ℓ-TASEP of STAR Methods and Figure S1), whose hydrodynamic limit, assuming it exists, can be derived from the associated master equation. More precisely, we obtained the hydrodynamic limit through Eulerian scaling of time and space by a factor a = N−1, and by following its dynamics on scale x such that , for 1 < k < N (Rezakhanlou, 1991). Implementing this limiting procedure for the ZRP and mapping it back to the inhomogeneous ℓ-TASEP, we found that the limiting occupation density , assuming its existence, satisfies the nonlinear PDE
| (1) |
where and λ is a differentiable extension of (p1, … , pN), such that λ(x) = λ(ka) = pk. More generally, this PDE takes the form of a conservation law with systematic and diffusive currents J and JD, given by
As a ≪ 1, the systematic current dominates and solutions of (1) generically converge locally uniformly on (0,1) to so-called entropy solutions of
| (2) |
Further details and relevant calculations are provided in The hydrodynamic limit of the inhomogeneous ℓ-TASEP of STAR Methods.
Particle densities, currents and phase transitions
The first order nonlinear PDE given by (2) can be solved using the method of characteristics (Evans, 2010), which describes the evolution of differently dense “patches” of particles over time. Solving for the characteristics yields two branches of solutions, which we call “upper” and “lower” branches, while the boundary conditions imposed by α and β determine which branch is taken by the stationary density of particles (see Phase transitions and profiles of STAR Methods). As a consequence, the behavior of the system is characterized by a phase diagram in α and β. Moreover, this phase diagram depends on only few parameters of the system (see Figure 1C): the size of particles ℓ, the jump rates at the boundaries, λ0 := λ(0) and λ1 := λ(1), and the minimum jump rate λmin := min{λ(x) : x ∈ [0,1]}. In particular, these parameters determine the critical initiation and termination rates, α* and β*, that are associated with phase transitions. More precisely, the critical initiation rate α* is given by
| (3) |
where . Note that α* is determined by the jump rates λ0 and λmin. In the context of translation dynamics, this means that α* will be specific to each gene, as different genes will likely have different values of λ0 and λmin. For a fixed λ0 the critical rate α* increases as λmin increases. For a fixed λmin it turns out that α* satisfies
| (4) |
where the lower bound is achieved as λ0 → ∞, while the upper bound is achieved when λ0 = λmin. More generally, for a fixed λmin, the critical initiation rate α* decreases as λ0 increases. The critical termination rate β* is obtained from (3) by replacing λ0 with λ1. Hence, for mRNA translation, β* is also gene-specific, determined by the key elongation rates λ1 and λmin.
The resulting phase diagram, which generalizes previous formulas for the homogeneous 1-TASEP (Derrida et al., 1993), is summarized as follows (see Figure 1D):
- If α < α* and β > β * (LD I): In this regime the flux is limited by the initiation rate, leading to a low density profile. The corresponding current assumed by the system is
while the site-specific particle density is(5) (6) If α > α* and β < β * (HD I): Now the flux is limited by the particle exit rate, resulting in a high density regime. The associated current JR and density ρR are identical to JL ((5)) and ρL ((6)), respectively, with λ0 and α replaced by λ1 and β.
If α < α* and β < β* (LD II and HD II): The steady state is determined by the sign of JL − JR (computed as above). If it is positive (JL > JR), the system is in a low density regime with current and density given by JL and ρL, respectively. Conversely, if it is negative, the system is in a high density regime with JR and ρR as the current and density.
- If α > α* and β > β* (MC): The system carries the maximum possible current (also referred to as the transport capacity of the system)
which is limited only by the minimum elongation rate λmin. Its density is characterized by qualitatively different profiles to the left and right of xmin = arg minx λ(x): For x < xmin, ρ(x) is described by the upper branch (obtained by replacing JR with Jmax in the equation for ρR), while for x > xmin, ρ(x) is described by the lower branch (obtained by replacing JL with Jmax in ρL). That is, a branch switch occurs at xmin (where ). We proved more generally that every global minimum of λ regulates the traffic of particles (like a toll reducing the traffic flow) in this fashion: incoming densities to the left of it are always described by the upper branch whereas outgoing particles on the right follow the lower branch. In particular, this implies that in the case of multiple global minima, the density between two consecutive minima must undergo a discontinuous jump from lower to upper branch (for more details, see Phase transitions and profiles of STAR Methods and Figure S2).(7)
Novel phenomena and applicability to discrete lattices
As shown in Figure 1E, for smooth rate functions the densities predicted by our analysis agree well with Monte Carlo simulations in all regimes of the phase diagram. In the context of translation dynamics, however, elongation rates are typically less regular, exhibiting substantial fluctuations throughout the entire transcript (see Figure 2A). Despite this lack of regularity, the hydrodynamic limit can still be employed to describe local averages of such a system. In particular, smoothing particle profiles by windows of length ℓ reproduces parameters that closely match hydrodynamic predictions (see Applicability to discrete lattices of STAR Methods and Figure S3). Hence, all subsequent analyses described below will pertain to elongation rate profiles smoothed by a ten-codon moving average. A noteworthy consequence of the above results is that local averages of elongation rates are more predictive of overall translation dynamics than their non-smoothed counterparts. In particular, the location at which branch switching occurs in the MC regime is governed by which may be, and in many cases is, considerably different from arg minx{px}/N (cf. Figure S3).
Figure 2. Local averaging reproduces hydrodynamic limit in lattices with discontinuous rate functions.
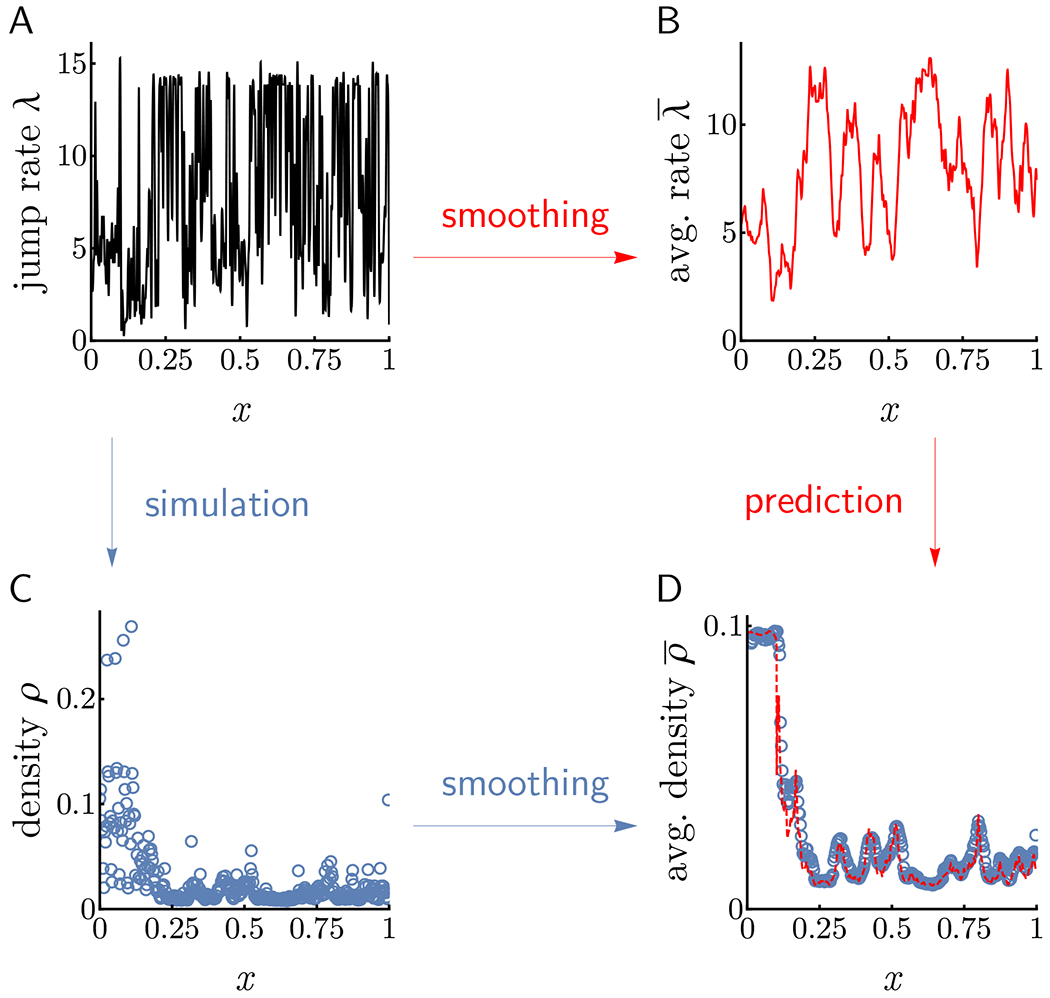
Applying the hydrodynamic theory to smoothed jump rates correctly predicts smoothed density profiles and currents. A: Elongation rates of the yeast gene YHR025W arbitrarily chosen from Dao Duc and Song (2018) (see Empirical Study: Translational Efficiency in Yeast for further details). B: Smoothed elongation rates obtained by applying a ten-codon moving average to the raw profile in A. C: Density profile resulting from simulation (as in Figure 1E except with ℓ = 10, N = 357) under discontinuous profile in A. D: The hydrodynamic density profile (dashed red) associated with the smoothed elongation rates of B reproduces the smoothed density profile obtained from averaging the raw densities in C by a moving ten-codon window. Similarly, simulated and predicted currents are in excellent agreement (0.1072 and 0.1077, respectively).
We highlight a few novel phenomena in our generalization of the homogeneous 1-TASEP: First, extending particles to size ℓ > 1 and lowering the limiting jump rate λmin reduces both the transport capacity Jmax and the critical rates (α* and β*) for entrance and exit, leading to an enlarged MC phase region. This is expected as fewer particles are needed to saturate the lattice, and distances between particles are larger, which in turn limits the number of particles able to cross a site per given time. This phenomenon is quantified precisely using our explicit expressions for α*, β*, and Jmax (see (3) and (7)). Second, the inhomogeneity in λ may deform the LD-HD phase separation from being a straight line in the homogeneous ℓ-TASEP (Chou and Lakatos, 2004) to a generally nonlinear curve (see Figure 1D) determined by solutions (α, β) of
corresponding to the condition JL = JR. This is a consequence of α and β affecting the system at different scales whenever λ0 ≠ λ1, resulting in a phase diagram that is no longer symmetric. Lastly, our observation of density profiles performing branch switching in the MC phase was indiscernible in the homogeneous case, as the high density and low density branches merge into a single value (viz. ).
Application: Design Principles for Translational Systems
We sought to apply our theoretical analysis to understand how the translational system can be regulated and optimized with regard to protein synthesis rate and ribosome usage. The hydrodynamic theory developed above singles out the key parameters that determine the current and particle densities. We illustrate in Figure 3 how λ0, λmin, and xmin impact the current capacity, its sensitivity to the initiation rate α, and the global particle density, suggesting the following principles:
The initiation rate α (and not termination rate β) should regulate the production rate J. As shown by our analysis of the current, any value of the current that lies below the system’s production capacity Jmax can be attained through either HD or LD regime. In order to avoid overuse of resources, however, a transcript should always operate in LD, where the main determinant for currents is the initiation rate α (cf. (5)). To guarantee LD profiles, termination rates merely need to exceed the critical value β*, whereas initiation rates are more tightly controlled, varying between 0 and α*. Within this interval, the current J increases with α according to (5), as illustrated in Figure 3A.
The minimum elongation rate λmin determines the production capacity Jmax. As α increases in the LD regime, the current J reaches a plateau that is associated with the maximal current (MC) regime (see Figure 3A). By (7), the maximum possible current is directly proportional to λmin, which therefore sets the range within which production rates may vary. Large values of λmin allow for both constitutively high expression of genes as well as highly variable protein levels, while small values of λmin guarantee constitutively low expression.
In the LD regime, the sensitivity of production rate J to α is moderated by λ0 and varies across different values of α. Our theory predicts that for β > β* (i.e., provided that the termination rate is sufficiently high), the dynamic range of the initiation rate (i.e., the range of α within which the overall protein production rate J varies with α) is given by (0,α*), where the critical initiation rate α* is defined in (3). Furthermore, the degree to which J varies with α is fully determined by the elongation rate λ0, as shown in (5). Indeed, λ0 controls the time spent by particles at the start of the lattice, and can induce significant buffering if α is large enough, thereby modulating the effective rate of entrance associated with J. We illustrate this in Figure 3A, where we compare how the current varies as a function of α for different values of λ0 relative to λmin. Recall that the critical initiation rate α* satisfies the inequalities in (4), and that α* increases as λ0 decreases. Figure 3A also shows that for λ0 fixed, the production rate of a system closer to the MC regime (i.e., with α just below α*) is less sensitive to changes in α, and that this effect is more pronounced the closer λ0 is to λmin. More generally, the α-sensitivity of J increases as λ0 increases. While the dependence of J in α is sublinear for λ0 = λmin, it becomes linear as λ0 gets large (see (5)). This suggests in particular that changes in the free ribosome pool (changing the initiation rate globally) can impact the protein production rate differently across different genes.
Positioning λmin close to the start site can reduce the amount of ribosomes used. At maximum production capacity (MC regime), we have shown that the density profile follows the high density branch from the start of the lattice until the location xmin of λmin whereafter it adopts the low density branch. This characteristic branch switching phenomenon makes xmin critical for the purpose of resource allocation. In Figure 3B, we illustrate how a small local change in the rate function can induce a large increase of average particle density when xmin changes substantially. Therefore, a way to limit the excessive usage of ribosomes induced by traffic jams at maximum capacity is to position the minimum rate close to the start. However, as previously shown, positioning it too close to the start (such that λ0 = λmin) would also decrease the sensitivity of the system to α.
Figure 3. Main determinants of current and particle densities.
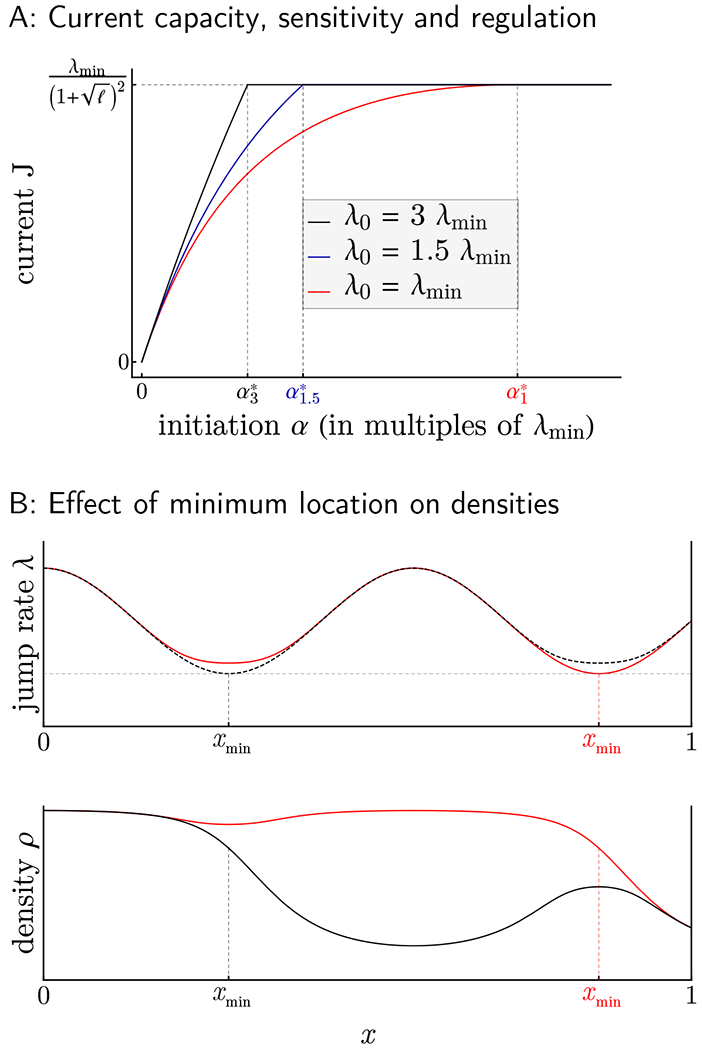
A: We plot the current J in LD and MC against the initiation rate α, for various choices of λ0. While λmin governs the maximum current at which J reaches a plateau (coinciding with the transition from LD to MC), changing the size of λ0 results in changes in ∂αJ, the sensitivity of J with respect to α. Distinct configurations of λmin and λ0 give rise to vastly different dependencies of J on α, suggesting different responses to global changes in the ribosome pool. , , and correspond to the α* value (in units of λmin) when λ0 = 3λmin, λ0 = 1.5λmin, and λ0 = λmin, respectively. B: Two elongation rate profiles that differ slightly in overall shape, but drastically in their position xmin of minimum elongation are plotted (top panel) together with their associated MC ribosome densities (bottom panel). The branch switching phenomenon has extreme consequences for equilibrium particle densities and hence ribosomal costs, with elongation rate profiles achieving minimum rates close to the initiation site (top, dotted black curve) benefiting from drastic savings (bottom, black curve) compared to otherwise similar profiles (red curves).
Empirical Study: Translational Efficiency in Yeast
In light of the aforementioned principles, we explored the extent to which the translational system in yeast is efficient. For this study, we used elongation rates previously inferred from ribosome profiling data for a set of 850 genes in S. cerevisiae (Dao Duc and Song, 2018) (see Data processing of STAR Methods). These genes were selected in Dao Duc and Song (2018) based on length and footprint coverage, to yield robust estimates of rates. The advantage of using this particular dataset over most others lies in the fact that the inferred rates for this subset of genes faithfully reproduce ribosome profiling data, incorporating several experimental artifacts of ribo-seq such as undetected stacked ribosomes, thereby minimizing confounding from technical biases. Furthermore, primarily analyzing high-coverage (and thus likely highly expressed) genes does not confound our study of design principles, but rather provides us an increased signal-to-noise ratio, as these genes are precisely those on which our design principles are expected to act most strongly.
We analyzed the location of these 850 genes in the phase diagram, and the distribution of the key parameters and variables that determine the ribosomal currents and densities. We found the aforementioned theoretical design principles being reflected as follows:
Translation mainly operates in LD regime. Upon computing α* and β*, we located the position of each gene in the phase diagram (see Figure 4A). Over the 850 genes in our dataset, we found 841 in LD and the remaining 9 in the MC region. No genes were found in HD, suggesting no excessive usage of ribosome to achieve any protein level. As a result, the initiation rate is the main determinant and limiting factor of the current (Spearman’s rank correlation coefficient ρ = 0.979). The strength of this correlation nevertheless decreases as genes get closer to the MC regime, since J becomes less sensitive to α and λmin becomes its rate limiting factor (see Figure 4C). To quantify this reduction in correlation, we binned the data by quartiles of J and computed Spearman correlations within each bin, which yielded (in order of quartiles): 0.93, 0.72, 0.64, and 0.58.
Wide ranges of currents are covered within production capacity. For each gene in our dataset, we examined the maximal protein production rate, which according to our theory is proportional to λmin. The data exhibit an overall range of λmin between 1.01 and 6.01 codons/second, and for any fixed λmin, currents are well spread out across [0, Jmax] (see Figure 4D). Given that genes cover almost all of the theoretically possible range of currents, we investigated whether certain configurations of λmin and J are associated with the biological function of specific genes. To do so, we compared ribosomal protein genes (known to be highly expressed) and genes related to stress response (requiring variable expression over time, see Data processing of STAR Methods). We found that, while both sets of genes display comparable λmin, ribosomal genes are more likely to be close to their maximal production capacity (p < 7 × 10−3, see QUANTIFICATION AND STATISTICAL ANALYSIS of STAR Methods) and more consistently so (the coefficient of variation is 0.22 for ribosomal genes and 0.36 for stress response).
λ0 (associated with sensitivity to α) is higher for genes that are either highly expressed or subject to varying expression demand. The impact of increasing α-sensitivity is primarily twofold: First, for fixed production capacity, large currents may be attained with smaller initiation rates; and second, more substantial changes in currents may be achieved with small changes in α. To investigate the former we computed α*, the critical rate necessary for a gene to attain maximum capacity, across all genes whose λmin exceeded the median λmin of the data set (as large currents presuppose large capacities). Further binning this range into quartiles (to isolate the dependence of α* on λ0), we found that genes whose currents are at least 90% of the production capacity are significantly more sensitive (p < 0.008, 0.01, 0.05, and 0.004, respectively; see Figure 4E), requiring smaller initiation rates to reach peak production rate (cf. Figure 4C). To inspect the second aspect of λ0 as facilitator or inhibitor of rapid changes in current, we explored the ratio of λ0 to λmin again in ribosomal and stress response genes. For constitutively highly expressed genes like ribosomal genes, we expect this ratio to be small to maintain stable current close to MC (cf. Figure 3), whereas genes with variable expression demands like the ones associated with stress response should exhibit larger ratios. Confirming this intuition, we found significantly reduced levels of λ0/λmin in ribosomal genes (p < 2 × 10−6), and significantly increased levels in stress response genes (p < 0.04).
The position of λmin is preferentially located early in the open reading frame. Upon analyzing the distribution of xmin from our dataset (see Figure 4B), we found it preferentially located in the codon positions between 30 to 40, consistent with genes forestalling excessive ribosome usage through enforcing branch switching early on. More specifically, we reasoned that both genes closer to MC and those highly sensitive to α run higher risk of incurring substantial ribosome cost and should thus locate xmin early in the coding sequence. Indeed, both the top quartile of genes close to MC (as measured by α/α*) and stress response associated genes showed significantly smaller xmin (p < 0.03 and 0.01, respectively). Moreover, genes with unusually large values of xmin are significantly less likely to be close to MC (top quartile of xmin: p < 1 × 10−3).
Figure 4. Translation machinery in S. cerevisiae optimizes for ribosomal cost, flexible regulation and production capacity.
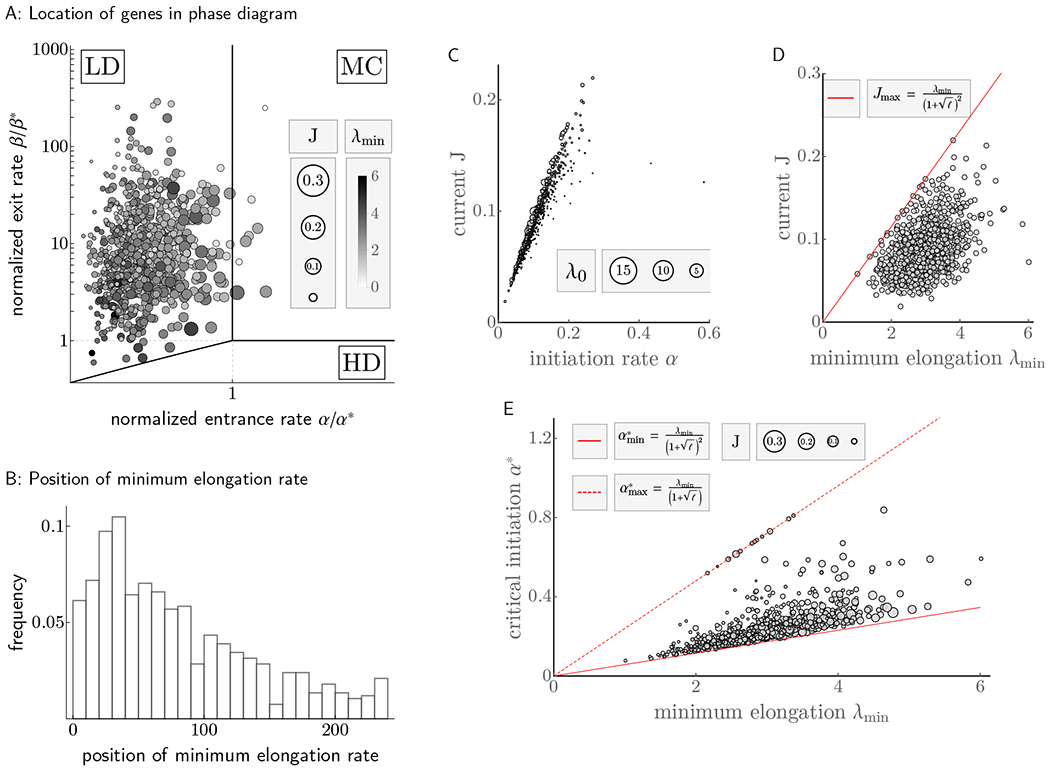
All rates are in codons per second, while currents are measured in ribosomes per second. A: 850 genes of S. cerevisiae are located in the phase diagram, with size and hue of each data point reflecting current and minimum elongation rate, respectively. On a population level, systems of comparable production capacities (∝ λmin) fully exploit their dynamic range by adjustment of α, with highly expressed proteins likely situated inside or close to MC. B: The resulting resource cost considerations drive a significant number of transcripts to position their minimum elongation rate early on in the codon sequence, forcing ribosomal traffic jams to remain short. C: Initiation α is the main determinant of currents, at least for low to average current genes. For highly expressed genes, the correlation between α and J decreases due to stronger variation in λ0 and transitions into MC. D: Genes utilize the full dynamical range of currents set by λmin, through variation in α and λ0. Constitutively highly expressed genes tend to be closer to maximum capacity (red line), while genes with variable expression demands are distributed more broadly (see main manuscript). E: For fixed production capacity ∝ λmin, α* (the critical initiation rate at which genes reach maximum production capacity) tends to be smaller for genes with larger production rates. That is, larger λ0 (which are inversely related to α* for fixed λmin) seem to facilitate attainment of large currents. Moreover, within highly expressed genes, those associated with variable expression patterns over time exhibit higher sensitivities (smaller α*), whereas genes with constitutive high expression are found closer towards maximal insensitivity (dotted red line) as these configurations ease stable expression.
To check for systematic biases potentially present in our subsampled gene set and to show replicability of our main biological conclusions, we also analyzed two other independent (and much larger) datasets from Williams et al. (2014) (combined with polysome profiling from MacKay et al. (2004)) and Pop et al. (2014) (see Data Processing of STAR Methods). We inverted the solution of (2) to obtain approximate estimates of initiation rates, termination rates, and smoothed elongation rates for these datasets, and repeated our analyses. As shown in Figure S4, the results are generally in excellent agreement with what is discussed above (Figure 4A,B).
DISCUSSION
While past quantitative studies of the TASEP under general conditions of extended particle size and/or rate heterogeneity have mostly been limited to numerical simulations or mean-field approximations, (Lakatos and Chou, 2003; Shaw et al., 2003, 2004; Chou and Lakatos, 2004; Dong et al., 2007), we used here a different approach that relies on studying the hydrodynamic limit of the process. In the case of homogeneous rates, previous studies (Schönherr, 2005; Schönherr and Schütz, 2004) established this hydrodynamic limit, but without further analyzing the subsequent PDE. After deriving this limit for inhomogeneous rates, we obtained closed-form formulas for the associated current, densities, and phase diagram, generalizing previous theoretical results for the TASEP (Derrida et al., 1993; Blythe and Evans, 2007) and its variants (Shaw et al., 2003; Chou and Lakatos, 2004; Stinchcombe and de Queiroz, 2011). Our approach has the advantage of revealing the key parameters that the current and densities depend on, enabling an immediate quantification of the process and its phase diagram. Such a quantification is difficult to achieve via conventional stochastic simulations or approximations used in the past several years (Zia et al., 2011; Zur and Tuller, 2016; Szavits-Nossan et al., 2018).
Our characterization of the current and densities in the phase diagram suggests that, in agreement with earlier experimental studies (Kosuri et al., 2013; Salis et al., 2009), translation dynamics should be mainly governed by the initiation rate, while the termination rate and most elongation rates have negligible impact. In particular, our results explain why having the initiation rate as the main limiting factor of the current (Plotkin and Kudla, 2011) minimizes ribosome usage. In addition, we discovered the importance of smoothed rather than raw elongation profiles in predicting translation dynamics, explaining the previously observed mild effect that any individual elongation change has compared to accumulated, neighboring changes (Levin and Tuller, 2018). This allowed us to identify two key parameters of the system, namely, the smoothed elongation rate λ0 immediately following initiation and the minimal smoothed elongation rate λmin. Previous studies have established some association between the sequence context in the early 5′ coding region and protein production levels (Frumkin et al., 2017; Boël et al., 2016; Ben-Yehezkel et al., 2015). For example, it has been shown that mRNA secondary structure in the first ~ 16 codons (which locally decreases the elongation rate) negatively affects the translation rate in E. Coli, while no significant contribution of mRNA folding in other regions was found (Frumkin et al., 2017). By exposing α and λ0 as the only parameters that currents in LD depend on, our analysis suggests a direct explanation for such contrast.
We also highlighted the impact of λ0 on the sensitivity of the current to changes in α. In practice, initiation rates can vary at the individual gene level (e.g., through interactions with specific miRNAs (Humphreys et al., 2005)). According to our theory, the way that these variations impact the protein production rate depends on λ0; we hence suggest that this may explain why genes associated with stress response present higher values of λ0, as it facilitates the response to changes in α. At a more global level, our study shows how protein levels can be more or less robust against changes in the ribosomal pool, which can simultaneously affect all initiation rates in a cell (Shah et al., 2013). Since the level of ribosomes present in a cell fluctuates over time (Wyant et al., 2018), it would be interesting to see if protein levels scale uniformly with these variations across genes, and if not, whether the differences in λ0 can explain it.
To the best of our knowledge, the role of the minimum elongation rate λmin has so far received attention only indirectly, through the study of what is known as the “5′ translational ramp” (Tuller et al., 2010). This ramp is a pattern of translational slowdown around codon position 30-50 followed by steadily accelerating elongation rates, which is mirrored by the spatial distribution of minimum elongation rates we found here. This ramp has been hypothesized to prevent crowding of ribosomes on the transcript (Tuller et al., 2010), for which we provide a theoretical basis, exposing λmin as a separator between crowded and freely elongating ribosomes. More generally, the complex interplay between the maximum current capacity, ribosome usage, and sensitivity to the initiation rate suggests various ways to set the parameters λ0, λmin and xmin, depending on the desired object to optimize. For example, allocating the minimum elongation rate near the beginning of the ramp region provides an optimal trade-off between high sensitivity and minimal traffic jams. On the other hand, it would be optimal for genes with housekeeping function to have a decreased sensitivity, which would push the minimum to earlier positions.
Our analysis can also help to answer the long-debated question regarding the implication of translation on codon usage bias (Hershberg and Petrov, 2008; Frumkin et al., 2018; Shah et al., 2013). Since highly expressed genes are enriched for synonymous codons translated by more abundant tRNAs (Yu et al., 2015; Hanson and Coller, 2018), it has been hypothesized that codon usage bias increases the overall protein synthesis rate by accelerating elongation (Hershberg and Petrov, 2008). However, recent studies have challenged such a hypothesis, suggesting that translational selection for speed is not sufficient to explain the observed variation in codon usage bias (Mahajan and Agashe, 2018). Synonymous changes of the coding sequence modify local elongation rates, but, according to our theory, such a modification impact the overall protein production rate only if the smoothed elongation rates λ0 or λmin are affected. In addition, our work implies that synonymous codon replacements that substantially change the location xmin of λmin affect the efficiency of ribosome usage, and hence are more likely to be under selective pressure. Aside from these cases, there should be little direct impact of synonymous codon usage on translation efficiency; this prediction is consistent with previous studies that tried to explain differences in expression using codon identity (Gustafsson et al., 2012), and to characterize the sensitivity of translational output with respect to changes in elongation (Levin and Tuller, 2018). Codon usage bias could affect the protein production rate indirectly, however, by reducing the cost of translation: replacing a codon by a “faster” synonymous codon helps to reduce the local ribosome density on the transcript, and this can in turn increase the availability of free ribosomes and therefore increase the initiation rate α slightly; in the LD regime, increasing α would increase the protein production rate. We note that other factors such as mRNA decay (Hanson and Coller, 2018), or reduction of nonsense errors or co-translational misfolding (Gilchrist, 2007; Frumkin et al., 2018) might be more important drivers of codon usage bias.
Finally, it would be interesting to experimentally test our theoretical predictions, e.g., using cell-free expression protocols such as lysate-based systems, which have been developed to optimize protein synthesis and more recently refined to study translation dynamics (Moore et al., 2017; Rosenblum and Cooperman, 2014; Katranidis and Fitter, 2019). By designing an appropriate mRNA sequence and controlling different components (NTPs, ribosomes, tRNAs, specific amino acids), these systems allow to manipulate the initiation and elongation rates, and hence tune the key parameters identified by our theoretical analysis. For example, one can modify λmin or λ0 by changing the level of corresponding amino acids, and vary α by modifying the 5′ UTR sequence or changing the ribosome concentration. The flexible nature of such cell-free expression systems, coupled with precise measurement of protein levels (e.g., via isotope-labeled amino acids or reporter proteins), should help to verify our theoretical results. In particular, it would be interesting to experimentally demonstrate the existence of phase transitions, and by modifying the mRNA sequence, test our predictions on how to effectively control the robustness and sensitivity of the translation system. We are currently pursuing these research directions.
STAR METHODS
LEAD CONTACT AND MATERIALS AVAILABILITY
Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Yun S. Song (yss@berkeley.edu).
This study did not generate new reagents.
METHOD DETAILS
The hydrodynamic limit of the inhomogeneous ℓ-TASEP
We derive here the PDE governing the hydrodynamic limit of the open-boundaries inhomogeneous ℓ-TASEP. To do so we exploit a representation of its dynamics in terms of another interacting particle system, the so-called zero range process (ZRP), whose hydrodynamics can be found explicitly. This TASEP-ZRP duality provides an expedient and general tool for identifying explicit TASEP formulas; however, rigorously proving the validity of these formulas often requires more technical tools from probability theory. Since this work’s emphasis is on the application of TASEP to unraveling the key parameters of translation dynamics, we will here concentrate on showcasing the TASEP-ZRP framework, and keep a rigorous existence proof of the hydrodynamic limit, combining techniques from Rezakhanlou (1991); Covert and Rezakhanlou (1997) and Bahadoran (2012), to a separate manuscript.
Reduction to periodic boundaries and mapping to the ZRP.
The purpose of the hydrodynamic limit is to describe the local evolution of the macroscopic particle density in the large system limit. As such, it does not explicitly rely on the precise formalism by which particles enter and exit the lattice at the boundaries (which will only later be needed to impose boundary conditions on the resulting PDE (Bahadoran, 2012)). In particular, we are free to choose periodic boundary conditions for our limiting procedure without changing the resulting PDE (Schönherr and Schütz, 2004). This has the advantage of preserving the total number of particles, which is essential for establishing the correspondence between TASEP and ZRP. In the following, we thus consider the ℓ-TASEP with M particles on a ring of N sites jumping to the right at rate pi, and take M, N → ∞ while M/N remains constant.
The ZRP is now obtained by reversing the roles of holes and particles: It consists of N − Mℓ particles (corresponding to the N − Mℓ holes in the TASEP) distributed across M sites (matching the TASEP particles) {1, … , M}, with multiple particles allowed to stack up on the same site. A ZRP configuration (ξi,t)1≤i≤M describes the number of particles ξi,t at each site i ∈ {1, … , M} and time t, and can be seen as a representation of spacings between particles i and i + 1 in the TASEP.
As a result, the TASEP dynamics are translated into ZRP dynamics as follows: If a site i at time t is occupied by at least one particle, then the topmost particle jumps to the left with rate mi,t = pk(i,t), where k(i, t) is the position of the ith TASEP particle (see formula (8) below) at time t. This jump occurs regardless of whether the destination site is occupied or not. That is, neither exclusion nor long range interactions are present, which will be key to establishing the hydrodynamic limit.
The correspondence between TASEP and ZRP states described above is so far only determined up to rotations of the TASEP lattice, hence we introduce one further variable ξ0,t ∈ {1, … , N} to trace the position of particle 1. More explicitly, at time t, TASEP particle i is located at site
| (8) |
on the TASEP ring. An illustration of this correspondence is given in Figure S1.
The hydrodynamic limits of the ZRP and TASEP.
The connection between the TASEP and the ZRP has been fruitfully used to derive hydrodynamic limits for homogeneous systems (Schönherr and Schütz, 2004; Schönherr, 2005). Here we generalize this approach to heterogeneous lattices and supply appropriate boundary conditions to the PDE, which become necessary when working with open rather than periodic boundaries.
We start with the master equation associated with the ZRP:
| (9) |
where is the probability that site i is non-empty at time t. Our goal is to identify a PDE that describes the limit of (9) under Euler scaling, i.e., on time scale at and spatial scale ia. Denoting these scaled variables as t again in time and x, y in space such that k = ⌊x/a⌋ and i = ⌊y/a⌋, and assuming the existence of a continuously differentiable rate function λ such that λ(x) = pk, the master equation (9) becomes
| (10) |
where c(y, t) and z(y, t) are the continuum limits of ξi,t and zi,t, respectively. Under local stationarity (Kipnis and Landim, 2013), we may replace z in (10) using the fugacity-density relation z = c(1 + c)−1 to obtain the final hydrodynamic limit of the inhomogeneous ZRP as
| (11) |
The assumption of local stationarity is essentially justified by the one-block estimates in Covert and Rezakhanlou (1997), as long as one can ensure slow enough variation of λ(x(y, t)) in t. In our case, this smooth dependency is given, since in a small (on the Eulerian scale) time interval NΔt, we expect a particle to perform O(NΔt) jumps, and whence λ(x(y, t + NΔt)) − λ(x(y, t)) ∈ O(Δt).
To derive the corresponding PDE for the TASEP, we use (8) to establish the continuum relation between x, y and t. More precisely,
| (12) |
Upon recognizing that particle densities are related by ρ = (c+ℓ)−1 and changing coordinates according to (12), (11) yields the hydrodynamic limit of the TASEP
| (13) |
where .
Phase diagram analysis
We now use (13) to provide a detailed derivation of the phase diagram described in the main text.
Reduction to conservation law.
Solutions of (13) converge locally uniformly (under mild conditions on λ, see Phase transitions and profiles) to viscosity solutions of the scalar conservation law
| (14) |
where H(ρ) = ρG(ρ), which thus determines the phase diagram in the hydrodynamic regime. Setting ∂tρ = 0 identifies the stationary profiles of the TASEP as distributions satisfying
| (15) |
where Jc = Jc(α, β, λ) is the critical current, set to belong to [0, Jmax], where Jmax is the transport capacity of the lattice
(15) has two solutions (see Figure S5A) of the form
any mixture of which may be a potential attractor picked by the system as t → ∞. Deciding precisely which mixture dominates requires analysis of the characteristic curves.
Solving the characteristic ODE.
Denoting the characteristic curves by xt and ρt with initial data x0, ρ0, their evolution is described by the system of ODE (Evans, 2010)
| (16) |
| (17) |
where H′ and λ′ respectively denote the derivatives of H and λ with respect to their arguments. The solutions are easily verified to be
| (18) |
| (19) |
as long as J(ρ0, x0) ∈ [0, Jmax]. The form of F follows from formally separating variables:
while H−1(J(ρ0, x0)/λ(xt)) is understood to be the preimage compatible with ρ0, see Figure S5A. For the homogeneous ℓ-TASEP (18) and (19) depend linearly on each other, giving rise to straight line characteristic curves (see Figure S5B). In the more general heterogeneous setting, however, more complicated behavior emerges (Figure S5C). In particular, if J(ρ0, x0) < Jmax, then for all t ≥ 0,
so for all t if , while for all t if . Hence, the sign of remains the same for all t, and any characteristic curve xt starting at the left lattice boundary x0 = 0 or right lattice boundary x0 = 1 propagates towards the opposite end and fills the lattice entirely.
On the other hand, if J(ρ0, x0) > Jmax, then , where xmin = arg minx λ(x), so . Recalling (19) and noting that it is physically not possible to have , we conclude that the characteristic curve xt cannot reach xmin. Indeed, it follows from (16) and (17) that at some critical time tc before reaching xmin, the characteristic curve xt reverses direction while ρt crosses , resulting in xt returning to its origin. Figure 1E of the main text and Figure S5D illustrate this behavior.
Computing initial densities ρ0.
As a consequence of the above, determining phase transitions in the α-β phase diagram reduces to establishing regimes in which J(ρ0, x0) exceeds or falls short of Jmax, which in turn is equivalent to finding an expression for ρ0 in terms of α and β. This is done by considering each lattice end separately and balancing currents:
The right lattice end x0 = 1:
As described in the main text, ρ1 = ρ(1) decomposes into a sum of two contributions, the periodic part and the troughs (Chou and Lakatos, 2004). More explicitly,
Since the current Jc is a conserved quantity of the system, the local currents across the last lattice site, the second to last lattice site and within the last ℓ sites must all be the same:
| (20) |
Solving for ρ1 gives exactly . Consequently, JR ≤ Jmax iff
The left lattice end x0 = 0:
Computing α* is more delicate as the effective jump rate is a combination of entrance rate and particle exclusion. To bypass this problem, we investigate the current of holes rather than particles, which is running in the opposite direction. With the loss of the particle-hole symmetry present in the simple 1-TASEP (Derrida et al., 1993), the hole density ρh here assumes a more complicated form. It satisfies its own conservation law given by
where
and th = ℓt is the time scale of the holes, moving slower as their density is higher. Thus by balancing hole currents rather than particle currents at x0 = 0, we obtain, noting that the effective exit rate (of holes) is still α (as ℓ holes need to accumulate for exiting to happen),
| (21) |
Solving for and using , we obtain ρ0 = α/[λ0+(ℓ−1)α]. Defining JL := J(ρ0, 0), we obtain α* by solving for α, JL = Jmax.
Phase transitions and profiles.
Using the densities obtained from (20) and (21) in the characteristic curves (16) and (17) yields the HD and LD regimes for parameter configurations (α > α*, β < β*) and (α < α*, β > β*), respectively. To describe the phase transition between HD and LD, we observe that for α < α* and β < β* both characteristic curves move into the lattice, meet, and move along a common shock with speed
where ρl and ρr are the densities left and right of the shock. As ρr − ρl > 0 as long as α < α* and β < β* (cf. Figure S5A), vshock > 0 if and only if JR > JL. That is, the slower current pushes the faster one past the lattice boundaries and dominates the stationary behavior of the system. The HD and LD regimes are thus separated by incoming currents of equal magnitudes
Lastly, we can use the behavior of characteristic curves for J(ρ0, x0) > Jmax to describe stationary profiles in the MC regime (α > α* and β > β*): Each characteristic curve reverses direction at a critical time tc and returns to its respective lattice boundary, while the density ρt it carries transitions from ρ− to ρ+ (on the left characteristic) or ρ+ to ρ− (on the right characteristic). Since the reversal of directions occurs strictly before reaching xmin, these characteristics provide density information on only part of the lattice. The uncovered regions are determined by the simultaneously propagating rarefaction waves (Evans, 2010), which interpolate between xt and the characteristic curve associated with J(ρ0, x0) = Jmax (see Figure S5D). Together, these observations combine to produce the high density and low density profiles to the left and right of xmin, respectively, with critical current Jc = Jmax, as described in the main manuscript.
If λ has exactly one global minimum xmin, this description captures the density profile on the entire lattice. In the case of multiple global minima at {xmin,1, … , xmin,n} however, it describes ρ on [0, xmin,1] ⋃ [xmin,n, 1] only, leaving open fluctuations on the middle segment (xmin,1, xmin,n). Although unlikely to be encountered in practice, these singular rate functions exhibit interesting stochastic phenomena: The presence of high densities on the initial interval and low densities on the terminal one suggest the formation of a coexistence phase in-between. Indeed, the subsystem restricted to [xmin,1, xmin,n] may be regarded as a TASEP with entrance and exit rates , positioning it at the triple point of the phase diagram, and computing the characteristics reveals one or multiple stationary shock fronts in the interior. Such macroscopic phenomenon in the homogeneous 1-TASEP has previously been associated on the microscopic level with a shock performing a random walk on the lattice with reflecting boundaries (Derrida et al., 1997). Numerical simulations seem to locate these shock around local maxima disproportionately often (cf. Figure S2), which might reflect dependencies of its diffusivity on λ.
Applicability to discrete lattices
The existence of a continuous limiting rate function extending the discrete jump rates pk = λ(ak) is an important ingredient in our treatment of the hydrodynamic limit. That is, in order for density profiles to be accurately approximated by solutions to the PDE (2), the pk must vary smoothly across lattice sites. Microscopic systems like the translation machinery in cells, however, are typically subjected to substantial amounts of fluctuations, resulting in far rougher elongation profiles (see Figure 2A). Despite this lack of regularity, the hydrodynamic limit can still be employed to describe local averages of such a system. More precisely, fixing r ∈ {1, … , N}, we associate with an elongation rate profile {p1, … , pN} and the corresponding density profile {ρ1, … , ρN} their smoothed profiles and , respectively, obtained through a moving r-codon average: , and . Moreover, we define {σ1, … , σN−r+1} to be the steady state density profile under the elongation rates . If {pk} extends to a smooth , then since , extends to this same λ, and hence {ρk}, and {σk} all converge to the solution ρ of (2). When {pk} does not extend to a continuous limit, then {ρk} generally does not either. However, by the same reasoning that establishes the hydrodynamics for the 1-TASEP with quenched disorder (Seppäläinen et al., 1999), should still be close to {σk}, which, due to the greater regularity of , is well approximated by the hydrodynamic density profile under . Thus, is ultimately well approximated by the hydrodynamic limit under .
To confirm this, we carried out an extensive simulation study on elongation rate profiles obtained from ribosome profiling data of yeast (see Data processing for more details on data). Specifically, we performed the smoothing (Figure 2A,B), simulated density profiles {ρk} under {pk} (Figure 2A,C), and compared the corresponding smoothed densities with the hydrodynamic prediction under (Figure 2D). A choice of r = 10, which is equal to the particle (ribosome) size ℓ in translation and the smallest window size guaranteeing smoothness of due to the ℓ-periodicity induced by traffic jams, resulted in excellent agreement both in densities and currents uniformly across transcripts while maintaining local structure.
Boundary conditions
The computation of initial densities in Solving the characteristic ODE yielded precise boundary values for x = 0 in the LD regime and x = 1 in the HD regime, respectively. Using the same principle of balancing currents, boundary conditions for all locations in the phase diagram can be computed. The results are listed in Table S1, which extend previous results obtained in (Lakatos and Chou, 2003) (who derived entries (1,1), (2,2) and (2,3) of Table S1). More precise information about the boundary layers can be gleaned from direct analysis of (13) rather than its limit (14).
Data processing
Initiation, elongation, and termination rates were obtained from an earlier work (Dao Duc and Song, 2018), where the rates were estimated from ribosome profiling data of S. cerevisiae for a set of 850 genes selected based on length and footprint coverage. The initiation and termination rates (α and β) were taken directly from that previous work. To compute the elongation rates relevant to the hydrodynamic limit, we applied a ten-codon moving average to their elongation rates (see Applicability to discrete lattices). To demonstrate replicability on larger datasets, we took ribosome profiles directly from Williams et al. (2014) and Pop et al. (2014) (combined with polysome profiling from MacKay et al. (2004) for normalization purposes, yielding 3098 and 2536 genes, respectively), smoothed them by moving averages of length ℓ = 10, and inverted the solution of (2) to obtain initiation rates, termination rates, and smoothed elongation profiles.
QUANTIFICATION AND STATISTICAL ANALYSIS
Hypothesis tests and p-values
To establish significance of a subset X of genes with respect to a statistic f (e.g., α, J or xmin) relative to a background set Y, we performed hypothesis testing on the median mf of f over samples in X. Under the null distribution of X being drawn uniformly at random, the probability of this test statistic exceeding m equals the probability of a hypergeometric variable with parameters N = |Y|, K = 2 |Ym|, n = |X|, where Ym is the set of genes in Y whose f exceeds m, exceeding ⌊|X/2|⌋. This p-value can be computed explicitly. Sets of ribosomal and stress response genes were taken from the Saccharomyces Genome Database (Cherry et al., 2011).
Agreement between theoretical prediction and simulation
In order to empirically verify our theoretical justification of the hydrodynamic limit, we simulated ribosome profiles and currents for all 850 S. cerevisiae genes studied in Dao Duc and Song (2018). For each gene, we considered four conditions: LD, HD, MC, and under the actual initiation and termination rates inferred in Dao Duc and Song (2018); these four conditions correspond to different rows in Figure S6. Absolute errors in ribosome density profiles and currents (first and last columns of Figure S6) are accurately predicted across all gene lengths—with a slight increase in prediction accuracy for longer genes (as expected, since the hydrodynamic limit becomes exact in the infinite length limit)—and across all regimes of the phase diagram. Due to two or more bottlenecks occasionally competing on the same transcript (i.e., when |{x : λ(x) = λmin}| > 1, cf. last paragraph of Phase transitions and profiles of STAR Methods), error distributions in MC exhibit heavier tails than in LD and HD. However, overall these outliers do not affect the quality of our theoretical prediction significantly. In particular, correlations between simulated and theoretical transcript-by-transcript quantities—ribosome density profiles and mean occupancies (middle column), as well as currents (last column)—are consistently high, demonstrating good predictive power of our hydrodynamic framework.
In HD, predicted and simulated ribosome density profiles had quite low mean squared differences (second row, first column of Figure S6), but poor correlation (histograms in second row, second column). This seemingly contradictory result can be explained by typical fluctuations in theoretical density profiles being of the same order as typical fluctuations in the random noise (mean ratio of fluctuations = 0.037). That is, generic HD profiles are close to flat, allowing uncorrelated site-by-site noise to substantially reduce overall correlations.
DATA AND CODE AVAILABILITY
This study did not generate new data. Code, including the code used to generate all figures, is publicly available at https://github.com/songlab-cal/l-TASEP.
Supplementary Material
ACKNOWLEDGEMENTS
This research is supported in part by NIH grants R01-GM094402 and R35-GM134922; a Packard Fellowship for Science and Engineering; and the Koret–UC Berkeley-Tel Aviv University Initiative in Computational Biology and Bioinformatics. YSS is a Chan Zuckerberg Biohub Investigator.
REFERENCES
- Bahadoran C (2012). Hydrodynamics and hydrostatics for a class of asymmetric particle systems with open boundaries. Communications in Mathematical Physics, 310(1):1–24. [Google Scholar]
- Ben-Yehezkel T, Atar S, Zur H, Diament A, Goz E, Marx T, Cohen R, Dana A, Feldman A, Shapiro E, et al. (2015). Rationally designed, heterologous s. cerevisiae transcripts expose novel expression determinants. RNA biology, 12(9):972–984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blythe RA and Evans MR (2007). Nonequilibrium steady states of matrix-product form: a solver’s guide. Journal of Physics A: Mathematical and Theoretical, 40(46):R333–R441. [Google Scholar]
- Boël G, Letso R, Neely H, Price WN, Wong K-H, Su M, Luff JD, Valecha M, Everett JK, Acton TB, et al. (2016). Codon influence on protein expression in E. coli correlates with mRNA levels. Nature, 529(7586):358–363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cherry JM, Hong EL, Amundsen C, Balakrishnan R, Binkley G, Chan ET, Christie KR, Costanzo MC, Dwight SS, Engel SR, et al. (2011). Saccharomyces Genome Database: the genomics resource of budding yeast. Nucleic Acids Research, 40(D1):D700–D705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chou T and Lakatos G (2004). Clustered bottlenecks in mRNA translation and protein synthesis. Phys. Rev. Lett, 93:198101. [DOI] [PubMed] [Google Scholar]
- Covert P and Rezakhanlou F (1997). Hydrodynamic limit for particle systems with nonconstant speed parameter. Journal of statistical physics, 88(1):383–426. [Google Scholar]
- Dao Duc K and Song YS (2018). The impact of ribosomal interference, codon usage, and exit tunnel interactions on translation elongation rate variation. PLoS Genetics, 14(e1007166):1–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Derrida B, Evans MR, Hakim V, and Pasquier V (1993). Exact solution of a 1D asymmetric exclusion model using a matrix formulation. Journal of Physics A: Mathematical and General, 26(7):1493–1517. [Google Scholar]
- Derrida B, Lebowitz J, and Speer E (1997). Shock profiles for the asymmetric simple exclusion process in one dimension. Journal of Statistical Physics, 89(1-2):135–167. [Google Scholar]
- Dever TE, Kinzy TG, and Pavitt GD (2016). Mechanism and regulation of protein synthesis in Saccharomyces cerevisiae. Genetics, 203(1):65–107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dong JJ, Schmittmann B, and Zia RKP (2007). Inhomogeneous exclusion processes with extended objects: The effect of defect locations. Phys. Rev. E, 76:051113. [DOI] [PubMed] [Google Scholar]
- Evans LC (2010). Partial Differential Equations, Vol. 19 of Graduate Studies in Mathematics American Mathematical Society. American Mathematical Society, Providence, Rhode Island. [Google Scholar]
- Frumkin I, Lajoie MJ, Gregg CJ, Hornung G, Church GM, and Pilpel Y (2018). Codon usage of highly expressed genes affects proteome-wide translation efficiency. Proceedings of the National Academy of Sciences, 115(21):E4940–E4949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frumkin I, Schirman D, Rotman A, Li F, Zahavi L, Mordret E, Asraf O, Wu S, Levy SF, and Pilpel Y (2017). Gene architectures that minimize cost of gene expression. Molecular Cell, 65(1):142–153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilchrist MA (2007). Combining models of protein translation and population genetics to predict protein production rates from codon usage patterns. Molecular Biology and Evolution, 24(11):2362–2372. [DOI] [PubMed] [Google Scholar]
- Gustafsson C, Minshull J, Govindarajan S, Ness J, Villalobos A, and Welch M (2012). Engineering genes for predictable protein expression. Protein Expression and Purification, 83(1):37–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanson G and Coller J (2018). Codon optimality, bias and usage in translation and mRNA decay. Nature Reviews Molecular Cell Biology, 19(1):20–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hershberg R and Petrov DA (2008). Selection on codon bias. Annual Review of Genetics, 42:287–299. [DOI] [PubMed] [Google Scholar]
- Humphreys DT, Westman BJ, Martin DI, and Preiss T (2005). MicroRNAs control translation initiation by inhibiting eukaryotic initiation factor 4E/cap and poly(A) tail function. Proceedings of the National Academy of Sciences, 102(47):16961–16966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katranidis A and Fitter J (2019). Single-molecule techniques and cell-free protein synthesis: A perfect marriage. Analytical Chemistry, 91(4):2570–2576. [DOI] [PubMed] [Google Scholar]
- Kipnis C and Landim C (2013). Scaling limits of interacting particle systems, volume 320 Springer Science & Business Media. [Google Scholar]
- Kosuri S, Goodman DB, Cambray G, Mutalik VK, Gao Y, Arkin AP, Endy D, and Church GM (2013). Composability of regulatory sequences controlling transcription and translation in Escherichia coli. Proceedings of the National Academy of Sciences, 110(34):14024–14029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kristensen AR, Gsponer J, and Foster LJ (2013). Protein synthesis rate is the predominant regulator of protein expression during differentiation. Molecular Systems Biology, 9(689):1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lakatos G and Chou T (2003). Totally asymmetric exclusion processes with particles of arbitrary size. Journal of Physics A: Mathematical and General, 36(8):2027–2041. [Google Scholar]
- Levin D and Tuller T (2018). Genome-scale analysis of perturbations in translation elongation based on a computational model. Scientific reports, 8(1):16191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu P, Vogel C, Wang R, Yao X, and Marcotte EM (2007). Absolute protein expression profiling estimates the relative contributions of transcriptional and translational regulation. Nature Biotechnology, 25(1):117–124. [DOI] [PubMed] [Google Scholar]
- MacDonald CT, Gibbs JH, and Pipkin AC (1968). Kinetics of biopolymerization on nucleic acid templates. Biopolymers, 6(1):1–25. [DOI] [PubMed] [Google Scholar]
- MacKay VL, Li X, Flory MR, Turcott E, Law GL, Serikawa KA, Xu X, Lee H, Goodlett DR, Aebersold R, et al. (2004). Gene expression analyzed by high-resolution state array analysis and quantitative proteomics response of yeast to mating pheromone. Molecular & Cellular Proteomics, 3(5):478–489. [DOI] [PubMed] [Google Scholar]
- Mahajan S and Agashe D (2018). Translational selection for speed is not sufficient to explain variation in bacterial codon usage bias. Genome Biology and Evolution, 10(2):562–576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moore SJ, MacDonald JT, and Freemont PS (2017). Cell-free synthetic biology for in vitro prototype engineering. Biochemical Society Transactions, 45(3):785–791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plotkin JB and Kudla G (2011). Synonymous but not the same: the causes and consequences of codon bias. Nature Reviews Genetics, 12(1):32–42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pop C, Rouskin S, Ingolia NT, Han L, Phizicky EM, Weissman JS, and Koller D (2014). Causal signals between codon bias, mrna structure, and the efficiency of translation and elongation. Molecular Systems Biology, 10(12):770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quax TE, Claassens NJ, Soll D, and van der Oost J (2015). Codon bias as a means to fine-tune gene expression. Molecular Cell, 59(2):149–161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rezakhanlou F (1991). Hydrodynamic limit for attractive particle systems on Zd. Communications in Mathematical Physics, 140(3):417–448. [Google Scholar]
- Rosenblum G and Cooperman BS (2014). Engine out of the chassis: Cell-free protein synthesis and its uses. FEBS letters, 588(2):261–268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salis HM, Mirsky EA, and Voigt CA (2009). Automated design of synthetic ribosome binding sites to control protein expression. Nature Biotechnology, 27(10):946–950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schönherr G (2005). Hard rod gas with long-range interactions: Exact predictions for hydrodynamic properties of continuum systems from discrete models. Phys. Rev. E, 71:026122. [DOI] [PubMed] [Google Scholar]
- Schönherr G and Schutz G (2004). Exclusion process for particles of arbitrary extension: hydrodynamic limit and algebraic properties. Journal of Physics A: Mathematical and General, 37(34):8215–8231. [Google Scholar]
- Seppäläinen T et al. (1999). Existence of hydrodynamics for the totally asymmetric simple k-exclusion process. The Annals of Probability, 27(1):361–415. [Google Scholar]
- Shah P, Ding Y, Niemczyk M, Kudla G, and Plotkin JB (2013). Rate-limiting steps in yeast protein translation. Cell, 153(7):1589–1601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaw LB, Sethna JP, and Lee KH (2004). Mean-field approaches to the totally asymmetric exclusion process with quenched disorder and large particles. Phys. Rev. E, 70:021901. [DOI] [PubMed] [Google Scholar]
- Shaw LB, Zia R, and Lee KH (2003). Totally asymmetric exclusion process with extended objects: a model for protein synthesis. Physical Review E, 68(2):021910(17). [DOI] [PubMed] [Google Scholar]
- Stinchcombe RB and de Queiroz SLA (2011). Smoothly varying hopping rates in driven flow with exclusion. Physical Review E, 83:061113. [DOI] [PubMed] [Google Scholar]
- Szavits-Nossan J, Ciandrini L, and Romano MC (2018). Deciphering mRNA sequence determinants of protein production rate. Phys. Rev. Lett, 120:128101. [DOI] [PubMed] [Google Scholar]
- Tuller T, Carmi A, Vestsigian K, Navon S, Dorfan Y, Zaborske J, Pan T, Dahan O, Furman I, and Pilpel Y (2010). An evolutionarily conserved mechanism for controlling the efficiency of protein translation. Cell, 141(2):344–354. [DOI] [PubMed] [Google Scholar]
- Williams CC, Jan CH, and Weissman JS (2014). Targeting and plasticity of mitochondrial proteins revealed by proximity-specific ribosome profiling. Science, 346(6210):748–751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wyant GA, Abu-Remaileh M, Frenkel EM, Laqtom NN, Dharamdasani V, Lewis CA, Chan SH, Heinze I, Ori A, and Sabatini DM (2018). NUFIP1 is a ribosome receptor for starvation-induced ribophagy. Science, 360:751–758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu C-H, Dang Y, Zhou Z, Wu C, Zhao F, Sachs MS, and Liu Y (2015). Codon usage influences the local rate of translation elongation to regulate co-translational protein folding. Molecular Cell, 59(5):744–754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zia RK, Dong J, and Schmittmann B (2011). Modeling translation in protein synthesis with TASEP: A tutorial and recent developments. Journal of Statistical Physics, 144(2):405–428. [Google Scholar]
- Zur H and Tuller T (2016). Predictive biophysical modeling and understanding of the dynamics of mrna translation and its evolution. Nucleic Acids Research, 44(19):9031–9049. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
This study did not generate new data. Code, including the code used to generate all figures, is publicly available at https://github.com/songlab-cal/l-TASEP.


