Repeatability of radiomics and machine learning for Diffusion Weighted Imaging: Short-term repeatability study of 112 patients with prostate cancer

Abstract

Purpose:

To evaluate repeatability of prostate DWI derived radiomics and machine leaning methods for prostate cancer (PCa) characterization.

Methods:

112 patients with diagnosed PCa underwent two prostate MRI examinations (Scan1 and Scan2) performed on the same day. DWI was performed using 12 b-values (0–2000 s/mm²), post-processed using kurtosis function and PCa areas were annotated using whole mount prostatectomy sections. 1694 radiomic features including Sobel, Kirch, Gradient, Zernike Moments, Gabor, Haralick, CoLIAGe, Haar wavelet coefficients, 3D analogue to Laws features, 2D contours and corner detectors, were calculated. Radiomics and four feature pruning methods (AUC, Maximum Relevance Minimum Redundancy (MRMR), Spearman ρ, Wilcoxon rank-sum) were evaluated in terms of Scan1-Scan2 repeatability using intraclass correlation coefficient, ICC(3,1). Classification performance for clinically significant and insignificant PCa with Gleason Grade Groups 1 vs >1 was evaluated by AUC in unseen random 30% data split.

Results:

The ICC(3,1) values for conventional radiomics and feature pruning methods were in the range of 0.28 to 0.90. The machine learning classifications varied between Scan1 and Scan2 with % of same class labels between Scan1 and Scan2 in the range of 61%−81%. Surface to volume ratio and corner detector based features were among the most represented features with high repeatability, ICC(3,1)>0.75, consistently high ranking using all four feature pruning methods, and classification performance with AUC>0.70.

Conclusion:

Surface to volume ratio and corner detectors for prostate DWI led to good classification of unseen data and performed similarly in Scan1 and Scan2 in contrast to multiple conventional radiomic features.

Introduction

Qualitative evaluation by means of visual inspection and interpretation of the medical images is a routine clinical practice, while image-derived measurements have been shown to be promising aides to a radiologist in lesion detection and characterization (1). During the last decade, radiomics (2–4) including textures and machine learning (ML) have been applied extensively in medical imaging in general (5–7). Adoption of these methods in routine clinical practice has been limited by concerns related to poor repeatability and reproducibility (8) due to different degree of noise in the imaging data sets obtained from different imaging sessions (9). An increasing number of research groups are applying radiomics for prostate cancer (PCa) imaging (10–18).

Prostate cancer is the most common solid cancer among men in the western world (19). Development of methods for accurate patient-tailored diagnostic process and treatment planning could have a major impact on improved PCa detection, characterization and treatment planning, ultimately leading to improved outcomes of men with suspected or diagnosed PCa. Diffusion weighted imaging (DWI) is a cornerstone of prostate magnetic resonance imaging (MRI) (20), which has an increasingly important role in PCa detection and characterization (21). Aggressiveness of PCa is histologically determined by Gleason Score which is classified into Gleason Grade Group (GGG) (22). Various radiomics and machine learning methods (ML) have already been developed for PCa detection and characterization e. g. (23,24). However, radiomics and ML methods have not been evaluated in terms of their repeatability, which contributes to reservations of making imaging applications that would use prostate MRI more extensively coupled with machine learning in routine clinical practice. High short-term repeatability is a prerequisite towards a quantitative tailored treatment planning and therapy monitoring, a major determining factor of the potential role of ML for prostate MRI in routine clinical practice in the future (25–28).

Repeatability of prostate DWI has been studied with measurements of raw signal (28–34) using intra-class correlation coefficient ICC(3,1) (35). In addition, repeatability of prostate DWI has already been assessed for advanced DWI models such as VERDICT model, which was evaluated (32) in 14 PCa patients who underwent two repeated prostate MRI examinations. Fedorov et al. (36) calculated ICC values for apparent diffusion coefficient maps calculated using mono-exponential function for tumor region in 15 PCa patients scanned with two different scanners. While differences in study subjects and applied MRI acquisition protocols of these studies make a direct comparison of ICC values difficult (37), these studies demonstrated that raw imaging signal and texture features can be repeatable (27). Recently, public access for prostate MRI of 15 subjects has been provided by Fedorov et al. (38). However, radiomic features for non-Gaussian DWI models (39–41) have not been evaluated in terms of short-term repeatability using the same scanner parameters.

While the area under the receiver operator characteristic curve (AUC) is conventionally used to evaluate binary classification performance for radiomic features, other techniques have been applied as well, particularly in conjunction with machine learning algorithms for PCa classification. In a study by Khalvati et al. (15), maximum relevance minimum redundancy (MRMR) (42) with classification sensitivity and specificity was used to maximize (AUC) in separation of prostate cancer from three non-cancer classes in 20 subjects, and MRMR was used together with Wilcoxon rank-sum test in (43). Spearman ρ value has already been used in feature selection process (44) as well. To the best of our knowledge, repeatability for feature selection and repeatability of machine learning has not been evaluated for prostate DWI.

In this study, we aim to answer three questions 1. How repeatable are DWI prostate radiomics? 2. Which features are to be considered to be both repeatable and with good performance? 3. How does repeatability affect machine learning performance in developing applications for PCa characterization? We evaluated radiomic features and feature selection methods, and trained classifier with machine learning using prostate DWI data, post-processed using kurtosis function. One-hundred-twelve patients with PCa underwent two MRI examinations performed on the same day. We evaluated the short-term repeatability of radiomics, feature selection methods and ML classifiers based on selected radiomics, for repeatability and PCa characterization.

Methods

The study was approved by the institutional review board and each patient gave written inform consent before enrollment to the study. Between March 2013 and February 2016, 115 patients with histologically confirmed PCa scheduled for robotic-assisted laparoscopic prostatectomy underwent MR examination performed using a 3T MR scanner (Ingenuity PET/MR, Philips, Cleveland, USA) and their whole mount prostatectomy sections were available for scientific studies. In one PCa patient, gonadotropin-releasing hormone antagonist (Degarelix, Ferring Pharmaceuticals) was started 10 days before the MR examination while none of the remaining patients had any hormonal, surgical and/or radiotherapy treatment related to prostate before or at the time of imaging.

Three patients were excluded from the final data set due to the presence of severe motion (n=1) and/or susceptibility artifacts (n=2). Patients’ characteristics of the 112 included patients are summarized in Supporting Information Table S1. 51 (45%) of the 112 included patients were part of previous studies optimizing b-value distributions for prostate DWI (29) and evaluating different mathematical models for PCa DWI (45–47).

MR examination

Two prostate MRI examinations (3 Tesla Philips Ingenuity PET/MR, Best, Netherlands) were performed on the same day shortly after each other. Following the first MRI examination, the patient was taken out of the MRI room and asked to rest for 10–15 minutes. Following re-positioning of the patient on the MR table, the second MR examination was performed.

Diffusion weighted imaging was performed with spin echo sequence, single-shot echo-planar read-out, monopolar diffusion gradient scheme, and the following parameters: repetition time/echo time (TR/TE) 3141 ms/51 ms, field of view (FOV) 250×250 mm², acquisition matrix 100×99, reconstruction matrix 224×224, slice thickness 5 mm, three diffusion directions per each b-value, diffusion gradient timing (Δ) 24.5 ms, diffusion gradient duration (δ) 12.6 ms, diffusion time (Δ − δ/3) 20.3 ms, 12 b-values of (number of signal averages) 0 (2), 100 (2), 300 (2), 500 (2) (2), 700 (2), 900 (2), 1100 (2), 1300 (2), 1500 (2), 1700 (3), 1900 (4), 2000 (4) s/mm². Transversal T₂-weighted images were acquired using a single-shot turbo spin-echo sequence with the following parameters: TR/TE 4668/130 ms, FOV 250×320 mm², acquisition matrix size 250×320, reconstruction matrix size 512×672, and slice thickness 2.5 mm. Additional MRI data were collected but not evaluated in the current study (48,49) since test-retest data for the additional MRI sequences were obtained only in a small sub-group of patients.

Histopathological analysis and cancer delineation on MRI

Following robotic-assisted laparoscopic prostatectomy, the prostate gland was fixed in formalin. The whole mount prostatectomy sections were processed at 5–6 mm intervals transversely in a plane perpendicular to the long axis of the prostate gland in a superior-inferior direction, similar to axial images of MRI (47,50). Four μm thick whole-mount sections from each macro-block were cut and stained with hematoxylin and eosin. Each individual tumor focus was graded separately based on International Society of Urological Pathology (ISUP) guidelines (22): Gleason Grade Group (GGG) 1 - Gleason score ≤ 3+3, GGG 2 - Gleason score 3+4, GGG 3 - Gleason score 4+3, GGG 4 - Gleason score 4+4/3+5/5+3, GGG 5 - Gleason score 4+5/5+4/5+5. Any Gleason pattern representing less than 5% of tumor volume was graded as tertiary grade (22). Only tumor foci >0.5 cm in diameter, defined using whole mount prostatectomy sections, were included in the analysis. The hematoxylin-eosin stained histological slides were first reviewed by one board certified staff pathologist and later re-reviewed by one experienced genitourinary pathologist. In case of disagreement between the two genitourinary pathologists, the opinion of a third genitourinary pathologist was asked for and consensus opinion was employed as the “ground truth” determination for diagnosis and grade.

Prostate cancer extent on each MRI acquisition (T2w, DWI) was manually delineated by one research fellow (8 years of prostate MRI experience) working in consensus with the genitourinary pathologist (8 years of prostate pathology experience), using whole mount prostatectomy sections as “ground truth”. Anatomical landmarks were used to align each MRI acquisition with mount prostatectomy sections.

Data analyses and modeling

Diffusion weighted imaging data sets were fitted using kurtosis function (34,47,51–53) to address potential non-Gaussian behavior when using high b-values in voxel-by-voxel basis, and apparent diffusion coefficient (ADCk) and kurtosity (K) maps were created. Broyden-Fletcher-Goldfarb-Shanno algorithm (54) was used to fit the kurtosis function to the DWI decay curve. Multiple initializations were used to minimize the possibility of local minima (29), and root mean squared error was used as the goodness of fit measure.

We applied a number of conventionally used feature extraction techniques (12,55) found in the literature such as Sobel (56), Kirch (57), Gradient magnitude, Zernike Moments (58), Gabor (59), Haralick (60), CoLlAGe (61), Haar wavelet coefficients (62) and Laws features (63) as texture methods. Additionally, features calculated with edge detector algorithms (64,65) and features derived from corner detectors were obtained.

First-order statistics were calculated (mean, standard deviation, median, range, 25th and 75th percentile) from ADCk and K signal intensities and included as part of feature extractions. Features relating to the shape of the lesion in 2D were acquired as curvature of level-set regions applied on transaxial slices of the ADCk and K parameter maps (referred here as 2D Curvature). Low and high-pass filters were implemented before extracting statistics from signal to evaluate the performance of other implemented feature extraction techniques in relation to simple noise filtering to the data.

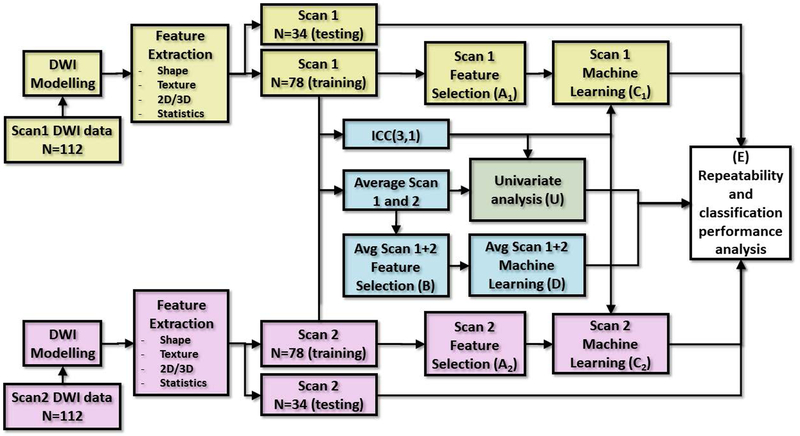
In order to utilize all three dimensions of the data, a three-dimensional version of Laws features was implemented (66). Shape feature of surface curvature (11,44) was extracted from 3D mesh after applying marching cubes algorithm to the binary lesion. All 3D feature extractions were preceded by resampling image data into isotropic voxel size. When applicable, all features were calculated from whole prostate, PCa lesions, and whole gland region excluding the lesion. Multiple parameters were applied to feature extraction algorithms where considered suitable. The feature extraction process was applied individually to first scan (Scan1), second scan within same day (Scan2), and using average feature value of two repetitions (see Fig. 1). In total, ADCk and K parametric maps were processed with 1694 features when statistics and different parameters were considered as separate features. The summary of applied features and number of features in their 18 respective groups is listed in Supporting Information Table S2.

Fig. 1:

Data flow of repeatability analysis for machine learning application using diffusion weighted imaging data of 112 patients with prostate cancer. The process for Scan1 and Scan2 is identical apart from data from acquisition time, containing DWI modelling, feature extraction and data split to training and testing sets. (A₁) and (A₂): Selection of features based on single repetition approach with Scan1 and Scan2, respectively. (B): Selection of features using average feature values of Scan1 and Scan2. (C₁), (C₂) and (D): Machine learning of classifier with single repetitions data Scan1, Scan2, and average of repetitions, respectively. (E): Final analysis of stability of trained classifiers and stability of final classifications. (U): Results of machine learning are compared to univariate analysis, including conventional DWI metrics.

Assessment of the repeatability of radiomics

Short-term repeatability was evaluated for individual radiomic features and machine learning classifiers with ICC, varying between [0..1], where 1 denotes perfectly repeatable individual measurement in relation to variation between subjects and scans, and 0 signifying no repeatability. While ICC values are not directly applicable to other related studies due to differences between subjects in other cohorts, it gives good estimates for comparing between features and between machine learning approaches within the same dataset. To study repeatability of classification between significant and insignificant PCa, the 112 patients were split randomly into 70–30% (as e. g. (44)) development-testing sets stratifying ratio of cases containing at least one lesion with GGG 1, as a trade-off between amount of training data and statistical power in final evaluations with test data. In test dataset 34 cases was considered sufficient to make reasonable performance estimations with unseen data, while rest of the subjects were left to training to make it possible to compare between numerous individual features, while able to apply machine learning. The full data flow of the experiment with radiomics applied to Scan1 and Scan2 in multivariate and univariate analysis, with and without help from information from ICC, is shown in Fig. 1.

Four conventionally used feature ranking methods were applied to reveal their effectiveness in terms of selecting features with high classification performance and repeatability:

1. Area under receiver operator characteristic curve (AUC) using leave-pair-out cross-validation (LPO-AUC) procedure to address for potential biases due to sample size (67) for estimating classification potential of individual features for differentiating PCa with GGG 1 vs >1. AUC is conventionally used as a performance metric for raw parameter map values of DWI models (15), giving expected classification potential between low and high groups.

2. Maximum Relevance Minimum Redundancy (MRMR) algorithm using GGG group 1–5 as target. MRMR is conventionally used as a feature pruning method and it considers also the correlation between variables within set of features, minimizing redundancy within chosen feature set.

3. Spearman correlation ρ between feature and GGG groups 1–5, which gives statistical test or non-linear association to all GGG, and used due to non-normality of used features.

4. Wilcoxon rank-sum test for classification of PCa with GGG 1 vs >1, with continuity correction. Like Spearman correlation, Wilcoxon rank-sum test is used as statistical test between low and high GGG groups in non-parametric manner.

Two of the feature ranking methods (LPO-AUC and Wilcoxon rank-sum test) are close to each other due to evaluating binary classification, while the other two (MRMR and Spearman) were applied to evaluate pruning of features when using more detailed information of the target variable GGG. All of the evaluated ranking methods have limitation of addressing signal noise only based on single repetition at hand. We evaluated the effect of refining the ranking method together with ICC values. In addition, we calculated the number of common features shared by selections from Scan1 and Scan2 and median(range) of ICC statistics of selected features.

Regularized least-squares (RLS) and ridge regression (68) were used to assess the classification potential of different multivariate radiomic procedures for differentiating PCa with GGG 1 vs >1 using selected features.

Machine learning and feature extraction techniques were implemented with publicly available tools in Python v. 2.7 and v. 3.6, using Meshlab (69) tool in 3D surface processing. Machine learning was implemented using the publicly available RLScore (version 0.8.1, https://github.com/aatapa/RLScore) with AUC (LPO-AUC) (67) when evaluating the number of used features (from 2 to 5), and regularization parameters (from 1.0⁻¹ to 1.0⁻⁶). Feature ranking criteria and statistical analyses were implemented using R (version 3.5.1, R Foundation for Statistical Computing, Vienna, Austria). Final comparison of radiomics performance was evaluated in testing set (51 lesions) in terms of agreement of their labeling (GGG 1 vs >1) between Scan1 and Scan2 (i. e. short-term labeling agreement), and AUC calculated with both scans using trapezoidal rule with 95% confidence interval (DeLong) to describe uncertainty in AUC measurements.

Overview of ROIs and DWI data sets (ADCk and K maps of the training data set) is provided at <<to be added upon acceptance of the manuscript>>. Free public access to post-processing code of most relevant features is provided at <<to be added upon acceptance of the manuscript>>. Imaging data sets are available for non-commercial development pending executed material transfer agreement.

Statistical analysis

We evaluated mutual agreement between feature pruning methods and repeatability of their rankings with Kendall’s W (70) having values from 0 (no agreement) to 1 (perfect agreement between rankings). Non-linear monotonic association between repeatability estimates ICC and feature rankings with averaged feature values over repetitions were tested with Spearman’s ρ test. We tested performance difference in terms of ICC and ranking values of AUC, MRMR, Spearman and Wilcoxon, with non-parametric Kruskal-Wallis test, followed by Wilcoxon post hoc test to see significance of differences between feature groups where p<3.27e-04 was considered statistically significant.

We also tested for difference of final classification potential AUC when classifier was trained with Scan1 and Scan2 data, between using top 10 features suggested by four pruning methods, and by using top 10 features after pre-excluding features not presenting repeatability with ICC>0.8. All tests were implemented with R (version 3.5.1), raw p-values were reported if found statistically significant with level p<0.05, unless otherwise noted.

Results

In total, 170 PCa lesions were present, of those (16%, 28/170), (45%, 77/170), (18%, 31/170), (17%, 29/170) and (3%, 5/170) tumors were to Gleason Grade Group (GGG) 1, 2, 3, 4, and 5, respectively. The training data sets (Fig. 1) consisted of 78 patients with 119 lesions, of those 17, 55, 22, 22 and 3 tumors were to GGG 1, 2, 3, 4, and 5, respectively. The testing data sets consisted of 34 patients with 51 lesions, of those 11, 22, 9, 7 and 2 tumors were to GGG 1, 2, 3, 4, and 5, respectively. The ICC of PCa lesion median intensity of the ADCk and K parameters was 0.786 (95%CI 0.784–0.789) and 0.780 (95%CI 0.778–0.783) in training set, and 0.889 (95%CI 0.887–0.891) and 0.857 (95%CI 0.855–0.860) in the testing set, correspondingly.

Classification Performance and Repeatability of Feature Groups

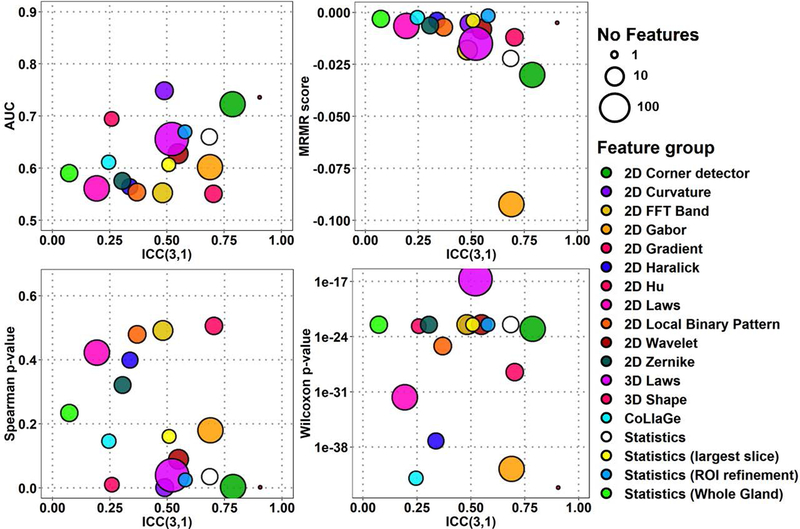
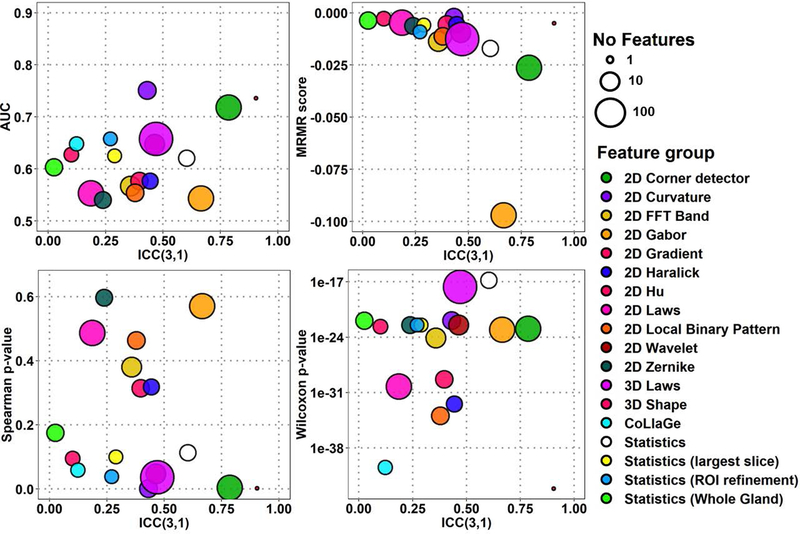
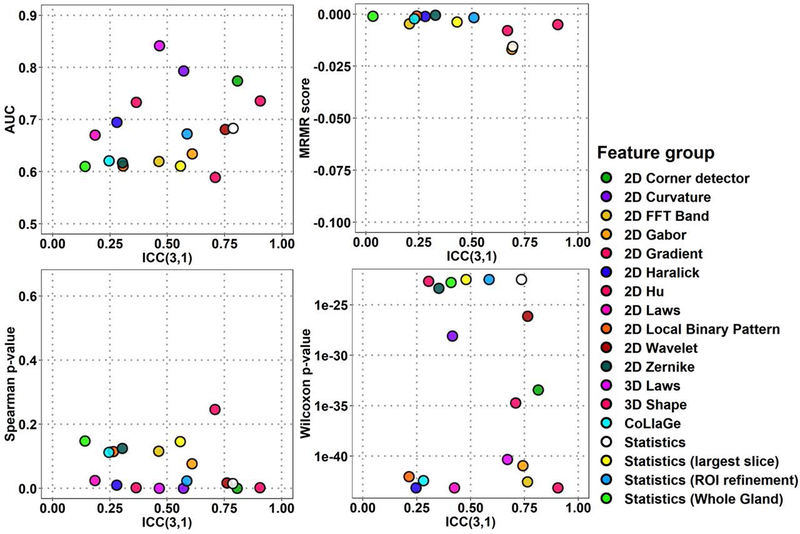
The classification performance and repeatability, ICC, of all 1694 radiomic features for median feature performance estimate values from Scan1 and Scan2 are presented in Fig. 2–3 for ADCk and K, performance of ten highest-ranking features in Fig. 4–5 of each of the 18 feature groups, and individual feature performance in Fig. 6–7. In Fig. 2–7, features with high repeatability but low classification performance in terms of AUC for GGG 1 vs >1 indicate that the feature contains a repeatable signal that is not useful for detection of PCa with GGG 1 vs >1, while these features might potentially still be useful due to their repeatability in other application. In contrast, features with low repeatability, together with high ranking, may contain more uncertainty in the ranking estimate itself. The corresponding plots for AUC, MRMR, Spearman ρ and Wilcoxon rank-sum methods are presented in Supporting Information Figures S1-S4 (ADCk) and S7-S10 (K). Feature group rankings with LPO-AUC and Spearman ρ demonstrated the biggest difference in their ranking of feature groups in comparison to other methods in Fig. 2–5, while differences between rankings were not found to be statistically significant (p>0.05).

Fig. 2:

Overall feature extraction scores of 1694 features in 18 feature groups, with four ranking methods and repeatability for ADCk (Apparent Diffusion Coefficient) of kurtosis function.

Fig. 3:

Overall feature extraction scores of 1694 features in 18 feature groups, with four ranking methods and repeatability for K (kurtosity) of kurtosis function.

Fig. 4:

Feature extraction rankings with four ranking methods and repeatability for top 10 features in each of 18 feature groups for ADCk (Apparent Diffusion Coefficient) of kurtosis function.

Fig. 5:

Feature extraction rankings with four ranking methods and repeatability for top 10 features in each of 18 feature groups for K (kurtosity) of kurtosis function.

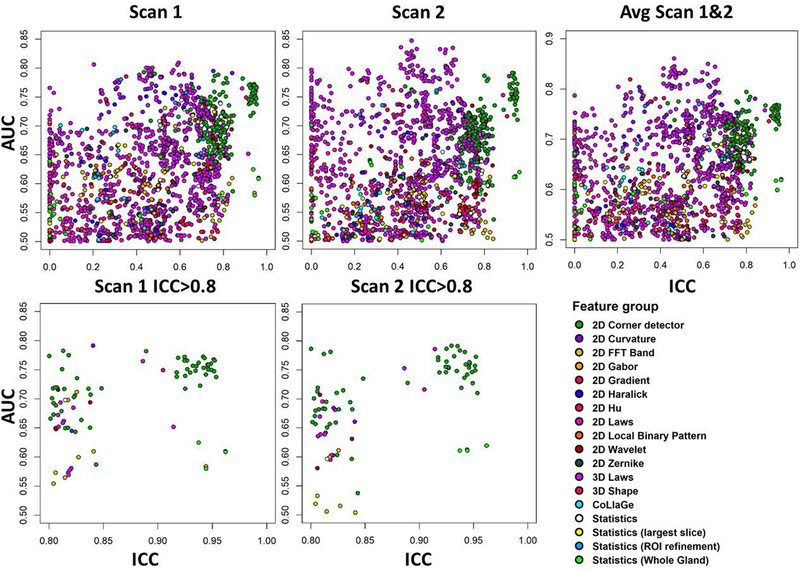
Fig. 6:

Classification performance for prostate cancer classification repeatability for 1694 features derived from ADCk (Apparent Diffusion Coefficient) of kurtosis function, using the area under receiver operator characteristic curve (AUC). The scatterplots show repeatability of radiomic features (x-axis) with respect to AUC (y-axis), for all features (top), and features having high repeatability only (ICC(3,1)>0.8, bottom). Measurements are from single DWI scan (Scan1 and Scan2) and when radiomic feature values are averaged (Avg Scan 1&2).

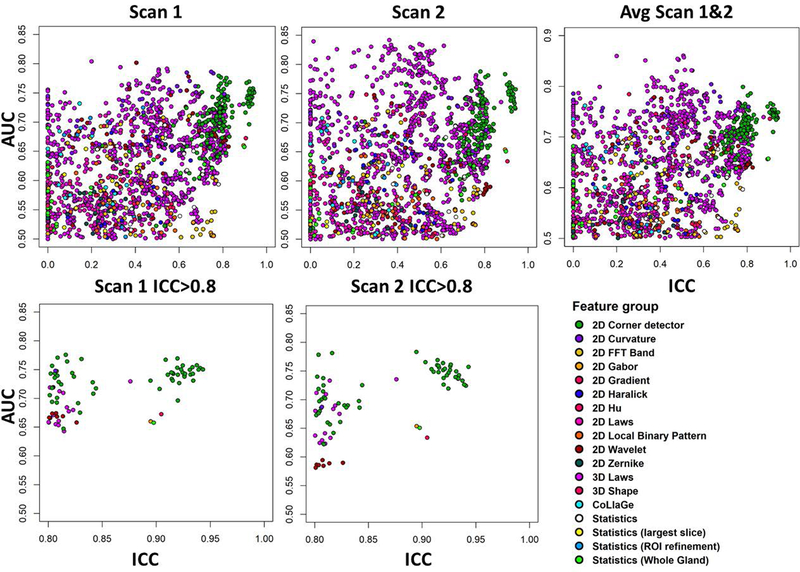
Fig. 7:

Classification performance for prostate cancer classification repeatability for 1694 features derived from K (kurtosity) of kurtosis function, using the area under receiver operator characteristic curve (AUC). The scatterplots show repeatability of radiomic features (x-axis) with respect to AUC (y-axis), for all features (top), and features having high repeatability only (ICC(3,1)>0.8, bottom). Measurements are from single DWI scan (Scan1 and Scan2) and when radiomic feature values are averaged (Avg Scan 1&2).

There were significant differences between ICC distributions of feature groups (Kruskal-Wallis p≤8.68e-11). A 3D Shape feature and 2D Corner detectors were found to be most repeatable groups in ADCk and K while their ICC difference was not found significant (p>0.05). With all features, 2D Corner detectors outperformed other feature groups in ADCk and K, except 3D Shape (p≤6.19e-05). Similarly, when only top 10 features were considered, 2D Corner detectors outperformed other feature groups (p≤3.0e-4) except five: 3D Shape, Statistics, Statistics (Whole Gland), 2D Wavelet and 2D FFT Band in ADCk, while no difference was found in K.

For performance estimates with all features (Fig. 2–3), in AUC estimates 2D Curvature features outperformed other feature groups except 3D Shape, 2D Corner detectors, 2D Hu and Statistics (ROI Refinement) in ADCk, and in K, 3D Shape and 2D Hu (p≤7.04e-06). Best performing feature group was less prominent with MRMR ranking as in ADCk, 2D Hu had higher scores than 2D Corner detectors and 2D Gabor (p≤2.93e-04), while in K, CoLlaGe features had higher score than 2D Local Binary Pattern, 3D Laws, 3D FFT Band, Statistics, 2D Corner Detector and 2D Gabor (p≤8.14e-06). CoLlaGe was found second best feature group after 3D Shape feature in Wilcoxon test based rankings, with significant difference only to 2D Wavelets and 3D Laws in ADCk, and to 3D Laws in K, while no other major differences were between two best groups to the others. Similar to AUC, 2D Curvature features had highest ranking with Spearman method, with significant difference to all other groups except 3D Shape feature, 2D Corner detectors, 2D Hu, Statistics (ROI Refinement) in ADCk, to all other groups except 3D Shape feature and 2D Hu in K.

Considering only six feature groups with highest ICC (see above), with top 10 features (Fig. 4–5) according to AUC ranking, 2D Corner detectors again outperformed all other feature groups except 3D Shape feature (p≤1.8e-04) with AUC=0.749 (95%CI 0.611..0.887) in ADCk, and all (p≤0.00167) except 3D Shape feature (p=0.154) and 2D Wavelets (p=0.00726) in K. In MRMR estimates, 2D Corner detector was considered significantly better only to Statistics, in ADCk and K (p≤7.15e-05). According to Spearman method rankings, 2D Corner detector was significantly better than Statistics (Whole Gland), 2D Wavelets and 2D FFT Band (p≤1.08e-5) in ADCk, while differences were not significant in K (p≥9.99e-4). Finally, with Wilcoxon performance estimate, 2D Corner detectors were ranked higher than 2D Wavelet, Statistics and Statistics (Whole Gland) (p≤1.6e-04) in ADCk, and Statistics in K (p≤1.7e-04).

Notably, conventionally used statistics from raw intensity values (Statistics, Statistics (Whole Gland), Statistics (ROI Refinements)) and naïve frequency-based filtering approaches (2D FFT Band) were shown to have good repeatability, in comparison to some texture features. Feature group of Statistics (i. e. basic statistics inside lesion), had better ICC than 2D Local Binary pattern, 2D Haralick, 2D Zernike, 2D Hu, CoLlaGe and 2D Laws features, although not found statistically significant (p≥1.3e-03) in ADCk and significantly better ICC in K than CoLlaGe features (p=4.33e-05). In overall terms, 2D Corner detectors and 3D Laws features provided good repeatability together with four performance metrics.

Repeatability Analysis of Feature Ranking Methods with Individual Features

There was a moderate negative association between ICC and MRMR rankings of Scan1, Scan2, and averaged features values in ADCk and K with Spearman ρ from −0.579 to −0.494 (all p≤1.08e-104). Correspondingly, rankings of Spearman and AUC had weak association with ρ from −0.358 to −0.158 (all p≤6.310e-11) and ρ from 0.173 to 0.360 (all p≤9.279e-13) in ADCk and K. Wilcoxon feature pruning method had very weak association with ρ from −0.168 to −0.150 (all p≤6.753e-10) in ADCk, while no significant association was found in K (p>0.05).

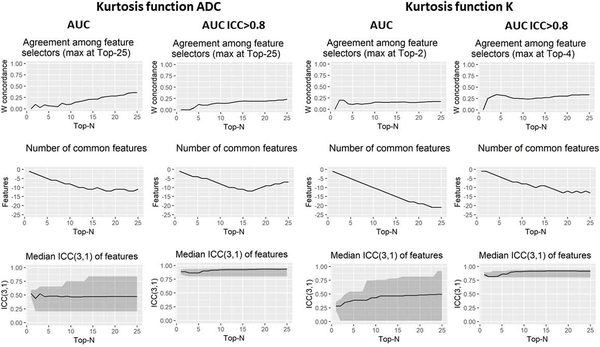
Three repeatability metrics of agreement between selected features over repetitions, number of common features, and ICC of selected features, are shown for taking best features ranging from top 2 to top 25 features in Fig. 8 for AUC as feature pruning method. All of the three metrics showed improvement when inclusion criteria of high ICC features were applied for AUC, and similarly for MRM, Spearman and Wilcoxon as feature pruning methods (see supporting information figures). MRMR and Wilcoxon feature pruning methods demonstrated significant agreement (Kendall’s W) between Scan1 and Scan2 in ADCk (p=0.030 and p= 1.469e-11) and K (p=0.045 and p=1.104e-11) and with Wilcoxon method when only ICC>0.8 was considered (p=0.041).

Fig. 8:

AUC feature selection associations with repeatability using ADC (Apparent Diffusion Coefficient) and K (kurtosity) of kurtosis function with and without pre-selection of highly repeatable (ICC(3,1)>0.8) features.

For averaged feature values, AUC was found to give concordant ranking with Wilcoxon (p=0.036) in ADCk, while other agreements between rankings were not considered statistically significant (p>0.05). Similar to analysis with overall feature groups, among highly repeatable features having also adequate AUC, most represented feature groups in Scan1 and Scan2 among top 10 selected features was 3D Laws in ADCk (60%) and in K (51.25%). 2D Corner detector features were most represented feature group when ICC>0.8 inclusion criteria was applied in ADCk (60%) and in K (76.25%). Also with ICC>0.8, 2D Corner detectors was the most represented feature group in all individual feature ranking methods in ADCk and K, except in Wilcoxon method, having 2D FFT Band (50%), 2D Corner detector (20%) and 3D Laws (20%).

Repeatability Analysis of Machine Learning

Repeatability analysis of ADCk parameter alone and combined ADCk and K are given in Table 1 and Table 2. Generally, the four ranking methods gave high rank to features which were fairly repeatable (Table 1, column C), while MRMR gave high ranking to features with low repeatability, resulting in selection of feature sets that had poor repeatability values. The final classification performance was not found to be significantly different between the four feature pruning methods (p>0.05). Classification labels (GGG 1 vs >1) varied between classifier trained with Scan1 and Scan2 (column F), meaning that classifiers labeled different cases in the test set to positive and negative depending on which repetition was used in training. There was a small variation between AUC estimates in the test Scan1 and Scan2 with largest difference of 0.07 with LPO-AUC and Spearman ρ in Table 2, while the differences were not found to be statistically significant (p>0.05). When additional information from repeatability was included (pre-inclusion of only features with high repeatability ICC>0.8), the selected feature sets were generally more consistent and labeling of classifiers trained with either Scan1 and Scan2 were in better agreement, particularly in Spearman ρ method.

Table 1:

Stability of machine learning results calculated independently in test (Scan1) and retest (Scan2) scans. (A) Feature pruning method. (B) Selection of 10 best ranking features according to pruning method. (C) Median and range of repeatability of features used in classifier training. (D) Agreement of binary classifications from classifiers trained with Scan1 and Scan2 data. (E) Area Under Receiver operator characteristic curve (AUC) when classifications are evaluated with Scan1 of test set. (F) AUC with Scan2. (G) Pooled estimate over Scan1 and Scan2 for AUC.

Pruning method (A)	Pruned features (B)	ICC median (range) (C)	% of same labels (D)	AUC (95% CI) Scan1 (E)	AUC (95% CI) Scan 2 (F)	AUC (95% CI) Scan 1 and 2 (G)
Wilcoxon rank-sum test	ADCk Top 10	0.438(0.000..0.953) 0.280(0.000..0.693)	80.4	0.682 (0.490..0.873)	0.495 (0.261..0.730)	0.586 (0.436..0.737)
MRMR	ADCk Top 10	0.296(0.000..0.813) 0.233(0.000..0.621)	70.6	0.673 (0.469..0.876)	0.630 (0.438..0.821)	0.649 (0.514..0.785)
Spearman ρ	ADCk Top 10	0.471(0.445..0.754) 0.476(0.414..0.654)	70.6	0.743 (0.558..0.928)	0.645 (0.465..0.826)	0.691 (0.563..0.819)
AUC	ADCk Top 10	0.471(0.445..0.754) 0.476(0.414..0.654)	70.6	0.743 (0.558..0.928)	0.645 (0.465..0.826)	0.691 (0.563..0.819)
Wilcoxon rank-sum test	ADCk ICC>0.8 & Top 10	0.823(0.804..0.953) 0.823(0.804..0.953)	84.3	0.783 (0.637..0.929)	0.750 (0.592..0.908)	0.770 (0.664..0.875)
MRMR	ADCk ICC>0.8 & Top 10	0.888(0.808..0.962) 0.836(0.800..0.962)	74.5	0.727 (0.538..0.916)	0.732 (0.566..0.897)	0.730 (0.607..0.852)
Spearman ρ	ADCk ICC>0.8 & Top 10	0.904(0.800..0.951) 0.927(0.800..0.942)	72.5	0.686 (0.503..0.870)	0.723 (0.566..0.880)	0.706 (0.589..0.822)
AUC	ADCk ICC>0.8 & Top 10	0.904(0.800..0.951) 0.927(0.800..0.942)	72.5	0.686 (0.503..0.870)	0.723 (0.566..0.880)	0.706 (0.589..0.822)

Table 2:

Stability and performance of machine learning optimizing repeatability using average of feature values extracted from prostate DWI with four feature ranking methods. The 95% confidence intervals are shown in parenthesis. Rows 1–4: Agreement between classifications and performance for Gleason Grade Group (GGG) 1 vs >1 classification. Rows 5–8: Agreement between classifications and performance for GGG 1,2 vs >2.

Feature ranking method	Pruned features	% of same labels	AUC (95% CI) Scan1	AUC (95% CI) Scan 2	AUC (95% CI) Scan 1 and 2
Wilcoxon rank-sum test	ADCk & K ICC>0.8 & Top 10	60.8	0.780 (0.607..0.952)	0.757 (0.572..0.942)	0.765 (0.640..0.890)
MRMR	ADCk & K ICC>0.8 & Top 10	80.4	0.781 (0.601..0.960)	0.725 (0.560..0.890)	0.747 (0.629..0.866)
Spearman ρ	ADCk & K ICC>0.8 & Top 10	72.5	0.686 (0.503..0.870)	0.723 (0.566..0.880)	0.706 (0.589..0.822)
AUC	ADCk & K ICC>0.8 & Top 10	64.7	0.782 (0.601..0.962)	0.709 (0.548..0.870)	0.743 (0.623..0.863)
Wilcoxon rank-sum test	ADCk & K ICC>0.8 & Top 10	72.5	0.705 (0.530..0.879)	0.791 (0.600..0.981)	0.745 (0.620..0.870)
MRMR	ADCk & K ICC>0.8 & Top 10	66.7	0.734 (0.550..0.918)	0.745 (0.557..0.934)	0.732 (0.606..0.858)
Spearman ρ	ADCk & K ICC>0.8 & Top 10	62.7	0.745 (0.551..0.940)	0.734 (0.563..0.905)	0.738 (0.613..0.863)
AUC	ADCk & K ICC>0.8 & Top 10	62.7	0.745 (0.551..0.940)	0.734 (0.563..0.905)	0.738 (0.613..0.863)

The performance of machine learning when feature extraction signal was pooled together from both parameters ADCk and K (top 5 from ADCk and top 5 from K) of kurtosis function is shown in Table 2. The difference in AUC between Scan1 and Scan2 of testing set, suggesting that the four applied feature ranking methods still contained unaddressed noise which further propagated as fitting model with a suboptimal group of features. In comparison to reference method of taking ADCk or K median value (0.63 and 0.68) inside the lesion, individual features as representatives of univariate models improved the classification, and RLS classifier gave performance estimate up to 0.77, and same feature sets resulted up to 0.75 for classification of GGG 1 and 2 vs >2.

Discussion

Radiomics including textures and shape feature, and ML methods hold promise for improved patient’s care by introducing objective optimized medical image evaluation. Performance of radiomics is often evaluated in terms of AUC. Despite an exponentially increasing number of studies using radiomics and ML in medical imaging, only a handful of these studies evaluated the repeatability and reproducible of these methods (8), and uncertainty of given AUC classification estimate is rarely given. Although in the current study the found differences in machine learning classifications were not found statistically significant, we observed improvement in both reliability and performance of final classifications between GGG 1 and >1, when repeatability of features was taken into account in DWI radiomic feature selection (Table 1) and in classifier training (Table 2), having AUC=0.77 (0.64..0.89) similar to study by Starmans et al. (71) with 40 subjects. Further, we observed significant differences between repeatability values of the feature groups, suggesting of using most repeatable features.

In the current study, we evaluated short-term repeatability and diagnostic performance of commonly used radiomics together with machine learning for PCa classification using DWI obtained with 12 b-values up to 2000 s/mm². Some of the conventional radiomics such as texture methods demonstrated high AUC but low repeatability, stressing the fact that high classification potential in training set does not necessarily mean good overall performance, specifically for classifying PCa between GGG 1 vs >1. Therefore, features with low repeatability but high classification performance for PCa classification should be considered with caution, as the feature may turn out to have poor short-term repeatability, while high short-term repeatability is needed for practical application of them in non-invasive PCa detection, characterization, therapy planning, and therapy monitory (5).

A number of factors affect the performance of radiomic features. For example, statistical descriptors can be particularly sensitive to the intensity of the image. Texture features of DWI, among other radiomic features, have already demonstrated some promise for PCa detection and management, e. g. (23,24). However, a large variation in radiomics performance has been observed in multi-institutional studies (5). Texture features find texture patterns from the image and are less dependent on the intensity than statistical descriptors, but are sensitive to voxel level variations. Shape features (11,27) can rely partially or solely on the human delineation, and as such are expected to be more robust against voxel level intensity variations within and between images. In agreement of our findings, surface-to-area ratio has been shown to perform well for the detection of clinically significant PCa (11). In a small study of 8 women with cervical cancer who underwent test–retest MRI, shape features and topological features demonstrated high repeatability (72) similar to the current study. Surface-to-area ratio has limitation of not incorporating information from absolute values of ADCk and K parameter maps which are known to correlate with PCa (46). However, their potential use may partially be in combination with other radiomic features.

Prostate MRI radiomic features as imaging-based markers are typically evaluated based on AUC values for PCa detection/characterization. Repeatability (same scanner/protocol) and reproducibility (different scanner/protocol) of radiomics and ML for prostate DWI in the same patients have not been evaluated so far. A study by Chirra et al. (73) evaluated external reproducibility of radiomics derived from prostate T2-weighted imaging but repeatability and reproducibility of radiomics and ML for prostate DWI in the same patients with PCa has not been evaluated. We found that the repeatability of the selected features was dependent on the applied feature ranking method. This may be due to all of the evaluated selection techniques focusing on metrics with which repeatability varies independently. We speculate that the within-subject variability propagates to the feature selection metrics, causing subsequently changes in the feature ranking order, depending on robustness of ranking methods. As the evaluated methods use only one repetition, they can potentially provide only indirect assessments of within-subject variations. We did not find any of the evaluated performance estimation methods to be considered as candidates for estimating repeatability, suggesting that to address repeatability, other means would need to be used, such as repeated scans. While we stress importance of direct measurements for repeatability, we suggest using Wilcoxon rank-sum test as feature selection criteria due to most consistent feature selections between repetitions. With our evaluated features using more top-ranking features caused the overall repeatability of feature selection to diminish. Thus, no warrant is given for blindly taking, for example, the top 10 of the best ranked features without knowledge of the repeatability of the feature selection process itself (Fig. 5). Careful optimization of radiomic parameters and feature ranking methods are needed to achieve both high diagnostic performance for PCa characterization as well as reliable labeling for clinical use.

This study has multiple limitations. We did not correct for possible correlation between multiple tumors in individual PCa patients. In 46 (41%, 46/112) patients, more than one PCa lesion was present. We focused on short-term repeatability of features extracted from the data and derived machine learning for practical application of separating GGG groups from each other. While most of the features have intuitive biophysical explanation such as shape or larger scale density variation in the tissue (textures, gradient methods) we did not perform separate evaluations for how well the radiomic features would correspond to histology. It is to be noted that repeatability and reproducibility of radiomic feature are additional requirements to good classification performance together with correspondence to histology. We addressed classification between significant and insignificant PCa, due to significant implication on patient’s management. Classification to other GGG is left for future work. Modeling of PCa DWI signal decay is most commonly performed using the mono-exponential model. However, kurtosis function has higher information content (fitting quality), similar repeatability, and robustness against noise (45–47), thus kurtosis function was used in the current study (39). Future studies are needed to evaluate the performance of radiomics derived using different function/models for prostate DWI. While we used kurtosis function to addresses the deviation of DWI signal decay at high b-values, it is important to stress that our results may still be influenced by the DWI acquisition parameters, such as TE, b-values (12 b-values in the range from 0 to 2000 s/mm²) and diffusion time (20.3 ms).

While we consider the applied features in this study to be a good representation of techniques given in related literature with all main types of features, the list does not consider all possibilities, and only one classifier was used in evaluations. Prostate cancer lesions on DWI data were manually delineated by one research fellow working in consensus with the genitourinary pathologist, using whole mount prostatectomy sections as “ground truth”. Other modalities besides DWI were not considered and it is left for future studies to explore effects of additional MRI sequences. Future studies are needed to evaluate the performance of calculated features using fully automatic tools for lesion delineation, as semi or fully automatic tool for ROI definition could be used in conjunction with feature selection methods in radiomics. Noting that only well repeatable features are to be expected to have link to underlying pathology, more detailed biophysical explanation of those features is left for future study. Although to best of our knowledge, the number of repeated DWI scans and radiomic features was the largest for evaluating short-term repeatability of prostate MRI derived features (38), it could be argued that the study is still limited by its sample size.

Conclusion

In this study, we have shown that: 1. Only a fraction of radiomics from ADCk and K had high repeatability, ICC(3,1)>0.8; 2. Shape and 2D Corner detector-based features were among the most represented features with high repeatability, ICC(3,1)>0.75 and high classification performance, AUC>0.70; 3. The applied feature selection method did have an a major effect on repeatability, ICC(3,1), and final classification performance, AUC, while the difference did not reach the level of statistical significance; 4. Although none of the feature selection methods selected the most repeatable features, Wilcoxon rank-sum test as feature selection criteria was found to be most consistent between repetitions. We demonstrated that radiomic features and ML methods should be addressed with caution if only single scan data are available and repeatability is unknown, and that repeatability improved performance in unseen data in terms of both absolute performance and stability of classifications between test and retest scan of unseen data.

Supplementary Material

Supp info

Supporting Information Figure S1: Selection of features extracted from Diffusion Weighted Imaging using ADC of kurtosis function. Feature performance with AUC against repeatability for Scan1 and Scan2 (left) and average of feature values (right). Plots describing stability of feature selection between Scan1 and Scan2 (middle) show Kendall’s W concordance of feature sets when top features from 1 to 25 are selected according to their AUC (top), number of common selected features (middle) and median of all selected features from both scans (bottom).

Supporting Information Figure S2: Selection of features extracted from Diffusion Weighted Imaging using ADC of kurtosis function. Feature performance with Maximum Relevance Minimum Redundancy scores against repeatability for Scan1 and Scan2 (left) and average of feature values (right). Plots describing stability of feature selection between Scan1 and Scan2 (middle) show Kendall’s W concordance of feature sets when top features from 1 to 25 are selected according to their score (top), number of common selected features (middle) and median (range) of all selected features from both scans (bottom).

Supporting Information Figure S3: Selection of features extracted from Diffusion Weighted Imaging using ADC of kurtosis function. Feature performance with Spearman Rho’s p-value against repeatability for Scan1 and Scan2 (left) and average of feature values (right). Plots describing stability of feature selection between Scan1 and Scan2 (middle) show Kendall’s W concordance of feature sets when top features from 1 to 25 are selected according to their p-value (top), number of common selected features (middle) and median (range) of all selected features from both scans (bottom).

Supporting Information Figure S4: Selection of features extracted from Diffusion Weighted Imaging using ADC of kurtosis function. Feature performance with Wilcoxon rank-sum test p-value against repeatability for Scan1 and Scan2 (left) and average of feature values (right). Plots describing stability of feature selection between Scan1 and Scan2 (middle) show Kendall’s W concordance of feature sets when top features from 1 to 25 are selected according to their p-value (top), number of common selected features (middle) and median (range) of all selected features from both scans (bottom).

Supporting Information Figure S5: Selection of features extracted from Diffusion Weighted Imaging using ADC of kurtosis function, show Kendall’s W concordance of feature sets when top features from 1 to 25 are selected according to their p-value (top), number of common selected features (middle) and median (range) of all selected features from both scans (bottom).

Supporting Information Figure S6: Stability of feature selection approaches using ADC of kurtosis function, when only highly repeatable (ICC(3,1)>0.8) features are pre-selected, show Kendall’s W concordance of feature sets when top features from 1 to 25 are selected according to their p-value (top), number of common selected features (middle) and median (range) of all selected features from both scans (bottom).

Supporting Information Figure S7: Selection of features extracted from Diffusion Weighted Imaging using kurtosity of kurtosis function. Feature performance with AUC against repeatability for Scan1 and Scan2 (left) and average of feature values (right). Plots describing stability of feature selection between Scan1 and Scan2 (middle) show Kendall’s W concordance of feature sets when top features from 1 to 25 are selected according to their AUC (top), number of common selected features (middle) and median of all selected features from both scans (bottom).

Supporting Information Figure S8: Selection of features extracted from Diffusion Weighted Imaging using ADC of kurtosity function. Feature performance with Maximum Relevance Minimum Redundancy scores against repeatability for Scan1 and Scan2 (left) and average of feature values (right). Plots describing stability of feature selection between Scan1 and Scan2 (middle) show Kendall’s W concordance of feature sets when top features from 1 to 25 are selected according to their score (top), number of common selected features (middle) and median (range) of all selected features from both scans (bottom).

Supporting Information Figure S9: Selection of features extracted from Diffusion Weighted Imaging using kurtosity of kurtosis function. Feature performance with Spearman Rho’s p-value against repeatability for Scan1 and Scan2 (left) and average of feature values (right). Plots describing stability of feature selection between Scan1 and Scan2 (middle) show Kendall’s W concordance of feature sets when top features from 1 to 25 are selected according to their p-value (top), number of common selected features (middle) and median (range) of all selected features from both scans (bottom).

Supporting Information Figure S10: Selection of features extracted from Diffusion Weighted Imaging using kurtosity of kurtosis function. Feature performance with Wilcoxon rank-sum p-value against repeatability for Scan1 and Scan2 (left) and average of feature values (right). Plots describing stability of feature selection between Scan1 and Scan2 (middle) show Kendall’s W concordance of feature sets when top features from 1 to 25 are selected according to their p-value (top), number of common selected features (middle) and median (range) of all selected features from both scans (bottom).

Supporting Information Figure S11: Selection of features extracted from Diffusion Weighted Imaging using kurtosity of kurtosis function, show Kendall’s W concordance of feature sets when top features from 1 to 25 are selected according to their p-value (top), number of common selected features (middle) and median (range) of all selected features from both scans (bottom).

Supporting Information Figure S12: Stability of feature selection approaches using kurtosity of kurtosis function, when only highly repeatable (ICC(3,1)>0.8) features are pre-selected, show Kendall’s W concordance of feature sets when top features from 1 to 25 are selected according to their p-value (top), number of common selected features (middle) and median (range) of all selected features from both scans (bottom).

Supporting Information Table S1

Patients’ characteristics

Supporting Information Table S2

Features used in this study grouped by their most essential characteristics.