X-ray Emission Spectroscopy at X-ray Free Electron Lasers: Limits to Observation of the Classical Spectroscopic Response for Electronic Structure Analysis

Abstract

X-ray free electron lasers (XFELs) provide ultrashort intense X-ray pulses suitable to probe electron dynamics, but can also induce a multitude of nonlinear excitation processes. These affect spectroscopic measurements and interpretation, particularly for upcoming brighter XFELs. Here we elaborate on the limits to observing classical spectroscopy, where only one photon is absorbed per atom for a Mn²⁺ in a light element (O, C, H) environment. X-ray emission spectroscopy (XES) with different incident photon energies, pulse intensities, and pulse durations is presented. A rate equation model based on sequential ionization and relaxation events is used to calculate populations of multiply ionized states during a single pulse and to explain the X-ray induced spectral lines shifts. This model provides easy estimation of spectral shifts, which is essential for experimental designs at XFELs, and illustrates that shorter X-ray pulses will not overcome sequential ionization but can reduce electron cascade effects.

Graphical Abstract

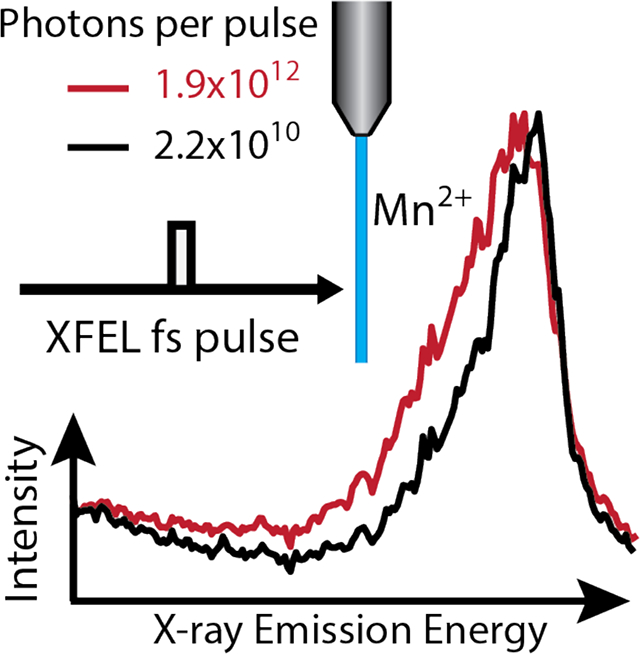
With the development of X-ray free electron laser (XFEL) sources there has been a paradigm shift in X-ray scattering and spectroscopy studies for physics, chemistry, biology and material sciences. With shorter (10–100 fs), more energetic (~10¹² photons) pulses, scientist can now study the atomic structure of nanocrystals¹, small molecules² and envision obtaining atomic resolution images for large single particles.³ Ultrashort pulses also enable X-ray spectroscopic studies of chemical reactions with sub-picosecond resolution^4–6, revealing fundamental transitions such as electron transfer and bond formation dynamics.⁷

While the X-ray community has been invigorated by these new opportunities, further research is required to understand the fundamental changes in the electronic structure of atoms due to the interaction with ultrashort (<100fs), intense X-ray pulses. In this regime, non-linear effects^8–11 become significant as they distort electron energy levels and create new excited states.^12–13 While there is limited understanding of how these modified electronic configurations can influence X-ray diffraction results or the single particle scattering analysis planned at future sources, X-ray spectroscopy can clearly be affected by the formation of electronic states beyond the one electron excitations typically analyzed at synchrotron sources, Figure 1. Understanding these effects will aid the development of the proper experimental protocols and interpretation of electronic structure measurements depending on time scales and intensities of the utilized X-ray pulses.

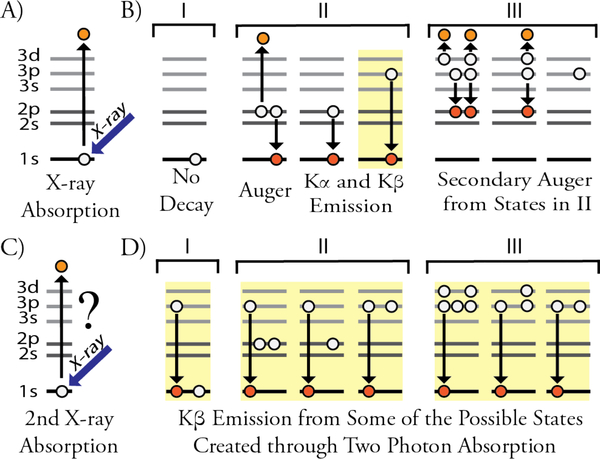
Figure 1.

Sequential ionization steps of the Mn²⁺ ion exposed to an intense X-ray pulse. Highlighted in yellow are the recorded emission processes. A) X-ray absorption creating a hole in the 1s orbital, B) possible electronic states obtained on different time scales: I) no decay, II) 1s hole is filled, and III) 2s and 2p holes are filled, C) a second 1s hole is create and D) subsequent decay (only Kβ shown) in the presence of various electronic configurations shown in Part B which alter spectral positions. Note that Auger processes can create a variety of different states in II and III that are not shown.”

Here ions of a 3d transition metal (Mn²⁺) in a lighter element (O, C, H) environment are used as a model system for 3d transition metals in general and for the biologically relevant Mn₄Ca cluster inside photosystem II¹⁴ in particular. Radiation induced damage to Mn centers in photosystem II at a synchrotron source is caused by chemical interaction of oxidized Mn ions with reactive species such as photoelectrons and OH radicals.¹⁵ As these damaging mechanisms require time for chemical redox processes to take place, they can be largely outrun at fs XFEL sources.^16–19 However, the two other major sources of electronic changes are sequential X-ray absorption by a single atom, Figure 1, and secondary ionizations caused by released photoelectrons and Auger electrons.^20–23 While these effects have been observed at XFELs previously, it remains unclear to what extent multiple ionization effects may impact interpretation of spectroscopic or crystallographic data.

Here effects of the intensity and duration of the XEFL pulse on the electronic structure of Mn ions was analyzed by X-ray emission spectroscopy (XES), Figure 2. The Kβ mainline emission spectrum is a result of the 3p to 1s transitions after a 1s core hole is created, Figure 1B–II. The exchange interaction between the newly created 3p hole and the valence electrons on the Mn 3d level leads to two spectral features with splitting sensitive to the oxidation state and spin state of Mn.^24–27 XES in conjunction with XFEL pulses, is used to probe fast dynamics, dilute samples and new electronic states including surface chemistry⁴, solvent shell dynamics²⁸, and electron transfer²⁹. However, all these applications require collection of the classical (or singly ionized) spectra for proper interpretation.

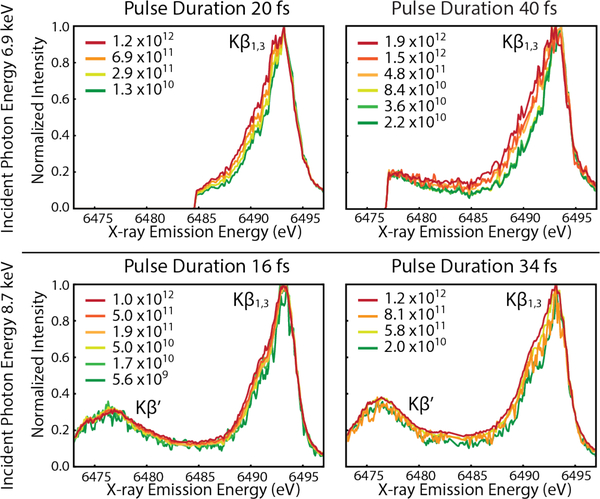
Figure 2.

Mn Kβ spectra recorded with varying photons per pulse colored green to red for increasing values. Different excitation energies (top: 6.9 keV and bottom: 8.7 keV), pulse intensity and pulse duration are also shown. Kβ’ region is only available in lower graphs due to differences in spectrometer positioning inside the vacuum chamber. Broadening of the low energy side of the Kβ_1,3 line with increased pulse intensity is visible.”

Here XES is used to monitor emission from atoms absorbing one or more X-rays, where multiple ionizations induces changes to the spectra for 3d transition metal in low-Z (O, C, N) environments, such as photosystem II. The Mn Kβ XES spectra recorded from Mn²⁺ ions (jetted 1 Molar MnCl₂ in H₂O or ethanol, see SI Methods) are shown in Figure 2. Each panel represents one of four different XFEL pulse configurations recorded: 20 fs and 40 fs pulse durations using 6.9 keV incident photon energy and 16 fs and 34 fs at 8.7 keV incident photon energy. For each pulse configuration, the Mn Kβ_1,3 peak shifts to lower energy as a function of pulse intensity. The onset of electronic structure changes in the Mn ion recorded using XFEL pulses creates a different XES spectra from the low flux regime, where only one X-ray is absorbed per atom, as Figures 1 & 2 illustrate.

To address the spectral shape change induced by sequential ionization we used theoretical modeling of electronic states obtained during a single XFEL pulse using rate equations^{20–21, 30} shown schematically in Figure 3A. The initial population starts in the ground state, $S_0^0$, as Mn²⁺ with no 1s holes. During X-ray exposure the Mn atom will populate the different states labelled as $S_k^j$ where j is the current number of 1s holes in the atom (maximum of two) and k shows the total number of 1s absorption events the atom has undergone. Any atom in a specific state can advance forward through ionization of a 1s electron. The rate for this process, or absorption rate, is written as

$$A^j=\mathrm{\Phi }{\sigma }^j$$

where Φ is the photon flux density, or photons per area per time, and σ^j is the atomic photoelectric cross section for the 1s orbital with j holes in the same orbital. The atom can also go to a lower j state, downward in Figure 3A, by filling a 1s hole through Auger decay or fluorescence. These effects combined form the decay rate, $D_k^j$, where j and k represent the state from which the decay occurs. The decay rate, the probability of Kβ emission, and the 1s cross sections were calculated using XATOM which has been described in detail elsewhere.^{23, 31–32} The beam profile was also assumed to be Gaussian making Φ radially dependent. The photon flux density was approximated stepwise to capture this dependence in the model as described in the SI Methods section.

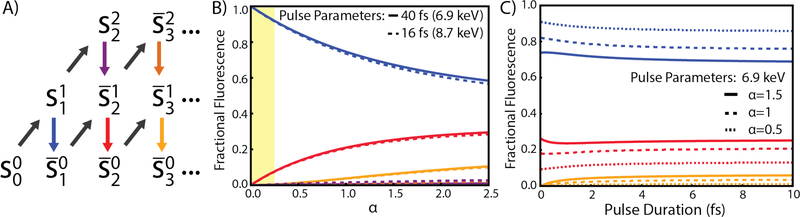
Figure 3.

A) The rate equation model with each state, S, labeled by the number of 1s holes (super script) and total 1s absorption events (subscript) and the bar above indicates that there are multiple electronic configurations in this state. Arrows going up indicate 1s absorption and arrows down are electronic relaxation filling a 1s hole. Colors are referenced to differentiate Kβ emission from different states with blue representing classical emission. B) The contributions to the total Kβ fluorescence based on decay from five different states with colors matching those in A) with an approximately linear regime is highlighted in yellow. C) The contributions to the total recorded Kβ fluorescence as a function of pulse duration.”

Using this model the fractional population of Mn centers that has absorbed at least one X-ray, i.e. no longer in the $S_0^0$ state, is

$$P_{abs}=1-e^{-A^{j}t},$$

where t is the pulse duration. Approximating the exponential portion, A^jt, as the parameter α which is defined in terms of basic experimental parameters using the full width half maximum of the X-ray spot size, the following is obtained

$$\alpha \equiv {\sigma }^0\frac{0.5(photonsperpulse)}{Area}$$

where σ⁰ is the photoelectric cross section for the filled 1s orbital of a single atom, half the photons per pulse is the number of photons in the FWHM profile of the x-ray beam and the Area is the spot size of the FWHM. Rewriting the absorbing fractional population, the following is obtained,

$$P_{abs}\cong 1-e^{-\alpha }.$$

The parameter α is introduced here as it encapsulates most of the pulse duration, photon density and spot size behavior in the model allowing for an easy comparison of datasets with different X-ray parameters.

The Figure 3B shows the proportion of the Kβ emission spectra that result from fluorescent decay depicted by the same colors in Figure 3A as a function of α. From this plot, the onset of sequential ionization effects can be clearly seen and the percent of the emission signal recorded which corresponds to the classical emission spectra, shown in blue. This percent can be estimated for values of α in the highlighted linear region to be

$$ClassicalFluorescence\cong 100\%-34\%\alpha ,where\alpha \le 0.25.$$

This is a useful measure for understanding the convolution of emitting states when planning XES measurements at an XFEL.

The rate equation model can also be used to predict the X-ray induced shifts in the first moment of the Kβ_1,3 peak by treating each electron hole as one oxidation state shift (see SI Methods). The first moment shift of each data set shown in Figure 2 is calculated as $FM=\frac{\sum E_i{I}_i}{\sum I_i}$ where E_i is the emission energy and I_i is the intensity of the spectrum using the energy between 6485–6495 eV with 0.1 eV bins. The change in first moment, typically used as an estimate for the oxidation state²⁵ or localized spin density changes³³, is shown for each data set in Figure 4 to indicate the sample’s electronic structure changes with increasing pulse intensity.

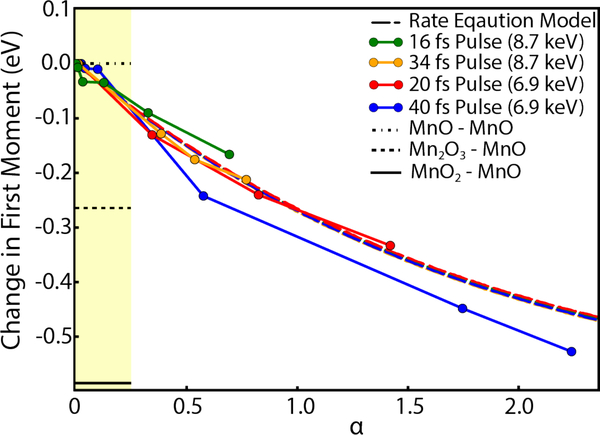
Figure 4.

The first moment dependence on α is shown for four data sets, for each set α is increasing with an increase of intensity. The rate equation predictions for the four datasets are represented by dashed lines with colors matching the respective dataset, however, all of the models overlap due to nearly identical dependence on the parameter α. The region with approximately linear dependence of the FM on α is highlighted. The three horizontal bars in the highlighted region show the difference between the FM values of Mn³⁺ and Mn⁴⁺ oxides from the reference Mn²⁺ oxide to indicate typical FM shifts between different oxidation states of Mn ions.”

The model predictions shown in Figure 4 appears to be in good agreement with the FM shifts in the data. We do note, however, that while the model predicts a nearly identical α dependence for each set of parameters, the data appear to have additional dependence on the pulse duration and incident photon energy. These effects are likely a result of additional ionization processes caused by Auger and photoelectrons. The increasing cross section of light elements at lower energy and more secondary ionizations during longer pulse durations will likely result in larger spectral changes and FM shifts. Additionally, the datasets with different incident photon energies were taken during different beamtimes and small changes in the FWHM of the beam may also be responsible for some of the FM shift between the two photon energies used.

To predict the FM shift in XES data for Mn ions and other high spin 3d ions we refer to the linear regime in Figure 4. Here the first moment shift in the linear regime can be estimated, Figure 3B, 4, as

$$F{M}_{shift}\cong -0.3\alpha ,when\alpha \le 0.25.$$

This simple analysis is useful in estimating tolerable photon densities based on XFEL parameters for experimental setups. This is important for some systems, such as photosystem II, where FM shifts of interest may be as small as ~0.02eV in the S₂ to S₃ state transition.^{25, 34} For detection of such small spectral changes it is clearly best to be removed from equivalent X-ray induced shifts estimated here, especially when additional effects from the electron cascade may be involved.

It is important to note that according to this prediction an α~0.5 was achieved in an earlier XFEL based study recording X-ray emission spectra of MnCl₂³⁵. An uncertainty of the study ~0.05 eV for comparing XFEL and synchrotron data³⁵ should not have precluded the detection of the expected shift of at least twice that of the uncertainty. As no detectable shift was observed the same X-ray beam parameters were used for XES analysis of PSII.³⁶ While the source of discrepancy is currently unknown, we do emphasize that predictions provided here should be carefully considered when planning XFEL experiments.

As XFEL sources move toward shorter and shorter pulses it is important to take into account the prospective of shorter pulses to limit electronic and structural changes. For the electron cascade, it seems to be clear that shorter pulses will lead to fewer electron-electron interactions. From a sequential ionization standpoint the picture is more complicated. As shorter pulse durations with the same photon densities are used, a larger population of the atoms will reach the empty 1s state. Atoms in this state will decay twice to fully repopulate the 1s orbital. Since the emission from atoms in the 1s0 state is likely to be significantly shifted relative to the 1s1 single hole state emission³⁷, the former emission is not expected to contribute to the final spectral shape and is not shown in Figure 3C. On the other hand, the subsequent emission will be from the 1s1 state and is expected to have spectral lines that overlap with the classical emission spectra. The second decay will have a higher probability of occurring in the presence of another low lying hole in the n=2 shell given the short amount of time after dual core hole decay and single core hole decay, Figure 1B–II. This is in contrast to longer pulses used here where the holes are in the n=3 level, Figure 1B–III, and are expected to lead to a different FM shift that that shown in Figure 4. Nevertheless, the percentage of classical emission spectra and spectra from sequential ionization will not be changed in as the race toward shorter X-ray pulses continues as is shown in Figure 3C.

Since sequential ionization is dependent on α, lowering the number of photons, increasing the beam spot size and increasing the incident photon energy all reduce the effect of sequential ionization. Out of the methods for reducing FM shifts, only increasing the X-ray spot size will not have a proportional reduction in the X-ray emission signal. Judging by our data, higher incident photon energies have the advantage over beam attenuation in that it will also reduce effects from photoelectrons of low z elements by lowering their cross section. Shorter pulses will also lead to fewer electron interactions within the sample during the duration of the pulse.

While the potential for outrunning the electron cascade is important, emission spectra will still have similar FM shift from sequential ionization, Figure 3C. Stimulated emission is one possible mechanism for increasing the emission intensity, however, the increased decay rate through stimulated emission may cause more sequential ionization events by refilling the 1s more rapidly allowing more ionizations. This process would lead to larger distortions to the spectra which explain this very phenomenon observed but not explained when recording stimulated emission spectra of Mn ions using this process.³⁸ Ultrashort pulses can also lead to dual core hole ionization which create hypersatellite emission lines, or emission lines from the 1s0 state, that don’t overlap spectroscopically with single core hole emission spectra. This allows X-ray pulses which create dual ionization but are much shorter than the decay rate of these states to capture unaltered atomic hypersatellites, though various holes in surrounding atoms will likely impact the spectra of metal complexes as well as direct absorption of orbitals other than the 1s. While some work has been done with hypersatellites experimentally³⁹, more groundwork will be required before hypersatellites can be validated as a widely applicable spectroscopic technique for XES.

Here we present a rate equation model that quantifies the percentages of recorded Kβ X-ray emission from atoms that have undergone a single or multiple sequential ionization events. Excellent agreement between the theoretical model and experimental observations has been demonstrated. Using these equations we provide a simple method to estimate the percent of classical vs sequential ionization spectra and the associated FM shift. Deviation from the sequential ionization model is attributed to electron cascade. Methods of avoiding effects from these two sources is also discussed. Additionally we note that shorter pulses do not overcome spectral changes that arise from sequential ionization and photon densities will have to be considered carefully in future facilities as more intense pulses become routinely available.