Interlaboratory comparison of nanoparticle size measurements between NMIJ and NIST using two different types of dynamic light scattering instruments

Abstract

The question of how to relate particle sizes measured using a fixed-angle dynamic light scattering (DLS) instrument with those measured using a multi-angle DLS instrument is addressed. A series of nearly monodisperse polystyrene latex (PSL) particles with nominal diameters of 100 nm, 70 nm, 50 nm, and 30 nm were measured using two different types of DLS instruments: one owned by the National Metrology Institute of Japan (NMIJ) of the multi-angle type and the other owned by the National Institute of Standards and Technology (NIST) of the fixed-angle type. The mean particle size of the PSL particles was measured using the multi-angle-type instrument at various scattering angles and at various concentrations of particle suspension. These data were used to establish the functional dependence of the measured particle size on the scattering angle and particle concentration through the least-squares fitting method. The established function was then used to predict the mean particle sizes that would have been obtained if the same scattering angle and particle concentrations as those used at NIST had been selected at NMIJ. The mean particle sizes obtained at NIST and at NMIJ agreed quite well for all four PSL particle samples after compensating for the angle and concentration differences. The result of this study clearly demonstrates that consideration for the dependence of measured particle sizes on the scattering angle and particle concentration is crucial in intra-method comparisons of mean particle sizes obtained using DLS.

1. Introduction

Nanoparticle sizing is critically important in the production of nanomaterials, evaluation of nanostructures, and risk assessment of nanomaterials with respect to human health and environmental regulations. Dynamic light scattering (DLS) is widely used as a convenient technique for determining nanoparticle size in liquids [1–7]. However, the accuracy of this technique has been questioned. Several international comparisons have been carried out to investigate the measurement accuracy of various techniques for nanoparticle sizing including DLS. In these comparisons, a conspicuous difference has generally been found between DLS and other methods. A major reason for the difference is that the measurement principle of DLS is based on the diffusion process of the particles, whereas most of the other methods are based more directly on the geometric particle sizes; however, before the inter-method differences can be addressed, we first must solve the problem of intra-method inconsistencies within the DLS method itself.

Several projects on nanoparticle sizing were carried out between 2005 to 2009 by the Asia-Pacific Economic Cooperation (APEC) with the Center for Measurement Standards, Industrial Technology Research Institute (CMS/ITRI) of Taiwan serving as the pilot laboratory [8, 9]. Interlaboratory comparisons of particle size were also conducted from 2009 to 2012 by the Institute for Reference Materials and Measurements (IRMM) in Belgium using silica particle suspensions as candidate standard reference materials [10–12]. Another typical example of interlaboratory comparisons is the Asia-Pacific Metrology Programme (APMP) Supplementary Comparison (APMP.L-S5), which is currently in progress. Under APMP.L-S5, comparisons are being made of particle sizes obtained by atomic force microscopy (AFM), transmission and scanning electron microscopy (TEM and SEM, respectively), differential mobility analysis (DMA), small-angle X-ray scattering (SAXS), and DLS. These comparisons reveal a tendency for particle sizes measured by DLS to have larger intra-method variations than particle sizes measured by other representative measurement methods including AFM, TEM, and SEM.

In the APMP.L-S5 project, DLS measurements at most of the participating laboratories were conducted using fixed-scattering-angle type instruments. Different particle concentrations were selected for sample suspensions by different laboratories. In the course of the project, the National Metrology Institute of Japan (NMIJ), a co-pilot laboratory of the project, proposed a procedure for adjusting particle size data obtained with the different DLS instruments to account for the effects of the scattering angle and particle concentration. This procedure was adopted by some of the participating laboratories, resulting in partially improved agreement of the DLS data between the different laboratories [13, 14]. The purpose of the present study is to examine in more detail the nature and validity of such an approach for the interpretation of DLS data on the basis of systematically collected experimental data.

In ISO 13321:1996 [15], a standard developed by the International Organization for Standardization (ISO), a DLS method protocol was described that utilized measurements made at a single angle and at a single concentration. The document recommended measuring in the low-concentration region, but it did not address the effect of changes in concentrations or angles. ISO 13321:1996 was recently developed into ISO 22412:2017 [16], which is applicable to a wide range of particle concentrations but still not to a wide range of scattering angles. In these two ISO standards, it is recommended that instrument performance be verified by using a dispersion of polystyrene latex (PSL) particles with a narrow size distribution and a certified mean particle size. However, the effect of scattering angle and concentration on the accuracy of the PSL particle size measured by DLS is not specified. Here, we show the applicability of interpolations made by using data at various concentrations and angles for obtaining valid intra-method comparisons between DLS instruments.

In this study, we evaluate the angular and concentration dependences of the DLS technique for nanoparticle sizing through an interlaboratory comparison conducted by NMIJ and the National Institute of Standards and Technology (NIST) for PSL suspensions with nominal particle diameters of 100 nm, 70 nm, 50 nm, and 30 nm. The angular and concentration dependences of the nano-sized PSL particle suspensions were measured with sufficient precision to permit fitting of the data to these two parameters. This method, based on a bilinear functional fit to these two dependences, is referred to as the dynamic Zimm-type plot analysis. The original Zimm plot method is used for static light scattering, whereas here it is applied to dynamic light scattering. The present estimation was performed by means of least-squares fitting involving several parameters including the angular and concentration dependences. Using this analysis, we compared the DLS data measured by NMIJ and NIST against each other, after accounting for the angular and concentration dependence of DLS.

2. Experimental

2.1. Sample Preparation

DLS measurements were performed on charge-stabilized PSL particles with nominal diameters of 100 nm, 70 nm, 50 nm, and 30 nm supplied by JSR Life Sciences Corporation (Ibaraki, Japan). Sample suspensions were supplied from the same sample lot, and dilutions of the PSL suspensions for DLS measurements were carried out in the same manner by NMIJ and NIST using pure water.

2.2. DLS measurements performed at NMIJ

The light scattering apparatus used at NMIJ was an ALV/compact goniometer system (ALV-Laser Vertriebsgesellschaft m.b.H., Langen/Hessen, Germany) with a yttriumaluminum-garnet (YAG) laser having a wavelength of 532 nm. The correlation function was measured at a minimum sampling time of 6.25 ns and logarithmically scaled delay times using an ALV-6010/160 Digital Correlator with Multiple Tau correlation channels in the Dual Mode (ALV-Laser Vertriebsgesellschaft m.b.H.). DLS measurements were performed at seven scattering angles θ ranging from 30° to 150° (θ = 30°, 50°, 70°, 90°, 110°, 130°, and 150°) for five suspensions with different particle concentrations for each nominal-particle-size sample. A sample cell with a diameter of 10 mm was set in a temperature bath of toluene for index matching with the quartz. The temperature of the toluene bath was maintained at 20.00 °C ± 0.01 °C.

The entire apparatus was set up in a clean enclosure, which was maintained at 23.0 °C ± 0.1 °C. The sample cell containing the PSL suspension was kept in the toluene bath for at least 30 minutes before measurements were made, for temperature equilibration. The standard count rate of the photon detector was 100 K counts/s. The run time of each DLS measurement was controlled within the range of 100 s to 300 s to obtain the same statistics for the correlation function. The run time for the most concentrated suspension at the scattering angle θ = 30° was only 100 s, whereas the lowest concentration at θ = 150° required 300 s to obtain the autocorrelation function (ACF) with the desired statistics. Each ACF obtained at a given scattering angle θ and particle concentration C was then analyzed to extract the apparent particle size diameter, d_app(θ, C).

2.3. DLS measurements performed at NIST

For the measurements performed at NIST, a Malvern Zetasizer Nano ZS¹ (Malvern Panalytical Ltd., Malvern, UK) was used with a 633 nm He-Ne laser source and a 173° scattering angle. The temperature of the sample and instrument was equilibrated at 23 °C. The default data acquisition settings for PSL were used for all measurements. The sample volume was 100 μL, and the count rate was > 400 K counts/s. The ACF was analyzed by the cumulant method using vendor-supplied software to obtain the z-average particle size Z_AVE. Sufficient statistics was assured by preparing and measuring three samples for each nominal-particle-size at different concentrations on different days with 3 replicate measurements per day.

2.4. Data analysis

Extraction of an average particle diameter in DLS is based on a cumulant analysis of the ACF. From theory [2], the electric-field correlation function g⁽¹⁾(τ) may be calculated from the scattered intensity correlation function g⁽²⁾(τ) using the Siegert relationship:

$$g^{(2)}(\mathit{\text{τ}})=A\left(1+B{\left|g^{(1)}(\mathit{\text{τ}})\right|}^2\right).$$ (1)

Here τ is the delay time, A is the baseline, and B is the intercept of the correlation function. The correlation function g⁽¹⁾(τ) was analyzed by the cumulant method, as described in ISO 22412:2017 [16], to evaluate the average decay rate, Γ, from the first cumulant:

$$\left|g^{(1)}(\tau )\right|=\text{exp}\left(-\mathit{\text{Γ}}\tau +\frac{1}{2}{\mu }_2{\tau }^2-\cdots \right).$$ (2)

Here, μ₂ is the second cumulant, which is related to the distribution of particle sizes. If particles are optically isotropic and there are no electrostatic interactions between particles, a diffusion coefficient D proportional to the decay rate may be calculated as

$$\mathit{\text{Γ}}=D{q}^2,$$ (3)

where q is the scattering vector defined as

$$q=\left(4\pi n_0/{\lambda }_0\right)\text{sin}(\theta /2).$$ (4)

In Equation 4, n₀ is the refractive index of the solvent, λ₀ is the vacuum wavelength of the incident light, and θ is the scattering angle. From the measured diffusion coefficient, D, a particle diameter, d, is obtained as the diameter of a geometrical sphere under the assumption of the Stokes-Einstein relationship

$$d=\frac{k_{B}T}{3\pi \eta D},$$ (5)

where k_B, T, and η are the Boltzmann constant, absolute temperature, and solvent viscosity, respectively.

In the following, the particle diameter obtained according to Equation (5) at NMIJ using the multi-angle type instrument is denoted by d_app, and that obtained at NIST using the fixed-angle-type instrument is denoted by Z_AVE.

3. Results

Figures 1, 2, 3, and 4 show d_app and Z_AVE for the nominal 100 nm, 70 nm, 50 nm, and 30 nm PSL particles, respectively. The apparent particle size diameters, d_app(θ, C) were obtained at the given scattering angles, θ, and particle concentrations, C. The NMIJ data are denoted by the marks ○, Δ, +, ×, and ◊, with the same marks indicating the same concentrations of the PSL particle suspensions, while the NIST data are denoted by filled squares (▪). These figures are drawn as dynamic Zimm-type plots, described previously [17, 18]; that is, the x-axis of each figure indicates a variable representing the sum of q² and C with an adequately selected weighting factor to show both the q² and C dependence of the observed particle size conveniently in a single figure.

Figure 1.

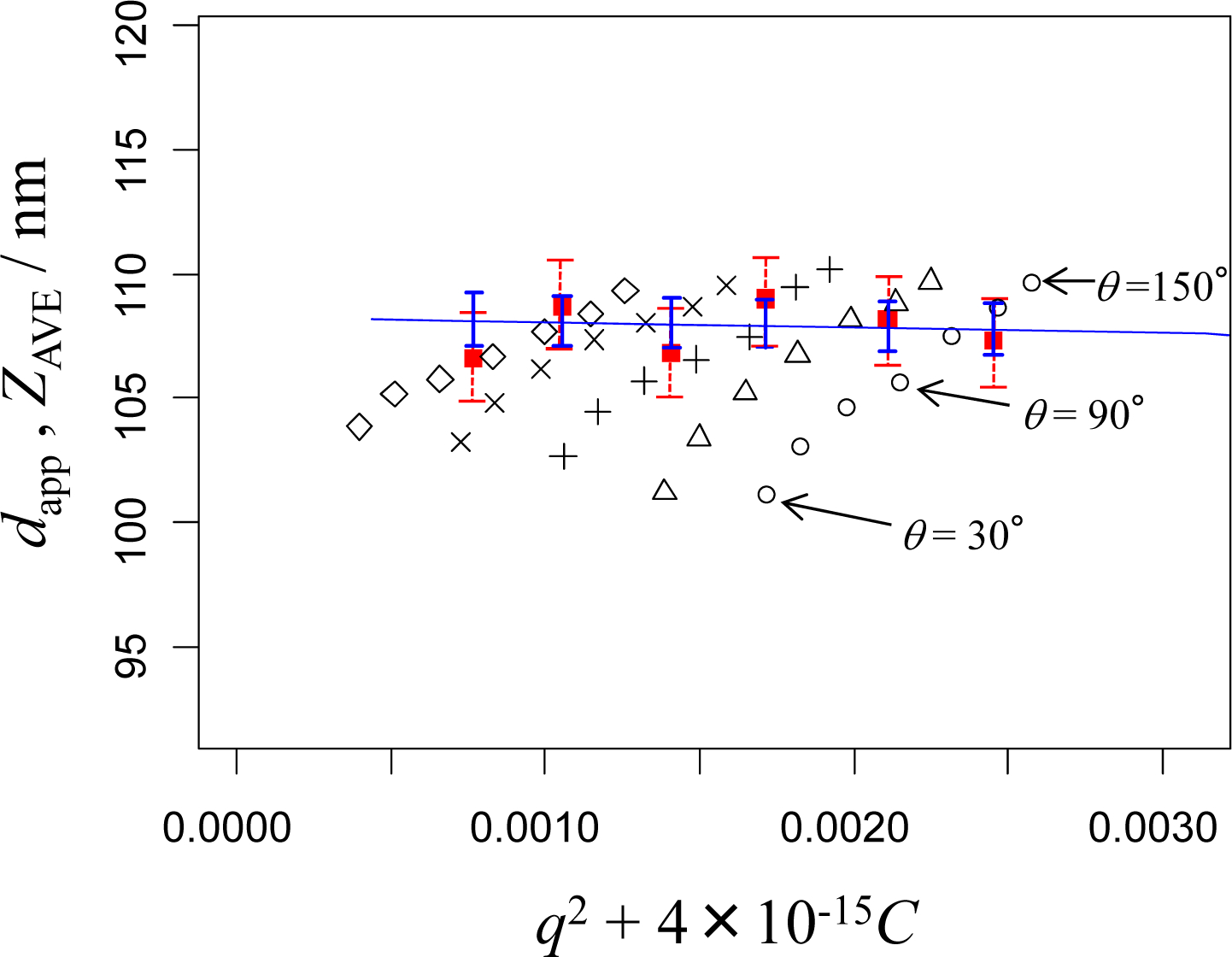
DLS measurements of the apparent diameter of 100 nm PSL particles obtained in pure water at NMIJ, d_app (○, Δ, +, ×, and ◊) and NIST, Z_AVE (filled squares). The straight line (with error bars indicating the ± confidence interval) is the calculated diameter based on the fit to the NMIJ data by Equation (10) for q_NIST. The dotted error bars of the NIST data show the ± expanded uncertainty based on the repeatability and reproducibility of the experiments. The concentrations (× 10¹⁰ particles mL⁻¹) at NMIJ are 41 (○), 33 (Δ), 25 (+), 16 (×), and 8.3 (◊). The concentrations (× 10¹⁰ particles mL⁻¹) at NIST are 44, 35, 25, 18, 9, and 2.

Figure 2.

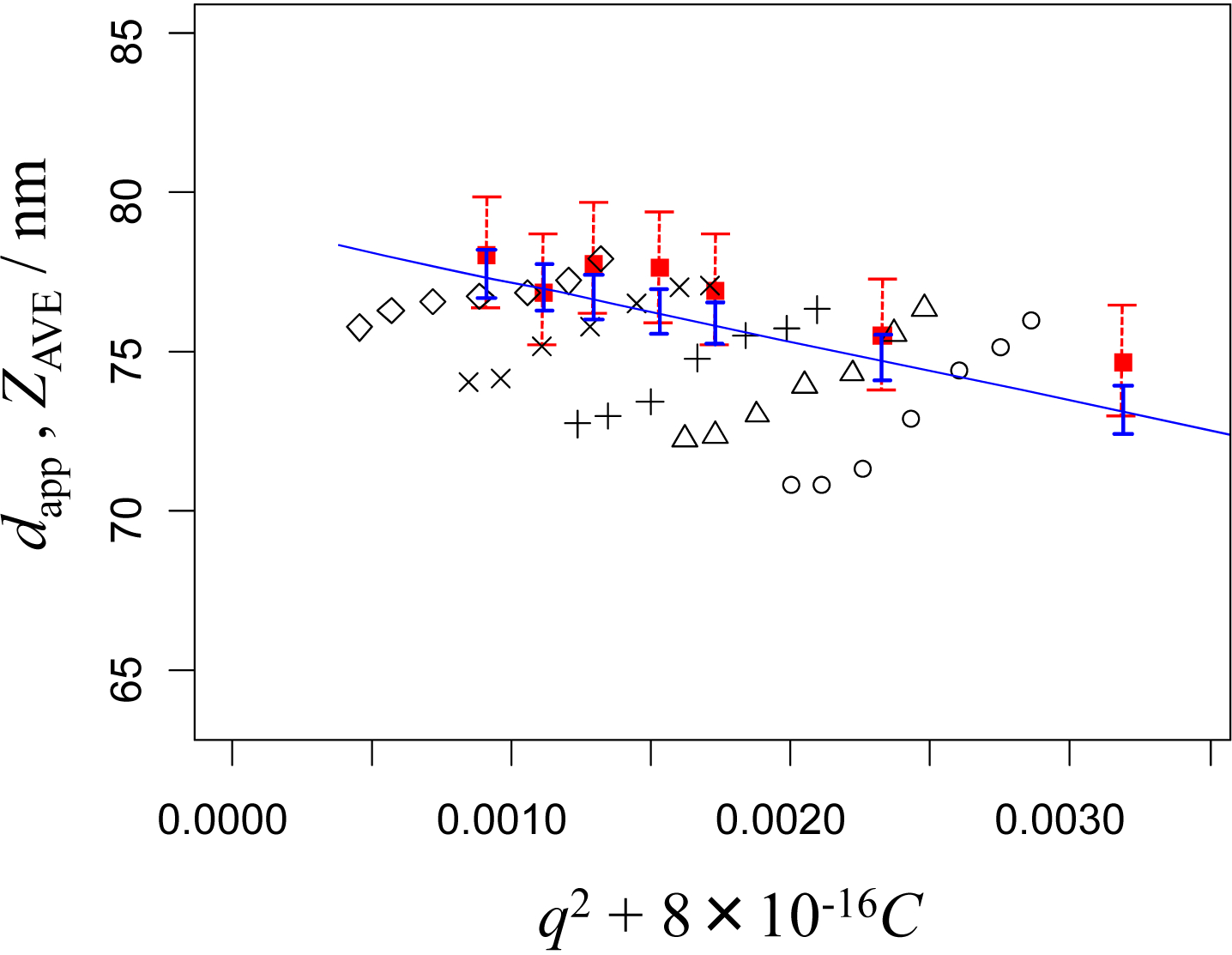
DLS measurements of the apparent diameter of 70 nm PSL particles obtained in pure water at NMIJ, d_app (○, Δ, +, ×, and ◊) and NIST, Z_AVE (filled squares). The concentrations (× 10¹¹ particles mL⁻¹) at NMIJ are 24 (○), 19 (Δ), 15 (+), 10 (×), and 4.9 (◊). The concentrations (× 10¹¹ particles mL⁻¹) at NIST are 31, 20, 13, 10, 7.5, 5.2, and 2.6. Error bars as in Fig. 1.

Figure 3.

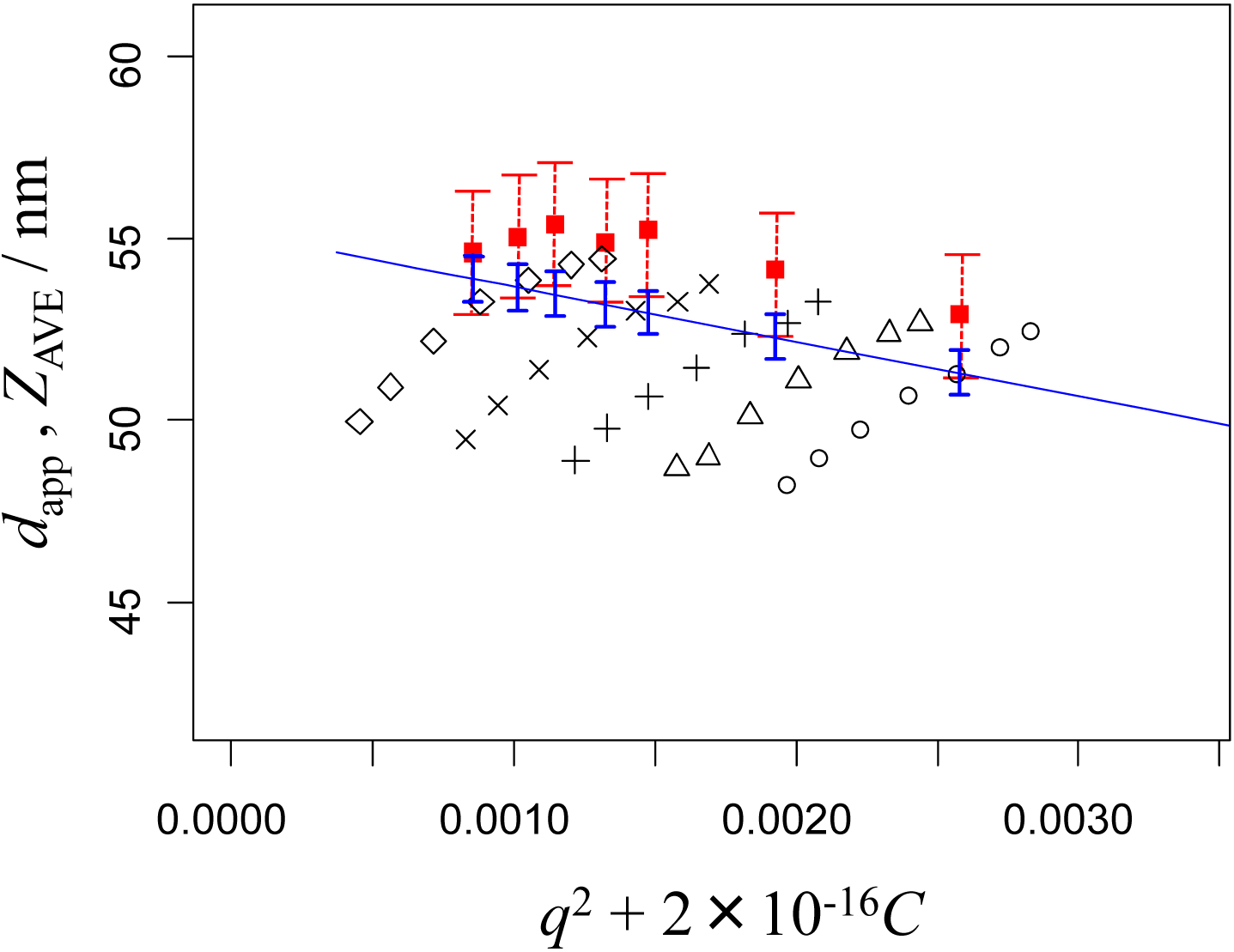
DLS measurements of the apparent diameter of 50 nm PSL particles obtained in pure water at NMIJ, d_app (○, Δ, +, ×, and ◊) and NIST, Z_AVE (filled squares). The concentrations (× 10¹¹ particles mL⁻¹) at NMIJ are 95 (○), 76 (Δ), 58 (+), 38 (×), and 19 (◊). The concentrations (× 10¹¹ particles mL⁻¹) at NIST are 94, 61, 39, 31, 22, 16, and 8. Error bars as in Fig. 1..

Figure 4.

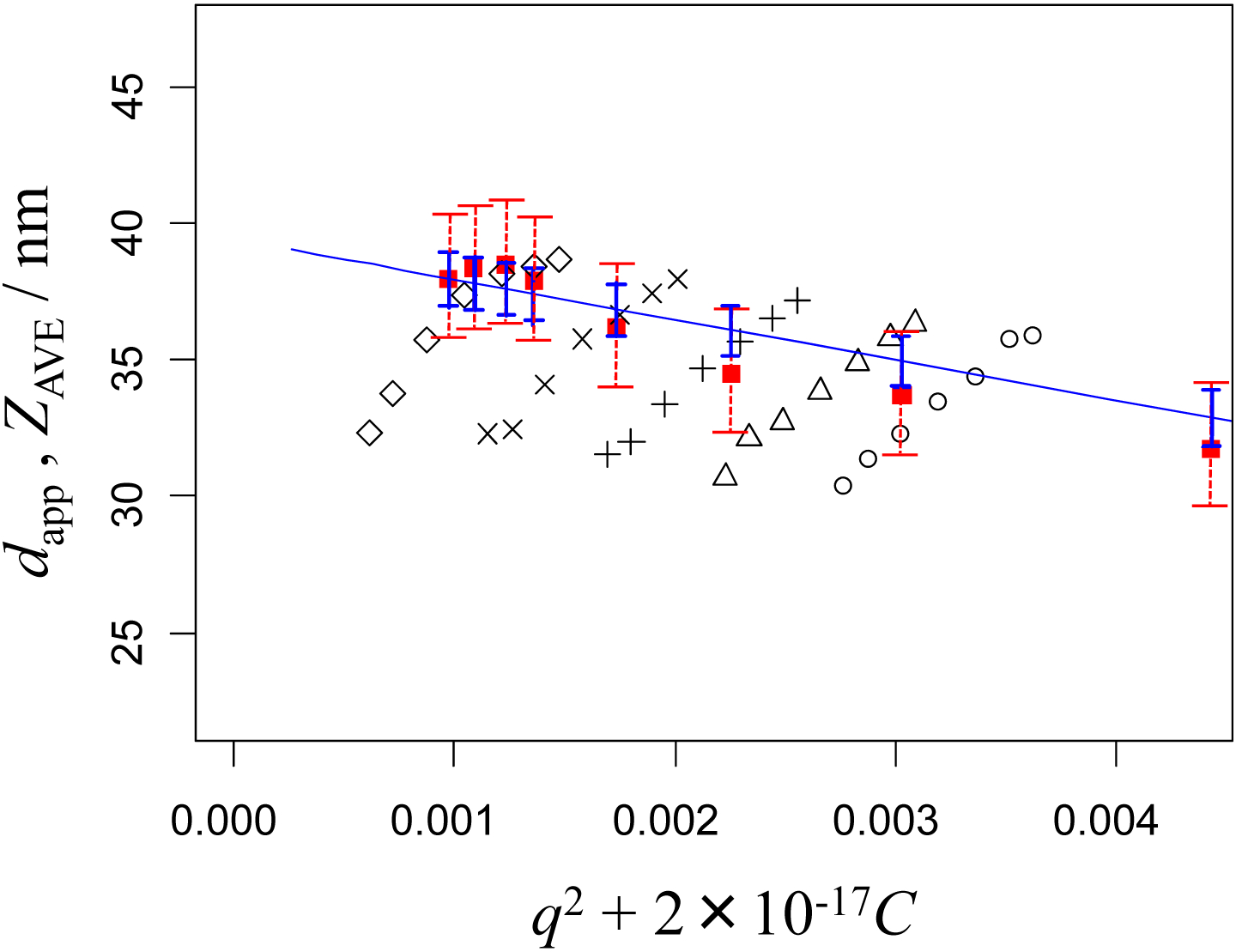
DLS measurements of the apparent diameter of 30 nm PSL particles obtained in pure water at NMIJ, d_app (○, Δ, +, ×, and ◊) and NIST, Z_AVE (filled squares). The concentrations (× 10¹² particles mL⁻¹) at NMIJ are 130 (○), 110 (Δ), 81 (+), 54 (×), and 27 (◊). The concentrations (× 10¹² particles mL⁻¹) at NIST are 190, 120, 78, 52, 33, 27, 19, and 14. Error bars as in Fig. 1.

In the Zimm-type plot analysis, observed particle sizes are extrapolated to infinite dilution, C = 0, and to zero angle, θ = 0, to obtain a unique value related to the particle size d_app(C = 0, θ = 0). It is customary [19, 20] to associate this unique value with purely Brownian translational diffusion described by the Stokes-Einstein equation, where mutual diffusion corresponds to self-diffusion. In the present study, however, we establish the functional dependence of d_app on C and q² through the least-squares fitting of the NMIJ data, and then use it to predict the value of d_app that would have been obtained at NMIJ for the wavelength, scattering angle and particle concentration conditions used at NIST. In this way, we can compare the observed mean particle sizes between NMIJ and NIST without the influence of differences in wavelength, scattering angle and particle concentration. These calculated values are shown on the plots by the straight lines with vertical error bars indicating the confidence interval. The dotted-line error bars on the plots show the expanded uncertainty of the NIST data based on the repeatability and reproducibility of the experiments. Details of the fitting calculations and comparisons are described in the next section.

4. Discussion

4.1. Comparison between NMIJ and NIST data with uncertainty analysis

The experimental data of NMIJ in Figures 1 to 4 suggest that d_app is well approximated by a bilinear function of C and q²:

$$d_{\text{app}}(C,q)=a_0+a_{1}C+a_2{q}^2+a_{3}C{q}^2.$$ (6)

Here, a₀ to a₃ are parameters to be determined by fitting this equation to the experimental data. Corresponding to five particle concentrations C_i (i = 1, 2, …, 5) and seven values of the magnitude of the scattering vector q_j (j = 1, 2, …, 7), we have 35 observations of d_app, which we denote by d = [d₁, d₂, …, d₃₅]^t. Here, “t” indicates transposition of a vector or matrix. Let a = [a₀, a₁, a₂, a₃]^t, and

$$X=\left[\begin{array}{cccc}1& C_1& q_1{}^2& C_1{q}_1{}^2\\ 1& C_1& q_2{}^2& C_1{q}_2{}^2\\ 1& C_1& q_3{}^2& C_1{q}_3{}^2\\ ⋮& ⋮& ⋮& ⋮\\ 1& C_5& q_7{}^2& C_5{q}_7{}^2\end{array}\right].$$ (7)

The NMIJ data d are then expressed by

$$d=X•a+e,$$ (8)

where e = [e₁, …, e₃₅]^t represents residuals in the fitting. Following the least-squares fitting procedure, we obtain the estimate of a from X and d as

$$a={\left(X^{\text{t}}X\right)}^{-1}{X}^{\text{t}}d.$$ (9)

In the NIST measurements, the value of q was 0.0264 nm⁻¹, corresponding to θ = 173° and λ₀ = 633 nm, and 6 to 10 levels of particle concentration (particles mL⁻¹) were selected depending on the PSL particles. We denote this value of q by q_NIST, and any one of the concentration levels by C_NIST, and let x = [1, C_NIST, q_NIST², C_NIST q_NIST²]^t. The particle size calculated according to

$$d_{\text{adj}}=x^{\text{t}}•a$$ (10)

represents a mean particle size that would have been obtained at NMIJ if C_NIST and q_NIST had been selected as the values of C and q, respectively. We will call d_adj the adjusted particle size. Assuming that measurement errors are contained in d, and hence in a, but not in x, which is a commonly adopted assumption in regression analysis, the Type A uncertainty of d_adj, u_A(d_adj), is given by applying the law of propagation of uncertainty to Equation (10). This results in

$$u_{\text{A}}{}^2\left(d_{\text{adj}}\right)=x^{\text{t}}\cdot V[a]\cdot x=s^2{x}^{\text{t}}\cdot {\left(X^{t}X\right)}^{-1}\cdot x,$$ (11)

where V[a] is the estimated variance-covariance matrix of a, and s is the experimental standard deviation of d that can be calculated from the residuals as

$$s^2={(d-Xa)}^{\text{t}}\cdot (d-Xa)/31.$$ (12)

In this equation, the denominator represents the degrees of freedom of the experimental variance s².

In Figures 1 to 4, the value of d_adj given in Equation (10) is drawn as a function of C for q = q_NIST (straight line). The vertical error bars indicate the intervals ±2u_A(d_adj), plotted at the C of the NIST data. The error bars of the NIST data are also shown, which indicate ±2u_NIST, where u_NIST are experimental standard deviations of the mean particle sizes based on the repeatability and reproducibility of the measurements. Here, 2u_NIST is 1.93 nm for the 100 nm PSL particles, 1.98 nm for the 70 nm PSL particles, 1.85 nm for the 50 nm PSL particles, and 1.86 nm for the 30 nm PSL particles.

In addition to these Type A uncertainties, there should also be Type B uncertainty components in both the NMIJ and NIST data. The uncertainty components associated with the physical parameters in Equations (4) and (5) (k_B, T, η, n₀, θ and λ₀) are negligible as compared with the Type A components. The uncertainty components associated with the finite widths of particle size distributions, as well as the thickness of the adsorption water layer on particle surfaces, are not negligible, but are considered to be the same at NMIJ and NIST because the same PSL particles and pure water were used in both sets of experiments. Hence, the Type B uncertainties are not included in the error bars in Figures 1 to 4, the main purpose of which is to compare the measured mean particle sizes obtained by NMIJ and NIST.

4.2. Physical aspects of dynamic Zimm-type plot

Table 1 lists the obtained parameters, a₀, a₁, a₂, and a₃. Since the NMIJ data are reasonably bilinear in C and q² for all particle sizes (as shown in Figures 1 to 4), the linearity assumption of Equation (6) is reasonable. It is important to note that the unique value d(0,0) simply coincides with the fitting parameter a₀ (in nm), which corresponds to the apparent particle size referenced to zero concentration and zero scattering vector. Note that these d(0, 0) (or a₀) are expected to be shifted from the certified values of the PSLs, because DLS measurements are based on particle diffusion and thus reflect the hydrodynamic size of the particles, which includes the water solvation shell, among other effects [17]. The parameter a₁ corresponds to the concentration dependence of the particle size. In all of the present PSL suspensions, the values of a₁ are negative. Since the particle size and diffusion constant have an inverse relationship, the observable diffusion constant has a positive slope with respect to the concentration indicating that the particle-particle interaction of the PSL is positive and that the PSL suspension is stable. The parameter a₂ corresponds to the angular dependence and is related to the structure function of the scattering system [18–20]. The parameter a₃ corresponds to the shape of the parallelogram, which is observed as the changes of angular dependence according to the increments in concentration. For example, the PSL 100 nm particles in Figure 1 and 70 nm particles in Figure 2 show the five slopes of angular dependence becoming steeper as the concentration increases. In contrast, the slopes of angular dependence for the PSL 50 nm particles in Figure 3 and 30 nm particles in Figure 4 are gentler at higher concentrations.

Table 1.

DLS angular and concentration fitting parameters obtained from NMIJ data. These parameters were obtained by fitting Equation (6) to the experimental data of the 100 nm, 70 nm, 50 nm, and 30 nm PSL reference materials.

nominal value	certified value (nm)	expanded uncertainty (nm) (k=2)	a0 (nm)	a1 (nm · mL)	a2 (nm3)	a3 (nm3 · mL)
100 nm	100	3	105	−9.03 × 10−12	5.00 × 103	1.17 × 10−8
70 nm	70	1	76.9	−2.93 × 10−12	1.33 × 103	2.06 × 10−9
50 nm	48	1	50.6	−2.79 × 10−13	5.07 × 103	−2.95 × 10−11
30 nm	29	1	33.2	−2.38 × 10−14	7.49 × 103	−8.50 × 10−12

The NIST data and the NMIJ data coincide remarkably well within the mutually valid concentration range. Within this range, it is possible to use Equation (6) and the parameters given in Table 1 to obtain a quantitative calculated value of d_app that corresponds to the fixed-angle data.

The important message is that the specific Z_AVE and d_app measurements do not generally refer to the same measurand and cannot be compared directly without proper adjustment. Before applying the calculated adjustments to account for the differing particle concentration, C, and the scattering vector, q, (which includes the scattering angle, θ and wavelength, λ₀), the apparent particle sizes are invariably observed to disagree with each other. Only when the adjusted values are calculated can we compare and validate particle sizes measured at different scattering angles, wavelengths, and particle concentrations.

5. Conclusions

In this study, we have shown that DLS intra-method comparisons may yield inconsistent results if the effect of the scattering vector and particle concentration on the measured particle size is neglected. Commonly used DLS instruments have a fixed scattering angle, and frequent practice is for only one particle concentration to be used for the particle size measurement. However, if different scattering angles or particle concentrations are used for the measurements, the apparent particle size will be affected, and the measurements cannot be directly compared It is therefore necessary for comparisons of particle sizes measured by different DLS instruments to be recalculated using fitting parameters obtained from multi-angle and multi-concentration measurements. From the results of the present study, we can conclude that the DLS data measured by NMIJ and NIST are in agreement to within their uncertainties after adjusting for the angular and concentration dependence of DLS.

The motivation for this work is to address the large intra-method variation reported in recent interlaboratory studies by DLS, not to deal with the inter-method deviation between DLS and other sizing techniques. We believe that the use of the dynamic Zimm-type plot analysis as described in this report represents a milestone in obtaining a solution to the intra-method inconsistency in the DLS method. The dynamic Zimm-type plot analysis is also applicable for other kinds of particles such as gold and silver colloids, as shown in the results of the APMP.L-S5 [14]. The ultimate benefit of the Zimm-type plot analysis is that it provides a means of comparing DLS results from measurements made at differing single angles and concentrations.