Abstract
This work presents precision measurements of quantized Hall array resistance devices using superconducting, crossover-free, multiple interconnections as well as graphene split contacts. These new techniques successfully eliminate the accumulation of internal resistances and leakage currents that typically occur at interconnections and crossing leads between interconnected devices. As a result, a scalable quantized Hall resistance array is obtained with a nominal value that is as precise and stable as that from single-element quantized Hall resistance standards.
Keywords: quantum Hall effect, quantized Hall array resistance standards, epitaxial graphene, superconducting contacts, multiple connection, split contacts
1. Introduction
Although the first graphene samples were isolated as micrometer-size flakes and found to have favorable electrical and optical properties,[1–5], more recently, high-quality and centimeter-scale graphene has been obtained through epitaxial growth on silicon carbide (SiC) [6–9]. The epitaxial graphene (EG) growth has improved to the point that one can realize devices suitable for general applications, like larger scale electronics, and more specialized applications, such as quantized Hall resistance (QHR) standards [9–17].
Limitations of reliable access to quantum Hall resistance plateaus other than RH = RK/2 = h/2e2, where RH is the Hall resistance, and RK is the von Klitzing constant, have motivated the development of quantum Hall array resistance standards (QHARS) based on series and in parallel connected devices [18–20]. These next-generation quantum resistance devices show promise in fulfilling the requirement of scalability for future applications in metrology. One issue for these scalable resistance networks, based on many Hall bar elements, is that they may suffer from accumulated internal resistances and Hall resistance contributions at thin-film metal contacts and interconnections. In addition, the crossover of electrical connections between Hall elements introduce other difficulties such as possible leakage currents through the dielectric where the voltage terminals need to cross the current path. Finally, because of limited chip mounting options, it is impossible to realize longitudinal resistance measurements as recommended in metrological guidelines for the QHR [21]. These challenges are the reason why state-of-the-art QHARS devices often cannot reach the level of quantization needed for resistance metrology.
In this work, we present new EG-based QHARS device design approaches to minimize the error contributions of undesired resistances at contacts and interconnections and ensure precise resistance quantization for series-parallel networks. The applied split contact geometry and superconducting interconnections ensure minimum deviation from the nominal resistance value on the order of 10−9. Furthermore, new quantization criteria are applied to verify the quantization of these resistance networks as a whole rather than by the characterization of single Hall devices in addition to previously discussed concepts [22,23].
2. Device preparation and characterization
2.1. Sample and contact design
Figure 1(a) shows the sample design based on six Hall bars (light grey), superconducting interconnections and contacts (dark grey), and positions of the bonding wires (blue) that were used for the four-terminal resistance measurements. Since there is no gradient in the electrical potential across the superconducting elements, the potential and current leads are interchangeable and can be bonded to any point. Each Hall bar was contacted by a multiple interconnection [20,24] that was optimized for a specific magnetic field direction such that the hot-spot forms in the lower left and upper right corner of each device as indicated in Figure 1(b). The device fabrication started with the deposition of a Pd/Au layer onto the EG. After the EG/Pd/Au layer was structured into the Hall bar shape by argon plasma etching, it was contacted with a ≈ 320 nm thick NbTiN layer and capped with a ≈ 30 nm thick Pt layer to prevent surface oxidation. A detailed description of the individual fabrication steps is given in a previous work [25]. The confocal laser scanning microscope (CLSM) image of the finished device is provided in Figure 1(b). Before the device was wire-bonded onto a chip carrier, covalent Cr(CO)3 functionalization was used to adjust the charge carrier density of the device as explained in Section 2.2. A previous work shows that by integrating the principle of the Delahaye triple-series interconnection for QHR devices into a single contact by means of split contacts (Figure 1(b) and Figure 1(c)), the resulting contact resistance in the quantum Hall regime is reduced to a level of 100 μΩ or less [25]. The vanishing contact resistance is the result of the current flowing through mainly one branch of the split contact, with each other branch experiencing a proportion of current that is smaller than the last. Thus, the connection voltage drop quickly approaches zero, bringing the superconductor to the potential of the quantized two-dimensional electron gas (2DEG). The condition for the branches to act as separate charge carrier reservoirs in the quantum Hall regime is separation by a minimum distance d, which must be larger than the inelastic scattering length of the charge carrier [26]. It is safe to assume that the condition is fulfilled for the distance d ≥ 5 μm indicated in Figure 1(c) between neighboring branches since inelastic scattering occurs at sub-micron length scales [27,28]. Additionally, the design accounts for the prevention of Andreev reflections that may occur at EG/superconductor interfaces and can lead to deviations of the Hall resistance from the nominal value [29–32]. As demonstrated in Figure 1(c), a several micrometer-wide Pd/Au stripe separates the EG edge from the NbTiN superconductor such that Andreev effects cannot occur. The results of a previous work [25] show that split contacts with in total six fingers are sufficient to minimize the effective contact resistance. Thus, the large number of interconnections along the Hall bar in the current design is not a requirement. More important is the last pair of Hall contacts/interconnections near the center of each element since it defines a Hall voltage that is theoretically unaltered by longitudinal resistance components. Figure 1(d) shows the array device mounted in a 32-pin leadless chip carrier (LCC03204) that was used for the pre-characterization. Precision measurements of the same sample were performed afterwards using a transistor outline (TO-8) package.
Figure 1.
Device design and sample characteristics. (a) The sample design of the graphene quantized Hall array resistance device shows the NbTiN interconnections (dark grey) of the individual QHR elements (light grey) and the positions of the bonding wires that were used for the measurement (blue). The red inset box marks the region shown in (b). (b) Confocal laser scanning microscope (CLSM) image of a graphene Hall bar device in the source/drain contact region using a multiple connection and superconducting split contacts (white). (c) CLSM image in the region of the graphene/NbTiN split contact shows the design used to realize negligible contact resistances. (d) The photo shows the contacted device (7.6 mm × 7.6 mm) mounted on a 32-pin chip carrier. (e) The scatter plot of Raman graphene 2D (G`) peak characteristics was evaluated from 50 μm × 50 μm area maps and shows a typical distribution of the FWHM and the peak position over centimeter-scale areas. (f) The graph shows the vanishing resistance across a superconducting element of the device for different temperatures and magnetic flux densities. The high critical magnetic field of the NbTiN superconductor ensures superconductivity even at T ≈ 10 K for magnetic flux densities B > 9 T. At B = 0 T, the typical critical transition temperature is around 12.5 K.
2.2. Graphene growth, device fabrication, and carrier density control
EG was obtained by thermally decomposing the Si-face of 4H-SiC(0001) semi-insulating substrates having a miscut of less than 0.10°. Substrates were first diced from a wafer with a diameter of ≈ 10 cm (4-inch) into squares with sides measuring 22.8 mm × 22.8 mm, cleaned by a piranha etch, immersed into diluted hydrofluoric acid, and surface-treated with polymer adsorbates for polymer-assisted sublimation growth (PASG) [8,9]. PASG involved spin coating a weak solution of 0.2 % (by volume) AZ5214E polymer in isopropanol. Prior to EG growth, the prepared substrates were then placed on a slab of polished graphite with the Si-face in direct contact with the slab for face-to-graphite growth [13,33]. The combination of the face-to-graphite growth and PASG methods supports the formation of a uniform surface morphology and suppresses the formation of high substrate steps and bilayer domains. Reducing the SiC terrace height to a sub-nanometer level is essential since it reduces variations of the doping level, the number of scattering centers, and strain caused by local detachment of the graphene layer at the edges of the terraces [34–37]. The annealing process at 1900 °C was performed in argon at atmospheric pressure with a graphite-lined resistive-element furnace. After growth, the EG quality was assessed using CLSM and optical microscopy, both being convenient and preparation-free methods for rapid identification of successful large-area growths [38].
Raman spectroscopy was performed to verify that the EG was undamaged before and after the functionalization process. Spectra were collected with a spectrometer using a 532.2 nm wavelength excitation laser source and a backscattering configuration. The spot size was about 1 μm, the acquisition times were 2 s, the laser power was 25 mW power, and the optical path included a 50 × objective and 600 mm−1 gratings. Square Raman maps were collected with step sizes of 0.5 μm in a 100 by 100 raster-style grid. The large-scale quality of the EG was assessed by monitoring only the 2D (G`) peak and its Raman shift, full width at half maximum (FWHM), and spatial location on the device. The 2D (G`) peak quantities are summarized in Figure 1 (e), with average FWHM of 33.16 cm−1 ± 0.93 cm−1 and average peak position of 2728.07 cm−1 ± 3.36 cm−1 (all uncertainties represent 1σ deviations). Figure 1 (d) shows a photo of the measured device which was fabricated using NbTiN contacts and interconnections.
Functionalization of EG with Cr(CO)3 was performed to have improved control over the carrier density, as it had been demonstrated in other reports [39–44]. To begin the functionalization process, the completed EG device was loaded onto a phosphor-bronze boat filled with approximately 100 mg of crystalline Cr(CO)6 (chromium hexacarbonyl) and placed within a homemade vacuum furnace. The deposition steps (well-documented in Ref. [44]) resulted in ring-centered Cr(CO)3 functionalization. By functionalizing the EG surface, the electron doping was reduced to a carrier density below 1011 cm−2 and produced limited drift of the carrier density in air. To adjust the carrier density to the level of about 2×1011 cm−2 for the measurement, the sample was annealed at 355 K for about 20 minutes in vacuum and was cooled down immediately afterwards.
2.3. Assessment of NbTiN properties
The measurement temperature and applied magnetic flux densities need to be far below the critical properties of the superconductor to allow voltage and current terminals to be the same by using multiple interconnections without crossing leads. This is not only important to avoid undesired ohmic resistance contributions but also to avoid the occurrence of non-zero Hall fluctuations at interconnections [45,46].
To assess the most important properties of the NbTiN superconductor, the four-wire resistance across a superconducting element of the device was monitored as a function of the magnetic flux density and temperature. Figure 1(f) shows that the resistance vanishes at a temperature of T = 10 K and magnetic flux densities up to B = 9 T. At this temperature the critical field is likely to be higher since a breakdown of the superconductivity was only observed above 11.5 K for the system’s highest available magnetic flux density of B = 9 T. At zero magnetic flux density, the typical critical temperature of this superconductor is T ≈ 12.5 K.
3. Results and discussion
Under the assumption of negligible resistance contributions from contacts and superconducting strip lines, the quantum Hall array device introduced in Figure 1 provides access to several measurement configurations resulting in different nominal resistance values. Here we focus on only those configurations in which the current splits equally among two or more paths and that provide access to null measurements that may be used to check for the uniformity and quantization of the resistance array. This characterization is complementary to the comparison to a calibrated 100 Ω standard resistor using a cryogenic current comparator (CCC) resistance bridge.
To precisely determine the array resistance values using the CCC bridge, a NIST 100 Ω standard resistor (Electro-Scientific Industries SR102) was used. The standard resistor has a well-known linear drift rate and was calibrated about 100 days prior to the characterization of the array device using a GaAs-AlGaAs quantized Hall resistance standard.
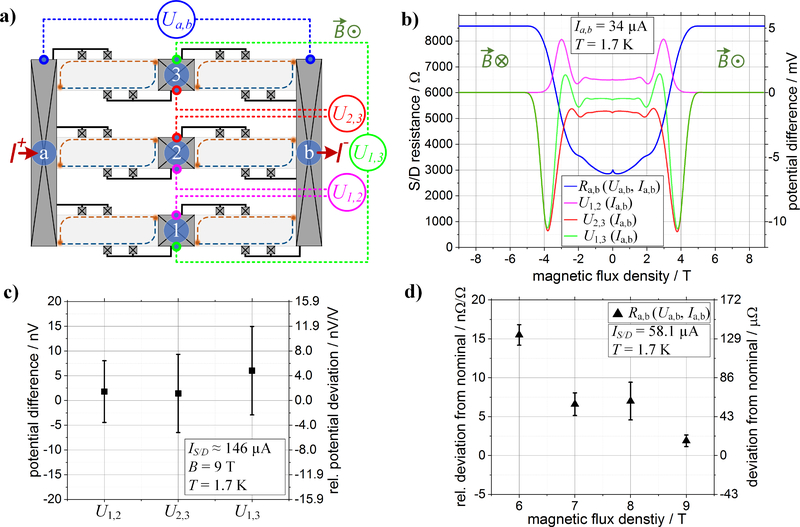
3.1. Measurement configuration 1 results, R = 2/6 RK ≈ 8604 Ω
Figure 2(a) shows the first configuration of three parallel pairs of series-connected quantized Hall devices with a resulting nominal resistance of Ra,b = Ua,b/Ia,b = 2/6 RK ≈ 8604 Ω. The voltage differences U1,2, U1,3, U2,3 at the terminals “1, 2, 3” in the center of the sample are monitored to detect a breakdown of the resistance quantization.
Figure 2.
Measurement configuration with a nominal resistance value of Ra/b = 2/6 RK ≈ 8604 Ω. (a) The simplified schematic of the array device shows the measurement configuration for the characterization of the source/drain (SD) resistance of Ra/b = Ua,b/Ia,b and the potential differences U1,2, U2,3 and U1,3. The indicated high (red) and low (blue) equipotential lines describe the case for a quantized device at positive flux densities. (b) The SD resistance and the potential differences Ui at the center locations 1,2,3 as a function of the magnetic flux density show wide plateaus for B > 5 T. (c) Measurements at B = 9 T show that once resistance quantization is obtained, the voltage differences at the center locations 1,2,3 become zero within the measurement uncertainty and thus serve as a simple quantization check of the device. (d) The precision CCC comparison of Ra/b with a 100 Ω standard resistor for B = 9 T shows a deviation of ≈ 2 nΩ/Ω from the expected nominal value.
Figure 2(b) shows lock-in measurements of the magnetic field dependence of the resistance Ra,b with a symmetrical behavior at low fields below ±5 T and a wide resistance plateau beyond ± 5 T. Due to similar carrier densities of the devices, the potential differences U1,2, U1,3, and U2,3 show Shubnikov-de Haas oscillations at lower fields and approach zero for ± 5 T.
Precision measurements of the potential differences at B = 9 T shown in Figure 2(c) were collected using a nanovoltmeter (EM N11) and a NIST-built ramping voltage source that is normally used in a CCC resistance bridge system [47]. The voltage source was operated at USD = Ua,b = 1.26 V to provide a stable current of Ia,b ≈ 146 μA, or ISD ≈ 49 μA through each of the six QHR devices. Measurements were performed by recording at least ten points, each using direct current (dc) reversal cycles to eliminate thermal voltages with a ramp time = 1 s, settle time = 8 s and an integration time = 8 s. Additionally, each data point Ui in Figure 2(c) is composed of two measurement sets with reversed nanovoltmeter potential terminals such that to reject constant voltage offsets that are typically < 10 nV. All three determined potential differences between the three parallel device branches with a mean value of 3.1 nV ± 7.6 nV were zero within the measurement uncertainty which indicates that all six devices were equal and thus almost certainly well quantized. To make measurements using different measurement conditions better comparable, the relative potential deviation δUdev = Ui/USD was determined resulting in a mean value of all three measurements of 2.5 nV/V ± 6.1 nV/V. This method achieves a metrological useful sensitivity to resistance differences below 10 nΩ/Ω with respect to a 12.9 kΩ resistor assuming a potential difference measurement with a statistical uncertainty < 10 nV and currents on the order of 100 μA.
A comparison of the QHARS and a 100 Ω standard resistor was realized using a binary cryogenic current comparator (BCCC) bridge [48]. Figure 2(d) shows the field-dependent deviation from the nominal resistance value Ra,b = 2/6 RK as a function of the magnetic flux density between B = 6 T and B = 9 T. The data points for B ≥ 7 T have a relative deviation well below 10 nΩ/Ω with the lowest value being 1.9 nΩ/Ω ± 0.75 nΩ/Ω at B = 9 T. The larger uncertainties of the measurements at 8 T, 7 T, and 6 T are related to the lower number of collected measurements of 25 points compared to 50 points at 9 T. The determined errors account for the type A (k = 1) uncertainties of the measurements.
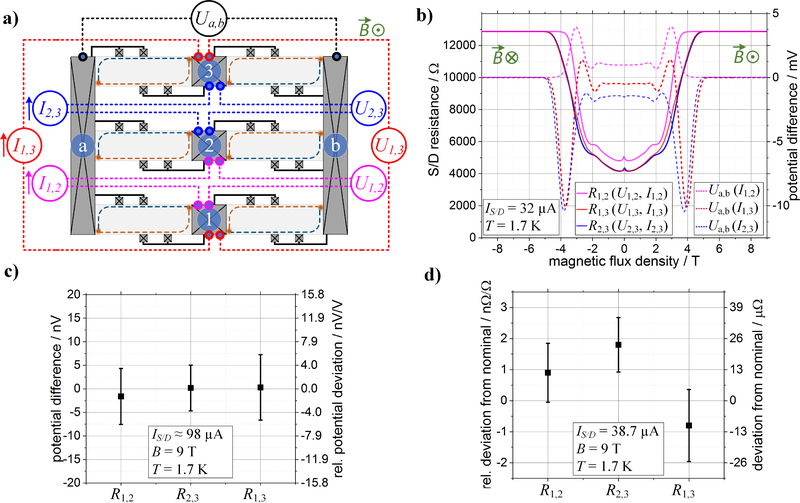
3.2. Measurement configuration 2 results, R = 1/2 RK ≈ 12906 Ω
In the second measurement set shown in Figure 3(a), the QHARS device was contacted such that only four out of the six devices contributed to the transport, creating a network with two parallel pairs of series-connected devices. This was achieved by using the terminals “1,2,3” as current terminals such that R1,2 = R2,3 = R1,3 with a nominal value of 1/2 RK ≈ 12906 Ω. The terminals “a” and “b” were used to identify asymmetries in the device by monitoring the potential difference Ua,b.
Figure 3.
Measurement configuration with a nominal resistance value of R1,2 = R2,3 = R1,3 = 1/2 RK ≈ 12906 Ω. (a) The simplified schematic of the array device shows the measurement configuration for the characterization of the source/drain (S/D) resistances R1,2 = R2,3 = R1,3 and the corresponding potential differences Ua,b. The indicated high (red) and low (blue) equipotential lines describe the case for a quantized device at positive flux densities. (b) The SD resistances as well as corresponding potential differences between port “a” and “b” as a function of the magnetic flux density show wide plateaus for B > 5 T. (c) At B = 9 T, the voltage differences Ua,b for each of the three SD resistances R1,2, R2,3, R1,3 are zero to within the measurement uncertainty and thus serve as a simple quantization check of the device. (d) The precision CCC comparison of the three SD resistances with a 100 Ω standard resistor at 9 T show near-zero deviations from the expected nominal value of R1,2 = R2,3 = R1,3.
Figure 3(b) shows the field dependence of R1,2, R2,3 and R1,3 and their corresponding potential differences Ua,b monitored with a lock-in measurement system within the range of available magnetic flux densities of −9 T ≤ B ≤ 9 T. Small differences in the charge carrier densities and low-field resistivities of the devices resulted in somewhat different onsets of the resistance plateaus at 1/2 RK ≈ 12906 Ω around ±5 T. Measurements of Ua,b in Figure 3(b) show that the potential differences of all three measurements with a mean value of −0.29 nV ± 4.7 nV are zero to within the measurement uncertainty and thus indicate the well quantization of all Hall elements.
The CCC resistance comparison of the QHARS against the same 100 Ω standard resistor in Figure 3(c) proves that all three resistances R1,2, R2,3 and R1,3 were well quantized at 1/2 RK with a deviation of ≈ ±2 nΩ/Ω.
4. Conclusions
We have demonstrated the fabrication and functionality of EG-based QHARS that provide variable resistances with excellent quantization properties resulting in deviations from its nominal value on the order of ± 2 nΩ/Ω. Additionally, the introduced relative potential deviation measurements between points of equal potential in the symmetric network design were successfully applied to verify the uniformity and quantization of the device. This technique does not require the assessment of individual devices and thus represents a straightforward quantization criterion of QHARS.
The reasons for the reported performance that matches that of single quantum Hall devices are the crossover-free, superconducting NbTiN interconnections that eliminate ohmic resistance contributions and Hall fluctuations as well as the applied split contacts with minimum contact resistances. By presenting a novel way to simplify device interconnections without altering the quantized resistance value this work brings the development of QHARS to the next stage.
Acknowledgments
The work of D.P. at NIST was made possible by arrangement with C.-T. Liang of National Taiwan University, and the work of M.M. at NIST was made possible by arrangement with M. Ortolano of Politecnico di Torino and L. Callegaro of the Istituto Nazionale di Ricerca Metrologica, Turin, Italy. The authors would like to thank S. Schlamminger and A. Biacchi for their assistance during the internal review at NIST. Commercial equipment, instruments, and materials are identified in this paper in order to specify the experimental procedure adequately. Such identification is not intended to imply recommendation or endorsement by the National Institute of Standards and Technology or the United States government, nor is it intended to imply that the materials or equipment identified are necessarily the best available for the purpose.
References
- [1].Geim AK and Novoselov KS 2007. The rise of graphene Nat. Mater 6 183–91 [DOI] [PubMed] [Google Scholar]
- [2].Castro Neto AH, Guinea F, Peres NMR, Novoselov KS and Geim AK 2009. The electronic properties of graphene Rev. Mod. Phys 81 109–62 [Google Scholar]
- [3].Novoselov KS, Fal′ko VI, Colombo L, Gellert PR, Schwab MG and Kim K 2012. A roadmap for graphene Nature 490 192–200 [DOI] [PubMed] [Google Scholar]
- [4].Das Sarma S, Adam S, Hwang EH and Rossi E 2011. Electronic transport in two-dimensional graphene Rev. Mod. Phys 83 407–70 [Google Scholar]
- [5].Berger C, Song Z, Li T, Li X, Ogbazghi AY, Feng R, Dai Z, Alexei N, Conrad MEH, First PN and De Heer WA 2004. Ultrathin epitaxial graphite: 2D electron gas properties and a route toward graphene-based nanoelectronics J. Phys. Chem. B 108 19912–6 [Google Scholar]
- [6].Virojanadara C, Syväjarvi M, Yakimova R, Johansson LI, Zakharov AA and Balasubramanian T 2008. Homogeneous large-area graphene layer growth on SiC(0001) Phys. Rev. B 78 245403 [Google Scholar]
- [7].Emtsev KV, Bostwick A, Horn K, Jobst J, Kellogg GL, Ley L, McChesney JL, Ohta T, Reshanov SA, Röhrl J, Rotenberg E, Schmid AK, Waldmann D, Weber HB and Seyller T 2009. Towards wafer-size graphene layers by atmospheric pressure graphitization of silicon carbide Nat. Mater 8 203–7 [DOI] [PubMed] [Google Scholar]
- [8].Kruskopf M, Pakdehi DM, Pierz K, Wundrack S, Stosch R, Dziomba T, Götz M, Baringhaus J, Aprojanz J, Tegenkamp C, Lidzba J, Seyller T, Hohls F, Ahlers FJ and Schumacher HW 2016. Comeback of epitaxial graphene for electronics: large-area growth of bilayer-free graphene on SiC 2D Mater. 3 041002 [Google Scholar]
- [9].Kruskopf M and Elmquist RE 2018. Epitaxial graphene for quantum resistance metrology Metrologia 55 R27–36 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Janssen TJBM, Tzalenchuk A, Yakimova R, Kubatkin S, Lara-Avila S, Kopylov S and Fal’ko VI 2011. Anomalously strong pinning of the filling factor ν=2 in epitaxial graphene Phys. Rev. B 83 233402 [Google Scholar]
- [11].Ribeiro-Palau R, Lafont F, Brun-Picard J, Kazazis D, Michon A, Cheynis F, Couturaud O, Consejo C, Jouault B, Poirier W and Schopfer F 2015. Quantum Hall resistance standard in graphene devices under relaxed experimental conditions Nat. Nanotechnol 10 965–71 [DOI] [PubMed] [Google Scholar]
- [12].Tzalenchuk A, Lara-Avila S, Kalaboukhov A, Paolillo S, Syväjärvi M, Yakimova R, Kazakova O, Janssen TJBM, Fal’ko V and Kubatkin S 2010. Towards a quantum resistance standard based on epitaxial graphene Nat. Nanotechnol 5 186–9 [DOI] [PubMed] [Google Scholar]
- [13].Real MA, Lass EA, Liu F-H, Shen T, Jones GR, Soons JA, Newell DB, Davydov AV. and Elmquist RE 2013. Graphene Epitaxial Growth on SiC(0001) for Resistance Standards IEEE Trans. Instrum. Meas 62 1454–60 [Google Scholar]
- [14].Lafont F, Ribeiro-Palau R, Kazazis D, Michon A, Couturaud O, Consejo C, Chassagne T, Zielinski M, Portail M, Jouault B, Schopfer F and Poirier W 2015. Quantum hall resistance standards from graphene grown by chemical vapour deposition on silicon carbide Nat. Commun 6 1–10 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Janssen TJBM, Rozhko S, Antonov I, Tzalenchuk A, Williams JM, Melhem Z, He H, Lara-Avila S, Kubatkin S and Yakimova R 2015. Operation of graphene quantum Hall resistance standard in a cryogen-free table-top system 2D Mater. 2 035015 [Google Scholar]
- [16].Jeckelmann B and Jeanneret B 2001. The quantum Hall effect as an electrical resistance standard Reports Prog. Phys 64 1603–55 [Google Scholar]
- [17].Rigosi AF, Panna AR, Payagala SU, Kruskopf M, Kraft ME, Jones GR, Wu B-Y, Lee H-Y, Yang Y, Hu J, Jarrett DG, Newell DB and Elmquist RE 2019. Graphene Devices for Tabletop and High-Current Quantized Hall Resistance Standards IEEE Trans. Instrum. Meas 68 1870–8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Novikov S, Lebedeva N, Hämäläinen J, Iisakka I, Immonen P, Manninen AJ and Satrapinski A 2016. Mini array of quantum Hall devices based on epitaxial graphene J. Appl. Phys 119 174504 [Google Scholar]
- [19].Lartsev A, Lara-Avila S, Danilov A, Kubatkin S, Tzalenchuk A and Yakimova R 2015. A prototype of R K /200 quantum Hall array resistance standard on epitaxial graphene J. Appl. Phys 118 044506 [Google Scholar]
- [20].Delahaye F 1993. Series and parallel connection of multiterminal quantum Hall-effect devices J. Appl. Phys 73 7914–20 [Google Scholar]
- [21].Delahaye F and Jeckelmann B 2003. Revised technical guidelines for reliable dc measurements of the quantized Hall resistance Metrologia 40 217–23 [Google Scholar]
- [22].Poirier W, Bounouh A, Piquemal F and André JP 2004. A new generation of QHARS: discussion about the technical criteria for quantization Metrologia 41 285–94 [Google Scholar]
- [23].Konemann J, Ahlers F-J, Pesel E, Pierz K and Schumacher HW 2011. Magnetic Field Reversible Serial Quantum Hall Arrays IEEE Trans. Instrum. Meas 60 2512–6 [Google Scholar]
- [24].Jeffery A, Elmquist RE and Cage ME 1995. Precision tests of quantum hall effect device DC equivalent circuit using double-series and triple-series connections J. Res. Natl. Inst. Stand. Technol 100 677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Kruskopf M, Rigosi AF, Panna AR, Patel DK, Jin H, Marzano M, Berilla M, Newell DB and Elmquist RE 2019. Two-Terminal and Multi-Terminal Designs for Next-Generation Quantized Hall Resistance Standards: Contact Material and Geometry IEEE Trans. Electron Devices 1–5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Büttiker M 1988. Absence of backscattering in the quantum Hall effect in multiprobe conductors Phys. Rev. B 38 9375–89 [DOI] [PubMed] [Google Scholar]
- [27].Baker AMR, Alexander-Webber JA, Altebaeumer T, Janssen TJBM, Tzalenchuk A, Lara-Avila S, Kubatkin S, Yakimova R, Lin C-T, Li L-J and Nicholas RJ 2012. Weak localization scattering lengths in epitaxial, and CVD graphene Phys. Rev. B 86 235441 [Google Scholar]
- [28].Drabińska A, Kamińska M, Wołoś A, Strupinski W, Wysmołek A, Bardyszewski W, Bożek R and Baranowski JM 2013. Enhancement of elastic and inelastic scattering lengths in quasi-free-standing graphene measured with contactless microwave spectroscopy Phys. Rev. B 88 165413 [Google Scholar]
- [29].Sahu MR, Liu X, Paul AK, Das S, Raychaudhuri P, Jain JK and Das A 2018. Inter-Landau-level Andreev Reflection at the Dirac Point in a Graphene Quantum Hall State Coupled to a NbSe2 Superconductor Phys. Rev. Lett 121 086809. [DOI] [PubMed] [Google Scholar]
- [30].Amet F, Ke CT, Borzenets IV, Wang J, Watanabe K, Taniguchi T, Deacon RS, Yamamoto M, Bomze Y, Tarucha S and Finkelstein G 2016. Supercurrent in the quantum Hall regime Science (80-. ). 352 966–9 [DOI] [PubMed] [Google Scholar]
- [31].Rickhaus P, Weiss M, Marot L and Schönenberger C 2012. Quantum Hall Effect in Graphene with Superconducting Electrodes Nano Lett. 12 1942–5 [DOI] [PubMed] [Google Scholar]
- [32].Hou Z, Xing Y, Guo A-M and Sun Q-F 2016. Crossed Andreev effects in two-dimensional quantum Hall systems Phys. Rev. B 94 064516 [Google Scholar]
- [33].Yang Y, Cheng G, Mende P, Calizo IG, Feenstra RM, Chuang C, Liu C-W, Liu C, Jones GR, Hight Walker AR and Elmquist RE 2017. Epitaxial graphene homogeneity and quantum Hall effect in millimeter-scale devices Carbon N. Y 115 229–36 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Nagase M, Hibino H, Kagashima H and Yamaguchi H 2008. Local conductance measurement of few-layer graphene on SiC substrate using an integrated nanogap probe J. Phys. Conf. Ser 100 052006 [Google Scholar]
- [35].Low T, Perebeinos V, Tersoff J and Avouris P 2012. Deformation and Scattering in Graphene over Substrate Steps Phys. Rev. Lett 108 096601. [DOI] [PubMed] [Google Scholar]
- [36].Willke P, Kotzott T, Pruschke T and Wenderoth M 2017. Magnetotransport on the nano scale Nat. Commun 8 15283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Momeni Pakdehi D, Aprojanz J, Sinterhauf A, Pierz K, Kruskopf M, Willke P, Baringhaus J, Stöckmann JP, Traeger GA, Hohls F, Tegenkamp C, Wenderoth M, Ahlers FJ and Schumacher HW 2018. Minimum Resistance Anisotropy of Epitaxial Graphene on SiC ACS Appl. Mater. Interfaces 10 [DOI] [PubMed] [Google Scholar]
- [38].Panchal V, Yang Y, Cheng G, Hu J, Kruskopf M, Liu C-I, Rigosi AF, Melios C, Hight Walker AR, Newell DB, Kazakova O and Elmquist RE 2018. Confocal laser scanning microscopy for rapid optical characterization of graphene Commun. Phys 1 83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Bekyarova E, Sarkar S, Niyogi S, Itkis ME and Haddon RC 2012. Advances in the chemical modification of epitaxial graphene J. Phys. D. Appl. Phys 45 154009 [Google Scholar]
- [40].Che S, Jasuja K, Behura SK, Nguyen P, Sreeprasad TS and Berry V 2017. Retained Carrier-Mobility and Enhanced Plasmonic-Photovoltaics of Graphene via ring-centered η 6 Functionalization and Nanointerfacing Nano Lett. 17 4381–9 [DOI] [PubMed] [Google Scholar]
- [41].Chen M, Pekker A, Li W, Itkis ME, Haddon RC and Bekyarova E 2018. Organometallic chemistry of graphene: Photochemical complexation of graphene with group 6 transition metals Carbon N. Y 129 450–5 [Google Scholar]
- [42].Pinto H and Markevich A 2014. Electronic and electrochemical doping of graphene by surface adsorbates Beilstein J. Nanotechnol 5 1842–8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Chuang C, Yang Y, Pookpanratana S, Hacker CA, Liang C-T and Elmquist RE 2017. Chemical-doping-driven crossover from graphene to “ordinary metal” in epitaxial graphene grown on SiC Nanoscale 9 11537–44 [DOI] [PubMed] [Google Scholar]
- [44].Rigosi AF, Kruskopf M, Hill HM, Jin H, Wu B-Y, Johnson PE, Zhang S, Berilla M, Hight Walker AR, Hacker CA, Newell DB and Elmquist RE 2019. Gateless and reversible Carrier density tunability in epitaxial graphene devices functionalized with chromium tricarbonyl Carbon N. Y 142 468–74 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Breznay NP and Kapitulnik A 2013. Observation of the ghost critical field for superconducting fluctuations in a disordered TaN thin film Phys. Rev. B 88 104510 [Google Scholar]
- [46].Destraz D, Ilin K, Siegel M, Schilling A and Chang J 2017. Superconducting fluctuations in a thin NbN film probed by the Hall effect Phys. Rev. B 95 1–6 [Google Scholar]
- [47].Hernandez-Marquez FL, Bierzychudek ME, Jones GR and Elmquist RE 2014. Precision high-value resistance scaling with a two-terminal cryogenic current comparator Rev. Sci. Instrum 85 044701. [DOI] [PubMed] [Google Scholar]
- [48].Götz M and Drung D 2017. Stability and Performance of the Binary Compensation Unit for Cryogenic Current Comparator Bridges IEEE Trans. Instrum. Meas 66 1467–74 [Google Scholar]