Optical Lattice with Torus Topology

Abstract

We propose an experimental scheme to construct an optical lattice where the atoms are confined to the surface of a torus. This construction can be realized with spatially shaped laser beams which could be realized with recently developed high resolution imaging techniques. We numerically study the feasibility of this proposal by calculating the tunneling strengths for atoms in the torus lattice. To illustrate the non-trivial role of topology in atomic dynamics on the torus, we study the quantized superfluid currents and fractional quantum Hall (FQH) states on such a structure. For FQH states, we numerically investigate the robustness of the topological degeneracy and propose an experimental way to detect such a degeneracy. Our scheme for torus construction can be generalized to surfaces with higher genus for exploration of richer topological physics.

Introduction.—

In the past decades, ultracold atoms in optical lattices have been widely used to study a range of interesting coherent and many-body physics [1]. In particular, there has been remarkable progress in investigating phenomena [2–5] in both different dimensions [6–8] and lattice geometries, such as square [2, 6], triangular [9], honeycomb [10], kagome [11], ring [12], cylinder [13], and more recently ribbon lattices with synthetic dimensions [14].

Meanwhile, intriguing physics can be explored in systems with non-trivial topologies. For example, it is theoretically predicted that there are topologically protected degeneracies on surfaces with non-zero genus, like the fractional quantum Hall (FQH) model [15, 16] or spin liquids [17–19]. Such systems are expected to not only contain rich many-body physics but also possibly be used in topological quantum computation [17]. While there have been interesting proposals to make torus surfaces in ultracold atomic systems, using synthetic dimensions [20] and semi-2D geometries by modifying cylinders [21, 22], the experimental construction of a torus in real space has remained challenging. Moreover, the presence of edge physics and the finite size effect have made the observation of FQH effect in ultracold atoms challenging.

In this Letter, we propose a scheme to construct an optical lattice in which atomic dynamics is confined to the surface of a torus. Our construction makes use of recent advances in beam shaping, in the context of ultracold atomic systems [23–27]. Specifically, we show that a rectangular square lattice with a hole in the middle can be turned into the surface of a torus by shaping a single beam perpendicular to the layers (Fig. 1). Moreover, we discuss that this construction could be generalized to surfaces with higher genus. To illustrate the non-trivial role of topology in atomic dynamics on the torus, we first investigate the hydrodynamics of bosonic superfluid on the torus. Specifically, we demonstrate a sequence of optical manipulations that generates quantized supercurrents in two intersecting non-contractible cycles. Furthermore, in the strongly correlated regime, we discuss a FQH model which can be realized on this torus. To numerically investigate the topological degeneracy on such system, we consider a relatively small square lattice (6 × 6) with torus topology. We show that the anticipated topological degeneracy exists and is robust against the discrepancy between inter- and intra-layer tunneling and disorder. Moreover, we propose a way to experimentally detect the topological degeneracy.

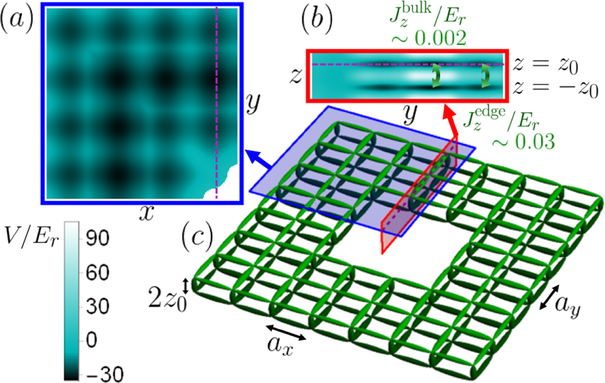
FIG. 1.

(a) Schematic beam configuration for a torus surface in an optical lattice. Plane wave beams in the horizontal directions generate a rectangular lattice in the xy plane. In the z direction, a superlattice structure created by pairs of blue-detuned and red-detuned beams confines atoms in two layers. The −z propagating blue-detuned beam has the beam shape of a square annulus. (Inset) Different laser intensities turn the inter-layer tunneling on and off in different regions. To complete the torus surface, only the inter-layer tunneling on in the edge region is allowed. (b) Generalization of the scheme to surfaces with higher genus (g = 2, 3 shown for example) can be achieved by puncturing more holes in the middle of the lattice.

Torus Construction.—

In the following, we show that by using several pairs of laser beams in the x, y, and z directions, one can build an optical lattice in which atomic dynamics is confined to the surface of a torus (Fig. 1). We first make a bilayer system by creating a superlattice structure in the z direction. Using high resolution optics, we then tailor one of the beams used in the superlattice structure to have the shape of a square annulus. This square annulus divides the xy plane into three regions: bulk, edge, and empty space [Fig. 1(a)]. By having a different set of intensities in these regions, the trap potential can be arranged to only allow atoms to vertically tunnel through lattice sites in the edge region, thus confining atoms to the surface of a torus.

To prepare a bilayer system, we use a 3D optical lattice with a superlattice structure in the z direction. Red-detuned laser beams with wavevectors $\pm k_x\widehat{x}$ and $\pm k_y\widehat{y}$ form a 2D rectangular lattice with lattice spacings (a_x, a_y) = (π/k_x, π/k_y). For the superlattice structure, we use a pair of blue-detuned lasers with wavevectors $\pm k_z\widehat{z}$ and another pair of red-detuned lasers with wavevectors $\pm q_z\widehat{z}$. When the ±z propagating beams do not vary in the xy plane, the combined vertical dipole potential is given by V_z(z) = V_b(z) + V_r(z) = V_blue cos²(k_zz) − V_red cos²(q_zz) for properly chosen relative phases, where V_blue (V_red) is the amplitude of the dipole potential generated by the blue-detuned (red-detuned) beam pair alone. Then atoms with atomic mass m can be confined at two neighboring minima, which we call the ±z₀, as shown in Fig. 2(b). Atoms in these minima constitute the bilayer system.

FIG. 2.

Numerically evaluated dipole potential and tunneling strengths. We consider Rb⁸⁷ atoms with a_x ≃ a_y = 480 nm and k_x = k_z/2 = 2q_z. In the unit of recoil energy $E_r\equiv {\hslash }^2{k}_x^2/2m\left(E_{r,z}\equiv {\hslash }^2{k}_z^2/2m\right)$, V₀ = 8E_r, V_E = 60E_r(15E_r,z), V_B = 120E_r(30E_r,z), and V_red = 20E_r(5E_r,z). (a) Dipole potentials in the xy plane on the upper layer. (b) Dipole potentials in the yz plane. Inter-layer tunneling strengths in bulk $\left(J_z^{\text{bulk }}\right)$ and edge $\left(J_z^{\text{edge}}\right)$ are shown for comparison. (c) Numerically evaluated tunneling strengths represented as the thickness of bonds in the 3D lattice. Shown tunneling strengths range from 0.03E_r to 0.04E_r.

To complete the torus surface, we tailor the −z propagating blue-detuned beam in the shape of a square annulus in the xy plane, adjusted to achieve the desired inter-layer tunneling only along edge sites. In particular, we make the laser intensity lower at the edge compared to the bulk region. The resulting potential barrier in the z direction is shallower at the edge than the bulk, which makes the inter-layer tunneling non-zero at the edge while negligible in the bulk region. With the laser intensity of the −z propagating beam set to zero in the empty space region, the +z propagating blue-detuned beam generates a higher dipole potential in the empty space compared to the edge and the bulk region. This difference in dipole potential energetically prevents atoms from escaping the designated square annulus.

To be concrete, we consider the following beam shapes for the blue-detuned beams:

$$\begin{gathered} E_{+}(r,t)=\widehat{y}\left(e^{+i{k}_z(z-ct)}+c.c.\right){\mathcal{E}}_{+}, \\ {E}_{-}(r,t)=\widehat{y}\left(e^{-i{k}_z(z+ct)}+\text{c}.\text{c}.\right)\{\begin{array}{cc}{\mathcal{E}}_{\text{B}}& \text{ bulk }\\ {\mathcal{E}}_{\text{E}}& \text{ edge }\\ 0& \text{ empty space }\end{array}. \end{gathered}$$ (1)

In this discrete setting, bulk and edge regions correspond to the zones around bulk and edge sites in the square annulus, within the distance a_x/2 (a_y/2) in the x (y) direction. The rest of the area is designated as empty space. For illustrative purposes, we assume the model beam has sharp boundaries between different regions, but in an experimental realization, one can relax this constraint and construct a good approximation of Eq. (1) using beams with sufficient numerical apertures (0.17 to 0.80) [28]. The recent progress in beam-shaping techniques for optical lattices [23–27, 29] could allow one to realize such a beam profile in the lab. Note that this beam profile should be placed properly in the xy plane in a way that regional distinctions in Eq. (1) to match with the horizontal lattice sites.

This beam profile gives rise to the combined vertical dipole potential including interference between the +z and −z propagating beams:

$$\begin{array}{l}{V}_z(r)=V_b(r)-V_{\text{red}}{\text{cos}}^2\left(q_{z}z\right),\\ V_b(r)=\{\begin{array}{cc}{V}_{\text{B}}{\text{cos}}^2\left(k_{z}z\right)+V_{\text{B}}^{(0)}& \text{ bulk }\\ V_{\text{E}}{\text{cos}}^2\left(k_{z}z\right)+V_{\text{E}}^{(0)}& \text{ edge }\\ V_{\text{S}}& \text{ empty space }\end{array},\end{array}$$ (2)

where the lattice potential amplitudes are $V_{\text{B}/\text{E}}=4f_0{\mathcal{E}}_{+}{\mathcal{E}}_{\text{B}/\text{E}}$, and the energy offsets are $V_{\text{B}/\text{E}}^{(0)}=f_0{({\mathcal{E}}_{+}-{\mathcal{E}}_{\text{B}/\text{E}})}^2$, $V_{\text{S}}=f_0{\mathcal{E}}_{+}^2$. Here, the proportionality constant f₀ depends on beam frequency, dipole elements, and transition frequency [30]. By setting ε_B > ε_E, the potential barrier between layers in the edge region is shallower than in the bulk region. This barrier difference leads to an inter-layer tunneling strength which is stronger in the edge than in the bulk. Moreover, we need to satisfy two additional conditions: (1) to have a smooth torus, the on-site energy in the edge and the bulk regions should be the same, and (2) this on-site energy should be smaller than the potential in the empty space, so that atoms are trapped in the designated square annulus. To find on-site energies in these conditions, we should include the zero point energies in the effective potentials as well. Then, these requirements can be summarized as

$$V_{\text{B}}^{(0)}+\frac{\hslash {\omega }_B}{2}=V_{\text{E}}^{(0)}+\frac{\hslash {\omega }_{\text{E}}}{2}<V_{\text{S}}$$ (3)

where the zero point energy of the harmonic confinements are $\hslash {\omega }_{\text{B}/\text{E}}/2=\frac{\hslash }{2}{\sum }_{s=x,y,z}\sqrt{m^{-1}{\partial }_s^{2}V(r){|}_{r\in \text{B}/\text{E}}}$. To evaluate this, we consider the total dipole potential V (r) = V_xy(x, y) + V_z(r), where the horizontal dipole potential is V_xy(x, y) = V₀{cos²(k_xx) + cos²(k_yy)} and V_z(r) is given in (Eq. 2). While it is not obvious to find a set of parameters satisfying these conditions simultaneously, it is possible to satisfy (Eq. 3) by tuning m, k_x, k_y, k_z, q_z, V₀, V_red, ε₊, ε_E, ε_B, f₀. For example, the parameters in Fig. 2 fulfill these requirements (see supplemental material [28]).

To verify that our beam design leads to the desired optical lattice, we numerically evaluate the total dipole potential for Rb⁸⁷ atoms [Figs. 2(a) and 2(b)]. We approximately evaluate the tunneling strengths by solving the Schrödinger equation over the region containing each pair of the nearest neighboring sites [28]. Fig. 2(c) shows that it is possible to suppress inter-layer tunneling in the bulk, while simultaneously setting inter-layer tunneling in the edge and intra-layer tunneling everywhere to be non-vanishing. Here, for boundaries between the different regions, we use more realistic resolution limited potentials [28] instead of the step functions in (Eq. 1).

Once our scheme for torus construction is realized, it is straightforward to extend the scheme to surfaces with higher genus [Fig. 1(b)]. The only requirement is to puncture more holes in the middle of the lattice, which requires no higher resolution in beam-shaping than puncturing a single hole. By generating surfaces with higher genus, one can explore richer topological physics, as we discuss later.

Quantized Supercurrents in Two Cycles.—

To demonstrate how topology plays a non-trivial role in the dynamics of ultracold atoms on a torus surface, we numerically investigated the hydrodynamics of weakly interacting bosonic superfluids. Previously, in a ring geometry, it has been experimentally demonstrated that the flow of supercurrents is quantized along the single quantization axis [12, 31]. The quantization of supercurrent results from the fact that wavefunction of the atomic condensate should be single-valued and its phase should be compact on a closed cycle. More interestingly, in the torus setting, there are two intersecting non-contractible cycles [Fig. 3(a)] which allow supercurrents to be quantized separately along each. In particular, the vorticity, which is defined as

$${\upsilon }_i=\frac{1}{2\pi {\rho }_{\text{avg}}}{\oint }_{\text{cycle }i}\text{Im}\left({\psi }^{*}\nabla \psi \right)\cdot \mathbf{\text{dl}}(i=1,2),$$ (4)

is quantized to an integer, up to a small finite-size fluctuation. Here, ρ_avg is the average condensate density and ψ(r) is the condensate wavefunction. To generate the supercurrents with non-zero vorticities, we stir the atomic condensate with an extra dipole potential [32]. In particular, we prepare a blue-detuned, focused beam and move it along each non-contractible cycle to generate the supercurrent flow in the stirring direction [Fig. 3(a)]. The supercurrent flows can be detected through established methods, such as time-of-flight imaging [31].

FIG. 3.

(a) A scheme to generate supercurrents in two cycles. A focused, blue-detuned laser beam acts as a stirrer along each cycle, namely, cycle 1 and 2. Note that the stirrer along cycle 2 is focused on the upper layer. A uniform condensate is loaded on the torus initially, then the stirring potential along cycle 1 (V₁) or cycle 2 (V₂) is ramped up and down. (b) Quantization of vorticity in two cycles. Dotted curves in the upper plots indicate the ramping sequences of V₁ and V₂. Solid lines in the upper plots indicate the number of completed cycles (m) in the stirring process. The lower plots show vorticities (v_i) changing over time. Steady-state wavefunctions of the different sequences are shown below.

To specifically show the quantization along the two non-contractible loops, we numerically simulate these stirring procedures [Fig. 3(b)]. In the weakly interacting and tight-binding regime, atomic dynamics in our optical lattice can be described in the mean-field approximation,

$$i\hslash {\partial }_t{\psi }_j^{\uparrow /\downarrow }=-J\sum _{k;|k-j|=1}{\psi }_k^{\uparrow /\downarrow }-\left(J{\psi }_j^{\downarrow /\uparrow }\right){\delta }_{j\in \text{edge}}+\left\{V^{\uparrow /\downarrow }\left(r_j,t\right)-\mu +U{\left|{\psi }_j^{\uparrow /\downarrow }\right|}^2\right\}{\psi }_j^{\uparrow /\downarrow },$$ (5)

where ${\psi }_j^l$ is the condensate wavefunction at site j on layer l, which can be ↑ / ↓ for the upper/lower layer. In this equation, |k−j| indicates the distance between site k and j within the same layer, while δ_j∈edge is 1 if j belongs to the edge region and 0 otherwise. J is the tunneling strength, U is the on-site interaction energy, V^l is the stirring potential on layer l and μ is the chemical potential. Superfluid remains stable if the stirring is slower than the sound speed, $\sqrt{\mu /m}$ [33]. This dynamics can be simulated with the numerical methods for the Gross-Pitaevskii equation [34–36]. See [28] for further details of the simulation.

In the simulation, we verify that the stirred superfluid exhibits the quantized vorticity along each cycle of stirring [Fig. 3(b)]. We also see that this vorticity increases with the stirring speed. As expected, the evaluated vorticity along each cycle coincides with the wavefunction winding numbers [Fig. 3(b)]. Also, we observe the creation and annihilation of vortex-antivortex pairs during the increment of vorticity [28].

Topological Degeneracy in FQH States.—

Our construction allows one to investigate the dynamics of strongly interacting ultracold atoms on a torus. As an example, we study a bosonic FQH model, which could be realized by laser-assisted tunneling [3, 4]. Specifically, the lattice FQH Hamiltonian for bosonic atoms on our torus can be written as

$$H=\sum _{n,m}\sum _{l=\uparrow ,\downarrow }(\frac{U}{2}{a}_{n,m}^{l†}{}^2{a}_{n,m}^l{}^2-J{e}^{i{\theta }_x^l}{a}_{n+1,m}^{l†}{a}_{n,m}^l-J{e}^{i{\theta }_y^l}{a}_{n,m+1}^{l†}{a}_{n,m}^l+\text{H}.\text{c}.)-\sum _{(n,m)\in \text{ edge }}\left(J^{\prime }{a}_{n,m}^{\uparrow †}{a}_{n,m}^{\downarrow }+\mathrm{ }\text{H.c.}\mathrm{ }\right),$$ (6)

where ${\theta }_x^{\uparrow /\downarrow }(n,m)=\frac{(n\mp m)\varphi }{2},{\theta }_y^{\uparrow /\downarrow }(n,m)=\frac{(m\pm n)\varphi }{2}$.

Here, $a_{n,m}^l$ annihilates an atom at site (n, m) on layer l. J and J′ are the effective intra- and inter-layer tunneling strengths, and U is the on-site interaction energy. With proper size of square annulus, the synthetic magnetic flux per unit cell can be set to ϕ [28]. To obtain the tunneling phases in (Eq. 6), we apply a magnetic field in such a way that the Zeeman energy gradient becomes Δ_x (Δ_y) per site in the x (y) direction. Then we apply Raman beams whose detuning matches with Δ_x (Δ_y) to induce the tunneling in the x (y) direction [Fig. 4(a)]. Since the surface orientations of two layers are opposite to each other, the required tunneling phases in each layer should be different as well. This can be achieved by targeting the different Raman beams on the different layers [Fig. 4(b)]. To do so, we use a triplet of beams for each tunneling term, namely T_i ≡ {i, i+, i−}, i = 1 to 4. Here, the beam i (i±) has the frequency ω_i (ω_i±) and the wavevector k_i (k_i±). In this triplet, the beams i+ and i− have the same x and y components and have the opposite z components in the wavevectors. These two beams then form a standing wave in z direction. By aligning the beams i+ and i− to destructively interfere at the lower (upper) layer, the beam triplet T_i can solely address the upper(lower) layer. In a rotating frame, these Raman beams result in the effective tunneling terms given in (Eq. 6) [28].

FIG. 4.

(a),(b) A scheme for FQH Hamiltonian. Different Raman beam triplets T₁ ~ T₄ give the different tunneling phases in Eq. (6). Schematic beam configuration of T₁ is shown for an example. Zeeman eneargy difference Δ_x (Δ_y) in the x (y) direction is matched with detuning of Raman beams in triplets T₁ and T₃ (T₂ and T₄) to give tunneling terms in the same direction. To address each layer independently, beam i+ and i− among triplet T₁ or T₂ (T₃ or T₄) destructively interfere at lower (upper) layer. (c) Exact diagonalization of FQH Hamiltonian for 3 hardcore bosonic atoms on a 6 × 6 square lattice (N_x = N_y = 6) with periodic boundary conditions and ϕ = π/3, magnetic length $l_B\equiv \sqrt{2\pi /\varphi }$. E_s(|ψ_s〉) indicates the s-th lowest eigenenergy (eigenstate). (d) Energy spectrums with distinct intra-layer (J) and inter-layer (J′) tunnelings. (e) Spectrum with a random disorder of scale 0.05J. Energy splitting between the ground states is 5×10⁻³J. (f) Inserting flux Φ_x through the handle of torus is equivalent to the boundary condition with twist angle α_x. (g) With additional potential V (y) = (0.01J/N_y)y, the spectral flows in α_x can be detected by measuring the y-coordinates of the states.

We numerically investigated the topological degeneracy in FQH system on the torus. In particular, FQH systems with filling fraction ν = 1/m on a torus surface have m-fold ground state degeneracies [15, 16]. To numerically diagonalize the FQH Hamiltonian, we put the upper layer part of Hamiltonian in (Eq. 6) on a 6 × 6 square lattice with periodic boundary conditions [Fig. 4(c)]. For filling fraction ν = 1/2, we have the anticipated two-fold degeneracy in the ground states [Fig. 4(d)].

To examine the robustness of this degeneracy, we diagonalize the same Hamiltonian with distinct intra-layer (J) and inter-layer (J′) tunnelings. As seen in Fig. 4(d), the two-fold degeneracy persists while J′ varies from J to 0.7J. As another test for the robustness of this degeneracy, we also diagonalize the same system with a disorder potential [Fig. 4(e)]. Here, we observe a slight splitting between the ground states, which is much smaller than disorder scale 0.05J and the excitation gap. Therefore, this topological degeneracy in a small FQH system is robust against potential experimental imperfections.

Furthermore, one can measure the topological degeneracy by measuring the spectral flow during the synthetic magnetic flux insertion though the handle of the torus. As shown in Fig. 4(f), the insertion of flux Φ_x is equivalent to the boundary condition ψ(x + N_x, y) = ψ(x, y) exp(iα_x) where α_x = (e/ħ)Φ_x. For ν = 1/m, the spectral flow of each ground state shows the 2mπ-periodicity in α_x [37, 38]. To observe this periodicity, we can introduce a small energy splitting by applying a potential V (y) ∝ y. Such a spectral flow is manifested in the y-coordinate expectation values of the ground states [Fig. 4(g)][28]. This average atom position can be experimentally detected through the density measurements.

Outlook.—

By introducing g punctures, we can generalize our scheme to a genus-g surface and leads to a topologically protected m^g-fold degenerate ground-state subspace for abelian and non-abelian FQH states. In that context, one can implement modular transformations to probe topological orders, measure fractional statistics, and realize fault-tolerant logical gates for topological quantum computations [39, 40].