Abstract
Influenza virus circulates in human, avian, and swine hosts, causing seasonal epidemic and occasional pandemic outbreaks. Influenza neuraminidase, a viral surface glycoprotein, has two sialic acid binding sites. The catalytic (primary) site, which also binds inhibitors such as oseltamivir carboxylate, is responsible for cleaving the sialic acid linkages that bind viral progeny to the host cell. In contrast, the functional annotation of the secondary site remains unclear. Here, we better characterize these two sites through the development of an all-atom, explicitly solvated, and experimentally based integrative model of the pandemic influenza A H1N1 2009 viral envelope, containing ∼160 million atoms and spanning ∼115 nm in diameter. Molecular dynamics simulations of this crowded subcellular environment, coupled with Markov state model theory, provide a novel framework for studying realistic molecular systems at the mesoscale and allow us to quantify the kinetics of the neuraminidase 150-loop transition between the open and closed states. An analysis of chloride ion occupancy along the neuraminidase surface implies a potential new role for the neuraminidase secondary site, wherein the terminal sialic acid residues of the linkages may bind before transfer to the primary site where enzymatic cleavage occurs. Altogether, our work breaks new ground for molecular simulation in terms of size, complexity, and methodological analyses of the components. It also provides fundamental insights into the understanding of substrate recognition processes for this vital influenza drug target, suggesting a new strategy for the development of anti-influenza therapeutics.
Short abstract
Molecular dynamics simulations and chloride ion analyses provide fundamental insights into the understanding of substrate recognition processes for two sialic binding sites of influenza neuraminidase.
Introduction
Influenza virus infection is responsible for millions of deaths worldwide each year. The Center for Disease Control estimates that pandemic influenza A H1N1 2009 (pH1N1) affected 60.8 million people, resulting in 12468 casualties in the United States alone.1,2 Along with others, this strain dramatically contributes to yearly epidemics, continuously fueling concerns about the emergence of a new pandemic strain. In addition, the increasingly widespread resistance to antiviral medications is compounding this threat,3 thus requiring the development of novel approaches for the prevention and treatment of influenza virus infection. One such strategy is to target the viral surface glycoprotein neuraminidase (NA), which promotes viral progeny release from the host cell by cleaving terminal sialic acid residues.4−6 Previous work has identified the importance of characterizing the dynamics of the NA catalytic site for drug design,7−12 understanding mechanisms of antiviral resistance,13 and deciphering the mechanisms underlying substrate binding.14−18
The catalytic (primary, 1°) site of NA is highly flexible, in part due to the adjacent 150- and 430-loops (residues 147–152 and 429–433, respectively, N2 numbering).11,14,19 The significance of this flexibility is highlighted by the structural comparison of the phylogenetically distinct group-1 (N1, N4, N5, and N8) and group-2 (N2, N3, N6, N7, and N9) NAs, which illustrates that the opening of the 150-loop in the group-1 structures leads to the formation of the so-called 150-cavity12 that can bind compounds with increased specificity and potency.10 However, crystal structures of pH1N1 NA (pN1) reveal that, unlike all other group-1 NAs, its 150-loop is closed, and therefore no 150-cavity is present.20 In contrast, previous investigations utilizing molecular dynamics (MD) simulations have found that the 150-loop of pN1 is in the open state ∼60–65% of the time.13,19,21
NA also contains a secondary (2°) sialic acid binding site adjacent to the catalytic site. This site was first identified as a hemadsorption site in avian-origin influenza NAs22−26 and was not initially believed to be present in swine-origin strains due to nonconservation of critical residues at this site.24,27 However, more recent studies provide support for the presence of a 2° site in swine-origin influenza NAs, including pN1.16,17 The precise mechanism by which this 2° site functions remains unclear; however, a number of studies have demonstrated its role in receptor binding28−32 and catalytic efficiency.28,29 In addition, previous Brownian dynamics (BD) simulations of single glycoproteins and various ligands suggested that both endogenous substrates and the drug oseltamivir carboxylate bind faster to the 2° site than the 1° site (i.e., the kon rate is 2- and 7-fold higher for the N1 and N2 2° site, respectively, vs the corresponding 1° site).17 Finally, the 2° site has recently been identified as a target for a novel influenza virus inhibitor,33,34 further highlighting the need to understand its role in viral infectivity.
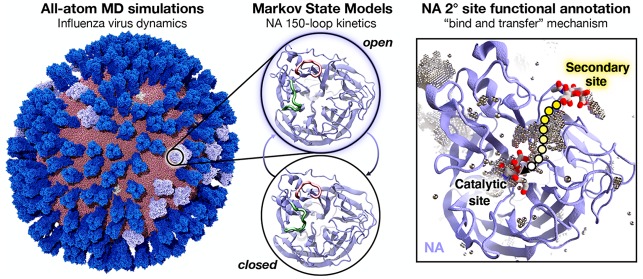
To study the 1° and 2° sites in the context of the viral surface, we used integrative modeling to construct a fully atomistic model of the pH1N1 viral envelope (Figure 1A, and Figure S1 of the Supporting Information (SI)). The model was built using high-resolution crystallographic structures of individual glycoproteins (∼1.9–2.6 Å resolution)20,35 that were spatially positioned according to a lower-resolution cryo-electron tomography (cryo-ET, ∼16–20 Å resolution) map of a viral particle.36 Our viral envelope construct includes 30 NA tetramers (120 monomers) and 236 hemagglutinin (HA) trimers (708 monomers) embedded in a phospholipid bilayer, with realistic density and patterning taken from the cryo-ET. The entire pH1N1 all-atom system modeled here amounts to ∼160 million atoms (fully solvated) and is ∼115 nm in diameter. As such, it is among the largest biophysical systems yet studied with all-atom molecular dynamics.37,38 A complete description of the integrative modeling and computational approaches used to build the viral envelope is provided in the SI (section S1.3). Additional details can also be found in Amaro et al.39
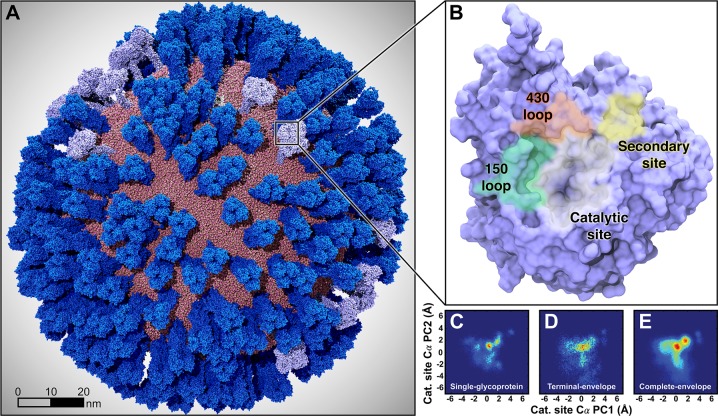
Figure 1.
Mesoscale simulations enhance conformational sampling of the viral glycoproteins. (A) A fully intact all-atom model of the influenza A H1N1 2009 (pH1N1) viral envelope, containing over 160 million atoms, shown without explicit water molecules, was simulated with all-atom MD simulations. Hemagglutinin (HA) glycoproteins shown in royal (dark) blue, neuraminidase (NA) glycoproteins shown in ice (light) blue. (B) Top view of a single NA monomer in surface representation with the catalytic site (white), secondary site (yellow), 150-loop (green), and 430-loop (red) highlighted. (C–E) Principal component analysis (PCA) was performed by considering the motions of the Cα atoms of 19 1° pocket residues. PCA histograms were independently normalized so the bins containing the minimum and maximum number of points were blue and red, respectively. (C) PCA of the four monomers sampled during a single-NA-tetramer simulation (“single-glycoprotein”). (D) PCA of the 120 monomeric trajectories extracted during the last 8.33 ns of the viral envelope simulation (“terminal-envelope”). (E) PCA of all 120 monomeric trajectories extracted from the full simulation of the viral envelope (“complete-envelope”).
Over the past decade, studies of viruses at the molecular and coarse-grained (CG) levels have given unique insights into these systems, complementing and extending available experimental data by providing highly detailed models at never-before-seen scales as well as suggesting testable biological hypotheses (predictions).40,41 Work by Schulten and co-workers established the first explicitly solvated atomic MD simulation of an intact virus, the satellite tobacco mosaic virus (∼17 nm diameter, ∼1 million atoms, 50 ns dynamics), in 2006.42 Zink and Grubmuller in 2009 used steered MD to explore the dynamics of the explicitly solvated icosahedral shell of the southern bean mosaic virus (∼36 nm diameter, ∼4.5 million atoms, 100 ns).43 In 2010, Ayton and Voth developed and simulated an implicitly solvated CG representation of the immature HIV-1 virion (∼125 nm diameter, 280,000 CG particles).44 In 2012, Larsson and co-workers simulated with explicitly solvated all-atom MD the satellite tobacco necrosis virus (∼17 nm diameter, ∼1.2 million atoms, ∼1 us),44 and Roberts et al. developed a fully atomic poliovirus (∼30 nm diameter, ∼2.8–4 million atoms, 50 ns).45 In 2013, Schulten and co-workers built and simulated a fully atomic representation of the HIV capsid (∼70 nm diameter, ∼64 million atoms, ∼100 ns),46 and Andoh et al. in 2014 simulated an all-atom poliovirus capsid (∼30 nm diameter, ∼6.5 million atoms, ∼200 ns).47 Sansom and colleagues in 2015 reported an explicitly solvated CG influenza virus simulation (∼80 nm diameter, 5 million particles).48 In two separate studies in 2016, Reddy and Sansom49 and Bond, Verma, and co-workers,50 reported CG simulations of the Dengue viral membrane (∼50 nm diameter, ∼1 million particles). In addition to the rich structural, dynamical, and biophysical insights that these studies each provided, the investigations have collectively pushed the capabilities of molecular simulation, often relying on the world’s fastest and most advanced computing architectures.
As the first explicitly solvated atomic-scale simulation of a viral lipid envelope (∼115 nm diameter, ∼160 million particles, ∼121 ns), the work reported here breaks new ground in molecular simulation. To further characterize the structural dynamics of the viral envelope and its glycoproteins, we combined our mesoscale all-atom MD simulations with Markov state model (MSM) theory,51−53 thus enabling the extraction of long-time-scale (e.g., microseconds) individual glycoprotein dynamics in a crowded environment from the short-time-scale MD (e.g., nanoseconds) of the fully intact viral surface. The accuracy and utility of MSMs have been demonstrated by experimental validation for many use cases, including protein–protein binding, small-molecule binding kinetics, and protein-folding rate prediction.54−56 Correspondingly, the approach reported here, which relies on the many copies of single glycoproteins present within a biologically accurate environment, provides a novel methodological advancement for extracting long-time-scale dynamics from short simulations through the powerful MSM theoretical framework at subcellular and cellular scales.
Here, we quantitatively compare how calculated protein dynamics differ when simulating many proteins in a single subcellular environment versus simulating single proteins in isolation. By exploiting the whole pH1N1 viral envelope treated entirely with atomic resolution, this study provides unique insights into the two sialic acid binding sites of NA (e.g., 1° and 2°). Our mesoscale atomic simulations suggest that the NA 1° site is even more flexible than previously appreciated and provide the first rigorous kinetic characterization of the 150-loop dynamics. Furthermore, our work suggests that the 2° site, which is more solvent exposed and, in some strains, has a higher kon rate than the 1° site,17,39 may be responsible for initially capturing sialic acid residues, which are then electrostatically guided to the 1° site for enzymatic cleavage. Within this context, our mesoscale simulations unveil an unprecedented cooperative interplay between the two sites that further illuminates the process of sialic acid/oseltamivir carboxylate recognition and 2° site functional annotation. This fundamental discovery may be used as a rationale for the development of novel anti-influenza small-molecule therapeutics targeting NA.
Influenza Virus All-Atom Simulations
All-atom MD simulations of the pH1N1 viral envelope were performed using NAMD2.1057 and CHARMM36 all-atom additive force fields.58 The system was fully solvated with explicit water molecules (TIP3P force field59), while ions were described using Beglov and Roux force fields.60 To broaden conformational sampling and more efficiently use supercomputer resources, the initial simulation was forked twice, generating two additional shorter daughter simulations (schematic representation in Figure S2). Taken together, these simulations achieved a comprehensive simulation time of ∼121 ns. The complete viral envelope simulation included 30 NA tetramers, yielding 14.5 μs of monomeric simulation (121 ns × 30 tetramers × 4 monomers/tetramer), and 236 HA tetramers, accounting for 85.6 μs of monomeric dynamics (121 ns × 236 tetramers × 3 monomers/trimer). Each glycoprotein structure used to build the initial viral envelope system was taken from fully equilibrated single-glycoprotein MD simulations (see sections S1.1–S1.2 for computational details relative to these sets of simulations). The viral envelope simulations were run on the Blue Waters petascale supercomputer using 114688 processors, equivalent to 16384 Blue Waters nodes or 4096 physical nodes. The simulation averaged 25.57 steps/sec. Frames were written every 10,000 steps (20 ps), ultimately occupying 11.66 terabytes of disk space. Data analysis drew upon conformations extracted at equally spaced time points from these trajectories. The adopted MD protocol for the viral envelope simulations is fully described in section S1.4, including the NAMD input file. The physical properties of the virus (RMSD, RMSF analyses) and its lipid bilayer (curvature, motions) per the simulations are reported in sections S1.5–S1.6 and shown in Figures S3–S9).
To explore the flexibility of the 1° pocket (shown in Figure S10), we concatenated the MD trajectories of all 120 NA monomers and performed principal component analysis (PCA) of 19 catalytic-pocket-lining NA residues by considering their Cα atoms (heatmap, Figure 1C–E). We selected these 19 residues because they are homologous to those within 5 Å of the crystallographic oseltamivir carboxylate from the 2HU4 structure.12 PCA details, including indices of the catalytic and active site residues used in the analysis, are provided in section S1.7.
To judge whether mesoscale simulations enhance conformational sampling, we compared the viral envelope full simulation (referred to as “complete-envelope”, Figure 1E) to five long time scale simulations of isolated NA tetramers embedded in small lipid-bilayer patches, described in a previous work (“single-glycoprotein”, Figure 1C).61 A fair comparison requires that the sampling of the two systems be consistent in terms of the actual simulation length. The viral envelope full simulation sampled 14.5 μs of monomeric dynamics, but the five simulations of isolated NA tetramers sampled only 1.0 μs of monomeric dynamics (5 simulations × 50 ns/simulation × 1 NA tetramer × 4 monomers/tetramer). Thus, to improve the comparison, we considered only the final 8.33 ns of the viral envelope simulation, which is equivalent to 1.0 μs of monomeric dynamics (1 simulation × 8.33 ns/simulation × 30 NA tetramers × 4 monomers/tetramer) (Figure 1D). We refer to this truncated segment of the full simulation as the “terminal-envelope” simulation. In all cases, the motions of the Cα atoms of the same 19 residues were projected onto the first two principal components of the viral envelope NA trajectories, and the resulting heatmaps were compared (Figure 1C–E). Strikingly, the PCA of the NA catalytic site residues indicates that the viral envelope simulation more thoroughly explored the conformational landscape, even after controlling for total simulation time.
To better study the 1° site conformations sampled by the viral envelope simulation, we applied k-means clustering to the PCA points of Figure 1E. A visual inspection of cluster centroids corresponding to four representative 1° site conformations (shown in Figure S10) reveals that R292 and R371, two key residues known to interact with the sialic acid carboxylate group, are the most flexible. In contrast, the carboxylate-stabilizing R152 residue moves outward in only one of the four representative conformations. Other pocket-lining residues such as R118 and D151, which previous works suggest may play a role in the molecular mechanisms of oseltamivir resistance,13 are also relatively flexible in the apo state.
The PCA analysis demonstrates that the viral envelope simulation more thoroughly sampled distinct 1° pocket states (Figure 1E) that are scarcely populated in the single glycoprotein (Figure 1C). This holds true even when comparing the terminal-envelope (Figure 1D) simulation to the single-glycoprotein simulations (where the total sampling time is equal). The enhanced conformational sampling may simply be a product of the large number of NA copies blanketed across the viral surface; however, we do expect some effects from the viral surface environment, including long-range electrostatic forces and glycoprotein–glycoprotein interactions that only the viral envelope simulation can capture.
pN1 Catalytic Site Structure and Dynamics
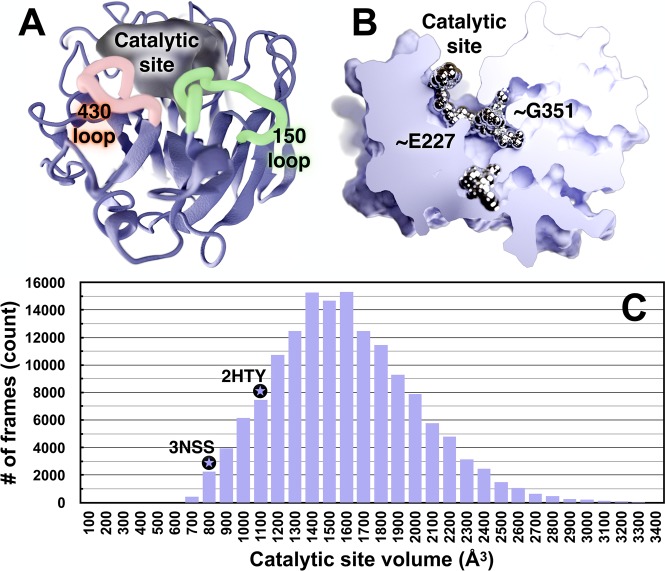
To explore the dynamics of the catalytic site, we analyzed the volumes of the 1° pocket and adjacent regions over the course of the entire viral envelope simulation (120 NA monomers, Figure 2).62 The volumes ranged from 450 to 4440 Å3, with an average of 1536 Å3 (Table S1 and section S1.8). By comparison, the starting crystal structure pN1 (PDB ID: 3NSS(20)) with a closed 150-cavity has a volume of 800 Å3, and the structure of a nonpandemic N1 (PDB ID: 2HTY(12)) with an open 150-cavity has a volume of 1088 Å3. This indicates that the volume and depth of the catalytic pocket and adjacent regions can increase remarkably over what has been observed in crystal structures (Figure 2C). Contributing to this additional cavity volume and depth are two novel subpockets near residues G351 and E227, buried deep inside, but contiguous with, the 1° site (Figure 2B). An analysis with FTMap, a server for mapping ligand binding hot spots in macromolecules,63 suggests that the G351 subpocket can accommodate small-molecule ligands. Similar to the 150-cavity and 430-cavity, the G351- and E227-adjacent subpockets may provide new ligand-binding opportunities.
Figure 2.
Volumetric and ligand binding “hot spot” analyses of the 1° catalytic site and adjacent regions. (A) NA is shown in ice blue ribbon, and the pocket volume is filled with semitransparent gel. The 1° active site, 430-loop, and 150-loop are visible. (B) NA is shown as a solid gradient, and ligand-binding hotspots are metallic. A portion of the surface-rendered protein was removed to facilitate visualization of internal cavities. This NA conformation has a notably open G351 pocket, which has a high propensity to bind ligands. (C) A histogram of the NA catalytic-site volumes sampled during the MD simulations. As reference, the volumes of the same active-site cavity from two crystal structures are indicated with black circled stars. The 3NSS(20) structure (pH1N1 with a closed 150-cavity) has a volume of 800 Å3, and the 2HTY(12) structure (H5N1 with an open 150-cavity) has a pocket volume of 1088 Å3. The simulated-pocket volumes range from ∼450 to 4440 Å3 (intervals 3500–4500 not shown), as reported in Table S1; the average pocket volume is 1536 Å3.
The volumetric and dynamical properties of the 1° site revealed in our simulations suggest that NA can bind many structurally distinct and complex sialoglycan receptors as part of the host-cell recognition process. Indeed, human glycans are vastly diverse in both their sugar composition and configuration (e.g., long, short, biantennary, triantennary, etc.).64 As such, the transient deepening and broadening of the 1° NA site may allow the glycoprotein to accommodate bulkier (e.g., long, bi/triantennary) and longer glycan receptors. Given that our simulations model the entire viral envelope, it may be that full-pocket opening only occurs in a crowded viral-surface environment. Alternatively, our simulations may capture full-pocket opening because the viral coat includes many replicates of individual glycoproteins, enabling extensive conformational sampling.
Using the intramolecular distance between the 150- and 430-loops as a metric for 150-cavity formation, we constructed a two-state MSM from the conformations sampled by the viral envelope simulation to estimate the time scales of 150-loop opening and closing motions. Ultimately, we find the stationary distribution (equilibrium probabilities) of the open and closed states to be similar (0.53 and 0.47, respectively). Correspondingly, the time to transition between the two states (i.e., the mean first-passage time (MFPT)) is also roughly equal (39 ± 15 ns for open to closed and 29 ± 11 ns from closed to open), indicating that loop opening and closing occur at similar rates (Figure 3). MSM calculations are detailed in section S1.9 and depicted in Figures S11–S14.
Figure 3.
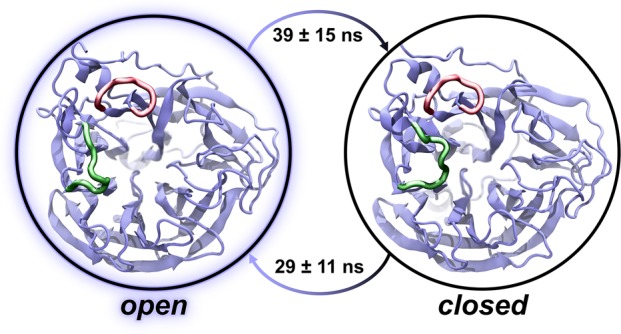
A two-state MSM with representative structures from the viral envelope simulation. The equilibrium populations of the open and closed states are approximately equal in both the viral envelope and single-glycoprotein simulations. Correspondingly, the mean first-passage times between the states are approximately equal. The 150-loop and 430-loop are represented as green and red ribbons, respectively.
To understand the impact of a crowded viral environment on loop sampling, we used the same protocol to construct an MSM from structures extracted from simulations of isolated NAs embedded in planar bilayer patches.61 The 150-loop dynamics of both the viral envelope and single-glycoprotein simulations are nearly equivalent; however, the error associated with the viral-envelope MSM is much smaller, likely due to the increased simulation time. The single-glycoprotein equilibrium probabilities of the open and closed states were 0.61 and 0.39, respectively, and the MFPT ranges (open to closed and closed to open after 50 ± 96 ns and 72 ± 44 ns, respectively) overlap with those calculated using the viral envelope simulations. This comparison suggests that 150-cavity dynamics are not influenced by the crowded environment of the viral envelope, an expected result given that this pocket is oriented inward (toward the neighboring three monomers of the same tetramer) rather than outward (toward the environment).
Secondary Binding Site: Functional Annotation
We note that all FDA-approved NA inhibitors, as well as the endogenous ligand sialic acid, contain negatively charged carboxylate groups. Considering the hypothesis that the 2° site contributes to catalytic efficiency by recruiting and keeping substrates within close proximity to the catalytic site28,29 and given that prior BD simulations indicate that substrates bind faster to the 2° site than the 1° site,17,39 we postulate that sialic acid first binds to the more solvent-exposed 2° site. Subsequently, the electrostatics of the NA surface guides the substrates to the 1° enzymatic site.
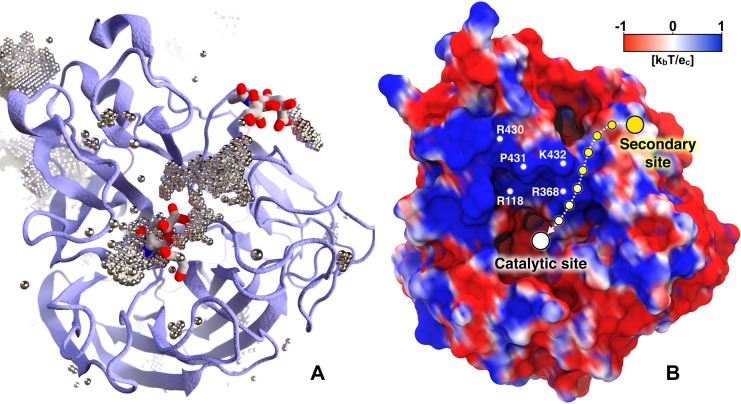
Although sialic acid substrates were not included in the viral envelope simulation, we propose that the negatively charged chloride anions in the bulk solvent surrounding the NA monomers serve as a rough surrogate for negatively charged ligand moieties that may associate with the glycoprotein surface. To identify regions favorable to chloride occupancy, we concatenated the 120 monomeric NA simulations and aligned them by the alpha carbons of the 1° site. The chloride atoms were binned into 3375000 voxels (0.67 Å × 0.67 Å × 0.67 Å each). We focused on voxels containing chloride counts greater than three standard deviations above the mean. Notably, our simulations reveal that a volume of high chloride occupancy connects the 1° and 2° sialic acid binding sites (Figure 4A). This path is wide enough to allow negatively charged small molecules such as sialic acid or oseltamivir carboxylate to move from the 2° site to the 1° catalytic site. Additional regions of high chloride density are also depicted in Figure 4A.
Figure 4.
Chlorine anion distribution within the NA binding sites. The chlorine anion distribution (A) and the projection of the electrostatic potential onto the NA surface (B) show the pathway between the 1° and 2° sites. In panel A, NA is drawn as ice blue cartoon. Regions of high chloride occupancy are illustrated as dotted silver bubbles. Two sialic acids (PDB ID: 1MWE(24)) are superimposed in the catalytic (center) and 2° (upper right) sites for reference.24 In panel B the NA surface is colored with a palette varying from red (negative) to royal blue (positive), representing electrostatic potential values of −1 kbT/ec and +1 kbT/ec, respectively. The path connecting the 2° site with the catalytic site is shown as a dashed arrow between circles fading from yellow (2° site) to white (catalytic site).
To further explore the role of electrostatics in the in this transfer mechanism, we calculated the electrostatic potential of the 120 NA monomers at the end of MD simulations using the adaptive Poisson–Boltzmann solver (APBS 1.4) software.65 When projected onto the NA surface, the electrostatic potential ranging from −1 kbT/ec to +1 kbT/ec shows a positive region connecting the two sites (Figure 4B). Positively charged residues such as R118, R368, R430, K432, and P431 (N2 numbering scheme) largely determine this profile. Interestingly, the same analysis performed on the representative NA structures with open and closed 150-loop pockets (extracted with MSM and shown in Figure 3) reveals that these residues are less exposed in the closed state (Figure S15). These results provide evidence that the two sites may act cooperatively, supporting the work of Lai et al.,16 which confirmed that pN1 has a 2° site that can bind sialic acid. It also supports the work of Le et al.,66 which suggested electrostatic funneling as being the main driving force for oseltamivir carboxylate association to the active site. Chloride anion and electrostatic analyses are detailed in section S1.10.
Taken together, these results suggest a biophysical mechanism for the previously uncharacterized 2° site. Sialic acid receptors may first bind the 2° site before being transferred to the 1° sialidase site (Figure 5). We propose that our chloride distribution analysis is well suited for studying these possible mechanisms of molecular transfer. In contrast to a simple electrostatic map, our simulation-based analysis accounts for both electrostatic and steric factors, as well as for the conformational dynamics sampled over all 14.5 μs of the monomeric simulation in the context of the whole viral-envelope environment. In addition, the proposed “bind and transfer” mechanism is in good agreement with prior experimental results and proposed mechanisms.28
Figure 5.
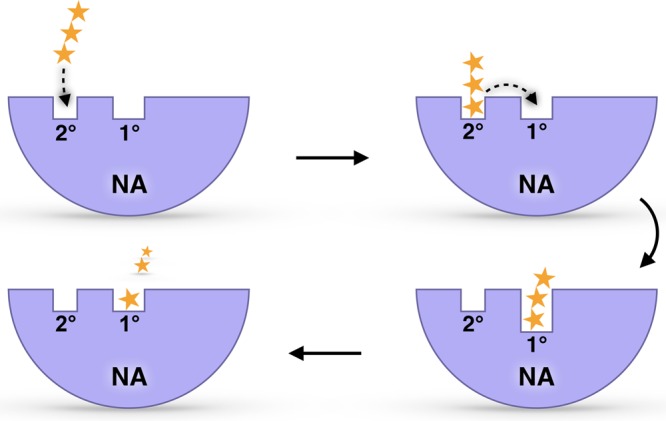
The predicted sialic acid “bind and transfer” mechanism. Yellow stars represent a sialic-acid-containing glycan receptor. Ice blue half circles represent NA. The 1° catalytic site and 2° site are also labeled.
Conclusions
Our work suggests a novel NA binding mechanism wherein a sialic acid-containing substrate (e.g., a glycan receptor) first binds the 2° site, as predicted by earlier BD simulations.17 After binding, the substrate is transferred to the catalytic site via electrostatic interactions. Finally, the catalytic site cleaves the terminal sialic acid substrate. In other words, a budding viral particle might use the 2° site to first attract the sialic acid-tipped receptors before these are cleaved within the catalytic site, ultimately allowing viral escape from the infected host-cell surface. MSM and volumetric analyses also further expand the functional annotation of the 1° site and surrounding regions, disclosing exceptionally deep and broad catalytic-pocket conformations. These findings can be exploited to design novel multipronged inhibitors capable of reaching the additional NA cavities unveiled in our multiscale simulations.
Taken together, this information provides fundamental insights into our understanding of sialic acid/oseltamivir carboxylate recognition, suggesting new strategies for the development of NA inhibitors. Our work also provides a novel methodological advancement for extracting long-time-scale dynamics from short-time-scale simulations by applying the powerful MSM theoretical framework at subcellular and cellular scales.
Acknowledgments
This work was funded in part by the Director’s New Innovator Award Program NIH DP2 OD007237 and the National Biomedical Computation Resource (NBCR) through NIH P41 GM103426 to R.E.A. Computing support on the NSF Blue Waters Petascale Computer was provided through NSF OAC-1811685. We thank the NSF for access to the TACC Stampede supercomputer through CHE060073N to R.E.A. and the Center for Research Computing at the University of Pittsburgh for a computing allocation to J.D.D.. The authors also thank Dr. Robert Malmstrom for providing sample MSM-building scripts and useful discussions. This work is dedicated to the memory of Klaus Schulten.
Supporting Information Available
Supporting Information available online. The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acscentsci.9b01071.
A NAMD input script used for the production run and the Jupyter notebook used to create the MSM are provided as Supporting Information. Additional analysis scripts are available upon request. In addition, the Supporting Information includes the following: supplementary materials and methods, information regarding building single-glycoprotein HA and NA structural models, details of the single-glycoprotein HA and NA MD simulations, information regarding building the viral envelope model from a simplified cryoelectron-tomography “point model”, complete viral envelope all-atom MD simulations, RMSD and RMSF analyses of the viral envelope MD simulations, viral envelope lipid and curvature analysis, NA catalytic-site PCA, volumetric and FTMap analysis, MSMs, and chloride anion and electrostatic analyses (PDF)
Author Contributions
§ J.D.D., S.E.K., and L.C. contributed equally. R.E.A. designed and oversaw the research project. J.D.D. built the structures and performed the MD simulations. R.E.A., J.D.D., S.E.K., L.C., P.U.L., and A.D. performed the simulation analyses. J.D.D, L.C., P.U.L., and A.D. created the figures. R.E.A., J.D.D., S.E.K., L.C., P.U.L., and A.D. wrote the paper.
The authors declare the following competing financial interest(s): R.E.A. is a cofounder and on the scientific advisory board of, and has equity interest in, Actavalon, Inc.
Supplementary Material
References
- Centers for Disease Control and Prevention . Summary of the 2017–2018 Influenza Season; United States Centers for Disease Control and Prevention: 2018; Vol. 11, pp. 7–10.
- Wang X.; et al. Epidemiology of avian influenza A H7N9 virus in human beings across five epidemics in mainland China, 2013–17: an epidemiological study of laboratory-confirmed case series. Lancet Infect. Dis. 2017, 17, 822–832. 10.1016/S1473-3099(17)30323-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Clercq E. Antiviral agents active against influenza A viruses. Nat. Rev. Drug Discovery 2006, 5, 1015–1025. 10.1038/nrd2175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamilton B. S.; Whittaker G. R.; Daniel S. Influenza virus-mediated membrane fusion: determinants of hemagglutinin fusogenic activity and experimental approaches for assessing virus fusion. Viruses 2012, 4, 1144–1168. 10.3390/v4071144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- von Itzstein M. The war against influenza: discovery and development of sialidase inhibitors. Nat. Rev. Drug Discovery 2007, 6, 967–974. 10.1038/nrd2400. [DOI] [PubMed] [Google Scholar]
- Gamblin S. J.; Skehel J. J. Influenza hemagglutinin and neuraminidase membrane glycoproteins. J. Biol. Chem. 2010, 285, 28403–28409. 10.1074/jbc.R110.129809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- An J.; et al. A novel small-molecule inhibitor of the avian influenza H5N1 virus determined through computational screening against the neuraminidase. J. Med. Chem. 2009, 52, 2667–2672. 10.1021/jm800455g. [DOI] [PubMed] [Google Scholar]
- Feng E.; et al. Structure-based design and synthesis of C-1- and C-4-modified analogs of zanamivir as neuraminidase inhibitors. J. Med. Chem. 2013, 56, 671–684. 10.1021/jm3009713. [DOI] [PubMed] [Google Scholar]
- Wen W. H.; et al. Analogs of zanamivir with modified C4-substituents as the inhibitors against the group-1 neuraminidases of influenza viruses. Bioorg. Med. Chem. 2010, 18, 4074–4084. 10.1016/j.bmc.2010.04.010. [DOI] [PubMed] [Google Scholar]
- Rudrawar S.; Dyason J. C.; Rameix-Welti M.-A.; Rose F. J.; Kerry P. S.; Russell R. J. M.; van der Werf S.; Thomson R. J.; Naffakh N.; von Itzstein M. Novel sialic acid derivatives lock open the 150-loop of an influenza A virus group-1 sialidase. Nat. Commun. 2010, 1, 113. 10.1038/ncomms1114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amaro R. E.; et al. Remarkable Loop Flexibility in Avian Influenza N1 and Its Implications for Antiviral Drug Design. J. Am. Chem. Soc. 2007, 129, 7764–7765. 10.1021/ja0723535. [DOI] [PubMed] [Google Scholar]
- Russell R. J.; et al. The structure of H5N1 avian influenza neuraminidase suggests new opportunities for drug design. Nature 2006, 443, 45–49. 10.1038/nature05114. [DOI] [PubMed] [Google Scholar]
- Woods C. J.; et al. Long time scale GPU dynamics reveal the mechanism of drug resistance of the dual mutant I223R/H275Y neuraminidase from H1N1–2009 influenza virus. Biochemistry 2012, 51, 4364–4375. 10.1021/bi300561n. [DOI] [PubMed] [Google Scholar]
- Amaro R. E.; Cheng X.; Ivanov I.; Xu D.; McCammon J. A. A. Characterizing Loop Dynamics and Ligand Recognition in Human- and Avian-Type Influenza Neuraminidases via Generalized Born Molecular Dynamics and End-Point Free Energy Calculations. J. Am. Chem. Soc. 2009, 131, 4702–4709. 10.1021/ja8085643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hausmann J.; Kretzschmar E.; Garten W.; Klenk H.-D. N1 neuraminidase of influenza virus A/FPV/Rostock/34 has haemadsorbing activity. J. Gen. Virol. 1995, 76, 1719–1728. 10.1099/0022-1317-76-7-1719. [DOI] [PubMed] [Google Scholar]
- Lai J. C. C.; et al. A secondary sialic acid binding site on influenza virus neuraminidase: Fact or fiction?. Angew. Chem., Int. Ed. 2012, 51, 2221–2224. 10.1002/anie.201108245. [DOI] [PubMed] [Google Scholar]
- Sung J. C.; Wynsberghe A. W. V.; Amaro R. E.; Li W. W.; McCammon J. A. Role of Secondary Sialic Acid Binding Sites in Influenza N1 Neuraminidase. J. Am. Chem. Soc. 2010, 132, 2883–2885. 10.1021/ja9073672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang T.; Wade R. C. Comparative Binding Energy (COMBINE) Analysis of Influenza Neuraminidase-Inhibitor Complexes. J. Med. Chem. 2001, 44, 961–971. 10.1021/jm001070j. [DOI] [PubMed] [Google Scholar]
- Amaro R. E.; Swift R. V.; Votapka L.; Li W. W.; Walker R. C.; Bush R. M. Mechanism of 150-cavity formation in influenza neuraminidase. Nat. Commun. 2011, 2, 388. 10.1038/ncomms1390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Q.; et al. The 2009 pandemic H1N1 neuraminidase N1 lacks the 150-cavity in its active site. Nat. Struct. Mol. Biol. 2010, 17, 1266–1268. 10.1038/nsmb.1909. [DOI] [PubMed] [Google Scholar]
- Han N.; Mu Y. Plasticity of 150-Loop in Influenza Neuraminidase Explored by Hamiltonian Replica Exchange Molecular Dynamics Simulations. PLoS One 2013, 8, e60995 10.1371/journal.pone.0060995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laver W. G.; Colman P. M.; Webster R. G.; Hinshaw V. S.; Air G. M. Influenza virus neuraminidase with hemagglutinin activity. Virology 1984, 137, 314–323. 10.1016/0042-6822(84)90223-X. [DOI] [PubMed] [Google Scholar]
- Webster R. G.; et al. Antigenic structure and variation in an influenza virus N9 neuraminidase. J. Virol. 1987, 61, 2910–6. 10.1128/JVI.61.9.2910-2916.1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varghese J. N.; et al. Structural evidence for a second sialic acid binding site in avian influenza virus neuraminidases. Proc. Natl. Acad. Sci. U. S. A. 1997, 94, 11808–11812. 10.1073/pnas.94.22.11808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Air G. M. Influenza neuraminidase. Influenza Other Respir. Viruses 2012, 6, 245–256. 10.1111/j.1750-2659.2011.00304.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Streltsov V. A.; Pilling P.; Barrett S.; McKimm-Breschkin J. L. Catalytic mechanism and novel receptor binding sites of human parainfluenza virus type 3 hemagglutinin-neuraminidase (hPIV3 HN). Antiviral Res. 2015, 123, 216–223. 10.1016/j.antiviral.2015.08.014. [DOI] [PubMed] [Google Scholar]
- Kobasa D.; Rodgers M. E.; Wells K.; Kawaoka Y. Neuraminidase hemadsorption activity, conserved in avian influenza A viruses, does not influence viral replication in ducks. J. Virol. 1997, 71, 6706–6713. 10.1128/JVI.71.9.6706-6713.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uhlendorff J.; Matrosovich T.; Klenk H.-D.; Matrosovich M. Functional significance of the hemadsorption activity of influenza virus neuraminidase and its alteration in pandemic viruses. Arch. Virol. 2009, 154, 945–957. 10.1007/s00705-009-0393-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dai M.; McBride R.; Dortmans J. C. F. M.; Peng W.; Bakkers M. J. G.; de Groot R. J.; van Kuppeveld F. J. M.; Paulson J. C.; de Vries E.; de Haan C. A. M. Mutation of the Second Sialic Acid-Binding Site, Resulting in Reduced Neuraminidase Activity, Preceded the Emergence of H7N9 Influenza A Virus. J. Virol. 2017, 91, 91. 10.1128/JVI.00049-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Du W.; Dai M.; Li Z.; Boons G. J.; Peeters B.; van Kuppeveld F. J. M.; de Vries E.; de Haan C. A. M. Substrate Binding by the Second Sialic Acid-Binding Site of Influenza A Virus N1 Neuraminidase Contributes to Enzymatic Activity. J. Virol. 2018, 92, e01243–18. 10.1128/JVI.01243-18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Du W.; et al. The 2nd sialic acid-binding site of influenza A virus neuraminidase is an important determinant of the hemagglutinin-neuraminidase-receptor balance. PLoS Pathog. 2019, 15, e1007860 10.1371/journal.ppat.1007860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeller F.; Luitz M. P.; Bomblies R.; Zacharias M. Multiscale Simulation of Receptor–Drug Association Kinetics: Application to Neuraminidase Inhibitors. J. Chem. Theory Comput. 2017, 13, 5097–5105. 10.1021/acs.jctc.7b00631. [DOI] [PubMed] [Google Scholar]
- Ivinson K.; Deliyannis G.; McNabb L.; Grollo L.; Gilbertson B.; Jackson D.; Brown L. E. Salivary Blockade Protects the Lower Respiratory Tract of Mice from Lethal Influenza Virus Infection. J. Virol. 2017, 91, e00624–17. 10.1128/JVI.00624-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilbertson B.; Ng W. C.; Crawford S.; McKimm-Breschkin J. L.; Brown L. E. Mouse Saliva Inhibits Transit of Influenza Virus to the Lower Respiratory Tract by Efficiently Blocking Influenza Virus Neuraminidase Activity. J. Virol. 2017, 91, e00145–17. 10.1128/JVI.00145-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu R.; et al. Structural Basis of Preexisting Immunity to the 2009 H1N1 Pandemic Influenza Virus. Science (Washington, DC, U. S.) 2010, 328, 357–360. 10.1126/science.1186430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris A.; et al. Influenza virus pleiomorphy characterized by cryoelectron tomography. Proc. Natl. Acad. Sci. U. S. A. 2006, 103, 19123–19127. 10.1073/pnas.0607614103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singharoy A.; et al. Atoms to Phenotypes: Molecular Design Principles of Cellular Energy Metabolism. Cell 2019, 179, 1098–1111. 10.1016/j.cell.2019.10.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karplus M. Development of Multiscale Models for Complex Chemical Systems: From H+H 2 to Biomolecules (Nobel Lecture). Angew. Chem., Int. Ed. 2014, 53, 9992–10005. 10.1002/anie.201403924. [DOI] [PubMed] [Google Scholar]
- Amaro R. E.; et al. A Computational Assay that Explores the Hemagglutinin/Neuraminidase Functional Balance Reveals the Neuraminidase Secondary Site as a Novel Anti-Influenza Target. ACS Cent. Sci. 2018, 4, 1570–1577. 10.1021/acscentsci.8b00666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hadden J. A.; Perilla J. R. All-atom virus simulations. Curr. Opin. Virol. 2018, 31, 82–91. 10.1016/j.coviro.2018.08.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huber R. G.; Marzinek J. K.; Holdbrook D. A.; Bond P. J. Multiscale molecular dynamics simulation approaches to the structure and dynamics of viruses. Prog. Biophys. Mol. Biol. 2017, 128, 121–132. 10.1016/j.pbiomolbio.2016.09.010. [DOI] [PubMed] [Google Scholar]
- Freddolino P. L.; Arkhipov A. S.; Larson S. B.; McPherson A.; Schulten K. Molecular dynamics simulations of the complete satellite tobacco mosaic virus. Structure 2006, 14, 437–449. 10.1016/j.str.2005.11.014. [DOI] [PubMed] [Google Scholar]
- Zink M.; Grubmüller H. Mechanical properties of the icosahedral shell of southern bean mosaic virus: A molecular dynamics study. Biophys. J. 2009, 96, 1350–1363. 10.1016/j.bpj.2008.11.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ayton G. S.; Voth G. A. Multiscale computer simulation of the immature HIV-1 virion. Biophys. J. 2010, 99, 2757–2765. 10.1016/j.bpj.2010.08.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roberts J. A.; Kuiper M. J.; Thorley B. R.; Smooker P. M.; Hung A. Investigation of a predicted N-terminal amphipathic α-helix using atomistic molecular dynamics simulation of a complete prototype poliovirus virion. J. Mol. Graphics Modell. 2012, 38, 165–173. 10.1016/j.jmgm.2012.06.009. [DOI] [PubMed] [Google Scholar]
- Zhao G.; et al. Mature HIV-1 capsid structure by cryo-electron microscopy and all-atom molecular dynamics. Nature 2013, 497, 643–646. 10.1038/nature12162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andoh Y.; et al. All-atom molecular dynamics calculation study of entire poliovirus empty capsids in solution. J. Chem. Phys. 2014, 141, 165101. 10.1063/1.4897557. [DOI] [PubMed] [Google Scholar]
- Reddy T.; et al. Nothing to Sneeze At: A Dynamic and Integrative Computational Model of an Influenza A Virion. Structure 2015, 23, 584–597. 10.1016/j.str.2014.12.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reddy T.; Sansom M. S. P. The Role of the Membrane in the Structure and Biophysical Robustness of the Dengue Virion Envelope. Structure 2016, 24, 375–382. 10.1016/j.str.2015.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marzinek J. K.; Holdbrook D. A.; Huber R. G.; Verma C.; Bond P. J. Pushing the Envelope: Dengue Viral Membrane Coaxed into Shape by Molecular Simulations. Structure 2016, 24, 1410–1420. 10.1016/j.str.2016.05.014. [DOI] [PubMed] [Google Scholar]
- Pande V. S.; Beauchamp K.; Bowman G. R. Everything you wanted to know about Markov State Models but were afraid to ask. Methods 2010, 52, 99–105. 10.1016/j.ymeth.2010.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prinz J. H.; et al. Markov models of molecular kinetics: Generation and validation. J. Chem. Phys. 2011, 134, 174105. 10.1063/1.3565032. [DOI] [PubMed] [Google Scholar]
- Chodera J. D.; Noé F. Markov state models of biomolecular conformational dynamics. Curr. Opin. Struct. Biol. 2014, 25, 135–144. 10.1016/j.sbi.2014.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plattner N.; Noé F. Protein conformational plasticity and complex ligand-binding kinetics explored by atomistic simulations and Markov models. Nat. Commun. 2015, 6, 7653. 10.1038/ncomms8653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plattner N.; Doerr S.; De Fabritiis G.; Noé F. Complete protein-protein association kinetics in atomic detail revealed by molecular dynamics simulations and Markov modelling. Nat. Chem. 2017, 9, 1005–1011. 10.1038/nchem.2785. [DOI] [PubMed] [Google Scholar]
- Voelz V. A.; Bowman G. R.; Beauchamp K.; Pande V. S. Molecular Simulation of ab Initio Protein Folding for a Millisecond Folder NTL9(1–39). J. Am. Chem. Soc. 2010, 132, 1526–1528. 10.1021/ja9090353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phillips J. C.; et al. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang J.; MacKerell A. D. CHARMM36 all-atom additive protein force field: Validation based on comparison to NMR data. J. Comput. Chem. 2013, 34, 2135–2145. 10.1002/jcc.23354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926. 10.1063/1.445869. [DOI] [Google Scholar]
- Beglov D.; Roux B. Finite representation of an infinite bulk system: Solvent boundary potential for computer simulations. J. Chem. Phys. 1994, 100, 9050–9063. 10.1063/1.466711. [DOI] [Google Scholar]
- Durrant J. D.; Bush R. M.; Amaro R. E. Microsecond Molecular Dynamics Simulations of Influenza Neuraminidase Suggest a Mechanism for the Increased Virulence of Stalk-Deletion Mutants. J. Phys. Chem. B 2016, 120, 8590–8599. 10.1021/acs.jpcb.6b02655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durrant J. D.; Votapka L.; Sørensen J.; Amaro R. E. POVME 2.0: An Enhanced Tool for Determining Pocket Shape and Volume Characteristics. J. Chem. Theory Comput. 2014, 10, 5047–5056. 10.1021/ct500381c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ngan C. H.; et al. FTMAP: extended protein mapping with user-selected probe molecules. Nucleic Acids Res. 2012, 40, W271–5. 10.1093/nar/gks441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marino K.; Bones J.; Kattla J. J.; Rudd P. M. A systematic approach to protein glycosylation analysis: a path through the maze. Nat. Chem. Biol. 2010, 6, 713–723. 10.1038/nchembio.437. [DOI] [PubMed] [Google Scholar]
- Baker N. A.; Sept D.; Joseph S.; Holst M. J.; McCammon J. A. Electrostatics of nanosystems: application to microtubules and the ribosome. Proc. Natl. Acad. Sci. U. S. A. 2001, 98, 10037–41. 10.1073/pnas.181342398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le L.; Lee E. H.; Hardy D. J.; Truong T. N.; Schulten K. Molecular Dynamics Simulations Suggest that Electrostatic Funnel Directs Binding of Tamiflu to Influenza N1 Neuraminidases. PLoS Comput. Biol. 2010, 6, e1000939 10.1371/journal.pcbi.1000939. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.