Significance
Unveiling the unusual atomic dynamics in superionic conductors is critical for the design of energy conversion and storage materials, for example to rationalize their thermal transport properties in thermoelectric applications or their fast ionic conductivity in solid-state electrolytes. We combine neutron/X-ray scattering techniques with first-principles calculations to discover hybrid lattice dynamics in , where the phonon wavelength controls the breakdown of transverse acoustic modes in the superionic phase. We attribute the ultralow thermal conductivity to strong phonon anharmonicity combined with disorder in the Ag sublattice. This understanding provides insights into the thermal conduction mechanism in superionic conductors and sheds light on the role of lattice dynamics in the emergence of superionic behavior.
Keywords: superionic conductor, thermoelectrics, thermal transport, anharmonic lattice dynamics
Abstract
Intrinsically low lattice thermal conductivity () in superionic conductors is of great interest for energy conversion applications in thermoelectrics. Yet, the complex atomic dynamics leading to superionicity and ultralow thermal conductivity remain poorly understood. Here, we report a comprehensive study of the lattice dynamics and superionic diffusion in from energy- and momentum-resolved neutron and X-ray scattering techniques, combined with first-principles calculations. Our results settle unresolved questions about the lattice dynamics and thermal conduction mechanism in . We find that the heat-carrying long-wavelength transverse acoustic (TA) phonons coexist with the ultrafast diffusion of Ag ions in the superionic phase, while the short-wavelength nondispersive TA phonons break down. Strong scattering of phonon quasiparticles by anharmonicity and Ag disorder are the origin of intrinsically low . The breakdown of short-wavelength TA phonons is directly related to the Ag diffusion, with the vibrational spectral weight associated to Ag oscillations evolving into stochastic decaying fluctuations. Furthermore, the origin of fast ionic diffusion is shown to arise from extended flat basins in the energy landscape and collective hopping behavior facilitated by strong repulsion between Ag ions. These results provide fundamental insights into the complex atomic dynamics of superionic conductors.
Superionic conductors (SICs) are materials with crystalline frameworks and liquid-like sublattices, harboring ionic conductivities comparable to those of liquids at room temperature (1). Fast ionic diffusion is attracting considerable interest for next-generation batteries, as high diffusivities and stable structures are required for high-efficiency solid-states electrolytes (1–3). Thermoelectric (TE) applications also benefit from SICs as they tend to exhibit intrinsically low lattice thermal conductivities (), boosting the TE conversion efficiency (4–6), and recent progress achieved stabilized SICs in TE devices (7). In conventional crystalline materials, strategies to suppress target the scattering of acoustic phonons, which tend to carry most of the heat. Common strategies include introducing defects via doping and alloying, using complex micro/nanostructures or engineering grain boundaries (8–12), as well as leveraging rattler vibrational modes in cage-like structures (13–15). Alternatively, the atomic dynamics of SIC spontaneously yield ultralow below 1 . In the superionic phase, a sublattice within the structure becomes unstable and its ions become highly mobile, diffusing from their equilibrium positions, while the electronic conductivity of the framework structure remains high, a behavior referred to as a phonon–liquid electron–crystal (PLEC) (4, 16–18).
Nevertheless, the precise mechanisms underlying these peculiar atomic dynamics and their role in the ultralow remain poorly understood. Centrally, it remains unclear whether long-wavelength, low-energy TA phonon modes, which are characteristic of shear elasticity in crystals, can persist in the superionic regime where part of the atomic structure is delocalized as in a liquid. In one scenario, a loss of shear modes propagating as TA phonons has been proposed to generate a liquid-like thermal conduction mechanism dominated by longitudinal phonons (compressive waves) with phonon mean free paths close to interatomic spacings (4, 19). Alternatively, strong anharmonicity, rattler modes, and disorder have been argued to be the main mechanisms of suppression (12, 20–24). Using inelastic neutron scattering (INS), inelastic X-ray scattering (IXS), and first-principles simulations of atomic dynamics, we obtain a detailed picture of atomic dynamics in that provides a much clearer understanding of its superionic and thermal transport properties.
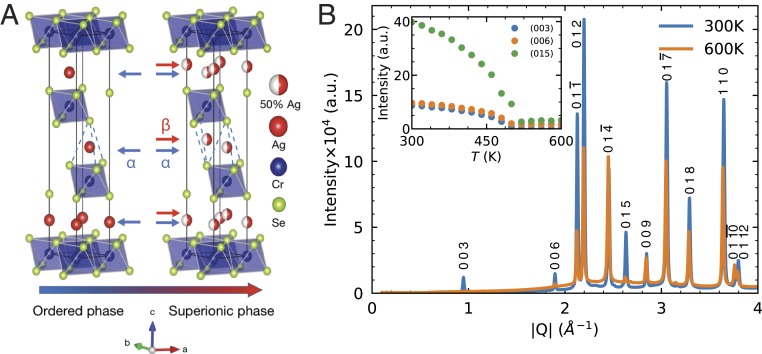
was recently reported to achieve promising TE performance, with a figure-of-merit of 0.81 at 773 K, in part enabled by an extremely low of 0.4 (25, 26). The was optimized to 1.4 in (AgCrSe2)0.5 (CuCrSe2)0.5 nanocomposites (25). AgCrSe2 belongs to the family of ternary triangular chalcogenides MM′X2 (M = Cu, Ag; M′ = Cr; X = S, Se), which crystallize in a rhombohedral primitive cell and display superionicity and very low at high temperature (17, 19, 27–32). A pseudohexagonal conventional cell is usually used to describe the structure with layers of octahedra (blue polyhedra) alternating with intercalation layers of Ag ions (red), as shown in Fig. 1A. At low temperatures, the structure adopts space group (no. 160), and all Ag ions occupy the tetrahedral sites coordinated by Se atoms (dashed blue lines). Above an order–disorder transition temperature 475 K (superionic transition), the Ag ions become disordered across sites and the symmetry equivalent sites (images of the former by an inversion symmetry), changing the space group into (no. 166). In this high- phase, the Ag ions hop between and sites with a high diffusion constant (30). The CrSe sublattice remains rigid and crystalline. The order–disorder transition in is reversible and somewhat gradual with the diffusion of Ag ions starting already 80 K below (19). In addition, antiferromagnetic ordering of spins sets in below 55 K (33, 34), but short-ranged dynamic magnetic correlations persist up to 200 K, far above , and strongly impact , which does not follow the regular dependence below 200 K (17).
Fig. 1.
Crystal structure and phase transition in . () Crystal structure of . Ag, Cr, and Se atoms are shown in red, blue, and green, respectively. Half-red–half-white spheres indicate 50% occupancy of Ag atoms. The blue dashed lines indicate the Se tetrahedron. Below 475 K, the sites are fully occupied. Above , both and sites are occupied with 50% probability. () X-ray powder diffraction pattern at 300 K (blue) and 600 K (orange), obtained from APS sector 11-ID-C ( 105.708 keV). Inset shows the integrated intensities of (003), (006), and (015) Bragg peaks as a function of temperature on heating, plotted as blue, orange, and green dots, respectively. The intensities are suppressed around nominal temperature 500 K.
Based on neutron scattering measurements on powder samples, a recent study attributed the low of to a disappearance of TA phonons, drawing an analogy with a liquid state, where vibrational degrees of freedom associated with shear modes are lost (19). A parallel investigation of the isostructural compound established the persistence of long-wavelength TA phonons in the superionic phase via IXS measurements on single crystals and attributed the suppression of to the strong lattice anharmonicity and the additional phonon scattering resulting from the disordered distribution of Cu ions between and sites above (22). Thus, the analogy between the superionic phase and the liquid state in needs to be further investigated.
Here, we report observations of the coexistence of long-wavelength dispersive TA phonons, which are important heat carriers, with superionic diffusion and the selective breakdown of the nondispersive TA phonons in using INS and IXS, which are further corroborated by computational modeling based on density functional theory (DFT) and molecular dynamics (AIMD) simulations. INS measurements on powder samples reveal the temperature evolution of the lattice dynamics via the phonon density of states (DOS) and quasielastic neutron scattering (QENS) signals and reveal that, in the superionic phase of , the low-frequency nondispersive phonons dampen significantly and transfer their spectral weight from vibrational modes to stochastic dynamics characteristic of fast diffusion. Additional IXS measurements on single crystals provide momentum-resolved phonon dispersions, which show that the dispersive TA phonons remain well defined in the superionic phase. DFT and AIMD simulations corroborate our experimental observations and further reveal a very small potential energy barrier for Ag hopping between and sites of 0.11 eV, in addition to a potential energy surface characterized by extended flat regions. Finally, the pair distribution function (PDF) obtained from X-ray diffraction and AIMD simulations reveals a repulsion between Ag atoms, which tends to facilitate the diffusion via collective hopping.
Results and Discussion
Superionic Phase Transition.
The structural phase transition in was tracked by -dependent X-ray diffraction (XRD) measurements on powders, performed at the Advanced Photon Source (APS) sector 11-ID-C (35) with incident energy 105.708 keV (Fig. 1B). By comparing the XRD patterns at 300 and 600 K, we can see that most Bragg intensities decrease as temperature increases, as a result of a larger Debye–Waller factor at high , combined with the disordering of Ag ions. The suppression of the (003), (006), and (015) Bragg intensities above reveals the disordering of Ag ions across and sites (Fig. 1B, Inset). From our power-law fits, a fully reversible and near second-order transition (SI Appendix, Fig. S1) occurs around a nominal temperature 500 K, both on heating and on cooling (SI Appendix, Figs. S2 and S3). The offset from the reported 475 K likely originates from the temperature gradient between sample and sensor.
Lattice Dynamics across Superionic Transition.
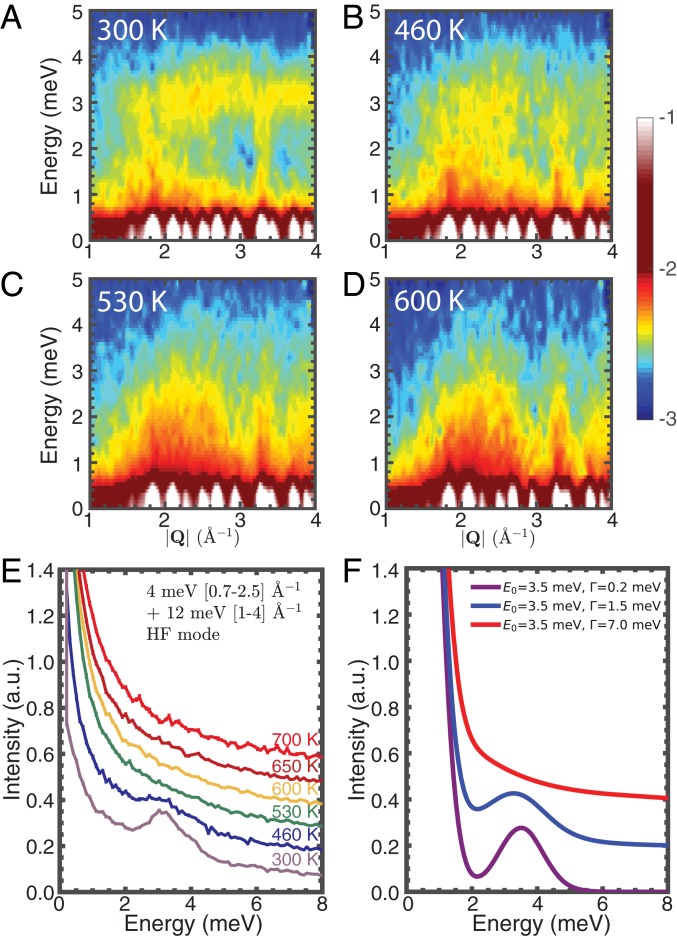
To understand the change in lattice dynamics across the superionic transition, we used INS to measure the dynamical structure factor, S(), which directly probes microscopic excitations (phonons, magnons). INS measurements were performed on powder samples with the cold neutron chopper spectrometer (CNCS) (36), using 4 and 12 meV, with elastic line energy resolution of 112 and 673 eV full width at half maximum (FWHM), respectively. Fig. 2 and SI Appendix, Fig. S4 present S() obtained with 12 meV at nominal temperatures 10, 40, 300, 460, 530, 600, and 700 K. At 10 and 40 K (SI Appendix, Fig. S4 A and B), we clearly observe spin-wave dispersions up to 2 meV emerging from magnetic Bragg peaks at 0.2 and 2.0 , as discussed by Damay et al. (17). Clear spin waves are no longer seen in the paramagnetic phase, but a magnetic quasielastic signal persists up to 0.6 even at room temperature, revealing damped fluctuations of spin correlations. Meanwhile, one can clearly see weak vertical streaks extending from the Bragg peaks at 0 meV (white) to 3.5 meV near = 1.8, 3.3 , as well as a horizontal band of intensity around 3.5 meV (Fig. 2A and SI Appendix, Fig. S4 A and B). The vertical streaks and band become more intense as temperature rises to 300 K, which confirms that the signals originate from phonons. From the DFT-calculated phonon dispersion (SI Appendix, Fig. S6B), the vertical streaks match the dispersive long-wavelength acoustic phonons, while the flat horizontal band around 3.5 meV originates from very flat TA dispersions away from the zone center. For below but close to , the flat signal dampens significantly (Fig. 2B). At , the flat mode completely broadens, revealing extreme phonon damping, and eventually merges with the quasielastic signal (Fig. 2 C and D). On the other hand, the dispersive portions of acoustic phonon dispersions remain clear, especially near the (018) Bragg peak at = 3.3 even at 600 K, far into the superionic regime (Fig. 2D). Consequently, two distinct behaviors are concurrent for different components of the acoustic phonons: the persistence of the dispersive acoustic phonons and the damping of the nondispersive acoustic phonons.
Fig. 2.
INS measurements reveal two behaviors in different portions of the acoustic phonon branch. (A–D) S() maps measured with = 12 meV at the CNCS in the ordered phase, () 300 K and () 460 K, and the superionic phase, () 530 K and () 600 K. The horizontal band around 3.5 meV at 300 K shows the nondispersive phonons. This mode damps and merges into the quasielastic lines at . The vertical streaks, which intensify with increasing temperature, represent the dispersive acoustic phonons especially at = 3.3 . () cuts from = 4 and 12 meV data, integrated over the range of 0.7 2.5 and 1 4 , respectively. The two datasets are stitched by matching intensities at 2 meV. The 3.5-meV peak broadens with temperature increase and smears out at and the quasielastic width increases. () Model S() from the DHO with energy and damping width , convoluted with the instrument resolution (FWHM = 1.5 meV). Elastic line is included. Purple, blue, and red represent S() at 300, 460, and 750 K.
The damping of the flat phonon branch at 3.5 meV was further investigated by integrating S() over (Fig. 2E). A peak can be seen at 3.5 meV at low temperatures, and it softens (shifts to lower energy) on warming to and smears out above the transition. This behavior follows the expected evolution for a damped harmonic oscillator (DHO) with increasing damping, as shown in Fig. 2F. A well-defined phonon mode (e.g., at 300 K) can be considered underdamped, where the DHO peak remains sharp, shown as the purple curve. As increases, the DHO width increases, and the energy slightly softens, shown in blue. At , the mode is overdamped, so that its spectral width becomes larger than its frequency, and the oscillation is no longer well defined. In this case, the spectral weight of the DHO is considerably shifted and leads to a central peak near zero frequency, shown in red. Consequently, at 2 meV, the S(E) behavior is no longer given by the Gaussian function of the instrument resolution (response to the elastic scattering from Bragg and incoherent static signal), but instead comprises a Lorentzian signal (QENS signal, discussed in detail in Fig. 5) in addition to the Gaussian component. The Lorentzian component is seen as a wide tail to the elastic line, whose width and intensity increase with temperature. The energy width of this Lorentzian is inversely proportional to the residence time of Ag ions on a site between hops, and thus the Lorentzian broadening indicates faster hopping of Ag ions in the superionic phase. Thus, we observe not only the damping of phonon-like oscillations, but also the transfer of spectral weight from vibrational dynamics to a diffusive dynamic.
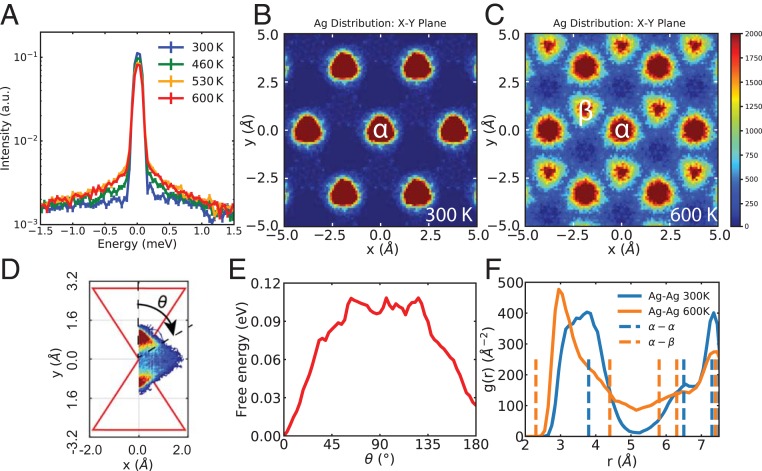
Fig. 5.
Superionic diffusion of Ag ions and the diffusion barrier. () Quasielastic neutron scattering from CNCS with 4 meV at 300, 460, 530, and 600 K, respectively, integrated over 1.4 1.6. The Lorentzian width increasing on heating represents faster diffusion. (B and C) In-plane probability distribution of Ag atoms from AIMD at () 300 K and () 600 K. At 300 K, Ag atoms vibrate near their equilibrium positions at sites. The diffusion occurs occasionally at 300 K and becomes dominant at 600 K. Threefold rotation symmetry and periodicity are applied to the plot. () The probability density of Ag atoms on the plane perpendicular to the shared edge of neighboring and sites. The upper red triangle is the projection of the -tetrahedron, and the lower one is the -tetrahedron. The angle between the Ag atom positions and the center of the -tetrahedron is defined as the reaction coordinate. () The free-energy barrier along the reaction pathway. A low barrier of 0.11 eV is observed along an extended region between and sites. () Pair distribution function projected on Ag–Ag bonds at 300 K (blue) and 600 K (orange). Dashed lines are the distances between – and the – sites. Strong repulsion between Ag atoms is observed, as no Ag–Ag bond with length of 2.3 Å (the nearest – distance) appears in AIMD.
It was proposed in ref. 19 that the damping of the 3.5-meV peak corresponds to a complete disappearance of the TA (shear) modes, akin to a liquid state, and that the LA phonons would thus dominate thermal transport. However, since the 3.5-meV modes are quite flat in energy across all Q at , they have very small group velocities ( , where ), and hence an already small contribution to in the ordered phase [, where is the heat capacity, and is the phonon lifetime for each phonon mode (37)]. The main contribution of TA phonons to actually comes from the dispersive part of the acoustic branches, and these still persist even at . Thus, it is crucial to identify the role of various modes and understand how they contribute to .
In-Plane Vibrations to Stochastic Diffusion.
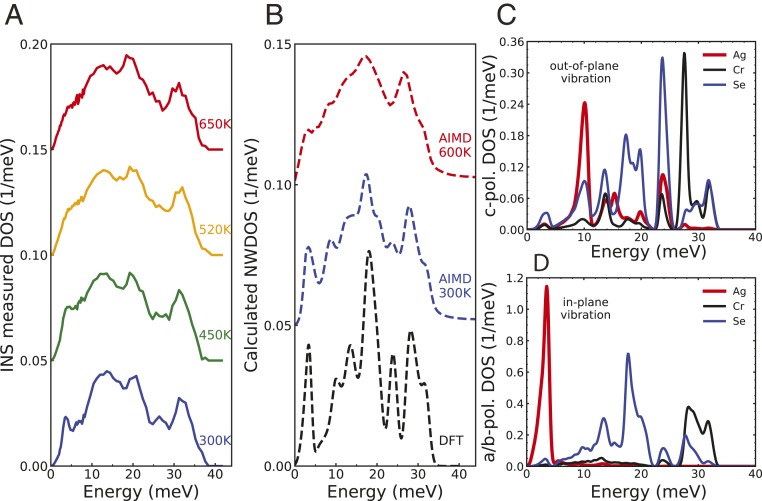
Next, we consider the evolution of the phonon density of states over the whole frequency range to contrast the strong damping behavior of the 3.5-meV modes with the higher-frequency vibrations of the stiff framework structure. The DOS was measured with INS using the wide angular-range chopper spectrometer (ARCS) (38), using 80 and 20 meV. The 80-meV gives the whole spectrum and the 20-meV data provides better resolution at the 3.5-meV peak. We merged the two datasets at 9 meV (Materials and Methods). As shown in Fig. 3A, at 300 K, a sharp peak is seen at 3.5 meV, similar to that observed in data from the CNCS. This peak drastically broadens at 450 K and smears out completely once enters the superionic regime (between 450 and 520 K). However, an overall milder broadening can be seen on warming for all features above 5 meV, which is a consequence of anharmonicity and increasing atomic vibration amplitudes. The mean energy, evaluated as the first moment of the phonon DOS, shows little change: less than 0.5 meV from 300 to 650 K, indicating that the overall crystalline framework remains stiff through the transition.
Fig. 3.
Phonon DOS from experiments and simulations. () INS powder measurements at the ARCS with and 80 meV to get fine resolution at the low-energy portion and the whole spectrum. Data are stitched together at 9 meV. Blue, green, orange, and red lines are measured at 300, 450, 520, and 650 K, respectively. () Calculated neutron-weighted DOS. Black dashed line is labeled as DFT, and AIMD at 300 and 600 K are blue and red dashed lines, respectively. ( and D) Site-projected DOS from DFT for the -axis polarized (C) and in-plane () motions in the – plane. Ag motions mainly contribute the strong peak around 3.5 meV for the in-plane vibration and a weaker peak near 10 meV for polarizations.
In Fig. 3B, we compare the experimental DOS to harmonic phonon simulations and AIMD simulations carried out at 300 and 600 K. All simulations are corrected to consider the neutron weighting factors and are convolved with the estimated energy resolution function of ARCS. The harmonic DOS exhibits sharp peaks as in low- INS data. The DOS from AIMD at 600 K qualitatively matches the overall broadening of features seen in INS data. Most importantly, the simulations closely reproduce the extreme damping of the 3.5-meV peak as temperature increases. Further, we calculated the atomic decomposition of the DOS and projected along the axis (Fig. 3C) or onto the – plane (Fig. 3D). This decomposition clearly reveals that the 3.5-meV peak arises overwhelmingly from Ag in-plane vibrations, and Ag atoms have much larger vibration amplitude than Cr and Se atoms (SI Appendix, Fig. S11). As Ag atoms are weakly bound to Cr and Se atoms, they tend to vibrate in-plane where they experience few constraints. Therefore, we may describe these local vibrations as “2D rattler modes,” which give rise to the large peak at 3.5 meV in the DOS. This behavior reflects the intercalated layer nature of , as discussed in previous studies (19, 23). The existence of such a mode in the normal phase could lead to low (39) below . Further, the weak bonding between layers and the intercalants creates easy hopping pathways for Ag between and sites at and enables fast long-range diffusion on the half-filled Ag sublattice. In the superionic regime, the in-plane Ag vibrations around either or sites are strongly disrupted and damped, leading to the smearing of the 3.5-meV peak in the vibrational spectrum.
Selective Breakdown of Transverse Acoustic Phonon.
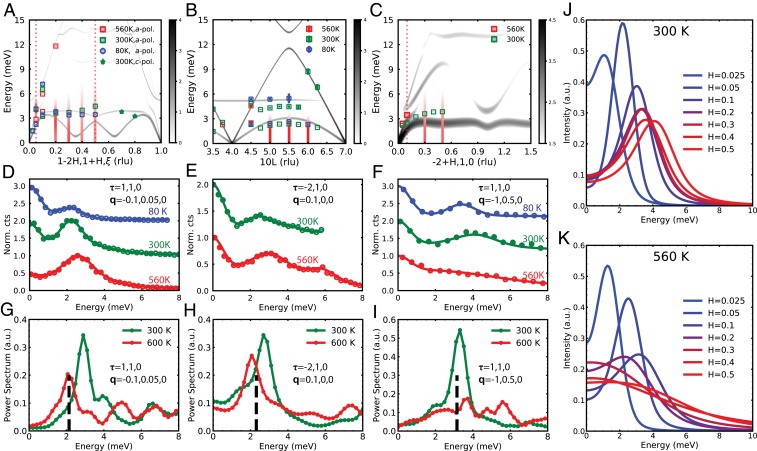
After describing how the flat portion of the TA branch breaks down in the superionic phase, we now establish the persistence of the dispersive TA phonons. The definite determination of phonon polarizations and dispersions requires momentum-resolved measurements, which we obtained from IXS measurements on small single crystals (SI Appendix, Fig. S5) using the high-energy resolution inelastic X-ray spectrometer (HERIX) spectrometer ( 23.7 keV) at the APS (40, 41). IXS spectra were collected in multiple Brillouin zones at three temperatures, 80, 300, and 560 K, across . The experimental phonon dispersions are shown as markers in Fig. 4 A–C, overlaid on the S(, E) from DFT (gray scale). The agreement between IXS data and DFT is quite good at low , especially at 80 K. At 300 and 560 K, the phonon energies are shifted, reflecting some anharmonic renormalization compared to the harmonic DFT results. This is seen especially for along . We evaluate the renormalization using mode Grüneisen parameters (SI Appendix, Fig. S6). The long-wavelength TA phonons have large negative values, possibly explaining their stiffening as the lattice expands with temperature. Additional intrinsically anharmonic renormalization can also be partially captured by AIMD (SI Appendix, Fig. S7), using the temperature-dependent effective potential (TDEP) method.
Fig. 4.
IXS measurements show selective breakdown of transverse acoustic phonon. (–) Momentum-resolved IXS measurements on single crystals with transverse polarization (markers), compared with DFT simulated S() (gray colormaps). Abscissa labels indicate the momentum transfer direction, and red vertical dashed lines indicate the locations of constant-Q spectra in –. Red vertical bars are plotted to show the overdamped phonon at 560 K using a fitted DHO, and intensities are shown with gradient color. 0 for -polarized modes, and 15 or 18 for -polarized modes. At 4.5, we measured at , which causes the energy difference in the plot. (–) IXS spectra at specific Q across the superionic transition, experimental data (markers), and the corresponding DHO fits (solid lines). All data are normalized by maximum intensities and are vertically offset. (–) The power spectrum calculated from AIMD at corresponding Q. Black dashed lines indicate the energies from harmonic approximation. The extra oscillations in and come from the incommensurate wave vectors because of the limited simulation supercell size. (J and K) DHO fits for TA phonons in at 300 K (J) and 560 K (K). 0.025 represents the zone center and 0.5 represents zone boundary in reciprocal space. At 300 K, the TA phonon energies increase and the peak widths broaden from zone center to zone boundary. All phonon modes are well defined. At 560 K, similar behaviors to 300 K are seen at 0.2 (dispersive portion), but modes at 0.2 are overdamped, representing the breakdown of nondispersive TA phonons in the superionic phase.
In Fig. 4A, we show the dispersions for the transverse modes along the q = [2H, H, 0] (0 H 1) direction, for both in-plane () and out-of-plane () polarizations. The TA phonons stiffen a little from 80 to 300 K. Still, all phonon peaks in the IXS spectra remain well defined. However, in the superionic phase ( 560 K), TA modes along the flat portion become extremely damped. For instance, at Q 0, 1.5, 0 (zone boundary, H 0.5), the IXS spectrum is captured with an overdamped DHO profile, with no obvious phonon peak, as shown in red in Fig. 4F. We use a rectangle with red gradient to denote the intensities of this DHO (energy range lower-bound cutoff is one-sixth of the maximum DHO intensity in all plots). Contrary to the overdamped behavior of the flat portion, the dispersive portion of TA at small q remains well defined even at 560 K. The same behavior is seen for other measured directions [1, 0, L] and [2+H, 1, 0] (Fig. 4 B and C). The constant-Q spectra at small q from IXS (Fig. 4 D and E) and corresponding AIMD simulations (Fig. 4 G and H) further illustrate the selective breakdown of the TA phonon by contrasting small and large q (Fig. 4 F and I). Compared to the case of (22), in which nondispersive phonons arise from a low-lying flat optical branch ( meV), the flat low-energy dispersion around 3.5 meV in is contributed by the top of the TA branch. Systematic trends for TA phonons at 300 and 600 K, obtained from DHO fits from zone center to zone boundary, are shown in Fig. 4 J and K. At 300 K the TA phonon energies increase with near the zone center and become constant near the zone boundary, mapping out the TA dispersion along [1 2H, 1+H, 0]. At 560 K, similar behaviors are seen at 0.2 (dispersive portion), but modes at 0.2 are severely damped, representing the breakdown of nondispersive TA phonons in the superionic phase. The persistence of the long-wavelength dispersive TA phonons is thus clearly established from IXS.
We further corroborate through simulations that the dispersive portions of the TA branches persist when their phonon eigenvectors are not dominated by Ag atoms. We note that the harmonic approximation predicts nondegenerate TA branches along the [1 2H, 1+H, 0] direction, while IXS yields nearly degenerate TA branches. This may reflect limitations of the harmonic approximation in systems with large anharmonicity, such as . The Ag contribution to the TA modes at varying was evaluated from the modulus of the computed eigenvectors. The Ag contributions for the nondispersive part of the TA branch (at short wavelengths) are 78%, 64%, and 83% at Q 0, 1.5, 0, Q 1, 0, 5.5, and Q −1.5, 1, 0, respectively. This large contribution from a single atom type gives these modes an optical character, similar to the picture of decoupled Einstein modes, reflecting the weak force constants between Ag ions and other atoms. On the other hand, the Ag contribution to the dispersive TA modes (long wavelengths) is 39% at Q 0.9, 1.05, 0, 45% at Q 1.05, 0, 4.5, and 31% at Q −1.9, 1, 0. Meanwhile, we note that the diffusion of the Ag atoms is via site hopping. Ag atoms still vibrate at both and sites between the intersite hops (as shown below using AIMD). Yet the random distribution of Ag among half-filled / sites yields strong disorder, which is expected to effectively scatter short-wavelength modes.
In summary, our IXS measurements on single crystals show that only the nondispersive short-wavelength TA modes break down in the superionic phase, corresponding to an optic-like character with strong Ag participation, while the dispersive long-wavelength TA modes are less sensitive and remain well defined, with limited damping at high temperature. A mixed lattice dynamic is therefore observed in where the framework of octahedra remains crystalline and the dispersive TA persists, while the order of the Ag sublattice “melts” in the superionic phase. We emphasize the importance of momentum-resolved techniques to track phonon modes with different polarizations and their temperature dependence. We also note that due to their low phonon group velocities, the flat portions of the TA dispersions contribute little to . The change in the experimentally reported thermal conductivity across is indeed quite small (19, 26).
Superionic Diffusion.
We now focus on the superionic behavior by investigating the diffusion of Ag ions via the QENS signal around the elastic line in . QENS is a powerful technique to probe stochastic diffusion of atoms. A strong QENS signal is seen in owing to its large ionic mobility at (30), as shown in Fig. 5A. The total signal consists of three portions: the QENS contribution in the form of a Lorentzian centered at zero energy transfer, a purely elastic delta function convolved with the instrumental (Gaussian) resolution, and a linear background. At 300 K, the QENS signal is very weak, and we mainly see the elastic line with the background signal. The QENS intensity increases with and saturates around 530 K, whereas the width of the Lorentzian tail continues broadening to 0.83 0.30 meV at 750 K, indicating a faster diffusion process upon heating (SI Appendix, Fig. S12).
To rationalize the QENS measurements, we use AIMD simulations to track the trajectories of Ag ions and correlations in their motions. In Fig. 5 B and C, we plot the in-plane probability distribution of Ag ions at 300 and 600 K, starting from the same configuration where all of the Ag ions occupy sites. While most Ag ions are distributed around their equilibrium positions at 300 K, simulations at 600 K clearly show the delocalization of Ag ions across both and sites, as observed in ref. 42. Some Ag ions are observed to hop to different sites when the previously occupied Ag ions at those sites hop away, enabling long-range diffusion. The diffusion distances are limited by the simulation supercell size, but a large enough simulation box should reproduce the long-range diffusion reported experimentally (30). All of the dynamical processes seen in experiments have been reproduced, although a longer trajectory (currently 13 ps long) is required for Ag ions to equally populate the and sites. The weak bonding at room temperature and diffusive behavior of Ag ions above can be seen from the mean-square displacement (MSD). As shown in SI Appendix, Fig. S11, at 300 K, the MSD of Ag atoms is larger than those of Cr and Se but stays constant during long simulation times. The MSD increases dramatically when the temperature reaches 600 K. While the Ag ions exhibit hopping dynamics, Cr and Se atoms retain oscillatory dynamics around their respective equilibrium positions, with vibration amplitudes characteristic of regular crystals (SI Appendix, Fig. S14), showing the rigid nature of the framework sublattice, which is an important reason for the persistence of dispersive TA modes. The diffusion constant estimated from the linear portion of the MSD at 600 K is 1.5 , in qualitative agreement with the experimentally measured value (30), further confirming the superionic behavior.
The diffusion pathway and the associated energy barrier were investigated from the free-energy landscape computed from AIMD trajectories of Ag ions (Materials and Methods), as shown in Fig. 5 D and E. The shape of the energy landscape in is unusual (43, 44). A very low and flat energy barrier about 0.11 eV in is found across an extended region between and sites, indicating a “frustrated environment” with no single optimal diffusion pathway, similar to recent findings in Li superionics (45). As we show in Fig. 5C and SI Appendix, Fig. S13, a quasi-2D probability distribution of Ag ions can be seen and represents the diffusion channel. The weak bonding of Ag ions enables large atomic displacements and low vibration frequencies, which results in a low free-energy barrier, matching the observations in Li SICs in ref. 46. In the “concerted migration” scheme, reported by ref. 3, multiple Li ions hop simultaneously along the diffusion channel and produce a similar shallow and flat energy landscape, but this scheme prefers a high Li concentration environment with the high-energy site occupied. We note that the hopping mechanism is different in , where the collective hopping might originate from the strong repulsion between nearby Ag ions discussed below.
To get more insight into such ion–ion interactions, we investigated the atomic correlations which describe microscopic interactions with characteristic length. In Fig. 5F and SI Appendix, Fig. S18, we plot the atomic PDF obtained from both XRD experiments (11-ID-C at APS with 105.708 keV) and AIMD simulations. Data at 300 and 600 K are represented in blue and yellow, respectively. The blue dashed lines in Fig. 5F indicate the Ag–Ag bond lengths in the theoretical relaxed structure at 0 K. The orange dashed lines are the Ag–Ag bond for the same structure but with Ag atoms occupying both and sites: An extra peak is clearly expected at Å. We first compare the reduced PDF () from the XRD in SI Appendix, Fig. S18A and from AIMD simulations in SI Appendix, Fig. S18E. The experimental PDF shows several important features: Upon heating, all of the peaks broaden considerably, but the temperature dependence of the first peak at around 2.5 Å is much less pronounced compared to the other peaks, which is the superposition of the nearest-neighbor Cr–Se and Ag–Se pairs. Our PDF from AIMD reproduces the experimental features quite well overall. We therefore proceed to analyze the behavior of individual atom pairs by decomposing the computed PDF. As seen in SI Appendix, Fig. S18B–D, the distributions of bonds involving at least one Ag atom change dramatically with temperature, but the PDF of Cr–Cr, Cr–Se, and Se–Se bonds varies little upon heating, consistent with the rigid nature of the octahedra framework (SI Appendix, Fig. S18F–H). Second, the normal PDF peak shape is expected to be a Gaussian within the harmonic approximation, when the atoms vibrate around their equilibrium position in a harmonic potential. Deviations from this Gaussian profile can be explained by large-amplitude anharmonic vibrations in . Most importantly, in Fig. 5F, the intensity and the lineshape of the Ag–Ag pair correlations smear out dramatically, and the predicted nearest – correlation length at 2.3 Å never appears. The circumvention of this bond length reveals a strong repulsion between nearest-neighbor Ag ions, which, because of the half-filled nature of the Ag sublattice, indicates necessarily correlated hopping dynamics of the Ag ions. This repulsion will tend to assist the hopping of other Ag atoms at sites once one Ag atom hops to the sites and a low free-energy barrier is achieved.
Conclusions
In this work, comprehensive experiments and first-principles calculations were performed to investigate the atomic dynamics in across its superionic transition. We conclude that long-wavelength dispersive TA phonon quasiparticles remain well defined in the superionic regime, while the nondispersive portions of TA branches at short phonon wavelengths break down due to the stochastic diffusive dynamics of Ag ions. This coexistence of fast diffusive atoms and a robust lattice framework in provides a clear picture of the mixed lattice dynamics in superionic conductors, beyond a simple “phonon–liquid” description. The contribution of extended flat portions of TA branches to the thermal conductivity is already very low at room temperature, and therefore the ultralow can be ascribed to very low group velocities (the flattening of TA dispersions reflecting the decoupled, Einstein-like nature of Ag vibrations) and large anharmonicity across the whole temperature range, in addition to Ag disorder at high . The superionic behavior in is enabled by a very low potential energy barrier between and sites and extended flat regions in the potential energy landscape. Strong repulsion between Ag ions enables collective hopping dynamics that facilitate the fast diffusion. These results shed light on the complex atomic dynamics leading to ultralow thermal conductivity and superionic diffusion and will enable the design of future materials for applications as thermoelectrics or as solid-state electrolytes in batteries.
Materials and Methods
For a detailed description of methods, see SI Appendix.
Data supporting this article are available from the authors upon reasonable request.
Neutron experiments were performed on powder using the time-of-flight CNCS and ARCS at the Spallation Neutron Source, Oak Ridge National Laboratory. The sample was sealed in a 3/8-inch diameter thin-walled aluminum can and placed in a high-temperature closed-cycle refrigerator.
XRD was performed on powders at Sector 11-ID-C ( 105.708 keV) of the Advanced Photon Source, Argonne National Laboratory. The powders were mounted and heated in a thin copper disk (1 mm) with an inner radius of 1 mm, clamped in a Linkam TS1500 stage in nitrogen atmosphere. IXS measurements were performed on small single crystals mounted on standard copper posts with a beryllium dome and heated with high- closed-cycle refrigerators in vacuum, using the high-resolution IXS beamline HERIX at Sector 30 ( 23.7 keV).
DFT and AIMD simulations were performed in the Vienna ab initio simulation package (VASP 5.4) (47–49), and the exchange-correlation function takes the generalized gradient approximation (GGA) in the Perdew–Burke–Ernzerhof (PBE) form (50, 51). The spin polarization effects are taken into account. Phonon calculations are processed with Phonopy (52) and the TDEP (53, 54) method was implemented to obtain the phonon shift with temperature. Power spectra at specific Q are obtained by projecting the AIMD trajectories onto the harmonic phonon eigenvectors and applying FFT as implemented in Dynaphopy (55).
Supplementary Material
Acknowledgments
We thank Olle Hellman for access to and support with the TDEP software package. X-ray and neutron scattering data collection and analysis and first-principles simulations by J.D. were supported the US Department of Energy (DOE), Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division, under Award DE-SC0019299. X-ray and neutron scattering work by J.L.N., D.B., X.H., and O.D. was supported by the US DOE, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division, under Early Career Award DE-SC0016166. Sample synthesis by A.F.M. was supported by the US DOE, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division. G.A. acknowledges Duke University startup funds for partial support. The use of the Advanced Photon Source was supported by the US DOE, Office of Science, Office of Basic Energy Sciences, under Contract DE-AC02-06CH11357. The use of Oak Ridge National Laboratory’s Spallation Neutron Source was sponsored by the Scientific User Facilities Division, Office of Basic Energy Sciences, US DOE. Theoretical calculations were performed using resources of the National Energy Research Scientific Computing Center, a US DOE Office of Science User Facility supported by the Office of Science of the US DOE under Contract DE-AC02-05CH11231.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission. G.C. is a guest editor invited by the Editorial Board.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.1913916117/-/DCSupplemental.
References
- 1.Kamaya N., et al. , A lithium superionic conductor. Nat. Mater. 10, 682–686 (2011). [DOI] [PubMed] [Google Scholar]
- 2.Kato Y., et al. , High-power all-solid-state batteries using sulfide superionic conductors. Nature Energy 1, 16030 (2016). [Google Scholar]
- 3.He X., Zhu Y., Mo Y., Origin of fast ion diffusion in super-ionic conductors. Nat. Commun. 8, 15893 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Liu H., et al. , Copper ion liquid-like thermoelectrics. Nat. Mater. 11, 422–425 (2012). [DOI] [PubMed] [Google Scholar]
- 5.Xiao C., et al. , Superionic phase transition in silver chalcogenide nanocrystals realizing optimized thermoelectric performance. J. Am. Chem. Soc. 134, 4287–4293 (2012). [DOI] [PubMed] [Google Scholar]
- 6.Weldert K. S., et al. , Thermoelectric transport in with high copper ionic mobility. J. Am. Chem. Soc. 136, 12035–12040 (2014). [DOI] [PubMed] [Google Scholar]
- 7.Qiu P., et al. , Suppression of atom motion and metal deposition in mixed ionic electronic conductors. Nat. Commun. 9, 2910 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Keppens V., et al. , Localized vibrational modes in metallic solids. Nature 395, 876–878 (1998). [Google Scholar]
- 9.Biswas K., et al. , High-performance bulk thermoelectrics with all-scale hierarchical architectures. Nature 489, 414–418 (2012). [DOI] [PubMed] [Google Scholar]
- 10.Zebarjadi M., et al. , Power factor enhancement by modulation doping in bulk nanocomposites. Nano Lett. 11, 2225–2230 (2011). [DOI] [PubMed] [Google Scholar]
- 11.Ma J., et al. , Glass-like phonon scattering from a spontaneous nanostructure in . Nat. Nanotechnol. 8, 445–451 (2013). [DOI] [PubMed] [Google Scholar]
- 12.Voneshen D. J., et al. , Suppression of thermal conductivity by rattling modes in thermoelectric sodium cobaltate. Nat. Mater. 12, 1028–1032 (2013). [DOI] [PubMed] [Google Scholar]
- 13.Christensen M., et al. , Avoided crossing of rattler modes in thermoelectric materials. Nat. Mater. 7, 811–815 (2008). [DOI] [PubMed] [Google Scholar]
- 14.Koza M. M., et al. , Breakdown of phonon glass paradigm in La- and Ce-filled skutterudites. Nat. Mater. 7, 805–810 (2008). [DOI] [PubMed] [Google Scholar]
- 15.Lee S., et al. , Resonant bonding leads to low lattice thermal conductivity. Nat. Commun. 5, 3525 (2014). [DOI] [PubMed] [Google Scholar]
- 16.Weldert K. S., Zeier W. G., Day T. W., Panthöfer M., Snyder G. J., Thermoelectric transport in Cu7SeP6 with high copper ionic mobility. J. Am. Chem. Soc. 136, 12035–12040 (2014). [DOI] [PubMed] [Google Scholar]
- 17.Damay F., et al. , Localised Ag+ vibrations at the origin of ultralow thermal conductivity in layered thermoelectric AgCrSe2. Sci. Rep. 6, 23415 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bailey T. P., Uher C., Potential for superionic conductors in thermoelectric applications. Curr. Opin. Green Sustainable Chem. 4, 58–63 (2017). [Google Scholar]
- 19.Li B., et al. , Liquid-like thermal conduction in intercalated layered crystalline solids. Nat. Mater. 17, 226–230 (2018). [DOI] [PubMed] [Google Scholar]
- 20.Voneshen D. J., Walker H. C., Refson K., Goff J. P., Hopping time scales and the phonon-liquid electron-crystal picture in thermoelectric copper selenide. Phys. Rev. Lett. 118, 145901 (2017). [DOI] [PubMed] [Google Scholar]
- 21.Danilkin S. A., et al. , Neutron scattering study of short-range correlations and ionic diffusion in copper selenide. Ionics 17, 75–80 (2011). [Google Scholar]
- 22.Niedziela J. L., et al. , Selective breakdown of phonon quasiparticles across superionic transition in . Nat. Phys. 15, 73–78 (2019). [Google Scholar]
- 23.Brüesch P., Hibma T., Bührer W., Dynamics of ions of the two-dimensional superionic conductor . Phys. Rev. B 27, 5052–5061 (1983). [Google Scholar]
- 24.Wakamura K., Miura F., Kojima A., Kanashiro T., Observation of anomalously increasing phonon damping constant in the phase of the fast-ionic conductor SI. Phys. Rev. B 41, 2758–2762 (1990). [DOI] [PubMed] [Google Scholar]
- 25.Bhattacharya S., et al. , High thermoelectric performance of (AgCrSe2)0.5 (CuCrSe2)0.5 nano-composites having all-scale natural hierarchical architectures. J. Mater. Chem. 2, 17122–17129 (2014). [Google Scholar]
- 26.Wu D., et al. , Revisiting AgCrSe2 as a promising thermoelectric material. Phys. Chem. Chem. Phys. 18, 23872–23878 (2016). [DOI] [PubMed] [Google Scholar]
- 27.Gascoin F., Maignan A., Order–disorder transition in : A new route to efficient thermoelectrics. Chem. Mater. 23, 2510–2513 (2011). [Google Scholar]
- 28.Bhattacharya S., et al. , .: A high performance phonon glass and electron crystal thermoelectric material. J. Mater. Chem. 1, 11289–11297 (2013). [Google Scholar]
- 29.Gagor A., Gnida D., Pietraszko A., Order–disorder phenomena in layered crystals. Mater. Chem. Phys. 146, 283–288 (2014). [Google Scholar]
- 30.Murphy D., Chen H., Tell B., Superionic conduction in and . J. Electrochem. Soc. 124, 1268–1271 (1977). [Google Scholar]
- 31.Wakamura K., Phonon spectra in superionic and normal states of the layered crystal . Solid State Ion. 40-41, 331–333 (1990). [Google Scholar]
- 32.Yakshibayev R., Zabolotsky V., Almukhametov R., Structural features and ionic transport in two-dimensional MxYSe2 (M = Cu, Ag; Y = Cr, Nb) mixed conductors. Solid State Ion. 31, 1–4 (1988). [Google Scholar]
- 33.Engelsman F., Wiegers G., Jellinek F., Van Laar B., Crystal structures and magnetic structures of some metal (i) chromium (iii) sulfides and selenides. J. Solid State Chem. 6, 574–582 (1973). [Google Scholar]
- 34.Gautam U. K., Seshadri R., Vasudevan S., Maignan A., Magnetic and transport properties, and electronic structure of the layered chalcogenide . Solid State Commun. 122, 607–612 (2002). [Google Scholar]
- 35.Ren Y., High-energy synchrotron x-ray diffraction and its application to in situ structural phase-transition studies in complex sample environments. JOM 64, 140–149 (2012). [Google Scholar]
- 36.Ehlers G., Podlesnyak A. A., Niedziela J. L., Iverson E. B., Sokol P. E., The new cold neutron chopper spectrometer at the Spallation Neutron Source: Design and performance. Rev. Sci. Instrum. 82, 085108 (2011). [DOI] [PubMed] [Google Scholar]
- 37.Tritt T. M., Thermal Conductivity: Theory, Properties, and Applications (Kluwer Academic/Plenum Publishers, New York, 2006). [Google Scholar]
- 38.Abernathy D. L., et al. , Design and operation of the wide angular-range chopper spectrometer ARCS at the Spallation Neutron Source. Rev. Sci. Instrum. 83, 015114 (2012). [DOI] [PubMed] [Google Scholar]
- 39.Qiu W., et al. , Part-crystalline part-liquid state and rattling-like thermal damping in materials with chemical-bond hierarchy. Proc. Natl. Acad. Sci. U.S.A. 111, 15031–15035 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Toellner T. S., Alatas A., Said A. H., Six-reflection meV-monochromator for synchrotron radiation. J. Synchrotron Radiat. 18, 605–611 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Said A. H., Sinn H., Divan R., New developments in fabrication of high-energy-resolution analyzers for inelastic X-ray spectroscopy. J. Synchrotron Radiat. 18, 492–496 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Xie L., et al. , Direct atomic-scale observation of Ag+ diffusion structure in the quasi-2D “liquid-like” state of superionic thermoelectric . J. Mater. Chem. C 7, 9263–9269 (2019). [Google Scholar]
- 43.Sagotra A. K., Chu D., Cazorla C., Influence of lattice dynamics on lithium-ion conductivity: A first-principles study. Phys. Rev. Mater. 3, 035405 (2019). [Google Scholar]
- 44.Bo S. H., Wang Y., Kim J. C., Richards W. D., Ceder G., Computational and experimental investigations of Na-ion conduction in cubic . Chem. Mater. 28, 252–258 (2015). [Google Scholar]
- 45.Di Stefano D., et al. , Superionic diffusion through frustrated energy landscape. Chem 5, 2450–2460 (2019). [Google Scholar]
- 46.Muy S., et al. , Tuning mobility and stability of lithium ion conductors based on lattice dynamics. Energy Environ. Sci. 11, 850–859 (2018). [Google Scholar]
- 47.Kresse G., Hafner J., Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558–561 (1993). [DOI] [PubMed] [Google Scholar]
- 48.Kresse G., Furthmüller J., Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996). [DOI] [PubMed] [Google Scholar]
- 49.Kresse G., Furthmüller J., Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996). [DOI] [PubMed] [Google Scholar]
- 50.Perdew J., Zunger A., Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 23, 5048–5079 (1981). [Google Scholar]
- 51.Perdew J., Burke K., Ernzerhof M., Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996). [DOI] [PubMed] [Google Scholar]
- 52.Togo A., Oba F., Tanaka I., First-principles calculations of the ferroelastic transition between rutile-type and -type at high pressures. Phys. Rev. B 78, 134106 (2008). [Google Scholar]
- 53.Hellman O., Abrikosov I. A., Simak S. I., Lattice dynamics of anharmonic solids from first principles. Phys. Rev. B 84, 180301(R) (2011). [Google Scholar]
- 54.Hellman O., Abrikosov I. A., Temperature-dependent effective third-order interatomic force constants from first principles. Phys. Rev. B 88, 144301 (2013). [Google Scholar]
- 55.Carreras A., Togo A., Tanaka I., Dynaphopy: A code for extracting phonon quasiparticles from molecular dynamics simulations. Comput. Phys. Commun. 221, 221–234 (2017). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.