Global Aromaticity at the Nanoscale

Abstract

Aromaticity can be defined by the ability of a molecule to sustain a ring current when placed in a magnetic field. Hückel’s rule states that molecular rings with [4n+2] π-electrons are aromatic, with an induced magnetisation that opposes the external field inside the ring, whereas those with 4n π-electrons are antiaromatic, with the opposite magnetisation. This rule reliably predicts the behaviour of small molecules, typically with fewer than 22 π-electrons (n = 5). It is not clear whether aromaticity has a size limit, or whether Hückel’s rule extends to much larger macrocycles. Here, we present evidence for global aromaticity in porphyrin nanorings with circuits of up to 162 π-electrons (n = 40); aromaticity is controlled by changing the constitution, oxidation state and conformation. Whenever a ring current is observed, its direction is correctly predicted by Hückel’s rule. The largest ring currents occur when the porphyrins units have fractional oxidation states.

The extent of electronic delocalisation in linear molecules is limited by the onset of symmetry-breaking transitions, which can be viewed as Peierls-type electron-vibration interactions or as shifts in mixed-valence behaviour¹. For example, cyanine dyes feature a linear chain of C–C bonds with bond order 1.5 and negligible bond length alternation (like the C–C bonds in benzene) resulting in charge delocalisation, but if the chain exceeds a critical length, the symmetry collapses, localising the charge^2,3. It is not clear whether similar effects limit the size of an aromatic ring, or whether molecular ring currents can extend into the domain of mesoscopic phenomena such as Aharonov–Bohm oscillations⁴. Many new globally aromatic macrocycles have been reported during the last few years^5–18, but apart from the porphyrin nanorings discussed here, there are no reports of aromatic rings with more than 62 π-electrons⁷.

Here we explore circuits of up to 162 π-electrons in a large family of nanorings in a wide range of oxidation states. In these nanorings, each porphyrin contributes 10 electrons to the Hückel π-electron count, and each linking alkyne contributes 2 electrons, so a nanoring cation c-PN[b_xe_y]^Q+ has an electron count of 10N + 4x + 2y – Q (where N is the number of porphyrin units; x and y are the number of butadiyne and ethyne links respectively). Recently, we reported that the butadiyne-linked six-porphyrin nanoring c-P6[b₆] displays global aromaticity when oxidised⁸, reduced¹⁷ or electronically excited¹⁸. According to Schleyer’s terminology¹⁹, all the nanorings discussed here are ‘trannulenes’ rather than ‘annulenes’, since the p-orbitals making up the aromatic π-system are oriented in the plane of the ring, whereas in annulenes the p-orbitals are perpendicular to the ring. Trannulenes follow Hückel’s rule in the same way as annulenes, although Hückel did not anticipate this type of system.²⁰

Results and discussion

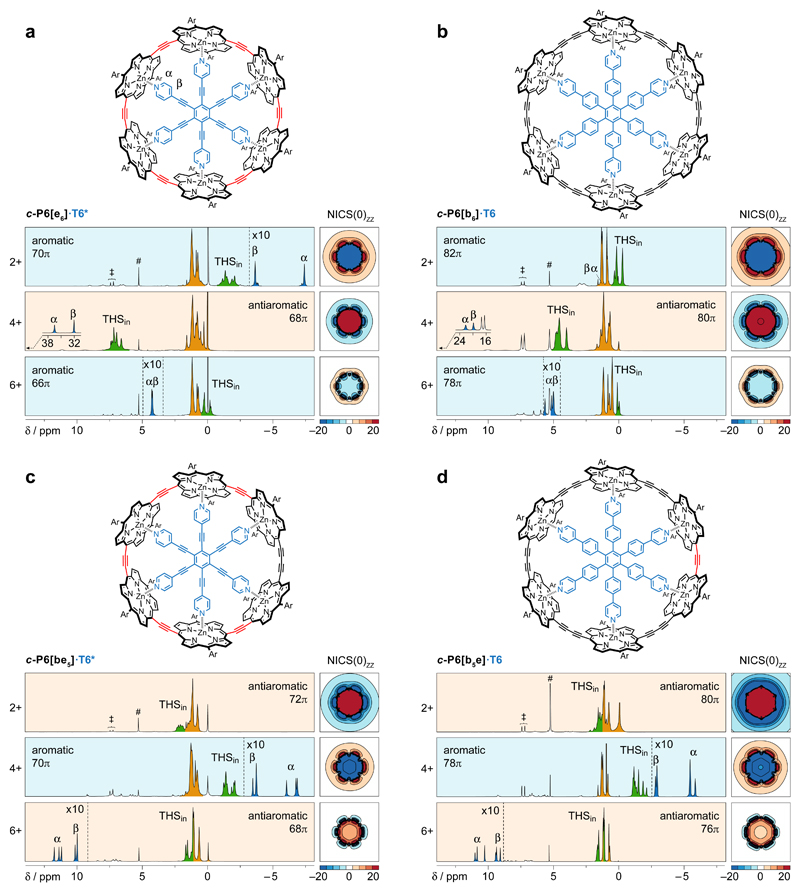
The six-porphyrin nanoring complexes c-P6[e₆]·T6*, c-P6[be₅]·T6*, c-P6[b₅e]·T6 and c-P6[b₆]·T6 provide a homologous series of compounds in which we systematically vary the number of π-electrons by changing the number of -C≡C- units, while preserving the circular geometry (which is locked by the template, T6* or T6, Fig. 1)^21,22. The ¹H NMR spectra of all four complexes were recorded in the 2+, 4+ and 6+ oxidation states, revealing the presence of aromatic or antiaromatic ring currents. The directions of these ring currents agree perfectly with Hückel’s rule. Thus, c-P6[e₆]·T6* (neutral: 72 πe) and c-P6[b₆]·T6 (neutral: 84 πe) are both aromatic in the 2+ and 6+ oxidation states and antiaromatic in the 4+ state, whereas c-P6[be₅]·T6* (neutral: 74 πe) and c-P6[b₅e]·T6 (neutral: 82 πe) are both antiaromatic in the 2+ and 6+ states and aromatic in the 4+ state.

Fig. 1. ¹H NMR spectra of the aromatic and antiaromatic six-porphyrin nanoring template complexes in oxidation states 2+, 4+ and 6+.

a, c-P6[e₆]·T6*; b, c-P6[be₅]·T6*; c, c-P6[b₅e]·T6 and d, c-P6[b₆]·T6. A grid plot of the NICS(0)_zz value in the xy plane of the nanoring, calculated without template, is shown for each oxidation state of each complex (5 × 5 nm; LC-ωhPBE/6-31G*, ω = 0.1; colour axis truncated above 20 and below –20 ppm; contours drawn every 5 ppm). ¹H NMR spectra recorded at 500 MHz in CD₂Cl₂; oxidised states are generated by titration with thianthrenium hexafluoroantimonate. # and ‡ denote CHDCl₂ and thianthrene, respectively. Detailed spectra are shown in Supplementary Figs. 9–12 and 19–34. Dashed vertical lines indicate 10-fold magnifications.

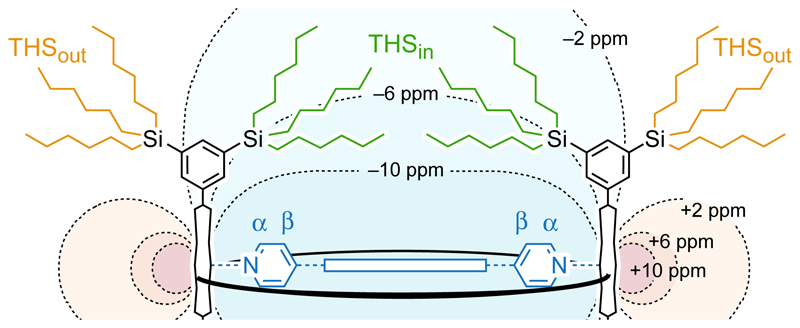
The most obvious evidence for these ring currents comes from the chemical shifts of the template α and β pyridyl ¹H resonances; for example, these protons are strongly shielded (δ_H = –7.3 and –3.6 ppm, vs. 8.7 and 7.5, respectively in the free template) in aromatic c-P6[e₆]·T6*²⁺ and strongly deshielded (δ_H = 36.0 and 30.1 ppm, respectively) in antiaromatic c-P6[e₆]·T6*⁴⁺. Further evidence is provided by the trihexylsilyl (THS) ¹H and ¹³C signals. In each spectrum, we observe one group of THS signals that is essentially unshifted, at 0–2 ppm as in the neutral compounds (peaks coloured orange in Fig. 1) which arises from the external THS group located near the zero-shielding cone of the nanoring (THS_out, Fig. 2), and one group of THS signals that is shielded or deshielded, depending on the direction of the ring current (THS_in, coloured green in Fig. 1 and 2). Interconversion of THS_in and THS_out is slow on the NMR timescale, and the assignment of THS_in signals is confirmed by the observation of NOEs to protons of the template (T6 or T6*). There is an excellent linear correlation between changes in the chemical shift of the α-pyridyl template ¹H and ¹³C signals and the THS CH₂-Si and CH₃ ¹H and ¹³C signals, showing that all six signals report on the same global ring currents (Supplementary Figs. 70–73).

Fig. 2. The magnetic shielding plotted in the xz plane perpendicular to the plane of the nanoring.

NICS_iso contours for (c-P6[e₆]·T6*)²⁺ from –10 to 10 ppm. Internal trihexylsilyl groups (THS_in, green) are sensitive to the global ring current whereas external ones (THS_out, orange-brown) are not.

The observed ring currents in this set of 12 species (four nanorings in three oxidation states) were compared with the results of nucleus-independent chemical shift (NICS) calculations^23,24. We screened a range of density functional theory (DFT) functionals for these NICS calculations (see Supplementary Figs. 80 and 83). The B3LYP functional²⁵ gave good agreement with the NMR results for most species, but it failed to reproduce the anti-aromaticity of the dications c-P6[be₅]²⁺ and c-P6[b₅e]²⁺. The LC-ωhPBE (ω = 0.1) functional²⁶ gave the best agreement with the observed NMR shifts (see plots on the right of each spectrum in Fig. 1) and we chose this functional for all the NICS calculations shown in this article.

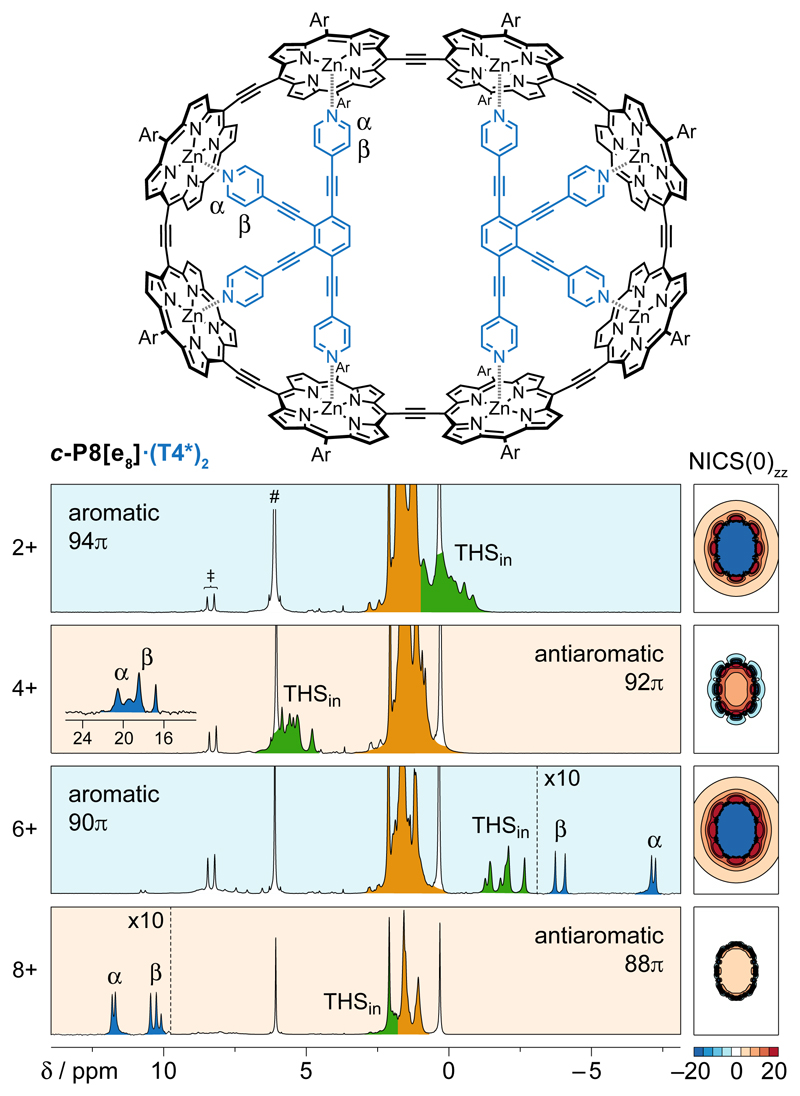
The evolution of the ring current with increasing ring size is illustrated by the ¹H NMR spectra of the 8-porphyrin nanoring complex c-P8[e₈]·(T4*)₂, which has a circuit of 96 πe when neutral (Fig. 3)²¹. The THS and template protons show clear evidence for aromaticity in the 2+ and 6+ oxidation states, whereas the 4+ and 8+ oxidation states are antiaromatic. These results match the predictions of Hückel’s rule and agree with calculated NICS values (Fig. 3). The magnitude of the ring current varies substantially between different oxidation states; thus the mean change in the chemical shift of the α-protons of the template (relative to unbound T4*, δ_α = 8.67 ppm) is Δδ_α = +11.8 ppm in the 4+ state, and –15.6 ppm in the 6+ state, but it dwindles to +1.9 ppm in the 8+ state.

Fig. 3. Hückel behaviour in a template-bound eight-porphyrin ring.

Molecular structure of c-P8[e₈]·(T4*)₂, Ar = 3,5-bis(trihexylsilyl))phenyl, and ¹H NMR spectra in oxidation states 2+, 4+, 6+ and 8+. Labels denote the key resonances THS_in (green), THS_out (orange), and template (α, β); # and ‡ denote CHDCl₂ and thianthrene, respectively. Detailed spectra are shown in Supplementary Figs. 14 and 45–47. NICS(0)_zz grids (LC-ωhPBE/6-31G*, ω = 0.1) in the xy plane for each state (without template).

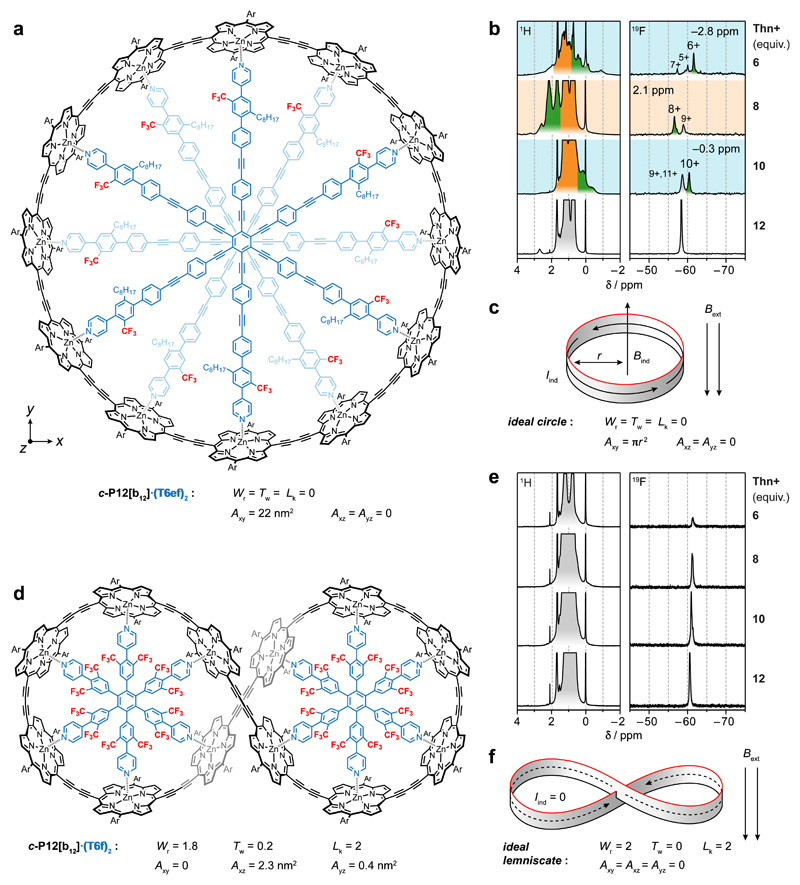
Fluorinated templates allow the aromaticity of nanorings to be evaluated using ¹⁹F NMR, as exemplified by the extended six-legged template T6ef (Fig. 4a). Two molecules of this template stack to form a stable 2:1 complex with the nanoring, c-P12[b₁₂]·(T6ef)₂ (circuit electron count: 168 πe when neutral²⁷), in which the CF₃ groups are positioned to probe the global ring current. The CF₃ ¹⁹F resonance is shielded in the aromatic 6+ and 10+ oxidation states, but deshielded in the antiaromatic 8+ oxidation state (Fig. 4b). The shifts of the CF₃ ¹⁹F resonance are fully consistent with shifts of the THS_in ¹H signals (shaded green, Fig. 4b) and they agree with the predictions of NICS calculations. A range of DFT functionals were tested for c-P12[b₁₂]ⁿ⁺ and, as for the 6-porphyrin rings, LC-ωhPBE (ω = 0.1) was found to give the best agreement with experimental ring current shifts (see Supplementary Figs. 88–90 and Supplementary Tables 7 and 8).

Fig. 4. Ring currents in topologically distinct twelve-porphyrin ring complexes.

a, Molecular structure of c-P12[b₁₂]·(T6ef)₂ with two stacked bound template units. b, ¹H and ¹⁹F NMR spectra of oxidised c-P12[b₁₂]·(T6ef)₂; green shading indicates the interior THS_in resonance; backgrounds indicate a global aromatic (blue) or antiaromatic (orange) state. c, A circular conformation is predicted to exhibit a ring current and thus an induced magnetic moment in an external magnetic field. d, Molecular structure of c-P12[b₁₂]·(T6f)₂ figure-of-eight complex. e, ¹H and ¹⁹F NMR spectra of oxidised c-P12[b₁₂]·(T6f)₂. f, In the lemniscate, the two loops induce opposite currents which cancel, and no ring current is expected. Detailed spectra are shown in Supplementary Figs. 17, 18 and 58–67. L_k, W_r and T_w are the linking number, writhe and twist that specify the topology of the loop^32–34. A_xy, A_xz and A_yz are the net cross section areas; for c-P12[b₁₂]·(T6f)₂, A_xy = 0 because the lemniscate has D₂ symmetry and the areas of the two loops cancel.

No aromatic or antiaromatic ring current was detected for the 12+ oxidation state, and this result is reproduced by the NICS calculations, although this 12+ state is expected to be antiaromatic (156 πe; 4n; n = 39). The ¹⁹F NMR titrations also show CF₃ signals attributed to the open-shell 7+, 9+ and 11+ oxidation states, at similar chemical shifts to the neutral compound — thus the shielding or deshielding effects in the open-shell cations are small compared with those in closed-shell species. EXSY NMR experiments show that the odd-electron oxidation states are in chemical exchange with the even-electron states, on a timescale of seconds. It is not surprising that mixtures of oxidation states are formed during these titrations, because the oxidation potentials are closely spaced (for calculated speciation curves, see Supplementary Fig. 79), but it is remarkable that these open-shell species give spectra that are sharp enough to be observed.

We used the 12-porphyrin nanoring c-P12[b₁₂] to explore the relationship between 3D conformation and aromaticity. The magnitude of the ring current induced in a macroscopic ring of metal wire depends on the total magnetic flux passing through the ring. If the ring has a figure-of-eight shape, with two equal lobes such that the magnetic flux passing through each loop induces equal and opposite currents, then there will be no net ring current. We sought to test whether this principle applies on the molecular scale, so we synthesised a small six-legged template, T6f, which forms a figure-of-eight shaped²⁷ 1:2 complex c-P12[b₁₂]·(T6f)₂ (which is doubly twisted, not Möbius^28,29, Fig. 4d) and investigated the ring currents in this system by ¹H and ¹⁹F NMR as a function of oxidation state, under identical conditions to those used for the circular c-P12[b₁₂]·(T6ef)₂. The resulting ¹H, ¹³C and ¹⁹F NMR spectra show the absence of any detectable ring currents (Δδ <0.1 ppm) in the figure-of-eight nanoring, confirming that aromaticity can be switched on/off by geometry (Fig. 4e). This result is reproduced by the NICS calculations (Supplementary Fig. 91).

The suppression of ring currents in figure-of-eight shaped annulenes has been predicted theoretically^28,30, but it has not been observed experimentally in other figure-of-eight shaped aromatic systems^{6,7,14,28,29,31}, probably because they were not the right shape to achieve cancellation of the ring current. The topology of a closed ribbon can be described by the linking number L_k, the writhe W_r and the twist T_w (ref. 32–34). Total cancellation of the ring current is expected for an ideal lemniscate geometry with W_r = 2, T_w = 0 and L_k = 2 with D₂ symmetry (Fig. 4f)²⁸, which is close to the geometry of c-P12[b₁₂]·(T6f)₂ (W_r = 1.8, T_w = 0.2 and L_k = 2, from the crystal structure of c-P12[b₁₂]·(T6)₂, ref: 35). The c-P12[b₁₂]·(T6ef)₂ ring has a large cross sectional area (A_xy = 22 nm²; A_xz = A_yz = 0; Fig. 4c) resulting in a substantial ring current, whereas the c-P12[b₁₂]·(T6f)₂ lemniscate has a small net cross section (A_xy = 0, A_xz = 2.3 nm², A_yz = 0.4 nm² and Supplementary Fig. 93) resulting in a weak response to magnetic field. The ring current in c-P12[b₁₂]·(T6f)₂ is blocked by the global topology (T_w ≈ 0 and W_r ≈ 2), not by any local break in π-conjugation.

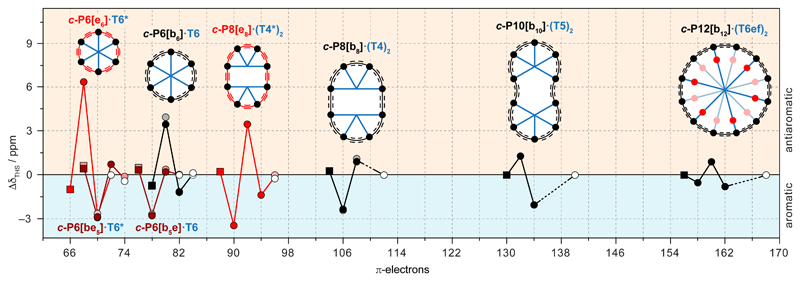
The ring currents observed in this whole family of nanorings are summarised in Fig. 5, which plots the shift in the THS_in resonances (Δδ_THSin) as a function of oxidation state. Whenever a ring current is observed, its direction (aromatic or antiaromatic) matches the prediction from Hückel’s rule. The magnitude of the ring current varies with the average oxidation state of the porphyrin units $(\overline{P_{\text{OX}}}=Q/N).$ The largest ring currents are observed in mixed-valence systems, where $\overline{P_{\text{OX}}}\approx +0.5\text{to}+\mathrm{0.7.}$ Global ring currents are not observed in the neutral rings $\left(\overline{P_{\text{OX}}}=0\right),$ where the local porphyrin ring current dominates; in the larger rings, the ring current also vanishes when $\overline{P_{\text{OX}}}=1$ (see square points for c-P8[b₈]·(T4)₂⁸⁺, c-P10[b₁₀]·(T5)₂¹⁰⁺ and c-P12[b₁₂]·(T6ef)₂¹²⁺ in Fig. 5). The formation of a mixed valence state appears to be essential for efficient nanoscale charge delocalisation, just as the presence of a partially filled band is essential for conductance in an extended lattice³⁶.

Fig. 5. Summary of the shielding and deshielding of the trihexylsilyl groups across eight different nanorings.

Schematic representation of related porphyrin rings; red indicates ethyne, black indicates butadiyne links; black dots indicate zinc-porphyrins; templates in blue. Plot of the observed ¹H chemical shift difference Δδ_THS = δ_THS(in) – δ_THS(out) between inner and outer THS protons for each oxidation state of the nanoring. Positive or negative shifts indicate a global antiaromatic or aromatic current, respectively. Empty circles indicate neutral rings (Δδ_THS = 0); squares indicate oxidation states with $\overline{P_{\text{OX}}}=1$. Vertical dashed lines denote oxidation states with 4n +2 π-electrons. Lines connecting the points are for visual guidance only. Δδ_THS is plotted for the CH₃ (dark points) and SiCH₂ signals (faded points) of the THS chains.

Hückel’s rule was originally formulated to explain the unusual properties of benzene, and other molecules with 6 π-electrons³⁷. It is remarkable that this simple rule correctly predicts the magnetic response of large oxidised nanorings with circuits of up to 162 π-electrons. This work shows that electronic delocalisation can extend coherently around molecular rings with circumferences of 16 nm. These supramolecular rings allow the magnitude of the ring current to be controlled by topology in a way that has not yet been demonstrated for small molecules.

Methods

All ¹H NMR oxidation titrations were carried out by adding a well-stirred suspension of thianthrenium hexafluoroantimonate to a solution of the porphyrin nanoring in CD₂Cl₂ at –60 °C to –20 °C under a counterflow of argon (see Supplementary Material for details). These oxidation experiments were conducted in NMR tubes fitted with J. Young greaseless PTFE stopcocks using CD₂Cl₂ stored over molecular sieves, using standard Schlenk line techniques to exclude moisture. Exposure to water is immediately deleterious to porphyrin polycations, but they are stable to oxygen (O₂). The neutral nanorings are only sparingly soluble in CD₂Cl₂ at low temperatures (< –40 °C), but solubility improves dramatically upon oxidation. The NMR measurements were performed on a Bruker AVII 500 (5 mm BBFO probe). ¹H NMR chemical shifts were calibrated to residual proton signals of the solvent (CHDCl₂ 5.32 ppm). ¹³C NMR chemical shifts were referenced to the solvent peak (CD₂Cl₂ 54.00 ppm). ¹⁹F NMR spectra were referenced to hexafluorobenzene (–164.8 ppm). At the end of each titration, decamethylferrocene (FeCp₂*) was added to reduce the porphyrin nanoring back to its neutral form; the whole oxidation process is highly reversible.

Supplementary Material

Supplementary information is available for this paper at https://doi.org/10.?????