Mathematical modeling reveals alternative JAK inhibitor treatment in myeloproliferative neoplasms

The identification of JAK-STAT pathway mutations in the majority of patients with myeloproliferative neoplasms (MPN) led to the clinical development of JAK inhibitors and resulted in the approval of ruxolitinib for MPN therapy.

Despite this important therapeutic advancement, there are significant limitations to JAK inhibitor therapy, both with respect to limited efficacy and dose-limiting toxicities. We hypothesized that alternate dosing regimens allowing for intermittent maximal target inhibition might increase efficacy without inducing added toxicity. Here, by combining experimental and mathematical techniques, we investigated the potential efficacy of varying dosing regimens. We first assessed the effect of ruxolitinib on the growth rate of JAKVV617-positive SET-2 cells exposed to a range of ruxolitinib concentrations. The in vitro data were integrated into a mathematical model to predict responses to varying ruxolitinib concentrations, which were then used to inform candidate dosing schedules to be validated in vivo on a JAKV617F knock-in mouse model. We found that a high-dose intermittent schedule was more efficacious than continuous dosing in vivo, without additional toxicity, suggesting that alternate, intermittent JAK inhibitor dosing strategies should be explored in MPN patients.

The BCR-ABL-negative myeloproliferative neoplasms (MPN) polycythemia vera (PV), essential thrombocythemia (ET), and primary myelofibrosis (PMF)¹ are clonal disorders of hematopoietic stem or progenitor cells leading to overproduction of myeloid cells.² Common to all three are systemic symptoms, increased risk of thrombosis, abnormal bleeding, and progression to acute myeloid leukemia (AML). The only curative treatment is allogeneic stem cell transplantation, which is reserved for patients with high-risk disease without significant comorbidities.³ The hallmark of BCR-ABL-negative MPN is constitutive activation of JAK-STAT signaling, including the somatic activating mutation V617F in JAK2 in the majority of MPN patients,^4,5 JAK2 exon 12 mutations in JAK2V617F-negative PV,⁶ and MPL and CALR mutations in JAK2 V617F-negative ET/PMF.^7,8 In each case, these mutations lead to constitutive JAK-STAT signaling^9,10 suggesting JAK2 as a potential therapeutic target. The first JAK2 inhibitor to enter clinical trials was ruxolitinib (INCB018424), which is approved by the Food and Drug Administration for treatment of MF¹¹ and refractory PV.¹² JAK2 inhibitors reduce spleen size, ameliorate systemic symptoms, and improve quality of life; however, they do not achieve significant disease modification in most MPN patients.¹³

The essential role of JAK kinases in hematopoiesis precludes safe, long-term, complete inhibition of JAK2. We therefore explored whether alternative intermittent dosing strategies might offer increased efficacy and/or reduced toxicity in MPN. Previous studies with dasatinib in chronic myeloid leukemia (CML) demonstrated an improved therapeutic window with once daily dosing that provides intermittent, potent BCR-ABL inhibition.¹⁴ We therefore sought to identify the optimal dosing schedule for ruxolitinib for MPN treatment by combining mathematical modeling, in vitro and in vivo efficacy and toxicity studies.

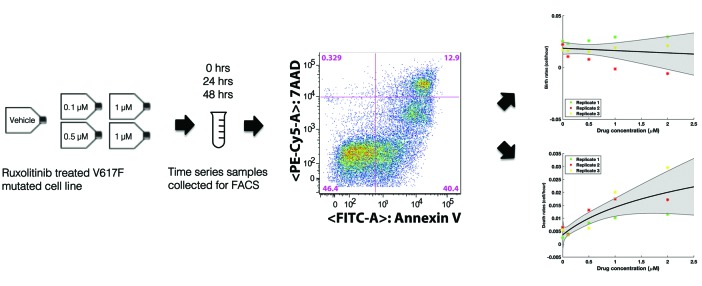
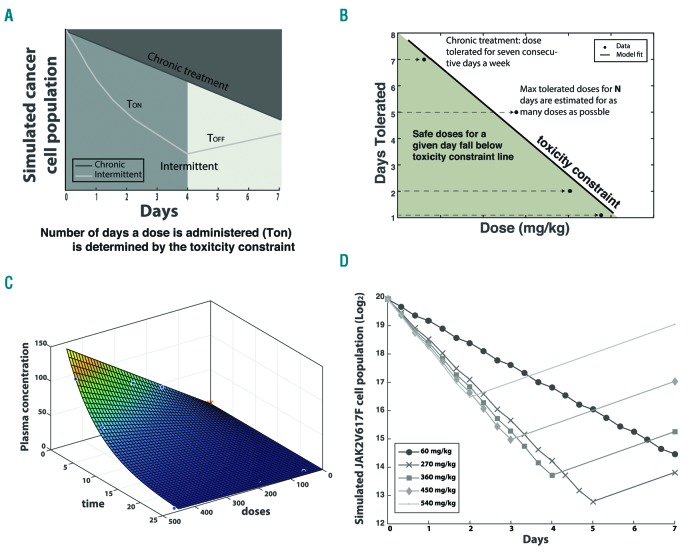
To guide our toxicity studies, growth rates of JAK2-mutant SET-2 cells under a range of ruxolitinib concentrations were estimated from flow cytometry apoptosis/viability assays using FITC-Annexin V and 7AAD staining, respectively (BD Pharmingen) (Figures 1 and Online Supplementary Figure S1). The estimated rates were used to parameterize a mathematical model of exponential expansion/decline of the cell population under different treatment schedules (Figure 2A and Online Supplementary Materials and Methods). The model was constrained by a toxicity curve, which indicates how many consecutive days a given dose is tolerated without inducing murine death (Figures 2B and Online Supplementary Figure S3 and Toxicity constraint section in the Online Supplementary Materials and Methods). Each treatment cycle consisted of a dose given for a certain number of days (the treatment pulse length, T_on) followed by a break, T_off. As the toxicity constraint determines how many consecutive days are safe to administer a certain dose (T_on), and the cycle length (T_on+ T_off) is fixed as one week, a chosen dose uniquely determines the treatment schedule as well as the birth and death rates of the cells. However, drug concentration is not constant over time in vivo but rather it decays exponentially. We fit an exponential decay surface to in vivo pharmacokinetic data in order to approximate the drug concentration at any given time (Figure 2C, Pharmacokinetic analysis section in the Online Supplementary Materials and Methods).

Figure 1.

In vitro experimental design using V617F mutated cell line. In vitro time series fluorescence activated cell sorting (FACS) measurement of Ruxolitinib-treated SET-2 cells were used to estimate the growth rates of cells over a range of Ruxolitinib concentrations (0, 0.1, 0.5, 1, and 2 µM). Birth and death rates were estimated from the time series FACS measurements of the cells stained with apoptosis and viability stains Annexin V and 7AAD, respectively. Each experimental replicate is represented by a different color. The x-axis shows the drug concentrations to which cells were exposed and the y-axes show the rates resulting from estimating the change in live and dead cells obtained from the FACS measurements over a time range of 48 hours for each concentrations of drug exposure. Mean line corresponds to the model fit to all the data and shaded region shows the 95% confidence interval obtained from fitting 100 bootstrapping samples.

Figure 2.

Mathematical modeling predicts optimal treatment schedule. (A) Mathematical model schema. Cell growth is simulated over a 1-week cycle based on in vitro growth rates for a period of continuous daily treatment (T_on) followed by a treatment break (T_off). In the case of chronic dosing, a non-stop treatment is simulated for the whole duration of the 1-week cycle. Treatment schedule (number of T_on days) is uniquely defined, given a chosen dose, by the toxicity constraint. (B) The toxicity constraint was built based on previous knowledge about how many consecutive days different doses could be tolerated in mice. (C) Pharmacokinetic surface. Drug concentration is not constant over time in vivo. An exponentially decaying surface describing the change in plasma concentration as a function of dose (mg/kg) and time is fit to in vivo pharmacokinetic data in order to approximate the drug concentration at any given time. (D) In vivo simulation based on In vitro data. Cell population growth is estimated for different treatment schedules and predicts the optimal treatment schedule of 270mpg for five consecutive days to minimize cancer cell population.

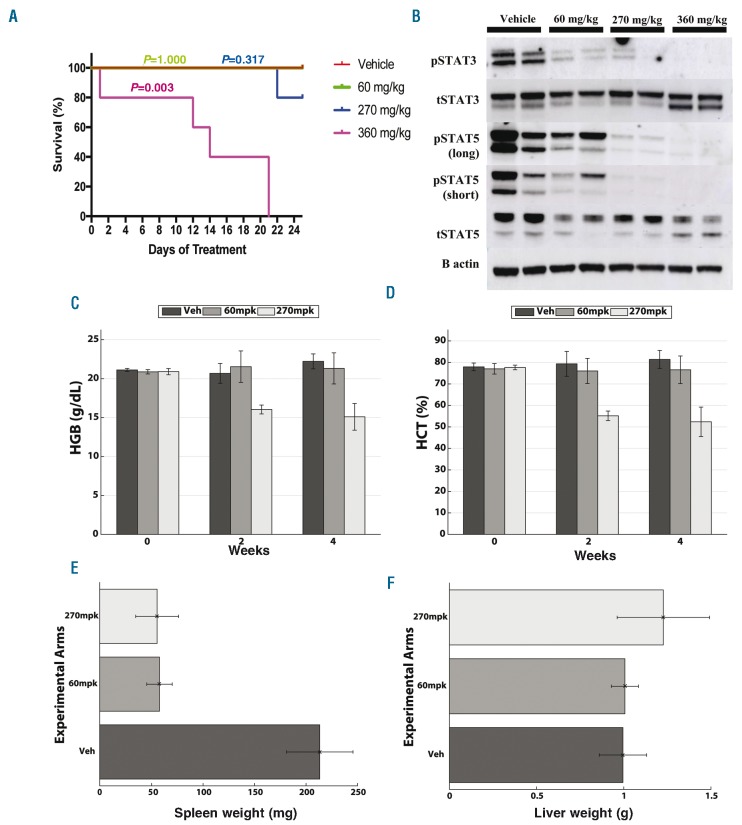
The efficacy and toxicity of the different treatments in vivo were evaluated based on cohort survival, complete blood counts, liver and spleen weights, and the histologic evaluation of the bone marrow, spleen, liver and gut (Figure 3, Online Supplementary Figures S5 and S6). A non-parametric Wilcoxon rank-sum test was used to determine the statistical significance of the pairwise comparisons of the treatment groups (Online Supplementary Table S1). All computer simulations were performed using MATLAB 8.5.0 (2015a, The MathWorks Inc., Natick, MA, USA). To enable the re-use of our materials and improve reproducibility and transparency we include the MATLAB code and data used for all the analysis and visualizations contained in this paper in the open repository https://github.com/answermyriddles/rux.

Figure 3.

In vivo data confirm in silico predictions. (A) Kaplan-Meier Survival Plot. Group 1 (red) was treated with vehicle twice daily. Group 2 (green) was treated with 60 mg/kg twice daily. Group 3 (blue) was treated with 270 mg/kg twice daily for five days followed by a two-day holiday. Group 4 (purple) was treated with 360 mg/kg twice daily for three days followed by a four-day holiday. The 360 mg/kg treatment group showed a significant decrease in survival (P=0.003) compared to other experimental arms. (B) Western blot. While mice treated with 60 mg/kg ruxolitinib showed partial pSTAT3 and pSTAT5 signaling, mice treated with 270 mg/kg showed nearly complete inhibition of pSTAT5 signaling, indicating there is improved signaling inhibition with increased dose. Complete blood counts measured before and after treatment revealed significant improvement in (C) hemoglobin and (D) hematocrit in group treated with 270 mg/kg bis in die (BID) (five times/week) in comparison to mice treated chronically with 60 mg/kg BID as well as vehicle starting at two weeks after treatment. A non-parametric Wilcoxon rank sum test revealed differences between the 270 mg/kg group and two others to be significant with P-values <0.016 for both hemoglobin and hematocrit. Complete results from statistical testing can be found in the Online Supplementary Table S1. (E) Mice treated with 270 mg/kg BID five times/week and chronic 60 mg/kg BID ruxolitinib showed marked reduction in spleen weight compared to vehicle treatment at the conclusion of 25 days of treatment (P-values of 0.007 comparing treatment groups to vehicle using a Wilcoxon rank sum test). (F) There was no significant change in liver weight between all groups supporting the absence of drug-related toxicity. All pairwise statistical test results for all three groups for liver and spleen can be found in Online Supplementary Table S1.

We created this mathematical modeling framework to investigate disease progression during intermittent and chronic treatment schedules of the JAK inhibitor, ruxolitinib. Our model was parameterized by the growth rates of JAK2V617-positive SET-2 cells exposed to varying doses of ruxolitinib to estimate cell population growth after a treatment cycle of one week (Figure 2D and Online Supplementary Materials and Methods). Our modeling approach resulted in two intermittent treatment schedules for which the final simulated cell population growth at the end of the one week treatment cycle was similar to that of a chronic one (Figure 2D). The two intermittent treatment schedules selected were 270 mg/kg bis in die (BID) and 360 mg/kg BID given for five and three consecutive days a week, respectively. Despite the one week predictions for the 360 mg/kg dosing resulting in a larger cell population compared to the chronic treatment (60 mg/kg), we decided to test it in vivo as well given the final simulated cell populations were of comparable size (Figure 2D and Online Supplementary Figure S4). By nature of being parameterized using in vitro data, our mathematical model is only an approximation and was intended for the purpose of hypothesis generation, pending further investigation in vivo. Instructed by our model we selected a chronic dosing schedule as well as the two aforementioned intermittent schedules to test in an MPN murine model.The in vivo trial demonstrated that in comparison to a chronic dose of 60 mg/kg BID, 270 mg/kg BID administered five days a week led to equivalent survival (P=0.31 according to a Log-rank test, Figure 3A) and was more effective at inhibiting JAK2 signaling (Figure 3B). Specifically, we observed greater pSTAT5 inhibition in the intermittent 270 mg/kg group compared to the 60 mg/kg chronic group (Figure 3B). The intermittent schedule also reduced hemoglobin counts by 25% (P<0.016) (Figure 3C) and hematocrit counts by 30% (P<0.016) (Figure 3D), without inducing additional hematopoietic or gastrointestinal toxicity (Online Supplementary Figure S6). Spleen weights was equivalently reduced for both the 60 mg/kg and 270 mg/kg groups compared to vehicle (Figure 3E and Online Supplementary Table S1). The intermittent 360 mg/kg schedule, however, induced gastrointestinal toxicity (apparent on gross examination with intestinal edema and erythema) and led to reduced survival compared to other dosing schedules (Figure 3A). These results suggest that the intermittent 270 mg/kg ruxolitinib dosing schedule is capable of increasing drug efficacy in the Jak2V617F model without inducing increased toxicity.

Through this study, we sought to test the effects of different ruxolitinib treatment schedules on survival, toxicity and allele burden in a JAKV617F knock-in mouse model. We designed a novel mathematical framework consisting of multiple components (exponential population growth constrained by toxicity and a time/dose dependent pharmacokinetic surface) that, when parameterized using in vitro data, predicted the efficacies of different dosing strategies in silico and allowed us to test hypotheses about the best intermittent treatment strategies to be validated in an in vivo MPN murine model. Based on our in silico model, we predicted that an intermittent treatment strategy could lead to increased efficacy and/or reduced toxicity. We confirmed that increased efficacy could be reached with a 270 mg/kg BID dose for five days followed by a two-day holiday without inducing hematopoietic or gut toxicity. Unfortunately, no treatment group showed differences in the reduction of allele burden, which has only been shown to date in a study by Vannucchi et al, which demonstrated progressive reduction in allele burden in JAK2 pV617F PV patients treated with ruxolitinib for up to 4 years.¹⁵ Of note, our study was of only 25-day duration, and it may take much longer-term studies to see an impact on allele burden, which is outside the scope of the current work.

It remains to be understood whether an intermittent treatment could have further beneficial effects such as preventing persistence to the JAK inhibitor after long-term use or whether treatment with JAK inhibitors alone will be enough to completely cure MPN because of the intrinsic limitation of the mechanism of action of the drug. We demonstrated that by combining in vitro data with mathematical modeling one can efficiently compare intermittent versus chronic dosing regimens and determined that an intermittent schedule is superior in the treatment of an MPN murine model. This study represents an innovative example of how mathematical modeling and biological data can be used to develop novel dosing regimens, an increasingly important question in the cancer and targeted therapy field.