Dynamics of strand slippage in DNA hairpins formed by CAG repeats: roles of sequence parity and trinucleotide interrupts

Abstract

DNA trinucleotide repeats (TRs) can exhibit dynamic expansions by integer numbers of trinucleotides that lead to neurodegenerative disorders. Strand slipped hairpins during DNA replication, repair and/or recombination may contribute to TR expansion. Here, we combine single-molecule FRET experiments and molecular dynamics studies to elucidate slipping dynamics and conformations of (CAG)_n TR hairpins. We directly resolve slipping by predominantly two CAG units. The slipping kinetics depends on the even/odd repeat parity. The populated states suggest greater stability for 5′-AGCA-3′ tetraloops, compared with alternative 5′-CAG-3′ triloops. To accommodate the tetraloop, even(odd)-numbered repeats have an even(odd) number of hanging bases in the hairpin stem. In particular, a paired-end tetraloop (no hanging TR) is stable in (CAG)_{n = even}, but such situation cannot occur in (CAG)_{n = odd}, where the hairpin is “frustrated’’ and slips back and forth between states with one TR hanging at the 5′ or 3′ end. Trinucleotide interrupts in the repeating CAG pattern associated with altered disease phenotypes select for specific conformers with favorable loop sequences. Molecular dynamics provide atomic-level insight into the loop configurations. Reducing strand slipping in TR hairpins by sequence interruptions at the loop suggests disease-associated variations impact expansion mechanisms at the level of slipped hairpins.

INTRODUCTION

Trinucleotide repeats (TRs) are a subset of microsatellite repeats in the human genome where a triplet of nucleotides is repeated multiple times (1). TR tracts may expand or contract in multiples of the trinucleotide unit (2,3). If an expansion within susceptible genes crosses a certain threshold, it gives rise to Trinucleotide Repeat Expansion Disorders (2,4–6). TR expansion is associated with more than 40 neurodegenerative and neuromuscular disorders (3,7–9), some of which display ‘anticipation’, where the age of disease onset can decrease coincidentally with intergenerational expansion of a TR (4,10–12).

Among all the possible TRs, CAG repeats are associated with the largest category of neurodegenerative diseases. CAG repeats in the exons of diverse genes cause a variety late-onset, progressive neurodegenerative disorders including Huntington’s disease (HD), dentatorubral-pallidoluysian atrophy (DRPLA), spinal and bulbar muscular atrophy (SBMA, popularly known as Kennedy’s disease) and several spinocerebellar ataxias (SCAs 1, 2, 3, 6, 7 and 17) of which SCA2 is related to amyotrophic lateral sclerosis (ALS) and parkinsonism (8,12,13). These pathologies are collectively referred to as polyglutamine (polyQ) diseases (14), since the CAG expansion in these genes leads to proteins with polyQ expansions, which ultimately form aggregates before eventual neuronal death (15–17).

Expansion of TR regions is believed to be related to the repetitive structure of TRs that could cause slippage during DNA replication, repair and/or recombination (7,8,12,18–22). Although mechanisms of TR expansion may be different for small scale (expansion of one trinucleotide) or large scale (expanding large runs of TR at once) mutations (23), there is broad consensus that secondary structures of TRs, including hairpins, contribute to both phenomena (24). Numerous experimental analyses dating back to 1995 (25,26) and extending to the present have confirmed that non-B DNA secondary structures in the expanded repeats contribute to TR expansion (3). In particular, CAG repeats are associated with hairpins in in vitro experiments with both DNA (27–34) and RNA (35), and although directly visualizing a TR hairpin in vivo is still not possible, indirect experimental data suggests CAG DNA hairpins form in vivo (36,37).

A key behavior of TR hairpins believed to be associated with TR expansion is their tendency for the two strands to slip along each other by integer units of the trinucleotide, a phenomenon known as strand-slipping. Strand-slipping in CAG DNA TR hairpins leading to overhanging single strand DNA regions has been inferred by indirect methods including single-strand nuclease susceptibility, polymerase-based extension, and chemical probing of exposed bases (28,30,38). The dynamics of the strand slipping behavior in TR hairpins has been estimated by observing temporal evolution of ensemble distributions, kinetics of conversion of hairpins to duplex, thermodynamic cycling and single molecule FRET (28–31,39).

Interruptions of the TR region by mutation of one repeat unit to a different codon can play important roles in TR disorders (40). Genetic studies find that interrupts increase the stability of alleles for several disease-related TRs (40–46). In particular, interruptions of a (CAG)_n repeat tract by mutation to CAA has strong phenotypic effects in several diseases (47). CAG TRs expand less and are associated with different disease age-of-onset phenotypes when interrupted by CAA in SCA17 (46) and SCA2 (13,48–50). In the Huntington gene, the (CAG) repeat region normally terminates with a CAA codon interrupting the (CAG) tract in the penultimate position. Rare mutations involving this interrupting codon in HD recently were linked to instability of the TR region and changes in the HD age-of-onset: earlier in individuals with the loss of CAA but later in those with duplicated CAACAG at the end of the TR region (51,52). Because CAG and CAA both code for glutamine, the impact of this change on disease phenotype, despite the unchanged polyQ protein produced, taken together with evidence that mRNA levels do not impact age-of-onset (52) confirms that at least some TR disorder phenomena occur at the level of the DNA.

In vitro studies showed that CAT interrupts in CAG TR and AGG interrupts in (CGG) TRs both reduce slipped strand configurations of hairpins (53). Interestingly, CAA interrupts also increase the fidelity of polymerase chain reaction (PCR) amplification of CAG repeated sequences (54) and reduced TR expansion in a yeast genetic assay (55). These biochemical characterizations support the hypothesis that interrupts enhance genomic stability of TRs by suppressing strand slippage in TR hairpins.

Despite the extensive evidence that CAG-containing TR DNA forms interconverting, slipped-strand hairpins, at present, there is neither a known molecular structure for a CAG-repeat hairpin nor a complete description of its strand slipping kinetics. Experimental structural studies of CAG repeats are limited to RNA using X-ray crystallography (56–58), and NMR (58,59). Given that the expansions that characterize TRs originate at the DNA level, an understanding of the dynamics of hairpin slipping along with a structural characterization of these repeats at the atomic level in DNA is particularly important.

In our previous work (60), we performed free energy and molecular dynamics (MD) studies to determine the preferred conformations of the A–A non-canonical pairs in (CAG)_n and (GAC)_n TRs (n = 1 to 4) and the consequent changes in the overall structure of both RNA and DNA duplexes. We found that the global free energy minimum corresponds to A–A pairs stacked inside the core of the helix with anti-anti conformations.

In this work, we combine experimental and computational investigations to directly probe the conformational ensemble and dynamic slipping of CAG TR hairpins. We use single-molecule fluorescence resonance energy transfer (smFRET) to directly observe dynamic slipping in CAG TR hairpins by integer numbers of CAG units, predominantly two CAG units. The observed hairpin dynamics, which agrees with previously reported parity-dependent behaviors (29–31), taken together with our molecular characterization of the conformers points toward the slipping dynamics being governed by a balance between free energies in the stem and loop of the TR hairpin that leads to more frequent slipping in hairpins with an odd number of repeat units. The details of the loop configuration and the impact on slipping are confirmed by studies using TR sequence interrupts that vary the specific loop sequence and result in strongly preferred conformers. We complement the smFRET studies with classical MD studies, which completely characterize the atomic configurations, and the structural origin of the competing energetic trends between loop and stem that drive the slipping of the odd-numbered hairpins. The simulations also provide insight into the triggering instability that initiates the slipping process. Our characterization of these spontaneous TR slips defines fundamental behaviors of TR hairpins that replication machinery or other repair or recombination-related proteins must manage.

MATERIALS AND METHODS

For smFRET experiments, we designed a two-strand system involving an anchor strand and a hairpin strand positioning donor (Cy3) and acceptor (Atto647N) fluorophores at consistent positions for all hairpins (see Figure 1(A), Supplementary Figures S1, S4 and S8) (61,62). All DNAs were purchased from IDT (Coralville, IA, USA), and the sequences are listed in Supplementary Table S1. Biotinylated DNAs were immobilized at widely spaced locations on biotinylated bovine serum albumin (biotin-BSA)/streptavidin coated quartz slides inside flow chambers. Single molecule FRET signals were recorded with a homebuilt, prism-based TIRF microscope as described in (63) using a 60× 1.2 N.A. objective, a Dualview image splitter with a 645dcxr dichroic mirror, HQ585/70m (donor) and HQ700/75m (acceptor) filters (Chroma) and an emCCD camera (Cascade 512B, Photometrics) recording at 15 ms per frame using 3 × 3 binning on chip before readout. Images were background subtracted, and then donor intensity (Id) and acceptor intensity (Ia) were extracted from the movie at each spot identified to have an active acceptor in the first 150 ms of the movie. FRET efficiency was defined and calculated as Ia/(Ia + Id) and not corrected for gamma factor (64). Histograms contain all the timepoints of FRET efficiency from multiple picked molecules. All the histograms are fit with multiple Gaussian functions to identify the peak locations. Estimates of the uncertainty in the reported peak locations are described in the Supplementary methods and Supplementary Table 2. We used automatic software (65) or manual identification to identify edges of transitions in FRET intensity traces (Supplementary Figure S2(A)). Histograms of dwell times in each state (Supplementary Figure S2B–F) were fit to single exponential decay function to extract fitting parameters. All measurements were conducted at 21°C in buffer containing 20 mM Tris–HCl pH 8.0, 10 mM NaCl, and an oxygen scavenging system of 1% glucose, glucose oxidase (100 units/ml), catalase (1000 units/ml), 0.05 mg/ml cycooctatetraene and 1% β-mercaptoethanol unless otherwise noted.

Figure 1.

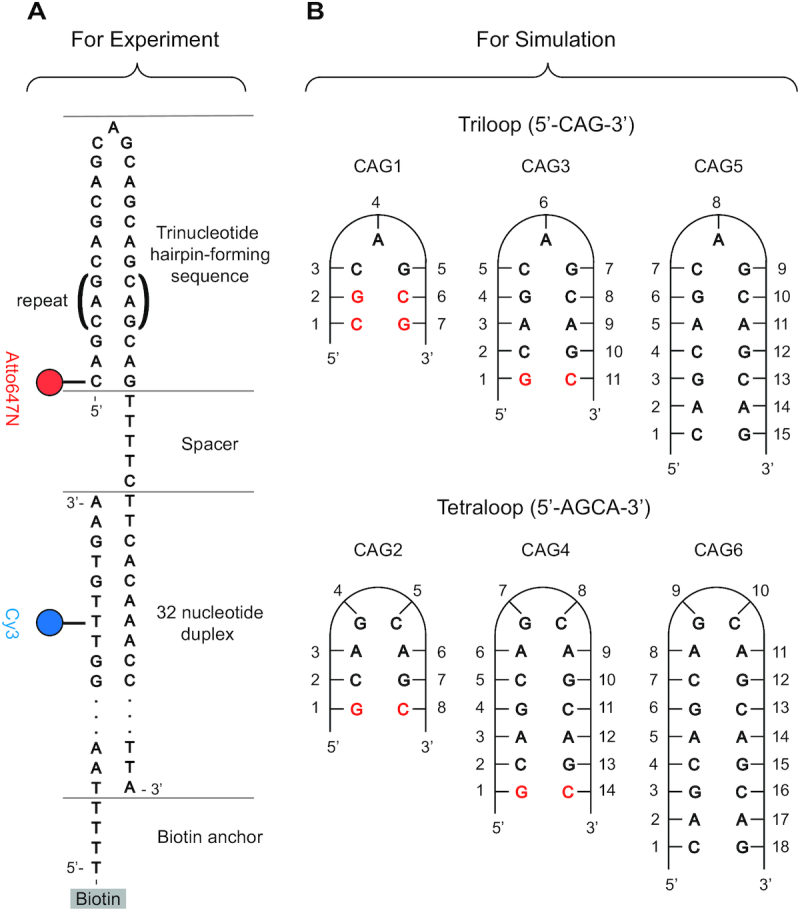
(A) Schematic DNA design for the smFRET analysis of CAG repeat hairpins, with donor in blue and acceptor in red. The CAG sequence in parenthesis is repeated for various hairpins. The hairpin loop of interest is immobilized to a surface by a partial complimentary DNA anchor strand. The TTTTC spacer helps reduce the interaction between the hairpin and junction duplex. (B) CAG hairpins sequences considered in the MD simulations. CG Watson-Crick pairs were added to the ends of short repeats to mimic long canonical stems.

The simulations were carried out using the PMEMD module of the AMBER v.16 (66) software package with force fields ff99 BSC1 (67) for DNA. For the waters, the TIP3P model (68) was used, as well as the standard AMBER force field parameters for the ions (69). The main CAG hairpins simulated are shown in Figure 1B. To model the long-range Coulomb interactions, the Particle-Mesh Ewald (PME) method (70) with a 9 Å cutoff and an Ewald coefficient of 0.30768 was used. The van der Waals interactions were calculated by means of a 9 Å atom-based nonbonded list, with a continuous correction applied to the long-range part. MD production runs were generated using the leap-frog algorithm with a 2 fs timestep utilizing Langevin dynamics with a collision frequency of 1 ps⁻¹ at 300 K. The pressure of the system was maintained at 1 bar using the Berendsen barostat, with isotropic position scaling and relaxation time of 1 ps. The SHAKE algorithm was applied to all bonds with hydrogen atoms. Regular long MD simulations up to 2 and even 3 μs were run for all sequences, using different initial conformational values for the glycosyl torsion angles χ as will be discussed.

Additional methodological detail in supplementary methods.

RESULTS

smFRET analysis of DNA containing CAG TRs

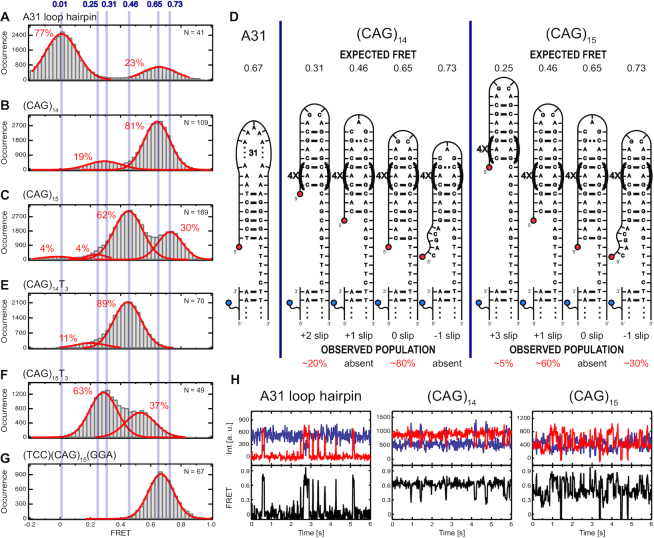
For smFRET studies, we used a two strand DNA system that allowed the specific hairpin to be changed while maintaining a consistent placement of the donor and acceptor dyes (Figure 1A). When the hairpin closes, the acceptor and donor are close and we expect high FRET. When the hairpin is open, we expect low FRET (near zero). We verified these expectations with a hairpin formed from a stem of 6 matched Watson-Crick base pairs and a loop of 31 adenine (A) bases. This A31 loop hairpin has 2 states with FRET efficiency 0.01 and 0.67, corresponding to open and closed respectively, see Figure 2A.

Figure 2.

smFRET analysis and interpretation of A31, (CAG)₁₄ and (CAG)₁₅ hairpin loops, as well as associated hairpin variants. Histograms contain all the timepoints of FRET efficiency from multiple molecules. All the histograms are fit with multiple Gaussian functions (red line) to identify the peak locations. Here we show results for (A) A31; (B) (CAG)₁₄; (C) (CAG)₁₅; (E) (CAG)₁₄T₃; (F) (CAG)₁₅T₃ and (G) (TCC)(CAG)₁₅(GGA). In (D), we present schematic diagrams to show molecular configurations, expected FRET values (upper edge) and the corresponding observed populations (lower edge) of the individual hairpins. The slip designation is indicated below each schematic. (H) Representative smFRET time traces (upper panels, donor signal in blue, acceptor signal in red) and calculated FRET values (lower panels, black) for A₃₁, (CAG)₁₄ and (CAG)₁₅ hairpin loops.

We measured smFRET signals from DNA containing 14 CAG repeats, which we designate (CAG)₁₄ (Figure 2B). When folded into a symmetric hairpin, MD simulations indicate a conformation of a tetraloop (AGCA) with the remaining bases paired in the stem containing G-C Watson-Crick base pairs and A–A mismatches, as shown in models shown in Figure 2D. smFRET time traces from (CAG)₁₄ have transitions among three different FRET efficiencies of 0.65, 0.31 and 0.01 (Figure 2B,D ). The 0.01 state was rarely visited, whereas there were many of transitions between the 0.31 and 0.65 states (Figure 2H). The 0.65 state was most stable with the hairpin populating that state for the majority of the time.

To assist identifying the configuration of the DNA generating these FRET efficiencies, we compare these results to the A31 loop hairpin (Figure 2A). The similarity in the highest and lowest smFRET efficiency states in the (CAG)₁₄ and the A31 hairpin experiments leads us to assign the lowest (0.01) state to the completely open state and the highest state to the folded hairpin state in both. The slight difference in the of the FRET efficiency of the closed states (0.67 for A31 and 0.65 for (CAG)₁₄), which is highly reproducible (beyond our uncertainty of ±0.01 for those FRET states. Error estimates and details on FRET efficiency measurements are described in Supplementary Tables S2 and S3.), is possibly due to transient unpairing of the CG terminal basepair of the (CAG)₁₄ as it is positioned beside an AA mismatch. There was no analogue in the A31 experiment for the 0.31 state observed in the (CAG)₁₄ experiments, which we will pursue further below.

We next measured DNA containing 15 CAG repeats, referred to as (CAG)₁₅. Surprisingly, smFRET measurements of (CAG)₁₅ revealed transitions among four states with FRET efficiencies 0.73, 0.46, 0.25 and 0.01 (Figure 2C, D). In agreement with the observation in the (CAG)₁₄ study, the 0.01 state was the rarest. Unlike the (CAG)₁₄ study, the 0.73 and 0.46 states were more equally populated, suggesting they have similar stabilities. We attribute the rare 0.01 state to the fully open state based on the similarity with (CAG)₁₄ and the A31 open state. The other states for (CAG)₁₅ (0.25, 0.46, 0.73) interleave with the states from (CAG)₁₄ (0.31 and 0.65). The highest state of (CAG)₁₅ (0.73) as higher than that of A31 and the (CAG)₁₄. This difference indicates that for the 0.73 state in (CAG)₁₅, the acceptor end is closer to the donor in the anchor compared to the 0.65 state of (CAG)₁₄, which could happen from the (CAG)₁₅ hairpin slipping by one CAG unit toward the donor on the anchor strand (Figure 2D), which we denote as ‘–1 slip’ in Figure 2(D). Similarly, the 0.46 state could be the (CAG)₁₅ hairpin slipping one CAG unit away from the donor, denoted as ‘+1 slip’ in Figure 2D. Slipping forward or backward by one CAG unit would allow (CAG)₁₅ to form an AGCA tetraloop turn with the stem assembling into the CAG/GAC aligned pairings, whereas aligning the CAG/GAC pair at the end of the (CAG)₁₅ hairpin (denoted ‘0 slip’ in Figure 2D) would require the loop to contain one CAG unit, a CAG triloop (Figure 2D). Previous studies indirectly observed odd repeat TR hairpins tolerating single trinucleotide stem overhangs to accommodate tetraloop structures as reported by nuclease susceptibility, polymerase extension, and chemical susceptibility of specific guanine bases (28,30,38). Additionally, our MD simulations (discussed below) indicate CAG triloops are substantially less stable than AGCA tetraloops. Continuing with this hypothesis, the 0.31 state of (CAG)₁₄ could be slipping two CAG units and the 0.25 state of (CAG)₁₅ slipping three CAG units (‘+2’ slip and ‘+3’ slip respectively).

We designed DNAs to test whether the intermediate states are consistent with hairpin slipping by multiples of trinucleotides. Adding unpaired T bases between the 3′ end of the hairpin and the anchor displaces the folded hairpin and associated acceptor fluorophore on the 5′ end by a known number of unpaired trinucleotides away from the donor. We inserted three extra Ts in CAG repeats containing 12, 13, 14 and 15 triplet units (called (CAG)₁₂T₃, (CAG)₁₃T₃, (CAG)₁₄T₃ and (CAG)₁₅T₃ respectively (Figure 2E, F and Supplementary Figure S1). Our models of (CAG)₁₄ and (CAG)₁₅ slipping (Figure 2D) suggest that the lower state of (CAG)₁₅ (E = 0.46 due to a slip of one CAG unit – 3 bases) should be similar to the highest state in (CAG)₁₄T₃, which has E = 0.45. Similarly, our model for the low state in (CAG)₁₄ being due to a slip of two CAG units (six bases) should compare well with the low state of (CAG)₁₅T₃ (assuming the low state in (CAG)₁₅ is due to one CAG unit slip), which they do, E = 0.29 versus 0.31. These results strongly suggest that the lower FRET state in (CAG)₁₅ is due to slipping by one CAG unit and the lower FRET state in (CAG)₁₄ is due to slipping two CAG units.

These observations highlight systematic differences in behavior of odd and even numbers of CAG repeats. Even-numbered repeats (e.g. (CAG)₁₄) accommodate an AGCA tetraloop with a fully strand-paired stem (without hanging trinucleotides) (Figure 2D). An alternate, less preferred configuration for even TR hairpins has the stem slipped by two CAG units, which also forms an AGCA tetraloop. In odd-numbered repeats (e.g. (CAG)₁₅), a paired-end stem requires formation of a CAG triloop, which we find spontaneously slips forward or backward by one trinucleotide to form an AGCA tetraloop with a hanging trinucleotide in the stem. We measured the dwell times in each state between transitions among these states in many single molecules for both (CAG)₁₄ and (CAG)₁₅ hairpins (Supplementary Figures S2 and S3). Fitting histograms of these dwell times with single exponential functions allows the characteristic lifetimes to be estimated. These quantitative dwell time measurements (Supplementary Table S4) confirm that the (CAG)₁₅ hairpin is more dynamic with more frequent slipping transitions than the (CAG)₁₄ hairpin (Figure 2H), suggesting the potential triloop for odd-parity hairpins frustrates their stability. We have verified this general pattern of states and kinetics is observed in other numbers of even and odd CAG repeats by measuring hairpins with 7–13 repeats (see Supplementary Figures S5 and S6). The dwell times become shorter as the hairpins become shorter. It is possible that the FRET states observed in the shortest hairpins (e.g. (CAG)₇) arise from rapid averaging of two underlying configurations interchanging at a rate just below our 15 ms resolution (71). Transitions between the fully open hairpin and any closed hairpin state (any degree of slipping) were rare compared to transitions between closed states of the hairpin with different degrees of slipping for both even and odd CAG repeat numbers suggesting the barriers to open are larger than to slip. The characteristic dwell time for (CAG)₁₄ were longer at 15°C compared to our standard 21°C measurements (Supplementary Table S4) while the populations of the states were not strongly affected (Supplementary Figure S7), suggesting the barriers between the states are on order of thermal energy around room temperature. In addition, higher cation concentration stabilized the symmetric folding state (indicated by an increase in the highest FRET state population) and slightly increase the FRET efficiency of the state (0.73 in 10 mM NaCl, 0.76 in 100 mM NaCl, 0.78 in 1000 mM NaCl, and 0.81 in 10 mM MgCl₂) for (CAG)₁₅ (Supplementary Figures S3 and S7). The difference in stability of the slipped CAG states in even and odd numbers of repeats suggests that a delicate balance between energies in the combination of the stem and either triloops or tetraloops that form in CAG repeat sequences make critical contributions to the overall stability of the slipped states of the CAG repeat hairpins.

CAA interrupts select preferred slipped strand conformers of (CAG)_n TRs

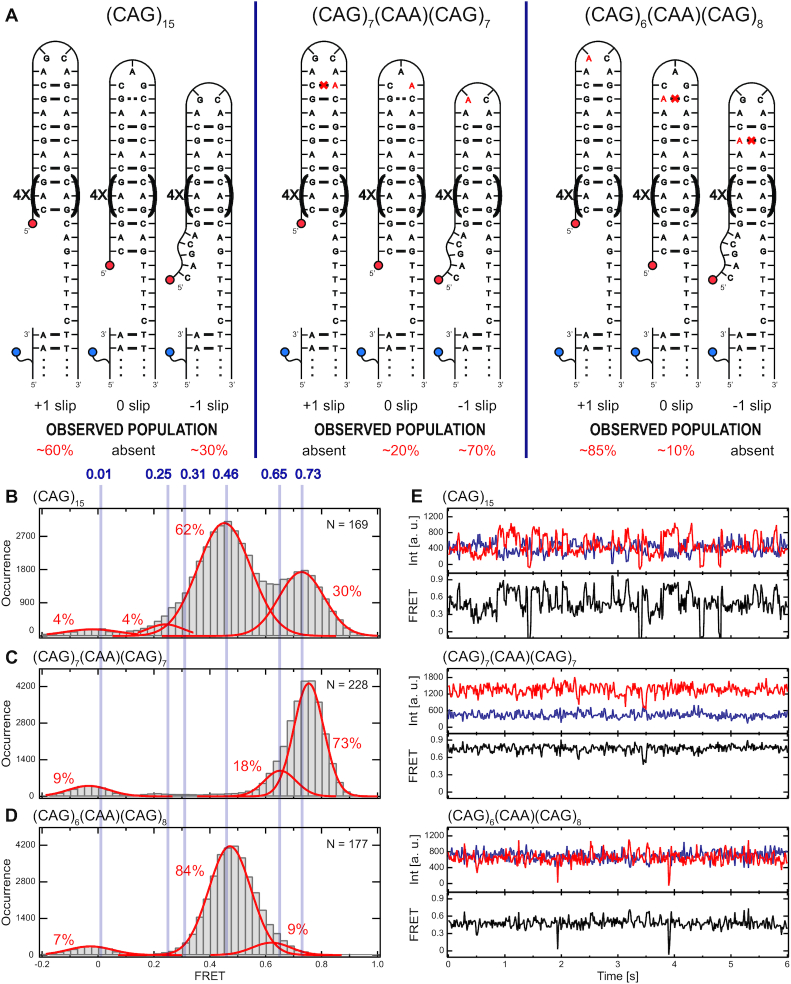
Because CAA interrupts within (CAG)_n tracts impact disease phenotypes in HD and in SCA2, we measured (CAG)₁₅ hairpins that were interrupted by CAA at the seventh and eighth position (noted as (CAG)₆(CAA)(CAG)₈ and (CAG)₇(CAA)(CAG)₇). The interrupt is located near the natural loop position in these constructs (Figure 3A). Placing the CAA interruption at position 7 (Figure 3D) dramatically stabilized the +1 slip with a new, minor population forming at 0 slip (FRET 0.65). The CAA interruption at position 8 (Figure 3(C)) stabilized the –1 slip state and also generated a small population of 0 slip not observed in (CAG)₁₅. For the seventh and eighth position CAA interrupts, slipping transitions were strongly suppressed compared to uninterrupted (CAG)₁₅ (Figure 3E).

Figure 3.

CAA Interrupts near the loop can stabilize (CAG)₁₅ strand-slipping transitions. (A) Schematics of possible folding configurations and smFRET results for (CAG)₁₅ and several CAA interrupted (CAG)₁₅ TR hairpins. Sequences are indicated at the top of the diagram. Slip designation and observed populations are indicated along the lower edge. Results of (CAG)₁₅ experiment from Figure 2 are listed for comparison. (B–D) Histograms of smFRET measurements for the hairpins diagramed in (A). (E) Representative time traces (upper panels, donor signal in blue, acceptor signal in red) and calculated FRET values (lower panels, black) for the (CAG)₁₅ and the CAA interrupted (CAG)₁₅ TR hairpins.

The stabilized states with the CAA interrupt at the seventh and eighth positions both are consistent with a tetraloop sequence of AACA closed by two G–C Watson–Crick bonds, differing from the AGCA loop that is present in the two states that interconvert for the (CAG)₁₅ hairpin. The minor 0 slip state in the CAA interrupted hairpins may be a larger, 7-base loop assuming the possible G–C basepair within that loop is not stabilized. Importantly, the slipping by two CAG units (between +1 and –1) that is characteristic of (CAG)₁₅ is eliminated by CAA near the loop. In total, these studies indicate that the presence of a point mutation generating a single CAA interrupt dramatically stabilizes the strand-slipping dynamics in the CAG TR hairpins when the sequence change occurs in the loop.

smFRET experiments of loop sequence variants

We tested additional interrupts in (CAG)₁₅ to investigate the relative influence between the loop and the closest base pairs in the stem on overall hairpin configuration bias. Changing the middle CAG in (CAG)₁₅ to AAA ((CAG)₇(AAA)(CAG)₇) results in a triloop configuration that has AAA or a tetraloop with AGAA and the loss of a G-C at the base of the loop (Supplementary Figure S8C). For this construct, we measured predominantly 0.65 with only short, rare excursions to 0.37 and nearly no open hairpin (0.01), indicating that the fully matched CAG/GAC paired stem (0 slip) with the AAA triloop was highly stabilized relative to the slipped stem with a tetraloop (middle model, Supplementary Figure S8C).

The triloop configuration of (CAG)₁₅ could be stabilized by adding three Watson–Crick base pairs to the end of the hairpin (Figure 2(G) and Supplementary Supplementary Figure S1F). For TCC(CAG)₁₅GGA, we observed only one state at E = 0.67, consistent with the ends of the hairpin being stable locked by the TCC/GGA basepairs. The (CAG)₁₅ middle section could either form a matched CAG/GAC stem with a CAG triloop, or yet another more complex configuration containing a bubble of unpaired bases. These sequence variants confirm that changes as small as 2 bases in the loop or 3 bases at the end of the stem dramatically change the configuration of (CAG)₁₅.

In another interrupt variant of (CAG)₁₅, (CAG)₆(CGG)(CAG)₈ (Supplementary Figure S8D), we observed preference for a different tetraloop. In this sequence, tetraloops can be either GGCA (+1 slip) or AGCA (−1 slip). smFRET measurements for this sequence found the 0.46 state to be nearly 10 times more populated indicating the GGCA loop is substantially favored over the AGCA. Notably, the potential CAG triloop that would accompany matched stem alignment was absent. Demonstrating the subtle energies of these configurations, the AGCA tetraloop can be stabilized relative to the TGCA tetraloop (left model 0.46 FRET, Supplementary Figure S8(E)) by changing a single base (G to T) as demonstrated in the variant (CAG)₆(CTG)(CAG)₈ (Supplementary Figure S8(E)). In this variant, the 0.73 state is dramatically stabilized compared to that state in (CAG)₆(CGG)(CAG)₈.

In contrast, an ACCA tetraloop with one CAG unit slip in the stem can be stabilized in the sequence (CAG)₆(CAC)(CAG)₈, which replaces only one G base of the loop in the original (CAG)₁₅ by a C (Supplementary Figure S8A). We observed (CAG)₆(CAC)(CAG)₈ primarily exists in the 0.46 FRET state, confirming that the ACCA tetraloop was preferred. A minor population was observed at 0.65, which could be a matched stem with larger loop ACCAGCA (expected E = 0.64) and seems unlikely to be the forward slipped AGCA tetraloop closed by one fewer basepairs in the adjacent stem (expected E = 0.73).

Shifting the G to C substitution to the other side of the loop has unexpected consequences. For (CAG)₈(CAC)(CAG)₆ we measure three states (in addition to the rare E = 0 open state): 0.25 (20% population), 0.46 (35% population) and 0.65 (40% population) (Supplementary Figure S8B). The 0.46 state is consistent with the hairpin slipped back by one CAG unit (+1 slip), forming an AGCA tetraloop. The G to C substitution sacrifices one W-C base pair far down the stem. Similarly, the 0.25 is similar to the hairpins slipped by two CAG units (+2 slip). The 0.65 state is substantially different than the E = 0.73 FRET level expected on forward slip by one CAG unit (−1 slip). It is closer to the values seen when the CAG/GAC pair symmetrically at the end of the stem with no slipping. In this case, the G to C substitution eliminates one C–G basepair in the lock between the stem and loop. This one base pair lock may not be sufficient and it could open to form a nine base pair loop.

Taken together, these result highlights the subtle balance between loop and stem free energies in determining the stability of the triloop and tetraloop configurations of CAG repeat sequences. Measurements of the energy differences for some hairpin states derived from DNA melting are reported in Supplementary Table S5 and Supplementary Figure S9.

Atomistic MD simulations

Our smFRET experiments indicate different hairpin slipping in odd and even number of repeats in CAG sequences but cannot unequivocally determine the number of bases that form the hairpin loop. Based on indirect evidence (27,72–74), it has been suggested that these loops can be tight, i.e. formed by a few bases. We used MD simulations to provide insight into the full atomic level conformations of CAG hairpins and relative stabilities of specific loops configurations (Figure 1B). Simulations with 27 different initial structures for triloops for a total time of 55.5 μs and 38 initial structures for tetraloops for a total time of 67.5 μs were performed. In addition, we ran CAA, AAA, CAC, CGG mutated sequences starting from both triloops and tetraloops (Supplementary Table S11), and (CAG)₉, (CAG)₁₁ and (CAG)₁₅ hairpins both at 0 and 100 mM NaCl in order to identify the spontaneous transition from the less stable triloop towards the tetraloop.

Triloop simulations

Simulations of the CAG1 hairpin (5′-CG-CAG-CG-3′, Figure 1(B)) considered four possibilities regarding the χ angles in the CG base pair closing the CAG triloop: C3(anti)-G5(anti), C3(anti)-G5(syn), C3(syn)-G5(anti) and C3(syn)-G5(syn). Combined with two conformations for the middle A base: A4(anti) and A4(syn) (Supplementary Figure S10), gives a total of eight different triloop conformations. All conformations for the CG pair in CAG involving a syn angle are unstable, and only C(anti)-G(anti) is stable. A4(syn) converts into A4(anti) after 10ns, which results in a stronger stacking of A4/G5, as shown in Supplementary Figure S10. The hairpin with every base in CAG in anti-conformation is stable after 1 μs simulation. This triloop shows a sheared C·G pair (Figure 4A), which has been reported on a GAC triloop (75). The sheared C·G pair has a typical C(O2)–G(N1-H1) hydrogen bond. A side view of the CAG triloop is shown in Figure 4B. The two G–C Watson–Crick base pairs in the stem help stabilize this triloop.

Figure 4.

(A) The sheared C·G pair with a C(O2)–G(H1) H-bond in the stable clamped triloop of CAG1 (Figure 1). (B) A side view of the CAG1 triloop with C3(blue), A4(orange) and G5(cyan). (C and D) Two long-lived loop conformations for CAG4 (Figure 1): (C) S(aa)-L(as)-G(a) (stable) and (D) S(as)-L(ss)-G(s) (kinetic trap). The cartoon only shows the residues from A3 to A12 with A6(blue), G7(orange), C8(red), A9(cyan) and A3–A12(green). (E) The strong stacking between the A–A mismatch in the tetraloop of CAG4 and the C–G Watson–Crick basepair immediately below: C5(yellow)/A6(blue) and A9(cyan)/G10(pink) in the S(aa)-L(as)-G(a) conformation (bases in the 5′-AGCA-3′ tetraloop in conformation anti–anti–anti–syn, with anti–anti conformation for the first mismatch closer to the loop, see text). (F) The two-stack loop in L(aa) (A–A in 5′-AGCA-3′ in anti-anti) for CAG2. Bases in colors: A3(blue), G4(orange), C5(red) and A6(cyan). (G) View for (F) of the stacking of A3(blue)/G4(orange) and C5(red)/A6(cyan).

To study the stability of hairpins with longer stems, we simulated CAG3 (5′-G-(CAG)₃-C-3′) and CAG5 (5′-(CAG)₅-3) (Figure 1(B)). Both were found to be unstable although there is increased stability as the stem length is increased. In particular, CAG5 begins unraveling at approximately 5 μs. See supplemental discussion for more details (Supplementary Table S6, Supplementary Figures S11–S13) as well as a discussion of an observed anti-syn versus anti-anti transitions in the A–A stem mismatches (60) as ion concentration is increased.

Tetraloop simulations

We simulated even CAG repeat numbers to examine 5′-AGCA-3′ tetraloops. For studies of CAG2 [5′-G-(CAG)₂-C-3′], numbering in the tetraloop as A3–G4–C5–A6, Figure 1B), we set initial conformation of the C5 base as anti because it can flip fast. There are four possibilities regarding the χ angles in the A–A base pair closing the loop: A3(anti)–A6(anti), A3(anti)–A6(syn), A3(syn)–A6(anti) and A3(syn)–A6(syn). We name them L(aa), L(as), L(sa), L(ss) (L stands for loop) (Supplementary Figure S14). The G4 base can have two conformations: G(anti) and G(syn), which results in eight different initial conformations.

Time courses for CAG2 demonstrate that loop A3–G4–C5–A6 populates possible stable conformations during the 2 μs simulation (Supplementary Table S7, Supplementary Figure S15). These include L(as)–G(a); L(sa)–G(s); L(ss)–G(s); and L(aa)–G(a) and L(sa)–G(a) that interconvert into each other. Additionally, a different type of loop structure with A/G and C/A stacked on different sides was found in L(aa)–G(a) and L(ss)–G(a) (see Figure 4F for L(aa)). We name it a two-stack loop since it has two stacks of overlapping bases. Stacking of A3/G4 and C5/A6 contribute to the relative stability of the structure (Figure 4G). Two-stack loops have not been observed experimentally in DNA but have been reported in some RNA tetraloops (PDB ID: 1K4A (76), 1AFX (77), 1K6G (78)). None of the tetraloops studied exhibit a full blown instability, as some of the triloops did. Supplementary Movie S1 in the supplemental discussion shows an example of a transition from L(aa)–G(s) to L(aa)–G(a) at ∼890 ns. This loop then transitions to a two-stack loop ∼1370 ns and it finally transitions back to the regular tetraloop ∼1500 ns.

We next simulated CAG4 [5′-G-(CAG)₄-C-3′], where an extra stem A–A mismatch may impact hairpin stability (Figure 1B). We considered three initial conformations for the A–A mismatch (A3(anti)–A12(anti), A3(anti)–A12(syn) and A3(syn)–A12(anti), named S(aa), S(as) and S(sa) respectively, where S stands for stem (Supplementary Figures S16– S18, Supplementary Table S8). We found that the S(aa)–L(as)–G(a) conformation has high stability in the 2 μs simulation and other initial states transition to this configuration frequently (Figure 4C). Another conformation of S(as)–L(ss)–G(s) in kinetic trap was also observed (Figure 4D). L(aa)–G(a) conformations (with different A–A arrangements) coexist with two-stack loops, and are also long-lived. The stability of S(aa)–L(as)–G(a) is enhanced by C5/A6 and A9/G10 stacking (Figure 4E). Other transitions to two-stack loops are discussed in the supplemental. The analysis of hydrogen bond and base-stacking are presented in Supplementary Tables S9–S10, while Supplementary Figure S19 gives a principle component analysis.

Since transitions between different hairpin conformations are relatively rare in the simulation time scales, we cannot carry out a strict cluster analysis but we can present an approximation to it, as shown in Figure 5. This figure is a schematic summary of the 72 times trajectories of the RMSD of the AGCA tetraloop in the CAG4 hairpin and of the χ angles of the neighboring A3–A12 mismatch, as well as of the associated transitions between different conformations (Supplementary Figure S16–S18). Circles represent the eight loop conformations and the three two-stack loops found in our simulations, averaged over the conformation of the A–A mismatch nearest to the loop. The area of each circle represents the percentage of the total simulation time that the hairpin spends on that conformation, while the width of the arrows is proportional to the frequency of transitions. We define a ‘well-connected’ circle as one that has at least two arrows linked to it. A growing circle is one where the net incoming arrows (incoming arrows minus outgoing arrows), weighed by their width, is positive. A shrinking circle has net weighted incoming arrows negative. Thus, the most favored conformations correspond to large, growing circles. The large circles corresponding to L(ss)–G(a) and L(ss)–G(s) are not well connected because they correspond to kinetic traps (see more details and principal component analysis in Supplementary Figure S19 in supplemental discussion). The most favored conformations correspond to large, growing circles. There are two net growing circles, the red L(as)–G(a); and the two versions of L(aa)–G(a): the blue circle (one stack) in coexistence with its two-stack alternate conformation (shaded circle). These are the most favored hairpin conformations for the tetraloops.

Figure 5.

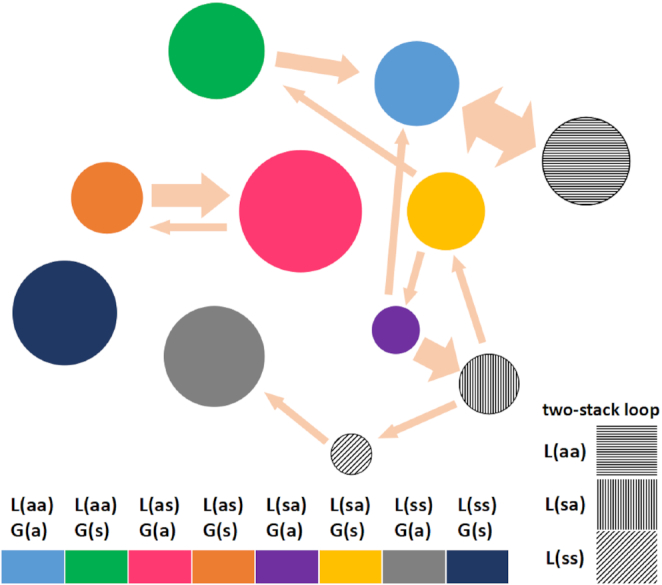
Results for the cluster-like analysis of different conformations for the AGCA tetraloop in the CAG4 hairpin. Different conformations are represented as different colors. Three different kinds of two-stack loops are shown in different shadows. The areas of the circles are representative of the percentage of time that the system spends in that conformation. Likewise the arrows indicate the observed transitions during the simulation with the width of the arrow representing the estimated frequency of transitions. Favorable conformations are indicated by large, growing circles. The simulation results show that the L(as)–G(a) (red; AGCA in anti–anti–anti–syn conformation) and the two versions of L(aa)–G(a) (blue, gray with horizontal line shading; AGCA all in anti conformation) are the most favorable conformations, as discussed in the text.

Interrupts in CAG hairpins to test loop stability

In simulations of hairpins containing variants of the CAG repeat sequences (Supplementary Table S11), we observe dynamic loop re-arrangements consistent with experimental results. For both triloops and tetraloops with CAA interrupts, we simulated the structures with the interrupt at different positions as the experiment did. First, we notice that the triloops (with the CAA interrupt in the middle or to either side of the triloop) tend to show weaker stability, in agreement with the smFRET results. The initial triloops convert into a heptaloop [(CAG)₆–CAA–(CAG)₈], or manifest a tendency to slip [(CAG)₇–CAA–(CAG)₇, which shifts one base towards the 5′ direction, consistent with the –1 slip behavior observed in experiments]. With respect to the tetraloops, our simulations show that a CAA interrupt in the 5′ side of an AGCA tetraloop is not stable, in agreement with the zero population for –1 slip in the (CAG)₆–CAA–(CAG)₈ smFRET result (Figure 3). The simulation where the bases C and A of the interrupt CAA form part of the tetraloop AGCA-A is not stable either, in agreement with the zero population for the +1 slip in the (CAG)₇–CAA–(CAG)₇ smFRET result (Figure 3). Finally, the AACA tetraloop shows good stability, in agreement with the –1 slip in in the smFRET (CAG)₇–CAA–(CAG)₇ hairpin (70% population) and the +1 slip in the smFRET (CAG)₆–CAA–(CAG)₈ hairpin (85% population).

With respect to the AAA mutation, the AAA-triloop remains stable during the simulation, in agreement with the smFRET AAA triloop hairpin. On the other hand, simulations show that the AAA-mutated tetraloop shifted to the usual GAA triloop. For CAC and CGG mutations, the triloop is not stable, also in agreement with the experiments. For the CAC and CGG mutations in tetraloop form, the simulations are stable. This supports the assumption in FRET experiments that the triloops with CAC and CGG mutations shifted to the lower free-energy tetraloops detected by FRET.

Structurally, these results can be explained as follows. When the synonymous point mutation G→A changes the 5′-AGCA-3′ tetraloop into the 5′-AACA-3′ tetraloop, the stacking previously described for the AGCA tetraloop is preserved, and the same stability considerations apply. However, when this mutation takes place anywhere else in or close to the loop in the hairpin, it either adds mismatches or destabilizes the stacking, therefore resulting in less stable hairpins.

The AAA triloop has a stronger purine-purine stacking (A/A) compared with the pyrimidine-purine (C/A) stacking in the CAG triloop, which enhances the AAA triloop stability. The AAA-mutated tetraloop morphs into a larger CAGAAA loop, which increases disorder and reduces the number of Watson-Crick base pairs. It becomes unstable and transitions to a stable GAA triloop. Similar explanations apply to the CAC and CGG triloop mutations. When the CAC and CGG mutations occur in tetraloops, the tetraloop stability is conserved due to the presence of purine-purine mismatches closing the loop: A–A in the ACCA tetraloop formed by the CAC mutation, and G–A in the GGCA tetraloop formed by the CGG mutation. In addition, they have a G–C Watson–Crick base pair immediately after, helping lock the tetraloop.

Extended (CAG)_n triloop

Both experiments and simulations indicate that CAG triloops are less stable than AGCA tetraloops. Thus, we carried out MD simulations on an initial (CAG)_n triloop (n = 9, 11, 15, at 0 and 100 mM NaCl) to gauge the steps in the transition towards a tetraloop. Depending on the case, base shifting produces GCA triloops and GCAG tetraloops (Supplementary Table S12). For instance, the (CAG)₁₅ hairpin under 100 mM NaCl excess salt undergoes large fluctuations after 1 μs, and at a certain point a base pairing shift results in a GCAG tetraloop. As shown in Supplementary Figure S20, the original A20–A26 mismatch immediately preceding the triloop breaks due to the flipping of the A26 base into the minor groove. This causes the C25 base to shift down along the 3′ direction to form an A20–C25 mismatch, leaving G21, C22, A23 and G24, in a temporary GCAG tetraloop conformation. We suggest that this is the first step in the mechanism of the shift transition from an unstable CAG triloop to a tetraloop. As experiments observed transitions between slipped states both involving tetraloops, it is suspected this transient, unstable triloop might be in intermediate state during the transition that is too short-lived to be resolved in experiments. A similar shifting behavior was observed in (CAG)₉ with zero salt, but a GCAG tetraloop with two-stack structure formed after transition from an intermittent unstable CAGC loop structure (see Supplementary Movie S2).

DISCUSSION

In this work, we have used smFRET measurements and MD simulations to characterize the structure and dynamics of DNA hairpins formed from CAG TRs. Including different lengths and/or mutations due to interrupting trinucleotides, the smFRET experiments have included 23 different sequences, and the MD simulations have included 13 different sequences with 71 different initial conditions. The smFRET results for the (CAG)₁₄ and (CAG)₁₅ oligomers show that the (CAG)₁₄ oligomer displays transitions between 0.65, 0.31 and 0.01 FRET states, while transitions for (CAG)₁₅ correspond to 0.73, 0.46, 0.25 and 0.01 FRET states (Figure 2). The 0.01 state corresponds to the open hairpin, a state that is rarely observed. These FRET values for even and odd hairpins interleave and represent sequential amounts of slipping of one strand of the hairpin stem with respect to the other by integer units of the CAG TR. Using the hairpin with paired ends as reference (zero slip), the FRET states and the associated slips are: 0.73 (–1 slip, 3′ → 5′, such that one TR overhangs at the 5′ end ), 0.65 (0 slip), 0.46 (+1 slip, 5′ → 3′, one TR overhanging at the 3′ end), 0.31 (+2 slip) and 0.25 (+3 slip) (Figure 2D). Using smFRET to observe real-time trinucleotide stem slipping dynamics confirms previous results using chemical probes of guanine accessibility, polymerase based extension, or single strand nuclease activity that support such configurations (28–30,38). However, there are subtle differences, such as the use of only even-numbered sequences (CAG)_n in those studies. For instance, the sequences employed in gel electrophoresis experiments in (29) are of the form (CAG)₁₆(CTG)₄ (where triloops are enforced through Watson-Crick pairing with the self-priming CTG repeats). In addition, smFRET directly reveals spontaneous, dynamic slipping between configurations with variable degrees of slip and underlines the completely different dynamic patterns between even- and odd-numbered sequences.

Folding CAG TRs into hairpins without any overhang in the stem requires triloops for odd repeat numbers and tetraloops for even numbers of repeats (Figure 2). Therefore, the offset in slipping number we observe between odd and even TR suggests slipping is driven to achieve the tetraloop configurations, as was previously suggested (29,30). The ability to stabilize triloops by changing only a few bases either in the loop or the stem indicates that a competition between loop and stem free energy is delicately balanced. Indeed, a recent smFRET study (79) of CAG repeat hairpins that intentionally removed the CAG pattern in the loop region and replaced it with polyA or polyT linkers (15 bases) did not observe slipped hairpin. These CAG stems with polynucleotide linkers were useful for studying stability of the stem region, but did not reveal spontaneous slipping of the stem, confirming the significance of the requirement of the CAG sequence in the loop for driving the phenomena.

MD simulations reveal details of the basic interactions that stabilize various configurations of CAG hairpins. CAG loops are marginally stable in a tight 5′-CAG-3′ triloop arrangement, as long as there is some clamping in the end of the stem, while tight 5′-AGCA-3′ tetraloops are stable even without clamping. Clamping can naturally occur in the cell when the ends of the loop interact with other molecules. Overall, all simulations indicate that tetraloops are more stable than triloops, in agreement with the experimental findings. In a 5′-CAG-3′ triloop, the three nucleotides are in anti conformation, the C base flips out and the weak sheared C·G pair is held by a single hydrogen bond (Figure 4A, B). The 5′-CAG-3′ triloop is then ‘locked’ by a weak AG/CA step (where the A bases are mismatched), whose melting temperature has been estimated as ∼13°C (29). In contrast, 5′-AGCA-3′ tetraloops (Figure 4C, D) are stabilized relative to triloops by favorable stacking energy within the loop, less bending deformation of the backbone; and locking by a GC/GC step, the strongest of all possible steps, whose melting energy has been estimated as ∼136°C (29). Considering the values of the glycosidic angle χ, the 5′-AGCA-3′ tetraloop shows two preferred conformations, where the four nucleotides are either in anti–anti–anti–syn, L(as)–G(a), or anti–anti–anti–anti L(aa)–G(a) conformations (Figure 5) The L(as)–G(a) conformation actually consists of two dynamically coexisting conformations with either single A/G or single G/C stacking (Supplementary Figure S19). The L(aa)–G(a) conformation also consists of two main dynamically coexisting conformations with (i) a single A/G or single G/C stacking similar to Supplementary Figure S19 that is not long-lived and dissolves into no stacking; or (ii) a long-lived double A/G and C/A stacking (Figure 4F, G).

In addition to the stability difference between the fundamental tri- and tetraloop configurations (including the locking basepair step at the base of the loop), one has to consider the free energy of the stem. Even-numbered sequences can accommodate a tetraloop while forming a paired-end stem without overhangs, which minimizes the free energy of the full hairpin. The stability of this state is reflected in the highly populated FRET 0.65 state of (CAG)₁₄. Odd-numbered sequences, on the other hand, can only accommodate an AGCA tetraloop if one strand is displaced with respect to the other by at least one TR (becoming di facto an even-numbered hairpin with a hanging base). However, the hanging base in the hairpin stem costs extra energy, although apparently not enough to deter the preference for tetraloops. Taking the paired-end state as reference, odd-numbered hairpins slip by odd (mainly 1 but also 3) CAG TR units. The resulting dynamics are therefore rather different: even-numbered hairpins reside most of the time in the paired-end state with occasional two CAG TR slips, while odd-numbered hairpins are essentially ‘frustrated’, never populating by a measurable amount of time the paired-end triloop, and slipping back and forth in one direction or the other. Of course, since the zero-slip reference for odd-numbered hairpins is not populated (at least in a measurable way), the odd-numbered hairpin is also slipping by two units as it goes from one state to the other. Molecular details of the mechanisms leading to these changes are further discussed in the supplemental discussion, where results for other hairpin lengths are also presented. We have carried out MD simulations to try to elucidate how the triloop favored by pairing the two strands of the stem would transition to a tetraloop. Although the simulations were not long enough to elucidate the mechanism of the transition, they indicate that the transition from a triloop in a (CAG)_odd sequence is triggered by the disruption of the A-A mismatch closest to the loop, where the A base on the 3′ strand switches towards the minor groove allowing the temporary formation of a GACG tetraloop.

Finally, we analyzed the effect of trinucleotide mutations in the hairpin stability. In principle, arbitrary trinucleotide mutations can alter hairpin structure and dynamics in a myriad of ways, and the effect of these on hairpin structure has been briefly discussed above and further presented in the supplemental discussion. Genetic studies find that interrupts increase the stability of alleles for several disease-related TRs (40–46). Of particular interest in the polyglutamine diseases is the synonymous point mutation G→A, which changes the CAG codon into the CAA codon, both coding for glutamine. Interruptions of a (CAG)_n repeat tract by mutation to CAA has a stabilizing effect in the polyglutamine diseases (47) such as Huntington’s disease (51,52), SCA17 (46) and SCA2 (13,48–50). For instance, the instability of expanded CAG repeats in SCA17 is up to 3-fold higher in patients with uninterrupted CAG repeats than in those with CAA interrupts (46). In this work we have shown that CAA interrupts in a CAG sequence can dramatically reduce strand slipping in the corresponding hairpins. In particular, when the mutation takes place in the second base in the tetraloop, i.e. the original 5′-AGCA-3′ tetraloop mutates into the 5′-AACA-3′ tetraloop, the stacking previously described for the AGCA tetraloop is preserved, and the same stability considerations apply. This results in the highly populated states of the -1 slip in the (CAG)₇-CAA-(CAG)₇ hairpin (70% population) and the +1 slip in the (CAG)₆–CAA–(CAG)₈ hairpin (85% population). However, when this mutation takes place anywhere else in or close to the loop in the hairpin, it either adds mismatches or destabilizes the stacking, therefore resulting in much less stable hairpins.

Interestingly, a recent smFRET study (80) of a pentanucleotide hairpin (TGGAA)_n found similar slipping by one repeat unit as we characterize for CAG TRs. The (TGGAA) study reported dramatically different behavior for even and odd numbers of repeats. That study concluded that the stem energies dominated the behaviors and formulated a local seeding model where the kinked GGA in the stem is key to the slipping transitions. Our results contrast with this result by highlighting the importance of the loop and the nuanced balance in energies between the loop and stem interactions for the CAG hairpins. Intriguingly, both sequences exhibit pathological expansion phenomena, which suggests that the mechanisms of the expansion might be similar after a hairpin slips, even if the molecular details driving the slip are different.

In summary, we have confirmed that the strands of a CAG TR hairpin slip with respect to each other by an integer number of CAG units, most commonly two, using smFRET, which is capable of directly resolving temporal kinetics of the slipping in comparison to previous, indirect approaches to assess slipped hairpins with single strand overhangs (28–30,38). We also present the first atomic structural and stability analysis of the possible CAG hairpin conformations. Our results are supported by previous thermodynamic studies of CAG hairpins showing that there are even/odd differences in unfolding energetic parameters (31,81). Our data suggest that slippage away from triloops is triggered by an instability in the A-A mismatch closest to the hairpin loop, giving rise to the formation of a temporary tetraloop.

Strand slippage may be crucial for the expansion of TRs. Although the in vivo context is long double-stranded DNA molecules, the results of our in vitro studies can inform aspects of a simple model that have been suggested previously (28). This model suggests that if strand separation were to occur in the region of the initial complementary (CAG)·(CTG) duplex, then CAG and CTG hairpins could form opposite each other in a cruciform-like stem structure. Strand slippage would thus allow these hairpins to travel apart in a soliton-like wave or ‘rollamers’ (28,82). This simple model proposes that single-stranded cleavage in one strand of a hairpin (nicking) would permit the hairpin be stretched open, leaving a single-stranded gap in the local duplex (28). The subsequent filling of this gap in the nicked strand would then result in TR expansion. Hairpin migration apart would enhance expansion because directly opposed, complementary hairpins (like the cruciform-like structure) might be more likely to collapse back to the (CAG)·(CTG) duplex, minimizing expansion. Notably, TR hairpins contain multiple mismatched bases, which are recognized by DNA mismatch repair proteins. Activation of the latent endonuclease activity of MutLα as part of the mismatch repair cascade upon detection of a mismatch in the hairpin could be the source of the nick required to permit the TR hairpins to open in this model. Such a mechanism would agree with the observation that suppressing DNA mismatch repair activity can reduce TR expansion (3,83). Within this model, suppression of strand-slipping when an interrupting trinucleotide selects for a specific hairpin configuration could suppress possible hairpin migration and reduce this pathway of TR expansion.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Institute of Health [NIH-R01GM118508]; National Science Foundation (NSF) [SI2-SEE-1534941]; Extreme Science and Engineering Discovery Environment (XSEDE) [TG-MCB160064]. Funding for open access charge: National Institute of Health [NIH-R01GM118508]; National Science Foundation (NSF) [SI2-SEE-1534941].

Conflict of interest statement. None declared.