Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Feb 3;124(8):1383–1391. doi: 10.1021/acs.jpcb.9b10396

Quantitative Determination of Dark Chromophore Population Explains the Apparent Low Quantum Yield of Red Fluorescent Proteins

Jord C Prangsma †, Robert Molenaar †, Laura van Weeren ‡, Daphne S Bindels ‡, Lindsay Haarbosch ‡, Jente Stouthamer ‡, Theodorus W J Gadella Jr ‡, Vinod Subramaniam †, Willem L Vos §, Christian Blum †,*
PMCID: PMC7049984  PMID: 32011884

Abstract

graphic file with name jp9b10396_0007.jpg

The fluorescence quantum yield of four representative red fluorescent proteins mCherry, mKate2, mRuby2, and the recently introduced mScarlet was investigated. The excited state lifetimes were measured as a function of the distance to a gold mirror in order to control the local density of optical states (LDOS). By analyzing the total emission rates as a function of the LDOS, we obtain separately the emission rate and the nonradiative rate of the bright states. We thus obtain for the first time the bright state quantum yield of the proteins without interference from dark, nonemitting states. The bright state quantum yields are considerably higher than previously reported quantum yields that average over both bright and dark states. We determine that mCherry, mKate2, and mRuby2 have a considerable fraction of dark chromophores up to 45%, which explains both the low measured quantum yields of red emitting proteins reported in the literature and the difficulties in developing high quantum yield variants of such proteins. For the recently developed bright mScarlet, we find a much smaller dark fraction of 14%, accompanied by a very high quantum yield of the bright state of 81%. The presence of a considerable fraction of dark chromophores has implications for numerous applications of fluorescent proteins, ranging from quantitative fluorescence microscopy to FRET studies to monitoring protein expression levels. We recommend that future optimization of red fluorescent proteins should pay more attention to minimizing the fraction of dark proteins.

Introduction

The discovery of genetically encodable visible fluorescent proteins (VFPs) has enabled revolutionary new insights into molecular and cellular biological processes.1−6 To date, the palette of available fluorescent proteins covers the whole visible spectrum, thereby allowing a myriad of applications. The unique properties of fluorescent proteins are also harnessed for technical applications. Lasing from a single cell and bioinspired light-emitting diodes containing different fluorescent proteins have been reported, as have solid state lasers that exploit the possibility to densely pack fluorescent proteins with little self-quenching.7−10

A key parameter in the optimization of VFPs is the fluorescence quantum yield that quantifies the efficiency of a fluorophore to convert an absorbed photon into an emitted fluorescence photon. Clearly, most applications require or benefit from VFPs with a high fluorescence quantum yield. Figure 1a shows that the reported quantum yields of VFPs as a function of their emission maximum wavelength reveals a strongly decreasing quantum yield with increasing wavelength. Indeed, in the blue-green part of the visible spectrum, cyan fluorescent proteins such as mTurquoise2 have a quantum yield of up to 93% at 474 nm, which rivals the quantum yield of highly efficient chemical fluorophores.11 In the red, the recently developed mScarlet reveals a quantum yield of Q = 70% near 594 nm.12 Moreover, efforts to develop efficient red emitting VFPs have only rarely succeeded. Current strategies to increase the quantum yield of VFPs are focused on minimizing nonradiative decay, yet with limited success.13,14

Figure 1.

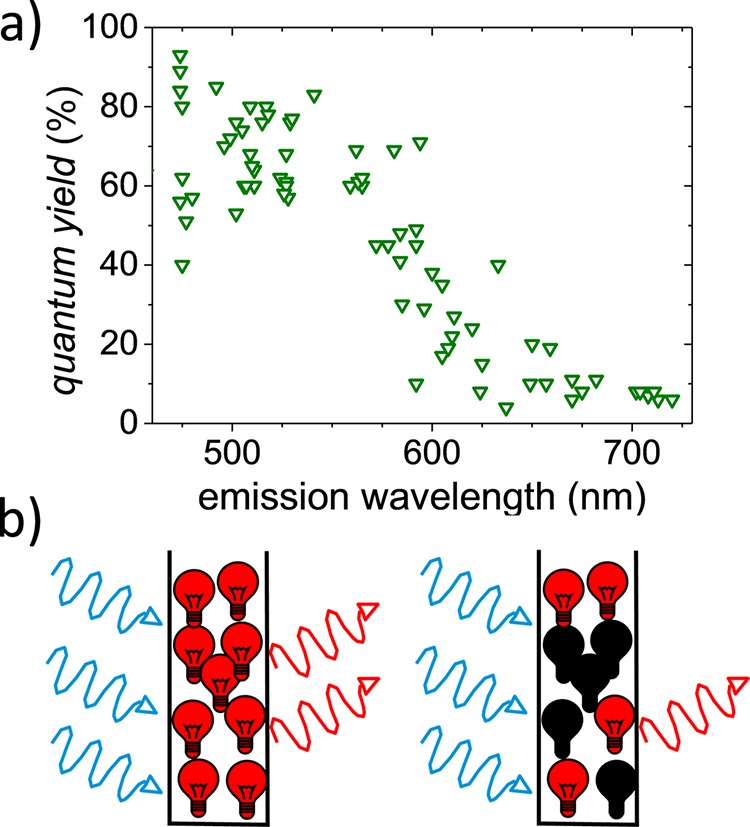
Figure 1

Open in a new tab

(a) Fluorescence quantum yield Qav of many types of visible fluorescent proteins (VFPs) versus their peak emission wavelengths obtained from the literature.21 The quantum yield was determined using ensemble-averaging methods that do not discriminate between dark and bright states. (b) (left) Cartoon of an ensemble of identical emitters that yield an accurate value for the fluorescence quantum yield when using a method that averages over the whole ensemble. (right) Cartoon of a heterogeneous ensemble of bright and dark emitters. The presence of dark emitters limits the apparent quantum yield determined by averaging methods.

The presence of dark—absorbing and nonemitting—fluorophores limits the observed quantum yield of VFPs in general and red emitting VFPs in particular. The underestimation of VFP fluorescence quantum yields in conventional measurement approaches has been previously noted15−20 and is schematically represented in Figure 1b. Figure 1b shows a cartoon of an ensemble of identical emitters that yield an accurate value for the fluorescence quantum yield even when using a method that averages over the whole ensemble. On the other hand, in a heterogeneous ensemble of bright and dark emitters, the ensemble-averaged quantum yield depends on the quantum yield of the bright emitters, as well as the ratio of bright versus dark fluorophores. The presence of a dark species limits the ensemble averaged quantum yield; the efficiency of the bright species remains obscured.

Currently, there are a number of methods available to determine the fluorescence quantum yield that were developed for ensembles of identical emitters; see refs (22 and 23) for reviews. These approaches average over all spectral species and are hence rigorously correct only for ensembles of identical emitters. Ensembles of chemically synthesized and purified fluorescent dyes fulfill this requirement well, while the assumption of identical emitters does not hold for VFPs.

The photophysics of VFPs has been extensively studied by both ensemble and single-molecule methods. These studies demonstrated rich photophysical behavior,24−26 including the presence of dark states that absorb but do not show fluorescence due to effective nonradiative deactivation.15,27−29 It is evident that the presence of such dark states limits the average quantum yield (see Figure 1b). Indeed, for the green fluorescent protein EGFP, we previously observed that the ensemble-averaged quantum yield (Qav = 60%) is smaller than the quantum yield of only the bright proteins (Qbright = 72%).30 Therefore, we hypothesize that the limited average quantum yield observed, especially from red emitting fluorescent proteins, does not originate from an inherently low quantum yield of the emitting state but from the presence of a considerable fraction of dark proteins.

In this paper, we determine the bright state quantum yield and the fraction of dark proteins of four frequently used red emitting fluorescent protein variants, by employing nanophotonic control.30−34 We find that the bright state quantum yield Qbright of all four red emitting VFPs is considerably higher than the quantum yield Qav determined with methods that average over bright and dark states. For the three earlier introduced proteins mCherry, mKate2, and mRuby2, we find a fraction of dark proteins up to about 45%, and for the recently introduced mScarlet, a significantly lower dark fraction of 14 ± 3%.

Experimental Section

Red Fluorescent Protein Purification

mRuby235 (40260, Addgene), mKate2,36 and mCherry37 were kind gifts from Michael Lam, Dmitriy Chudakov, and Roger Tsien, respectively. The development of mScarlet is described elsewhere.12 DNA encoding the RFPs was transferred into a rhamnose-inducible bacterial expression vector. To this end, the pDRESS vectors containing these RFPs (fused to mTurquoise2 and an antiFRET linker,12 for mScarlet see 130509, Addgene) were cut with NheI to excise the mTurquoise2 antiFRETlinker P2A sequence and ligated again. All RFPs contained an N-terminal 6xHis tag. Chemically competent or electrocompetent E. cloni 5-alpha (Lucigen corporation) were used and transformed according to the manufacturer’s heatshock or electroporation protocol. After transformation, they were transferred to 50 mL of growth medium (super optimal broth (SOB), 0.5% (w/v) yeast extract, 2% (w/v) tryptone, 10 mM NaCl, 20 mM MgSO4, 2.5 mM KCl, 100 mg/mL kanamycin, and 0.4% (w/v) rhamnose to induce transcription). The cultures were grown overnight (200 rpm, 37 °C), and an additional 6 h of incubation at 21 °C was conducted to improve maturation. The cultures were washed once in 20 mL of ST buffer (20 mM Tris–HCl, 200 mM NaCl, pH 8.0), and pellets were resuspended in 5 mL of ST buffer and stored at −20 °C. The pellets were defrosted on ice and incubated in ST buffer supplemented with lysozyme (1 mg/mL, L7651, Sigma-Aldrich) and benzoase nuclease (5 unit/ml, Merck/Millipore, 71205-3) for at least 30 min. A volume of 100 μL of 100 mM PMSF and 100 μL of 10% NP40 was added to the bacterial suspension. The lysate was centrifuged (30 min, 40,000g, 4 °C). The supernatant was added to 1 mL of Ni2+ loaded His-Bind resin (Novagen, 69670-2) and incubated for at least 1 h at 4 °C. The resin was washed three times with ST buffer and eluted with 0.5 mL of 0.6 M imidazole in ST buffer (final concentration 0.2–0.3 M imidazole). The eluent was filtered (0.22 μm), and the protein solution was dialyzed overnight in 10 mM Tris–HCl pH 8.0 using 3.5 kDa membrane tubing (132720, Spectrum Laboratories). Proteins were short-term stored at 4 °C or flash frozen and stored at −80 °C for long-term storage.

Sample Preparation

Fluorophores were diluted to nM concentrations in a 1% by weight aqueous poly(vinyl alcohol) (PVA, Sigma-Aldrich, MW = 13000–23000) solution. This solution was spin-coated onto a microscopy cover slide, resulting in an ∼15 nm thick film of PVA embedded fluorophores. The uniformity of each sample was verified using confocal microscopy prior to each measurement.

Fluorescence Lifetime Microscopy

Fluorescence decay curves were determined using a custom-built, time-correlated single-photon-counting (TCSPC)-based, confocal microscope. For details, see refs (38) and (39). In short, a supercontinuum white light source (Fianium, SC-400-PP) operating at a repetition rate of 20 MHz serves as the excitation source. The excitation wavelength of 550 nm was selected using an AOTF (Crystal Technologies, PC NI-VIS). The excitation light was coupled through a single-mode fiber and collimated, linear polarized, and spectrally limited further by a 561 nm low pass filter (Semrock, SP01-561RU-25) before entering the backport of an inverted microscope (Olympus, IX71). Instead of a dichroic mirror, a glass wedge was used to direct the collimated light toward the objective (Olympus, UPLSAPO 100× NA1.4). The same objective also collected the fluorescence. Fluorescence was spatially filtered by a pinhole and spectrally filtered to remove remaining excitation light with a 561 nm long pass filter (Semrock, LP02-561RU-25). An additional short pass filter (Semrock, FF01-770/SP-25) was used to suppress stray light from the AFM. Photon counts were detected using a single-photon avalanche detector (MPD, PD1CTC); photon arrival times were determined and registered using a TCSPC Counter Card (Becker&Hickl, SPC-830) providing the lifetime histogram.

Control of the Local Density of States (LDOS)

To control the LDOS, we used a gold-coated sphere (Duke Standards, 100 μm, coated with 3 nm of Cr and 100 nm of Au) that approached the fluorophores embedded in the PVA film. The gold-coated sphere was glued to the base of an AFM cantilever. To control the distance between the gold-coated sphere and the fluorophores, and hence the LDOS the fluorophores experience, we used an approach we recently developed; see ref (40) and the schematic in Figure 2a. In short: We used the deflection from the in contact microcantilever to control the distance between the metallic mirror consisting of a 100 μm gold-coated sphere (see Figure 2b) and the sample surface. Before measuring, we calibrated the instrument using the z displacement of the sample scanning stage (PI P-527.3CD) to relate deflection to absolute surface–mirror distance. The short- and long-term positioning accuracy lies within 3 nm. To measure the change in fluorescence lifetime induced by the LDOS change, the gold-coated sphere was positioned exactly above the laser focus of the confocal microscope. Considering that the radius of the diffraction limited excitation is much smaller than the 100 μm sphere, the LDOS modifying gold surface can be approximated as flat.

Figure 2.

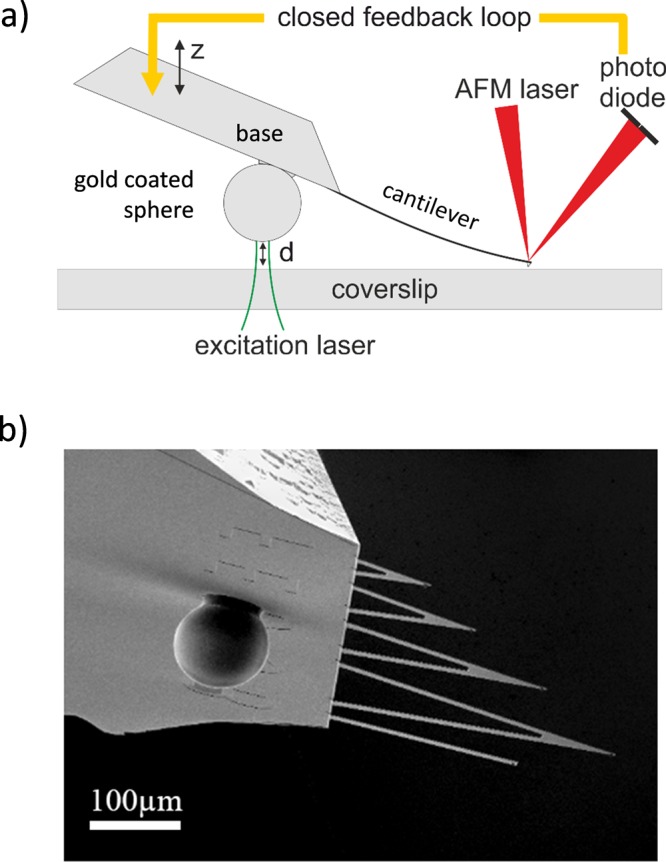
Figure 2

Open in a new tab

(a) Schematic of the method to control the mirror–sample distance. A microcantilever with a gold-coated sphere serving as LDOS manipulating probe attached to the rigid base of the cantilever is brought into contact with a coverslip serving as sample substrate. The mirror-to-surface distance d is precisely controlled via the angular deflection when the microcantilever tip is in contact. (b) SEM image of the microcantilevers and the LDOS manipulating probe consisting of a 100 μm gold-coated sphere attached to the microcantilever base.

Changing the axial position of the mirror results in different LDOS experienced by the fluorophores. The effect of changing the LDOS was sampled by determining the fluorescence lifetime. A typical fluorescence lifetime measurement was set to collect over 50 kcounts to ensure an accurate lifetime fit. LDOS-lifetime measurements consisted of a series of lifetime measurements recorded every 8 nm, starting typically at 600 nm above the VFP layer and then approaching the VFP layer. Each data set consisted of a sequence of lifetime decay histograms recorded over a time of approximately 100 s, controlled by a custom written LabView software.

Data Analysis

The modeling of the fluorescence decay was done using a description of the LDOS based on a multilayer model41 and is done analogous to ref (34). The multilayer consisted of a very thick glass substrate (n = 1.52), a 15 nm thick PVA layer (n = 1.46), an air layer (n = 1) of variable width depending on the mirror sample distance, and a pure Au layer of 100 nm (n = 0.44 + 2.43i42). To account for the fluorophore orientation dependent excitation and collection as well as the fluorophore to mirror orientation dependence of the LDOS, the orientation of the fluorophores in the PVA film was taken into account analogous to ref 34. The fit thus had as free parameters the radiative decay in a homogeneous PVA layer, the nonradiative decay, and a parameter describing the ratio of the detection efficiency of parallel to perpendicular oriented fluorophores.

Results

Verification of the Method

To determine the bright state quantum yield of the fluorescent proteins, we use the well-known fact that the radiative decay rate krad of a fluorophore is proportional to the local density of optical states (LDOS), while the nonradiative decay rate knonrad is independent of the LDOS. We tune the LDOS while observing the resulting fluorescence lifetime τ.30−34,43 Since the lifetime is the inverse of the sum ktot of the radiative and nonradiative decay rates, we can write

graphic file with name jp9b10396_m001.jpg 1

The radiative krad and nonradiative decay rates knonrad can be derived by interpreting the varying lifetime in terms of the varying LDOS changing krad while knonrad remains unaffected. From the radiative and nonradiative decay rates, the fluorescence quantum yield is obtained:

graphic file with name jp9b10396_m002.jpg 2

For mixtures of a bright and a dark state, this method gives access to the quantum yield of solely the emitting state Qbright, since nonemitting fluorophores hardly emit photons and thus do not contribute to the observed lifetime.

To control the LDOS, we position the fluorophores in a thin polymer film at precisely defined distances d from a metallic mirror. As first shown by Drexhage in a pioneering experiment,44 the lifetime characteristically oscillates with distance to the metallic mirror due to changes in the LDOS. We use a classical model developed by Chance et al.45 to calculate the lifetime versus distance to the mirror, while taking into account the material properties of the mirror and dielectric environment. Modeling the lifetime versus distance using the single-mirror model41 yields the radiative and nonradiative decay rates of the emitters in the embedding, isotropic medium in the absence of the mirror that effectively corresponds to the infinite distance limit (d → ∞).

To control the distance d between the emitters and the metallic mirror, we used a recently developed method40 whereby a large (diameter = 100 μm) gold-coated polystyrene sphere serves as a movable mirror. To this end, the sphere is rigidly attached to the stiff base of an AFM microcantilever chip. The deflection from an in-contact AFM cantilever is used as a feedback signal to control the distance d between the mirror and the sample. We obtain a displacement range from in-contact (d = 0 μm) up to d = 2 μm and an axial positioning accuracy of better than Δd = 3 nm.40

We validate our experimental approach using the well-characterized synthetic fluorophore rhodamine 101, a dye without dark fraction that is often used as a standard reference dye in fluorescence quantum yield measurements.46 Moreover, Figure 3 shows that it emits in a similar wavelength range as the fluorescent proteins studied here. The fluorescence quantum yield of rhodamine 101 has been reported to be Q = 95% and to be insensitive to solvent and temperature.47 To immobilize the fluorophores, we used a standard method for photophysical studies by embedding them in a thin film of poly(vinyl alcohol) (PVA) that is spin-coated onto a microscopy coverslip.15,48 We then approach the gold-coated sphere toward the fluorophore containing film in steps of ∂d = 8 nm. At each sample to mirror distance d, a fluorescence decay curve is recorded, as is shown in Figure 4a for two different distances, d = 152 and 304 nm. Figure 4a shows that the decay curves change markedly for these different distances. Moreover, Figure 4a shows that both decay curves agree well with a single-exponential decay. Therefore, the fluorescence lifetime τ is obtained with high precision by matching a single-exponential model to each decay curve.

Figure 3.

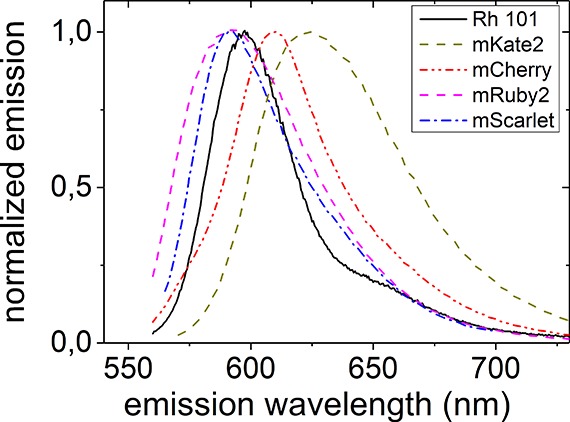
Figure 3

Open in a new tab

Emission spectra of the fluorophores studied here. Rhodamine 101 (Rh 101) is a well-characterized synthetic fluorescent dye used to validate our approach. mCherry, mKate2, and mRuby2 are three commonly used red emitting fluorescent proteins, and mScarlet is a newly developed protein.

Figure 4.

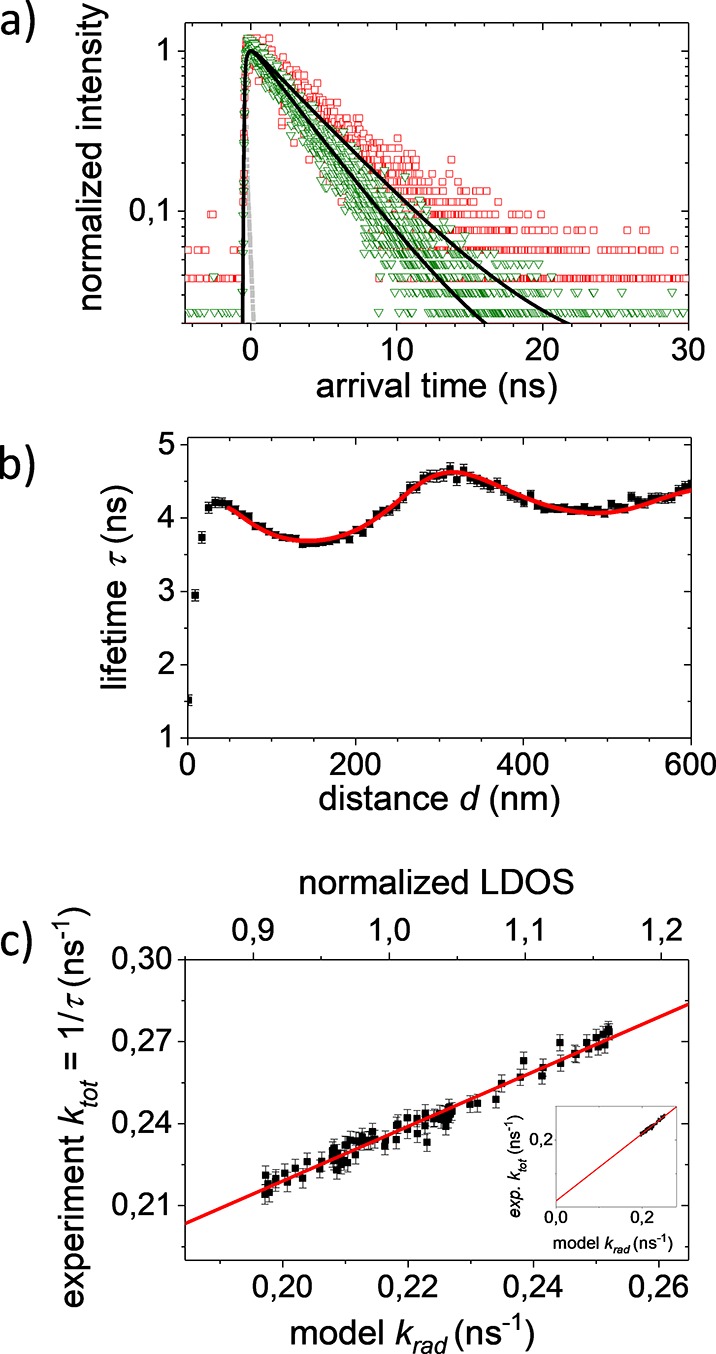
Figure 4

Open in a new tab

(a) Fluorescence decay curves of R101 recorded for two distances d = 304 nm (red) and d = 152 nm (green) between the LDOS modifying gold mirror probe and the fluorophore film. The instrument response function (IRF) is shown in gray. The decays are fitted with a single exponential (black lines), yielding τ = 4.6 ns and τ = 3.7 ns, respectively. (b) Lifetime determined from decay curves versus fluorophore-to-mirror distance. The fluorescence lifetime clearly shows the expected Drexhage oscillation due to the modified LDOS. Our data (black squares) agree very well with the fit using the single-mirror model (red line). (c) Observed kexp versus modeled krad which is proportional to the normalized LDOS (normalized to d → ∞). The line represents a linear fit with slope krad and intercept with the ordinate equal to knonrad (see inset). We derive a radiative decay rate kradPVA = 0.260 ± 0.005 ns–1 in the homogeneous medium PVA (n = 1.46) and a nonradiative decay rate knonrad = 0.019 ± 0.004 ns–1.

Plotting the determined lifetimes τ versus the mirror distance d, as shown in Figure 4b, reveals the well-known Drexhage-like oscillation of lifetime. Interpreting the varying lifetime in terms of the varying LDOS gives access to the radiative decay rate krad and the nonradiative decay rate knonrad as adjustable parameters. We find very good agreement between the Chance model and the observed lifetimes down to sample to mirror distances between d = 50 and 100 nm, depending on the sample. At small sample to mirror distances, the predicted and observed lifetimes start to deviate, for currently unknown reasons and in agreement with observations elsewhere.33,49

A robust and precise way to determine the radiative and nonradiative rates is to parametrically plot the experimentally observed total decay rates ktot (that is, the inverse of the lifetime τ) as a function of the calculated LDOS at each emitter–mirror distance d, as is shown in Figure 4c. As is described above, the total decay rate increases linearly with the radiative rate and thus linearly with the LDOS. By suitably normalizing the LDOS to the LDOS for an emitter in the polymer film in the absence of the mirror (corresponding to the limit d → ∞ in Figure 4b), we indeed observe the expected linear relation with slope equal to the radiative rate krad and an intercept with the ordinate equal to the nonradiative rate knonrad (see Figure 4c). From krad which is the radiative decay rate of the fluorophores in the polymer film, we obtain the bright state radiative decay rate kradPVA in isotropic embedding medium of PVA, which has a refractive index of 1.46.

To compare our results to the literature that is usually determined in aqueous solution, we used the Strickler–Berg relation50 to compensate for the different refractive indices. While there are different models for the change in radiative decay rate with refractive index (for a review, see ref (51)), we note that differences between the models are small for our study. Moreover, the validity of the Strickler–Berg relation for fluorescent proteins has been experimentally demonstrated in a systematic study by Suhling.52 Upon using the Strickler–Berg relation, we obtain kradwater = 0.216 ± 0.004 ns–1 for rhodamine 101 in water. The nonradiative decay rate knonrad is independent of the refractive index of the embedding medium. Using the determined decay rates knonrad = 0.019 ± 0.004 ns–1 and krad = 0.216 ± 0.004 ns–1, we derive the fluorescence lifetime of rhodamine 101 in water to be τ = 4.25 ± 0.10 ns and the bright state quantum yield to be Qbright = 92 ± 4%. Both values are in very good agreement with previous results, τ = 4.32 ns53 and Q = 95%,47 which verifies the precision of our approach and confirms the expected absence of dark fluorophores for the well-known laser dye rhodamine 101.

Red Fluorescent Proteins

We now turn to the red fluorescing VFPs mKate2, mRuby2, mCherry, and mScarlet, where mKate2, mRuby2, and mCherry are commonly used and well established, and the recently developed mScarlet was chosen because of its record quantum yield for red emitting proteins of 71%. We observe single-exponential decays for all four studied red emitting fluorescent proteins (for examples of observed decays, see Supporting Information Figure S1), which indicates the presence of only a single emitting species.

For all four fluorescent proteins, we find the expected oscillation of the fluorescence lifetime with the approaching mirror (see Supporting Information Figure S2). Clear differences in the modulation depth between the samples are visible, giving a first indication for differences in the bright state quantum yields. mRuby2 and mKate2 show a pronounced modulation depth from 2.0 to 2.5 ns and from 2.5 to 3.0 ns, respectively, and mScarlet shows a modulation from 3.2 to 4 ns, whereas mCherry shows a comparatively moderate lifetime modulation from 1.6 to 1.8 ns.

Modeling the observed lifetimes versus the calculated LDOS yields the radiative decay in bulk PVA and the nonradiative decay rates for the four different fluorescent proteins; see Figure 5. Taking the difference in refractive index into account by using the Strickler–Berg relation, we obtain the fluorescence lifetimes in aqueous solution to be 2.39 ± 0.09 ns (literature: 2.5 ns12) for mRuby2, 2.64 ± 0.15 ns (literature: 2.5 ns12) for mKate2, 1.77 ± 0.11 ns (literature: 1.4 ns54) for mCherry, and 3.73 ± 0.07 ns (literature: 3.9 ns12) for mScarlet. The lifetimes obtained here agree well with literature values in aqueous environment, further confirming the validity of our approach.

Figure 5.

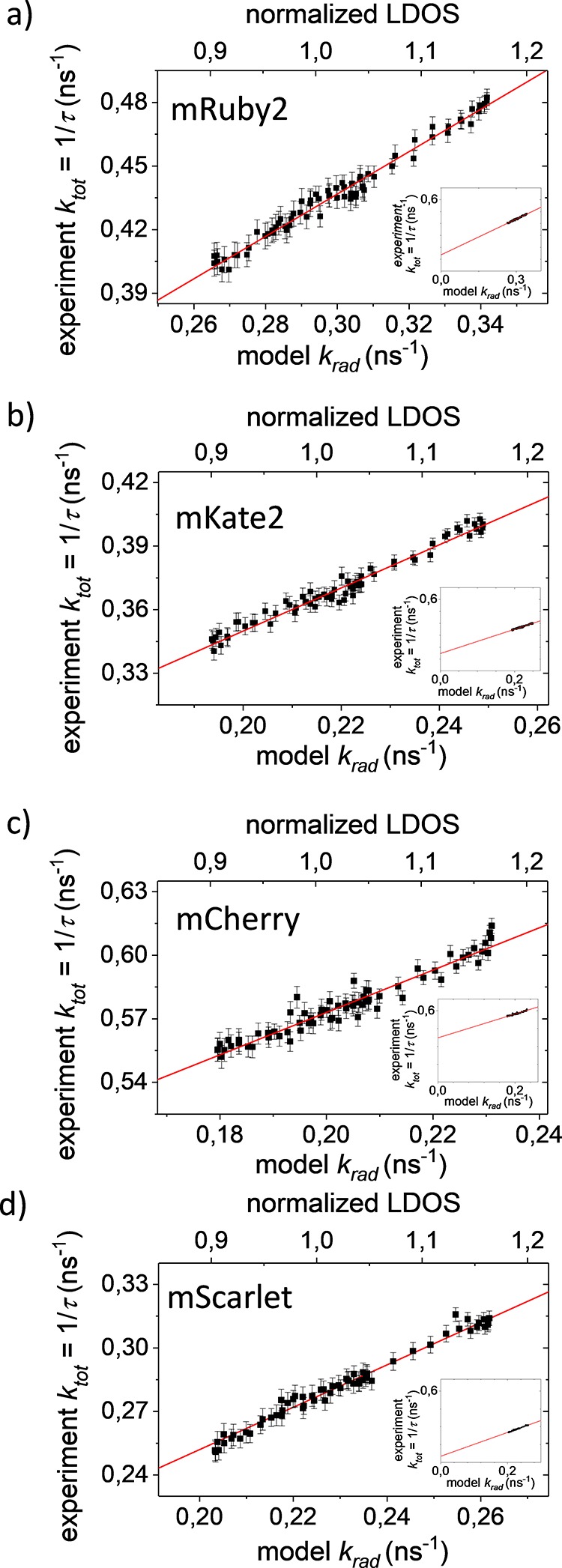
Figure 5

Open in a new tab

Experimentally observed kexp versus modeled krad that is proportional to the LDOS (normalized to d → ∞) for the red fluorescent proteins mKate2, mRuby2, mCherry, and mScarlet. The recorded data (black squares) agree very well with the model (red lines). Modeling the data gives the radiative decay rates in homogeneous medium PVA kradPVA and nonradiative decay rates knonrad (see insets): (a) mRuby2: krad = 0.340 ± 0.005 ns–1 and knonrad = 0.137 ± 0.016 ns–1; (b) mKate2: kradPVA = 0.275 ± 0.001 ns–1 and knonrad = 0.151 ± 0.22 ns–1; (c) mCherry: krad = 0.230 ± 0.007 ns–1 and knonrad = 0.373 ± 0.033 ns–1; (d) mScarlet: kradPVA = 0.260 ± 0.004 ns–1 and knonrad = 0.052 ± 0.004 ns–1.

Now we are in the position to derive the bright state quantum yields of the fluorescent proteins in aqueous solution from the decay rates above; see Figure 6a. We find Qbright = 60 ± 4% for mKate2, Qbright = 67 ± 3% for mRuby2, Qbright = 34 ± 3% for mCherry, and Qbright = 81 ± 3% for mScarlet. All experiments have been repeated at least twice, and all results are within the quoted error. For comparison, the reported averaged quantum yields determined by conventional ensemble-averaging methods are Qav = 40% for mKate2,36Qav = 38% for mRuby2,35Qav = 22% for mCherry,55 and Qav = 70% for mScarlet.12 The first important result from our study is that the quantum yield of the bright state of the studied fluorescent proteins is strikingly higher than the earlier reported ensemble-averaged quantum yields that average over bright and dark states. This result shows that there is a considerable fraction of proteins in dark states, in other words, absorbing but not emitting states in each red fluorescent protein sample.

Figure 6.

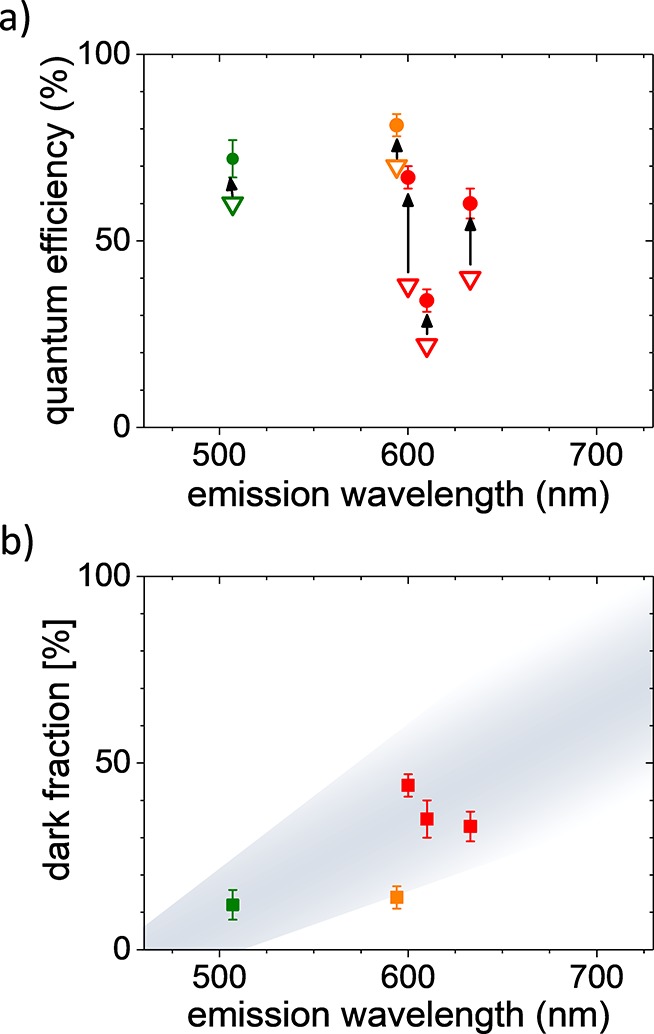
Figure 6

Open in a new tab

(a) Averaged quantum yields (open triangles) are considerably lower than the bright state quantum yields (filled circles) for the studied red emitting fluorescent proteins (red: earlier developed mRuby2, mKate2, and mCherry; orange: mScarlet) as well as for the protein EGFP (green, studied earlier30). (b) A considerable fraction of the studied red emitting proteins are dark (red: earlier developed mRuby2, mKate2, and mCherry; orange: mScarlet). These proteins absorb excitation light but do not show fluorescence. Using data from ref (30), we find the dark fraction of EGFP (green) to be significantly smaller. Gray shading in the background represents our hypothesis of increasing dark fraction with emission wavelength and serves as a guide to the eye.

Discussion

If we assume the averaged quantum yield Qav to be composed of a mixture of two states, namely, one bright and one dark state, then the average Qav is given by the weighted sum of the quantum yields of the two states

graphic file with name jp9b10396_m003.jpg 3

with fdark being the fraction of the dark proteins and where we make the reasonable assumption that both states have the same absorbance (dark states due to nonradiative decay; for a discussion, see below). [For a general discussion of the quantum yield in inhomogeneous emitters, see van Driel et al.,100]. Any emitting species gives one decay component in the observed decay curves. Since we observe single-exponential decay for all of our measurements, we conclude that there is only one emitting species and that the quantum yield of the dark state is essentially zero. Using Qdark = 0 allows us to rewrite eq 3 to find the fraction fdark of the dark states:

graphic file with name jp9b10396_m004.jpg 4

Using the reported average quantum yield Qav from the literature and the bright state quantum yield Qbright determined above, we find a dark fraction of fdark = 33 ± 4% for mKate2, fdark = 44 ± 3% for mRuby2, and fdark = 35 ± 6% for mCherry, as shown in Figure 6b. Interestingly, despite the large differences in bright state quantum yield, the older, established red emitting fluorescent proteins all have a considerable dark state fraction of >33%. In contrast, for mScarlet, we find a dark fraction of fdark = 14 ± 3% only. mScarlet was recently developed from a synthetic starting template that was further improved by systematic spectroscopic screening.12 Our results show that mScarlet’s record quantum yield for red emitting fluorescent proteins is not just the result of increasing the quantum yield. The observed high average quantum yield of mScarlet is in fact due to two factors: (1) a very high bright state quantum yield and (2) a clear reduction of the fraction of dark states. This finding clearly opens new directions in fluorescent protein optimization.

Considering that the quantum yield of fluorescent proteins that emit at lower wavelengths is generally higher than that for red emitting VFPs, one would expect lower dark state fractions for these proteins. To the best of our knowledge, only the bright state quantum yield of the green emitting fluorescent protein EGFP has been determined so far. The EGFP bright state quantum yield has been determined to be Qbright = 72 ± 5%.30 Using the conventionally determined quantum yield of EGFP Qav = 60%,56 we calculate a dark fraction for EGFP of fdark = 12 ± 4%. The considerably lower dark fraction for the green emitting EGFP compared to the red emitting fluorescent proteins mKate2, mRuby2, and mCherry studied here further supports the hypothesis that the observed decrease in quantum yield originates not only from a decrease in quantum yield of the chromophores per se, as observed for synthetic chemical fluorescent dyes,57 but from an increase of the fraction of dark proteins with increasing emission wavelength. Only recently with the development of mScarlet does it seem that this limit has been overcome.

It has been known since the early days of the photophysics of fluorescent proteins that the rigid embedding of the fluorophore in the protein is key to the emergence of fluorescence. The isolated fluorophore in solution shows no fluorescence because of efficient radiationless deactivation channels caused by rapid cis–trans isomerization of the chromophore.29 The embedding of the fluorophore within the protein hampers this cis–trans movement and hence the radiationless deactivation of the fluorophore, which results in the known efficient fluorescence. It has been shown by many studies that the nanoenvironment of the fluorophore that is formed by the surrounding protein not only defines the exact spectral properties but is also related to transitions between dark and bright states.15,58−60 Conformational changes in the protein that allow for a decrease in the rigidity of the embedding of the fluorophore are linked to the appearance of a dark state. Rigid embedding, however, is associated with the bright state. The rigidity of the embedding of the chromophore might be responsible for the observed increase of the dark fraction with increasing emission wavelength. The red emitting chromophore is larger and has a more extended chromophoric π-system than the blue/green emitting chromophore, which may result in more possibilities of radiationless deactivation by vibrations and conformational rearrangements. To rigidly embed this larger chromophore into the surrounding protein, a larger, exactly defined protein pocket is necessary. With increasing size, the probability that the surrounding protein supplies exactly this local context decreases. Imperfect folding and the exact side chain arrangement have an increasing effect on the embedding of a larger chromophore. The crystal structure of mScarlet supports the hypothesis that rigid embedding of the chromophore plays a crucial role. In mScarlet, the chromophore is extraordinarily rigidly embedded into the protein12—which is likely key to the low fraction of dark proteins.

A significant fraction of dark chromophores not only results in dimmer than expected emission, but the presence of dark chromophores also has severe consequences for fluorescent protein based quantitative fluorescence microscopy and spectroscopy. Recently, a number of methods have been developed to determine absolute protein numbers based on quantitative fluorescence microscopy and single-molecule photobleaching.61,62 Other studies used the emission of single fluorescent proteins to monitor gene expression on the single cell level.3,63 Dark chromophores evade detection in all of these studies, resulting in an underestimation of the determined number of fluorescent protein copies. Other studies affected by dark fluorescent protein chromophores are fluorescence resonance energy transfer (FRET) studies.64 FRET between fluorescent proteins is a much-used method to probe conformational changes and molecular interactions. In such studies, FRET is read out as the ratio of emission intensity of the two fluorescent proteins forming the FRET pair. Clearly, the presence of dark chromophores, either as FRET donor or as FRET acceptor, results in a bias of the data.

Conclusions

Our results demonstrate the significance of dark states in fluorescent proteins for the measured fluorescence quantum yield. We find that the generally low quantum yields reported for red fluorescent proteins can be attributed to a large fraction of proteins in a dark state. This relation can be rationalized in the context of the flexibility of the fluorophore embedding and dark state formation. Our data shows that the current barrier in quantum yield encountered for red emitting fluorescent proteins does not necessarily only result from an inherently low quantum yield of the red emitting chromophore but that the large fraction of proteins containing a dark chromophore plays a crucial role. We suggest to pay increased attention to the exact folding and formation of the chromophore embedding in the development of new fluorescent proteins to decrease the fraction of dark fluorophores and thereby increase the overall, averaged quantum yield.

Acknowledgments

The authors acknowledge support from the Dutch Technology Foundation STW, Project No. 12149, which is part of a STW Perspective program on Optical Nanoscopy.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcb.9b10396.

  • Typical decays and the oscillation of lifetimes with approaching mirror (PDF)

Author Present Address

∥ V.S.: Vrije Universiteit Amsterdam, The Netherlands.

Author Contributions

The manuscript was written by C.B. J.C.P., R.M., L.v.W., T.W.J.G., V.S., and W.L.V. contributed sections and edited the manuscript. L.v.W., D.S.B., L.H., and J.S. performed cloning and purification of the RFPs. J.C.P., R.M., W.L.V., and C.B. performed the LDOS experiments. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.

Supplementary Material

jp9b10396_si_001.pdf (694.6KB, pdf)

References

  1. Chalfie M.; Tu Y.; Euskirchen G.; Ward W. W.; Prasher D. C. Green Fluorescent Protein as a Marker for Gene-Expression. Science 1994, 263, 802–805. 10.1126/science.8303295. [DOI] [PubMed] [Google Scholar]
  2. Lippincott-Schwartz J.; Patterson G. H. Development and Use of Fluorescent Protein Markers in Living Cells. Science 2003, 300, 87–91. 10.1126/science.1082520. [DOI] [PubMed] [Google Scholar]
  3. Yu J.; Xiao J.; Ren X. J.; Lao K. Q.; Xie X. S. Probing Gene Expression in Live Cells, One Protein Molecule at a Time. Science 2006, 311, 1600–1603. 10.1126/science.1119623. [DOI] [PubMed] [Google Scholar]
  4. Dean K. M.; Palmer A. E. Advances in Fluorescence Labeling Strategies for Dynamic Cellular Imaging. Nat. Chem. Biol. 2014, 10, 512–523. 10.1038/nchembio.1556. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Betzig E.; Patterson G. H.; Sougrat R.; Lindwasser O. W.; Olenych S.; Bonifacino J. S.; Davidson M. W.; Lippincott-Schwartz J.; Hess H. F. Imaging Intracellular Fluorescent Proteins at Nanometer Resolution. Science 2006, 313, 1642–1645. 10.1126/science.1127344. [DOI] [PubMed] [Google Scholar]
  6. Zhang X.; Zhang M. S.; Li D.; He W. T.; Peng J. X.; Betzig E.; Xu P. Y. Highly Photostable, Reversibly Photoswitchable Fluorescent Protein with High Contrast Ratio for Live-Cell Superresolution Microscopy. Proc. Natl. Acad. Sci. U. S. A. 2016, 113, 10364–10369. 10.1073/pnas.1611038113. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Gather M. C.; Yun S. H. Single-Cell Biological Lasers. Nat. Photonics 2011, 5, 406–410. 10.1038/nphoton.2011.99. [DOI] [Google Scholar]
  8. Weber M. D.; Niklaus L.; Proschel M.; Coto P. B.; Sonnewald U.; Costa R. D. Bioinspired Hybrid White Light-Emitting Diodes. Adv. Mater. 2015, 27, 5493–5498. 10.1002/adma.201502349. [DOI] [PubMed] [Google Scholar]
  9. Gather M. C.; Yun S. H. Bio-Optimized Energy Transfer in Densely Packed Fluorescent Protein Enables near-Maximal Luminescence and Solid-State Lasers. Nat. Commun. 2014, 5, 5722. 10.1038/ncomms6722. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Press D. A.; Melikov R.; Conkar D.; Firat-Karalar E. N.; Nizamoglu S. Fluorescent Protein Integrated White Leds for Displays. Nanotechnology 2016, 27, 45LT01. 10.1088/0957-4484/27/45/45LT01. [DOI] [PubMed] [Google Scholar]
  11. Goedhart J.; von Stetten D.; Noirclerc-Savoye M.; Lelimousin M.; Joosen L.; Hink M. A.; van Weeren L.; Gadella T. W. J.; Royant A. Structure-Guided Evolution of Cyan Fluorescent Proteins Towards a Quantum Yield of 93%. Nat. Commun. 2012, 3, 751. 10.1038/ncomms1738. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Bindels D. S.; Haarbosch L.; van Weeren L.; Postma M.; Wiese K. E.; Mastop M.; Aumonier S.; Gotthard G.; Royant A.; Hink M. A.; et al. mScarlet: A Bright Monomeric Red Fluorescent Protein for Cellular Imaging. Nat. Methods 2017, 14, 53–56. 10.1038/nmeth.4074. [DOI] [PubMed] [Google Scholar]
  13. Shcherbakova D. M.; Verkhusha V. V. Near-Infrared Fluorescent Proteins for Multicolor in Vivo Imaging. Nat. Methods 2013, 10, 751. 10.1038/nmeth.2521. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Morozova K. S.; Piatkevich K. D.; Gould T. J.; Zhang J. H.; Bewersdorf J.; Verkhusha V. V. Far-Red Fluorescent Protein Excitable with Red Lasers for Flow Cytometry and Superresolution Sted Nanoscopy. Biophys. J. 2010, 99, L13–L15. 10.1016/j.bpj.2010.04.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Hendrix J.; Flors C.; Dedecker P.; Hofkens J.; Engelborghs Y. Dark States in Monomeric Red Fluorescent Proteins Studied by Fluorescence Correlation and Single Molecule Spectroscopy. Biophys. J. 2008, 94, 4103–4113. 10.1529/biophysj.107.123596. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Hillesheim L. N.; Chen Y.; Muller J. D. Dual-Color Photon Counting Histogram Analysis of Mrfp1 and Egfp in Living Cells. Biophys. J. 2006, 91, 4273–4284. 10.1529/biophysj.106.085845. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Manna P.; Jimenez R. Time and Frequency-Domain Measurement of Ground-State Recovery Times in Red Fluorescent Proteins. J. Phys. Chem. B 2015, 119, 4944–4954. 10.1021/acs.jpcb.5b00950. [DOI] [PubMed] [Google Scholar]
  18. Siegel A. P.; Baird M. A.; Davidson M. W.; Day R. N. Strengths and Weaknesses of Recently Engineered Red Fluorescent Proteins Evaluated in Live Cells Using Fluorescence Correlation Spectroscopy. Int. J. Mol. Sci. 2013, 14, 20340–20358. 10.3390/ijms141020340. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Dunsing V.; Luckner M.; Zuhlke B.; Petazzi R. A.; Herrmann A.; Chiantia S. Optimal Fluorescent Protein Tags for Quantifying Protein Oligomerization in Living Cells. Sci. Rep. 2018, 8, 10634. 10.1038/s41598-018-28858-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Klementieva N. V.; Pavlikov A. I.; Moiseev A. A.; Bozhanova N. G.; Mishina N. M.; Lukyanov S. A.; Zagaynova E. V.; Lukyanov K. A.; Mishin A. S. Intrinsic Blinking of Red Fluorescent Proteins for Super-Resolution Microscopy. Chem. Commun. 2017, 53, 949–951. 10.1039/C6CC09200D. [DOI] [PubMed] [Google Scholar]
  21. Data were obtained from Http://Nic.Ucsf.Edu/FPvisualization/ under the Creative Commons License.
  22. Rurack K.Fluorescence Quantum Yields: Methods of Determination and Standards. In Standardization and Quality Assurance in Fluorescence Measurements I: Techniques; Resch-Genger U., Ed.; Springer: Berlin, Heidelberg, 2008; pp 101–145. [Google Scholar]
  23. Würth C.; Geißler D.; Behnke T.; Kaiser M.; Resch-Genger U. Critical Review of the Determination of Photoluminescence Quantum Yields of Luminescent Reporters. Anal. Bioanal. Chem. 2015, 407, 59–78. 10.1007/s00216-014-8130-z. [DOI] [PubMed] [Google Scholar]
  24. Remington S. J. Fluorescent Proteins: Maturation, Photochemistry and Photophysics. Curr. Opin. Struct. Biol. 2006, 16, 714–721. 10.1016/j.sbi.2006.10.001. [DOI] [PubMed] [Google Scholar]
  25. Lounis B.; Deich J.; Rosell F. I.; Boxer S. G.; Moerner W. E. Photophysics of Dsred, a Red Fluorescent Protein, from the Ensemble to the Single-Molecule Level. J. Phys. Chem. B 2001, 105, 5048–5054. 10.1021/jp010116x. [DOI] [Google Scholar]
  26. Blum C.; Meixner A. J.; Subramaniam V. Spectral Versatility Off Single Reef Coral Fluorescent Proteins Detected by Spectrally-Resolved Single Molecule Spectroscopy. ChemPhysChem 2008, 9, 310–315. 10.1002/cphc.200700784. [DOI] [PubMed] [Google Scholar]
  27. McAnaney T. B.; Zeng W.; Doe C. F. E.; Bhanji N.; Wakelin S.; Pearson D. S.; Abbyad P.; Shi X. H.; Boxer S. G.; Bagshaw C. R. Protonation, Photobleaching, and Photoactivation of Yellow Fluorescent Protein (Yfp 10c): A Unifying Mechanism. Biochemistry 2005, 44, 5510–5524. 10.1021/bi047581f. [DOI] [PubMed] [Google Scholar]
  28. Garcia-Parajo M. F.; Veerman J. A.; Bouwhuis R.; Vallee R.; van Hulst N. F. Optical Probing of Single Fluorescent Molecules and Proteins. ChemPhysChem 2001, 2, 347–360. . [DOI] [PubMed] [Google Scholar]
  29. Ward W. W.; Bokman S. H. Reversible Denaturation of Aequorea Green-Fluorescent Protein: Physical Separation and Characterization of the Renatured Protein. Biochemistry 1982, 21, 4535–4540. 10.1021/bi00262a003. [DOI] [PubMed] [Google Scholar]
  30. Cesa Y.; Blum C.; van den Broek J. M.; Mosk A. P.; Vos W. L.; Subramaniam V. Manipulation of the Local Density of Photonic States to Elucidate Fluorescent Protein Emission Rates. Phys. Chem. Chem. Phys. 2009, 11, 2525–2531. 10.1039/b817902f. [DOI] [PubMed] [Google Scholar]
  31. de Dood M. J. A.; Knoester J.; Tip A.; Polman A. Forster Transfer and the Local Optical Density of States in Erbium-Doped Silica. Phys. Rev. B: Condens. Matter Mater. Phys. 2005, 71, 115102. 10.1103/PhysRevB.71.115102. [DOI] [Google Scholar]
  32. Leistikow M. D.; Johansen J.; Kettelarij A. J.; Lodahl P.; Vos W. L. Size-Dependent Oscillator Strength and Quantum Efficiency of Cdse Quantum Dots Controlled Via the Local Density of States. Phys. Rev. B: Condens. Matter Mater. Phys. 2009, 79, 045301. 10.1103/PhysRevB.79.045301. [DOI] [Google Scholar]
  33. Kwadrin A.; Koenderink A. F. Gray-Tone Lithography Implementation of Drexhage’s Method for Calibrating Radiative and Nonradiative Decay Constants of Fluorophores. J. Phys. Chem. C 2012, 116, 16666–16673. 10.1021/jp3048423. [DOI] [Google Scholar]
  34. Chizhik A. I.; Gregor I.; Ernst B.; Enderlein J. Nanocavity-Based Determination of Absolute Values of Photoluminescence Quantum Yields. ChemPhysChem 2013, 14, 505–513. 10.1002/cphc.201200931. [DOI] [PubMed] [Google Scholar]
  35. Lam A. J.; St-Pierre F.; Gong Y. Y.; Marshall J. D.; Cranfill P. J.; Baird M. A.; McKeown M. R.; Wiedenmann J.; Davidson M. W.; Schnitzer M. J.; et al. Improving Fret Dynamic Range with Bright Green and Red Fluorescent Proteins. Nat. Methods 2012, 9, 1005. 10.1038/nmeth.2171. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Shcherbo D.; Murphy C. S.; Ermakova G. V.; Solovieva E. A.; Chepurnykh T. V.; Shcheglov A. S.; Verkhusha V. V.; Pletnev V. Z.; Hazelwood K. L.; Roche P. M.; et al. Far-Red Fluorescent Tags for Protein Imaging in Living Tissues. Biochem. J. 2009, 418, 567–574. 10.1042/BJ20081949. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Shaner N. C.; Campbell R. E.; Steinbach P. A.; Giepmans B. N. G.; Palmer A. E.; Tsien R. Y. Improved Monomeric Red, Orange and Yellow Fluorescent Proteins Derived from Discosoma Sp. Red Fluorescent Protein. Nat. Biotechnol. 2004, 22, 1567–1572. 10.1038/nbt1037. [DOI] [PubMed] [Google Scholar]
  38. Stopel M. H. W.; Prangsma J. C.; Blum C.; Subramaniam V. Blinking Statistics of Colloidal Quantum Dots at Different Excitation Wavelengths. RSC Adv. 2013, 3, 17440–17445. 10.1039/c3ra43637c. [DOI] [Google Scholar]
  39. Blum C.; Cesa Y.; Escalante M.; Subramaniam V. Multimode Microscopy: Spectral and Lifetime Imaging. J. R. Soc., Interface 2009, 6, S35–S43. 10.1098/rsif.2008.0356.focus. [DOI] [Google Scholar]
  40. Molenaar R.; Prangsma J. C.; van der Werf K. O.; Bennink M. L.; Blum C.; Subramaniam V. Microcantilever Based Distance Control between a Probe and a Surface. Rev. Sci. Instrum. 2015, 86, 063706. 10.1063/1.4922885. [DOI] [PubMed] [Google Scholar]
  41. Novotny L.; Hecht B.. Principles of Nano-Optics; Cambridge University Press: 2006. [Google Scholar]
  42. Etchegoin P. G.; Le Ru E. C.; Meyer M. An Analytic Model for the Optical Properties of Gold. J. Chem. Phys. 2006, 125, 164705. 10.1063/1.2360270. [DOI] [PubMed] [Google Scholar]
  43. Johansen J.; Stobbe S.; Nikolaev I. S.; Lund-Hansen T.; Kristensen P. T.; Hvam J. M.; Vos W. L.; Lodahl P. Size Dependence of the Wavefunction of Self-Assembled Inas Quantum Dots from Time-Resolved Optical Measurements. Phys. Rev. B: Condens. Matter Mater. Phys. 2008, 77, 073303. 10.1103/PhysRevB.77.073303. [DOI] [Google Scholar]
  44. Drexhage K. H. Influence of a Dielectric Interface on Fluorescence Decay Time. J. Lumin. 1970, 1–2, 693–701. 10.1016/0022-2313(70)90082-7. [DOI] [Google Scholar]
  45. Chance R. R.; Prock A.; Silbey R. In Molecular Fluorescence and Energy Transfer near Interfaces; Prigogine I., Rice S. A., Eds.; Wiley & Sons: New York, 1978; Vol. 37, pp 1–64. [Google Scholar]
  46. Karstens T.; Kobs K. Rhodamine B and Rhodamine 101 as Reference Substances for Fluorescence Quantum Yield Measurements. J. Phys. Chem. 1980, 84, 1871–1872. 10.1021/j100451a030. [DOI] [Google Scholar]
  47. Velapoldi R. A.; Tønnesen H. H. Corrected Emission Spectra and Quantum Yields for a Series of Fluorescent Compounds in the Visible Spectral Region. J. Fluoresc. 2004, 14, 465–472. 10.1023/B:JOFL.0000031828.96368.c1. [DOI] [PubMed] [Google Scholar]
  48. Blum C.; Meixner A. J.; Subramaniam V. Single Oligomer Spectra Probe Chromophore Nanoenvironments of Tetrameric Fluorescent Proteins. J. Am. Chem. Soc. 2006, 128, 8664–8670. 10.1021/ja060726g. [DOI] [PubMed] [Google Scholar]
  49. Stobbe S.; Johansen J.; Kristensen P. T.; Hvam J. M.; Lodahl P. Frequency Dependence of the Radiative Decay Rate of Excitons in Self-Assembled Quantum Dots: Experiment and Theory. Phys. Rev. B: Condens. Matter Mater. Phys. 2009, 80, 155307. 10.1103/PhysRevB.80.155307. [DOI] [Google Scholar]
  50. Strickler S. J.; Berg R. A. Relationship between Absorption Intensity and Fluorescence Lifetime of Molecules. J. Chem. Phys. 1962, 37, 814. 10.1063/1.1733166. [DOI] [Google Scholar]
  51. Toptygin D. Effects of the Solvent Refractive Index and Its Dispersion on the Radiative Decay Rate and Extinction Coefficient of a Fluorescent Solute. J. Fluoresc. 2003, 13, 201–219. 10.1023/A:1025033731377. [DOI] [Google Scholar]
  52. Suhling K.; Siegel J.; Phillips D.; French P. M. W.; Leveque-Fort S.; Webb S. E. D.; Davis D. M. Imaging the Environment of Green Fluorescent Protein. Biophys. J. 2002, 83, 3589–3595. 10.1016/S0006-3495(02)75359-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Magde D.; Rojas G. E.; Seybold P. G. Solvent Dependence of the Fluorescence Lifetimes of Xanthene Dyes. Photochem. Photobiol. 1999, 70, 737–744. 10.1111/j.1751-1097.1999.tb08277.x. [DOI] [Google Scholar]
  54. Merzlyak E. M.; Goedhart J.; Shcherbo D.; Bulina M. E.; Shcheglov A. S.; Fradkov A. F.; Gaintzeva A.; Lukyanov K. A.; Lukyanov S.; Gadella T. W. J.; et al. Bright Monomeric Red Fluorescent Protein with an Extended Fluorescence Lifetime. Nat. Methods 2007, 4, 555. 10.1038/nmeth1062. [DOI] [PubMed] [Google Scholar]
  55. Seefeldt B.; Kasper R.; Seidel T.; Tinnefeld P.; Dietz K. J.; Heilemann M.; Sauer M. Fluorescent Proteins for Single-Molecule Fluorescence Applications. J. Biophotonics 2008, 1, 74–82. 10.1002/jbio.200710024. [DOI] [PubMed] [Google Scholar]
  56. van Driel A. F.; Nikolaev I. S.; Vergeer P.; Lodahl P.; Vanmaekelbergh D.; Vos W. L. Statistical analysis of time-resolved emission from ensembles of semiconductor quantum dots: Interpretation of exponential decay models. Phys. Rev. B: Condens. Matter Mater. Phys. 2007, 75, 8. 10.1103/PhysRevB.75.035329. [DOI] [Google Scholar]
  57. Patterson G.; Day R. N.; Piston D. Fluorescent Protein Spectra. J. Cell Sci. 2001, 114, 837–838. [DOI] [PubMed] [Google Scholar]
  58. Rurack K.; Spieles M. Fluorescence Quantum Yields of a Series of Red and near-Infrared Dyes Emitting at 600–1000 Nm. Anal. Chem. 2011, 83, 1232–1242. 10.1021/ac101329h. [DOI] [PubMed] [Google Scholar]
  59. Weber W.; Helms V.; McCammon J. A.; Langhoff P. W. Shedding Light on the Dark and Weakly Fluorescent States of Green Fluorescent Proteins. Proc. Natl. Acad. Sci. U. S. A. 1999, 96, 6177–6182. 10.1073/pnas.96.11.6177. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Kummer A. D.; Kompa C.; Lossau H.; Pollinger-Dammer F.; Michel-Beyerle M. E.; Silva C. M.; Bylina E. J.; Coleman W. J.; Yang M. M.; Youvan D. C. Dramatic Reduction in Fluorescence Quantum Yield in Mutants of Green Fluorescent Protein Due to Fast Internal Conversion. Chem. Phys. 1998, 237, 183–193. 10.1016/S0301-0104(98)00245-6. [DOI] [Google Scholar]
  61. Addison K.; Conyard J.; Dixon T.; Page P. C. B.; Solntsev K. M.; Meech S. R. Ultrafast Studies of the Photophysics of Cis and Trans States of the Green Fluorescent Protein Chromophore. J. Phys. Chem. Lett. 2012, 3, 2298–2302. 10.1021/jz3008408. [DOI] [PubMed] [Google Scholar]
  62. Verdaasdonk J. S.; Lawrimore J.; Bloom K.. Determining Absolute Protein Numbers by Quantitative Fluorescence Microscopy. In Quantitative Imaging in Cell Biology; Waters J. C., Wittmann T., Eds.; Elsevier Academic Press Inc: San Diego, CA, 2014; Vol. 123, pp 347–365. [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Leake M. C.; Chandler J. H.; Wadhams G. H.; Bai F.; Berry R. M.; Armitage J. P. Stoichiometry and Turnover in Single, Functioning Membrane Protein Complexes. Nature 2006, 443, 355–358. 10.1038/nature05135. [DOI] [PubMed] [Google Scholar]
  64. Taniguchi Y.; Choi P. J.; Li G. W.; Chen H. Y.; Babu M.; Hearn J.; Emili A.; Xie X. S. Quantifying E-Coli Proteome and Transcriptome with Single-Molecule Sensitivity in Single Cells. Science 2010, 329, 533–538. 10.1126/science.1188308. [DOI] [PMC free article] [PubMed] [Google Scholar]
  65. Shrestha D.; Jenei A.; Nagy P.; Vereb G.; Szollosi J. Understanding Fret as a Research Tool for Cellular Studies. Int. J. Mol. Sci. 2015, 16, 6718–6756. 10.3390/ijms16046718. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp9b10396_si_001.pdf (694.6KB, pdf)

Articles from The Journal of Physical Chemistry. B are provided here courtesy of American Chemical Society

RESOURCES