An Algorithm for Creating Virtual Controls Using Integrated and Harmonized Longitudinal Data

Abstract

We introduce a strategy for creating virtual control groups – cases generated through computer algorithms that, when aggregated, may serve as experimental comparators where live controls are difficult to recruit, such as when programs are widely disseminated and randomization is not feasible. We integrated and harmonized data from eight archived longitudinal adolescent-focused datasets spanning the decades from 1980 to 2010. Collectively, these studies examined numerous psychosocial variables and assessed past 30-day alcohol, cigarette and marijuana use. Additional treatment and control group data from two archived randomized control trials were used to test the virtual control algorithm. Both RCTs assessed intentions, normative beliefs and values as well as past 30-day alcohol, cigarette and marijuana use. We developed an algorithm that used percentile scores from the integrated dataset to create age- and gender-specific latent psychosocial scores. The algorithm matched treatment case observed psychosocial scores at pretest to create a virtual control case that figuratively “matured” based on age-related changes, holding the virtual case’s percentile constant. Virtual controls matched treatment case occurrence, eliminating differential attrition as a threat to validity. Virtual case substance use was estimated from the virtual case’s latent psychosocial score using logistic regression coefficients derived from analyzing the treatment group. Averaging across virtual cases created group estimates of prevalence. Two criteria were established to evaluate the adequacy of virtual control cases: (1) virtual control group pretest drug prevalence rates should match those of the treatment group, (2) virtual control group patterns of drug prevalence over time should match live controls. The algorithm successfully matched pretest prevalence for both RCTs. Increases in prevalence were observed; although, there were discrepancies between live and virtual control outcomes. This study provides an initial framework for creating virtual controls using a step-by-step procedure that can now be revised and validated using other prevention trial data.

Introduction

Despite both long-standing (e.g., Feinstein, 1983) and more recent challenges (Cartwright, 2007; Chaulk & Kazandjian, 2004; Concato, Shah, & Horowitz, 2000; Grossman & Mackenzie, 2005) randomized controlled trial (RCT) designs continue to be regarded as the gold standard of experimental intervention research. This benchmark exists both generally for scientific research and specifically for drug prevention studies (Flay, Biglan, Boruch et al., 2005). The most basic research design has two conditions; one receives the intervention and the other serves as a control group. The control group serves as the counterfactual against which experimental manipulations are evaluated for evidence of program effects. Particularly when studies are well-designed and well-executed, randomized “live” control groups have the benefit of reducing major threats to internal validity, including selection bias, history, maturation, instrumentation, and regression artifacts (Campbell & Stanley, 1963). For these reasons alone RCTs will remain the preferred method for conducting drug prevention research. They enable researchers to document the contemporaneous rate of change, which is valuable in that general trends of alcohol and other substance use vary from year-to-year (Miech, Johnston, O’Malley, et al., 2016).

Although RCTs are valuable for establishing program efficacy, they face different concerns when used to establish effectiveness once a program is disseminated (Flay, 1986; Glasgow, Lichtenstein & Marcus, 2003). This usually arises because circumstances exist where RCTs are not possible or practical. For example, once local service providers adopt drug prevention programs and invest time and resources to receive training and purchase materials, asking them to forego implementation and serve as controls is not a realistic option. This is even more true should one desire to evaluate the effectiveness of programs that have been routinely delivered for several years. Nonetheless, understanding effectiveness remains a priority for justifying funding and effort and for noting instances where program design and quality of implementation can be improved.

An Alternative: Virtual Controls

When interventions are newly developed, researchers do not know what magnitude of effect might be achieved. Estimating an effect size is a crucial prerequisite to conducting independent and valid scientific enquiries. In drug prevention studies, controls represent normative development and depict the natural course of drug use onset. National surveillance data shows that prevalence increases as young people grow older (Miech et al., 2016). As evidence accumulates and predictive models are developed, the expected course of normal development becomes less obscure and, given sufficient appropriate data, the normal onset of use can be modeled. We now have a fundamentally sufficient understanding of the normal pattern of drug use onset and the psychosocial factors that drive behavior to create models that can be used to this end.

This paper discusses the potential for algorithmically creating suitable comparators – virtual controls. We describe a method for creating virtual controls that can serve as counterfactuals against which the effectiveness of prevention programs can be documented and evaluated. We expect virtual controls to have multiple definable benefits for prevention research and evaluation, including (1) the ability to evaluate disseminated interventions, (2) increased speed of results delivery, (3) increased flexibility to test alternatives and adaptions, (4) reduced cost, (5) increased equivalence of controls and treated subjects, (6) increased external validity, and (7) the elimination of differential attrition as a threat to validity.

There are multiple ways in which alternatives to live controls might be created. For example, “propensity score matching” provides one alternative (e.g., Caliendo & Kopeinig, 2008; Li & Greene, 2013; Stuart, Cole, Bradshaw, & Leaf, 2001). In addition, others have suggested strategies for creating “synthetic” comparators using extant survey data (Abadie, Diamond, & Hainmueller, 2010; Abadie & Gardeazabal, 2003; Hansen, Derzon, & Reese, 2012). Such methods are, without question, useful. However, there are documented challenges associated with applying these methods (e.g., Austin, 2008). Among the more practical concerns are challenges with finding suitable longitudinal datasets that match a treated cohort’s risk status and demographic profile precisely. Even if pretest scores can be matched, there may be problems with differential attrition (Biglan, Severson, Ary et al., 1987; Hansen, Collins, Malotte, et al., 1985; Hansen, Tobler & Graham, 1990), which can affect the internal validity of a study’s findings. Further, regression artifacts remain a potential threat to internal and external validity when matching approaches are applied to analyses involving longitudinal data (Campbell, 1996; Campbell & Kenny, 1999).

We propose an alternative algorithm-based approach that relies on modeling gender-specific and age-related changes in key psychosocial variables that represent the active ingredients of prevention trials. Data from multiple studies will be used to derive latent¹ psychosocial scores for all levels of risk. Latent psychosocial scores will serve as data points against which a treatment case’s pretest observed psychosocial scores, adjusted for age and gender, can be used to define a virtual case. For subsequent waves of data, the virtual cases’ latent psychosocial variable scores will figuratively “mature” based on modeled age-related changes in these variables. Probability of substance use for the virtual control case will then be estimated using the statistical relations between psychosocial variables and behaviors, calculated from empirical data supplied by the treatment group.

Deriving latent psychosocial scores will rely on statistical relations between demographic and psychosocial variables on the one hand and targeted behaviors on the other (Hansen & McNeal, 1996). This analytic framework is consistent with a prevention trial where the focus rests with relations between target mediators and behavior outcomes adjusted for covariates. Moreover, trends in drug prevalence fluctuate from year-to-year; nonetheless, past research has shown that the strength of relations between psychosocial variables and substance use have remained remarkably constant over decades (Hansen & Hansen, 2016; Miech et al., 2016). We postulate that when data from multiple generations of research are integrated, variables that have lasting importance will emerge.

Our goal is to develop a method for generating virtual controls that will function as reasonable comparators against which the effectiveness of an intervention can be evaluated. The algorithm should be flexible in that it is adaptive to the risk level of the groups and individuals being studied and produces virtual control pretest scores that match treated participants’ pretest scores (i.e., pretest equivalence), while at the same time produces outcomes that mimic normal developmental trends and closely match the prevalence rates of established “live” control groups. The potential benefit is that this approach can meet the needs of a wide variety of situations, including evaluating programs delivered to groups that may vary in their risk of alcohol and drug use. Once an algorithm is successfully developed and programming completed to automate the process of generating virtual controls, it can be readily applied to a variety of evaluation projects.

To accomplish this goal, we propose a three-step process that involves: (1) assembling, integrating and harmonizing multiple relevant datasets, including developing strategies for addressing missing data, (2) devising algorithms that allow cases from a prevention trial to generate virtual control cases that will be matched at pretest and subsequently mature independently of the treatment case, and (3) testing the algorithm against known outcomes to demonstrate its feasibility.

Step 1: Integration, Harmonization and Missing Data Imputation

Integration.

There are many reasons to integrate data from multiple datasets (Cooper & Patall, 2009). This may include an increased ability to generate new knowledge, provide increased access to key findings needed for intervention development, provide tools needed for evaluating state-of-the-art interventions, and provide a means to increase the involvement of non-researchers in how information might be used (Murdock & Detsky, 2013). Among the specific purposes we envision is the use of data from multiple datasets to create models of alcohol, cigarette, and marijuana use onset. In this paper, we demonstrate a method for integrating data that will allow us to model age- and gender-related changes in psychosocial variables and the model relations between key measures of psychosocial functioning and adolescent alcohol, cigarette and marijuana use onset.

The idea of integrating datasets to create suitable comparison groups is not new. Several researchers have recently promoted the use of databases as a rich source of comparative data (Babalola & Kincaid, 2009; Booth & Tannock, 2014; Derzon, 2000; Glasgow, 2008; Harvey, Rowan, Harrison & Black, 2010; Wang, 2013; Wang & Shen, 2014). For example, Mun and colleagues (2015) analyzed integrative data that included individual-level data pooled from 24 previously completed alcohol college-age intervention studies. Whereas the average independently conducted study included 272 control subjects, once pooled a much larger sample of 4,893 control subjects became available for analyses.

In assembling multiple datasets, we assume that we will find commonalities among them such that associations between psychosocial and behavioral variables will be consistent. Data will be gathered from diverse populations at different points in time and from different geographic locations. Such assumptions may be unwarranted and unjustified. Nonetheless, as far as we know, this is the way forward that is mostly likely to provide data needed for modeling drug use onset.

Harmonization.

Harmonization refers to the process of creating a common set of metrics that permit comparability among initially dissimilar datasets. When researchers plan project, they focus on specific populations and include a variety of predictor and outcome measures that address their specific hypotheses. Adopting a “big data” and an “integrated data” approach allows the various measures to be harmonized, allowing investigators to then work with similar and comparable constructs (Cooper & Patall, 2009; Curran & Hussong, 2009). Meta-analytic studies routinely harmonize variables to allow common concepts to be examined (e.g., Cooper, Hardy, Sayer, et al., 2011; Doiron, Burton, Marcon, et al., 2013; Evangelou & Ioannidis, 2013). In nearly all cases where harmonization is attempted, there is a tension between rigor and flexibility and between specificity and generalizability (Fortier, Doiron, Burton, & Raina, 2011). However, the end benefit is having access to large numbers of similar cases that can be used to model important relations between predictors and outcomes.

There have been prior attempts in the alcohol and drug use field to harmonize multiple datasets. For example, using data from 53 studies, Fortier, Doiron, Little et al. (2011) used a key word approach to attempt to harmonize 148 variables with only modest success; 38% of variables were successfully harmonized. Harmonization has been applied to measures of personality (Kern, Hampson, Goldberg, & Friedman, 2014) and alcohol use (Mun, de la Torre, Atkins, et al., 2015). There have also been previous attempts to harmonize psychosocial variables in a general conceptual manner that provides a useful initial starting point for the current study (Derzon & Lipsey, 1999; Hansen, Dusenbury, Bishop, & Derzon, 2007; Hawkins, Catalano, & Miller, 1992).

In addition to grouping variables based on the constructs being measured, there is also a need to harmonize measurement characteristics (Conway, Vullo, Kennedy, et al., 2014). In some cases, surveys include response options that need to be re-coded to allow statistical comparability across studies. Curran and Hussong (2009; Curran, Hussong, Cai et al., 2008) have used item response theory (IRT) to harmonize responses from multiple studies. We propose a strategy that stretches all individual items within scales to fit a 0-to-10 metric with values of 10 always being assigned the most theoretically and socially desirable outcome. Items are then averaged within scales to form observed composites. The reason for adopting this approach is that in future applications of this methodology we plan to automate the virtual control group application. Importing data pre-coded to meet this standard will simplify and streamline the application.

Imputing Missing Data.

A typical challenge of integrating loosely related datasets is the problem of missing data. There often exist missing values that arise because respondents do not provide answers to all questions on a survey. We refer to this as “local” missing data. The most likely scenario for missing data in integrated datasets is because each study collects data for only some psychosocial and behavioral variables. This creates a different kind of missing data, which we refer to as “global.” Both types of missing values, item non-response, and design missing, limit the availability of data for analysis. However, it is particularly global missing data that requires remediation. The local versus global imputation concept has been successfully used in genetics to improve the quality of imputed missing data. An example is epistatic mini-array profiling where 30% of data may be missing (Pan, Tian, Huang, & Shen, 2011).

A variety of imputation methods have been extensively used in the behavioral science literature for handling missing values. Multiple imputation (MI) is one such prevalent method for handling missing data (Rubin, 2004; Schafer, 1997). Most MI methods assume data to be missing-at-random (Rubin, 1976), which is the approach we use in this study. In MI, a single missing value is imputed with several copies (e.g., 5) that are generated from a predictive model using relevant observed data. Eventually multiple copies of imputed data sets in which all the missing values are filled are made available for analysis. Parameter estimates are averaged across these datasets adjusting for varying levels of missing data uncertainty in each one (Schafer, 1997).

Current innovations in the use of MI reflect three broad approaches: (1) joint modeling of all involved variables such as PROC MI in SAS; (2) conditional specification of the full joint distribution such as MICE (van Buuren, 2007); and (3) nonparametric approaches such as Random Forest (Breiman, 2001) and missForest (Stekhoven & Buhlmann, 2012). Both joint modeling and conditional specification approaches have drawbacks that limit their appropriateness for use with our integrative dataset, in part because of assumptions about the nature of the data that can be accommodated using these approaches (Deng et al., 2016). We adopt a non-parametric approach in this project.

Method

Sample Datasets

We used our knowledge of the field of drug prevention as well as electronic searches conducted using Google Scholar and the NIH Reporter to identify two types of longitudinal studies that addressed adolescent alcohol, cigarette, or marijuana use. These included: (1) epidemiological studies that assess risk and protection; and (2) two-condition preventive intervention studies that included an untreated control group. In line with the aims of the grant that funded this project, we contacted principal investigators for 13 studies and requested access to their data. Ultimately, we plan to assess many more datasets; however, funds were limited and we therefore attempted to secure datasets from principal investigators whose work was well known to the research community. Modest funds were offered to offset any time required to prepare or transmit the data. Researchers associated with the parent data were responsible for securing any required IRB permission to permit transfer of datasets. Researchers were guaranteed that neither they nor their studies would be identified in published reports.

We received 10 of 13 requested datasets, codebooks, and sample surveys. Principal investigators who did not contribute requested data either failed to archive their data (two studies) or failed to respond to repeated attempts to discuss transfer of their data (one study). Three datasets were eliminated because they failed to contain data about substance use behaviors. We supplemented the datasets received from other researchers with datasets from three prevention trials associated with our research team, bringing the total number of datasets to 10 available for creating virtual controls.

Two of the 10 datasets were epidemiologic studies (datasets C and F) and six included untreated control groups obtained from drug prevention trials (datasets A, B, D, E, G and H). Two intervention studies, RCT-1 and RCT-2, included both treatment and control cases and were set aside for algorithm testing, the remaining eight were used in algorithm development. The datasets spanned the mid-1980s through the 2010 decade. Data were de-identified; however, some form of participant ID not linked to a name was required for linking study participants across time in multi-wave studies. We also set the requirement for inclusion that study participants needed at least two surveys separated in time within each dataset with gender and age included as measures. Table 1 includes characteristics of the different datasets.

Table 1.

Gender, race/ethnicity and average ages for each of the datasets included in this project

	Dataset
	A	B	C	D	E	F	G	H	RCT-1	RCT-2
N	369	896	5,909	2,782	5,308	1,174	1,704	382	15,705	6,763
Gender (percent)
Female	51.2	53.2	54.8	50.7	49.6	47.1	47.2	100.0	56.4	55.7
Male	48.8	46.8	45.2	49.3	50.4	52.9	52.8	0.0	43.6	44.3
Racial/Ethnic (percent)
Black/African American	80.8	22.7	- - -	10.5	- - -	0.7	12.9	22.3	11.3	13.5
White	4.9	69.7	- - -	40.6	- - -	94.0	83.6	55.9	58.5	70.3
Native American	0.0	1.3	- - -	4.0	- - -	0.0	0.0	1.3	5.0	0.6
Hispanic	0.0	1.6	- - -	27.2	- - -	1.9	0.0	10.5	22.0	5.5
Asian	0.0	2.9	- - -	9.7	- - -	0.6	0.0	2.6	4.9	2.4
Pacific Islander	0.0	0.0	- - -	2.0	- - -	0.0	0.0	0.3	- - -	0.9
Other	14.3	1.8	- - -	6.1	- - -	2.9	3.5	7.1	9.0	6.7
Average Age
Wave 1	10.3	12.1	12.5	11.5	13.9	12.5	11.0	13.9	12.4	14.4
Wave 2	10.9	12.8	13.5	12.8	14.3	13.0	11.5	14.4	12.9	15.2
Wave 3	11.8	13.6	14.5	13.8	14.1	14.2	12.4	15.1	13.6	15.7
Wave 4	12.7			20.1	14.7	14.7	13.5		14.4
Wave 5	13.4						15.5		14.9
Wave 6	13.5						15.9		15.4
Wave 7	13.8						17.8		16.4

Data Harmonization Procedures

For each dataset, a systematic set of coding procedures were followed to standardize and harmonize data across sources. Table 2 shows the step-by-step coding procedure to achieve data harmonization. (Data in Table 1 reflect the application of harmonization procedures applied to age and race/ethnicity.)

Table 2.

Steps to achieve data harmonization

1. We identified control groups and, if intervention groups were included we eliminated non-control cases.

2. We applied standard gender codes and checked for consistency of gender across waves of data.

3. Where feasible, we coded race and ethnicity so that coded values for African American, White, Native American, Hispanic, Asian, Pacific Islander, and Other were consistent across datasets. In cases where multiple races were listed, the category “Other” was used. When Hispanic was selected in addition to any other single race, Hispanic was used. Race and ethnicity coding was checked to ensure consistency across waves of data. Inconsistencies were resolved when possible by looking for most commonly reported values. When inconsistencies could not be resolved, race and ethnicity were coded as missing.

4. We examined original coding for age, which varied from dataset to dataset. Several datasets included age specified as a decimal value (e.g., 12.5). Several datasets included month of birth and month of survey delivery in addition to age as an integer that allowed a similar decimal system to be employed in estimating age. In these cases, age was rounded to the half year. The remaining datasets included age only as an integer. It was not uncommon to discover that the same age was listed for multiple waves of data. Because we anticipated that age would be an important component of any future algorithm used to predict probability of becoming an alcohol, cigarette or marijuana user, making some adjustment in these cases was crucial. When age did not advance from an initial to a subsequent wave of data, half-year increments were applied to the subsequent wave of data. Thus, for example, if a participant reported being 13 years old at both wave 1 and wave 2 of data, the second value was augmented to 13.5.

5. We analyzed the constructs employed represented by the survey items and used psychosocial variable names developed in a previous meta-analysis of National Registry of Evidence-based Programs and Practices (NREPP) programs as a method for aligning the disparate concepts that psychosocial variables represent (Hansen et al., 2007; Hawkins, Catalano, & Miller, 1992).

6. Each project also used individualized methods for coding responses to psychosocial items. We recoded all individual psychosocial items to have values from 0 to 10 and oriented each so that a theoretically more desirable response had a higher score (e.g., greater social competence and more assertiveness skills). For example, questions that had four responses were recoded to have respective values of 0.00, 3.33, 6.67 and 10.00 for theoretically least desirable to most desirable responses. Items with five response categories were recoded to have values of 0.00, 2.50, 5.00, 7.50, and 10.00. This system of recoding data allowed all variables to have the same metric with identical scaling. We checked to ensure that there were no out-of-range values.

7. We used both Cronbach’s alpha (1951) and McDonald’s omega (1999) to test the reliability of all multi-item scales that were formed by averaging across items within a construct. When alpha and omega coefficients were greater than .60, we created composite scales. When partially successful (typically this resulted when there were inadequate numbers of cases list-wise for reliability calculation), we created scales and correlated values across waves of data and included only scales where test-retest correlations exceeded .40. When unsuccessful, we eliminated the possible scale from further consideration.

8. Measures used to assess alcohol, cigarette, and marijuana use were inconsistent across datasets including both how questions were asked as well as how response categories were framed. We categorized measures of alcohol, cigarette, and marijuana use to reflect both the time frame being assessed (e.g., the past day, week, month, year or ever in one’s lifetime). We also provided a categorization scheme to reflect whether the variable measured frequency or quantity or assessed dichotomous use (i.e., yes/no). When no dichotomous measure was included, we calculated values from frequency or quantity measures with 0 referring to non-use and 1 indicating use. In the case of assessing alcohol, some studies included a “sips” category, which was coded as non-use.

9. We eliminated cases within datasets that did not have multiple measurement time points (setting two as the minimum threshold).

Imputing missing data.

Once we completed harmonization procedures, we imputed missing values. For the current data harmonization, we used global imputation methods (Collins, Schafer, & Kam, 200). We used a random forest method (Breiman, 2001) to complete imputation. This nonparametric imputation approach used a tree-based method. It fully addresses our needs because it: (1) does not require distributional assumptions regarding the model variables, (2) can simultaneously handle mixed types of data (e.g., ordinal and dichotomous), (3) can capture nonlinear interaction effects among variables, and (4) can scale up and is applicable to datasets that have high dimensionality.

We followed these steps to impute missing data:

1. We duplicated the dataset five times, labeling each iteration.

2. We established a list of candidate predictor variables for predicting a specific measure. Because temporality is a feature present in all the databases, we also include the measures from the most recent non-missing time point (except for the first-time point) as predictors.

3. We ran the random forest imputation procedure, using the R-based program missForest (Stekhoven & Buhlmann, 2012) for each unique combination of iteration, gender, and age, where age includes half years from 10.0 through 18.5. In missForest, values are randomly generated for successive iterations. After each iteration the difference between the previous and the new imputed data table is assessed. The procedure stops when differences become larger than the prior iteration.

Algorithm Development

We developed an algorithm, programmed in JavaScript, that allowed a latent psychosocial variable to serve as the basis for defining the probability of substance use for virtual control cases. The algorithm created one virtual case for each treatment case, matched on age and gender. To ensure that the latent psychosocial variable included in the algorithm would be viable indicators of substance use we calculated Receiver Operating Characteristic curves (ROC) for each psychosocial variable from the integrated/harmonized/imputed dataset. The ROC analysis included gender and age as interaction terms in addition to psychosocial variables. These data allowed us to define which variables would be promising predictors of alcohol consumption, cigarette smoking, and marijuana use. This statistical procedure also allowed us to model age-related developmental patterns associated with psychosocial variables that we could then use to create latent psychosocial scores.

The algorithm included three JavaScript Object Notation (JSON) tables.

The percentile table consisted of latent psychosocial scores (which range from 0 to 10) for each percentile derived from the integrated/harmonized/imputed dataset. Latent psychosocial scores were calculated for all half-percentiles (0.5, 1.0, 1.5, 2.0, … 98.0, 98.5, 99.0, 99.5, and 100.0²) based on gender and age (11 through 19.0 with half-years included).

Added to this table were values representing the probability of using each substance for each gender, age, and percentile element of the table associated with each latent psychosocial score (Psych in the equation that follows). Puse (the probability of use for each gender, age, substance, and percentile) for all entries in the table was calculated using latent psychosocial scores from the percentile table with B weights from logistic regression results. Weights were derived based on the relations between observed psychosocial scores and behaviors in the treatment group. Female and male probability estimates were calculated separately.

$$P\text{use}=\frac{\mathit{EXP}(\mathit{Intercept}+(\mathit{Age}\times B\text{Age})+(\mathit{Psych}\times B\mathrm{Psych})+(\mathit{Age}\times \mathit{Psych}\times B(\mathit{Age}\times \mathit{Psych})))}{1+\mathit{EXP}(\mathit{Intercept}+(\mathit{Age}\times B\text{Age})+(\mathit{Psych}\times B\mathrm{Psych})+(\mathit{Age}\times \mathit{Psych}\times B(\mathit{Age}\times \mathit{Psych})))}$$

The treatment case table consisted of the data from treatment cases: ID number, gender, age at each wave of data collection, pretest psychosocial value score and dichotomous 30-day alcohol, cigarette and marijuana use at each wave.

A virtual case table was created that included a case that corresponded to each treatment case. These cases initially had only ID numbers; the remaining values (alcohol, cigarette and marijuana probabilities at each wave) were initialized to be null.

The algorithm used treatment case gender and age at pretest to find a near match to that case’s observed psychosocial score in the percentile table. For each virtual case, a probability of use (Puse) value was recorded. Once pretest values were established for virtual control cases, the algorithm maintained the percentile of the virtual control and used latent psychosocial scores associated with each treatment case’s age at subsequent surveys completed to estimate probability of use. Thus, virtual cases figuratively “matured”. If the treatment case did not provide data at any given wave of data collection, the virtual case also had missing data. Because the age and sequence of treatment and virtual cases match precisely, there was no differential attrition between groups.

Results

Harmonization

Psychosocial Constructs.

We followed steps 5, 6, and 7 in Table 2 to harmonize psychosocial constructs. When possible, we used codebook descriptions and variable names to ascribe which psychosocial construct was being measured. For the most part, researchers used terms very similar to the content of Table 3 to describe the psychosocial measures assessed in their surveys, making classification relatively straightforward. On rare occasions, there was a lack of clarity or a failure for descriptions to align with concepts associated with the meta-analysis described in step 5 of the procedures (Hansen et al., 2007). When this happened, we analyzed the construct-specific items assessed and, whenever possible, compared survey question content with the content of surveys for which classification had already occurred. Some exceptions had to do with researchers combining conceptually related items into a single multi-item composite score. For example, questions that assessed beliefs regarding drug effects were split into those that addressed possible positive (e.g., relaxation or enjoyment) or negative expectancies (e.g., disease or social rejection).

Table 3.

Reliability estimates (McDonald’s omega) for psychosocial measures averaged across waves

	Dataset
Variable (Datasets Including)	A*	B	C	D	E	F	G	H
Motivation
Attitude (2)						.928	.677
Beliefs Negative (5)	.798		.590	.914	.762		.780
Beliefs Positive (3)			.610		.881		.833
Intentions (5)	.663	.852	.657	.748			.856
Knowledge (1)							.403
Normative Beliefs (8)	.874	.891	.888	.866	.458†	.900	.869	.887
Risk-Taking (1)	.765
Sensation Seeking (1)		.873
Values (3)	.753	.722	.716
Personal Competence
Decide Skill (5)	.587	.782	.734	.585				.849
Emotion Skill (3)			.764	.816				.732
Goal Skill (2)			.779					.856
Self-Efficacy (2)	.795						.575
Self-Esteem (6)	.454	.887	.817	.731			.666	.904
Social Competence
Media Skill (1)								.809
Refusal Skill (5)			.821	.967		.908	.844	.925
Social Skill (1)			.652
Environment
Access/Availability (2)	.755						.594
Bonding to School (3)	.655	.800					.638
Parenting (5)	.666	.769		.670		.900	.763

^*For dataset A, coefficients could be calculated for only one wave of data for Normative Beliefs, Values, Decision Skill, Self-Efficacy, Self-Esteem, and Parenting.

^†Only one measure per wave; value is the average correlation coefficient across waves.

Despite these efforts, we were unable to harmonize all items within surveys. As a rule, we excluded survey questions that would not normally be related to evaluating the efficacy of an alcohol and drug prevention program. Examples of constructs not retained included:

• knowledge, attitudes, beliefs, values and activity related to hygiene, exercise, sexual activity, violence, delinquency, and nutrition,

• items assessing experiential stress or anxiety (versus the ability to respond, which was included), and

• degree of ethnic or racial identity and experiences related to prejudice or discrimination.

For each set of items related to a targeted construct, we computed internal estimates of consistency using the alpha (Cronbach, 1951) and the more recently proposed omega (McDonald, 1999) statistics. Both alpha and omega reliability analyses yielded essentially equal coefficients. Calculations were completed separately for each wave of data collection. Table 3 presents omega reliability estimates that have been averaged across waves of data. Of the 64 values presented, 8 (12.5%) had average omega coefficients that were greater than or equal to .90. An additional 20 psychosocial measures (31.3%) had values greater than or equal to .80 and less than .90. Eighteen (28.1%) had values between .70 and .80, 10 (15.6%) had values between .60 and .70 and 8 (12.5%) had values lower than .60.

Alcohol, Cigarette and Marijuana Use.

The various datasets contained a variety of approaches for assessing self-reported drug use. Frequency and intensity measures of alcohol, cigarette, and marijuana use are generally focal measures for evaluating adolescent drug prevention interventions. Table 4 documents the measures included in each of the 10 databases for past 30-day drinking alcohol, smoking cigarettes, and using marijuana.

Table 4.

Number of Cases Available for Analysis in Each of Eight Datasets

	Dataset
Past 30-Day Behavior	A	B	C	D	E	F	G	H
Alcohol	987	2,234	5,122	7,601		4,030	5,148	1,136
Cigarettes	988	2,255	12,507	7,608	14,325	4,043	5,102	1,136
Marijuana		2,236	12,493	7,597		4,041	5,116	1,136

In Table 4, “number of cases” refers to the number of times survey participants responded to particular items. For example, in a study with four waves of data collection, an individual participant may have contributed as many as four data points for any given measure. Past month cigarette smoking had the largest numbers of available cases (47,964). There were also relatively large numbers of cases available across studies for past month marijuana use (32,619) and for past thirty-day alcohol use (26,258).

Imputed Missing Data.

Table 5 shows the descriptive statistics by gender for the key variables averaged for the imputed data sets. The far-right columns show the same information for the original data set. The sample size of the imputed data set (number of participants and number of surveys imputed within each) for females is 23,148 and for males it is 20,769. The means of the imputed data sets generally agree with the mean of the original data set. The average absolute discrepancy between the imputed and original means is .09 on 0-to-10 scales and the same computation for the standard deviations is .36. An exception is Access (Access/Availability in the Environment), which for both males and females was .5 for the mean and 1.3 and 1.4, respectively for the SD. The discrepancy might be due to the relatively small sample size available for this measure, which was included in only two studies.

Table 5.

Distributions of variables used for imputed and original data.

Gender	Variable Name	Imputed*: Mean of Means (Range of Means)	Imputed*: Mean of Standard Deviation	Original: N	Original: Mean	Original: Standard Deviation
Female	Access/Availability	5.7 (5.7-5.8)	2.4	2,284	5.2	3.7
	Age	13.4 (13.4-13.4)	13.4	23,148	13.4	13.4
	Beliefs Negative	7.6 (7.6-7.6)	1.8	18,401	7.7	2.0
	Beliefs Positive	8.0 (8.0-8.0)	2.0	18,302	8.2	2.1
	Decision Skill	6.9 (6.8-7.0)	1.8	11,890	6.5	2.1
	Intention	7.6 (7.5-7.6)	2.2	7,192	7.9	2.7
	Normative Beliefs	7.9 (7.9-7.9)	1.9	16,575	7.8	2.1
	Refusal Skill	8.3 (8.3-8.3)	2.0	14,251	8.2	2.3
	Self-Esteem	7.9 (7.9-7.9)	1.6	13,571	7.9	2.0
	Values	8.3 (8.3-8.3)	1.8	7,858	8.5	2.0
Male	Access/Availability	5.3 (5.1-5.5)	2.4	2,296	4.8	3.8
	Age	13.5 (13.5-13.5)	13.5	20,769	13.5	13.5
	Beliefs Negative	7.3 (7.3-7.3)	2.1	17,034	7.4	2.2
	Beliefs Positive	7.7 (7.7-7.7)	2.2	16,854	7.8	2.3
	Decision Skill	7.1 (7.0-7.1)	1.8	9,217	6.4	2.2
	Intention	7.6 (7.6-7.6)	2.2	6,947	7.8	2.7
	Normative Beliefs	7.9 (7.9-7.9)	1.9	14,356	7.6	2.1
	Refusal Skill	8.3 (8.3-8.3)	2.1	12,028	8.1	2.4
	Self-Esteem	8.4 (8.4-8.4)	1.4	10,842	8.3	1.7
	Values	8.3 (8.3-8.4)	1.7	6,531	8.2	2.1

Note.

^*Imputed dataset size, female (N= 23,148), male (N=20,769)

Algorithm Application

Evidence of Predictive Value.

Table 6 presents the results from the ROC analyses predicting alcohol consumption, smoking, and marijuana use, respectively. The best single predictor of all three substances in the imputed dataset was Intentions. Values, Normative Beliefs, Refusal Skill, Beliefs about Positive Consequences were also efficient predictors.

Table 6.

Area under the curve in ROC analyses. (Higher number indicates better prediction.)

	Alcohol	Cigarettes	Marijuana
Intentions	0.929	0.913	0.940
Values	0.900	0.879	0.937
Normative Beliefs	0.862	0.831	0.889
Refusal Skill	0.856	0.841	0.891
Beliefs Positive	0.836	0.810	0.882
Access/Availability	0.830	0.812	0.847
Beliefs Negative	0.759	0.722	0.807
Decision Skill	0.731	0.735	0.748
Self-Esteem	0.712	0.705	0.727
Age / Gender only	0.686	0.653	0.690

Note. Models are additive with Age / Gender as a base model.

The algorithm required both treatment and the percentile tables to each have a single psychosocial variable on which cases could be matched at pretest. In the treatment table, the variable reflected observed values. In the percentile table, the variable consisted of latent psychosocial scores. For values to be comparable, the specific variables that constituted each would be ideally composed of similar sets of variables. Both RCT-1 and RCT-2 included three variables examined in ROC analyses (Intentions, Values, and Normative Beliefs). Previous work (Hansen &Hansen, 2016) included these same variables and found they were highly intercorrelated and reliable. Therefore, in both the treatment and percentile table, we created a single psychosocial variable that was an average of these values. In the case of the treatment dataset, these scores were the average of observed scores. For the imputed dataset, these were latent psychosocial scores derived from the integrated/harmonized/imputed dataset.

As noted in the description of the algorithm, after the percentile value associated with the treatment case was identified, a specific latent psychosocial score was linked to the age at which any given treatment case was subsequently measured. It was generally the case that latent psychosocial scores decreased over time. For example, the 50^th percentile female had latent psychosocial score values of 8.65 at age 12, 7.86 at age 14, 7.31 at age 16, and 6.99 at age 18. The 50^th percentile male’s latent psychosocial score values were 8.57, 7.88, 7.15 and 6.40 for ages 12, 14, 16 and 18, respectively³. Along with the treatment case’s age, these values were used as indicators in the logistic regression formula used to estimate probability of use. In all instances, with a decline in latent psychosocial scores, the probability of substance use increases.

Virtual Control Results When Applied to Known Datasets.

The goal of the virtual controls algorithm was to create virtual cases that, when aggregated (1) matched the treatment group substance use prevalence at pretest and (2) at subsequent waves of data, matched live control group prevalence. Averaging probabilities across all virtual cases for each wave of data provided an estimate of the virtual control prevalence of each substance. Results for past 30-day alcohol use for each of the two RCTs is presented in Figures 1 and 2, 30-day cigarette use is presented in Figures 3 and 4, and 30-day marijuana use is presented in Figures 5 and 6.

Figure 1.

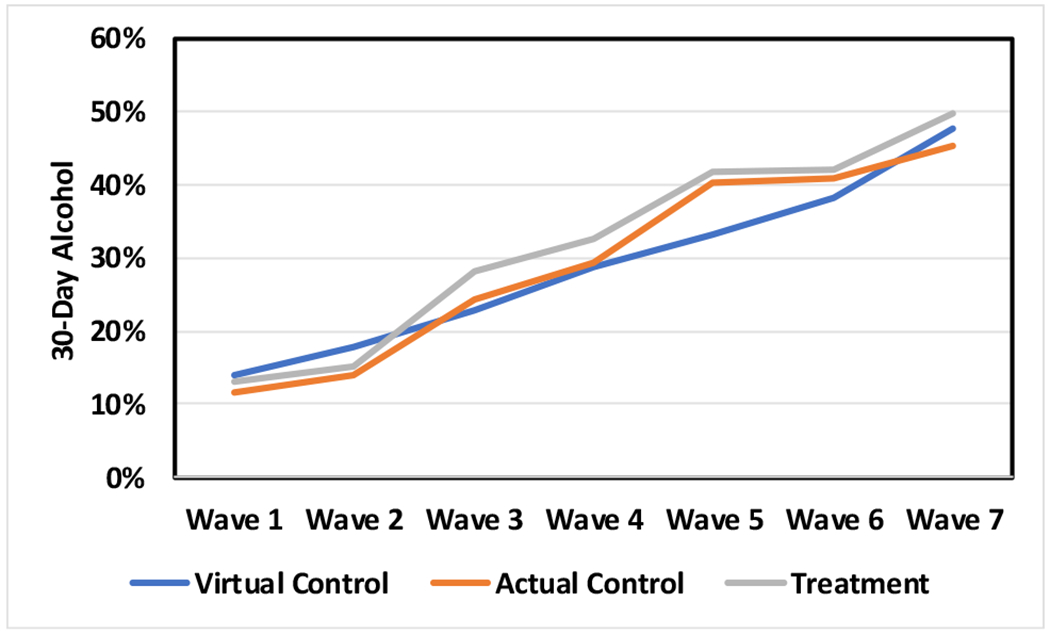
Virtual control group estimates of alcohol prevalence compared to treatment and actual control group observed values in a study that included seven waves of data collection.

Figure 2.

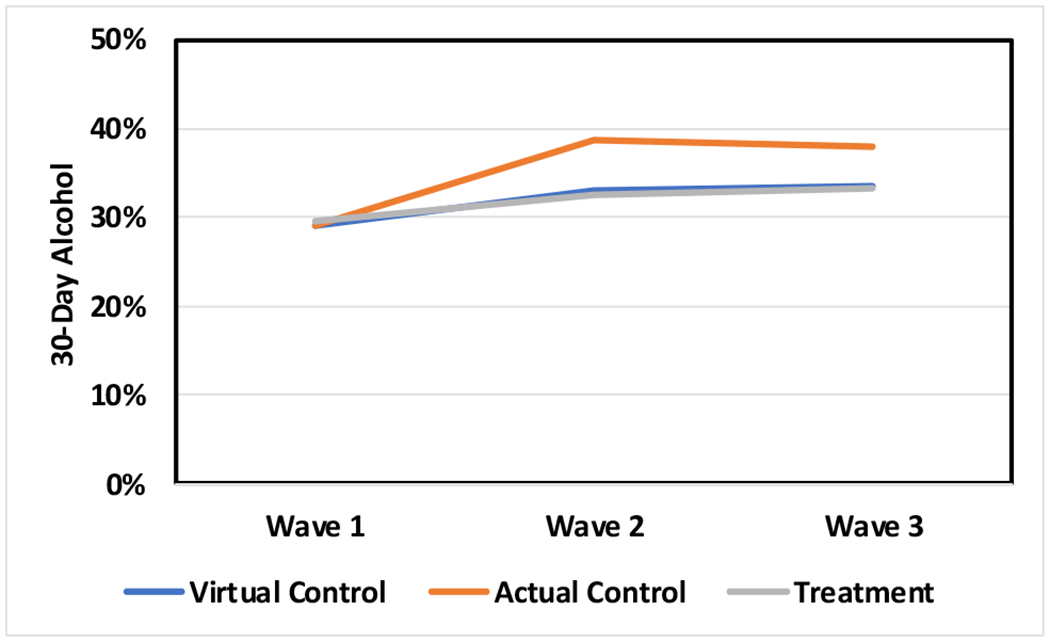
Virtual control group estimates of alcohol prevalence compared to treatment and actual control group observed values in a study that included three waves of data collection.

Figure 3.

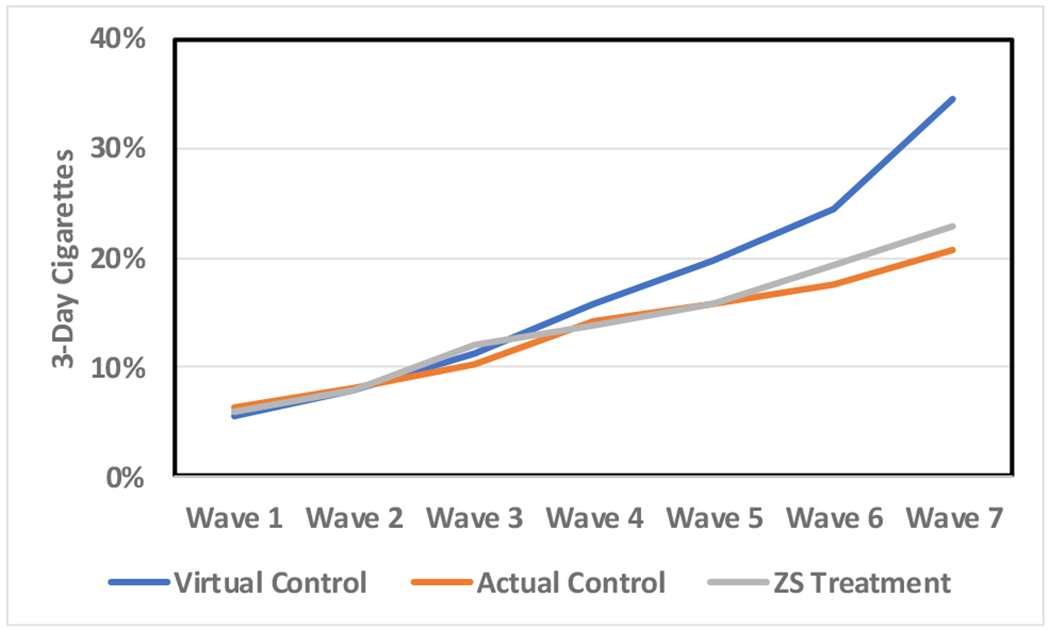
Virtual control group estimates of cigarette prevalence compared to treatment and actual control group observed values in a study that included seven waves of data collection.

Figure 4.

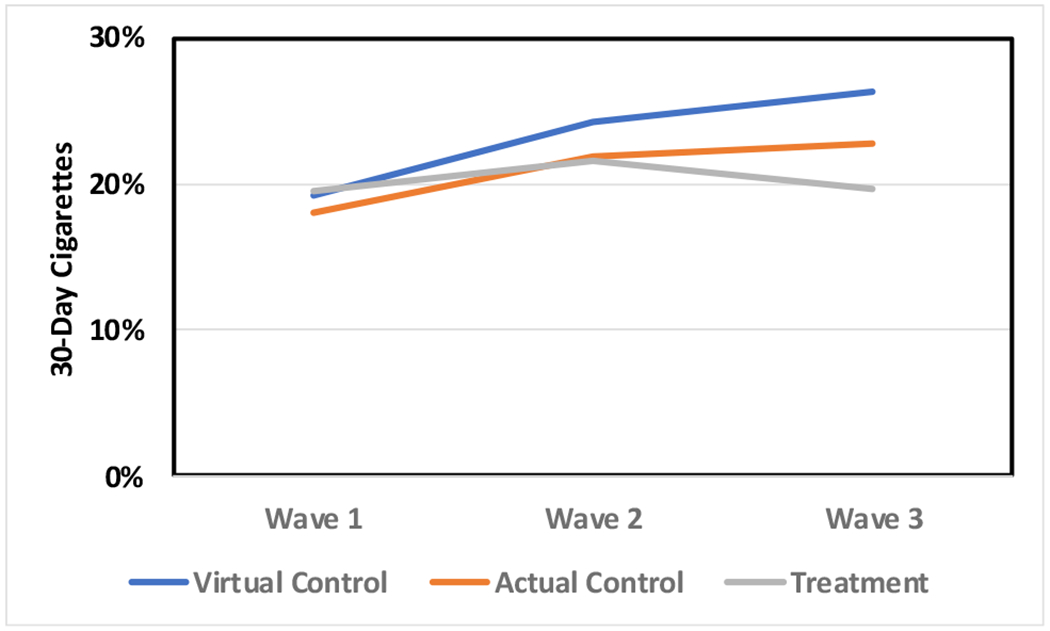
Virtual control group estimates of cigarette prevalence compared to treatment and actual control group observed values in a study that included three waves of data collection.

Figure 5.

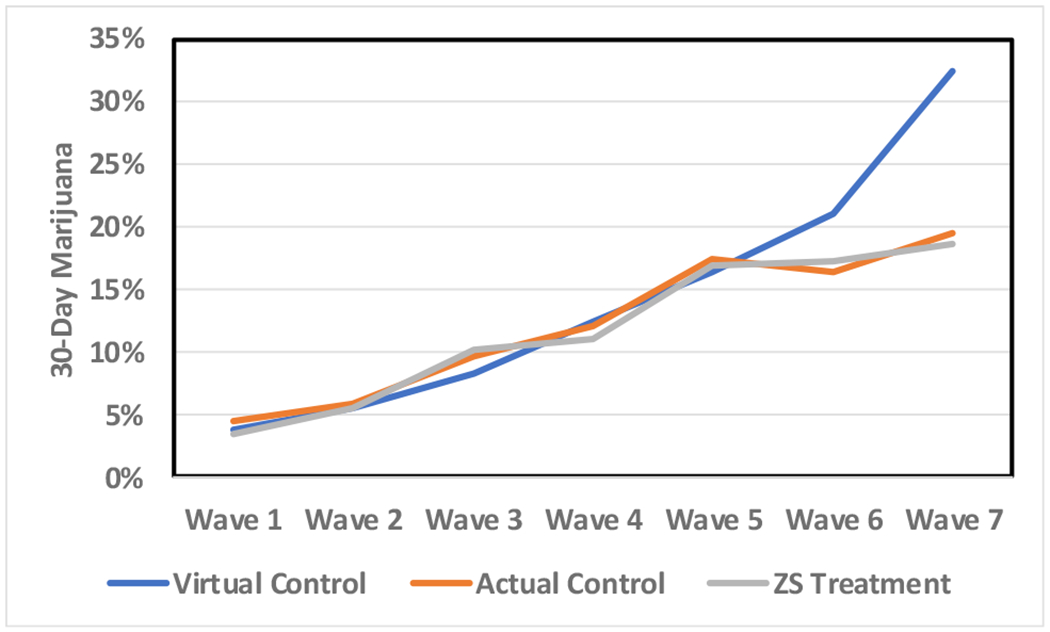
Virtual control group estimates of marijuana prevalence compared to treatment and actual control group observed values in a study that included seven waves of data collection.

Figure 6.

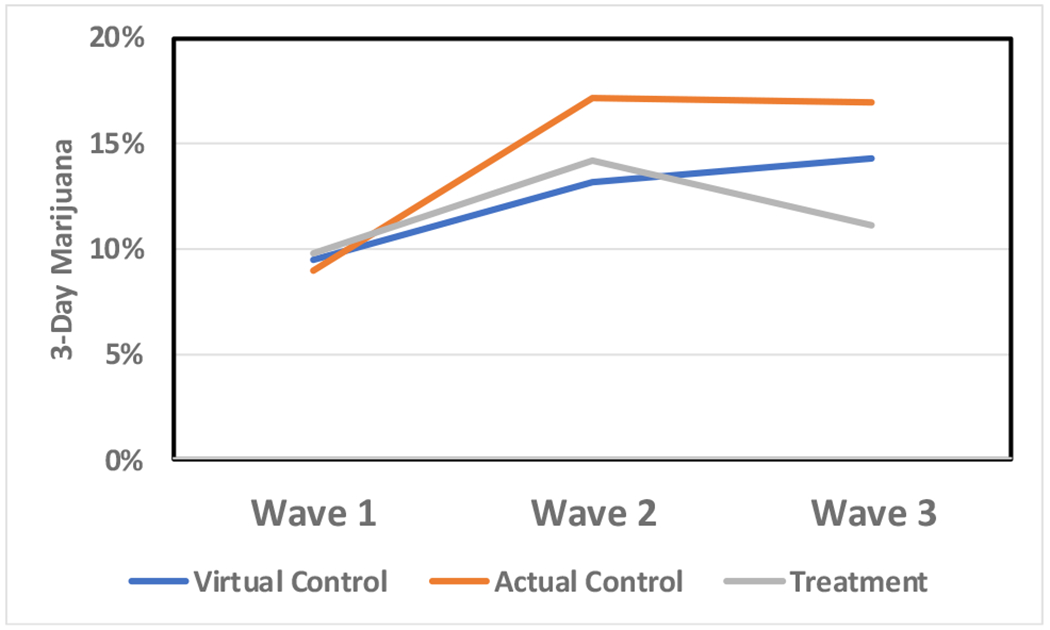
Virtual control group estimates of marijuana prevalence compared to treatment and actual control group observed values in a study that included three waves of data collection.

We assessed how closely virtual control estimates of prevalence mimicked live control reports of prevalence. Using means and standard deviations, effect sizes for the difference between virtual and live controls were calculated for each wave of data (Cohen, 1977). Unlike intervention research where large effect sizes are hoped for, the goal of the virtual control algorithm was to minimize effect sizes when virtual and live controls were compared. If the algorithm were operating adequately, all effect sizes would be near zero. Larger effect sizes indicate that the algorithm provided a poor match between virtual and live controls. For our purposes, Cohen’s d values of less than the absolute value of 0.15 were thought of as adequately providing a virtual control value that mimicked the observed live control value.

Pretest Treatment Group Similarity.

Pretest alcohol use was 13.0% in the RCT-1 treatment group compared to 14.0% in the virtual control group. Pretest cigarette smoking was 5.8% and 6.3% for RCT-1 treatment and virtual controls, respectively. Marijuana use at pretest was 3.4% for RCT-1 treatment and 3.8% for virtual controls. RCT-1 virtual controls were similar to treatment cases with d = 0.04 for alcohol, d = 0.03 for cigarettes and d = 0.02 for marijuana.

Results for RCT-2 pretest alcohol prevalence for treatment and virtual controls was 29.0% and 29.5%, respectively. Pretest prevalence for treatment and virtual controls for cigarettes was 19.5% and 19.2%, respectively, and for marijuana was 9.8% and 9.5%, respectively. In RCT-2, the alcohol effect size was zero, the cigarette and marijuana effect sizes were each −0.02. Thus, at pretest, analyses showed that virtual control group prevalence closely matched treatment group prevalence at pretest, satisfying the first requirement.

Posttest Control Group Similarity.

Prevalence estimates increased for virtual controls at each successive wave for both RCT-1 and RCT-2. To assess success at achieving the second goal, mimicking live control group onset, virtual and live control group prevalence rates were compared (see Table 7). About half of the RCT-1 comparisons met the d = 0.15 criterion. For alcohol prevalence, only one effect size (wave 5) failed to meet this criterion. In contrast, after wave 4, the RCT-1 virtual control prevalence of cigarette smoking increases much more rapidly than was observed in the live controls. five of six analyses failed to meet the d = 0.15 criterion. For marijuana, two effect sizes (waves 6 and 7) failed to meet the criterion. In both cases, treatment and control groups suddenly level off.

Table 7.

Effect Size Differences (Cohen’s d) Between Virtual and Live Control Groups at Posttest Waves of Data for Two RCTs

Study	Wave	Alcohol	Cigarettes	Marijuana
RCT-1	2	0.14	0.05	−0.02
	3	−0.04	0.15	−0.06
	4	−0.02	0.21	0.02
	5	−0.19	0.34	−0.04
	6	−0.08	0.47	0.16
	7	0.07	0.80	0.41
RCT-2	2	−0.16	0.05	−0.14
	3	−0.12	0.08	−0.10

In RCT-2, the virtual controls’ increase in alcohol prevalence most nearly matches the treatment, not the control group. However, only one comparison (alcohol at wave 2) failed to meet the d = 0.15 criterion. The increase in cigarette prevalence is more pronounced in the virtual control group than the live controls. This pattern was reversed for marijuana use, where virtual controls nearly matched the treatment group between waves 1 and 2 and then continued to increase through wave 3. If a more restrictive standard were imposed (e.g., 0.10), fewer than half (4 of 6) of the virtual control group comparisons would be considered to mimic live control group outcomes.

Discussion

This article describes procedures we employed to create an integrated, harmonized and imputed dataset that was then used as the basis for creating virtual control cases. Our goal is to use an algorithm to create suitable virtual control cases when live control cases cannot be acquired. We used data from the integrated dataset to create latent psychosocial scores for gender- and age-specific percentiles ranging from 0.5 to 100.0 and used logistic regression coefficients from treatment groups to estimate probability of use for alcohol, cigarettes and marijuana. The algorithm matched treatment case age, gender and observed psychosocial scores at pretest to create a virtual control case that was then allowed to figuratively “mature” based on age-related changes in the percentile table. We examined resulting virtual controls, live controls and treated cases for two drug prevention randomized control trials. We set two criteria for judging the adequacy of virtual control case generation. The first was that prevalence rates for aggregated virtual control cases’ alcohol, cigarette and marijuana use should match treatment group pretest prevalence. The second was that patterns of onset should mimic prevalence rates for live control cases as their prevalence of use changes over time.

Harmonization

We tackled harmonization by developing a systematic means of coding diverse data obtained from several independent research programs; reflecting both epidemiologic and intervention studies. While a more formal statistical treatment of data integration is dealt with more extensively in other papers (Curran et al., this issue), the conceptual and data management concerns addressed in this paper represent important and pervasive concerns.

Demographics.

Overall, we found tremendous consistency between data sources in the coding of gender and race/ethnicity from wave-to-wave of data collection. Any discrepancies were easily resolved.

We found age to be the most problematic demographic variable to address because the studies we included involved multiple data collection strategies to assess age. Some studies calculated age as a floating-point number at the time of the survey by subtracting birth date from survey date, which created the most precise chronological measure. On the other extreme were studies that asked respondents to indicate their age in years as an integer. For these studies, the challenge became dealing with multiple measures (e.g., pretest, posttest or follow-up) where participants gave the same response given there was only a small lapse in time between assessments. Integrating across datasets requires adopting a strategy that produces consistent age estimates across trials based on a replicable data coding scheme. In our case, when we encountered repeated measures of age for the same individual that were identical, we advanced the second measure of age by half a year.

Combing through the data also highlighted rampant coding issues for age that should have been resolved as part of normal data quality control. Logical inconsistencies, for example, when a youth was older at pretest than posttest, were of particular note. Such discrepancies were attributed to coding errors and were corrected.

Psychosocial Constructs.

We benefited in the coding of psychosocial measures from prior work examining the need for theoretical integration in drug prevention (Hansen et al., 2007). The framework for sorting and classifying these measures elaborated nine constructs tapping motivational dispositions toward drug use, five personal competence constructs, three social competence constructs and three environmental constructs. No two studies shared the same set of psychosocial constructs nor were constructs that shared the same theoretical basis measured precisely the same way. Studies that included similar measures often did so without necessarily referencing the same theoretical axioms. Nonetheless, there seemed to be considerable conceptual overlap applying the data coding scheme we devised. Importantly, our conceptual coding scheme reflected similar strategies that have been used to organize and classify psychosocial variables in the alcohol and drug prevention literature (Derzon, 2000; Hansen et al., 2007; Hawkins et al., 1992).

Generally, the high reliability estimates we obtained across the numerous measures reinforces that each of the original investigators cast a keen eye toward writing well-conceived items or using psychometrically sound items from previous questionnaires. Normative beliefs about substance use was the most commonly assessed psychosocial construct followed by measures of self-esteem, intentions, decision making skill, beliefs about the negative consequences and positive consequences of substance use, and youths’ assessments of parenting. Knowledge, media literacy skills, social skills, sensation seeking and risk-taking personalities were measured in only one study, limiting their value for the predictive analytic component.

One challenge to harmonizing psychosocial measures across studies was the variation in response categories from study-to-study. We resolved this issue by instituting a standardization procedure that recast the response format using a 0-to-10 metric. We then scaled this metric based on drug prevention theory so that higher levels reflected more favorable program outcomes (i.e., more self-esteem and less perceived benefit to drug use). All response categories that fell in between were equidistant in the values assigned. This scheme allowed us to compare standardized scale scores (averaged item scores) across studies.

Alcohol, Cigarette, and Marijuana Use.

We limited our analyses to dichotomous (use/nonuse) measures of past 30-day alcohol, cigarette and marijuana use. In studies that lacked dichotomous use variables, we transformed quantity/frequency measures of consumption into these measures. For alcohol, two additional measures that we expected to be more commonly assessed, binge drinking or self-reported drunkenness, were much less frequently present among the different studies and were excluded from our analyses.

Imputation

We applied existing tried and true imputation methods to handle missing values in the harmonized dataset. The harmonization steps ensured that there would be no missing data for gender and age. On the other hand, because of the variety of measures included in each of the assembled datasets, there was extensive missing for many psychosocial variables. We paid special attention to the benefits of “global” versus “local” imputation within the context of integrative data analysis. An important advantage of global imputation is that complete datasets are relevant for modeling the underlying statistical relations between psychosocial and behavioral variables. Local imputation may still be advantageous when data sets are highly heterogeneous (Curran & Hussong, 2009).

Global imputation appeared to be successful for many of the psychosocial variables. When the preponderance of datasets contained a specific variable (e.g., normative beliefs, self-esteem, beliefs about positive and negative consequences, decision making skills, self-esteem, and intentionality), global imputation appeared to work well. However, results were not always usable. For example, for Access/Availability to Environment, which was only assessed in two of eight studies, global imputation did not create stable values.

Researchers should weigh the value of various imputation schemes in terms of similarity between datasets, the magnitude of missing data, and other measurement as well as substantive factors. In the future, it may also be possible to adopt a hybrid approach of conducting local imputation for some data sets prior to integration and global imputation after integration for those for which there are design-generated missing values (i.e., planned “missingness” strategies).

Performance of Virtual Controls.

The first criterion for evaluating the functional utility of the virtual control algorithm – pretest equivalence – was successfully met. In both RTC-1 and RTC-2, pretest prevalence of alcohol, cigarettes and marijuana, for virtual control groups were similar to observed treatment group prevalence.

The strategy for projecting the probability of using substances at posttests was only partially successful. For the algorithm to be successful, there is clearly a need for refinement and further study. For RCT-1 and RCT-2, alcohol, cigarette and marijuana use prevalence estimates increased wave-over-wave as would generally be expected. However, as results in each of the figures and effect size calculations attests, virtual controls failed to mimic the precise changes in prevalence observed in live control groups.

In RCT-1, prevalence of alcohol use between virtual and live controls was most consistently similar as participants aged. After wave 3 for cigarettes and after wave 5 for marijuana, RCT-1 virtual controls diverged and portrayed use as being much higher in the virtual versus live controls. RCT-2 showed slightly different results. The virtual control mimicked the treatment group, not the control group when alcohol was analyzed. On the other hand, virtual controls somewhat mimicked live controls for cigarette and marijuana use. The second criterion for evaluating the heuristic value of the virtual control algorithm was thus less clearly successful and presents challenges that need to be overcome before a methodology is available for use. Prevalence of substance use increased with age, as was expected. However, there were several instances where the predicted prevalence deviated from live control group outcomes.

There are several possible reasons for the obtained discrepancies and lack of precision matching live and virtual control groups. Some of these may be faults with the algorithm or data that formed the basis of the algorithm. It is also possible that some discrepancies may be attributable to the specific control groups that had been included in each study. For example, it is possible that there was some form of experimental error attributable to control groups. Large numbers of cases and randomization to condition does not guarantee equivalence. It may have been, particularly in RCT-2, that controls were different in undefined ways than those who received treatment. Even with equivalence at pretest, differential attrition may still have plagued control groups, causing their equivalence to diminish over time (Hansen, Collins, Malotte, et al., 1985). In the case for RCT-1, 48% of treatment and 42% of control cases were retained. RCT-2 had a similar greater retention rate with 83% of treatment and 69% of control cases being included in at least one posttest survey.

Challenges and Limitations

As with any new procedure, creating virtual controls using the algorithm proposed will require further refinement. We note Francis Bacon’s dictum: Truth emerges more readily from error than from confusion. We hope that our results will encourage discussion and improvement of our methods to make creating virtual controls a viable methodology.

The algorithm as executed only partially fulfilled our goals. There are specific issues we are aware of that will require further attention. Modeling substance use onset may require many more cases than were available to this project. Data mining and “big data” modeling often relies on numbers of cases that exceed the number of cases we included by orders of magnitude. However, even within the confines of this study, there were relatively fewer older adolescent cases contributing to the integrated dataset that were used to derive latent psychosocial scores. Being able to include more data can be expected to change the performance of the algorithm primarily because there will be changes in latent psychosocial scores. The selection of variables that were used as predictors of substance use (intentionality, normative beliefs, and values) may also be a source of challenge. These variables were selected because they were the strongest predictors and were also included in each of the RCTs that we used to test the algorithm. Future research may wish to explore other variables and combinations of variables; essentially broadening not only the data sources but also the underlying theory driving data collection.

Some of the inability to mirror control group prevalence longitudinally may be due to random fluctuations in consumption rates that are normal in field research. Unlike live controls, such issues as what time of year they were tested did not influence virtual controls (i.e., before or after summer break), changing historical trends, and situational issues such as the setting in which surveys are administered. These factors may individually or collectively influence self-reported behavior and subtly alter responses to psychosocial questions.

Because some of the contributing datasets did not include race/ethnicity, we were not able to model the moderating influence of these characteristics on latent psychosocial variables. Adding race/ethnicity may increase the precision required for carving out virtual controls. Other issues, such as location and setting of data collection may also influence how data can be assembled and interpreted.

We had access to two RCTs for testing the algorithm. One was graciously donated; one came from our research team. In the future, we plan to refine the algorithm using additional data from a variety of research projects and test the algorithm using additional RCTs. However, it became apparent to us as we sought access to data that many researchers who have conducted RCTs, especially if they have begun the process of commercialization, are hesitant to share raw data. We are hopeful this will not prove to be a barrier to further development and testing.

There may be a continuing issue related to not being able to procure data from contemporaneous studies. Our earliest research dataset was from the 1980s. Sadly, many longitudinal datasets we sought from the 1970s, 1980s, 1990s and even into the current century have apparently disappeared. Our most recent dataset had its final assessment collected in 2010. Dataset creation will always lag current research practice. It is only after datasets become available from researchers that integration is possible. Researchers seem disinclined to share data until their own analyses have been completed, often years after the final wave of data has been collected. Other researchers are simply unwilling to share. The lack of contemporaneous data is a challenge that all forms of meta-analysis and integrated data analysis will continue to face that may affect the ability to create suitable virtual control groups.