Cherenkov imaging for total skin electron therapy (TSET)

Abstract

Background

Total skin electron therapy (TSET) utilizes high-energy electrons to treat malignancies on the entire body surface. The otherwise invisible radiation beam can be observed via the optical Cherenkov photons emitted from interactions between the high-energy electron beam and tissue.

Methods and materials

With a time-gated intensified camera system, the Cherenkov emission can be used to evaluate the dose uniformity on the surface of the patient in real time. Fifteen patients undergoing TSET in various conditions (whole body and half body) were imaged and analyzed. Each patient was monitored during TSET via in vivo detectors (IVD) in nine locations. For accurate Cherenkov imaging, a comparison between IVD and Cherenkov profiles was conducted using a polyvinyl chloride board to establish the perspective corrections.

Results and discussion

With proper corrections developed in this study including the perspective and inverse square corrections, the Cherenkov imaging provided two-dimensional maps proportional to dose and projected on patient skin. The results of ratio between chest and umbilicus points were in good agreement with in vivo point dose measurements, with a standard deviation of 2.4% compared to OSLD measurements.

Conclusions

Cherenkov imaging is a viable tool for validating patient-specific dose distributions during TSET.

1. INTRODUCTION

Total skin electron beam therapy (TSET) has been widely used in the treatment of cutaneous lymphoma and leukemia.^1–6 In TSET treatment, the high-energy electron beam (typically 6 MeV) is delivered toward the patient, and the patients stands at a source-to-surface-distance (SSD) of more than 300 cm.⁷ In 3–9 weeks of treatment, a total of 12 to 36 Gy dose is delivered.^8,9 In most centers, the Stanford standing technique with six beam angles is used to ensure full coverage of the patient’s skin.¹⁰ At each beam angle, the treatment beam contains two sequential fields, covering the patient’s upper and lower body.¹¹

Total skin electron beam therapy treatment has a goal of uniform dose distribution over the patient’s skin area within the tolerance of ±10%, except for feet, peritoneum, vertex, and axilla, where lower dose is expected because the body contour causes electron beams to be incident obliquely.⁷ Even though the positioning tools, such as patient stands, are used to fix the patient position, the dose delivery is still affected by other factors in the treatment, such as the body shape and unexpected movement of patient in the long period of treatment. Classical dosimetry tools, such as ionization chamber, diodes, thermoluminescent detector (TLD), and film, have been used to measure the cumulative dose deposition in selected parts of the patient’s body throughout each fraction.^12–15 Newer optical dosimetry tools, such as scintillators,¹⁶ can measure the dose delivery under electron beams using a Cherenkov imaging camera and appropriate calibration procedures. Even though diodes and optical stimulated luminescent dosimeters (OSLDs) provide accurate point dose measurement, the dose distribution of the entire skin area may not be reconstructed accurately from limited point dose measurements. Classical two-dimensional (2D) dose measurement has been implemented with arrays of dosimeters, but most of the applications measure the dose distribution in flat surfaces and the resolution is limited by the size of the individual dosimeter.^17,18 In the case of TSET treatment, the curvature of the body is not flat. Thus, physicists need to attach the dosimeters to the representative locations, such as the center of the chest and umbilicus, or at locations in the boundaries and corners, such as the boundaries of the front and back skin, which are covered in different standing positions of the patient.¹² This manual placement process is time-consuming and may introduce discomfort for patients as well.

Cherenkov imaging is an emerging technology to analyze the dose distribution over the patient’s body or phantom in radiation therapy.^19,20 Cherenkov light signal is generated from the transmission of high-energy photons and electrons through dielectric materials, such as water, plastic phantoms, and human tissues when the speed of charged particle exceeds the speed of light in the medium.^21,22 This requires in water the minimum kinetic energy of electrons to exceed 0.256 MeV (or half of rest mass of electrons).²³ The wavelength of resulting Cherenkov emission covers the visible light range (200–1000 nm) but due to the tissue absorption and scattering, only light in the near-infrared (NIR) region are emitted out from body.²⁴ Experiments have shown that, for beams with the same energy, there is a linear relationship between the Cherenkov signal intensity and dose deposited on the surface of the phantom with uniform optical properties.¹⁹ Based on the linearity between Cherenkov signal and radiation dose, QA tools have even been developed to acquire three-dimensional (3D) dose distribution in a water tank derived from Cherenkov image intensity, which is acquired by a time-gated intensified camera.^20,25,26 Compared with classical dosimetry tools, Cherenkov imaging shows greater potential for acquiring high-resolution 2D relative dose distribution on the surface and 3D relative dose distribution of transparent materials with uniform optical property. However, further studies are necessary to ensure the accuracy of the conversion between Cherenkov image intensity to dose in patients due to complications arising from tissue optical property variations, patient anatomic correction, radiation beam incident angle dependence, optical diffusion, and others.

In the clinical environment, Cherenkov imaging has also been used to evaluate surface dose distribution and photon beam shape in breast treatment.^27,28 The imaged beam shape can be compared with the plan predictions created by the treatment planning system, showing how Cherenkov imaging can be used as a verification tool for treatment planning.^28,29 Studies have been done to verify the uniformity of dose distribution of the TSET beam on the vertical plane where the patient stands.^30–33 A recent study showed the feasibility to determine dose using the Cherenkov camera to perform scintillator dosimetry for TSE.³⁴ In this study, we present the first analysis of a comparison between Cherenkov intensity and in vivo dose measurements for a large cohort of adult subjects undergoing TSE treatment to validate Cherenkov imaging dosimetry.

2. MATERIALS AND METHODS

2.A. Patient diagnosis and demography

A clinical trial entitled “Cherenkov imaging in radiation therapy—application for total skin electron (TSE) and other sites” was reviewed and approved by the institutional review board (IRB) of the University of Pennsylvania since May 2017 and was reviewed annually since then. Informed consent was obtained for all subjects. There were 18 adult subjects enrolled in the protocol. Among the subjects, most (94%, 17/18) received TSE for treatment for mycosis fungoides, a chronic cutaneous T-cell lymphoma, one received TSE for breast cancer. 39% (7/18) of subjects had partial body treatments (including shields of head, upper body, lower body, or both upper and lower body) while the rest (61%) had whole body treatments. They are shown in Table I for each patient. Ages ranged from 33 to 83 yr. 11% (2/18) were female while the rest (89%) were male. 22% (4/18) of subjects were African American, no patients were Asian (0%), while the rest (78%, 14/18) were Caucasian.

Table I.

Dosimetrical comparison between diode and optical stimulated luminescent dosimeter (OSLD) results at different locations (x,y) on polyvinyl chloride (PVC) board for three different patient positions: anterior–posterior (AP), right–anterior oblique (RAO), left–anterior oblique (LAO), and two different radiation incident configurations: 90° and dual. The mean and relative standard deviation (stdev, %) are calculated using ∑σ/n and $\sqrt{\sum \frac{{\sigma }^2}{n-1}}$. The overall standard deviation of all data between diode and OSLD is 3.6%.

x (cm)	y (cm)	Angles	AP			RAO			LAO
			Diode norm	OSLD norm	% diff	Diode norm	OSLD norm	% diff	Diode norm	OSLD norm	% diff
0	−100		0.593	0.579	2.5%	0.573	0.549	4.5%	0.589	0.569	3.5%
0	−80		0.722	0.657	10.0%	0.710	0.723	−1.8%	0.716	0.711	0.8%
0	−60			0.845			0.786			0.823
0	−40		0.924	0.921	0.3%	0.913	0.858	6.3%	0.922	0.891	3.4%
0	−20			0.965			0.933			0.969
0	0		1.000	1.000	0.0%	1.000	1.000	0.0%	1.000	1.000	0.0%
0	20	90°		1.009			0.961			0.985
0	40		0.928	0.967	−4.0%	0.916	0.906	1.1%	0.922	0.947	−2.7%
0	60			0.883			0.780			0.873
0	70		0.806	0.846	−4.7%	0.787	0.824	−4.5%	0.794	0.814	−2.4%
−40	0		0.871	0.855	1.8%	1.021	1.041	−1.9%	0.823	0.785	4.8%
−20	0		0.970	0.988	−1.9%	1.042	1.041	0.1%	0.933	0.929	0.4%
20	0		0.985	1.005	−2.0%	0.948	0.916	3.5%	1.021	1.030	−0.8%
40	0		0.878	0.904	−2.9%	0.825	0.814	1.3%	0.982	1.068	−8.1%
0	−100		1.011	1.021	−1.0%	0.990	1.037	−4.5%	1.013	1.029	−1.6%
0	−80		1.043	1.057	−1.3%	1.027	1.017	1.0%	1.034	1.080	−4.3%
0	−60			1.026			0.987			1.067
0	−40		1.000	1.000	0.0%	1.007	1.042	−3.4%	1.017	1.076	−5.5%
0	−20			1.025			1.008			1.009
0	0		1.000	1.000	0.0%	1.000	1.000	0.0%	1.000	1.000	0.0%
0	20	Dual		1.064			0.983			1.081
0	40		1.004	1.017	−1.4%	1.003	1.028	−2.4%	0.997	1.065	−6.4%
0	60			1.043			1.016			1.052
0	70		1.014	1.026	−1.2%	1.007	1.005	0.1%	1.010	1.134	−10.9%
−40	0		0.850	0.879	−3.3%	1.010	1.042	−3.1%	0.812	0.785	3.4%
−20	0		0.961	0.975	−1.5%	1.040	1.077	−3.5%	0.926	0.888	4.2%
20	0		0.975	0.952	2.4%	0.943	0.944	−0.1%	1.020	0.978	4.3%
40	0		0.875	0.845	3.5%	0.830	0.832	−0.2%	0.990	1.005	−1.5%
Mean ± SD (%)					−0.24 ± 3.3%			−0.38 ± 2.9%			−0.97 ± 4.5%

2.B. Setup of patient, linac, camera, and dosimeters

During the TSET treatment, the linac gantry rotates to 90° for treatment setup, and the patient stands in the radiation field region, with source-surface-distance (SSD) of 500 cm. Each patient stands in six postures through the whole treatment according to the Stanford technique. A beam spoiler made of a transparent 3 mm thick Lucite sheet is used for all TSET patients. The treatment is conducted in a 2-day cycle with three dual fields per day. At our institution, a Truebeam linac (Varian, Palo Alto, CA) with 6 MeV high dose rate electron mode (HDTSE) is commissioned to treat TSE patients to achieve shorter treatment time compared to conventional electron mode. For each patient posture, the patient is irradiated with a set of dual field composed of an upper and a lower field with gantry angles at 74° and 106°. The gantry angles are chosen to be 16° above and below the horizontal, which are optimized to deliver uniform dose given the vault-specific geometry. In each of the upper and lower fields, 2226 Monitor Units (MU) are delivered in the specific TSE high dose rate mode at 2500 MU/min.

A time-gated intensified camera (C-Dose Camera System, DoseOptics, Lebanon, NH) was used to capture the Cherenkov signal emitted from the subject’s skin surface during the TSET treatment. The camera was positioned next to the linac head at a height of 132 cm, with a 24 mm F/1.8 lens pointing to the center of the patient, to ensure the field of view covered the patient whole body.^26,30 In the first treatment cycle, both in vivo diodes (IVDs) and optical stimulated luminescent dosimeters were taped to the subject’s chest and umbilicus to monitor the in vivo and accumulative dose delivered to these two locations. These independently measured dose values were used to verify the dose calculation from Cherenkov signals.

To ensure the OSLDs provide doses readings with <5% error, Landauer Nanodots™ were calibrated per batch with 6 MV at dmax (1.5 cm depth) at 100 SSD. The experimental setup included 1.5 cm solid water with 10 cm of backscatter, which was a combination of 0.5 cm bolus and 9.5 cm of solid water. Four OSLDs were irradiated at low dose (3, 5, 8, and 10 cGy) and high dose (50, 100, 150, 200, 300cGy). A bilinear calibration curve was generated based on the average counts during readout with the vendor provided sensitivity corrections applied. Readings from the four OSLDs per dose level showed standard deviations below <2.5%.

Ten diode detectors (SunNuclear, FL, QED scatter diode) were also used for in vivo dosimetry. The diodes were calibrated at SSD = 100 cm at depth 1.5 cm in solid water for 6 MeV electron beams using the standard calibration procedure.³⁵ The diode calibrations were also cross-checked with an ADCL calibrated Farmer ionization chamber (Exradin, A12) using AAPM TG21³⁶ and AAPM TG51³⁷ protocols as well as IROC (IROC, Houston) OSLDs at SSD = 500 cm to be better than 1% for the TSE electron beams with the beam spoiler. It has been proven that energy dependence of Silicon diodes is negligible as long as adequate buildup corresponding to the electron energy is used.³⁸ Our diodes are calibrated for 6 MeV electrons at 100 cm and then used at 500 cm, where the electron energy is 3.5 MeV. Routine calibrations were performed annually, and the variation of diodes was less than 5%. The same diode detectors were also used to commission the TSE flatness for the dual field annually at SSD = 500 cm.

2.C. Measurement of Cherenkov light

The Cherenkov light emission was measured with the C-Dose camera (DoseOptics, Lebanon, NH), which utilized the klystron’s pulse signals for electron bunching in the linac as an input for time-gated acquisition of the optical signal in an image intensifier. During the treatment, the room light was dimmed slightly to a level at which the therapist could still monitor the patient from the closed-circuit TV (CCTV) camera installed in the treatment room. For each radiation field, a video was recorded by the C-Dose camera and the background images were automatically acquired concurrently during the beam delivery for background subtraction to remove room light interference.²⁹ In the end, a cumulative image was summed over each video for each posture with background subtraction to derive the total Cherenkov emission signal distribution. With the intensity to dose calibration obtained from the phantom, the Cherenkov intensity distributions were converted to dose distributions on the subject’s body surface for different postures.

2.D. Cherenkov intensity calibration

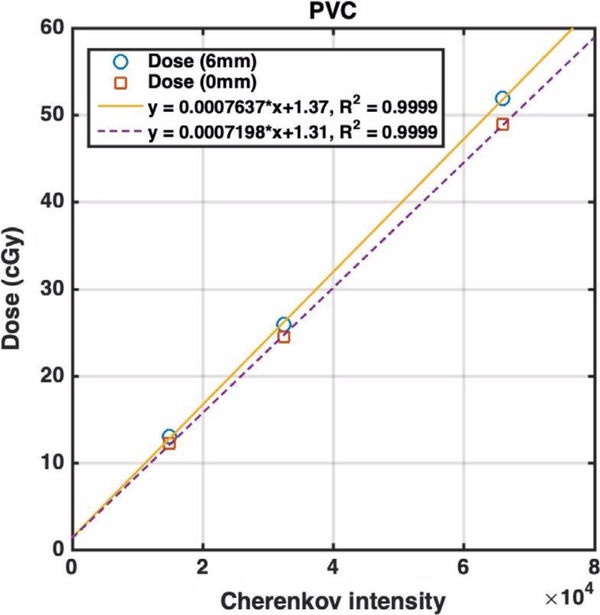
A white flat polyvinyl chloride (PVC) board was used to obtain the calibration factor for converting the Cherenkov light intensity to absorbed dose, as shown in Fig. 1(a). The phantom was placed at the location equivalent to the center of the subject’s body during the treatment and the C-Dose camera was set to the same position as in the subject treatment. The linac delivered electron beams at gantry angle of 90°, pointing toward the phantom. The same phantom was irradiated with same electron field to different doses and the corresponding Cherenkov signals were recorded by the C-Dose camera separately. The corresponding conversion of Cherenkov intensity to dose was derived and used as a generic conversion for all patients.

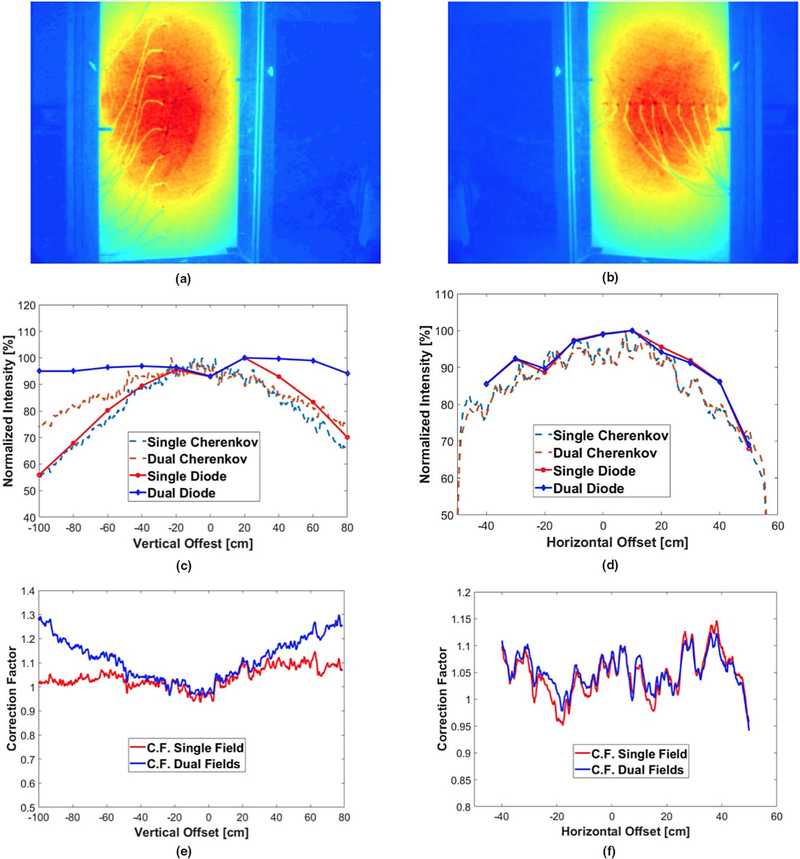
FIG. 1.

Setup for Cherenkov imaging with C-Dose camera: (a) Diodes measurements for dose-to-calibration in vertical direction; (b) Diode measurements for dose-to-calibration in horizontal direction. (c) in vivo acquisition for patients in total skin electron stand box. [Color figure can be viewed at wileyonlinelibrary.com]

In this study, we propose a generic conversion to relate the dose and Cherenkov intensity all tissues:

$$\begin{gathered} Dose(cGy)=a\left(E,\mathit{r},\widehat{s},R_d,SDD\right)\cdot Cherenkov \\ =a^{\prime }(E)\cdot b^{\prime }\left(R_d\right)\cdot c^{\prime }(\mathit{r},\widehat{s}) \\ \cdot {\left(\frac{CD{D}_0}{CDD}\right)}^2\cdot Cherenkov \end{gathered}$$ (1)

where a is the Cherenkov-to-dose conversion factor and is a function of the electron energy (E), pixel position and radiation incident direction, $(\mathbf{r},\widehat{s})$, material optical properties (represented here using the diffuse reflectance R_d), and Camera-to-detector distance (CDD), that is, the distance between the patient surface to the Cherenkov camera. a can be separated into multiplication factors a′, b′, c′, and the inverse square factor (CCD₀/CDD)² (see Section 4.D): a(E) is the Cherenkov-to-dose conversion factor for a radiation energy E and a reference tissue optical properties on the central axis, b′ is the tissue optical property correction factor relative to a reference tissue optical properties (see Section 4.B), c′ is the perspective correction factor that includes both camera sensitivity variations as well as radiation incident angle dependence (see Section 4.C). All correction factors except for a′(E), which has the unit of cGy/Cherenkov intensity, are unitless. For our camera, one detected photon within wavelength range 600–800 nm, typical Cherenkov emission spectrum range from tissue,^39,40 can approximately convert to 40 counts in Cherenkov images. In this study, optical diffusion was not considered, therefore not addressed in Eq. (1).

2.E. Perspective (geometrical) correction of Cherenkov reading

Each pixel of image sensors may have different sensitivity to the same flux due to the vignetting effect, lens correction, and individual pixel response.⁴¹ Thus, a geometrical calibration was acquired to correct this in the Cherenkov reading, to ensure that the signal was consistent with the dose reading. In this study, a flat white PVC board was aligned at the same location of the patient mid-plane with an SSD = 500 cm for the geometrical calibration (see Fig. 1).

The calibration was measured and applied in two directions: horizontal and vertical. In the calibration of each direction (2), nine IVDs were taped with an interval of 20 cm/10 cm in vertical/horizontal direction, respectively. The electron beams were delivered in two different groups: the enface field with gantry angle of 90° and the dual-field set used in TSET treatment. The Cherenkov signal on the PVC board was recorded by the C-Dose camera and the IVD readings were taken as the delivered dose at different locations. The correction factors were then derived from the readings of IVD doses and Cherenkov intensity in each direction separately. The discrepancy between the diode measurements and Cherenkov signal intensity is more pronounced for pixels close to field edges than those near-field center. This perspective correction factor was calculated and applied to the Cherenkov signal so that the intensity could be matched to the dose readings of diodes. Figures 3(e) and 3(f) are the correction factors calculated from the ratio of the Cherenkov signal and diode measurements are shown in vertical and horizontal directions, respectively. The a 3-by-3 median filter (medfilt2.m function in the “Image Processing Toolbox” of MATLAB ver. R2017b) has been applied to all the Cherenkov profiles before correction factor calculations.

FIG. 3.

Correction of Cherenkov to dose in vertical and horizontal direction: Accumulated Cherenkov image with diodes in (a) vertical and (b) horizontal directions; comparison of Cherenkov intensity and diode dose measurement in (c) vertical and (d) horizontal directions; plot of perspective geometrical correction factors used to convert Cherenkov to dose in (e) vertical and (f) horizontal directions, with reference point at the center of the board. All profiles have been smoothed with a median filter. [Color figure can be viewed at wileyonlinelibrary.com]

3. RESULTS

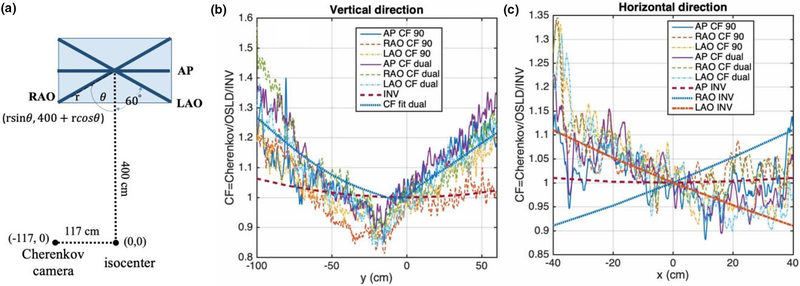
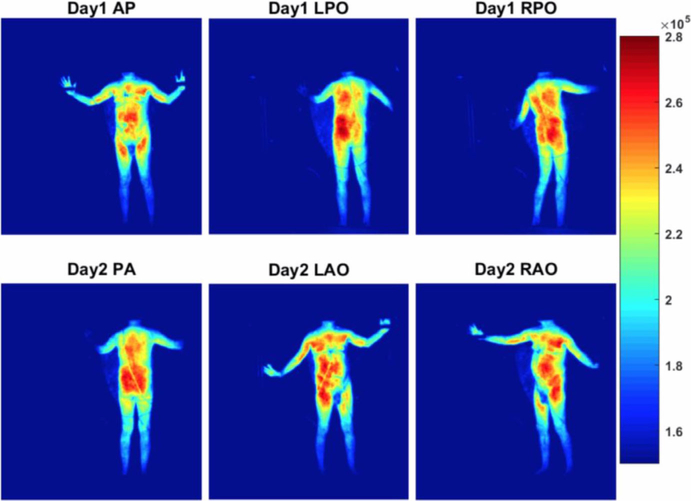
In Fig. 2, the dependence of Cherenkov signal intensity vs delivered dose on the central axis for a normal incident electron beam at the TSET treatment condition is shown for the calibration phantoms. In Fig. 3, a comparison between diode-measured profile (dashed line) and the Cherenkov intensity profile (solid line) on a white PVC board is shown in the vertical (upper panel) and horizontal (lower panel) directions for a dual TSET field. The resulting perspective correction factors are plotted for the vertical and horizontal directions in Figs. 3(e) and 3(f). In Fig. 3, a comparison is also performed for a single enface field, which was not used for patient treatments due to its inferior dose uniformity. In the Cherenkov images, the diode detectors are visible as well as the connection cables. We identified the chest and umbilicus detectors’ locations by following the corresponding cables to the pixels nearest to the diodes. Then, the pixel values averaged over 9 pixels were taken as the Cherenkov signals. Figure 4 compares the perspective correction factors for different patient (phantom) positions [anterior–posterior (AP), right anterior oblique (RAO), and left anterior oblique (LAO)] in the horizontal and vertical directions by comparing the Cherenkov intensity and dose measured by OSLD and diodes. A comparison between the (relative) diode/OSLD results is shown in Table I. Figures 5 and 6 compare the Cherenkov intensity distribution for the dual fields before and after perspective corrections, respectively, for patient 6. They are generally in agreement except for one case, patient 5, when the chest point fell into the large gradient region of the radiation field (as shown by the corrected Cherenkov profile). Table II summarizes the dose comparison for all 15 patients between diode and Cherenkov dose reading. We define a new variable, R

$$R=\frac{r_{OSLD}-r_{Cherenkov,corr}}{r_{Cherenkov,corr}},$$ (2)

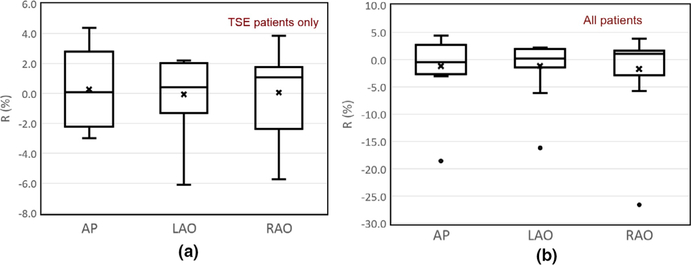
where r_OSLD and r_{Cherenkov,corr} are the chest-to-umbilicus dose ratio for OSLD measurement and perspective-corrected Cherenkov imaging, respectively. The R represents the difference between in vivo OSLD measurements and Cherenkov imaging. Figure 7 shows the box-and-whisker plot comparison of the chest-to-umbilicus dose ratio between in vivo OSLD measurements and Cherenkov imaging, R, for (a) TSE patient only and (b) all patients.

FIG. 2.

Delivered dose (in unit of cGy) vs Cherenkov intensity for the calibration polyvinyl chloride (PVC) phantom in the total skin electron (TSE) stand with spoiler at SSD = 500 cm on the central axis. The gantry angle is 90° and 6 MeV electron for TSE is used. The solid line is for dose measured at depth of maximum dose (6 mm) and the dashed line is for the dose measured at surface. The slope of the linear dependence, corresponding to a in Eq. (2), is a function of electron energy, incident angle, pixel position, material optical properties, and inverse square law. The offset reflects the background signal from the Cherenkov intensity and is instrument specific. [Color figure can be viewed at wileyonlinelibrary.com]

FIG. 4.

Comparison of perspective correction factor, c’, of Cherenkov-to-dose in vertical and horizontal directions for right anterior oblique (RAO), left anterior oblique (LAO), and anterior–posterior (AP): (a) Schematics of the experimental setup that shows the positions of RAO, LAO, and AP board in the TSE stand and location of the Cherenkov camera, the isocenter, and their corresponding coordinates from the top view. (b) CF in vertical direction. (c) CF in horizontal directions. The dose was determined by optical stimulated luminescent dosimeter and verified by diode measurements in all three polyvinyl chloride (PVC) board orientations (Table I). “CF fit dual” in Fig. 4b is obtained by fitting the perspective correction factor in Fig. 3e for the dual fields. The inverse square factor, ${\text{CDD}}_0^2/{\text{CDD}}^2$, for AP, RAO, LAO in the vertical positions are the same (INV) in Fig. 4a and in the horizontal positions (AP INV, RAO INV, and LAO INV) in Fig. 4b. All profiles have been smoothed with a median filter. [Color figure can be viewed at wileyonlinelibrary.com]

FIG. 5.

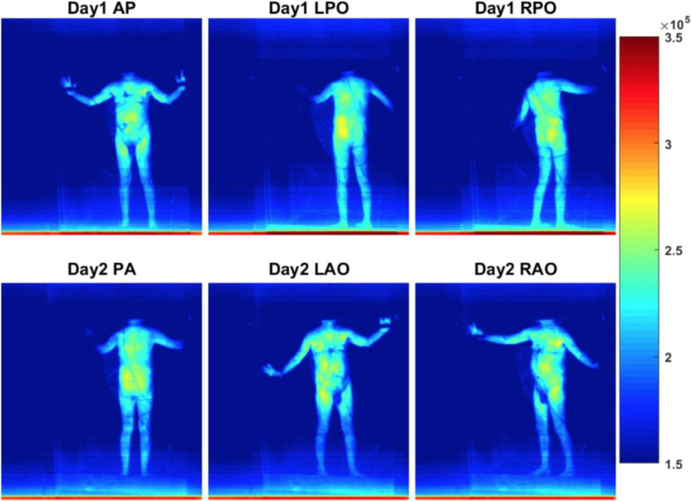
Comparison of accumulative Cherenkov intensity of Patient 6 in treatment day 1 and 2 for dual fields without perspective geometrical correction. The color palette on the right represents the raw Cherenkov intensity per pixel. [Color figure can be viewed at wileyonlinelibrary.com]

FIG. 6.

Comparison of accumulative Cherenkov intensity of Patient 6 in treatment day 1 and 2 for dual fields with perspective geometrical correction. The color palette on the right represents the raw Cherenkov intensity per pixel. [Color figure can be viewed at wileyonlinelibrary.com]

Table II.

Comparison of relative dose of chest to umbilicus calculated from measurements of Cherenkov (after prospective correction), IVD, and optical stimulated luminescent dosimeter (OSLD). The IVD values labeled with “*” are corrected with the OSLD measurements while those in parentheses are excluded from the study due to compromised diode readings. The mean and overall relative standard deviation (stdev, %) is calculated using ∑σ/n and $\sqrt{\sum \frac{{\sigma }^2}{n-1}}$. For OSLD, patient 5 data were excluded; for diodes, data in () were excluded. Data for patients 7 and 11 were affected by room light and thus excluded from data analysis. Cherenkov data for AP of patient 14 and 15 were not taken. Treatment types: W—whole body; P—partial body, including shielding of the head, upper, and/or lower bodies.

Patient label	Type	Postures	Cherenkov w prospective corr.	OSLD	Error, OSLD to Cherenkov (%)	Diode	Error, diode to Cherenkov (%)
2	P	AP	0.92	0.90	−2.2	0.85	−7.5
		LAO	0.90	0.85	−6.1	0.94	4.5
		RAO	0.90	0.85	−5.7	1.05	16.4
3	W	AP	0.97	1.00	2.8	1.02*	4.4*
		LAO	1.00	0.99	−1.6	1.03*	2.6*
		RAO	0.96	0.99	3.9	1.01	5.9
4	W	AP	0.94	0.97	3.5	1.10	17.5
		LAO	0.98	1.00	2.1	1.08	10.8
		RAO	0.99	1.00	1.4	1.03	4.9
5	P	AP	0.42	0.34	−18.6	0.38	−9.2
		LAO	0.46	0.38	−16.2	0.44	−2.8
		RAO	0.52	0.38	−26.5	0.45	−13.3
6	P	AP	0.92	0.90	−2.1	0.92	0.0
		LAO	0.97	0.99	2.0	0.89*	−8.8*
		RAO	1.03	0.99	−4.2	0.97	−6.0
8	P	AP	0.95	0.96	0.6	1.01	6.0
		LAO	0.93	0.94	0.9	1.05	12.7
		RAO	0.96	0.94	−2.2	1.06	9.7
9	P	AP	0.92	0.91	−0.4	0.99	7.4
		LAO	0.96	0.94	−1.2	1.24*	30.0*
		RAO	0.93	0.94	1.1	1.01	7.8
10	W	AP	1.00	0.99	−0.8	1.00	0.1
		LAO	0.99	0.98	−1.3	1.13*	15.9*
		RAO	0.97	0.98	0.5	1.05	6.4
12	W	AP	0.96	0.97	0.9	0.97	0.8
		LAO	0.99	0.99	−0.2	−0.71	(−28.0)
		RAO	0.98	0.99	0.5	−0.77	(−21.7)
13	W	AP	0.86	0.88	2.7	1.04	22.0
		LAO	0.97	0.99	2.2	1.00	2.2
		RAO	0.98	0.99	1.1	1.22*	26.6*
14	W	LAO	0.97	0.98	0.6	1.00	3.0
		RAO	0.97	0.98	1.0	1.13*	16.0*
15	P	LAO	0.92	0.93	0.8	0.57	(−37.8)
		RAO	0.90	0.93	2.6	0.61	(−32.3)
16	W	AP	0.99	0.96	−3.0	1.00	5.9
		LAO	1.02	1.01	−1.4	1.10	1.5
		RAO	0.99	1.01	2.1	1.08	6.0
17	W	AP	0.98	1.02	4.4	1.04	5.9
		LAO	1.00	1.00	0.2	1.05	1.5
		RAO	1.03	1.00	−2.9	1.06	6.0
18	W	AP	1.00	1.01	1.0	0.98	−2.1
		LAO	1.01	1.03	2.2	1.07	5.6
		RAO	1.01	1.03	1.6	1.14	13.0
				Mean ± SD (%)	0.2 ± 2.4		7.1 ± 11.5

FIG. 7.

The comparison of the chest-to-umbilicus dose ratio between in vivo optical stimulated luminescent dosimeter measurements and perspective corrected Cherenkov intensity, $R=\frac{r_{OSLD}-r_{Cherenkov,corr}}{r_{Cherenkov,corr}}$, for (a) total skin electron (TSE) patients only and (b) all patients. The mean values are shown as crosses, the median values are the central line, the boxes are the standard deviation, and the bars are the 25% and 75% percentiles. The black dots in Figure 7(b) represent the measurements for the non-TSE patient #5 in this study. [Color figure can be viewed at wileyonlinelibrary.com]

4. DISCUSSIONS

4.A. General relationship between dose and Cherenkov intensity

The total Cherenkov photons visible from outside a patient (and/or a phantom) are emitted from depths typically ranging from 0 to 5 mm from tissue surface depending on tissue optical properties.²⁴ The dependence of emitted Cherenkov photons with tissue optical properties is accounted for by the b’ (see Section 4.B). In our studies, electron doses are used to correlating to the total Cherenkov intensity emitted at both surface and the depth of maximum dose, which is 6 mm depth in our case, corresponding to the depth of maximum dose for the enface TSE beam at SSD = 500 cm. Figure 3 shows that the Cherenkov signal intensity is proportional to either dose on the patient surface (dashed line) or dose at depth of maximum dose (6 mm depth, solid line) with different slopes. The camera-to-detector distance (CDD) depends on the patient anatomy and it is mostly defined by the inverse-square law (CDD/CDD₀)², where CDD₀ is the camera-to-detector distance for the point on the patient surface intersecting the radiation axis [cross-hair, CDD₀ = 416 cm, see Fig. 4(a)]. For this study, only the dose and Cherenkov ratios between chest and umbilicus points are compared. Therefore, r_dose = D(chest)/D(umbilicus) and r_Cherenkov = Cherenkov(chest)/Cherenkov (umbilicus) can be expressed as:

$$\begin{gathered} r_{dose}={\left(\frac{CD{D}_{umbilicus}}{CD{D}_{chest}}\right)}^2\cdot \frac{c^{\prime }{(\mathit{r},\widehat{s})}_{chest}}{c^{\prime }{(\mathit{r},\widehat{s})}_{umbilicus}}\cdot r_{Chereknov} \\ ={\left(\frac{CD{D}_{umbilicus}}{CD{D}_{chest}}\right)}^2\cdot r_{Chereknov,corr} \end{gathered}$$ (3)

where r_{Cherenkov,corr}, a′, and b′, is the perspective corrected Cherenkov intensity ratio, the energy, and the optical properties dependence, respectively. In this study, we have assumed, a’, and b’ are the same at the chest and umbilicus points for the same patient and the same electron energy. We have calculated the inverse square ratio between umbilicus and chest points to be <1% for Camera to detector distance, CDD₀ = 416 cm [see Fig. 4(b)].

4.B. Optical properties dependence, b′(R_d)

Even though there is a linear correlation between Cherenkov intensity and dose deposition, the proportional constant, b′(R_d), between Cherenkov intensity and maximal dose is dependent on the tissue optical properties for a given electron energy, CDD, and incident angle. In other words, the conversion of Cherenkov intensity to dose differs with material optical properties because of the light transport escape function of the tissue.⁴² The optical property values including the scattering and absorption coefficients of human tissues vary across patients and over the patient’s body; thus, the Cherenkov-to-dose conversion ratio may differ for different patients, which makes it invalid to use one universal factor to perform the dose conversion. With the measurement of the patient’s body diffuse reflectance, R_d, the Cherenkov-dose conversion ratio can be estimated, and the dose distribution can be derived from the Cherenkov images of the TSET patient.³⁹ Thus, a calibration is needed between the Cherenkov-to-dose conversion and the measured macroscopic optical properties of the tissue where light travels through to exit the skin surface. Further studies are under investigation to establish the relationship between the delivered dose and Cherenkov intensity for tissues with known optical properties, b′(R_d). Details of the optical property dependence were presented elsewhere.³⁹

4.C. Perspective (geometrical) correction, ${\mathit{c}}^{\prime }(\mathit{r},\widehat{\mathit{s}})$

The dual-field technique is designed and utilized to deliver the uniform dose to the patient body surface, which is consistent with the in vivo diode measurements. However, in this study, we observed that the Cherenkov intensity recorded by C-Dose camera system had a strong dependence on the pixel position (r) relative to the center of the field of view, which was close to center of the patient body in general. This geometrical dependence was visible mostly in vertical and somewhat less in horizontal directions as shown in Figs. 3 and 4. It is clear that the perspective correction factor was also a function of electron beam incident angle, $\widehat{s}$, as has been pointed out from previous experimental³¹ and theoretical studies.^43–45 The light transport escape function^43,44 is a kernel to correlate the Cherenkov light to the dose and mainly affects the dose distribution shape near penumbra regions. There is also a possibility that the escaped Cherenkov light has a preferred direction as a function of the incident radiation angles⁴⁵ rather than strictly Lambertian, that is, isotropic light emission typical for completely scattered visible photons from a turbid medium.

Figure 4 shows that the position dependence of the perspective correction factor is independent of the phantom locations (AP, LAO, RAO) in the vertical and horizontal directions [Figs. 4(b) and 4(c)]. The perspective correction factor in the vertical direction in Fig. 3(f) for the dual field can be fitted by a rational function:

$$c^{\prime }=\frac{p1\cdot y^5+p2\cdot y^4+p3\cdot y^3+p4\cdot y^2+p5\cdot y+p6}{y^5+q1\cdot y^4+q2\cdot y^3+q3\cdot y^2+q4\cdot y+q5},$$

where p1 = −0.004524, p2 = 1.694, p3 = −76.3, p4 = 1.935e4, p5 = 7.869e4, p6 = 2.873e6, q1 = −97.49, q2 = 1.843e4, q3 = 6.795e4, q4 = 6.795e4, q5 = 2.867e6, and y is the vertical position relative to central axis. The rational function with lowest rank was chosen to fit the data as smoothly as possible without introducing many ripples. This perspective correction factor agrees very well with the additional measurements in Fig. 4(b), where both OSLDs and diodes were used to determine the actual dose. This is the perspective correction factor for all patient analysis in the vertical direction. We have also shown in Fig. 4(b) that the inverse square law factor in the vertical direction is relatively small (up to 6%) for our camera located at CDD > 400 cm from the phantom [see Fig. 4(a)]. However, the inverse square law effect can be quite large (~10%) for RAO and LAO geometries [see Fig. 4(c)] thus making it necessary to correct for the inverse square factor (CDD₀/CDD)² to the camera for those phantom geometries (RAO and LAO). The measured perspective factor is larger for 90° beams in Fig. 4(b) than those in Fig. 3(e), we hypothesize that this difference is due to the fact that different pixel position (r) was used in our repeat experiment in Fig. 4(b) compared to the original experiment in Fig. 3(e). This is the same reason for the perspective correction factor in Fig. 4(c) is different from that in Fig. 3(f).

Figures 5 and 6 show the Cherenkov intensity distributions for the same patient (patient 6 as an example) before and after applying the perspective correction. It is obvious that perspective correction is necessary before we can compare Cherenkov intensity with radiation dose distribution.

4.D. Inverse square (patient anatomy) correction, (CDD₀/CDD)²

The inverse square law effect can be calculated as (CDD₀/CDD)² between the distance from the camera to the central axis and the distance from the camera to the point of interest on the patient. For any point (x, y) on a flat panel with angle, CDD is calculated as CDD² = y² + (xsinθ + 117)² + (400 + xcosθ)² [see Fig. 4(a)]. This is because Cherenkov light will decay following the inverse square law if it travels different distances to the camera. This effect is <1% for points in the middle of the patient (e.g., chest or umbilicus) as shown in Fig. 4(b) for all three positions. However, it can be large in the lateral distances for RAO and LAO positions. Fortunately, our measurement points are located near the center of the patient so that this effect is negligible for the points we are comparing between IVD and the Cherenkov.

4.E. Comparison between IVD and Cherenkov imaging for patients

The IVD dose ratio between chest and umbilicus (dose prescription point) are compared with the ratio from Cherenkov intensity with the perspective correction. They are generally in agreement except for one case when the chest point fell into the large gradient region of the radiation field. Table I shows that OSLD gives good results compared to calibrated diodes (SD 3.6%). However, it is possible that the maximum difference can be as large as 10% (see Table I). In order to minimize the uncertainties from OSLD, every patient measurement was taken with two OSLDs and the average was taken as the final results for the patients. As a result, we believe that OSLD can achieve accuracy of ±5%. Table II summarizes the dose comparison results for all 15 patients with available Cherenkov imaging. Between Cherenkov and OSLD results, they agree within 6.1% for most of the patients except for patient 5, whose chest point was located in the sharp dose gradient region close to field edges formed by lead blocks. During patient treatment delivery, it happened occasionally that some IVD diode detectors fell off or were placed in the wrong direction, which resulted in unreliable diode readings of some fields. To maximize the usage of our recorded data, we corrected the diode reading for the cases when the OSLD measurements were available. For the AP field of patient 3, we used the OSLD reading of umbilicus and diode reading of chest to calculate the chest to umbilicus ratio. For either LAO or RAO fields, we summed the corresponding OSLDs and subtracted the diode reading from the other oblique field to calculate the diode chest-to-umbilicus ratios. In the case where both diode readings of the two oblique fields were suspicious, such that no remedy could be applied to correct the dose, we excluded those diode reading data points from the study. The comparisons between Cherenkov and diode readings have relatively larger uncertainties (10.9%) than the OSLD results (2.4%). The OSLD has gone through a rigorous QA process to ensure that its accuracy is better than ±2.5% if two OSLDs, which is the case for all OSLD in vivo measurements, are used to determine dose eliminate large outlier (>10%). Although there is a possibility of tissue optical properties variation for the same patient, including skin pigmentation, our study seems to indicate that this effect is <6.1% for the patient population. This partially reflects the expected larger variation of diode detector response resulting from leakage and other unknown reasons. Although the cause of this large (1–27%) correction is still unclear, there are three possible causes for larger errors included in the diode measurements: (a) Diode orientation effect (if the diode is off by more than 20° from the normal incident direction, it can produce an error of up to 15%; (b) Diode falling off part way through the TSE treatment due to the wires pulling the detector either during a TSE treatment session or in-between different beam orientations (e.g., AP, RAO, LAO) when the patient position was changed; (c) The detectors placed on the wrong side facing the patient, which can cause 10% error due to asymmetry of the inherent buildup. Further investigation will be conducted to determine the root cause with dedicated 2D studies. Based on the current study of the comparison between diode and OSLD in AP, RAO, and LAO positions, we believe that the angular dependence of the diode can cause the diode dose reading to be higher for LAO and RAO directions by up to 15%.

As shown in Fig. 7(b), the black dots are the ratios for the non-TSE patient (patient #5) who was treated in the TSE setup to deliver uniform dose to the whole abdomen skin without the multiple electron field matchings. The OSLD detector placed on the patient chest was in the gradient region near-field edges, as defined by the lead blocks, which resulted in the large deviations from all other TSE patients. After excluding this non-TSE patient, the Cherenkov imaging agreed well with the in vivo OSLD measurements with a mean value of 0.1% and relative standard deviation of 2.4%.

5. CONCLUSIONS

Cherenkov imaging is a viable tool, providing valuable information for patient-specific dose distributions delivered during TSET. A comparison between IVD and Cherenkov profiles was conducted using a flat PVC board and this ratio metric data could be used to establish the vertical and lateral perspective corrections needed for accurate Cherenkov imaging. For the 15 TSE patients studied, the relative standard deviation between IVD and Cherenkov intensity is 2.4% excluding patient 5, when all chest detectors were in the gradient region.