Enhanced cavitation activity in a slab-shaped optical absorber during photo-mediated ultrasound therapy

Abstract

Recently, new studies have shown that combined laser and ultrasound, or photo-mediated ultrasound therapy (PUT), can enhance cavitation in optically absorptive targets to disrupt tissues through photoacoustic (PA) effect. These studies, including both experimental and theoretical investigations, have largely focused on blood vessels, which are modeled as cylindrically-shaped optical absorbers for PA wave generation and propagation. However, in many clinical situations, target tissues may not be cylindrically-shaped. In this paper we investigated the effect of PUT on a slab-shaped optical absorber, much larger than the size of the laser beam or the ultrasound focal point. Our results demonstrated that laser light could generate a PA wave that could enhance cavitation not only at the surface of a slab, but also at depths when combined with ultrasound, suggesting that PUT may be effective in enhancing cavitation in a large range of soft tissues. Our results also demonstrated that the cavitation enhancement was based on the optical absorption of the targeted tissue, allowing for self-targeting treatments when optical contrast is present. Additionally, we demonstrated that for the greatest cavitation enhancement in deeper layers a focused laser beam geometry would be most effective.

Introduction

Cavitation is a potentially destructive process where a void or vapor bubble is created in a liquid phase, generally due to a strong rarefaction pressure located at some bubble nucleation sites (Leighton 1994). When these bubbles collapse, through a process known as inertial cavitation, strong shock waves are emitted. The shock waves can cause significant damage, but their range is limited to approximately the size of the bubble prior to collapse. Traditionally research has been performed to predict and prevent cavitation due to diagnostic ultrasound for the safety of the patient (Apfel and Holland 1991). On the other hand new applications using high intensity focused ultrasound (HIFU) are being developed to utilize the destructive nature of cavitation for therapeutic effects such as disrupting dense fibrous tissues (Yeh, Li et al. 2013), opening the blood brain barrier (Tung, Vlachos et al. 2011, Burgess, Apostolakis et al. 2018), and occluding veins (Hwang, Zhou et al. 2010, Yeh, Li et al. 2013).

In biomedical applications, cavitation can be induced through several different mechanisms. It can be directly induced by ultrasound, for example, in the applications of ultrasound-assisted thrombolysis (ter Haar 1999, Everbach and Francis 2000, Holland, Vaidya et al. 2008, Parikh, Motarjeme et al. 2008, Maxwell, Cain et al. 2009, Maxwell, Owens et al. 2011, Wright, Hynynen et al. 2012) and high intensity focused ultrasound (HIFU) surgery (Hynynen 1991, Holt and Roy 2001, Yang, Roy et al. 2004, Hanajiri, Maruyama et al. 2006, Coussios and Roy 2008), or by laser light. Optical breakdown can efficiently produce cavitation and has found a list of applications in laser ablation surgeries (Brujan, Nahen et al. 2001, Brujan, Nahen et al. 2001, Vogel and Venugopalan 2003, Brujan and Vogel 2006). In addition to optical breakdown where high optical fluence is needed, cavitation can also be created though a photomechanical process termed photospallation (Paltauf and Dyer 2003, Vogel and Venugopalan 2003). This process is also sometimes termed photoacoustic (PA) cavitation (Paltauf and Schmidt-Kloiber 1999), where a laser pulse with a very short duration causes concentrated thermal expansion in an optical absorber in what is known as the PA effect (McDonald and Wetsel 1978). This thermal expansion can cause strong stresses waves in and around the optical absorber. The shape of the emitted stress wave is determined by the geometry of the optical absorber, with spherical and cylindrical geometries generating the strongest rarefaction pressures (Paltauf and Schmidt-Kloiber 1999). The resulting pressure wave can cause cavitation in and around the optical absorber. Cavitation induced by this mechanism is through the photomechanical process, which causes the tissue to fracture as opposed to causing a phase change (Paltauf and Dyer 2003). Among the advantages of photomechanical cavitation is that it occurs at a temperatures that are much lower than what is required for vaporization or ionization which is utilized in optical breakdown. Additionally, fracturing the material is significantly more energy efficient than other methods of inducing cavitation with lasers

Based on the abilities of ultrasound and laser to create cavitation, a growing body of research is developing new treatments based on the synergistic effects of combined HIFU and laser therapies in a process sometimes called photo-mediated ultrasound therapy (PUT) (Cui and Yang 2011, Cui and Yang 2013, Jo and Yang 2016, Hu, Zhang et al. 2017, Hazlewood, Feng et al. 2018, Zhang, Xie et al. 2018, Hazlewood and Yang 2019). PUT delivers synchronized laser pulses and HIFU bursts. Ideally the intensity of the treatments would be adjusted such that the ultrasound and PA pressures alone are not enough to cause inertial cavitation, but when the pressure waves are combined inertial cavitation occurs. Optical contrast can be used to selectively target tissues with high optical absorption, while leaving the surrounding tissue with lower optical absorption undamaged.

PUT has shown promise in targeting blood vessels (Cui and Yang 2013, Hu, Zhang et al. 2017, Zhang, Xie et al. 2018), and a computer model of the process has been created to explore cavitation from PUT in blood vessels (Li, Qin et al. 2018). Li et al. found that when targeting blood vessels with PUT, the cylindrical geometry of the blood vessel created a very high amplitude pressure wave along the central axis, which greatly enhanced cavitation.

In the current study, we are modeling the effects of PUT on a flat slab-shaped optical absorber, mimicking the surface of the skin, and just below the surface. The model will consist of slabs of homogenous tissue without small optical absorbers such as blood vessels, and the illumination geometry of the laser beam will be cylindrical geometry. We have previously demonstrated that enhanced ablation occurs on tissue surfaces during PUT (Hazlewood and Yang 2019). The current investigation will provide a theoretic explanation for these results by modeling the enhanced cavitation activity while simultaneous PA and ultrasound pressure waves are applied.

Methods

PA model

The PA pressure generated by a very short laser pulse (under stress and thermal confinement) can be simulated through the general PA equation (1) as described by Wang and Wu (Wang and Wu 2007),

$$p(\overrightarrow{r},t)=\frac{1}{4\pi c^2}\frac{\partial }{\partial t}\left(\frac{1}{ct}\int p_0({\overrightarrow{r}}^{\prime })\delta \left(t-\frac{\mid \overrightarrow{r}-{\overrightarrow{r}}^{\prime }\mid }{c}\right)d{\overrightarrow{r}}^{\prime }\right)$$ (1)

where c is the speed of sound (1500 m/s), t is time, δ is Dirac delta function, and $\overrightarrow{r}$ is a location vector. The Dirac delta function in (1) is due to the travel time of pressure waves. The pressure that effects a given point over time is related to the generated pressure in an expanding spherical shell around that point. The integral in (1) is the summation of all the initial pressures along the shell.

The shell expands at the speed of sound allowing us to substitute ct for the radius of the shell. By using an axisymmetric geometry, and applying the Dirac delta function, the volume integral is simplified to a one-dimensional integral resulting in (2),

$$p(d,t)=\frac{1}{2}\frac{\partial }{\partial t}(t\int {\mathrm{p}}_0(t,\theta )\sin \theta d\theta )$$ (2)

where d is the depth into the sample along the axis, and θ is the polar angle from the central axis.

To use Equation (2) it is important to have an accurate model of initial pressure p_o, which is defined as

$$p_0(\overrightarrow{r})=\Gamma A(\overrightarrow{r})=\Gamma {\mu }_{a}F(\overrightarrow{r})$$ (3)

where Γ is the Gruneisen parameter which was 0.81 in this study (Yao, Zhang et al. 2014), A is the local absorbance, μ_a is the optical absorption coefficient, and F is the local fluence. The relationship between the temperature increase and the local absorbance is defined by Wang and Wu in (4) (Wang and Wu 2007),

$$\Delta T=\frac{A}{\rho C_v}$$ (4)

Where ΔT is the temperature increase, ρ is the density of the medium (1000 kg/m³) and C_v is the specific heat at a constant volume (4000 J/(kg K)). By relating Equation (3) and Equation (4) an initial pressure of 1 MPa results in a temperature increase of 0.31 K.

The distribution of absorbance/fluence were determined by performing Monte Carlo photon transport simulation through MCML (Wang, Jacques et al. 1995). The pencil beam results of MCML were then convolved to describe the actual beam geometry. Equation (2) was solved to generate the PA pressure at various points along the central axis of the laser beam. In this study some of the simulations examined a normal incident beam, while others examined a focused laser beam as seen in some PA imaging systems (Jo and Yang 2016) where the laser beam was spread into a ring and then refocused. Modeling of the focused beam geometry were performed by changing the launch conditions of the photon in the MCML simulation.

Bubble model

To model the dynamics of bubble expansion and collapse, the following equation (5) from Keller and Miksis was solved (Keller and Miksis 1980):

$$\left(1-\frac{\stackrel{.}{R}}{c}\right)R\ddot{R}+\frac{3}{2}\left(1-\frac{R}{3c}\right){\stackrel{.}{R}}^2=\frac{R}{\rho c}\frac{d}{dt}[p_B]+\frac{1}{\rho }\left(1+\frac{\stackrel{.}{R}}{c}\right)\left(p_B-p_{\infty }-p\left(t+\frac{R}{c}\right)\right)$$ (5)

Where R is the radius of the bubble, c is the speed of sound (1500 m/s), p_∞ is the pressure at infinity (101 kPa), p(t + R/c) is the driving pressure, and p_B is the pressure in the medium at the boundary defined by:

$$p_B=\left(p_{\infty }+\frac{2\sigma }{R_0}\right){\left(\frac{R_0}{R}\right)}^{3\eta }-\frac{2\sigma }{R}-\frac{4\mu }{R}\stackrel{.}{R}$$ (6)

Where σ is the surface tension (0.0725 N/m), R_o is the initial bubble radius, η is the polytropic exponent of the gas (1.4), and μ is the fluid viscosity (0.005 Pa·s).

The driving pressure was applied as a sinusoidal wave, representing the HIFU contribution, superimposed with the pressure wave derived by the PA model. The timing of the PA wave and the HIFU wave were synchronized so that the negative peak of the PA wave was aligned with the negative peak of the second ultrasound cycle. An initial bubble nucleation site can be assumed to be present in the soft tissue as an initial nucleation site as described by Hynynen (Hynynen 1991), therefore an initial bubble radius was supplied to the equation.

Simulations

Various samples were simulated through MCML and then Equation (2) was solved resulting in the PA wave over time at various depths. These results were then used as the driving pressure in Equation (5) to model the bubble dynamics. When solving Equation (5), two additional parameters, the amplitude of the ultrasound wave and the initial bubble radius, were supplied in two sets of simulations. The first was using an initial bubble radius of 100 nm, while varying the amplitude of the ultrasound. The second used a constant amplitude for the ultrasound wave and varied the initial bubble size. The change in bubble radius was modeled with the maximum bubble size relative to the initial bubble size being recorded. The relative increase in maximum bubble size of 2 was used as the threshold for the transition between a stably oscillating bubble and inertial cavitation (Yang and Church 2005, Fabiilli, Haworth et al. 2009), and this assumption was based on the earlier work of Apfel (Apfel 1981). A simulation using the ultrasound wave without the addition of the PA waves, i.e., ultrasound-alone, was used as the reference. An example of these simulations is shown in Figure 2 with the results from ultrasound-alone and the changes caused by the addition of a PA wave. From these results three main values were extracted to represent the changes in cavitation. First was the cavitation threshold pressure for a 100 nm bubble, which represents the ultrasound pressure needed to cause an increase in bubble radius by a factor of 2. If the cavitation threshold pressure is lowered by the addition of a PA wave, then a weaker ultrasound intensity could to initiate cavitation. Second was the cavitation threshold when using a constant ultrasound pressure wave and the initial bubble radius was varied. A decrease in this second cavitation threshold would indicate that smaller initial nucleation sites could be used to initiate cavitation. Finally, the maximum relative increase in bubble radius with a constant ultrasound wave represents the intensity of the resulting cavitation, where a larger maximum bubble radius causes stronger shockwaves upon bubble collapse. These three values were determined when ultrasound-alone was applied and compared to the results of the combined PA + ultrasound treatment. Simulations were performed using two main ultrasound parameters. The first was a 1 MHz wave with a 1 MPa amplitude, while the second was a 5 MHz wave with a 1.2 MHz amplitude. The amplitude of the wave was increased for the simulations using 5 MHz ultrasound wave so that the cavitation thresholds when using ultrasound-alone were similar.

Figure 2:

Example simulations of the relative maximum bubble size. Simulations using 1 MHz ultrasound alone and combined PUT are shown. (a) The results of the bubble simulation using a range of ultrasound amplitudes with a constant initial bubble size of 100 nm. The cavitation threshold is defined as the lowest pressure in which the maximum bubble size is twice the initial bubble size. (b) The results of the bubble simulations using a range of initial bubble sizes with a constant ultrasound pressure of 1 MPa at 1 MHz. The peak nucleation size is the bubbles size which has the largest relative maximum increase. The three identified values (cavitation threshold at constant initial bubble and constant ultrasound pressure, and the maximum relative increase in radius are used for comparisons further in the study to compare the level cavitation enhancement compared to ultrasound alone. The following parameters were used: Radiant exposure- 20 mJ/cm², Beam 1/e radius – 1 mm, μ_a – 100 cm⁻¹, μ_s – 100 cm⁻¹, g – 0.9, ultrasound wave 1 MHz with a 1 MPa amplitude.

Three main sets of simulation were used in this study. Group 1 involves the modeling of a single semi-infinite layer of tissue with changes to the optical absorption coefficient. Group 2 modeled multi-layer tissue, in this case, two layers of tissue, to examine the penetration ability of the treatments. The optical absorption coefficient was changed in the second layer, and all other variable were held constant. Group 3 replicates the results in group 2, but the geometry of the laser beam was changed to a focused laser beam instead of a direct laser beam.

In vitro verification

Targeted ablation of internal tissue phantoms during PUT was demonstrated. Agar based slab-shaped tissue phantoms were created using a 2% solution of powdered agar (Agar pure powder, ThermoFisher Scientific, Waltham, MA) in the method described by Zell et al. (Zell, Sperl et al. 2007). The mechanical properties of the agar phantom were measured with a dynamic mechanical analyzer (Q800, TA Instruments, New Castle, DE) through a compression test. The measured elastic modulus was 0.55 MPa, and the yield strength was 70 kPa.

In order to create increased optical absorption a 0.06% concentration of black tattoo ink (True Black, Intenze Products, Rochelle Park, NJ) was added to darken the samples. The samples were made in two layers. The top layer (4 mm thick) was left undyed, while the bottom layer was divided into two parts with the right half dyed and the left half undyed.

The tissue phantoms were then placed in our treatment system(Hazlewood and Yang 2019) seen in Figure 3. A spherically focused 5 MHz HIFU transducer (SU-108–013, Sonic Concepts, Bothell, WA) was used to apply a 1 ms burst of ultrasound waves at 5 MHz with a peak negative pressure of 1.2 MPa. A 532 nm laser (Surelight SLI-30, Continuum, Santa Clara, CA) was used to deliver 5 ns pulses with a radiant exposure of 20 mJ/cm². An additional 30 MHz focused transducer was used to detect the scattered ultrasound and photoacoustic pressure waves. The detection transducer was placed in a position slightly offset from orthogonal position to avoid the direct path of the ultrasound waves, while allowing the tissue phantom to pass underneath the transducer. The focal point of the laser and both ultrasound transducers was the top of the second layer of the tissue phantom, and arrival of the laser pulse was adjusted so that the negative peak of the photoacoustic wave overlapped with the negative phase of the ultrasound burst. The detection transducer was used to monitor the strength of the photoacoustic signal and to detect cavitation in the sample. An electric motor was used to move the sample under the system to apply a combined laser and ultrasound treatment across both halves of the second layer. The sample was moved at a speed of 5 μm/s. After the treatment, the top layer of the sample was removed, and all surfaces were inspected for damage.

Figure 3:

A diagram of the combined treatment system and detector. The 2 % agar sample was comprised of a top layer and a bottom layer. One half of the bottom layer was dyed with a 0.06% concentration of black ink to increase the optical absorption. The focal point of the system was located at the top of the bottom layer. A motorized stage moved the sample horizontally so that the system could be focused on the light or dark side of the sample.

Results

Group 1: Single semi-infinite slab

When the optical absorption for the tissue samples was modeled, the region of high absorption was a half spheroid (as seen in Figure 4), where the width of the half spheroid was based on the radius of the laser beam, and the depth was related to the optical properties of the sample. The resulting PA pressure wave had a positive and a negative portion. In PA waves near the surface (shown in Figure 5a) the positive portion had a much larger amplitude than the negative portion. However, the negative portion of the wave had a much longer duration. The PA waves deeper in the slab (shown in Figure 5c) had a more symmetric shape where the positive and negative portions of the wave were more similar in amplitude and duration. Additionally, the duration of the PA waves was shorter deeper in the slab. The shape and behavior of the PA waves is in agreement with those previously simulated (Paltauf and Dyer 2003). When the PA waves were superimposed and synchronized with the 1 MHz ultrasound waves (shown in Figure 5b and 5d) it can be seen that the negative portion of the surface PA wave completely encompassed the negative portion of the ultrasound wave. The deeper PA wave on the other hand, had a shorter duration therefore the positive phase of the PA wave canceled out a portion of the negative phase of the ultrasound. However, deeper PA wave had a stronger a peak negative pressure than the surface PA wave. When the 5 MHz ultrasound wave was superimposed over the deeper PA waves the duration of the negative phases were more similar, resulting in changes to the amplitude without dramatically changing the shape of the negative phase.

Figure 4:

Contour plots of the initial pressure p_o found in group 1, which were 3 single slabs with different optical absorption coefficients. All three simulations were performed with constant laser parameters with a gaussian beam width of 1 mm, and a radiant exposure of 20 mJ/cm². The simulations used constant values for optical scattering coefficients (μ_s = 100 cm⁻¹) and anisotropy (g = 0.9), while the optical absorption coefficient was varied with (μ_a) = 5 cm⁻¹, 50 cm⁻¹, and 100 cm⁻¹ for (a), (b), and (c) respectively. It can be seen that increased optical absorption increases the maximum initial pressure while decreasing the effective depth.

Figure 5:

(a) The photoacoustic (PA) pressure wave generated at the surface of an optically absorbent slab. (b) The total pressure wave generated at the surface by PUT accounting for both the 1 MHz ultrasound and the PA wave. The most negative portion of the PA wave was synchronized with the bottom of the ultrasound wave. (c) The PA wave generated 1.5 mm inside an optically absorbent slab. (d) The total pressure 1.5 mm in the slab with both the PA wave and the 1 MHz ultrasound wave. The synchronization of the most negative portion of both waves was maintained. Simulations were performed with the following parameters: Radiant exposure- 20 mJ/cm², Beam 1/e radius – 1 mm, μ_a – 100 cm⁻¹, μ_s – 100 cm⁻¹, g – 0.9.

Figure 6 presents the results of the bubble dynamic simulations of three different semi-infinite slabs with the following optical properties: μ_a = 5, 50, and 100 cm⁻¹, μ_s = 200 cm⁻¹, and g = 0.9. These optical properties are similar to those seen in soft tissue using green laser light (Tuchin 2007). The cavitation pressure threshold with constant initial bubble radius, the cavitation initial radius threshold with constant ultrasound pressure, and the maximum relative bubble radius under constant ultrasound pressure are all presented for each of the three slabs at a range of depths from the surface to 5 mm into the slab.

Figure 6:

The overall results of group 1. A single layer was modeled with the following optical properties: μ_a = 5, 50, and 100 cm⁻¹, μ_s = 200 cm⁻¹, and g = 0.9. The laser beam had a 1/e radius of 1 mm and a radiant energy of 20 mJ/cm². All results are compared to an ultrasound-only control. (a-c) Simulations were performed with a 1 MHz ultrasound wave. (d-f) Simulations were performed with a 5 MHz ultrasound wave. (a,d) The change in the inertial cavitation pressure threshold when a constant initial bubble radius of 100 nm was used, and the amplitude of the ultrasound pressure wave was changed. Lower values represent that cavitation can be initiated with a lower ultrasound intensity. (b,e) The change in inertial cavitation radius threshold when a constant ultrasound wave was used, and the initial bubble radius was changed. Lower values represent that smaller nucleation sites can be used to initiate cavitation. (c,f) The change in maximum relative bubble radius increase when the constant ultrasound wave. Increased maximum bubble size is associated with stronger shockwaves upon bubble collapse.

Increased optical absorption in the slab increases cavitation by reducing the threshold values or enhancing the maximum bubble radius through all three of the evaluated parameters as shown in Figure 6. The greatest reduction in the cavitation thresholds is seen deeper in the samples with higher optical absorption, despite the results in Figure 3 showing that increased optical absorption decreases the penetration of the laser energy. The PA wave generated at the surface traveled into the slab to enhance cavitation. The change in the shape of the PA wave seen in Figure 5 affect cavitation activities. The wave generated at the surface, which has a wide but shallow negative phase, is less effective at lowering the cavitation thresholds. On the other hand, the PA waves seen deeper in the slab are more effective at lowering the cavitation thresholds. There is a small range, in the simulations using the 1 MHz ultrasound wave, where there is a transition between the surface PA wave and the deeper PA wave which did not enhance cavitation (Figure 6c). During the transition the negative phase had a duration shorter than the ultrasound negative phase and had not developed the stronger peak negative pressures found in the deeper waves. These transitionary waves were less effective at enhancing cavitation. The simulations using the 5 MHz ultrasound wave did not have this effect and demonstrated greater relative increase in maximum bubble radius with the deeper waves than the more surface waves. However, the relative changes in cavitation thresholds were very similar when either 1 MHz of 5 MHz ultrasound was used.

Group 2: Two slab model

It was found in preliminary simulations that when there was higher absorption in the top layer, there was not enough light absorbed by the deeper layer regardless of how high the optical absorption was. Instead the results were largely driven by the PA signal seen at the surface of the sample, leading to results nearly identical to those seen in group 1. This effect could result in enhanced cavitation in the deeper layer, but since the results were not related to the optical properties of the deeper layer, the optical selectivity of the treatment was based on surface optical absorption, not the underlying tissues.

To better target the deeper layer, a new set of simulations with the following optical properties were performed: Top layer - μ_a = 0.2 cm⁻¹, μ_s = 10 cm⁻¹, g = 0.8, and thickness of 1.0 mm. Bottom layer - μ_a = 0.2, 10, 20 cm⁻¹, μ_s = 10 cm⁻¹, g = 0.8. These optical properties are similar to skin in the near infrared (NIR) range (Tuchin 2007). The results are shown in Figure 7.

Figure 7:

The overall results of group 2. A double layer model was used in three simulations with a constant top layer (μ_a = 0.2 cm⁻¹, μ_s = 10 cm⁻¹, g = 0.8, and thickness of 1.0 mm), and a second layer with various optical absorption coefficient values (μ_a = 0.2, 10, 20 cm⁻¹.) Vertical dashed line represents the interface between the two slabs. The laser beam had a 1/e radius of 1 mm and a radiant energy of 20 mJ/cm². All results are relative to an ultrasound-only control. (a-c) A 1 MHz ultrasound wave was used. (d-f) A 5 MHz ultrasound wave was used. (a,d) Shows the changes in the inertial cavitation threshold when a constant initial bubble is used. (b,e) The change in inertial cavitation threshold when a constant ultrasound wave was used. (c,f) The change in peak nucleation. The simulation with the highest optical absorption caused the greatest enhancement in cavitation across all three metrics.

A slight enhancement in the second layer, indicated by reduced cavitation threshold due to the addition of the PA wave was observed in Figure 7. However, it was generally less enhancement than was seen previously in Group 1. This is largely due to the increased spreading of the light as it propagated through the first layer. The absorption of the light in the second layer was more diffuse, leading to a weaker PA signal that had a much smaller rarefaction pressure. Additionally, there was cavitation enhancement in the top layer due to a propagation of the PA wave from the deeper sample. The PA wave was largely generated in the second layer near the boundary, but it propagated both with and against the travel direction of the ultrasound wave. In these simulations, the peak negative portions of the PA and ultrasound waves were synchronized at every point to determine maximum cavitation enhancement. In practice, the cavitation enhancement in the first layer would be partially alleviated through the fact the negative peaks of the ultrasound and PA waves would drift out of and back into synchronization across the wavelength of the ultrasound.

Group 3: Two slab model with a focused laser illumination.

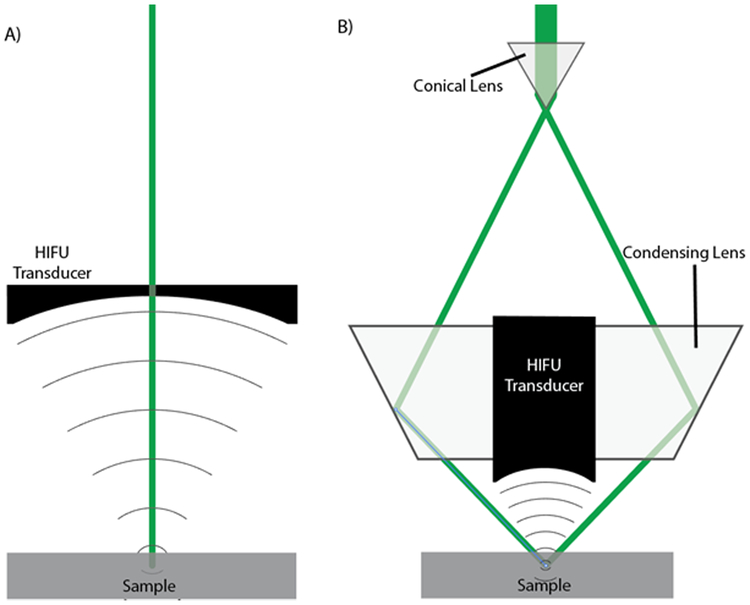
The focused laser beam geometry (Figure 1b) was applied to the NIR simulations performed in group 2 to increase the light fluence in the deep tissue. By selecting the laser ring radius to match the depth of the second layer, we focused the light on the surface of the second layer. A comparison between the initial pressure generated by the illumination seen using the direct geometry and the focused geometry is seen in Figure 8. A constant surface radiant exposure of 20 mJ/cm² was used for both illuminations, however it should be noted that this allowed for a greater total beam energy to be used with the focused laser geometry which had a larger surface area of illumination. The increased beam energy with a constant radiant exposure is one of the advantages of the focused geometry. Despite the higher total laser energy was used, the penetration into the second layer was shallower in the focused geometry than in the direct laser geometry.

Figure 1:

Cross sectional diagrams of two PUT treatment systems. (a) The laser beam is directed through a hole in the center of an ultrasound transducer. (b) The laser beam is shaped into a ring by a conical lens and then refocused using a condensing lens, directing the laser around an ultrasound transducer. In both configurations the laser and ultrasound are aligned and an optically transparent ultrasound coupling medium is used between the ultrasound transducer and the sample.

Figure 8:

A comparison between two different illumination geometries (as seen in Figure 1) using the dual slab model in group 2 (bottom layer μ_a = 20 cm⁻¹). (a) Using the direct illumination as performed in group 2 with a 1/e radius of 1 mm. In this geometry the beam is normal to the surface of the sample. (b) Using a focused ring illumination, the entry angle of the laser was 45 degrees and internal and external 1/e radii of the ring were 0.5 and 1.5 mm respectively. A constant radiant exposure of 20 mJ/cm² was used for both illuminations. The focused illumination not only has a higher peak initial pressure, but it also results in a more rapid drop off in pressure moving away from the focal point, which increases the negative pressure in the resulting PA wave.

After simulating bubble dynamics for group 3 (shown in Figure 9), stronger cavitation enhancement was found at all depths when using the focused laser geometry compared the direct laser geometry. Additionally, cavitation enhancement was found in the second layer that was greater compared than the first layer, as demonstrated by the reduced cavitation thresholds and increased maximum bubble size. The increased contrast in cavitation enhancement seen in the two layers results in superior targeting of the targeted tissue.

Figure 9:

The results of the group 3 simulation using two slabs and a focused laser ring illumination. The optical properties of the slabs were identical to those used in group 2, but only the illumination geometry changed. The vertical dashed line identifies the interface between the two slabs. (a-c) A 1 MHz, ultrasound wave was used. (d-f) A 5 MHz ultrasound wave was used. (a,d) Shows the changes in the inertial cavitation threshold when a constant initial bubble is used. (b,e) The change in inertial cavitation threshold when a constant ultrasound pressure amplitude is used. (c,f) The change in peak nucleation. The change in bubble behavior just before the interface between the two slabs is due to a brief change in synchronization from PA waves arriving from multiple directions.

When the focused geometry was used, there were two main sources of PA waves. The first was from the path of the laser through the top layer, and the second was from the illuminated area in the bottom layer. There was a point just outside of the second layer where these two PA waves interacted to create a second negative pressure peak with a very short duration when 1 MHz ultrasound wave was used. This second negative peak changed the synchronization for a small number of points, which dramatically reduced the cavitation enhancement. When 5 MHz ultrasound wave was used, the amplitude of this second negative peak, however, was much less significant..

Tissue phantom experiment

The above computer simulations suggest that cavitation can occur at significantly lower intensities than previously observed. To demonstrate this, we used long treatment times so that small amounts of damage would be able to accumulate into visible damage. The goal of the experiment is to demonstrate that PUT was able to selectively damage deeper tissue phantoms based on optical absorption in a slab, without damaging the top layer or the lighter side of the sample.

The ultrasound-only and PUT treatments used 1-ms bursts of 5 MHz waves with a peak negative pressure of 1.2 MPa. The laser-only and PUT treatments used a 5 ns pulse of 532 nm light with a radiant exposure of 20 mJ/cm² on the top surface with a pulse repetition frequency (PRF) of 10 Hz. The peak negative pressure and radiant exposure of these treatments were lower than the 15.7 MPa (Zhou and Gao 2013) and 8 J/cm² (Ross, Naseef et al. 1998) used in other studies for ablations with ultrasound-only and laser-only, and less than we had previously achieved using PUT with 4.3 MPa and 1.2 J/cm² (Hazlewood and Yang 2019).

The photoacoustic signals for the dark and light portions of the sample can be seen in Figure 10a and 10b. The photoacoustic signal from the dark side of the sample had an amplitude that was 7.2 times greater than the light side of the sample, indicating much stronger optical absorption on the dark side. Figure 10c shows the scattered ultrasound signal from the combined treatment. A stable signal from the ultrasound burst can be seen prior to the arrival of the laser, but after the arrival of the laser the signal becomes unstable and has a larger amplitude, indicating enhanced cavitation activity.

Figure 10:

The experimental results using agar tissue phantoms. (a,b) The average of 32 photoacoustic signals from the dark and light sides of the sample. Time is relative the beginning of the photoacoustic signal. (c) The detected signal during PUT on the darker side of the tissue phantom. A steady sinusoidal wave can be seen from the ultrasound wave prior to the arrival of the laser pulse, while after the arrival of the laser pulse the signal becomes unstable and has a greater amplitude. (d) The image of the damage done to the second layer of the sample on the dark side. No damage was seen in the top layer or the light side of the sample. The scale mare represents 1 mm.

Removal of the tissue phantom material was clearly seen in the dyed region in the second layer but was not seen in the undyed region in Figure 10d. These results demonstrated the connection between increased PA signal and increased ablation during combined laser and ultrasound ablation and the selectivity of PUT. Furthermore, no damage was seen in the top layer, demonstrating that PUT is truly non-invasive and can penetrate several millimeters. The change to the detected signal from before and after the laser pulse arrival is suspected to be due to the presence of cavitation bubbles, which are then driven by the rest of the ultrasound burst causing increased damage to the sample (Hu, Zhang et al. 2017).

Discussion

These results showed that PA pressure waves can be used to supplement HIFU on a wide slab-shaped tissue without cylindrical or spherical optical absorbers such as blood vessels or particles. Instead, the width of the laser beam provides a region of illumination that has an axisymmetric geometry. The axisymmetric geometry allows for the generation of a PA pressure wave with a rarefaction portion. Compared to more ideal optical absorbers such as spherical tattoo particles or cylindrical blood vessels the PA pressure wave may not be as strong, however when it is used to supplement HIFU, it can increase cavitation activity in several ways. First, the maximum relative bubble radius is increased, resulting in stronger shock waves when the bubbles collapse. Secondly, the nucleation threshold is reduced allowing for smaller initial nucleation sites to initiate cavitation. Finally, the cavitation pressure threshold for a given bubble size is reduced allowing for cavitation to be triggered with a weaker ultrasound pulse.

Our simulations have also revealed that the PA wave that is generated at the surface of the soft tissue can propagate much deeper into the tissue than the penetration of the light directly. This may be beneficial towards treating tissues that are normally beyond the reach of laser therapies, such as tumors or thick scars. In fact, increased optical absorption reduces the effective depth of traditional laser treatments, however, using PA waves, the treatment on deeper tissues is more effective with increased optical absorption. It should be noted that under these conditions the optical selectivity of the laser treatment will be based on the optical absorption at the surface instead of the deeper tissues.

The simulations presented in this study support our previously published experimental findings, which demonstrated that surface ablation of tissue mimicking phantoms when PUT was applied to the surface, and studied parametric variations on the treatment dosages (Hazlewood and Yang, 2019). In addition, the current results demonstrated that PUT could have increased effectiveness when targeting optically absorptive tissue below the surface, and it was also experimentally demonstrated in this study. Although the full range of parametric variations is not presented in this study, the similarity in experimental results suggests that the previous results are applicable when targeted below the surface.

To selectively treat underlying tissue, our simulations have shown that a focused laser beam geometry is more effective than a direct beam that is normal to the tissue surface. To properly target the underlying tissue, it is important that an appropriate wavelength is selected that has good penetration depth through the surface tissues to prevent a strong PA signal from the surface. Near infrared light is likely to be the preferred wavelength for such treatments as it can penetrate through skin easily. A potential target for those treatments would be collagen due to its relatively high optical absorption in the IR range. Additionally, it may be possible to artificially alter the optical properties of the tissue through dyes and/or optical clearing (Yu, Qi et al. 2018), in order to properly target the desired tissues.

When comparing the results of simulations using 1 MHz and 5 MHz ultrasound waves, a similar effect on the cavitation thresholds was seen with the addition PA waves. The 5 MHz ultrasound simulations had a larger relative increase in maximum bubble radius when comparing the combined treatments to the ultrasound-alone, however this is largely due to the fact that 5 MHz ultrasound alone is less effective at causing cavitation than 1 MHz ultrasound alone.

It should be noted that the simulations in this study are limited to the initiation of inertial cavitation. Once bubble collapse has occurred the dynamics of the system dramatically increase in complexity due to shockwaves and microjets which may interact with nearby nucleation sites. It is expected that once cavitation is initiated through PUT it will follow a similar process as that seen in cavitation initiated through optical breakdown, which has been studied in detail through high speed photography (Brujan, Nahen et al. 2001, Brujan, Nahen et al. 2001, Vogel and Venugopalan 2003, Brujan and Vogel 2006). The optical breakdown studies have demonstrated that upon bubble collapse extremely high-speed jets can causing ejection and fracturing of nearby material. Our in vitro experiment showed that the resulting acoustic signal after cavitation was initiated was chaotic, however the damage to the sample was highly localized.

There are some notable limitations to this study, however the overall conclusions drawn from these simulations are expected to hold. First among them is the lack or accurate and consistent data on the optical properties of soft tissue over a wide range, and the nonhomogeneous nature of biological tissue. As such, the optical properties used in this study are approximations only. Second limitation to this study is the heterogeneity of biological tissues, including the presence of reflections amongst different tissues. Due to the similarities in acoustic impedance in soft tissues, these reflections are expected to have approximately 1% of the amplitude of the incoming wave. Reflections of the acoustic waves at the surface can be minimized through the use of appropriate ultrasound coupling medium, which will be used to apply HIFU.

The other limitation of this study is that the effects of material properties are not considered. Our tissue contained 98% water, so we used water as the medium in our simulation. As a result, the conclusions will be more relevant in soft tissue than in stiffer tissues, such as articular cartilage. Different material properties can significantly affect cavitation dynamics, as demonstrated by a series of previous studies (Brujan, Nahen et al. 2001, Brujan, Nahen et al. 2001, Vogel and Venugopalan 2003, Brujan and Vogel 2006) in cavitation induced by nanosecond optical breakdown in a tissue phantom. These studies have shown the elastic/plastic response of the medium could lead to a significant decrease in cavitation size and oscillation period. The decrease in cavitation activity will subsequently reduce the cavitation-induced tissue damage, indicating higher HIFU or laser energy will be needed during PUT for stiffer tissues. In addition, this study consider cavitation inside the tissue phantom, and the effect of boundary is not considered.

Conclusion

We have presented the results of simulations of slabs of tissue under PUT. The bubble dynamics under combined ultrasound and PA pressure waves were simulated, and changes in cavitation thresholds and maximum relative increase in bubble radius were used to quantify the enhancement in cavitation. It was found that the PA wave generated by the laser would enhance cavitation when compared to focused ultrasound treatments alone when optically absorbent semi-infinite slabs were targeted. The PA wave can travel deeper into the tissue than the laser light itself, allowing for treatment beyond the range of typical laser therapies. We have also presented results showing that when targeting internal tissue, it is more effective to use a focused laser geometry, which counteracts the spreading of the laser light though the surface layers. These results show that PUT is effective in slabs of optically absorbent tissue even when cylindrical or spherical optical absorbers are not present, which allows PUT to be used in a wider range of applications.