Cell Boundary Confinement Sets the Size and Position of the E. coli Chromosome

SUMMARY

Although the spatiotemporal structure of the genome is crucial to its biological function, many basic questions remain unanswered on the morphology and segregation of chromosomes. Here, we experimentally show in Escherichia coli that spatial confinement plays a dominant role in determining both the chromosome size and position. In non-dividing cells with lengths increased to 10 times normal, single chromosomes are observed to expand > 4-fold in size. Chromosomes show pronounced internal dynamics but exhibit a robust positioning where single nucleoids reside robustly at mid-cell, whereas two nucleoids self-organize at 1/4 and 3/4 positions. The cell-size-dependent expansion of the nucleoid is only modestly influenced by deletions of nucleoid-associated proteins, whereas osmotic manipulation experiments reveal a prominent role of molecular crowding. Molecular dynamics simulations with model chromosomes and crowders recapitulate the observed phenomena and highlight the role of entropic effects caused by confinement and molecular crowding in the spatial organization of the chromosome.

Graphical Abstract

In Brief

Imaging chromosomes in E. coli within a broad length range, Wu et al. observe that chromosome size and position strongly depend on cell size. They provide evidence that this arises from a confinement-modulated entropic repulsion between chromosome and cytosolic crowders, highlighting the importance of confinement effects in cellular organization.

INTRODUCTION

Chromosomes are spatially confined by physical boundaries. Although interphase eukaryotic chromosomes reside in distinct territories within the nucleus [1], bacterial nucleoids occupy a large sub-volume of the cytoplasm that is itself bounded by the cell membrane [2]. Historically, boundary confinement had been considered to be the sole factor constraining the structure of the bacterial and interphase-eukaryotic chromosomes, in contrast to the intrinsically condensed rod-shaped eukaryotic chromosomes in metaphase. Studies in the past few decades revised this view by showing that chromosomes in all cell types and all phases of the cell cycle are structurally organized by various types of proteins interacting with DNA [3–5]. However, it remains elusive how the size of chromosomes is precisely determined in bacteria, archaea, and interphase-eukaryotic cells. Similarly, a general understanding of mechanisms underlying chromosome positioning in bacteria without mitotic spindles is lacking. This is largely due to the fact that to date the confinement-dependent effects could not be controlled independently, making it hard to disentangle the various proposed mechanisms.

The 4.6-Mbp circular chromosome of the rod-shaped Escherichia coli (E. coli) is generally visualized as an ovoid nucleoid, occupying ~60% of the cell volume. PALM/STORM-type super-resolution microscopy was unable to resolve its detailed architecture [6] because of its small size and fast dynamics, whereas live-cell imaging of a widened E. coli allowed an expansion of the ellipsoidal nucleoid into a torus that exhibited a strong density heterogeneity [7]. This finding is consistent with various approaches indicating that E. coli chromosome organizes into a filamentous bundle with non-crosslinked left and right arms flanking the origin of replication, although the exact conformation of the arms can differ depending on nutrient conditions, cell width, and cell cycle [8–12]. By contrast, some other bacteria such as C. crescentus show two arms that are crosslinked by condensin structural maintenance of chromosome (SMC) protein complexes, but the individual arms are likely to also organize into filaments as inferred from 3C data [13]. These studies of the shape and topology of bacterial chromosomes converge to a picture where, in elongated bacterial cells, an internally compacted chromosome with or without arm crosslinking is constrained by the lateral cell wall into an ellipsoidal shape. Many proteins have been found to be associated with the internal compaction of DNA in bacteria, including nucleoid-associated proteins (NAPs) (such as HU, Fis, and H-NS [14–16]) and SMCs such as MukBEF in E. coli [17–19]). However, it remains elusive how these proteins contribute to the overall size of the chromosome, even at the qualitative level.

The mechanism of chromosome positioning within the E. coli cell also remains an open question. During a cell cycle, a single nucleoid localizes around the cell center before DNA replication, whereas sister chromosomes localize to the two cell halves after they are replicated and segregated [11]. So far, three main classes of mechanisms have been considered in the positional homeostasis and sister segregation of E. coli chromosomes: (1) physical effects of the intrinsic DNA polymer conformation and mechanics, (2) external forces acting on the whole chromosome, and (3) external forces acting on the OriC-proximal region. Numerical simulations showed that two long polymers can spontaneously separate from each other due to conformational entropy [20], whereas dynamic imaging led to a proposal that chromosomes in live cells might be mechanically strained and repulse each other like loaded springs [12]. Other models proposed transertion (the tethering of DNA to the membrane through transcription-translation coupling of transmembrane proteins [21]) and a coupling to the Min system (binding of DNA by membrane-bound MinD proteins which oscillate between the two poles [22]). Finally, the Ori region is the first to be replicated and segregated during the cell cycle, and it showed distinct localization patterns [11, 23], prompting hypotheses that chromosome segregation and positioning are dictated by mechanisms acting on or near the Ori. Various factors were proposed to drive Ori migration, although both the potential binding sites and the potential force-generating mechanisms are yet to be further elucidated [18, 23–25]. Broadly speaking, it remains unclear whether chromosome segregation and positioning primarily rely on intrinsic or extrinsic driving forces, and whether these forces act locally or globally.

The study presented here is inspired by the increasing realization that the behavior of cellular structures is governed not only by specific molecular interactions, but also by the generically aspecific physical properties of the intracellular environment such as molecular crowding [26–29] and by the boundary geometry [30]. In particular, mechanisms involved in cell growth and division depend on cell geometry to achieve organizational homeostasis [31–33]. Given the fact that the chromosome occupies a large fraction of the total cell volume, it stands to reason that chromosome sizing and positioning should be understood in the context of cell size and cell shape.

Here, we study the size and position of a single nonreplicating chromosome in E. coli cells that range in length from 2 to 30 microns. We explored the principles by which chromosomes respond to cell size change and disentangled the roles of extrinsic and intrinsic factors to elucidate the underlying physical mechanism. We first combined genetic perturbation and quantitative imaging to show that the E. coli chromosome can reach a significantly larger size that depends nonlinearly on cell length, even though it is not in direct physical contact with the cell poles. We identified molecular crowding as one of the factors that can directly impact nucleoid size. In contrast, various nucleoid-associated proteins are shown to play secondary roles in quantitatively modulating the nucleoid-cell-length relation. We used molecular dynamic simulations to show that depletion forces arising from molecular crowding provide a plausible mechanistic basis for capturing this behavior. We next investigated the morphological and positional dynamics of chromosome at various length scales. We found that in all cell lengths, a single nucleoid is positioned precisely at the cell center, whereas two sister chromosomes are positioned, non-self-evidently, at the 1/4 and 3/4 locations along the cell length. This persistent chromosome positioning is independent of Ori localization and of other proposed membrane-associated mechanisms, and can be recaptured by simulations, which identify the intrinsically slow global diffusion of the chromosomes and the entropically favorable distribution of newly synthesized crowders as the governing factors.

RESULTS

Maintaining a Single Chromosome in a Growing Cell Allows Studying the Effects of Boundary Confinement

In E. coli cells at steady-state growth conditions, the DNA replication is tightly regulated to scale the DNA copy number with the cell volume [34], making it hard to probe the effect of cell-size changes on the size of a single chromosome. Here, we decouple DNA replication and cell growth so as to obtain cells that maintain only a single chromosome copy while sustaining a continued growth to very long lengths. Via a dnaC2(ts) mutant [35], a rapid shift from a permissive (30°C) to non-permissive temperature (40°C) will disable DnaC’s function in loading DnaB, an essential component of the replisome, which in turn prevents the cell from initiating new rounds of DNA replication. A second element of our approach was that we prevented cell division at any stage of the growth by adding cephalexin, an antibiotic which inhibits enzymes responsible for the septum-cell-wall constriction. The nucleoids in the cells were labeled by HU-mYPet, which are endogenously expressed fluorescent-fusion proteins of a NAP that binds DNA in a sequence-nonspecific manner [36, 37]. Origin- and terminus-proximal foci were labeled by fluorescent repressor-operator systems (FROS), as described previously [38].

We inoculated these bacteria in microfabricated channels [31] that were 1-µm wide, 1-µm high, and 60-µm long (Figure 1A; Methods Details). These channels guided single E. coli cells to grow linearly in one dimension. As cell division was prevented, cells containing a single chromosome could reach very large lengths of 20–30 µm. Supplementing the agarose pad with chloramphenicol to inhibit translation led to immediate cell growth arrest (Figures S1A and S1B), in line with the recent finding that functional accumulation of cell mass underlies cell growth even when DNA replication initiation is inhibited [34]. These single-nucleoid dnaC2(ts) cells form the core system for studying the effects of boundary confinement on the bacterial chromosome.

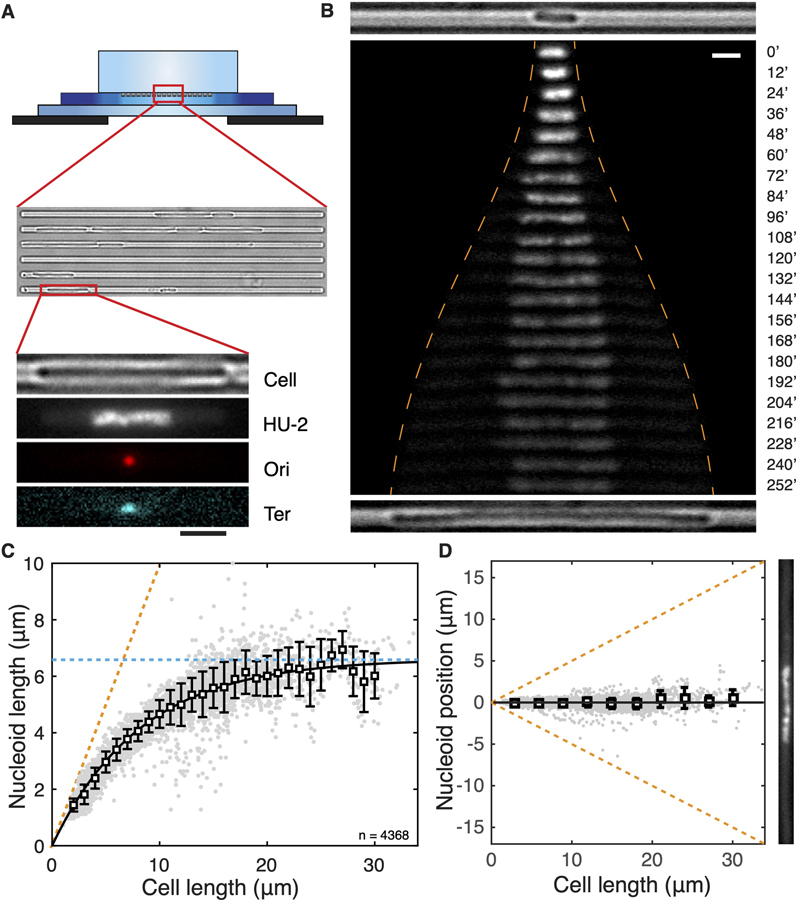
Figure 1. Chromosome Size and Positioning Are Dependent on Cell Size in E. coli.

(A) Schematic of the experimental set-up. The top illustration shows the cross section of the device composed of an agarose containing nutrient and drugs (top), a thin PDMS layer containing 1-μm-wide channels containing E. coli bacteria (middle), and a glass coverslip (bottom). On the bottom is shown, from top to bottom, a cell, its nucleoid, the Ori locus, and the Ter locus.

(B) Time-lapse images of a HU-mYPet-labeled chromosome as it expands with cell growth at nonpermissive temperature defected in DNA replication initiation. The orange dashed line indicates the positions of the cell poles. Time is indicated in m. The top and bottom, respectively, show the bright-field images of the cell at t = 0′ and t = 252′.

(C) The length of single nucleoids in relation to the cell length. Grey dots are single data points (n = 4,585). Squares and error bars are mean and standard deviations calculated with a bin size of 1 μm. The line shows a phenomenological fit by exponential approaching saturation L_nucleoid = 6.61*(1-exp( 0.12*L_cell)). The orange dashed line denotes a scenario where nucleoid occupies full cell length. The blue dashed line indicates the maximal (intrinsic) cell length of 6.6 μm.

(D) Localization of nucleoid center of mass in relation to cell center. Squares and error bars are mean and SD values calculated with a bin of 1 μm, plotted every 3 μm. n = 4,585. An image of a nucleoid in a long cell is exemplified at the right. Scale bars in (A) and (B), 2 μm. See also Figure S1.

Nucleoid Size Scales Nonlinearly with Cell Size

Systematic manipulation of the cell size allowed measuring the response of the nucleoid length to the degree of longitudinal confinement by the cellular boundary. Shown in Figure 1B, a 2.8-µm-long cell at inoculation contains a single 1.6-µm-long nucleoid. As cell growth became apparent, the nucleoid did not retain this size, but instead started expanding longitudinally. The initial phase of nucleoid expansion was pronounced, doubling in length in an hour as the cell length doubled, indicating a near-linear relation. In the following time course of cell growth, however, the chromosome expanded even further in a nonlinear way, ultimately reaching a length of almost 7 μm, about 4 times larger than its initial length. Although the cell size and nucleoid size increased, the total number of nucleoid-bound HU-mYPet is steadily maintained (Figure S1C), resulting in a drop of HU-mYPet intensity on the expanded nucleoid as well as a concomitant increase of it in the cytosol (Figure 1B). The dramatic nucleoid-size expansion was surprising, given that it was not predicted by the existing body of literature attributing chromosome size of bacteria to a combined effect of protein-mediated intra-nucleoid interactions [19] and extrinsic cytosolic crowding [26] and thus warrants a thorough quantitative and mechanistic investigation.

We quantified the nucleoid-cell-length relation in 4,585 single-cell snapshots collected at different stages of cell growth. This led to a nucleoid-cell-length relation that is well described by an exponential approach to saturation at 6.6 ± 0.2 μm, i.e., $L_{nucleoid}=L_{sat}(1-e^{-L_{cell}/L_c})$(Figure 1C, coefficient of determination R² = 0.97, L_sat = 6.6± 0.2μm, L_c = 8.3± 0.5μm, errors show 95% confidence). This phenomenological fit captured both the early stage of near-linear increase of nucleoid size with cell size as well as the slowing down of expansion as cells grew larger until it approached saturation when the cells reached a length above 17 μm. This saturating behavior indicates that the nucleoid has an intrinsic length of 6.6 μm in the cylindrical cell geometry in the absence of longitudinal confinement.

The Nucleoid Localizes Robustly at Mid-cell Position

Single nucleoids were found to strictly localize at the mid-cell position with a striking accuracy. As shown in Figure 1D, the nucleoid center of mass is observed to coincide with the cell center, on average deviating from the mid-cell position over a distance less than 4% of the cell length (Figure 1D). It is to be noted that, in conjunction with the above-described nonlinear relation between nucleoid and cell length, a very significant nucleoid-free cytosolic volume is observed near the two cell poles, whose size increased continuously without any saturation with cell length (Figure S1D). This poses an intriguing question on how the nucleoid appears to ‘‘sense’’ the polar cell walls without any direct physical contact, a sensing that appears effective over long distances and remains operative beyond the cell length range within which the nucleoid length changes.

The Nucleoid Contracts in Size upon Cell Division

Given that a wide range of proteins were previously proposed to bind to DNA and influence the DNA compaction at various levels, it is conceivable that their concentrations or activities can quantitatively affect the chromosome size under the altered DNA/cytosol content ratio in our experiments. If confinement alone, rather than any potential changes in the activities of DNA-binding proteins or the overall degree of molecular crowding in the cytosol, were to determine the quantitative response of the nucleoid size to cell size observed above, the nucleoid would be expected to contract if the cell size were to be reduced.

To verify this experimentally, we examined the nucleoid sizes before and after cell division in a ΔslmA/dnaC2 mutant at different times (Figures 2 and S2). SlmA is known to bind DNA and depolymerize FtsZ to prevent cell division at positions across the nucleoid [39]. When SlmA is omitted in our single-nucleoid cells (in the absence of cephalexin), the cells were found to frequently divide at the nonpermissive temperature (Figure S2A), and interestingly, they were observed to distribute DNA copies unequally among progenies. Notably, only the daughter cells that inherited DNA continued to grow. The ΔslmA/dnaC2 mutant thus demonstrated that the single-nucleoid cells are metabolically active as that cell growth is fueled by active transcription from DNA.

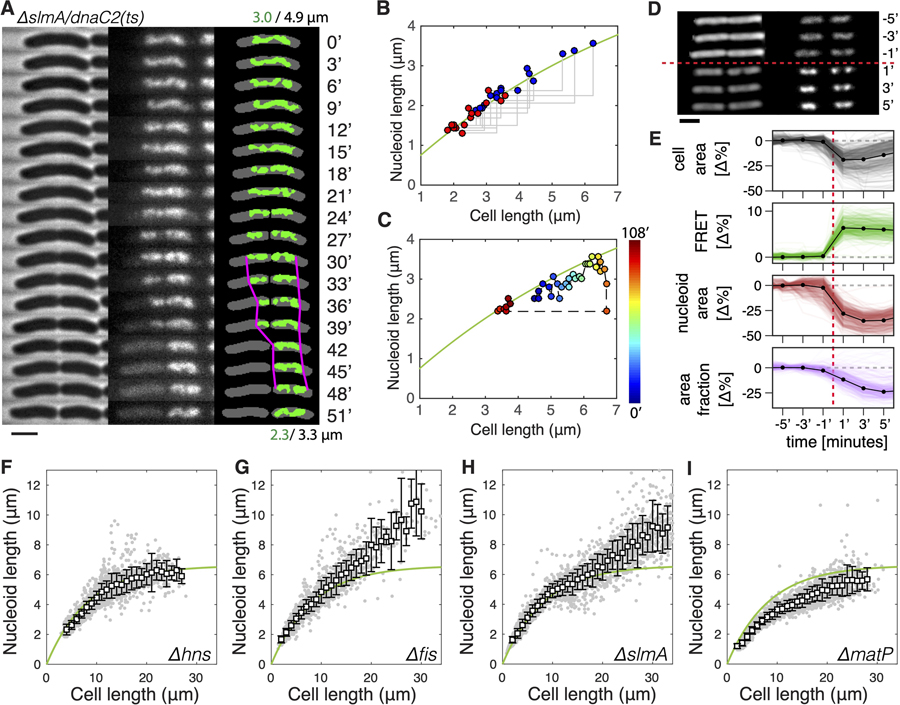
Figure 2. Cell-Size-Dependent Chromosome Sizing under Extrinsic and Intrinsic Perturbations.

(A) Time-lapse images of slmA/dnaC2 cell growth and division at 3 min intervals. On the left are phase contrast images. In the middle is DNA visualized through HU-mYPet. On the right is a binary overlay of the cell body and the nucleoid with nucleoid tips highlighted in magenta around the time of cell division. Time is indicated in m. Scale bar, 2 μm.

(B) Nucleoid length versus cell length before (blue) and after (red) cell division in ΔslmA/dnaC2 cells (n = 16). The green line is identical to the dependence in Figure 1C.

(C) Nucleoid length versus cell length during a full growth and division cycle of a single ΔslmA/dnaC2 cell. The color bar shows time. The green line is identical to the dependence in Figure 1C.

(D) Time-lapse phase-contrast (left, shown in inversed color) images of two cells and the associated nucleoid (right, labeled with HU-mRuby), before (top) and after (bottom) hyperosmotic shock induced by 0.6 M sucrose, which is added at t = 0′. Times are indicated in m. Scale bar, 2 μm.

(E) Changes in cell area, FRET ratio, nucleoid area, and area fraction (the ratio of nucleoid size over cell size). Black dots indicate mean value at each frame. Data at each time point are average values obtained from 301 channels (colored lines) that contain in total about 2,000 cells.

(F–I) Nucleoid length versus cell length in cells lacking hns (n = 2,175) (F), fis (n = 2,291) (G), slmA (n = 3,125) (H), or matP (n = 2,678) (I) genes. The smooth green line represents the WT data as shown in Figure 1C, for comparison.

See also Figure S2 and Figure S3.

These manipulations thus led to a ‘‘reverse’’ control system for examining chromosome sizing upon cell shortening, as the nucleoid traversed from one long cell into one shorter daughter cell. Time-lapse imaging at 3 min intervals showed that the single-genome copy residing in the mother cell was first pinched by the constricting septum and then rapidly translocated to one compartment before cell scission (Figure 2A; for more examples see Figure S2B). These translocations are unidirectional (always toward the cell halves containing the Ori) (Figure S2C) and occurred with a 5 kbp/s maximum speed (Figure S2D), in agreement with the in-vitro-measured speed of DNA translocase FtsK [40]. Strikingly, the nucleoids became smaller in the (smaller) daughter cell but again did not fill up the volume of the latter (Figures 2A, S2A, and S2B). Figure 2B shows the quantitative analyses of individual cell division events, which all yielded nucleoid-cell size data from mother-daughter pairs that collapsed onto the same curve that describes the chromosome expansion with cell elongation (Figure 1C). Notably, nucleoid contraction took place in a ~5–10 min time frame near the septation event (Figures 2A and S2B), too short for significant changes in the cellular crowding, metabolic state, or NAP concentrations to occur. Quantitative mapping of nucleoid-cell size relation in a single cell over time showed that they consistently fluctuate around the same curve (Figure 2C), even in cells that have undergone two consecutive growth-division cycles (Figure S2E). Therefore, we conclude that a change in longitudinal confinement alone is responsible for the observed rapid and reversible nonlinear scaling of the nucleoid size with cell size.

The Size of the Nucleoid Responds to Changes in Intracellular Crowding

It has long ago been suggested that molecular crowding can contribute to the compaction of DNA [41, 42]. In principle, all cytosolic components that are large enough to be sterically hindered by the presence of the chromosome might to some extent contribute to depletion forces, which are of entropic origin. This was shown in vitro for DNA molecules that were modulated in their compaction by using synthetic crowders with dimensions comparable to that of proteins (i.e., a few nm) [26, 43, 44]. Monte-Carlo simulations revealed that at the scale of a bacterial cell, large biomolecular complexes such as ribosomes and polysomes (mRNA molecules bound by ribosomes) impose a major depletion force against a model chromosome, leading to the expulsion of these complexes to the cell poles [45]. This was corroborated by subsequent experimental observations in E. coli, where fully transcribed mRNA and ribosomes preferentially localize outside of the nucleoid region [46, 47].

To directly test the influence of intracellular crowding on the size of the nucleoid, we subjected E. coli bacteria of wild-type sizes to osmotic shocks in a so-called ‘‘mother-machine’’ setup (Figure S3) [48], which allows continuous imaging at single-cell resolution and high throughput. To quantify the degree of crowding, we employed a recently developed genetically encoded fluorescence resonance energy transfer (FRET) sensor [49], which reports on the spatial proximity between a donor and acceptor moiety located on the arms of a clamp-like protein (Figure S3; STAR Methods). Upon a hyperosmotic shock induced via exchange of the growth medium by the same medium with 0.6 M sucrose, we observed a direct step-like increase in FRET signal, indicating an immediate increase in molecular crowding in these cells (Figures 2D and 2E). Simultaneously, the nucleoids underwent a drastic compaction, as is evident from the quantification of both the nucleoid size as well as the nucleoid-cell size ratio (Figures 2D and 2E). These results thus indicate that molecular crowding indeed plays a clear role in nucleoid sizing.

NAPs Exhibit Modest Effects on the Nucleoid Size

Next, we explored the roles of intrinsic packaging agents on the nucleoid size by independently omitting various NAPs in our wild-type (WT) strain background described in Figure 1. Specifically, we probed the abundant and well-studied NAPs Fis and H-NS, which distribute across the genome and have long been proposed to induce chromosome compaction [14, 16], as well as SlmA and MatP, which target binding sites away from and close to the terminus region, respectively [39, 50].

Nucleoids of the Δhns cells exhibited a nonlinear increase with cell size (Figure 2F) that, remarkably, was almost identical to NAPs⁺ cells (NAPs⁺ denotes the control strain described in Figure 1), showing a saturation at 6.7 ± 0.2 μm (R² = 0.98). This finding is unexpected, given that H-NS has long been thought to play an essential role in chromosome compaction and was recently observed to promote short-range interactions. Through PCR and sequencing, we found no extra copy of the hns gene elsewhere in the genome and no mutation in the hns-paralog stpA gene. We also examined the physiological effect of Δhns and found that, at the permissive temperature of 30°C, these cells grew much more slowly than hns⁺ cells (doubling time 165 min versus 83 min in M9 glycerol medium with 0.25% amino acids). We thus conclude that H-NS proteins, despite being essential for the homeostasis of cellular metabolism as a global transcription repressor, have virtually no effect on the global nucleoid size.

Omitting Fis and SlmA also showed little effect in cells shorter than 15 μm, but removal of either of these NAPs was observed to lead to clearly longer nucleoids compared with those in NAPs⁺ strains in cells longer than 15 μm (Figures 2G and 2H). At the maximum cell length of ~30 μm in these two mutants, the nucleoid length reached 10.2 ± 1.8 μm and 9.2 ± 1.7 μm, respectively, significantly above the 6.6 μm plateau for WT nucleoids. These data strongly indicate that Fis and SlmA both play a role in determining the degree of intrinsic DNA-cross-linking that contribute to the observed maximal nucleoid length of 6.6 μm. The effect of Fis can be attributed to its previously reported functions of bending DNA in vitro [51] and stabilizing supercoils in vivo [14]. The effect of SlmA is surprising as its role in chromosome organization was so far barely investigated, although 3C data did show that SlmA-binding sites have higher interactions with their neighboring sequences [52]. Despite the strong effect at larger cell lengths, however, in cells with a size smaller than 15 μm (5 times the regular cell sizes), the strong effect of boundary confinement overruled any effects of changes in local DNA crosslinking by Fis and SlmA.

Omitting MatP led to a 20% reduction in nucleoid size compared with that of WT (Figure 2I). This observation is in line with recent finding that MatP proteins modulate the actions of MukBEF [18, 19] and are responsible for inducing a thin Ter region [7], rather than condensing the Ter region [50, 53]. Unlike Fis and SlmA, the effect of MatP is apparent across all cell lengths, showing that its role in condensing the chromosome acts in parallel to the effect of boundary-confinement and is relevant to the nucleoid size in regular cells at steady-state growth conditions.

Polymer Modeling Captures the Sizing and Positioning of Nucleoids when Including Molecular Crowders

To explore the physical mechanisms underlying the experimentally observed intrinsic nucleoid length, i.e., the 6.6-μm saturation, as well as its compaction by longitudinal confinement, we carried out molecular dynamic simulations. In the absence of detailed experimental data on the internal structure of the chromosome, we opted for a simple polymeric DNA model [20, 54, 55]. This model captures a loop-based chromosomal organization principle [56, 57] by considering a self-avoiding polymer consisting of a circular backbone chain to which a large number of side-loops are attached (Figure 3A), a so-called ‘‘bottle brush’’ structure [58]. Recent evidence obtained from observation of the nucleoid in expanded disk-like cell morphologies of mutant E. coli, provides further support for this type of internal organization [7]. The impact of the side-loops is further coarse-grained by representing their free-energetic contribution in terms of an effective repulsive Gaussian core interaction [59] between the backbone monomers (Figure 3A) (see STAR Methods for model details). The strength of this effective interaction is chosen to be intermediate between that of linear side chains [60], appropriate, for example, to fully supercoiled side chains [45], and the upper values obtained for closed loops [61]. The model partitions the 4.6 Mbp genome into a circular main chain to which ~600 loops are attached, which are spaced at a uniform separation and that have an equal size close to the experimentally reported mean loop size [57]. Such a coarse-graining approach retains the key property of the chromosome in this context, viz., to resist compaction due to its internal structure.

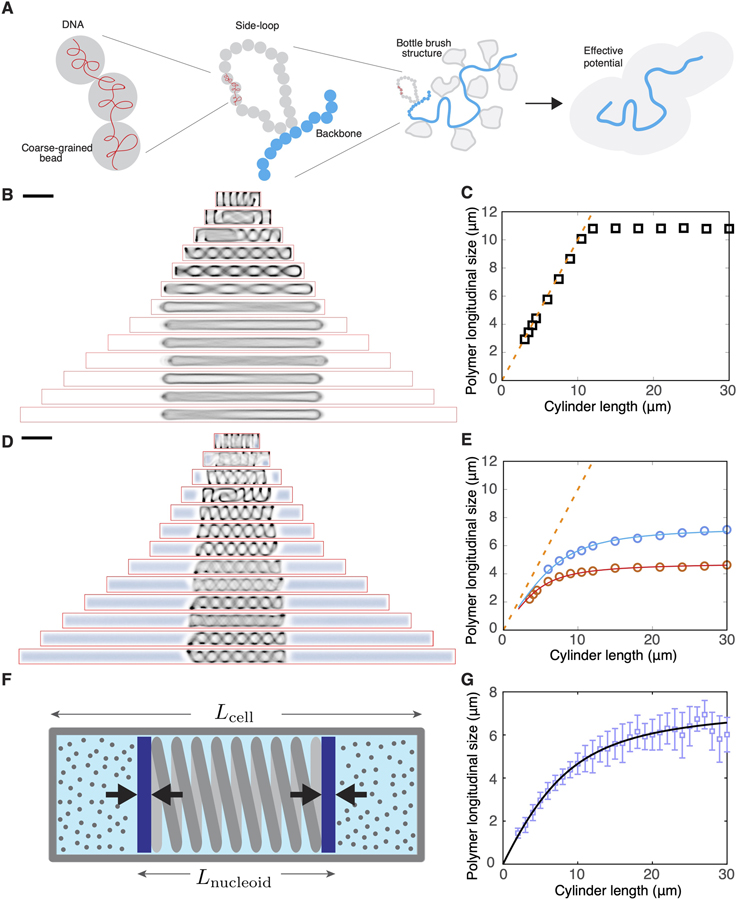
Figure 3. A Polymer Model Captures the Effect of Boundary Confinement on Nucleoid Size and Position.

(A) Schematic of the construction of our coarse-grained polymer model of bottle-brush type, with a bead-chain circular backbone and side loops represented by a parametrized effective potential.

(B) Time-averaged conformations of our model chromosome simulated in cylindrical cells of different lengths in the absence of depletants.

(C) Longitudinal size (FWHM of the backbone) of the modeled chromosome polymer as a function of cell size, simulated without depletants. The orange dashed line indicates the cell length.

(D) Time-averaged conformations of our model chromosome simulated in cylindrical cells of different lengths in the presence of depletants at density of 212 μm³.

(E) Longitudinal size (FWHM of the backbone) of the modeled chromosome polymer as a function of cell size, simulated with two different concentrations of depletants. Blue circles indicate a depletant density of 212 μm⁻³, and red circles indicate a depletant density of 1,060 μm⁻³. The orange dashed line indicates the cell length. The two solid lines represent fits to the piston model, Equation 1.

(F) Schematic describing the piston model.

(G) Fit of the piston model (green line) to the experimental data.

Scale bars in (B) and (D), 2 μm. See also Figure S4.

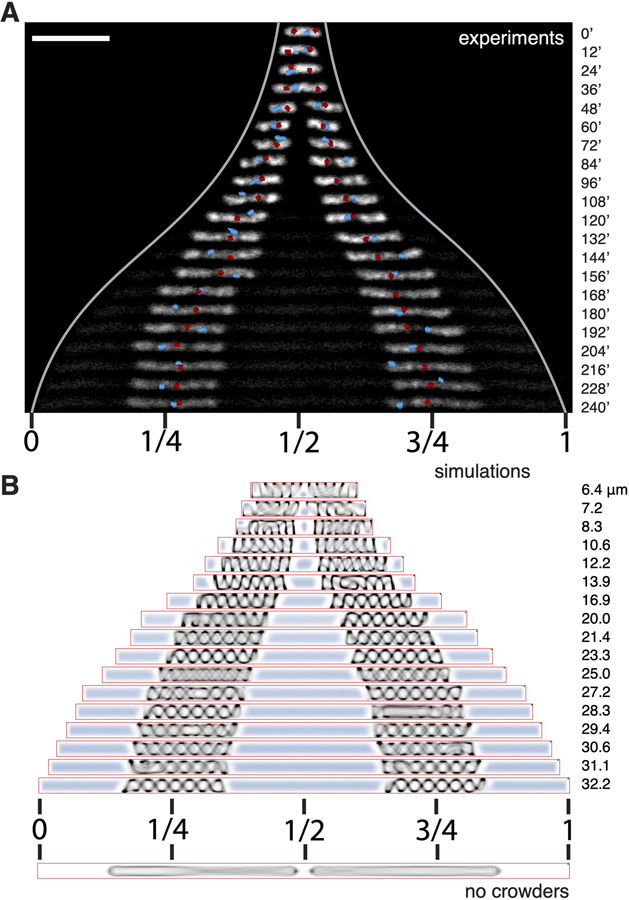
We first simulated such a bottle-brush-structured nucleoid inside a cylindrical volume of 1.0 μm diameter and various length without considering crowders (non-nucleoid-bound cytosolic components). We observed that the polymer pushed against the poles of the cylinder and formed helical conformations in the shorter cells. When the cylinders were sufficiently long, the polymer backbone was found to completely stretch out (Figure 3B), and a sharp transition occurred to the regime where no nucleoid length change was observed upon increasing the cell length further (Figure 3C).

The results of the osmotic manipulation experiments shown in Figures 2D and 2E suggest that intracellular crowding influences the size of the nucleoid. We therefore incorporated depletion effects induced by cytosolic crowding agents by including non-additive crowder particles [62, 63] to the simulation of the confined chromosome. These crowders spontaneously segregated spatially from the DNA polymer, localizing at the polar volumes of the cell. Upon changing the cell size, the cellular concentration of the crowders was maintained constant by inserting new crowders by using a Boltzmann-weighted acceptance criterion (STAR Methods), which resulted in their insertion in the space outside of the chromosome, but otherwise without any spatial bias.

Upon elongating the cell, we observed two key effects of the crowders on the longitudinal size of the chromosome. First, the crowders were observed to exert an inward pressure on the chromosome generating a much more compact shape (Figures 3D and 3E). Second, the chromosome hardly displayed any center of mass motion, and thus consistently maintained a central localization (Figure 3D)–notably reproducing the key experimental observations shown in Figure 1D. The magnitude of the inward pressure as measurable in the simulation was of the order of a few Pa (corresponding to forces of few piconewtons in a cell of diameter ~1 μm) and was a decreasing function of cell length (Figure S4A). Furthermore, unlike the entirely stretched backbone in the large cells in Figure 3B, the presence of crowders maintained the helical morphology of the backbone with a micron-sized helical pitch even in the longest cylinders (Figure 3D), a phenomenon also captured by our structured illumination microscopy (SIM) images (Figure S4B). Finally, the simulation estimate of the chromosome size as a function of cell size now was nonlinear and much more gradual, in much better agreement with experimental findings (Figure 3D). Numerically, the two simulation datasets shown in Figure 3E yielded saturation values of 6.7 and 4.9 μm for two different levels of crowder densities, close to the experimentally observed value, which is gratifying in view of the simplicity of the model.

These effects are readily understood in a simple physical picture: as the cell size increases continuously, the relative size of the cytosolic volume that is occupied by the crowders increases compared with the excluded volume of the nucleoid, which gradually decreases the inward pressure on the nucleoid, in turn allowing the nucleoid to expand. This idea can be translated in a very simple mechanical toy model (Figure 3F) which represents the nucleoid by a two-sided piston that is loaded by a spring with a spring constant K and a rest length L_max that equals the nucleoid length in an infinitely long cylinder without crowders. This piston was embedded in a finite cylinder with a length L_cell and a diameter D_cell equal to that of the bacterium. To the right and left of the piston, we then confined equal amounts of an ideal gas, representing the cytosol with crowders with the total number of gas particles N_gas = ρA_cell L_cell scaling with the volume (and hence the length) of the cell, where $A_{cell}=\left(\pi /4\right)D_{cell}^2$ is the fixed cross-sectional area of the cell. The pressure of the ideal gas representing the crowders that were expelled from the nucleoid, balances the expansive force of the compressed nucleoid, which yields the equilibrium condition

$$P{A}_{cell}=\frac{N_{gas}{k}_{B}T}{V_{gas}}{A}_{cell}=\rho k_{B}T{A}_{cell}\frac{L_{cell}}{L_{cell}-L_{nucleoid}}=K(L_{max}-L_{nucleoid})$$ (Equation 1)

where k_B is Boltzmann’s constant and T is temperature. Solving for L_nucleoid then yielded the fitted nucleoid expansion curves shown in Figure 3E, which were fully determined by just two parameters: the value of L_max and the effective stiffness of the coupled piston-gas system $\kappa \stackrel{\text{def}}{=}K/\rho k_{B}T{A}_{cell}$. Thus, this piston model, in spite of its simplicity, was shown to be able to reproduce the salient aspects of the actual coupled nucleoid-crowders system. From these fits, we can determine a value for the spring constant which is in the order of pN/μm, consistent with the directly computed pressures (see Figure S4A) which are in the order of a few Pa, acting on a cross-sectional area of ~1 μm². Interestingly, we can also fit the piston model to our experimental data and obtain a very good fit, see Figure 3G, with fit parameters L_max = 10.7± 0.2μm and k = 0.31 ± 0.01mm, the latter being of the same order of magnitude as the stiffness extracted from the simulations (≲1/μm, weakly dependent on the crowder density). The fit captures both the early stage of near-linear increase of nucleoid size with cell size as well as the slowing down of expansion as cells grew larger. Note that the value of the fit parameter L_max = 10.7 μm captures the intrinsic length of the fully expanded nucleoid in a cylindrical cell geometry in the absence of any crowders (cf. also Figure 3C), which, as expected, is larger than the experimentally observed saturation value L_sat = 6.6 μm for the crowded cellular environment.

Although our elementary model with a uniform loop size and constant crowder density captured the experimentally observed trends remarkably well, more refined modeling of the nucleoid size versus cell length relation as well as the ultrastructure of the chromosome will benefit from including potentially important effects such as the heterogeneous and dynamic nature of DNA loop distribution [7, 57], the plectonemic structure due to super-coiling and its associated packing effects [45] and the distribution of cytosolic particle sizes [64].

Chromosomes Show Strong Local Dynamics but Weak Global Diffusivity

In live cells, chromosomes exhibited strong intrinsic morphological dynamics. Time-lapse SIM imaging in live cells revealed rapid morphological transformations and density drifts within the long helical chromosomes at sub-minute timescale (Figure 4A). The co-efficient of variation (C_v = s.d./mean) of the nucleoid length stayed rather constant at around C_v ~0.13 across all cell lengths (Figure 4B).

Figure 4. The E. coli Chromosome Shows Strong Internal Dynamic but Weak Global Diffusivity.

(A) Structured illumination microscopy (SIM) images showing rapid density drifts and morphological changes within a long nucleoid. The red arrows indicate areas with significant changes. The blue arrow indicates the cross-section along which intensity profiles are taken as displayed in the plot below the images. Scale bar, 2 μm.

(B) Comparison of the co-efficient of variance of the nucleoid lengths in different cell lengths. The mean value is shown in magenta.

(C) MSD of nucleoid center of mass (black), Ori foci (red), and Ter foci (cyan) along the long axis in 3-μm-long cells versus time. Circles indicate experimental data, and lines indicate fits for sub-diffusion.

(D) MSD of nucleoid center of mass versus time in different cell lengths.

(E) Exponent of the fits describing sub-diffusion of nucleoids in different cell lengths (diffusion co-efficients are all 1.9 × 10⁻⁴ μm²/s^α). The dashed line denotes an exponential approach to saturation fit, f(x) = 0.84 – 0.48e^−0.31x. Note that for 2 μm cells the exponent was calculated for the first m, where the profile follows the power law, before the trajectory plateaus.

We compared the local and global behavior of the chromosome by measuring the mean-square displacement (MSD) in time lapse experiments for the Ori and Ter foci as well as for the chromosome center of mass (COM) at 10 s time resolution at 40°C. Figure 4C shows the data for 3-micron-long cells. The MSD of the Ori and Ter foci were seen to scale as a power law with time, as expected for sub-diffusion, < Δx² > = D t^α. Note that for α = 1, the constant D in this equation is the diffusion constant, whereas for α < 1, D merely is a fitting constant with dimensions of μm²/s^α–which is often used in describing sub-diffusive behavior. The Ori and Ter traces were fitted by very similar exponents α (0.31 versus 0.33, respectively), whereas the MSD of Ter is much larger than Ori (with fitted D of 2 × 10⁻³ μm²/s^0.3 for Ter foci and 5 × 10⁻³ μm²/s^0.3 for Ori foci). Interestingly, the COM of the entire nucleoid also followed a sub-diffusive behavior, albeit with a much lower mean square displacement with D = 1.9 × 10⁻⁴ μm²/s^0.6 and an exponent of 0.62.

These data show that the diffusive behavior of the chromosome as a whole is distinct from its local dynamics. Although local DNA loops are strongly dynamic, they are restricted to a certain region due to the polymeric nature of the chromosome as well as the local compaction density. By contrast, the chromosome is in principle free to explore the whole cellular space, but its large size and the high cytosolic viscosity together constrain its diffusivity.

We next examined how the longitudinal boundary confinement played a role in the diffusivity of the chromosomes. It is commonly known that confinement affects the MSD because of the finite length that can be traveled. This was indeed observed in the shortest, 2-μm-long cells, where the MSD saturated after 1 min of imaging (Figure 4D). In cells longer than 3 μm, no saturation in MSD was observed within the 10 min duration of the experiments (Figure 4D). Surprisingly, however, we observed an additional effect of confinement on the sub-diffusion behavior of the nucleoid COM: although it maintained a near-constant co-efficient D, it exhibited a pronounced dependence of the exponent α that increased from < 0.6 to > 0.8 with increasing cell length (Figure 4E).

Persistent Chromosome Central Positioning Independent of Ori and Ter Localization

The above data on chromosome dynamics suggests that, although strong morphological dynamics of chromosomes can arise through active transcription and metabolism (Figures 4A and 4B), confinement and crowding play the major role in constraining their global dynamics to sub-diffusion behavior (Figures 4C–4E) and contributing to their persistent long-term positioning (Figure 1D).

Previous work suggested various Ori- and Ter-associated active biological mechanisms to play a role in chromosome segregation and distribution [65, 66]. We thus analyzed the localization patterns of Ori and Ter loci positioning in our experiments during cell growth, comparing the results to the nucleoid COM. As shown in Figure 5A, Ori loci localize near the center of the cell and had a standard deviation close to that of the nucleoid COM, whereas the localization of Ter loci are, on average, observed to be farther from the cell center. Quantitative analyses of fluorescent Ori loci revealed an accurate localization of the origin of replication to the nucleoid center in WT cells, whereas Ter loci exhibited a larger spatial freedom (Figures 5B and 5C).

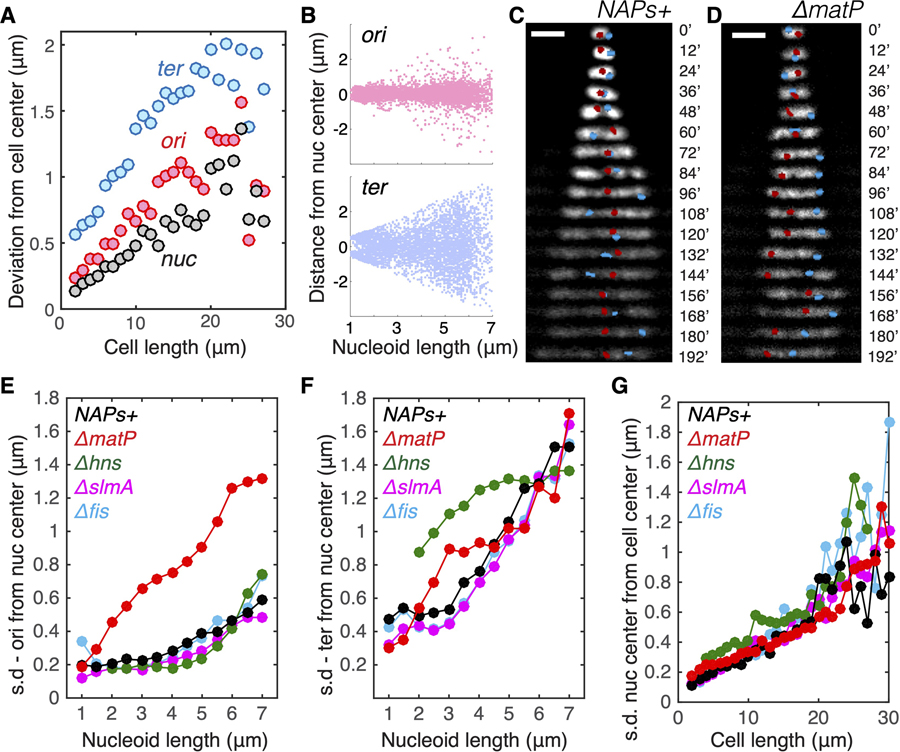
Figure 5. Persistent Positioning of Single Chromosome Independent of NAP-Modulated Sub-structuring.

(A) Deviation (mean square root distance) of the nucleoid center, Ori locus, and Ter locus from the cell center in cells of different lengths.

(B) Distances of Ori and Ter loci from the center of nucleoids in relation to nucleoid length.

(C) Time-lapse images showing the positioning of Ori locus (red) and Ter locus (blue) in single nucleoids over time. Scale bars, 2 μm.

(D) Time-lapse images showing the positioning of Ori locus and Ter locus in single nucleoids over time for the DmatP strain.

(E) Deviation (mean square root distance) of the Ori foci from the nucleoid center in different mutants in different cell lengths. NAPs⁺ denote the control strain with all NAPs present.

(F) Deviation (mean square root distance) of the Ter foci from the nucleoid center in different mutants in different cell lengths.

(G) Deviation (mean square root distance) of the nucleoid center of mass from the cell center in different mutants in different cell lengths.

See also Figure S5.

These data suggest that the nucleoid localizes its COM more accurately to the cell center than the labeled Ori locus. However, given that chromosomes are significantly larger and inherently less diffusive than individual OriC loci (Figure 4A), the causal relation between the localization of Ori region and nucleoid COM to the cell center remains insufficiently resolved. To elucidate it further, we examined the nucleoid loci and COM positioning in various NAP mutants and found that ΔmatP cells lost the central localization pattern of the Ori foci (Figures 5D–5F and S5). This is consistent with recent finding that MatP regulates MukBEF and TopoIV to modulate Ori organization [18] and affect their local DNA structure [7]. Surprisingly, however, the persistent localization of the nucleoid COM to the cell center did not alter in ΔmatP cells (Figure 5G). In addition, the nucleoid COM was also observed to persist at the cell center in Δhns cells where Ter loci resided at the side of the nucleoid, and in Δfis and ΔslmA cells where Ori/Ter localizations are similar to the NAP⁺ strain (Figures 5D–5G and S5). Hence, the persistence of single chromosome at cell center is found to be independent of the localization of Ori or Ter region.

Sister Chromosomes Position at 1/4 and 3/4 of All Cell Lengths

Next, we examined cells containing two chromosomes. Here, we observed a highly specific positioning of the two nucleoids in the cells. Upon sustained cell growth, the two sister chromosomes separated and accurately localized to the two quarter positions along the long axis, that is, at 1/4 and 3/4 of the cell length (Figure 6A). This is by no means trivial, as a priori one might expect them to be free to localize anywhere along the cell length, provided they do not overlap. Or perhaps, one might have anticipated that on average they would localize near 1/3 and 2/3 positions. However, a 1/4 and 3/4 positioning pattern was robustly seen for almost all cells with two completely replicated chromosomes and, strikingly, this persisted for all cell lengths (Figure S6A).

Figure 6. Positioning of Two Replicated Chromosomes.

(A) Time-lapse images of nucleoid positioning in cells that contain two chromosomes. Cell poles are indicated by the light grey lines. Center and quarter positions in the final cell length is indicated below the image. Ori loci are shown in red, and the Ter loci are shown in cyan.

(B) 2D projection of simulated sister chromosomes that are moving apart because of cell growth and the associated depletant addition. Cell lengths are indicated on the right. Scale bars, 5 μm.

See also Figure S6.

The remarkable accuracy of the nucleoid localization prompted us to explore the possible role of active mechanisms that had been proposed. We first deleted the minDE genes in light of the proposal that Min oscillations might affect the positioning of chromosomes [22]. However, we found no effect (Figure S6B). We next examined the involvement of transertion that might tether chromosomes to the membrane [21]. To test this, we treated the elongated cells with a combination of chloramphenicol and rifampicin (see Method Details) to inhibit both transcription and translation, but we did not observe a change in the nucleoid positioning (Figures S6C and S6D). We concluded that these active mechanisms do not play a major role in the nucleoid localization.

Subsequently, we explored the effect of entropic repulsion in sister chromosome segregation by using molecular dynamics simulations of two copies of nucleoid in a growing cylindrical confinement (Figure 6B, bottom). In the absence of crowders, the chromosomes were initially able to localize to the 1/4 and 3/4 positions because of direct repulsion between the chromosomes in small cells, but proper spatial segregation failed for cells longer than 20 μm where the direct chromosomal overlap disappears beyond the length of two fully stretched nucleoids (gray lines in Figure S6E). This approach thus did not fully recapitulate the experimental finding.

The correspondence to the experiments, however, drastically improved when we examined the effect of macromolecular crowding. As new crowders are equally likely to be inserted on either side of each chromosome, the initially established 1/4 and 3/4 positioning is maintained by the crowders that are homogeneously expelled and distributed in a 1:2:1 ratio to the space between one cell end and the first chromosome, the space between the two chromosomes, and the space between the second chromosome and the other cell end, respectively. This resulted in a balanced compression force exerted on the chromosomes by the crowders, which, together with the absence of any significant center-of-mass diffusion, led to robust positioning at the 1/4 and 3/4 positions. This result was found even in the longest cells that are far beyond the regime of direct chromosomal overlap (Figure 6B), where the bare model without crowders failed (Figure S6E).

The 1/4 and 3/4 positioning is thus due to two mechanisms: (1) direct inter-nucleoid repulsion in smaller cells and (2) longer ranged effective repulsion between chromosomes through continued homogeneous protein production in the space outside of the chromosomes. Both of these driving mechanisms are entropic in origin.

DISCUSSION

In this paper, we demonstrated how the size and position of E. coli chromosomes depend on the cell size. Quantitation and modeling of the chromosome-boundary relation allowed us to identify the driving forces that govern chromosome organization and disentangle the roles of diverse factors known to interact with DNA.

The first key finding of this study is that, without directly pushing against the cell poles, the E. coli nucleoid senses the level of longitudinal confinement and varies its size accordingly. Previous studies have explored the effects of the binding of NAPs [14–16] as well as the aspecific depletion effect of crowders outside of the nucleoids on nucleoid compaction [26, 41, 42]. Here, by probing cell lengths across an order of magnitude, including the WT size, we found that NAPs have very little effect on the nucleoid size in cell lengths close to the WT regime. Furthermore, we observed that, strikingly, the magnitude of depletion effect depends on the level of boundary confinement and not only, as reported before, on the crowder size and crowder concentration. Although we cannot exclude that changing the cytosol/DNA ratio in our approach led to some degree of shift in the proteome, the invariance of the nucleoid-cell size relation in both growing cells and dividing cells demonstrated the robustness of our findings, suggesting a universality of the confinement effect.

The extent to which the chromosome size reacts to changes in longitudinal confinement is surprising. The existence of a distinct nucleoid region within E. coli was reported as early as the 1950s [2]. As the nucleoid was seen to push against its cell envelope transversely, but not longitudinally, discussions on the effect of confinement primarily focused on how the small cell diameter influences the chromosome morphology [10, 12], whereas the longitudinal compaction of nucleoid has been mainly considered to be determined by intrinsic packaging by NAPs and SMCs [19]. In principle, chromosome compaction can be well achieved by protein-mediated DNA-crosslinking alone [3]. However, the merit of relying on confinement becomes apparent once we consider its physiological advantages. Strong protein-mediated DNA condensation can be found in metaphase eukaryotic cells or deep-stationary-phase bacterial cells, but such a highly packaged state imposes a disadvantage for its accessibility to transcription and replication machineries. By taking advantage of the confinement effect for physiologically relevant levels of crowding, the chromosome can achieve a relatively small size with a modest level of intranucleoid organization while allowing both dynamics and accessibility.

Our quantitative data of the confinement effects in cells with various genetic perturbations have strong implications on the understanding of the intranucleoid interactions mediated by various NAPs. H-NS and Fis have been shown to bridge DNA and change its conformations in vitro [14, 16]. Recent Hi-C studies also showed that these two NAPS respectively promote short- and long-range DNA-DNA interactions [19]. The functional consequences of these interactions on nucleoid size were, however, not as expected. Here, we showed that the interactions mediated by Fis and H-NS did not influence nucleoid size in cells smaller than 15 μm, which is 5 times larger than a regular G1-phase E. coli cell with a single nucleoid. This would suggest that the reported Fis- and H-NS-mediated DNA-DNA interactions are instead important in transcription regulation, in line with recent finding that Fis is essential for the emergence of transient domain boundaries across the dynamic genome in a live cell [7]. A confinement-driven mechanism underlying nucleoid size homeostasis thus shows an advantage in tolerating changes in local DNA topology as influenced by transcription. The nucleoid size can, however, be tuned by MatP proteins, which expanded the nucleoid by 20% at all cell sizes. This can be explained by the recent finding that MatP reduces DNA compaction at Ter and Ori region [7]. This study indicates that this structural modulation by MatP also appears to be essential for the internal conformation (Ori centering) of the nucleoid.

The second key finding of this study is that confinement-modulated depletion forces place the nucleoids persistently at a defined position. The fact that the chromosome positions persist across an order of magnitude in cell sizes, and correspondingly, in depletion forces (Figure S4A) suggests that such a mechanism might apply to bacteria of various cell sizes and cytosolic crowding levels. For example, 1/4 and 3/4 positioning of sister chromosomes was observed in filamentous symbionts of marine nematodes [67]. Previous experiments showed that various hydrophilic synthetic crowders (e.g., PEG and Dextran) with a size similar to small proteins can induce DNA compaction at high enough concentrations [26, 43, 44]. The most relevant crowders in our experiments are likely large cellular components such as ribosomes and polysomes [45, 47], which effectively partition to the cell poles because of the depletion forces against the chromosome. Such depletion forces are entropic in origin and weak in magnitude, estimated to generate on the order of one to tens of Pa pressure in our model, or equivalently exerting forces of one to tens of pN to the chromosome. These forces appear strong enough to curb full-chromosome mobility at the larger scales but stay weak enough to allow prominent morphological dynamics at the local scale. The essential role of the depletion forces that we observe is notably in line with the recent prediction that a weak force, larger than purely entropic polymer-polymer repulsion force but much smaller than that generated by canonical motors, drives chromosome segregation in E. coli [23]. It is also in line with recent experimental data showing that replicated chromosomes do not spatially separate without new mRNA and protein synthesis [68]. Clearly, the small magnitude of the force responsible for the positioning homeostasis of the chromosome allows it to be easily overcome by active ATP/ GTP-driven processes that involve DNA transport across the cell length, such as FtsK-mediated DNA translocation [69] (also see Figure 2), or RecA-mediated DNA repair [70]. It is known that bacteria such as C. crecentus use active mitotic-lime mechanism to segregate chromosomes, raising the intriguing question whether mitotic and non-mitotic mechanisms result in different evolutionary advantages. We can speculate that whereas a motor-driven mechanism enables polar localization and daughter-cell differentiation, an entropy-driven mechanism is arguably more free-energy efficient.

All cellular processes occur in the context of confinement. Recent studies of the effect of boundary geometry largely focused on nonequilibrium self-organized systems such as reaction-diffusion patterns [31] and molecular-motor-driven active fluids [71]. Here, we showed how the confinement determines the chromosome size, its dynamics, as well as its positioning. These findings have broad implications on the organization of bacterial, archaeal, and eukaryotic-interphase chromosomes under their confining envelopes, as well as the confinement-dependence of diffusivity in cytoplasm in general.

STAR ★ METHODS

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Cees Dekker (c.dekker@tudelft.nl).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

All experimental models in this study are nonpathogenic E. coli K12 derivatives. Chromosomes are labeled through an endogenous hupA-mYPet fusion (strain FW1551 [36]). For Ori1/Ter3 labeling, we used strain RRL189, a kind gift from Rodrigo Reyes-Lamothe. The P1 lysate of FW1551 was transduced into RRL189, which was cured of kanamycin resistance using pCP20 [73] to produce strain FW2177. Strain REP1329 (dnaC2(ts) allele [35], a kind gift from Jean-Luc Ferat), was introduced a aph::frt fragment amplified from JW5794 ([72]) to yield strain FW1957, which allows the transduction of dnaC2 through a kanamycin resistance marker. The lysate of FW1957 was transduced into FW2177 to produce FW2179 for majority of the experiments in this study. For NAP deletions, lysates of strain JW3229–1, JW1225–2, JW0939, and JW5641 [72] were transduced into strain FW2177, cured of kanamycin resistance, and then transduced with lysate the FW1957 to produce final strains FW2254, FW2442, FW2444 and FW2479. To construct strain FW2502, strain FW2179 was transduced with P1 phage FW1363 [31] and selected for chloramphenicol resistance. For nucleoid-size readout in the osmotic shock experiment, we made a functional fluorescent fusion protein HupA-mRuby2, expressed from its native hupA chromosomal locus in strain SJ540, a derivative of E. coli strain MG1655, using λ\RED recombination at 30°C [71]. To measure intracellular crowding, we transformed SJ540 with pSJAB159, a plasmid encoding a recently developed FRET sensor [49] to yield strain TSS1961. The sensor consists of a clamp-like protein composed of two arms with a donor CFP (mCerulean) and acceptor YFP (mCitrine) fluorescent protein respectively on the tip of each of its arms. Increased crowding forces the two domains into closer spatial proximity, resulting in an increased FRET signal (acceptor-to-donor fluorescence ratio; I_YFP/I_CFP). The FRET sensor has been shown to robustly measure crowding changes both in vitro and in vivo, and under variation in relevant environmental parameters (temperature, pH, salt concentration, osmoprotectant concentrations), crowder type (Ficoll, PEG, sucrose), crowder size, as well as sensor concentration [49]. All the insertions were confirmed by PCR amplification and sequencing. All strains used in this study are listed in the Key Resources Table.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Bacterial and Virus Strains
RRL189[AB1157, ori1:: lacOx240::hygR, ter3::tetOx240::accC1 ΔgalK::tetR-mCerulean:: frt, ΔleuB::lacI-mCherry:: frt]	[38]	N/A
FW1551[W3110, hupA-mYPet:: aph frt]	[36]	N/A
REP1329[CM735, dnaC2(ts) ΔmdoB::Tn10]	[35]	N/A
JW5794[BW25113, ΔmdoB::aph frt]	[72]	N/A
JW3229–1[BW25113, Δfis::aph frt]	[72]	N/A
JW1225–2[BW25113, Δhns::aph frt]	[72]	N/A
JW0939[BW25113, ΔmatP::aph frt]	[72]	N/A
JW5641[BW25113, ΔslmA::aph frt]	[72]	N/A
FW1363[W3110, ΔminDE::cat:: frt:: sacB]	[31]	N/A
FW1957[CM735, dnaC2(ts) ΔmdoB::aph frt]	This paper	N/A
FW2177[RRL189, hupA-mYPet:: frt]	This paper	N/A
FW2179[FW2177, dnaC2 ΔmdoB:: aph frt]	This paper	N/A
FW2254[FW2177 ΔmatP::frt, dnaC2 ΔmdoB:: aph frt]	This paper	N/A
FW2442[FW2177 ΔslmA::frt, dnaC2 ΔmdoB:: aph frt]	This paper	N/A
FW2444[FW2177 Δfis::frt, dnaC2 ΔmdoB:: aph frt]	This paper	N/A
FW2479[FW2177 Δhns::frt, dnaC2 ΔmdoB:: aph frt]	This paper	N/A
FW2502[FW2179 ΔminDE::cat frt:: sacB]	This paper	N/A
SJ540[MG1655, hupA-mRuby2:: frt]	This paper	N/A
SJ545[MG1655, hupA-mRuby2:: frt cat frt]	This paper	N/A
TSS1961[SJ540, pSJAB159]	This paper	N/A
Chemicals, Peptides, and Recombinant Proteins
Silicone elastomer	Sylgard	Sylgard 184
tridecafluoro-1,1,2,2-tetrahydroocytaltrichloro-silane	ABCR	Product#AB111444
Chloramphenicol	Sigma-Aldrich	Product#C0378
Cephalexin	Sigma-Aldrich	Product#PHR1848
Recombinant DNA
Plasmid pSJAB159	[49]	N/A
Plasmid pKD46	[73]	N/A
Plasmid pCP20	[73]	N/A
Software and Algorithms
MATLAB	Mathwork	www.mathworks.com
DipImage	Quantitative Imaging Group, TU Delft	www.diplib.org
Python	Python Software Foundation	www.python.org
ESPResSo	Institute of Computational Physics, University of Stuttgart	espressomd.org

For genetic engineering, E. coli cells were incubated in lysogeny broth (LB) supplemented, when required, with 100 μg/mL ampicillin (Sigma-Aldrich), 50 μg/mL kanamycin (Sigma-Aldrich), or 34 μg/mL chloramphenicol (Sigma-Aldrich) for plasmid selection, and with 25 μg/mL kanamycin or 11 μg/mL chloramphenicol for selection of the genomic insertions of gene cassettes. For on-chip experiments, we grew cells in liquid M9 minimum medium (Fluka Analytical) supplemented with 2 mM MgSO₄, 0.1mM CaCl₂, 0.4% glycerol (Sigma-Aldrich), and 0.01% protein hydrolysate amicase (PHA) (Fluka Analytical). For comparing the growth rates of different NAP mutants at permissive temperature in liquid medium, we grew cells at 30°C in liquid M9 minimum medium supplemented with 2 mM MgSO₄, 0.1mM CaCl₂, 0.4% glycerol, and 0.25% PHA. Under this growth condition, strain FW2179 showed a doubling time of 83 min.

METHOD DETAILS

Mask microfabrication

The silicon mask of the microchannels was microfabricated as described previously [31]. A silicon wafer (universitywafer.com) was spin-coated with resist NEB-22 (Sumitomo Chemical). Predesigned features were patterned through an electron-beam lithography system (Leica EBPG 5000+) with a beam step size of 20 nm. The exposed resist was removed by solvent Microposit MF-322 solution (Rohm and Haas) and the exposed wafer surface was etched using an AMS Bosch Etcher. The remaining resist was removed using oxygen plasma.

PDMS microchamber patterning

The patterned silicon wafer was silanized by tridecafluoro-1,1,2,2-tetrahydroocytaltrichloro-silane (97%, ABCR), and used as a mold for creating microchannels. A 5-ml mixture of Sylgard elastomer 184 (base-to-curing agent ratio 5:1) was applied onto the microstructures of the silicon surface and subsequently covered with a clean microscope coverglass (thickness 0.13–0.17 μm) to spread the mixture throughout the area of the glass [31]. The wafer attached to the coverglass was baked in an oven at 70°C for 3 hours until the solvent was fully evaporated, which resulted in a ~10-μm-thick layer of polydimethylsiloxane (PDMS) between the coverglass and the silicon substrate. The coverglass with the patterned PDMS layer was subsequently recovered from the silicon wafer using a razor blade.

On-chip experiments

E. coli bacteria from a freezer stock were inoculated into M9 medium supplemented with 0.4% glycerol and 0.01% of PHA, and incubated overnight at 30°C to reach late exponential. The PDMS/glass chip was treated with oxygen plasma for 5 s to make the surface of the microchambers hydrophilic. 1 ml of the overnight bacterial culture was then pipetted onto the PDMS/glass chip that was clamped onto a custom-made baseplate. The droplet was then immediately covered by a 4.8% agarose pad supplemented with M9 broth, 0.4% glycerol, 0.01% PHA and 25 mg/mL cephalexin (Sigma-Aldrich). The baseplate was well sealed by a piece of parafilm to prevent drying and enable long-term imaging [74] and placed onto the microscope stage. For imaging the cell division event of dnaC2(ts)/ΔslmA cells, cephalexin was omitted in the agarose pad. To inhibit transertion, 34 μg/mL chloramphenicol (Sigma-Aldrich) and 100 μg/mL rifampicin are used in the agarose pad.

Fluorescence imaging

Wide-field fluorescence imaging was carried out using Nikon Ti-E microscope with CFI Apo TIRF objective with an NA of 1.49. The microscope was enclosed by a custom-made chamber that was pre-heated overnight and kept at 39–40°C. For excitation of mCerulean, mYPet, and mCherry signal, cells were illuminated by Nikon-Intensilight illumination lamp through a CFP filter set (λ_ex / λ_bs / λ_em = 426–446 / 455 / 460–500 nm), YFP filter set (λ_ex / λ_bs / λ_em = 490–510 / 515 / 520–550 nm), or an RFP filter set (λ_ex / λ_bs / λ_em = 540–580 / 585 / 592 – 668). The fluorescence signal was recorded by an Andor iXon EMCCD camera. For time-lapse imaging during single cell growth, images were acquired every 12 min for about 8 hours or until the cell growth stopped. The structured illumination microscopy images were taken using Nikon-Ti microscope equipped with a N-SIM module with a 100X objective (1.49), 515nm laser, and an Andor iXon EMCCD camera.

Osmotic shock experiments

Osmotic shock experiments were conducted in a PDMS-based ‘‘mother machine’’ microfluidic device, which enables microscopic imaging of thousands of individual cells during steady-state growth in an array of parallel microchannels flanking a wider feeder channel [48] (Figure S3), fabricated as described previously [75].

Microscopy was carried out in a temperature-controlled room (37C) on an inverted microscope (Nikon Ti-E) equipped with a 60X phase objective (Nikon CFI Plan Apochromat DM60x oil), an sCMOS camera (Andor Neo sCMOS 5.5), a LED fluorescence excitation light source (Lumencor Spectra X), a multiband dichroic (Chroma 69008bs), multiband excitation filters (Chroma 69008x) and multiband emission filter (Chroma 69008 m). The size of the cells’ cytoplasm, that of the nucleoid, as well as the crowding FRET signal were monitored in four image channels (phase contrast, mRuby2, CFP and YFP), with rapid switching (~0.2 s) between channels by use of a motorized filter-cube turret of an inverted fluorescence microscope (Nikon Ti-E), and a motorized filter wheel (Nikon TI-FLBW-E) attached at the microscope’s emission output port. The total exposure time across all four channels in each image frame was ~0.7 s (30ms for phase contrast, 50ms for YFP, 400ms for CFP and 200ms for mRuby), so that the duration of each four-channel frame acquisition was ~1.5 s. Image acquisition (including excitation light pulses, filter switching, and translation of the motorized microscope stage) was automated using custom-written scripts in NIS-Elements software (Nikon Instruments, NIS-Elements Advanced Research). The script executed the four-channel acquisition at 3 s intervals across a set of 30 FOVs pre-selected by the user, and this acquisition sequence across FOVs was repeated at 2-min intervals.

Growth both before and after cell loading into the mother machine was in AB medium [76] (solution A: 2.0 g (NH₄)₂SO₄, 6.0 g Na₂HPO₄, 3.0 g KH₂PO₄, 3.0 g NaCl, 0.011 g Na₂SO₄, dissolved in 200 mL of water; solution B: 0.2 g MgCl2, 0.010 g CaCl2 and 0.0005 g FeCl₃,7H₂O dissolved in 800 mL water), supplemented with EZ Supplement (Teknova) and all 4 nucleotides (10X ACGU solution, Teknova) to a final concentration of 0.02 mM and 0.5% glycerol, which supported fast growth (doubling time ≈25 min) at 37C. Cells were first grown overnight to saturation in this medium, then diluted 1:10 into fresh medium and grown for another 4hrs, concentrated 10-fold by centrifugation before injection into the device’s feeder channel by pipetting. Once the feeder channel was filled with cells, they were driven into the flanking cell-growth channels by gently centrifuging the loaded device (10 min at 800 rpm). A syringe pump (PHD ULTRA, Harvard Apparatus, MA, USA) provided steady flow of fresh growth medium or growth medium with added sucrose (0.6 M) through the feeder channel, connected via PTFE tubing (24AWG, Zeus, SC, USA) and a fluidic valve near the device inlet to switch between the two media. The osmotic shock stimulus was delivered after allowing the cells to reach steady-state growth, by switching the growth medium flowing in the device to the same growth medium supplemented with 0.6 M sucrose.

Theoretical model

The 4.6 Mbp circular genome of E. coli was modeled as a polymer of beads that form a backbone chain consisting of a number (n_b) of monomers, each with side-loop attached that contained ns monomers, totaling 4 × 10⁴ beads (bead diameter σ = 0.04 μm, or 115 bp) that stretched out to a length of 1.6μm (Figure 2A). Here, each side loop was taken to be n_s = 62 beads long, which represented 7.2 kbp DNA that amounts to 2.4 μm of length that folded into a loop, and a main chain with n_b = 636 beads that corresponded to a length of 24.8 μm. Thus, the total chain length l= n_b σ + n_b (n_s σ). The polymer was simulated by beads connected by a finitely extensible nonlinear elastic (FENE) potential

$${\mathrm{\beta }\text{V}}_{FENE}=-1/2K R^{2}ln\left[1-{\left((r-\sigma )/R\right)}^2\right],$$

with K= 30 and R = 1.5 σ. The self-avoidance in the chain was incorporated via the repulsive part of the Lennard-Jones potential

$$\mathrm{\beta }\text{V}\left({\text{r}}_{\text{ij}}\right)=4\left[{\left(\sigma /{\text{r}}_{\text{ij}}\right)}^{12}-{\left(\sigma /{\text{r}}_{\text{ij}}\right)}^6\right]+1/4.$$

The presence of side loops generated both an effective bending stiffness as well as a ‘‘thickening’’ of the main chain. The latter effect led to a soft repulsion between spatially close but contour-wise distant parts of the chromosome. Both effects were well captured by approximating the soft effective repulsion between side-loops in terms of an excess Gaussian core (GC) potential

$$\mathrm{\beta }{V}_{\text{gc}}=\text{a}\hspace{0.17em}\exp \left[-\text{r}2/2{\text{ζ}}^2\right]$$

between the main-chain beads, in addition to the self-avoidance [54]. The interaction range between two side-loops is given by ζ² = 2 (R_g)² where R_g is the radius of gyration of side-loops given by R_g = c n_s^3/5 σ = 0.14 μm where the numerical factor c = 0.323 was confirmed from independent molecular dynamics (MD) simulations [54]. Thus, the impact of side loops of length 2.4 μm can be incorporated through an additional GC interaction, of a width 0.21 μm and a strength proportional to the side-loop size, between backbone beads. As the side loop size R_g is small with respect to the confining diameter D, the effective interaction between side loops remains unaffected by confinement (Jun and Mulder, PNAS 2006). While the interaction strength between two linear chains can be described by a ≈ 2 [60], that between loops depend on the details of the loop topology and remains in between a ≈2 and 6 [61]. Given that some of the loops may furthermore acquire plectoneme structures associated with locally maintained supercoiling, we assume an intermediate interaction strength a= 3 for all loops.

Crowders were modeled as non-additive depletants, so they did not interact among themselves but repel the beads of the polymer. To avoid introducing more interactions parameters, we assume this repulsion to be the same as that between monomers, having both repulsive Lennard-Jones and GC repulsion components.

The confinement is introduced through repulsive interaction between all beads (monomer and depletant) and walls of the confining cylindrical cell geometry. For this purpose, an integrated WCA repulsion

$$\mathrm{\beta }\text{V}\left({\text{r}}_{\text{ij}}\right)=4\left[{\left(\sigma /{\text{r}}_{\text{ij}}\right)}^{12}-{\left(\sigma /{\text{r}}_{\text{ij}}\right)}^6\right]+1/4,$$

and Gaussian core with half the strength and width, a/2 and ζ/2 are used. To model a cylindrical cell of diameter 1μm, we used D = 26.67s and we varied the length of the cell.

To keep the density of depletants constant in a growing cell, we used a Widom insertion scheme that ensured that new depletants were added in a spatially homogeneously distributed manner near the simulated chromosome(s) consistent with the equilibrium state. This was done by a trial move in a Monte-Carlo sense in which a new depletant particle was placed inside the cell within a 22 range of the chain and the change in energy ΔE due to the trial insertion was calculated. The insertion move was accepted with a probability proportional to the Boltzmann weight exp(−βΔE).

QUANTIFICATION AND STATISTICAL ANALYSIS

For experiments under agarose pad, image analysis was carried out using custom MATLAB codes. The bright-field images showing the micro-channels and cells were used to correct for drift between frames, based on the design that each patch contains 21 parallel channels that are 1 μm wide, 60 μm long, and 2 μm apart. After alignment, raw images of each channel were cropped automatically along with all fluorescence channels and saved for further data processing. Montages of these channels were generated in parallel for a manual omission of out-of-focus image frames as well as frames after cell growth has stopped. The recorded coordinates were then used to omit the disqualified frames from the cropped raw images.

Further morphological analysis and quantification were carried out through automatic shape recognition and foci identification based on the DipImage Toolbox (http://www.diplib.org) as described previously [31, 36]. For the quantification of total HU concentrations on the nucleoids, the binary images of the identified nucleoids were used as a mask to isolate the nucleoid signals. The mean fluorescence intensity of the fluorescence signals inside the cells but outside of nucleoid (at least 2 pixels away from the HU mask to avoid interference of the nucleoid-bound HU signal) were used for background subtraction. All intensity values inside the nucleoid was subtracted by the background value and the sum of the background subtracted intensity was used as a measure of the total nucleoid-bound HU.

For data representation in the figures with overlaid signals of HU, Ori, and Ter, HU image was scaled into 8 bit in greyscale. Ori and Ter images were background subtracted using a Gaussian filter and scaled to show sufficiently bright signals [Figure S5A]. The signals above a threshold was false-colored and used to replace the pixels on the HU images. Such an operation was to ensure a visualization of both HU morphology and the foci positioning. The exact morphology and spread of the Ori/Ter foci are subject to thresholding.

Image analysis of hyperosmotic shock data utilized custom-written Python code that automates detection and segmentation of growth channels of the mother machine device, and subsequently applies background subtraction and image segmentation to each of four imaging channels. Segmentation of phase contrast and nucleoid (mRuby) channels utilized a watershed transform method [77] seeded by the same image distance-thresholded at 1.5 pixels (163 nm) from pre-segment perimeters after pre-segmenting by Otsu thresholding [78]. Segmentation of the FRET donor (CFP) and acceptor (YFP) channels utilized the segmentation masks of the phase contrast channel to identify for each cell rectangular regions of interest (ROIs) for segmentation. Cell and nucleoid areas were computed by counting the number of pixels of each segmented area in the phase contrast and mRuby channels, respectively. FRET donor (I_CFP) and acceptor (I_YFP) intensities were computed by integrating pixel values of each segmented area in the CFP and YFP channels, respectively.

Highlights.

• A single E. coli chromosome changes size in response to cell size

• Sister chromosomes maintain positions at 1/4 and 3/4 of the cell length

• Cytosolic crowders compress the chromosome through entropic repulsion of crowders

• Boundary confinement level quantitatively modulates chromosome-crowder repulsion