SHARP: hyperfast and accurate processing of single-cell RNA-seq data via ensemble random projection

Abstract

To process large-scale single-cell RNA-sequencing (scRNA-seq) data effectively without excessive distortion during dimension reduction, we present SHARP, an ensemble random projection-based algorithm that is scalable to clustering 10 million cells. Comprehensive benchmarking tests on 17 public scRNA-seq data sets show that SHARP outperforms existing methods in terms of speed and accuracy. Particularly, for large-size data sets (more than 40,000 cells), SHARP runs faster than other competitors while maintaining high clustering accuracy and robustness. To the best of our knowledge, SHARP is the only R-based tool that is scalable to clustering scRNA-seq data with 10 million cells.

By enabling transcriptomic profiling at the individual-cell level, scRNA-seq has been widely applied in various domains of biology and medicine to characterize novel cell types and detect intra-population heterogeneity (Potter 2018). The amount of scRNA-seq data in the public domain has increased owing to technological development and the efforts to obtain large-scale transcriptomic profiling of cells (Han et al. 2018). Computational algorithms to process and analyze large-scale high-dimensional single-cell data are essential. To cluster high-dimensional scRNA-seq data, dimension-reduction algorithms such as principal component analysis (PCA) (Joliffe and Morgan 1992) or independent component analysis (ICA) (Hyvärinen and Oja 2000) have been successfully applied to process and to visualize high-dimensional scRNA-seq data. However, it requires considerable time to obtain principal or independent components as the number of cells increases. Dimension reduction decreases processing time at the cost of losing original cell-to-cell distances. For instance, t-distributed stochastic neighbor embedding (t-SNE) (van der Maaten 2014) effectively visualizes multidimensional data into a reduced-dimensional space. However, t-SNE distorts the distance between cells for its visualization. Besides, t-SNE requires considerable time for large-scale scRNA-seq data visualization and clustering.

Random projection (RP) (Bingham and Mannila 2001) has been suggested as a powerful dimension-reduction method. Based on the Johnson–Lindenstrauss lemma (Johnson and Lindenstrauss 1984), RP reduces the dimension while the distances between the points are approximately preserved (Frankl and Maehara 1988). Theoretically, RP is very fast because it does not require calculation of pairwise cell-to-cell distances or principle components.

To effectively handle very large-scale scRNA-seq data without excessive distortion of cell-to-cell distances, we developed SHARP (Supplemental Code), a hyperfast clustering algorithm based on ensemble RP (Methods) (Fig. 1A). RP (Bingham and Mannila 2001) projects the original D-dimensional data into a d-dimensional subspace, using a d × D-dimensional random matrix, R, whose elements conform to a distribution with zero mean and unit variance. RP preserves cell-to-cell distances even in a much lower dimensional space and is robust to missing values, which provides a well-suited condition for clustering high-dimensional scRNA-seq data. SHARP reduced the running cost for clustering, whereas clustering performance is robust especially for large-size scRNA-seq data sets. SHARP requires the time complexity of only $O\left(N\log \left(N\right)\sqrt{D}\right)$ for scRNA-seq data with N cells and D genes. Compared with it, a simple hierarchical clustering algorithm requires O(N²D) (Murtagh and Legendre 2014) to calculate the distance between cells. t-SNE combined with the k-means algorithm requires O(DN log(N)) (van der Maaten 2014), and a simple PCA requires O(ND · min(N, D)) for data reduction (Bingham and Mannila 2001).

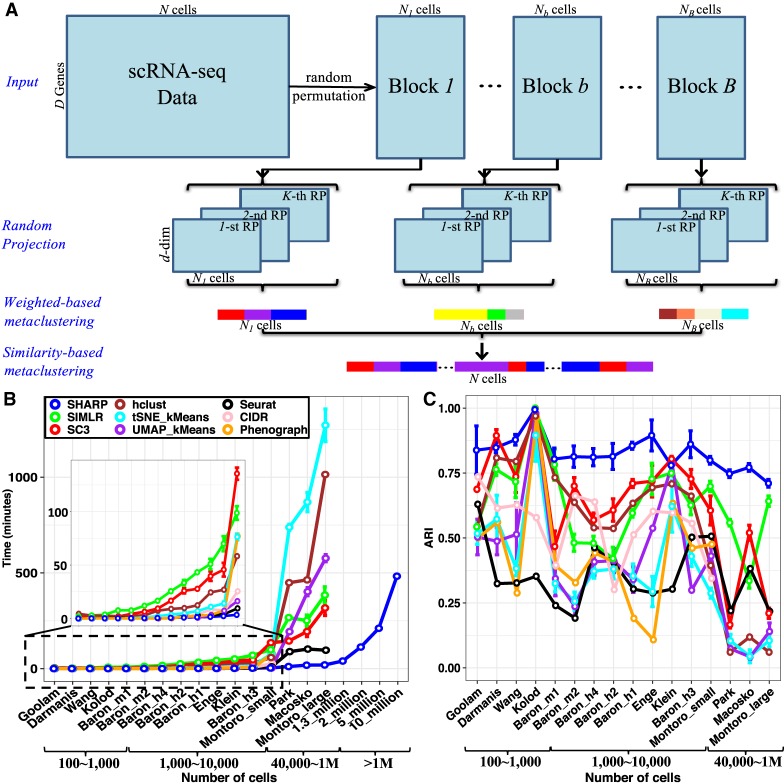
Figure 1.

The framework of SHARP. (A) SHARP has four steps for clustering: divide-and-conquer, random projection (RP), weighted-based metaclustering, and similarity-based metaclustering. (B,C) Running time (B) and clustering performance (C) based on ARI (Hubert and Arabie 1985) of SHARP in 20 single-cell RNA-seq data sets with numbers of single cells ranging from 124 to 10 million (where data sets with 2 million, 5 million, and 10 million cells were generated by randomly oversampling the data set with 1.3 million single cells). For the data sets with more than 1 million cells, only SHARP can run, and only the running time was provided owing to lack of the ground-truth clustering labels. All of the results for SHARP were based on 100 runs of SHARP on each data set. All the tests except for the larger-than-1-million-cell data sets were performed using a single core on an Intel Xeon CPU E5-2699 v4 @ 2.20-GHz system with 500-GB memory. To run data sets with more than 1 million cells, we used 16 cores on the same system. CIDR and PhenoGraph were unable to produce clustering results for those data sets with number of cells larger than 40,000 (i.e., Park, Macosko, and Montoro_large).

There have been previous ensemble-based approaches for RP (Fern and Brodley 2003; Bertoni and Valentini 2006). Compared with them, we developed a strategy specifically for handling scRNA-seq data by using (1) a divide-and-conquer approach for very large-scale scRNA-seq data clustering, (2) a two-layer metaclustering approach for robust clustering, and (3) a very sparse RP embedded into ensemble clustering for hyperfast clustering.

In this study, we aim to present SHARP, an R-based (R Core Team 2016) ensemble RP-based algorithm that can be scalable to 10 million cells while maintaining clustering performance. We perform comprehensive benchmarking to assess the performance of SHARP and further investigate the characteristics that contribute to its performance.

Results

SHARP uses RP for ultrafast scRNA-seq clustering

SHARP uses a divide-and-conquer strategy followed by RP to accommodate effective processing of large-scale scRNA-seq data (Fig. 1A and Methods). SHARP processes scRNA-seq data in four interconnected steps: (1) data partition, (2) RP based clustering, (3) weighted ensemble clustering, and (4) similarity-based metaclustering (sMetaC). During data partition, the scRNA-seq data are divided into small blocks (random size). It is noted that currently R lacks 64-bit integers support, and a scRNA-seq data matrix with more than 1 million cells (so that the number of elements is usually significantly larger than 2³¹ − 1) cannot be directly loaded into R. The divide-and-conquer strategy enables SHARP to upload and process more than 1 million cells. The divided data blocks are further processed by RP followed by a hierarchical clustering algorithm. Because the performance of an individual RP-based clustering is volatile, the ensemble of several runs of RPs is used. A weighted-ensemble clustering (i.e., wMetaC) algorithm merges individual RP-based clustering results. Finally, a similarity-based ensemble clustering (i.e., sMetaC) approach is to integrate clustering results of each block (Fig. 1A and Methods).

SHARP is faster than other predictors and is scalable to 1.3 million cells and even up to 10 million cells

We performed comprehensive benchmarking of SHARP against existing scRNA-seq clustering algorithms, including SC3 (Kiselev et al. 2017), SIMLR (Wang et al. 2017), hierarchical clustering and t-SNE combined with k-means, UMAP (Becht et al. 2019) with k-means, Seurat (Butler et al. 2018), CIDR (Lin et al. 2017), and PhenoGraph (Levine et al. 2015) (Fig. 1B,C; Supplemental Methods) using 17 publicly available scRNA-seq data sets whose cell numbers range from 124 to 1.3 million cells (Supplemental Table S1; Darmanis et al. 2015; Klein et al. 2015; Kolodziejczyk et al. 2015; Macosko et al. 2015; Baron et al. 2016; Goolam et al. 2016; Wang et al. 2016; 10x Genomics 2017; Enge et al. 2017; Montoro et al. 2018; Park et al. 2018).

The benchmarking tests showed cost reduction by SHARP (Fig. 1B). Reflecting the theoretical running costs, the two classical algorithms (t-SNE + k-means, hierarchical clustering) manifested exponential increase in their processing time as the number of cells increased (Fig. 1B). SC3 (Kiselev et al. 2017) and SIMLR (Wang et al. 2017) showed better performance than the classical clustering approaches, but they still required a considerable amount of time for clustering. The computing cost of SHARP was substantially lower than other clustering algorithms. The required computing cost of SHARP rose roughly linearly even with the very large size of the data sets. For data sets with more than 40,000 single cells, SHARP ran at least 20 times faster than SC3 (Kiselev et al. 2017) and SIMLR (Wang et al. 2017). Although CIDR and PhenoGraph were reported to perform very fast and robustly (Levine et al. 2015; Lin et al. 2017), they were unable to produce clustering results for those data sets with more than 40,000 single cells, such as the Park (Park et al. 2018), Macosko (Macosko et al. 2015), and Montoro_large (Montoro et al. 2018) data sets (Fig. 1B).

SHARP clustered the scRNA-seq with 1.3 million cells in 42 min when using a multicore system (Fig. 1B). Because of the data loading problem (and potential exhaustive memory use), we could not show the running time of other approaches for 1.3 million cells. When using a multicore system (16 cores) on the Montoro_large data set (Montoro et al. 2018) with 66,265 cells, SHARP ran more than 40 times faster than SC3 and SIMLR (Supplemental Fig. S1; Supplemental Methods). The running time of SHARP for 1.3 million cells was two times (42 min vs. 96 min) faster than that of Seurat for 66,255 cells. We expect superior performance of SHARP against its competitors when data loading is feasible.

To evaluate the performance of SHARP and show its scalability, we performed random oversampling of the mouse brain data set consisting of 1.3 million cells (10x Genomics 2017) so that we were able to construct even larger scRNA-seq data sets. For this simulation, we tested up to 10 million cells. The running time of SHARP was simply linearly increased with the increasing of cell numbers from 1 million to 10 million. In our system and using 16 cores, SHARP needed ∼8 h (i.e., 482.8 min) to cluster 10 million cells into 1175 clusters (Fig. 1B).

The clustering performance of SHARP is not highly affected by the number of cells

In parallel, we compared the clustering performance using the predefined cell types for each data set (Supplemental Table S1). To evaluate clustering performance, we used the adjusted Rand index (ARI) (Hubert and Arabie 1985). ARI (Supplemental Methods) is a similarity metric to measure how accurately a prediction of clustering is made in the unsupervised learning scenarios, which is similar to the accuracy measurement in supervised classification problems. Generally, the larger ARI, the better the predicted clustering is, with +1 indicating that the predicted clustering is perfectly consistent with the reference, whereas 0 (or negative value) indicates that the predicted clustering is as good as (or worse than) a random guess.

For almost all data sets we tested, SHARP showed better performance (Fig. 1C). The performance of other algorithms became generally worse for large data sets (more than 40,000 single cells). In contrast, SHARP showed an ARI larger than 0.7 regardless of the size of the data sets, showing its robustness. The ARI of Seurat was poor, in general, even for the small-sized data sets. Seurat showed relatively faster speed (despite worse clustering performance) even with its implementation of t-SNE compared with other existing methods except SHARP. This is because Seurat only uses genes with high variation in their expression, which could affect the clustering performance (Fig. 1C).

For robust assessment of the clustered results, we also used artificial data sets by mixing cells with known cell types obtained from the Tabula Muris Consortium (Supplemental Fig. S2; The Tabula Muris Consortium 2018). SHARP again outperformed other methods in terms of both clustering performance (Supplemental Fig. S3) and running time (Supplemental Table S2).

SHARP preserves cell-to-cell distance

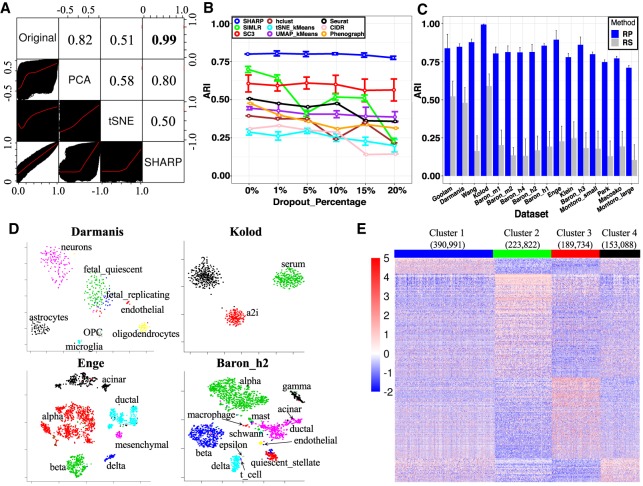
To explain the robust clustering performance of SHARP, we investigated the degree of distortion caused by dimension reduction and compared the correlation of cell-to-cell distances after reducing dimension using SHARP, PCA, and t-SNE, respectively. For this, we calculated the pairwise Pearson correlation between each pair of cells for the original scRNA-seq data and the dimension-reduced data. Reflecting the property of RP, SHARP showed almost perfect similarities in cell-to-cell distance with a correlation coefficient >0.94 even in a dimensional space that is 74 times lower (from 20,862 to 279) than the original one (Fig. 2A; Supplemental Fig. S4; Supplemental Methods). Cell-to-cell distances were distorted when dimension reduction was performed to the same number of dimensions using PCA (Fig. 2A). t-SNE, an algorithm to visualize high-dimensional data into two- or three-dimensional space, showed a lower correlation as expected (Fig. 2A).

Figure 2.

The properties of SHARP. (A) Cell-to-cell distance preservation in SHARP space compared with that in t-SNE and PCA for the Enge data set (Enge et al. 2017). The lower triangular part shows the scatter plots of the cell-to-cell distances, whereas the upper triangular part shows the Pearson's correlation coefficient (PCC) of the corresponding two spaces. (B) SHARP is robust to the additional dropout events on the Montoro_small (Montoro et al. 2018) data set. (C) Comparing RP (SHARP uses RP) with random gene selection (RS) in 16 single-cell RNA-seq data sets (Darmanis et al. 2015; Klein et al. 2015; Kolodziejczyk et al. 2015; Macosko et al. 2015; Baron et al. 2016; Goolam et al. 2016; Wang et al. 2016; Enge et al. 2017; Montoro et al. 2018; Park et al. 2018) with the number of single cells ranging from 124 to 66,265. (D) Visualization capabilities of SHARP in the Darmanis (Darmanis et al. 2015), Kolod (Kolodziejczyk et al. 2015), Enge (Enge et al. 2017), and Baron_h2 (Baron et al. 2016) data sets. (E) Cluster-specific marker gene expression of the top four major clusters for 1.3 million single cells (10x Genomics 2017) by SHARP. The total number of clusters predicted by SHARP is 244. The number in brackets represents the number of single cells in the corresponding cluster.

SHARP is robust to dropouts

scRNA-seq suffers a high frequency of dropouts where many of the true expressions are not captured. To evaluate the robustness of SHARP against dropouts, we tested SHARP while increasing dropout rates in the Montoro_small (Montoro et al. 2018) data set (Fig. 2B). We also applied additional random dropouts. For instance, originally the Montoro_small data set has the dropout rate of 79.6% for the top 8000 genes in terms of nonzero gene expression. Based on the original high dropout rate, additional artificial dropouts were imposed, which provide more difficult conditions for clustering. Our test results showed that additional 20% of dropout was enough to evaluate the robustness of the clustering algorithms.

We found that both SHARP and SC3 were robust to the added dropouts (Methods), whereas we observed poorer performance of other methods for the added dropouts in general (Fig. 2B). The performance of SIMLR, even though it was better than SC3 when there were no added dropouts, became worse when the added dropout rates were increased > 5%.

Cell-to-cell distance is important for clustering results

To evaluate the contribution of RP for clustering, we performed clustering after replaying RP with random selection (RS) of genes while other procedures are unchanged. This violates the condition for RP (a matrix with zero mean and unit variance), and therefore, rough preservation of cell-to-cell distance is no longer guaranteed. RS of genes severely undermined the performance (Fig. 2C), suggesting that RP is a major component contributing to the performance of SHARP.

Furthermore, to show the effectiveness of wMetaC, we compared wMetaC with the method of averaging gene expression after multiple runs of RP (“RP_avg”) while other configurations were unchanged. We observed that wMetaC performs better than simply averaging the expression profiles after RP across all data sets (Supplemental Fig. S5). The superiority of SHARP was more evident for those large-size scRNA-seq data sets when the number of cells is larger than 40,000 (e.g., Park, Macosko, and Montoro_large).

SHARP is equipped with visualization

SHARP is equipped with t-SNE (Fig. 2D; Supplemental Fig. S6) and heatmaps (Supplemental Fig. S7) to visualize its clustering results (Methods). For instance, the heat map for the Enge data set (Enge et al. 2017) clearly showed the cell types in pancreas, including α (GCG), β (INS), acinar (PRSS1), and δ (SST) cells (Supplemental Fig. S7).

Clustering 1.3-million-cell data using SHARP

Of note, SHARP provides an opportunity to study the million-cell-level data set. Previous analysis on the scRNA-seq data with 1,306,127 cells from embryonic mouse brains (10x Genomics 2017) was performed using k-means and graph clustering (equivalent to kernel k-means) algorithms (10x Genomics 2017). However, k-means cannot identify the optimal number of clusters, and it depends on the initial seeds for clustering. By using SHARP, we identified a total of 244 clusters from this data set (17 clusters with more than 1000 cells) (Supplemental Table S3). The top four clusters among them were found to have clear different expression patterns (Fig. 2E). Gene Ontology (GO) analysis (Supplemental Table S3) shows that cluster 2 is associated with dendrites and cluster 3 is associated with axons. We also identified a cluster (cluster 8) enriched for the genes associated with “nonmotile cilium assembly”, which is important for brain development and function (Guemez-Gamboa et al. 2014), and immune cells with high IL4 expression (cluster 14).

Discussion

In this study, we showed that SHARP preserves the cell-to-cell distance during dimension reduction and performs clustering much faster than other competing methods while the clustering performance is robust. We also showed that SHARP is robust to dropouts. By benchmarking various clustering algorithms, we found that SHARP is the only R-based (R Core Team 2016) algorithm to perform clustering of 1.3 million cells (10x Genomics 2017) and to handle clustering up to 10 million cells.

The size of scRNA-seq data sets has been increasing exponentially in recent years. Besides the 1.3-million brain-cell data set we used, we expect larger-sized data sets to be generated. We found the majority of the computational algorithms cannot efficiently handle very large size data sets (Fig. 1B). Furthermore, the clustering performance became worse as the number of cells increased (Fig. 1C). Thus, there is an urgent need for a computational approach to handle large data sets efficiently.

To address these problems, we developed SHARP based on RP, which, to the best of our knowledge, has not been introduced for scRNA-seq data analysis. RP preserves the distance of the data points, even in a lower dimension. Reflecting this, the cell-to-cell distance was well preserved after running SHARP (Fig. 2A). The performance comparison showed that SHARP outperforms other state-of-the-art methods in terms of computation cost and clustering performance (Fig. 1B,C).

To further show the scalability of SHARP, we have extended our comparison against some scalable scRNA-seq analysis methods, including bigSCale (Iacono et al. 2018), geometric sketching (GeoSketch) (Hie et al. 2019b), and Scanorama (Hie et al. 2019a). As they were designed for different purposes, we only evaluated their scalability by running them with scRNA-seq data sets with different cell sizes and measured the running costs. Results (Supplemental Fig. S8) suggested that the computing time for bigSCale and Scanorama increased exponentially, whereas SHARP and GeoSketch exerted more powerful scalability. For data sets with cell numbers larger than 200,000, bigSCale and Scanorama did not work. These results show that SHARP's scalability is comparable with other state-of-the-art algorithms.

SHARP is composed of many indispensable components. To evaluate the contribution of RP, we replaced RP with RS, so that the Johnson–Lindenstrauss lemma (Johnson and Lindenstrauss 1984) is no longer valid. We observed that the performance became much worse by RS, suggesting that the theoretical background by RP is a major contributor toward the performance of SHARP. Also, SHARP uses an ensemble clustering method to combine the results of several runs of RP. We found that the ensemble strategy provides robust performance in clustering (Supplemental Fig. S9; Supplemental Methods). SHARP was robust to the ensemble size when the size is larger than five (Supplemental Fig. S10, S11; Supplemental Methods). Moreover, SHARP's performance was not highly affected by the size of the block when the size was larger than 1000 cells (Supplemental Fig. S12; Supplemental Methods). SHARP is also roughly insensitive to the degree of dimension reduction (Supplemental Fig. S13; Supplemental Methods).

It should be noted that the superior performance of SHARP is not owing to a single run of RP outperforming traditional dimension-reduction methods, such as PCA. On the contrary, the performance of a single run of RP is volatile (Supplemental Fig. S9). Instead, the superior performance of SHARP is because of the following reasons: (1) Multiple runs of RP generated diversity, and then they were combined with the weighted-ensemble clustering approach for robust clustering, and (2) RP's dimension reduction with the property of preserving cell-to-cell distance in the lower-dimensional space. Besides, our metaclustering strategies were able to effectively handle tiny clusters generated during the data partition stage (Supplemental Fig. S14; Supplemental Methods).

We noticed that some studies reported better clustering results for the same data sets (e.g., Darmanis and Baron data sets) when comparing some of the same clustering algorithms (Huh et al. 2019; Yang et al. 2019). This is because in these studies several preprocessing steps have been manually calibrated by using additional methods to polish different parameters for each of the state-of-the-art methods. For example, SAFE-clustering (Yang et al. 2019) used a stratified random sampling strategy to determine the best parameter, like the resolution for Seurat for the Darmanis data set. Similarly, SAME-clustering (Huh et al. 2019) reduced the dimension for Seurat according to the number of principal coordinates determined by CIDR (Lin et al. 2017). Further, both studies added an intermediate step for t-SNE + k-means to detect the cluster number and the cluster centroids to mitigate fluctuations of t-SNE plus k-means. For a fair comparison, we used the same criteria (i.e., let the methods themselves automatically determine their hyperparameters) for all of the methods, including SHARP, to test all of the data sets without parameter tuning.

To assess the robustness of SHARP, we performed various tests: (1) We ran SHARP 100 times and reported the mean ± standard deviation of ARI and computational time for almost all scRNA-seq data sets used here; (2) we tested SHARP on a variety of scRNA-seq data sets with different numbers of cells ranging from several hundred to 10 million; and (3) we used SHARP to process scRNA-seq with various additional dropout rates. In these series of tests, SHARP showed robustness across different cases.

Randomness has been widely used in multiple different domains, like scalable dimensionality reduction and matrix decomposition approximation (Halko et al. 2011). The randomized method like the Gaussian random matrix, which also belongs to one kind of RPs, was used for low-rank matrix decomposition approximation (Halko et al. 2011), whereas we used RP for dimension reduction and clustering in large-scale scRNA-seq data. Further, the random matrix that we used for SHARP was highly sparse, whereas the one used by Halko et al. (2011) was not.

Clustering involves extensive use of computational resources in calculating distances and/or dimension reduction. We showed that SHARP is scalable to processing even 10 million cells. Currently, SHARP is not designed to detect rare cell populations, which could be a future application of RP. Besides clustering, the property of RP to preserve cell-to-cell distance in the reduced dimension will be useful for other applications for scRNA-seq data.

Methods

The framework of SHARP

SHARP accepts gene expression data arranged in a matrix, $\mathbf{M}\in {\mathcal{R}}^{D\times N}$, where each of the D rows corresponds to a gene (or transcript), and each of the N columns corresponds to a single cell. The type of input data can be either fragments/reads per kilo base per million mapped reads (FPKM/RPKM), counts per million mapped reads (CPM), transcripts per million (TPM), or unique molecule identifiers (UMI). For consistency, FPKM/RPKM values are converted into TPM values, and UMI values are converted into CPM values.

Data partition

For a large-scale data set, SHARP performs data partition using a divide-and-conquer strategy. SHARP divides scRNA-seq data $\mathbf{M}\in {\mathcal{R}}^{D\times N}$ into B blocks, where each block may contain different numbers of cells (i.e., N₁, …, N_B, where ${\sum }_{i=1}^B{N}_i=N$). To avoid bias during data partition, we randomly permuted the original single-cell data before partitioning. In practice, SHARP roughly equally divides M and allows users to assign the base number of single cells in each block (e.g., n). In this case, $B=\lceil N/n\rceil$, where $\lceil x\rceil$ is the minimum integer no less than x. The numbers of single cells ${\left\{N_b\right\}}_{b=1}^B$ in each block are as follows:

1. If B = 1, N_b = N, where b = B = 1;

2. If B = 2, $N_b=\{\begin{array}{c}\lfloor {\displaystyle \frac{N}{2}\rfloor ,\mathrm{where}b=\left\{B-1\right\}}\\ \lceil {\displaystyle \frac{N}{2}\rceil ,\mathrm{where}b=\left\{B\right\}}\end{array};$

3. If B ≥ 3, $N_b=\{\begin{array}{cc}n,& \mathrm{where}b=\left\{1,\dots ,B-2\right\}\\ \lfloor {\displaystyle \frac{N-n\left(B-2\right)}{2}\rfloor ,}& \mathrm{where}b=\left\{B-1\right\}\\ \lceil {\displaystyle \frac{N-n\left(B-2\right)}{2}\rceil ,}& \mathrm{where}b=\left\{B\right\}\end{array}.$

This enables SHARP to maximize the usage of local computational resources and avoid memory overflow while minimizing the negative impact from imbalanced numbers of data for each block.

Random projection

RP is a group of simple yet powerful dimension-reduction techniques. It is based on the Johnson–Lindenstrauss lemma (Supplemental Methods; Johnson and Lindenstrauss 1984). Specifically, the original D-dimensional data are projected onto a d-dimensional subspace, using a random matrix whose column are unit length; namely,

$$\mathbf{P}=\frac{1}{\sqrt{d}}\mathbf{R}\mathbf{M}\in {\mathcal{R}}^{d\times N},\mathbf{M}\in {\mathcal{R}}^{D\times N},\mathbf{R}\in {\mathcal{R}}^{d\times D}.$$

As long as the elements of R conform to any distributions with zero mean and unit variance, R gives a mapping that satisfies the Johnson–Lindenstrauss lemma.

Choice of random matrix R

To reduce the computational complexity, we adopted a very sparse RP proposed by Li et al. (2006), where the elements of R (i.e., r_i,j) are defined as

$$r_{i,j}=\sqrt{s}\{\begin{array}{cc}1& \mathrm{with}\mathrm{probability}\frac{1}{2s},\\ 0& \mathrm{with}\mathrm{probability}1-\frac{1}{s},\\ -1& \mathrm{with}\mathrm{probability}\frac{1}{2s},\end{array}\mathrm{where}i=\left\{1,\dots ,d\right\},j=\left\{1,\dots ,D\right\}.$$

As suggested by Li et al. (2006), we selected $s=\sqrt{D}$.

Choice of the subspace dimension d

To balance between maintaining robust performance and yielding a solution as parsimonious as possible, we selected d = log₂(N)/ε², where ε ∈ (0, 1] as suggested by the Johnson–Lindenstrauss lemma.

Ensemble RP

After RP, pairwise Pearson correlation coefficients between each pair of single cells were calculated using the dimension-reduced feature matrix. An agglomerative hierarchical clustering (hclust) with the “ward.D” (Ward 1963) method was used to cluster the correlation-based distance matrix. We first applied RP K times to obtain K RP-based dimension-reduced feature matrices and then further K distance matrices. Each of the K matrices was clustered by a “ward.D”-based hclust. As a result, K different clustering results were obtained, each from a RP-based distance matrix, that would be combined by a weighted-based metaclustering (wMetaC) algorithm (Ren et al. 2017) detailed in the next step.

wMetaC

Compared with the traditional cluster-based similarity partitioning algorithm (CSPA) (Strehl and Ghosh 2002) that treats each instance and each cluster equally important, wMetaC assigns different weights to different instances (or instance pairs) and different clusters to improve the clustering performance. wMetaC includes four steps: (1) calculating cell weights, (2) calculating weighted cluster-to-cluster pairwise similarity, (3) clustering on a weighted cluster-based similarity matrix, and (4) determining final results by a voting scheme. Note that wMetaC was applied to each block of single cells. The flowchart of the wMetaC ensemble clustering method is shown in Supplemental Figure S15.

Specifically, for calculating cell weights, similar to the first several steps in CSPA, we first converted the individual RP-based clustering results into a colocation similarity matrix, S, whose element s_i,j represents the similarity between the ith and jth single cells. Then, based on the idea that the weight for each pair of single cells is determined by the degree of consistency of the colocation clustering results of these two single cells, we converted the similarity matrix S to the weight matrix W according to the following equation:

$$w_{i,j}=s_{i,j}\left(1-s_{i,j}\right),$$

where w_i,j is the element in the ith row and the jth column of W. It is easy to see that when s_i,j = 1 (i.e., the ith cell and the jth cell are with 100% probability in the same cluster) or s_i,j = 0 (i.e., the ith cell and the jth cell are with 0% probability in the same cluster), w_i,j reaches the minimum at zero; when s_i,j = 0.5 (i.e., the colocation probability of the ith cell and the jth cell in the same cluster is 0.5, whereas the probability of them in different clusters is also 0.5, which means this is the most difficult-to-cluster case), w_i,j reaches the maximum at 0.25. In other words, zero weight is assigned to those most “easy-to-cluster” pairs of single cells, and the highest cell-to-cell weight is assigned for the most “difficult-to-cluster” pairs. Then, a weight associated with each cell was calculated as the accumulation of all the cell-to-cell weights related with the corresponding cell. To calculate the weighted cluster-to-cluster similarity, we first noted that the size of the similarity matrix is |C| × |C|, where C is the union set of all the clusters obtained in each individual RP-based clustering results in the previous step, and | · | is the cardinality of a set. Then, for any two clusters, their similarity is determined by the sum of weights of their overlapped elements (i.e., cells) divided by that of their combined ones. Specifically, given two clusters C_u and C_v, the cluster-to-cluster similarity in wMetaC is defined as

$$S_{wMetaC}=\frac{{\sum }_{t\in C_u\cap C_v}{\sum }_{j=1}^N{w}_{t,j}+\delta }{{\sum }_{t\in C_u\cup C_v}{\sum }_{j=1}^N{w}_{t,j}+\delta },$$

where w_t,j is the colocation weight for the tth cell and jth cell derived above, N is the number of cells, and δ is a very small positive number (by default, we used δ = 0.01) to avoid the denominator being zero. We can treat ${\sum }_{j=1}^N{w}_{t,j}$ as the overall colocation weights for the tth cell because it sums up all the possible colocation weights between the tth cell and all cells. Thus, in the equation, the numerator represents the sum of the colocation weights of the cells that are found in both Cluster C_u and Cluster C_v, whereas the denominator represents the sum of the colocation weights of the cells that are found in either Cluster C_u or Cluster C_v.

Then, in the third step (i.e., metaclustering), we used a hierarchical clustering with “ward.D” to cluster the obtained similarity matrix. After clustering, we understood which cluster in the first RP-based clustering corresponds to which cluster(s) in the second, third,…, Kth RP-based clustering. Then, in the final step, we reorganized the K RP-based clustering results according to the result in the third step, and then we used a voting scheme (see below) to determine the final clustering results. These procedures were repeated for each of the B blocks.

Voting scheme

Given K runs of RPs, we obtained K different individual clustering results by using hierarchical clustering on each of the K RP-based dimension-reduced feature matrices. Suppose that the kth (k ∈ {1, …, K}) individual clustering results in |C^k| clusters, that is, $\left\{C_1^k,C_2^k,\dots ,C_{\left|C_k\right|}^k\right\}$. Then, by using the first three steps of wMetaC, we obtained a weighted-based cluster-wise similarity matrix, and then we used hierarchical clustering again for this metaclustering problem. After metaclustering, assume that the number of clusters is |G|, namely, {G₁, …, G_g, …, G_|G|}, where $\left|G\right|\le {\sum }_{k=1}^K\left|C^k\right|$. Thus, G_g corresponds to one or more clusters from the individual clustering set. Finally, a single cell was assigned to the metacluster to which it belongs with the highest ratio. Ties were broken randomly. For example, given K = 5, suppose for a single cell, its five RP-based individual clustering results are $\left(C_3^1,C_1^2,C_6^3,C_3^4,C_2^5\right)$; that is, it belongs to the third cluster in the first RP clustering results, the first cluster in the second RP, the sixth cluster in the third RP, the third cluster in the fourth RP, and the second cluster in the fifth RP (note that the individual clusters are not necessarily consistent with each other and that is why metaclustering method like wMetaC is required). After metaclustering, suppose that $C_3^1$, $C_6^3$, and $C_2^5$ belong to the same metacluster G₃, while $C_1^2$ and $C_3^4$ belong to G₁ and G₂, respectively. Because this single cell is predicted to belong to Cluster G₃ with the highest ratio (i.e., 3/5), the final predicted cluster of this cell is Cluster G₃.

Similarity-based metaclustering

To integrate the clustering results of the B blocks obtained by wMetaC, we proposed a similarity-based metaclustering (sMetaC) approach, which is similar to wMetaC. The major differences between wMetaC and sMetaC are (1) the cluster-to-cluster pairwise similarity of the former is calculated based on colocation weights of single cells in each cluster, whereas that of the latter is calculated based on the mean of the cell-to-cell correlation coefficients; (2) the individual clustering results of the former actually correspond to the same block of single cells but in different lower-dimensional space, whereas those of the latter correspond to different blocks of single cells; and (3) the former requires a voting scheme to integrate K individual clustering results, whereas the latter does not, and it just needs to reorganize the clusters to make clusters consistent across blocks.

The cluster-to-cluster pairwise similarity of wMetaC is calculated based on colocation weights of single cells in each cluster, whereas that of the sMetaC is calculated based on the Pearson's correlation coefficient of the mean cluster-wise feature vectors after ensemble RP. Specifically, in sMetaC, given two clusters G^u and G^v that were obtained by wMetaC (note that these two clusters may or may not belong to the same block of single cells), we calculated the similarity between these two clusters in sMetaC as follows

$$S_{sMetaC}\left(G^u,G^v\right)=\mathbf{c}\mathbf{o}\mathbf{r}\left(\frac{1}{\left|G^u\right|}{\sum }_{i\in G^u}{\mathit{p}}_i^u,\frac{1}{\left|G^v\right|}{\sum }_{j\in G^v}{\mathit{p}}_j^v\right),$$

where cor(·, ·) is the Pearson's correlation coefficient of two vectors, ${\mathit{p}}_i^u$ and ${\mathit{p}}_j^v$ are the dimension-reduced feature vectors after ensemble RP for the ith cell in Cluster G^u and the jth cell in Cluster G^v, and |G^u| and |G^v| are the numbers of cells in Cluster G^u and Cluster G^v, respectively.

Determining the optimal number of clusters

SHARP determines the optimal number of clusters by using three criteria that are based on internal evaluations of the clustering results (Supplemental Methods).

Time complexity analysis

SHARP includes four steps for clustering: (1) data partition, (2) RP, (3) wMetaC, and (4) sMetaC. For the scRNA-seq data matrix $\mathit{M}\in {\mathcal{R}}^{D\times N}$, SHARP first divides the data into B blocks, the bth block with N_b single cells. According to the “data partition” section, N_b ≤ n, where n is a fixed user-defined parameter enabling that one application of RP-based clustering runs sufficiently fast. Our analysis (Supplemental Fig. S12) shows that $n=1500\mathrm{or}2000$ is a good balance between performance and speed in our case. Then, for each block, one run of RP requires time complexity of $O\left(nd\sqrt{D}\right)$ (Johnson and Lindenstrauss 1984), where $d=\lceil \log \left(N\right)/{\in }^2\rceil \ll D$. Note here, d is calculated based on N rather than n for dimension-reduction consistency across blocks. Practically, in the 13 reported scRNA-seq data sets with numbers of cells smaller than 10,000, the dimension can be reduced by 42 to 238 times (i.e., D/d), depending on the number of single cells and the number of genes. SHARP requires several (i.e., K) runs of RPs (with complexity of $O\left(Knd\sqrt{D}\right)$). Subsequently, SHARP uses a hierarchical clustering (hclust) with “ward.D” for each of the K RPs, thus with an overall time complexity of $O\left(K\left(nd\sqrt{D}+n^2\right)\right)$ (note that the time complexity of hclust in R package is O(n²)) (Murtagh and Legendre 2014). Later, wMetaC, essentially a hclust for the individual predicted clusters (also without loss of generality, suppose the number of clusters for each RP-based clustering is equally C₁, where C₁ ≪ n), was applied to each block (in total, time complexity of $O(K\left(nd\sqrt{D}+n^2\right)+{(K{C}_1)}^2)$). Finally, SHARP integrated the results of all blocks by proposing a method called sMetaC, whose time complexity is similar to wMetaC except the number of instances is different (similarly, we can suppose the number of clusters in each block is equally C₂, where C₂ ≪ n). In this case, the total time complexity is $O\left(B\right[K\left(nd\sqrt{D}+n^2\right)+{\left(K{C}_1\right)}^2]+{\left(B{C}_2\right)}^2)$. Practically, K, B, C₁, and C₂ are very small; thus, the time complexity of SHARP can be written as $O\left(KN\left(d\sqrt{D}+n\right)\right)$. Because n is fixed across different data sets, $d=\lceil \log \left(N\right)/{\in }^2\rceil$ and D is usually larger than 10,000; thus $d\sqrt{D}>n$, and therefore, the time complexity of SHARP is essentially $O\left(N\log \left(N\right)\sqrt{D}\right)$.

On the other hand, among the compared state-of-the-art methods, t-SNE plus k-means is arguably the fastest. Theoretically, t-SNE requires O(DN log(N)) for dimension reduction to two- or three-dimensional space (van der Maaten 2014). For t-SNE plus k-means for clustering, the time complexity is O(DN log(N) + 2Nki), where k is the number of clusters, and i is the number of iterations. Thus, the total time complexity for t-SNE + k-means is O(DNlog(N)).

All the tests except for the 1.3-million-cell data set were performed using a single core on an Intel Xeon CPU E5-2699 v4 @ 2.20-GHz system with 500-GB memory. To run 1.3 million cells, we used 16 cores on the same system.

Visualization

For visualization, SHARP uses a weighted combination of the dimension-reduced feature matrix and the cell-to-cluster matrix derived from the clustering results. The former matrix is obtained by three steps: (1) applying K runs of RPs for each block of the large-scale scRNA-seq data, (2) combining these block-wise matrices to obtain K RP-based dimension-reduced matrices, and (3) averaging these K matrices into one ensemble matrix. For the latter matrix, we constructed a N × pC matrix, where N is the number of single cells, and pC is the predicted number of clusters. If the ith single cell is predicted to be in the jth cluster, then the element of the ith row and jth column is one; otherwise, it is zero. Subsequently, these two matrices were combined with different weights to formulate the visualization matrix, which is the input matrix of t-SNE for visualization.

First, both the dimension-reduced feature matrix $\mathit{A}\in {\mathcal{R}}^{N\times d}$ (where N is the number of cells, and d is the number of dimensions after dimension reduction) and the cell-to-cluster matrix $\mathit{B}\in {\mathcal{R}}^{N\times pC}$ (where pC is the predicted number of clusters) are centered and scaled along each dimension across cells, and we notate the results as $\overline{\mathit{A}}$ and $\overline{\mathit{B}}$. Then, these two matrices are combined as follows: $\overline{\mathit{V}}=\left[w\overline{\mathit{A}},\overline{\mathit{B}}\right]$, where $\overline{\mathit{V}}$ is the input matrix to t-SNE for visualization, and w > 0 is the weight ratio of the dimension-reduction feature matrix over the cell-to-cluster matrix. If 0 < w < 1, more weight will be given to cell-to-cluster matrix, suggesting that the clustering results are believed to be better for visualization; if w > 1, more weight will be given to the dimension-reduced feature matrix, which indicates that the data in dimension-reduced space can be more suitable for visualization. Although it is possible to use some algorithms to optimize w, we adopted an empirical value (i.e., w = 2) by default, which is robust for better visualization across different scRNA-seq data sets. For flexibility, we also provided an extra option to allow users to define their own w.

Based on the clustering results, SHARP can further detect cell-type-associated genes for each cluster. We adopted a method similar to SC3 except for three points: (1) Besides P-value and area under receiver operating curve (AUROC), SHARP uses two more criteria to select marker genes, namely, cluster-mean fold change (FC) and expression sparsity (i.e., the percentage of expressions across all cells); (2) SHARP uses an adaptive threshold instead of a hard-threshold (i.e., P-value < 0.01 and AUROC > 0.85); and (3) SHARP uses a parallelization way to calculate all of the criteria mentioned above.

Simulated data

In this study, we have generated three simulated scRNA-seq data from the Tabula Muris Consortium (The Tabula Muris Consortium 2018). Specifically, we only selected the data from the microfluidic droplet–based method, and three simulated data were generated, namely, mdata3, mdata6, and mdata8. mdata3 was generated by mixing scRNA-seq data from three organs, including heart and aorta, thymus, and liver; mdata6 was generated from six organs, including heart and aorta, thymus, liver, bladder, kidney, and tongue; and mdata8 was generated from eight organs, including heart and aorta, thymus, liver, bladder, kidney, tongue, spleen, and trachea. Note that only those filtered data by the original paper were used. The total numbers of single cells for mdata3, mdata6, and mdata8 are 3898, 16,717, and 37,538, respectively.

Adding dropouts

To further show the robustness of SHARP against scRNA-seq dropout events, we artificially added dropouts to a benchmarking data set (e.g., Montoro_small). Specifically, we randomly selected a percentage (e.g., 1%, 5%, 10%, 15%, and 20%) of nonzero expressions from the Montoro_small data set and then set them to be zero. In other words, the dropout percentage here refers to the added dropout percentage.

Public data sets used in this study

Single-cell RNA-seq data were obtained from the NCBI Gene Expression Omnibus (GEO; https://www.ncbi.nlm.nih.gov/geo/) accession numbers provided by their respective original publications. We downloaded the 1.3-million single-cell data set from the 10x Genomics website: https://support.10xgenomics.com/single-cell-gene-expression/datasets/1.3.0/1M_neurons. The scRNA-seq data from the Tabula Muris Consortium was downloaded from figshare: https://figshare.com/projects/Tabula_Muris_Transcriptomic_characterization_of_20_organs_and_tissues_from_Mus_musculus_at_single_cell_resolution/27733.

Software availability

The source code for SHARP is available at GitHub (https://github.com/shibiaowan/SHARP) and as Supplemental Code.

Competing interest statement

The authors declare no competing interests.