netNMF-sc: leveraging gene–gene interactions for imputation and dimensionality reduction in single-cell expression analysis

Abstract

Single-cell RNA-sequencing (scRNA-seq) enables high-throughput measurement of RNA expression in single cells. However, because of technical limitations, scRNA-seq data often contain zero counts for many transcripts in individual cells. These zero counts, or dropout events, complicate the analysis of scRNA-seq data using standard methods developed for bulk RNA-seq data. Current scRNA-seq analysis methods typically overcome dropout by combining information across cells in a lower-dimensional space, leveraging the observation that cells generally occupy a small number of RNA expression states. We introduce netNMF-sc, an algorithm for scRNA-seq analysis that leverages information across both cells and genes. netNMF-sc learns a low-dimensional representation of scRNA-seq transcript counts using network-regularized non-negative matrix factorization. The network regularization takes advantage of prior knowledge of gene–gene interactions, encouraging pairs of genes with known interactions to be nearby each other in the low-dimensional representation. The resulting matrix factorization imputes gene abundance for both zero and nonzero counts and can be used to cluster cells into meaningful subpopulations. We show that netNMF-sc outperforms existing methods at clustering cells and estimating gene–gene covariance using both simulated and real scRNA-seq data, with increasing advantages at higher dropout rates (e.g., >60%). We also show that the results from netNMF-sc are robust to variation in the input network, with more representative networks leading to greater performance gains.

Single-cell RNA-sequencing (scRNA-seq) technologies provide the ability to measure gene expression within/among organisms, tissues, and disease states at the resolution of a single cell. These technologies combine high-throughput single-cell isolation techniques with second-generation sequencing, enabling the measurement of gene expression in hundreds to thousands of cells in a single experiment. This capability overcomes the limitations of microarray and RNA-seq technologies, which measure the average expression in a bulk sample, and thus have limited ability to quantify gene expression in individual cells or subpopulations of cells present in low proportion in the sample (Wang et al. 2009).

The advantages of scRNA-seq are tempered by undersampling of transcript counts in single cells caused by inefficient RNA capture and low numbers of reads per cell. The result of scRNA-seq is a gene × cell matrix of transcript counts containing many dropout events that occur when no reads from a gene are measured in a cell, even though the gene is expressed in the cell. The frequency of dropout events depends on the sequencing protocol and depth of sequencing. Cell-capture technologies, such as Fluidigm C1, sequence hundreds of cells with high coverage (1–2 million reads) per cell, resulting in dropout rates ≈20%–40% (Ziegenhain et al. 2017). Microfluidic scRNA-seq technologies, such as 10x Genomics Chromium platform, Drop-Seq, and inDrops sequence thousands of cells with low coverage (1000–200,000 reads) per cell, resulting in higher dropout rates, up to 90% (Zilionis et al. 2017). Furthermore, transcripts are not dropped out uniformly at random, but in proportion to their true expression levels in that cell.

In recent years, multiple methods have been introduced to analyze scRNA-seq data in the presence of dropout events. The first three steps that constitute most scRNA-seq pipelines are (1) imputation of dropout events; (2) dimensionality reduction to identify lower-dimensional representations that explain most of the variance in the data; and (3) clustering to group cells with similar expression. Imputation methods include MAGIC (Van Dijk et al. 2018), a Markov affinity-based graph method; scImpute (Li and Li 2018), a method that distinguishes dropout events from true zeros using dropout probabilities estimated by a mixture model; and SAVER (Huang et al. 2018), a method that uses gene–gene relationships to infer the expression values for each gene across cells. Dimensionality reduction methods include ZIFA (Pierson and Yau 2015), a method that uses a zero-inflated factor analysis model; SIMLR (Wang et al. 2017), a method that uses kernel based similarity learning; and two matrix factorization methods, pCMF (Durif et al. 2019) and scNBMF (Sun et al. 2019), which use a gamma-Poisson and negative binomial model factor model, respectively. Clustering methods include BISCUIT, which uses a Dirichlet process mixture model to perform both imputation and clustering (Azizi et al. 2017); and CIDR, which uses principal coordinate analysis to cluster and impute cells (Lin et al. 2017b). Other methods, such as Scanorama, attempt to overcome limitations of scRNA-seq by merging data across multiple experiments (Hie et al. 2019). Supplemental Table S1 gives a list of these and other related methods.

We introduce a new method, netNMF-sc, which leverages prior information in the form of a gene coexpression or physical interaction network during imputation and dimensionality reduction of scRNA-seq data. netNMF-sc uses network-regularized non-negative matrix factorization (NMF) to factor the transcript count matrix into two low-dimensional matrices: a gene matrix and a cell matrix. The network regularization encourages two genes connected in the network to have a similar representation in the low-dimensional gene matrix, recovering structure that was obscured by dropout in the transcript count matrix. The resulting matrix factors can be used to cluster cells and impute values for dropout events. Although netNMF-sc may use any type of network as prior information, a particularly promising approach is to leverage tissue-specific gene coexpression networks derived from earlier RNA-seq and microarray studies of bulk tissue and recorded in large databases such as COXPRESdb (Okamura et al. 2015), COEXPEDIA (Yang et al. 2017), GeneSigDB (Culhane et al. 2010), and others (Lee et al. 2004; Wu et al. 2010). netNMF-sc provides a flexible and robust approach for incorporating prior information about genes in imputation and dimensionality reduction of scRNA-seq data.

Results

netNMF-sc algorithm

Let X ∈ ℝ^m×n be a matrix of transcript counts from an scRNA-seq experiment for m transcripts and n single cells. It has been observed that the majority of variation in transcript counts is explained by a small number of gene expression signatures that represent cell types or cell states. Because X is a non-negative matrix, non-negative matrix factorization (NMF) (Lee and Seung 1999) can be used to find a lower-dimensional representation. NMF factors X into an m × d gene matrix W and a d × n cell matrix H, where d ≪ m, n, and the elements of both W and H are non-negative. We formulate this factorization as a minimization problem,

$$\underset{\mathbf{W}\ge 0,\mathbf{H}\ge 0}{min}\sum _{i,j}\left(x_{ij}\log \frac{x_{ij}}{\mathbf{W}\mathbf{H}{|}_{ij}}-x_{ij}+\mathbf{W}\mathbf{H}{|}_{ij}\right)$$

in which ≥ indicates non-negative matrices whose entries are ≥0.

The original NMF publication (Lee and Seung 1999) proposed two cost functions to measure the difference between X and WH: the the Kullback-Leibler (KL) divergence given above and the Euclidean distance, ${\parallel \mathbf{X}-\mathbf{W}\mathbf{H}\parallel }^2$. We use KL divergence because it is equivalent to maximizing the likelihood of the Poisson model $x_{ij}\sim \mathrm{Pois}\left(\widehat{x_{ij}}\right)$, where $\hat{\mathbf{X}}=\mathbf{W}\mathbf{H}$ (Févotte and Cemgil 2009). The Poisson distribution (Townes et al. 2019) and the negative binomial distribution (Hafemeister and Satija 2019; Svensson 2020) without zero inflation have been shown to provide a good fit for droplet-based transcript (UMI) count data. The Poisson model can be applied directly to transcript count matrices, eliminating the need to log-transform the transcript counts to better fit a Gaussian distribution (Prabhakaran et al. 2016; Li and Li 2018).

Log-transformation has been shown to introduce bias transcript in count data (Hafemeister and Satija 2019; Townes et al. 2019). Because of high dropout rates and other sources of variability in scRNA-seq data, the direct application of NMF to the transcript count matrix X may lead to components of W and H that primarily reflect technical artifacts rather than biological variation in the data. For example, Finak et al. (2015) observe that the number of dropped-out transcripts in a cell is the primary source of variation in several scRNA-seq experiments.

To reduce the effect of technical artifacts on the factorization, we propose to combine information across transcripts using prior knowledge in the form of a gene–gene interaction network. We incorporate network information using graph-regularized NMF (Cai et al. 2008), which includes a regularization term to constrain W based on prior knowledge of gene coexpression. The resulting method, netNMF-sc, performs matrix factorization by solving the following optimization problem:

$$\underset{\mathbf{W}\ge 0,\mathbf{H}\ge 0}{min}\sum _{i,j}\left(x_{ij}\log \frac{x_{ij}}{\mathbf{W}\mathbf{H}{|}_{ij}}-x_{ij}+\mathbf{W}\mathbf{H}{|}_{ij}\right)+\lambda \mathrm{Tr}({\mathbf{W}}^T\mathbf{L}\mathbf{W})$$

where λ is a positive real constant, L is the Laplacian matrix of the gene–gene interaction network, and Tr(·) indicates the trace of the matrix.

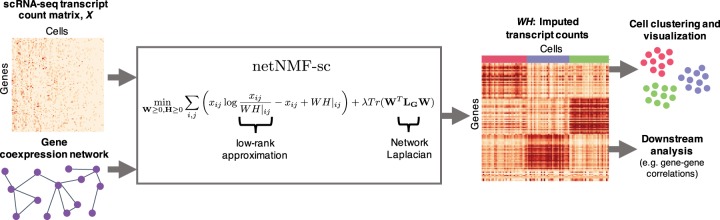
netNMF-sc uses the resulting matrix H to cluster cells and the product matrix $\hat{\mathbf{X}}=\mathbf{W}\mathbf{H}$ to impute values in the transcript count matrix X, including dropout events (Fig. 1).

Figure 1.

Overview of netNMF-sc. Inputs to netNMF-sc are: a transcript count matrix X from scRNA-seq and a gene coexpression network. netNMF-sc factors X into two lower-dimensional matrices, a gene matrix W and a cell matrix H, using the network to constrain the factorization. The product matrix $\hat{\mathbf{X}}=\mathbf{W}\mathbf{H}$ imputes dropped-out values in the transcript count matrix X. H is useful for clustering and visualizing cells in lower-dimensional space, whereas WH is useful for downstream analysis such as quantifying gene–gene correlations.

We also derive a formulation of netNMF-sc with the Euclidean distance cost function ${\parallel \mathbf{X}-\mathbf{W}\mathbf{H}\parallel }^2$ (Supplemental Section S1), which is useful for (log-transformed) data with zero inflation, for example, read count data lacking UMIs. We show that netNMF-sc with the Euclidean distance cost function has similar clustering performance (ARI) to netNMF-sc with the KL divergence cost function on read count data from Supplemental Figure S1A–D and Buettner et al. (2015).

We select the regularization parameter λ as well as the dimension d of the factor via holdout validation (Supplemental Section S2; Supplemental Fig. S2).

Evaluation on simulated data

We compared netNMF-sc and several other methods for scRNA-seq analysis on a simulated data set containing 5000 genes and 1000 cells and consisting of six clusters with 300, 250, 200, 100, 100, and 50 cells per cluster, respectively. We generated this data using a modified version of the Splatter simulator (Zappia et al. 2017), modeling gene–gene correlations using a gene coexpression network from Yang et al. (2017). We simulated dropout events using one of two models: a multinomial dropout model (Linderman et al. 2018; Zhu et al. 2018) and a double exponential dropout model (Azizi et al. 2017; Li and Li 2018). Further details are in Methods.

We compared the performance of netNMF-sc to PCA, scNBMF, MAGIC, scImpute, and NMF at dropout rates ranging from 0 (no dropout) to 0.80 (80% of the values in the data are zero), using 20 simulated data sets for each dropout rate. We clustered the output from each method using k-means clustering with k = 6 to match the number of simulated clusters (for more details on clustering, see Supplemental Section S4). We selected d = 10 for NMF, scNBMF, and netNMF-sc, and λ = 10 for netNMF-sc based on holdout validation (Supplemental Section S2).

For netNMF-sc, we used a randomly selected subnetwork S = (V_S, E_S) of the same gene coexpression network G = (V,E) (Yang et al. 2017) used to create the simulated data (Supplemental Section S5). This is intended as a positive control, to show the benefit of netNMF-sc when a highly informative network is available. We note that although S may correlate more strongly with the underlying coexpression structure of the data than we would expect from biological data sets, the edges in S do not perfectly correspond to coexpressed genes in the simulated data. This is because only a subset of genes from S are differentially expressed in the simulated data and some pairs of differentially expressed genes in the simulated data are not represented by an edge in S. When we compare the correlation matrix of the simulated data to S, we observe 317 gene pairs with R² ≥ 0.5 are captured by edges in S, but 828 gene pairs with R² ≥ 0.5 are not.

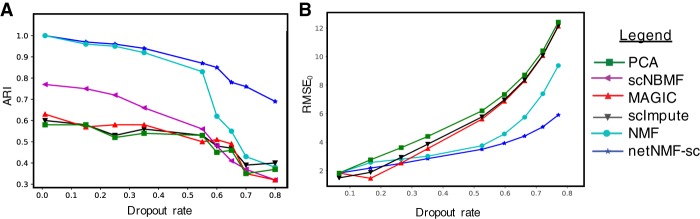
We found that the clusters identified using netNMF-sc across all dropout rates had higher overlap with true clusters compared to the clusters identified using other methods (Fig. 2A). The improvement for netNMF-sc was especially pronounced at higher dropout rates; for example, at a dropout rate of 0.7, netNMF-sc had an adjusted Rand index (ARI) = 0.78, compared to 0.47 for the next best performing method, NMF. We observe a similar improvement in clustering performance using the double exponential dropout model (Supplemental Fig. S8A,B). At a dropout rate of 0.7, netNMF-sc had ARI = 0.79, compared to 0.41 for the next best performing method, scImpute (Supplemental Fig. S8A).

Figure 2.

Comparison of netNMF-sc and other methods on a simulated scRNA-seq data set containing 1000 cells and 5000 genes, with dropout simulated using a multinomial dropout model. (A) Adjusted Rand Index (ARI) between the true and inferred cell clusters obtained as a function of dropout rate. (B) RMSE at dropped-out entries (RMSE₀) between true and imputed transcript counts.

We compared the performance of netNMF-sc and other methods on the task of imputation by computing the RMSE between X′, the simulated transcript count matrix before dropout, and the imputed matrix $\hat{\mathbf{X}}=\mathbf{W}\mathbf{H}$. We first compute RMSE₀, the RMSE between X′ and the imputed matrix $\hat{\mathbf{X}}$ restricted to entries for which dropout events were simulated. At low dropout rates (<0.25), netNMF-sc had similar RMSE₀ as other methods; at higher dropout rates, netNMF-sc had lower values of RMSE₀ (Fig. 2B). For example, at a dropout rate of 0.7, netNMF-sc had RMSE₀ = 4.8 compared to 7.4 for the next best performing method, NMF (Fig. 2B). Similar results were observed on data simulated using the double exponential dropout model. At a dropout rate of 0.7, netNMF-sc had RMSE₀ = 8.3, slightly above MAGIC (RMSE₀ = 7.9) but substantially better than NMF (RMSE₀ = 15.9) and scImpute (RMSE₀ = 18.3). When we compute the RMSE between all entries of the transcript count matrix, scImpute outperforms other methods at low dropout rates (<0.25) because scImpute does not attempt to impute nonzero counts. However, at dropout rates above 0.6, netNMF-sc has the lowest RMSE (Supplemental Fig. S5). Additionally, we investigated the contribution of the input network to the performance of netNMF-sc. We found that the addition of up to 70% random edges did not have a large effect on the performance (Supplemental Fig. S7).

Evaluation on cell clustering

We compared netNMF-sc and other scRNA-seq methods in their ability to cluster cells into meaningful cell types using three scRNA-seq data sets. For all data sets, we normalized the transcript count matrices following Zheng et al. (2017) to reduce the effect of differences in the library size or total number of transcripts sequenced in each cell (Supplemental Section S3). We used the normalized count data for all methods except PCA and scImpute. For these two methods, we applied a log-transformation (log ₂(X + 1)) to the transcript count matrix because these methods assume the data were generated from a Gaussian distribution.

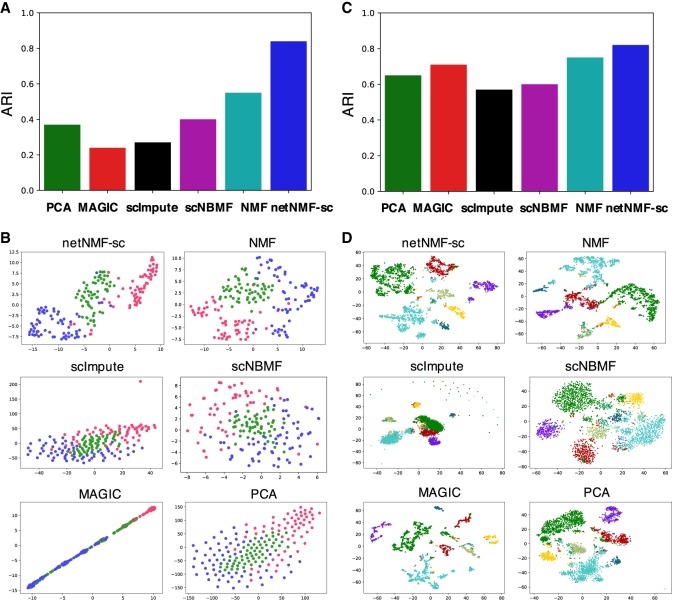
The first data set contains 182 mouse embryonic stem cells (mESCs) that were flow sorted into one of three cell cycle phases—G, S, and G2/M—and sequenced using the Fluidigm C1 platform combined with Illumina sequencing (Buettner et al. 2015). The data contain 9571 genes and a zero-proportion of 0.41. We computed cell clusters for each method as described in Supplemental Section S4. We ran NMF, scNBMF, and netNMF-sc with d = 5 dimensions, a value selected via holdout validation. For netNMF-sc, we used a network from the ESCAPE database (Xu et al. 2014), which contains 153,920 protein-mRNA regulatory interactions from mESCs, with edge weights of 1 for positive correlations and −1 for negative correlations. We selected λ = 5 via holdout validation. For PCA we used the top 136 principal components, which explained 90% of the variance. We compared the cell clusters obtained by running each method followed by k-means clustering on the low-dimensional representation, using both the true cluster number k = 3 as well as the value k that produced the highest silhouette score in the range 2 ≤ k ≤ 20. We also ran PhenoGraph (Levine et al. 2015), a graph clustering method, but found that performance was similar or worse than k-means for all methods (Supplemental Fig. S10A–D). We found that netNMF-sc outperformed other methods at clustering cells into the three cell cycle stages with an adjusted Rand index (ARI) = 0.84 compared to 0.24 for MAGIC and 0.37 for scImpute (Fig. 3A,B). Although MAGIC did not perform as well as netNMF-sc in clustering the cells into distinct cell cycle phases, it did identify a trajectory between the phases of the cell cycle, which may be biologically meaningful. However, MAGIC also identified a trajectory between clusters in the simulated data above, although no trajectory was present (Supplemental Fig. S6).

Figure 3.

Clustering performance on scRNA-seq data. (A) Adjusted Rand index (ARI) for cell clusters obtained by methods on mouse embryonic stem cell (mESC) scRNA-seq data from Buettner et al. (2015), with cell cycle labels obtained by flow sorting. (B) t-SNE projections of cells in reduced dimensional space. (C) Clustering results on brain cell data set from Zeisel et al. (2015) into nine cell types. (D) t-SNE projections of cells in reduced dimensional space.

To quantify the contribution of the network to the performance of netNMF-sc, we ran netNMF-sc with three additional networks: a generic gene coexpression network from COEXPEDIA (Yang et al. 2017), a k-nearest neighbors network (KNN), and a random network with the same degree distribution as the ESCAPE network. The k-nearest neighbors network was constructed by placing an edge between the 10 nearest neighbors of each gene in the input data matrix X, based on Euclidean distance (for more details, see Supplemental Section S6). We found that the ESCAPE coexpression network gave the best performance, with an ARI of 0.84 compared to 0.76 for COEXPEDIA, 0.68 for KNN, 0.63 for the random network, and 0.60 for NMF (Supplemental Fig. S9A,B). This result is consistent with the fact that the ESCAPE network was constructed using the same cell type as the scRNA-seq data, mESCs, whereas the COEXPEDIA network was constructed using cells from many different cell types. This shows the benefit of prior knowledge that is matched to the cell types in the scRNA-seq data. We note that netNMF-sc with any of the networks outperformed NMF, although the difference for the random network was negligible, suggesting that some of the advantage of netNMF-sc may result from enforcing sparsity on W.

The second data set, from Zeisel et al. (2015), contains 3005 mouse brain cells from nine cell types sequenced with the Single-Cell Tagged Reverse Transcription (STRT-Seq) protocol. The data contain 8345 genes and a zero-proportion of 0.60. For netNMF-sc we used a gene coexpression network from McKenzie et al. (2018) containing 157,306 gene–gene correlations across brain cell types (astrocytes, neurons, endothelial cells, microglia, and oligodendrodytes), and selected λ = 1 via holdout validation. NMF, scNBMF, and netNMF-sc were run with d = 30 dimensions, selected via holdout validation. For PCA we used the top 82 principal components, which explained 90% of the variance. For each method we ran k-means with k = 9. We found that netNMF-sc outperformed other methods with an ARI = 0.82 compared to the next best performing methods, NMF and MAGIC, with ARI = 0.72 and 0.71, respectively (Fig. 3C,D). netNMF-sc also outperformed other methods with k selected using the silhouette score as well as using the clustering method PhenoGraph, with scNBMF performing second best (Supplemental Fig. S11A–D).

The third data set contains 2022 brain cells from an E18 mouse sequenced using 10x Genomics scRNA-seq platform (https://support.10xgenomics.com/single-cell-gene-expression/datasets/2.1.0/neuron_2000). The data contain 13,509 genes with transcript counts ≥10 and a zero-proportion of 0.84. Because this data set does not have known cell clusters, we compare the cell clusters computed by each method with the 16 brain cell types reported in a separate 10x Genomics scRNA-seq data set of 1.3 million cells from the forebrains of two different E18 mice that was analyzed using bigSCale (Iacono et al. 2018), a framework for analyzing large-scale transcript count data. For netNMF-sc, we used a gene coexpression network from McKenzie et al. (2018) containing 157,306 gene–gene correlations across brain cell types (astrocytes, neurons, endothelial cells, microglia, and oligodendrodytes) and selected λ = 50 via holdout validation. NMF and netNMF-sc were run with d = 20 dimensions, selected via holdout validation. For PCA we used the top 372 principal components, which explained 90% of the variance. We used k = 16 in k-means clustering to match the number of brain cell types reported in bigSCale. We matched the cell clusters output by each method to the 16 cell types reported in bigSCale as follows. We computed the overlap between the top 200 overexpressed genes in each cluster (calculated with a one-sided t-test between cells in and out of the cluster) and the published marker genes for each of the 16 cell types, and selected the cell type with the lowest P-value of overlap (Fisher's exact test). If the cluster was not enriched for any cell type with Bonferroni-corrected P < 0.05, then we marked the cluster as unclassified.

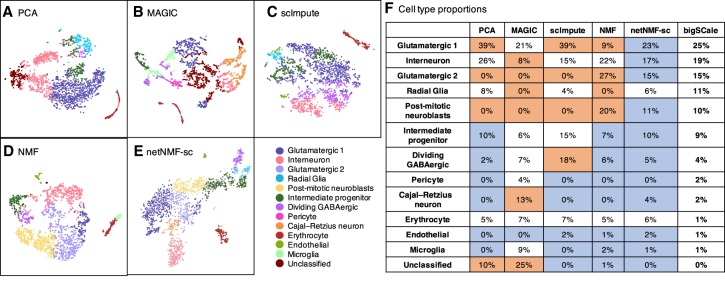
Although the true class assignment for each cell is unknown, both scRNA-seq data sets were generated from the forebrains of E18 mice, and thus we expect that the proportions of each cell type should be similar across both data sets. We found that the proportions of each cell type identified by netNMF-sc (Fig. 4E) were the closest (many within 2%) to the proportions reported (Fig. 4F; Iacono et al. 2018). In both cases, the cell type with the largest proportion is glutamatergic neurons, followed by interneurons, and then radial glia and post-mitotic neuroblasts. Other cell types, such as dividing GABAergic progenitors and Cajal–Retzius neurons, were found in smaller proportions. In contrast, MAGIC (Fig. 4B) finds a large population (13%) of Cajal–Retzius neurons, but scImpute (Fig. 4C) finds a large population (18%) of dividing GABAergic progenitor cells—both proportions more than threefold greater than in bigSCale or netNMF-sc. Clusters computed from PCA (Fig. 4A) and from NMF (Fig. 4D) also differed substantially from the proportions reported in bigSCale (Fig. 4F); for example, the proportion of post-mitotic neuroblasts was 0% in PCA, 20% in NMF, but 10% in bigSCale. We found that the number of unclassified cells varied substantially across the methods. Clusters computed from scImpute and netNMF-sc had no unclassified cells, whereas PCA, MAGIC, and NMF had 10%, 25%, and 1% of cells unclassified, respectively.

Figure 4.

Identification of mouse brain cell types. (A–E) t-SNE projections of scRNA-seq data from 2022 brain cells from an E18 mouse. Colors indicate cell types as derived in bigSCale analysis of 1.3 million E18 mouse brain cells (Iacono et al. 2018). (F) Proportions of each cell type predicted by each method. Entries highlighted in blue are within 2% of the proportions from bigSCale. Entries highlighted in orange differ by >10% from the proportions from bigSCale.

We further examined the smallest cell cluster identified by netNMF-sc, containing only 14 cells. This cluster was enriched (P ≤ 2.2 × 10⁻¹⁶) for microglia marker genes reported by bigSCale, including well-studied marker genes such as Csf1r, Olfml3, and P2ry12 (Wes et al. 2016). These 14 cells represented 0.7% of the 2022 sequenced cells, closely matching the proportion of microglia reported by bigSCale (1%). NMF and MAGIC also identified clusters of microglia cells, but the differentially expressed genes in these clusters were less enriched for microglia marker genes (P ≤ 4.1 × 10⁻¹³ and P ≤ 5.5 × 10⁻³, respectively). The NMF cluster contained 65 cells but did not include any of the 14 cells classified as microglia by netNMF-sc. In addition, these 65 cells were equally enriched for erythrocyte marker genes (P ≤ 3.2 × 10⁻¹¹). The MAGIC cluster contained 174 cells, a much larger proportion (9%) of the cell population than the 1% reported by bigSCale. This cluster included the 14 microglia identified by netNMF-sc but also 160 other cells. The additional 160 cells present in the cluster were not enriched for microglia marker genes (P ≤ 1.2 × 10⁻¹) but were enriched for glutamatergic marker genes (P ≤ 1.5 × 10⁻²). This suggests that MAGIC erroneously grouped together different types of cells.

We found 436 genes were differentially expressed between the 14 microglia identified by netNMF-sc and the other 2008 cells (FDR ≤ 0.01). All 50 microglia marker genes from bigSCale were included in this set, including the two most highly differentially expressed genes Ccl4 (fold change 12.5) and C1qc (fold change 8.7). Of the top 20 differentially expressed genes identified in the netNMF-sc microglial cells, several were reported in other studies as microglia genes (Sousa et al. 2017) but not in bigSCale; these include Hexb (fold change 7.8) and Lgmn (fold change 5.8). Several potential novel marker genes were in the 20 differentially expressed genes, including Cstdc5 (fold change 4.5) and Stfa1 (fold change 4.2). These results suggest that netNMF-sc improves clustering of cells into biologically meaningful cell types from scRNA-seq data with high dropout—even when the cell type is represented by only a small number (<20) of cells—and facilitates the identification of potentially novel marker genes.

Recovering marker genes and gene–gene correlations

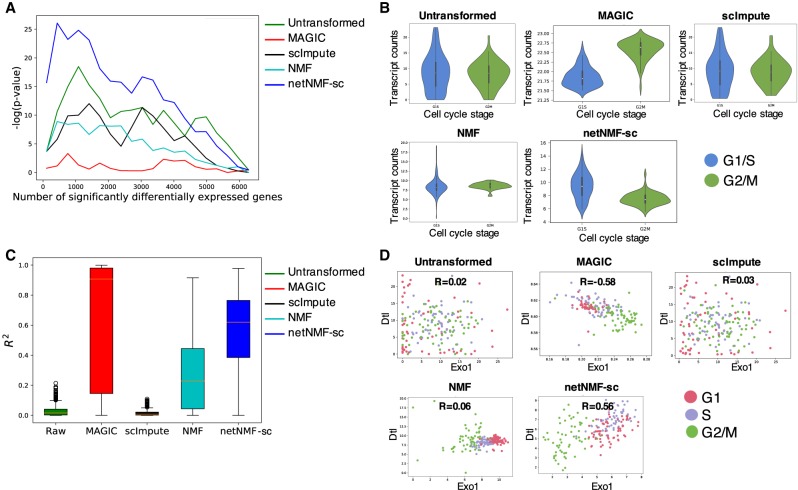
Finally, we investigated how well each method recovers differentially expressed marker genes and gene–gene correlations from scRNA-seq data. First, we examined cell cycle marker genes. We obtained a set of 67 periodic marker genes whose expression has been shown to vary over the cell cycle across multiple cell types (Dominguez et al. 2016). This set contains 16 genes with peak expression in G1/S phase and 51 genes with peak expression during G2/M phase. We expect to observe a significant number of these periodic genes among the top differentially expressed genes between G1/S phase and G2/M phase cells in the cell cycle data set from Buettner et al. (2015). We compared the ranked list of differentially expressed genes from data imputed by netNMF-sc to the ranked lists of differentially expressed genes from the untransformed data and data imputed NMF, MAGIC, scImpute. We found that periodic genes ranked very highly in netNMF-sc results (P ≤ 3.2 × 10⁻¹¹, Wilcoxon rank-sum test), an improvement compared to their ranking in the untransformed data (P ≤ 4.5 × 10⁻³, Wilcoxon rank-sum test) (Fig. 5A). In contrast, the data imputed with NMF, MAGIC, and scImpute resulted in a lower ranking of the periodic genes (P ≥ 0.05, Wilcoxon rank-sum test). Additionally, we found that in data imputed by MAGIC, some periodic genes had expression patterns that were out of phase with the cell cycle. For example, Exo1, which peaks in G1/S phase, had lower expression in G1/S phase cells compared to G2/M phase cells (P ≤ 2.2 × 10⁻¹⁶, Wilcoxon rank-sum test) in MAGIC-imputed data (Fig. 5B). In contrast, the peak in Exo1 expression during G1/S phase is observed in the results from netNMF-sc (P ≤ 6.7 × 10⁻¹², Wilcoxon rank-sum test), whereas Exo1 is not differentially expressed in the untransformed data (P ≤ 0.17, Wilcoxon rank-sum test) (Fig. 5B).

Figure 5.

Comparison of differential expression of marker genes and gene–gene correlations in untransformed data from Buettner et al. (2015) and data imputed using netNMF-sc, NMF, scImpute, and MAGIC. (A) Overlap between differentially expressed genes and periodic genes (log P-values from Fisher's exact test). (B) Expression of the G1/S phase marker gene Exo1 in cells labeled as G1/S (blue) and cells labeled as G2/M (green) in data imputed by each method. In netNMF-sc inputed data, Exo1 is overexpressed in G1/S cells compared to G2/M cells (P ≤ 6.7 × 10⁻¹²), as expected. In contrast, in data imputed by MAGIC, Exo1 is underexpressed in G1/S cells compared to G2/M cells (P ≤ 2.2 × 10⁻¹⁶). Exo1 shows no difference in expression in untransformed and scImpute data. (C) Distribution of R² correlation coefficients between pairs of periodic genes in the cell cycle data. (D) Scatter plot of expression of two G1/S phase genes, Dtl and Exo1, across cells. These genes are positively correlated in data imputed by netNMF-sc (P ≤ 2.2 × 10⁻¹⁶), negatively correlated in data imputed by MAGIC (P ≤ 2.2 × 10⁻¹⁶), and uncorrelated in other methods.

We also investigated whether each method could recover gene–gene correlations between periodic marker genes in the cell cycle data. We expect pairs of periodic genes whose expression peaks during the same phase of the cell cycle to be positively correlated and pairs of genes that peak during different phases to be negatively correlated. Across all 2211 pairs of periodic marker genes, we found that the mean R² was 0.54 for netNMF-sc, compared to 0.73 for MAGIC, 0.29 for NMF, 0.02 for scImpute and 0.03 for untransformed data (Fig. 5C). Setting a stringent cutoff for significant correlation (R² ≥ 0.8, P ≤ 2.2 × 10⁻¹⁶), we found that 15% of the pairs of periodic genes were correlated in data imputed by netNMF-sc compared to 68% in data imputed by MAGIC, 0.8% in data imputed by NMF, and nearly 0% in data imputed by scImpute. Although the higher percentage of correlated gene pairs in MAGIC seems to be an advantage, the MAGIC-imputed data also contained a number of cell cycle marker genes, such as Exo1, whose expression signature was the opposite of what was expected. Such cases can result in incorrect correlations between pairs of marker genes. For example, marker genes Exo1 and Dtl both peak during G1/S phase and are expected to be positively correlated. However, MAGIC found negative correlation (R = −0.58, P ≤ 3.6 × 10⁻¹⁶) between these two genes. In contrast, netNMF-sc recovers the positive correlation (R = 0.56, P ≤ 2.2 × 10⁻¹⁶), but scImpute (R = 0.03, P ≤ 0.66) and NMF (R = 0.06, P ≤ 0.46) do not (Fig. 5D).

Overall, we found that in the data imputed by MAGIC, 19% of correlated periodic genes were correlated in the opposite direction than expected; that is, genes that peaked during the same phase were negatively correlated or genes which peaked during different phases were positively correlated. In contrast, in the data imputed by netNMF-sc, only 1% of the correlated periodic genes were correlated in the opposite direction than expected (Table 1). These results from MAGIC may be explained by the fact that MAGIC introduces a large number of gene–gene correlations during imputation, many of which may be spurious, as was previously reported (Huang et al. 2018). In fact, the majority (78%) of the gene pairs in the correlation matrix generated from data imputed by MAGIC were correlated (R² ≥ 0.8, P ≤ 2.2 × 10⁻¹⁶), compared to only 0.2% in the correlation matrix generated from data imputed by netNMF-sc and 0.005% in the correlation matrix generated from the untransformed data (Table 1).

Table 1.

Fraction of all pairs of genes and pairs of periodic genes with correlations (R² ≥ 0.8, P ≤ 2.2 × 10⁻¹⁶, Student's t-test) in the cell cycle data set

To examine whether these correlations identified by MAGIC and netNMF-sc represented real biological signal, we ran both methods on permuted data where the transcript counts were permuted independently in each cell. We found that 85% of the gene pairs were correlated (R² ≥ 0.8, P ≤ 2.2 × 10⁻¹⁶) in MAGIC-imputed data compared to only 0.2% of gene pairs in netNMF-sc imputed data (Table 1). This observation suggests that many of the gene–gene correlations found in the MAGIC-imputed cell cycle data may be spurious. Further investigation on simulated data suggests that such spurious correlations may be a consequence of the small number of cells: We found that MAGIC-imputed data had many correlations in transcript count matrices with approximately 200 cells but fewer correlations in imputed data with many (∼1000) cells (Supplemental Fig. S13). We also observed the number of gene–gene correlations found by MAGIC on permuted data increased rapidly with the diffusion parameter t before reaching a plateau (Supplemental Fig. S12B). In contrast, the number of gene–gene correlations found by netNMF-sc on permuted data decreased as the number of latent dimensions d increased (Supplemental Fig. S12A).

We performed a second analysis of differentially expressed marker genes and gene–gene correlations in scRNA-seq data from the MAGIC publication (Van Dijk et al. 2018) containing 7415 human transformed mammary epithelial cells (HMLEs), which were induced to undergo epithelial to mesenchymal transition (EMT) and then sequenced using the inDrops platform (Klein et al. 2015). We assessed how well each method recovered differential expression of 16 canonical EMT marker genes from Gibbons and Creighton (2018) (three genes with high expression in epithelial [E] cells and 13 genes with high expression in mesenchymal [M] cells). We found that the EMT marker genes ranked highly in netNMF-sc results (P ≤ 1.4 × 10⁻⁵, Wilcoxon rank-sum test), an improvement compared to their ranking in the untransformed data (P ≤ 3.1 × 10⁻³, Wilcoxon rank-sum test) (Supplemental Fig. S14A). MAGIC was the second-best method, ranking EMT genes highly (P ≤ 1.1 × 10⁻⁴, Wilcoxon rank-sum test) but below the performance of netNMF-sc. We observed that in data imputed by MAGIC, the E marker gene TJP1 had higher average expression in M cells than E cells (P ≤ 2.2 × 10⁻¹⁶) (Supplemental Fig. S14B). This resulted in TJP1 being negatively correlated (R = −0.57, P ≤ 2.2 × 10⁻¹⁶) with another epithelial marker gene, CDH1 in the MAGIC-imputed data. In contrast, these E marker genes showed positive correlation (R = 0.66, P ≤ 6.4 × 10⁻¹⁶) in the netNMF-sc imputed data and this correlation that was not apparent in the untransformed data (Supplemental Fig. S14C). We also investigated whether netNMF-sc could recover gene–gene correlations between EMT marker genes in E and M cells. We expect that pairs of E or M genes would show positive correlation, and pairs containing one E and one M gene would show negative correlations. In data imputed by netNMF-sc, 12% of the EMT gene pairs were correlated (R² ≥ 0.8, P ≤ 2.2 × 10⁻¹⁶), with all gene pairs correlated in the expected orientation (Supplemental Fig. S15). In data imputed by MAGIC, 23% of EMT gene pairs were correlated, but 5% were correlated in the opposite direction than expected (Supplemental Fig. S14D). Full details of this analysis are in the Supplemental Section S7.

Discussion

We present netNMF-sc, a method for performing dimensionality reduction and imputation of scRNA-seq data in the presence of high (>60%) dropout rates. These high dropout rates are common in droplet-based sequencing technologies, such as 10x Genomics Chromium, which are becoming the dominant technology for scRNA-seq. netNMF-sc leverages prior knowledge in the form of a gene coexpression network. Such networks are readily available for many tissue types, having been constructed from bulk RNA-sequencing data, or from other experimental approaches. To our knowledge, the only other method that uses network information to perform dimensionality reduction on scRNA-seq data is Lin et al. (2017a). However, this method assumes that there is no dropout in the data, and its performance with high dropout rates is unknown. Moreover, this method uses a neural network that is trained on a specific protein–protein interaction (PPI) network, whereas netNMF-sc can use any gene–gene interaction network. Another method, netSmooth (published during the preparation of this paper) (Ronen and Akalin 2018), uses network information to smooth noisy scRNA-seq matrices but does not perform dimensionality reduction.

We show that netNMF-sc outperforms state-of-the-art methods in clustering cells in both simulated and real scRNA-seq data. In addition, netNMF-sc is better able to distinguish cells in different stages of the cell cycle and to classify mouse embryonic brain cells into distinct cell types whose proportions mirror the cellular diversity reported in another study with a substantially greater number of sequenced cells. netNMF-sc imputes values for every entry in the input matrix, similar to MAGIC and in contrast to scImpute, which imputes values only for zero counts. Because transcript counts in scRNA-seq data are reduced for all genes, imputation of all values can improve clustering performance and better recover biologically meaningful gene–gene correlations. On multiple data sets, we show that netNMF-sc yields more biologically meaningful gene–gene correlations than other methods. However, one potential downside of imputation is “oversmoothing” of the data resulting in the introduction of artificial gene–gene correlations.

There are multiple directions for future improvement of netNMF-sc. First, netNMF-sc relies on existing gene–gene interaction networks. Although we have shown that generic gene coexpression networks (Yang et al. 2017) can improve clustering performance on human and mouse scRNA-seq data, netNMF-sc may not offer substantial improvements over existing methods on tissues or organisms where high-quality gene–gene interaction networks are not available. In the future, other prior knowledge could be incorporated into netNMF-sc, such as cell–cell correlations, which might be obtained from underlying knowledge of cell types or from spatial or temporal information. Second, there are several additional sources of variation in scRNA-seq data in addition to dropout, such as cell cycle and batch effects. netNMF-sc may be able to assist in removing these confounding effects by encouraging correlations between genes that are connected in the network, thus down-weighting correlations induced by these or other confounding effects. Evaluating the effectiveness of netNMF-sc in the presence of these additional sources of variation is left as future work. Finally, there remains the issue of whether one should identify discrete cell clusters or continuous trajectories in scRNA-seq data. Here, we focused on clustering cells in the low-dimensional space obtained from netNMF-sc. A potential future direction is to investigate how to leverage prior knowledge in trajectory inference from scRNA-seq data.

Methods

netNMF-sc algorithm

netNMF-sc uses graph-regularized NMF (Cai et al. 2008) with KL divergence, which solves the following optimization problem:

$$\underset{\mathbf{W}\ge 0,\mathbf{H}\ge 0}{min}\sum _{i,j}\left(x_{ij}\log \frac{x_{ij}}{\mathbf{W}\mathbf{H}{|}_{ij}}-x_{ij}+\mathbf{W}\mathbf{H}{|}_{ij}\right)+\lambda \mathrm{Tr}({\mathbf{W}}^T\mathbf{L}\mathbf{W}),$$

for a positive real constant λ, where L is the Laplacian matrix of the gene–gene interaction network, and Tr(·) indicates the trace of the matrix. The regularization term Tr(W^TLW) encourages pairs of genes to have similar representations in the matrix W when they are connected in the network. Graph-regularized NMF has previously been used in bioinformatics to analyze somatic mutations in cancer (Hofree et al. 2013).

We derive the graph Laplacian L for the gene–gene interaction network as follows. Let S = [s_ij] ∈ ℝ^m×m denote a gene–gene similarity matrix whose entry s_ij is the weight of an interaction between genes i and j. A positive weight s_ij indicates a positive correlation between gene i and gene j, whereas a negative weight indicates negative correlation. We use the signed graph Laplacian L = D − S, where D = Diag(|S|1) is the degree matrix and |S| is the entrywise absolute value of S. The signed Laplacian, like the Laplacian, is symmetric and positive semidefinite (Kunegis et al. 2010; Gong et al. 2014). Performing Laplacian embedding using the signed version of the graph Laplacian produces an embedding where positive edges between a pair of genes correspond to high similarity and negative edges correspond to low similarity (Kunegis et al. 2010).

We implemented netNMF-sc using the TensorFlow Python library (Abadi et al. 2016) and tested the performance of netNMF-sc with four different optimizers: Adam, momentum, gradient descent, and Adagrad. We found Adam to perform the best at recovering clusters embedded in the data as well as reducing error between the imputed data and the original data before dropout (Supplemental Fig. S3A–D). Adaptive moment estimation (Adam) uses the first and second moments of gradient of the cost function to adapt the learning rate for each parameter (Kingma and Ba 2014). This allows Adam to perform well on noisy data as well as sparse matrices (Kingma and Ba 2014).

netNMF-sc has a shorter runtime on large-scale scRNA-seq data sets than other methods. On a simulated data set with 5000 genes and 2000 cells, netNMF-sc ran in 1.2 min on one 2.60 GHz Intel Xeon CPU and in 34 sec on one NVidia Tesla P100 GPU. In comparison, MAGIC was the fastest method, taking only 13 sec, whereas scNBMF and scImpute were both significantly slower than netNMF-sc, taking 2.1 and 6.9 min, respectively (Supplemental Fig. S4). On a real data set from Macosko et al. (2015) with 9291 genes and 44,808 mouse retinal cells, netNMF-sc ran in 34 min on one NVidia Tesla P100 GPU. In comparison, MAGIC was the fastest, running in 1.3 min, but scNBMF and scImpute were significantly slower than netNMF-sc, failing to complete in 5 h.

Generation of simulated scRNA-seq data

We used the simulator Splatter (Zappia et al. 2017) to generate transcript count data, estimating the parameters of the model from mouse embryonic stem cell scRNA-seq data (Buettner et al. 2015) using the SplatEstimate command. We modified Splatter to introduce correlations between genes that are differentially expressed in each cluster using a gene coexpression network from Yang et al. (2017). See Supplemental Section S5 for further details.

After simulating transcript counts to obtain a count matrix X′, we generated dropout events using one of two models. The first is a multinomial dropout model, used previously to model dropout in scRNA-seq data (Linderman et al. 2018; Zhu et al. 2018). In this model, the observed transcript counts in a cell are multinomial distributed, where the probability of observing a transcript from gene i in cell j is $x_{ij}^{\mathrm{\prime }}/{\sum }_{r,s}{x}_{rs}^{\mathrm{\prime }}$ and the number of trials is the sum of all transcripts in the count matrix, $\sum _{r,s}{x}_{rs}^{\mathrm{\prime }}$, multiplied by the capture efficiency, ranging from 0 to 1. The resulting count matrix X contains dropout proportional to the capture efficiency. The second model is the double exponential dropout model, used previously in the scImpute (Li and Li 2018) and BISCUIT (Azizi et al. 2017) publications. In this model, an entry x_ij of the count matrix is set to zero with probability $P=\exp (-\delta x_{ij}^{\mathrm{\prime }2})$, where δ is the dropout rate.

Software availability

netNMF-sc is available as Supplemental Code and at GitHub (https://github.com/raphael-group/netNMF-sc).

Competing interest statement

B.E.E. is on the Scientific Advisory Board for Celsius Therapeutics and Freenome and is currently employed by Genomics plc. B.J.R. is a cofounder and consultant for Medley Genomics.