Abstract
Continuum manipulators are flexible robots which undergo continuous deformation as they are actuated. To describe the elastic deformation of such robots, kinematic models have been developed and successfully applied to a large variety of designs and to various levels of constitutive stiffness. Independent of the design, kinematic models need to be calibrated to best describe the deformation of the manipulator. However, even after calibration, unmodeled effects such as friction, nonlinear elastic and/or spatially varying material properties as well as manufacturing imprecision reduce the accuracy of these models. In this paper, we present a method for improving the accuracy of kinematic models of continuum manipulators through the incorporation of orientation sensor feedback. We achieve this through the use of a “disturbance wrench”, which is used to compensate for these unmodeled effects, and is continuously estimated based on orientation sensor feedback as the robot moves through its workspace. The presented method is applied to the HydroJet, a waterjet-actuated soft continuum manipulator, and shows an average of 40% reduction in root mean square position and orientation error in the two most common types of kinematic models for continuum manipulators, a Cosserat rod model and a pseudo-rigid body model.
Index Terms—: Medical Robots and Systems, Kinematics, Flexible Robots
I. Introduction
CONTINUUM manipulators (CM) have captured attention within the research community for their unique capabilities, including whole-arm grasping and manipulation [1], navigation through complex and unpredictable environments [2], and passive compliance, which can make them safer for human interaction [3]. A variety of different designs for CMs have been proposed by researchers, including tendon-actuated arms [4], manipulators driven by multiple push-pull rods [5], concentric tube robots [6], [7], pneumatic and hydraulic soft manipulators [8], and even robots actuated by the motion of external magnets [9]. While the flexible nature of these robots provides many benefits, it also presents kinematic modeling challenges not seen in traditional rigid-link robotic arms, and as a result, tip accuracies for these robots tend to be lower than that of their rigid counterparts [10].
A number of different types of kinematic models for continuum robots have been developed, ranging in complexity from simple constant curvature models [11] to more elaborate models based on Cosserat rod theory [12]. The choice of modeling approach for a specific manipulator depends on a number of factors, including the mechanism of actuation, the significance of the effect of external loads like gravity, the required level of accuracy, and in some cases computation speed. All of these modeling approaches include parameters which typically require calibration, including material properties and geometric/structural characteristics of the robot [13]. However, even after calibration of these parameters, kinematic accuracy may still be less than desired, due to unmodeled effects such as friction, nonlinear elastic and/or spatially varying material properties, and manufacturing imprecision.
One option for further improving kinematic accuracy is to incorporate some of these effects into the model. For example, for certain designs, researchers have integrated more complex, nonlinear constitutive laws within the models [14]. However, accurately determining these constitutive laws requires tedious material testing processes. Friction and manufacturing uncertainties can also be modeled in principle, but for many designs, these are extremely difficult to accurately describe in practice [15], [16]. In addition, incorporating these effects increases overall model complexity and can significantly increase the number of parameters, thereby requiring an even more complex calibration procedure.
Another approach to improving kinematic accuracy is to incorporate feedback from sensors. One of the most commonly used method is to embed strain sensors along the principal bending directions and then use the kinematic model to predict the shape of the manipulator based on strain measurement [17], [18]. This approach, however, is not suitable for all types of continuum manipulators, as these sensors do not scale down well to small designs and require precise alignment, complicating the fabrication process. Another common method is to use fiber optic shape sensors [19], [20]. However, this method begins to lose accuracy at high curvatures due to propagation losses, and cannot be implemented for many low-stiffness designs, as the fiber optic sensor is often stiffer than the manipulator itself. As an alternative which does not require any mechanical interaction between the robot and the sensors, much work has focused on reconstructing the shape from an external camera [21], [22]. The use of an external camera, however, can become problematic when direct visualization is limited by occlusions, such as during operation in a confined environment.
In this paper, we present a new method to improve the accuracy of the kinematic model for CMs by utilizing sensory information from two inclinometers, one at the base of the manipulator and one at the tip. These sensors avoid the problem of occlusions associated with camera-based sensing modalities, while remaining compatible with low-stiffness CMs undergoing large deflections, as the sensors themselves do not need to bend with the structure of the CM. In addition, this type of sensor is inexpensive, making it well-suited to cost-sensitive applications. Utilizing this sensor feedback, our approach is to include a “disturbance” parameter in the model, which can compensate for a variety of unmodeled effects, and then calibrate this parameter in real time, based on the sensor data. The disturbance is in the form of an external point wrench, which is not meant to describe any particular external loads or actuation forces, both of which are considered separately within the CM modeling framework. The update of the disturbance can be performed by iteratively sensing the end effector’s orientation through the inclinometers. Since the disturbance represents a set of additional model parameters, it is possible to numerically evaluate a sensitivity matrix that expresses how changes in the disturbance affect the end effector’s angular velocity. The sensitivity matrix can then be inverted to update the disturbance estimate. This can then be applied back to the model, with the process being repeated iteratively to find a disturbance wrench that minimizes orientation error.
The contributions of this paper can be summarized as follows. First, we propose a calibration method for CMs that considers the addition of a disturbance wrench to compensate for unmodeled effects such as friction, nonlinear elasticity, non-uniform geometric and material properties, and inaccuracies in manufacturing and assembly. Second, we propose a method to update the disturbance wrench using the absolute orientation provided by two inclinometers located at the proximal and distal ends of the manipulator through the use of the sensitivity matrix. Lastly, to demonstrate the presented method on a physical robot, we present a case study on a soft continuum robot actuated by waterjets at the tip and undergoing large deflections in three dimensional space. The improvement in kinematic model accuracy is seen for both a kinematic-based model (Pseudo Rigid Body (PRB) Model) and a mechanics-based model (Cosserat Model), which are the two most commonly used frameworks for CMs.
II. Disturbance Estimation Approach
In this section, we describe the estimation procedure used to find a disturbance wrench which minimizes the tip rotation error associated with the kinematics. We approach this problem by first calibrating geometric and material properties of the manipulator with the additional disturbance wrench parameter to find a solution for the manipulator parameters which is optimal across the initial calibration data set. Then, during robot operation, the calibrated value of the tip disturbance is iteratively changed by using sensory information to minimize the orientation error at the current position within the workspace.
To describe the disturbance estimation approach, we begin by assuming a general kinematic model for the continuum robot which can be expressed in the form:
| (1) |
where g represents the pose of the end effector as a function of the actuation inputs q, and a set of manipulator’s parameters ζ = [η wd]T composed by geometric and material properties of the manipulator η, (such as length, Young’s Modulus, etc.), and by the disturbance wrench wd. The nominal mapping between end effector pose and actuator inputs can be used to calibrate the manipulator’s parameters by using the scalar product of end effector absolute orientations as the error metric [23]. After calibration, the resulting parameters (indicated as ζ*) are used to estimate the equilibrium pose of the end effector that corresponds to the inputs q.
A. Iterative Disturbance Estimation
The sensing of absolute orientations can help to correct the rotation error iteratively through the use of the sensitivity matrix:
| (2) |
which maps body frame end-effector velocities to changes in the manipulator’s calibrated parameters ζ*. Independent of which kinematic modelling approach is used, the sensitivity matrix can be computed numerically using a finite difference approximation [24]. Each column can be computed as:
| (3) |
where gj is the homogeneous transformation describing the end effector pose obtained after perturbing g with a small change in the ith calibrated parameter by Δζi. Using this method, each column of the sensitivity matrix can be obtained after 2 solutions of the kinematic equations.
The rotation error is iteratively minimized by using a gradient descent approach where the change in the disturbance wrench is calculated by:
| (4) |
where Swd represents the columns of the sensitivity matrix which map changes in the disturbance parameter to changes in the tip orientation, ωdes can be calculated by using the orientation error between the current estimated rotation Ri and the measured value from the sensors Rm expressed in body coordinate, λ represents a gain correction coefficient which can be experimentally tuned, μ is a damping factor and I3 is the identity matrix (Fig. 1). The calculated change can then be added to the previously estimated value of the disturbance and applied to the model where and .
Fig. 1.
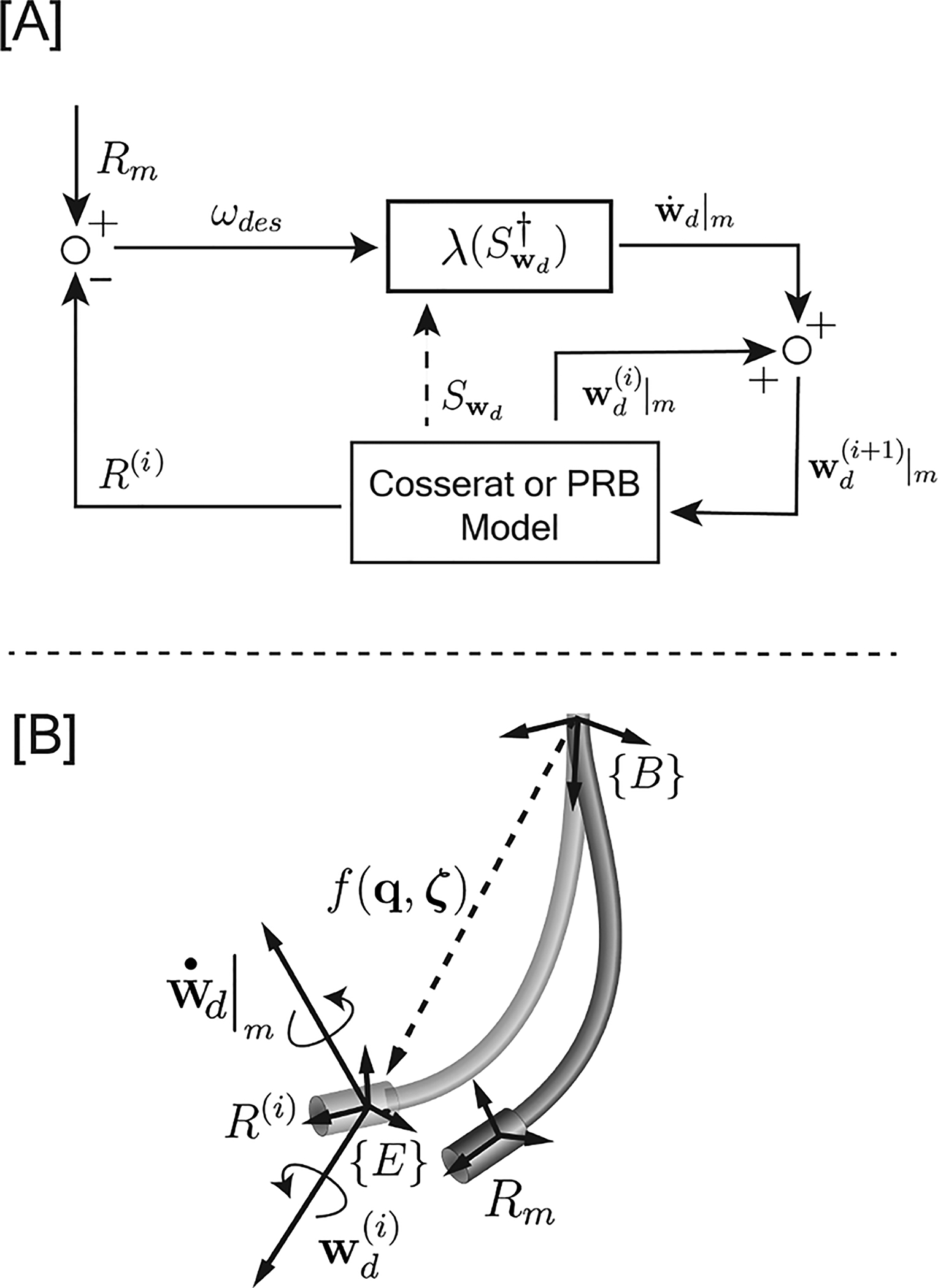
Iterative disturbance estimation algorithm. [A] Block diagram illustrating the iterative update of the disturbance based on inclinometer data. The initial value for is obtained after initial calibration. [B] The compliance matrix Swd is used to minimize the orientation error between current estimated orientation R(i) and the measured value from the sensors Rm.
III. Case study: The Hydrojet System
The HydroJet Endoscopic Device (HJ) was introduced in [25]. It is a soft continuum endoscope that addresses the need for upper GI cancer screening in Low and Middle Income Countries (LMIC) and remote areas. The device uses three miniature waterjet actuators, spaced 120 degrees apart around the diameter (Fig. 2), to directly maneuver the camera located at the tip. The pressurized water is carried through a multilumen catheter that is connected directly to three solenoid valves which control the flow to each nozzle. The deflection is facilitated by a soft elastomer sleeve (Ecoflex 00–30), located at the distal end of the multilumen catheter, which wraps around three flexible single lumen tubes that are connected to the capsule. This structure is designed to be soft and flexible to allow for high curvatures and thereby large deflections of the capsule. By controlling each jet’s actuation force individually, the deflection generated by the three waterjets creates a resultant motion in two DoFs. The net applied wrench in the body frame acting on the tip of the manipulator due to the waterjet forces is defined as:
| (5) |
where q1, q2, and q3 are the three applied forces due to the water jets and Fa|xy represents the x and y components of the tip force in the frame of the tip of the manipulator, as defined in Fig. 2. Since the three actuators are all coplanar with the tip of the endoscope, the z component of the force is zero.
Fig. 2.
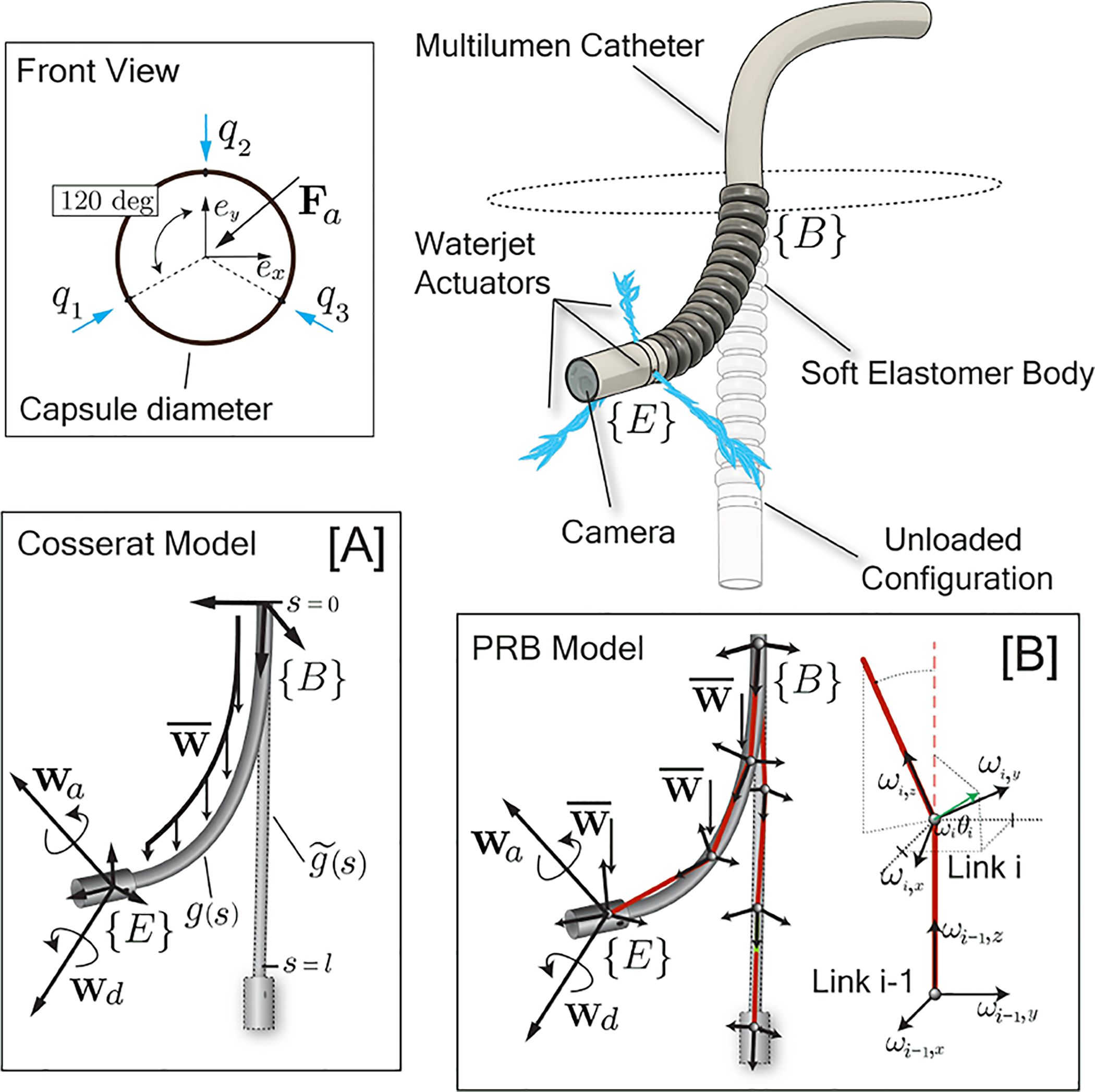
Mechanical deflection for the HydroJet endoscopic device expressed in both PRB and Cosserat frameworks. The waterjet actuators are spaced 120 degrees around the capsule diameter and modeled as a tip follower force.
IV. Kinematic Modelling for the Hydrojet System
In this section we present two commonly used kinematic models for continuum manipulators and describe how they can be applied to decribe deflection of the HydroJet Device.
A. Pseudo-Rigid Body Kinematics
The PRB model is based on the approximation of subdividing the elastic body of the continuum manipulator into a series of rigid links connected by conventional revolute, universal, or spherical joints. In this case, the continuum structure is modeled as n + 1 uniformly spaced rigid links connected by n spherical joints (Fig. 2 (B)) [26]. The rotation of each joint i with respect to the orientation of the previous joint i − 1 is described using a rotation vector ωiθi = ωixθix + ωiyθiy + ωizθiz, where ωix, ωiy, ωiz are the three orthonormal axes attached to the ith joint and θix, θiy, θiz are the rotation angles around each axis. The resulting rotation axis and magnitude of rotation are indicated with ωi and θi respectively. Considering that the magnitude and the direction of rotation of the ith joint can be calculated as ϕi = ‖θi‖ and ωi = θi/‖θi‖, the corresponding twist, results in:
| (6) |
where qi is a vector pointing from the origin to any location on the axis ωi, and is the skew-symmetric matrix:
| (7) |
The homogeneous transformation matrix of each joint can be determined using the twists of equation (6), the rotation angle ϕi and the product of exponentials formula [27]:
| (8) |
where gsi(θ) ∈ SE(3) is the configuration of joint i in the space frame for joint angles [θ1 θ2 … θi]T and gsi(0) represents the initial configurations of joint i.
The relationship between the internal bending moment and deflection angle at each joint i can be modeled as:
| (9) |
where is a vector representing the internal bending moment and Ki is the stiffness matrix of joint i with components in x, y and z directions. The effective torsional spring constant can be found in terms of the elastic material properties by comparing spring energy and strain energy due to bending, as explained in [20]:
| (10) |
where ls is the length of the ith link, lc ∈ [0, L] is an incremental counter with ls increments, and E is varying along the length of the body, with E0,x and EL,x representing the Young’s modulus of the joints i in the direction x at l = 0 and l = L, respectively. A similar expression can be found for y and z directions.
The Jacobian matrix can be calculated using [26], [27]:
| (11) |
where
| (12) |
The Jacobian for the end-effector can be expressed as:
| (13) |
The mapping of forces applied on the body (i.e distributed loads and actuations) are modeled through the manipulator Jacobian. The effect of a distributed load on the body can be modeled as:
| (14) |
where represents a distributed force expressed in body frame at the ith joint. The effect of the actuators can be modeled as
| (15) |
where Fa represents force and Ma moment due to the actuators, wd|f represents the disturbance force at the tip and wd|m represents the disturbance wrench.
The configuration vector θ is obtained by equalizing internal and external moments applied on the body. The solution to this equation cannot be obtained analytically, and is thus obtained through the following minimization:
| (16) |
The first term in the objective function is the internal moment due to the stiffness of the body, where Kω(θ) is the internal bending moment of the whole body. The second and third terms represent the external moments acting on the body, which are related to the configuration vector θ through the manipulator Jacobian, and q represents the actuation forces (e.g. forces applied by the water jets).
B. Cosserat Rod Kinematics
A Cosserat rod-based kinematic model for continuum manipulators has been derived in [12]. In this section, we review the model using the notation provided in [7]. The centerline of an unloaded rod is expressed using a homogenoeous reference frame consisting of an arc length-parameterized space curve and a rotation matrix , with s denoting arc length. Under an external load, the parametric curve deflects to the curve p(s), and rotates to R(s) (Fig. 2 (A)). The homogeneous frames (g(s)), defined by:
| (17) |
are assigned so that the z-axis of each frame is tangent to the curve. The rotation of each point on the rod may be expressed in terms of a local curvature vector u(s), which can be found using the relationship [27]:
| (18) |
where the operator ∨ denotes conversion of an element of so(3) to its corresponding element in . The constitutive relationship between the curvature vector and internal moments, expressed in the local coordinate frame at s, is:
| (19) |
where Mb(s) is the internal moment and K represents the stiffness matrix, defined as:
| (20) |
where Ex, Ey are the the Young’s modulus, Ix and Iy are the second moments of area of the tube cross-section, G is the shear modulus and J is the polar moment of inertia of the tube cross-section. The Young’s modulus is considered to be linearly varying along the length of the body going from a value E0 at the base to EL at the tip following the equations: E = sEL,x + (1 − s)E0,x. A similar expression can be found for the y and z directions. The resulting Cosserat rod equations that govern the rod shape expressed in local frame coordinates are:
| (21) |
where nb is the internal force, is the distributed force and and are the skew-symmetric versions of vectors ez and u, respectively. In the equations listed above, we have ignored the contribution of distributed moments along the body.
In the Cosserat framework, forces and moments applied at the tip represent boundary conditions on equation (21). The boundary conditions at s = L can be expressed as:
| (22) |
while is already included in eq. (21). The boundary conditions at s = 0 are:
| (23) |
and solution of the resulting boundary value problem provides the full pose of the manipulators as a function of arc length.
V. Experimental Validation
A. HydroJet System Testbed
The testbed was assembled as depicted in Fig. 3. The capsule was manufactured from a durable plastic (Clear resin, FormLabs, Sommerville, MA, USA) through rapid prototyping. The capsule’s outer diameter and length are 9.8 mm and 28 mm, respectively. A 6 DoF electromagnetic sensor (EM) (Northern Digital Inc., Canada), with 0.48 mm and 0.70 deg accuracy, was integrated within the capsule, with its frame aligned to the capsule in a known orientation. The wire of the electromagnetic sensor runs through the soft elastomer sleeve together with the three single-lumen water lines connecting the tip to the base connector. The base was connected to three solenoid water valves (A352273, Asco Numatics, USA) using standard hydraulic tubing (1/16”ID × 1/8”OD Tygon E-3603, Cole-Parmer, USA). The base connector was held in the desired orientation using a custom 3D printed holder. The assembly was secured in place through attachment to an aluminum frame (Rexroth, Bosch, Germany). A second 6-DoF EM sensor was attached to the base holder to sense the orientation of this frame as well and compute the direction of gravity with respect to the capsule and tether.
Fig. 3.

Experimental bench test setup consisting of the Hydrojet Endoscopic Device. A 3D printed holder anchors the base of the device while the waterjets at the tip cause deflection of the soft elastomer body.
B. Initial Calibration
The purpose of calibration is to find values for the parameters of the model that best describe the deflection of the manipulator for a set of N poses distributed throughout the workspace of the manipulator. This means that the intrinsic parameters found during calibration may not be the optimal for a single actuation value. The parameters of both models are optimized such that the rotation at the tip and at the base closely approximate those of the experimental data under the same set of actuations. In these experiments, the data used for calibration consist of a set of 40 randomly distributed equilibrium configurations within the workspace. The overall collection time was around 3 min and 30 sec. The parameter optimization problem is defined as follows:
| (24) |
where hm = a + bi + cj + dk represents the quaternion associated with the rotation of the tip with respect to the base, as computed by solving for the equilibrium configuration (eq. (16) for the PRB model and eqs. (21), (22), (23) for the Cosserat model) with inputs qi and manipulator parameters ζ. Similarly, hi represents the quaternion associated with the measured experimental rotation, which is obtained by calculating the relative rotations of the two EM sensors. The operator < · > represents the scalar product of two vectors and is chosen as the distance metric between two elements of SO(3) [23].
Assuming the soft elastomer body to have a cylindrical shape with radially isotropic properties results in EL,x = EL,y = EL, E0,x = E0,y = E0 and GL = EL/2γ and G0 = E0/2γ, where γ is the Poisson’s ratio. The manipulator’s parameters that we seek to calibrate are then ζ = [E0 El L wd]T. The results of calibration using both models are summarized in Table I.
TABLE I.
Calibrated values of model parameters
| Parameter | PRB Model (Value) |
Cosserat Model (Value) |
|---|---|---|
| E0 | 2.35 · 105 N/m2 | 3.00 · 105 N/m2 |
| El | 1.68 · 105 N/m2 | 2.00 · 105 N/m2 |
| L | 0.0705 m | 0.0698 m |
| ωd,x|f | −0.99 · 10−3 N | −1.54 · 10−2 N |
| ωd,y|f | 0.02 · 10−3 N | −9.07 · 10−3 N |
| ωd,z|f | 0.01 · 10−3 N | 2.07 · 10−2 N |
| ωd,x|m | −0.04 · 10−3 Nm | 2.71 · 10−2 Nm |
| ωd,y|m | −0.15 · 10−3 Nm | −2.33 · 10−2 Nm |
| ωd,z|m | 4.69 · 10−3 Nm | −1.74 · 10−1 Nm |
C. Constant Disturbance Results
The optimal value for the manipulator parameters ζ* was obtained for both PRB and Cosserat models using the calibration procedure described in the previous section. To validate the accuracy of both models after calibration, the soft manipulator was moved throughout its workspace by gradually increasing the actuation force of one waterjet at a time until the maximum force was reached. This resulted in three sweeping motions, shown in different colors in Fig. 4. During this motion, the orientations of the base and the tip of the manipulator were recorded through the EM sensors. The force generated by the waterjet was directly controlled by input signals to the solenoid valves. To facilitate quasi-static motion, each command was sent with a delay of 5 seconds, which is higher than the settling time of the body to its equilibrium. This delay time is primarily a requirement of the actuator dynamics for this particular robot design. The sweeping motion corresponding to each of the three jets was repeated three times, for a resulting total of nine separate motions. For each actuation force, each model was evaluated with the parameters obtained during calibration (ζ*) to compute the end-effector pose. The results are shown in Figs. 4 and 5. The position error (‖ϵ‖2) is defined as the Euclidean norm of the difference between model-predicted tip position and measured tip position obtained from the EM sensors, while the rotation error Δψ is calculated as in section V-B. To enable similar discretization of the body of the manipulator for both frameworks, the length of the links for the PRB model was chosen to be the same as the integration step size used for the Cosserat model (20 links in total were chosen for the PRB model). This allows for a more direct correlation between analogous parameters in the two models. The root-mean-square (RMS) and standard deviation (SD) position and orientation error resulting from the nine sweeps was 0.69 cm ± 0.20 cm with 6.85 deg ± 3.41 deg for the PRB and 0.51 cm ± 0.20 cm with 5.66 deg ± 4.21deg for the Cosserat model, showing similar behavior of the two modelling frameworks.
Fig. 4.
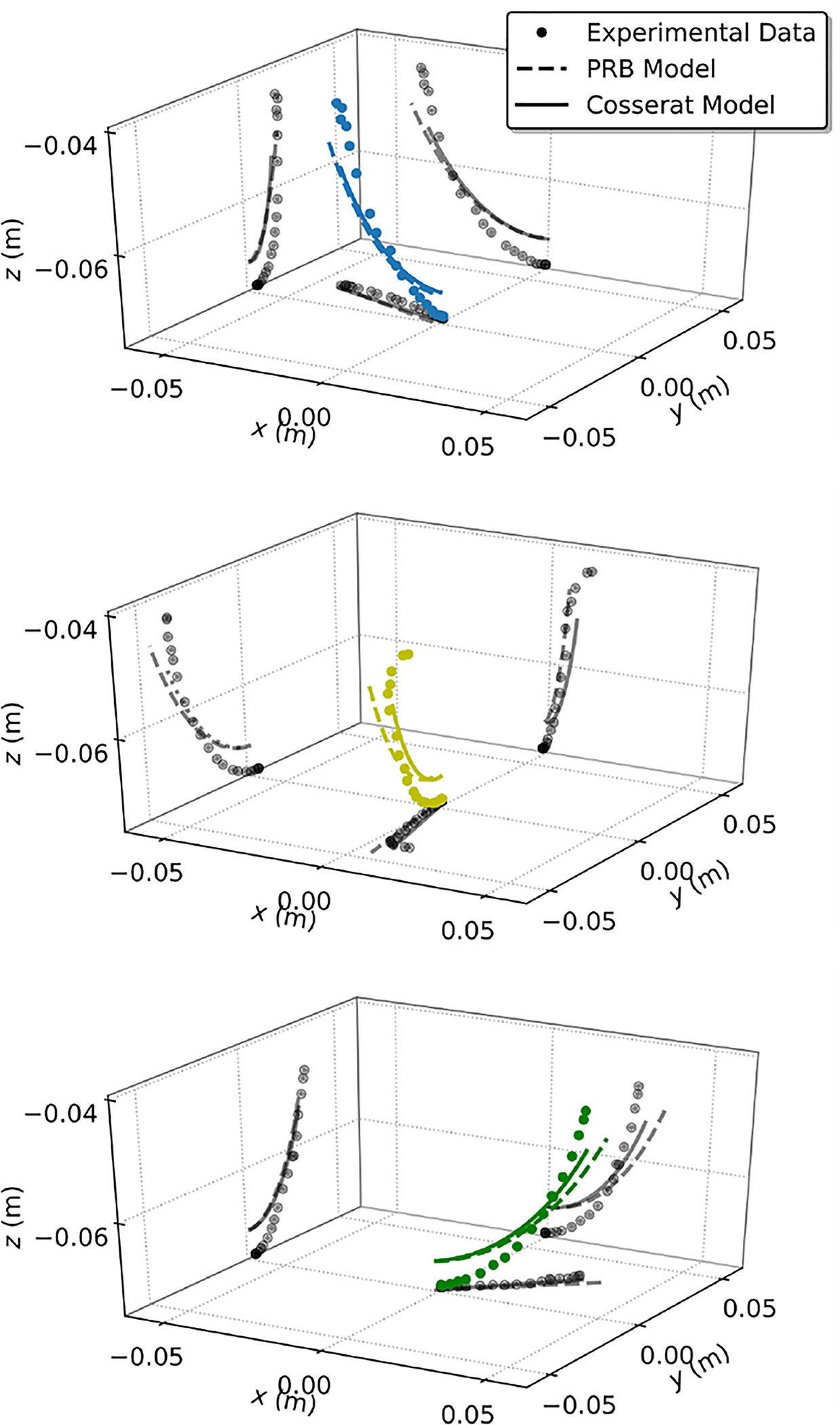
Experimental validation of the calibrated coefficient ζ*. Each sweep is marked with a different color. The experimental deflection (dots) is projected on xy, xz, yz planes together with the corresponding position estimated from both PRB (black dashed line) and Cosserat (black continuous line) frameworks.
Fig. 5.
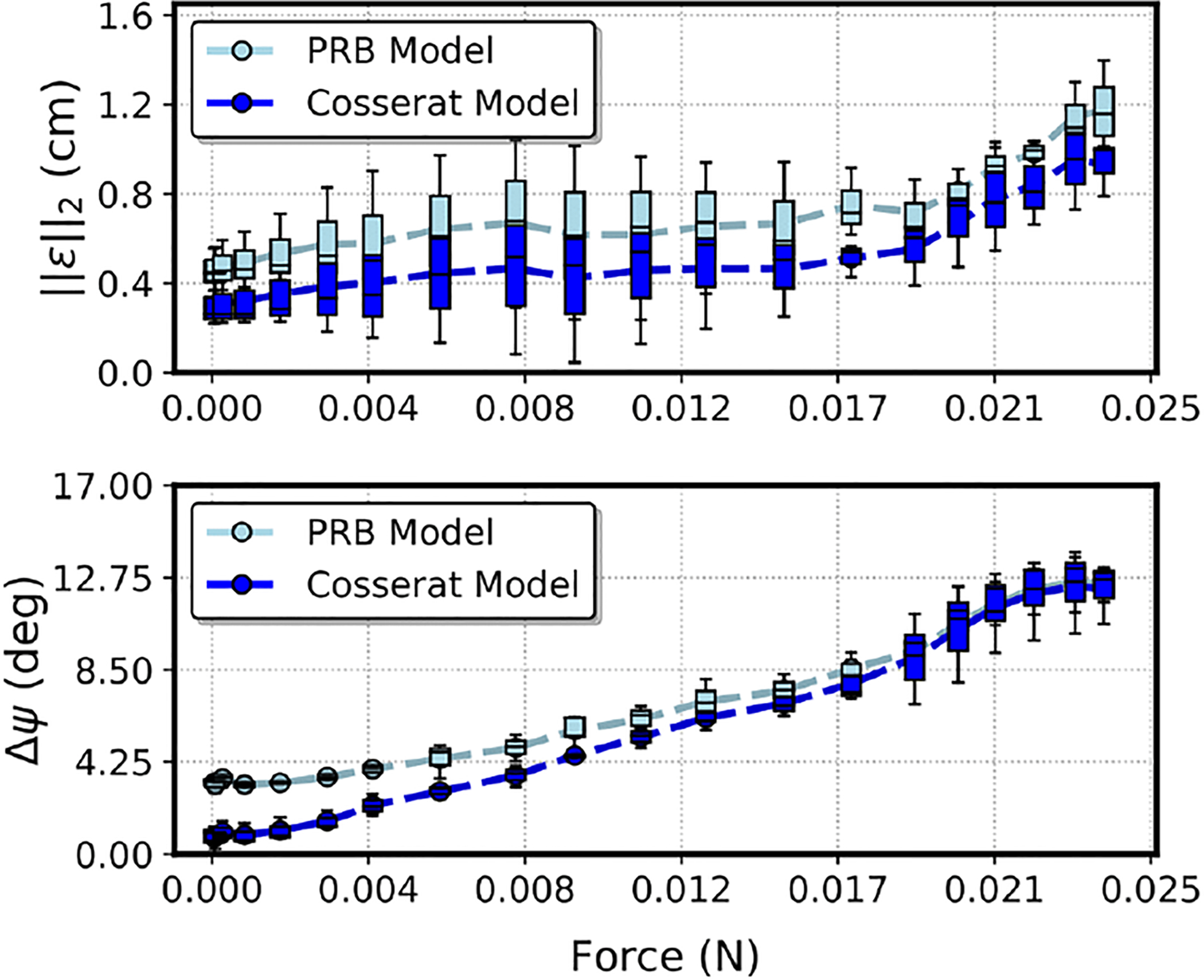
Box Plot Comparison of PRB and Cosserat Models. Position and orientation errors with constant disturbance wrench.
D. Iterative Disturbance Estimation Results
The same sweeping motions described in the previous section were used with online adjustment of the disturbance wrench based on sensor orientation. The disturbance wrench was iteratively adjusted following the gradient descent minimization approach described in Section 3 using a gain correction coefficient of λ = 0.4. The local minimum was generally reached after one to two iterations per time step. Results are shown in Fig. 6. Compared to the constant disturbance approach, the iterative estimation reduces the orientation error by 43%, going from an average error of 6.85 deg to 3.96 deg in the case of PRB model, and by 42%, from 5.66 deg to 3.29 deg for the Cosserat model. While the error in orientation is significantly reduced, there is no significant variation in positional error, which remains confined within the same range of the values observed for the PRB model without online disturbance estimation, and is slightly improved for the Cosserat model. In Table II, the RMS errors calculated using the iterative estimation method (Proposed) are compared to the standard geometric calibration (Ref.). The proposed method significantly improves both positional and orientation error over the standard calibration method showing 42% positional error reduction (from 17.9% of the robot length to 10.7%) and 32% orientation error reduction for 75° deflection of the end effector.
Fig. 6.
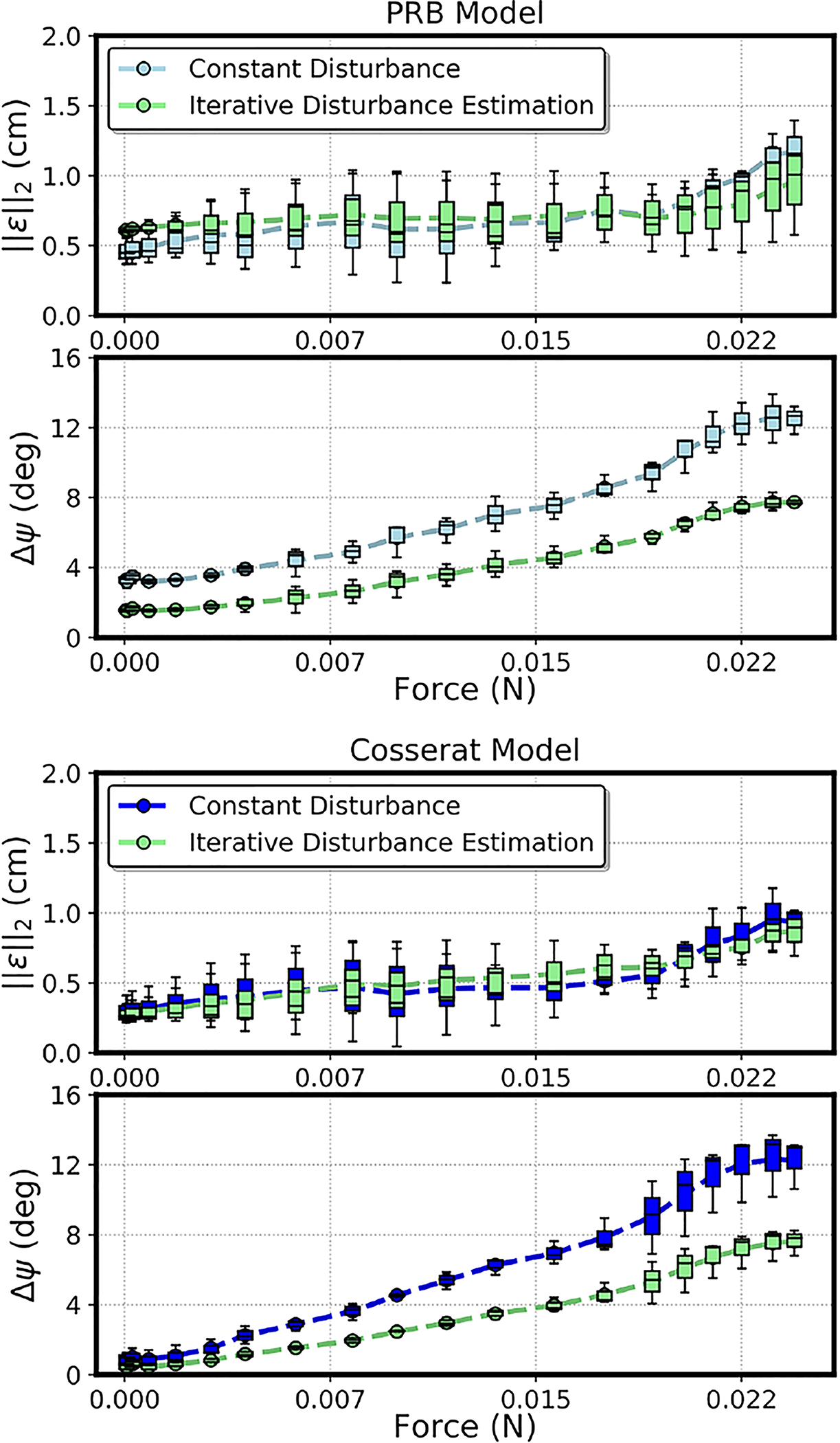
Box plot showing error distribution and variability over the nine sweeping motions. The iterative estimation of the disturbance wrench using sensor data allows for significant reduction in the rotation error for both modelling frameworks.
TABLE II.
RMSE Position and Orientation of Iterative Disturbance Estimation compared to Standard Geometric Calibration
| Bending Angle | 10° | 25° | 50° | 75° | ||
|---|---|---|---|---|---|---|
| PRB Model |
Position RMSE (cm) | Ref. | 0.44 | 0.75 | 1.16 | 1.34 |
| Proposed. | 0.66 | 0.69 | 0.74 | 0.79 | ||
| Orientation RMSE (deg) | Ref. | 9.06 | 9.89 | 10.02 | 10.75 | |
| Proposed. | 1.74 | 3.18 | 5.18 | 7.07 | ||
| Cosserat Model |
Position RMSE (cm) | Ref. | 0.52 | 0.78 | 1.01 | 1.25 |
| Proposed. | 0.37 | 0.47 | 0.56 | 0.75 | ||
| Orientation RMSE (deg) | Ref. | 9.17 | 9.81 | 9.27 | 10.04 | |
| Proposed. | 0.82 | 2.46 | 3.96 | 7.18 | ||
VI. Discussion
In this paper, we have presented a new method for using sensory feedback from orientation sensors to improve the kinematic modeling accuracy for continuum manipulators. We achieve this by incorporating a “disturbance wrench” to account for unmodeled phenomena, which is continually updated based on the sensor data. While this method could in principle be used to estimate external loads due to contact with the environment, force estimation and contact detection are substantial research problems in their own right, and typically depend on the design and actuator methodology of the specific CM. The validation of our method with external environmental forces is thus left for future work. In addition, future work will focus also on the integration of this method into a Jacobian-based motion controller; the improved modeling accuracy demonstrated in this work is expected to improve trajectory following abilities as well.
The improved modeling and control accuracy which this approach can enable is expected to be highly valuable, as improving kinematic modelling accuracy is still a very active area of research for CMs in particular. For the HydroJet System described in Section III, we anticipate that this improved accuracy will enable medical providers to more precisely control the device within the stomach during upper gastrointestinal endoscopy. It is expected that this approach could provide similar benefits for a wide range of soft robotics applications, both in and outside of the medical field. In this paper we have used EM sensors to calculate absolute orientations; however, these sensors can be replaced by cheaper inertial motion units (IMUs) without changing the proposed disturbance estimation method. Absolute orientation can be obtained from IMUs through an orientation filter, as the one proposed in [28], which provides static accuracy comparable to that of the EM sensors (0.6 degrees). While IMUs are well suited to the HydroJet device, integrating even these low cost sensors will not be practical for all applications, making the need for adding sensors one of the primary limitations of our method.
VII. Conclusion
This paper presents a method for augmenting the kinematic models for continuum manipulators with information from orientation sensors in order to improve model accuracy. The method is based on online calibration of a “disturbance wrench” used to account for various unmodeled phenomena. We apply this method in particular to continuum manipulators actuated by a tip follower wrench and experiencing external loading, and demonstrate the performance of the method on a soft continuum endoscope actuated by waterjet propulsion. Our results indicate that the method is effective for both PRB and Cosserat rod modeling frameworks.
Acknowledgment
The authors would like to thank the Vanderbilt Institute for Surgery and Engineering (ViSE) for their support of our work and utilization of space. Any opinions, findings and conclusions, or recommendations expressed in this article are those of the authors and do not necessarily reflect the views of the Royal Society, EPSRC, NIH, NIHR, the UK Department of Health and Social Care or the ERC.
This paper was recommended for publication by Editor D. Song upon evaluation of the Associate Editor and Reviewers’ comments. Research reported in this article was supported by the Royal Society, by the Engineering and Physical Sciences Research Council (EPSRC) under grant number EP/P027938/1, by the National Institute of Biomedical Imaging and Bioengineering of the National Institute of Health under Award Number R01EB018992, by the National Institute for Health Research (NIHR) (16/137/44) using UK aid from the UK Government to support global health research, and by the European Research Council (ERC) under the European Unions Horizon 2020 research and innovation programme (grant agreement No 818045).
References
- [1].Giri N and Walker I, “Continuum robots and underactuated grasping,” Mechanical Sciences, vol. 2, no. 1, pp. 51–58, 2011. [Google Scholar]
- [2].Chirikjian GS and Burdick JW, “The kinematics of hyper-redundant robot locomotion,” IEEE transactions on robotics and automation, vol. 11, no. 6, pp. 781–793, 1995. [Google Scholar]
- [3].Sanan S, Moidel J, and Atkeson CG, “A continuum approach to safe robots for physical human interaction,” in Intl Symposium on Quality of Life Technology. Citeseer, 2011. [Google Scholar]
- [4].Simaan N, Xu K, Wei W, Kapoor A, Kazanzides P, Taylor R, and Flint P, “Design and integration of a telerobotic system for minimally invasive surgery of the throat,” The International journal of robotics research, vol. 28, no. 9, pp. 1134–1153, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Xu K, Zhao J, and Fu M, “Development of the sjtu unfoldable robotic system (surs) for single port laparoscopy,” IEEE/ASME Transactions on Mechatronics, vol. 20, no. 5, pp. 2133–2145, 2014. [Google Scholar]
- [6].Dupont PE, Lock J, Itkowitz B, and Butler E, “Design and control of concentric-tube robots,” IEEE Transactions on Robotics, vol. 26, no. 2, pp. 209–225, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Rucker DC, Jones BA, and Webster III RJ, “A geometrically exact model for externally loaded concentric-tube continuum robots,” IEEE transactions on robotics: a publication of the IEEE Robotics and Automation Society, vol. 26, no. 5, p. 769, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Ranzani T, Gerboni G, Cianchetti M, and Menciassi A, “A bioinspired soft manipulator for minimally invasive surgery,” Bioinspiration & biomimetics, vol. 10, no. 3, p. 035008, 2015. [DOI] [PubMed] [Google Scholar]
- [9].Taddese AZ, Slawinski PR, Obstein KL, and Valdastri P, “Closed loop control of a tethered magnetic capsule endoscope,” Robotics science and systems: online proceedings, vol. 2016, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Hughes J, Culha U, Giardina F, Guenther F, Rosendo A, and Iida F, “Soft manipulators and grippers: a review,” Frontiers in Robotics and AI, vol. 3, p. 69, 2016. [Google Scholar]
- [11].Webster III RJ and Jones BA, “Design and kinematic modeling of constant curvature continuum robots: A review,” The International Journal of Robotics Research, vol. 29, no. 13, pp. 1661–1683, 2010. [Google Scholar]
- [12].Trivedi D, Lotfi A, and Rahn CD, “Geometrically exact models for soft robotic manipulators,” IEEE Transactions on Robotics, vol. 24, no. 4, pp. 773–780, 2008. [Google Scholar]
- [13].Webster RJ, Romano JM, and Cowan NJ, “Kinematics and calibration of active cannulas,” in 2008 IEEE International Conference on Robotics and Automation. IEEE, 2008, pp. 3888–3895. [Google Scholar]
- [14].Grazioso S, Di Gironimo G, and Siciliano B, “A geometrically exact model for soft continuum robots: The finite element deformation space formulation,” Soft robotics, 2018. [DOI] [PubMed] [Google Scholar]
- [15].Lock J and Dupont PE, “Friction modeling in concentric tube robots,” in 2011 IEEE International Conference on Robotics and Automation. IEEE, 2011, pp. 1139–1146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Subramani G and Zinn MR, “Tackling friction-an analytical modeling approach to understanding friction in single tendon driven continuum manipulators,” in 2015 IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2015, pp. 610–617. [Google Scholar]
- [17].Leleu S, Abou-Kandil H, and Bonnassieux Y, “Piezoelectric actuators and sensors location for active control of flexible structures,” in Proceedings of the 17th IEEE Instrumentation and Measurement Technology Conference [Cat. No. 00CH37066], vol. 2 IEEE, 2000, pp. 818–823. [Google Scholar]
- [18].Lyshevski SE, “Data-intensive analysis and control of flexible pointing systems with pzt actuators,” in IEEE International Frequency Control Symposium and PDA Exhibition Jointly with the 17th European Frequency and Time Forum, 2003. Proceedings of the 2003. IEEE, 2003, pp. 948–956. [Google Scholar]
- [19].Yi X, Qian J, Shen L, Zhang Y, and Zhang Z, “An innovative 3d colonoscope shape sensing sensor based on fbg sensor array,” in 2007 International Conference on Information Acquisition. IEEE, 2007, pp. 227–232. [Google Scholar]
- [20].Roesthuis RJ and Misra S, “Steering of multisegment continuum manipulators using rigid-link modeling and fbg-based shape sensing,” IEEE transactions on robotics, vol. 32, no. 2, pp. 372–382, 2016. [Google Scholar]
- [21].Camarillo DB, Loewke KE, Carlson CR, and Salisbury JK, “Vision based 3-d shape sensing of flexible manipulators,” in 2008 IEEE International Conference on Robotics and Automation. IEEE, 2008, pp. 2940–2947. [Google Scholar]
- [22].Hannan MW and Walker ID, “Real-time shape estimation for continuum robots using vision,” Robotica, vol. 23, no. 5, pp. 645–651, 2005. [Google Scholar]
- [23].Huynh DQ, “Metrics for 3d rotations: Comparison and analysis,” Journal of Mathematical Imaging and Vision, vol. 35, no. 2, pp. 155–164, 2009. [Google Scholar]
- [24].Rucker DC and Webster RJ, “Computing jacobians and compliance matrices for externally loaded continuum robots,” in Robotics and Automation (ICRA), 2011 IEEE International Conference on. IEEE, 2011, pp. 945–950. [Google Scholar]
- [25].Campisano F, Gramuglia F, Dawson IR, Lyne CT, Izmaylov ML, Misra S, De Momi E, Morgan DR, Obstein KL, and Valdastri P, “Gastric cancer screening in low-income countries: System design, fabrication, and analysis for an ultralow-cost endoscopy procedure,” IEEE robotics & automation magazine, vol. 24, no. 2, pp. 73–81, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Greigarn T and Çavuşoğlu MC, “Pseudo-rigid-body model and kinematic analysis of mri-actuated catheters,” in 2015 IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2015, pp. 2236–2243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Murray RM, Li Z, Sastry SS, and Sastry SS, A mathematical introduction to robotic manipulation. CRC press, 1994. [Google Scholar]
- [28].Madgwick S, “An efficient orientation filter for inertial and inertial/magnetic sensor arrays,” Report x-io and University of Bristol (UK), vol. 25, pp. 113–118, 2010. [Google Scholar]


