2’-Deoxy-2’-fluoro-arabinonucleic acid: A valid alternative to DNA for biotechnological applications using charge transport

Abstract

The non-biological 2’-deoxy-2’-fluoro-arabinonucleic acid (2’F-ANA) may be used as a valid alternative to DNA in biomedical and electronic applications because of its higher resistance to hydrolysis and nuclease degradation. However, the advantage of using 2’F-ANA in such applications also depends on its charge-transfer properties compared to DNA. In this study, we compare the charge conduction properties of model 2’F-ANA and DNA double-strands, using structural snapshots from MD simulations to calculate the electronic couplings and reorganization energies associated with the hole transfer steps between adjacent nucleobase pairs. Inserting these charge-transfer parameters into a kinetic model for charge conduction, we find similar conductive properties for DNA and 2’F-ANA. Moreover, we find that 2’F-ANA’s enhanced chemical stability does not correspond to a reduction in the nucleobase π-stack structural flexibility relevant to both electronic couplings and reorganization free energies. Our results promote the use of 2’F-ANA in applications that can be based on charge transport, such as biosensing and chip technology, where its chemical stability and conductivity can advantageously combine.

Graphical Abstract

1. Introduction

In the past decade, we have witnessed considerable advances in DNA-based nanotechnology, for applications in areas such as bioimaging¹, sequencing and detection relevant to biomedicine^2–4 and ecology⁵, biosensing,^{6, 7} drug delivery,⁸ electronic materials^9–11 and devices.^12–15 Experiments on synthetic DNA structures,^15–22 DNA hairpins,^23–28 and diblock DNA hairpins,^{27, 29–31} as well as their theoretical interpretation, have provided important opportunities for fundamental understanding of charge injection and transfer in DNA systems. DNA variants and related systems have also been explored to improve on DNA conduction and chemical stability in such applications^{13, 32–36} or because of their medical relevance.^36–40 In particular, 2’F-ANA⁴¹ (which belongs to the family of xeno-nucleic acids³⁶) has a greater resistance to acid hydrolysis^{42, 43} and a wider operating pH range⁴² than DNA or RNA. These and other properties investigated in previous studies^{36, 41, 42, 44, 45} make 2’F-ANA a potentially advantageous nucleic acid analog for uses ranging from oligonucleotide oral absorption^{46, 47} to developing biosensing and chip technologies in which DNA is commonly employed.^{48, 49}

Most of the biotechnological applications mentioned above require charge transfer (CT). Thus, as we pointed out in a previous study,⁵⁰ 2’F-ANA may outperform DNA in such applications if it combines its enhanced chemical/structural characteristics with a charge conductivity similar to or greater than that through DNA. This fact motivates the present study, which aims to compare the hole transport properties of DNA and 2’F-ANA.

In ref. 50, we showed that the effective^{51, 52} electronic couplings between nucleobase pairs, as a function of the nuclear conformation, are similar in DNA and the nucleic acid analog. In order to establish the relative quality of the two systems in terms of charge conduction, we further need to (i) model the hole transfer through the π-stacked base pairs, (ii) evaluate the free energy parameters involved, (iii) estimate the CT rate constants from the coupling and free energy parameters, and (iv) insert such rates into a suitable kinetic model for the hole transport through the double strands. Points (i)-(iv) are tackled in this study, in which we sample the conformational spaces of DNA and 2’F-ANA (as provided by MD simulations on the model structures shown in Fig. 1) to calculate the necessary CT parameters, and then we insert these parameters into a charge transport model to compare the charge conductivity of the two systems (section 2). Our results indicate that 2’F-ANA may transfer electron holes more rapidly than DNA, or with comparable speed, (section 3), thus supporting the use of 2’F-ANA in nanobiotechnology applications (section 4).

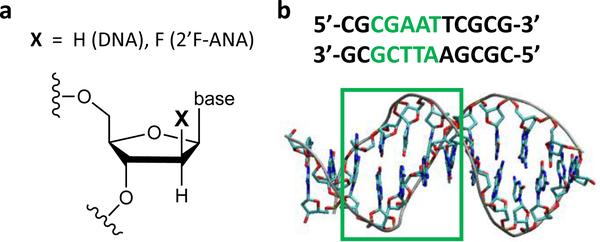
Fig. 1.

Schematic representation of the molecular systems studied. (a) Modification of the DNA sugar moiety that produces 2’F-ANA. (b) Molecular structure and nucleobase pair sequence of the Dickerson-Drew dodecamer (PDB: 4C64⁵³). The CT analysis is performed on the sequence portion highlighted in green. The A-T base pairs in the 5’-to-3’ direction are denoted A₁T, A₂T, and TA.

2. Methods

2.1. System and charge dynamics modeling

DNA and 2’F-ANA are modelled as Dickerson-Drew dodecamers (see Fig. 1). The DNA structure is provided by the PDB file with code 4C64,⁵³ while the 2’F-ANA structure is derived from the 2LSC⁵⁴ PDB file as is detailed in ref. 50. The part of the base-pair sequence studied (after excluding the two terminal nucleobase pairs on each end) is highlighted in Fig. 1b. The choice of this portion takes into account the palindromic nature of the system and incorporates the seam of the two half sequences, so as to include all different types of base pairs in the double strand. The MD simulations were performed in a previous study⁵⁰ where the electronic couplings between adjacent base pairs in the sequences were calculated for structural snapshots spaced 1 ns apart along the MD simulations. Here, a denser conformational sampling is used to enhance the statistical accuracy of the results, considering MD snapshots intercalated with those in ref. 50 and with the same time spacing of 1 ns. Thus, the resulting conformational ensemble consists of 81 structural snapshots extracted each 0.5 ns from the 10–50 ns time window in the MD production run. The electronic couplings are calculated for the conformations missing in the study of ref. 50. The coupling calculations of this previous study are combined with the present ones for the statistical analysis giving Table 1. All other CT parameters are computed using the 81 selected MD snapshots.

Table 1.

Mean-square electronic coupling $<V_{D-A}^2>$(in meV ²) and coherence parameter C for the indicated nucleobase pair dimers in DNA and 2’F-ANA. These parameters are computed using the V_D–A values in Table S1 of the Supplementary Information and Table S1 of ref. 50.

	DNA		2’F-ANA
Base pair dimer	$<V_{D-A}^2>$	C	$<V_{D-A}^2>$	C
CG-GC	241	0.47	267	0.48
GC-A1T	9353	0.57	1444	0.73
A1T-A2T	3599	0.51	1914	0.47
A2T-TA	2547	0.30	3055	0.24

We focus on hole transfer, for which more detailed experimental and theoretical information is available, compared to excess electron transfer, in the case of DNA.⁵⁵ Based on the coupling values (section 3) the rate constant k for CT between adjacent nucleobase pairs can be approximated using the Marcus’ expression for the nonadiabatic, high-temperature limit of charge transfer:^{56, 57}

$$k=\sqrt{\frac{\pi }{\lambda k_{\text{B}}T}}\frac{<V^2>}{\hslash }\exp \left[-\frac{{\left(\mathrm{\Delta }{G}^0+\lambda \right)}^2}{4\lambda k_{\text{B}}T}\right]$$ (1)

The average over the square effective electronic coupling in eqn (1) accounts for the slow modulation of the coupling, V, by nuclear fluctuations, while neglecting the dynamical coupling of the electron and nuclear dynamics.⁵⁷ In eqn (1), △G⁰ and λ are the reaction free energy and reorganization energy associated with the CT, respectively; k_B is Boltzmann’s constant and T is the temperature.

We describe the hole transport as sequential hopping through the stacked nucleobase pairs. The rationale for such approximation is provided by recent multiscale simulations of CT through DNA showing that, on average, the hole localizes almost completely on a single nucleobase because of the hole localizing effects of polarizable solvents (i.e., water in this study), as well as of static and dynamic disorder of the nuclear degrees of freedom.⁵⁸ At any rate, here we do not tackle the thorny issue of charge localization/delocalization in DNA,^{58, 59} as well as the possibility that the electronic states involved in the charge transport are delocalized in technological contexts where a voltage is applied to the DNA.⁶⁰ We assume that the simple description of the hole transport employed here can characterize the relative charge conductivities of DNA and 2’F-ANA with sufficient accuracy.

To define the kinetic model for the charge transport, we combine the charge sequential hopping mechanism with boundary conditions that may describe, for example, situations in which the DNA or 2’F-ANA is used as a probe in biosensing or other chip technology. We consider two cases. In one case, the excess charge (i.e., the hole) is injected near one end of the double strand and travels to the other end or to some intermediate point in contact with a charge drain (such as the tip of an electrode) that quickly sweeps the excess charge away. In the other case, the hole is injected within the DNA or 2’F-ANA double strand and travels towards one of its terminal regions in contact with the charge drain. With this kinetic model, the mean residence time, or travel time, τ of the hole on the relevant double strand portion is described by the equation⁶¹

$$\begin{gathered} \tau =\sum _{n=0}^{N-1}\frac{1}{k_{n\to n+1}}\left(\sum _{j=0}^{N-n-1}\prod _{i=n+1}^{N-j}\frac{k_{i\to i-1}}{k_{i\to i+1}}+1\right)+\frac{1}{k_{N\to N+1}} \\ \cong \sum _{n=0}^N\frac{1}{k_{n\to n+1}}\text{for}{k}_{n+1\to n}<<k_{n\to n+1}(0\le n<N) \\ \cong \frac{1}{k_{p\to p+1}}\text{for}\{\begin{array}{l}{k}_{n+1\to n}<<k_{n\to n+1}(0\le n<N)\hfill \\ k_{p\to p+1}<<k_{n\to n+1}(0\le n\le N,n\ne p)\hfill \end{array} \end{gathered}$$ (2)

where the conditions in the last line are sufficient ones. Here, eqn (2) is applied to the hole (thus, hole occupation probabilities are used in the kinetic model⁶¹ leading to eqn (2)). n=0 denotes the nucleobase into which the hole is created, the N+1 site is the arrival nucleobase in contact with the charge drain, and 1 ≤ n ≤ N distinguishes the nucleobases in the middle. The boundary condition involving the drain⁶¹ differs from the one usually associated with the standard “birth and death” master equation,^{62, 63} which changes the transient evolution of the kinetic model, but not its solution in terms of mean residence times.^{61, 62} The first τ expression in eqn (2) exactly solves the kinetic model, by taking into account all forward and backward CT rates with respect to the charge transport direction that is determined by the positions of the injection and arrival sites. This solution was obtained applying the concept of mean first passage time to the different hopping sites in ref. 62, following the work in ref. 63, while the kinetic problem was solved by use of the induction method in ref. 61. The second well-known approximate expression in eqn (2) can be used when all backward CT rates are negligible compared to their respective forward ones. Under this condition, the last approximate expression of eqn (2) is obtained in the presence of a rate-limiting CT step. Considering the palindromic nature of the nucleobase-pair sequence and our purpose to compare the relative rapidity of charge transport in the two systems, we limit the application of eqn (2) to the double-strand portion highlighted in Fig. 2b, where we also exclude from the analysis the two external base pairs that are more subject to structural fluctuations (cf. ref. 64).

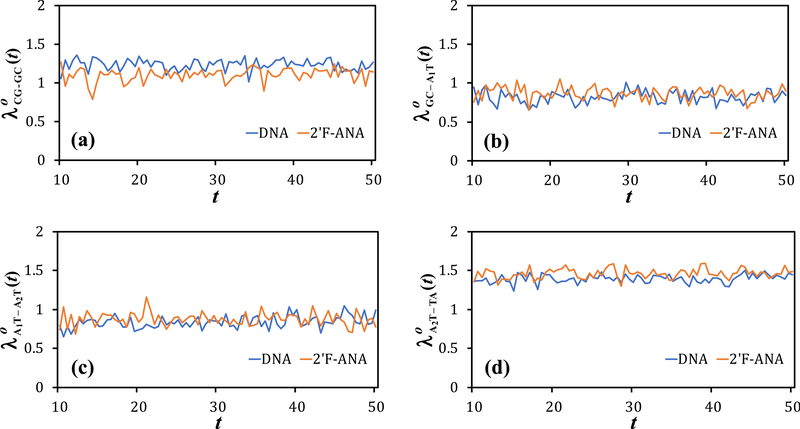
Fig. 2.

(a) V_CG–GC, (b) V_GC–A1T, (c) V_A1T–A2T, and (d) V_A2T–TA versus the MD simulation time for DNA and 2’F-ANA. The diagrammed values are listed in Table S1.

2.2. Effective electronic couplings

The effective electronic couplings $(V_{D-A},D-A=\text{CG}-\text{GC},\text{GC}-{\text{A}}_1\text{T},{\text{A}}_1\text{T}-{\text{A}}_2\text{T},{\text{A}}_2\text{T}-\text{TA})$ are computed between adjacent base pairs pruned from the backbone as detailed in ref. 50, using the theoretical method of ref. 65. This method allows the use of electronic states with a large overlap, as long as the two-state approximation is sufficiently well satisfied^{65, 66} (Supplementary Information, Table S2), therefore avoiding the limitations that may arise from the use of orthogonal diabatic electronic states and the calculation of dipole matrix elements,^{67, 68} or the need for a strict localization of the diabatic states.⁶⁹ The theoretical method⁶⁵ (i) results from exact solution of the secular equation for two non-orthogonal electronic states;⁶⁵ (ii) provides directly the effective electronic coupling to be used in the expressions for both⁷⁰ CT rates and electronic transition probabilities (which is symmetric with respect to the energies of the initial and final diabatic states^{51, 66}); (iii) reconciles the long-standing, puzzling discrepancy raised by the use of different Hamiltonians in the previous time-dependent and secular equation approaches to two-state CT problems;^{52, 66, 70, 71} and (iv) can be reduced to the generalized Mulliken-Hush method^{67, 68} in the particular case of orthogonal diabatic electronic states, using the pertinent dipole moments.⁶⁶

Following the vast DFT analysis in ref. 70, this method is implemented using hybrid DFT, with the M11⁷² density functional and the 6–311g** basis set. This computational setup produces an optimal description of the electronic ground state, avoiding the excessive spreading of the net charge between the donor and acceptor groups that is generally due to electron self-interaction errors and would otherwise lead to overestimation of the couplings.⁷⁰ While the theoretical method of ref. 65 can be implemented using any of the available methods for diabatic state construction (for example, the generalization of the Boys algorithm proposed in ref. 69), constrained DFT (CDFT)^{73, 74} affords a natural approach to the localization of the excess (transferring) charge within DFT computational schemes, because it searches for the minimum-energy distributions of the charge on the donor and acceptor atomic groups. Here, we obtain the diabatic electronic states using the CDFT approach that was formulated in refs. 75, 76 and implemented in the NWChem software package.⁷⁷ Using the variance ${\sigma }^2=<V_{D-A}^2>-<V_{D-A}{>}^2$, the variations in the effective electronic coupling caused by nuclear fluctuations are characterized by means of the coherence parameter $C=1-{\sigma }^2/<V_{D-A}^2>=<V_{D-A}{>}^2/<V_{D-A}^2>$.⁷⁸ $C\cong 1$ in very rigid systems, since ${\sigma }^2\cong 0$, while $C\cong 0$ in very flexible systems with strong conformation dependence of the coupling.

2.3. Free energy parameters

We calculate the free energy parameters △G⁰ and λ (eqn (1)) using simple recipes that can be useful in simulations of complex systems of biological or technological relevance, in which the nucleic acid is interfaced with macromolecules^{61, 64, 79, 80} or electrodes.^{14, 81}

The reaction free energy for the hole transfer between the donor (D) and acceptor (A) base pairs,$\mathrm{\Delta }{G}_{D-A}^0$ , is approximated as the difference in oxidation potential between the A and D purine bases. Using the experimental values of 1.29 V^{82, 83} and 1.42 V⁸² (with respect to the normal hydrogen electrode) for the oxidation potentials of G and A, respectively, we obtain $\mathrm{\Delta }{G}^0=0.13\text{eV}(-0.13\text{eV})$for the $\text{GC}-\text{to}-{\text{A}}_1\text{T}\left({\text{A}}_1\text{T}-\text{to}-\text{GC}\right)$ hole transfer, while $\mathrm{\Delta }{G}^0=0$for all other CT steps.

The reorganization energy is calculated using the Marcus’ expression^{56, 84}

$${\lambda }_{D-A}={\lambda }_{D-A}^i+\left(\frac{1}{{\epsilon }_o}-\frac{1}{{\epsilon }_s}\right)\left(\frac{1}{2R_D}+\frac{1}{2R_A}-\frac{1}{R_{D-A}}\right)e^2$$ (3)

In eqn (3), ${\lambda }_{D-A}^i$denotes the inner-sphere contribution to the reorganization energy; ε_o and ε_s are the optical and static dielectric constants that describe the CT medium; e is the transferred elementary charge; R_D and R_A are the D and A effective radii, respectively; and R_D–A is the center-to-center distance between D and A. ${\lambda }_{G-G}^i$and ${\lambda }_{A-A}^i$ are obtained using Nelsen’s four-point method,^{85, 86} with gas-phase B3LYP/6311++g** computations on the G and A nucleobases, respectively. The values thus obtained are ${\lambda }_{G-G}^i=0.618\text{eV}$ and ${\lambda }_{A-A}^i=0.414\text{eV}$, which are relatively similar to the values found in ^{ref. 87} for the corresponding nucleobase-pair dimers. ${\lambda }_{\text{G}-\text{A}}^i=0.516\text{eV}$ is obtained as the average of these two values, according to Marcus’ prescription.^{88, 89} ${\lambda }_{\text{G}-\text{A}}^i$is close to the value obtained by DFT computations on the corresponding base-pair dimer in ref. 87.

The choice of calculating ${\lambda }_{D-A}^i$for the individual G and A purine bases relies on the substantial localization of the hole on such nucleobases and is consistent with the following recipe to estimate the effective radii in the outer-sphere contribution to the reorganization energy, which is given by the second term on the right side of eqn (3)). This term is hereafter denoted ${\lambda }_{D-A}^0$. In order to maintain the simple picture of eqn (3)), we first obtain the centers of the hole localizations in the G and A bases using the standard formula $r_c=\sum q_i{r}_i$, where r_i is the position vector of atom i in the given nucleobase and q_i is its Löwdin charge, which is calculated with the M11/6–311g** method (consistently with the coupling calculations) for each purine nucleobase and snapshot (e.g., the atomic coordinates and Löwdin charges of the DNA and 2’F-ANA nucleobases in the first MD snapshot are reported in Tables S3–S12 of the Supplementary Information). The center-to-center distance R_D–A is given by the distance between the D and A centers of charge (see Tables S13 and S14 in the Supplementary Information).

Born’s expression for the (dielectric) solvation energy involved in Marcus’ formulation of ${\lambda }_{D-A}^0$ suggests the two simplest ways to define R_D and R_A. One way results from the description of the Born model for a charged sphere and consists in defining the average size of the charge distribution on the nucleobase through the weighted average distance between the calculated center of charge and the nucleobase atoms, using the atomic charges as weights. This approach may give an effective radius that is appreciably smaller than the geometric size of the cavity produced by the nucleobase in the surrounding environment described by the dielectric constants, thus leading to inconsistency with the ${\lambda }_{D-A}^i$calculation using the entire nucleobase. The other way is inspired by the same expression of Born solvation energy, but as meant for a point charge in a spherical cavity. In fact, considering that the center of charge is near the C4-C6 atoms (i.e., on the side of the pyrimidine ring, close to the edge in common with the imidazole ring) and thus near the geometric center, in both G and A, one can define the nucleobase effective radius as the geometric average distance between the center of charge and the nucleobase atoms. This approximation, which is used here, is consistent with our calculation of ${\lambda }_{D-A}^i$, while other limitations of both approaches remain, e.g. regarding the planar conformation of purines. However, such limitations do not preclude profitable uses of models that decompose the CT system in spheres for free energy calculations.⁹⁰

Since the reorganization energy is, actually, a free energy, even neglecting entropic effects, the use of eqn (3) requires to average the D and A effective radii and distance over the thermal fluctuations of the system. Considering the structural stability of the DNA and 2’F-ANA systems over the MD production runs that emerges from their RMSDs,⁵⁰ we assume that the ergodic hypothesis is valid and sufficiently well approximated by averaging over the set of 81 selected MD snapshots. Therefore, we calculate the reorganization energy using the formula

$${\lambda }_{D-A}={\lambda }_{D-A}^i+\frac{1}{N_s}\sum _i{\lambda }_{D-A}^o\left(t_i\right)$$ (4a)

with

$${\lambda }_{D-A}^o(t)=\left(\frac{1}{{\epsilon }_o}-\frac{1}{{\epsilon }_s}\right)\left[\frac{1}{2R_D(t)}+\frac{1}{2R_A(t)}-\frac{1}{R_{D-A}(t)}\right]e^2$$ (4b)

where R_D, R_A, and R_D–A are calculated at the time t_i of the ith selected MD snapshot, N_s is the number of snapshots, and the summation runs over the selected MD snapshots. ${\lambda }_{D-A}^i$is constructed as a time-independent quantity, following a standard approximation scheme.⁸⁵ We apply eqn (4) using three sets of dielectric constants that correspond to different physical limits and therefore serve to test the robustness of our results with respect to the theoretical-computational approach used. The set $S_1=\left\{{\epsilon }_o=2.27,{\epsilon }_s=12.4\right\}$ ⁹⁰ describes the limiting case in which the base stack environment (namely, the complementary and flanking nucleobases) dominates the effective dielectric constants. The set $S_2=\left\{{\epsilon }_o=1.8,{\epsilon }_s=80\right\}$represents cases in which the contribution of surrounding water is dominant. $S_3=\left\{{\epsilon }_o=2,{\epsilon }_s=8\right\}$combines the ε_o value in ref.⁹¹ (which is intermediate to the other two ε_o values used) with the experimental ε_s value from ref.⁹². Depending on the context in which DNA or 2’F-ANA is used, the dielectric constants may be approximated by one of these choices or need to be described using multiple dielectric zones.^{90, 93} The above approach is used to calculate consistently the reorganization energies in DNA and 2’F-ANA, whereas ${\lambda }_{D-A}^o$was only estimated for DNA in previous studies.^{94, 95}

3. Results and discussion

3.1. Effective electronic couplings

The V_D–A values obtained in the present study are listed in Table S1 of the Supplementary Information and diagrammed in Figs. 2a–d. Table S2 shows that the two-state approximation is well satisfied. The parameters in Table 1 are obtained using the V_D–A values in Table S1 and in ref. 50. Due to the palindromic nature of the two base-pair sequences, we expect similar electronic couplings for the nucleobase pairs in the part of the system not considered, thus ruling out substantial differences that could otherwise arise from the directional asymmetry of hole transfer through nucleic acids.⁹⁶

The comparison of Table 1 with Table 2 of ref. 50 shows an inversion in the relative $<V_{{\text{A}}_1\text{T}-{\text{A}}_2\text{T}}^2>$values for DNA and 2’F-ANA, as well as an increase in the $<V_{{\text{A}}_2\text{T}-\text{TA}}^2>$ value for DNA. However, the denser sampling of MD snapshots that leads to Table 1 does not change the order of magnitude of any electronic coupling value. In fact, $<V_{{\text{A}}_2\text{T}-\text{TA}}^2>$in DNA undergoes the largest change, which amounts to an increase of only a factor ~ 1.5 in the average size of electronic coupling.

Table 2.

Reorganization energy (λ_D–A) and hole-transfer rate (k_D–A) values for the indicated base-pair dimers in DNA, using the S₁, S₂ and S₃ dielectric constant sets.

DNA	S1		S2		S3
	${\lambda }_{D-A}(\text{eV})$	$k_{D-A}\left({\text{s}}^{-1}\right)$	${\lambda }_{D-A}(\text{eV})$	$k_{D-A}\left({\text{s}}^{-1}\right)$	${\lambda }_{D-A}(\text{eV})$	$k_{D-A}\left({\text{s}}^{-1}\right)$
TA-A2T	1.81	7.08 × 105	2.52	5.97 × 102	1.87	3.88 × 105
A2T-A1T	1.25	2.81 × 108	1.68	3.68 × 106	1.29	1.87 × 108
A1T-GC GC- A1T	1.33	3.60 × 109 2.28 × 107	1.75	5.42 × 107 3.43 × 105	1.37	2.41 × 109 1.53 × 107
GC-CG	1.85	4.49 × 104	2.48	8.41 × 101	1.90	2.72 × 104

The values of $<V_{\text{CG}-\text{GC}}^2>$ and $<V_{{\text{A}}_2\text{T}-\text{TA}}^2>$in 2′F-ANA and DNA are very similar (the ratios of these mean-square couplings are about 1.1 and 1.2, respectively), thus reflecting in even smaller differences in the electronic couplings. On the contrary, we obtain appreciable differences for the $<V_{\text{GC}-{\text{A}}_1\text{T}}^2>$and $<V_{{\text{A}}_1\text{T}-{\text{A}}_2\text{T}}^2>$ values, which are about 6 and 2 times larger in DNA than in 2′F-ANA (namely, their square roots differ by factors of about 2.5 and 1.4, respectively). These differences correlate with the $<R_{\text{GC}-{\text{A}}_1\text{T}}>$and $<R_{{\text{A}}_1\text{T}-{\text{A}}_2\text{T}}>$values (as calculated from Tables S13–S14), which are 3.80 Å and 3.70 Å in DNA versus 3.94 Å and 3.80 Å, respectively, in 2′F-ANA. From structural analysis using the CPPTRAJ software,⁹⁷ we see that the slide parameter is mainly different in the two systems. In fact, for the GC-A₁T and A₁T-A₂T dimers in the DNA system, the average (absolute) values of the slide are 0.40 Å and 0.68 Å, respectively, while the corresponding values in 2′F-ANA are 1.21 Å and 1.22 Å, thus slightly impairing the corresponding electronic couplings in 2′FANA compared to DNA.

The average coherence parameters for the DNA and 2’FANA nucleobase pairs are 0.46 and 0.48, respectively, thereby indicating similar fluctuations of the base-pair electronic couplings. Considering the connection between the coupling and the nucleobase π-stacking, the denser sampling of the nucleic acid structures further supports our conclusion⁵⁰ that the enhanced chemical stability of 2’F-ANA compared to DNA does not entail reduced fluctuations of the nucleobase π-stack involved in the charge conduction.

3.2. Reorganization energies

The effective center-to-center D-A distances in Tables S13–S14 and the effective D and A radii in Tables S15–S16 give the outer-sphere ${\lambda }_{D-A}^o\left(t_i\right)$ values shown in Fig. 3. The ${\lambda }_{D-A}^i+{\lambda }_{D-A}^{°}\left(t_i\right)$values are reported in Tables S17–S22, while Tables 2 and 3 contain the values of the total reorganization energy ${\lambda }_{D-A}$ for each nucleobase pair in DNA and 2’F-ANA derived from eqn (4) using the dielectric constant sets S₁, S₂, and S₃. The outer-sphere reorganization energy ${\lambda }_{D-A}^o$ (see Table S23) for the intra-strand adenine dimer A₁-A₂ spans the range 0.84–1.27 eV depending on the dielectric constants used. This range includes previous estimates of Steinbrecher et al.⁹⁴ (1.08 eV) and Kubař et al.⁹⁵ (1.21 eV). Our estimate of 1.26 eV using the dielectric constants of water is close to the one of Kubař and Elstner⁹⁵ for DNA in water. This agreement promotes the theoretical framework detailed in Section 2.3, although more accurate approaches to calculate the reorganization energy^{85, 90, 93–95, 98-108} may be needed depending on the structure and dynamics of a specific system studied. Tables 2 and 3 show similar reorganization energies for the DNA and 2’F-ANA nucleobase pairs. Therefore, according to our results, the DNA modification leading to 2’F-ANA does not influence significantly the reorganization free energies associated with hole transfer through the nucleobases.

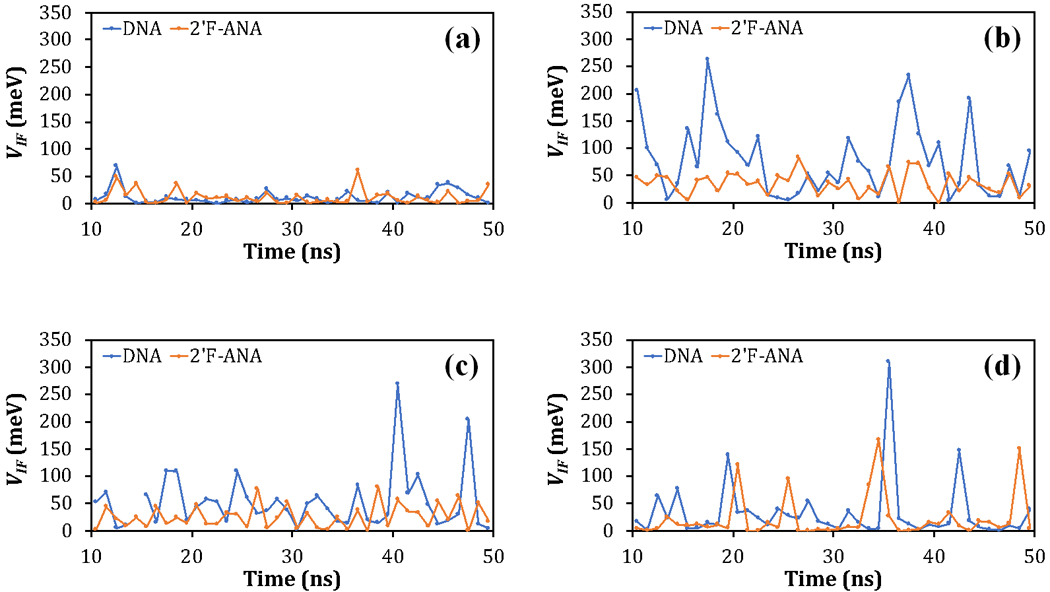
Fig. 3.

Instantaneous value of the Marcus expression for the outer-sphere reorganization energy ${\lambda }_{D-A}^o(t)$(eqn (4b)), in eV, vs. the MD simulation time, in ns, for the D-A dimers (a) CG-GC, (b) GC-A₁T, (c) A₁T -A₂T, and (d) A₂T-TA in DNA and 2’F-ANA. The S₁ set of dielectric constants is used. The curves are linear interpolations of the data points listed in Tables S17 and S18, which are taken each 0.5 ns in the 10–50 ns time window of the MD production runs.

Table 3.

Reorganization energy (λ_D–A) and hole-transfer rate (k_D–A) values for the indicated base-pair dimers in 2’-FANA, using the S₁, S₂ and S₃ dielectric constant sets.

2’F-ANA	S1		S2		S3
	${\lambda }_{D-A}(\text{eV})$	$k_{D-A}\left({\text{s}}^{-1}\right)$	${\lambda }_{D-A}(\text{eV})$	$k_{D-A}\left({\text{s}}^{-1}\right)$	${\lambda }_{D-A}(\text{eV})$	$k_{D-A}\left({\text{s}}^{-1}\right)$
TA-A2T	1.88	4.21 × 105	2.62	2.65 × 102	1.94	2.31 × 105
A2T-A1T	1.29	9.95 × 107	1.73	1.19 × 106	1.33	6.64 × 107
A1T-GC GC- A1T	1.38	3.37 × 108 2.13 × 106	1.82	4.17 × 106 2.64 × 104	1.42	2.26 × 108 1.43 × 106
GC-CG	1.72	1.83 × 105	2.28	6.81 × 102	1.77	1.11 × 105

3.3. Charge transport

The CT rate constants for the hole-transfer steps in DNA and 2’F-ANA are reported in Tables 2 and 3, respectively. The approximations in section 2 lead to equal CT rates for the two opposite CT steps between given nucleobase-pairs if purine nucleobases of the same kind are involved, while the reaction free energy causes different $k_{D-A}$values for the A₁T-GC and GC-A₁T hole-transfer steps (therefore, both values are reported in Tables 2 and 3).

The theoretical calculation of the rate constant for the A₁T-to-GC hole-transfer step is relevant to experiments on photoinduced charge separation and transport in (diblock) DNA hairpins,^25,26,36 in which the hole transfer between A and G nucleobases protracts the charge separation.³⁰ Experiments on DNA hairpins with a perylenediimide chromophore and a single G base working as the hole acceptor produced an A-to-G hole-transfer rate that ranges from ~10¹⁰ to ~10¹² S⁻¹ depending on the length of the adenine block separating the chromophore from the guanine acceptor.²⁵ More recent experiments using a diphenylacetylenedicarboxamide chromophore obtained a rate constant ranging from ~10⁸ to ~10¹⁰ s^−1,26 This range encloses our theoretical values for the A₁T-GC nucleobase dimer in DNA and 2’F-ANA using the S₁ and S₂ dielectric constant sets (Tables 2 and 3). Experiments on diblock DNA hairpins (where the hole acceptor consists of more than one G nucleobase) give a CT rate of ~ 10¹² s^–1.³⁰ However, we expect that hole trapping in the G tract is favored by the presence of more guanines, namely, the free energy difference between the A and G tracts is increased compared to the case in which only one G is present. In fact, a value of $\mathrm{\Delta }{G}^0=-0.45\text{eV}$ was predicted^{23, 30, 109} (note that part of the difference between this value and the value of −013. eV used in our study can also be attributed to the different experimental conditions in the investigations of DNA diblock hairpins^{23, 30, 109} and in the studies that provided the A and G oxidation potentials used here^{82, 83}). Furthermore, partial charge delocalization within the A and G blocks may reduce^{110, 111} the reorganization energy compared to our estimate for the A-G dimer. Using $\mathrm{\Delta }{G}^0=-0.45\text{eV}$and the reorganization energy values corresponding to the S₁ and S₃ dielectric constant sets (Table 2), we would obtain a ps time scale for the hole transfer from A₁T to GC, in agreement with the experiment in ref. 30 (see Scheme 2B therein). This agreement supports our theoretical value for the A₁T-GC mean-square electronic coupling in the DNA sequence and, more generally, our theoretical-computational approach to the calculation of electronic couplings between adjacent base-pair dimers in either DNA or 2’F-ANA. This fact, as well as the general agreement between the reorganization energy values obtained in this study and the available values, for comparison, in the DNA literature (Section 3.2), help delimit the theoretical uncertainty of our treatment in relation to our main conclusions. In fact, such uncertainty is expected to be similar for the DNA and 2’F-ANA systems (which contain the same nucleobases and experience similar structural fluctuations⁵⁰) and, in both cases, smaller than the differences in the CT rates resulting from use of different dielectric constant sets. Yet, the similarity of the DNA and 2’F-ANA conductivities is not affected by the different dielectric environments.

Table 4 shows the mean residence time, τ, of the hole along the path from the TA pair to CG, namely, the average time spent by a hole injected in the middle of DNA or 2’F-ANA (for example, by contact with an analyte) to travel towards the edge of the double strand (where, e.g., the hole is delivered to an electrode that functions as a charge drain). τ is calculated using the different sets of dielectric constants. The value of the effective rate constant $k_{\text{eff}}\equiv 1/\tau$ obtained using the S₁ set is also explicitly shown. Table 5 reports the analogous quantities for the path from CG to TA. S₂ leads to τ values significantly larger than those resulting from S₁ and S₃, as a consequence of the greater localization of the transferring hole in the more polarizable medium, which entails a larger reorganization energy.^{110, 111} However, environments characterized by dielectric constants closer to S₁ and S₃ are expected in most technological applications, where, generally, the nucleic acid is not completely surrounded by a polar solvent such as water.

Table 4.

Mean travel time (τ) spent by the hole to traverse the path from TA to a charge drain in contact with CG. The τ values corresponding to the S₁, S₂ and S₃ dielectric constants sets are denoted τ₁, τ₂, and τ₃, respectively, and are computed inserting the CT rates of Tables 2 and 3 into the exact expression of eqn (2). The value of the effective rate $k_{\text{eff},1}=1/{\tau }_1$ is also shown.

TA to CG	τ1(s)	keff,1 (s–1)	τ2 (s)	τ3 (s)
DNA	2.41 × 10−5	4.14 × 104	1.38 × 10−2	4.00 × 10−5
2’F-ANA	7.98 × 10−6	1.25 × 105	5.27 × 10−3	1.36 × 10−5

Table 5.

Mean travel time (τ) spent by the hole to traverse the path from CG to a charge drain in contact with TA. The notation is the same as in Table 4.

CG to TA	τ1(s)	keff,1 (s–1)	τ2 (s)	τ3 (s)
DNA	4.73 × 10−4	2.12 × 103	5.44 × 10−1	8.57 × 10−4
2’F-ANA	7.64 × 10−4	1.31 × 103	1.20	1.39 × 10−3

In the path from TA to CG (see base-pair sequence in Fig. 1), the rate of the forward CT from A₁T to GC is much larger than the backward CT rate (note that we are considering the two opposite hole-transfer processes for the same GC-A₁T dimer in the 5’-to-3’ direction; we are not comparing GC-A₁T and A₁T-GC dimers in the 5’-to-3’ direction, for which the electronic couplings would be considerably different⁹⁶). The forward and backward CT rates for the other self-exchange steps are the same, but the backward CT rate from CG to GC is not at play, because, in our model, the charge is immediately delivered to a drain when it arrives at CG. In both DNA and 2’F-ANA, k_eff is only slightly smaller than k_D–A for the rate-limiting CT step from GC to CG (i.e., 4.49 × 10⁴ s^–1 in DNA and 1.83 × 10⁵ s^–1 in 2’F-ANA; cf. Tables 2 and 3, respectively). For the path from TA to CG, it is $k_{\text{GC}-\text{CG}}=k_{N\to N+1}$, and the $1/k_{N\to N+1}$ term in the first τ expression of eqn (2) is much larger than all the other terms, so that $\tau \approx 1/k_{\text{GC}-\text{CG}}$although the backward CT rates are not negligible for most of the other CT steps, i.e., the first condition associated with the last τ expression in eqn (2) is not satisfied. For the route from CG to TA, k_CG–GC and k_GC–CG are both at play, and the rate k_A1T–GC of backward CT from A₁T to GC is two orders of magnitude larger than the corresponding forward rate $k_{\text{GC}-{\text{A}}_1\text{T}}$ in both DNA and 2’F-ANA (see Tables 2 and 3, respectively). Therefore, the last expression for τ in eqn (2) does not apply although k_CG–GC is much smaller than all other forward CT rates, that is, the second condition associated with the last τ expression in eqn (2) is satisfied. This condition needs to be combined with the negligibility of the backward CT rates to provide a sufficient condition of general validity to approximate τ as the inverse of the slowest CT rate.

The results in Tables 4 and 5 indicate that DNA and 2’F-ANA have comparable conductivities. Conduction through 2’F-ANA is somewhat faster than through DNA in the predominant direction of charge transport (from the TA base pair to CG) that would be privileged in most applications of the nucleobase-pair sequences studied. The DNA hole conduction is a little faster in the opposite direction. Clearly, the approximations used in the theoretical models do not allow us to establish with certainty which of the two systems supports faster hole conduction, while from our results it clearly emerges that the DNA and 2’F-ANA conductivities have the same order of magnitude in different CT environments, as are here modeled using different dielectric constants. A more detailed analysis of the CT rates associated with the individual base-pair dimers (cf. Tables 2 and 3) shows that: the CT through the TA-A₂T dimer is similarly fast in the two systems; the difference in CT rate is significantly less than one order of magnitude for A₂T-A₁T; the CT rate for the A₁T-GC or GC-A₁T step is about one order of magnitude larger in DNA than in 2’F-ANA, and the converse holds for the slow GC-CG step. This comparison highlights that appreciable differences in DNA and 2’F-ANA conductivities may be observed for sequences with an appreciable prevalence of intra-strand A-G or inter-strand G-G stacks. For mixed sequences such as the ones considered in this study, comparable conduction properties are expected, and 2’FANA might prevail due to the faster hole transfer in the guanine dimer. Future studies on a variety of base-pair sequences and nucleic acid lengths would be desirable to refine the comparison between the charge conduction properties of DNA and 2’F-ANA. Nonetheless, we expect that the strong indication in support of their similar charge transport properties is confirmed, especially since our theoretical-computational approach, or more refined ones, cannot achieve confidence intervals for the values of the CT rates (which depend exponentially on the activation barrier) narrower than one order of magnitude.

The τ values in Tables 4 and 5 are less than doubled, and thus the timescales are the same, for the 8-base-pair palindromes obtained from the model systems of Fig. 1 excluding two base pairs in each terminal region. Considering the predominant hole transport direction (Table 4) and using the S₁ and S₃ dielectric constants to describe the polarization of the CT environment, we obtain a timescale on the order of 10 μs for the charge transport through the 8-base-pair DNA and 2’F-ANA palindromes. A much slower conduction, on a 10 ms timescale, would be obtained using dielectric constants of water (S₂). However, we expect that S₁ and S₃ are more realistic choices of dielectric constants to describe the charge transport through DNA and 2’F-ANA in technologically relevant contexts. The use of an intermediate static dielectric constant (namely, between the limiting values in S₃ and S₂) would lead to a timescale in the ms-to-μs range. This timescale is clearly reduced if a bias voltage is applied to the system in a device. More importantly, the reorganization energies at play might be smaller than those calculated by us and in previous studies, and thus the hole transport timescale might be correspondingly smaller. In this regard, it is important to investigate if a significantly smaller effective reaction reorganization energy as the one defined by Matyushov and coworkers¹⁰⁷ for proteins can also be defined for nucleic acids, thus leading to much faster hole transport through DNA and 2’F-ANA.

The present analysis only considers the effects of the different backbones in DNA and 2’F-ANA on the structural fluctuations that influence both the base-pair π-stacking (which is the main factor determining the base-pair electronic couplings) and the reorganization energies associated with the hole transport. Future studies should ascertain whether the backbone difference may produce any appreciable change in the electronic couplings and in the reorganization energies, as computed by including the backbone connecting the two stacked base pairs involved in each CT step.

Hole delocalization over more than one nucleobase pair may change the charge conductivity of the nucleobase π-stack in both the DNA and 2′F-ANA systems. This charge delocalization should be improbable in polar environments^{58, 59} (see Section 2.1) and, anyhow, our results for structural fluctuations,⁵⁰ electronic couplings (ref. 50 and present study) and reorganization energies (present study) produce the expectation that this charge delocalization, if at play, should influence to similar extents the charge conductivities of DNA and 2′F-ANA.

4. Conclusions

This study shows that the electron-hole conduction occurs on the same timescale in DNA and 2’F-ANA. We provide a simple scheme for rapid and yet sufficiently accurate description of the charge transport through nucleic acid-like systems, which may be conveniently applied to systems larger than the ones studied here. We also discuss some possible improvements of such scheme that may lead to more accurate quantitative evaluation of CT timescales in DNA and DNA-inspired systems.

According to our results, the greater chemical stability of 2’F-ANA compared to DNA does not entail significant changes in the conformational properties of the base-pair pattern, concerning the electronic structure and free energy properties relevant to the hole transport. In fact, the results of this study, combined with those of ref. 50, show (i) similar fluctuations of the inter-nucleobase pair electronic couplings as a function of the nuclear motion, despite the chemical stability enhancement produced by the backbone mutation in 2’F-ANA, and (ii) similar free energy parameters (in particular, reorganization energies) for the pertinent CT steps. These parameters mainly depend on the nucleobase pairs, which are the same in the two nucleic acid systems, and on the theoretical-computational modeling of the environment around the hole-transfer partners, which includes the nucleic acid backbones. Since the environment neutralizes the backbone charges in both systems (which is crucial for their stability), we expect that more refined theoretical modeling of the base-pair surroundings would not change our conclusion on the similarity of the reorganization energies associated with the CT processes in the two nucleic acid systems. Future studies that include explicitly the (solvated) backbone connecting adjacent base pairs could investigate this expectation.

Our results indicate a slightly faster hole transport through 2’F-ANA than through DNA in the predominant charge transport direction, but the theoretical uncertainty in the absolute values of the effective CT rates is such not to allow such a strict comparison of the two conductivities. Although the absolute value of the timescale depends on the base-pair sequence and the approximations used in the theoretical modeling of the actual systems, we expect that none of these approximations can affect the main physical-chemical conclusion of this study, namely, the fact 2’F-ANA can conduct electron-holes comparably to DNA, thereby providing a valid alternative to DNA for technological applications that use nucleic acid charge transport and, at the same, can benefit from the enhanced 2’FANA’s chemical stability.