Deterministic epidemic model for ($SV{C}_{Sy}{C}_{Asy}IR$) pneumonia dynamics, with vaccination and temporal immunity

Abstract

Streptococcus pneumonia is one of the leading causes of mobility and mortality in children under 6 years and the elderly especially in developing countries in which Ghana, the study area is not an exception.In this paper, a model of the spread and control of bacterial pneumonia that include symptomatic carriers, asymptomatic carriers and vaccination is formulated and analyzed to determine the effect of the vaccination intervention.Analysis of the system show that the disease free equilibrium is stable if and only if the basic reproductive number $R_0<1$. For $R_0\ge 1$, the endemic equilibrium is globally stable and the disease persist. Numerical simulation on the system show that with effective vaccine intervention pneumonia infection can be eradicated in the long term.

1. Introduction

Pneumonia has been rated as the leading cause of under six morbidity and mortality in Ghana, with an up setting annual death toll record of 16,200 children, representing 20 percent deaths per year, according to Ghana Health Service (Ghana Health Service, 2018; GhanaHomePage).

According to World Health Organisation the leading causes of death among children under six in 2016 were preterm birth complications, pneumonia, intrapartum-related complications, diarrhoea and congenital abnormalities. Neonatal deaths accounted for 45% of under-five deaths in 2016.Pneumonia is the single largest infectious cause of death in children worldwide. Pneumonia killed 920,136 children under the age of six in 2016, accounting for 16% of all deaths of children under six years old (WHO and UNICEF, 2016; World Health Organization, 2016).Globally, about 1.58 million children under six years die from pneumonia annually,it is the single biggest child-killer in the world according to the United Nations Children Emergency Fund, more children die from pneumonia than from Human Immured Virus and Acquired Immured Deficiency Syndrome (HIV/AIDS), diarrhea and malaria combined,the disease kills a child every 35 s (United Nations Children Emergency Fund, 2015).

Pneumonia is a respiratory infection that affects the lungs, resulting in an inflammation of the alveoli, the air sacs that make up the bulk of the lungs and help us breathe. Infection causes them to fill with fluid or mucus, limiting the amount of oxygen entering the sacs and making it painful to breathe.Pneumonia are mainly caused by bacteria, viruses, fungal. But Bacteria are the most common cause of pneumonia with the bacterium called Streptococcus pneumoniae being the primary causative agent of most common cause of pneumonia in children, with an incubation period between 1 and 4 weeks.The most common cause of viral pneumonia in adults is the influenza virus that accounts for approximately a third and in children for about 15% of pneumonia cases. A number of different respiratory viruses cause pneumonia in children such as respiratory syncytial virus (RSV) and Influenza are the most common viral cause of pneumonia (United Nations Children Emergency Fund, 2015; World Health Organization, 2016,(Center for Disease Control and Prevention, 2017)).

There is a risk of developing secondary bacterial pneumonia when viral pneumonia is present. However, it is more common in elderly people over 65 years and young children under six years of age. Some people are at higher risk of pneumonia because they have pre existing lung diseases, poor nutrition, difficulty in swallowing, other chronic health problems or problems with their immune system, other higher risk factors that can course pneumonia are smoking, alcoholism neurological problems or sustaining injuries that interfere with swallowing or coughing.

Basically, pneumonia is classified in to two;

• (a)Community-acquired pneumonia (CAP) which is acquired outside of the health-care setting and
• (b)Hospital-acquired (or health-care-acquired)pneumonia (HAP) which is typically more serious but about 20% of those with CAP require treatment in a hospital (mayoclinic).

Pneumonia is preventable through vaccination, proper diagnosis, screening, environmental control measures and appropriate treatment of other diseases (Singh & Aneja, 2011; Wardlaw, Salama, Johansson, & Mason, 2006). Vaccination is the most effective way to prevent certain bacterial and viral pneumonia in children under six years of age. The two types of vaccines available against S. pneumoniae are the pneumococcal polysaccharide vaccine (PPV), based on purified capsular (PS) and pneumococcal conjugate vaccine (PCV), obtained by chemical conjugation of the capsular (PS) to a protein carrier (Dunn, 2005). PCVs were developed for use in children only and PPV for vaccination of the at-risk adults and the elderly (Moberley, Holden, Tatham, & Andrews, 2013; Russell & Mulholland, 2004). Pneumococcus spreads through micro aspiration of oropharyngeal organisms and inhalation of aerosols containing bacteria or viruses especially in children that carry the bacteria in their throats without being sick. Newborn babies can again, be protected from pneumonia infection through early recognition and treatment at the level of the community or the primary-care health facility, testing of pregnant mothers for streptococcus and giving antibiotic treatment and vaccination with PPV that has a proven record of safety in pregnant and breastfeeding mothers for pneumococcal pneumonia prevention in infants. Suctioning the mouth and throat of babies with meconium-stained amniotic fluid decreases the rate of aspiration pneumonia (Mulholland, 2007(Ngari et al., 2014)).

Environmental measures for pneumonia prevention include reduction of indoor air pollution by encouraging good hygiene in crowded homes and smoking cessation that reduces risks of pneumonia infections among children and adults. Since the bacteria and viruses can also be spread to your hands and then to your mouth, it is important to wash hands with soap when around a person with pneumonia infection (Kizito & Tumwiine, 2018).

Appropriate antibiotics are used for treatment of bacterial pneumonia,it treatment depends on the underlying cause of infection. Effective and timely treatment together with better diagnostic tools and education prevents antibiotic resistance (Rodrigues, 2017, Effelterre et al., 2010).

These are some of literatures of the mathematical models developed to study transmission dynamics of pneumonia using different procedures.

Tilahun et al. (Tilahun et al., 2017). Proposed and analyse a nonlinear mathematical model for the transmission dynamics of pneumonia disease cost-effective strategies. They used deterministic compartmental model and stability theory of differential equations in their study. They also consider possibility of bifurcation of the model and the sensitivity indices.

Ndelwa et al. (Ndelwa et al., 2015). Used a mathematical model of the transmission dynamics of pneumonia with screening and treatment to formulate and analyse the disease with the aim of understanding its transmission dynamics and the effects of these interventions that lead to the causes of serious illness and deaths among children under five years of age in Tanzania and around the world.

Ong’ala et al. (Jacob Otieno, Joseph, & John, 2012). Used a mathematical model of the transmission dynamics of pneumonia among children under five years of age and they considered four compartments based on the disease status, that is Susceptible, Carriers, Infectious and Recovered (SICR). The model is analyzed using the theory of ordinary differential equations, dynamical systems and possibility of bifurcation. They only considered the S.pneumonia since it is the most common among children under five years of age.

Kizito et al. (Kizito & Tumwiine, 2018). They study, a model of the spread and control of bacterial pneumonia under public health interventions that involve treatment and vaccination. They also infer the effect of these interventions on the dynamics of the pneumonia through sensitivity analysis on the effective reproduction number. From which it is revealed that treatment and vaccination interventions combined can eradicate pneumonia infection. A numerical simulation was done to illustrate the analytical results and establish the long-term behavior of the disease. It is revealed that, with treatment and vaccination interventions combined, pneumonia can be wiped out. However, with treatment intervention alone, pneumonia persists in the population.

Temime et al. (Temime, Guillemot, & Böelle, 2004). Developed a mathematical model of selection for S. pneumoniae resistance to penicillin G in an age structured population. The model considered three age classes, that is, [0, 2) years, [2, 15) years and 15 + years. The model incorporated vaccination and sought to understand the epidemiological characteristics of S. pneumoniae in a vaccinated population and also the distribution of resistance levels in children and adult carriers after introduction of vaccination. The results suggested that because of serotype replacement, the effects of vaccination observed at a particular instant would not be sustained in the long run.

Sutton et al. (Sutton, Banks, & Castillo-Chavez, 2010). Developed a mathematical model for pneumococcal infection with vaccination. It was made up of partial differential equations with time and age as independent variables, though in the analysis these were reduced to differential equations. The model was used to evaluate the impact of vaccines at population level and parameters were estimated using data.The use of vaccination as an intervention, age dependence and estimation of parameters were important aspects that informed our work.

2. Model description and formulation

The model divides the total population(N) into six sub-classes according to their disease status. susceptible S(t),vaccinated V(t),symptomatic carrier $C_{sy}\left(t\right)$, asymptomatic carrier $C_{Asy}\left(t\right)$, infected I(t), recovery R(t).

In the model the disease is assumed to have several progress stages, and so individual move between these stages with a specific rates.

The total population size:

$$N=V+S+C_{Sy}+C_{Asy}+I+R\text{.}$$ (1)

The model assume that a proportion of the population p has been vaccinated and $1-p$ is the proportion of the population that are susceptible before the disease outbreak,at a rate of ω. In Africa, specifically Ghana most of the new born infants do not take in the Pneumoccocal Conjugate Vaccine(PVC) due to lack of education, traditional and cultural believes of parents and individuals. The susceptible population decrease to become symptomatic carrier q and asymptomatic carrier $1-q$ with a rate of φ. The symptomatic carrier decreased to become infected at a rate of β and asymptomatic carrier also decrease to become infected at a rate of α Symptomatic and Asymptomatic carriers decreases to recovery stage after undergoing treatment with a rate of σ and τ respectively. The symptomatic carriers becomes asymptomatic carrier at a rate of θ whiles asymptomatic carriers becomes symptomatic carrier at rate of $\text{Ω}$ due to natural immunity of the individual and each of the compartment have a natural mortality rate of μ. Individual who loses their temporary immunity at a rate of ϕ becomes susceptible. Vaccinated individuals decreased to become symptomatic or asymptomatic carriers at a rate of η with a proportion of k and $1-k$ respectively Vaccinated individuals decreased to become susceptible at a rate of δ and Infected individuals turn to recovery state at a rate of γ.Vaccinated individuals becomes infected at a rate of ρ and infected individuals become vaccinated at a rate of χ. Symptomatic and Asymptomatic carriers decreases to become susceptible at a rate of π and ξ respectively. Asymptomatic and Symptomatic carries decrease to become infected at a rate α and β respectively. New infection can be due to effective contact with either the symptomatic carrier or asymptomatic carriers.Recovery individuals turn to susceptible state at a rate of ϕ.

3. $SV{C}_{Sy}{C}_{Asy}IR$ Model

A model depicting pneumonia transmission dynamics with a flow from the host organism to the susceptible S(t),vaccinated V(t),symptomatic carrier $C_{sy}\left(t\right)$, asymptomatic carrier $C_{Asy}\left(t\right)$, infected I(t) and recovery R(t) compartment.As a result we have this $SV{C}_{Sy}{C}_{Asy}IR$ model (Table 1, Table 2).

Table 1.

Variables and variable definition.

Variables	Variable Definition
S(t)	Susceptible individual at time t
V(t)	Vaccinated individual at time t
$C_{sy}\left(t\right)$	Symptomatic carrier at time t
$C_{Asy}\left(t\right)$	Asymptomatic carrier at time t
I(t)	Infected individual at time t
R(t)	Recovered individual at time t

Table 2.

Parameters and parameter definition.

Parameters	Parameters Definition
P	proportion of the population that have been vaccinated before and after the outbreak.
$1-p$	proportion of the population that are susceptible.
ω	Recruitment rate.
q	proportion susceptible decrease to become symptomatic carriers.
1-q	proportion of susceptible decrease to become asymptomatic carriers.
φ	rate at which susceptible population decrease to symptomatic or asymptomatic carriers.
β	the rate at which symptomatic carriers decrease to become infected.
α	the rate at which asymptomatic carriers decrease to become infected.
σ	the rate at which symptomatic carriers decrease to recovered stage after treatment.
Parameters	Parameters Definition
τ	the rate at which asymptomatic carriers decrease to recovery stage after treatment.
θ	the rate at which symptomatic carriers become asymptomatic carries.
$\text{Ω}$	the rate at which asymptomatic carriers become symptomatic carries.
μ	the natural mortality rate.
ϕ	the rate of loss of temporary immunity to become susceptible.
k	the proportion of vaccinated population decrease to become symptomatic carriers.
1-k	the proportion of vaccinated population decrease to become asymptomatic carriers.
η	rate at which vaccinated population decrease to symptomatic and asymptomatic.
δ	the rate at which vaccinated population decrease to become susceptible.
γ	the rate at which infected individuals turn to recovered state.
ρ	the rate at which vaccinated population decrease to become infected.
$\text{Π}$	the rate at which the symptomatic carriers decrease to become susceptible.
ξ	the rate at which the asymptomatic carriers decrease to become susceptible.
a	the rate at which infected decrease to asymptomatic carrier.
$\ell$	the rate at which infected decrease to symptomatic.
χ	the rate at which susceptible become infected.
ν	the rate at which susceptible become vaccinated.
ς	the disease induced death rate.

4. Equations of the model

$$\begin{array}{ll}\frac{dS\left(t\right)}{dt}\hfill & =\delta V\left(t\right)+\text{Π}{C}_{Sy}\left(t\right)+\xi C_{Asy}\left(t\right)+\phi R\left(t\right)+\left(1-p\right)\omega -[\mu +\left(q+\left(1-q\right)\lambda \right)\varphi +\chi \lambda +\nu ]S\left(t\right)\hfill \\ \frac{dV\left(t\right)}{dt}\hfill & =p\omega -\rho \lambda V\left(t\right)+\nu S\left(t\right)-\left(\delta +\mu +k\lambda \eta +\left(1-k\right)\lambda \eta \right)V\left(t\right)\hfill \\ \frac{d{C}_{Sy}\left(t\right)}{dt}\hfill & =q\varphi S\left(t\right)+\text{Ω}{C}_{Sy}\left(t\right)+\eta k\lambda V\left(t\right)+\ell I\left(t\right)-[\text{Π}+\theta +\mu +\beta +\sigma ]C_{Sy}\left(t\right)\hfill \\ \frac{d{C}_{Asy}\left(t\right)}{dt}\hfill & =\left(1-q\right)\varphi S\left(t\right)+\theta C_{Sy}\left(t\right)+\eta \lambda \left(1-k\right)V\left(t\right)+aI\left(t\right)-[\xi +\text{Ω}+\mu +\alpha +\tau ]C_{Asy}\left(t\right)\hfill \\ \frac{dI\left(t\right)}{dt}\hfill & =\rho \lambda V\left(t\right)+\alpha C_{Asy}\left(t\right)+\beta C_{Sy}\left(t\right)+\chi \lambda S\left(t\right)-[\mu +\zeta +\gamma +a+\ell ]I\left(t\right)\hfill \\ \frac{dR\left(t\right)}{dt}\hfill & =\gamma I\left(t\right)+\tau C_{Asy}\left(t\right)+\sigma C_{Sy}\left(t\right)-[\mu +\phi ]R\left(t\right)\hfill \end{array}\}$$ (2)

with force of infection:

$$\lambda =T\left(\frac{I+{\mathrm{\epsilon }}_{sy}{C}_{Sy}+{\mathrm{\epsilon }}_{Asy}{C}_{Asy}}{N}\right).$$ (3)

where;

$T=mz.$$m=$the rate of contact or the average number of effective contacts.

$z=$the probability that a contact is effective to cause infection.

${\mathrm{\epsilon }}_{sy}=$transmission coefficient of symptomatic carrier.

${\mathrm{\epsilon }}_{Asy}=$transmission coefficient of asymptomatic carrier.

Adding the equations, we have

$$\begin{array}{l}\frac{dV\left(t\right)}{dt}+\frac{dS\left(t\right)}{dt}+\frac{d{C}_{Sy}\left(t\right)}{dt}+\frac{d{C}_{Asy}\left(t\right)}{dt}+\frac{dI\left(t\right)}{dt}+\frac{dR\left(t\right)}{dt}=\\ p\omega -\rho \lambda V\left(t\right)+\nu S\left(t\right)-\left(\delta +\mu +k\lambda \eta +\left(1-k\right)\lambda \eta \right)V\left(t\right)+\delta V\left(t\right)\\ +\text{Π}{C}_{Sy}\left(t\right)+\xi C_{Asy}\left(t\right)+R\varphi +\left(1-p\right)\omega -[\mu +\left(q+\left(1-q\right)\lambda \right)\phi +\chi \lambda +\nu ]S\left(t\right)\\ +q\lambda \phi S\left(t\right)+\text{Ω}{C}_{Asy}\left(t\right)+\ell I\left(t\right)+\eta \lambda kV\left(t\right)-[\text{Π}+\theta +\mu +\beta +\sigma ]C_{Sy}\left(t\right)\\ +\left(1-q\right)\lambda \phi S\left(t\right)+\theta C_{Sy}\left(t\right)+\eta \lambda \left(1-k\right)V\left(t\right)+\text{a}I\left(t\right)-[\xi +\text{Ω}+\mu +\alpha +\tau ]C_{Asy}\left(t\right)\\ +\rho \lambda V\left(t\right)+\alpha C_{Asy}\left(t\right)+\beta C_{Sy}\left(t\right)+\chi \lambda S\left(t\right)-[\mu +\zeta +\gamma +\text{a}+\ell ]I\left(t\right)\\ +\gamma I\left(t\right)+\tau C_{Asy}\left(t\right)+\sigma C_{Sy}\left(t\right)-[\mu +\varphi ]R\left(t\right)\\ \Rightarrow \frac{d\left(V+S+C_{Sy}+C_{Asy}+I+R\right)}{dt}=\omega -(V+S+C_{Sy}+C_{Asy}+I+R)+\zeta I\\ \frac{dN}{dt}=\omega -N\mu +\zeta I.\end{array}$$ (4)

5. Properties of the model equations

In this section, we show a description of some basic properties of the system (2), such as feasible solution and the positivity of solutions. The feasible solution shows the region in which the solutions of the system (2) are biologically meaningful and the positivity and boundedness of the solutions describes the non-negativity of the solutions of the equations.

5.1. Region of feasibility

The feasible solution set which is positively invariant set of the model is given by,

$$\mathbf{\Psi }=\left\{\left(V+S+C_{Sy}+C_{Asy}+I+R\right)\in {\mathfrak{R}}_{+}^6:V+S+C_{Sy}+C_{Asy}+I+R=N\le \frac{\omega +\zeta I}{\mu }\right\}$$

From the model system (2) It will be shown that the region is positively invariant. Consider the steps below;

From the system (2), the total population of individuals is given by

$$N=V+S+C_{Sy}+C_{Asy}+I+R.$$

Therefore adding the system $\left(2\right)$, the results become

$$\frac{dN}{dt}=\omega -N\mu +\zeta I.$$

And by solving equation $\left(4\right)$leads to:

$$\frac{dN}{\omega -N\mu +\zeta I}=dt$$

$$\int \frac{dN}{\omega -N\mu +\zeta I}=\int dt$$

$$\frac{-1}{\mu }\text{ln}|\omega -N\mu +\zeta I|=t+c$$

$$\text{ln}|\omega -N\mu +\zeta I|=-\mu t+c$$

$$\omega -N\mu +\zeta I=e^{-\mu t+c}$$

$$\omega -N\mu +\zeta I=c_1{e}^{-\mu t}$$

$$-N\mu =c_1{e}^{-\mu t}-\omega -\zeta I$$

$$\therefore N\left(t\right)=\frac{-c_1{e}^{-\mu t}+\omega +\zeta I\left(t\right)}{\mu }.$$

now at t = 0

$$N\left(0\right)=\frac{-c_1{e}^{-\mu 0}+\omega +\zeta I\left(0\right)}{\mu }.$$

$$c_1=\omega +\zeta I\left(0\right)-N\left(0\right)\mu .$$

now the equation is

$$N\left(t\right)=\frac{\omega +\zeta I\left(t\right)-[\omega +\zeta I\left(0\right)-N\left(0\right)\mu ]e^{-\mu t}}{\mu }.$$ (5)

now as $t\to \infty$

$$N\left(t\right)\le \frac{\omega +\zeta I\left(t\right)}{\mu }.$$

Therefore, Ψ is positively invariant.

5.2. Positivity and boundedness of solutions

We have proved that the state variables are non-negative and the solutions remain positive for all time $t\ge 0$.Here the parameters in the model are assumed to be positive. We also prove that the feasible solutions are bounded in a region:

$$\mathbf{\Psi }=\left\{\left(V+S+C_{Sy}+C_{Asy}+I+R\right)\in {\mathfrak{R}}_{+}^6:V+S+C_{Sy}+C_{Asy}+I+R=N\le \frac{\omega +\zeta I}{\mu }\right\}$$

Lemma 5.2.1

Let the initial values of the parameters be $\{V\ge 0,S\ge 0,C_{Sy}\ge 0,C_{Asy}\ge 0I\ge 0,R\ge 0\}\in \Psi$,then the solution set $\left\{V\left(t\right),S\left(t\right),C_{Sy}\left(t\right),C_{Asy}\left(t\right),I\left(t\right),R\left(t\right)\right\}$is positive for all $t\ge 0$

Proof First, we consider the second equation of system(2)

$$\frac{dV\left(t\right)}{dt}=p\omega +\nu S\left(t\right)-\left(\delta +\mu +\lambda \eta +\rho \lambda \right)V\left(t\right)$$

we have

$$\frac{dV\left(t\right)}{dt}\ge -\left(\delta +\mu +\lambda \eta +\rho \lambda \right)V\left(t\right)$$

$$\frac{dV\left(t\right)}{V\left(t\right)}\ge -\left(\delta +\mu +\lambda \eta +\lambda \rho \right)dt$$

integrating both sides

$$\int \frac{dV\left(t\right)}{V\left(t\right)}\ge \int -\left(\delta +\mu +\lambda \eta +\lambda \rho \right)dt$$

$$\text{ln}\left|V\left(t\right)\right|\ge -\left(\delta +\mu +\lambda \eta +\lambda \rho \right)t+c$$

$$V\left(t\right)\ge e^{-\left(\delta +\mu +\lambda \eta +\lambda \rho \right)t+c}$$

And at $t=0$

$$V\left(t\right)\ge V\left(0\right)e^{-\left(\delta +\mu +\lambda \eta +\lambda \rho \right)t}$$

$$V\left(t\right)\ge V\left(0\right)e^{-\left(\delta +\mu +\lambda \eta +\lambda \rho \right)t}\ge 0$$

hence

$$V\left(t\right)\ge 0$$

Next, we consider the first equation of system (2)

$$\frac{dS\left(t\right)}{dt}=\delta V\left(t\right)+\text{Π}{C}_{Sy}\left(t\right)+\xi c+R\varphi +\left(1-p\right)\omega -[\mu +\left(q+\left(1-q\right)\right)\lambda \phi +\chi \lambda +\nu ]S\left(t\right)$$

we have

$$\begin{array}{c}\frac{dS\left(t\right)}{dt}\ge -[\mu +\lambda \phi +\chi \lambda +\nu ]S\left(t\right)\\ \frac{dS\left(t\right)}{S\left(t\right)}\ge -[\mu +\lambda \phi +\chi \lambda +\nu ]dt\end{array}$$

integrating both sides

$$\begin{array}{l}\int \frac{dS\left(t\right)}{S\left(t\right)}\ge \int -[\mu +\lambda \phi +\chi \lambda +\nu ]dt\\ \text{ln}\left|S\left(t\right)\right|\ge -\left(\mu +\lambda \phi +\chi \lambda +\nu \right)t+c\\ S\left(t\right)\ge e^{-\left(\mu +\lambda \phi +\chi \lambda +\nu \right)t+c}\end{array}$$

And at $t=0$,

$$\begin{array}{l}S\left(t\right)\ge S\left(0\right)e^{-\left(\mu +\left(q+\left(1-q\right)\right)\phi +\chi +\nu \right)t}\\ S\left(t\right)\ge S\left(0\right)e^{-\left(\mu +\left(q+\left(1-q\right)\right)\phi +\chi +\nu \right)t}\ge 0\end{array}$$

hence

$$S\left(t\right)\ge 0$$

We can proceed in a similar way to prove the positivity of $C_{Sy}\left(t\right)$, $C_{Asy}\left(t\right)$$I\left(t\right)$,$R\left(t\right)$ and $N\left(t\right)$ Hence, all the variables are positive.

Lemma 5.2.2

The solutions for the Systems are contained and remain in the region Ψ for all time $t\ge 0$.

6. Model analysis

In this section the model is qualitatively analyzed by determining the model equilibrium point,and carry out their corresponding stability analysis and interpreting the results.

6.1. Disease free equilibrium (DFE)

The disease free equilibrium of the system(2) is obtained by setting;

$\frac{dV\left(t\right)}{dt}=\frac{dS\left(t\right)}{dt}=\frac{d{C}_{Sy}\left(t\right)}{dt}=\frac{d{C}_{Asy}\left(t\right)}{dt}=\frac{dI\left(t\right)}{dt}=\frac{dR\left(t\right)}{dt}=0$$\begin{array}{ll}p\omega -\lambda \rho V\left(t\right)+\nu S\left(t\right)-\left(\delta +\mu +k\lambda \eta +\left(1-k\right)\lambda \eta \right)V\left(t\right)\hfill & =0\hfill \\ \delta V\left(t\right)+\text{Π}{C}_{Sy}\left(t\right)+\xi C_{Asy}\left(t\right)+R\phi +\left(1-p\right)\omega -[\mu +\left(q+\left(1-q\right)\right)\lambda \varphi +\chi \lambda +\nu ]S\left(t\right)\hfill & =0\hfill \\ q\lambda \varphi S\left(t\right)+\text{Ω}{C}_{Asy}\left(t\right)+\ell I\left(t\right)+\eta \lambda kV\left(t\right)-[\text{Π}+\theta +\mu +\beta +\sigma ]C_{Sy}\left(t\right)\hfill & =0\hfill \\ \left(1-q\right)\lambda \varphi S\left(t\right)+\theta C_{Sy}\left(t\right)+\eta \lambda \left(1-k\right)V\left(t\right)+aI\left(t\right)-[\xi +\text{Ω}+\mu +\alpha +\tau ]C_{Asy}\left(t\right)\hfill & =0\hfill \\ \rho \lambda V\left(t\right)+\alpha C_{Asy}\left(t\right)+\beta C_{Sy}\left(t\right)+\chi \lambda S\left(t\right)-[\mu +\zeta +\gamma +a+\ell ]I\left(t\right)\hfill & =0\hfill \\ \gamma I\left(t\right)+\tau C_{Asy}\left(t\right)+\sigma C_{Sy}\left(t\right)-[\mu +\phi ]R\left(t\right)=0\hfill & =0\hfill \end{array}\}$ (6)

now from system (6) we have

$$V^{\text{*}}=\frac{p\omega +\nu S^{\text{*}}}{\left(\delta +\mu +k\lambda \eta +\left(1-k\right)\lambda \eta +\rho \lambda \right)}$$ (7)

$$S^{\text{*}}=\frac{\delta V^{\text{*}}+\text{Π}{C}_{Sy}^{\text{*}}+\xi C_{Asy}^{\text{*}}+R^{\text{*}}\varphi +\left(1-p\right)\omega }{[\mu +\left(q+\left(1-q\right)\right)\lambda \phi +\chi \lambda +\nu ]}$$ (8)

$$\begin{array}{c}{C}_{Sy}^{\text{*}}=\frac{q\lambda \phi S^{\text{*}}+\text{Ω}{C}_{Asy}^{\text{*}}+\ell I^{\text{*}}+\eta \lambda k{V}^{\text{*}}}{[\text{Π}+\theta +\mu +\beta +\sigma ]}\\ C_{Asy}^{\text{*}}=\frac{\left(1-q\right)\lambda \phi S^{\text{*}}+\theta C_{Sy}^{\text{*}}+\eta \lambda \left(1-k\right)V^{\text{*}}+a{I}^{\text{*}}}{[\xi +\text{Ω}+\mu +\alpha +\tau ]}\\ I^{\text{*}}=\frac{\rho \lambda V^{\text{*}}+\alpha C_{Asy}^{\text{*}}+\beta C_{Sy}^{\text{*}}+\chi \lambda S^{\text{*}}}{[\mu +\zeta +\gamma +a+\ell ]}\\ R^{\text{*}}=\frac{\gamma I\left(t\right)+\tau C_{Asy}\left(t\right)+\sigma C_{Sy}\left(t\right)}{[\mu +\varphi ]}\end{array}\}$$ (9)

from equation (9) $C_{Sy}^{\text{*}}=C_{Asy}^{\text{*}}=I^{\text{*}}=R^{\text{*}}=0$

$$V^{\text{*}}=\frac{p\omega +\nu \frac{\delta V^{\text{*}}+\text{Π}{C}_{Sy}^{\text{*}}+\xi C_{Asy}^{\text{*}}+R^{\text{*}}\varphi +\left(1-p\right)\omega }{[\mu +\lambda \phi +\chi \lambda +\nu ]}}{\left(\delta +\mu +\lambda \eta +\rho \lambda \right)}$$

$$V^{\text{*}}=\frac{p\omega +\nu \frac{\left(1-p\right)\omega +\delta V^{\text{*}}}{[\mu +\lambda \phi +\chi \lambda +\nu ]}}{\left(\delta +\mu +\lambda \eta +\rho \lambda \right)}$$

$$V^{\text{*}}=\frac{p\omega [\mu +\lambda \phi +\chi \lambda +\nu ]+\nu \left(1-p\right)\omega +\nu \delta V^{\text{*}}}{\left(\delta +\mu +\lambda \eta +\rho \lambda \right)\left(\mu +\lambda \phi +\chi \lambda +\nu \right)}$$

letting

$$H_1=\left(\delta +\mu +\lambda \eta +\rho \lambda \right)$$

$$H_2=\left(\mu +\lambda \phi +\chi \lambda +\nu \right)$$

We have

$$\begin{array}{l}{V}^{\text{*}}=\frac{p\omega H_2+\nu \left(1-p\right)\omega +\nu \delta V^{\text{*}}}{H_1{H}_2}\\ V^{\text{*}}=\frac{p\omega H_2+\nu \left(1-p\right)\omega }{H_1{H}_2-\nu \delta }\\ \therefore V^{\text{*}}=\frac{p\omega \left(\mu +\lambda \phi +\chi \lambda +\nu \right)+\nu \left(1-p\right)\omega }{\left(\delta +\mu +\lambda \eta +\rho \lambda \right)\left(\mu +\lambda \phi +\chi \lambda +\nu \right)-\nu \delta }\end{array}$$

for $C_{Sy}^{\text{*}}=C_{Asy}^{\text{*}}=I^{\text{*}}=R^{\text{*}}=0$ and solving for $S^{\text{*}}$

$$S^{\text{*}}=\frac{\delta V^{\text{*}}+\text{Π}{C}_{Sy}^{\text{*}}+\xi C_{Asy}^{\text{*}}+R^{\text{*}}\varphi +\left(1-p\right)\omega }{[\mu +\lambda \phi +\lambda \chi +\nu ]}$$

$$S^{\text{*}}=\frac{\delta \frac{p\omega H_2+\nu \left(1-p\right)\omega }{H_1{H}_2-\nu \delta }+\text{Π}{C}_{Sy}^{\text{*}}+\xi C_{Asy}^{\text{*}}+R^{\text{*}}\varphi +\left(1-p\right)\omega }{[\mu +\lambda \phi +\chi \lambda +\nu ]}$$

$$S^{\text{*}}=\frac{\delta \frac{p\omega H_2+\nu \left(1-p\right)\omega }{H_1{H}_2-\nu \delta }+\left(1-p\right)\omega }{[\mu +\lambda \phi +\lambda \chi +\nu ]}$$

$$S^{\text{*}}=\frac{\delta \frac{p\omega H_2+\nu \left(1-p\right)\omega }{H_1{H}_2-\nu \delta }+\left(1-p\right)\omega }{H_2}$$

$$S^{\text{*}}=\frac{\delta \left(p\omega H_2+\nu \left(1-p\right)\omega \right)+\left(1-p\right)\omega \left(H_1{H}_2-\nu \delta \right)}{H_2\left(H_1{H}_2-\nu \delta \right)}$$

$$\text{Now the equilibrium point}{Q}^{\text{*}}=Q^{\text{*}}\left(V^{\text{*}},S^{\text{*}},C_{Sy}^{\text{*}},C_{Asy}^{\text{*}},I^{\text{*}},R^{\text{*}}\right)$$

$$=Q^{\text{*}}\left(\frac{p\omega H_2+\nu \left(1-p\right)\omega }{H_1{H}_2-\nu \delta },\frac{\delta \left(p\omega H_2+\nu \left(1-p\right)\omega \right)+\left(1-p\right)\omega \left(H_1{H}_2-\nu \delta \right)}{H_2\left(H_1{H}_2-\nu \delta \right)},\mathrm{0,0,0,0}\right)$$

where.

$H_3=[\text{Π}+\theta +\mu +\beta +\sigma ]$$H_4=[\xi +\text{Ω}+\mu +\alpha +\tau ]$$H_5=[\mu +\zeta +\gamma +a+\ell ]$$H_6=[\mu +\varphi ]$

6.2. The basic reproduction number $R_0$

Epidemiologists have always been interested in finding the basic reproduction number of an emerging disease because its threshold parameter can tell whether a disease will die out or persist in a population. Denoted by $R_0$, this parameter is arguably the most important quantity in infectious disease epidemiology (WuMSc et al., 2012, Bonita et al., 2006). It is defined as the average number of new cases (infections) produced by a single infective when introduced into an entirely susceptible population. It is one of the first quantities estimated for emerging infectious diseases in outbreak situations.It is a key epidemiological quantity, because it determines the size and duration of epidemics and is an important factor in determining targets for vaccination coverage.The basic reproduction number is sought after principally because (Stephen et al., 2015, pp. 396–408; WuMSc et al., 2012). If $R_0<1$, then throughout the infectious period, each infective will produce less than one new infective on the average. This in turn implies that the disease will die out as the DFE is stable.If $R_0>1$, then throughout the infectious period, each infective will produce more than one new infective on the average. This in turn implies that the disease will persist as the DFE is unstable. In other words, there will be an outbreak. If $R_0$ can be determined, then the transmission parameters which will force $R_0$ to be or greater than 1 can easily be identified and control measures effectively designed. We shall find the basic reproduction number of the system using the next generation method. To calculate the basic reproduction number by using a next-generation matrix, the whole population is divided into n compartments in which there are $m<n$ infected compartments (Diekmann, Heesterbeek, & Roberts, 2009, Herbert and Hethcote, 2000). In our model among six compartments we have three infected compartments. Let $x_i,i=\mathrm{1,2,3},\dots ,m$ be the numbers of infected individuals in the $i^{th}$ infected compartment at time t.

$F_i\left(x\right)$ be the rate of appearance of new infections in compartment. $V_i\left(x\right)$ be the difference between rates of transfer of individuals between $i^{th}$ compartments. $V_i^{+}\left(x\right)$ be the rate of transfer of individuals into $i^{th}$ compartment by all other means.$V_i^{-}\left(x\right)$ be the rate of transfer of individuals out of $i^{th}$ compartment (Diekmann et al., 2009; Stephen et al., 2015, pp. 396–408).

$$\frac{d{x}_i}{dt}=F_i\left(x\right)-V_i\left(x\right)$$

where

$$V_i\left(x\right)=[V_i^{-}\left(x\right)-V_i^{+}\left(x\right)]$$

now we have

$$\frac{d{x}_i}{dt}=F\left(x\right)-V\left(x\right)$$

where

$$F\left(x\right)=\left[\begin{array}{c}{F}_1\left(x\right)\\ F_2\left(x\right)\\ \dots \\ F_m\left(x\right)\end{array}\right],V\left(x\right)=\left[\begin{array}{c}{V}_1\left(x\right)\\ V_2\left(x\right)\\ \dots \\ V_m\left(x\right)\end{array}\right]$$

$$\begin{array}{c}\frac{d{C}_{Sy}\left(t\right)}{dt}=q\lambda \phi S\left(t\right)+\text{Ω}{C}_{Asy}\left(t\right)+\ell I\left(t\right)+\lambda \eta kV\left(t\right)-[\text{Π}+\theta +\mu +\beta +\sigma ]C_{Sy}\left(t\right)\\ \frac{d{C}_{Asy}\left(t\right)}{dt}=\left(1-q\right)\lambda \phi S\left(t\right)+\theta C_{Sy}\left(t\right)+\lambda \eta \left(1-k\right)V\left(t\right)+aI\left(t\right)-[\xi +\text{Ω}+\mu +\alpha +\tau ]C_{Asy}\left(t\right)\\ \frac{dI\left(t\right)}{dt}=\lambda \rho V\left(t\right)+\alpha C_{Asy}\left(t\right)+\beta C_{Sy}\left(t\right)+\lambda \chi S\left(t\right)-[\mu +\zeta +\gamma +a+\ell ]I\left(t\right)\end{array}\}$$ (10)

we can say from our explanation above that $x_1=C_{Sy}\left(t\right)$,$x_2=C_{Asy}\left(t\right)$ and $x_3=I\left(t\right)$now with $N=V+S+C_{Sy}+C_{Asy}+I+R$. This system has three infected states, $C_{Sy}\left(t\right)$, $C_{Asy}\left(t\right)$ and $I\left(t\right)$; and three uninfected states,V,S and R. Although there are six states in the model, it is five-dimensional as the total population size is constant.At the infection-free steady state $C_{Sy}\left(t\right)$ = $C_{Asy}\left(t\right)$ = $I\left(t\right)$ = $R\left(t\right)$ = $V\left(t\right)$ = 0,hence S=N,now we define $F_i\left(x\right)$and $V_i\left(x\right)$ as

$$F_i\left(x\right)=\left[\begin{array}{c}q\lambda \phi S\left(t\right)+\lambda \eta kV\left(t\right)\\ \left(1-q\right)\lambda \phi S\left(t\right)+\lambda \eta \left(1-k\right)V\left(t\right)\\ \lambda \chi S\left(t\right)+\lambda \rho V\left(t\right)\end{array}\right],V_i\left(x\right)=\left[\begin{array}{c}-H_3{C}_{Sy}\left(t\right)+\text{Ω}{C}_{Asy}\left(t\right)+\ell I\left(t\right)\\ \theta C_{Sy}\left(t\right)-H_4{C}_{Asy}\left(t\right)+aI\left(t\right)\\ \beta C_{Sy}\left(t\right)+\alpha C_{Asy}\left(t\right)-H_{5}I\left(t\right)\end{array}\right]$$

Let $x_0$ be the disease-free equilibrium. The values of the Jacobian matrices F(x) and V(x) are:

We differentiate $F_i\left(x\right)$ with respect to $C_{Sy}\left(t\right)$, $C_{Asy}\left(t\right)$ and $I\left(t\right)$ and get

$$F=\frac{\partial F_i\left(x_0\right)}{d{x}_j}$$

$$F=\left[\begin{array}{ccc}\frac{\partial F_1}{\partial C_{Sy}\left(t\right)}& \frac{\partial F_1}{\partial C_{ASy}\left(t\right)}& \frac{\partial F_1}{\partial I\left(t\right)}\\ \frac{\partial F_2}{\partial C_{Sy}\left(t\right)}& \frac{\partial F_2}{\partial C_{ASy}\left(t\right)}& \frac{\partial F_2}{\partial I\left(t\right)}\\ \frac{\partial F_3}{\partial C_{Sy}\left(t\right)}& \frac{\partial F_3}{\partial C_{ASy}\left(t\right)}& \frac{\partial F_3}{\partial I\left(t\right)}\end{array}\right]$$

$$F=\left[\begin{array}{ccc}T{\mathrm{\epsilon }}_{sy}\frac{\left(q\phi \right)S^0+\eta k{V}^0}{S^0}& T{\mathrm{\epsilon }}_{Asy}\frac{\left(q\phi \right)S^0+\eta k{V}^0}{S^0}& T\frac{\left(q\phi \right)S^0+\eta k{V}^0}{S^0}\\ T{\mathrm{\epsilon }}_{sy}\frac{\left(\left(1-q\right)\phi \right)S^0+\eta \left(1-k\right)V^0}{S^0}& T{\mathrm{\epsilon }}_{Asy}\frac{\left(\left(1-q\right)\phi \right)S^0+\eta \left(1-k\right)V^0}{S^0}& T\frac{\left(\left(1-q\right)\phi \right)S^0+\eta \left(1-k\right)V^0}{S^0}\\ T{\mathrm{\epsilon }}_{sy}\frac{\chi S^0+\rho V^0}{S^0}& T{\mathrm{\epsilon }}_{Asy}\frac{\chi S^0+\rho V^0}{S^0}& T\frac{\chi S^0+\rho V^0}{S^0}\end{array}\right]$$

We differentiate $V_i\left(x\right)$ with respect to $C_{Sy}\left(t\right)$, $C_{Asy}\left(t\right)$ and $I\left(t\right)$

$$V=\frac{\partial V_i\left(x_0\right)}{d{x}_j}$$

$$V=\left(\begin{array}{ccc}\frac{\partial V_1}{\partial C_{Sy}\left(t\right)}& \frac{\partial V_1}{\partial C_{ASy}\left(t\right)}& \frac{\partial V_1}{\partial I\left(t\right)}\\ \frac{\partial V_2}{\partial C_{Sy}\left(t\right)}& \frac{\partial V_2}{\partial C_{ASy}\left(t\right)}& \frac{\partial V_2}{\partial I\left(t\right)}\\ \frac{\partial V_3}{\partial C_{Sy}\left(t\right)}& \frac{\partial V_3}{\partial C_{ASy}\left(t\right)}& \frac{\partial V_3}{\partial I\left(t\right)}\end{array}\right)$$

$$V=\left(\begin{array}{ccc}-H_3& \text{Ω}& \ell \\ \theta & -H_4& a\\ \beta & \alpha & -H_5\end{array}\right)$$

and

$$V^{-1}=\left(\begin{array}{ccc}\frac{H_4{H}_5-a\alpha }{Z}& \frac{H_5\text{Ω}+\alpha \ell }{Z}& \frac{H_4\ell +a\text{Ω}}{Z}\\ \frac{H_5\theta +a\beta }{Z}& \frac{H_3{H}_5-\beta \ell }{Z}& \frac{H_{3}a+\theta \ell }{Z}\\ \frac{\theta \alpha +H_4\beta }{Z}& \frac{H_3\alpha +\beta \text{Ω}}{Z}& \frac{H_3{H}_4-\text{Ω}\theta }{Z}\end{array}\right)$$

where:

$Z=\left(H_5\text{Ω}\theta -H_5{H}_3{H}_4+H_{3}a\alpha +\text{Ω}a\beta +H_4\beta \ell +\alpha \ell \theta \right)$$H_7=[\left(1-q\right)\phi T{\mathrm{\epsilon }}_{sy}+\eta \left(1-k\right)T{\mathrm{\epsilon }}_{Asy}]-H_4$$H_8=[q\phi T{\mathrm{\epsilon }}_{sy}+\eta kT{\mathrm{\epsilon }}_{Asy}]-H_3$

The matrix $F{V}^{-1}$ is known as the next-generation matrix and the largest eigenvalue or spectral radius of $F{V}^{-1}$ is the effective reproduction number of the model (Diekmann et al., 2009; WuMSc et al., 2012).

$${F{V}^{-1}=\left(\begin{array}{c}\frac{\partial F_i\left(x_0\right)}{d{x}_j}\end{array}\right)\left(\begin{array}{c}\frac{\partial V_i\left(x_0\right)}{d{x}_j}\end{array}\right)}^{-1}$$

Let.

$B_1=T{\mathrm{\epsilon }}_{sy}\frac{\left(q\phi \right)S^0+\eta k{V}^0}{S^0}$$B_2=T{\mathrm{\epsilon }}_{Asy}\frac{\left(q\phi \right)S^0+\eta k{V}^0}{S^0}$$B_3=T\frac{\left(q\phi \right)S^0+\eta k{V}^0}{S^0}$$G_1=T{\mathrm{\epsilon }}_{sy}\frac{\left(\left(1-q\right)\phi \right)S^0+\eta \left(1-k\right)V^0}{S^0}$$G_2=T{\mathrm{\epsilon }}_{Asy}\frac{\left(\left(1-q\right)\phi \right)S^0+\eta \left(1-k\right)V^0}{S^0}$$G_3=T\frac{\left(\left(1-q\right)\phi \right)S^0+\eta \left(1-k\right)V^0}{S^0}$$J_1=T{\mathrm{\epsilon }}_{sy}\frac{\chi S^0+\rho V^0}{S^0}$$J_2=T{\mathrm{\epsilon }}_{Asy}\frac{\chi S^0+\rho V^0}{S^0}$$J_3=T\frac{\chi S^0+\rho V^0}{S^0}$$Q_1=\frac{H_4{H}_5-a\alpha }{Z}$$Q_2=\frac{H_5\text{Ω}+\alpha \ell }{Z}$$Q_3=\frac{H_4\ell +a\text{Ω}}{Z}$$M_1=\frac{H_5\theta +a\beta }{Z}$$M_2=\frac{H_3{H}_5-\beta \ell }{Z}$$M_3=\frac{H_{3}a+\theta \ell }{Z}$$F_1=\frac{\theta \alpha +H_4\beta }{Z}$$F_2=\frac{H_3\alpha +\beta \text{Ω}}{Z}$$F_3=\frac{H_3{H}_4-\text{Ω}\theta }{Z}$

$$F{V}^{-1}=\left(\begin{array}{ccc}\left(B_1{Q}_1+B_2{M}_1+B_3{F}_1\right)& \left(B_1{Q}_2+B_2{M}_2+B_3{F}_2\right)& \left(B_1{Q}_3+B_2{M}_3+B_3{F}_3\right)\\ \left(G_1{Q}_1+G_2{M}_1+G_3{F}_1\right)& \left(G_1{Q}_2+G_2{M}_2+G_3{F}_2\right)& \left(G_1{Q}_3+G_2{M}_3+G_3{F}_3\right)\\ \left(J_1{Q}_1+J_2{M}_1+J_3{F}_1\right)& \left(J_1{Q}_2+J_2{M}_2+J_3{F}_2\right)& \left(J_1{Q}_3+J_2{M}_3+J_3{F}_3\right)\end{array}\right)$$

The eigenvalues,W of the equation can be computed from the characteristic equation:

$$\left|\begin{array}{c}F{V}^{-1}-WI\end{array}\right|=0$$

$$F{V}^{-1}=\left(\begin{array}{ccc}\left(B_1{Q}_1+B_2{M}_1+B_3{F}_1\right)-W& \left(B_1{Q}_2+B_2{M}_2+B_3{F}_2\right)& \left(B_1{Q}_3+B_2{M}_3+B_3{F}_3\right)\\ \left(G_1{Q}_1+G_2{M}_1+G_3{F}_1\right)& \left(G_1{Q}_2+G_2{M}_2+G_3{F}_2\right)-W& \left(G_1{Q}_3+G_2{M}_3+G_3{F}_3\right)\\ \left(J_1{Q}_1+J_2{M}_1+J_3{F}_1\right)& \left(J_1{Q}_2+J_2{M}_2+J_3{F}_2\right)& \left(J_1{Q}_3+J_2{M}_3+J_3{F}_3\right)-W\end{array}\right)$$

$$W_1=0$$

and

$$W_2=\frac{H_7^2\left(h_1{h}_4{H}_6+h_2{h}_5{H}_6+h_2{h}_3{h}_6{H}_6+h_1{h}_3{H}_6^2\right)-h_4\left(h_1{H}_6{H}_7{h}_6+h_2{H}_7{h}_5{h}_6+h_1{h}_4{h}_5{h}_6{H}_7+h_2{h}_6^2{h}_3\right)}{\left([\rho T+\chi T]-H_5\right)\left(H_6\left(H_7\right)-h_6{h}_4\right)\left(H_6{\left(H_7\right)}^2-h_6{h}_4\right)}$$

where.

$h_1=\rho T{\mathrm{\epsilon }}_{sy}+\chi T{\mathrm{\epsilon }}_{Asy}+\beta$$h_2=\rho T{\mathrm{\epsilon }}_{sy}+\chi T{\mathrm{\epsilon }}_{Asy}+\alpha$$h_3=q\phi T+\eta kT+\ell$$h_4=q\phi T{\mathrm{\epsilon }}_{sy}+\eta kT{\mathrm{\epsilon }}_{Asy}+\text{Ω}$$h_5=\left(1-q\right)\phi T+\eta \left(1-k\right)T+a$$h_6=\left(1-q\right)\phi T{\mathrm{\epsilon }}_{sy}+\eta \left(1-k\right)T{\mathrm{\epsilon }}_{Asy}+\theta$

The eigenvalue of the model is in the form.

$$R_0=\frac{H_7^2\left(h_1{h}_4{H}_6+h_2{h}_5{H}_6+h_2{h}_3{h}_6{H}_6+h_1{h}_3{H}_6^2\right)-h_4\left(h_1{H}_6{H}_7{h}_6+h_2{H}_7{h}_5{h}_6+h_1{h}_4{h}_5{h}_6{H}_7+h_2{h}_6^2{h}_3\right)}{\left([\rho T+\chi T]-H_5\right)\left(H_6\left(H_7\right)-h_6{h}_4\right)\left(H_6{\left(H_7\right)}^2-h_6{h}_4\right)}$$

7. The endemic equilibrium

The endemic equilibrium is denoted by $E^e$ and defined as a steady-state solutions for the model. This can occur when there is a persistence of the disease. It can be obtained by equating the system of Equation to zero. Then we obtained

$$V^{\text{*}}=\frac{p\omega +\nu S^{\text{*}}}{\left(\lambda \rho +\delta +\mu +\lambda \eta \right)}$$

$$S^{\text{*}}=\frac{\delta V^{\text{*}}+\text{Π}{C}_{sy}^{\text{*}}+\xi C_{Asy}^{\text{*}}+R^{\text{*}}\varphi +\left(1-p\right)\omega }{[\mu +\lambda \phi +\chi \lambda +\nu ]}$$

$$C_{Sy}^{\text{*}}=\frac{q\lambda \phi S^{\text{*}}+\text{Ω}{C}_{Asy}^{\text{*}}+\ell I^{\text{*}}+\lambda \eta k{V}^{\text{*}}}{[\text{Π}+\theta +\mu +\beta +\sigma ]}$$

$$C_{Asy}^{\text{*}}=\frac{\left(1-q\right)\lambda \phi S^{\text{*}}+\theta C_{Sy}^{\text{*}}+\lambda \eta \left(1-k\right)V^{\text{*}}+a{I}^{\text{*}}}{[\xi +\text{Ω}+\mu +\alpha +\tau ]}$$

$$I^{\text{*}}=\frac{\rho \lambda V^{\text{*}}+\alpha C_{Asy}^{\text{*}}+\beta C_{Sy}^{\text{*}}+\lambda \chi S^{\text{*}}}{[\mu +\zeta +\gamma +a+\ell ]}$$

$$R^{\text{*}}=\frac{\gamma I^{\text{*}}+\tau C_{Asy}^{\text{*}}+\sigma C_{Sy}^{\text{*}}}{[\mu +\varphi ]}$$

Hence $E^e=\left\{V^{\text{*}},S^{\text{*}},C_{Sy}^{\text{*}},C_{Asy}^{\text{*}},I^{\text{*}},R^{\text{*}}\right\}$ is the endemic equilibrium of system(2).

Lemma 7.0.1

For $R_0>1$a unique endemic equilibrium point $E^e$exist and vice versa.

Proof:

For the disease to be endemic, $\frac{d{C}_{Asy}}{dt}>0,\frac{d{C}_{Sy}}{dt}>0,\frac{dI}{dt}>0$, that is

$$\frac{d{C}_{Sy}\left(t\right)}{dt}=q\lambda \phi S\left(t\right)+\text{Ω}{C}_{Asy}\left(t\right)+\ell I\left(t\right)+\lambda \eta kV\left(t\right)-[\text{Π}+\theta +\mu +\beta +\sigma ]C_{Sy}\left(t\right)>0$$

$$\frac{d{C}_{Asy}\left(t\right)}{dt}=(1-q)\lambda \phi S\left(t\right)+\theta C_{Sy}\left(t\right)+\lambda \eta (1-k)V\left(t\right)+aI\left(t\right)-[\xi +\text{Ω}+\mu +\alpha +\tau ]C_{Asy}\left(t\right)>0$$

$$\frac{dI\left(t\right)}{dt}=\rho \lambda V\left(t\right)+\alpha C_{Asy}\left(t\right)+\beta C_{Sy}\left(t\right)+\lambda \chi S\left(t\right)-[\mu +\zeta +\gamma +a+\ell ]I\left(t\right)>0$$

now From the inequality of system (10)

$$[\mu +\zeta +\gamma +a+\ell ]I\left(t\right)<\lambda \rho V\left(t\right)+\alpha C_{Asy}\left(t\right)+\beta C_{Sy}\left(t\right)+\chi \lambda S\left(t\right)$$

$$I<\frac{\rho T\frac{I+{\mathrm{\epsilon }}_{sy}{C}_{Sy}+{\mathrm{\epsilon }}_{Asy}{C}_{Asy}}{N}V\left(t\right)+\alpha C_{Asy}\left(t\right)+\beta C_{Sy}\left(t\right)+\chi T\frac{I+{\mathrm{\epsilon }}_{sy}{C}_{Sy}+{\mathrm{\epsilon }}_{Asy}{C}_{Asy}}{N}S\left(t\right)}{[\mu +\zeta +\gamma +a+\ell ]}$$

From the fact $\frac{S\left(t\right)}{N}\le 1,and\frac{V\left(t\right)}{N}\le 1$

$$I<\frac{\left(\rho T{\mathrm{\epsilon }}_{sy}+\chi T{\mathrm{\epsilon }}_{sy}+\beta \right)C_{Sy}+\left(\rho T{\mathrm{\epsilon }}_{Asy}+\chi T{\mathrm{\epsilon }}_{Asy}+\alpha \right)C_{Asy}}{[\rho T+\chi T]-H_5}$$

$$I<\frac{h_1{C}_{Sy}+h_2{C}_{Asy}}{[\rho T+\chi T]-H_5}$$

From the inequality of system (10)

$$C_{Sy}\left(t\right)<\frac{q\phi T\frac{I+{\mathrm{\epsilon }}_{sy}{C}_{Sy}+{\mathrm{\epsilon }}_{Asy}{C}_{Asy}}{N}S\left(t\right)+\eta kT\frac{I+{\mathrm{\epsilon }}_{sy}{C}_{Sy}+{\mathrm{\epsilon }}_{Asy}{C}_{Asy}}{N}V\left(t\right)+\text{Ω}{C}_{Asy}\left(t\right)+\ell I\left(t\right)}{[\text{Π}+\theta +\mu +\beta +\sigma ]}$$

From the fact $\frac{S\left(t\right)}{N}\le 1,and\frac{V\left(t\right)}{N}\le 1$

$$C_{Sy}\left(t\right)<\frac{\left(q\phi T+\eta kT+\ell \right)I\left(t\right)+\left(q\phi T{\mathrm{\epsilon }}_{sy}+\eta kT{\mathrm{\epsilon }}_{Asy}+\text{Ω}\right)C_{Asy}}{[q\phi T{\mathrm{\epsilon }}_{sy}+\eta kT{\mathrm{\epsilon }}_{Asy}]-H_3}$$

$$C_{Sy}\left(t\right)<\frac{h_{3}I\left(t\right)+h_4{C}_{Asy}}{H_7}$$

$$C_{Sy}\left(t\right)<\frac{h_3\left(H_6\left(H_7\right)\right)I\left(t\right)+h_4\left(\left(H_7\right)h_5\right)I\left(t\right)}{H_6{\left(H_7\right)}^2-h_6{h}_4}$$

From the inequality of system (10)

$$C_{Asy}<\frac{\left(1-q\right)\phi T\frac{I+{\mathrm{\epsilon }}_{sy}{C}_{Sy}+{\mathrm{\epsilon }}_{Asy}{C}_{Asy}}{N}S\left(t\right)+\eta \left(1-k\right)T\frac{I+{\mathrm{\epsilon }}_{sy}{C}_{Sy}+{\mathrm{\epsilon }}_{Asy}{C}_{Asy}}{N}V\left(t\right)+\theta C_{Sy}\left(t\right)+aI\left(t\right)}{[\xi +\text{Ω}+\mu +\alpha +\tau ]}$$

From the fact $\frac{S\left(t\right)}{N}\le 1,and\frac{V\left(t\right)}{N}\le 1$

$$C_{Asy}<\frac{\left(\left(1-q\right)\phi T+\eta \left(1-k\right)T+a\right)I\left(t\right)+\left(\left(1-q\right)\phi T{\mathrm{\epsilon }}_{sy}+\eta \left(1-k\right)T{\mathrm{\epsilon }}_{Asy}+\theta \right)C_{Sy}}{[\left(1-q\right)\phi T{\mathrm{\epsilon }}_{Asy}+\eta \left(1-k\right)T{\mathrm{\epsilon }}_{Asy}]-H_4}$$

$$C_{Asy}<\frac{h_{5}I\left(t\right)+h_6{C}_{Sy}}{[\left(1-q\right)\phi T{\mathrm{\epsilon }}_{Asy}+\eta \left(1-k\right)T{\mathrm{\epsilon }}_{Asy}]-H_4}$$

$$C_{Asy}<\frac{\left(\left([H_7\right)h_5+h_6{h}_3\right)I\left(t\right)}{H_6\left(H_7\right)-h_6{h}_4}$$

By substituting $C_{Sy}$ and $C_{Asy}$ into I we have.

$$I<\frac{h_1\frac{\left(h_3{H}_6\left(H_7\right)+h_4\left(H_7\right)h_5\right)I\left(t\right)}{H_6{\left(H_7\right)}^2-h_6{h}_4}+h_2\frac{\left(\left([H_7\right)h_5+h_6{h}_3\right)I\left(t\right)}{H_6\left(H_7\right)-h_6{h}_4}}{[\rho T+\chi T]-H_5}$$

$$I<\frac{h_1\left(h_3{H}_6\left(H_7\right)+h_4\left(H_7\right)h_5\right)\left(H_6\left(H_7\right)-h_6{h}_4\right)I\left(t\right)+h_2\left(\left(H_7\right)h_5+h_6{h}_3\right)\left(H_6{\left(H_7\right)}^2-h_6{h}_4\right)I\left(t\right)}{\left([\rho T+\chi T]-H_5\right)\left(H_6\left(H_7\right)-h_6{h}_4\right)\left(H_6{\left(H_7\right)}^2-h_6{h}_4\right)}$$

$$1<\frac{H_7^2\left(h_1{h}_4{H}_6+h_2{h}_5{H}_6+h_2{h}_3{h}_6{H}_6+h_1{h}_3{H}_6^2\right)-h_4\left(h_1{H}_6{H}_7{h}_6+h_2{H}_7{h}_5{h}_6+h_1{h}_4{h}_5{h}_6{H}_7+h_2{h}_6^2{h}_3\right)}{\left([\rho T+\chi T]-H_5\right)\left(H_6\left(H_7\right)-h_6{h}_4\right)\left(H_6{\left(H_7\right)}^2-h_6{h}_4\right)}$$

$$\Rightarrow 1<R_0$$

Thus a unique endemic equilibrium exist when. $R_0>1.$

8. Numerical simulation

We observe the dynamics of pneumonia model over time and analyzing the results of our model by performing numerical simulations using Matlab software.The parameters used in our simulation are based on data from Brong Ahafo Regional Health Directorate on children under six years of age and some values assigned to other parameters have been derived from epidemiological literature.The table below shows the parameters with their respective values peculiar to Brong Ahafo Region (Table 3).

Table 3.

Parameter estimates for a pneumonia model.

parameters	value	source
p	0.867	Estimated
ω	389772	Estimated
q	0.234	Estimated
φ	0.05	Jacob.O, 2012 (Jacob Otieno et al., 2012)
β	0.001–0.00196 per day	Jacob.O, 2012 (Jacob Otieno et al., 2012)
α	0.001–0.00196 per day	Jacob.O, 2012 (Jacob Otieno et al., 2012)
σ	0.0115	Jacob.O, 2012 (Jacob Otieno et al., 2012)
τ	0.0076	Estimated
θ	0.014	Estimated
$\text{Ω}$	0.15	Estimated
μ	0.01	Getachew Teshome Tilahun,2017 (Tilahun et al., 2017)
k	0.2	Estimated
η	0.002	Emile.J, 2012 (Ndelwa et al., 2015)
δ	0.0025	Emile.J, 2012 (Ndelwa et al., 2015)
γ	0.8	Estimated
ρ	0.002	Estimated
$\text{Π}$	0.002	Estimated
ξ	0.057	Getachew Teshome Tilahun,2017 (Tilahun et al., 2017)
a	0.11	Estimated
$\ell$	0.073	Estimated
χ	0.095	Jacob.O, 2012 (Jacob Otieno et al., 2012)
ν	0.008	Getachew Teshome Tilahun,2017 (Tilahun et al., 2017)
ς	0.0026	Estimated
ϕ	0.02	Estimated

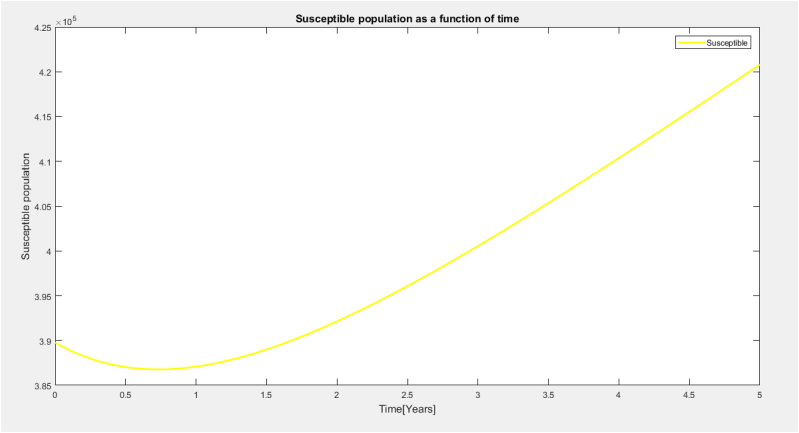
It is observed from Fig. 2 above that the susceptible population decrease as a result of mass vaccination and education to period of half a year.It is again observed that the susceptible population increases as a result of societal perception about the vaccines and lack of awareness and education of this population.

Fig. 1.

Flow chart of the $SV{C}_{Sy}{C}_{Asy}IR$ model.

Fig. 2.

Susceptible population as a function of time.

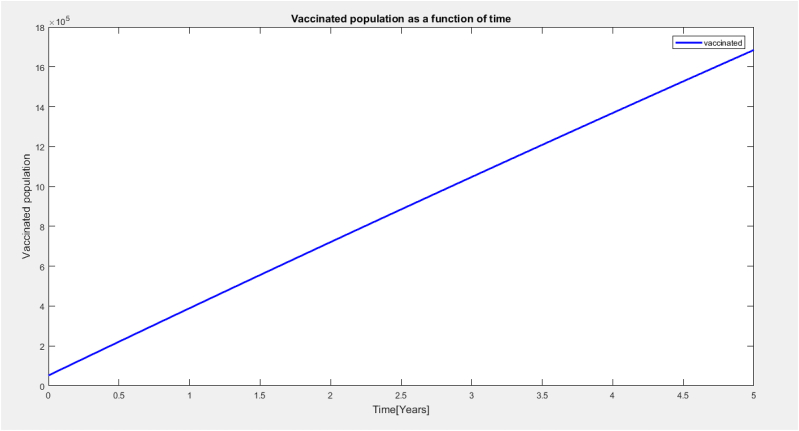
It is observed from Fig. 3 above that the vaccinated population increases as time increases due to the mass immunization coverage in the region.

Fig. 3.

Vaccinated population as a function of time.

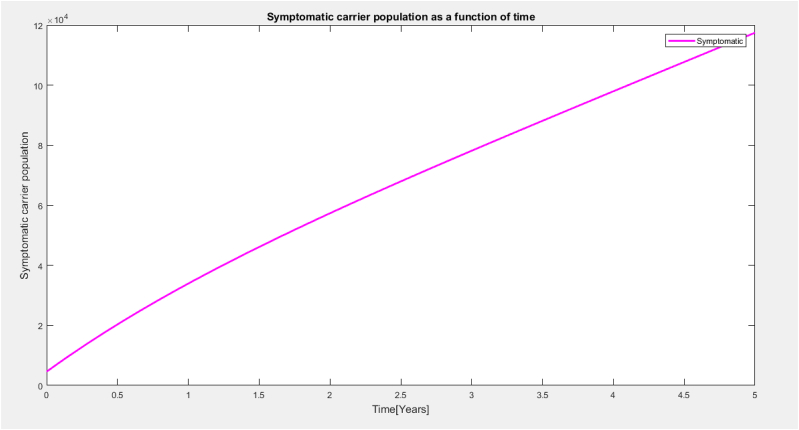
It is observed from Fig. 4 that the symptomatic population increases with respect to time. within a space of 6 months the symptomatic population showed a steady increase in population and within a time range of 1 year there was a slightly curved increase in the population and later there was a steady increase in the symptomatic population within a space of 3 years.All this increases came as a result of the waning ability of the individuals in the population and the efficacy rate of the vaccine.

Fig. 4.

Symptomatic carrier as a function of time.

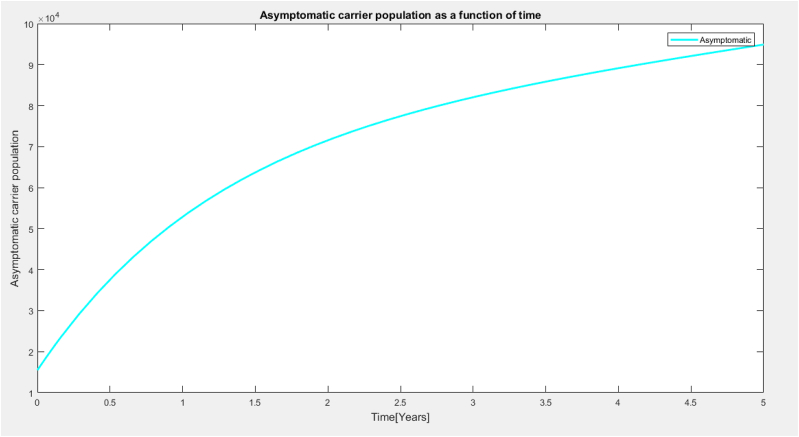
It is observed from Fig. 5 that the asymptomatic carrier population showed a sharp curved increase in population within 4years and then increases steadily as time increases. This rapid increase of the asymptomatic individuals is as a result of the strong immune system and efficacy of the vaccine.

Fig. 5.

Asymptomatic carrier as a function of time.

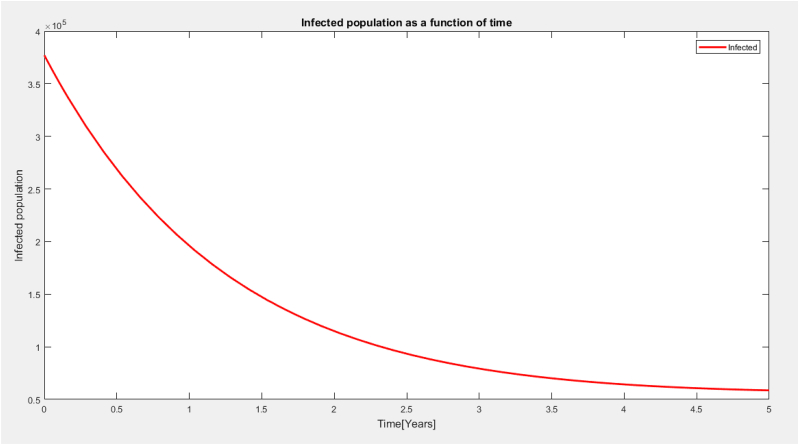
From Fig. 6 the infected population decreases rapidly with respect to time.This decrease came as a result of the mass vaccination of the population and individual gaining temporary immunity of the disease.As the contact rate is high with respect to time[years] the infected population will begin to increase again.

Fig. 6.

Infected population as a function of time.

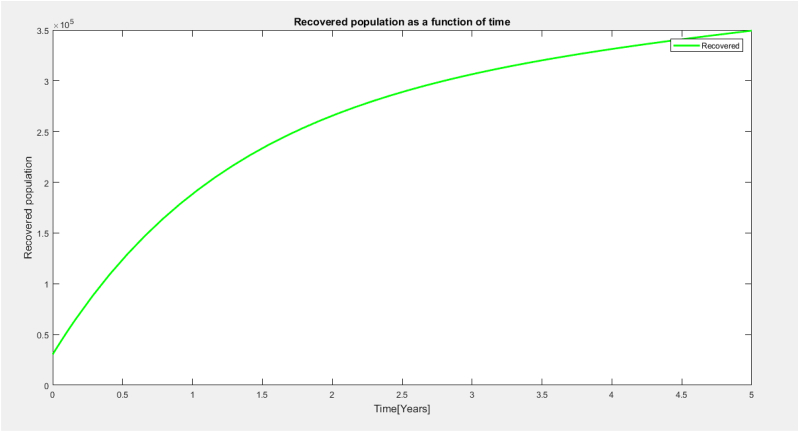
From Fig. 7 the recovery population increases sharply within 3 years and later showed a steady increase with respect to time.This is as a result of the mass vaccination of the individual and the symptomatic carrier, asymptomatic carrier and the infected population gaining temporary immunity to join the recovered population.

Fig. 7.

Recovered population as a function of time.

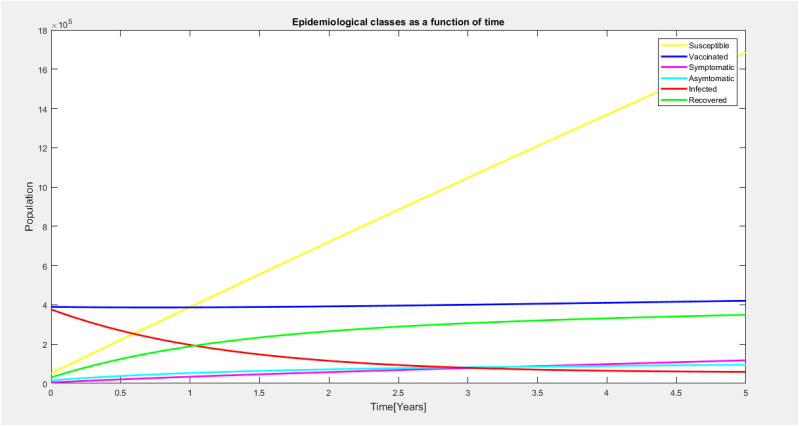
The graph in Fig. 8 shows the various epidemiological classes seen as a function of time. It comprises the graphs Figs. 2, Figure 3, Fig. 4,Fig. 5,Figs. 6 and 7

Fig. 8.

Epidemiological classes as a function of time.

9. Conclusion

The model has shown the importance of pneumonia vaccination in reducing the transmission dynamics of the disease within the population in Brong Ahafo region.The model depicted strongly that the spread of the disease is largely due to the effective contact rate of the infected population as well as symptomatic and asymptomatic carriers of individuals within the entire population.It is also realized that the efficacy of the vaccination is not $100\text{\%}$ effective so individuals within the population can become susceptible with respect to time.Hence intensive public education should be given to parents and individual to complete all the three doses of the vaccine to avert any possible outbreak of pneumonia in the region.

Handling Editor: Dr. J Wu

Appendix A. Supplementary data

The following are the Supplementary data to this article: