Pharmacokinetic-Pharmacodynamic Models that Incorporate Drug-Target Binding Kinetics

Abstract

Pharmacokinetic/pharmacodynamic (PK/PD) models predict the effect time course resulting from a drug dose. In this review we summarize the development of mechanistic PK/PD models that explicitly integrate the kinetics of drug-target interactions into predictions of drug activity. Such mechanistic models are expected to have several advantages over approaches in which concentration and effect are linked using variations of the Hill equation and where preclinical data is often used as a starting point for modeling drug activity. Instead, explicit use of the full kinetic scheme for drug binding enables time-dependent changes in target occupancy to be calculated using the kinetics of drug-target interactions and drug PK, providing a more precise picture of target engagement and drug action in the non-equilibrium environment of the human body. The mechanistic PK/PD models also generate target vulnerability functions that link target occupancy and effect, and inform on the sensitivity of a target to engagement by a drug. Key factors such as the rate of target turnover can also be integrated into the modeling which, together with target vulnerability, provide additional information on the PK profile required to achieve the desired pharmacological effect and on the utility of kinetic selectivity in developing drugs for specific targets.

Introduction

Pharmacokinetic/pharmacodynamic (PK/PD) models are mathematical expressions that predict the effect time course resulting from a drug dose. Pharmacokinetics (PK, what the body does to the drug) analyzes the time dependent change in drug concentration as a result of drug absorption, distribution, metabolism and excretion (ADME), whilst pharmacodynamics (PD, what the drug does to the body) relates the drug concentration to the pharmacological effect of the drug. PK/PD modeling plays a critical role in both preclinical and clinical drug development, for example by assisting in the selection and optimization of drug candidates, and designing dosing regimens for clinical trials [1].

Most current PK/PD models use data primarily from preclinical studies to predict the optimum dosing regimen in humans and are not heavily reliant on in vitro data such as the kinetics of drug-target interactions. In these models target occupancy is accounted for by Hill-based terms (Hill logistic), such as the sigmoidal E_max equation (Figure 1) [2], and thus do not directly inform on the design and development of compounds with altered target-binding profiles. In contrast, PK/PD models that utilize both preclinical data and information obtained from the kinetics of binding to purified target or target in cells, provide useful guidelines for both compound selection and optimization in the early stage of drug discovery as well as dose selection in the clinical phases. In this review we first introduce Hill-based models, and then we discuss models that directly include both the kinetics and thermodynamics of drug-target interactions.

Figure 1. Common PK-PD models.

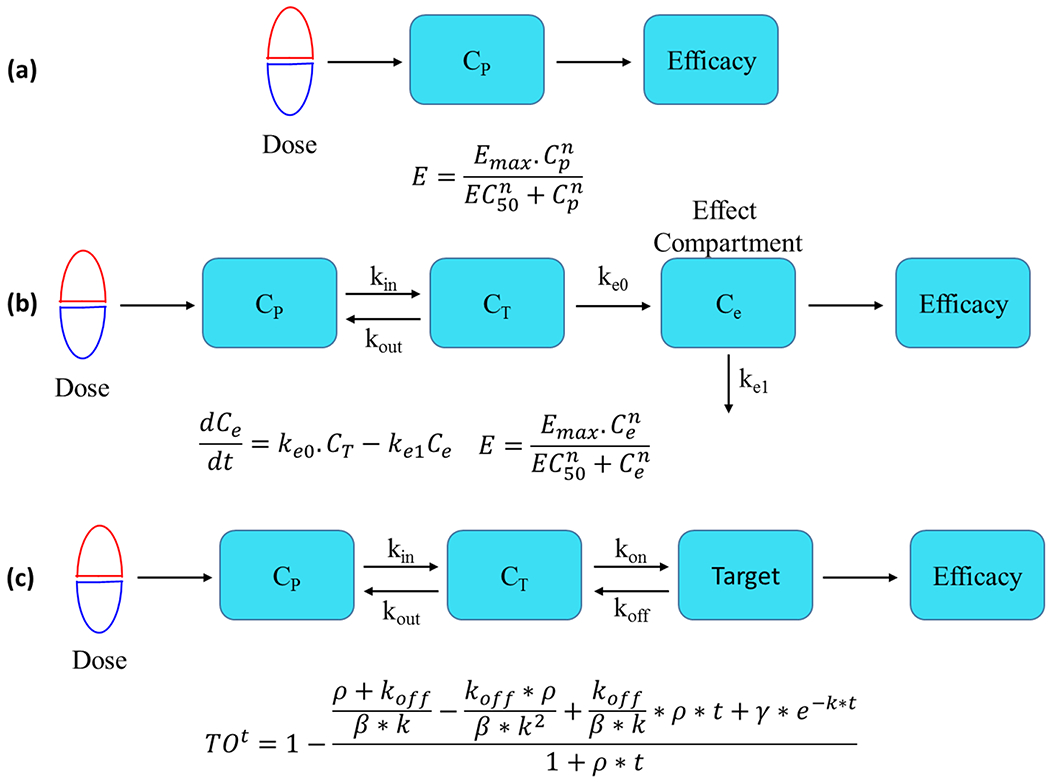
(a) A simple Hill-based direct link-direct response model. C_P is the concentration of drug in plasma, and drug concentration and response are connected by a sigmoidal E_max model where E is the observed efficacy, E_max is the maximum efficacy and n is the Hill coefficient that describes the steepness of the response. (b) A Hill-based model with an effect compartment. C_p, C_T and C_e, are the drug concentrations in plasma, target tissue and effect compartment, respectively. k_in and k_out are the first order rate constants for the distribution of drug from the plasma to the tissue and drug release from the tissue to the plasma, respectively, and k_eo and k_e1 are first order rate constants for drug entering and leaving the effect compartment which is included to compensate for the temporal dissociation between concentration and response, and thus to account for hysteresis. In the absence of hysteresis, the effect compartment is excluded from the model. In the sigmoidal E_max model, C_e is the drug concentration in the effect compartment. (c) A target occupancy (TO)-based model that includes a term for the rate of target turnover (ρ). The model has two dynamic sections including a PK term that defines the time-dependent change in drug concentration in plasma/tissue, and a binding kinetics term that controls the time-dependent change in target occupancy (TO) as a function of drug concentration at the target site. Drug-target complex formation is assumed to occur in a single step where k_on is the second order rate constant for binding and k_off is the first order rate constant for dissociation. TO^t is the fractional target occupancy as a function of time (t), where ρ is the rate of target turnover, $\beta =1+\frac{K_m}{\left[S\right]}$ where K_m is the Michaelis-Menten constant and [S] is the substrate concentration, $\kappa =k_{off}*\left(1+\frac{\left[I\right]}{K_i^{app}}\right)$ where [I] is the inhibitor concentration and $K_i^{app}=\frac{k_{off}}{k_{on}}$, is the apparent equilibrium inhibition dissociation constant for the one-step binding mechanism, and $\gamma \mathrm{ }=\mathrm{ }\frac{k_{off}*\rho }{\beta *k^2}-\frac{\rho +k_{off}}{\beta *k}$.

Hill-based PK/PD models

In most PK/PD models, the concentration response relationship which links drug concentration and effect is described by the sigmoidal E_max model which is based on the Hill equation and classical receptor occupancy theory (Figure 1) [2]. In this model, E_max is the maximum effect, EC₅₀ is the concentration of drug that results in 50% of the maximum effect, and n is the slope factor (Hill coefficient) that desribes the steepness of the correlation between drug concentration and effect [3,4]. At the simplest level, there is no time delay between drug PK and the observed effect so that drug concentration in the plasma is correlated directly with PD through the Hill equation (Figure 1(a)). However, there can also be a delay or hysteresis between changes in drug concentration and effect [4]. Although there are several mechanistic explanations for hysteresis, including slow distribution of drug to the site of action [5,6], time-dependent binding to plasma proteins [7], time-dependent drug-target interactions [8], and up or downregulation of the target [4], many PK/PD models account for hysteresis by including a hypothetical effect compartment [9]. In this case, the time delay between changes in drug concentration in the central compartment and the development of activity at the site of action are compensated for by adjusting the rate constants for transfer of drug into and out of the effect compartment. Drug concentration in the effect compartment is then linked to PD through a Hill equation (Figure 1(b)).

The biological response described by the E_max term can directly reflect a quantitative effect on one or more physiological processes, or be indirectly linked to physiological changes using a biomarker. For instance, the effect of morphine on electroencephalograms (EEGs) in rats was simulated through a direct correlation between morphine concentration at the site of action and EEG amplitude [10]. In addition, lysergic acid diethylamide (LSD) concentration at the site of action was directly correlated to the quantitative changes in heart rate, body temperature, and diastolic and systolic blood pressure [11]. However, many models are constructed using biomarkers to connect drug concentration and efficacy, such as the level of kinase phosphorylation when kinase inhibitors are being modeled. In this case, the concentration of drug in the plasma, tissue, or site of action is first correlated to the level of the biomarker using a Hill equation, which is then incorporated into a differential equation to connect the biomarker to a quantitative read out of efficacy, such as tumor volume (oncology) or ankle diameter (collagen-induced arthritis) [3,12,13].

The dynamic change in effect predicted by the Hill-based models described above is directly controlled by the dynamic change in drug concentration which is itself dependent on the drug PK. These models assume that free and bound drug are in rapid equilibrium, and can successfully model preclinical data and then predict clinical outcome when drug is eliminated from the body more slowly than it dissociates from the target [10]. However, for those drugs that dissociate slowly from their targets, the maintenance of the drug effect is not solely dependent on PK [14–16], and an effect compartment has to be included [4,10,17]. As we discuss below, the inclusion of the thermodynamics and kinetics of drug-target interactions enable PK/PD models to take into account time-dependent binding.

Binding kinetics-based PK/PD models

Many biological interactions, including those between drug and target, are often assumed to be at rapid equilibrium so that changes in concentration of the free ligand (drug) are immediately reflected in an alteration in the amount of bound ligand (drug-target complex). However, an analysis by Swinney in 2006 concluded that approximately 80% of drugs approved by the FDA between 2001 and 2004, operated through a non-equilibrium mode of action [16], and thus that in vivo drug activity was controlled by the both the thermodynamics and kinetics of drug-target interactions. At about the same time, Copeland et al noted that many drugs dissociate slowly from their targets supporting the concept that the kinetics of drug-target interactions provide a more realistic insight into the mode of drug action [18]. These authors went on to propose that drug-target residence should be integrated into lead optimization programs, and noted the importance of long residence time for prolonging drug efficacy. Since then there have been many reviews and commentaries that have discussed the value of including binding kinetics in lead selection and optimization [19–23], as well as ongoing efforts to understand the mechanistic basis for alterations in on and off rates [24]. Below we discuss a PK/PD model that explicitly incorporates drug-target kinetics and then go onto describe the importance of factors such as drug PK, target vulnerability and target turnover in the utility of a kinetics-driven approach to drug discovery.

An antibacterial PK/PD model for inhibition of LpxC

In order to include time-dependent drug-target binding in the modeling, Walkup et al replaced the Hill logistic in a standard antibacterial PK/PD model with the full kinetic scheme for enzyme inhibition (Figure 2) and used this model to simulate the activity of inhibitors of paLpxC, an antibacterial target involved in cell wall biosynthesis in Pseudomonas aeruginosa [14] (Figure 3).

Figure 2: PK/PD Model that integrates drug-target kinetics.

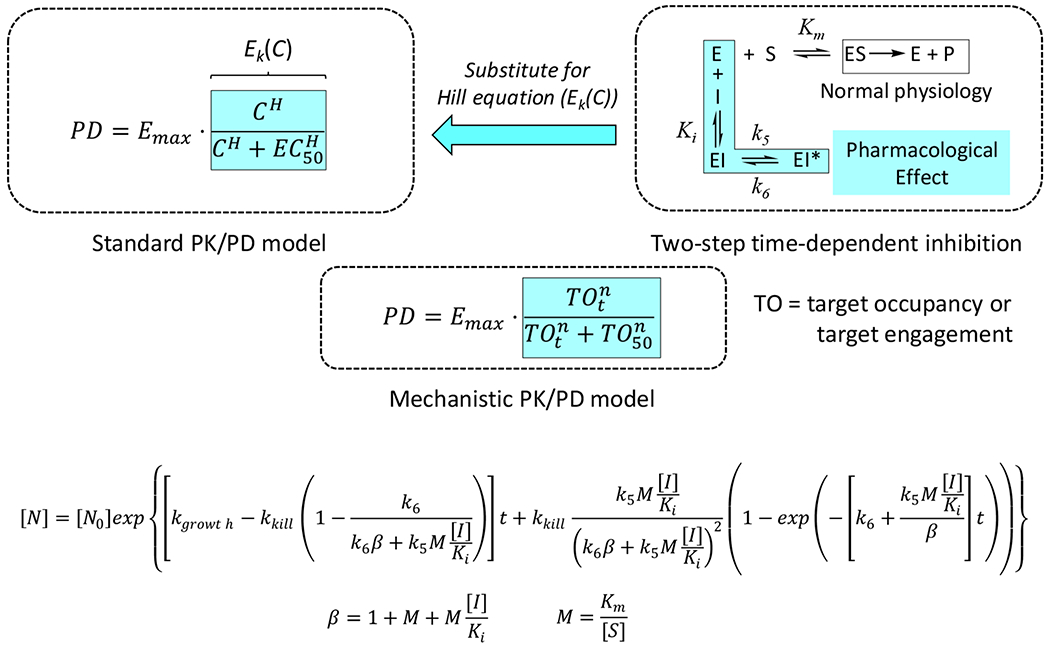
The kinetic scheme for inhibition of a drug target (E) through a two-step mechanism (K_i, k₅ and k₆) replaces the concentration-dependent ‘enhancement of kill’ function, E_k(C), in a standard antibacterial PD model where E_k(C) is the Hill logistic function which assumes rapid equilibrium between and drug and target. In the two-step mechanism, K_i = k₄/k₃, where k₃ and k₄ are the forward and reverse rate constants for the first inhibitor binding step, and k₅ and k₆ are the forward and reverse rate constants for the second step. By convention, the inhibition rate constants are numbered k₃, k₄, k₅ and k₆ as k₁ and k₂ are used to define formation of ES from E+S. The full derivation of the PD model is given in Walkup et al. [14].

Figure 3: Prediction of antibacterial activity using a PK/PD model that incorporates binding kinetics.

(a) In vitro PAE data for inhibition of P. aeruginosa PAO1 growth by a LpxC inhibitor (PF5081090). Cells were treated for 1 hour with different concentrations of inhibitor (fold over MIC from 0x to 16xMIC) prior to washout at t=0. The solid lines are from fitting the data to the PK/PD model. (b) Output parameters from model fitting in (a) were used to simulate bacterial load following administration of three different drug doses to a preclinical model of P. aeruginosa infection. The solid lines are the simulated change in bacterial CFUs and the symbols are the experimental data, blue, 10 mg/kg; red, 50 mg/kg and black, 250 mg/kg. The dashed lines were calculated assuming the inhibitor was in rapid equilibrium with LpxC. The figure is adapted from Figures 3c and 5 in Walkup et al. [14].

Time-dependent inhibition of paLpxC translates to a delay in bacterial regrowth following compound washout which is termed the post-antibiotic effect (PAE). In order to obtain parameters for in vivo modeling, the PAE of a paLpxC inhibitor was first determined for P. aeruginosa cells grown in culture as a function of compound concentration (Figure 3(a)). Global fitting of the PK/PD model to the PAE data returned optimized parameters for enzyme inhibition and also for a permeability parameter that accounted for the difference in inhibitor concentration at the target site and in bulk medium. Subsequently, the PK/PD model was used to successfully predict the antibacterial activity of the paLpxC inhibitor in a preclinical model of P. aeruginosa infection (Figure 3(b)). An important conclusion from this work was the observation that modeling the activity of the inhibitor assuming rapid equilibrium between drug and target significantly underestimated the experimentally observed efficacy. Thus, use of a traditional rapid-equilibrium model would predict a much higher dose of drug than is actually needed.

Target vulnerability

The link between target occupancy and effect is of critical importance to the action of any drug. In addition to the model described by Walkup et al., there have been other reports of mechanistic PK-PD models that have been used either to predict the level of bound target in vivo [25–27], or to predict efficacy assuming a linear relationship between the fraction of drug-target complex and the pharmacological response [28–30]. However, a one-to-one relationship may not exist between occupancy and effect. For instance in animal models of Btk-driven rheumatoid arthritis [12], ALK-dependent anaplastic large cell lymphoma [13], and ALK-dependent non-small cell lung cancer [13], a sigmoidal relationship exists between target inhibition and the pharmacological effect. In order to account for this possibility, we have developed kinetics-driven PK/PD models (Figure 1(c)), in which target occupancy (TO) and effect are linked through a target vulnerability function (Figure 4(a) and Figure 5(d)). Target vulnerability defines the threshold and strength of correlation between target-occupancy and effect, and is of critical importance since high vulnerability targets are much easier to drug than low vulnerability targets. A PK/PD model similar to that shown in Figure 1(c) but lacking a term for target turnover, was used to predict the activity of inhibitors of the Staphylococcus aureus enoyl-ACP reductase (saFabI). Subsequently, vulnerability functions were generated for both saFabI and paLpxC which revealed that saFabI is less vulnerable than paLpxC [15].

Figure 4: Btk vulnerability function in the CIA model and fractional occupancy in humans treated with acalabrutinib.

(a) The target vulnerability function for Btk in a preclinical model of collagen induced arthritis (adapted from Figure 8 in Daryaee et al. [31]. (b) Variability of Btk occupancy in patients with CLL treated with acalabrutinib. 12 h: 100 mg BID (twice per day) of acalabrutinib on day 3 of treatment, 12h after receiving the dose. 24 h: 200 mg QD (once per day) of acalabrutinib on day 3 of treatment, 24h after receiving the dose. The variability in occupancy is proposed to result from differences in Btk synthesis rates across subjects. The data has been extracted from Alsadhan et al. [32].

Figure 5: Kinetic selectivity: PK, turnover and vulnerability.

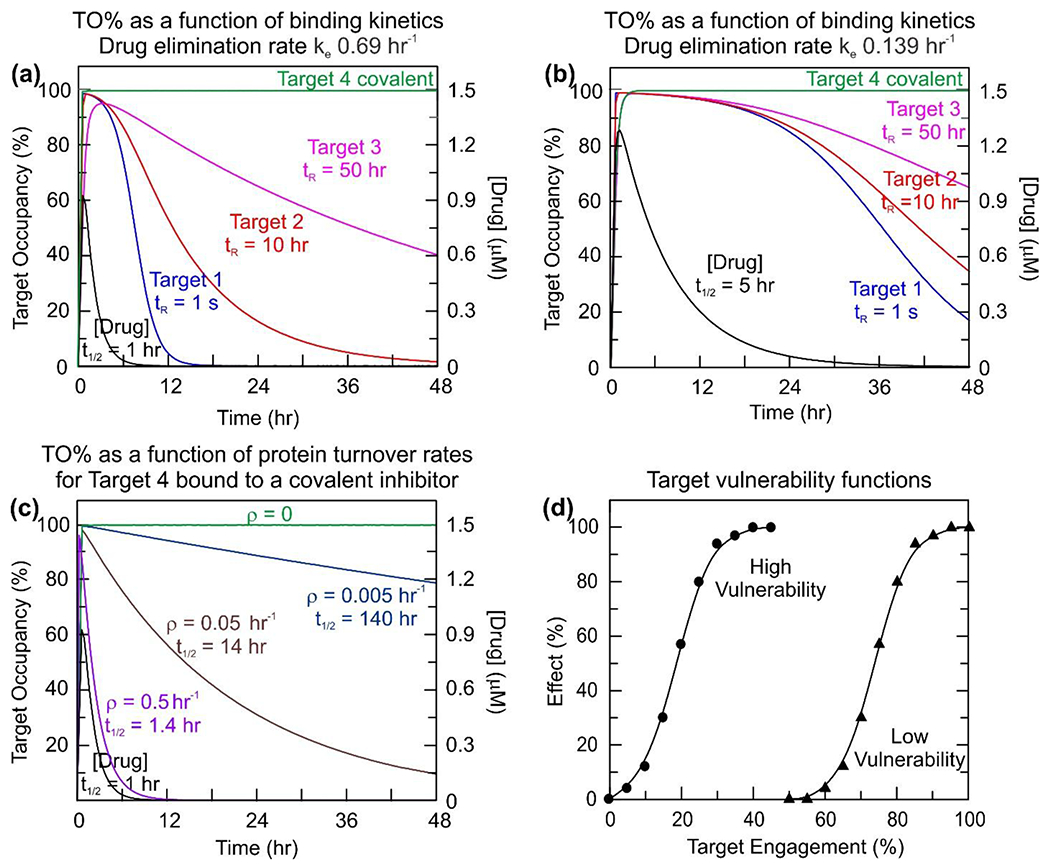
Panels (a) and (b) compare the effect of reducing the rate of elimination on the occupancy of 4 targets with different binding kinetics (Targets 1-4). Panels (a) and (c) compare the effect of target turnover on the occupancy of Target 4. In panel (a) there is no protein turnover whereas in panel (c) the effect of different turnover rates on target occupancy has been modeled. (a) The effect of drug-target kinetics on time-dependent target occupancy. A compound is assumed to bind reversibly to three targets with the same thermodynamic affinity (10 nM) but have different residence times on the three targets: Target 1, 1 s, Target 2, 10 hr and Target 3, 50 hr. In addition, the compound is assumed to bind covalently to a fourth target (Target 4). Target occupancy has been simulated using Kintek [39], assuming a 1.5 μM dose of compound that is absorbed with k_a 3 hr⁻¹ and eliminated with k_e 0.69 hr⁻¹ (t_1/2 1 hr). Reversible binding is assumed to occur via a one-step mechanism with the following on and off-rates. Target 1: k_on 100 μM⁻¹ s⁻¹, k_off 1 s⁻¹. Target 2: k_on 2.78×10⁻³ μM⁻¹ s⁻¹, k_off 2.78×10⁻⁵ s⁻¹. Target 3: k_on 5.56×10⁻⁴ μM⁻¹ s⁻¹, k_off 5.56×10⁻⁶ s⁻¹. For Target 4 it is assumed that the compound binds in a two-step mechanism in which the initial rapid binding of the compound to the target, defined by k_on 100 μM⁻¹ s⁻¹ and k_off 1 s⁻¹ is followed by a second step with k_inact 5.56×10⁻⁴ s⁻¹ leading to the covalent drug-target complex. In each case the target concentration is fixed at 1 nM (i.e. no target turnover). (b) The role of PK in kinetic selectivity. The modeling performed in (a) has been repeated using identical parameters except now assuming that the drug eliminates more slowly with k_e 0.139 hr⁻¹ (t_1/2 5 hr). (c) The impact of turnover on target occupancy. Target 4 in panel (a) is now assumed to turnover linearly at different rates (ρ) of 0.5, 0.05 and 0.005 hr⁻¹ and thus has a half-life of 1.4, 14 and 140 hr, respectively. (d) Target vulnerability plots. Vulnerability functions are shown for low (red) and high (blue) vulnerability targets. The vulnerability function is defined by the minimum level of engagement required for any effect to be observed (TO_min) and the level of engagement that leads to the maximal efficacy (TO_max). The third parameter required to define the function is the Hill coefficient or slope factor that determines the steepness of the effect response between TO_min and TO_max. For the low vulnerability target, the full physiological effect of the drug requires close to 100% target engagement, whereas only ∼35% engagement is needed for the high vulnerability target. The Hill coefficients for the two functions are 4.6 (high) and 16.4 (low). Figures (a), (b) and (d) are adapted from Tonge, 2018 [20].

The mechanistic PK/PD models described above use a permeability function to account for the difference in concentration of drug in the cell (at the target site) and in bulk medium, acknowledging the often-significant concentration gradient across Gram negative bacterial cell walls. The next step in the development of kinetics-driven PK/PD modeling was the use of a covalent probe to directly quantify the level of target occupancy for a covalent inhibitor of Bruton’s tyrosine kinase (Btk), a target for diseases caused by B cell dysregulation [31]. This approach assumes that all unbound protein interacts with either the inhibitor or the probe. Using this probe, inhibition of Btk by CC-292, a covalent inhibitor developed by Avila Therapeutics, was quantified in cells expressing Btk and in B cells isolated from rats dosed with CC-292. This enabled intracellular Btk occupancy to be quantified as a function of extracellular drug concentration, negating the need for a permeability function in the modeling, and also for the rate of Btk turnover to be incorporated into the model. The resulting PK/PD model was then used to predict the activity of CC-292 in a preclinical model of collagen induced arthritis. Quantification of CC-292 efficacy as a function of Btk occupancy resulted in an experimental target vulnerability function for Btk that was in excellent agreement with the vulnerability function generated by the PK/PD model, and which showed that Btk has to be more than 50% occupied for any efficacy to be observed and more than 90% occupied for maximum effect (Figure 4(a)).

Target turnover

Target turnover is a key factor that will limit the extent and duration of target-occupancy once free drug has been removed from the system. The rate of target turnover is thus of key importance for the application of kinetic selectivity in drug development since rapid target resynthesis will impact the translation of slow drug-target dissociation to prolonged drug activity at low drug concentration. This factor is of particular importance for kinase drug targets given the emphasis on developing irreversible inhibitors [33]. Alsadhan et al. have proposed that the differences in Btk occupancy observed in patients with chronic lymphocytic leukemia (CLL) treated with acalabrutinib is due to variation in the rate of Btk synthesis [32]. In particular, it was observed that a much greater variation in Btk occupancy was observed for patients dosed 200 mg QD (once per day) rather than 100 mg BID (twice per day) (Figure 4(b)), and that BID dosing was required to keep Btk occupancy above 90%. The benefit of BID dosing over QD also reflects the relatively rapid elimination of acalabrutinib [32,34,35]. Indeed, when the rate of target turnover is rapid relative to the rate of drug-target dissociation, then the duration and level of target-occupancy will be dependent on both rates, highlighting the importance of including the rate of target turnover in mechanistic PK/PD models in addition to drug-target binding kinetics. Thus, drugs with high affinity, slow dissociation rates, and slow systemic elimination will be needed to maintain the occupancy of targets that turnover rapidly.

Kinetic Selectivity

Selectivity has both thermodynamic and kinetic components, and thus differential occupancy of on and off target molecules can be achieved either by differences in affinity (IC₅₀ values) or in the on and off rates for formation and breakdown of the drug-target complex [20]. Whilst kinetic selectivity therefore offers an additional approach to widening the therapeutic window, for example in situations where occupancy of the desired target persists after drug has been eliminated, the utility of kinetic selectivity depends on target vulnerability and target turnover (Figure 5). Assuming that the duration of target occupancy drives the effect, then low vulnerability targets that turn over rapidly will be unsuitable for kinetic selectivity since drug concentration will have to be maintained at a level that continuously drives drug onto the target, and therefore onto other off-target molecules.

Modeling approaches that integrate drug-target kinetics inform on target vulnerability and can be used to determine which targets might benefit from kinetic selectivity through the development of compounds, such as covalent inhibitors, that dissociate slowly from their targets. As noted above, and in many other articles [10,20,36], the expression of kinetic selectivity is intimately related to drug PK since the rate of elimination must be fast relative to the rate of drug-target complex breakdown [37]. However, the normal emphasis in medicinal chemistry campaigns is on the development of compounds with reduced metabolism that eliminate slowly, even if in some cases the desired mechanism of action is through irreversible inhibition of the target. This may partly account for the observation made by Georgi et al who surveyed 270 kinase inhibitors and concluded that time-dependent kinase occupancy was driven to a large extent by drug PK [38]. Thus, optimization of drug-target kinetics should procced in concert with the development of compounds with appropriate PK to take advantage of kinetic selectivity.

Summary

Time-dependent target occupancy is controlled by several factors including the thermodynamics and kinetics of drug-target interactions, dynamic changes in drug and target concentration, and the rate of target turnover. The subsequent translation of occupancy to effect is controlled by factors such as target vulnerability which includes the physiological response to target engagement. This review summarizes our efforts to develop PK/PD models that integrate binding kinetics and target turnover into predictions of drug activity. Although we have made progress, there are still a number of factors that are not explicitly included in the modeling process such as target concentration and changes in target levels caused by drug treatment. In addition, it is assumed that the drug only works when it is bound to the target. However, the ability to quantify target occupancy directly using covalent inhibitors and probes in cells, animals and humans, is a major advantage since an experimental link between occupancy and effect can be directly obtained. Such experimental vulnerability functions can then be used to check some of the assumptions used in the modeling process and also to predict the activity of reversible inhibitors of the same target. In systems where only reversible ligands are available, the ability to measure binding kinetics in cells, such as with NanoBRET [38], will be an advantage since this should enable the drug concentration gradient across the cell membrane to be factored into the modeling. Ultimately, such mechanistic models present the opportunity to inform the selection and optimization of drug candidates using both in vitro measurements of drug-target binding as well as data from preclinical studies. In addition, these models are expected to improve the prediction of drug activity in the non-equilibrium environment of the human body where drug and target may not be at equilibrium.

Highlights.

• PK/PD models that integrate drug-target kinetics.

• Predictions of drug activity in the non-equilibrium environment of the human body.

• Inclusion of the rate of target turnover in modeling and generation of target vulnerability functions.