Quantitative Hemodynamic Analysis of Brain Aneurysms at Different Locations

Abstract

BACKGROUND AND PURPOSE:

Studies have shown that the occurrence of brain aneurysms and risk of rupture vary between locations. However, the reason that aneurysms at different branches of the cerebral arteries have different clinical presentations is not clear. Because research has indicated that aneurysm hemodynamics may be one of the important factors related to aneurysm growth and rupture, our aim was to analyze and compare the flow parameters in aneurysms at different locations.

MATERIALS AND METHODS:

A total of 24 patient-specific aneurysm models were constructed by using 3D rotational angiographic data for the hemodynamic simulation. Previously developed computational fluid dynamics software was applied to each aneurysm to simulate the blood-flow properties. Hemodynamic data at peak pulsatile flow were recorded, and wall shear stress (WSS) and flow rate in the aneurysms and parent arteries were quantitatively compared. To validate our method, a comparison with a previously reported technique was also performed.

RESULTS:

WSS and flow rate in the aneurysms at the peak of the cardiac cycle were found to differ in magnitude between different locations. Multiple comparisons among locations showed higher WSS and flow rate in middle cerebral artery aneurysms and lower WSS and flow rate in basilar artery and anterior communicating artery aneurysms.

CONCLUSIONS:

We observed changes in hemodynamic values that may be related to aneurysm location. Further study of aneurysm locations with a large number of cases is needed to test this hypothesis.

Brain aneurysm rupture is one cause of subarachnoid hemorrhage and results in substantial rates of morbidity and mortality. Autopsy studies have reported that intracranial aneurysms are common lesions and certain locations tend to have a higher rate of incidence.¹ Recent international studies have reported that some aneurysm locations have a higher risk of rupture than others.^2–4 Because little is known about the cause of brain aneurysms or the process by which they grow and rupture, studies of how anatomic location may affect brain aneurysms can help further understand this disease.⁵

Vascular geometry, branching angles, and surrounding anatomic structures, the features used to identify and specify an aneurysm, have previously been studied to find their relationships with the natural history of aneurysms.^6–8 Analyzing differences in parent artery geometry revealed that aneurysms with a large caliber of the proximal artery tended to rupture at a larger size.⁶ Bifurcations beyond the circle of Willis approximated optimality principles, unlike those within the circle of Willis.⁷ Moreover, the perianeurysmal environment has been suggested to influence aneurysm shape and risk of rupture, especially for locations with unbalanced contact constraint.⁸

Intra-aneurysmal hemodynamic characteristics are also believed to be an important factor for aneurysm growth and rupture.^9–16 With the help of advancements in medical imaging, realistic aneurysm geometry and vascular structure can be incorporated into simulations to perform patient-specific hemodynamic analysis. This type of image-based hemodynamic research has shown that ruptured aneurysms tend to have a more complicated flow pattern.^14,17 Using a longitudinal data base, a recent hemodynamic study of aneurysm growth also reported that aneurysms are more likely to grow in regions of low wall shear stress (WSS).¹⁸ Although studies have suggested that aneurysms at different locations tend to differ geometrically and clinically,^1–4 to our knowledge, whether aneurysms at different locations have different hemodynamic properties has not yet been reported. The aim of this study was to examine the hemodynamic parameters in aneurysms at different locations.

Materials and Methods

Data Collection and Imaging Technique

Twenty-four aneurysms from 4 of the common locations in cerebral arteries (anterior communicating artery [AcomA], middle cerebral artery [MCA], internal carotid artery [ICA], basilar artery [BA]) were selected from the University of California, Los Angeles interventional neuroradiology data base from November 2007 to June 2008. 3D rotational angiographic (3DRA) images (Integris; Philips Medical Systems, Best, the Netherlands) obtained before aneurysm embolization were collected and transferred to an Integris workstation (Philips Medical Systems) for 3D voxel generation. The Table summarizes the details of the cases.

Summary of aneurysm cases^*

Characteristics	Group 1	Group 2	Group 3	Group 4	Summary
Age (year)
Mean	65.2	64.2	51.3	57.3	59.5
Range	48–81	42–79	24–70	47–70	24–81
Sex (No. of patients)
Female	5	5	6	3	19
Male	1	1	0	3	5
Unruptured-ruptured aneurysms (No. of patients)	4–2	4–2	4–2	4–2	16–8
Total No. of aneurysms	6	6	6	6	24
Largest diameter of aneurysm (mm)
Mean	5.2	6.25	7.2	11.0	7.4
Range	3.6–8.2	5.1–8.1	5–8	6–15	3.6–15
Diameter of aneurysm neck (mm)
Mean	3.5	3.7	4.4	7.17	4.7
Range	2.3–6.5	3.3–4	2.7–7	4–14.6	2.3–14.6
Size of aneurysm (No. of patients)
<7 mm	5	4	2	1	12
7–12 mm	1	2	4	2	9
13–24 mm	0	0	0	3	3
Diameter of parent artery vessel lumen (mm)
Mean	2.1	2.2	3.9	3.4	2.9
Range	1.3–3.2	1.6–2.7	3.4–5.3	2.7–4.4	1.3–4.4

^*Groups 1, 2, 3, and 4 are aneurysms located at the AComA, MCA, ICA, and BA, respectively.

Hemodynamic Modeling of Aneurysms

The computational model for each aneurysm was reconstructed by using patient-specific computational fluid dynamics−simulation software developed by George Mason University.^{14,15,17,19–25} All 3DRA images were denoised and later segmented by using a region-growing algorithm.^14,15,20,24 A volumetric model generated by a 3D advancing front technique was used to define the geometry of the computational domain. To have the same inflow settings for all the aneurysm simulations, aneurysms located at the anterior circulation were all modeled from the ICA cavernous segment, and aneurysms located at posterior circulation were all modeled from the BA segment.

Previously reported pulsatile flow profiles for the ICA and BA measured from a healthy subject by using phase-contrast MR imaging (Signa 1.5T scanner; GE Healthcare, Waukesha, Wis) were imposed as the inflow for the computational fluid dynamics models.^14,21,26 The flow profiles were prescribed by using the Womersley solution for the fully developed pulsatile flow in a rigid straight tube^13–15,27 and were scaled according to the cross-sectional area of the inflow vessels for each model.²⁸ Assuming that all the distal vascular beds have similar total resistance to flow, traction-free boundary conditions with the same pressure level were applied to all the model outlets. Blood flow was modeled as an incompressible Newtonian fluid. The governing equations were the unsteady Navier-Stokes equations in 3D. The blood attenuation was 1.0 g/cm³ and the viscosity was 0.04 poise. Vessel walls were assumed rigid, and no-slip boundary conditions were applied at the walls. Numeric solutions of the Navier-Stokes equations were obtained by using a fully implicit finite-element formulation. Two cardiac cycles were computed by using 100 steps per cycle, and all the results presented corresponded to the second cardiac cycle.^13–15,27 Details of the simulation settings have been previously described.^{14,15,17,19–25}

Quantitative Hemodynamic Analysis and Validation Method

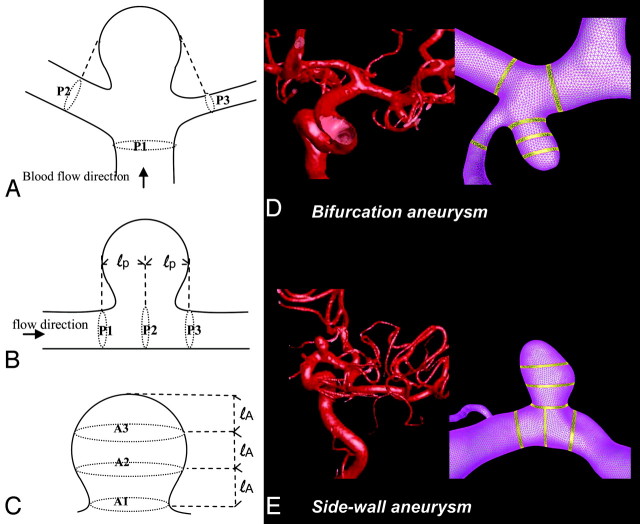
After the hemodynamic simulation, for each aneurysm, the blood-flow rate and WSS at the peak of the cardiac cycle were collected both from the aneurysm and the parent artery. We applied a previously developed technique to perform quantitative analyses by using a predefined 6-region method.²⁹ Hemodynamic data were collected from 3 equal sections in the aneurysm dome, with regions defined crossing the aneurysm dome at the level of the aneurysm neck, middle, and top (Fig 1). Likewise, data in the vessel were recorded from 3 regions of the parent artery—crossing at the proximal end of the aneurysm, the center of the aneurysm, and the distal end of the aneurysm. For aneurysms located at multi-avenue terminals or bifurcations, 1 region crossed the proximal point of the bifurcation at the main artery and 2 regions crossed the arteries at the distal end of the aneurysm.

Fig 1.

Schematic representations of regions for hemodynamic data analysis. A, Regions in the arteries of terminal or bifurcation aneurysms. B, Regions in the arteries of sidewall aneurysms. C, Regions in the aneurysm dome. D and E, Application to patient-specific aneurysm models are shown for a bifurcation aneurysm (D) and a sidewall aneurysm (E).

Although the 6-region method reduces the complexity of hemodynamic results, its consistency with hemodynamic data collected from the entire aneurysm dome and parent artery needed to be evaluated. Due to the complexity of the data-analysis process, few studies have detailed the collection of hemodynamic data from the entire aneurysm dome and parent artery. However, one relatively recent report by Shojima et al¹³ extracted data from the entire aneurysm dome and MCA to study MCA aneurysms. We reproduced their approach and compared results collected from the entire dome and parent artery with the 6-region method. Because the method of Shojima et al¹³ was only applicable to study WSS in MCA aneurysms, 10 MCA aneurysms from the University of California, Los Angeles interventional neuroradiology data base (from November 2007 to June 2008) were selected for the method comparison.

Statistical Methods

Results were expressed as mean value and SD. Repeated measurements and analysis of variance were used. Multivariate tests and multiple comparisons between location groups were performed to see the relationship of hemodynamic properties and locations. The sign test³⁰ was used for the method comparison. The Spearman rank correlation was used to find the relationship between vessel dimensions and hemodynamic values. The statistical significance level was set at .05.

Results

Hemodynamic Properties in Aneurysms

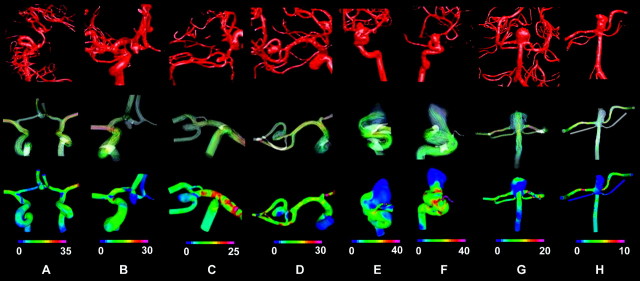
The representative hemodynamic properties of brain aneurysms from different locations are shown in Fig 2. Patient-specific aneurysm models were reconstructed based on the 3DRA images (Fig 2, top row). The instantaneous streamlines at the peak of systole, recorded from the trajectory of the instantaneous 3D velocity field,²⁹ show the flow pattern in the aneurysms (Fig 2, the second row). The third row is the distribution of WSS for each aneurysm. As previously shown, the patient-specific hemodynamic simulation allowed us to study flow properties in various aneurysms; however, the results yielded from the simulation can be complicated and difficult to compare, especially when studies include a variety of aneurysms.

Fig 2.

Representative hemodynamic results for AcomA (A and B), MCA (C and D ), ICA (E and F ), and BA (G and H ) aneurysms. Top row is the 3DRA images obtained for each aneurysm during the clinical procedure. A diversity of aneurysms and complicated arterial structures can be observed. The middle row (flow pattern) and the bottom row (WSS) are the hemodynamic results obtained from the simulation. Flow pattern and WSS show differences among aneurysms, and each one has a unique pattern in the arteries and the aneurysms. WSS is in pascal units.

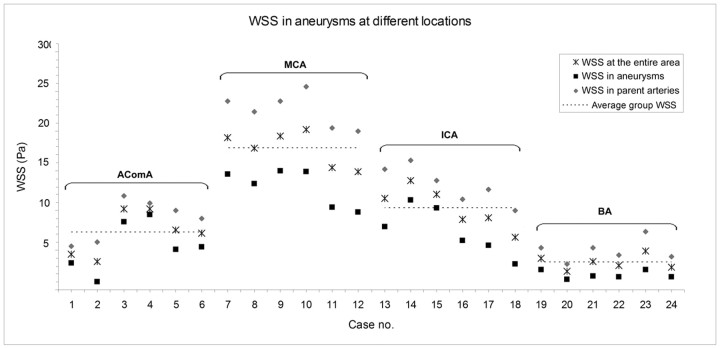
For quantitative comparison of hemodynamic properties, we calculated the WSS and flow rate from different regions of aneurysms. The average WSS in the aneurysms, parent arteries, and the entire aneurysm area (both aneurysm and parent artery regions) is shown in Fig 3. WSS was found to differ among locations in aneurysms (P = .01) and in parent arteries (P = .009). Multiple comparisons showed that the BA aneurysms had the lowest average WSS, lower than AcomA (P = .009), ICA (P < .001), and MCA (P < .001) aneurysms. WSS in AcomA aneurysms was lower than that in MCA aneurysms (P < .001).

Fig 3.

WSS in aneurysms at each location. Note the average WSS in arteries and aneurysms and the average WSS in the entire aneurysm area.

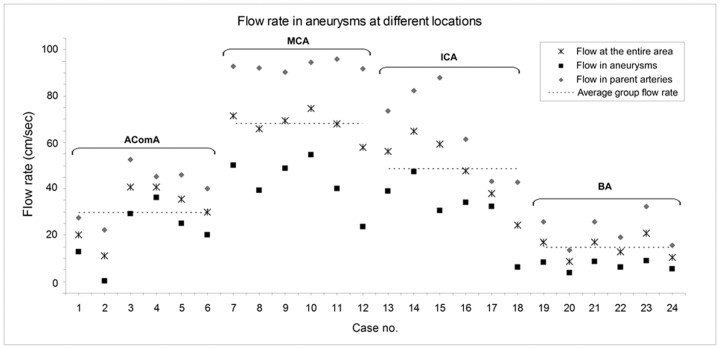
The average blood-flow rate calculated for the aneurysms, parent arteries, and the entire aneurysm area is shown in Fig 4. We found the trend of flow rate in the parent arteries (P < .001) and aneurysms (P = .071) also differed among locations. Aneurysms at the BA had the lowest average flow rate, and multiple comparisons showed that the flow rate in BA aneurysms was lower than that in AcomA (P = .018), ICA (P < .001), and MCA (P < .001) aneurysms. Flow in AcomA aneurysms was slower than that in MCA (P < .001) and ICA (P = .05) aneurysms.

Fig 4.

Flow rates in aneurysms at different locations. Note the average flow in arteries and aneurysms and the average flow velocity in the entire aneurysm area.

Technique Validation

Figure 5shows the average WSS in 10 MCA aneurysms obtained by the present method, which collected data from 6 regions, and by the method of Shojima et al,¹³ which found WSS averages in the aneurysm dome and parent artery. The average WSS in the aneurysms obtained by the present method and by Shojima et al were 10.3 ± 5.2 Pa and 11.7 ± 3.6 Pa, respectively (Fig 5A). The average WSS in the parent arteries was 19.3 ± 4.6 Pa and 17.4 ± 5.9 Pa, respectively (Fig 5B). We found that the present method and that of Shojima et al yielded similar results and there was no statistical difference between the techniques (P = .344).

Fig 5.

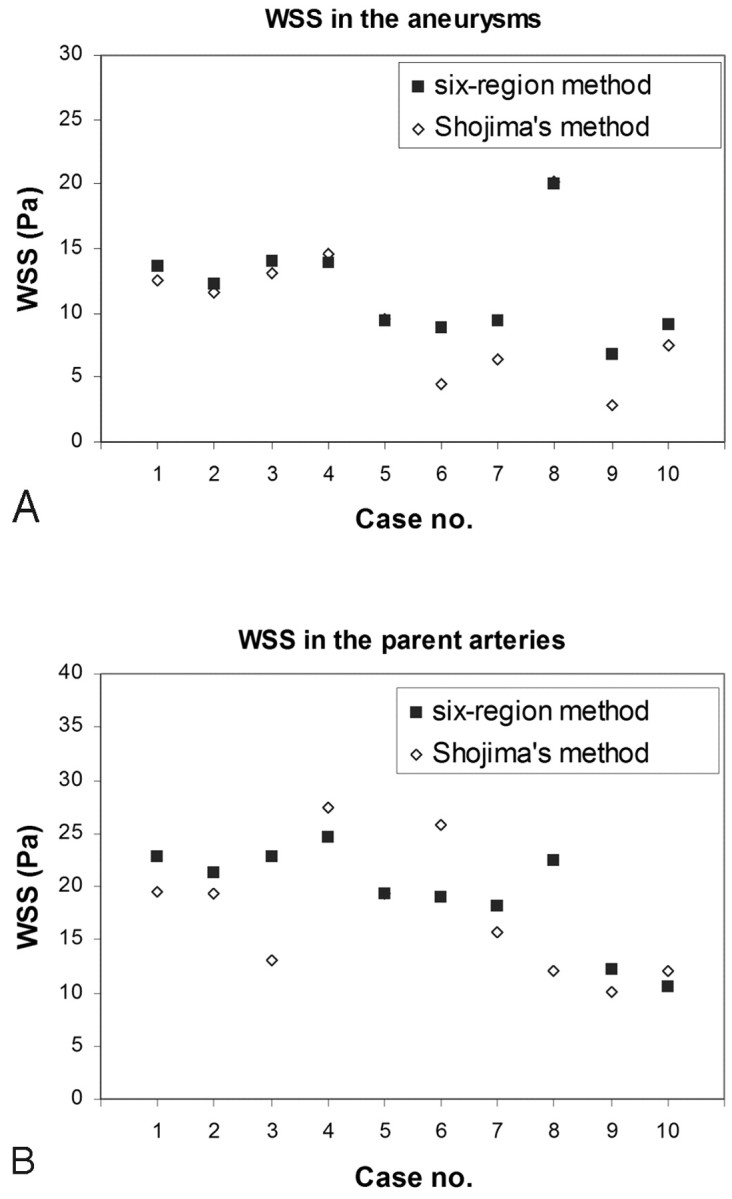
A and B, Validation study comparing the hemodynamic results by using 6 regions (solid) and values collected from the entire dome and parent artery (method of Shojima et al¹³) (hollow) shows the average WSS in the aneurysms (A ) and the average WSS in the parent arteries (B). Note in cases 5 and 8 that both methods show the same average WSS in the aneurysm.

Discussion

Patient-specific hemodynamic analysis enabled us to simulate intra-aneurysmal flow properties for a diversity of aneurysm shapes and complicated vascular structures. In this study, we quantitatively analyzed hemodynamic data in aneurysms and found that there were hemodynamic differences among aneurysms at different locations. Many causes may produce differences in aneurysmal hemodynamic values among locations: aneurysm geometry, vessel geometry, parent artery size and curvature, or blood flow rates. From this study, we were not able to determine the reason for such hemodynamic differences because of the small number of cases. Furthermore, many other factors affecting aneurysms were not considered, including aneurysm size, patient age and sex, and population. Studies incorporating those groups with more cases are also important to find out how hemodynamic changes among locations are associated with these parameters.

We found different hemodynamics properties according to location. The results may not be surprising because different-sized vessels have different flow.³¹ Such evidence has not yet been shown in human brain aneurysms; instead, many hemodynamic studies have combined aneurysms in various locations.^14,18,32 Although this is a preliminary study and further proof of this finding is needed, we think that on the basis of our results, consideration of hemodynamic variation between locations will be important for future studies. Furthermore, in our cases, no significant correlations were found between parent artery size and aneurysm WSS (ρ = −0.357; P = .086) and flow rate (ρ = −0.286, P = .175), suggesting that due to the complexity of the brain vascular structure, using only the size of the vessel may not be enough to understand the flow properties in aneurysms.

Hemodynamic influences have important effects on vascular diseases.^28,33–36 WSS, caused by blood flow, is a tangential force acting on the endothelial surface. Studies have shown that though WSS is a small force that is insufficient to tear the vessel wall, it is an important determinant of endothelial cell function especially when WSS is low.^28,34,35 Recently, studies evaluated the presence of endothelial cells in human aneurysms^37,38 and reported that low WSS in aneurysms may relate to the risk of rupture and aneurysm growth.^13,18 Consistent with previous studies,^13,29 our results showed that WSS was low in aneurysms, compared with the arteries (P = .005). Moreover, because the low WSS in aneurysms varies among locations, whether this variation associates with the rate of endothelium function deterioration or the rate of aneurysm growth is a question needing further investigation. Studies combining histological findings and flow simulation in aneurysms will be helpful in understanding the meaning of the different ranges of WSS found in each location.

Limitations

We compared hemodynamic properties in aneurysms among various aneurysm locations; however, even aneurysms at the same location have anatomic variations that may also affect the hemodynamic properties. Because of the limited number of cases, we were not able to compare how these anatomic differences affect aneurysm hemodynamics. Moreover, the case selection in this study was not ideal, with, for example, more large aneurysms in the BA group than in other locations. This case selection was affected by the patients' enrollment patterns in our medical center. Although we found a statistically significant difference among groups in our cases, these variations in anatomy and size were included. Further research with more detailed anatomic categorization and combining a multicenter data base would still be needed to provide thorough understanding of the association among aneurysm hemodynamics and locations and anatomic variations.

Our hemodynamic study used a human pulsatile profile with inflow conditions scaled according to the patients' inflow vessel sizes. A simulation with patient-specific inflow conditions will be the most ideal flow conditions to use. A recent study has shown success by using patient-specific blood-flow information collected from phase-contrast MR imaging to perform hemodynamic simulations.¹⁸ However, obtaining sufficient aneurysm cases with patients' intracranial vessel geometry and flow information is technically challenging. One of our future tasks will be collecting patient-specific inflow information to incorporate into the hemodynamic simulation to test our findings.

In this study, we used the 6-region method to study hemodynamic properties and showed that it was a comparable and more computationally efficient approach in comparison with results collected from the entire aneurysm dome and parent artery. This data-collection method is a useful tool to reduce the amount of data and accelerate the data-collection process, which is suitable for larger case numbers. However, this is just one way to perform data analysis, and efforts to improve the analysis methods for various aneurysms are still needed to develop accurate and efficient hemodynamic analysis tools for studies including a large number of cases. In this study, we analyzed the hemodynamic value at the peak of systole as our first step to study aneurysms at different locations. Further study comparing the entire cardiac cycle with patient-specific flow profiles will be needed to study whether hemodynamic differences among locations change during the course of the cardiac cycle.

The current analysis still used hemodynamic simulation focused on a particular segment of the artery. Because asymmetric effects may be important to aneurysms within the circle of Willis,³⁹ future studies with the simulation incorporating the entire circle of Willis will facilitate in-depth understanding of the influence of location, especially lateral influence.

Conclusions

On the basis of the results of this study, our hypothesis is that aneurysmal hemodynamic properties may vary according to location. Consideration of hemodynamic variation among locations may be needed when studying aneurysm hemodynamics, such as aneurysm natural history or aneurysm rupture. Further study of aneurysm locations with more cases and incorporation of factors such as sex and medical history are needed to test this hypothesis.