Abstract
Objective
Schizophrenia is a chronic and debilitating neuropsychiatric disorder. It has been suggested that impaired brain connectivity underlies the pathophysiology of schizophrenia. Network analysis has thus recently emerged in the field of schizophrenia research.
Methods
We investigated 48 schizophrenia patients and 24 healthy controls using network analysis and a machine learning method. A number of global and nodal network properties were estimated from graphs that were reconstructed using probabilistic brain tractography. These network properties were then compared between groups and used for machine learning to classify schizophrenia patients and healthy controls.
Results
In classifying schizophrenia patients and healthy controls via network properties, the support vector machine, random forest, naïve Bayes, and gradient boosting machine learning models showed an encouraging level of performance. The overall connectivity was revealed as the most significant contributing feature to this classification among the global network properties. Among the nodal network properties, although the relative importance of each region of interest was not identical, there were still some patterns.
Conclusion
In conclusion, the possibility exists to classify schizophrenia patients and healthy controls using network properties, and we have found that there is a provisional pattern of involved brain regions among patients with schizophrenia.
Keywords: brain imaging, machine learning, network analysis, schizophrenia
1. INTRODUCTION
Schizophrenia is a chronic and debilitating mental disorder with a considerable disease burden (Rossler, Salize, van Os, & Riecher‐Rossler, 2005). Following on from previous postmortem studies (Bogerts, 1993), there have been efforts to identify anatomical alterations in brains with schizophrenia, particularly in light of advancements in brain imaging techniques (Dietsche, Kircher, & Falkenberg, 2017; Haijma et al., 2013; Shepherd, Laurens, Matheson, Carr, & Green, 2012; van Erp et al., 2018). Although there have been some significant findings to date on the anatomical alterations in the brains of schizophrenia patients, the pathophysiology of this disorder has not yet been comprehensively explained by these findings. It has been recently suggested that it is not alterations in individual anatomical regions but the connectivity between multiple brain regions that underlies the core pathophysiology of schizophrenia (Cui et al., 2019; Fitzsimmons, Kubicki, & Shenton, 2013; Nelson, Bassett, Camchong, Bullmore, & Lim, 2017).
In terms of connectivity, network analysis based on the graph theory has recently emerged in the area of schizophrenia research (Bullmore & Sporns, 2009; van den Heuvel, Mandl, Stam, Kahn, & Hulshoff Pol, 2010) since its first application with the electroencephalogram and magnetoencephalogram methods (Stam, 2004). Graph theory is a branch of mathematics that describes a complex system, such as the brain, as a graph with nodes and edges (Deo, 2017). Brain networks can also be presented in this way as graphs, with nodes and edges representing neural elements and synaptic connections. Although each graph can only represent topological relationships between brain regions, it is known that topological distances are related to physical distances in the brain (Laughlin & Sejnowski, 2003), which indicates that network analysis with a structural brain image is possible.
It is possible to analyze the brain network after reconstructing it as a conceptual graph. Such analysis is based on multiple graph features or network properties (Bullmore & Sporns, 2009). Some prior studies that have investigated network properties within conceptualized brain networks in schizophrenia (Fornito & Bullmore, 2015; Jalili & Knyazeva, 2011; Lord et al., 2011; Nelson et al., 2017) have reported significant differences between patients and healthy controls. We have also previously compared brain structural networks between patients with schizophrenia and healthy controls and found significant difference in network properties (Shon et al., 2018). Notably, however, most prior studies have focused only on group differences in network properties, which has limited their clinical utility in terms of assessing individual patients or healthy controls.
We have here evaluated machine learning as a method of enhancing the clinical utility of network properties in individual patients with schizophrenia and healthy controls. Machine learning is a field of computer science that assesses the use of algorithms to perform a specific task without specified human instructions (Mohri, Rostamizadeh, & Talwalkar, 2018). It has seen recent widespread application in various fields including biology and neuroscience. Various machine learning techniques have shown great efficacy in this regard, particularly in classifying items by multiple features. These have also now been applied also to schizophrenia research (Rozycki et al., 2017; Winterburn et al., 2017) and have shown high disease classification accuracy from various nonpathognomonic features.
In our present analyses of a schizophrenia and normal cohort, we applied the machine learning method to the results of structural brain network analysis in these subjects, on the basis of graph theory. By conceptualizing hypothetical graphs with the brain tractography, the brain networks of both schizophrenia patients and healthy controls were reconstructed for network analysis. Both the global and nodal network properties of the brain were then compared between schizophrenia patients and healthy controls. Through the use of machine learning methods, we attempted to create a possible disease classification model of schizophrenia based on these network properties, which would have significant future clinical implications. Also, the relative importance of each network property or region of interest (ROI) in the machine learning model was evaluated for further insight.
2. METHODS
2.1. Study participants
Study participants were recruited from Asan Medical Center, Seoul, Korea. This included 48 patients diagnosed with schizophrenia using the Diagnostic and Statistical Manual of Mental Disorders, Fourth Edition, Text Revision (American Psychiatric Association, 2011), who had presented with psychotic symptoms within 5 years. We also enrolled 24 healthy controls without an Axis I psychiatric diagnosis or any first‐degree relative with an Axis I psychiatric diagnosis. All subjects were between the ages of 20 and 40 years, were right‐handed, and had no previously known organic disease that could affect the brain structure or function. Written informed consent was obtained from all study participants. This study was approved by the Institutional Review Board of Asan Medical Center (2012‐0485).
2.2. Clinical assessments
Full Scale Intelligence Quotient scores obtained using the short form of the Wechsler Adult Intelligence Scale—III were used to measure overall intelligence in all study participants. The Wisconsin Card Sorting Test: Computer Version 2 (Heaton, Chelune, Talley, Kay, & Curtiss, 1993) was additionally applied to measure executive function in each study participant. In addition, the Korean version of the Positive and Negative Syndrome Scale (Yi et al., 2001) was used to evaluate psychiatric symptom severity in the patients with schizophrenia.
2.3. Image acquisition
Imaging was conducted on a 3T scanner with an 8‐channel SENSE head coil (Achieva; Philips Healthcare, Best, The Netherlands). T1‐weighted images were acquired using a turbo field echo sequence (TR [repetition time]/TE [echo time], 4.9/4.6 ms; field of view, 240 × 240 × 170 mm; and voxel size, 1 mm3). Diffusion‐weighted echo planar imaging was conducted (TR [repetition time]/TE [echo time], 5,422/70 ms; flip angle, 90°; field of view, 224 × 224 × 135 mm; and voxel size, 2 × 2 × 3 mm) for one baseline (b value, 0 s/mm2) and 32 gradient directions (b value, 1,000 s/mm2). All acquired images were then visually inspected again to exclude inappropriate images from further analysis. The data for one patient were therefore replaced with those for a newly enrolled patient in comparison with our previous study findings (Shon et al., 2018). This did not alter the results of either study.
2.4. Image processing
Because anisotropic voxels can cause undesirable problems such as low signal intensity‐to‐noise ratio and a directional error with the fiber tracking algorithm, the importance of making each voxel isotropic for analysis has been stressed (P. Mukherjee, Chung, Berman, Hess, & Henry, 2008). Hence, diffusion‐weighted images in this current study were upsampled and converted to an isotropic voxel size of 2 mm using Slicer Version 4.4 (Fedorov et al., 2012). Corrections for motion and eddy current distortions were then conducted through the affine transformation of all gradient volumes to the b = 0 baseline using FLIRT (FMRIB's Linear Image Registration Tool; Jenkinson, Beckmann, Behrens, Woolrich, & Smith, 2012; Jenkinson & Smith, 2001). T1‐weighted images were parcellated into discrete anatomical ROIs using the Desikan–Killiany Atlas of FreeSurfer Version 5.3 (Fischl, 2012; Fischl et al., 2002). For each anatomical structure, white and grey matter ROIs were combined into a single ROI, which resulted in a total of 87 ROIs across the brain. These T1‐weighted images were then registered into diffusion‐weighted images with six degrees of freedom using FLIRT. Table S1 presents the list of 87 ROIs.
2.5. Network reconstruction
FMRIB's Diffusion Toolbox (Behrens et al., 2003; Behrens, Berg, Jbabdi, Rushworth, & Woolrich, 2007) was used for analyzing processed diffusion‐weighted images. By using BEDPOSTX, the distribution of the diffusion parameters at each voxel was modeled through the Metropolis–Hastings Markov chain Monte Carlo method. Probabilistic tractography was then employed by PROBTRACKX, with resampling conducted 5,000 times from the distribution for each ROI. As a result, a set of passing “probabilistic” streamlines was generated for each ROI. The degree of connectivity was estimated as the number of streamlines from one ROI to another, divided by the total number of generated streamlines. The nondirectional connectivity was the average of both unidirectional connectivities. The brain network of each study subject was then reconstructed from the ROIs and estimated connectivities and represented as a graph with nodes representing ROIs and edges representing connectivities. The threshold for the 10th percentile among the total connections was applied to remove weak or false positive connections in each brain network.
2.6. Network examination
After reconstructing brain networks, a number of network properties were calculated via the MATLAB‐based Brain Connectivity Toolbox (Rubinov & Sporns, 2010), on the basis of nondirectional weighted matrices. Considering the regional differences of general topology in the brain, both global and nodal network properties were separately calculated.
As global network properties, global and local efficiency, clustering coefficient, mean betweenness centrality, small coefficient, and overall connectivity were measured to represent the topological characteristic of each brain network. In the first instance, the efficiency (Latora & Marchiori, 2001, 2003) of a network is a measure of how efficiently it transports information across itself. Global efficiency quantifies the integrity of the whole network, whereas local efficiency represents the communication between neighbors. The clustering coefficient (Watts & Strogatz, 1998) comes from transitivity and is a measure of how closely a network clusters together. The betweenness centrality (Barthélemy, 2004), the fraction of shortest paths passing through each node, is a general measure of centrality. The mean betweenness centrality, calculated as the average of all betweenness centralities for each node, is a global property representing the whole network characteristic in general. Moreover, the small coefficient (Humphries & Gurney, 2008) is a measure of “small‐worldness,” which means the characteristic of a network with a short mean path length and clusters of tightly interconnected nodes. This coefficient is calculated by dividing the ratio of the clustering coefficient by that of the path length clustering among a given network to a random network. Lastly, overall connectivity (Beineke, Oellermann, & Pippert, 2002) is the average of all connection probabilities across the network, representing the overall strength of the network itself.
As nodal properties, local efficiency, degree, and betweenness centrality were measured for each specific brain region. Local efficiency, which represents the regional efficiency of information transference by the shortest path length between neighbors, quantifies how much the network is segregated (Latora & Marchiori, 2001). The degree, which denotes the number of connections to a single given node, and betweenness centrality both represent the importance of the individual node (Freeman, 1977; Rubinov & Sporns, 2010).
2.7. Statistical analysis
For demographics, clinical characteristics, and network properties, group differences were analyzed by the Statistical Package for the Social Sciences Version 21.0 (IBM Corporation, Armonk, New York). After the normality of each variable was determined by the Kolmogorov–Smirnov test, the independent t test or the Mann–Whitney U test was applied for comparisons. A p value <.05 was considered statistically significant, and the false discovery rate method was used for correcting multiple comparisons of nodal network properties.
2.8. Machine learning model
We built several machine learning models based on the aforementioned brain network properties. The models were first built on the basis of global network properties. Other models were then built on the basis of nodal network properties, in which case each model was separately built according to the single nodal network property to prevent overcomplexity. We used various algorithms including support vector machine (SVM), multinomial naïve Bayes (NB), random forest (RF), and gradient boosting. SVM (Vapnik, 2000) is a classical supervised machine learning method that can classify different classes via the optimal “hyperplane” in a multidimensional space created with multiple trained features. It has been used in a number of schizophrenia studies (Lu et al., 2016; Pina‐Camacho et al., 2015; Xiao et al., 2017). NB classifier, which is based on a simple theorem of probability known as Bayes' rule, is one of the classic machine learning methods but still shows significant performance in classification problems (Lewis, 1998; Zhou et al., 2015). RF (Breiman, 2001) is one of the ensemble learning methods composed of numerous decision trees. It is a popular machine learning method and shows strong predictive power in classification problems (Dahinden, 2011; Lee et al., 2018). Gradient boosting (Friedman, 2002) is also an alternative ensemble learning method with decision trees, which achieved noticeable outcomes in recent Kaggle competitions (Ben Taieb & Hyndman, 2014; Hoch, 2015).
Python 3.7.1 (https://www.python.org/) on CentOS 7 (https://www.centos.org) was used for machine learning in this present study. Previously developed python modules from Scikit‐learn 0.20.1 (Pedregosa et al., 2011; http://scikit-learn.org/) were applied for model building and testing. XGBoost 0.82 (Chen & Guestrin, 2016; https://xgboost.readthedocs.io/) was additionally used as a gradient boosting algorithm. The hyperparameters of each model were optimized using a grid search method. Because the patient and healthy control sample sizes were imbalanced, the “class_weight” hyperparameter was set as “balanced” in all algorithms.
Cross‐validation was used to test the model and assess its predictive performance with stratified k‐fold (k = 10; Purushotham & Tripathy, 2011). The accuracy of each model was measured, as was the area under curve (AUC), which represents the area under the receiver operating characteristic curve, because this is considered to be a more appropriate performance measure in classification problems compared with accuracy (Bradley, 1997). Cross‐validation was independently done 1,000 times, and the mean and standard deviation of the accuracy and AUC measures were calculated. After testing the model and performance assessment, the importance of each network property within a single machine learning model was estimated. The mean and standard deviation of each network property's importance were calculated with 1,000 independent estimations. This was done only in the decision tree‐based models.
3. RESULTS
3.1. Demographics and clinical characteristics
There was no significant difference between the age and sex of the schizophrenia patients and healthy controls. The mean Full Scale Intelligence Quotient of the schizophrenia patients was 97.6 ± 15.8, which was significantly lower than that for the healthy controls (120.1 ± 9.2; p < .001). In the Wisconsin Card Sorting Test, our patients achieved lower scores than the healthy controls, although the t score of the perseverative responses did not reach statistical significance (p = .201). Table 1 presents the demographics and clinical characteristics of our current study patients in detail.
Table 1.
Demographic and clinical characteristics of the study participants
| Variable | Schizophrenia | Healthy | t or Mann–Whitney U | p value |
|---|---|---|---|---|
| Age (year) | 28.9 [6.3] | 30.0 [5.3] | 495.0 | .444 |
| Sex (male/female) | 18/30 | 9/15 | ||
| PANSS | 61.3 [14.8] | |||
| FSIQ | 97.6 [15.8] | 120.1 [9.2] | 110.5 | <.001* |
| WCST (t score) | ||||
| Total errors | 42.2 [15.4] | 53.5 [4.9] | 236.0 | .001* |
| Perseverative responses | 48.3 [16.7] | 53.9 [7.7] | 343.5 | .201 |
| Perseverative errors | 47.6 [14.7] | 54.8 [7.1] | 306.0 | .037* |
| Nonperseverative errors | 45.9 [11.9] | 52.3 [4.0] | 248.0 | .003* |
| Conceptual‐level responses | 45.5 [11.4] | 53.7 [4.5] | 4.179 | .001* |
Note: Values are presented as a mean [standard deviation]; independent t test or Mann–Whitney U test.
Abbreviations: FSIQ, Full Scale Intelligence Quotient; PANSS, Positive and Negative Syndrome Scale; WCST, Wisconsin Card Sorting Test.
Statistical significance was set at p < .05.
3.2. Comparisons of global network properties
The global and local efficiency, clustering coefficient, and overall connectivity of the network were all significantly lower in the schizophrenia group than among the healthy controls. The mean betweenness centrality and small‐coefficient measures were both higher in the schizophrenia patients, although this difference did not reach statistical significance in the case of the small coefficient (1.06 ± 4.43E − 2, 1.04 ± 5.90E − 2, Mann–Whitney U = 420.0, p = .062). Table S2 presents the group differences in the global network properties.
3.3. Comparisons of nodal network properties
Among the schizophrenia patients in our current study cohort, a number of the ROIs across the fronto–temporo–parietal brain area showed a lower nodal local efficiency compared with the healthy controls. Furthermore, a few ROIs at the cingulate cortex and diencephalon also showed a lower nodal local efficiency in these cases. For the nodal degree, however, the tendency was inconsistent. Although schizophrenia patients showed a decreased nodal degree value in the right transverse temporal gyrus, right supramarginal gyrus, and right nucleus accumbens, they also showed an increased nodal degree value in the left pars orbitalis, right lateral orbitofrontal cortex, right hippocampus, and right ventral diencephalon. Nodal betweenness centrality in the right entorhinal cortex was higher among schizophrenia patients compared with the healthy controls. However, none of these results were maintained following a false discovery rate correction. Table S3 lists all of the significant (uncorrected) group differences in the nodal network properties.
3.4. Machine learning model: Global
The SVM model showed a 58.2% mean accuracy and a mean AUC of 0.631, whereas the multinomial NB model showed a 66.9% mean accuracy and mean AUC of 0.638. The RF model on the other hand showed a 68.6% mean accuracy and a mean AUC of 0.680. Moreover, the gradient boosting (XGBoost) model showed a 66.3% mean accuracy and a mean AUC of 0.633. Among all of the tested models, the RF model achieved the highest performance (Table 2). Furthermore, among the six network properties that were evaluated, overall connectivity was revealed as the most important feature in classifying schizophrenia patients and healthy controls. Figure 1 shows the relative importance of each network property in each machine learning model.
Table 2.
Performance of the machine learning models: Global
| Model | Accuracy (%) | AUC |
|---|---|---|
| SVM | 58.2 [17.5] | 0.631 [0.202] |
| Multinomial NB | 66.9 [4.0] | 0.638 [0.233] |
| RF | 68.6 [16.0] | 0.680 [0.229] |
| XGBoost | 66.3 [14.5] | 0.633 [0.232] |
Note: Values shown are the mean [standard deviation].
Abbreviations: AUC, area under curve; NB, naïve Bayes; RF, random forest; SVM, support vector machine.
Figure 1.
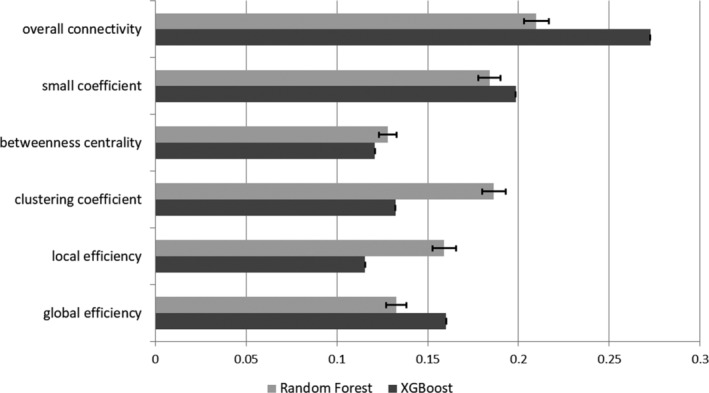
Relative importance of each network property in the machine learning model. Random forest models are denoted in grey and XGBoost models in black. Error bars indicate the standard deviation. Error bars cannot be visualized in the XGBoost models due to small standard deviations
3.5. Machine learning model: Nodal
All 12 machine learning models, four per nodal network property, showed a maximum accuracy of around 66% and an AUC of approximately 0.66. Considering both of these values, the XGBoost model based on the nodal degree showed the highest performance with a 66.3% accuracy and an AUC of 0.656. All models showed relatively weaker performances comparing with those based on global network properties. Table 3 indicates the performance of all machine learning models tested. Furthermore, for all machine learning models, the importance of each ROI was investigated. Due to the characteristics of the gradient boosting model that uses a rather smaller number of features, there were differences in the relative importance of each ROI between the RF and XGBoost models. However, there were still a few regions contributing to both RF and XGBoost models at the same time, indicating patterns of involved brain regions. Also, ROIs in right hemisphere showed more contribution to the model than ROIs in left hemisphere (right: 37; left: 16). Figure 2 shows the relative importance of each network property ROI in each machine learning model.
Table 3.
Performance of machine learning models: Nodal
| Model | Accuracy | AUC |
|---|---|---|
| I. Local efficiency | ||
| SVM | 66.0 [13.7] | 0.665 [0.239] |
| Multinomial NB | 66.9 [4.0] | 0.347 [0.240] |
| RF | 66.1 [14.9] | 0.619 [0.249] |
| XGBoost | 63.0 [11.2] | 0.540 [0.237] |
| II. Degree | ||
| SVM | 66.7 [4.4] | 0.518 [0.055] |
| Multinomial NB | 54.8 [16.7] | 0.538 [0.225] |
| RF | 56.9 [17.2] | 0.545 [0.228] |
| XGBoost | 66.3 [8.9] | 0.656 [0.219] |
| III. Betweenness centrality | ||
| SVM | 66.9 [4.0] | 0.519 [0.040] |
| Multinomial NB | 47.0 [17.4] | 0.410 [0.192] |
| RF | 52.5 [14.8] | 0.363 [0.129] |
| XGBoost | 63.5 [9.8] | 0.513 [0.223] |
Note: Values shown are a mean [standard deviation].
Abbreviations: AUC, area under curve; NB, naïve Bayes; RF, random forest; SVM, support vector machine.
Figure 2.
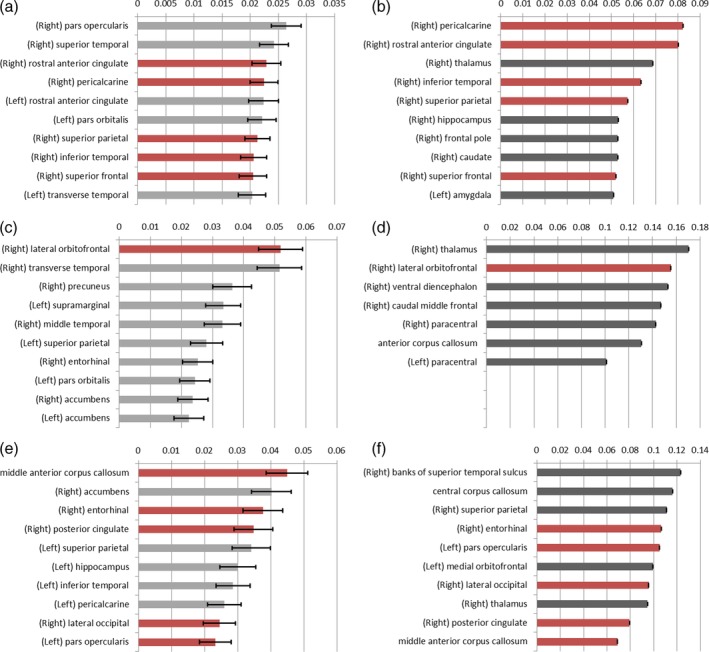
Relative importance of each network property—regions of interest (ROIs) in the machine learning model. The 10 ranking ROIs in each machine learning model are presented. Random forest models are indicated in grey. XGBoost models are denoted in black. The error bars indicate the standard deviation. Error bars could not be visualized for the XGBoost models due to small standard deviations. The ROIs contributing to both RF and XGBoost models for each nodal feature are indicated in red. (a) Local efficiency (RF), (b) local efficiency (XGBoost), (c) degree (RF), (d) degree (XGBoost), (e) betweenness centrality (RF), and (f) betweenness centrality (XGBoost)
4. DISCUSSION
Our study has revealed some significant group differences in the brain network properties between schizophrenia patients and healthy controls. We first found that the global network properties, global and local efficiency, clustering coefficient, and overall connectivity of the networks were significantly lower in the schizophrenia patients than in the healthy controls. Considering the definition of each network property (Beineke et al., 2002; Latora & Marchiori, 2001, 2003; Watts & Strogatz, 1998), these results suggested that there is an impaired transformation of information across the network of a brain with schizophrenia, which is poorly clustered and has weak overall strength. These observations were also strongly consistent with the findings of many previous studies indicating brain network alterations in schizophrenia (Cui et al., 2019; Griffa et al., 2015; Micheloyannis, 2012; Nelson et al., 2017; Shon et al., 2018; van den Heuvel et al., 2013).
In contrast, the betweenness centrality was revealed to be higher in a brain with schizophrenia than in a healthy brain. This is not consistent with the current literature (Rubinov & Bullmore, 2013; van den Heuvel et al., 2013), which has indicated that schizophrenia may be associated with a deterioration in network hub organization. According to Cheng et al. (2015), however, the mean betweenness centrality value may not properly reflect regional impairment in a brain network because only a small fraction of the nodes in a network show a high value for this parameter. It has been suggested in fact that the global properties of the brain are not sensitive enough to regional abnormalities (Tomasi & Volkow, 2014). Thus, the observed higher mean betweenness centrality in the brain networks of patients with schizophrenia in this study may be due to the increased betweenness centrality among less significant regions and decreased betweenness centrality among network hubs.
We further observed that in terms of nodal network properties, schizophrenia patients showed a lower nodal efficiency in a number of brain regions across the fronto–temporo–parietal area, cingulate cortex, and diencephalon, when compared with healthy controls. These results were consistent with the data from previous studies that indicated impaired connectivity in the frontal and temporal lobe (van den Heuvel et al., 2010), parietal lobe (Kahn, Andrews‐Hanna, Vincent, Snyder, & Buckner, 2008; Peters et al., 2016), thalamus (Anticevic et al., 2014), and cingulate (Cui et al., 2015; Wang et al., 2015). Also, schizophrenia patients showed higher nodal betweenness centrality in the right entorhinal cortex in our study.
Furthermore, we attempted to generate a disease prediction model of schizophrenia using the machine learning method, which would have significant clinical applications. We thus built a number of models based on either global or nodal network properties, all of which showed a noticeable level of performance in classifying and distinguishing schizophrenia patients and healthy controls, with encouraging accuracy and AUC scores. Although previous studies (Greenstein, Weisinger, Malley, Clasen, & Gogtay, 2012; Lee et al., 2018; Schnack et al., 2014) have reported an even higher accuracy from 70% to 80% in classifying schizophrenia, the lower accuracy we obtained in our present study may have been due to our small sample size, considering sufficient sample size is required to reach a target performance (Figueroa, Zeng‐Treitler, Kandula, & Ngo, 2012; S. Mukherjee et al., 2003; Tam, Kabbara, Yeh, & Leary, 2006). In addition, most of the previously reported models were based on features directly related to structural measures such as grey matter density (Schnack et al., 2014; D. Sun et al., 2009) or cortical thickness (Greenstein et al., 2012). The models we used in our present study were based on the features of conceptually reconstructed brain networks. Despite the large number of reports to date on the modern network analysis of the brain with schizophrenia (Micheloyannis, 2012), most have only focused on group comparisons of network properties between schizophrenia patients and healthy controls. Therefore, the possibility is noticeable that schizophrenia patients and healthy controls can actually be classified on the basis of these network properties.
By investigating the importance of each feature of each machine learning model, the overall connectivity was revealed as the most important feature in classifying schizophrenia. This was not unexpected because the disconnection of the brain has been considered to play a significant role in the underlying pathophysiology of schizophrenia (Friston, 2002). Moreover, as multiple regions were reported to show altered connectivity in brains with schizophrenia (Fitzsimmons et al., 2013; Lynall et al., 2010), the overall brain connectivity must also be altered. Of note in this regard, the global connectivity measure was previously revealed to be decreased in brains with schizophrenia (Skudlarski et al., 2010).
We observed a noticeable contributing pattern of ROIs in our machine learning models based on nodal network properties. Moreover, a number of the ROIs that were revealed to be significant in classifying schizophrenia patients and healthy controls in our current analysis were previously well‐studied brain regions among schizophrenia patients. In terms of nodal local efficiency, the rostral anterior cingulate cortex, pericalcarine cortex, superior parietal cortex, inferior temporal cortex, and superior frontal cortex were revealed as significant by our present analyses. The rostral anterior cingulate cortex, located in the frontal part of the cingulate cortex, has been considered to be the error‐checking system of brain (Kiehl, Liddle, & Hopfinger, 2000). Notably in this regard, patients with schizophrenia have been reported to show dysfunction of the rostral anterior cingulate cortex during error processing (Laurens, Ngan, Bates, Kiehl, & Liddle, 2003; Polli et al., 2008) and even a decreased volume of the rostral anterior cingulate cortex (Baiano et al., 2007). Impaired connectivity in the parietal lobe (Kahn et al., 2008; Peters et al., 2016) and frontal lobe (van den Heuvel et al., 2010) have also been described previously. Furthermore, the inferior temporal gyrus, which is known to be involved in visual processes (Papadelis et al., 2016; Zhang, Mlynaryk, Ahmed, Japee, & Ungerleider, 2018), has shown significant anatomical connectivity abnormalities in schizophrenia patients (Jeong, Wible, Hashimoto, & Kubicki, 2009).
With respect to the nodal degree, the lateral orbitofrontal cortex was also revealed by our analysis to be significant in classifying schizophrenia patients and healthy controls. The lateral orbitofrontal cortex, one of the prefrontal cortex regions, is known to be involved in the decision‐making process (Domenech & Koechlin, 2015). According to a previous study, the sulcogyral pattern of orbitofrontal cortex is altered in schizophrenia patients (Isomura et al., 2017), and even the grey matter volume is decreased (Nakamura et al., 2008). Lastly, in terms of nodal betweenness centrality, the middle anterior corpus callosum, entorhinal cortex, posterior cingulate cortex, lateral occipital cortex, and pars opercularis were revealed by our current data to be important regions in classifying schizophrenia patients and healthy controls. Most of these regions have shown anatomical or functional brain alterations in previous studies of schizophrenia. A significant reduction of the corpus callosum in the brain with schizophrenia has also been reported (del Re et al., 2016), and reduced fractional anisotropy was revealed in a prior meta‐analysis study (Zhuo, Liu, Wang, Tian, & Tang, 2016). In another prior study of the posterior cingulated cortex, although no brain connectivity was found to be altered, alterations of muscarinic and GABA receptors were observed among schizophrenia patients (Newell, Zavitsanou, Jew, & Huang, 2007). Postmortem studies have revealed a limbic pathology in schizophrenia patients, represented by a volume reduction of the entorhinal cortex (Falkai, Bogerts, & Rozumek, 1988). Another study similarly reported cytoarchitectural abnormalities in the entorhinal cortex of the brain with schizophrenia (Arnold, Hyman, Vanhoesen, & Damasio, 1991). The lateral occipital complex, which is known to process visual perception, has also shown impairment in the brain with schizophrenia, as reflected by an altered connectivity measured using functional magnetic resonance imaging (Harvey et al., 2011).
Interestingly, it has been revealed that contributing ROIs in the machine learning models were located more commonly in the right hemisphere of the brain. Because it is known that the normal brain asymmetry may be attenuated in schizophrenia (Ribolsi, Daskalakis, Siracusano, & Koch, 2014), an asymmetrical hemispheric contribution could be expected in the machine learning model. Notably in this regard, alteration of the hemispheric asymmetry has long been recognized in the brain with schizophrenia (Newlin, Carpenter, & Golden, 1981) and was recently advocated also in a number of brain imaging studies (Joo et al., 2018; Okada et al., 2016; Y. Sun, Chen, Collinson, Bezerianos, & Sim, 2015). Although the current literature generally supports mainly left hemisphere anomalies in schizophrenia (Ribolsi et al., 2009), there have been a number of studies suggesting a relationship between the right cerebral hemisphere and psychiatric disorders (Cutting, 1990), including schizophrenia (Cutting, 1994).
Our present study had some limitations of note. In the first instance, the network properties chosen for our machine learning models were intercorrelated. There are various different network properties representing the characteristics of each network. Some attributes are correlated, and some even can be derived from others. Because machine learning models such as SVM can be affected significantly by feature selection (Nguyen & de la Torre, 2010), overall model performance and feature importance could be altered. Hence, we attempted to choose the most frequently studied network properties from previous studies (Alexander‐Bloch et al., 2010; Lynall et al., 2010; Zalesky et al., 2011). In addition, the RF and Gradient Boosting models, which were based on a decision tree algorithm, were not significantly affected by correlated features because the decision tree discarded redundant features (Hall, 1999). Another limitation of our present analysis was that a relatively small number of study participants was included. A small sample size makes it hard to correctly evaluate the model in machine learning (Raudys & Jain, 1991). It can also cause a large deviation in prediction (Lemm, Blankertz, Dickhaus, & Muller, 2011). In addition, it is known that a classification model based on a small sample size is more unstable, particularly because of the overfitting problem (Arbabshirani, Plis, Sui, & Calhoun, 2017). We thus used a cross‐validation method to minimize overfitting and also inspected the accuracy and AUC in both the training and test sets among each fold. The scores from the training and test sets showed similar values in every fold, which suggested the absence of overfitting. However, considering the statistical power issues with our small patient population, further studies with larger sample sizes are recommended.
In conclusion, we have here found significant differences in the network properties of a brain with schizophrenia compared with a healthy brain and also found that schizophrenia patients and healthy controls can be properly classified by these properties based on machine learning models. Because there have already been a number of studies on machine learning and network analysis in schizophrenia, it is meaningful to evaluate the possibility of integrating both methods. Further investigations with large sample sizes and extensive network properties are warranted.
CONFLICT OF INTEREST
The authors declare no conflicts of interest in relation to this study.
Supporting information
Table S1 List of 87 Regions of Interest (ROIs).
Table S2. Comparison of global network properties.
Table S3. Comparison of nodal network properties.
ACKNOWLEDGMENT
This work was supported by the National Research Foundation of Korea (NRF‐2012R1A1A1006514 and NRF‐2017R1D1A1B03032707 to Jungsun Lee).
Jo YT, Joo SW, Shon S‐H, Kim H, Kim Y, Lee J. Diagnosing schizophrenia with network analysis and a machine learning method. Int J Methods Psychiatr Res. 2020;29:e1818 10.1002/mpr.1818
Funding information National Research Foundation of Korea, Grant/Award Numbers: NRF‐2012R1A1A1006514, NRF‐2017R1D1A1B03032707
REFERENCES
- Alexander‐Bloch, A. F. , Gogtay, N. , Meunier, D. , Birn, R. , Clasen, L. , Lalonde, F. , … Bullmore, E. T. (2010). Disrupted modularity and local connectivity of brain functional networks in childhood‐onset schizophrenia. Frontiers in Systems Neuroscience, 4(147), 147 10.3389/fnsys.2010.00147 [DOI] [PMC free article] [PubMed] [Google Scholar]
- American Psychiatric Association . (2011). Diagnostic and statistical manual of mental disorders, text revision (DSM‐IV‐TR®) (4th ed.). Arlington: American Psychiatric Association Publishing. [Google Scholar]
- Anticevic, A. , Cole, M. W. , Repovs, G. , Murray, J. D. , Brumbaugh, M. S. , Winkler, A. M. , … Glahn, D. C. (2014). Characterizing thalamo‐cortical disturbances in schizophrenia and bipolar illness. Cerebral Cortex, 24(12), 3116–3130. 10.1093/cercor/bht165 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arbabshirani, M. R. , Plis, S. , Sui, J. , & Calhoun, V. D. (2017). Single subject prediction of brain disorders in neuroimaging: Promises and pitfalls. NeuroImage, 145, 137–165. 10.1016/j.neuroimage.2016.02.079 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arnold, S. E. , Hyman, B. T. , Vanhoesen, G. W. , & Damasio, A. R. (1991). Some cytoarchitectural abnormalities of the entorhinal cortex in schizophrenia. Archives of General Psychiatry, 48(7), 625–632. 10.1001/archpsyc.1991.01810310043008 [DOI] [PubMed] [Google Scholar]
- Baiano, M. , David, A. , Versace, A. , Churchill, R. , Balestrieri, M. , & Brambilla, P. (2007). Anterior cingulate volumes in schizophrenia: A systematic review and a meta‐analysis of MRI studies. Schizophrenia Research, 93(1–3), 1–12. 10.1016/j.schres.2007.02.012 [DOI] [PubMed] [Google Scholar]
- Barthélemy, M. (2004). Betweenness centrality in large complex networks. European Physical Journal B, 38(2), 163–168. 10.1140/epjb/e2004-00111-4 [DOI] [Google Scholar]
- Behrens, T. E. , Berg, H. J. , Jbabdi, S. , Rushworth, M. F. , & Woolrich, M. W. (2007). Probabilistic diffusion tractography with multiple fibre orientations: What can we gain? NeuroImage, 34(1), 144–155. 10.1016/j.neuroimage.2006.09.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Behrens, T. E. , Woolrich, M. W. , Jenkinson, M. , Johansen‐Berg, H. , Nunes, R. G. , Clare, S. , … Smith, S. M. (2003). Characterization and propagation of uncertainty in diffusion‐weighted MR imaging. Magnetic Resonance in Medicine, 50(5), 1077–1088. 10.1002/mrm.10609 [DOI] [PubMed] [Google Scholar]
- Beineke, L. W. , Oellermann, O. R. , & Pippert, R. E. (2002). The average connectivity of a graph. Discrete Mathematics, 252(1–3), 31–45. 10.1016/S0012-365x(01)00180-7 [DOI] [Google Scholar]
- Ben Taieb, S. , & Hyndman, R. J. (2014). A gradient boosting approach to the Kaggle load forecasting competition. International Journal of Forecasting, 30(2), 382–394. 10.1016/j.ijforecast.2013.07.005 [DOI] [Google Scholar]
- Bogerts, B. (1993). Recent advances in the neuropathology of schizophrenia. Schizophrenia Bulletin, 19(2), 431–445. 10.1093/schbul/19.2.431 [DOI] [PubMed] [Google Scholar]
- Bradley, A. P. (1997). The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recognition, 30(7), 1145–1159. 10.1016/S0031-3203(96)00142-2 [DOI] [Google Scholar]
- Breiman, L. (2001). Random forests. Machine Learning, 45(1), 5–32. 10.1023/A:1010933404324 [DOI] [Google Scholar]
- Bullmore, E. , & Sporns, O. (2009). Complex brain networks: Graph theoretical analysis of structural and functional systems. Nature Reviews Neuroscience, 10(3), 186–198. 10.1038/nrn2575 [DOI] [PubMed] [Google Scholar]
- Chen, T. , & Guestrin, C. (2016). XGBoost: A scalable tree boosting system. Paper Presented at the KDD 2016: Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA. [Google Scholar]
- Cheng, H. , Newman, S. , Goni, J. , Kent, J. S. , Howell, J. , Bolbecker, A. , … Hetrick, W. P. (2015). Nodal centrality of functional network in the differentiation of schizophrenia. Schizophrenia Research, 168(1–2), 345–352. 10.1016/j.schres.2015.08.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cui, L.‐B. , Liu, J. , Wang, L.‐X. , Li, C. , Xi, Y.‐B. , Guo, F. , … Lu, H. (2015). Anterior cingulate cortex‐related connectivity in first‐episode schizophrenia: A spectral dynamic causal modeling study with functional magnetic resonance imaging. Frontiers in Human Neuroscience, 9, 589 10.3389/fnhum.2015.00589 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cui, L.‐B. , Wei, Y. , Xi, Y.‐B. , Griffa, A. , De Lange, S. C. , Kahn, R. S. , … Van den Heuvel, M. P. (2019). Connectome‐based patterns of first‐episode medication‐naïve patients with schizophrenia. Schizophrenia Bulletin, 45(6), 1291–1299. 10.1093/schbul/sbz014%J [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cutting, J. C. (1990). The right cerebral hemisphere and psychiatric disorders. New York: Oxford University Press. [Google Scholar]
- Cutting, J. C. (1994). Evidence for right hemisphere dysfunction in schizophrenia In David A. S., Cutting J. C., & Lawrence Erlbaum Associates (Eds.), The neuropsychology of schizophrenia (pp. 231–242). Hove: Lawrence Erlbaum Associates. [Google Scholar]
- Dahinden, C. (2011). An improved random forests approach with application to the performance prediction challenge datasets In Guyon I., Cawley G., & Dror G. (Eds.), Hands‐on pattern recognition: Challenges in machine learning (pp. 223–230). Brookline: Microtome Publishing. [Google Scholar]
- Deo, N. (2017). Graph theory with applications to engineering and computer science. Mineola: Courier Dover Publications. [Google Scholar]
- Dietsche, B. , Kircher, T. , & Falkenberg, I. (2017). Structural brain changes in schizophrenia at different stages of the illness: A selective review of longitudinal magnetic resonance imaging studies. Australian & New Zealand Journal of Psychiatry, 51(5), 500–508. 10.1177/0004867417699473 [DOI] [PubMed] [Google Scholar]
- Domenech, P. , & Koechlin, E. (2015). Executive control and decision‐making in the prefrontal cortex. Current Opinion in Behavioral Sciences, 1, 101–106. 10.1016/j.cobeha.2014.10.007 [DOI] [Google Scholar]
- van Erp, T. G. M. , Walton, E. , Hibar, D. P. , Schmaal, L. , Jiang, W. , Glahn, D. C. , … Turner, J. A. (2018). Cortical brain abnormalities in 4474 individuals with schizophrenia and 5098 control subjects via the Enhancing Neuro Imaging Genetics Through Meta Analysis (ENIGMA) Consortium. Biological Psychiatry, 84(9), 644–654. 10.1016/j.biopsych.2018.04.023 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Falkai, P. , Bogerts, B. , & Rozumek, M. (1988). Limbic pathology in schizophrenia: The entorhinal region—A morphometric study. Biological Psychiatry, 24(5), 515–521. 10.1016/0006-3223(88)90162-X [DOI] [PubMed] [Google Scholar]
- Fedorov, A. , Beichel, R. , Kalpathy‐Cramer, J. , Finet, J. , Fillion‐Robin, J. C. , Pujol, S. , … Kikinis, R. (2012). 3D Slicer as an image computing platform for the Quantitative Imaging Network. Magnetic Resonance Imaging, 30(9), 1323–1341. 10.1016/j.mri.2012.05.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Figueroa, R. L. , Zeng‐Treitler, Q. , Kandula, S. , & Ngo, L. H. (2012). Predicting sample size required for classification performance. BMC Medical Informatics and Decision Making, 12, 8 10.1186/1472-6947-12-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl, B. (2012). FreeSurfer. NeuroImage, 62(2), 774–781. 10.1016/j.neuroimage.2012.01.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl, B. , Salat, D. H. , Busa, E. , Albert, M. , Dieterich, M. , Haselgrove, C. , … Dale, A. M. (2002). Whole brain segmentation: Automated labeling of neuroanatomical structures in the human brain. Neuron, 33(3), 341–355. 10.1016/S0896-6273(02)00569-X [DOI] [PubMed] [Google Scholar]
- Fitzsimmons, J. , Kubicki, M. , & Shenton, M. E. (2013). Review of functional and anatomical brain connectivity findings in schizophrenia. Current Opinion in Psychiatry, 26(2), 172–187. 10.1097/YCO.0b013e32835d9e6a [DOI] [PubMed] [Google Scholar]
- Fornito, A. , & Bullmore, E. T. (2015). Reconciling abnormalities of brain network structure and function in schizophrenia. Current Opinion in Neurobiology, 30, 44–50. 10.1016/j.conb.2014.08.006 [DOI] [PubMed] [Google Scholar]
- Freeman, L. C. (1977). A set of measures of centrality based on betweenness. Sociometry, 40(1), 35–41. 10.2307/3033543 [DOI] [Google Scholar]
- Friedman, J. H. (2002). Stochastic gradient boosting. Computational Statistics & Data Analysis, 38(4), 367–378. 10.1016/S0167-9473(01)00065-2 [DOI] [Google Scholar]
- Friston, K. J. (2002). Dysfunctional connectivity in schizophrenia. World Psychiatry, 1(2), 66–71. [PMC free article] [PubMed] [Google Scholar]
- Greenstein, D. , Weisinger, B. , Malley, J. , Clasen, L. , & Gogtay, N. (2012). Using multivariate machine learning methods and structural MRI to classify childhood onset schizophrenia and healthy controls. Frontiers in Psychiatry, 3, 53 10.3389/fpsyt.2012.00053 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Griffa, A. , Baumann, P. S. , Ferrari, C. , Do, K. Q. , Conus, P. , Thiran, J. P. , & Hagmann, P. (2015). Characterizing the connectome in schizophrenia with diffusion spectrum imaging. Human Brain Mapping, 36(1), 354–366. 10.1002/hbm.22633 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haijma, S. V. , Van Haren, N. , Cahn, W. , Koolschijn, P. C. , Hulshoff Pol, H. E. , & Kahn, R. S. (2013). Brain volumes in schizophrenia: A meta‐analysis in over 18 000 subjects. Schizophrenia Bulletin, 39(5), 1129–1138. 10.1093/schbul/sbs118 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hall, M. A. (1999). Correlation‐based feature selection for machine learning [Doctor dissertation]. The University of Waikato, Hamilton, New Zealand.
- Harvey, P. O. , Lee, J. , Cohen, M. S. , Engel, S. A. , Glahn, D. C. , Nuechterlein, K. H. , … Green, M. F. (2011). Altered dynamic coupling of lateral occipital complex during visual perception in schizophrenia. NeuroImage, 55(3), 1219–1226. 10.1016/j.neuroimage.2010.12.045 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heaton, R. K. , Chelune, G. J. , Talley, J. L. , Kay, G. G. , & Curtiss, G. (1993). Wisconsin card sorting test (Vol. 4). Odessa Psychological Assessment Resources (PAR).
- van den Heuvel, M. P. , Mandl, R. C. , Stam, C. J. , Kahn, R. S. , & Hulshoff Pol, H. E. (2010). Aberrant frontal and temporal complex network structure in schizophrenia: A graph theoretical analysis. Journal of Neuroscience, 30(47), 15915–15926. 10.1523/JNEUROSCI.2874-10.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- van den Heuvel, M. P. , Sporns, O. , Collin, G. , Scheewe, T. , Mandl, R. C. , Cahn, W. , … Kahn, R. S. (2013). Abnormal rich club organization and functional brain dynamics in schizophrenia. JAMA Psychiatry, 70(8), 783–792. 10.1001/jamapsychiatry.2013.1328 [DOI] [PubMed] [Google Scholar]
- Hoch, T. (2015). An ensemble learning approach for the Kaggle taxi travel time prediction challenge. Paper Presented at the DC@PKDD/ECML 2015: Proceedings of the ECML/PKDD 2015 Discovery Challenges, Porto, Portugal. http://ceur-ws.org/Vol-1526/paper22.pdf [Google Scholar]
- Humphries, M. D. , & Gurney, K. (2008). Network ‘small‐world‐ness’: A quantitative method for determining canonical network equivalence. PLoS One, 3(4), e0002051 10.1371/journal.pone.0002051 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Isomura, S. , Hashimoto, R. , Nakamura, M. , Hirano, Y. , Yamashita, F. , Jimbo, S. , … Onitsuka, T. (2017). Altered sulcogyral patterns of orbitofrontal cortex in a large cohort of patients with schizophrenia. NPJ Schizophrenia, 3(1), 3 10.1038/s41537-016-0008-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jalili, M. , & Knyazeva, M. G. (2011). EEG‐based functional networks in schizophrenia. Computers in Biology and Medicine, 41(12), 1178–1186. 10.1016/j.compbiomed.2011.05.004 [DOI] [PubMed] [Google Scholar]
- Jenkinson, M. , Beckmann, C. F. , Behrens, T. E. , Woolrich, M. W. , & Smith, S. M. (2012). FSL. NeuroImage, 62(2), 782–790. 10.1016/j.neuroimage.2011.09.015 [DOI] [PubMed] [Google Scholar]
- Jenkinson, M. , & Smith, S. (2001). A global optimisation method for robust affine registration of brain images. Medical Image Analysis, 5(2), 143–156. [DOI] [PubMed] [Google Scholar]
- Jeong, B. , Wible, C. G. , Hashimoto, R.‐I. , & Kubicki, M. (2009). Functional and anatomical connectivity abnormalities in left inferior frontal gyrus in schizophrenia. Human Brain Mapping, 30(12), 4138–4151. 10.1002/hbm.20835 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joo, S. W. , Chon, M. W. , Rathi, Y. , Shenton, M. E. , Kubicki, M. , & Lee, J. (2018). Abnormal asymmetry of white matter tracts between ventral posterior cingulate cortex and middle temporal gyrus in recent‐onset schizophrenia. Schizophrenia Research, 192, 159–166. 10.1016/j.schres.2017.05.008 [DOI] [PubMed] [Google Scholar]
- Kahn, I. , Andrews‐Hanna, J. R. , Vincent, J. L. , Snyder, A. Z. , & Buckner, R. L. (2008). Distinct cortical anatomy linked to subregions of the medial temporal lobe revealed by intrinsic functional connectivity. Journal of Neurophysiology, 100(1), 129–139. 10.1152/jn.00077.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiehl, K. A. , Liddle, P. F. , & Hopfinger, J. B. (2000). Error processing and the rostral anterior cingulate: An event‐related fMRI study. Psychophysiology, 37(2), 216–223. 10.1111/1469-8986.3720216 [DOI] [PubMed] [Google Scholar]
- Latora, V. , & Marchiori, M. (2001). Efficient behavior of small‐world networks. Physical Review Letters, 87(19), 198701 10.1103/PhysRevLett.87.198701 [DOI] [PubMed] [Google Scholar]
- Latora, V. , & Marchiori, M. (2003). Economic small‐world behavior in weighted networks. European Physical Journal B, 32(2), 249–263. 10.1140/epjb/e2003-00095-5 [DOI] [Google Scholar]
- Laughlin, S. B. , & Sejnowski, T. J. (2003). Communication in neuronal networks. Science, 301(5641), 1870–1874. 10.1126/science.1089662 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laurens, K. R. , Ngan, E. T. , Bates, A. T. , Kiehl, K. A. , & Liddle, P. F. (2003). Rostral anterior cingulate cortex dysfunction during error processing in schizophrenia. Brain, 126(Pt 3), 610–622. 10.1093/brain/awg056 [DOI] [PubMed] [Google Scholar]
- Lee, J. , Chon, M. W. , Kim, H. , Rathi, Y. , Bouix, S. , Shenton, M. E. , & Kubicki, M. (2018). Diagnostic value of structural and diffusion imaging measures in schizophrenia. NeuroImage: Clinical, 18, 467–474. 10.1016/j.nicl.2018.02.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lemm, S. , Blankertz, B. , Dickhaus, T. , & Muller, K. R. (2011). Introduction to machine learning for brain imaging. NeuroImage, 56(2), 387–399. 10.1016/j.neuroimage.2010.11.004 [DOI] [PubMed] [Google Scholar]
- Lewis, D. D. (1998). Naive (Bayes) at forty: The independence assumption in information retrieval. Paper Presented at the ECML 1998: Machine Learning: ECML‐98, Chemnitz, Germany. [Google Scholar]
- Lord, L. D. , Allen, P. , Expert, P. , Howes, O. , Lambiotte, R. , McGuire, P. , … Turkheimer, F. E. (2011). Characterization of the anterior cingulate's role in the at‐risk mental state using graph theory. NeuroImage, 56(3), 1531–1539. 10.1016/j.neuroimage.2011.02.012 [DOI] [PubMed] [Google Scholar]
- Lu, X. , Yang, Y. , Wu, F. , Gao, M. , Xu, Y. , Zhang, Y. , … Wu, K. (2016). Discriminative analysis of schizophrenia using support vector machine and recursive feature elimination on structural MRI images. Medicine, 95(30), e3973 10.1097/MD.0000000000003973 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynall, M. E. , Bassett, D. S. , Kerwin, R. , McKenna, P. J. , Kitzbichler, M. , Muller, U. , & Bullmore, E. (2010). Functional connectivity and brain networks in schizophrenia. Journal of Neuroscience, 30(28), 9477–9487. 10.1523/jneurosci.0333-10.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Micheloyannis, S. (2012). Graph‐based network analysis in schizophrenia. World Journal of Psychiatry, 2(1), 1–12. 10.5498/wjp.v2.i1.1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mohri, M. , Rostamizadeh, A. , & Talwalkar, A. (2018). Foundations of machine learning. Cambridge: MIT Press. [Google Scholar]
- Mukherjee, P. , Chung, S. W. , Berman, J. I. , Hess, C. P. , & Henry, R. G. (2008). Diffusion tensor MR imaging and fiber tractography: Technical considerations. American Journal of Neuroradiology, 29(5), 843–852. 10.3174/ajnr.A1052 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mukherjee, S. , Tamayo, P. , Rogers, S. , Rifkin, R. , Engle, A. , Campbell, C. , … Mesirov, J. P. (2003). Estimating dataset size requirements for classifying DNA microarray data. Journal of Computational Biology, 10(2), 119–142. 10.1089/106652703321825928 [DOI] [PubMed] [Google Scholar]
- Nakamura, M. , Nestor, P. G. , Levitt, J. J. , Cohen, A. S. , Kawashima, T. , Shenton, M. E. , & McCarley, R. W. (2008). Orbitofrontal volume deficit in schizophrenia and thought disorder. Brain, 131(Pt 1), 180–195. 10.1093/brain/awm265 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson, B. G. , Bassett, D. S. , Camchong, J. , Bullmore, E. T. , & Lim, K. O. (2017). Comparison of large‐scale human brain functional and anatomical networks in schizophrenia. NeuroImage: Clinical, 15, 439–448. 10.1016/j.nicl.2017.05.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newell, K. A. , Zavitsanou, K. , Jew, S. K. , & Huang, X. F. (2007). Alterations of muscarinic and GABA receptor binding in the posterior cingulate cortex in schizophrenia. Progress in Neuro‐Psychopharmacology & Biological Psychiatry, 31(1), 225–233. 10.1016/j.pnpbp.2006.07.004 [DOI] [PubMed] [Google Scholar]
- Newlin, D. B. , Carpenter, B. , & Golden, C. J. (1981). Hemispheric asymmetries in schizophrenia. Biological Psychiatry, 16(6), 561–582. [PubMed] [Google Scholar]
- Nguyen, M. H. , & de la Torre, F. (2010). Optimal feature selection for support vector machines. Pattern Recognition, 43(3), 584–591. 10.1016/j.patcog.2009.09.003 [DOI] [Google Scholar]
- Okada, N. , Fukunaga, M. , Yamashita, F. , Koshiyama, D. , Yamamori, H. , Ohi, K. , … Hashimoto, R. (2016). Abnormal asymmetries in subcortical brain volume in schizophrenia. Molecular Psychiatry, 21(10), 1460–1466. 10.1038/mp.2015.209 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Papadelis, C. , Arfeller, C. , Erla, S. , Nollo, G. , Cattaneo, L. , & Braun, C. (2016). Inferior frontal gyrus links visual and motor cortices during a visuomotor precision grip force task. Brain Research, 1650, 252–266. 10.1016/j.brainres.2016.09.011 [DOI] [PubMed] [Google Scholar]
- Pedregosa, F. , Varoquaux, G. , Gramfort, A. , Michel, V. , Thirion, B. , Grisel, O. , … Duchesnay, E. (2011). Scikit‐learn: Machine learning in Python. Journal of Machine Learning Research, 12(Oct), 2825–2830. [Google Scholar]
- Peters, H. , Shao, J. , Scherr, M. , Schwerthöffer, D. , Zimmer, C. , Förstl, H. , … Sorg, C. (2016). More consistently altered connectivity patterns for cerebellum and medial temporal lobes than for amygdala and striatum in schizophrenia. Frontiers in Human Neuroscience, 10, 55 10.3389/fnhum.2016.00055 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pina‐Camacho, L. , Garcia‐Prieto, J. , Parellada, M. , Castro‐Fornieles, J. , Gonzalez‐Pinto, A. M. , Bombin, I. , … Arango, C. (2015). Predictors of schizophrenia spectrum disorders in early‐onset first episodes of psychosis: A support vector machine model. European Child & Adolescent Psychiatry, 24(4), 427–440. 10.1007/s00787-014-0593-0 [DOI] [PubMed] [Google Scholar]
- Polli, F. E. , Barton, J. J. , Thakkar, K. N. , Greve, D. N. , Goff, D. C. , Rauch, S. L. , & Manoach, D. S. (2008). Reduced error‐related activation in two anterior cingulate circuits is related to impaired performance in schizophrenia. Brain, 131(Pt 4), 971–986. 10.1093/brain/awm307 [DOI] [PubMed] [Google Scholar]
- Purushotham, S. , & Tripathy, B. (2011). Evaluation of classifier models using stratified tenfold cross validation techniques. Paper Presented at the ObCom 2011: Global Trends in Information Systems and Software Applications, Vellore, India. [Google Scholar]
- Raudys, S. J. , & Jain, A. K. (1991). Small sample size effects in statistical pattern recognition: Recommendations for practitioners. IEEE Transactions on Pattern Analysis and Machine Intelligence, 13(3), 252–264. 10.1109/34.75512 [DOI] [Google Scholar]
- del Re, E. C. , Konishi, J. , Bouix, S. , Blokland, G. A. M. , Mesholam‐Gately, R. I. , Goldstein, J. , … McCarley, R. W. (2016). Enlarged lateral ventricles inversely correlate with reduced corpus callosum central volume in first episode schizophrenia: Association with functional measures. Brain Imaging and Behavior, 10(4), 1264–1273. 10.1007/s11682-015-9493-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ribolsi, M. , Daskalakis, Z. J. , Siracusano, A. , & Koch, G. (2014). Abnormal asymmetry of brain connectivity in schizophrenia. Frontiers in Human Neuroscience, 8, 1010 10.3389/fnhum.2014.01010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ribolsi, M. , Koch, G. , Magni, V. , Di Lorenzo, G. , Rubino, I. A. , Siracusano, A. , & Centonze, D. (2009). Abnormal brain lateralization and connectivity in schizophrenia. Reviews in the Neurosciences, 20(1), 61–70. 10.1515/REVNEURO.2009.20.1.61 [DOI] [PubMed] [Google Scholar]
- Rossler, W. , Salize, H. J. , van Os, J. , & Riecher‐Rossler, A. (2005). Size of burden of schizophrenia and psychotic disorders. European Neuropsychopharmacology, 15(4), 399–409. 10.1016/j.euroneuro.2005.04.009 [DOI] [PubMed] [Google Scholar]
- Rozycki, M. , Satterthwaite, T. D. , Koutsouleris, N. , Erus, G. , Doshi, J. , Wolf, D. H. , … Davatzikos, C. (2017). Multisite machine learning analysis provides a robust structural imaging signature of schizophrenia detectable across diverse patient populations and within individuals. Schizophrenia Bulletin, 44(5), 1035–1044. 10.1093/schbul/sbx137 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubinov, M. , & Bullmore, E. (2013). Schizophrenia and abnormal brain network hubs. Dialogues in Clinical Neuroscience, 15(3), 339–349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubinov, M. , & Sporns, O. (2010). Complex network measures of brain connectivity: Uses and interpretations. NeuroImage, 52(3), 1059–1069. 10.1016/j.neuroimage.2009.10.003 [DOI] [PubMed] [Google Scholar]
- Schnack, H. G. , Nieuwenhuis, M. , van Haren, N. E. , Abramovic, L. , Scheewe, T. W. , Brouwer, R. M. , … Kahn, R. S. (2014). Can structural MRI aid in clinical classification? A machine learning study in two independent samples of patients with schizophrenia, bipolar disorder and healthy subjects. NeuroImage, 84, 299–306. 10.1016/j.neuroimage.2013.08.053 [DOI] [PubMed] [Google Scholar]
- Shepherd, A. M. , Laurens, K. R. , Matheson, S. L. , Carr, V. J. , & Green, M. J. (2012). Systematic meta‐review and quality assessment of the structural brain alterations in schizophrenia. Neuroscience & Biobehavioral Reviews, 36(4), 1342–1356. 10.1016/j.neubiorev.2011.12.015 [DOI] [PubMed] [Google Scholar]
- Shon, S. H. , Yoon, W. , Kim, H. , Joo, S. W. , Kim, Y. , & Lee, J. (2018). Deterioration in global organization of structural brain networks in schizophrenia: A diffusion MRI tractography study. Frontiers in Psychiatry, 9(272), 272 10.3389/fpsyt.2018.00272 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skudlarski, P. , Jagannathan, K. , Anderson, K. , Stevens, M. C. , Calhoun, V. D. , Skudlarska, B. A. , & Pearlson, G. (2010). Brain connectivity is not only lower but different in schizophrenia: A combined anatomical and functional approach. Biological Psychiatry, 68(1), 61–69. 10.1016/j.biopsych.2010.03.035 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stam, C. J. (2004). Functional connectivity patterns of human magnetoencephalographic recordings: A ‘small‐world’ network? Neuroscience Letters, 355(1–2), 25–28. [DOI] [PubMed] [Google Scholar]
- Sun, D. , van Erp, T. G. M. , Thompson, P. M. , Bearden, C. E. , Daley, M. , Kushan, L. , … Cannon, T. D. (2009). Elucidating a magnetic resonance imaging‐based neuroanatomic biomarker for psychosis: Classification analysis using probabilistic brain atlas and machine learning algorithms. Biological Psychiatry, 66(11), 1055–1060. 10.1016/j.biopsych.2009.07.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun, Y. , Chen, Y. , Collinson, S. L. , Bezerianos, A. , & Sim, K. (2015). Reduced hemispheric asymmetry of brain anatomical networks is linked to schizophrenia: A connectome study. Cerebral Cortex, 27(1), 602–615. [DOI] [PubMed] [Google Scholar]
- Tam, V. H. , Kabbara, S. , Yeh, R. F. , & Leary, R. H. (2006). Impact of sample size on the performance of multiple‐model pharmacokinetic simulations. Antimicrobial Agents and Chemotherapy, 50(11), 3950–3952. 10.1128/AAC.00337-06 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tomasi, D. , & Volkow, N. D. (2014). Mapping small‐world properties through development in the human brain: Disruption in schizophrenia. PLoS One, 9(4), e96176 10.1371/journal.pone.0096176 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vapnik, V. (2000). The nature of statistical learning theory (2nd ed.). New York: Springer. [Google Scholar]
- Wang, D. , Zhou, Y. , Zhuo, C. , Qin, W. , Zhu, J. , Liu, H. , … Yu, C. (2015). Altered functional connectivity of the cingulate subregions in schizophrenia. Translational Psychiatry, 5(6), e575–e575. 10.1038/tp.2015.69 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watts, D. J. , & Strogatz, S. H. (1998). Collective dynamics of ‘small‐world’ networks. Nature, 393(6684), 440–442. 10.1038/30918 [DOI] [PubMed] [Google Scholar]
- Winterburn, J. L. , Voineskos, A. N. , Devenyi, G. A. , Plitman, E. , Fuente‐Sandoval, C. , Bhagwat, N. , … Chakravarty, M. M. (2017). Can we accurately classify schizophrenia patients from healthy controls using magnetic resonance imaging and machine learning? A multi‐method and multi‐dataset study. Schizophrenia Research, 214, 3–10. 10.1016/j.schres.2017.11.038 [DOI] [PubMed] [Google Scholar]
- Xiao, Y. , Yan, Z. , Zhao, Y. , Tao, B. , Sun, H. , Li, F. , … Lui, S. (2017). Support vector machine‐based classification of first episode drug‐naïve schizophrenia patients and healthy controls using structural MRI. Schizophrenia Research, 214, 11–17. 10.1016/j.schres.2017.11.037 [DOI] [PubMed] [Google Scholar]
- Yi, J. S. , Ahn, Y. M. , Shin, H. K. , An, S. K. , Joo, Y. H. , Kim, S. H. , … Lee, J. Y. (2001). Reliability and validity of the Korean version of the Positive and Negative Syndrome Scale. Journal of Korean Neuropsychiatric Association, 40(6), 1090–1105. [Google Scholar]
- Zalesky, A. , Fornito, A. , Seal, M. L. , Cocchi, L. , Westin, C. F. , Bullmore, E. T. , … Pantelis, C. (2011). Disrupted axonal fiber connectivity in schizophrenia. Biological Psychiatry, 69(1), 80–89. 10.1016/j.biopsych.2010.08.022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, X. , Mlynaryk, N. , Ahmed, S. , Japee, S. , & Ungerleider, L. G. (2018). The role of inferior frontal junction in controlling the spatially global effect of feature‐based attention in human visual areas. PLoS Biology, 16(6), e2005399 10.1371/journal.pbio.2005399 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou, X. , Wang, S. , Xu, W. , Ji, G. , Phillips, P. , Sun, P. , & Zhang, Y. (2015). Detection of pathological brain in MRI scanning based on wavelet‐entropy and naive Bayes classifier In International conference on bioinformatics and biomedical engineering (pp. 201–209). Cham: Springer. [Google Scholar]
- Zhuo, C. , Liu, M. , Wang, L. , Tian, H. , & Tang, J. (2016). Diffusion tensor MR imaging evaluation of callosal abnormalities in schizophrenia: A meta‐analysis. PLoS One, 11(8), e0161406 10.1371/journal.pone.0161406 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Table S1 List of 87 Regions of Interest (ROIs).
Table S2. Comparison of global network properties.
Table S3. Comparison of nodal network properties.


