Abstract
Objective:
This work presents a novel approach to handle the inter-subject variations existing in the population analysis of ECG, applied for localizing the origin of ventricular tachycardia (VT) from 12-lead electrocardiograms (ECGs).
Methods:
The presented method involves a factor disentangling sequential autoencoder (f-SAE) – realized in both long short-term memory (LSTM) and gated recurrent unit (GRU) networks – to learn to disentangle the inter-subject variations from the factor relating to the location of origin of VT. To perform such disentanglement, a pair-wise contrastive loss is introduced.
Results:
The presented methods are evaluated on ECG dataset with 1012 distinct pacing sites collected from scar-related VT patients during routine pace-mapping procedures. Experiments demonstrate that, for classifying the origin of VT into the predefined segments, the presented f-SAE improves the classification accuracy by 8.94% from using prescribed QRS features, by 1.5% from the supervised deep CNN network, and 5.15% from the standard SAE without factor disentanglement. Similarly, when predicting the coordinates of the VT origin, the presented f-SAE improves the performance by 2.25 mm from using prescribed QRS features, by 1.18 mm from the supervised deep CNN network and 1.6 mm from the standard SAE.
Conclusion:
These results demonstrate the importance as well as the feasibility of the presented f-SAE approach for separating inter-subject variations when using 12-lead ECG to localize the origin of VT.
Significance:
This work suggests the important research direction to deal with the well-known challenge posed by inter-subject variations during population analysis from ECG signals.
Index Terms—: Ventricular Tachycardia, Electrophysiology, Disentangled Representations, Sequential Autoencoder
I. Introduction
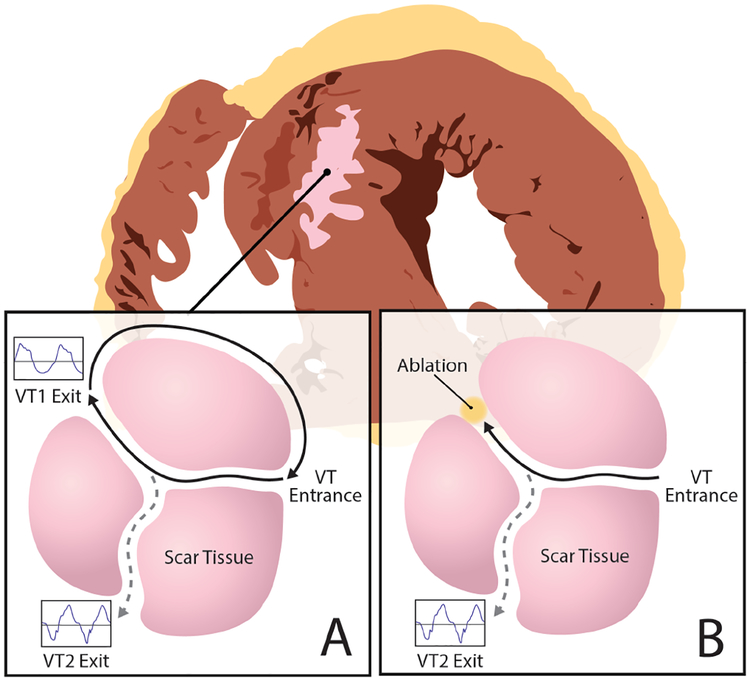
MONOMORPHIC ventricular tachycardia (VT) involves abnormal electrical activation in the lower chambers of the heart (ventricles) [1]. These abnormal origins of activation may exist in structurally healthy hearts giving rise to focal arrhythmia patterns (e.g., in premature ventricular contractions (PVCs)), or serve as an exit from a narrow strand of surviving tissue inside the myocardial scar and form reentrant ”short” circuits as illustrated in Fig. 1A (i.e., in scar-related VT) [2]. In either case, an important treatment to terminate and prevent the future recurrence of VT is to destroy the abnormal origin of ventricular activation by radiofrequency ablation, as illustrated in Fig. 1B.
Fig. 1:
Schematics of a VT reentry circuit. A: An electrical ”short circuit” travels and exits through narrow strands of surviving tissue inside the scar tissue to depolarize the rest of the ventricles. B: Ablation procedure that cuts off this ”short circuit” by blocking its exit from the scar tissue.
To localize this target for ablation, a widely accepted principle is that the origin of ventricular activation largely determines the QRS morphology in 12-lead electrocardiograms (ECGs) [2]. Based on this principle, a standard clinical procedure used to identify VT ablation targets – known as pace-mapping – involves electrically stimulating (i.e., pacing) different sites of the heart point by point, until locating the site at which pacing reproduces the QRS morphology of the VT on all 12 ECG leads [1]. This practice is of a ”trial-and-error” nature, requiring extensive invasive catheter maneuvers and prolonging procedural time, especially when there are multiple origins of VT to locate in the same heart.
A computer model to automatically localize the origin of ventricular activation from 12-lead ECG can be used to guide the clinicians to the potential ablation targets in real time, which can be expected to reduce the duration and improve the efficacy of ablation procedures. This model can be built by learning from a large amount of ECG data obtained during pacing of different myocardial locations in routine pace-mapping procedures. This notion was pioneered in [3], where a set of rules was derived from retrospective pace-mapping data to correlate four hand-engineered features – location of infarction, bundle branch block configuration, quadrant of QRS axis, and precordial R wave progression pattern – to the site of the origin of ventricular activation in terms of ten ventricular segments. These rules were then used by human operators (i.e., not automated) to localize the origin of ventricular activation from 12-lead ECG. To automate this prediction, however, a significant challenge arises from inter-subject anatomical variations that can modify the expected surface ECG patterns for a given arrhythmia origin [2]. Examples include general geometrical variations such as the location and orientation of the heart about the chest wall, the shape of the body torso, and the positioning of surface ECG leads. Examples also include disease-specific structural remodeling of the heart such as the presence, extent, and spatial distribution of scar tissue. Existing works, accordingly, can be divided into two categories: patient-specific models, and population-based models.
Patient-specific models are learned from ECG data for each patient, thereby removing the challenge of inter-subject anatomical variations in the data. In [4], a multiple linear regression model was designed to predict the origin of ventricular activation from 12-lead ECG. It is, however, difficult to collect a large amount of pace-mapping data on each patient. As a result, it was evident in [4] that the prediction accuracy is heavily reliant on the proximity of training sites with the actual target sites. To overcome this lack of patient-specific training data, recent work explored training a localization model from image-based patient-specific simulation data, using principal component analysis [5] or deep convolutional neural networks (CNN) [6]. Recent works also considered various means to further transfer and adapt the knowledge from simulation data to the real data [7] [8]. However, to either generate patient-specific simulation data [6], [8] or adapt simulation data to patient-specific anatomy [7], these approaches require patient-specific anatomical data that are not routinely available in patients undergoing pace-mapping procedures.
Population-based models, on the contrary, are learned from pace-mapping ECG data from a group of patients [9], [10]. In [9], the origin of VT was localized into one of ten predefined ventricular segments using support vector machine on prescribed ECG morphology. In [10], template matching was used to localize the origin of VT into sixteen segments based on the time-integrals of QRS complexes. None of these methods, however, addressed the presence of inter-subject variations in ECG data. As a result, they often report limited accuracy when applied to new patients.
To bridge this gap, we propose a population-based deep network that learns to separate inter-subject variations from the typical relationship between QRS complexes and origins of ventricular activation. Our work is motivated by a general challenge in machine learning that has gained increasing traction: how to learn a task-relevant representation that is invariant to other generative factors in the data? In [11], a bilinear model was presented to capture sufficiently expressive representations of factors of variations in the data, demonstrated in separating handwriting styles from the content when recognizing hand written digits. In [12] and [13], restricted Boltzman machine was used to model multiplicative interactions between latent factors of variation, separating identity from emotion [12] or expression from pose [13] in facial images. In [14], an autoencoder was trained to separate the discriminative and non-discriminant features for facial expression recognition, assuming orthogonality between the two types of, w features and discarding the latter in expression recognition. Most recently, [15] proposed a deep autoencoder that learns hidden factors of variation under a supervised cost. These existing works, however, mostly considered image-based applications and rarely investigated disentangling for sequential data. While recurrent neural networks (RNNs) such as Long Short-Term Memory (LSTM) networks have been increasingly used for ECG-based machine learning tasks because of their ability to handle long-term dependency [16], [17], to our knowledge, disentangled representation learning using sequential networks have not been explored for ECG signals.
In this paper, we present a novel sequential deep framework to explicitly separate the factors of variation within time-series ECG data when learning to predict the origin of ventricular activation. The overall concept is a sequential autoencoder augmented with a contrastive regularization for decomposing the raw ECG signal into two latent representation: individual-level variations and the common factor in QRS complex that relates to the origin of ventricular activation. We realize the proposed concept of factor-disentangling sequential autoencoder using both the commonly used LSTM and the recently proposed Gated Recurrent Unit (GRU). We evaluated the presented methods on an ECG dataset with 1012 distinct pacing sites collected from 39 scar-related VT patients during routine pace-mapping procedures. To demonstrate the effect of removing inter-subject variations on localizing the origin of ventricular activation, we benchmarked the presented methods with three different baselines: regression using prescribed QRS features, standard sequential autoencoders, and supervised deep CNN.
II. Methods
Our primary motivation is to separate the factor of variations while learning the abstract task-relevant representation from the data. The success of such separation depends on data representation on different hierarchy [18], naturally motivating the use of deep networks. Furthermore, given the temporal nature of ECG data, RNN is a natural choice for learning their latent representations. In this section, we first introduce RNN (LSTM and GRU in specific) followed by sequential autoencoders. We then describe, in the setting of sequential autoencoders, the strategy for separating VT-related factors from individual variations. Finally, we outline the procedure to fine tune the learned factorized representations with a supervised objective to localize the origin of ventricular activation.
A. Recurrent Neural Networks: LSTM & GRU
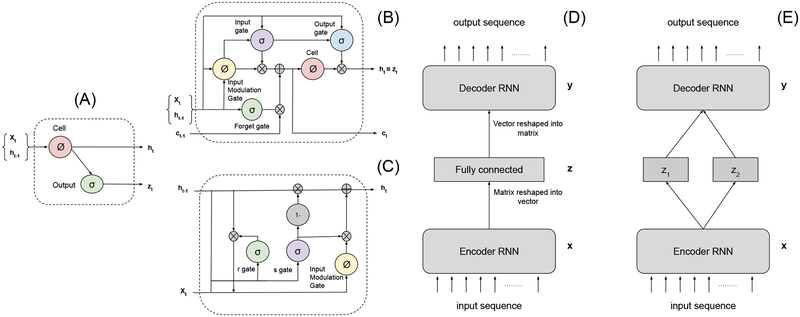
RNNs (Figure 2(A)) are suitable for capturing relationships among sequential data xt (defined in II-B) using a recurrent hidden state whose activation at each time is dependent on that of the previous time. The hidden state of such network is updated as:
| (1) |
where g is a (pointwise) activation function, ht is the hidden state at time t and W, U are the parameters to be learned. We omit the bias terms from all the presented RNN structures for brevity. It has been showed [19] that RNNs expressed in (1) have difficulties in capturing long-term dependencies because of vanishing or exploding gradients. To address this challenge, two particular models, LSTM [20] and GRU [21] have been proposed. As illustrated in Figure 2(B), LSTM realizes equation (1) by the following set of computations:
| (2) |
| (3) |
| (4) |
where c refers to the cell state, responsible for internal memory state, it, ft and ot denote, respectively, the input, forget and output gating signals at time t. The gating signals are expressed as:
| (5) |
| (6) |
| (7) |
where σ is the logistic sigmoid function and Wk, Uk with k ∈ {c, i, f, o} are the parameters to be learned for the three gates and memory cell. The parameters space is increased four folds from the simple RNN expressed in equation (1).
Fig. 2:
(A) A diagram of a basic RNN cell. (B) A diagram of a basic LSTM cell. (C) A diagram of a basic GRU cell. (D) Illustration of the Sequential Autoencoder (SAE). (E) The proposed two-way factored Sequential Autoencoder (f-SAE).
Alternatively, recently proposed GRU performs the computation as illustrated in Figure 2(C):
| (8) |
| (9) |
where two gates st and rt at time t is expressed as:
| (10) |
| (11) |
GRU and LSTM are related as both are utilizing a gating mechanism to prevent the gradient related problems. In comparison, the GRU unit controls the flow of information without having to use a memory unit like LSTM, resulting in a smaller number of parameters. LSTMs, on the other hand, in theory, may remember more extended sequences than GRUs due to the presence of internal memory mechanism. For more detailed comparisons between these two sequence learners and other variants, we refer readers to [22] [23]. Here we will consider and compare the use of both LSTM and GRU in the presented factor-disentangling sequential autoencoders.
B. Sequential Autoencoder (SAE)
The sequential autoencoder learns representations from sequential data in an unsupervised manner. In this paper, as shown in Figure 2(D), from an input sequence , an LSTM or GRU network first obtains an embedded sequence representation where . This matrix is then reshaped into a single vector by row concatenation and input into non-linear MLPs (multilayer perceptrons) to obtain a vector latent representation z. Note that different strategies can be considered while taking the output of RNN encoders. As an example, in sequence-to-sequence learning [24], the output of the last sequential unit of the RNN encoder is used as the input for the decoding network. Here, in comparison, the non-linear MLP is used for a stronger global aggregation of information from all the temporal aspects of the input sequence. The resulting latent representation z is then fed to non-linear MLPs, symmetrical to the ones used in the encoder, to obtain a vector which is reshaped into a matrix by forming a row from every elements. Finally, a LSTM or GRU decoder, symmetrical to the sequence encoder, is used to “reconstruct” an output sequence .
We denote the overall encoding process by parameterized by θ, and the overall decoding process by parameterized by θ′.
The parameters θ and θ′ are optimized by minimizing the average reconstruction error over n training examples:
| (12) |
where Lr is the loss function, such as mean square errors and cross entropy functions, which could be optimized using stochastic gradient descent.
C. Factorized Sequential Autoencoder (f-SAE)
Although disentangling factor of variations in the data is often considered as a natural ability of deep networks[25], without specific design, the extent of disentangling that can be achieved could be limited [26]. Specifically, for the framework of autoencoders, latent representations z learned by minimizing the reconstruction loss does not guarantee disentanglement of factors of variations in the data [27]. Given a bijective function f(·)1, the same reconstruction error can be obtained by replacing the encoder function by and decoder function by . Initially, the reconstruction loss will force decoder function to learn roughly the inverse of encoder function, , even though is initially a random mapping (weights are randomly initialized). All of this can remain true even when the reconstruction loss is 0 as the network approximates the corresponding encoding and decoding function. This, however, does not necessarily imply that different dimensions of latent representation are individually meaningful since any bijective function could entangle the representation while keeping the reconstruction the same. The projection space of the encoding function can be any transformations but lacks incentive for any dimension of that encoding to have any particular causal meaning. This motivates us to design objective functions to explicitly encourage the disentangling of factors of variations in the data.
In this work, we propose that the encoding process can be used to map the input data to two different latent representations, z1 and z2, that represent different generative factors within the data (Figure 2(E)). Formally, from an input sequence , similar to section II-B, the encoder first obtains a sequence representation which is then reshaped into a single vector by row concatenation. This vector representation is used as input to two different nonlinear MLPs to obtain the latent representation and . In the application of localizing the origin of ventricular activation, z1 represents the common relationship between the origins of ventricular activation and QRS data, and z2 represents other individual-level physiological and pathological variations that modify the ECG data. We make the following fundamental assumptions. For QRS data originating from nearby locations, the location representation z1 should be similar regardless of the data are collected from the same patient; otherwise, z1 should be different. On the other hand, for QRS data from the same patient, the patient-level variation representation z2 should be similar regardless of the origin of activation. Importantly, for QRS data from different patients, we do not make any assumption on the similarity between the embedded z2 considering our absence of knowledge about the similarity among the anatomical and other relevant physiological factors among patients. This factorized embedding will be realized by a a contrastive loss which requires a pair-wise comparison of the factorized representations learned by SAE [28]. Training pairs Xp = (x(i),x(j)) are randomly generated from the training data ensuring different beats from the same pacing location are not paired together. Each pair is given a label : is 1 if QRS data pair is from the same patient, and 0 otherwise; is 1 if QRS data pair originates from the same ventricular segment, and 0 otherwise. The contrastive loss is formulated as:
| (13) |
where
and
where β is an empirically determined margin. This contrastive loss is added as a weakly-supervised regularization term to the standard reconstruction loss (equation (12) of the sequential autoencoder, giving rise to the overall objective function:
| (14) |
where α is the weight given to the contrastive regularization. The training architecture of the proposed f-SAE is a siamese architecture which consists of two copies of the encoding mapping and two copies of decoding mapping which share the same set of parameters, respectively, θ and θ′, and the objective function (14). The paired input signals (x(i), x(j)) are passed through the mapping functions, yielding two pairs of latent representation and the pairs of reconstructed input signals (y(i), y(j)). The loss function of (14) combines these outputs to generate scalar loss. The parameters θ and θ′ are optimized using stochastic gradient-based optimization methods such as SGD, RMSprop, or ADAM [29]. Our experimental results were obtained using ADAM.
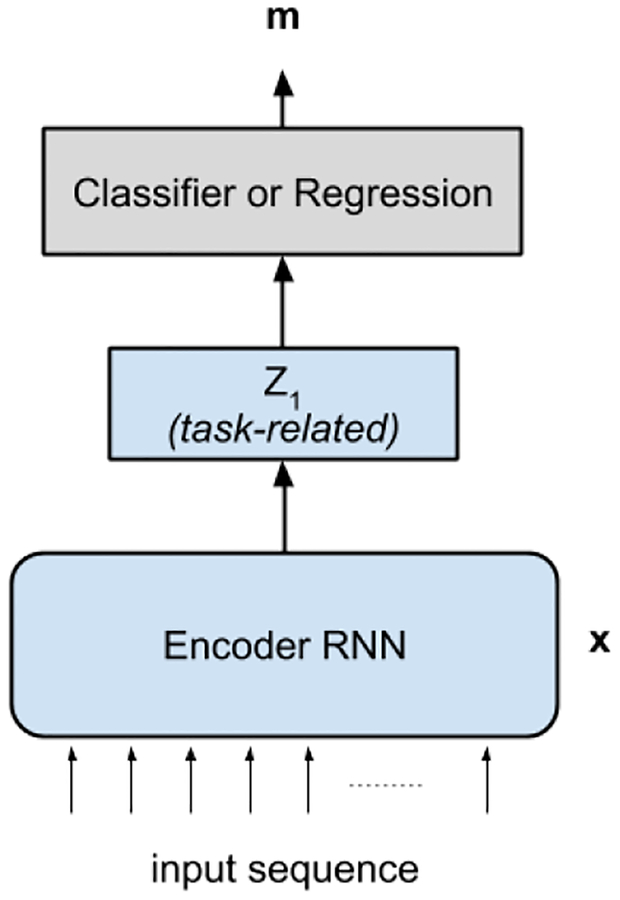
D. Supervised Fine-tuning
The parameters of the deep networks trained in a weakly-supervised manner, as described in section II-C, are fine-tuned to a supervised training criterion. The encoder of the trained f-SAE is used during the fine-tuning procedure. In specific, the parameters involved only in the encoding process for z1 is considered, since z1 is the representation used to localize the origin of ventricular activation. The schematic of the fine-tuning network is presented in Figure 3. We consider localization in two settings: localization into one of ten predefined ventricular segments in the form of a classification task, and prediction of the 3D x-y-z coordinates in the form of a regression task. In the classification task, the classifier network fc(z1) is created by adding a one-layer MLP to convert the learned representation to a prediction that corresponds to the probability of the input belonging to each of the L pre-defined ventricular segments. The f-SAE encoder and the classification network fc(z1) is trained by using the supervised cross-entropy loss given as:
where represents the ground truth label and N represents the total number of the training data.
Fig. 3:
Supervised fine-tuning network using the learned parameters from the f-SAE (light blue) for the localization of the origin of VT in the form of classification or regression task.
Similarly, for the coordinate prediction task, the regression network fr(z1) is created by adding a one-layer MLP to convert the learned representation to a prediction that corresponds to the 3D x-y-z coordinates of the origin of ventricular activation. The f-SAE encoder and the regression network fr(z1) is trained by minimizing the mean square error cost given as:
For both supervised task, to avoid overfitting, both implicit regularization in the form of early stopping and explicit regularization in the form of dropout [30] are used. In early stopping, model validation is performed in each training epoch to stop training if the model prediction no longer improves on the held-out validation data set. In case of dropout, during training, model neglects (drop) some hidden units with probability p and during testing, all of the hidden units are used to calculate the network output, resembling an ensemble learning approach.
III. Experiments
A. Experimental data and data processing
Experimental data were collected from routine pace-mapping procedures on 39 patients who underwent ablation of scar-related VT. Study protocols were approved by the Nova Scotia Health Authority Research Ethics Board. The database includes 15-second 12-lead ECG recordings produced from 1012 distinctive pacing sites on the left-ventricular (LV) endocardium, where the 3D coordinates of all pacing sites were identified on an electroanatomic mapping system (CARTO3, Biosense Webster Inc., Irvine, CA).
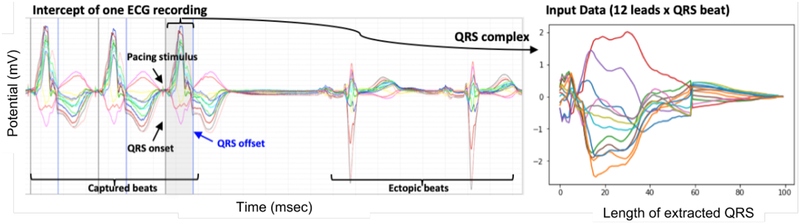
All ECG data were processed for noise removal and baseline correction using an open-source software2. As illustrated in Figure 4, QRS complexes were manually extracted by student trainees to avoid motion artifacts, ectopic beats, and non-capture beats. Each QRS complex, acquired initially at 1024 Hz frequency, was down-sampled to 100 dimension in time. Because many quality beats can be extracted from each ECG recording, we obtain in-total 16848 QRS complexes, each with 100 × 12 in dimension.
Fig. 4:
(Left) Illustration of experimental data and processing, in which 15-second ECG recordings are pre-processed for extraction of a successfully-paced QRS complex. (Right) The final input data for prediction represented as sequence of 12×100 (i.e. 12 leads × QRS beat).
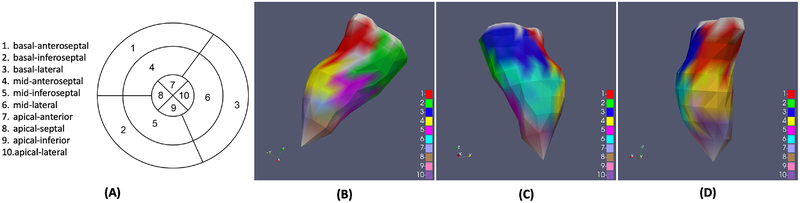
Each QRS complex was associated with a label of the spatial location of the pacing site exported from the CARTO3 system. These CARTO3 coordinates were processed in two ways as described in [4], using a common LV endocardial surface model as shown in Figure 6. This endocardial model was derived from the necropsy specimen of a normal human heart and comprised 275 triangles in the surface mesh. Each pacing site from the CARTO data was inspected and associated with one of the 275 triangles, and the center of the triangle was used to represent the label of x-y-z coordinate for each QRS complex for regression purpose. Second, the endocardial surface model was further divided into ten ventricular segments as defined in [9]: the nomenclature of these segments is provided in Figure 5(A) and their distribution on the endocardial surface is visualized in Figure 5(B)–(D). Each of the pacing sites was then assigned into one of the ten ventricular segments, generating a label of segment ID for each QRS complex for classification purpose.
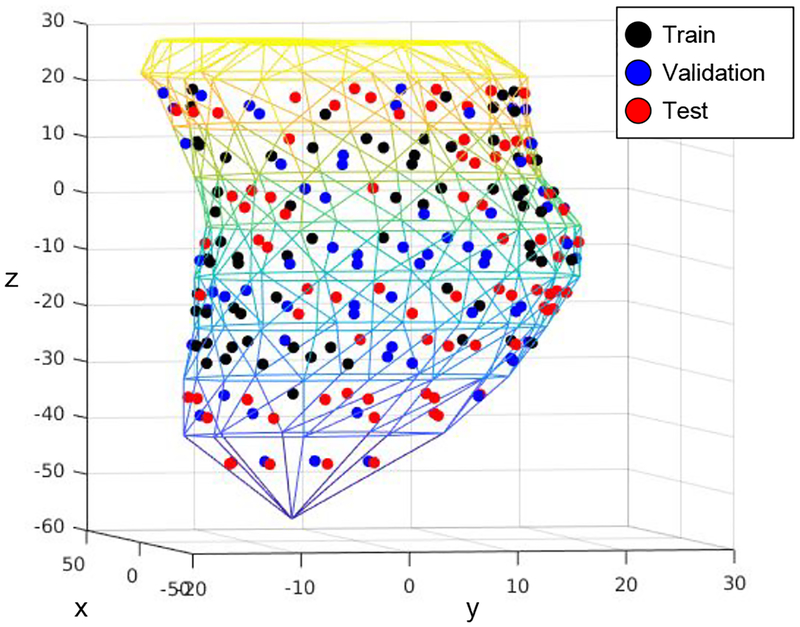
Fig. 6:
[Best viewed in color] The triangulated left ventricular (LV) endocardial surface on which all pacing sites are projected. The pacing sites for train, validation and test set are shown with different colors.
Fig. 5:
(A) Schematics of the 10-segment division of the left ventricle. (B)-(D) Visualization of distribution of the ten segments on the LV endocardial surface model in three different views.
We test the presented f-SAE for both regressing the 3D coordinates or classifying the segment ID of the pacing site using the QRS complex in ECG data. The accuracy of the predicted 3D coordinates is measured by its Euclidean distance (in millimeter) to the coordinate label. For segment classification, the accuracy is measured by correctly predicting the segment ID of the pacing site.
B. Model training, testing, and comparison
The entire dataset is split into training (10292 beats from 22 patients), validation (3017 beats from 5 patients), and test sets (3539 beats from 12 patients) making sure that the data from the same patient are not shared between any two sets. The spatial distributions of the pacing sites among the three sets are shown in Figure 6, and the training data distribution among ten segment classes is demonstrated in Figure 7. The presented f-SAE models are compared with three alternative models as detailed below:
f-SAE (presented): We tested the following f-SAE architecture with both GRU and LSTM units. The sequential encoder with two hidden layers (output temporal dimensions of 8) is followed by two fully-connected layers, respectively with dimensions 500 and 50, before the latent representation is factorized into two components as described in section II-C. The decoder then concatenates the factored representations and passes it through two fully-connected layers. The output is then reshaped and moved into the sequential decoder with two hidden layers. All the dimensions of layers of the decoder network are set mirroring the hidden layers of the encoder network. Finally, one extra fully-connected layer, without any activation is used to reconstruct the input signal. This choice is made because tanh activation – commonly used in LSTM and GRU networks – would squash the output into [−1, 1], an undesirable effect for the ECG data used in our experiments.
SAE: The architecture of the SAE is identical to that of the f-SAE except that there is no factorization of the latent representation at the end of the encoder. Similar to the case of f-SAE, the encoder is fine-tuned along with a linear classifier for segment classification, and a linear regression model for coordinate prediction.
CNN: Given the success of supervised CNNs in a wide variety of tasks including ECG-based analyses, we also compared the presented methods with a specific supervised CNN model. Our design choice is inspired by recent work reported in [6], where CNN is used for premature ventricular contraction (PVC) localization from 12-lead ECG. The CNN takes in the input signal as 1×12×100 and consists of three blocks of convolution layers with the following structure: Dropout d [30], 2d convolution layer with input channel cip and output channel cop of kernel size (kw, kh), batch normalization layer [31], ReLU [32] activation and pooling layer of 2d max pool with window size (winw, winh) and stride of (sw, sh). Three convolution layers are designed with d = {0.2,0.5, 0.5}, (cip, cop) = {(1,32), (32, 24), (24, 12), (kw, kh) = {(3,5), (3, 3), (1, 2)}, batch normalization only first and second CNN block, (winw, winh) = {(1,2), (1,2), (1, 1)} and (sw, sh) = {(2,2), (1, 1), (1, 1)}. These CNN blocks are followed by two fully connected neural networks with hidden units = {200, h}, where h is 10 for segment classification and 3 for coordinate prediction.
QRS integral (QRSi): As a baseline, we also included a linear model using commonly-used prescribed features of 120-ms QRS-integrals [10], calculated as the 120-ms time-integral of the QRS complex using the standard trapezoidal rule.
Hyper-parameters for all models, such as learning rate and the margin value β (equation 13) and weight value α (equation 14) in the presented methods, are selected based on their performance on the validation set. The dropout, with probability p = 0.5, is used during the fine-tuning as presented in II-D. All the models were implemented using PyTorch [33].
Fig. 7:
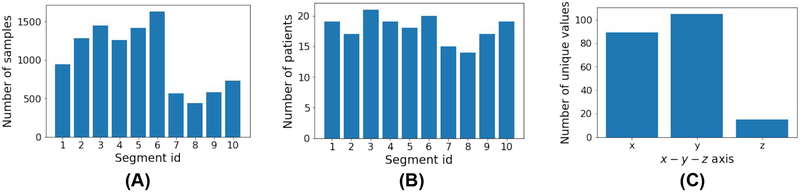
Training data distribution in bar diagrams. (A): Number of samples in each segment ID. (B): Number of unique patients in each segment ID. (C): Number of unique values along each of the x-, y-, and z-axes.
C. Quantitative prediction results
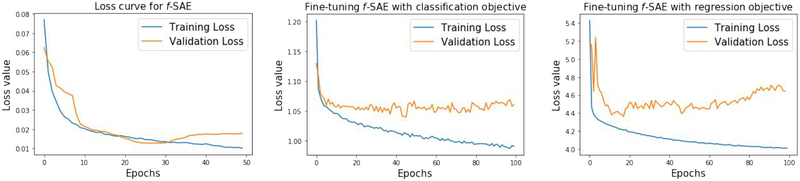
Table I presents the accuracy of coordinate prediction and segment classification by the presented model f-SAE compared against the three other models. In Figure 8, we include the training and validation loss for the unsupervised presentation learning (left), fine-tuning for segment classification (middle), and fine turning for coordinate regression (right). With early stopping, we selected the unsupervised f-SAE model trained until epoch 30 before the validation error started to increase. Similarly, fine-tuning for segment classification and coordinate regression was stopped at 46 and 18 epochs, respectively.
TABLE I:
Coordinate prediction accuracy and segment classification of the two presented models versus the three comparison methods as described in section III-C. For coordinate prediction, we report a mean error (in millimeters) and its 95% confidence interval. For segment classification, we report the percentage of correctly classified segments. All results are reported on a separately held-out test set.
| Model/Task | Coordinate Prediction (in mm) | Classification (in %) |
|---|---|---|
| QRSi | 15.09±0.20 | 47.35 |
| CNN | 14.02 ±0.22 | 54.79 |
| SAE (LSTM) | 14.63±0.22 | 52.16 |
| SAE (GRU) | 14.44±0.20 | 51.14 |
| f-SAE (LSTM) | 13.14±0.23 | 53.29 |
| f-SAE (GRU) | 12.84±0.22 | 56.29 |
Fig. 8:
Training and validation loss over training epochs. Left: regularized reconstruction loss as defined in (14) of the unsupervised f-SAE (GRU). Middle: Classification loss during fine-tuning f-SAE (GRU) for segment classification. Right: Regression loss during fine-tuning of f-SAE (GRU) for coordinate regression.
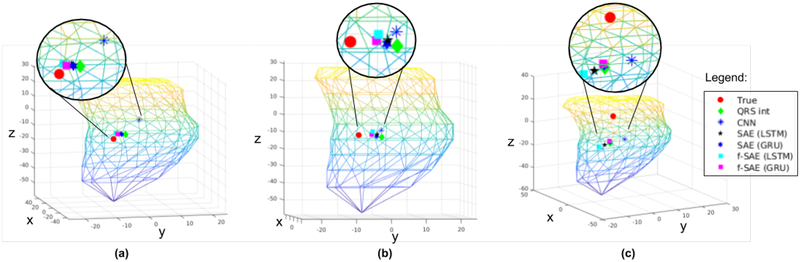
In predicting coordinates, compared with the use of prescribed QRSi as input features, the use of deep networks in the form of supervised CNN improved the prediction accuracy by approximately 1 millimeter. While the use of SAE (both GRU and LSTM) was able to achieve higher performance than QRSi-based localization, it was not able to improve upon the prediction capability of the supervised CNN. In comparison, using the presented f-SAE, a significant improvement can be seen with both GRU and LSTM. In particular, GRU based f-SAE was able to improve the localization prediction performance by approximately millimeters against the prescribed QRSi-based approach and millimeters against the supervised CNN. Figure 9 shows three examples of true pacing sites compared with the predicted location using the presented as well as three comparison methods.
Fig. 9:
Three examples of true pacing sites and the predicted locations using the presented methods and the three comparison methods as described in III-C. For brevity, actual and predicted sites are zoomed-in.
As a further investigation into the model performance, we list the prediction accuracy in each of the x, y, and z-axis in the 3D coordinate, as shown in Table II for the presented f-SAE. As we can quickly notice, the error of prediction on the z-axis is more significant than those on the x- and y-axis. This can be explained by the distribution of the pacing points on the dataset. As illustrated in Figure 7C, there are only 15 unique values along the z-axis among the pacing sites in the training set, compared to 89 and 105 unique values along the x- and y-axis. Furthermore, the pacing sites are distributed throughout 66 millimeters along the z-axis, more extensive compared to the span along the x- and y-axis (36 and 46 millimeters, respectively).
TABLE II:
Coordinate prediction accuracy for each coordinate axis. We report the mean error (Euclidean distance in millimeters) in the separately held-out test set.
| Coordinate axis | x (in mm) | y (in mm) | z (in mm) |
|---|---|---|---|
| f-SAE (LSTM) | 5.09 | 4.80 | 9.16 |
| f-SAE (GRU) | 5.41 | 4.81 | 8.69 |
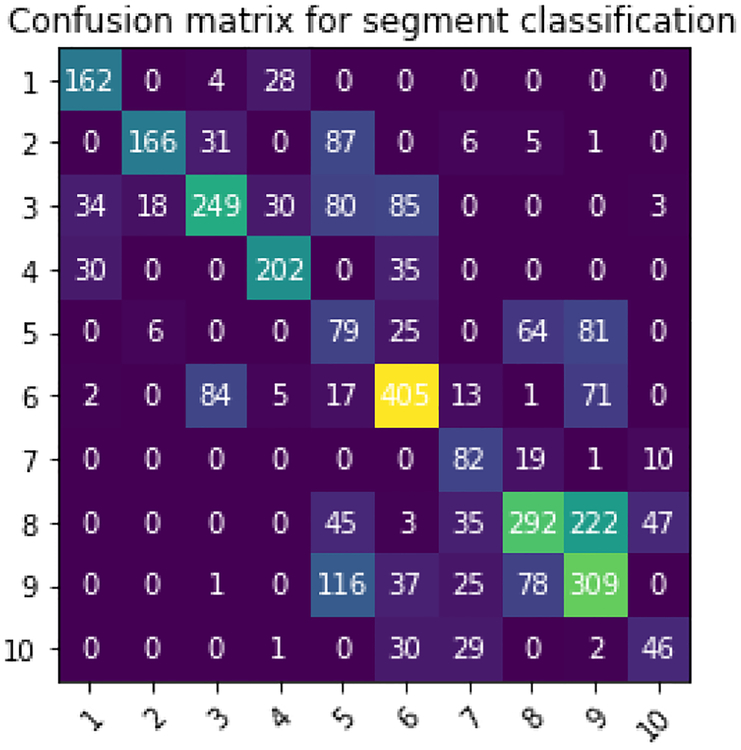
Regarding segment classification, similar to coordinate prediction task, we see consistent improvement as we go from feature-based approaches to deep network and further improvement is observed with presented f-SAE as shown in Table I. In Figure 10, we show the confusion matrix for segment classification from the presented f-SAE (GRU) model. As we can notice, the main confusion is between segments 7, 8 and 9 corroborated by the training data distribution of the number of samples in Figure 7A. Besides, origins in segment 3 also tend to be confused with other segments. To further understand the difficulty in localizing the origin of ventricular activation from different anatomical segments of the heart, we present in Table III the average coordinate prediction error made by the presented f-SAE (GRU) model within each segment. As shown, the accuracy of coordinate prediction also appeared to differ among different segments, with relatively lower accuracy in segments 2, 3, 8, 9, and 10, similar to the observation draws from the confusion matrix.
Fig. 10:
The confusion matrix for segment classification for the f-SAE (GRU) model.
TABLE III:
Average coordinate prediction errors by the presented f-SAE (GRU) model within each pre-defined LV segment, evaluated on the held-out test set.
| Segment number | Coordinate prediction (in mm) | Segment name | Coordinate prediction (in mm) |
|---|---|---|---|
| 1 | 10.296 | 6 | 10.574 |
| 2 | 15.021 | 7 | 12.986 |
| 3 | 15.174 | 8 | 14.388 |
| 4 | 10.306 | 9 | 13.200 |
| 5 | 10.323 | 10 | 14.130 |
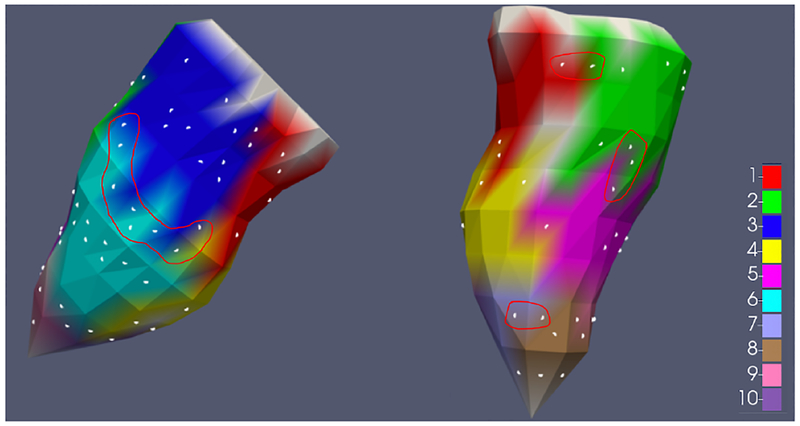
To further understand the relation between the segment classification and coordinate prediction tasks, we approximated the average surface area of the ten segments to be 8.4 cm2 and a corresponding average radius of approximately 16 mm (assuming circular shape) on the given endocardial surface model. Interestingly, this radius is larger than the average error obtained by the coordinate prediction model. This is potentially because many of the pacing sites in the test set were located close to the boundary of the segments, as illustrated in Fig. 11, in which scenario an incorrect classification can be made even though the distance error is small. Quantitatively, among all the test-set samples incorrectly classified by the presented f-SAE (GRU) model (n = 1547), on 48% of them (n = 745) the true segment was correctly classified by the second most probable prediction while the first most probable prediction was located in the immediate neighboring segment to the true segment. This is consistent with our previous findings [8] and suggests that the accuracy of segment classification may be improved by incorporating the spatial relation between ventricular segments in the classification model.
Fig. 11:
Visualization of the distribution of pacing sites in the held-out test set (white dots) on the endocardial surface model in two different views. The red curve is manually drawn to demonstrate that many test set samples are located near segment boundaries.
In both tasks of coordinate prediction and segment classification, the highest training accuracy – following early-stopping using the validation set – is obtained by the CNN: a prediction error of 6.04 ±0.10 mm for coordinate prediction, and a classification accuracy of 76.04% for segment classification in specific. In comparison the presented f-SAE (GRU) obtains 10.97 ±0.12 mm and 67.83%, SAE (GRU) obtains 9.64 ±0.13 mm and 69.16%, and QRSi-based method obtains 13.71 ±0.17 mm and 52.60%, respectively in coordinate prediction and segment classification during training following early-stopping using the validation set. This suggests that CNN was not able to generalize as well as the presented methods to data from unseen patients.
D. Analyzing disentanglement
To gain further insight into the effect of factor disentangling, we analyze to which extent we can use each of the learned representation z1 and z2 to classify the origin of ventricular activation as well as the patient ID. The results are presented in Table IV: as shown, the patient-specific factor z2 is much better in associating with different patient IDs compared to z1, while z1 is better at localizing the origin of ventricular activation.
TABLE IV:
Classification accuracy (in %) when one factor is used to classify the label of its own as well as the other factor. The results involving patient-specific factor z2 is reported on train set because no patients are shared between datasets.
| factor | segment classification | patient ID classification |
|---|---|---|
| z1 | 56.29 | 40.74 |
| z2 | 37.36 | 62.60 |
| random-chance | 10 | 4.5 |
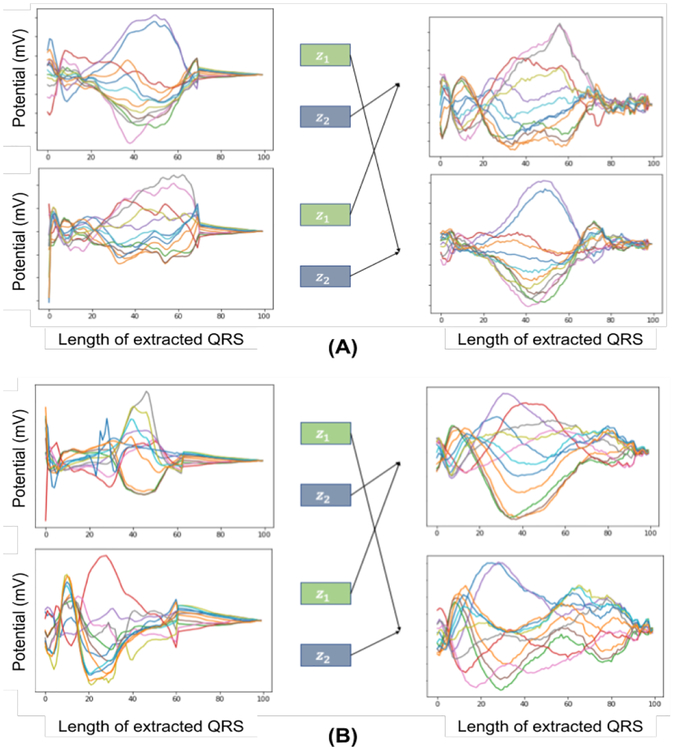
Besides, we demonstrate the ability to swap the encoded representations to generate different signals in Figure 12. Note that, by swapping z1 (which is learned to represent the origins of ventricular activation) between a pair of signals, the critical morphology in specific leads (e.g. the amplitude and duration of the R wave of the aVR lead, represented by red color) is transferred.
Fig. 12:
The encoded representation, z1 and z2, from two ECG signals (left) are swapped to generate the signals (right) for two different cases (A) and (B).
E. Effect of hyperparameters
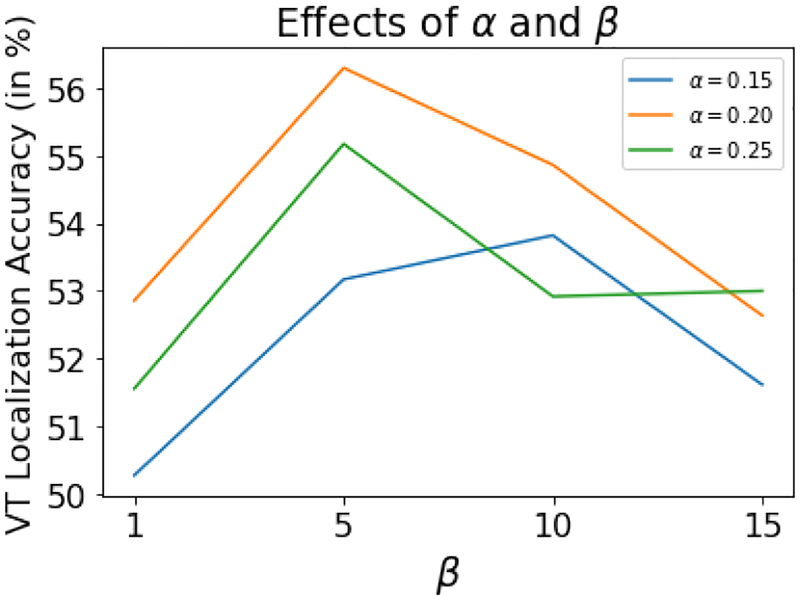
The hyper-parameters, margin value β (equation 13) and weight value α (equation 14), are tuned for different values: {1, 5, 10, 15} and {0.15, 0.20, 0.25} demonstrates respectively. Figure 13 the results, in terms of VT localization accuracy on test data, for the different combination of α and β values. As shown, the best results were obtained for β = 5 and α = 0.2 and presented results earlier in Table I are reported using these values.
Fig. 13:
The effects of α and β for VT localization accuracy for the presented f-SAE (GRU) model on test data.
IV. Discussion
While the presented disentangling of inter-subject variations improved ECG-based localization of the origin of ventricular activation, the overall performance obtained by the different approaches tested – including the state-of-the-art CNN architecture – was limited (Table I). This was especially true for the segmentation classification task. This may be attributed to several challenges that will be discussed below.
1). The challenge of data acquisition:
First and foremost, while the paced ECG data set considered in this paper is large by the clinical standard considering the invasive nature of the acquisition process, it is quite moderate compared with data sets commonly used for deep learning in domains such as computer vision. In particular, the disentanglement of inter-subject variations was learned from only a training set of 22 patients. Furthermore, the collected pacing sites on each patient typically covered only a local region of the myocardium of interest to the clinicians (i.e., in and around the region of the scar), resulting in an imbalance in training and the test set distribution. This is evident in the analysis of localization accuracy along each of the x-y-z axis: the larger span of values along the z-axis together with the smaller number of samples contributed to a reduced performance in predicting along the z-axis compared to the other two axes. Future work will investigate the presented methods on a more extensive set of data, through our continued effort in data collection as well as the exploration of transfer learning approaches utilizing related public ECG data sets.
2). The effect and challenge of registration:
The location of the pacing sites in the experimental data considered in this work were identified on an electroanatomic mapping system (CARTO3) that measures electrical signals on a spatial location in the heart along with its 3D coordinate. The coordinate system used by the CARTO3 system, however, is specific to each patient. To pool data from all patients, therefore, it is necessary to register all the pacing sites to a common heart model. For the data used in this paper, this was done via a semi-qualitative process as described in [4] and briefly summarized in section III-A. This introduced unknown registration errors that may have affected the result of the presented prediction models. In our ongoing collection of new pace-mapping data, efforts are made to collect both CARTO mapping and tomographic imaging (e.g., CT) data whenever possible to allow more quantitative registration processes as well as the evaluation of registration errors in our future work.
While the regression of 3D coordinates presents a more difficult task due to the aforementioned challenge of registration, we believe that it complements segment-based classification by providing continuous localization that can potentially meet the clinical need of a localization accuracy of 5–10 mm (size of ablation catheters). Given the ongoing effort in registering CARTO and other tomographic images [34], we envision that a prediction model of 3D coordinates can be accommodated into clinical practice when integrated with pre- and intra-procedural registration software such as CARTOMerge (Biosense Webster Inc., Diamond Bar, CA, USA).
3). The challenge of myocardial scar tissue:
The presence of fibrosis or scar tissue in the myocardium – which is typical for the patient group of reentrant VT – will affect the electrical activation pattern. This will in turn influence the QRS pattern on the ECG, constituting a significant challenge for machine learning approaches to localize the origin of activation from ECG data. This was studied in detail via a 3D simulation study in [35]. In this paper, we are motivated to address this challenge by using deep representation learning to disentangle this factor of variations, along with other geometrical factors that affect the ECG morphology such as the position and orientation of the heart, the size, and shape of the thorax, and the positioning of the surface electrodes. This is a challenging problem given that there is a large variety of factors of variations that contribute to the ECG data through a complex process that is difficult to characterize precisely. Future work utilizing simulation studies such as that presented in [35] may provide better insight into how to correctly separate the effect of these factors from the machine learning models for localizing the origin of electrical activation in the heart. This may also help the development of machine learning models that can incorporate imaging data, such as patient-specific scar characteristics and geometrical parameters, for more accurate localization of the origin of electrical activation.
4). The effect of the location of activation origin:
In this study, the presented models performed differently in localizing the origin of ventricular activation in different segments of the heart, as suggested by both the confusion matrix of the segment classification model and the within-segment coordinate prediction errors obtained by the regression model. This may be due to several different reasons.
First, as shown in Fig. 7, the distribution of training data can be expected to play a significant role in the performance of the machine learning model: regions with less or more narrowly distributed training data are expected to be more challenging to localize. This challenge can be overcome by a future effort to balance the data distribution throughout the ventricles during clinical data acquisition, utilizing simulation data that allows virtually complete coverage of the ventricles in data generation [8], or specialized techniques for balancing the data set before training a machine learning model [36].
Second, because electrical information at different regions of the heart contributes differently to ECG depending on their relative position to surface electrodes, origins from some regions of the heart may be less captured in the 12-lead ECG. Similar observations were made in the atria in a recent study [37], where ectopic foci in certain regions of the atria make more significant contributions to the body surface potential maps. Furthermore, as recently reported in [38], electrical activation originated from some regions of the atria may produce very similar ECG patterns on the body surface. A similar phenomenon can be expected for the ventricles, which may further suggest that origins in some regions of the heart are more difficult to localize than others.
Finally, in the presented model for segment classification, the spatial relationship between the segments was ignored. In our previous work [8], we have found that it is common for a model to predict a site of origin to a segment next to that with the true label. To overcome this, future work may consider a hierarchical classification task that considers the spatial relationship among the anatomical segments of the ventricles at different resolutions.
5). Relation to existing works and other future directions:
This paper extends the ideas of our initial works presented in [39], [40]. The primary extension is made with the novel factorizing sequential deep framework, yielding an improvement of more than 1% in segment classification. Furthermore, while the high-level features in our previous works were learned through greedy layer-wise pre-training, here we increased the depth of both the encoder and decoder. This decision is made as the single joint optimization of global reconstruction objective seems to allow more natural convergence compared to stacked-autoencoders with multiple local reconstruction objectives. Finally, in this work, we also examined the presented disentangled autoencoder with widely used CNN architecture.
The primary innovation in this work is to show that removing patient-specific factors from the task representation can improve the subsequent task of localizing the activation origin from ECGs. While this innovation is realized in the setting of SAE in this paper, it is orthogonal to the choice of deep architectures. To extend the proposed idea to other deep architectures will be a primary direction of future work. For example, unsupervised disentanglement learning has gained increasing traction in the machine learning community [18] [41]. These recent works have mostly considered deep generative models like Variational Autoencoder (VAE) [42] for disentangling simple data generating factors from a highly complex input space. Moreover, several disentanglement metrics are also introduced for such deep generative models, making evaluation much easier. To extend the present work in such deep generative models for disentangling the data generative factors of ECG data would be a natural future work. It is, however, important to note that, in digital images in the visual domain, the primary generative factors – such as the style of handwriting or the pose of a face – are intuitive to interpret and visualize in the data domain. In comparison, the generative factors in our application – such as patient-specific anatomical factors – are related to the ECG data through a much more complex physical process and are quite challenging to visualize directly in the data domain. This is especially a challenge in real clinical datasets, in which values of the true generative factors are not always known for each patient. Therefore, controlled simulation – with known heart and torso geometries that can be manipulated to generate EGG data corresponding to controlled changes in known generative factors – could provide a valuable dataset to understand and analyze disentanglement in the application of interest and will be investigated in our future work. Furthermore, the autoencoder in this work is designed to utilize the sequential nature of the ECG data via LSTM and GRU. Since the CNN architecture has been successful across various domains, an immediate future work is to investigate the use of a convolutional autoencoder [43] for the presented disentangling idea.
V. Conclusion
This paper presents a novel sequential factorized autoencoder for disentangling inter-subject variations during localization of the origin of ventricular activation from 12-lead ECG. We demonstrated the presented sequential autoencoder for two different recurrent neural networks: GRU and LSTM. The presented methods are evaluated for regression and classification tasks in real clinical data of unseen patients, demonstrating improved performance compared with several baseline models including feature-based regression, supervised CNN, and sequential autoencoding without factor disentangling. To our knowledge, this is the first effort in attempting to disentangling different generative factors – especially those related to patient-specific anatomy – from ECG data, which may have important clinical implications in improving the accuracy of ECG-based applications such as the localization of ventricular activation origin and beyond.
Acknowledgment:
This work is supported in part by National Institute of Health (Award No.: R15HL140500 and R01HL145590), National Science Foundataion (Award No.: ACI-1350374) and investigator-initiated research grant from Biosense Webster.
Footnotes
Not to be confused with the forget gate of LSTM as expressed in Equation (6)
Contributor Information
Prashnna Kumar Gyawali, B. Thomas Golisano College of COmputing and Information Science, Rochester Institute of Technology, Rochester, NY, USA (see http://pkgyawali.com).
B. Milan Horac̀ek, School of Biomedical Engineering, Dalhousie University, Halifax, NS, Canada..
John L. Sapp, School of Biomedical Engineering, Dalhousie University, Halifax, NS, Canada.
Linwei Wang, B. Thomas Golisano College of COmputing and Information Science, Rochester Institute of Technology, Rochester, NY, USA.
References
- [1].Stevenson William G, “Ventricular scars and ventricular tachycardia,” Transactions of the American Clinical and Climatological Association, vol. 120, pp. 403, 2009. [PMC free article] [PubMed] [Google Scholar]
- [2].PARK KYOUNG-MIN, KIM YOU-HO, and Marchlinski Francis E, “Using the surface electrocardiogram to localize the origin of idiopathic ventricular tachycardia,” Pacing and Clinical Electrophysiology, vol. 35, no. 12, pp. 1516–1527, 2012. [DOI] [PubMed] [Google Scholar]
- [3].Miller JOHNM, Marchlinski FRANCISE, Buxton Alfred E, and Josephson Mark E, “Relationship between the 12-lead electrocardiogram during ventricular tachycardia and endocardial site of origin in patients with coronary artery disease.,” Circulation, vol. 77, no. 4, pp. 759–766, 1988. [DOI] [PubMed] [Google Scholar]
- [4].Sapp John L, Bar-Tal Meir, Howes Adam J, Toma Jonathan E, El-Damaty Ahmed, Warren James W, MacInnis Paul J, Zhou Shijie, and Horáček B Milan, “Real-time localization of ventricular tachycardia origin from the 12-lead electrocardiogram,” JACC: Clinical Electrophysiology, vol. 3, no. 7, pp. 687–699, 2017. [DOI] [PubMed] [Google Scholar]
- [5].Potse Mark, Linnenbank André C, Peeters Heidi AP, Sippens-Groenewegen Arne, and Crimbergen CA, “Continuous localization of cardiac activation sites using a database of multichannel ecg recordings,” IEEE transactions on biomedical engineering, vol. 47, no. 5, pp. 682–689, 2000. [DOI] [PubMed] [Google Scholar]
- [6].Yang Ting, Yu Long, Jin Qi, Wu Liqun, and He Bin, “Localization of origins of premature ventricular contraction by means of convolutional neural network from 12-lead ecg,” IEEE Transactions on Biomedical Engineering, vol. 65, no. 7, pp. 1662–1671, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Giffard-Roisin Sophie, Delingette Hervé, Jackson Thomas, Webb Jessica, Fovargue Lauren, Lee Jack, Rinaldi C Aldo, Razavi Reza, Ayache Nicholas, and Sermesant Maxime, “Transfer learning from simulations on a reference anatomy for ecgi in personalised cardiac resynchronization therapy,” IEEE Transactions on Biomedical Engineering, 2018. [DOI] [PubMed] [Google Scholar]
- [8].Alawad M and Wang L, “Learning domain shift in simulated and clinical data: Localizing the origin of ventricular activation from 12-lead electrocardiograms,” IEEE Transactions on Medical Imaging, pp. 1–1, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Yokokawa Miki, Liu Tzu-Yu, Yoshida Kentaro, Scott Clayton, Hero Alfred, Good Eric, Morady Fred, and Bogun Frank, “Automated analysis of the 12-lead electrocardiogram to identify the exit site of postinfarction ventricular tachycardia,” Heart Rhythm, vol. 9, no. 3, pp. 330–334, 2012. [DOI] [PubMed] [Google Scholar]
- [10].Sapp John L, El-Damaty Ahmed, MacInnis Paul J, Warren James W, and Horáček B Milan, “Automated localization of pacing sites in postinfarction patients from the 12-lead electrocardiogram and body-surface potential maps,” Computing in Cardiology, 2012. [Google Scholar]
- [11].Tenenbaum Joshua B and Freeman William T, “Separating style and content with bilinear models,” Neural computation, vol. 12, no. 6, pp. 1247–1283, 2000. [DOI] [PubMed] [Google Scholar]
- [12].Desjardins Guillaume, Courville Aaron, and Bengio Yoshua, “Disentangling factors of variation via generative entangling,” arXiv preprint arXiv:1210.5474, 2012. [Google Scholar]
- [13].Reed Scott, Sohn Kihyuk, Zhang Yuting, and Lee Honglak, “Learning to disentangle factors of variation with manifold interaction,” in Proceedings of the 31st International Conference on Machine Learning (ICML-14), 2014, pp. 1431–1439. [Google Scholar]
- [14].Rifai Salah, Bengio Yoshua, Courville Aaron, Vincent Pascal, and Mirza Mehdi, “Disentangling factors of variation for facial expression recognition,” in Computer Vision–ECCV 2012, pp. 808–822. Springer, 2012. [Google Scholar]
- [15].Cheung Brian, Livezey Jesse A, Bansal Arjun K, and Olshausen Bruno A, “Discovering hidden factors of variation in deep networks,” arXiv preprint arXiv:1412.6583, 2014. [Google Scholar]
- [16].Lipton Zachary C, Kale David C, Elkan Charles, and Wetzel Randall, “Learning to diagnose with lstm recurrent neural networks,” arXiv preprint arXiv:1511.03677, 2015. [Google Scholar]
- [17].Yildirim Özal, “A novel wavelet sequence based on deep bidirectional lstm network model for ecg signal classification,” Computers in biology and medicine, vol. 96, pp. 189–202, 2018. [DOI] [PubMed] [Google Scholar]
- [18].Bengio Y, Courville A, and Vincent P, “Representation learning: A review and new perspectives,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 35, no. 8, pp. 1798–1828, August 2013. [DOI] [PubMed] [Google Scholar]
- [19].Bengio Yoshua, Simard Patrice, and Frasconi Paolo, “Learning long-term dependencies with gradient descent is difficult,” IEEE transactions on neural networks, vol. 5, no. 2, pp. 157–166, 1994. [DOI] [PubMed] [Google Scholar]
- [20].Hochreiter Sepp and Schmidhuber Jürgen, “Long short-term memory,” Neural computation, vol. 9, no. 8, pp. 1735–1780, 1997. [DOI] [PubMed] [Google Scholar]
- [21].Bahdanau Dzmitry, Cho Kyunghyun, and Bengio Yoshua, “Neural machine translation by jointly learning to align and translate,” arXiv preprint arXiv:1409.0473, 2014. [Google Scholar]
- [22].Chung Junyoung, Gulcehre Caglar, Cho KyungHyun, and Bengio Yoshua, “Empirical evaluation of gated recurrent neural networks on sequence modeling,” arXiv preprint arXiv:1412.3555, 2014. [Google Scholar]
- [23].Dey Rahul and Salemt Fathi M, “Gate-variants of gated recurrent unit (gru) neural networks,” in Circuits and Systems (MWSCAS), 2017 IEEE 60th International Midwest Symposium on IEEE, 2017, pp. 1597–1600. [Google Scholar]
- [24].Sutskever Ilya, Vinyals Oriol, and Le Quoc V, “Sequence to sequence learning with neural networks,” in Advances in neural information processing systems, 2014, pp. 3104–3112. [Google Scholar]
- [25].Bengio Yoshua et al. , “Learning deep architectures for ai,” Foundations and trends® in Machine Learning, vol. 2, no. 1, pp. 1–127, 2009. [Google Scholar]
- [26].Achille Alessandro and Soatto Stefano, “Emergence of invariance and disentanglement in deep representations,” Journal of Machine Learning Research, vol. 19, no. 50, 2018. [Google Scholar]
- [27].Bengio Emmanuel, Thomas Valentin, Pineau Joelle, Precup Doina, and Bengio Yoshua, “Independently controllable features,” CoRR, vol.abs/1703.07718, 2017. [Google Scholar]
- [28].Hadsell Raia, Chopra Sumit, and LeCun Yann, “Dimensionality reduction by learning an invariant mapping,” in Computer vision and pattern recognition, 2006 IEEE computer society conference on IEEE, 2006, vol. 2, pp. 1735–1742. [Google Scholar]
- [29].Kingma Diederik and Ba Jimmy, “Adam: A method for stochastic optimization,” arXiv preprint arXiv:1412.6980, 2014. [Google Scholar]
- [30].Srivastava Nitish, Hinton Geoffrey, Krizhevsky Alex, Sutskever Ilya, and Salakhutdinov Ruslan, “Dropout: A simple way to prevent neural networks from overfitting,” The Journal of Machine Learning Research, vol. 15, no. 1, pp. 1929–1958, 2014. [Google Scholar]
- [31].Ioffe Sergey and Szegedy Christian, “Batch normalization: Accelerating deep network training by reducing internal covariate shift,” arXiv preprint arXiv:1502.03167, 2015. [Google Scholar]
- [32].Nair Vinod and Hinton Geoffrey E, “Rectified linear units improve restricted boltzmann machines,” in Proceedings of the 27th international conference on machine learning (ICML-10), 2010, pp. 807–814. [Google Scholar]
- [33].Paszke Adam, Gross Sam, Chintala Soumith, Chanan Gregory, Yang Edward, DeVito Zachary, Lin Zeming, Desmaison Alban, Antiga Luca, and Lerer Adam, “Automatic differentiation in pytorch,” 2017.
- [34].Alam Fakhre, Rahman Sami Ur, Ullah Sehat, and Gulati Kamal, “Medical image registration in image guided surgery: Issues, challenges and research opportunities,” Biocybernetics and Biomedical Engineering, vol. 38, no. 1, pp. 71–89, 2018. [Google Scholar]
- [35].Godoy Eduardo Jorge, Lozano Miguel, Garcia-Fernandez Ignacio, Ferrer-Albero Ana, Saiz Javier, and Sebastian Rafael, “Atrial fibrosis hampers non-invasive localization of atrial ectopic foci from multi-electrode signals: a 3d simulation study,” Frontiers in physiology, vol. 9, pp. 404, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Coppola Erin E, Gyawali Prashnna K, Vanjara Nihar, Giaime Daniel, and Wang Linwei, “Atrial fibrillation classification from a short single lead ecg recording using hierarchical classifier,” in 2017 Computing in Cardiology (CinC). IEEE, 2017, pp. 1–4. [Google Scholar]
- [37].Ferrer Ana, Sebastián Rafael, Sánchez-Quintana Damián, Rodríguez José F, Godoy Eduardo J, Martínez Laura, and Saiz Javier, “Detailed anatomical and electrophysiological models of human atria and torso for the simulation of atrial activation,” PloS one, vol. 10, no. 11, pp. e0141573, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Ferrer-Albero Ana, Godoy Eduardo J, Lozano Miguel, Martínez-Mateu Laura, Atienza Felipe, Saiz Javier, and Sebastian Rafael, “Non-invasive localization of atrial ectopic beats by using simulated body surface p-wave integral maps,” PloS one, vol. 12, no. 7, pp. e0181263, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Gyawali Prashnna K, Chen Shuhang, Liu Huafeng, Horacek B Milan, Sapp John L, and Wang Linwei, “Automatic coordinate prediction of the exit of ventricular tachycardia from 12-lead electrocardiogram,” in 2017 Computing in Cardiology (CinC). IEEE, 2017, pp. 1–4. [Google Scholar]
- [40].Chen Shuhang, Gyawali Prashnna K, Liu Huafeng, Horacek B Milan, Sapp John L, and Wang Linwei, “Disentangling inter-subject variations: Automatic localization of ventricular tachycardia origin from 12-lead electrocardiograms,” in 2017 IEEE 14th International Symposium on Biomedical Imaging (ISBI 2017) IEEE, 2017, pp. 616–619. [Google Scholar]
- [41].Achille A and Soatto S, “On the emergence of invariance and disentangling in deep representations. arxiv 2017,” arXiv preprint arXiv:1706.01350. [Google Scholar]
- [42].Kingma Diederik P and Welling Max, “Auto-encoding variational bayes,” in Proceedings of the 2nd International Conference on Learning Representations (ICLR), 2013, number 2014. [Google Scholar]
- [43].Yildirim Ozal, San Tan Ru, and Acharya U Rajendra, “An efficient compression of ecg signals using deep convolutional autoencoders,” Cognitive Systems Research, vol. 52, pp. 198–211, 2018. [Google Scholar]