Graphical abstract
Abbreviations: aacomp, amino acid composition descriptors; CNN, convolutional neural network; const, constitutional descriptors; ctd, composition transition and distribution descriptors; HMM, hidden Markov model; kappa, Kappa shape indices; LSTM, long short-term memory; MD, molecular dynamics; MM/GBSA, molecular mechanics/generalized born surface area; MM/PBSA, molecular mechanics/Poisson-Boltzmann surface area; paacomp, type 1 pseudo amino acid composition descriptors; RF, random forest; RMSD, root-mean-square deviation; RNN, recurrent neural network; SASA, solvent accessible surface area; top, topological descriptors; WTP, wildtype protein
Keywords: Missense mutation, Mutation impact, Protein-ligand binding affinity, Molecular dynamics (MD) simulations, Local geometrical features, Time series features, Deep learning
Abstract
Purpose
Mutation-induced variation of protein-ligand binding affinity is the key to many genetic diseases and the emergence of drug resistance, and therefore predicting such mutation impacts is of great importance. In this work, we aim to predict the mutation impacts on protein-ligand binding affinity using efficient structure-based, computational methods.
Methods
Relying on consolidated databases of experimentally determined data we characterize the affinity change upon mutation based on a number of local geometrical features and monitor such feature differences upon mutation during molecular dynamics (MD) simulations. The differences are quantified according to average difference, trajectory-wise distance or time-vary differences. Machine-learning methods are employed to predict the mutation impacts using the resulting conventional or time-series features. Predictions based on estimation of energy and based on investigation of molecular descriptors were conducted as benchmarks.
Results
Our method (machine-learning techniques using time-series features) outperformed the benchmark methods, especially in terms of the balanced F1 score. Particularly, deep-learning models led to the best prediction performance with distinct improvements in balanced F1 score and a sustained accuracy.
Conclusion
Our work highlights the effectiveness of the characterization of affinity change upon mutations. Furthermore, deep-learning techniques are well designed for handling the extracted time-series features. This study can lead to a deeper understanding of mutation-induced diseases and resistance, and further guide the development of innovative drug design.
1. Introduction
As exposed by the next-generation sequencing (NGS) techniques, a wide variety of genetic mutations exist in different organisms [38]. Such genetic mutations, particularly missense mutations, can cause proteins to malfunction by modulating their stability as well as altering their affinity with other biological molecules [38], [44], [22], [43]. The stability changes (thermodynamic) upon mutations can be quantified by the change of folding free energy (), which is a result of collective contributions from multiple structural features (e.g. hydrogen bonds, etc.) and physico-chemical properties (e.g. polarity, solvation energy, etc.) [26]. Besides experimental measurements, various computational methods have been developed to decipher , which fall into sequence-based machine-learning approaches and structure-based approaches involving statistical potentials, biophysics knowledge or intensive sampling (e.g. free energy perturbation, thermodynamic integration, etc.) [50]. Disease-causing mutations frequently destabilize proteins () with accompanied structural changes [31]. However, local changes of geometry without necessarily affecting the folding free energy () can still be disease-causing [26]. This reflects the importance of local geometrical changes upon mutations, and makes predicting the impact and associated phenotypes of mutations a challenging problem. Arguably, the phenotypes of mutations depend principally on the changes in protein-partner binding affinity, which can be measured by the binding free energy changes () and determines the magnitude of physiological effect. In general, any mutation-induced affinity change may be disease-causing with high risk [45], [56]. Aside from experimental investigation, computational methods designed for deciphering binding free energy changes can be categorized similarly to those determining the folding free energy changes [26].
Particularly, the effects of missense mutations on small molecule ligand binding to proteins can respond to many genetic diseases and the emergence of drug resistance [44], [43]. Deciphering the protein-ligand affinity changes upon mutations has therefore been an essential step towards more innovative and personalized therapeutic interventions. Although high-throughput DNA sequencing allows vast amounts of mutations to be identified rapidly, determining the mutation impacts often requires time-consuming and expensive experiments (e.g. isothermal titration calorimetry [13], FRET [42], surface plasmon resonance [34], etc.). To computationally decode the impacts of mutations on protein-ligand binding affinity, efforts have also been made, mostly based on molecular dynamics (MD) simulations. These works either focused on the direct estimation of binding free energy () or employed machine-learning techniques to monitor specific structural/physico-chemical features in protein dynamics. For a pair of wild-type type 1 human immunodeficiency virus (HIV-1) protease and its drug-resistant mutant, Perryman et al. implemented all-atom MD simulations in explicit solvent and examined the structural properties sampled during the simulations, which demonstrated decreased binding affinities of inhibitors to the mutant [39]. In [21], for a group of homologically modeled mutants of HIV-1 protease, implicit-solvent MD simulations were conducted, based on which the free energy decomposition analysis coupled with machine-learning techniques was applied to quantitatively estimate the protease-drug binding affinity for different mutations. Similarly, by incorporating binding free energy components extracted from explicit-solvent MD simulations and personalized characteristics, drug-resistant epidermal growth factor receptor (EGFR) mutations or EGFR-mutated lung cancer patients were recognized using machine-learning approaches in [53]. Ma et al. predicted drug-resistant EGFR mutants that generally have lower binding affinity with inhibitors by combining MD simulations and local surface geometrical properties, represented by the curvature of atoms in drug-binding pockets [33]. Zou et al. investigated the relationships between mutations and EGFR-inhibitor interactions by investigating atom connectivity dynamics, which indicate longitudinal distance changes between an inhibitor and its target [62]. Aside from these MD simulation-based studies, molecular descriptors can also be a potential alternative for deducing molecular affinity or its change upon mutation [7], [57]. Molecular descriptors can be used to encode useful molecular information as numerical features by characterizing the structural and physico-chemical properties of molecules according to distinct aspects of molecular topology. In the past decades, a variety of descriptors ranging from simple constitutional/count descriptors to complicated steric/quantum-chemical descriptors have been developed for chemical structures [1], [1], [8], [18], [10], [2], [9] and proteins [29], [11], [55], [6], [37]. Chemical-protein interaction descriptors can be designed on top of them by a simple concatenation or tensor product [10]. Such descriptors can easily be adopted by the machine-learning community for determining the impact of mutations on protein-ligand binding affinity.
To mitigate the limitations in these studies, such as scarcity of samples, unavailability of experimentally-determined mutant structures and lack of experimental affinity measurements for verification, attempts have been made over the past decades to establish comprehensive databases that link missense mutations with experimentally measured affinity changes of protein-partner binding systems [43], [27], [3], [35]. Among them, Platinum [43] is a manually curated and literature-derived database that compiles ligand-affinity measurements (experimental) for wild-type proteins (WTPs) and their mutants under the same experiment conditions, and links such protein-ligand complexes to their three-dimensional structural information deposited in the Protein Data Bank (PDB) [4]. This provides a valid resource for designing structure-guided, computational approaches to predict the impacts of mutations on protein-ligand binding affinity. Standing on these consolidated databases and the importance of local geometrical changes upon mutations, we proposed a number of local geometrical/structural features (closeness, local surface area, orientation, contacts and interfacial hydrogen bonds) and monitored their differences between the WTP-ligand and mutant-ligand systems in the dynamics simulations. Such feature differences were further employed by machine-learning methods to predict the mutation impact on protein-ligand binding affinity. To compromise on the discrepancy among different experiment conditions for deriving the ligand-affinity measurements, we only learned an increased or decreased affinity upon mutation (categorical). The energy-based and descriptor-based predictions were performed as benchmarks for our method. An overall framework of this study is shown in Fig. 1.
Fig. 1.
Overall framework for predicting the impacts of mutations on protein-ligand binding affinity. In the data-collection phase, mutation, affinity (ligand-binding affinity measurements for each pair of wild-type protein (WTP) and its mutant), experimental (experiment conditions for deriving the ligand-binding affinity) and structural (crystal structures of WTP-ligand and mutant-ligand complexes) data were conjunctionally collected from Platinum and Protein Data Bank. The molecular dynamics (MD) simulation step involved each WTP-ligand or mutant-ligand system, and adopted the explicit-solvent model. Next, the trajectory frames for each system were collected, and the difference between each pair of WTP-ligand and mutant-ligand systems was quantified according to several local geometrical features (closeness, local surface area, orientation, contacts and interfacial hydrogen bonds) in these frames. Finally, in the prediction phase we adopted machine-learning methods to relate such feature differences to the mutation impact on protein-ligand binding affinity. Prediction based on direct estimation of binding free energy and that based on molecular descriptors were also implemented as benchmarks.
2. Material and methods
2.1. Data collection
In this work, we mainly adopted the protein-ligand affinity information in Platinum [43] and the associated crystallographic structures in PDB [4] for a supervised study of mutation impacts on protein-ligand binding affinity. Specifically, we filtered the mutations using criteria that (1) the molecular structures of both the WTP and mutant have been released in PDB, avoiding structural modeling with no ground truth, (2) the structures should have a high resolution ( angstrom ()), guaranteeing high-quality data, and (3) the involved ligands belong to the ligand library of AMBER software suite, leading to accurate MD simulations. For the impacts of mutations on protein-ligand binding affinity, ‘decreased affinity’ (D) and ‘increased affinity’ (I) comprise the two types. The impact of each mutation on protein-ligand binding affinity is defined on the triplet .
2.2. Molecular dynamics (MD) simulations
For a triplet , the mutation impact on protein-ligand binding affinity is highly associated with the discrepancy between the WTP-ligand and the mutant-ligand binding systems in their dynamics. For each mutation, the WTP and mutant were structurally aligned [40] in advance to ensure a more compatible analysis. Only the ligand-binding protein chains were remained. An online program H++ [15] was employed to protonate these chains and add missing hydrogen atoms for them according to the experimental pH values in Platinum, where a non-specified pH was regarded as the neutral pH (7.0). The gaps (missing residues), most of which are not located in the ligand-binding vicinity, of these protonated proteins were capped with acetyl group at the N terminus and amide residue at the C terminus prior to MD simulations. Proteins with multiple binding sites were considered separately for each site.
Depending on the AMBER software suite [5], MD simulations in explicit solvent with periodic boundaries were conducted for each WTP-ligand or mutant-ligand complex. AMBER ff14SB and gaff force fields were used separately for proteins and ligands. Compulsory metal ions were handled using the 12-6 Lennard-Jones (LJ) non-bonded model [28], which is broadly applied due to its simplicity and excellent transferability. Cofactors such as heme groups (all-atom model in [14]) were regarded as non-standard units, with the parameters imported from AMBER parameter database ( http://research.bmh.manchester.ac.uk/bryce/amber/ http://research.bmh.manchester.ac.uk/bryce/amber/). A 12 buffer of TIP3P water around each neutralized complex in any direction, constituting a truncated octahedron water box, was imposed. Prior to the production MD simulation, each system was subsequently minimized and equilibrated, and the equilibration includes heating the system to the experimental temperature (a missing value assigned to 298 Kelvin) and equilibrating the system at constant pressure. All equilibration simulations were conducted with shake on hydrogen atoms and Langevin dynamics for temperature control [5]. To guarantee a valid production simulation, the equilibration of each system was verified through investigating the root-mean-square deviation (RMSD) of atomic positions to a reference structure. The production simulation for each system lasted for 2 ns and resulted in 1000 trajectory frames, which were collected at a time step of 2 picoseconds (ps). All the simulations were GPU-accelerated [16], [48].
For each WTP-ligand or mutant-ligand system, the production MD trajectory is composed of a series of structural snapshots , and represents the i-th structure.
2.3. Characterizing affinity change upon mutation using local geometrical features
2.3.1. Local geometrical features of protein-ligand systems
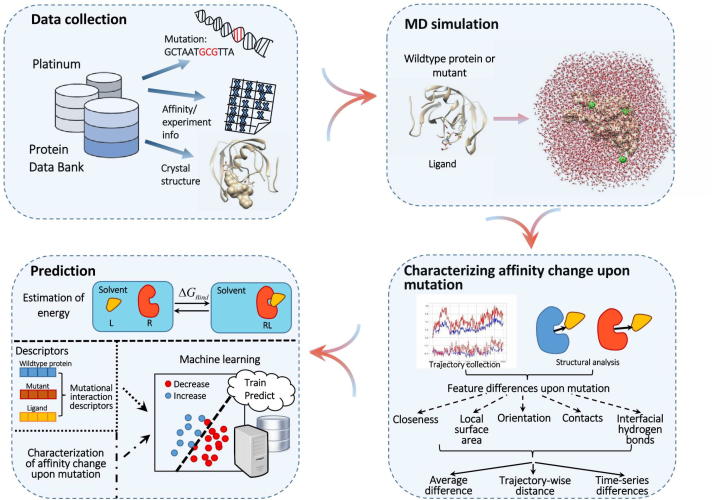
Protein-ligand closeness. For a protein-ligand system, distance between the ligand and its binding site on the protein is a common measure for the affinity [62], [61]. Here we define the closeness of a protein-ligand system based on the distance (Fig. 2a) expressed in Eq. (1).
| (1) |
where i and j indicate atoms in amino acid residue and the ligand LIG respectively, represents the coordinates of atom denotes the binding-site residues, is the cardinality of set S and means the Euclidean distance between a and b. This measures the negative average of the pairwise residue-ligand distances based on their geometric centers. Here we only consider heavy atoms to ease the computations.
Fig. 2.
Local geometrical features of protein-ligand systems. (a) Closeness. (b) Solvent accessible surface area of ligand-binding site. (c) Orientation. (d) Contacts. (e) Interfacial hydrogen bonds.
Solvent accessible surface area of ligand-binding site. Solvent accessible surface area (SASA) of a biomolecule measures the surface area that is accessible to a solvent, and the SASA of the ligand-binding site plays an important role in protein-ligand binding affinity. For each protein-ligand system, the SASA () of the binding-site atoms can be calculated to characterize the protein-ligand binding affinity (Fig. 2b), according to the LCPO algorithm [54].
Protein-ligand orientation. We define protein-ligand orientation as Eq. (2). Each angle is between two rays diverging from the center of the whole binding site B, with one ray passing through the center of a binding-site residue and the other the center of the ligand L. The absolute deviations of these angles to were averaged to yield the protein-ligand orientation (Fig. 2c). This orientation also measures protein-ligand binding affinity. Here we consider geometric centers and the heavy atoms only.
| (2) |
Protein-ligand contacts. For a protein-ligand system, the atomic contacts within a distance cutoff between the ligand and binding site also measure the protein-ligand binding affinity, and we define the total contacts (Fig. 2d) for the system as in Eq. (3).
| (3) |
where is the indicator function where only if x is fulfilled, and t is the distance cutoff. Cutoff of was selected in this work.
Interfacial hydrogen bonds for protein-ligand system. Hydrogen bonds play a significant role in protein-ligand interactions as they control the binding specificity and stabilization of various molecular binding systems in solvent [60]. Determining hydrogen bonds follows simple geometric rules including basic structure (heavy-atom acceptor A, hydrogen-atom donor H and heavy-atom donor D), component atoms (specified atom types for donors and acceptors) and formation criteria (the A-to-D distance is less than a cutoff and angle is greater than a cutoff). Following the CPPTRAJ module in AMBER, the cutoff for the A-to-D distance was set as the default value of 3 and that for the angle the default value of 135 [5]. For a protein-ligand system, the number of hydrogen bonds connecting the system is defined as follows.
| (4) |
where indicates the number of hydrogen bonds formed by donors in a binding-site residue and acceptors in the ligand LIG, and is similarly defined (Fig. 2e).
2.3.2. Characterizing affinity change upon mutation
Considering the dynamics of a protein-ligand system, we can characterize its affinity using , where corresponds to the ith MD structural snapshot (). By comparing the difference of such features between each pair of WTP-ligand and mutant-ligand systems, we can characterize the affinity change upon mutation. Such difference can be defined using following strategies.
First, it can be defined as the average difference over all the MD snapshots of each feature (Eq. (5)).
| (5) |
where , and and indicate the mutant-ligand and WTP-ligand systems respectively.
Another strategy is to calculate the trajectory-wise distance between a pair of WTP-ligand and mutant-ligand systems based on each feature (Eq. (6)).
| (6) |
where is the distance between two time series and , and can be the Euclidean, correlation, cosine or Dynamic Time Warping (DTW) distance (Eq. (7)). The correlation distance is calculated based on the Pearson correlation coefficient. The DTW distance is computed as the Euclidean distance between the two aligned time series according to the alignment path P.
| (7) |
An alternative strategy is to simply use the trajectory of feature differences between a pair of WTP-ligand and mutant-ligand systems (Eq. (8)).
| (8) |
Accordingly, the affinity change upon mutation can be characterized by or (time series).
2.4. Prediction of mutation impact on protein-ligand binding affinity
2.4.1. Prediction based on machine-learning techniques
Based on the extracted features, we can apply machine-learning techniques to the prediction of mutation impacts on protein-ligand binding affinity. We used a simple train-test mechanism with a random half-half partition. Features were standardized to zero mean and unit variance before fed to the training machines. For each setting, we repeated the experiments 10 times and averaged the performance. As we face an imbalanced classification problem, the performance was evaluated by both the accuracy and balanced F1 score. The balanced F1 score is simply computed as the average of the F1 scores concerning the two mutation impacts (D and I) separately, as shown in Eq. (9).
| (9) |
Conventional features. For conventional features like or , we employed traditional random forests (RFs) [20], which have been successfully applied to extensive machine-learning tasks [58]. RFs are an ensemble learning method that depends on a multitude of decision-tree learners in training and outputs the averaged prediction from individual tree learners. RFs have mitigated the overfitting problem of individual decision trees in the training phase. Specifically, RFs apply the general bagging technique to tree learners, which repeatedly selects a random sample from the training set, fits trees to those samples, and finally averages the prediction (or takes the majority vote). In addition, RFs adopt feature bagging (a random subset of features) in the learning process to reduce the correlated trees in the original bagging algorithm. Normally the optimal number of trees can be determined by cross validation or observing the out-of-bag error. For simplicity in this work, we fix this parameter as 50 for handling our medium-sized dataset, with the maximum depth of each tree set as 2.
Single time-series features. Aside from conventional features, the time-series features () should have high classification power. It is well acknowledged that hidden Markov models (HMMs) are designed for analyzing time-series data, although they can merely cope with individual sequences. Here use HMMs to deal with single time-series features ( or ). Specifically, an HMM is a probabilistic model for learning systems that can be assumed as a Markov process with hidden states, and each state can independently generate observations according to emission probabilities [46]. An HMM is commonly composed of the hidden-state space (state at time t denoted as ), the set of distinct observation symbols generated from the states (observation at time t denoted as ), transition probabilities between hidden states (considering first-order Markov chains only), emission probabilities for the states to produce observations and probabilities of initial hidden states . These probabilities are defined in Eq. (10). Emissions for continuous observations can come from distributions such as a Gaussian, and we merely consider univariate emission probabilities in this work.
| (10) |
An HMM can thereupon determined by . Given observations can be trained by the Baum-Welch algorithm to maximize . For a given observation sequence and multiple HMMs , the model that best matches the observations can be determined by , where can be computed through the Viterbi algorithm. In this work, we separately trained HMMs for the two mutation impacts (D and I) using the training set, based on single time-series features. The cardinality of the state space is assumed to be 3, which is commonly used in speech recognition [46]. Gaussian emissions were adopted. A test trajectory is assigned with an HMM if it corresponds to a higher .
Multiple time-series features. To deal with multiple time-series features (), we adopted several machine-learning and deep-learning models. The first model is a simple densely connected neural network (multilayer perceptron - MLP), which is composed of an input layer that flattens the times series into a vector, a densely connected layer, a dropout layer and an output layer. Specifically, we employed 50 nodes in the densely connected layer, with the ReLU activation function. The sigmoid function was used as the activation function for the output layer. A dropout layer [49] was added between the densely connected and output layers to mitigate the overfitting issues, and we adopted a dropout ratio of 25%. During the training process, the binary cross-entropy function was selected to calculate the loss, and the efficient Adam optimizer [23] was adopted for updating the network parameters. In addition, we set the class weight of the minority class the two times as that of the majority during training, to balance the samples.
An alternative model is the convolutional neural networks (CNNs), which have been successfully applied to abundant applications such as image classification and speech recognition [30]. CNNs are well designed for image classification due to their consideration of spatial structure of the images [25], where neighboring pixels are correlated. The essence of CNNs includes local receptive fields, shared weights and pooling. Local receptive fields correspond to localized regions of the input image that are connected to different hidden neurons. A map of hidden neurons connected to their local receptive fields share the same weights and bias, implying the detection of the same feature (such as a horizontal edge) by these neurons. This highlights the translation invariance nature of images. Accordingly, the shared weights and bias define a specific kernel of filter for the input image, corresponding to a feature map in the hidden layer. For a filter of size with weights and bias b, a hidden neuron in the feature map will output as follows,
| (11) |
where denotes the inputs and is an activation function (ReLU in most CNNs). This corresponds to a convolution operation. A full convolution layer in a CNN normally consists of multiple feature maps (filters), to learn different types of features. A pooling layer frequently follows a convolutional layer, which condenses each feature map in the convolutional layer into a smaller one by summarizing regions of the map as the max or average value. Overall, a complete CNN is composed of an input layer, consecutive convolutional and pooling layers, a layer for flattening the feature maps, a densely connected layer and a final output layer. For inputs of multiple time-series features, it may differ from the original spatial structures of images as the order of the time series may vary. However, such data still possess the sequential structures along the time axis, which can be beneficial from the convolutional layers. Specifically in this work, we implemented both two-dimensional (2D) and one-dimensional (1D) convolutions in CNN models. For a 2D case, we assembled a CNN with a convolutional layer including 50 filters of size (5 types of time series ), a 1D pooling layer of size 2 that maximizes feature-map regions and the following layers. In the 1D case, we replaced the 2D convolution filters with 1D filters of size 3. Similarly, two dropout layers, one after the pooling layer and the other after the densely connected layer, were inserted to mitigate the overfitting problem. The optimizer, loss function, class weights, dropout ratio and activation functions for training were set the same as aforementioned.
The third model is the recurrent neural networks (RNNs) where the activation of hidden/output neurons is determined by both the current and earlier inputs (time-varying behavior), thus perfectly designed for time-series features. RNNs are extremely useful in speech recognition [17]. Basic RNNs organize neuron-like nodes into successive layers, with each node having a time-varying activation. Unfortunately, RNNs suffer from short-term memory and the vanishing gradient problem during back propagation. Long short-term memory (LSTM) has been broadly incorporated as a solution to the short-term memory. LSTM uses gates to regulate the flow of information, which can deliver relevant information along the sequences to make prediction. Specifically, in an LSTM cell its state carries the relevant information throughout the processing of the sequences, and it adds information to the state or removes from it via different gates. Three types of gates, namely the forget gate, input gate and output gate, are used in an LSTM cell. A forget gate decides what memory (previous hidden state ) to keep or forget. An input gate handles the new coming information and decides how much to memorize it. The cell state is then defined as the combination of the remaining memory and the processed new information. The output gate then decides the next hidden state. Practically, many LSTM cells will be used in an application, and the network can be summarized as follows,
| (12) |
where denotes the overall state of many LSTM cells, are the gates to regulate different LSTM cells, means pointwise multiplication, and and represent the input, hidden state and the output respectively. tanh is the activation function for the new coming information and the hidden state. The gates are normally controlled by the current input , the previous hidden state and the sigmoid activation function. For RNNs in this work, we simply set the number of hidden units in the LSTM cell as 50 and collected the hidden state outputs for each time step in the LSTM. To avoid overfitting, dropout layers between recurrent layers were embedded. LSTM is then followed by a feature-flattening layer and an output layer. Parameters like optimizer, loss function, class weights, dropout ratio and activation functions for training were similarly selected as earlier. In addition, we also attempted to combine CNN and RNN models. CNNs are good at learning the spatial structure in the inputs, and we applied convolutional layers to extract invariant features of the time-series data before feeding them into an LSTM layer. Here 1D convolutional and max pooling layers were used, with all the other parameters set the same as above.
2.4.2. Prediction based on energy estimation
Based on MD simulations, computational estimation of binding free energies can be used to uncover the mutation impacts on protein-ligand binding affinity [53], [32], [52]. The assembly of molecular mechanics (MM) energies, Poisson-Boltzmann (PB) or generalized Born (GB) models, and surface area (SA) continuum solvation yields popular MM/PBSA or MM/GBSA method to estimate the free energy of binding of a ligand to a protein [12]. In these methods, the free energy G of a state is estimated as follows.
| (13) |
where is the MM energy term contributed by bonded, electrostatic and van der Waals interactions. and are the polar and non-polar contributions to the solvation free energies. can be estimated by the PB equation or the GB model [12]. The non-polar contribution is typically obtained based on the SASA. T indicates the temperature of the system and S is the entropy contribution, which is frequently ignored because of its high computational cost. Additionally, for similar systems like a WTP and its mutant, such contributions can be quite similar and therefore ignored. It is common to only simulate the dynamics of the protein-ligand complex (PL) and extract the dynamics of free ligand (L) and protein (P) respectively, leading to the estimation of the free energy of binding as Eq. (12), where indicates the energies are averaged from the simulation of the complex.
| (14) |
To predict the mutation impacts on protein-ligand binding affinity, we computed the difference of binding free energy between each pair of WTP-ligand and mutant-ligand complexes (Eq. (13)). As a largely negative binding free energy indicates a higher affinity, a negative difference represents type I and otherwise type D. MM/PBSA or MM/GBSA calculates relative binding free energies with the ignorance of conformational rearrangement upon binding, therefore considering the sign of the difference instead of the value can compromise on the discrepancy among different pairs of WTP-ligand and mutant-ligand systems.
| (15) |
2.4.3. Prediction based on molecular descriptors
Molecular descriptors, which play an important role in cheminformatics and bioinformatics, are a potential alternative for deducing the affinity change upon mutation. For chemical structures, commonly used structural and physicochemical descriptors include constitutional descriptors [1], topological descriptors [1], [8], Kappa shape indices [18], charge descriptors [10], Basak information indices [2], autocorrelation descriptors [9], etc. Those for proteins and peptides incorporate amino acid composition descriptors [29], composition, translation and distribution (CTD) of various structural and physicochemical properties [11], autocorrelation descriptors [55], pseudo amino acid composition descriptors [6], [37], etc. Chemical-protein interaction descriptors can be defined on top of these chemical and protein descriptors by a simple concatenation or tensor product [10].
We attempted to decode the mutation impacts on protein-ligand binding affinity from the perspective of molecular descriptors. A number of widely-used descriptors for the ligands and proteins were employed in this study. For ligands, the following descriptors were adopted.
-
•
Constitutional descriptors (const): 30 features including molecular weight, average molecular weight, count of all atoms, counts of different types of atoms (hydrogen, halogen, Carbon, nitrogen, etc.), number of rings, number of different types of bonds (rotatable, single, aromatic, etc.), number of hydrogen bond acceptors/donors and molecular path counts (length of ). The full list can be found in [10]).
-
•
Kappa shape indices (kappa): 7 features including first-, second- and third-order topological shape descriptors, Kier molecular flexibility index, and first-, second- and third-order Kier alpha-modified shape descriptors [51].
-
•
Topological descriptors (top): 30 topological features including (average) Weiner index, Balaban’s J index, Schiultz index, graph distance index, Xu index, Pogliani index, Ipc index, BertzCT, Gutman molecular topological index, Zagreb index with order , quadratic index, topological indices proposed by Narumi, Harary number, Platt number, Polarity number, maximum value in distance matrix, topological radius and topological Petitjean [10]).
For proteins and peptides, we calculated the following descriptors based on the sequences.
-
•
Amino acid composition descriptors (aacomp): 20 features indicating the fractions of each type of amino acid in the whole protein sequence.
-
•
CTD descriptors (ctd): 147 features. The amino acids are first encoded according to each of the attributes including hydrophobicity, normalized van der Waals volume, polarity, polarizability, etc. For each encoded class, the composition (fractions in the whole sequence), transition (frequency of being neighbors to another encoded class) and distribution (quantile-based) descriptors can be calculated [11]).
-
•
Type 1 pseudo amino acid composition descriptors (paacomp): 50 features. On the basis of normalized attribute values (hydrophobicity, hydrophilicity, side chain mass, etc.) of each type of amino acids, a set of sequence order-correlated factors (first-tier, second-tier, -tier) can be calculated. The pseudo amino acid composition descriptors can be derived depending on such factors, the normalized frequency of amino acids and some weight factors (w) for the sequence-order effect [6]. Default parameters in [10] were used in our study.
Depending on sequential information or structural topology, these descriptors are invariant to structural deformation. Based on each pair of descriptors respectively for the ligands and proteins, we can construct several mutational interaction descriptors (MIDs) to characterize the protein-ligand binding affinity change upon mutation. As an example, using the constitutional descriptors for the ligands () and the amino acid composition descriptors for the proteins (wtp: and mutant: ) leads to the following types of MIDs.
| (16) |
| (17) |
| (18) |
| (19) |
We also trained RFs to deal with such MIDs and evaluated the performance using the accuracy and balanced F1 score (9). For a given pair of descriptors (such as const for ligands and aacomp for proteins), we only reported the best performance among the four types of MIDs (Eqs. (16)–(19)). Additionally, we combined all descriptors for the liand (const, kappa and top) and those for the proteins (aacomp, ctd and paacomp), for a further prediction.
3. Results
3.1. Collected data
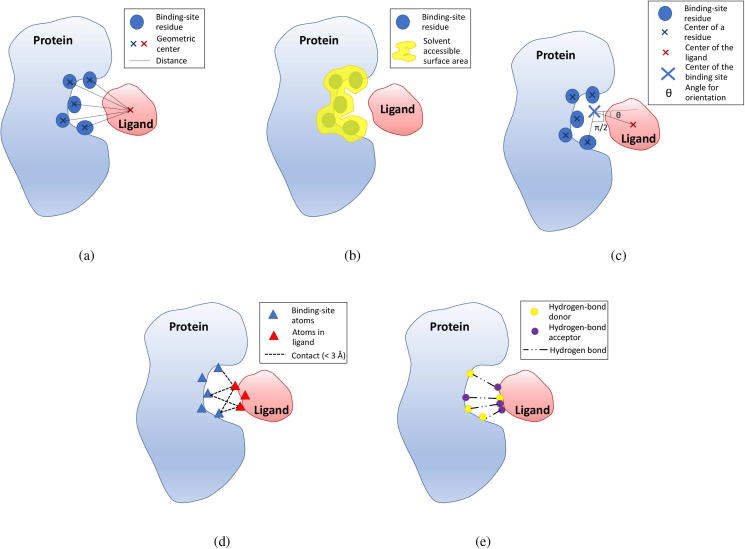
110 protein mutations, corresponding to 160 wildtype or mutant proteins in PDB, passed this filter. The statistics for these mutations are presented in Supplementary Table S1. Among them, 94 are single-point mutations and the rest double- or multi-point mutations. Majority of the proteins belong to classes of oxidoreductase (54), hydrolase (25), transferase (9) and plasma protein (9). A wide range of organisms are involved, belonging to animalia kingdom (58, including human), viral (26), bacterium (19), protist kingdom (4) and fungi kingdom (2). As affected by the mutations, 85 mutants had decreased binding affinities (D) with the associated ligands compared to the WTPs, and 25 ones corresponded to increased affinities (I). For these two groups of mutations, statistics on the lengths of proteins and the organisms where the proteins belong are presented in Fig. 3, Fig. 3b. A further investigation of the affinity changes was conducted in case of trivial changes. Generally, protein-ligand affinities are experimentally measured by inhibitor constant (Ki), and can be associated to via (R: ideal gas constant, T: temperature, : quotient of activity coefficients). A smaller Ki indicates a higher binding affinity. Considering the WTP-ligand and mutant-ligand affinities ( and ), the fold change can be used to evaluate the affinity change, where a value represents an increased affinity and a value an decreased affinity. The density of the mutations inducing an absolute affinity fold change larger or equal to a threshold () is shown in Fig. 3c, where we can see that 98.2% mutations have induced affinity changes () and 86.4% mutations affinity changes (). This guarantees that the majority of our mutation samples correspond to nontrivial affinity changes.
Fig. 3.
Statistics of mutations. (a) Lengths of mutant proteins that cause a decreased ligand-binding affinity or an increased one. (b) Organisms where the proteins belong. (c) The density of the mutations inducing an absolute affinity fold change () larger or equal to a threshold (t). Results for and have been further marked.
3.2. MD simulations with verification of the equilibration
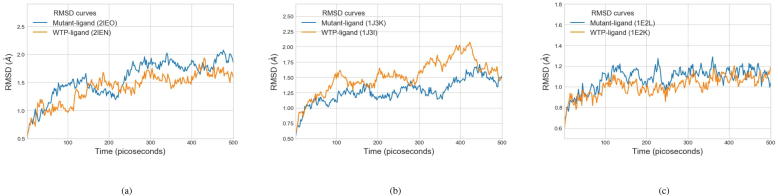
For each WTP-ligand or mutant-ligand system, the explicit-solvent MD simulations were implemented. For each solvated and neutralized system, we carried out a short minimization, heated the system to the experimental temperature, equilibrated the system at constant pressure, and implemented a production simulation that produced the trajectory for analysis. To guarantee reliable production simulations, we investigated the backbone RMSD curves of the protein-ligand systems, referring to their starting structures. Fig. 4 shows the backbone RMSD curves, at an interval of 2 ps in the equilibration period, of several examples. As presented in Fig. 4, equilibration of these systems can be verified by the stable RMSD curves, and mutant-ligand systems mostly have a larger RMSD than WTP-ligand systems. For computational loads, a solvated complex comprising a protein of 311 residues and a ligand in explicit solvent costed 2.65 h for running a 2 ns production simulation on our server (NVIDIA Tesla K40c GPU).
Fig. 4.
Equilibration verification of several protein-ligand systems using backbone RMSD curves referring to their starting structures. RMSD curves at an interval of 2 ps of both the wildtype protein (WTP)-ligand and mutant-ligand systems are displayed. (a) Mutant-ligand: PDB ID of 2IEO (protein length: 99), and WTP-ligand: ID of 2IEN (protein length: 99). (b) 1J3K (mutant-ligand, protein length: 231) and 1J3I (WTP-ligand, protein length: 233). (c) 1E2L (mutant-ligand, protein length: 329) and 1E2K (WTP-ligand, protein length: 329).
3.3. Local geometrical features for characterizing protein-ligand binding affinity change upon mutation
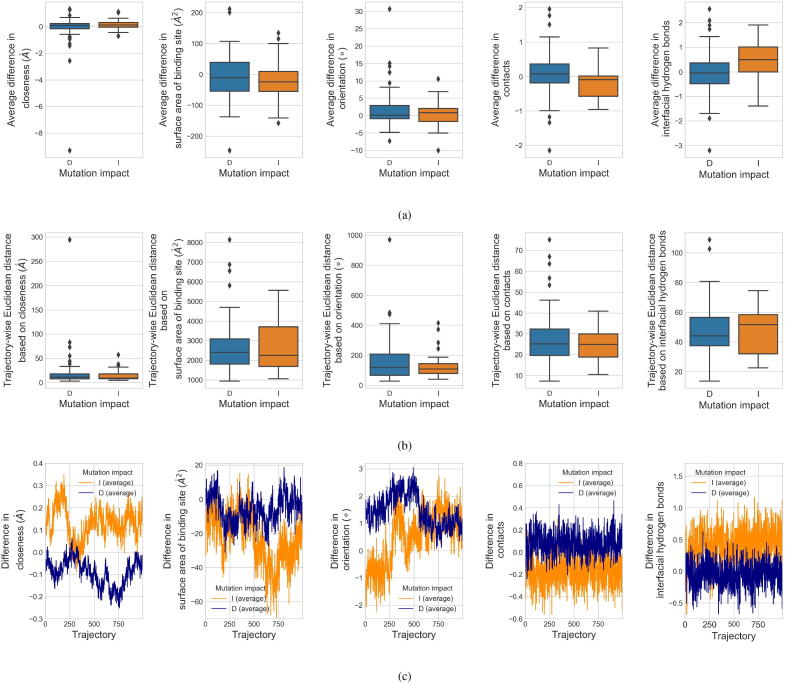
Based on a number of local geometrical features including closeness, SASA of ligand-binding site, orientation, contacts and interfacial hydrogen bonds, we characterized the difference between each pair of WTP-ligand and mutant-ligand systems using average difference, trajectory-wise distance and difference trajectory (Section 2.3.2). For the two groups of mutations (D and I), the distributions of the features extracted as average differences are presented in Fig. 5a. Upon mutations, the average closeness differences in group I are slightly higher than those in group D, indicating that the increase in closeness from the WTP-ligand systems to the mutant-ligand systems is higher in group I. Upon mutations, group I has a lower negative average difference in binding-site SASA than group D, implying more buried area from the WTPs to their mutants in group I than that in group D. The tendency in average orientation differences is not clear enough. Considering the more negative values in group I, mutant-ligand complexes have a more equilibrated orientation compared to the WTP-ligand systems in group I than those in group D. In addition, group I has a lower average difference in overall contacts but a higher average difference in interfacial hydrogen bonds (effective contacts), suggesting hydrogen bonds may be more useful than the total contacts in this prediction.
Fig. 5.
To characterize the affinity change upon mutation, difference between each pair of WTP-ligand and mutant-ligand systems was quantified by local geometrical features (closeness, surface area of binding site, orientation, contacts and interfacial hydrogen bonds) extracted from the molecular dynamics (MD) trajectories of the systems. Feature distributions for the two mutation impacts, decreased affinity (D) and increased affinity (I), are shown. Panel (a) shows the differences in each feature averaged over all the MD structural snapshots for each mutation. Panel (b) shows the trajectory-wise Euclidean distance based on each feature for the mutations. Panel (c) shows the time-vary differences in each feature during the 2 ns-simulation, averaged in each mutation group.
Besides, the trajectory-wise feature distance between each pair of mutant-ligand and WTP-ligand systems was computed to quantify their discrepancy. Distance metrics, including Euclidean, correlation, cosine and DTW, were investigated and the scenario for Euclidean distance is displayed in Fig. 5b (the rest scenarios are presented in Supplementary Fig. S1). Similar as above, the tendency in Fig. 5b seems weaker. Considering the larger span of values and a higher median in group D, it may indicate a larger orientation adjustment from the WTP-ligand systems to the mutant-ligand systems in this group. Simply considering the medians only, all the remaining features are similarly distributed as those in the earlier scenario. Here the distance calculated between two systems lacks of an explicit order (from the mutant to the WTP or the opposite), which may be a potential aspect for further refinement.
Apart from above conventional features, time-varying feature differences between the WTP-ligand and mutant-ligand systems were extracted as well. For the two mutation groups (D and I), we averaged such time series and now present them in Fig. 5c. Except for the orientation differences whose tendency is not clear enough, the others are consistent with those observed in the previous scenarios.
3.4. Prediction results of mutation impacts on protein-ligand binding affinity
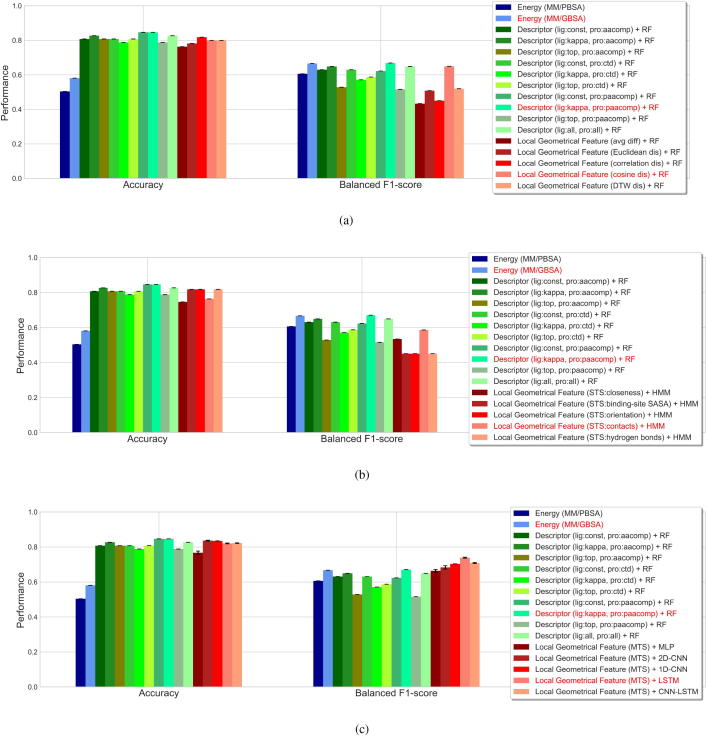
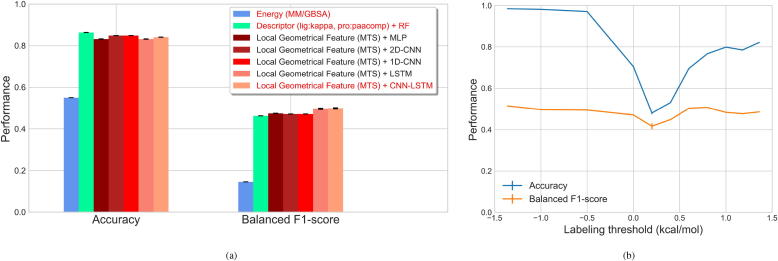
We predicted the mutation impacts on protein-ligand binding affinity using machine-learning methods in three scenarios. In all these scenarios, we adopted a simple train-test mechanism with a random selection of half samples for training. After standardizing the features, we repeated the experiments 10 times based on different classification machines and averaged the performance for evaluation. Evaluation was based on the overall accuracy and balanced F1 score. Energy-based prediction (MD simulation-dependent) and descriptor-based prediction were also performed as benchmarks. Both MM/PBSA and MM/GBSA protocols for the energy calculations were employed. As descriptors for affinity change upon mutation, MIDs (Eqs. (16)–(19)) were constructed based on descriptors for ligands and proteins (lig:const, pro:aacomp; lig:kappa, pro:aacomp; lig:top, pro:aacomp; lig:const, pro:ctd; lig:kappa, pro:ctd; lig:top, pro:ctd; lig:const, pro:paacomp; lig:kappa, pro:paacomp; lig:top, pro:paacomp or lig:all, pro:all), and handled by RFs (same setting as above). The best performance on different MIDs (Eqs. (16)–(19)) for each descriptor combination was reported.
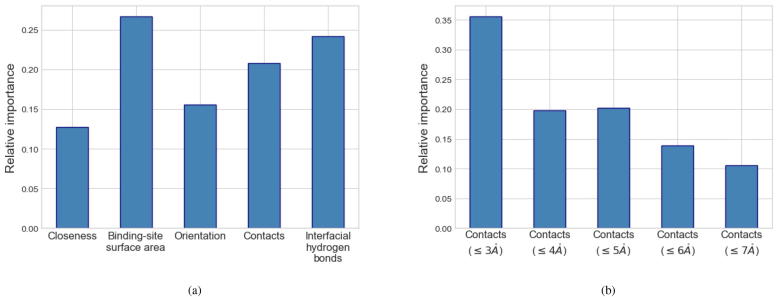
In the first scenario, conventional features, which were extracted as the average difference between each pair of WTP-ligand and mutant-ligand systems or as the trajectory-wise distance between them, were handled by RFs. 50 trees with the maximum depth of 2 were employed in RFs. The performance is now shown in Fig. 6a. Comparing these conventional features, the best performance corresponds to those extracted as trajectory-wise cosine distance (accuracy: 0.8, balanced F1 score: 0.650). Using such conventional features generally resulted in a better accuracy than energy-based prediction (MM/GBSA: 0.581, MM/PBSA: 0.505) while a lower or comparable balanced F1 score (MM/GBSA: 0.667, MM/PBSA: 0.606). Additionally, it underperformed the descriptor-based prediction in both accuracy and balanced F1 score (best descriptor-based prediction: lig:kappa, pro:paacomp; accuracy: 0.846, F1 score: 0.670). Although the prediction depending on average difference or trajectory-wise distance was barely satisfactory, they can still provide some clues on the importance of involved local geometrical features in the prediction, which can be quantified by a tree ensemble like RFs. Here we used the best performer (trajectory-wise cosine distance + RF) to measure the relative importance of these features. As shown in Fig. 7a, SASA of the binding site has the highest importance in this prediction, followed by interfacial hydrogen bonds, contacts, orientation and closeness. In this prediction, we imposed a relatively stringent threshold () on the contacts features. To further investigate the effects of thresholds on such features, we measured the importance of contacts features extracted based on different thresholds ( to ) using the best performer (Fig. 7b). It partly shows a higher importance of closer protein-ligand contacts in such prediction.
Fig. 6.
Performance evaluation of predicting mutation impacts on protein-ligand binding affinity. Performance was evaluated based on the overall accuracy and balanced F1 score. Results from the estimation of binding-free-energy difference and from the prediction based on molecular descriptors are provided as benchmarks. In the energy-based predictions, MM/PBSA and MM/GBSA methods were employed for estimating the binding free energy. In the descriptor-based predictions, generally used descriptors for the ligands (Constitutional descriptors (const), Kappa shape indices (kappa) and Topological descriptors (top)) and proteins (Amino acid composition descriptors (aacomp), Composition, translation and distribution descriptors (ctd) and Type 1 pseudo amino acid composition descriptors (paacomp)) were adopted. On top of these descriptors, the mutational interaction descriptors were constructed by concatenations or tensor products, and used for the prediction of mutation impact by random forests (RFs). Our method characterized protein-ligand binding affinity change upon mutation by several local geometrical features (closeness, solvent accessible surface area (SASA) of binding site, orientation, contacts and interfacial hydrogen bonds) and monitored such feature differences upon mutation in the molecular dynamics (MD) simulations, after which a number of machine-learning methods were adopted for prediction of mutation impact. (a) RF-based predictions according to the features extracted as the average differences or trajectory-wise distances between each WTP-ligand and mutant-ligand systems. Distance metrics of the Euclidean, Pearson correlation, cosine and dynamic time warping (DTW) were considered. (b) Hidden Markov models (HMMs)-based predictions according to single time-series (STS) features, extracted as the time-varying differences in each of the five local geometrical features. (c) Prediction according to multiple time-series (MTS) features (based on all of the five local geometrical features) by shallow or deep neural networks. These neural networks include multilayer perceptron (MLP), convolutional neural networks (CNNs) with 2D convolutional layers, CNNs with 1D convolutional layers, recurrent neural networks (RNNs) with long short-term memory (LSTM) cells, and neural networks composed of CNNs and LSTM (CNN-LSTM).
Fig. 7.
Feature importance evaluated by the random forest model, with the features extracted as trajectory-wise Cosine distances upon mutation based on local geometrical features. (a) The relative importance of five local geometrical features was evaluated. (b) The relative importance of contacts features, based on different thresholds (), was evaluated.
Single time-series features outputted as the time-varying difference upon mutation in the MD simulations were considered in the second scenario. HMMs were applied with the number of hidden states set as 3, the emissions assumed to be Gaussian, and the model parameters randomly initiated and trained using the Baum-Welch algorithm. Concerning the five time-series features generated based on the local geometrical features, the prediction performance is shown in Fig. 6b. Similar as in the first scenario, combining single time-series features and HMMs failed to refine the balanced F1 score. The best performance was derived when employing the time-series contacts differences, corresponding to an accuracy of 0.764 and a balanced F1 score of 0.586. This failed to mitigate the imbalanced classification problem; therefore, we combined all the time-series features and attempted to handle them using deep-learning techniques in what follows.
In the third scenario, we combined all the time-series features as two-dimensional features and employed shallow or deep neural networks to predict the mutation impacts. The binary cross-entropy loss function and Adam optimizer were used in each training process, and a higher class-weight was assigned to the minority class (I) to balance the samples. MLP with a feature-flattening layer, a densely connected layer (50 hidden nodes, ReLU activation), a dropout layer (ratio of 25%) and an output layer (sigmoid activation) was first constructed. We then applied CNNs with a 2D () or 1D () convolutional layer, a 1D max pooling layer (), a dropout layer, a densely connected layer, a dropout layer and an output layer. The other parameters were similarly assigned. Additionally, RNNs with LSTM were assembled to process the time-series features. The LSTM model contains recurrent LSTM layers (50 hidden units, combined outputs for each time step), dropout layers between the recurrent layers, a feature-flattening layer, a densely connected layer and an output layer. Lastly, we assembled an CNN-LSTM model that is composed of a 1D CNN part and an LSTM part for the prediction, with all the other parameters set the same as above. The prediction performance is now shown in Fig. 6c. Aside from the shallow neural networks (MLP), all the other deep learning models improved both the accuracy (0.820 0.836) and balanced F1 score (0.683 0.738), compared to the energy estimation methods. Compared to the descriptor-based predictions (best performance: lig:kappa, pro:paacomp, accuracy: 0.846, F1 score: 0.670), these deep learning models improved the balanced F1 score (0.683 0.738). Especially for the LSTM model, the best performance (accuracy: 0.820, balanced F1 score: 0.738) was obtained, guaranteeing its capacity for analyzing such time-series data. CNNs resulted in a slightly weaker performance (in balanced F1 score), which is due in part to the lack of spatial structures of our input data.
4. Discussion
4.1. Sampling frequency in MD simulations
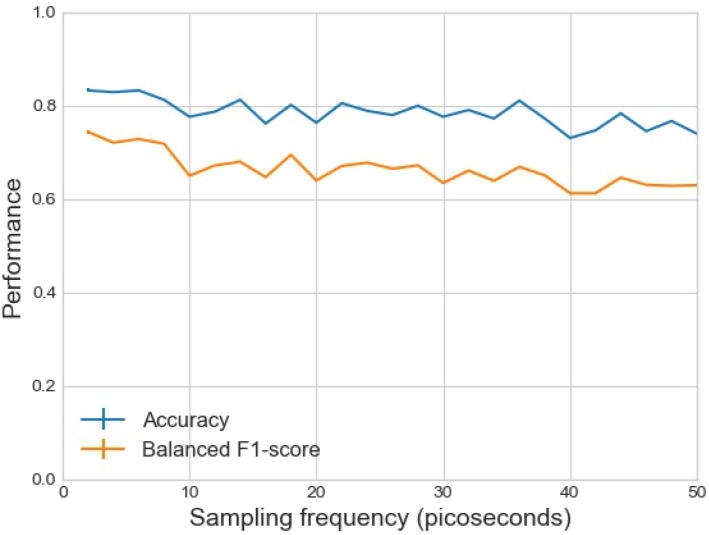
In our study, the trajectory frames were collected every 2 ps in the MD simulations for feature extraction. Here, we investigated whether the sampling frequency of trajectory frames will influence the prediction performance. Specifically, based on the multiple time-series features (Section 2.3.2) and LSTM model, we used different sampling frequencies (per ps) for collecting trajectory frames. The prediction results corresponding to different sampling frequencies are plotted in Fig. 8, where a gradual decline of performance is exhibited and a higher sampling frequency (such as per 10 ps) should be used to guarantee a fair performance.
Fig. 8.
Investigation of how the sampling frequency of trajectory frames in MD production simulations influences the prediction performance. Features were extracted as multiple time series based on the local geometrical features and MD trajectories. Prediction was conducted using the long short-term memory (LSTM) model, and the performance was evaluated by accuracy and balanced F1 score.
4.2. Duration for MD simulations
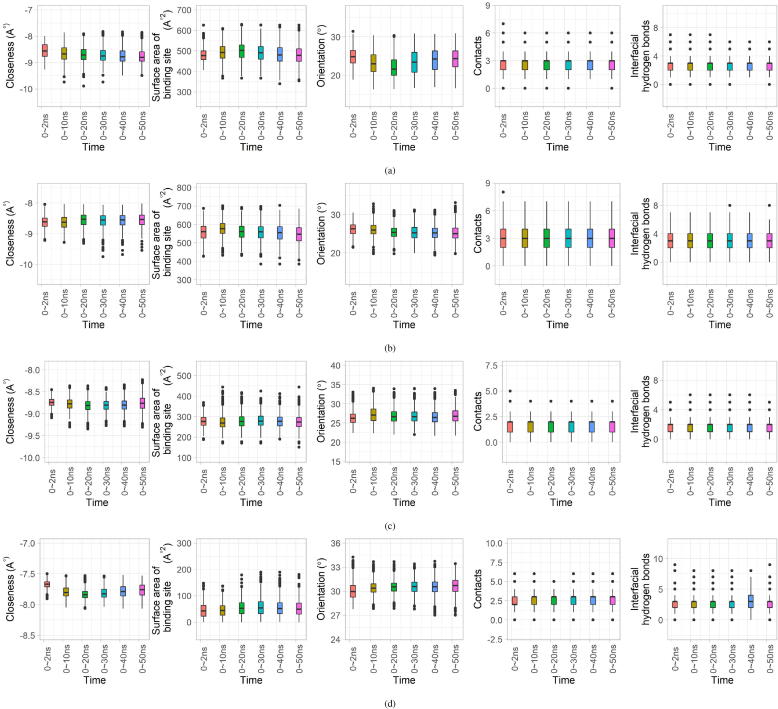
Due to the large-scale calculations imposed by the group of protein-ligand systems, we performed a 2 ns-simulation on each system in this study. In order to explore the influence of simulation times on the extracted affinity features and the prediction, we tested a number of systems with different simulation times (2 ns, 10 ns, 20 ns, 30 ns, 40 ns and 50 ns). 1000 frames were collected from each simulation at fixed intervals. The distributions of the five local geometrical features during these simulations have been presented in Fig. 9. Fig. 9a shows the feature distributions for the protein-ligand system labeled as 1BV9 (PDB ID). For 1BV9, the distributions of the five local geometrical features in the simulations with different durations possess minor differences (slightly wider or thinner spans of values), while they share quite similar quantiles. 2IEN in Fig. 9b and 1J3K in Fig. 9c are analogous to 1BV9. For 1E2K in Fig. 9d, the contacts features in the 2 ns-similation and the interfacial-hydrogen-bond features in the 40 ns-simulation differ more from the remaining simulations. Accordingly, it is difficult to decide a ‘proper’ simulation time for the systems. However, considering the similar feature distributions in these simulations and the efficiency of large-scale calculations, we recommend simulations of ns when facing a large number of systems. On the other hand, rapider MD simulations with the implicit-solvent model can be an alternative when involving larger scale calculations, but with some compromise on the accuracy [59].
Fig. 9.
Investigation of how the MD simulation time influences the extracted local geometrical features using a number of protein-ligand systems. The distributions of the features in the MD simulations (durations of 2 ns, 10 ns, 20 ns, 30 ns, 40 ns and 50 ns) for several systems are displayed. Panel (a) shows the feature distributions for the system with a PDB ID of 1BV9 (protein length: 99). Panel (b) shows scenario for 2IEN (protein length: 99). Panel (c) shows the scenario for 1J3K (protein length: 231). Panel (d) shows the scenario for 1E2K (protein length: 329).
4.3. The availability of mutant structures
To further test our method, another data set was compiled from [19]. In [19], Hauser and co-workers have proposed a physics-based potential for calculating alchemical free-energy, which facilitated the prediction of how mutations modulate inhibitor affinities to Abl kinase (a primary therapeutic target in chronic myelogenous leukemia). This data set (Abl-mut for short) differs from Platinum with respect to data integrity (most of the mutant structures in Abl-mut have not been experimentally resolved while the mutations we examined in Platinum were all structurally available for the WT/mutant proteins), variety of data (Abl-mut merely concers Abl kinase proteins while Platinum involves a variety of proteins), experimental measurements of affinity ( for Abl-mut while binding constants / for Platinum) and prediction labels (the sign of was considered in the study of Platinum while a threshold of 1.36 kcal for was used in Abl-mut to classify the mutations into susceptible or resistant). In total, Abl-mut consists of 144 mutation-inhibitor systems, regarding eight kinase inhibitors (axitinib, bosutinib, dasatinib, imatinib, nilotinib, ponatinib, gefitinib and erlotinib) and 31 clinically identified point mutations [19]. Due to the lack of experimental structures of Abl mutants and mutant-inhibitor complexes, techniques such as homology modeling (with an experimentally-resolved template structure) and docking (without a template) were frequently involved in the preparation of the work in [19]. Since our work is highly dependent on complex structures, we only retained the 131 mutation-inhibitor systems each with a structural template in order to minimize the interventions (only homology model required) in the data preparation, and docking-based systems (Abl-gefitinib and Abl-erlotinib) were pruned. The re-compilation of this subset includes the following steps.
-
•
Refining the template structures. The experimental X-ray structures of the WT Abl-inhibitor complexes were collected from PDB as the template structures for mutant-inhibitor systems (Abl-axitinib: 4WA9 (chain B), Abl-bosutinib: 3UE4 (chain A), Abl-dasatinib: 4XEY (chain A), Abl-imatinib: 1OPJ (chain B), Abl-nilotinib: 3CS9 (chain A), Abl-ponatinib: 3OXZ (chain A)) [4]. The residue indexes were standardized to a convention that places the Thr gatekeeper residue at position 315. Shared residues at positions 233 500 of these templates were remained as therefore no intervention is required (e.g. homology modeling). Missing residues of the Abl-dasatinib structure were modeled according to PDB2GQG (both kinases in active conformations) instead of PDB3IK3 (inactive conformation) used in [19]. Similarly, Abl-nilotinib structure was filled using PDB3IK3 (both kinases in inactive conformations) and Abl-ponatinib was modeled based on PDB3OY3 (both kinases in inactive conformations).
-
•
All Abl mutant structures were computed based on above templates using comparative modeling protocols in Rosetta [47]. Rosetta application [24] was performed to score mutant thermostability by calculating the folding free energy differences between the WTPs and mutants. In such modeling, high-level precision protocol (all atoms with backbone flexibility) and pre-minimizations were adopted. Remaining parameters were set as default.
-
•
H++ was employed to protonate these structures and add missing hydrogen atoms for them with pH = 7.0. Then the protonated proteins were capped with acetyl group at the N terminus and amide residue at the C terminus, and were aligned to the templates to form the complexes with the inhibitors.
Similarly as in Section 2.2, 2-ns explicit-solvent MD simulations of the Abl-inhibitor systems were conducted after energy minimization and equilibration of the systems. 1000 trajectory frames were collected for each system. Subsequently, we characterized the mutation-induced local geometrical differences (Section 2.3) and applied machine-learning models (Section 2.4.1) for classifying the mutations into susceptible or resistant (threshold of 1.36 kcal for ). The best performers in energy-based (MM/GBSA, Sections 2.4.2) and descriptor-based predictions (lig:kappa, pro:paacomp, Sections 2.4.3) were performed for comparisons. Different from our main data set, Abl-mut only concerns the Abl kinase protein and therefore has a simpler structure. Simpler parameter setting, such as that the number of trees in RFs and the size of neural network layers were tuned from 10 to 20, was adopted to avoid overfitting. The weights of the two classes were set as 1:4 (negative:positive) during training, as Abl-mut has lesser positive samples than the main data set (1:2). The prediction results are presented in Fig. 10a. Aside from MM/GBSA (accuracy of 0.55), the descriptor-based predictions and the machine-learning-based predictions both achieved an accuracy greater than 0.8. Due to factors such as the ignorance or underestimation of the entropy contributions in free energy calculations, using a specific labeling threshold for the absolute binding free energy can be a huge challenge to MM/GBSA, which induces the deficiency of such methods in this prediction scenario. Compared to the descriptor-based predictions, predictions based on our method achieved slightly better performance in balanced F1-score, with the best performer of CNN-LSTM (accuracy: 0.841, balanced F1 score: 0.500). This indicates the potential of machine-learning techniques in such prediction scenarios. However, the overall performance is still not satisfying enough, which may be largely due to the deficiency of initial mutant structures and the inaccuracy of structure-modeling processes. In future studies, collecting more quality data will always be an important task to refine our method. Since 1.36 kcal was used as the labeling threshold in [19], which seems arbitrary, we additionally tested the effects of different labeling thresholds on the prediction performance. A series of thresholds (−1.36, −1, −0.5, 0, 0.2, 0.4, 0.6, 0.8, 1, 1.18, 1.36) were adopted, and the performance of LSTM (parameters: 15 epochs, 15 LSTM units, 15 nodes in the densely-connected layer and class weights of 1:4) on the time-varying local geometrical features was examined. The results are now displayed in Fig. 10b. As shown in Fig. 10b, the balanced F1-score fluctuates slightly, while the accuracy depends heavily on the labeling thresholds (valley: 0.2). It may imply that highly resistant samples such as those determined by a labeling threshold of 1.36 kcal (corresponding to a 10-fold change in affinity [19]) and highly susceptible samples defined by a lower labeling threshold are more predictable in this data set.
Fig. 10.
Performance evaluation of predicting mutation impacts on protein-ligand binding affinity for the Abl-mut data set. Performance was evaluated based on the overall accuracy and balanced F1 score. (a) Results of our method, which uses machine-learning techniques to monitor the time-varying local geometrical feature differences upon mutation in the molecular dynamics (MD) simulations, are displayed. Shallow or deep neural networks include multilayer perceptron (MLP), convolutional neural networks (CNNs) with 2D convolutional layers, CNNs with 1D convolutional layers, recurrent neural networks (RNNs) with long short-term memory (LSTM) cells, and neural networks composed of CNNs and LSTM (CNN-LSTM) were used. Results from the estimation of binding-free-energy difference (MM/GBSA) and from the prediction based on molecular descriptors (Kappa shape indices (kappa) for ligands and Type 1 pseudo amino acid composition descriptors (paacomp) for proteins, and random forests (RFs) for predictions) are provided for comparisons. (b) Evaluation of the effects of different labeling cutoffs on the prediction performance. Prediction performance was evaluated based on LSTM.
4.4. pH-dependence and protonation states in protein-ligand binding
Practically, all biological processes in different compartments of the cell are pH-dependent, and macromolecules normally maintain specific pH-dependent characteristics to function properly and interact with the partners [50]. The pH-dependence in receptor-ligand interactions is principally due to the protonation-state changes of some titratable groups (with unusual pKa’s) upon binding, which may involve proton uptake/release [41]. These protonation states must be properly predicted prior to or after binding, which can be accomplished accurately with the unbound or complex structures provided and with the pH of binding known. However, the modeling becomes more complicated if the unbound or complex structures are not available or if the pH of binding is unknown (frequently true). Additionally, predicting the protonation states during the binding process, involving factors such as binding-induced conformational changes, becomes much more complicated. We focused on characterizing the bound protein-ligand complexes in their MD simulations, and therefore the changes of protonation states upon binding were not considered here. For accurately assigning the protonation states to the bound complexes, we employed H++ [15] based on the experimental pH values in the Platinum database. For any experiment with a non-specific pH value, a default value of 7.0 was used. For these experiments, such setting may affect the assignments of protonation states to the complexes, which may also downgrade our following prediction performance. As a potential refinement of our work, non-standard MD simulations, such as those based on constant-pH protocols [36], can be explored to more carefully monitor the protonation-state changes of titratable groups during the dynamics.
5. Conclusion
In this paper we have described our study on predicting the impacts of mutations on protein-ligand binding affinity based on MD simulations and local geometrical features. Different from many computational studies in this field that lack of experimental validation, we initiated our study based on consolidated databases of experimentally determined data (from Platinum and PDB). For evaluating affinity change upon mutation, we measured the feature differences between each pair of WTP-ligand and mutant-ligand systems in their dynamics simulations. Such differences were quantified according to average difference over all structural snapshots, trajectory-wise distance or time-vary differences. For the resulting conventional or time-series features, we employed a number of machine-learning methods to predict the impacts of mutations. Compared to the benchmark performances yielded by the energy estimation and by the molecular-descriptor investigation, our method induced an improved balanced F1 score while sustained the accuracy. Especially, deep-learning (LSTM) models well handled the extracted time-series features, resulting in the best prediction performance in balanced F1 score. This highlights the effectiveness of the extracted features and the deep-learning techniques in this problem.
In future studies, more efficient methods to evaluate the protein-ligand binding affinity and to longitudinally analyze such affinity measures in molecular dynamics will be explored. Additionally, sophisticated strategies such as generative models for mitigating the imbalance of samples will be investigated. Overall, such studies will contribute to a better understanding of the protein-ligand recognition and of the role of missense mutations in genetic diseases and the emergence of drug resistance.
CRediT authorship contribution statement
Debby D. Wang: Conceptualization, Methodology, Software, Formal analysis, Writing - original draft. Le Ou-Yang: Methodology, Formal analysis, Visualization. Haoran Xie: Software, Resources, Writing - review & editing. Mengxu Zhu: Data curation, Investigation. Hong Yan: Supervision, Writing - review & editing.
Acknowledgment
This work was support by the Hong Kong Research Grants Council [Project CityU 11200818]; City University of Hong Kong [Projects 9610034 and 9610460]; the Shenzhen Fundamental Research Program [Grant JCYJ20170817095210760]; National Natural Science Foundation of China [Grant 61602309]; Guangdong Basic and Applied Basic Research Foundation [Grant 2019A1515011384]; the Interdisciplinary Research Scheme of the Dean’s Research Fund 2018-19 [FLASS/DRF/IDS-3] and Departmental Collaborative Research Fund 2019 [MIT/DCRF-R2/18-19] of The Education University of Hong Kong.
Footnotes
Supplementary data associated with this article can be found, in the online version, at https://doi.org/10.1016/j.csbj.2020.02.007.
Contributor Information
Debby D. Wang, Email: d.wang@usst.edu.cn.
Le Ou-Yang, Email: leouyang@szu.edu.cn.
Supplementary data
The following are the Supplementary data to this article:
Fig. S1. To characterize the affinity change upon mutation, difference between each pair of WTP-ligand and mutant-ligand systems was quantified by local geometrical features (closeness, surface area of binding site, orientation, contacts and interfacial hydrogen bonds) extracted from the MD trajectories of the systems. Feature distributions for the two mutation impacts, decreased affinity (D) and increased affinity (I), are shown. Panel (a) shows the trajectory-wise Correlation distance based on each feature for the mutations. Panel (b) shows the trajectory-wise Cosine distance based on each feature for the mutations. Panel (c) shows the trajectory-wise dynamic time warping (DTW) distance based on each feature for the mutations.
Table S1. Statistics of the original data set, including the mutation type, the ID of the corresponding mutant in the protein data bank (PDB), the PDB ID of the wild type protein, the ID of the ligand, the type of ligand-binding sites (multiple or single), the impact of mutation on the protein-ligand affinity (decreased or increased) and the affinity fold change. For mutation types, XIY means a substitution from residue X to residue Y at position I, and XIY/AIIB indicates a dual mutation at positions I and II.
References
- 1.Agatonovic-Kustrin S., Beresford R., Yusof A.P.M. Theoretically-derived molecular descriptors important in human intestinal absorption. J Pharm Biomed Anal. 2001;25:227–237. doi: 10.1016/s0731-7085(00)00492-1. [DOI] [PubMed] [Google Scholar]
- 2.Basak S.C., Balaban A.T., Grunwald G.D., Gute B.D. Topological indices: their nature and mutual relatedness. J Chem Inf Comput Sci. 2000;40:891–898. doi: 10.1021/ci990114y. [DOI] [PubMed] [Google Scholar]
- 3.Bava K.A., Gromiha M.M., Uedaira H., Kitajima K., Sarai A. Protherm, version 4.0: thermodynamic database for proteins and mutants. Nucleic Acids Res. 2004;32:D120–D121. doi: 10.1093/nar/gkh082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Berman H.M., Bourne P.E., Westbrook J., Zardecki C. Protein structure. CRC Press; 2003. The protein data bank; pp. 394–410. [Google Scholar]
- 5.Case D, Ben-Shalom I, Brozell S, Cerutti D, Cheatham III, T, Cruzeiro V, Darden T, Duke R, Ghoreishi D, Gilson M, et al. Amber 2018: San francisco; 2018.
- 6.Chou K.-C. Prediction of protein cellular attributes using pseudo-amino acid composition. Proteins: Struct Funct Bioinf. 2001;43:246–255. doi: 10.1002/prot.1035. [DOI] [PubMed] [Google Scholar]
- 7.Deng W., Breneman C., Embrechts M.J. Predicting protein- ligand binding affinities using novel geometrical descriptors and machine-learning methods. J Chem Inf Comput Sci. 2004;44:699–703. doi: 10.1021/ci034246+. [DOI] [PubMed] [Google Scholar]
- 8.Devillers J., Balaban A.T. CRC Press; 2000. Topological indices and related descriptors in QSAR and QSPAR. [Google Scholar]
- 9.Devillers J., Domine D., Guillon C., Bintein S., Karcher W. Prediction of partition coefficients (log p oct) using autocorrelation descriptors. SAR QSAR Environ Res. 1997;7:151–172. [Google Scholar]
- 10.Dong J., Yao Z.-J., Zhang L., Luo F., Lin Q., Lu A.-P., Chen A.F., Cao D.-S. Pybiomed: a python library for various molecular representations of chemicals, proteins and dnas and their interactions. J Cheminf. 2018;10:16. doi: 10.1186/s13321-018-0270-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Dubchak I., Muchnik I., Holbrook S.R., Kim S.-H. Prediction of protein folding class using global description of amino acid sequence. Proc Natl Acad Sci. 1995;92:8700–8704. doi: 10.1073/pnas.92.19.8700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Genheden S., Ryde U. The mm/pbsa and mm/gbsa methods to estimate ligand-binding affinities. Expert Opin Drug Discov. 2015;10:449–461. doi: 10.1517/17460441.2015.1032936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ghai R., Falconer R.J., Collins B.M. Applications of isothermal titration calorimetry in pure and applied research-survey of the literature from 2010. J Mol Recogn. 2012;25:32–52. doi: 10.1002/jmr.1167. [DOI] [PubMed] [Google Scholar]
- 14.Giammona DA. An examination of conformational flexibility in porphyrins and bulky-ligand binding in myoglobin; 1984.
- 15.Gordon J.C., Myers J.B., Folta T., Shoja V., Heath L.S., Onufriev A. H++: a server for estimating p k as and adding missing hydrogens to macromolecules. Nucleic Acids Res. 2005;33:W368–W371. doi: 10.1093/nar/gki464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Gotz A.W., Williamson M.J., Xu D., Poole D., Le Grand S., Walker R.C. Routine microsecond molecular dynamics simulations with amber on gpus. 1. Generalized born. J Chem Theory Comput. 2012;8:1542–1555. doi: 10.1021/ct200909j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Graves A, Mohamed A-r, Hinton G. Speech recognition with deep recurrent neural networks. In 2013 IEEE international conference on acoustics, speech and signal processing. IEEE; 2013. pp. 6645–6649.
- 18.Hall L.H., Kier L.B. The molecular connectivity chi indexes and kappa shape indexes in structure-property modeling. Rev Comput Chem. 1991;5:367–422. [Google Scholar]
- 19.Hauser K., Negron C., Albanese S.K., Ray S., Steinbrecher T., Abel R., Chodera J.D., Wang L. Predicting resistance of clinical abl mutations to targeted kinase inhibitors using alchemical free-energy calculations. Commun Biol. 2018;1:70. doi: 10.1038/s42003-018-0075-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ho TK. Random decision forests. In Proceedings of 3rd international conference on document analysis and recognition. IEEE. vol. 1; 1995. pp. 278–282
- 21.Hou T., Zhang W., Wang J., Wang W. Predicting drug resistance of the hiv-1 protease using molecular interaction energy components. Proteins: Struct Funct Bioinf. 2009;74:837–846. doi: 10.1002/prot.22192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Jubb H.C., Pandurangan A.P., Turner M.A., Ochoa-Montano B., Blundell T.L., Ascher D.B. Mutations at protein-protein interfaces: small changes over big surfaces have large impacts on human health. Prog Biophys Mol Biol. 2017;128:3–13. doi: 10.1016/j.pbiomolbio.2016.10.002. [DOI] [PubMed] [Google Scholar]
- 23.Kingma DP, Ba J. Adam: a method for stochastic optimization. arXiv:1412.6980; 2014.
- 24.Kortemme T., Baker D. A simple physical model for binding energy hot spots in protein–protein complexes. Proc Natl Acad Sci. 2002;99:14116–14121. doi: 10.1073/pnas.202485799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Krizhevsky A, Sutskever I, Hinton GE. Imagenet classification with deep convolutional neural networks. In Advances in neural information processing systems; 2012. pp. 1097–1105.
- 26.Kucukkal T.G., Petukh M., Li L., Alexov E. Structural and physico-chemical effects of disease and non-disease nssnps on proteins. Curr Opin Struct Biol. 2015;32:18–24. doi: 10.1016/j.sbi.2015.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kumar M.S., Bava K.A., Gromiha M.M., Prabakaran P., Kitajima K., Uedaira H., Sarai A. Protherm and pronit: thermodynamic databases for proteins and protein–nucleic acid interactions. Nucleic Acids Res. 2006;34:D204–D206. doi: 10.1093/nar/gkj103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Li P., Roberts B.P., Chakravorty D.K., Merz K.M., Jr Rational design of particle mesh ewald compatible lennard-jones parameters for+ 2 metal cations in explicit solvent. J Chem Theory Comput. 2013;9:2733–2748. doi: 10.1021/ct400146w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Li Z.-R., Lin H.H., Han L., Jiang L., Chen X., Chen Y.Z. Profeat: a web server for computing structural and physicochemical features of proteins and peptides from amino acid sequence. Nucleic Acids Res. 2006;34:W32–W37. doi: 10.1093/nar/gkl305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Liu W., Wang Z., Liu X., Zeng N., Liu Y., Alsaadi F.E. A survey of deep neural network architectures and their applications. Neurocomputing. 2017;234:11–26. [Google Scholar]
- 31.Lori C., Lantella A., Pasquo A., Alexander L.T., Knapp S., Chiaraluce R., Consalvi V. Effect of single amino acid substitution observed in cancer on pim-1 kinase thermodynamic stability and structure. PloS One. 2013;8 doi: 10.1371/journal.pone.0064824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ma L., Wang D.D., Huang Y., Yan H., Wong M.P., Lee V.H. Egfr mutant structural database: computationally predicted 3d structures and the corresponding binding free energies with gefitinib and erlotinib. BMC Bioinf. 2015;16:85. doi: 10.1186/s12859-015-0522-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ma L., Zou B., Yan H. Identifying egfr mutation-induced drug resistance based on alpha shape model analysis of the dynamics. Proteome Sci. 2016;14:12. doi: 10.1186/s12953-016-0102-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Masi A., Cicchi R., Carloni A., Pavone F.S., Arcangeli A. Integrins and Ion Channels. Springer; 2010. Optical methods in the study of protein-protein interactions; pp. 33–42. [DOI] [PubMed] [Google Scholar]
- 35.Moal I.H., Fernández-Recio J. Skempi: a structural kinetic and energetic database of mutant protein interactions and its use in empirical models. Bioinformatics. 2012;28:2600–2607. doi: 10.1093/bioinformatics/bts489. [DOI] [PubMed] [Google Scholar]
- 36.Mongan J., Case D.A., McCAMMON J.A. Constant ph molecular dynamics in generalized born implicit solvent. J Comput Chem. 2004;25:2038–2048. doi: 10.1002/jcc.20139. [DOI] [PubMed] [Google Scholar]
- 37.Nanni L., Brahnam S., Lumini A. Prediction of protein structure classes by incorporating different protein descriptors into general chou’s pseudo amino acid composition. J Theor Biol. 2014;360:109–116. doi: 10.1016/j.jtbi.2014.07.003. [DOI] [PubMed] [Google Scholar]
- 38.Pandurangan A.P., Ochoa-Monta no B., Ascher D.B., Blundell T.L. Sdm: a server for predicting effects of mutations on protein stability. Nucleic Acids Res. 2017;45:W229–W235. doi: 10.1093/nar/gkx439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Perryman A.L., Lin J.-H., McCammon J.A. Hiv-1 protease molecular dynamics of a wild-type and of the v82f/i84v mutant: possible contributions to drug resistance and a potential new target site for drugs. Protein Sci. 2004;13:1108–1123. doi: 10.1110/ps.03468904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Pettersen E.F., Goddard T.D., Huang C.C., Couch G.S., Greenblatt D.M., Meng E.C., Ferrin T.E. Ucsf chimera-a visualization system for exploratory research and analysis. J Comput Chem. 2004;25:1605–1612. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]
- 41.Petukh M., Stefl S., Alexov E. The role of protonation states in ligand-receptor recognition and binding. Curr Pharmaceutical Design. 2013;19:4182–4190. doi: 10.2174/1381612811319230004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Phillip Y., Kiss V., Schreiber G. Protein-binding dynamics imaged in a living cell. Proc Natl Acad Sci. 2012;109:1461–1466. doi: 10.1073/pnas.1112171109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Pires D.E., Blundell T.L., Ascher D.B. Platinum: a database of experimentally measured effects of mutations on structurally defined protein–ligand complexes. Nucleic Acids Res. 2014;43:D387–D391. doi: 10.1093/nar/gku966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Pires D.E., Blundell T.L., Ascher D.B. mcsm-lig: quantifying the effects of mutations on protein-small molecule affinity in genetic disease and emergence of drug resistance. Scientific Rep. 2016;6:29575. doi: 10.1038/srep29575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Placone J., He L., Del Piccolo N., Hristova K. Strong dimerization of wild-type erbb2/neu transmembrane domain and the oncogenic val664glu mutant in mammalian plasma membranes. Biochim Biophys Acta. 2014;1838:2326–2330. doi: 10.1016/j.bbamem.2014.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Rabiner L.R. A tutorial on hidden markov models and selected applications in speech recognition. Proc IEEE. 1989;77:257–286. [Google Scholar]
- 47.Rohl CA, Strauss CE, Misura KM, Baker D. Protein structure prediction using rosetta. In Methods in enzymology. Elsevier. vol. 383; 2004. pp. 66–93. [DOI] [PubMed]
- 48.Salomon-Ferrer R., Gotz A.W., Poole D., Le Grand S., Walker R.C. Routine microsecond molecular dynamics simulations with amber on gpus. 2. explicit solvent particle mesh ewald. J Chem Theory Comput. 2013;9:3878–3888. doi: 10.1021/ct400314y. [DOI] [PubMed] [Google Scholar]
- 49.Srivastava N., Hinton G., Krizhevsky A., Sutskever I., Salakhutdinov R. Dropout: a simple way to prevent neural networks from overfitting. J Mach Learn Res. 2014;15:1929–1958. [Google Scholar]
- 50.Stefl S., Nishi H., Petukh M., Panchenko A.R., Alexov E. Molecular mechanisms of disease-causing missense mutations. J Mol Biol. 2013;425:3919–3936. doi: 10.1016/j.jmb.2013.07.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Todeschini R., Consonni V. vol. 11. John Wiley & Sons; 2008. (Handbook of molecular descriptors). [Google Scholar]
- 52.Wang D.D., Lee V.H., Zhu G., Zou B., Ma L., Yan H. Selectivity profile of afatinib for egfr-mutated non-small-cell lung cancer. Mol BioSyst. 2016;12:1552–1563. doi: 10.1039/c6mb00038j. [DOI] [PubMed] [Google Scholar]
- 53.Wang D.D., Zhou W., Yan H., Wong M., Lee V. Personalized prediction of egfr mutation-induced drug resistance in lung cancer. Scientific Rep. 2013;3:2855. doi: 10.1038/srep02855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Weiser J., Shenkin P.S., Still W.C. Approximate atomic surfaces from linear combinations of pairwise overlaps (lcpo) J Comput Chem. 1999;20:217–230. [Google Scholar]
- 55.Xia J.-F., Han K., Huang D.-S. Sequence-based prediction of protein-protein interactions by means of rotation forest and autocorrelation descriptor. Protein Peptide Lett. 2010;17:137–145. doi: 10.2174/092986610789909403. [DOI] [PubMed] [Google Scholar]
- 56.Yang F., Wu M., Li Y., Zheng G.-Y., Cao H.-Q., Sun W., Yang R., Zhang H., Sheng Y.-H., Kong X.-Q. Mutation p. s335x in gata4 reduces its dna binding affinity and enhances cell apoptosis associated with ventricular septal defect. Curr Mol Med. 2013;13:993–999. doi: 10.2174/15665240113139990053. [DOI] [PubMed] [Google Scholar]
- 57.Zamora I., Oprea T., Cruciani G., Pastor M., Ungell A.-L. Surface descriptors for protein- ligand affinity prediction. J Med Chem. 2003;46:25–33. doi: 10.1021/jm011051p. [DOI] [PubMed] [Google Scholar]
- 58.Zhang C., Ma Y. Springer; 2012. Ensemble machine learning: methods and applications. [Google Scholar]
- 59.Zhang J., Zhang H., Wu T., Wang Q., van der Spoel D. Comparison of implicit and explicit solvent models for the calculation of solvation free energy in organic solvents. J Chem Theory Comput. 2017;13:1034–1043. doi: 10.1021/acs.jctc.7b00169. [DOI] [PubMed] [Google Scholar]
- 60.Zhou W, Wang DD, Yan H, Wong M, Lee V. Prediction of anti-egfr drug resistance base on binding free energy and hydrogen bond analysis. In 2013 IEEE Symposium on Computational Intelligence in Bioinformatics and Computational Biology (CIBCB). IEEE; 2013. pp. 193–197.
- 61.Zou B., Lee V.H., Chen L., Ma L., Wang D.D., Yan H. Deciphering mechanisms of acquired t790m mutation after egfr inhibitors for nsclc by computational simulations. Scientific Rep. 2017;7:6595. doi: 10.1038/s41598-017-06632-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Zou B., Wang D.D., Ma L., Chen L., Yan H. Analysis of the relationship between lung cancer drug response level and atom connectivity dynamics based on trimmed delaunay triangulation. Chem Phys Lett. 2016;652:117–122. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Fig. S1. To characterize the affinity change upon mutation, difference between each pair of WTP-ligand and mutant-ligand systems was quantified by local geometrical features (closeness, surface area of binding site, orientation, contacts and interfacial hydrogen bonds) extracted from the MD trajectories of the systems. Feature distributions for the two mutation impacts, decreased affinity (D) and increased affinity (I), are shown. Panel (a) shows the trajectory-wise Correlation distance based on each feature for the mutations. Panel (b) shows the trajectory-wise Cosine distance based on each feature for the mutations. Panel (c) shows the trajectory-wise dynamic time warping (DTW) distance based on each feature for the mutations.
Table S1. Statistics of the original data set, including the mutation type, the ID of the corresponding mutant in the protein data bank (PDB), the PDB ID of the wild type protein, the ID of the ligand, the type of ligand-binding sites (multiple or single), the impact of mutation on the protein-ligand affinity (decreased or increased) and the affinity fold change. For mutation types, XIY means a substitution from residue X to residue Y at position I, and XIY/AIIB indicates a dual mutation at positions I and II.