Abstract
Background
Recent developments in literature on sample size calculations for time-to-event outcomes involve assumption of Weibull distributed times. These methods require a point estimate of the Weibull shape parameter obtained from historical studies. However, very limited guidance exists in published literature to assess how reliable this point estimate is when it is obtained from published results of a historical study.
Methods
We conduct simulations to assess how accurate and reliable the point estimate of the Weibull shape parameter is when it is estimated from published results of median survival time and/or corresponding interquartile range. Accuracy of this estimate is assessed using the criteria of average relative bias, root mean square error, and coefficient of variation for various combinations of sample sizes and censoring rates. Sensitivity of these calculations is assessed first, by increasing the number of survival quantiles used to calculate accuracy, and second, by using the full Kaplan Meier (KM) curve from the historical study.
Results
Our simulations suggest that point estimate of the shape parameter is reasonably accurate when estimated from historical studies with sample size ≥ 50 with censoring rate approximately 20%. Knowledge of the median and inter-quartile range seems to be adequate for this purpose. For historical studies with small sample sizes or higher censoring rates, more information needs to be abstracted from the published KM curves to improve accuracy.
Conclusions
We conclude that assessing the accuracy of Weibull shape parameter estimate is important before it can be used to conduct sample size calculations for a subsequent trial.
Keywords: Censoring, Historical data, KM curves, Sample size, Shape parameter, Weibull
1. Introduction
Sample size calculation is an integral component of designing clinical trials. While randomized two-arm trials are considered the gold standard in biomedical research in assessing the clinical effect of a new treatment relative to a control, there are situations where single-arm trials are inevitable owing to certain practical constraints. In case of clinical trials with a time-to-event endpoint, traditional methods of sample size calculation for the two-arm case involve the nonparametric log-rank test, assumption of exponential distribution for the survival times, or the assumption of proportional hazards between the two arms. While standard statistics software can be used to conduct sample size calculations using these traditional methods for two-arm trials, surprisingly few options are available for the single-arm and multi-arm scenarios. In the single-arm case, the most popular option available in standard software and in online calculators (for example, see SWOG [1]) assumes that the survival time for the single-arm trial follows an exponential distribution. However, when the assumption of exponentially distributed survival times (resulting in hazard that is constant over time) is inappropriate, a statistician designing the trial is left with limited options. Although some methods using the weighted logrank test have been proposed in literature in the single-arm case (see for example, Finkelstein et al. [2], Kwak and Jung [3], Jung [4], and Sun et al. [5]), the logrank test proposed by Wu [6] is the only option available in commercial software such as PASS [7] and nQuery [8]. By assuming that survival times follows a Weibull distribution (thereby providing the flexibility to account for hazards that are increasing or decreasing over time) Wu [6] has improved on the earlier versions of the logrank test and has provided sample size formula based on the exact variance of the test statistic. More recently, Phadnis [9] has extended the exact parametric approach of Narula and Li [10] for sample size calculation using the assumption of Weibull distribution for single-arm trial with time-to-event endpoint. While the Weibull distribution has been used in reliability and manufacturing engineering with regularity (see for example, Gerokostopoulos et al. [11], Yang et al. [12], Jeng [13], Meeker Jr. [14], and Pina-Monarrrez et al. [15] for approximate methods of sample size calculation) its use in biomedical settings for the purpose of sample size calculation has been limited. While Heo et al. [16] and Han et al. [17] have proposed approximate methods in the biomedical setting, Phadnis et al. [18] have provided exact method of sample size calculation supported by simulations. The methods of Wu [6] and Phadnis [9] (single-arm trials), and, Phadnis et al. [18] (two-arm trials) can be used to calculate sample sizes for a clinical trial. However, their accuracy depends on a user-provided value for the shape parameter of the Weibull distribution. All these authors have recommended that such an estimate can be obtained from historically published data on previously conducted trials. As the sample size calculation of these methods depends on multiple factors such as effect size, type I error, target power, drop-out rate, accrual and follow-up times, small changes in the point estimate may lead to widely varying sample sizes. Thus, while the Weibull distribution offers the flexibility to model non-constant hazards and is being considered in recent literature for designing both single-arm and multi-arm trials, it is important to justify the choice of the point estimate of the shape parameter used in the sample size calculation. If a reasonably strong justification is available for choosing a specific value for this point estimate, a statistician designing a clinical trial will able to correctly utilize the properties of the Weibull distribution.
To obtain a reliable point estimate of the Weibull shape parameter from historical sources, a statistician has to approach his/her clinical collaborators and often this information is provided in the form of previously published papers that either {i} provide a descriptive summary (median, and/or inter-quartile range of survival quantiles, or {ii} Kaplan Meier (KM) plot of a standard control (either as a single curve, or as part of a prior study comparing the standard control to some other treatment). The statistician must use this information to obtain a point estimate of the shape parameter to be able to conduct sample size calculations for the current trial. It is therefore important to assess how accurate this point estimate and its impact on the sensitivity of sample size calculations. For example, a point estimate obtained from a large-sample historical study is expected to be more accurate (closer to the true value) than the one obtained from small-sample historical study. Since many historical phase II trials in cancer are themselves small-to-moderate sized trials, the statistician has to be careful in using this point estimate in his/her calculations. A point estimate that is greater than 1 (increasing Weibull hazard) will result in a smaller sample size compared to a point estimate of 1 (constant hazard – exponential distribution). Conversely, a point estimate less than 1 (decreasing Weibull hazard) will lead to large sample size for the trial under consideration. That is, an inaccurately estimated shape parameter may result in underestimation or overestimation of the sample size for the current trial adversely impacting the study design and future analysis considerations.
To address these concerns, it is important to conduct a simulation study to assess the accuracy of the Weibull shape parameter when it is estimated from historical data. To the best of our knowledge, there is limited guidance in previously published literature on how to assess this accuracy when historical information is available from KM curves or median (and IQR) and our work aims to fill this gap. In this paper, we focus on the following ideas – first, the minimum sample size needed from a historical study to obtain a reliable estimate of the shape parameter is assessed. Secondly, the optimum number of survival quantiles needed from the historical study for fixed sample size is assessed. Accuracy of these estimates is calculated for various combinations of sample size, information points from the Kaplan Meier curve, and varying levels of right-censoring proportions. This accuracy is assessed using the criteria of average relative bias, average coefficient of variation, and root mean square error. A real-life example from a clinical trial on cholangiocarcinoma with progression-free survival (PFS) as the time-to-event endpoint is used throughout our discussion. Results from our simulation study can be used to justify the choice of the point estimate of the Weibull shape parameter when using it to perform sample size calculation for a new study.
2. Methods
2.1. Background
The probability density function (PDF) for two-parameter Weibull distribution is given by
| (1) |
Here, is the scale parameter and is the shape parameter. The hazard or failure function of Weibull distribution can be written as
| (2) |
When , the hazard increases over time. When , hazard decreases over time, and, when (exponential distribution), the hazard is constant over time. We also note that when at least two (or more) Weibull times are known along with their corresponding survival probabilities, the Weibull shape parameter can be estimated by fitting a least squares regression line using the relationship given below.
| (3) |
This procedure is also known as median rank regression estimators (MRRS) and it allows us to obtain a point estimate of as the slope of the fitted regression line. For example, consider a historical study that has published results related to 25th, 50th (median), and 75th percentile of survival times related to the performance of a standard-of-care control arm. Then and its corresponding standard error can be estimated using equation (3). If only two survival quantiles (say, median and 75th percentile) are available, we can still obtain a point estimate of even though the standard error cannot be estimated. The scale parameter can then be estimated from the intercept, or, simply as: . However, doing this calculation does not guarantee accurate estimation of due to multiple reasons. Firstly, the historical study may be a small sample study and hence our estimate of may be inaccurate. Secondly, if we use only 25th, 50th, and 75th percentile of survival times for this estimation, then there is a possibility that information from very early and late failures may not be utilized. Further, some studies may have been terminated early and so only the 25th percentile and median may have been reported, allowing us only two points of information to estimate . Thirdly, many published studies provide a KM curve but only the median survival time is reported and so we would have to use this curve to obtain additional information to estimate . On some occasions, the published KM curves are presented in small sized figures making it difficult to obtain such information. Further, visual assessment of such KM curves for obtaining this information may itself contribute to the inaccuracy in estimating due to human error and therefore it may be important to use customized software for this purpose. Thus, overall it can be said that there is no known general strategy on how to choose a point estimate of when it is obtained from historical sources.
2.2. Simulation study design
We conducted an extensive simulation study to assess the accuracy of the Weibull shape parameter for different values of to reflect the decreasing, constant and increasing hazard functions. The event time distribution was simulated from Weibull () for each of the values mentioned above. The value of the scale parameter was taken as to be consistent with a median survival time of 2.5 months as described in the example discussed in Phadnis [9]. The censoring time distribution was also generated from Weibull () with for predefined event rate m using the technique discussed in Wan [19]. We considered the right-censoring mechanism with a censoring rate of 0%, 20% and more extreme case of 40%, and N = 10,000 simulations were run for small to moderately large sample sizes of n = 25, 50, 100, 200, 500. For each of these 10,000 simulations, we obtained the KM estimates of the survival quantiles. Next, we considered various scenarios representing the “number of information points (NIP)” that were used to obtain the point estimate of using (3). That is, following scenarios were considered:
{i} NIP = 2: Estimating from only the 25th and 50th percentile of KM curve
{ii} NIP = 2: Estimating from only the 25th and 75th percentile of KM curve
{iii} NIP = 3: Estimating from the 25th, 50th and 75th percentile of KM curve
{iv} NIP = 4: Estimating from the 20th, 40th, 60th and 80th percentile of KM curve
{v} NIP = 5: Estimating from the 17th, 33rd, 50th, 67th, and 83rd percentile of KM curve
This approach was adopted to assess the minimum NIP required to obtain reasonably accurate estimate of as a function of sample size and predefined censoring rate. While scenarios {i} – {iii} are likely to occur in practice, scenarios {iv} and {v} were used to obtain a better idea of how accuracy of changes as NIP increases. In case of smaller sample sizes of n = 25 or n = 50 with 40% censoring, some of simulations did not yield KM estimates for “low” values of survival probability and in such cases we modified the simulations to capture the event times at the closest step boundary. For example, with NIP = 4, say a particular simulation provided an estimate of the 20th, 40th, 60th percentile but did not yield an estimate for the 80th percentile. In this case we took the lowest possible value (say 70th percentile as the fourth piece of information).
2.3. Metrics
We used the following metrics to assess the accuracy of the Weibull shape parameter from our simulation study. Note that is the estimate of from the ith simulation (i = 1, 2, …, N) and is the average of all values.
-
(a)
The average relative bias of the parameter estimate is defined as:
| (4) |
-
(b)
Root mean square (RMSE) of the parameter estimate defined as:
| (5) |
-
(c)
Scaled Root mean square (SRMSE) of the parameter estimate defined as:
| (6) |
-
(d)
Coefficient of variation (CV) of the parameter estimate defined as:
| (7) |
-
(e)
The bias of relative to the maximum likelihood estimate is calculated as:
| (8) |
where is the estimate of obtained from maximum likelihood estimation method.
2.4. Shape parameter estimation using the full KM curve
The five scenarios discussed in Section 2.2 allow estimation of when such survival quantiles have been reported in literature. Literature on historical study data is often in the form of a KM plot and hence it is important to evaluate the accuracy of the point estimate of when it is estimated by all points from a published KM plot. This can be done in two ways described below.
{i} Using customized software to estimate all possible survival quantiles:
We used the DigitizeIt [20] software to perform this task. This software allows a user to generate X and Y coordinate values from any “Y vs X” plot. To do this, a figure of a previously published KM curve is loaded into the software. The range of values on the x-axis (time values ranging from 0 to tmax) and the y-axis (survival probability ranging from 0 to 1) is entered by the user. On selecting the KM curve with a mouse, the software can generate a dataset with corresponding values of time and survival probabilities. These values can then be used to estimate using (3). It is possible to create datasets corresponding to NIP ranging from as less as 2 or 3 observations to as large as a few hundred observations. That is, for each value of NIP we can obtain a point estimate of . Accuracy of this estimate can be assessed numerically by the metrics defined in Section 2.3 and visually by plotting the estimated versus NIP to assess the how the point estimate changes as a function of NIP. See Section 3.2 for results related to a real-life application discussing this approach.
{ii} Approximate manual observation of KM plot to estimate all possible survival quantiles:
In cases, where a software like DigitizeIt [20] is not available to a statistician, he/she can try to perform the same task manually. However, this would require the statistician to visually scrutinize the published KM plot inducing additional source of variation due to human error in the calculations. If the published KM plot is in the form of a small-sized figure, then it is possible that manual approximation may not be accurate. It is therefore important to assess the performance of such an approximation using simulations. We have therefore conducted an additional simulation study to assess the accuracy of obtaining all point estimates from a KM curve when this task is performed manually. Our simulations assumed that the human eye can capture measurements from a plot with moderate accuracy (neither very accurate nor very inaccurate). That is, approximate estimates of event times and corresponding survival probabilities can be obtained through eyeballing of the figure, but that some error is inevitable in this approach. This task was accomplished in the following way:
Step 1. Generate right-censored Weibull data representing a hypothetical historical trial as described in Section 2.2. Obtain the KM estimates from this data and denote them as at survival times for .
Step 2. Assume that the researchers working on this historical trial have published a KM plot, and that, we as a statistician, intend to first obtain estimates of time and corresponding survival probabilities, and then to obtain a point estimate of using (3). We assume that the time axis on this plot has the time values marked on it at regular intervals (say, in increments of 1 month) and that we are now required to estimate the KM survival probabilities at each of these time values. We further assume that in performing this visual abstraction task, the human eye errs in estimating the survival probability by a magnitude that is equal to half the standard error of the actual KM estimates available to us in Step 1. As an example, say, the true KM estimate at time = 6 months was 0.775 with a standard error of 0.05. A statistician would “inaccurately” estimate this as somewhere between 0.75 and 0.80.
Step 3. At each time point of interest (marked on the time-axis), make a single random draw from a uniform representing the corresponding visually estimated survival probability and denote these as . Since the may not always exactly coincide with , linear interpolation may be used to obtain estimates of survival probability from .
Step 4. Obtain point estimate of using (3). Denote this estimate by .
Step 5. Compare to obtained from NIP = 2 and NIP = 3 from Section 2.2. That is, we ask ourselves the question “Is the point estimate obtained from using multiple points on a published KM plot incorporating the human eye error due to visual abstraction more or less accurate than the point estimate obtained from published results of 25th, 50th and 75th KM estimates if such results were available to the statistician?”
The R statistical software [21] was used to conduct all the simulations.
3. Results
3.1. Simulation study results related to Section 2.2
The results of our simulation studies are displayed in Table 1, Table 2, Table 3, Table 4, Table 5. The first three columns are arranged by censoring rate, the true value of the shape parameter used in the simulation, and varying samples sizes. The fourth column displays the estimated value of obtained from the simulation. In cases where NIP >2, the fifth column contains the values of the standard error of estimate of . When NIP = 2, the standard error of estimate of cannot be calculated. The remainder of the columns are arranged by bias, ARB, RMSE, SRMSE, CV (included only when NIP > 2), MLE of , MARB (this is the bias of the MLE of relative to the true value of ) and RARB respectively. We primarily rely on ARB, RMSE and SRMSE to assess the accuracy of . We assume a threshold value of 5% as the “maximum value of ARB” at which we are willing to use the point estimate of for sample size calculations in a subsequent clinical trial (although in real life, a statistician may be willing to relax this threshold at a higher value such as 10%).
Table 1.
Simulation result for NIP = 2 (25th and 50th percentile) under various censoring proportions.
| Censor | 2 data points |
Complete data set |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| N | BIAS | ARB | RMSE | SRMSE | MARB | RARB | ||||
| 0% | 0.50 | 25 | 0.613 | 0.113 | 0.225 | 0.195 | 0.390 | 0.529 | 0.057 | 0.329 |
| 50 | 0.534 | 0.034 | 0.064 | 0.110 | 0.220 | 0.514 | 0.027 | 0.192 | ||
| 100 | 0.517 | 0.017 | 0.035 | 0.074 | 0.148 | 0.507 | 0.014 | 0.131 | ||
| 200 | 0.508 | 0.008 | 0.016 | 0.052 | 0.104 | 0.503 | 0.007 | 0.093 | ||
| 500 | 0.504 | 0.004 | 0.007 | 0.033 | 0.066 | 0.501 | 0.003 | 0.059 | ||
| 0.75 | 25 | 0.919 | 0.169 | 0.225 | 0.292 | 0.389 | 0.793 | 0.057 | 0.329 | |
| 50 | 0.801 | 0.051 | 0.064 | 0.162 | 0.216 | 0.770 | 0.027 | 0.192 | ||
| 100 | 0.776 | 0.026 | 0.035 | 0.111 | 0.148 | 0.076 | 0.014 | 0.131 | ||
| 200 | 0.762 | 0.012 | 0.016 | 0.077 | 0.103 | 0.755 | 0.007 | 0.093 | ||
| 500 | 0.755 | 0.005 | 0.007 | 0.049 | 0.065 | 0.752 | 0.003 | 0.059 | ||
| 1 | 25 | 1.225 | 0.225 | 0.225 | 0.390 | 0.390 | 1.057 | 0.057 | 0.329 | |
| 50 | 1.067 | 0.064 | 0.064 | 0.219 | 0.219 | 1.027 | 0.027 | 0.192 | ||
| 100 | 1.035 | 0.035 | 0.035 | 0.148 | 0.148 | 0.014 | 0.014 | 0.131 | ||
| 200 | 1.016 | 0.016 | 0.016 | 0.103 | 0.103 | 0.007 | 0.007 | 0.093 | ||
| 500 | 1.007 | 0.007 | 0.007 | 0.065 | 0.065 | 0.003 | 0.003 | 0.059 | ||
| 1.25 | 25 | 1.531 | 0.281 | 0.225 | 0.487 | 0.389 | 1.321 | 0.057 | 0.329 | |
| 50 | 1.334 | 0.084 | 0.064 | 0.274 | 0.219 | 1.284 | 0.027 | 0.192 | ||
| 100 | 1.293 | 0.043 | 0.035 | 0.185 | 0.148 | 1.267 | 0.014 | 0.131 | ||
| 200 | 1.269 | 0.019 | 0.016 | 0.129 | 0.103 | 1.259 | 0.007 | 0.093 | ||
| 500 | 1.259 | 0.009 | 0.007 | 0.082 | 0.065 | 1.253 | 0.003 | 0.059 | ||
| 1.50 | 25 | 1.838 | 0.338 | 0.225 | 0.585 | 0.390 | 1.586 | 0.057 | 0.329 | |
| 50 | 1.600 | 0.100 | 0.064 | 0.328 | 0.218 | 1.541 | 0.027 | 0.192 | ||
| 100 | 1.552 | 0.052 | 0.035 | 0.222 | 0.148 | 1.521 | 0.014 | 0.131 | ||
| 200 | 1.523 | 0.023 | 0.016 | 0.155 | 0.103 | 1.510 | 0.007 | 0.093 | ||
| 500 | 1.511 | 0.011 | 0.007 | 0.098 | 0.065 | 1.504 | 0.003 | 0.059 | ||
| 20% | 0.50 | 25 | 0.617 | 0.117 | 0.234 | 0.209 | 0.418 | 0.532 | 0.064 | 0.356 |
| 50 | 0.550 | 0.050 | 0.101 | 0.125 | 0.250 | 0.515 | 0.031 | 0.217 | ||
| 100 | 0.525 | 0.025 | 0.050 | 0.082 | 0.164 | 0.508 | 0.016 | 0.145 | ||
| 200 | 0.513 | 0.013 | 0.026 | 0.052 | 0.104 | 0.504 | 0.008 | 0.100 | ||
| 500 | 0.505 | 0.005 | 0.010 | 0.036 | 0.072 | 0.501 | 0.003 | 0.064 | ||
| 0.75 | 25 | 0.926 | 0.176 | 0.234 | 0.313 | 0.417 | 0.798 | 0.064 | 0.356 | |
| 50 | 0.826 | 0.076 | 0.101 | 0.187 | 0.249 | 0.773 | 0.031 | 0.217 | ||
| 100 | 0.788 | 0.038 | 0.050 | 0.123 | 0.164 | 0.762 | 0.016 | 0.145 | ||
| 200 | 0.769 | 0.019 | 0.026 | 0.085 | 0.113 | 0.756 | 0.008 | 0.100 | ||
| 500 | 0.757 | 0.007 | 0.010 | 0.054 | 0.072 | 0.752 | 0.003 | 0.064 | ||
| 1 | 25 | 1.234 | 0.234 | 0.234 | 0.417 | 0.417 | 1.064 | 0.064 | 0.356 | |
| 50 | 1.101 | 0.101 | 0.101 | 0.249 | 0.249 | 1.031 | 0.031 | 0.217 | ||
| 100 | 1.050 | 0.050 | 0.050 | 0.163 | 0.163 | 1.016 | 0.016 | 0.145 | ||
| 200 | 1.026 | 0.026 | 0.026 | 0.114 | 0.114 | 1.008 | 0.008 | 0.100 | ||
| 500 | 1.010 | 0.010 | 0.010 | 0.071 | 0.071 | 1.003 | 0.003 | 0.064 | ||
| 1.25 | 25 | 1.543 | 0.293 | 0.234 | 0.521 | 0.416 | 1.330 | 0.064 | 0.356 | |
| 50 | 1.376 | 0.126 | 0.101 | 0.312 | 0.249 | 1.288 | 0.031 | 0.217 | ||
| 100 | 1.313 | 0.063 | 0.050 | 0.204 | 0.163 | 1.270 | 0.016 | 0.145 | ||
| 200 | 1.282 | 0.032 | 0.026 | 0.142 | 0.114 | 1.260 | 0.008 | 0.100 | ||
| 500 | 1.262 | 0.012 | 0.010 | 0.089 | 0.071 | 1.254 | 0.003 | 0.064 | ||
| 1.50 | 25 | 1.851 | 0.351 | 0.234 | 0.626 | 0.417 | 1.596 | 0.064 | 0.356 | |
| 50 | 1.651 | 0.151 | 0.101 | 0.374 | 0.249 | 1.546 | 0.031 | 0.217 | ||
| 100 | 1.575 | 0.075 | 0.050 | 0.245 | 0.163 | 1.524 | 0.016 | 0.145 | ||
| 200 | 1.539 | 0.039 | 0.026 | 0.171 | 0.114 | 1.512 | 0.008 | 0.100 | ||
| 500 | 1.514 | 0.014 | 0.010 | 0.107 | 0.071 | 1.504 | 0.003 | 0.064 | ||
| 40% | 0.50 | 25 | 0.849 | 0.349 | 0.698 | 0.442 | 0.884 | 0.538 | 0.075 | 0.825 |
| 50 | 0.601 | 0.101 | 0.202 | 0.176 | 0.353 | 0.517 | 0.034 | 0.314 | ||
| 100 | 0.550 | 0.050 | 0.100 | 0.107 | 0.214 | 0.509 | 0.018 | 0.194 | ||
| 200 | 0.530 | 0.030 | 0.060 | 0.073 | 0.146 | 0.505 | 0.009 | 0.131 | ||
| 500 | 0.514 | 0.014 | 0.028 | 0.045 | 0.091 | 0.502 | 0.003 | 0.083 | ||
| 0.75 | 25 | 1.274 | 0.524 | 0.698 | 0.663 | 0.883 | 0.806 | 0.075 | 0.825 | |
| 50 | 0.902 | 0.152 | 0.202 | 0.264 | 0.353 | 0.776 | 0.034 | 0.314 | ||
| 100 | 0.825 | 0.075 | 0.100 | 0.161 | 0.214 | 0.764 | 0.018 | 0.194 | ||
| 200 | 0.795 | 0.045 | 0.060 | 0.109 | 0.146 | 0.757 | 0.009 | 0.131 | ||
| 500 | 0.771 | 0.021 | 0.028 | 0.068 | 0.091 | 0.752 | 0.003 | 0.083 | ||
| 1 | 25 | 1.698 | 0.698 | 0.698 | 0.883 | 0.883 | 1.075 | 0.075 | 0.825 | |
| 50 | 1.202 | 0.202 | 0.202 | 0.353 | 0.353 | 1.034 | 0.034 | 0.314 | ||
| 100 | 1.100 | 0.100 | 0.100 | 0.214 | 0.214 | 1.018 | 0.018 | 0.194 | ||
| 200 | 1.060 | 0.060 | 0.060 | 0.146 | 0.146 | 1.009 | 0.009 | 0.131 | ||
| 500 | 1.028 | 0.028 | 0.028 | 0.091 | 0.091 | 1.003 | 0.003 | 0.083 | ||
| 1.25 | 25 | 2.123 | 0.873 | 0.698 | 1.104 | 0.883 | 1.344 | 0.075 | 0.825 | |
| 50 | 1.503 | 0.253 | 0.202 | 0.441 | 0.353 | 1.293 | 0.034 | 0.314 | ||
| 100 | 1.375 | 0.125 | 0.100 | 0.268 | 0.214 | 1.273 | 0.018 | 0.194 | ||
| 200 | 1.324 | 0.074 | 0.060 | 0.182 | 0.146 | 1.261 | 0.009 | 0.131 | ||
| 500 | 1.285 | 0.035 | 0.028 | 0.114 | 0.091 | 1.254 | 0.003 | 0.083 | ||
| 1.50 | 25 | 2.547 | 1.047 | 0.698 | 1.325 | 0.883 | 1.613 | 0.075 | 0.825 | |
| 50 | 1.807 | 0.303 | 0.202 | 0.529 | 0.353 | 1.552 | 0.034 | 0.314 | ||
| 100 | 1.650 | 0.150 | 0.100 | 0.321 | 0.214 | 1.527 | 0.018 | 0.194 | ||
| 200 | 1.589 | 0.089 | 0.060 | 0.218 | 0.146 | 1.514 | 0.009 | 0.131 | ||
| 500 | 1.542 | 0.042 | 0.028 | 0.136 | 0.091 | 1.505 | 0.003 | 0.083 | ||
Table 2.
Simulation result for NIP = 2 (25th and 75th percentile) under various censoring proportions.
| Censor | 2 data points |
Complete data set |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| N | BIAS | ARB | RMSE | SRMSE | MARB | RARB | ||||
| 0% | 0.50 | 25 | 0.562 | 0.062 | 0.124 | 0.121 | 0.241 | 0.529 | 0.057 | 0.173 |
| 50 | 0.516 | 0.016 | 0.033 | 0.075 | 0.149 | 0.514 | 0.027 | 0.112 | ||
| 100 | 0.508 | 0.008 | 0.016 | 0.051 | 0.101 | 0.507 | 0.014 | 0.079 | ||
| 200 | 0.504 | 0.004 | 0.009 | 0.036 | 0.072 | 0.503 | 0.007 | 0.056 | ||
| 500 | 0.502 | 0.002 | 0.003 | 0.023 | 0.046 | 0.501 | 0.003 | 0.036 | ||
| 0.75 | 25 | 0.843 | 0.093 | 0.124 | 0.181 | 0.241 | 0.793 | 0.057 | 0.173 | |
| 50 | 0.774 | 0.024 | 0.033 | 0.112 | 0.149 | 0.770 | 0.027 | 0.112 | ||
| 100 | 0.762 | 0.012 | 0.016 | 0.076 | 0.101 | 0.760 | 0.014 | 0.079 | ||
| 200 | 0.757 | 0.007 | 0.009 | 0.054 | 0.072 | 0.755 | 0.007 | 0.056 | ||
| 500 | 0.753 | 0.003 | 0.003 | 0.034 | 0.046 | 0.752 | 0.003 | 0.036 | ||
| 1 | 25 | 1.124 | 0.124 | 0.124 | 0.241 | 0.241 | 1.057 | 0.057 | 0.173 | |
| 50 | 1.033 | 0.033 | 0.033 | 0.149 | 0.149 | 1.027 | 0.027 | 0.112 | ||
| 100 | 1.016 | 0.016 | 0.016 | 0.101 | 0.101 | 1.014 | 0.014 | 0.079 | ||
| 200 | 1.009 | 0.009 | 0.009 | 0.072 | 0.072 | 1.007 | 0.007 | 0.056 | ||
| 500 | 1.003 | 0.003 | 0.003 | 0.046 | 0.046 | 1.003 | 0.003 | 0.036 | ||
| 1.25 | 25 | 1.405 | 0.155 | 0.124 | 0.301 | 0.241 | 1.321 | 0.057 | 0.173 | |
| 50 | 1.291 | 0.041 | 0.033 | 0.187 | 0.149 | 1.284 | 0.027 | 0.112 | ||
| 100 | 1.270 | 0.020 | 0.016 | 0.127 | 0.101 | 1.267 | 0.014 | 0.079 | ||
| 200 | 1.261 | 0.011 | 0.009 | 0.090 | 0.072 | 1.259 | 0.007 | 0.056 | ||
| 500 | 1.254 | 0.004 | 0.003 | 0.057 | 0.046 | 1.253 | 0.003 | 0.036 | ||
| 1.50 | 25 | 1.686 | 0.186 | 0.124 | 0.362 | 0.241 | 1.586 | 0.057 | 0.173 | |
| 50 | 1.549 | 0.049 | 0.033 | 0.224 | 0.149 | 1.541 | 0.027 | 0.112 | ||
| 100 | 1.524 | 0.024 | 0.016 | 0.152 | 0.101 | 1.521 | 0.014 | 0.079 | ||
| 200 | 1.513 | 0.013 | 0.009 | 0.108 | 0.072 | 1.510 | 0.007 | 0.056 | ||
| 500 | 1.505 | 0.005 | 0.003 | 0.069 | 0.046 | 1.504 | 0.003 | 0.036 | ||
| 20% | 0.50 | 25 | 0.551 | 0.051 | 0.103 | 0.118 | 0.236 | 0.532 | 0.064 | 0.169 |
| 50 | 0.524 | 0.024 | 0.048 | 0.078 | 0.156 | 0.515 | 0.031 | 0.113 | ||
| 100 | 0.512 | 0.012 | 0.025 | 0.054 | 0.107 | 0.508 | 0.016 | 0.079 | ||
| 200 | 0.507 | 0.007 | 0.013 | 0.038 | 0.076 | 0.504 | 0.008 | 0.056 | ||
| 500 | 0.502 | 0.002 | 0.005 | 0.024 | 0.048 | 0.501 | 0.003 | 0.036 | ||
| 0.75 | 25 | 0.827 | 0.077 | 0.103 | 0.177 | 0.236 | 0.798 | 0.064 | 0.169 | |
| 50 | 0.786 | 0.036 | 0.048 | 0.117 | 0.156 | 0.773 | 0.031 | 0.113 | ||
| 100 | 0.768 | 0.018 | 0.025 | 0.080 | 0.107 | 0.762 | 0.016 | 0.079 | ||
| 200 | 0.760 | 0.010 | 0.013 | 0.057 | 0.076 | 0.756 | 0.008 | 0.056 | ||
| 500 | 0.754 | 0.004 | 0.005 | 0.036 | 0.048 | 0.752 | 0.003 | 0.036 | ||
| 1 | 25 | 1.102 | 0.103 | 0.103 | 0.236 | 0.236 | 1.064 | 0.064 | 0.169 | |
| 50 | 1.048 | 0.048 | 0.048 | 0.156 | 0.156 | 1.031 | 0.031 | 0.113 | ||
| 100 | 1.025 | 0.025 | 0.025 | 0.107 | 0.107 | 1.016 | 0.016 | 0.079 | ||
| 200 | 1.013 | 0.013 | 0.013 | 0.076 | 0.076 | 1.008 | 0.008 | 0.056 | ||
| 500 | 1.006 | 0.005 | 0.005 | 0.048 | 0.048 | 1.003 | 0.003 | 0.036 | ||
| 1.25 | 25 | 1.378 | 0.128 | 0.103 | 0.295 | 0.236 | 1.330 | 0.064 | 0.169 | |
| 50 | 1.310 | 0.060 | 0.048 | 0.194 | 0.156 | 1.288 | 0.031 | 0.113 | ||
| 100 | 1.281 | 0.031 | 0.025 | 0.134 | 0.107 | 1.270 | 0.016 | 0.079 | ||
| 200 | 1.266 | 0.016 | 0.013 | 0.095 | 0.076 | 1.260 | 0.008 | 0.056 | ||
| 500 | 1.256 | 0.006 | 0.005 | 0.06 | 0.048 | 1.254 | 0.003 | 0.036 | ||
| 1.50 | 25 | 1.653 | 0.153 | 0.103 | 0.354 | 0.236 | 1.596 | 0.064 | 0.169 | |
| 50 | 1.572 | 0.072 | 0.048 | 0.233 | 0.156 | 1.546 | 0.031 | 0.113 | ||
| 100 | 1.537 | 0.037 | 0.025 | 0.161 | 0.107 | 1.524 | 0.016 | 0.079 | ||
| 200 | 1.520 | 0.020 | 0.013 | 0.114 | 0.076 | 1.512 | 0.008 | 0.056 | ||
| 500 | 1.507 | 0.007 | 0.005 | 0.072 | 0.048 | 1.504 | 0.003 | 0.036 | ||
| 40% | 0.50 | 25 | 0.576 | 0.076 | 0.152 | 0.149 | 0.298 | 0.538 | 0.075 | 0.215 |
| 50 | 0.537 | 0.037 | 0.075 | 0.093 | 0.186 | 0.517 | 0.034 | 0.136 | ||
| 100 | 0.523 | 0.023 | 0.045 | 0.063 | 0.126 | 0.509 | 0.018 | 0.093 | ||
| 200 | 0.515 | 0.015 | 0.031 | 0.044 | 0.089 | 0.505 | 0.009 | 0.063 | ||
| 500 | 0.507 | 0.007 | 0.015 | 0.028 | 0.057 | 0.502 | 0.003 | 0.044 | ||
| 0.75 | 25 | 0.864 | 0.114 | 0.152 | 0.224 | 0.298 | 0.806 | 0.075 | 0.215 | |
| 50 | 0.806 | 0.056 | 0.075 | 0.139 | 0.186 | 0.776 | 0.034 | 0.136 | ||
| 100 | 0.784 | 0.034 | 0.045 | 0.095 | 0.126 | 0.018 | 0.018 | 0.093 | ||
| 200 | 0.773 | 0.023 | 0.031 | 0.067 | 0.089 | 0.009 | 0.009 | 0.063 | ||
| 500 | 0.761 | 0.011 | 0.015 | 0.043 | 0.057 | 0.003 | 0.003 | 0.044 | ||
| 1 | 25 | 1.152 | 0.152 | 0.152 | 0.298 | 0.298 | 1.075 | 0.075 | 0.215 | |
| 50 | 1.075 | 0.075 | 0.075 | 0.186 | 0.186 | 1.034 | 0.034 | 0.136 | ||
| 100 | 1.045 | 0.045 | 0.045 | 0.126 | 0.126 | 1.015 | 0.018 | 0.093 | ||
| 200 | 1.031 | 0.031 | 0.031 | 0.089 | 0.089 | 1.009 | 0.009 | 0.063 | ||
| 500 | 1.015 | 0.015 | 0.015 | 0.057 | 0.057 | 1.003 | 0.003 | 0.044 | ||
| 1.25 | 25 | 1.440 | 0.190 | 0.152 | 0.373 | 0.298 | 1.344 | 0.075 | 0.215 | |
| 50 | 1.344 | 0.094 | 0.075 | 0.232 | 0.186 | 1.293 | 0.034 | 0.136 | ||
| 100 | 1.307 | 0.057 | 0.045 | 0.158 | 0.126 | 1.273 | 0.018 | 0.093 | ||
| 200 | 1.289 | 0.039 | 0.031 | 0.111 | 0.089 | 1.261 | 0.009 | 0.063 | ||
| 500 | 1.269 | 0.019 | 0.015 | 0.071 | 0.057 | 1.254 | 0.003 | 0.044 | ||
| 1.50 | 25 | 1.728 | 0.228 | 0.152 | 0.448 | 0.298 | 1.613 | 0.075 | 0.215 | |
| 50 | 1.612 | 0.112 | 0.075 | 0.278 | 0.186 | 1.552 | 0.034 | 0.136 | ||
| 100 | 1.568 | 0.068 | 0.045 | 0.189 | 0.126 | 1.527 | 0.018 | 0.093 | ||
| 200 | 1.546 | 0.046 | 0.031 | 0.133 | 0.089 | 1.514 | 0.009 | 0.063 | ||
| 500 | 1.269 | 0.019 | 0.015 | 0.071 | 0.057 | 1.254 | 0.003 | 0.044 | ||
Table 3.
Simulation result for NIP = 3 (25th, 50th and 75th percentile) under various censoring proportions.
| Censor | 3 data points (25th, 50th,75th) |
Complete data set |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | SE | BIAS | ARB | RMSE | SRMSE | CV | MARB | RARB | ||||
| 0% | 0.5 | 25 | 0.550 | 0.067 | 0.050 | 0.100 | 0.117 | 0.233 | 0.125 | 0.529 | 0.057 | 0.170 |
| 50 | 0.511 | 0.043 | 0.011 | 0.022 | 0.074 | 0.148 | 0.085 | 0.514 | 0.027 | 0.114 | ||
| 100 | 0.505 | 0.030 | 0.005 | 0.011 | 0.051 | 0.101 | 0.06 | 0.507 | 0.014 | 0.079 | ||
| 200 | 0.503 | 0.022 | 0.003 | 0.006 | 0.036 | 0.072 | 0.044 | 0.503 | 0.007 | 0.056 | ||
| 500 | 0.501 | 0.014 | 0.001 | 0.002 | 0.023 | 0.046 | 0.028 | 0.501 | 0.003 | 0.036 | ||
| 0.75 | 25 | 0.825 | 0.101 | 0.075 | 0.100 | 0.175 | 0.233 | 0.125 | 0.793 | 0.057 | 0.170 | |
| 50 | 0.766 | 0.064 | 0.016 | 0.022 | 0.111 | 0.148 | 0.085 | 0.770 | 0.027 | 0.114 | ||
| 100 | 0.758 | 0.045 | 0.008 | 0.011 | 0.076 | 0.101 | 0.060 | 0.760 | 0.014 | 0.079 | ||
| 200 | 0.755 | 0.033 | 0.005 | 0.006 | 0.540 | 0.072 | 0.044 | 0.755 | 0.007 | 0.056 | ||
| 500 | 0.752 | 0.021 | 0.002 | 0.002 | 0.035 | 0.046 | 0.028 | 0.752 | 0.003 | 0.036 | ||
| 1 | 25 | 1.100 | 0.135 | 0.100 | 0.100 | 0.233 | 0.233 | 0.125 | 1.057 | 0.057 | 0.170 | |
| 50 | 1.022 | 0.086 | 0.022 | 0.022 | 0.148 | 0.148 | 0.085 | 1.027 | 0.027 | 0.114 | ||
| 100 | 1.011 | 0.061 | 0.011 | 0.011 | 0.101 | 0.101 | 0.06 | 1.014 | 0.014 | 0.079 | ||
| 200 | 1.006 | 0.044 | 0.006 | 0.006 | 0.072 | 0.072 | 0.044 | 1.007 | 0.007 | 0.056 | ||
| 500 | 1.002 | 0.028 | 0.002 | 0.002 | 0.046 | 0.046 | 0.028 | 1.003 | 0.003 | 0.036 | ||
| 1.25 | 25 | 1.374 | 0.169 | 0.124 | 0.100 | 0.292 | 0.233 | 0.125 | 1.321 | 0.057 | 0.170 | |
| 50 | 1.277 | 0.107 | 0.027 | 0.022 | 0.186 | 0.148 | 0.085 | 1.284 | 0.027 | 0.114 | ||
| 100 | 1.263 | 0.076 | 0.013 | 0.011 | 0.127 | 0.101 | 0.060 | 1.267 | 0.014 | 0.079 | ||
| 200 | 1.257 | 0.055 | 0.007 | 0.006 | 0.090 | 0.072 | 0.044 | 1.259 | 0.007 | 0.056 | ||
| 500 | 1.253 | 0.035 | 0.003 | 0.002 | 0.058 | 0.046 | 0.028 | 1.253 | 0.003 | 0.036 | ||
| 1.50 | 25 | 1.649 | 0.202 | 0.149 | 0.100 | 0.350 | 0.233 | 0.125 | 1.586 | 0.057 | 0.170 | |
| 50 | 1.533 | 0.129 | 0.033 | 0.022 | 0.223 | 0.148 | 0.085 | 1.541 | 0.027 | 0.114 | ||
| 100 | 1.516 | 0.091 | 0.016 | 0.011 | 0.152 | 0.101 | 0.060 | 1.521 | 0.014 | 0.079 | ||
| 200 | 1.509 | 0.066 | 0.009 | 0.006 | 0.108 | 0.072 | 0.044 | 1.51 | 0.007 | 0.056 | ||
| 500 | 1.503 | 0.042 | 0.003 | 0.002 | 0.069 | 0.046 | 0.028 | 1.504 | 0.003 | 0.036 | ||
| 20% | 0.5 | 25 | 0.538 | 0.071 | 0.038 | 0.076 | 0.114 | 0.229 | 0.133 | 0.532 | 0.064 | 0.168 |
| 50 | 0.518 | 0.048 | 0.018 | 0.035 | 0.077 | 0.154 | 0.093 | 0.515 | 0.031 | 0.114 | ||
| 100 | 0.509 | 0.033 | 0.009 | 0.018 | 0.054 | 0.107 | 0.065 | 0.508 | 0.016 | 0.08 | ||
| 200 | 0.505 | 0.023 | 0.005 | 0.01 | 0.038 | 0.076 | 0.045 | 0.504 | 0.008 | 0.057 | ||
| 500 | 0.502 | 0.014 | 0.002 | 0.004 | 0.024 | 0.048 | 0.029 | 0.501 | 0.003 | 0.037 | ||
| 0.75 | 25 | 0.807 | 0.106 | 0.057 | 0.076 | 0.172 | 0.229 | 0.133 | 0.798 | 0.064 | 0.168 | |
| 50 | 0.777 | 0.071 | 0.027 | 0.035 | 0.115 | 0.154 | 0.093 | 0.773 | 0.031 | 0.114 | ||
| 100 | 0.764 | 0.050 | 0.014 | 0.018 | 0.080 | 0.107 | 0.065 | 0.762 | 0.016 | 0.080 | ||
| 200 | 0.758 | 0.034 | 0.008 | 0.010 | 0.057 | 0.076 | 0.045 | 0.756 | 0.008 | 0.057 | ||
| 500 | 0.753 | 0.022 | 0.003 | 0.004 | 0.036 | 0.048 | 0.029 | 0.752 | 0.003 | 0.037 | ||
| 1 | 25 | 1.075 | 0.141 | 0.075 | 0.075 | 0.229 | 0.229 | 0.133 | 1.064 | 0.064 | 0.168 | |
| 50 | 1.035 | 0.095 | 0.035 | 0.035 | 0.154 | 0.154 | 0.093 | 1.031 | 0.031 | 0.114 | ||
| 100 | 1.018 | 0.066 | 0.018 | 0.018 | 0.107 | 0.107 | 0.065 | 1.016 | 0.016 | 0.080 | ||
| 200 | 1.010 | 0.046 | 0.010 | 0.010 | 0.076 | 0.076 | 0.045 | 1.008 | 0.008 | 0.057 | ||
| 500 | 1.004 | 0.029 | 0.004 | 0.004 | 0.048 | 0.048 | 0.029 | 1.003 | 0.003 | 0.037 | ||
| 1.25 | 25 | 1.344 | 0.176 | 0.094 | 0.075 | 0.286 | 0.229 | 0.133 | 1.33 | 0.064 | 0.168 | |
| 50 | 1.294 | 0.119 | 0.044 | 0.035 | 0.192 | 0.154 | 0.093 | 1.288 | 0.031 | 0.114 | ||
| 100 | 1.273 | 0.083 | 0.023 | 0.018 | 0.134 | 0.107 | 0.065 | 1.27 | 0.016 | 0.080 | ||
| 200 | 1.263 | 0.057 | 0.013 | 0.010 | 0.095 | 0.076 | 0.045 | 1.26 | 0.008 | 0.057 | ||
| 500 | 1.254 | 0.036 | 0.004 | 0.004 | 0.06 | 0.048 | 0.029 | 1.254 | 0.003 | 0.037 | ||
| 1.50 | 25 | 1.613 | 0.212 | 0.113 | 0.075 | 0.343 | 0.229 | 0.133 | 1.596 | 0.064 | 0.168 | |
| 50 | 1.553 | 0.143 | 0.053 | 0.035 | 0.231 | 0.154 | 0.093 | 1.546 | 0.031 | 0.114 | ||
| 100 | 1.528 | 0.099 | 0.028 | 0.018 | 0.161 | 0.107 | 0.065 | 1.524 | 0.016 | 0.08 | ||
| 200 | 1.515 | 0.069 | 0.015 | 0.01 | 0.114 | 0.076 | 0.045 | 1.512 | 0.008 | 0.057 | ||
| 500 | 1.505 | 0.043 | 0.005 | 0.005 | 0.072 | 0.048 | 0.029 | 1.504 | 0.003 | 0.037 | ||
| 40% | 0.50 | 25 | 0.555 | 0.088 | 0.055 | 0.11 | 0.143 | 0.286 | 0.163 | 0.538 | 0.075 | 0.210 |
| 50 | 0.528 | 0.058 | 0.028 | 0.057 | 0.091 | 0.181 | 0.111 | 0.517 | 0.034 | 0.134 | ||
| 100 | 0.519 | 0.04 | 0.019 | 0.037 | 0.062 | 0.125 | 0.077 | 0.509 | 0.018 | 0.093 | ||
| 200 | 0.514 | 0.027 | 0.014 | 0.028 | 0.045 | 0.089 | 0.053 | 0.505 | 0.009 | 0.067 | ||
| 500 | 0.507 | 0.017 | 0.007 | 0.014 | 0.029 | 0.057 | 0.034 | 0.502 | 0.003 | 0.045 | ||
| 0.75 | 25 | 0.833 | 0.132 | 0.083 | 0.110 | 0.214 | 0.286 | 0.163 | 0.806 | 0.075 | 0.210 | |
| 50 | 0.793 | 0.087 | 0.043 | 0.057 | 0.136 | 0.181 | 0.111 | 0.776 | 0.034 | 0.134 | ||
| 100 | 0.778 | 0.060 | 0.028 | 0.037 | 0.094 | 0.125 | 0.077 | 0.764 | 0.018 | 0.093 | ||
| 200 | 0.771 | 0.041 | 0.021 | 0.028 | 0.067 | 0.089 | 0.053 | 0.757 | 0.009 | 0.067 | ||
| 500 | 0.761 | 0.026 | 0.011 | 0.014 | 0.043 | 0.057 | 0.034 | 0.751 | 0.003 | 0.045 | ||
| 1 | 25 | 1.110 | 0.175 | 0.11 | 0.11 | 0.286 | 0.286 | 0.163 | 1.075 | 0.075 | 0.210 | |
| 50 | 1.057 | 0.116 | 0.057 | 0.057 | 0.181 | 0.181 | 0.111 | 1.034 | 0.034 | 0.134 | ||
| 100 | 1.037 | 0.08 | 0.037 | 0.037 | 0.125 | 0.125 | 0.077 | 1.018 | 0.018 | 0.093 | ||
| 200 | 1.028 | 0.055 | 0.028 | 0.028 | 0.089 | 0.089 | 0.053 | 1.009 | 0.009 | 0.067 | ||
| 500 | 1.014 | 0.034 | 0.014 | 0.014 | 0.057 | 0.057 | 0.034 | 1.003 | 0.003 | 0.045 | ||
| 1.25 | 25 | 1.388 | 0.219 | 0.138 | 0.110 | 0.357 | 0.286 | 0.163 | 1.344 | 0.075 | 0.210 | |
| 50 | 1.321 | 0.144 | 0.071 | 0.057 | 0.227 | 0.181 | 0.111 | 1.293 | 0.034 | 0.134 | ||
| 100 | 1.297 | 0.099 | 0.047 | 0.037 | 0.156 | 0.125 | 0.077 | 1.273 | 0.018 | 0.093 | ||
| 200 | 1.285 | 0.068 | 0.035 | 0.028 | 0.111 | 0.089 | 0.053 | 1.261 | 0.009 | 0.067 | ||
| 500 | 1.268 | 0.043 | 0.018 | 0.014 | 0.072 | 0.057 | 0.034 | 1.254 | 0.003 | 0.045 | ||
| 1.50 | 25 | 1.665 | 0.263 | 0.165 | 0.110 | 0.428 | 0.286 | 0.163 | 1.613 | 0.075 | 0.21 | |
| 50 | 1.585 | 0.173 | 0.085 | 0.057 | 0.272 | 0.181 | 0.111 | 1.552 | 0.034 | 0.134 | ||
| 100 | 1.556 | 0.119 | 0.056 | 0.037 | 0.187 | 0.125 | 0.077 | 1.527 | 0.018 | 0.093 | ||
| 200 | 1.542 | 0.082 | 0.042 | 0.028 | 0.134 | 0.089 | 0.053 | 1.514 | 0.009 | 0.067 | ||
| 500 | 1.521 | 0.051 | 0.021 | 0.014 | 0.086 | 0.057 | 0.034 | 1.505 | 0.003 | 0.045 | ||
Table 4.
Simulation result for NIP = 4 (20th, 40th, 60th & 80th percentile) under various censoring proportions.
| Censor | 4 data points (20th, 40th, 60th 80th) |
Complete data set |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | SE | BIAS | ARB | RMSE | SRMSE | CV | MARB | RARB | ||||
| 0% | 0.50 | 25 | 0.517 | 0.051 | 0.017 | 0.034 | 0.093 | 0.186 | 0.099 | 0.529 | 0.057 | 0.127 |
| 50 | 0.507 | 0.037 | 0.007 | 0.015 | 0.066 | 0.131 | 0.073 | 0.514 | 0.027 | 0.094 | ||
| 100 | 0.503 | 0.027 | 0.003 | 0.007 | 0.046 | 0.092 | 0.053 | 0.507 | 0.014 | 0.068 | ||
| 200 | 0.502 | 0.019 | 0.002 | 0.003 | 0.033 | 0.065 | 0.038 | 0.503 | 0.007 | 0.048 | ||
| 500 | 0.500 | 0.012 | <0.001 | 0.001 | 0.021 | 0.042 | 0.024 | 0.501 | 0.003 | 0.030 | ||
| 0.75 | 25 | 0.773 | 0.076 | 0.023 | 0.031 | 0.140 | 0.186 | 0.099 | 0.793 | 0.057 | 0.127 | |
| 50 | 0.760 | 0.055 | 0.010 | 0.014 | 0.099 | 0.131 | 0.073 | 0.770 | 0.027 | 0.094 | ||
| 100 | 0.755 | 0.040 | 0.005 | 0.007 | 0.069 | 0.092 | 0.053 | 0.760 | 0.014 | 0.068 | ||
| 200 | 0.753 | 0.029 | 0.003 | 0.003 | 0.049 | 0.065 | 0.038 | 0.755 | 0.007 | 0.048 | ||
| 500 | 0.751 | 0.018 | <0.001 | 0.001 | 0.031 | 0.042 | 0.024 | 0.752 | 0.003 | 0.030 | ||
| 1 | 25 | 1.030 | 0.101 | 0.030 | 0.03 | 0.186 | 0.186 | 0.099 | 1.057 | 0.057 | 0.128 | |
| 50 | 1.014 | 0.074 | 0.014 | 0.014 | 0.131 | 0.131 | 0.073 | 1.027 | 0.027 | 0.094 | ||
| 100 | 1.007 | 0.053 | 0.007 | 0.007 | 0.092 | 0.092 | 0.053 | 1.014 | 0.014 | 0.068 | ||
| 200 | 1.003 | 0.038 | 0.003 | 0.003 | 0.065 | 0.065 | 0.038 | 1.007 | 0.007 | 0.048 | ||
| 500 | 1.001 | 0.024 | 0.001 | 0.001 | 0.042 | 0.042 | 0.024 | 1.003 | 0.003 | 0.030 | ||
| 1.25 | 25 | 1.286 | 0.126 | 0.036 | 0.029 | 0.233 | 0.186 | 0.099 | 1.321 | 0.057 | 0.128 | |
| 50 | 1.267 | 0.092 | 0.017 | 0.013 | 0.164 | 0.131 | 0.073 | 1.284 | 0.027 | 0.094 | ||
| 100 | 1.258 | 0.066 | 0.008 | 0.007 | 0.115 | 0.092 | 0.053 | 1.267 | 0.014 | 0.068 | ||
| 200 | 1.254 | 0.048 | 0.004 | 0.003 | 0.081 | 0.065 | 0.038 | 1.259 | 0.007 | 0.048 | ||
| 500 | 1.251 | 0.031 | 0.001 | 0.001 | 0.052 | 0.042 | 0.024 | 1.253 | 0.003 | 0.03 | ||
| 1.50 | 25 | 1.543 | 0.152 | 0.043 | 0.028 | 0.280 | 0.186 | 0.099 | 1.586 | 0.057 | 0.128 | |
| 50 | 1.520 | 0.111 | 0.020 | 0.013 | 0.197 | 0.131 | 0.073 | 1.541 | 0.027 | 0.094 | ||
| 100 | 1.510 | 0.08 | 0.010 | 0.007 | 0.138 | 0.092 | 0.053 | 1.521 | 0.014 | 0.068 | ||
| 200 | 1.505 | 0.058 | 0.005 | 0.003 | 0.098 | 0.065 | 0.038 | 1.510 | 0.007 | 0.048 | ||
| 500 | 1.501 | 0.037 | 0.001 | 0.001 | 0.063 | 0.042 | 0.024 | 1.504 | 0.003 | 0.030 | ||
| 20% | 0.50 | 25 | 0.511 | 0.058 | 0.011 | 0.022 | 0.099 | 0.198 | 0.115 | 0.532 | 0.064 | 0.137 |
| 50 | 0.506 | 0.042 | 0.006 | 0.012 | 0.069 | 0.139 | 0.083 | 0.515 | 0.031 | 0.095 | ||
| 100 | 0.505 | 0.03 | 0.005 | 0.011 | 0.049 | 0.098 | 0.059 | 0.508 | 0.016 | 0.066 | ||
| 200 | 0.504 | 0.021 | 0.004 | 0.008 | 0.034 | 0.069 | 0.041 | 0.504 | 0.008 | 0.047 | ||
| 500 | 0.501 | 0.013 | 0.001 | 0.003 | 0.022 | 0.044 | 0.026 | 0.501 | 0.003 | 0.031 | ||
| 0.75 | 25 | 0.766 | 0.087 | 0.016 | 0.021 | 0.148 | 0.198 | 0.115 | 0.798 | 0.064 | 0.137 | |
| 50 | 0.759 | 0.063 | 0.009 | 0.012 | 0.104 | 0.139 | 0.083 | 0.773 | 0.031 | 0.095 | ||
| 100 | 0.758 | 0.044 | 0.008 | 0.011 | 0.073 | 0.098 | 0.059 | 0.762 | 0.016 | 0.066 | ||
| 200 | 0.756 | 0.031 | 0.006 | 0.008 | 0.052 | 0.069 | 0.041 | 0.756 | 0.008 | 0.047 | ||
| 500 | 0.752 | 0.020 | 0.002 | 0.003 | 0.033 | 0.044 | 0.026 | 0.752 | 0.003 | 0.031 | ||
| 1 | 25 | 1.020 | 0.116 | 0.020 | 0.020 | 0.198 | 0.198 | 0.115 | 1.064 | 0.064 | 0.137 | |
| 50 | 1.012 | 0.083 | 0.012 | 0.012 | 0.139 | 0.139 | 0.083 | 1.031 | 0.031 | 0.095 | ||
| 100 | 1.011 | 0.059 | 0.011 | 0.011 | 0.098 | 0.098 | 0.059 | 1.016 | 0.016 | 0.066 | ||
| 200 | 1.008 | 0.042 | 0.008 | 0.008 | 0.069 | 0.069 | 0.041 | 1.008 | 0.008 | 0.047 | ||
| 500 | 1.003 | 0.026 | 0.003 | 0.003 | 0.044 | 0.044 | 0.026 | 1.003 | 0.003 | 0.031 | ||
| 1.25 | 25 | 1.275 | 0.145 | 0.025 | 0.020 | 0.247 | 0.198 | 0.115 | 1.330 | 0.064 | 0.137 | |
| 50 | 1.265 | 0.104 | 0.015 | 0.012 | 0.174 | 0.139 | 0.083 | 1.288 | 0.031 | 0.095 | ||
| 100 | 1.263 | 0.074 | 0.013 | 0.011 | 0.122 | 0.098 | 0.059 | 1.27 | 0.016 | 0.066 | ||
| 200 | 1.26 | 0.052 | 0.010 | 0.008 | 0.086 | 0.069 | 0.041 | 1.26 | 0.008 | 0.047 | ||
| 500 | 1.253 | 0.033 | 0.003 | 0.003 | 0.055 | 0.044 | 0.026 | 1.254 | 0.003 | 0.031 | ||
| 1.50 | 25 | 1.529 | 0.174 | 0.029 | 0.020 | 0.297 | 0.198 | 0.115 | 1.596 | 0.064 | 0.137 | |
| 50 | 1.517 | 0.125 | 0.017 | 0.012 | 0.209 | 0.139 | 0.083 | 1.546 | 0.031 | 0.095 | ||
| 100 | 1.516 | 0.089 | 0.016 | 0.011 | 0.147 | 0.098 | 0.059 | 1.524 | 0.016 | 0.066 | ||
| 200 | 1.512 | 0.062 | 0.012 | 0.008 | 0.103 | 0.069 | 0.041 | 1.512 | 0.008 | 0.047 | ||
| 500 | 1.504 | 0.039 | 0.004 | 0.003 | 0.066 | 0.044 | 0.026 | 1.504 | 0.003 | 0.031 | ||
| 40% | 0.50 | 25 | 0.532 | 0.074 | 0.032 | 0.063 | 0.124 | 0.249 | 0.142 | 0.538 | 0.075 | 0.166 |
| 50 | 0.519 | 0.051 | 0.019 | 0.038 | 0.081 | 0.162 | 0.100 | 0.517 | 0.034 | 0.11 | ||
| 100 | 0.513 | 0.036 | 0.013 | 0.025 | 0.056 | 0.112 | 0.070 | 0.509 | 0.018 | 0.076 | ||
| 200 | 0.511 | 0.025 | 0.011 | 0.021 | 0.040 | 0.079 | 0.049 | 0.505 | 0.009 | 0.055 | ||
| 500 | 0.506 | 0.016 | 0.006 | 0.011 | 0.026 | 0.051 | 0.031 | 0.502 | 0.003 | 0.037 | ||
| 0.75 | 25 | 0.797 | 0.112 | 0.047 | 0.063 | 0.186 | 0.249 | 0.142 | 0.806 | 0.075 | 0.166 | |
| 50 | 0.778 | 0.077 | 0.028 | 0.038 | 0.121 | 0.162 | 0.100 | 0.776 | 0.034 | 0.11 | ||
| 100 | 0.769 | 0.054 | 0.019 | 0.025 | 0.084 | 0.112 | 0.07 | 0.764 | 0.018 | 0.076 | ||
| 200 | 0.766 | 0.038 | 0.016 | 0.021 | 0.059 | 0.079 | 0.049 | 0.757 | 0.009 | 0.055 | ||
| 500 | 0.758 | 0.023 | 0.008 | 0.011 | 0.039 | 0.051 | 0.031 | 0.752 | 0.003 | 0.037 | ||
| 1 | 25 | 1.062 | 0.149 | 0.062 | 0.062 | 0.249 | 0.249 | 0.142 | 1.075 | 0.075 | 0.166 | |
| 50 | 1.038 | 0.103 | 0.038 | 0.038 | 0.162 | 0.162 | 0.100 | 1.034 | 0.034 | 0.11 | ||
| 100 | 1.025 | 0.072 | 0.025 | 0.025 | 0.112 | 0.112 | 0.070 | 1.018 | 0.018 | 0.076 | ||
| 200 | 1.021 | 0.05 | 0.021 | 0.021 | 0.079 | 0.079 | 0.049 | 1.009 | 0.009 | 0.055 | ||
| 500 | 1.011 | 0.031 | 0.011 | 0.011 | 0.051 | 0.051 | 0.031 | 1.003 | 0.003 | 0.037 | ||
| 1.25 | 25 | 1.328 | 0.186 | 0.078 | 0.062 | 0.311 | 0.249 | 0.142 | 1.344 | 0.075 | 0.166 | |
| 50 | 1.297 | 0.129 | 0.047 | 0.038 | 0.202 | 0.162 | 0.100 | 1.293 | 0.034 | 0.11 | ||
| 100 | 1.282 | 0.089 | 0.032 | 0.025 | 0.139 | 0.112 | 0.070 | 1.273 | 0.018 | 0.076 | ||
| 200 | 1.277 | 0.063 | 0.027 | 0.021 | 0.099 | 0.079 | 0.049 | 1.261 | 0.009 | 0.055 | ||
| 500 | 1.264 | 0.039 | 0.014 | 0.011 | 0.064 | 0.051 | 0.031 | 1.254 | 0.003 | 0.037 | ||
| 1.50 | 25 | 1.593 | 0.223 | 0.093 | 0.062 | 0.373 | 0.249 | 0.142 | 1.613 | 0.075 | 0.166 | |
| 50 | 1.556 | 0.154 | 0.056 | 0.038 | 0.243 | 0.162 | 0.100 | 1.552 | 0.034 | 0.11 | ||
| 100 | 1.538 | 0.107 | 0.038 | 0.025 | 0.167 | 0.112 | 0.070 | 1.527 | 0.018 | 0.076 | ||
| 200 | 1.532 | 0.076 | 0.032 | 0.021 | 0.119 | 0.079 | 0.049 | 1.514 | 0.009 | 0.055 | ||
| 500 | 1.517 | 0.047 | 0.017 | 0.011 | 0.077 | 0.051 | 0.031 | 1.505 | 0.003 | 0.037 | ||
Table 5.
Simulation result for NIP = 5 (17th, 34th, 50th, 67th & 84th percentile) under various censoring proportions.
| Censor | 5 data points (17th, 34th, 50st, 67th and 84th) |
Complete data set |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | SE | BIAS | ARB | RMSE | SRMSE | CV | MARB | RARB | ||||
| 0% | 0.50 | 25 | 0.515 | 0.049 | 0.015 | 0.030 | 0.088 | 0.177 | 0.095 | 0.529 | 0.057 | 0.114 |
| 50 | 0.504 | 0.033 | 0.004 | 0.008 | 0.062 | 0.124 | 0.066 | 0.514 | 0.027 | 0.084 | ||
| 100 | 0.502 | 0.023 | 0.002 | 0.004 | 0.043 | 0.086 | 0.046 | 0.507 | 0.014 | 0.058 | ||
| 200 | 0.501 | 0.017 | 0.001 | 0.002 | 0.030 | 0.060 | 0.034 | 0.503 | 0.007 | 0.041 | ||
| 500 | 0.500 | 0.011 | <0.001 | 0.001 | 0.019 | 0.039 | 0.021 | 0.501 | 0.003 | 0.026 | ||
| 0.75 | 25 | 0.772 | 0.074 | 0.022 | 0.030 | 0.133 | 0.177 | 0.095 | 0.793 | 0.057 | 0.114 | |
| 50 | 0.756 | 0.050 | 0.006 | 0.008 | 0.093 | 0.124 | 0.066 | 0.770 | 0.027 | 0.084 | ||
| 100 | 0.753 | 0.035 | 0.003 | 0.004 | 0.064 | 0.086 | 0.046 | 0.760 | 0.014 | 0.058 | ||
| 200 | 0.752 | 0.025 | 0.002 | 0.002 | 0.045 | 0.060 | 0.034 | 0.755 | 0.007 | 0.041 | ||
| 500 | 0.751 | 0.016 | 0.001 | 0.001 | 0.029 | 0.039 | 0.021 | 0.752 | 0.003 | 0.026 | ||
| 1 | 25 | 1.030 | 0.098 | 0.030 | 0.030 | 0.177 | 0.177 | 0.095 | 1.057 | 0.057 | 0.114 | |
| 50 | 1.008 | 0.066 | 0.008 | 0.008 | 0.124 | 0.124 | 0.066 | 1.027 | 0.027 | 0.084 | ||
| 100 | 1.004 | 0.046 | 0.004 | 0.004 | 0.086 | 0.086 | 0.046 | 1.014 | 0.014 | 0.058 | ||
| 200 | 1.002 | 0.034 | 0.002 | 0.002 | 0.060 | 0.060 | 0.034 | 1.007 | 0.007 | 0.041 | ||
| 500 | 1.001 | 0.021 | 0.001 | 0.001 | 0.039 | 0.039 | 0.021 | 1.003 | 0.003 | 0.026 | ||
| 1.25 | 25 | 1.288 | 0.123 | 0.038 | 0.030 | 0.221 | 0.177 | 0.096 | 1.321 | 0.057 | 0.113 | |
| 50 | 1.260 | 0.083 | 0.010 | 0.008 | 0.155 | 0.124 | 0.066 | 1.284 | 0.027 | 0.084 | ||
| 100 | 1.255 | 0.058 | 0.005 | 0.004 | 0.107 | 0.086 | 0.046 | 1.267 | 0.014 | 0.058 | ||
| 200 | 1.253 | 0.042 | 0.003 | 0.002 | 0.076 | 0.060 | 0.034 | 1.259 | 0.007 | 0.041 | ||
| 500 | 1.251 | 0.027 | 0.001 | 0.001 | 0.049 | 0.039 | 0.021 | 1.253 | 0.003 | 0.026 | ||
| 1.50 | 25 | 1.545 | 0.147 | 0.045 | 0.030 | 0.265 | 0.177 | 0.096 | 1.586 | 0.057 | 0.113 | |
| 50 | 1.512 | 0.099 | 0.012 | 0.008 | 0.186 | 0.124 | 0.066 | 1.541 | 0.027 | 0.084 | ||
| 100 | 1.506 | 0.070 | 0.006 | 0.004 | 0.128 | 0.086 | 0.046 | 1.521 | 0.014 | 0.058 | ||
| 200 | 1.503 | 0.050 | 0.003 | 0.002 | 0.091 | 0.060 | 0.034 | 1.510 | 0.007 | 0.041 | ||
| 500 | 1.501 | 0.032 | 0.001 | 0.001 | 0.058 | 0.039 | 0.021 | 1.504 | 0.003 | 0.026 | ||
| 20% | 0.50 | 25 | 0.525 | 0.055 | 0.025 | 0.050 | 0.095 | 0.191 | 0.107 | 0.532 | 0.064 | 0.119 |
| 50 | 0.510 | 0.038 | 0.010 | 0.021 | 0.065 | 0.130 | 0.074 | 0.515 | 0.031 | 0.081 | ||
| 100 | 0.503 | 0.026 | 0.003 | 0.006 | 0.046 | 0.092 | 0.052 | 0.508 | 0.016 | 0.058 | ||
| 200 | 0.503 | 0.018 | 0.003 | 0.006 | 0.032 | 0.064 | 0.037 | 0.504 | 0.008 | 0.041 | ||
| 500 | 0.501 | 0.012 | 0.001 | 0.002 | 0.02 | 0.041 | 0.023 | 0.501 | 0.003 | 0.027 | ||
| 0.75 | 25 | 0.787 | 0.083 | 0.037 | 0.050 | 0.143 | 0.191 | 0.107 | 0.798 | 0.064 | 0.119 | |
| 50 | 0.766 | 0.057 | 0.016 | 0.021 | 0.098 | 0.130 | 0.074 | 0.773 | 0.031 | 0.081 | ||
| 100 | 0.755 | 0.039 | 0.005 | 0.006 | 0.069 | 0.092 | 0.052 | 0.762 | 0.016 | 0.058 | ||
| 200 | 0.754 | 0.028 | 0.004 | 0.006 | 0.048 | 0.064 | 0.037 | 0.756 | 0.008 | 0.041 | ||
| 500 | 0.751 | 0.018 | 0.001 | 0.002 | 0.031 | 0.041 | 0.023 | 0.752 | 0.003 | 0.027 | ||
| 1 | 25 | 1.050 | 0.111 | 0.050 | 0.050 | 0.191 | 0.191 | 0.107 | 1.064 | 0.064 | 0.119 | |
| 50 | 1.021 | 0.076 | 0.021 | 0.021 | 0.130 | 0.130 | 0.074 | 1.031 | 0.031 | 0.081 | ||
| 100 | 1.006 | 0.052 | 0.006 | 0.006 | 0.092 | 0.092 | 0.052 | 1.016 | 0.016 | 0.058 | ||
| 200 | 1.006 | 0.037 | 0.006 | 0.006 | 0.064 | 0.064 | 0.037 | 1.008 | 0.008 | 0.041 | ||
| 500 | 1.002 | 0.023 | 0.002 | 0.002 | 0.041 | 0.041 | 0.023 | 1.003 | 0.003 | 0.027 | ||
| 1.25 | 25 | 1.312 | 0.139 | 0.062 | 0.05 | 0.238 | 0.191 | 0.107 | 1.33 | 0.064 | 0.119 | |
| 50 | 1.276 | 0.094 | 0.026 | 0.021 | 0.163 | 0.130 | 0.074 | 1.288 | 0.031 | 0.081 | ||
| 100 | 1.258 | 0.065 | 0.008 | 0.006 | 0.114 | 0.092 | 0.052 | 1.27 | 0.016 | 0.058 | ||
| 200 | 1.257 | 0.046 | 0.007 | 0.006 | 0.08 | 0.064 | 0.037 | 1.26 | 0.008 | 0.041 | ||
| 500 | 1.252 | 0.029 | 0.002 | 0.002 | 0.051 | 0.041 | 0.023 | 1.254 | 0.003 | 0.027 | ||
| 1.50 | 25 | 1.575 | 0.166 | 0.075 | 0.05 | 0.286 | 0.191 | 0.107 | 1.596 | 0.064 | 0.119 | |
| 50 | 1.531 | 0.113 | 0.031 | 0.021 | 0.196 | 0.130 | 0.074 | 1.546 | 0.031 | 0.081 | ||
| 100 | 1.509 | 0.079 | 0.009 | 0.006 | 0.137 | 0.092 | 0.052 | 1.524 | 0.016 | 0.058 | ||
| 200 | 1.508 | 0.055 | 0.008 | 0.006 | 0.096 | 0.064 | 0.037 | 1.512 | 0.008 | 0.041 | ||
| 500 | 1.503 | 0.035 | 0.003 | 0.002 | 0.061 | 0.041 | 0.023 | 1.504 | 0.003 | 0.027 | ||
| 40% | 0.50 | 25 | 0.532 | 0.066 | 0.032 | 0.065 | 0.112 | 0.224 | 0.125 | 0.538 | 0.075 | 0.148 |
| 50 | 0.514 | 0.045 | 0.014 | 0.028 | 0.074 | 0.148 | 0.089 | 0.517 | 0.034 | 0.094 | ||
| 100 | 0.509 | 0.032 | 0.009 | 0.018 | 0.052 | 0.104 | 0.063 | 0.509 | 0.018 | 0.065 | ||
| 200 | 0.508 | 0.023 | 0.008 | 0.015 | 0.037 | 0.074 | 0.045 | 0.505 | 0.009 | 0.046 | ||
| 500 | 0.504 | 0.014 | 0.004 | 0.009 | 0.024 | 0.048 | 0.028 | 0.502 | 0.003 | 0.032 | ||
| 0.75 | 25 | 0.799 | 0.099 | 0.049 | 0.065 | 0.168 | 0.224 | 0.125 | 0.806 | 0.075 | 0.148 | |
| 50 | 0.771 | 0.068 | 0.021 | 0.028 | 0.111 | 0.148 | 0.089 | 0.776 | 0.034 | 0.094 | ||
| 100 | 0.764 | 0.048 | 0.014 | 0.018 | 0.078 | 0.104 | 0.063 | 0.764 | 0.018 | 0.065 | ||
| 200 | 0.762 | 0.034 | 0.012 | 0.015 | 0.055 | 0.074 | 0.045 | 0.757 | 0.009 | 0.046 | ||
| 500 | 0.757 | 0.021 | 0.007 | 0.009 | 0.036 | 0.048 | 0.028 | 0.752 | 0.003 | 0.032 | ||
| 1 | 25 | 1.065 | 0.132 | 0.065 | 0.065 | 0.224 | 0.224 | 0.125 | 1.075 | 0.075 | 0.148 | |
| 50 | 1.028 | 0.091 | 0.028 | 0.028 | 0.148 | 0.148 | 0.089 | 1.034 | 0.034 | 0.094 | ||
| 100 | 1.018 | 0.064 | 0.018 | 0.018 | 0.104 | 0.104 | 0.063 | 1.018 | 0.018 | 0.065 | ||
| 200 | 1.015 | 0.045 | 0.015 | 0.015 | 0.074 | 0.074 | 0.045 | 1.009 | 0.009 | 0.046 | ||
| 500 | 1.009 | 0.029 | 0.009 | 0.009 | 0.048 | 0.048 | 0.028 | 1.003 | 0.003 | 0.032 | ||
| 1.25 | 25 | 1.331 | 0.164 | 0.081 | 0.065 | 0.279 | 0.224 | 0.125 | 1.344 | 0.075 | 0.148 | |
| 50 | 1.284 | 0.113 | 0.034 | 0.028 | 0.185 | 0.148 | 0.089 | 1.293 | 0.034 | 0.094 | ||
| 100 | 1.273 | 0.08 | 0.023 | 0.018 | 0.129 | 0.104 | 0.063 | 1.273 | 0.018 | 0.065 | ||
| 200 | 1.269 | 0.057 | 0.019 | 0.015 | 0.092 | 0.074 | 0.045 | 1.261 | 0.009 | 0.046 | ||
| 500 | 1.261 | 0.036 | 0.011 | 0.009 | 0.059 | 0.048 | 0.028 | 1.254 | 0.003 | 0.032 | ||
| 1.50 | 25 | 1.597 | 0.197 | 0.097 | 0.065 | 0.335 | 0.224 | 0.125 | 1.613 | 0.075 | 0.148 | |
| 50 | 1.541 | 0.136 | 0.041 | 0.028 | 0.221 | 0.148 | 0.089 | 1.552 | 0.034 | 0.094 | ||
| 100 | 1.527 | 0.096 | 0.027 | 0.018 | 0.155 | 0.104 | 0.063 | 1.527 | 0.018 | 0.065 | ||
| 200 | 1.523 | 0.068 | 0.023 | 0.015 | 0.111 | 0.074 | 0.045 | 1.514 | 0.009 | 0.046 | ||
| 500 | 1.513 | 0.043 | 0.013 | 0.009 | 0.071 | 0.048 | 0.028 | 1.505 | 0.003 | 0.032 | ||
Table 1 shows the simulation results obtained at two quantile points (25th, and 50th percentile) from the KM curve. The overall bias remains small for different values of . Table 1 shows that for decreasing hazard ( = 0.5) with 0% censoring, and with small sample size of 25, the estimated shape parameter is 0.613 and the bias is 0.113. Similarly, for increasing hazard shape ( = 1.50) with 0% censoring and similar sample size gives the estimate 1.838 with a bias value of 0.338. We can observe that with no censoring, if the sample size increase from small to large (n = 500), bias decreases and the estimated shape parameter converges to the true parameter value. A similar pattern is captured through the second assessment criteria, RMSE. If we consider the same combination as earlier, we see that RMSE = 0.195 for the former, and RMSE = 0.585 for the latter. However, the value of SRMSE remains same at 0.390 irrespective of the true value of . Comparison between and also shows expected results. The MLE relies on the full dataset and for small sample sizes, is closer to the true value than . For example, and = 0.613 for the combination of = 0.5, c = 0, and n = 25. As expected, for larger samples sizes, estimated with only two quantiles (NIP = 2) is closer to the . We can see that, for a sample size of 500, estimated shape parameter using KM estimates is and , suggesting that even with two information points, the KM estimate converges in a similar manner as the MLE estimate. However, when censoring is introduced, we see higher deviations in the results. With no censoring, = 0.5 and n = 25, we obtain (ARB = 0.225, RMSE = 0.195, SRMSE = 0.390). At 20% censoring, the estimated (ARB = 0.234, RMSE = 0.209, SRMSE = 0.418). We observe that with small sample sizes (n = 25) with censoring, the estimate is relatively higher than the one obtained from the no censoring dataset. At 40% censoring, it is observed that there is a substantial increase in estimate of the Weibull shape parameter () with ARB = 0.698, RMSE = 0.442 and SRMSE = 0.884. Using the maximum likelihood estimation, the estimated shape parameter and the corresponding relative bias is ARB = 0.075. We can see that for small sample sizes and relatively high censoring rate, maximum likelihood estimate is much better performing than the KM estimate with NIP = 2. However, for large sample sizes, KM estimate provides similar shape parameter as the MLE estimate. In addition to that, at very high censoring rate, ARB is also higher than the acceptable threshold value of 5%. For example, even if we consider the moderately large sample size of 200 with 40% censoring rate, the relative bias is still greater than 5% (ARB = 0.060) which suggests that historical studies with high censoring rates are poor references to estimate the shape parameter.
Table 2 shows simulation results obtained at two different quantile points (25th and 75th percentile). Results are comparable to Table 1 with one noteworthy distinction: is closer to true shape parameter. At 0% censoring, = 0.50, n = 25, Table 1 shows that the KM point estimate is = 0.613 (ARB = 0.225, RMSE = 0.195, SRMSE = 0.390) whereas Table 2 with the same simulation, estimated shape parameter is (ARB = 0.124, RMSE = 0.121, SRMSE = 0.241). This suggests that when partial information is limited to just two data points, it is better to obtain information from quantiles that are spread out wider so as to capture a wider range of the survival curve. results in Table 2 are identical to Table 1 since this estimation method utilizes the full dataset. We also performed simulation studies obtained at three equal quantile points, 25th, 50th, and 75th displayed in Table 3. With the addition of one information point (NIP = 3), the deviation between and is reduced. In Table 2, the combination = 0.50, c = 0, and n = 25, 50, 100 gives = 0.562, 0.516, 0.508 respectively. With one more information point from Table 3, for n = 25, 50, 100 we get = 0.550, 0.511, 0.505 respectively. This is also a significant reduction in bias, RMSE, ARB and CV, and slight reduction in SRMSE. The reduction is negligible for larger sample sizes. For n = 500, with similar criteria mentioned above, Table 2 gives the estimate as and Table 3 gives the estimate as . Thus, for larger sample size, accuracy of Weibull shape parameter is quite similar with two or three quantile points and with the maximum likelihood estimates. The trends mentioned above are also observed in the case of 20% and 40% censoring when comparing Table 3 to Table 2. Similarly, Table 4 shows the simulation results obtained at four equally spaced quantile points (20th, 40th, 60th, and 80th. The addition of a second information point (NIP = 4 in this case) further reduces the deviation between and. The combination = 0.50, c = 0.2, and n = 25 provides = 0.511 (Table 4) compared to = 0.538 (Table 3). As expected, the results in Table 4 show lower values for RMSE, SRMSE and CV. We also observe that RARB has decreased significantly as the sample size increases, suggesting that, with the inclusion of additional data points, provide a similar estimate as . Table 5 displays the simulation results obtained at five equal quantile points, 17th, 34th, 50th, 67th, and 84th. While we obtain a closer estimate of , the marginal benefit from an additional information point has reduced. For = 0.50, c = 0, and n = 25, Table 4 provides = 0.517 and Table 5 provides = 0.515. Through a simulation study, we observe that the ARB and CV does not depend on the shape parameter hence remain constant for various values of used in the simulation study.
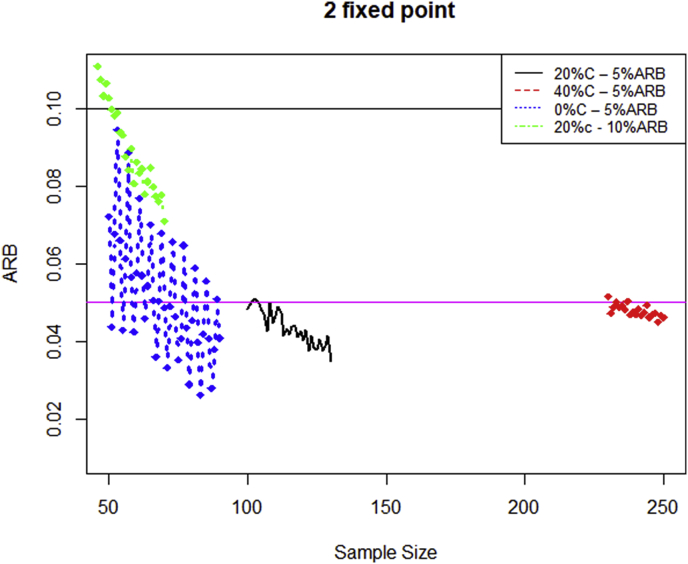
The above-mentioned results demonstrate how ARB changes for different combinations of sample size, NIP and censoring proportion. From a practical standpoint, however, we wish to assess if the historical study has a large enough sample size, so as to give us confidence to use it to estimate and use this estimate in a subsequent sample size calculation. We would also like to know the minimum value of NIP that we should use to estimate for a fixed value of the sample size of the historical study. Fig. 1 displays a plot of ARB versus sample size n for NIP = 2 (25th, 75th percentiles) for four combinations of censoring proportion and acceptable threshold levels. The jittery (unsmooth) shape of the curve is due to the fact that owing to the randomness inherent to the simulation process, occasionally it is possible that for a fixed value of NIP, a sample size of n+1 may result in a higher ARB compared to a sample size of n. Even so, in general, ARB goes down as n increases and Fig. 1 clearly displays this characteristic. If we choose an acceptable threshold of 5% for the ARB, Fig. 1 shows that the minimum value of n at which ARB remains at or below 5% is around 74 (for 0% censoring), 104 (for 20% censoring) and 238 (for 40% censoring). When the acceptable threshold for ARB is increased to 10%, the minimum value of n at which ARB remains at or below 10% is around 51. That is, when a statistician is tasked with using a point estimate of and if he/she has been provided with the IQR of a historical study with 20% censoring by his/her collaborators, then it is required that this historical study have a sample at least as large as 51 for the statistician to accept the point estimate as “reasonably accurate” using an ARB of 10% as the threshold value.
Fig. 1.
ARB vs Sample size for different censoring rates.
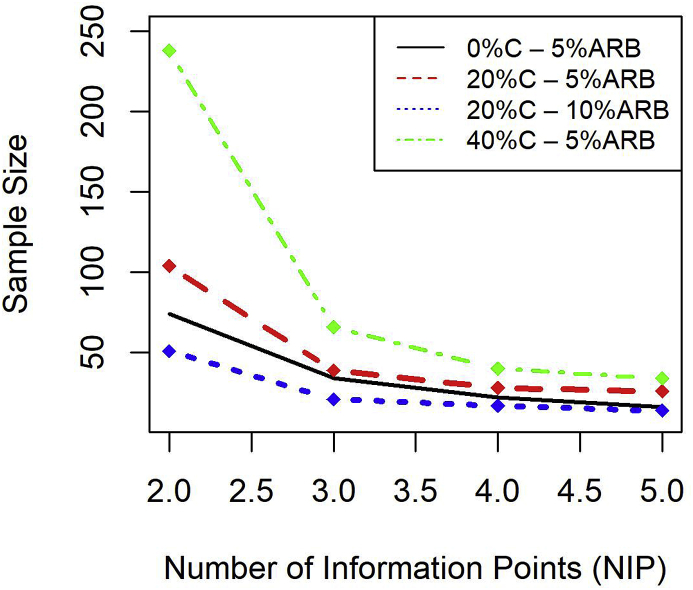
Since Fig. 1 is constructed for a fixed value of NIP, we would also like to evaluate the minimum sample size (assessed through studying Fig. 1) as a function of NIP for a fixed ARB threshold value. Fig. 2 displays such a plot (when true = 1.25) for various combinations of censoring proportion (0%, 20%, 40%) and ARB threshold levels (5% and 10%). From this plot, we see that for a fixed value of censoring proportion and ARB threshold, the minimum sample size required by us to call an accurate estimate of decreases as NIP increases. Likewise, higher censoring proportion adversely effects the minimum sample size required for us to call an accurate estimate of for any given value of NIP.
Fig. 2.
Sample size vs NIP for different censoring rates and ARB threshold levels.
3.2. Real-life application
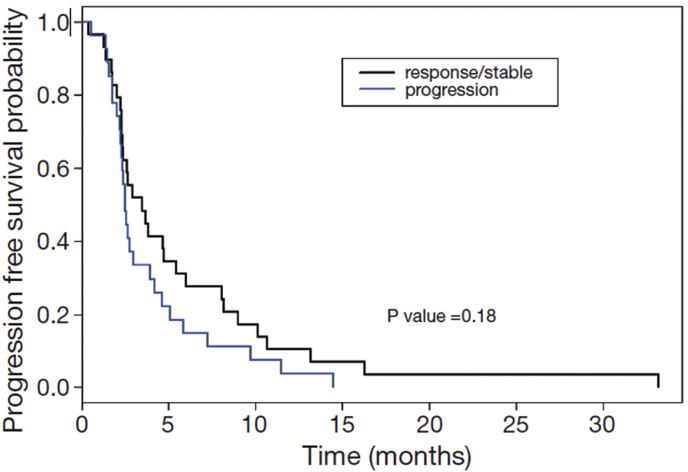
Phadnis [9] discusses a real-life example pertaining to designing a single-arm phase II clinical trial for treating patients suffering from chemotherapy refractory advanced metastatic biliary cholangiocarcinoma. For this study with PFS as the end-point of clinical interest, a point estimate of = 1.25 was used in the sample size calculations. Based on the design parameters (a hypothesized improvement in median PFS from 2.5 months to 3.75 months, accrual time of 24 months, follow-up time was 36 months, 20% loss to-follow-up, type I error of 0.05, one-sided test, power = 80%), the required number of events was calculated as 24. Accounting for the accrual and follow-up time and drop outs, the required sample size was calculated as 30. The point estimate of 1.25 was estimated from a KM curve of a prior study of sample size n = 56 conducted by Rogers at al [22]. and this KM curve has been reproduced here as Fig. 3 (see blue curve representing a standard control arm). The median PFS was reported by Rogers at al [22]. as 2.5 months, but the 25th and 75th percentiles were visually abstracted from the KM curve as 2 months and 4.75 months by Phadnis [9].
Fig. 3.
Kaplan Meier plot of PFS from historical study data (standard-of-care control).
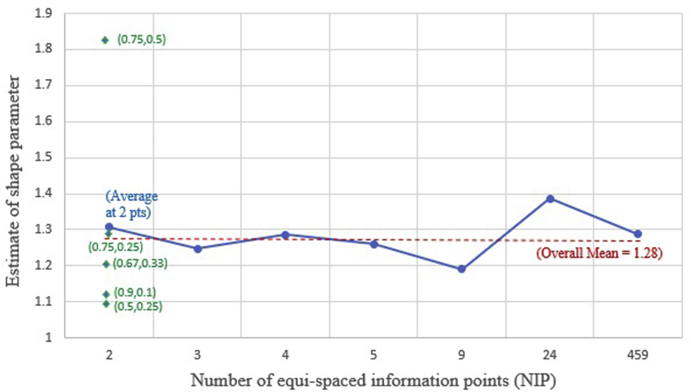
We used the DigitizeIt [20] software to assess the sensitivity of these calculations pertaining to obtaining a point estimate of for NIP = 2, 3, 4, 5, 9, 24, and 459. For NIP = 2, various possibilities were considered such as: {i} 25th and 50th percentile {ii} 50th and 75th percentile{iii} 25th and 75th percentile {iv} 33rd and 67th percentile {v} 10th and 90th percentile. For NIP = 3, 4, 5, 9 and 24, the percentiles were equally spaced. So for example, NIP = 9 meant that all deciles were considered. The last value of NIP = 459 was auto-generated by the DigitizeIt software when we selected the whole (blue) curve. Then equation (3) was used to obtain the point estimate of . Fig. 4 displays a plot of this point estimate versus NIP. From this figure we see that when NIP = 2, the five different percentile combinations mentioned above yield a point estimate of 1.098, 1.823, 1.289, 1.205 and 1.123 respectively. The lowest of these values (1.098) results from 25th and 50th percentiles on the KM curve and the highest of these values (1.823) result from 50th and 75th percentiles on the KM curve. This suggests that when NIP = 2 is chosen, we may be better off choosing widely (and equally) spaced percentiles that are capture do not ignore the two extreme ends of the KM curve. The average of the 5 values for NIP = 2 is found to be 1.308. When using NIP = 3, the point estimate obtained from using the software was 1.248 which is nearly identical to 1.25 used by visual abstraction. For all other values of NIP, the point estimate obtained from equation (3) is similar in magnitude. The overall mean of these estimates for different values of NIP is found to be 1.280. Overall, we see that the historical study of sample size n = 56 was adequate to obtain a reasonably accurate estimate of whether by visual abstraction or by the use of software. However, there could be other examples where software could be preferred to visual abstraction (especially when the published KM curves are of small size or of sub-optimal quality).
Fig. 4.
Weibull shape estimate vs Number of Information Points (NIP).
4. Conclusion
In this paper we have presented simulation study results for assessing the accuracy of Weibull shape parameter when it is estimated from historical data made available through published results of the median survival time and IQR, or, by using the entire KM curve. These results will enable a statistician to make informed decisions in designing clinical trials that assume a Weibull distribution for the survival times. When such an assumption is viable, statisticians will find our simulation results quite useful in that they will be able to decide whether the historical study data has a large enough sample size to warrant estimating the Weibull shape parameter with reasonable accuracy. Our results suggest that for historical studies with n = 50 or more, an estimate of the shape parameter obtained by using NIP = 3 is reasonably accurate with an ARB <5% for up to 20% censoring. In our experience, this is a typical occurrence in designing phase II single arm trials in cancer where biomedical researchers investigating a new treatment often base their research hypothesis after looking at the study results of a standard control in a previously conducted historical trial. Occasionally, the historical trials may have a combination of low sample size (say 25–45) and/or greater than 20% censoring (say 30%–40% is common in cancer) and in such cases the statistician may have to use a software to extract information from all points on the KM curve. Where such a software is not available, it may be advisable to do visual abstraction for as many points as possible. If sample sizes are small with even higher censoring rates, the acceptable threshold for ARB may increased from 5% to 10% or a more conservative estimate of the Weibull shape parameter may be used than the one obtained from the KM curve. Further, plots such as Figs. 1 and 2 (specific to the research hypothesis under consideration) may prove to be very handy when deciding on the choice of a point estimate for the shape parameter.
Our simulation study also provides two important guidelines. Firstly, many studies are conducted assuming exponentially distributed survival times for the simple reason that it is easy to conduct the sample size calculations. Since the exponential distribution is a special case of the Weibull (with = 1), our results can be used as a warning that the assumption of exponentially distributed times may be inappropriate when KM curves from a suitable historical study indicate otherwise (when a reasonably accurate estimate of is obtained with less than 5% ARB). This is important because assuming = 1 when historical study suggests otherwise may underestimate or overestimate the sample size for the current trial. Second, our simulation results discourage the practice of just reporting the median survival time in biomedical journals. In cases where the KM curve is not published, our results encourage the research community to report at least the IQR along with the median survival time so that this information (NIP = 3) can be used for designing future trials. We recommend that in the absence of a high-quality KM plot, information about the 10th and 90th percentile of the survival time should be reported in addition to the median and the IQR. We also warn against using our method when the assumption of Weibull distribution is inappropriate. In this regard, we suggest using a Weibull plot or a goodness-of-fit test to the data abstracted from the KM curve before proceeding to estimate for subsequent use in sample size calculations. For example, if the DigitizeIt [20] software is used to abstract data from the KM curve, then we can obtain a large sample dataset and can use the chi-square goodness-of-fit test recommended by Ross [23] to assess the Weibull fit. As this test is applicable to both continuous and discrete right censored data, the discrete choices of coordinate points {t, S(t)} selected by using the DigitizeIt software should work reasonably well. Alternatively, when such customized software is not available, Mann's test (see Mann et al. [24]) specific to the Weibull can be used to assess the Weibull fit when the abstracted data set is of moderate size. Another option to assess the Weibull fit is by obtaining a log-survival plot of Cox-Snell residuals using the technique mentioned in Allison [25].
Overall, we feel that our work will provide an additional insight to statisticians planning a clinical trial design using the assumption of Weibull distributed survival times.
Disclaimer
None.
Declaration of competing interest
The authors have no relevant conflicts of interest to declare.
Acknowledgment
None.
References
- 1.SWOG: cancer research network – cancer research and biostatistics. https://stattools.crab.org/Calculators/oneArmSurvivalColored.html Available at:
- 2.Finkelstein D.M., Muzikansky A., Schoenfeld D.A. Comparing survival of a sample to that of a standard population. J. Natl. Cancer Inst. 2003;95:1434–1439. doi: 10.1093/jnci/djg052. [DOI] [PubMed] [Google Scholar]
- 3.Kwak M., Jung S.H. Phase II clinical trials with time-to-event endpoints: optimal two-stage designs with one-sample log-rank test. Stat. Med. 2014;33:2004–2016. doi: 10.1002/sim.6073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Jung S.H. CRC Press: Chapman and Hall; 2013. Randomized Phase II Cancer Clinical Trial. [Google Scholar]
- 5.Sun X., Peng P., Tu D. Phase II cancer clinical trials with a one-sample log-rabk test and its corrections based on the Edgeworth expansion. Contemp. Clin. Trials. 2011;32:108–113. doi: 10.1016/j.cct.2010.09.009. [DOI] [PubMed] [Google Scholar]
- 6.Wu J. Sample size calculation for the one-sample log-rank test. Pharmaceut. Stat. 2015;14:26–33. doi: 10.1002/pst.1654. [DOI] [PubMed] [Google Scholar]
- 7.PASS 14 Power Analysis and Sample Size Software. NCSS, LLC; Kaysville, Utah, USA,: 2015. ncss.com/software/pass [Google Scholar]
- 8.nQuery 8 Power and Sample Size for Group Sequential Trials . 2019. “Statsols” (Statistical Solutions Limited), Cork, Ireland, statsols.Com/nquery. [Google Scholar]
- 9.Phadnis M.A. Sample size calculation for small sample single-arm trials for time-to-event data: logrank test with normal approximation or test statistic based on exact chi-square distribution? Contemp. Clin. Trials. 2019;15 doi: 10.1016/j.conctc.2019.100360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Narula S.C., Li F.S. Sample size calculations in exponential life testing. Technometrics. 1975;17(2):229–231. [Google Scholar]
- 11.Gerokostopoulos A., Guo H., Pohl E. Determining the right sample size for your test: theory and Application. 2015. https://www.weibull.com/pubs/2015_RAMS_right_sample_size.pdf Available from:
- 12.Yang Y., Li W., Tang W., Li B., Zhang D. Sample sizes based on the Weibull distribution and Normal distribution for FRP tensile coupon test. Materials. 2019;12(1) doi: 10.3390/ma12010126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Jeng S. Exact sample siuze determination in a Weibull test plan when there is time censoring. J Stat Compul Simul. 2003;73(6):389–408. [Google Scholar]
- 14.Meeker W.Q., Jr., Escobar L.A., Hill D.A. Sample sizes for estimating the Weibull hazard function from censored samples. IEEE Trans. Reliab. 1992;41(1):133–138. [Google Scholar]
- 15.Pina-Moarrez M.R., Ramos-Lopez M.L., Alvarado-Iniesta A., Molina-Arredondo R.D. Robust sample size for Weibull demonstration test plan. Dyna. 2016;83(197):52–57. [Google Scholar]
- 16.Heo M., Faith M.S., Allison D.B. Power and sample size for survival analysis under the Weibull distribution when the whole lifespan is of interest. Mech. Ageing Dev. 1998;102:45–53. doi: 10.1016/s0047-6374(98)00010-4. [DOI] [PubMed] [Google Scholar]
- 17.Han D., Cheen Z., Hou Y. Sample size for a non-inferiority clinical trial with time-to-event data in the presence of competing risks. J. Biopharm. Stat. 2018;28:797–807. doi: 10.1080/10543406.2017.1399897. [DOI] [PubMed] [Google Scholar]
- 18.Phadnis M.A., Wetmore J.B., Mayo M.S. A clinical trial design using the concept of proportional time using the generalized gamma ratio distribution. Stat. Med. 2017;6:4121–4140. doi: 10.1002/sim.7421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wan F. Simulating survival data with predefined censoring rates for proportional hazards models. Stat. Med. 2017;36(5):838–854. doi: 10.1002/sim.7178. [DOI] [PubMed] [Google Scholar]
- 20.DigitizeIt 2.3.3. 2019. http://www.digitizeit.de Braunschweig, Germany.
- 21.R Core Team . R Foundation for Statistical Computing; Vienna, Austria: 2018. R: A Language and Environment for Statistical Computing.https://www.R-project.org/ [Google Scholar]
- 22.Rogers J.E., Law L., Nguyen V.D., Qiao W., Javle M.M., Kaseb A., Shroff R.T. Second-line systemic treatment for advanced cholangiocarcinoma. J. Gastrointest. Oncol. 2014;5(6):408–413. doi: 10.3978/j.issn.2078-6891.2014.072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ross S.M. John Wiley & Sons; 1987. Introduction to Probability and Statistics for Engineers and Scientists. [Google Scholar]
- 24.Mann N.R., Schafer R.E., Singpurwalla N.D. John Wiley & Sons; 1974. Methods for Statistical Analysis of Reliability and Life Data. [Google Scholar]
- 25.Allison P.D. SAS Institute Inc; Cary, NC: 2010. Survival Analysis Using SAS: A Practical Guide. [Google Scholar]