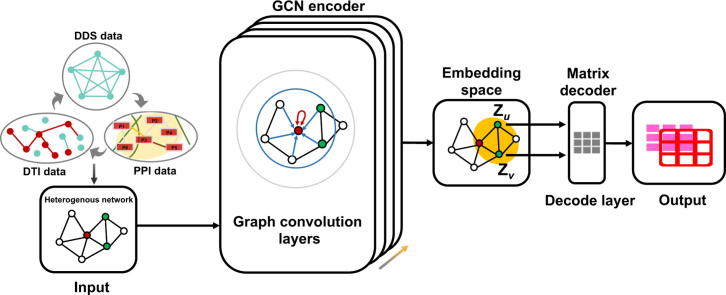
Graphical abstract
Abbreviations: GCN, graph convolutional network; AUC, area under the curve; HTS, high throughput screening; RF, random forest; XGBoost, extreme gradient boosting; DDS, drug-drug synergy; DTI, drug-target interaction; PPI, protein–protein interaction; CNN, convolutional neural network; ROC, receiver operating characteristic; TPR, true positive rate; FPR, false positive rate; SVM, support vector machine; DNN, deep neural network; ACC, accuracy; SD, standard deviation; ER, estrogen receptor; TNBC, triple negative breast cancer; GBM, glioblastoma multiforme
Keywords: Synergistic drug combination, Cancer, Cell line, Graph convolutional network, Heterogenous network
Abstract
Drug combinations are frequently used for the treatment of cancer patients in order to increase efficacy, decrease adverse side effects, or overcome drug resistance. Given the enormous number of drug combinations, it is cost- and time-consuming to screen all possible drug pairs experimentally. Currently, it has not been fully explored to integrate multiple networks to predict synergistic drug combinations using recently developed deep learning technologies. In this study, we proposed a Graph Convolutional Network (GCN) model to predict synergistic drug combinations in particular cancer cell lines. Specifically, the GCN method used a convolutional neural network model to do heterogeneous graph embedding, and thus solved a link prediction task. The graph in this study was a multimodal graph, which was constructed by integrating the drug-drug combination, drug-protein interaction, and protein–protein interaction networks. We found that the GCN model was able to correctly predict cell line-specific synergistic drug combinations from a large heterogonous network. The majority (30) of the 39 cell line-specific models show an area under the receiver operational characteristic curve (AUC) larger than 0.80, resulting in a mean AUC of 0.84. Moreover, we conducted an in-depth literature survey to investigate the top predicted drug combinations in specific cancer cell lines and found that many of them have been found to show synergistic antitumor activity against the same or other cancers in vitro or in vivo. Taken together, the results indicate that our study provides a promising way to better predict and optimize synergistic drug pairs in silico.
1. Introduction
Drug combinations, also known as combinatorial therapies, are frequently prescribed to treat patients with complex diseases especially cancers [1], [2], which have been driven by many mechanisms concurrently [3]. The rationale of drug combination is that targeting multiple molecular mechanisms in cancer cells simultaneously can typically increase the potency of the treatment [1], [2]. Thus, compared to monotherapies (i.e., single drug treatments), whose effectiveness may be limited, drug combinations have been reported with the potential to increase efficacy [1], [2], decrease adverse side effects [4], or overcome drug resistance in cancer treatment [5]. However, a concurrent use of multiple drugs may sometimes cause adverse effects [6]. For example, the addition of panitumumab to bevacizumab and oxaliplatin- or irinotecan-based chemotherapy has been shown to lead to an increased toxicity and decreased progression free survival of metastatic colorectal cancer patients [6]. Therefore, it is critical to evaluate the effects of drug combinations in cancer cells and thereby identify those showing synergistic effects in a particular cancer type. Synergistic drug combinations exhibit greater total effect of the drugs than the additive effects of the individual drugs [7].
One of the challenges in studying drug synergy is that the possible number of drug combinations grows exponentially with the number of drugs under consideration, further expanded by the number of cancer types and drug dosages. Conventionally, effective drug combinations were proposed according to clinical trials, which are time- and cost-consuming, and what was worse, may expose patients to unnecessary or even harmful treatments [8], [9]. More recently, high throughput screening (HTS) approaches have been extensively used to determine and evaluate effective combination strategies in a preclinical setting, which test an enormous number of drug combinations prescribed with different dosages and applied to different cancer cell lines [4], [10], [11]. With the advancement of HTS, informatics approaches for systems-level data management and analysis are booming such as DrugComb, an Integrative Cancer Drug Combination Data Portal [12]. An example of HTS is the study performed by O’Neil and colleagues [4]. This study carried out 23,062 experiments on 583 drug combinations across 39 cell lines from various cancer types, recapitulating in vivo response profiles. Although they don’t perfectly represent the original tumor tissues, cancer cell lines can be used to provide an alternative way for assessing the synergistic properties across drugs. Thus, data generated by HTS strategies enables the possibility of silico prediction of novel synergistic drug pairs, which can further guide in vitro and in vivo discovery of rational combination therapies.
A number of computational methods have been developed to predict anti-cancer drug synergy using chemical information from drugs, or molecular data from cancer cell lines, or both. The approaches rang from traditional machine learning models to deep learning methods. Sidorov and colleagues utilized two machine learning methods (random forest (RF) and extreme gradient boosting (XGBoost)) to develop models for drug synergy prediction [13]. The models took the physicochemical properties of drugs as input and were trained on a per-cell line basis, which means each method (RF or XGBoost) was used to generate a model for each cell line. The XGBoost method demonstrated a slightly better prediction performance than the RF technique when they were evaluated in a new data set. As shown in [7], given a drug pair comprising drugs A and B and a particular cell line C, a deep learning-based regression model (termed DeepSynergy) was developed using both the chemical descriptors for drugs A and drug B and the gene expression profiles of the cell line C to predict the synergy scores of specific drug combinations on a given cell line. DeepSynergy demonstrated an improvement of 7.2% in its performance over Gradient Boosting Machines for drug synergy prediction task. Zhang and collogues [14] also proposed a deep learning-based model named AuDNNsynergy by integrating multi-omics data (i.e., the gene expression, copy number and genetic mutation data) from cancer cell lines to predict synergistic drug combinations. AuDNNsynergy outperformed the other four approaches, namely DeepSynergy, gradient boosting machines, random forests, and elastic nets. Other studies, such as Hsu et al. [14], explored gene set-based approaches to predict the synergy of drug pairs. However, there are limited works applying the recently developed graph convolutional network (GCN) approaches [15] to predict drug synergy in cancers by integrating multiple biological networks. This study tried to develop GCN models to predict synergistic drug combinations in cancer cell lines by performing heterogeneous graph embedding from an integrated drug-drug combination, drug-protein interaction, and protein–protein interaction network.
2. Material and methods
2.1. Data collection
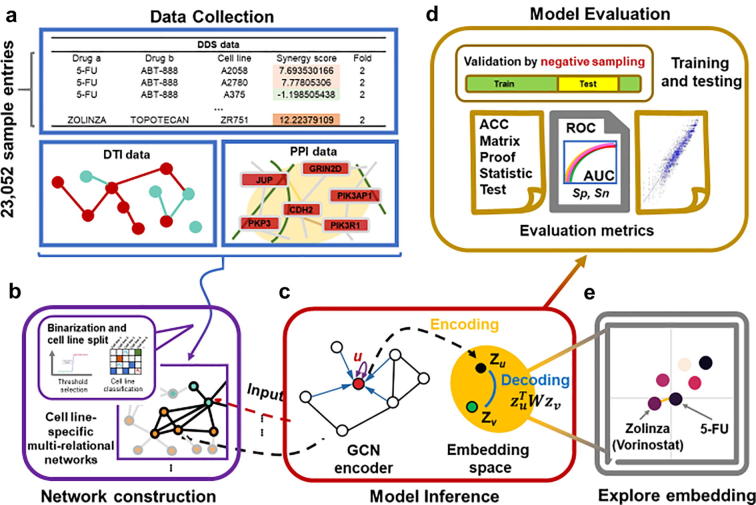
Our study design is depicted in Fig. 1. The GCN model for synergistic drug combination prediction was cell line-specific and based on three different types of subnetworks: drug-drug synergy (DDS) network, drug-target interaction (DTI) network, and protein–protein interaction (PPI) network. Data from various sources such as online databases and the published literature were collected to build the three networks (Table 1). We obtained the DDS data from O’Neil et al.’s study [4]. This study contains 23,052 drug-drug combinations with the corresponding Loewe synergy scores tested across 38 drugs in 39 cell lines derived from 6 human cancer types. The measured Loewe synergy score for most drug pairs in the O’neil et al.’s data ranges from −60 to 60. According to the definition of the Loewe synergy score, any score greater than 0 indicates the synergistic effect between the two drugs [16]. Drug pairs with a high synergy score indicate a highly synergistic effect [7]. We used 30 as the threshold to define the positive and negative samples as described in Preue et al.’s study [7]. Drug pairs with a measured synergy score higher than 30 were considered as positive (i.e., synergistic). Drug pairs with a measured score lower than 30 and not reported were considered as negative (i.e., non-synergistic). In this way, we obtained 20,971 negative drug pairs and 2,081 positive drug pairs.
Fig. 1.
The study designs. (a) Data collection. The drug-drug synergy (DDS) data, the drug-target interaction (DTI) data, and the protein–protein interaction (PPI) data were collected for the three subnetworks. (b) Network construction. For a given cell line, the synergy scores of drug pairs were binarized to construct the DDS subnetwork, which together with the DTI and PPI networks was further built the cell line-specific heterogenous network. (c) Model inference. The heterogenous network for a specific cell line is the input of the GCN encoder. Each encoded node is then mapped to an embedding space for representing the drug-drug synergy prediction in the new space. (d) Model evaluation. The negative sampling method together the accuracy, AUC, and Pearson correlation coefficient metrics were used. (e) Exploration of embedding space. t-SNE method was used to find the distribution of synergistic drug combinations.
Table 1.
The data sources of three types of interactions.
| Data sources | Number of links | Number of entries | Number of entities |
|---|---|---|---|
| Ⅰ(DDS) | 23,052 DDS | 23,052 DDS | 38 drugs, 39 cell lines |
| II(DTIs) | 8,083,600 DTIs | 871 DTIs | 519,022 drugs, 8,934 proteins |
| III(PPIs) | 719,402 PPIs | 5,296 PPIs | 19,085 proteins |
The DTI data were extracted from the STITCH Version 5.0 database [17], which provides voluminous interactions between chemical compounds and target proteins. We obtained a total of 8,083,600 interactions between more than 500,000 compounds and 8,900 proteins.
We collected the PPI data from two comprehensive open access repositories, the STRING Version 11.0 database [18] and the BioGRID Version 3.5.174 database [19]. Both the computationally predicted and experimentally validated interactions were included, resulting in a total of 719,402 interactions over 19,085 unique proteins. We listed the total number of links extracted for each of the three networks (DDS, DTI and PPI) in Table 1.
The three types of subnetworks were used to construct a heterogenous network interactively. This final heterogeneous network is the intersection of the heterogenous entities (i.e., proteins and drugs), and has their links from the three subnetworks [15]. The exact number of entries from DDS, DTIs and PPIs are also shown in Table 1. The entry number is the total statistics mapped in all 39 cell lines. Cell line specific networks were constructed by focusing on the links in a given cell line (Fig. 2). The construction process is as follows: the DDS samples were binarized using a synergy score of 30 as the cutoff and grouped by different cell lines. For each cell line, we mapped the DDS data to the DTI data to find the protein targets. We then mapped the DTI data to the PPI data to add the protein–protein sub-network into the heterogeneous network. The final cell line-specific heterogeneous network is the maximum connected component after aforementioned operations. As a result, 39 cell line-specific heterogeneous networks were established.
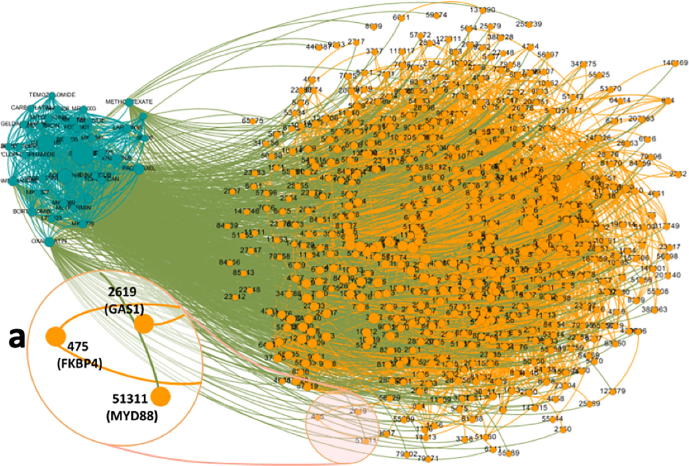
Fig. 2.
The cell line-specific heterogenous network derived from the cell line CAOV3. The teal color represents the drugs (nodes) and their interactions (edges), which consist the DDS network. The orange color represents the proteins (nodes) and their interactions (edges), which consist the PPI network. The olive color represents the interactions (edges) between the drugs and the proteins, which consist the DTI network. For the cell line CAOV3, the cell line-specific DDS network was first linked to the DTI network and then connected to the PPI network. We can choose any area of the network to zoom in and see that area in more detail. For example, (a) displays the entry number, names, and linkages of proteins in the selected area. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
2.2. Graph convolutional network encoder
As shown in [20], the prediction of synergistic drug combinations can be formulized as a link prediction problem using complex networks. In this study, we represented the different types of known links in the heterogeneous network belonging to each of the unique cell lines. Our research aim is to predict drug-drug synergic links using all the link information in the heterogeneous network [21]. The kind of prediction is related to semi-supervised learning in graphs such as GCN.
The GCN model is a neural network that operates on graphs and enables learning over graph structures. It is widely used as an encoder in different deep learning architectures. An encoder is a tool for mathematical transformation to map information from a space to another space (i.e., the embedding space).
To elucidate the GCN more clearly, the entities and their links in a network are usually represented by a defined graph G = (V, E), where V is a set of N nodes such as drugs and proteins, and E is a set of M edges such as drug-drug links and drug-protein links. These N nodes have numerical node feature vectors x1, x2, x3, …, xN ∈d, where d is the dimension of the feature vector. As for the edges, for example, (, ) represents the link between node and . In regular Euclidean arrays such as matrices and pixels in images, convolutional neural network (CNN) is of great efficiency. However, when considering graphs, the traditional CNN model is not as powerful as it in Euclidean space.
Many approaches were proposed to solve this problem in the past several years. In 2016, Kipf et al. introduced a semi-supervised GCN model [22]. In this model, graph convolution operation on a graph was defined as a multi-layer propagation process. For the graph G = (V, E), an adjacency matrix A∈N×N and a degree matrix D () can be defined. The multi-layer model follows a layer-wise propagation rule as shown below:
| (1) |
Here, is the adjacency matrix of the undirected graph G with added self-connections, I is the identity matrix, , is a layer-specific weight matrix that is able to be trained, is characterized as the activation function (i.e. ), ∈N×D is the matrix of activations of the layer. Specially, ( is the feature matrix consisting of x1, x2, x3, …, xN). The final outcome after k layers of feature vector xi is the embedding vector zi. A general GCN model can be considered as a function ( is the embedding feature matrix consisting of z1, z2, z3, …, zN).
However, for the complex network-based drug-drug synergy prediction using the above mentioned GCN model, there is an obvious limitation. It considers only single node type and link type. This drawback restricts the usage of the GCN model in heterogenous networks. In 2018, Marinka et al. developed a multi-relational link prediction model called Decagon [15]. They applied this model to predict polypharmacy side effects and achieved state-of-the-art performance. In this study, we adopted the Decagon-based GCN algorithm, which is capable to extract information of different types of nodes and edges. For a given node in a graph, successive operations of graph convolutional layers integrate and transform information from its neighbors. In this architecture, the edges (vi, vj) from a given graph G = (V, E) are divided into r types. Hence, the new representation of the edges is (vi, r, vj). For instance, 964 different relation types of drugs (side effects) were considered in Decagon. We continued to use this strategy for efficiently aggregating information from different edge types. There are 3 types of interactions (r = 1, 2, 3) in our drug-drug synergy prediction. The layer-wise propagation rule can be formulated as:
| (2) |
Here, is the adjusted Laplace matrix and , where is the number of the neighbors of node by link type r. This number is a constant for a given graph. is a trainable edge type-specific weight matrix of layer l. The same input and output forms as original GCN are maintained in this architecture. The first input layer could be numerical features, adjacency information or unique code of each node such as one-hot. Finally, the feature vector xi of a given node arrives in the ultimate embedding space as zi.
2.3. Matrix bilinear decoder
After mapping each node into the embedding space, the primary task is to represent the drug-drug synergy in the new space. This process is defined as decoding. The goal of decoding is to reconstruct edge or node labels by the integrated information from the embedding space. Voluminous methods have been introduced to decode the embeddings. Matrix factorization is one of the easiest and most efficient way to perform the operation.
From the GCN encoder each node including either drugs or proteins is first encoded into a unique vector in the embedding space (Fig. 3). Then we observe the embedding node set of all the drugs. Utilizing the embedding vectors zu and zv, the synergy score between drug u and drug v is calculated by the following matrix in the bilinear form:
| (3) |
where is a cell line-specific matrix to decode edges from node embedding vectors. is also trainable. The training process of is based on the cell line-specific heterogenous network. This is due to two reasons. Firstly, the synergistic effect is experimentally measured in different cell lines. Secondly, we expect to acquire the prediction among all the drug combinations across all the cell lines. is the predicted synergy score of the combination of drug u and drug v. Not like the original Loewe synergy score, the predicted score is between 0 and 1. The higher value represents the larger potential of synergy. Using this approach, the matrix bilinear decoder is able to well comprehend the embedding space.
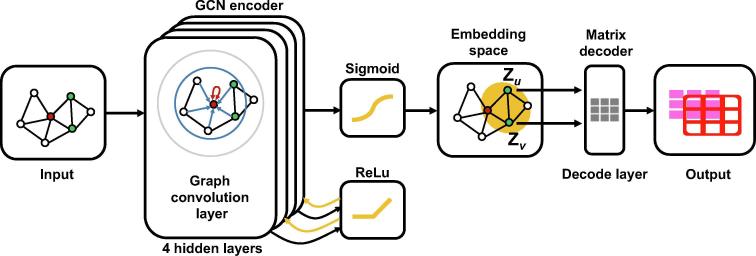
Fig. 3.
The workflow of GCN encoder and matrix decoder. There are 4 hidden layers in the GCN encoder. Between each of two hidden layers, there is a ReLu activation function. The output of the ReLu is the input for the next hidden layer. For the last hidden layer, we adopt a sigmoid activation function. The input of the GCN model is a graph and the output is an embedding vector for each node. Matrix decoder decodes the embedding vectors to predict the synergy score of any given drug combination.
2.4. Model construction
To build the model for drug-drug synergy prediction, we first constructed the GCN deep encoder (Fig. 1c and Fig. 3). Our GCN encoder had an input layer and 4 hidden layers. Between each of two hidden layers, there was a ReLu activation function. The activation function of the last hidden layer was the sigmoid function:
| (4) |
Here, y is the output of previous layer and is the embedding vector. 39 cell line specific-heterogeneous networks were input into the GCN encoder and the output was 39 cell line specific-embedding spaces including the embedding vectors for each drug.
Then from the embedding space, matrix decoder performed the mathematic operations to decode all given embedding vectors mentioned above. The matrix decoding was the 5th hidden layer. Finally, the result of the decoder was a cell line-specific synergy score matrix.
Optimization was implemented using the cross-entropy loss function:
| (5) |
Here, is the real synergistic state of each drug combination, is the predicted synergy score for each combination, and N is the number of drug combinations respectively. Backpropagation was carried out from the final loss back to each of the previous layers (Fig. 3). We trained our full model including all the trainable parameters by this end-to-end method. It has been shown that the end-to-end learning can greatly improve the model performance because all the trainable parameters receive the gradients from the loss function jointly [23]. In this study, the loss propagates through both the GCN encoder and matrix decoder.
2.5. Model comparison
To benchmark the performance of our method, we compared the GCN model to the other state-of-art machine learning and deep learning approaches, including support vector machine (SVM) [24], random forest [25], elastic net [26], and deep neural network (DNN) [27]. For the input features of these models, we utilized physiochemical properties of drugs including 1-D descriptors (i.e., molecular weight, molar refractivity, and logarithm of the octanol/water partition coefficient), 2-D descriptors (i.e., number of atoms, number of bonds, and connectivity indices), and PubChem fingerprints which represent unique molecular structure and properties in a particular complex form. We extracted these properties of each drug using the PaDEL software [28] with default settings. As a result, a total of 2,325 features were obtained to construct the feature vector for each drug. For a drug-drug pair, the two individual feature vectors were concatenated into a 4,650-dimensional input feature vector.
In order to verify the power of graph structure in predicting drug-drug synergy, we also used the adjacency from the adjacency matrix as the features for DNN. For a given drug, the feature was the corresponding adjacency vector of the adjacency matrix in the cell-line specific heterogenous network. The true feature vector of a sample (drug-drug pair) was the concatenated vector of two drugs.
The DNN models maintained similar architectures as the GCN to avoid extra factors. There were 4 hidden layers in both the DNN using adjacency-specific features and the DNN using physiochemical-related features. The number of nodes in each of the 4 hidden layers was 1280, 640, 128, 48, respectively. For the activation function, ReLu was utilized between each of two hidden layers. The loss function was also cross-entropy loss.
2.6. Model evaluation and comparison
To evaluate the performance of our proposed GCN model, we used the recently developed negative sampling method. Negative sampling is a technique used to train machine learning models that generally have several order of magnitudes more negative samples compared to positive ones. Negative sampling can precisely and robustly estimate the performance of network-based models by generating a given proportion of negative samples from the sample distribution [29]. The sampling is achieved by randomly selecting nodes instead of links since selection of a link in a graph will lead to selection of two nodes. We used 10% of all the positive samples for testing. We also randomly selected the same number of negative samples as the number of the positive ones for testing. In this case, the testing set was balanced.
To compare the performance of the GCN model with the other five models: support vector machine (SVM), random forest (RF), elastic net (EN), physiochemical features-based deep neural network (DNN) and adjacency features-based DNN, we used the 10-fold cross-validation (CV) strategy. The five models were based on matrix-like feature vectors and the 10-fold CV method could be directly used to measure their performance. However, for the GCN model, if we directly divide all links (both positive samples and negative samples) into 10 subsets and repeatedly use different 9 subsets for training and the hold-out subset for testing, the structure of the original networks will be destroyed since the input feature vectors in GCN are not matrix-based. Therefore, we performed the 10-fold CV method in a different way. In the training process, the test subset was kept in the network but masked to avoid changes of the model parameters [30]. Based on this, we conducted the 10-fold CV method by taking each of the 10 positive subsets for testing and the left 9 subsets for training with the negative sampling method in each run.
We utilized four performance metrics, area under the curve (AUC) of a receiver operating characteristic (ROC) curve, area under the curve of a precision-recall curve (AUPRC), accuracy, and kappa coefficient. Performance of the models was evaluated individually in each cell line.
2.7. Software and global parameters
For the deep learning-based methods (GCN and DNN), our software environment used the Keras version 2.2.4 (with tensorflow 1.13.1 backend) from http://github.com/fchollet/keras, which is a high-level neural network API, written in Python and capable of running fast parallel computing. For the other methods (SVM, RF and EN), we implemented scikit-learn version 0.21.2 (a powerful open source machined learning package in python) to achieve the performance.
We set mini batch size as 256 to ensure fast training and high accuracy. 20% dropout rate and 200 epochs of Adam optimizer [31] were used to avoid overfitting. The learning rate was set to 0.0001. Other training parameters, including degree of momentum, strength of parameter regularization and initial weights, were updated and optimized at the same time to reach optimal performance.
3. Results
3.1. Cell line-specific drug synergy prediction
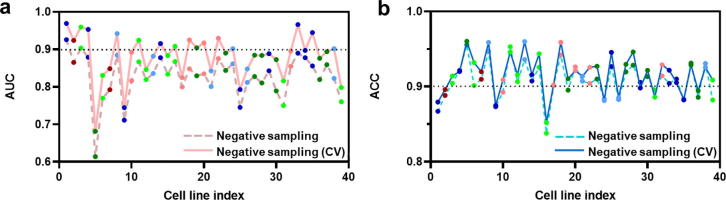
The trained model was used to predict the synergy scores of all drug combinations included in the network. The predicted values range from 0 to 1 and can be treated as probabilities of the synergistic effect of the drug combinations. Higher predicted values mean that the probability of the corresponding drug pairs to show synergistic effect is higher. In order to assess the performance of our model, we calculated the sensitivity and specificity for each cell line at different probability thresholds. The ROC curves were plotted and the AUC was obtained for each cell line (Fig. 4a). The average AUC of all cell lines is 0.84 using the negative sampling method and 0.88 using the 10-fold CV method which was incorporated with negative sampling. The accuracy for all cell line-specific GCNs ranges from 0.83 to 0.96 using the negative sampling with the mean of 0.84 (Fig. 4b). The accuracy for all cell line-specific GCNs ranges from 0.85 to 0.96 using the 10-fold CV method with the mean of 0.92 (Fig. 4b). In general, the performance in terms of AUC and accuracy for most cell line-specific GCN models is consistent and the majority of these models have the accuracy and AUC greater than 0.80.
Fig. 4.
The performance of DDS prediction for all cell lines. The x-axis is the cell line index. The y-axis is numeric ranging from 0 to 1. (a) The line chart shows the AUC of the negative sampling method (the dash line) and the 10-fold CV method (the solid line) across cell lines. (b) The line chart shows the accuracy (ACC) of the negative sampling method (the dash line) and the 10-fold CV method (the solid line) across cell lines.
3.2. Investigation of prediction performance among tissues and drugs
To further understand the varied performance, we evaluated the correlation of the observed synergy scores and the predicted synergy scores at tissue and drug levels, respectively. We utilized Pearson correlation coefficient, a powerful and understandable method to check the consistency between the two variables, to further investigate the variability.
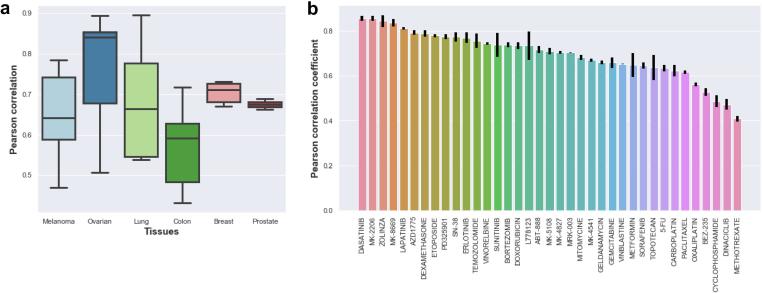
By integrating the predicted synergy scores with the measured synergy scores in the 39 cell lines from six tissues, we calculated the Pearson correlation (Fig. 5a). The median of the coefficients is 0.64 for melanoma, 0.83 for ovarian, 0.67 for lung, 0.59 for colon, 0.71 for breast, and 0.68 for prostate. Among all the tissues, cell lines from ovarian show the highest median whereas those from prostate show the most concentrated distribution. The relatively high correlation suggests our model’s consistency in tissue-wise aspects.
Fig. 5.
The Pearson correlation coefficients of the GCN models. (a) The boxplot shows the Pearson correlation coefficients between true and predicted synergy scores per tissue types. On the x-axis tissue names and the number of cell lines are displayed. (b) The bar plot shows the Pearson correlation coefficients between true and predicted synergy scores per drugs. On the x-axis the drug names are displayed. The error bar, which was calculated by repeating 10 times across all cell lines, was shown for each drug.
We further investigated the drug-wise correlation between predicted and measured synergy scores. For each drug, the correlation coefficient was averaged across all cell lines and existing drug combinations. The coefficients of drugs ranged from 0.39 to 0.90 (Fig. 5b). For example, dasatinib used for treatment of chronic myeloid leukemia [32] has the highest correlation coefficient of 0.89. MK-2206, zolinza and MK-8669 also exhibit high correlation in the drug-specific prediction. The drug-wise analysis suggests that complicated pharmacological actions contribute to the variability of drug-drug synergy prediction.
3.3. Data visualization and regression analysis
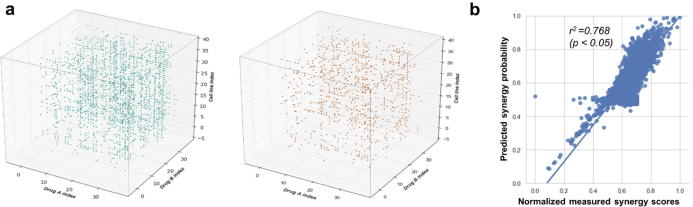
To better understand the consistency of the drug combinations in different cell lines at the same time, we constructed the 3-D matrix to illustrate the synergy distribution. Both experimental (blue dots) and predicted (orange dots) data were shown together in Fig. 6a. Generally speaking, data from the two measurements indicate the similar patterns. Since the predicted scores covered both training and testing data, the 3-D synergy score distribution significantly supports that our model was well-trained and reached relatively high accuracy in the testing data.
Fig. 6.
The diagram of visualization and regression. (a) The 3-D matrix representation for experimentally measured drug synergy scores and predicted drug synergy scores. Each dot represents an experimental (blue, cutoff = 60, more than 60) or a predicted (orange, cutoff = 0.75) measurement of the synergy effect of drugs A and B in a specific cell line. The x axis is first drug index. The y axis is the second drug index. The z axis is the cell line index. (b) The regression of the predicted and measured synergy scores for all cell lines. Dots here are also flattened dots from the two 3-D matrices. The x-axis is the normalized measured synergy scores and y-axis is the predicted synergy probability (from 0 to 1). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Furthermore, in order to eliminate the potential bias in regression and illustrate the synergy score distribution more properly, we scaled the experimentally observed Loewe synergy scores to a fixed range of 0 to 1 using the min–max scaling method. We regressed the predicted synergy scores on the normalized measured synergy scores, which is shown in Fig. 6b with an R-squared value of 0.768 (p-value <0.05). This demonstrates that the predicted synergy score is highly consistent with the measured ones.
3.4. Model comparison
We compared our GCN mode with the other five methods. The performance of GCN is based on 10-fold CV with negative sampling. The mean and standard deviation (std) of all cell lines for each method are listed in Table 2. Our proposed GCN approach achieved the best performance in terms of AUC, AUPRC, Accuracy and Kappa coefficient. GCN demonstrated an improvement of 10% in AUC compared to the second-best method, the DNN with physiochemical features. Among the other five methods, the DNN approach using either the adjacency features or the physiochemical features showed a decent result. The DNN model with the physiochemical features was slightly better than that with the adjacency features in terms of AUC. The former is inferior to the latter in terms of AUPRC, accuracy and Kappa. We also found that the performance of deep learning-based methods (GCN and DNN) is better than that of other relatively traditional machine learning-based methods (SVM, EN and RF).
Table 2.
Compare the Performance of GCN with other different traditional methods.
| Performance metrics | AUC |
AUPRC |
Accuracy |
Kappa |
Evaluation method | ||||
|---|---|---|---|---|---|---|---|---|---|
| mean | std | mean | std | mean | std | mean | std | ||
| GCN | 0.892 | 0.008 | 0.794 | 0.015 | 0.919 | 0.018 | 0.584 | 0.031 | 10-fold CV (Negative sampling) |
| DNN (adjacency) | 0.752 | 0.052 | 0.691 | 0.029 | 0.882 | 0.029 | 0.541 | 0.021 | 10-fold CV |
| DNN (physiochemical) | 0.811 | 0.021 | 0.666 | 0.041 | 0.833 | 0.045 | 0.486 | 0.044 | 10-fold CV |
| SVM | 0.762 | 0.072 | 0.682 | 0.13 | 0.872 | 0.059 | 0.514 | 0.14 | 10-fold CV |
| EN | 0.741 | 0.059 | 0.522 | 0.09 | 0.881 | 0.051 | 0.531 | 0.062 | 10-fold CV |
| RF | 0.779 | 0.054 | 0.534 | 0.043 | 0.873 | 0.043 | 0.522 | 0.056 | 10-fold CV |
We also compared the performance of GCN against the DeepSynergy method proposed by Preuer et al. [7], which also used O’Neil et al.’s dataset. We re-ran the DeepSynergy model using the same evaluation strategy as the GCN model and showed the results in Table 3. GCN shows better performance than DeepSynergy in terms of AUPRC and Kappa. However, DeepSynergy shows higher accuracy than GCN. The two models do not differ too much in terms of AUC.
Table 3.
Compare the Performance of GCN with the state-of-the-art method DeepSynergy.
| Performance metrics | AUC |
AUPRC |
Accuracy |
Kappa |
Evaluation method | ||||
|---|---|---|---|---|---|---|---|---|---|
| mean | std | mean | std | mean | std | mean | std | ||
| GCN | 0.892 | 0.008 | 0.794 | 0.015 | 0.919 | 0.018 | 0.584 | 0.031 | 10-fold CV (Negative sampling) |
| DeepSynergy | 0.893 | 0.034 | 0.568 | 0.089 | 0.929 | 0.014 | 0.568 | 0.106 | 10-CV |
3.5. De novo prediction of drug synergy for particular cell lines
The drug pairs with the highest predicted probability for synergy were selected for each cell line. Of these 39 drug pairs, the BEZ-235/MK-2206 combination and the oxaliplatin/sunitinib combination ranked highest for the colon cancer cell line COLO320DM and the lung cancer cell line NCIH520, respectively. However, both of the two pairs show a low predicted probability of 0.1, and were thus removed. The remaining cell line-specific top predictions are listed in Table 4. To further examine the reliability of these top predicted drug combinations, we performed an in-depth literature survey and found that many of these pairs have been reported to show synergistic effects in cancer treatment. For instance, bortezomib and dasatinib have been used as lung cancer therapy recently (i.e. small cell lung cancer and non-small cell lung cancer) according to the studies [33], [34]. Although some literatures reported that there was lung toxicity when using these two drugs [6], [35], our model predicted them to have synergistic effect in lung cancer cell lines. Evidence from both cell line-level experiments [36] and clinic trials [37] indicate bortezomib has synergistic effect with dasatinib by inhibiting cell viability and promoting apoptosis within dasatinib-treated cells. This evidence is an example that our de novo predictions of drug-drug synergy are strongly supported by previous experiments.
Table 4.
Top predicted synergistic drug combinations for each of the 39 cancer cell lines.
| Cell line | Cancer | Drug A | Drug B | Probability for synergy |
|---|---|---|---|---|
| OCUBM | Breast | ABT-888 | MK-8669 | 0.98 |
| ZR751 | Breast | AZD1775 | BEZ-235 | 0.92 |
| MDAMB436 | Breast | BEZ-235 | Temozolomide | 0.86 |
| T47D | Breast | Sunitinib | BEZ-235 | 0.86 |
| KPL1 | Breast | MK-8669 | MK-2206 | 0.82 |
| EFM192B | Breast | Dasatinib | MK-8669 | 0.78 |
| HT29 | Colon | MK-4827 | Temozolomide | 0.95 |
| RKO | Colon | MK-2206 | MK-8669 | 0.88 |
| SW620 | Colon | Dasatinib | Sunitinib | 0.87 |
| SW837 | Colon | Lapatinib | MK-2206 | 0.87 |
| HCT116 | Colon | BEZ-235 | MK-8776 | 0.82 |
| LOVO | Colon | Lapatinib | Dasatinib | 0.82 |
| DLD1 | Colon | Sunitinib | Temozolomide | 0.73 |
| SKMES1 | Lung | MK-4827 | SN-38 | 0.93 |
| NCIH460 | Lung | BEZ-235 | MK-4827 | 0.90 |
| MSTO | Lung | Bortezomib | Dasatinib | 0.87 |
| NCIH23 | Lung | Temozolomide | MK-4827 | 0.84 |
| A427 | Lung | MK-8669 | Temozolomide | 0.82 |
| NCIH1650 | Lung | Dasatinib | MK-8669 | 0.81 |
| NCIH2122 | Lung | MK-4827 | Temozolomide | 0.68 |
| NCIH520 | Lung | Oxaliplatin | Sunitinib | 0.10 |
| SKMEL30 | Melanoma | MK-8776 | MK-8669 | 0.98 |
| A375 | Melanoma | BEZ-235 | Temozolomide | 0.96 |
| UACC62 | Melanoma | MK-8669 | MK-4827 | 0.96 |
| A2058 | Melanoma | MK-8776 | Temozolomide | 0.89 |
| RPMI7951 | Melanoma | AZD1775 | MK-8669 | 0.84 |
| HT144 | Melanoma | BEZ-235 | MK-8669 | 0.62 |
| OV90 | Ovarian | Vinorelbine | MK-8776 | 0.97 |
| PA1 | Ovarian | BEZ-235 | MK-4827 | 0.94 |
| SKOV3 | Ovarian | MK-8669 | MK-4827 | 0.93 |
| UWB1289BRCA1 | Ovarian | BEZ-235 | Temozolomide | 0.91 |
| A2780 | Ovarian | MK-8669 | MK-2206 | 0.85 |
| CAOV3 | Ovarian | Etoposide | MK-2206 | 0.83 |
| OVCAR3 | Ovarian | Dasatinib | MK-8776 | 0.82 |
| UWB1289 | Ovarian | AZD1775 | BEZ-235 | 0.80 |
| ES2 | Ovarian | Sunitinib | BEZ-235 | 0.75 |
| VCAP | Prostate | BEZ-235 | MK-4541 | 0.93 |
| LNCAP | Prostate | BEZ-235 | Geldanamycin | 0.77 |
Colon cancer cell line COLO320DM and the lung cancer cell line NCIH520 were not included in the table due to the low predicted probability synergy score of the top drug combinations in the two cell lines.
3.6. Evaluation of drug synergy data and negative sampling
In order to have a clearer speculation about the contribution factors that might explain the synergy predictions from additional sub-network types (DTIs and PPIs) and to make it unambiguous about information sources contributing to the DDS prediction. We have implemented prediction by only taking the DDS data. This experiment was conducted by re-running our GCN model using 2325 physiochemical features for each drug node with freshly end-to-end trained encoders and decoders.
We also evaluated the effects of negative sampling. The network link prediction problems are inherently unbalanced since only a small fraction of pairs interact [30], [38]. Properly leveraging unlabeled data in training can improve prediction performance significantly [38]. Because of the small number of positive samples in the dataset, we needed to find negative samples for semi-supervised training to find a prediction model. Performance is heavily dependent on how the negative set is selected. So, we evaluated the influence of the size of the negative samples to that of the positive samples. We defined p, the percentage of selected negative sample number to the number of benchmark positive samples (the sum of training and testing positive samples) and r, the ratio of the size of the negative dataset to that of the positive dataset in both training process and prediction performance process. For instance, p = 20%, r = 2:1, 10-fold cross validation means that in each run, 90% of the benchmark positive samples with two times negative samples are used for training while 10% left positive samples with two times negative samples. The results are shown in Table 5, different p and r could shape the different unbalances regarding negative and positive samples. Among different settings of negative sampling, p = 10%, r = 1:1 is suggested to be a good parameter combo. This parameter combo was also the one we used for the heterogenous network-based training in Section 2.6.
Table 5.
Performance comparison of AUC in 10-fold CV using different settings of negative sampling (GCN with only DDI data).
| Values of p* | 5% | 10% | 15% | 20% | 25% | 50% |
| Values of r* | 0.5:1 | 1:1 | 1.5:1 | 2:1 | 2.5:1 | 5:1 |
| Average AUC | 0.809 ± 0.05 | 0.857 ± 0.04 | 0.853 ± 0.04 | 0.837 ± 0.04 | 0.803 ± 0.04 | 0.753 ± 0.04 |
p, the percentage of selected negative sample number to the number of benchmark positive samples.
r, the ratio of the size of the negative dataset to that of the positive dataset in both training process and prediction performance process.
3.7. Exploration of embedding space of drug synergy prediction
In particular, we are curious about whether the clustering structure is existed in the embedding space. If the GCN model can capture the interdependence of synergistic effects, the embedding vectors of synergy pairs should enjoy a short “distance” since the similarity we used is the “distance” after the linear transformation of Rc. The data dimension reduction method t-SNE [41] maintained the distance between one node and its neighbors precisely. Moreover our training process also follows the rational to make prominent synergistic pairs in one cluster.
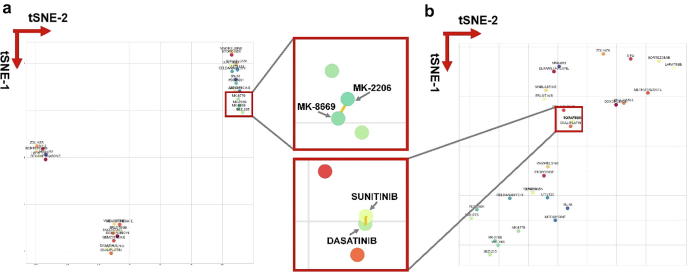
We plotted the result of t-SNE in a particular embedding space of cell line COLO320DM in Fig. 7. It shows the drugs with higher probability of the synergistic effect, such as MK-8669/MK-2206 and sunitinib/dasatinib, were clustered together in the 2-D space. MK-8669 and MK-2206 share a short distance in the cluster and their synergistic effect has been reported by a previous study [39]. Zitnik et al. [15] revealed the existence of clustering structure in side effects’ representations. They observed that side effects embedded close together in the 2D space tend to co-occur in drug combinations. Our work proved that clustering structure also existed in drug synergy representations.
Fig. 7.
Visualization of synergistic effects by t-SNE to explore the embedding space. The left panel (a) is the t-SNE result of the cell line KPL1-specific embedding space and the right panel (b) is the t-SNE result of the cell line SW620-specific embedding space. Two red frames in the middle are the magnifications in particular areas in (a) and (b). The x-axis is the first dimension of t-SNE and the y-axis is the second dimension of t-SNE. Each dot is a representation of a specific drug. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
4. Discussion
Given the enormous number of drug combinations, experimentally screening all possible pairs is unfeasible in terms of cost and time. Thus, computational methods have been extensively used to predict potential synergistic drug combinations. In this study, we have developed a GCN-based model, which can predict synergy scores of drug combinations in particular cancer cell lines. Although it has been widely used in social network and knowledge graph prediction problems, GCNs have not until recently been introduced to the field of computational biology to predict sides effects caused by drug-drug interactions [15]. GCNs have not yet been used for prediction problems in drug synergy. Our GCN-based model for predicting synergistic drug combination was trained for each cell line and demonstrated a high accuracy, with a mean AUC of 0.84 (the minimum is 0.61, the maximum is 0.93) and a mean ACC of 0.91 (the minimum is 0.83, the maximum is 0.96), respectively. When treating the prediction task as a regression instead of a classification problem, the mean Pearson correlation coefficient between the measured and the predicted synergy scores of our GCN method for drug pairs in all cell lines was 0.70.
It is noteworthy that the GCN models from some cell lines performed better than others in terms of AUC. As an example, models for the CAOV3 (ovarian cancer) and A427 (lung cancer) cell lines are the two best-performing ones among the 39 cell line-specific GCN models, with an AUC larger than 0.90. The variability could be partly explained by the difference in the number of all conceivable drug combinations from each cell line. For example, some cell lines comprise ~700 tested drug combinations whereas others include approximate 500 screened drug combinations, leading to the varying training set size among cell lines. In addition, each cell line constitutes a different problem instance in this study. Even if training set size, features and classifiers are the same, the modeled relationship between drug synergy and features depends on training set composition and cell line properties due to the fact that the performance of supervised learning algorithms varies depending on the problem instance [40].
Among the top predicted drug pairs for the 39 cell lines (Table 4), many of them have been reported to be synergistic in the literature. For example, MK-8669 is a mTOR inhibitor [41] while MK-2206 is an Akt inhibitor [42]. For the estrogen receptor (ER)-positive breast cancer cell line KPL1 [43], the combination of these two agents shows the highest predicted synergy score, which is in accordance with a phase I clinical trial [39]. In this clinical study [39], a combination of MK-8669 and MK-2206, with the aim to completely block the PI3K/Akt/mTOR signaling pathway required for tumor growth, showed promising activity and good tolerability in ER-positive breast cancer patients with the PI3K/Akt/mTOR pathway addiction. The combination of MK-8669 and MK-2206 also shows the highest synergistic score predicted by both the RKO- and A2780-specific GCN models. RKO is a colon cancer cell line while A2780 is an ovarian cancer cell line. Since the PI3K/Akt/mTOR signaling pathway is aberrantly activated to sustain the growth and survival of tumor cells in many cancer types, including human breast, colon, and ovarian cancers [44], MK-8669 in combination with MK-2206 may act synergistically to block the PI3K/Akt/mTOR pathway in colon and ovarian cancer cells. For another triple negative breast cancer (TNBC) cell line MDAMB436 [45], BEZ-235 and temozolomide were predicted as the top synergistic pair. BEZ-235 is a novel dual PI3K and mTOR inhibitor and has been widely used in preclinical studies for various cancers including glioblastoma multiforme (GBM), breast, colorectal and lung cancers [46]. Temozolomide is a DNA alkylating agent and has been reported to induce cell apoptosis by the inhibition of mTOR signaling in GBM cells [47]. Compared with temozolomide or BEZ-235 monotherapy, a combination of the two drugs has been found to more effectively inhibit GBM cell proliferation, invasion, migration and induce apoptosis in vitro by repressing the PI3K/Akt/mTOR pathway singling activity [48]. The PI3K/Akt/mTOR signaling pathway is one of the most frequently altered pathways in TNBC [49]. Thus, the combination of temozolomide and BEZ-235 may be an effective treatment for TNBC, for which very limited targeted therapies exist currently. The combination of BEZ-235 and temozolomide was also predicted as the top synergistic pair for another two cell lines, the melanoma cell line A375 and the ovarian cancer cell line UWB1289BRCA1, for which constitutive PI3K/Akt/mTOR pathway activation has been observed [44]. Thus, our data suggests that BEZ-235 combined with temozolomide may have the potential to treat melanoma and ovarian cancer patients. Another combination of bortezomib and dasatinib has been predicted as synergistic pair in the lung cancer cell line MSTO by our GCN model and has experimentally shown synergistic antitumor activity in myeloma cell lines [50] and gastrointestinal stromal tumor cell lines [36]. Bortezomib is a small-molecule proteasome inhibitor and has activity in lung cancer both as a single drug and in combination with drugs commonly used in lung cancer [51]. Dasatinib is an inhibitor of Src family kinases and has modest clinical activity in lung cancer patients as a single drug in a phase II study [52]. Therefore, the combination of dasatinib and bortezomib may improve the treatment of lung cancer. The GCN model has also predicted some novel synergistic drug combinations, such as BEZ-235/geldanamycin in LNCAP (prostate cancer) and BEZ-235/MK-4541 in VCAP (prostate cancer). Geldanamycin is the first natural HSP90 inhibitor and has demonstrated antiproliferative and cytotoxic effects in both human prostate cancer cell lines [53] and prostate xenograft tumors [54]. The PI3K/mTOR dual inhibitor BEZ-235 combined with an HSP90 inhibitor (NVP-AUY922) has been reported to act synergistically to inhibit tumor cell proliferation and induce apoptosis in cholangiocarcinoma cell lines [55]. HSP90 is often overexpressed in prostate cancer cells, making it a potential therapeutic target for prostate cancer [56]. The PI3K/Akt/mTOR pathway also plays an important role in prostate cancer cell survival, apoptosis, metabolism, motility, and angiogenesis [44]. These findings suggest that the combination of BEZ-235/geldanamycin may exhibit synergistic antitumor activity against prostate cancer, for which further experimental validation is needed. MK-4541 is a novel selective androgen receptor modulator and found to exert anti-androgenic activity in the prostate cancer xenograft mouse model [57]. Androgens are critical for the development, growth, and maintenance of male sex organs and can drive prostate cancer initiation [57]. Therefore, the dual PI3K/mTOR inhibitor BEZ-235 might synergize with the androgen receptor inhibitor MK-4541 to treat prostate cancer.
Although the GCN model achieved the state-of-the-art performance, there are some limitations in the study. The drug-protein interaction data is highly limited and biased with only a small subset of targets known for each drug. This may mask some hidden associations in cell line-specific networks. Besides, there are also some study biases, incompleteness and noises in the other two used sub-networks. Binarization of DDS data is needed but more different thresholds or study should be checked for selection. This limitation could be overcome by filtering out noises, incorporating more well-validated to construct the complete network, and well-tuning model to downgrade biases.
Another limitation is the size of our benchmark dataset. Although a large publicly available synergy dataset has been used in this study [4], there is a limited number of different cell lines, drugs, and drug combinations. In this cell line-specific GCN method, some drugs have been tested in combination with only a few other drugs.
Finally, the complexity of drug combination determined that the drug side effects, drug synergistic effects, drug antagonism and drug sensitivities are interdependent. Current computational tools assess only the synergy but not the sensitivity of drug combinations, which might lead to false positive discoveries because a strong synergy does not necessarily render the drug combination effective [12]. In the future, prediction of drug synergy should incorporate at least sensitivity. Computational methods could shape and model drug combination better by considering multi-relations between drugs simultaneously.
5. Conclusions
In this study, we utilized the graph convolutional network method to develop GCN models, which can predict synergistic drug combinations for 39 cell lines derived from six major cancer types, including breast, colon, lung, melanoma, ovarian, and prostate cancers. For the 39 cell line-specific GCN models we built, the mean AUC is 0.84 while the mean Pearson correlation coefficient between the measured and the predicted synergy scores is 0.70. Remarkably, we found that many synergistic combinations among our top predictions for a particular cancer type have been reported in the treatment of the same or other cancer types in the literature. Overall, given the prediction performance, the GCN models could be a valuable in silico tool for predicting novel synergistic drug combinations and thus guide in vitro and in vivo discovery of rational combination therapies.
Conflicts of interest
The authors declare no conflict of interest.
Funding
This research was supported in part by Canadian Breast Cancer Foundation, Natural Sciences and Engineering Research Council of Canada, Mitacs and University of Manitoba.
CRediT authorship contribution statement
Peiran Jiang: Conceptualization, Formal analysis, Methodology, Software, Validation, Visualization, Writing - original draft. Shujun Huang: Conceptualization, Data curation, Resources, Investigation, Writing - original draft. Zhenyuan Fu: Formal analysis, Resources. Zexuan Sun: Formal analysis, Resources, Software. Ted M. Lakowski: Supervision, Funding acquisition, Writing - review & editing. Pingzhao Hu: Conceptualization, Supervision, Methodology, Investigation, Project administration, Resources, Funding acquisition, Writing - review & editing.
Acknowledgements
We thank the Supercomputing Center of Wuhan University for supporting the numerical calculations.
Contributor Information
Peiran Jiang, Email: peiran@hust.edu.cn.
Shujun Huang, Email: huangs12@myumanitoba.ca.
Zhenyuan Fu, Email: u201612472@hust.edu.cn.
Zexuan Sun, Email: zexuansun@outlook.com.
Ted M. Lakowski, Email: ted.lakowski@umanitoba.ca.
Pingzhao Hu, Email: pingzhao.hu@umanitoba.ca.
References
- 1.Csermely P., Korcsmáros T., Kiss H.J.M., London G., Nussinov R. Structure and dynamics of molecular networks: a novel paradigm of drug discovery: a comprehensive review. Pharmacol Ther. 2013;138:333–408. doi: 10.1016/j.pharmthera.2013.01.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Jia J., Zhu F., Ma X., Cao Z.W., Li Y.X., Chen Y.Z. Mechanisms of drug combinations: interaction and network perspectives. Nat Rev Drug Discov. 2009;8:111. doi: 10.1038/nrd2683. [DOI] [PubMed] [Google Scholar]
- 3.Hanahan D., Weinberg R.A. Hallmarks of cancer: the next generation. Cell. 2011;144:646–674. doi: 10.1016/j.cell.2011.02.013. [DOI] [PubMed] [Google Scholar]
- 4.O’Neil J., Benita Y., Feldman I., Chenard M., Roberts B., Liu Y. An unbiased oncology compound screen to identify novel combination strategies. Mol Cancer Ther. 2016;15:1155–1162. doi: 10.1158/1535-7163.MCT-15-0843. [DOI] [PubMed] [Google Scholar]
- 5.Huang Y., Jiang D., Sui M., Wang X., Fan W. Fulvestrant reverses doxorubicin resistance in multidrug-resistant breast cell lines independent of estrogen receptor expression. Oncol Rep. 2017;37:705–712. doi: 10.3892/or.2016.5315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Guignabert C., Phan C., Seferian A., Huertas A., Tu L., Thuillet R. Dasatinib induces lung vascular toxicity and predisposes to pulmonary hypertension. J Clin Invest. 2016;126:3207–3218. doi: 10.1172/JCI86249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Preuer K., Lewis R.P.I., Hochreiter S., Bender A., Bulusu K.C., Klambauer G. DeepSynergy: predicting anti-cancer drug synergy with deep learning. Bioinformatics. 2018;34:1538–1546. doi: 10.1093/bioinformatics/btx806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Pang K., Wan Y.-W., Choi W.T., Donehower L.A., Sun J., Pant D. Combinatorial therapy discovery using mixed integer linear programming. Bioinformatics. 2014;30:1456–1463. doi: 10.1093/bioinformatics/btu046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Day D., Siu L.L. Approaches to modernize the combination drug development paradigm. Genome Med. 2016;8:115. doi: 10.1186/s13073-016-0369-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Menden M.P., Wang D., Guan Y., Mason M.M.J., Szalai B., Bulusu K.C. A cancer pharmacogenomic screen powering crowd-sourced advancement of drug combination prediction. BioRxiv. 2018;200451 [Google Scholar]
- 11.He L., Kulesskiy E., Saarela J., Turunen L., Wennerberg K., Aittokallio T. Methods for high-throughput drug combination screening and synergy scoring. Cancer Syst. Biol., Springer. 2018:351–398. doi: 10.1007/978-1-4939-7493-1_17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Zagidullin B., Aldahdooh J., Zheng S., Wang W., Wang Y., Saad J. DrugComb: an integrative cancer drug combination data portal. Nucleic Acids Res. 2019;47:W43–W51. doi: 10.1093/nar/gkz337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Sidorov P., Naulaerts S., Ariey-Bonnet J.J., Pasquier E., Ballester P.J. Predicting synergism of cancer drug combinations using NCI-ALMANAC data. Front Chem. 2019;7 doi: 10.3389/fchem.2019.00509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Zhang T., Zhang L., Payne P.R.O., Li F. Synergistic drug combination prediction by integrating multi-omics data in deep learning models. ArXiv Prepr ArXiv181107054. 2018 doi: 10.1007/978-1-0716-0849-4_12. [DOI] [PubMed] [Google Scholar]
- 15.Zitnik M., Agrawal M., Leskovec J. Modeling polypharmacy side effects with graph convolutional networks. Bioinformatics. 2018;34:i457–i466. doi: 10.1093/bioinformatics/bty294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Loewe S. The problem of synergism and antagonism of combined drugs. Arzneimittelforschung. 1953;3:285–290. [PubMed] [Google Scholar]
- 17.Szklarczyk D., Santos A., von Mering C., Jensen L.J., Bork P., Kuhn M. STITCH 5: augmenting protein–chemical interaction networks with tissue and affinity data. Nucleic Acids Res. 2015;44:D380–D384. doi: 10.1093/nar/gkv1277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Szklarczyk D., Morris J.H., Cook H., Kuhn M., Wyder S., Simonovic M. The STRING database in 2017: quality-controlled protein–protein association networks, made broadly accessible. Nucleic Acids Res. 2016 doi: 10.1093/nar/gkw937. gkw937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Chatr-Aryamontri A., Breitkreutz B.-J., Oughtred R., Boucher L., Heinicke S., Chen D. The BioGRID interaction database: 2015 update. Nucleic Acids Res. 2014;43:D470–D478. doi: 10.1093/nar/gku1204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Coley C.W., Jin W., Rogers L., Jamison T.F., Jaakkola T.S., Green W.H. A graph-convolutional neural network model for the prediction of chemical reactivity. Chem Sci. 2019;10:370–377. doi: 10.1039/c8sc04228d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Sun M., Zhao S., Gilvary C., Elemento O., Zhou J., Wang F. Graph convolutional networks for computational drug development and discovery. Brief Bioinform. 2019 doi: 10.1093/bib/bbz042. [DOI] [PubMed] [Google Scholar]
- 22.Kipf T.N., Welling M. Semi-supervised classification with graph convolutional networks. ArXiv Prepr ArXiv160902907. 2016 [Google Scholar]
- 23.Defferrard M., Bresson X., Vandergheynst P. Convolutional neural networks on graphs with fast localized spectral filtering. Adv Neural Inf Process Syst. 2016:3844–3852. [Google Scholar]
- 24.Cortes C., Vapnik V. Support-vector networks. Mach Learn. 1995;20:273–297. [Google Scholar]
- 25.Breiman L. Random forests. Mach Learn. 2001;45:5–32. [Google Scholar]
- 26.Zou H., Hastie T. Regularization and variable selection via the elastic net. J R Stat Soc Ser B (Statistical Methodol) 2005;67:301–320. [Google Scholar]
- 27.Schmidhuber J. Deep learning in neural networks: an overview. Neural Networks. 2015;61:85–117. doi: 10.1016/j.neunet.2014.09.003. [DOI] [PubMed] [Google Scholar]
- 28.Yap C.W. PaDEL-descriptor: an open source software to calculate molecular descriptors and fingerprints. J Comput Chem. 2011;32:1466–1474. doi: 10.1002/jcc.21707. [DOI] [PubMed] [Google Scholar]
- 29.Trouillon T., Welbl J., Riedel S., Gaussier É., Bouchard G. Complex embeddings for simple link prediction. Int Conf Mach Learn. 2016:2071–2080. [Google Scholar]
- 30.Huang J., Shen H., Hou L., Cheng X. Signed graph attention networks. Int Conf Artif Neural Networks, Springer. 2019:566–577. [Google Scholar]
- 31.Kingma D.P., Adam Ba.J. A method for stochastic optimization. ArXiv Prepr ArXiv14126980. 2014 [Google Scholar]
- 32.Haslam S. Dasatinib: the emerging evidence of its potential in the treatment of chronic myeloid leukemia. Core Evid. 2005;1:1. [PMC free article] [PubMed] [Google Scholar]
- 33.Taromi S., Lewens F., Arsenic R., Sedding D., Sänger J., Kunze A. Proteasome inhibitor bortezomib enhances the effect of standard chemotherapy in small cell lung cancer. Oncotarget. 2017;8:97061. doi: 10.18632/oncotarget.21221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Kelley M.J., Jha G., Shoemaker D., Herndon J.E., Gu L., Barry W.T. Phase II study of dasatinib in previously treated patients with advanced non-small cell lung cancer. Cancer Invest. 2017;35:32–35. doi: 10.1080/07357907.2016.1253710. [DOI] [PubMed] [Google Scholar]
- 35.Martínez M.S., Cid N.B., Quintas R.D. Bortezomib-induced lung toxicity. Arch Bronconeumol (English Ed) 2014;12:564–565. doi: 10.1016/j.arbres.2013.11.027. [DOI] [PubMed] [Google Scholar]
- 36.Dong Y., Liang C., Zhang B., Ma J., He X., Chen S. Bortezomib enhances the therapeutic efficacy of dasatinib by promoting c-KIT internalization-induced apoptosis in gastrointestinal stromal tumor cells. Cancer Lett. 2015;361:137–146. doi: 10.1016/j.canlet.2015.02.044. [DOI] [PubMed] [Google Scholar]
- 37.Wright J.J. Combination therapy of bortezomib with novel targeted agents: an emerging treatment strategy. Clin Cancer Res. 2010;16:4094–4104. doi: 10.1158/1078-0432.CCR-09-2882. [DOI] [PubMed] [Google Scholar]
- 38.Zhu X., Goldberg A.B. Introduction to semi-supervised learning. Synth Lect Artif Intell Mach Learn. 2009;3:1–130. [Google Scholar]
- 39.Gupta S., Argilés G., Munster P.N., Hollebecque A., Dajani O., Cheng J.D. A phase I trial of combined ridaforolimus and MK-2206 in patients with advanced malignancies. Clin Cancer Res. 2015;21:5235–5244. doi: 10.1158/1078-0432.CCR-15-0180. [DOI] [PubMed] [Google Scholar]
- 40.Fernández-Delgado M., Cernadas E., Barro S., Amorim D. Do we need hundreds of classifiers to solve real world classification problems? J Mach Learn Res. 2014;15:3133–3181. [Google Scholar]
- 41.Rivera V.M., Squillace R.M., Miller D., Berk L., Wardwell S.D., Ning Y. Ridaforolimus (AP23573; MK-8669), a potent mTOR inhibitor, has broad antitumor activity and can be optimally administered using intermittent dosing regimens. Mol Cancer Ther. 2011;10:1059–1071. doi: 10.1158/1535-7163.MCT-10-0792. [DOI] [PubMed] [Google Scholar]
- 42.Fouladi M., Perentesis J.P., Phillips C.L., Leary S., Reid J.M., McGovern R.M. A phase I trial of MK-2206 in children with refractory malignancies: a Children’s Oncology Group study. Pediatr Blood Cancer. 2014;61:1246–1251. doi: 10.1002/pbc.25023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Kinoshita Y., Yoshizawa K., Hamazaki K., Emoto Y., Yuri T., Yuki M. Mead acid inhibits the growth of KPL-1 human breast cancer cells in vitro and in vivo. Oncol Rep. 2014;32:1385–1394. doi: 10.3892/or.2014.3390. [DOI] [PubMed] [Google Scholar]
- 44.Markman B., Dienstmann R., Tabernero J. Targeting the PI3K/Akt/mTOR pathway–beyond rapalogs. Oncotarget. 2010;1:530. doi: 10.18632/oncotarget.188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Chavez K.J., Garimella S.V., Lipkowitz S. For better treatment of triple negative breast cancer. Breast Dis. 2010;32:35–48. doi: 10.3233/BD-2010-0307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Zhao H.F., Wang J., Shao W., Wu C.P., Chen Z.P., To S.T. Recent advances in the use of PI3K inhibitors for glioblastoma multiforme: current preclinical and clinical development. Mol Cancer. 2017;16:1–16. doi: 10.1186/s12943-017-0670-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Zhang W., Wang Z., Shu F., Jin Y., Liu H., Wang Q. Activation of AMP-activated protein kinase by temozolomide contributes to apoptosis in glioblastoma cells via p53 activation and mTORC1 inhibition. J Biol Chem. 2010;285:40461–40471. doi: 10.1074/jbc.M110.164046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Yu Z., Xie G., Zhou G., Cheng Y., Zhang G., Yao G. NVP-BEZ235, a novel dual PI3K-mTOR inhibitor displays anti-glioma activity and reduces chemoresistance to temozolomide in human glioma cells. Cancer Lett. 2015;367:58–68. doi: 10.1016/j.canlet.2015.07.007. [DOI] [PubMed] [Google Scholar]
- 49.Gupta I., Sareyeldin R.M., Al-Hashimi I., Al-Thawadi H.A., Al Farsi H., Vranic S. Triple negative breast cancer profile, from gene to microRNA, in relation to ethnicity. Cancers (Basel) 2019;11:363. doi: 10.3390/cancers11030363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Coluccia A.M.L., Cirulli T., Neri P., Dammacco F., Tassone P., Gambacorti C. Dasatinib inhibits multiple myeloma growth by blocking PDGF-Rb and c-Src activity in patient-derived tumor and endothelial. Cells. 2007 [Google Scholar]
- 51.Davies A.M., Lara P.N., Mack P.C., Gandara D.R. Incorporating bortezomib into the treatment of lung cancer. Clin Cancer Res. 2007;13:4647s–4651s. doi: 10.1158/1078-0432.CCR-07-0334. [DOI] [PubMed] [Google Scholar]
- 52.Johnson F.M., Bekele B.N., Feng L., Wistuba I., Tang X.M., Tran H.T. Phase II study of dasatinib in patients with advanced non–small-cell lung cancer. J Clin Oncol. 2010;28:4609. doi: 10.1200/JCO.2010.30.5474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Ma Y., Lakshmikanthan V., Lewis R.W., Kumar M.V. Sensitization of TRAIL–resistant cells by inhibition of heat shock protein 90 with low-dose geldanamycin. Mol Cancer Ther. 2006;5:170–178. doi: 10.1158/1535-7163.MCT-05-0129. [DOI] [PubMed] [Google Scholar]
- 54.Gan Y., Au J.L.-S., Lu J., Wientjes M.G. Antiproliferative and cytotoxic effects of geldanamycin, cytochalasin E, suramin and thiacetazone in human prostate xenograft tumor histocultures. Pharm Res. 1998;15:1760–1766. doi: 10.1023/a:1011921031564. [DOI] [PubMed] [Google Scholar]
- 55.Chen M.-H., Chiang K.-C., Cheng C.-T., Huang S.-C., Chen Y.-Y., Chen T.-W. Antitumor activity of the combination of an HSP90 inhibitor and a PI3K/mTOR dual inhibitor against cholangiocarcinoma. Oncotarget. 2014;5:2372. doi: 10.18632/oncotarget.1706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Peng R., Li Z., Lin Z., Wang Y., Wang W., Hu B. The HSP90 inhibitor 17-PAG effectively inhibits the proliferation and migration of androgen-independent prostate cancer cells. Am J Cancer Res. 2015;5:3198. [PMC free article] [PubMed] [Google Scholar]
- 57.Chisamore M.J., Gentile M.A., Dillon G.M., Baran M., Gambone C., Riley S. A novel selective androgen receptor modulator (SARM) MK-4541 exerts anti-androgenic activity in the prostate cancer xenograft R–3327G and anabolic activity on skeletal muscle mass & function in castrated mice. J Steroid Biochem Mol Biol. 2016;163:88–97. doi: 10.1016/j.jsbmb.2016.04.007. [DOI] [PubMed] [Google Scholar]