The fractal geometry of bronchial trees differs by strain in mice

Abstract

Fractal biological structures are pervasive throughout the plant and animal kingdoms, with the mammalian lung being a quintessential example. The lung airway and vascular trees are generated during embryogenesis from a small set of building codes similar to Turing mechanisms that create robust trees ideally suited to their functions. Whereas the blood flow pattern generated by these fractal trees has been shown to be genetically determined, the geometry of the trees has not. We explored a newly established repository providing high-resolution bronchial trees from the four most commonly studied laboratory mice (B6C3F1, BALB/c, C57BL/6 and CD-1). The data fit a fractal model well for all animals with the fractal dimensions ranging from 1.54 to 1.67, indicating that the conducting airway of mice can be considered a self-similar and space-filling structure. We determined that the fractal dimensions of these airway trees differed by strain but not sex, reinforcing the concept that airway branching patterns are encoded within the DNA. The observations also highlight that future study design and interpretations may need to consider differences in airway geometry between mouse strains.

NEW & NOTEWORTHY Similar to larger mammals such as humans, the geometries of the bronchial tree in mice are fractal structures that have repeating patterns from the trachea to the terminal branches. The airway geometries of the four most commonly studied mice are different and need to be considered when comparing results that employ different mouse strains. This variability in mouse airway geometries should be incorporated into computer models exploring toxicology and aerosol deposition in mouse models.

INTRODUCTION

The mammalian lung is constructed around three intertwined trees (bronchial, arterial, and venous systems) that are ideally suited for their unique functions and matched with each other during development. These trees are created from bifurcating processes that resemble mathematical models of Turing (36) in which two diffusible proteins interact through feedforward and feedback mechanisms to direct this branching morphogenesis (28, 29). It has been demonstrated that such structures are mechanically optimized for their functions and, therefore, have been selected for through evolutionary advantages and conserved across phyla and kingdoms (39, 40).

The resultant trees have been characterized as fractal structures because of their scale independence and the fact that they can be constructed through simple recursive rules (20, 30). Fractal dimensions, originally defined by Mandelbrot, provide a simplified estimate of the complexity and self-similarity of objects in nature that follow fractal patterns (25). We now use a newly created and publicly available data set (2, 3) of murine airway geometries to test the hypotheses that fractal dimensions of these trees are different across strains or sexes. The data are unique in that they provide high-resolution geometries of 34 mice across four commonly used laboratory strains in both sexes.

MATERIALS AND METHODS

Animals.

Data from 34 mice are available: B6C3F1 (n = 8), BALB/C (n = 11), C57Bl/6 (n = 8), and CD-1 (n = 7), as well as both sexes (males: 16; females: 18). Table 1 provides descriptive information for the different strains. The tree length is the total sum of all segment lengths. The weight, tree length, number of airway segments, and number of outlets differ statistically by strain. There is no statistical difference in lung volume or number of generations by strain.

Table 1.

Descriptive information for the different strains of mice

Measurement	B6C3F1	BALB/c	C57BL/6	CD-1
No. of animals	8	11	8	7
Sex	4 males	5 males	4 males	3 males
Weight, g	21.7 ± 1.8	23.4 ± 1.5	22.7 ± 1.7	24.4 ± 1.0
Lung volume, mm3	1,104.6 ± 39.3	1,093.2 ± 132.5	1,155.9 ± 123.7	1,195.6 ± 30.4
Tree length, mm	627.4 ± 8.1	567.9 ± 51.3	646.2 ± 46.7	554.8 ± 54.1
No. of generations	25.0 ± 1.1	26.3 ± 1.4	25.7 ± 1.2	25.0 ± 1.8
No. of segments	1,773.4 ± 219.8	1,448.5 ± 168.1	1,900.2 ± 264.2	1,379.0 ± 214.4
No. of outlets	2,075.8 ± 227.5	1,972.1 ± 248.5	2,092.1 ± 305.9	1,700.7 ± 301.8

Values are means ± SE.

Airway geometries.

The repository provides a rich data set of very high-resolution geometric airway models and measurements from the four most commonly studied mouse strains. The data for the bronchial trees were gathered with an imaging system with x-, y-, and z-resolution of 9.4 × 9.4 × 9.5 µm. This voxel size determines the side lengths of our boxes for determining the fractal dimensions of the bronchial trees (see below). A number of different reconstructions, including full 3D airway meshes and centerline-based skeletonizations, are available from the website (3). We elected to use the skeletonized representation of the bronchial tree to focus primarily on the network topology rather than the volumes occupied by the tree. Typical airway geometries from mice of the four different strains included in the repository and their skeletonized airway trees are shown in Fig. 1.

Fig. 1.

Top: reconstructed bronchial trees from 4 different mouse strains. Bottom: skeletonized trees of the same mice.

Box-counting method.

The box-counting method is a well-established approach to estimating the fractal dimension of a structure (4). Although initially applied to two-dimensional objects, three-dimensional structures can be characterized using cubes (Fig. 2). Given that the skeletonized data in our application are sparse compared with the entire imaging volume, we use a box-counting method similar to that provided by Liebovitch and Toth (21). We only need to consider those points representing the airway skeleton instead of exhaustively searching each box for the existence of any skeleton inside it. Our three-dimensional skeleton locations, written originally in millimeters, are converted into x-, y-, and z-indices by dividing each location by the image voxel size in millimeters.

Fig. 2.

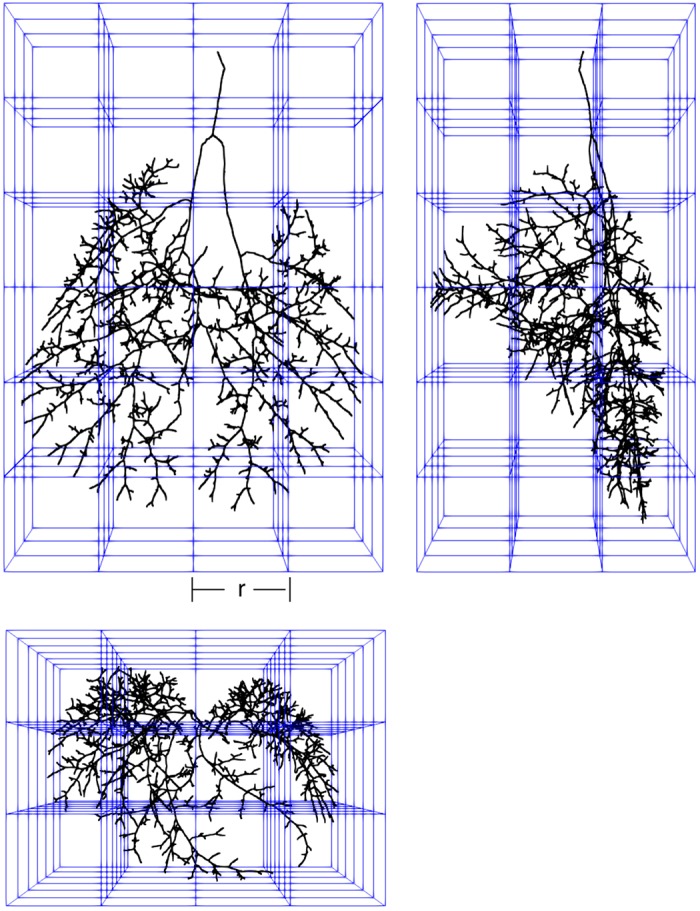
Front, side, and top projections of skeletonized airway tree within cubes (blue lines) used for box-counting method. The numbers of cubes containing a part of the tree (N_r) are determined for a range of different box sizes, r.

For each box size r, we down sample the skeleton points x by dividing each by the box side length using integer math. For each point i, we calculate a new xyz triplet ${x\prime }_i$ as

$${x\prime }_i=\frac{x_i}{r}.$$ (1)

The box count for a given r is the number of unique triplets remaining in the matrix x'.

We expanded the Liebovitch and Toth (21) method to include multiple measurements for each r to reduce the influence of the original grid. The number of repeats for a box of side r is the square root of the box volume, with a maximum of 500. The repeats are implemented as a random integer offset vector, x_offset, with all members within the range of 0 to r-1. This can be envisioned as moving the origin of the data to a random point lying inside a box of the current sampling size. With the offset, the new triplets are given by replacing x_i with x_i + x_offsett in Eq. 1.

None of the offsets may be repeated within each r group. The box count for a given r is the mean of all repeats.

Fractal dimensions can only be defined over the range of observations. Per the recommendations of Bouda et al. (6), we limit the range of our boxes from the largest structure (the entire bronchial tree, r = 2,048 voxels) to the smallest structure (terminal airway lengths, r = 32 voxels). The fractal dimension for each bronchial tree is determined from the slope of the linear regression of the number of boxes containing an airway tree element against the reciprocal of the box size (Fig. 3).

Fig. 3.

Fractal plot from 1 mouse bronchial tree showing the linear relationship between the no. of intersecting boxes and the box size on a log-log plot.

Statistical methods.

Linear regression was fit using MATLAB (Mathworks.com). One-way ANOVA in R (r-project.org) was used to test for differences in the slopes and intercepts of the linear fits across strains and sexes. Tukey’s honestly significant difference post hoc test in R was used to determine which groups were statistically different and accounted for multiple comparisons. Statistical significance was set at P < 0.05. The regression diagnostic plots provided in R were used to check the assumptions of linear regression. Pearson’s correlation was used to explore relationships between fractal dimensions and the physical characteristics of the mice presented in Table 1.

RESULTS

All of the data were well fit with linear regression (r² ranged from 0.994 to 0.995), supporting the concept that the geometries of the bronchial trees are fractal. The fractal dimensions (slopes) ranged from 1.54 to 1.67, and the intercepts ranged from 3.45 to 3.62. The slopes and intercepts were significantly different across strains but not sexes (Fig. 4). A two-way ANOVA looking for interactions between strain and sex demonstrated a statistically significant difference due to strain but not sex for both the slope (P < 0.001) and intercept (P < 0.01). The within-group and between-group sums of squares for the fractal dimensions were 0.00037 and 0.0030, respectively.

Fig. 4.

Left: slopes (fractal dimensions) from linear regression of all 34 mice grouped by strain. The fractal dimensions differ statistically among strains. Right: intercepts from linear regression of all 34 mice grouped by strain. The intercepts differ statistically by strain. *P < 0.05.

Strong correlations exist between the fractal dimension of each mouse airway tree and the number of airway segments, number of outlets and centerline length, and the fractal dimension for each animal.

DISCUSSION

This study clearly shows that the geometry of the bronchial tree in mice is a self-repeating and scale-independent structure, fitting the definition of a fractal. Furthermore, the observation that the fractal dimension of the airway tree differs across strains of mice suggests that this robust and complicated tree is genetically influenced.

Other studies have explored the fractal nature of the lung and its physiology. Horsfield and Cumming (17) were the first to recognize and quantify the repeating (self-similar) nature of the human bronchial tree. Mandelbrot (24) introduced the concepts of fractals in nature in in the late 1960s, and Ewald Weibel (38) applied these theories to the design of the lung across multitudes of scale, all the way down to the mitochondria. Others have demonstrated the spatial patterns of blood flow (14) and ventilation (1), determined by the trees to be fractal in nature. Fractal analyses have been used to characterize interstitial lung disease (18) and more recently applied to airways segmented from computerized tomography from human patients with COPD (5).

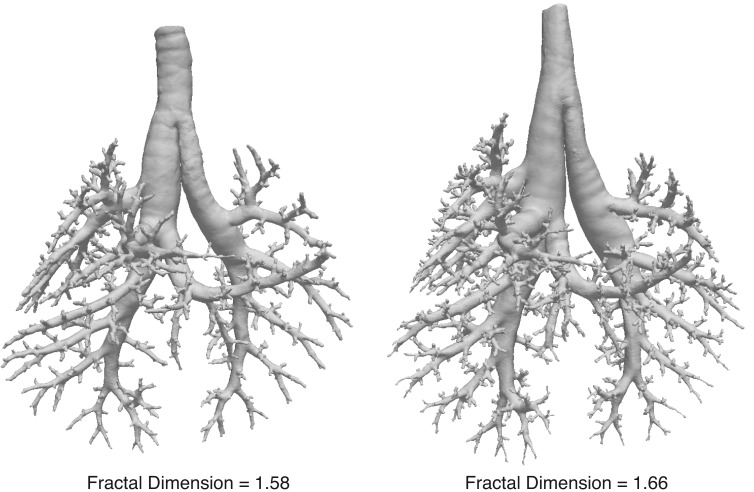
Fractal dimensions provide a measure of the complexity and space-filling nature of a structure. A geometrical structure with more complexity will appear to change more as the spatial resolution of observation is reduced. Using the box-counting method, a more complex structure will have a greater change in the number of boxes that contain an element of the structure as the box size gets smaller. Therefore, the slope of the line generated with the box-counting method is a reflection of how a structure changes shape as the scale of resolution is altered. The number of generations and hence, number of terminal airway segments in the bronchial tree also affect the fractal dimension. As expected for fractal structures, the range of fractal dimensions for these airway trees fall between their topological and the Euclidean dimensions (15). The skeletonized trees in this study have topological dimensions of 1 because they are a connection of lines of width 1 and they fill a three-dimensional Euclidean space. The fractal dimensions of 1.54 to 1.67 indicate that the trees do not fill the entire three-dimensional space, leaving ample room for gas exchanging surface area. The range of fractal dimensions is similar to other three-dimensional biological structures such as plant root systems (33), tree crowns (41), plant identification (8), and the retinal vasculature (26), to name only a few. Airway trees from two mice with fractal dimensions of 1.58 and 1.67 are depicted in Fig. 5 to allow the reader to judge differences between these fractal values.

Fig. 5.

Reconstructed bronchial trees from 2 mice with fractal dimensions of 1.58 and 1.66 to visually demonstrate the differences in structural complexity for these fractal values. Note that the tree with the smaller fractal dimension has fewer airway segments.

The intercept of the fractal plot represents the numbers of boxes that contain at least one part of the skeletonized bronchial tree at a box size of 0 µL. Therefore, the intercepts of the fractal plots would correspond to the leaves of a tree if the tree continued to branch in the same self-similar process down to a box size of 0 µL. However, the bronchial tree does not continue to ramify after the terminal bronchi, and it is not likely that the fractal process remains self-similar beyond this point. Given these qualifiers, the observation that the intercepts differ by strain suggests that the airway trees may ramify into more terminal airways in some mouse strains compared with others. We did not see a correlation between the numbers of generations in the tree or the numbers of identified outlets and the intercepts of the corresponding fractal plots.

Others have looked specifically at the bronchial tree using various imaging methods. Van de Moortele et al. (37) used in vivo computed tomography and in vitro MRI to characterize the geometry of the bronchial tree in humans and derived a fractal dimension of 1.89. The larger fractal dimension compared with this study may be explained by their use of the bronchial tree volume rather than the skeletonized airway. Stypa (32) used a box-counting method to find a fractal dimension of the surface of two human bronchial trees and estimated fractal dimensions of 2.74 and 2.84. Because a surface has topological dimension of 2, fractal dimensions of these surfaces should be >2 and <3. Canals et al. (9) used two-dimensional projections of rat bronchograms and found a fractal dimension of 1.587. They did not find any differences in the fractal dimensions across sex or age all within a single rat species (Rattus norvegicus).

West et al. (39, 40) noted that fractal vascular and air distribution systems are used by a broad range of species, from plants to insects to animals. For such structures to be conserved across such a wide array of organisms, there must be a strong evolutionary advantage. They proposed that fractal trees have three important characteristics that confer significant advantages. First, fractal trees fill three-dimensional space (such as a chest cavity), with the largest possible surface area for gas or nutrition exchange. This is central to the lung’s primary role in gas exchange. Second, a fractal tree requires the least amount of material (least cost to the organism) to fill the three-dimensional space. This also means that the volume of the tree takes up the least amount of volume within the lung, leaving more space for gas exchange. And third, a fractal structure requires the least amount of energy to transport fluids or air.

However, for the geometries of the airway tree to confer evolutionary advantages, they must be heritable traits that can be passed on to subsequent generations. The observation that branching morphogenesis is controlled by a limited number of proteins (28) does not necessarily mean that the final shape of the airway tree is determined genetically. The current study is not able to prove that the bronchial tree is genetically determined; however the finding of similarities among genetically identical animals and difference between genetically different animals is supportive of this hypothesis. Other supporting evidence is provided from the pulmonary vascular tree that determines the distribution of blood flow, where two-thirds of the regional variability in organ blood flow is genetically controlled (13).

Determining fractal dimensions of biological structures is subject to errors arising from the shortcomings of linear regression and arbitrary grid placement when using the box-counting method (6, 16). There are four assumptions of linear regression that should be assessed for greater confidence in the results (11). First, the relationship between the independent and dependent data should be linear. Second, all errors from the linear relationship should be normally distributed to about zero. Third, the variance in the errors should be similar across the range of independent values. And finally, the errors should be independent of each other. Using the R regression diagnostic plots, we confirmed that our data adhere to these assumptions. We mitigated the influence of grid placement by obtaining multiple box count measures at the same box sizes while randomly offsetting the starting grid position in space and then reporting the average box count at that size. Any of the above potential pitfalls would lead to greater noise in the slopes estimated and potentially mask the true existing differences.

The mouse is the most common animal model used to investigate inhaled toxicology, tobacco-related diseases, and environmental exposures (27). Whereas inbred strains remove the variability in response caused by genetic variations (31), inconsistent inhalation toxicology results have been noted across different strains (12, 23). Recent studies have demonstrated significant anatomic differences in airway morphometry between mouse strains (34), suggesting that differences in local airway deposition could account for the variability in outcomes across strains (27). Although mice provide an invaluable model for obtaining experimental data on exposure and toxicities, it is not possible or humane to study all substances or exposure conditions. Therefore, computational models are employed to fill the gap or to extend the range of experimental data and for analyzing the exposure-dose relationship under varying inhalation conditions (19). These computational models now need to incorporate differences in the bronchial tree geometries of different mouse strains.

It is well recognized that there are significant differences among mouse strains with regard to airway responsiveness to methacholine (10, 22), ozone exposure (7), and cigarette smoke inhalation (35), to name only a few. Particle deposition in the airway tree is highly influenced by the geometry of the conducting airways. More tortuous branching airways will generate greater airflow turbulence, impacting both the location and amount of particle deposition in the airways. Airway geometries of higher fractal dimensions will be more complex, increasing the likelihood of particle deposition around ranching points. Although speculative, mouse strains with airway geometries with different fractal dimensions may have different particle deposition patterns and possibly greater total deposition. The relationships between airway fractal dimensions and particle deposition can now be explored with the publicly available data sets (2, 3).

GRANTS

This study was supported by National Institute of Environmental Health Sciences R01 ES023863-01.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

R.W.G. conceived and designed research; M.A.K. performed experiments; R.W.G. and M.A.K. analyzed data; R.W.G. interpreted results of experiments; R.W.G. prepared figures; R.W.G. drafted manuscript; R.W.G., M.A.K., C.B., and R.R.B. edited and revised manuscript; R.W.G., M.A.K., C.B., and R.R.B. approved final version of manuscript.