Abstract
Neurons within early visual cortex are selective for basic image statistics, including spatial frequency. However, these neurons are thought to act as band-pass filters, with the window of spatial frequency sensitivity varying across the visual field and across visual areas. Although a handful of previous functional (f)MRI studies have examined human spatial frequency sensitivity using conventional designs and analysis methods, these measurements are time consuming and fail to capture the precision of spatial frequency tuning (bandwidth). In this study, we introduce a model-driven approach to fMRI analyses that allows for fast and efficient estimation of population spatial frequency tuning (pSFT) for individual voxels. Blood oxygen level-dependent (BOLD) responses within early visual cortex were acquired while subjects viewed a series of full-field stimuli that swept through a large range of spatial frequency content. Each stimulus was generated by band-pass filtering white noise with a central frequency that changed periodically between a minimum of 0.5 cycles/degree (cpd) and a maximum of 12 cpd. To estimate the underlying frequency tuning of each voxel, we assumed a log-Gaussian pSFT and optimized the parameters of this function by comparing our model output against the measured BOLD time series. Consistent with previous studies, our results show that an increase in eccentricity within each visual area is accompanied by a drop in the peak spatial frequency of the pSFT. Moreover, we found that pSFT bandwidth depends on eccentricity and is correlated with the pSFT peak; populations with lower peaks possess broader bandwidths in logarithmic scale, whereas in linear scale this relationship is reversed.
NEW & NOTEWORTHY Spatial frequency selectivity is a hallmark property of early visuocortical neurons, and mapping these sensitivities gives us crucial insight into the hierarchical organization of information within visual areas. Due to technical obstacles, we lack a comprehensive picture of the properties of this sensitivity in humans. Here, we introduce a new method, coined population spatial frequency tuning mapping, which circumvents the limitations of the conventional neuroimaging methods, yielding a fuller visuocortical map of spatial frequency sensitivity.
Keywords: fMRI, spatial frequency, visual cortex
INTRODUCTION
The initial stages of visual perception are constructed from a handful of building blocks residing within early visual cortex, including spatial frequency (SF; Watanabe et al. 1968; Wilson et al. 1983). Spatial frequency sensitivity plays a crucial role in determining the degree to which a neural population can discern the spatial scale of information processed within a visual scene. For instance, neural populations that prefer low spatial frequency content can detect coarse luminance variations but are blind to fine details. Recordings from visual cortexes in nonhuman primates have typically found band-pass selectivity, wherein a visuocortical neuron displays peak sensitivity for a particular SF, which is narrowly tuned to a range of neighboring frequencies. The neuronal response to frequencies lower or higher than the peaked preference, however, drops off rapidly (Campbell et al. 1969; De Valois et al. 1982; Movshon et al. 1978b).
Spatial frequency preferences in animal V1 indicate coarse structural organization, wherein the distribution of spatial frequencies changes continuously across primary visual cortex (Everson et al. 1998; Issa et al. 2000). Although neurons with receptive fields corresponding to the same visual eccentricity tend to exhibit a wide range of SF sensitivities, the overall distribution of SF tuning preferences gradually shifts toward lower SFs as a function of eccentricity (Xu et al. 2007; Yu et al. 2010). In addition to this retinotopically organized drop-off in spatial frequency with eccentricity, systematic variations of the peak preference have been observed across the visuocortical hierarchy, as well. The mean peak SF preference at a particular eccentricity is roughly one third of the SF preference found in the preceding visual area along the visuocortical hierarchy (Foster et al. 1985; Issa et al. 2000; Movshon et al. 1978b). Interestingly, the bandwidth of spatial frequency tuning appears to change as well, with electrophysiological recordings in cat V1 revealing an inversely proportional relation between peak and bandwidth of spatial frequency tuning, wherein neurons with preferences for higher spatial frequencies tend to have narrower bandwidths (De Valois et al. 1982).
To investigate the retinotopic organization of spatial frequency tuning in humans, a handful of studies have used functional magnetic resonance imaging (fMRI). From a methodological point of view, these studies can be categorized into two groups: phase-encoding and stimulus-blocked designs. The phase-encoding approach is advantageous because it allows the peak spatial frequency tuning to be efficiently estimated for every individual voxel. Results using this approach are consistent with animal studies, replicating the negative correlation between peak SF preference and eccentricity (Sasaki et al. 2001). Although methodologically efficient, this approach is incapable of estimating the entire shape of the tuning curve for every voxel. Alternatively, other studies have employed conventional stimulus-blocked designs to estimate the shape of the tuning curve. Based on these results, neural populations have been shown to act as simple linear filters, ranging from band-pass filters within V1 up to low-pass filters in V5 (Henriksson et al. 2008; Singh et al. 2000). In addition, similar to previous animal studies, the peak of the estimated tuning for V2 is less than that of V1, and the same is true for V3 relative to V2. Although blocked design studies have estimated the overall tuning function for certain visual areas, the estimation of the tuning curve per voxel requires the use of a large set of stimuli to attain enough statistical power, which becomes much less feasible when considering time constraints.
In this study, we set out to circumvent the aforementioned methodological limitations by proposing an alternative, model-based fMRI analyses approach (Dumoulin and Wandell 2008; Kay et al. 2013; Zhou et al. 2018), which allows for the fast and efficient estimation of population spatial frequency tuning (pSFT) functions, at a voxel-wise level. By employing this novel technique, we were able to demonstrate rich and reliable measurements of spatial frequency tuning, both within and across early visual areas, allowing us to better examine the organization of spatial frequency selectivity in humans.
METHODS
Participants.
Eight subjects (3 women, median age = 28) participated in the study. Participants had normal or corrected-to-normal vision and gave written informed consent to participate. The study was approved by the Boston University Institutional Review Board.
Stimuli and procedures.
Across each scan, participants viewed a set of stimuli that varied in spatial frequency content, ranging from a low 0.5 cycles/degree (cpd) to a high 12 cpd. Specifically, each stimulus was generated by filtering uniformly distributed noise with a narrow band-pass filter. The central SF of the band-pass filter (filter fixed-width: 0.1 cpd) spanned between 0.5 and 12 cpd, sampled at 40 logarithmically spaced frequencies (Fig. 1A). For each central SF, 10 different versions were generated, each from a different initial noise distribution. The stimuli had a Michelson contrast of 90% and were presented as a large annulus around fixation (outer diameter: 19.6°; inner diameter: 0.32°). A fixation point was displayed at the center of the display, throughout the experiment (diameter of 0.1°). To promote fixation, the fixation point’s color changed pseudorandomly on average every 4.5 s, and participants reported via key press the detection of these changes. All visual stimuli were generated using MATLAB (R2013a) in conjunction with the Psychophysics Toolbox-3 (Brainard 1997; Kleiner et al. 2007; Pelli 1997). All stimuli were displayed using a linearized VPixx PROPixx projector (maximum luminance: 389 cd/m2).
Fig. 1.
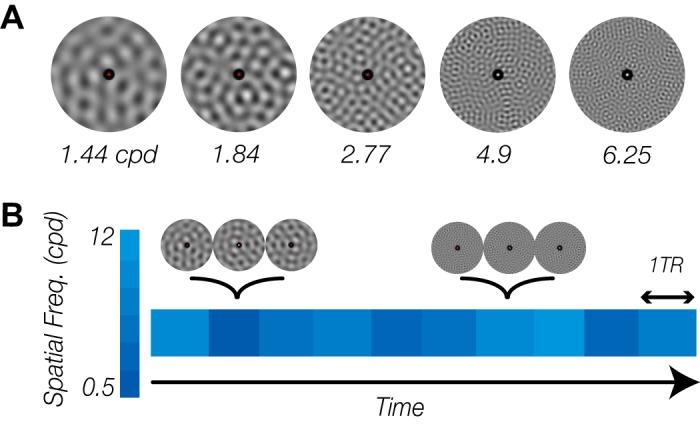
Stimulus and experimental procedure. A: example stimuli varying in spatial frequency content. Each stimulus was generated by filtering uniform noise with a narrow band-pass filter that had a central spatial frequency equal to the desired spatial frequency content. The 5 presented frequencies are only a subset of 40 different frequencies that were used for data collection; cpd, cycles/degree. B: exemplar time course of stimulus presentation. During each run, subjects viewed a series of visual stimuli that changed constantly and rapidly. In spite of the temporal dynamics of the visual stimuli, the spatial frequency content of the stimuli remained the same for 1 repetition time (TR) and then randomly changed to a new spatial frequency.
During each run, participants maintained their gaze on a fixation point at the center of the display, detecting the color change of the fixation dot. Simultaneously, a set of stimuli with varying spatial frequency content was displayed in the periphery. The peripheral stimulus changed continuously with a temporal frequency of 10 Hz; however, the spatial frequency was updated in-synch with the scan sequence repetition time (TR = 1,000 ms, 1 Hz) (Fig. 1B). Each spatial frequency from our selected set was presented six times during a run, and the order of presenting the frequencies was determined in a pseudorandom manner. Presentation of the stimuli started and also ended with a 10-s blank fixation period. Each participant completed a total number of 14 runs.
fMRI acquisition and analyses.
All MRI data were collected on a Siemens 3T Prisma scanner using a 64-channel head coil. Responses to the varying spatial frequencies were measured during one 2-h session, and population receptive fields (pRF) were mapped during a separate session. In both sessions, blood oxygen level-dependent (BOLD) activity was measured with simultaneous multislice echoplanar T2*-weighted imaging (Moeller et al. 2010; Xu et al. 2013) with a field of view (FOV) oriented perpendicular to the calcarine sulcus [2 mm3; TR = 1,000 ms; echo time (TE) = 35.40 ms; flip angle (FA) = 64°; FOV = 136 × 136 × 72 mm]. At the beginning of the main experiment, a T1-weighted anatomical volume with the same positioning as the functional runs was acquired (MPRAGE; 2 mm3; TR = 2,530 ms; TE = 1.35 ms; FA = 7°; FOV = 136 × 136 × 72 mm). We registered the functional-matched T1 volume to a high-resolution reference anatomical T1-weighted whole brain volume (MPRAGE; 1 mm3; TR = 2200 ms; TE = 1.54 ms; FA = 7; FOV = 256 × 256 × 256 mm) acquired during a separate session. For each subject, this allowed us to align all the functional runs with the high-resolution anatomical volume, using an automated robust image registration algorithm (Nestares and Heeger 2000). The mrTools neuroimaging analysis package (http://gru.stanford.edu/mrTools) was used to perform registration and standard preprocessing steps including motion correction, linear detrending, and applying a temporal high-pass filter (0.01 Hz). Before concatenation of all times series across runs for each subject in preparation for the modeling fitting procedure, the within-run percent signal change for each voxel was computed by dividing the BOLD signal during each run by the mean. Additional data analyses were then carried out using custom code written in MATLAB. We used population receptive field mapping (pRF) to delineate regions of interest (ROIs) V1–V3. The maps were acquired using standard techniques and stimuli (Dumoulin and Wandell 2008; Kay et al. 2013), and data analysis was performed using the analyze pRF MATLAB toolbox (Kay et al. 2013). Only voxels lying within the occipital region were included in the pRF analysis, which were identified using an occipital lobe label generated from an atlas based on intrinsic functional connectivity (Yeo et al. 2011). The investigation of the spatial frequency preference dependency on the preferred visual field position required having the parameters of both the pSFT and pRF analyses in alignment for each voxel. We used Freesurfer’s boundary-based registration (Greve and Fischl 2009) to bring the pRF analysis results into the pSFT functional session space. Then, by taking advantage of the capacity of mrTools to register individual functional runs to each other, while maintaining voxel-to-voxel correspondence across different runs, we were able to extract BOLD responses of functional runs and the estimated pRF parameters for the same voxels across all ROIs.
Population spatial frequency tuning modeling and estimation.
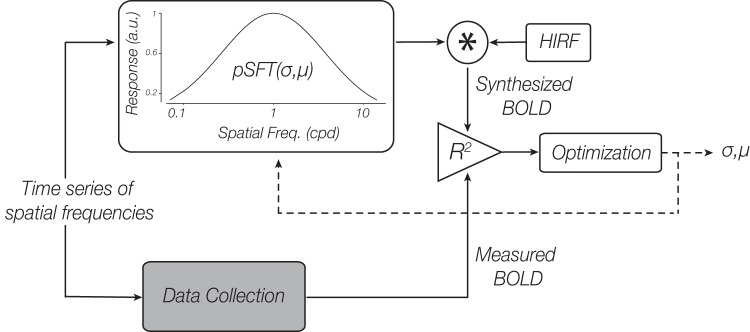
Our modeling approach assumed a linear relation between the neural response and the BOLD response (Birn et al. 2001; Boynton et al. 1996; Hansen et al. 2004), allowing the concatenated BOLD response time series to be predicted by convolving the estimated population responses to the spatial frequencies of the stimuli that were presented, with a hemodynamic impulse response function (HIRF). In this study, we estimated the population spatial frequency tuning (pSFT) using a Gaussian function, for which the precise shape parameters are unknown (Farivar et al. 2017; Henriksson et al. 2008). With this assumed underlying model, we were able to synthesize an estimated BOLD response time series given the set of spatial frequency-varying stimuli presented in our imaging experiment. Since we were interested in assessing the unknown parameters in our pSFT model (preference and bandwidth) for each voxel, the synthesized time series from our pSFT estimates were iteratively fit to the measured BOLD response time series using a grid search to find the Gaussian model parameters that best aligned our synthesized and measured BOLD responses. We estimated the most accurate pSFT per voxel by assuming a hypothetical model for the pSFT and forcing its unknown parameters toward values that would result in the best fit between the synthesized and actual responses, given the examined spatial frequencies (Fig. 2). Specifically, we assumed that the neural response to many different spatial frequencies is best captured by a log Gaussian distribution (Eq. 1 ), expressed as:
| (1) |
with two unknown parameters: µ represents the peak, and σ is the standard deviation that determines the spatial frequency tuning bandwidth. To find the parameters that best characterized the spatial frequency preferences of a voxel, we treated the BOLD signal as the product of a linear system (Boynton et al. 1996; Cohen 1997; Friston et al. 1994). This assumption allowed us to synthesize the BOLD response to the time series of spatial frequencies, f(t), that were presented to subjects. The synthesized BOLD response B(t) is expressed as
| (2) |
which is the product of the convolution of the neural response to the spatial frequencies, R[f(t)] with the HIRF, h(t). The other two parameters, B0, the baseline value, and β, the scaling factor, represent the changes in the baseline and scaling coefficient for the BOLD signal, respectively. Following the convention in neuroimaging analysis, both of these parameters were estimated using a general linear model (Dumoulin and Wandell 2008). To model the HIRF, we used a simple gamma function (Boynton et al. 1996):
Fig. 2.
Schematic diagram of the proposed model-based approach. Blood oxygen level-dependent (BOLD) time series containing responses to varying spatial frequencies were both measured and synthesized. The synthesized BOLD response was calculated by convolving the hypothetical neural responses to the frequencies, i.e., the pSFT values at the tested frequencies with the hemodynamic impulse response function. The population spatial frequency tuning (pSFT) was modeled as a log Gaussian function (Eq. 1) with unknown mean (µ) and SD (σ). Through comparison of the measured BOLD response with the synthesized one, the unknown parameters of the pSFT were estimated. The R2 of the fit of the 2 time series is the index of similarity, and the final estimated parameters are the outputs of a recursive optimization procedure, with the goal of maximizing the similarity index; cpd, cycles/degree; a.u., arbitrary units; HIRF, hemodynamic impulse response function; *, convolution operation.
| (3) |
In the equation, t is again time, n is the phase delay fixed at a value of 3, and the time constant τ was set to 1.08. Moreover, in synthesizing the BOLD response, the delay between the stimulus onset and the fMRI response was fixed at 2.05 s (Boynton et al. 1996). This model of the HIRF was selected over the two-gamma HIRF (Glover 1999) mainly due to its simplicity. Reanalysis of the data with a two-gamma function did not result in any substantial improvements nor changes in the qualitative pattern of results.
The coefficient of determination, R2, between the synthesized signal, B(t), and the real measured BOLD was used as a goodness-of-fit index. The two pSFT parameters, peak and bandwidth, that produced the highest R2 value yielded the optimal set of pSFT parameters. To find the optimal parameters that maximized the R2, we used exhaustive search. A grid comprised of the combination of 400 points for µ, and 400 points for σ was used to search the peak SD space for optimal parameters. The µ values were logarithmically spaced between 0.009 and 6, and the σ values were equally spaced between 0.1 and 1. To exclude the estimations that tended toward the limits, in the final analysis, only voxels with peaks between 0.01 and 5 and bandwidths between 0.2 and 0.9 were included.
Voxel selection.
Considering the size of the stimuli, only voxels with pRF centers falling within the eccentricity range of 0.16–9.8° were included in the final analyses. Moreover, voxels with poor fits in either the pRF or pSFT analyses were excluded. An R2 of 10% was set as the lowest acceptable goodness of fit for the pRF analysis. To set a threshold for the pSFT analysis, we carried out a permutation test, wherein sampling without replacement was used to shuffle the order of presented frequencies, generating a null distribution. The 95th percentile of the R2 of these estimates, across each cortical region, was calculated per subject, and finally, the average of this value across all the subjects was set as the threshold for selecting voxels within that cortical area.
RESULTS
To evaluate population spatial frequency tuning (pSFT) profiles, we deployed a generative model-based analysis (Dumoulin and Wandell 2008; Harvey et al. 2013; Kay et al. 2008; Zhou et al. 2018), which allowed us to fit BOLD time series data with assumed underlying tuning parameters (detailed in methods). We modeled the pSFT function as log Gaussian, with two primary unknown parameters: 1) mean, the peak spatial frequency preference; and 2) the standard deviation, which affects the selectivity bandwidth. Gaussian models have previously been used in neuroimaging studies to characterize spatial frequency tuning (Farivar et al. 2017; Henriksson et al. 2008), and the log Gaussian function fitted our data better in comparison to a linear Gaussian (one-tailed t-test of the difference of the medians of the R2 values; P < 0.05 for V1–V2). The model-based analysis involved iteratively fitting the BOLD time series data by changing the parameters of an assumed underlying model to predict the best input/output relationship between the spatial frequency presented at a given moment and neural response. For any given sequence of spatial frequencies presented to an observer in a scan, the modeled neural response is transformed into a simulated BOLD response through convolution with an assumed hemodynamic impulse response function. The parameters (peak and SD) that maximized the R2 of this fit were taken to be the final estimates for the pSFT of that particular voxel. Note that while the assumption of linearity between neural and BOLD response fails in certain regimes, the linearity approximation holds across quite a large range of conditions (Birn et al. 2001; Boynton et al. 1996; Hansen et al. 2004).
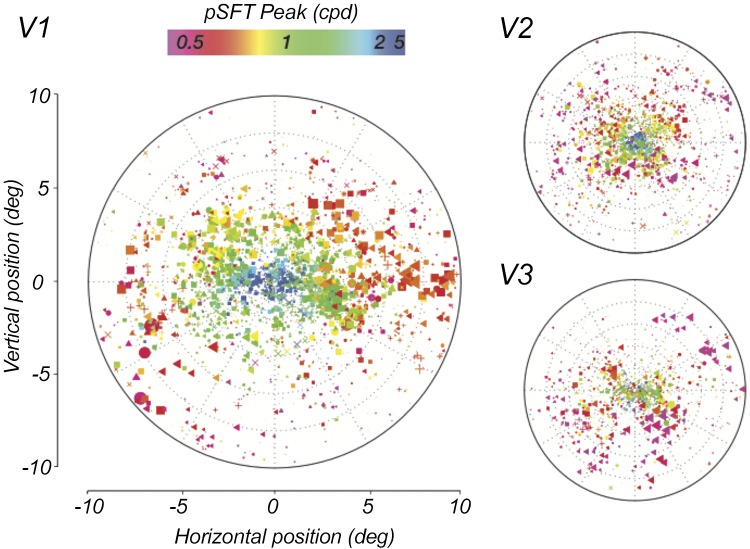
After estimation of the parameters, we first set out to qualitatively assess the organization of the estimated pSFT peaks across the visual field (Fig. 3), using voxel-based retinotopic preferences derived from independent pRF mapping, per participant. Doing so revealed systematic changes in the peak spatial frequency selectivity with eccentricity. Consistent with previous reports (Henriksson et al. 2008; Hess et al. 2009; Sasaki et al. 2001), voxels with retinotopic preferences closest to the foveal confluence were selective for higher spatial frequencies, and this peak preference dropped off as a function of eccentricity. To focus on the eccentricity-based effects, in subsequent analyses we collapsed our results across polar angles (Fig. 4A). This decline in peak spatial frequency preference with eccentricity emerged across all participants and across visual areas V1–V3 (Fig. 4B).
Fig. 3.
Voxel-wise map of the population spatial frequency tuning (pSFT) peak across the visual field. Each point represents a single voxel. The color codes the magnitude of the estimated pSFT peak of the voxel, and the size of the points are scaled with their R2 of the pSFT fits. The locations of the points are selected according to the population receptive fields polar angle and eccentricity coordinates of the corresponding voxels. The symbols correspond to different subjects. In all 3 regions, the foveal voxels prefer the highest spatial frequencies and this value drops when moving toward the more peripheral regions. Moreover, the frequencies represented in V1 seem to be higher in comparison to the higher cortical regions.
Fig. 4.
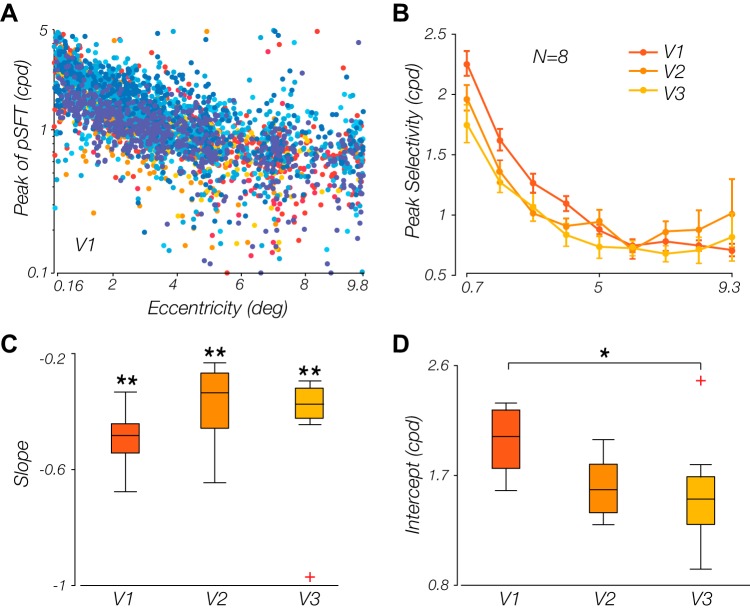
Relationship between the population spatial frequency tuning (pSFT) peak and retinotopic eccentricity. A: peak of the pSFT declines with eccentricity in area V1. Each point is a voxel. Data from each subject is displayed with a certain color; cpd, cycles/degree. B: mean subject-wise pSFT peak estimates within each eccentricity bin. Nine bins linearly spaced within the eccentricity range of [0.16°, 9.8°] have been used. Error bars show the means ± SE. C and D: parameters of the line that models the relationship between the peak pSFT and the eccentricity (both in logarithmic scale); slopes (C) and intercepts (D) of such lines, fitted per subject on the binned data (bins similar to B), are shown. The slopes are significantly <0 in all 3 cortical regions. The intercept of the V1 area is significantly larger than this value in V3 area and almost significantly larger than the corresponding value in V2 (*P < 0.05; **P < 0.001).
To quantify the precise nature of the relationship between eccentricity and peak spatial frequency preference, we fit the binned data with three candidate models proposed by previous work: Linear, Multiplicative Inverse (M-Inverse), and a Hinged Line (H-Line). These three models that were fit on the mean peaks within eccentricity bins are expressed as Eq. 4 to Eq. 6, respectively.
| (4) |
| (5) |
| (6) |
In the equations, µ is the peak, eccen is the eccentricity, and A–C are the unknown parameters, estimated separately for each function.
While a linear relationship has some support by Hess et al. (2009) and D’Souza et al. (2016), a hinged line relationship has been proposed as a plausible model, as well. Indeed, the hinged line has been used for describing the relationship between eccentricity and RF size in the past (Freeman and Simoncelli 2011). Moreover, this relationship between receptive field size and spatial frequency preference has been recently proposed as the central assumption behind the proposed single-unit receptive field (suRF) procedure (Keliris et al. 2019). To test the assumption that pRF size and spatial frequency sensitivity are related, we included this as a candidate for modeling the eccentricity-spatial frequency sensitivity relationship, as well. This assumption is based on findings in simple cell recordings (Enroth-Cugell and Freeman 1987; Cleland et al. 1979). However, it is worth noting that evidence suggests that complex cells may diverge from this rule (Movshon et al. 1978a), and the existence of such relationship has been debated (Welbourne et al. 2018). Considering that there is evidence in favor of both possibilities, and we have measurements of both spatial frequency and pRF eccentricities acquired directly during an imaging session, we were able to test the possibility of a hinged line relationship in humans.
Alternatively, a multiplicative inverse function has been used as an approximation of the cortical magnification factor that changes along with visual eccentricity (Harvey and Dumoulin 2011). The relationship between visual field coordinates and the corresponding retinotopic location of the representation across the early visual cortex has been shown to be well described by a complex logarithm function (Schwartz 1977), the derivative of which is approximated by multiplicative inverse function (Schira et al. 2007). Although it has been argued that the exact magnification is not polar invariant, this relationship is claimed to be a valid first order approximation (Schira et al. 2010). To determine which model provided the best and simplest description of our results, we compared the corrected Akaike’s information criterion (AICc) values of each model fit, which is a corrected variant that better accounts for a lower sample size (Hurvich and Tsai 1989). The AICc values for each model were transformed into the ΔAICc values, which is simply the differences in AICc values between a candidate model, and the minimum AICc across the three models (Burnham and Anderson 2002). The closer a ΔAICc is to zero, the better that model is believed to account for the data relative to the other candidate models. Figure 5 is the mean ΔAICc value across subjects, indicating that across V1–V3, the lowest AICc value supports a multiplicative inverse relationship, wherein peak spatial frequency preference is the reciprocal of eccentricity (for individual subjects’ fits, refer to the Supplemental Materials that are deposited in the Figshare repository at https://doi.org/10.6084/m9.figshare.11499801.v1). On a log-log scale, this manifests as a linear relationship between peak and eccentricity, from which we could then derive a parsimonious quantification of the drop-off with eccentricity (slope) and the peak spatial frequency tuning at the innermost eccentricity (intercept). Turning first to the slope estimates, the means of the fitted lines across subjects for V1, V2, and V3 were, respectively, −0.49 (SD = 0.10), −0.37 (SD = 0.14), and −0.44 (SD = 0.22), with all slopes being significantly negative (P < 0.001 for all regions) (Fig. 4C). Despite a decrease in the overall spatial frequency preference from V1 to V3, the rate of drop-off in preference was preserved across visual areas, with no significant differences in slope found between areas (one-way ANOVA, F2,21 = 1.05, P = 0.37). However, the intercept parameter, which served as a proxy for the peak preference at the innermost eccentricity, varied significantly across areas (one-way ANOVA, F2,21 = 3.93, P = 0.04) (Fig. 4D). A post hoc Tukey test indicated that the differences were primarily between V1 and extrastriate visual areas (significant between V1 and V3, P = 0.045; close to significant in V1 vs. V2, P = 0.086). We converted the intercept back to spatial frequency by taking the exponential of the intercept, as this indicates the maximal SF represented within each of our cortical ROIs, and found the highest value in V1 (1.99 cpd, SD = 0.28), which drops down in V2 (1.60 cpd, SD = 0.24) and V3 (1.55 cpd, SD = 0.46).
Fig. 5.
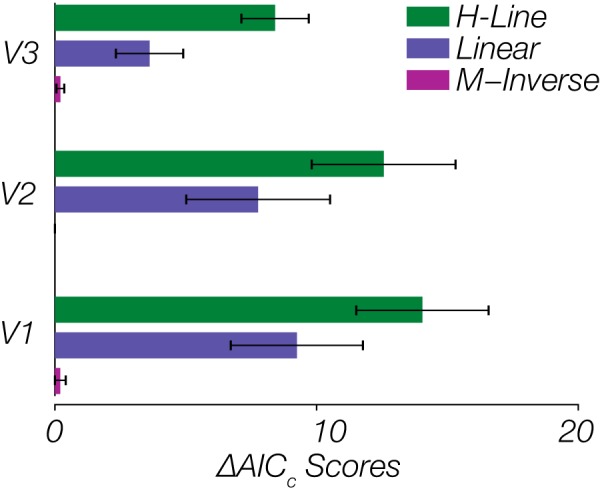
Comparison of model fits for peak-eccentricity relationship. The lowest change in corrected Akaike’s information criterion (ΔAICc) score across all visual areas of V1 to V3 belongs to the M-Inverse function. Performances of the Linear and H-Line models are very similar and poorer than the M-Inverse. Each bar shows the mean ΔAICc value across all eight subjects and the error bars represent the standard error of the mean. Note that the values for the M-Inverse are very small (indicating the best candidate model) and not very variable and thus difficult to see.
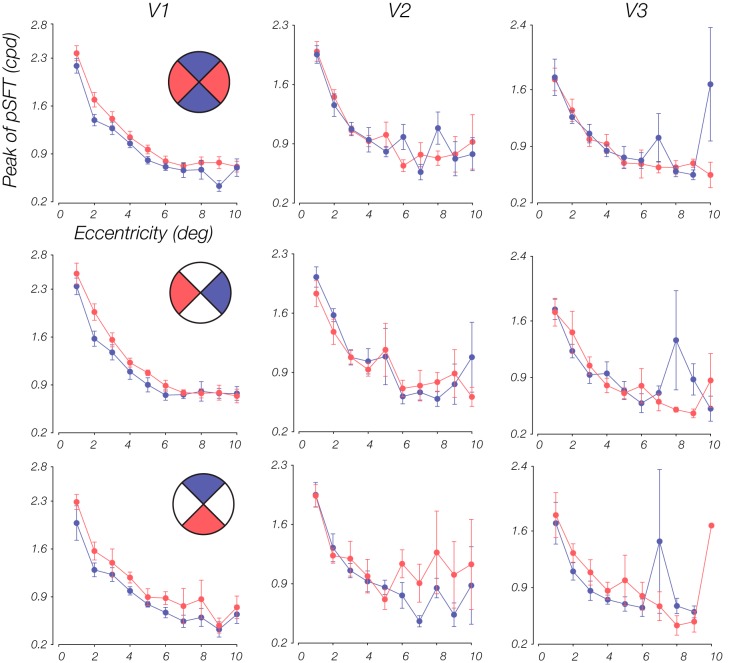
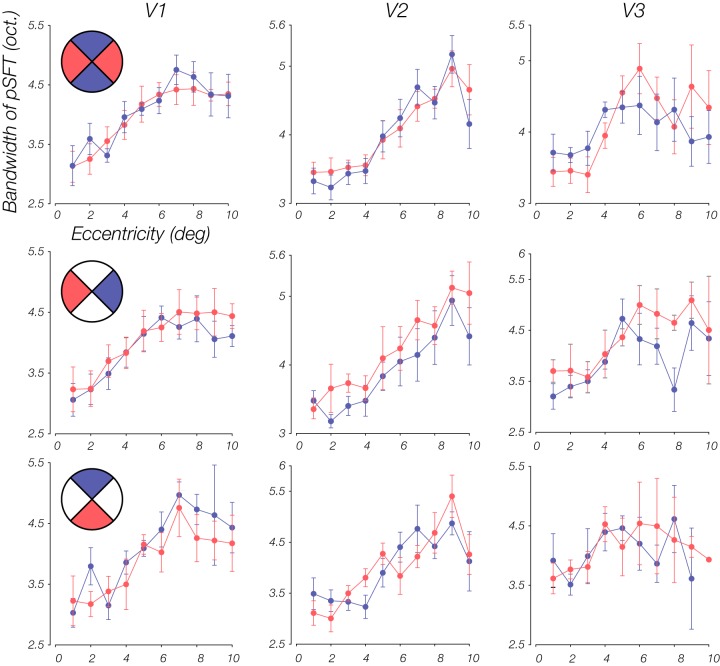
Psychophysical and neurophysiological studies suggest that perceptual sensitivity is impacted not only by eccentricity but by anisotropies in perceptual sensitivity across polar angle, as well (Carrasco et al. 2001, 2002; Karim and Kojima 2010; Levine and McAnany 2005; Rijsdijk et al. 1980). To examine whether our estimated pSFTs reveal nonuniformities across the visual field, we leveraged pRF mapping to split the visual field into sections (Silva et al. 2018), allowing us to simply test for differences in the pSFT parameters between sets of quadrants of the visual field. The quadrants were comprised of 90° wedges above, below, left, and right of fixation. In addition, the eccentricity range was divided into 10 equally spaced bins. Figure 6 shows the mean of the pSFT peaks lying within these eccentricity bins for different sets of quadrants. In V1, the peak in horizontal meridian quadrants is higher than the vertical meridian quadrants. Moreover, lower and left fields were slightly higher in SF preference, compared with the upper and right fields, respectively. Similar to Silva et al. (2018), we found differences in the mean peak within each bin, between the two opposing quadrants for every subject and then carried out a two-tailed, one-sample t test on these differences combined across subjects. For each subject, only bins that had at least one voxel within each of the two quadrants were included in the analysis. Differences were significant in V1 between horizontal and vertical meridian quadrants [V1: t(74) = 5.06, P < 0.001; V2: t(76) = −0.42, P = 0.67; V3: t(68) = −1.89, P = 0.06], as well as upper versus lower [V1: t(61) = −3.86, P < 0.001; V2: t(63) = −2.32, P = 0.02; V3: t(51) = 0.01, P = 1.00], and right versus left [V1: t(77) = −3.67, P < 0.001; V2: t(73) = 0.48, P = 0.63; V3: t(64) = 1.05, P = 0.30]. Except for the difference between upper and lower quadrants in V2, which primarily emerged in the periphery (Fig. 6), we did not find meaningful differences in V2 and V3.
Fig. 6.
Comparison of peak spatial frequency (SF) between different quadrants of the visual field. Each column is a visual area (V1–V3), and each row is a comparison of retinotopic coverage. Specifically, each plot shows the mean estimated peak within an eccentricity bin, across subjects, for 2 opposing quadrant sets that are designated with red and blue colors in the insets of the plots on the left. In V1, horizontal, left, and lower quadrants have higher peaks in comparison with the vertical, right, and upper quadrants [horizontal vs. vertical: t(74) = 5.06, P < 0.001; upper vs. lower: t(61) = −3.86, P < 0.001; right vs. left: t(77) = −3.67, P < 0.001]. Results of a t test also revealed significant differences between upper and lower quadrants in V2 [t(63) = −2.32, P = 0.02]. Quadrant ranges include [−45°,45°], [45°,135°], [135°,225°], and [225°,315°]. Error bars represent means ± 1 SE.
To investigate voxel-wise SF selectivity, we first used the estimated parameters to calculate the pSFT bandwidths in octaves. The bandwidth of spatial frequency selectivity has traditionally been indexed in octave units in neurophysiological studies, due to the assumed logarithmic representational scaling of spatial frequency coding within the visual system (e.g., De Valois et al. 1982; Foster et al. 1985; Movshon et al. 1978b). Using octaves as a measure of bandwidth adheres to this ratio-based representation of spatial frequency, while also allowing for a symmetric measure of frequency tuning width. Considering that an octave is a frequency ratio of 2:1, the full bandwidth at half-amplitude in octave units (BW) is defined as the log transform of the ratio of the SFs at half-amplitude of the pSFT (Eq. 7).
SF0.5H and SF0.5L: higher and lower cutoff SFs at half-amplitude
| (7) |
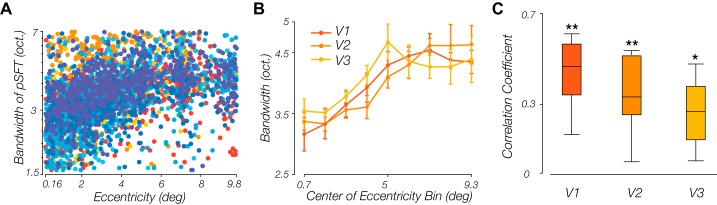
Figure 7 illustrates the retinotopic organization of these bandwidth estimates. We observed a modest increase in the estimated bandwidth of tuning in parafoveal regions, compared with foveal regions, especially in V1. To quantify the relationship between eccentricity and tuning bandwidth, we collapsed the data across polar angle (Fig. 8A). When dividing the data into equal sized eccentricity bins and examining the average tuning bandwidth as a function of eccentricity across subjects, a positive trend in V1–V3 was found (Fig. 8B), with the correlation coefficients significantly greater than zero in all three areas of V1 [t(7) = 8.31, P < 0.001], V2 [t(7) = 5.84, P < 0.001], and V3 [t(7) = 5.14, P = 0.001] (Fig. 8C).
Fig. 7.
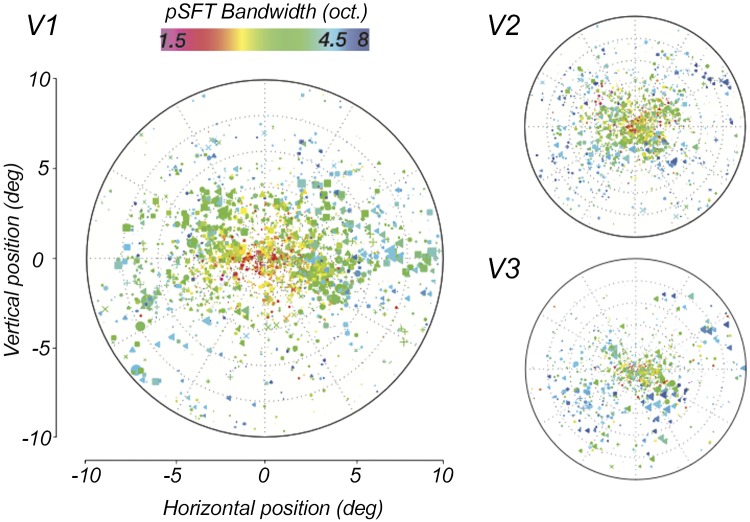
Voxel-wise map of the population spatial frequency tuning (pSFT) bandwidth estimates across visual field and area. Each point represents a single voxel. The color codes the magnitude of the estimated pSFT peak of the voxel, and the size of the points are scaled with their R2 of the pSFT fits. The locations of the points are selected according to the population receptive fields polar angle and eccentricity coordinates of the corresponding voxels. The symbols distinguish data from different subjects. In all 3 areas, the bandwidth is narrower in the foveal regions and increases slightly in the periphery.
Fig. 8.
Relationship between the population spatial frequency tuning (pSFT) bandwidth and retinotopic eccentricity. A: bandwidth increases slightly with eccentricity in V1. Each point illustrates a voxel. Data from every single subject has been displayed with a certain color. B: average of the mean pSFT bandwidth within each eccentricity bin, across subjects. Error bars show means ± SE. C: distributions of the correlation coefficients between bandwidth and eccentricity, estimated per subject. Coefficients are significantly different than zero in all three areas (*P < 0.05; **P < 0.001).
To test for visual field anisotropies in SF tuning bandwidth, we conducted the same analysis previously described for the SF peak estimates. The changes of bandwidth with eccentricity for different quadrants are plotted in Fig. 9. The statistical tests indicated significant differences between right and left quadrants in both V2 and V3 [V1: t(77) = −1.59, P = 0.12; V2: t(73) = −2.14, P = 0.04; V3: t(64) = −2.86, P = 0.01]. However, there were no differences between either the horizontal and vertical quadrants [V1: t(74) = −1.21, P = 0.23; V2: t(76) = 1.22, P = 0.23; V3: t(68) = 0.29, P = 0.77] or the upper and lower quadrants [V1: t(61) = 1.94, P = 0.06; V2: t(63) = −0.06, P = 0.96; V3: t(51) = −0.24, P = 0.81].
Fig. 9.
Comparison of bandwidth estimates between different quadrants sets of the visual field. The t tests on the differences between right and left quadrants in V2 and V3 were significant [V2: t(73) = −2.14, P = 0.04; V3: t(64) = −2.86, P = 0.01]. In other cases, the null hypothesis was not rejected. Quadrant ranges include [−45°,45°], [45°,135°], [135°,225°], and [225°,315°]. Error bars represent means ± 1 SE. pSFT, population spatial frequency tuning.
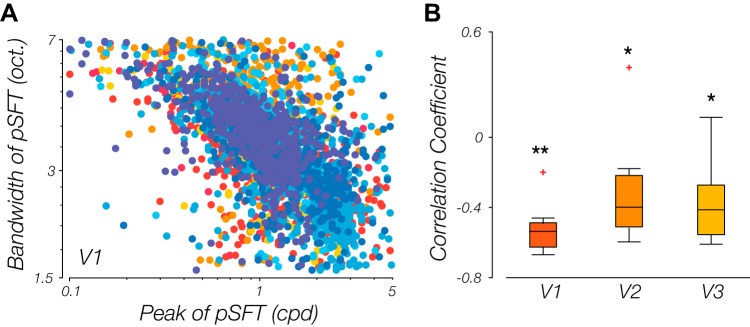
What relationship, if any, is there between pSFT peak preference and the corresponding bandwidth in human visual cortex? To examine this, we carried out a voxel-wise correlational analysis between these two parameters and found a clear decline in bandwidth for voxels that prefer higher spatial frequencies (Fig. 10A). Across all subjects, the negative correlation coefficients for pSFT bandwidth, in octaves, and pSFT peak proved significantly different from zero across all ROIs [V1: t(7) = −10.05, P < 0.001; V2: t(7) = −2.72, P = 0.03; V3: t(7) = −4.43, P = 0.003] (Fig. 10B). To the best of our knowledge, this is the first report of an inverse relationship between spatial frequency preference and bandwidth within human visual cortex; an observation made possible by employing the model-based analysis approach.
Fig. 10.
Voxels with higher population spatial frequency tuning (pSFT) peaks have narrower tuning. A: bandwidth decreases with increase in pSFT peak. Each point illustrates a voxel. Data from every single subject has been displayed with a certain color. B: distributions of the correlation coefficients between the peak and the bandwidth estimates of the pSFT, across subjects. The coefficients are significantly negative in all 3 regions of V1, V2, and V3 (*P < 0.05; **P < 0.001).
Note that the derived relationships for estimated bandwidths in logarithmic scale (i.e., octave units) can change qualitatively when bandwidths are assessed in linear scale (i.e., cpd units). To explore the influence of the particular units used for assessing bandwidth, we assessed the bandwidth in cpd units, as well. The bandwidth in cpd units is equal to the full-width at half-maximum (FWHM) of the pSFT. Across subjects, the mean correlation between these cpd bandwidth values and eccentricity were, in V1, V2, and V3, respectively, −0.38 (SD = 0.14), −0.2 (SD = 0.10), and −0.31 (SD = 0.16), suggesting a significant negative relationship [V1: t(7) = −7.55, P < 0.001; V2: t(7) = −5.65, P < 0.001; V3: t(7) = −5.4, P = 0.001]. In addition, the conversion of units led to a significant positive relationship between the FWHM and the pSFT peak [V1: t(7) = 18.95, P < 0.001; V2: t(7) = 26.02, P < 0.001; V3: t(7) = 22.63, P < 0.001], with the mean correlations in V1, V2, and V3, respectively, being 0.65 (SD = 0.10), 0.68 (SD = 0.07), and 0.68 (SD = 0.09). Although the direction of these relationships appeared to be the reverse of what we had reported with the bandwidths in log scale (octaves), the estimated bandwidths in the two different scales were not inversely related. Mean correlation coefficients between bandwidth in octave units and FWHM in cpd units [V1: 0.16 (SD = 0.15); V2: 0.29 (SD = 0.22); V3: (0.24 (SD = 0.18)] were significantly positive in all three visual areas [V1: t(7) = 3.06, P = 0.018; V2: t(7) = 3.76, P = 0.007; V3: t(7) = 3.73, P = 0.007]. To shed light on this seemingly contradictory trend, we examined the interconnected relationship between mean values of the FWHM, bandwidth in log scale, and the pSFT peaks within different eccentricity (Fig. 11). The direction of the relationship between FWHM and bandwidth in octave units depended on the pattern of modulation of the peak with eccentricity. The decline of the peak with eccentricity occurs along with an increase of the bandwidth in log scale, and a decrease of the FWHM.
Fig. 11.
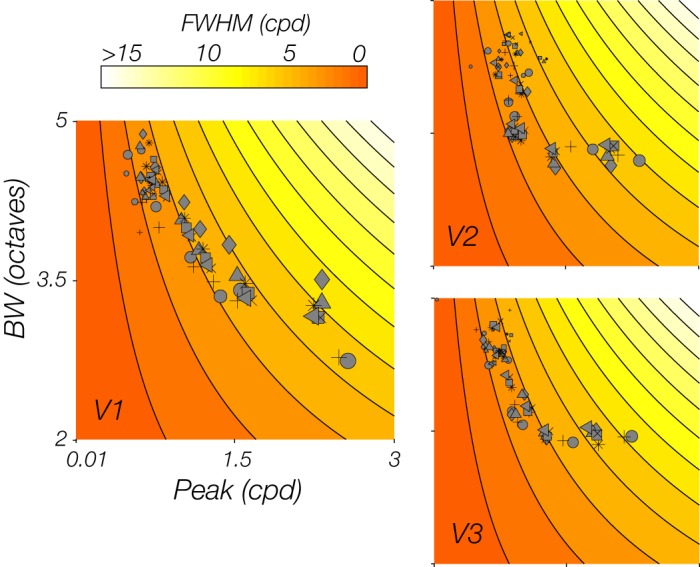
Relationship between measures of bandwidths in octave scale, absolute full-width at half-max (FWHM), and peak spatial frequency preferences, over the eccentricity range. Tuning width, as measured by the absolute FWHM, decreases as a function of increasing eccentricity; cpd, cycles/degree. However, when tuning width is expressed as octave bandwidths, we observed an increase of the bandwidth in logarithmic scale (BW) with eccentricity, as well as with the decrease of the population spatial frequency tuning (pSFT) peak, in V1–V3. Each point represents the average parameter estimates of voxels lying within an eccentricity bin, for an individual subject (symbols represent different subjects). The size of each point is inversely scaled relative to eccentricity, wherein largest points are near-eccentricities, and smallest are far eccentricities. Nine bins, equally distanced within the range of 0.16–9.8°, were used in the analysis.
DISCUSSION
Estimation of voxel-wise spatial frequency tuning within human visual cortexes has been proven difficult primarily due to methodological constraints: the variety and number of measurements necessary to fully capture a spatial frequency tuning function using traditional imaging approaches would be unreasonably time consuming. To circumvent this obstacle, we devised a computational approach paired with fMRI that allowed us to estimate the preference and shape of population spatial frequency tuning (pSFT) at a voxel-wise level. This generative model-driven analytic approach has the advantage that it allows for much more flexible and dynamic experimental designs, with event presentations and timing that would not be feasible when using conventional imaging designs (i.e., phase-encoding or stimulus-blocked designs). Here, we applied our novel approach to assess BOLD responses to the presentation of stimuli that rapidly changed in spatial frequency to estimate pSFT functions across early visual cortex. Based on prior studies, we assumed that the pSFT took on the properties akin to a band-pass filter, with the pSFT for any particular voxel characterized by two key parameters: peak spatial frequency (cpd) and bandwidth (octave). With this approach, we were then able to thoroughly investigate the dependency of spatial frequency preferences on retinotopy, examining the precise relationship between voxel-wise spatial frequency preference and bandwidth, as well as its relation to the eccentricity of voxel-wise receptive field properties. Our results support previously reported declines in the peak SF with eccentricity in all visual areas (Campbell et al. 1969; De Valois et al. 1982; Movshon et al. 1978b). Interestingly, our findings suggest that the rate of peak spatial frequency decline is comparable across V1–V3. However, V1 appears distinct from extrastriate cortex in some domains, with the peak SF at the innermost eccentricity being higher in V1, which appears to drop across higher visual areas. The spatial frequency selectivity of the voxels appears to change with eccentricity as well, wherein estimated bandwidths gradually become larger in more peripheral regions for all three areas of V1–V3. Moreover, comparison of the pSFTs between opposing quadrants of the visual field indicated a radial bias in the SF preferences of the voxels. We found higher sensitivities in horizontal and lower sides of the visual field in comparison to their opposite sides in V1. These patterns match with the previous reports of higher perceptual performances (Carrasco et al. 2001, 2002; Levine and McAnany 2005; Rijsdijk et al. 1980) and smaller pRF sizes in these sectors compared with the vertical and upper fields (Silva et al. 2018). Our results also pointed to higher peak SFs in the left field in V1 that are consistent with the previously reported smaller pRF sizes of this hemifield in V2 and V3 (Silva et al. 2018) and advantage of the left hemifield in detection task (Silva et al. 2008). We are aware, though, that the superiority of visual performance in the left visual field is not true for all types of stimuli and there has been reports of better performance of the right hemifields as well (Kitterle et al. 1992; Peyrin et al. 2005). This inconsistency, however, does not undermine the pattern that we have found, as our results are not completely devoid of such mismatch either; left visual field pSFTs have higher bandwidths in V2, which theoretically can result in poorer performance on this side. Future work directly comparing perceptual sensitivity across the visual field within an individual participant and comparing that to the individual’s pSFT estimates could shed further light on this. Finally, building on previous results in the literature, we observed a novel relationship between the voxel-wise peak selectivity preference and tuning bandwidth, in which voxels that were responsive to higher frequencies had also tighter bandwidths. We should emphasize that the direction of the derived relationship between the bandwidth and the other parameters depended on the scale of the bandwidth; when we converted the scale of our measurements of the bandwidth from octave to the absolute units of cpd, the direction of the relationships switched.
The decline of the peak spatial frequency with eccentricity has been reported in neurophysiological studies of both cat and monkey (De Valois et al. 1982; Movshon et al. 1978b). In addition, the interdependency of the bandwidth and the peak that we observed is consistent with studies conducted within macaque visual cortexes, wherein the bandwidth on octave scale appears to be inversely related to peak preference, but the bandwidth in linear scale is smaller for neurons that prefer lower SFs (De Valois et al. 1982; Foster et al. 1985). Interestingly, the negative correlation between bandwidth and eccentricity is not readily predicted from previous animal findings. Whereas De Valois et al. (1982) found no significant differences between bandwidths in foveal (<1.5°) and parafoveal (3–5°) regions, Foster et al. (1985) reported a mean bandwidth of 1.8 octaves for the parafoveal region (2–5°) and 1.4 octaves in foveal areas (<1°) of V1. Considering the gradual increase of bandwidth with eccentricity that we observed, these previously reported results do not contradict our findings. The mean bandwidths within the region-specific eccentricity bins that these previous studies examined (<5°) varies by 1–2 octaves in our study, and without having the measurements for all voxels we might have easily overlooked this relationship as well. However, by leveraging our pSFT technique across large swaths of visual cortex, our voxel-wise estimations can reveal an existing relationship that would otherwise be difficult to detect without obtaining detailed estimations of tuning profiles across a large population.
While human spatial frequency tuning has been estimated in previous studies (Henriksson et al. 2008; Sasaki et al. 2001; Singh et al. 2000), our approach differs in a number of meaningful ways, in terms of granularity or measurement, potential efficiency of time, and flexibility. First, none of the previous neuroimaging work on SF tuning had been carried out to measure tuning for individual voxels. Henriksson et al. (2008) measured mean responses within bins comprised of voxels spanning one of three eccentricity ranges. With this approach, they concluded that SF preference is conversely dependent on eccentricity: a finding that squares with our results. Although these three points were sufficient for finding this relationship, our approach allows us to gather a richer data set, bringing into focus a more fine-grained picture of tuning properties per voxel, additional details that further aid in understanding other aspects of frequency selectivity within human visual areas. For instance, our voxel-wise approach allowed us to examine the negative relationship between peak frequency and bandwidth of each voxel. In addition, we were able to detect an increase in bandwidth with eccentricity, which mostly occurred within the perifovea. Without the fine-grained sampling of eccentricity afforded by our paradigm, it would not have been feasible to detect such trends across retinotopic space.
In terms of efficiency, our method offers advantages, as well. Because traditional approaches involve discrete, repeated sampling of responses to a set of spatial frequencies, as was done in Henriksson et al. (2008), the upper bound of what could be measured within one scanning session was limited to the estimation of an average tuning curve per eccentricity range, for only three eccentricities. This is because traditional fMRI approaches, such as block designs and event-related designs, necessitate a fixed number of spatial frequencies, selected in advance, for which multiple measures are acquired. In theory, this traditional approach could yield a fine-grained picture of tuning properties, but in practice this would be much more time costly. In contrast, our model-driven paradigm allowed us to sweep through a broad range of spatial frequencies, allowing us to efficiently sample more eccentricity ranges. In terms of flexibility, this model-based approach also allows us to, in principle, estimate tuning curves in the absence of any repeated instances of a particular spatial frequency presented. The flexibility of this approach thus lends itself nicely to experimental designs that were previously less feasible within the scanner, such as staircase procedures to estimate thresholds, or other dynamic experimental designs that have limited-to-no repeats of a given stimulus intensity/quality.
For first-order simplicity, our approach ignores a set of known nonlinearities, one nonlinearity in neurovascular coupling, and the other being inherent nonlinearities in neural response. Regarding neurovascular coupling, although we cannot deny that there are, in some regimes, nonlinear relationships between the BOLD signal and neural response, we do not believe the assumption of linearity is a determining factor in the qualitative patterns of results we report. Note that while the assumption of linearity between neural and BOLD response fails in certain regimes, the linearity approximation holds across quite a large range of conditions (Boynton et al. 1996). Indeed, this linear relationship is assumed in not only the lion’s share of model-based approaches to fMRI analyses, including population receptive field mapping, but is the underlying assumption for the bulk of fMRI analyses. For simplicity, paucity of ground truth, and adherence to the convention in fMRI analyses, we have opted to stick with the assumption of linearity but acknowledge that the approach, along with most model-driven approaches, would benefit in the future from incorporation of a better model of the putative nonlinearity of neurovascular coupling (Buxton et al. 1998).
Regarding inherent neural nonlinearities, such as compressive nonlinearities brought about by temporal (Zhou et al. 2018) or spatial dynamics (Kay et al. 2013), we did not incorporate such nonlinearities into our current pSFT modeling procedure. Although it would certainly be interesting to incorporate spatiotemporal models to investigate how the preference of a particular voxel to a certain frequency is formed and how it is affected by the surrounding population, or extensions of time, these questions stand outside the scope of our current study, necessitating acquisition of compressive nonlinearities in the spatiotemporal domain, to properly test and constrain nonlinear models. Here, the focus was on estimating what frequency a particular voxel is most sensitive to and its envelope of sensitivity. This does not imply that the nonlinear relationship between the peak and eccentricity is the product of such a nonlinearity that we have opted to overtly ignore. Rather, our estimated values represent the final sensitivity of a voxel, and we remain agnostic as to any spatiotemporal nonlinearities that may underlie this sensitivity. In other words, while the host of linear or nonlinear interactions that underlie each voxel’s preference is not explained in our data set, and can be investigated in another set of studies and with a model incorporating such aspects, it is clear that the net preferences change with eccentricity.
Our approach rides on the assumption that all voxels within our target visual areas can be qualitatively characterized as band-pass filters. The weight of the evidence currently in the literature suggests that within most spatial frequency regimes this band-pass filter assumption is reasonably accurate. Neuroimaging studies have shown that when the range of the spatial frequencies used in stimulating the occipital cortex is centered in the ideal low end of the spatial frequency spectrum for a particular visual area, then under these conditions most visual areas have been found to act as band-pass filters (Henriksson et al. 2008; Singh et al. 2000). Furthermore, the majority of recorded cells in neurophysiological studies have been shown to be narrowly tuned, with only a low percentage being identified as truly resembling low-pass filters (De Valois et al. 1982; Foster et al. 1985). However, one potential follow-up to this study would be to model the voxel-wise pSFT using a combination of different filter types, to test the degree to which adding more complex, heterogeneous filter banks to the model could capture more variability in the BOLD response.
The typical spatial resolution of human fMRI experiments permits the measurement of population responses, with the pooled response of neurons within an individual voxel representing a wide range of spatial frequency preferences. Despite the much coarser scale of analyses accessible with fMRI, our pattern of results in humans succeed in demonstrating a high correspondence with the patterns often reported by animal studies using invasive recording techniques. Recently, similar computational modeling approaches have also been able to successfully estimate receptive field size in human visual cortex using solely fMRI measurements, while also demonstrating a close correspondence to direct measurements in nonhuman primates (Keliris et al. 2019). The high level of correspondence between these different methodologies and recording techniques offers strong support for the generative modeling approach employed in this study as a means for reproducing homologous animal electrophysiology results in human subjects.
GRANTS
This work was supported by National Eye Institute Grant EY-028163 (to S. Ling) and National Science Foundation Grant NSF-1625552.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
S.L. conceived and designed research; S.A. and L.N.V. performed experiments; S.A. and L.N.V. analyzed data; S.A. and S.L. interpreted results of experiments; S.A. prepared figures; S.A. drafted manuscript; S.A., L.N.V., and S.L. edited and revised manuscript; S.A., L.N.V., and S.L. approved final version of manuscript.
REFERENCES
- Birn RM, Saad ZS, Bandettini PA. Spatial heterogeneity of the nonlinear dynamics in the FMRI BOLD response. Neuroimage 14: 817–826, 2001. doi: 10.1006/nimg.2001.0873. [DOI] [PubMed] [Google Scholar]
- Boynton GM, Engel SA, Glover GH, Heeger DJ. Linear systems analysis of functional magnetic resonance imaging in human V1. J Neurosci 16: 4207–4221, 1996. doi: 10.1523/JNEUROSCI.16-13-04207.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brainard DH. The Psychophysics Toolbox. Spat Vis 10: 433–436, 1997. doi: 10.1163/156856897X00357. [DOI] [PubMed] [Google Scholar]
- Burnham KP, Anderson DR. Model Selection and Multimodel Inference: a Practical Information-Theoretic Approach (2nd ed.). New York: Springer, 2002. [Google Scholar]
- Buxton RB, Wong EC, Frank LR. Dynamics of blood flow and oxygenation changes during brain activation: the balloon model. Magn Reson Med 39: 855–864, 1998. doi: 10.1002/mrm.1910390602. [DOI] [PubMed] [Google Scholar]
- Campbell FW, Cooper GF, Enroth-Cugell C. The spatial selectivity of the visual cells of the cat. J Physiol 203: 223–235, 1969. doi: 10.1113/jphysiol.1969.sp008861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carrasco M, Talgar CP, Cameron EL. Characterizing visual performance fields: effects of transient covert attention, spatial frequency, eccentricity, task and set size. Spat Vis 15: 61–75, 2001. doi: 10.1163/15685680152692015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carrasco M, Williams PE, Yeshurun Y. Covert attention increases spatial resolution with or without masks: support for signal enhancement. J Vis 2: 467–479, 2002. doi: 10.1167/2.6.4. [DOI] [PubMed] [Google Scholar]
- Cleland BG, Harding TH, Tulunay-Keesey U. Visual resolution and receptive field size: examination of two kinds of cat retinal ganglion cell. Science 205: 1015–1017, 1979. doi: 10.1126/science.472720. [DOI] [PubMed] [Google Scholar]
- Cohen MS. Parametric analysis of fMRI data using linear systems methods. Neuroimage 6: 93–103, 1997. doi: 10.1006/nimg.1997.0278. [DOI] [PubMed] [Google Scholar]
- De Valois RL, Albrecht DG, Thorell LG. Spatial frequency selectivity of cells in macaque visual cortex. Vision Res 22: 545–559, 1982. doi: 10.1016/0042-6989(82)90113-4. [DOI] [PubMed] [Google Scholar]
- D’Souza DV, Auer T, Frahm J, Strasburger H, Lee BB. Dependence of chromatic responses in V1 on visual field eccentricity and spatial frequency: an fMRI study. J Opt Soc Am A Opt Image Sci Vis 33: A53–A64, 2016. doi: 10.1364/JOSAA.33.000A53. [DOI] [PubMed] [Google Scholar]
- Dumoulin SO, Wandell BA. Population receptive field estimates in human visual cortex. Neuroimage 39: 647–660, 2008. doi: 10.1016/j.neuroimage.2007.09.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Enroth-Cugell C, Freeman AW. The receptive-field spatial structure of cat retinal Y cells. J Physiol 384: 49–79, 1987. doi: 10.1113/jphysiol.1987.sp016443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Everson RM, Prashanth AK, Gabbay M, Knight BW, Sirovich L, Kaplan E. Representation of spatial frequency and orientation in the visual cortex. Proc Natl Acad Sci USA 95: 8334–8338, 1998. doi: 10.1073/pnas.95.14.8334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farivar R, Clavagnier S, Hansen BC, Thompson B, Hess RF. Non-uniform phase sensitivity in spatial frequency maps of the human visual cortex. J Physiol 595: 1351–1363, 2017. doi: 10.1113/JP273206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foster KH, Gaska JP, Nagler M, Pollen DA. Spatial and temporal frequency selectivity of neurones in visual cortical areas V1 and V2 of the macaque monkey. J Physiol 365: 331–363, 1985. doi: 10.1113/jphysiol.1985.sp015776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freeman J, Simoncelli EP. Metamers of the ventral stream. Nat Neurosci 14: 1195–1201, 2011. doi: 10.1038/nn.2889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston KJ, Jezzard P, Turner R. Analysis of functional MRI time‐series. Hum Brain Mapp 1: 153–171, 1994. doi: 10.1002/hbm.460010207. [DOI] [Google Scholar]
- Glover GH. Deconvolution of impulse response in event-related BOLD fMRI. Neuroimage 9: 416–429, 1999. doi: 10.1006/nimg.1998.0419. [DOI] [PubMed] [Google Scholar]
- Greve DN, Fischl B. Accurate and robust brain image alignment using boundary-based registration. Neuroimage 48: 63–72, 2009. doi: 10.1016/j.neuroimage.2009.06.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansen KA, David SV, Gallant JL. Parametric reverse correlation reveals spatial linearity of retinotopic human V1 BOLD response. Neuroimage 23: 233–241, 2004. doi: 10.1016/j.neuroimage.2004.05.012. [DOI] [PubMed] [Google Scholar]
- Harvey BM, Dumoulin SO. The relationship between cortical magnification factor and population receptive field size in human visual cortex: constancies in cortical architecture. J Neurosci 31: 13604–13612, 2011. doi: 10.1523/JNEUROSCI.2572-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harvey BM, Klein BP, Petridou N, Dumoulin SO. Topographic representation of numerosity in the human parietal cortex. Science 341: 1123–1126, 2013. doi: 10.1126/science.1239052. [DOI] [PubMed] [Google Scholar]
- Henriksson L, Nurminen L, Hyvärinen A, Vanni S. Spatial frequency tuning in human retinotopic visual areas. J Vis 8: 5.1–13, 2008. doi: 10.1167/8.10.5. [DOI] [PubMed] [Google Scholar]
- Hess RF, Li X, Mansouri B, Thompson B, Hansen BC. Selectivity as well as sensitivity loss characterizes the cortical spatial frequency deficit in amblyopia. Hum Brain Mapp 30: 4054–4069, 2009. doi: 10.1002/hbm.20829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hurvich CM, Tsai CL. Regression and time series model selection in small samples. Biometrika 76: 297–307, 1989. doi: 10.1093/biomet/76.2.297. [DOI] [Google Scholar]
- Issa NP, Trepel C, Stryker MP. Spatial frequency maps in cat visual cortex. J Neurosci 20: 8504–8514, 2000. doi: 10.1523/JNEUROSCI.20-22-08504.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karim AK, Kojima H. The what and why of perceptual asymmetries in the visual domain. Adv Cogn Psychol 6: 103–115, 2010. doi: 10.2478/v10053-008-0080-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kay KN, Naselaris T, Prenger RJ, Gallant JL. Identifying natural images from human brain activity. Nature 452: 352–355, 2008. doi: 10.1038/nature06713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kay KN, Winawer J, Mezer A, Wandell BA. Compressive spatial summation in human visual cortex. J Neurophysiol 110: 481–494, 2013. doi: 10.1152/jn.00105.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keliris GA, Li Q, Papanikolaou A, Logothetis NK, Smirnakis SM. Estimating average single-neuron visual receptive field sizes by fMRI. Proc Natl Acad Sci USA 116: 6425–6434, 2019. doi: 10.1073/pnas.1809612116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kitterle FL, Hellige JB, Christman S. Visual hemispheric asymmetries depend on which spatial frequencies are task relevant. Brain Cogn 20: 308–314, 1992. doi: 10.1016/0278-2626(92)90023-F. [DOI] [PubMed] [Google Scholar]
- Kleiner M, Brainard D, Pelli D. What’s new in Psychtoolbox-3? Perception 36 (ECVP Abstract Supplement), 2007. [Google Scholar]
- Levine MW, McAnany JJ. The relative capabilities of the upper and lower visual hemifields. Vision Res 45: 2820–2830, 2005. doi: 10.1016/j.visres.2005.04.001. [DOI] [PubMed] [Google Scholar]
- Moeller S, Yacoub E, Olman CA, Auerbach E, Strupp J, Harel N, Uğurbil K. Multiband multislice GE-EPI at 7 tesla, with 16-fold acceleration using partial parallel imaging with application to high spatial and temporal whole-brain fMRI. Magn Reson Med 63: 1144–1153, 2010. doi: 10.1002/mrm.22361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Movshon JA, Thompson ID, Tolhurst DJ. Receptive field organization of complex cells in the cat’s striate cortex. J Physiol 283: 79–99, 1978a. doi: 10.1113/jphysiol.1978.sp012489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Movshon JA, Thompson ID, Tolhurst DJ. Spatial and temporal contrast sensitivity of neurones in areas 17 and 18 of the cat’s visual cortex. J Physiol 283: 101–120, 1978b. doi: 10.1113/jphysiol.1978.sp012490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nestares O, Heeger DJ. Robust multiresolution alignment of MRI brain volumes. Magn Reson Med 43: 705–715, 2000. doi:. [DOI] [PubMed] [Google Scholar]
- Pelli DG. The VideoToolbox software for visual psychophysics: transforming numbers into movies. Spat Vis 10: 437–442, 1997. doi: 10.1163/156856897X00366. [DOI] [PubMed] [Google Scholar]
- Peyrin C, Schwartz S, Seghier M, Michel C, Landis T, Vuilleumier P. Hemispheric specialization of human inferior temporal cortex during coarse-to-fine and fine-to-coarse analysis of natural visual scenes. Neuroimage 28: 464–473, 2005. doi: 10.1016/j.neuroimage.2005.06.006. [DOI] [PubMed] [Google Scholar]
- Rijsdijk JP, Kroon JN, van der Wildt GJ. Contrast sensitivity as a function of position on the retina. Vision Res 20: 235–241, 1980. doi: 10.1016/0042-6989(80)90108-X. [DOI] [PubMed] [Google Scholar]
- Sasaki Y, Hadjikhani N, Fischl B, Liu AK, Marrett S, Dale AM, Tootell RB. Local and global attention are mapped retinotopically in human occipital cortex. Proc Natl Acad Sci USA 98: 2077–2082, 2001. [Erratum in Proc Natl Acad Sci USA 99: 4752, 2002.] doi: 10.1073/pnas.98.4.2077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schira MM, Tyler CW, Spehar B, Breakspear M. Modeling magnification and anisotropy in the primate foveal confluence. PLOS Comput Biol 6: e1000651, 2010. doi: 10.1371/journal.pcbi.1000651. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schira MM, Wade AR, Tyler CW. Two-dimensional mapping of the central and parafoveal visual field to human visual cortex. J Neurophysiol 97: 4284–4295, 2007. doi: 10.1152/jn.00972.2006. [DOI] [PubMed] [Google Scholar]
- Schwartz EL. Spatial mapping in the primate sensory projection: analytic structure and relevance to perception. Biol Cybern 25: 181–194, 1977. doi: 10.1007/BF01885636. [DOI] [PubMed] [Google Scholar]
- Silva MF, Brascamp JW, Ferreira S, Castelo-Branco M, Dumoulin SO, Harvey BM. Radial asymmetries in population receptive field size and cortical magnification factor in early visual cortex. Neuroimage 167: 41–52, 2018. doi: 10.1016/j.neuroimage.2017.11.021. [DOI] [PubMed] [Google Scholar]
- Silva MF, Maia-Lopes S, Mateus C, Guerreiro M, Sampaio J, Faria P, Castelo-Branco M. Retinal and cortical patterns of spatial anisotropy in contrast sensitivity tasks. Vision Res 48: 127–135, 2008. doi: 10.1016/j.visres.2007.10.018. [DOI] [PubMed] [Google Scholar]
- Singh KD, Smith AT, Greenlee MW. Spatiotemporal frequency and direction sensitivities of human visual areas measured using fMRI. Neuroimage 12: 550–564, 2000. doi: 10.1006/nimg.2000.0642. [DOI] [PubMed] [Google Scholar]
- Watanabe A, Mori T, Nagata S, Hiwatashi K. Spatial sine-wave responses of the human visual system. Vision Res 8: 1245–1263, 1968. doi: 10.1016/0042-6989(68)90031-X. [DOI] [PubMed] [Google Scholar]
- Welbourne LE, Morland AB, Wade AR. Population receptive field (pRF) measurements of chromatic responses in human visual cortex using fMRI. Neuroimage 167: 84–94, 2018. doi: 10.1016/j.neuroimage.2017.11.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson HR, McFarlane DK, Phillips GC. Spatial frequency tuning of orientation selective units estimated by oblique masking. Vision Res 23: 873–882, 1983. doi: 10.1016/0042-6989(83)90055-X. [DOI] [PubMed] [Google Scholar]
- Xu J, Moeller S, Auerbach EJ, Strupp J, Smith SM, Feinberg DA, Yacoub E, Uğurbil K. Evaluation of slice accelerations using multiband echo planar imaging at 3 T. Neuroimage 83: 991–1001, 2013. doi: 10.1016/j.neuroimage.2013.07.055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu X, Anderson TJ, Casagrande VA. How do functional maps in primary visual cortex vary with eccentricity? J Comp Neurol 501: 741–755, 2007. doi: 10.1002/cne.21277. [DOI] [PubMed] [Google Scholar]
- Yeo BT, Krienen FM, Sepulcre J, Sabuncu MR, Lashkari D, Hollinshead M, Roffman JL, Smoller JW, Zöllei L, Polimeni JR, Fischl B, Liu H, Buckner RL. The organization of the human cerebral cortex estimated by intrinsic functional connectivity. J Neurophysiol 106: 1125–1165, 2011. doi: 10.1152/jn.00338.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu HH, Verma R, Yang Y, Tibballs HA, Lui LL, Reser DH, Rosa MG. Spatial and temporal frequency tuning in striate cortex: functional uniformity and specializations related to receptive field eccentricity. Eur J Neurosci 31: 1043–1062, 2010. doi: 10.1111/j.1460-9568.2010.07118.x. [DOI] [PubMed] [Google Scholar]
- Zhou J, Benson NC, Kay KN, Winawer J. Compressive temporal summation in human visual cortex. J Neurosci 38: 691–709, 2018. doi: 10.1523/JNEUROSCI.1724-17.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]