Surface-Volume Consistent Construction of Longitudinal Atlases for the Early Developing Brain

Abstract

Infant brain atlases are essential for characterizing structural changes in the developing brain. Volumetric and cortical atlases are typically constructed independently, potentially causing discrepancies between tissue boundaries and cortical surfaces. In this paper, we present a method for surface-volume consistent construction of longitudinal brain atlases of infants from 2 weeks to 12 months of age. We first construct the 12-month atlas via groupwise surface-constrained volumetric registration. The longitudinal displacements of each subject with respect to different time points are then transported parallelly to the 12-month atlas space. The 12-month cortico-volumetric atlas is finally warped temporally to each month prior to the 12th month using the transported displacements. Experimental results indicate that the longitudinal atlases generated are consistent in terms of tissue boundaries and cortical surfaces, hence allowing joint surface-volume analysis to be performed in a common space.

1. Introduction

A brain atlas is an anatomical representation of the brain, encapsulating population-wise brain features. Infant atlases are constructed to capture normative growth trajectories that are essential for understanding brain maturation during infancy and for early diagnosis of neurodevelopmental abnormalities [6]. Volumetric atlases facilitate the analysis of cortical and subcortical structures whereas cortical atlases provide additional information for studying cortical attributes, such as thickness, curvature, and convexity, as well as cortico-cortical connectivity [8,13,15].

Existing research focuses on constructing either volumetric or cortical atlases. For instance, Serag et al. [11] constructed spatio-temporal volumetric brain atlases of infants scanned between 28 and 44 weeks of age. Shi et al. [12] constructed a volumetric neonatal atlas using unbiased group-wise registration and patch-based sparse representation. Zhang et al. [17] constructed a volumetric neonatal brain atlas by combining spatial and frequency information using patch-based sparse representation. Bozek et al. [2] constructed neonatal cortical surface atlases for nine time points between 36–44 weeks of age. Multimodal surface matching [10] was used to align the features on the cortical surface and then temporal adaptive kernel regression was employed to generate the atlases. Li et al. [7] constructed infant cortical surface atlases for seven time points between 1- and 24-months of age using longitudinally consistent and unbiased group-wise registration.

Volumetric and cortical atlases are typically constructed independently, causing the following problems: (i) Misalignment of tissue boundaries in the volumetric atlas, and the pial and white matter surfaces of the cortical atlas. (ii) Blurred cortical structures in the volumetric atlas due to not using the geometry of the cortical surfaces in guiding registration. (iii) Cortical surface registration disregarding the image volume results in deformations that will unrealistically deform the brain. (iv) The volumetric and surface atlases do not reside in the same space, complicating concurrent analysis of the two entities. (v) Alignment inconsistency and inaccuracy can diminish the detectability of true but subtle longitudinal changes.

To overcome these problems, we present in this paper a method to construct longitudinal surface-volume consistent atlases for infants from 2 weeks to 12 months of age. We construct the cortical and volumetric atlases simultaneously, such that the boundaries of white matter (WM), gray matter (GM), and cerebrospinal fluid (CSF) are consistently aligned, in both volumetric and surface spaces. This allows surface and volumetric analyses to be conducted consistently in a single atlas space.

2. Methods

Our surface-volume consistent atlas construction method consists of two steps (see Fig. 1) (i) Construct the cortico-volumetric atlas at the 12-month time point; and (ii) Construct longitudinal month-specific cortico-volumetric atlases prior to the 12th month via parallel transport of displacement fields.

Fig. 1.

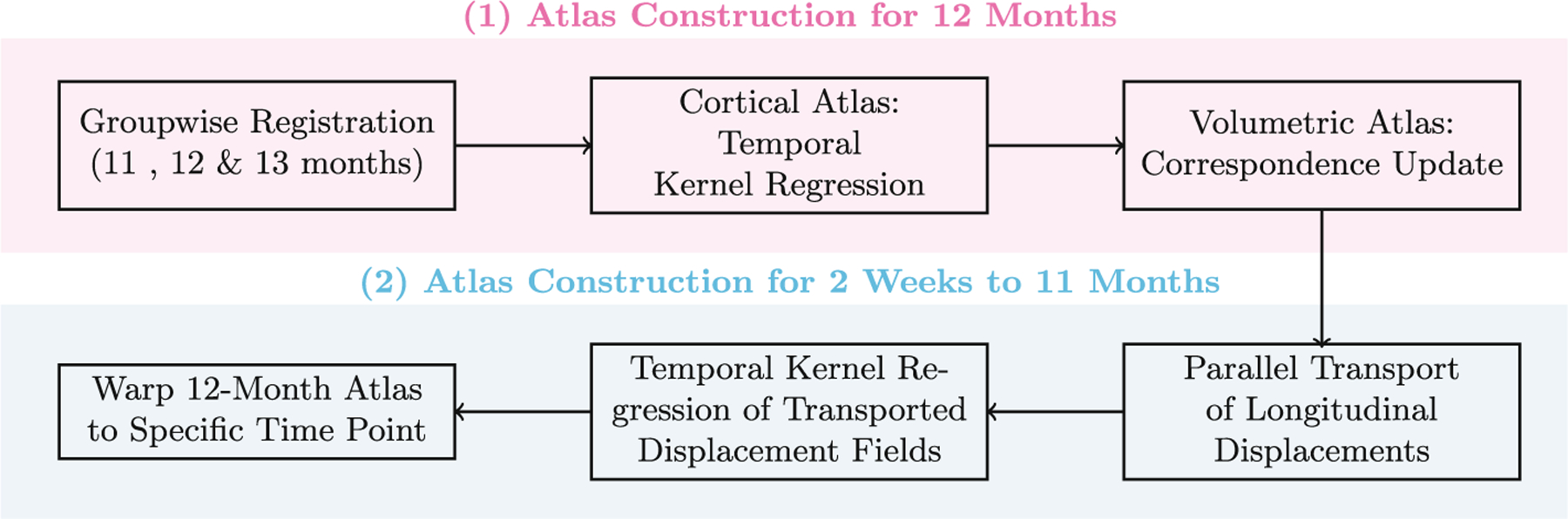
Construction of cortico-volumetric atlases.

2.1. Construction of 12-Month Atlas

Groupwise Surface-Constrained Volumetric Registration –

We first construct the 12-month atlas via group-wise registration using subjects scanned at either 11, 12 or 13 months of age. Group-wise registration simultaneously registers all the images to a hidden common space by (i) selecting as reference the image with the minimum dissimilarity to the other images and (ii) iteratively updating the reference by averaging all the images registered to it. The registration of infant brain MR images is challenging owing to the dramatic contrast changes during the first year of life. To overcome this problem, we propose to register the segmented tissue maps instead of the intensity images. We use a surface-constrained dynamic elasticity model (SCDEM) [1] as the underlying transformation model for cross-sectional group-wise registration. The SCDEM registration algorithm determines the volumetric displacement field ϕ that matches a pair of images, constrained by the surface displacement field ψ computed as vertex-wise displacements between cortical surfaces given by Spherical Demons [16]. The volumetric displacement field is estimated using the following hyperbolic wave equation:

$$\alpha {\nabla }^2\varphi (x)+\alpha \nabla (\nabla \cdot \varphi (x))+\beta f^{\text{v}}(x)+\gamma f^{\text{s}}(x)=\frac{{\partial }^2\varphi (x)}{\partial t^2},$$ (1)

where the volumetric force field f^v measures the discrepancies between the warped and reference segmented tissue maps. The surface force field f^s is computed as the error between the surface displacement field estimated by ϕ and the pre-computed surface displacement field ψ. α, β, and γ are parameters that control the smoothness of the displacement field, and the contributions of f^v and f^s, respectively. The two force fields recede gradually and eventually balance the smoothness terms in (1), causing the displacement field to converge. Once the dataset has been registered in a group-wise manner, the aligned cortical surfaces and segmented tissue maps are subsequently used to compute the 12-month cortico-volumetric atlas.

Construction of Cortical Atlas –

The cortical surface atlas at the 12th month (366 days) is constructed via temporal kernel regression. Let {S_i|i = 1, …, N} be the cortical surface (left/right, white matter/pial) of the i-th subject scanned at t_i days. Let ${\widehat{S}}_i$ be the corresponding cortical surface registered as described in the previous step. The cortical surface atlas $A_{12}^{\text{s}}$ is obtained by weighted averaging of the vertex coordinates:

$$A_{12}^{\text{s}}=\frac{{\sum }_{i=1}^N{w}_i{\widehat{S}}_i}{{\sum }_{i=1}^N{w}_i}\text{ with }{w}_i=\frac{1}{\sigma \sqrt{2\pi }}\text{exp}\left(\frac{-{\left(t_i-366\right)}^2}{2{\sigma }^2}\right),$$ (2)

where σ² = 15.25 days. The constructed cortical surface atlas will be used to guide the construction of the volumetric atlas.

Construction of Volumetric Atlas –

The volumetric atlas $A_{12}^{\text{v}}$ at the 12th month is constructed by correcting the alignment of the segmented tissue maps based on the cortical atlas $A_{12}^{\text{s}}$. The correspondences are updated by first computing the vertex-wise surface displacement field between ${\widehat{S}}_i$ and $A_{12}^{\text{s}}$, i.e., Δψ, and then extrapolating it over the volumetric space. More specifically, this is carried out by generating the cortical surface mesh using Delaunay triangulation and then, for each voxel location x, finding the mesh triangle, with vertices {y_j|j = 1, …, 3}, that contains the voxel. The corrective volumetric displacement field Δϕ(x) is computed from the surface transformation Δψ using Gaussian interpolation:

$$\Delta \varphi (x)=\frac{{\sum }_{j=1}^3{w}_j\Delta \psi \left(y_j\right)}{{\sum }_{j=1}^3{w}_j}\text{ with }{w}_j=\frac{1}{{\sigma }_g\sqrt{2\pi }}\text{exp}\left(\frac{-{\Vert x-y_j\Vert }^2}{2{\sigma }_g^2}\right),$$ (3)

where ${\sigma }_g^2=9$ is set to ensure that the displacement at the tissue interfaces is smooth. This correspondence update step ensures that the segmented tissue maps are well-aligned with the cortical atlas. After warping each segmented tissue map with its respective final displacement field ϕ + Δϕ, the volumetric atlas is computed via majority-voting fusion. The atlases at other time points are constructed based on $A_{12}^{\text{v}}$ and $A_{12}^{\text{s}}$.

2.2. Construction of Longitudinal Atlases

Age-dependent cortico-volumetric atlases prior to the 12th month are constructed by determining the longitudinal change of each subject with respect to either 11-, 12- or 13-month scan of the subject (see Fig. 2) and then transporting this change to the 12-month atlas space. The within-subject longitudinal changes are represented by longitudinal displacement fields estimated via SCDEM intra-subject registration.

Fig. 2.

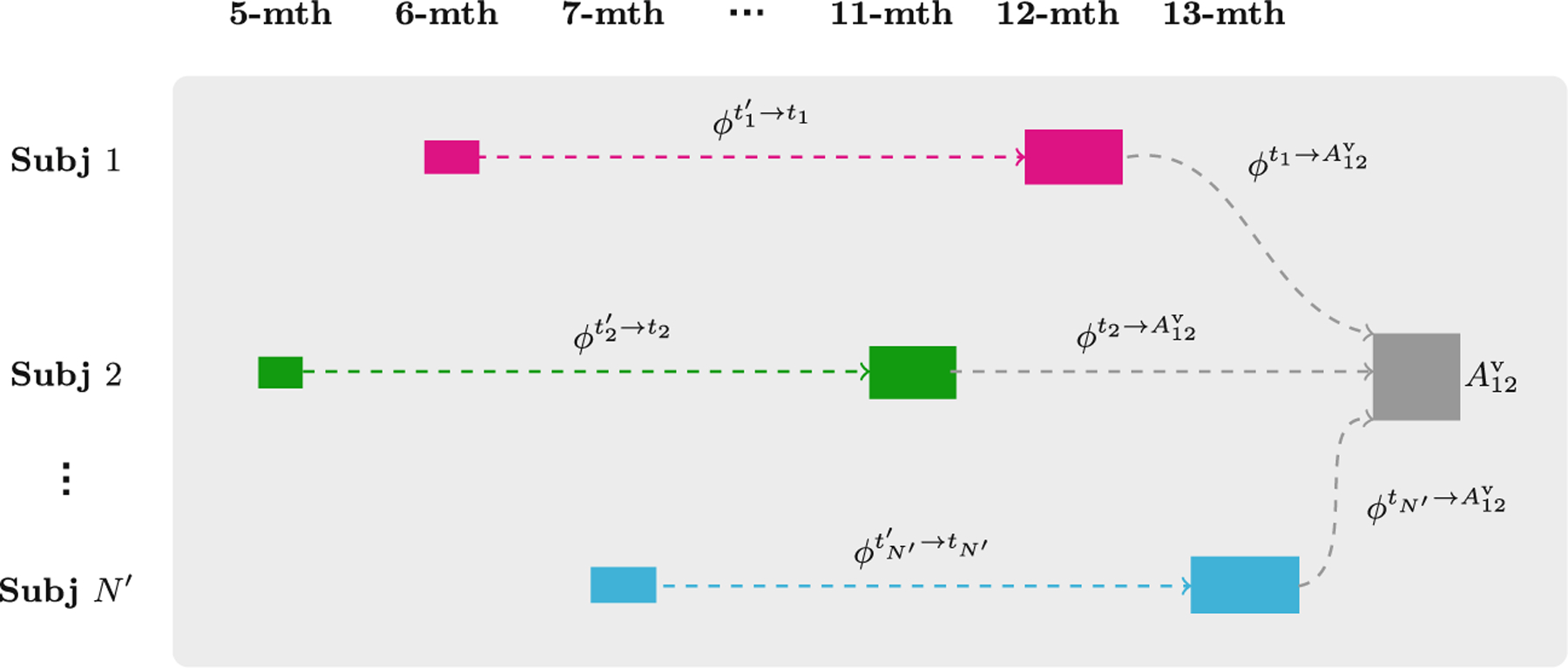
Longitudinal and cross-sectional displacements used to construct the 6-month atlas via parallel transport

Parallel Transport of Longitudinal Displacements –

Each longitudinal displacement field encodes the within-subject growth from an earlier time $t_i^{\prime }$ to time t_i. To characterize growth without the confound of inter-subject variability, the longitudinal displacement fields of each subject are normalized by parallel transport to the common space defined by the 12-month atlas ($A_{12}^{\text{v}}$). The 12-month atlas is warped by the inverse of the averaged transported displacement fields to construct the atlas at each time point. Figure 2 shows the longitudinal displacement fields ${\varphi }^{t_i^{\prime }\to t_i}$ and the cross-sectional displacement field ${\varphi }^{t_i\to A_{12}^{\text{v}}}$ of the i-th subject. Parallel transport is implemented by reorienting the displacement vectors [5,9] using the Jacobian matrix of cross-sectional deformation field ${\Phi }^{t_i\to A_{12}^{\text{v}}}=x+{\varphi }^{t_i\to A_{12}^{\text{v}}}$, which is computed as $J_i=D{\Phi }^{t_i\to A_{12}^{\text{v}2}}$. The transported longitudinal displacement field is given as $J_i{\varphi }^{t_i^{\prime }\to t_i}$.

Temporal Kernel Regression of Transported Displacements –

The displacement field from time t to the 12th month time point, ${\phi }^{t\to A_{12}^{\text{v}}}$, is generated via weight averaging of the transported longitudinal displacement fields:

$${\phi }^{t\to A_{12}^{\text{v}}}=\frac{{\sum }_{i=1}^{N^{\prime }}{w}_i^{\prime }{w}_i{J}_i{\varphi }^{t_i^{\prime }\to t_i}}{{\sum }_{i=1}^{N^{\prime }}{w}_i^{\prime }{w}_i},$$ (4)

where N′ is the total number of subjects used to construct the month-specific atlases and,

$$w_i^{\prime }=\frac{1}{\sigma \sqrt{2\pi }}\text{exp}\left(\frac{-{\left(t_i^{\prime }-t\right)}^2}{2{\sigma }^2}\right),w_i=\frac{1}{\sigma \sqrt{2\pi }}\text{exp}\left(\frac{-{\left(t_i-366\right)}^2}{2{\sigma }^2}\right).$$ (5)

The inverse of the computed displacement field ${\phi }^{t\to A_{12}^{\text{v}}}$ is used to warp the 12-month cortico-volumetric atlas to time t.

3. Results

The dataset consisted of T1- and T2-weighted images of 29 infant subjects enrolled as part of the UNC/UMN baby connectome project (BCP). The subjects were divided into three cohorts according to their first scheduled visits: 2 weeks, 1 month and 2 months. These subjects were scanned every three months, using a 3T Siemens Prisma MRI scanner with 320 × 320 × 208 voxels and 0.8 mm³ resolution. The images were segmented into WM, GM, and CSF and the cortical surfaces were reconstructed. 34 cortical ROIs were also delineated for evaluation, by first parcellating the cortical surfaces using FreeSurfer [3] and then labeling each voxel in the GM cortical ribbon according to the cortical surface vertex nearest to the voxel.

We compared our results with those generated using diffeomorphic demons [14] (i.e., the baseline method) instead of SCDEM registration. Figure 4 shows the results in terms of consistency between the cortical surfaces and volumetric atlases for all thirteen time points. These results indicate that the cortico-volumetric atlases constructed by our method are more consistent than the baseline method. The baseline method shows greater discrepancies at the gray-white matter interface, which is more convoluted than the pial surface. From Fig. 4, it is evident that the atlases constructed by the proposed method preserve more cortical details. Figure 3 shows the quantitative results in terms of Dice ratio over different tissue types and cortical ROIs, and a modified Hausdorff distance [4] for surfaces. These metrics were computed between the 11-, 12- and 13-month registered volumes and surfaces, and the 12-month atlases constructed by the two methods. The improvements given by the proposed method, quantified using these metrics, are statistically significant (p < 0.01).

Fig. 4.

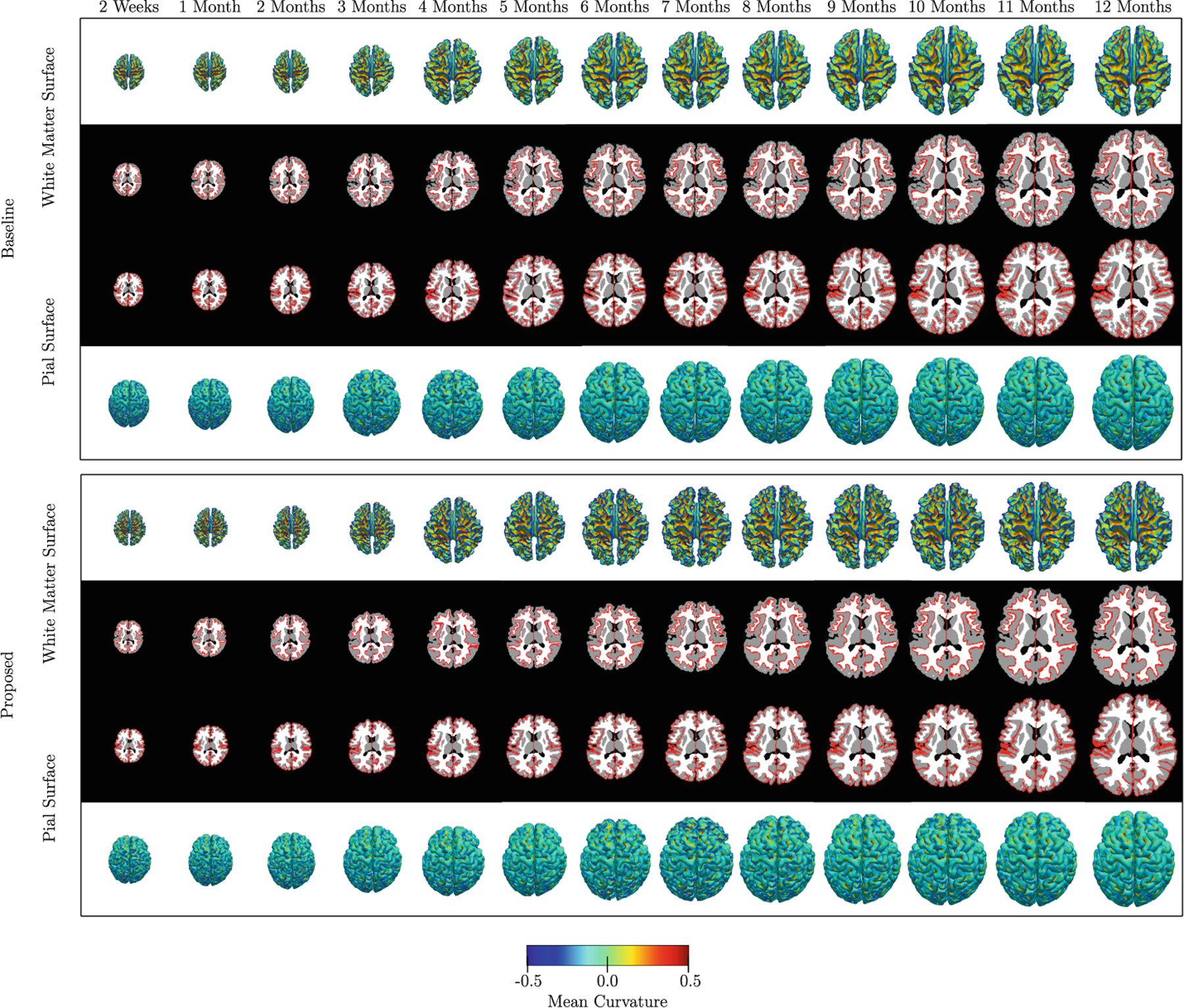
Cortical surface atlases overlaid onto the volumetric atlases constructed by the proposed and baseline methods

Fig. 3.

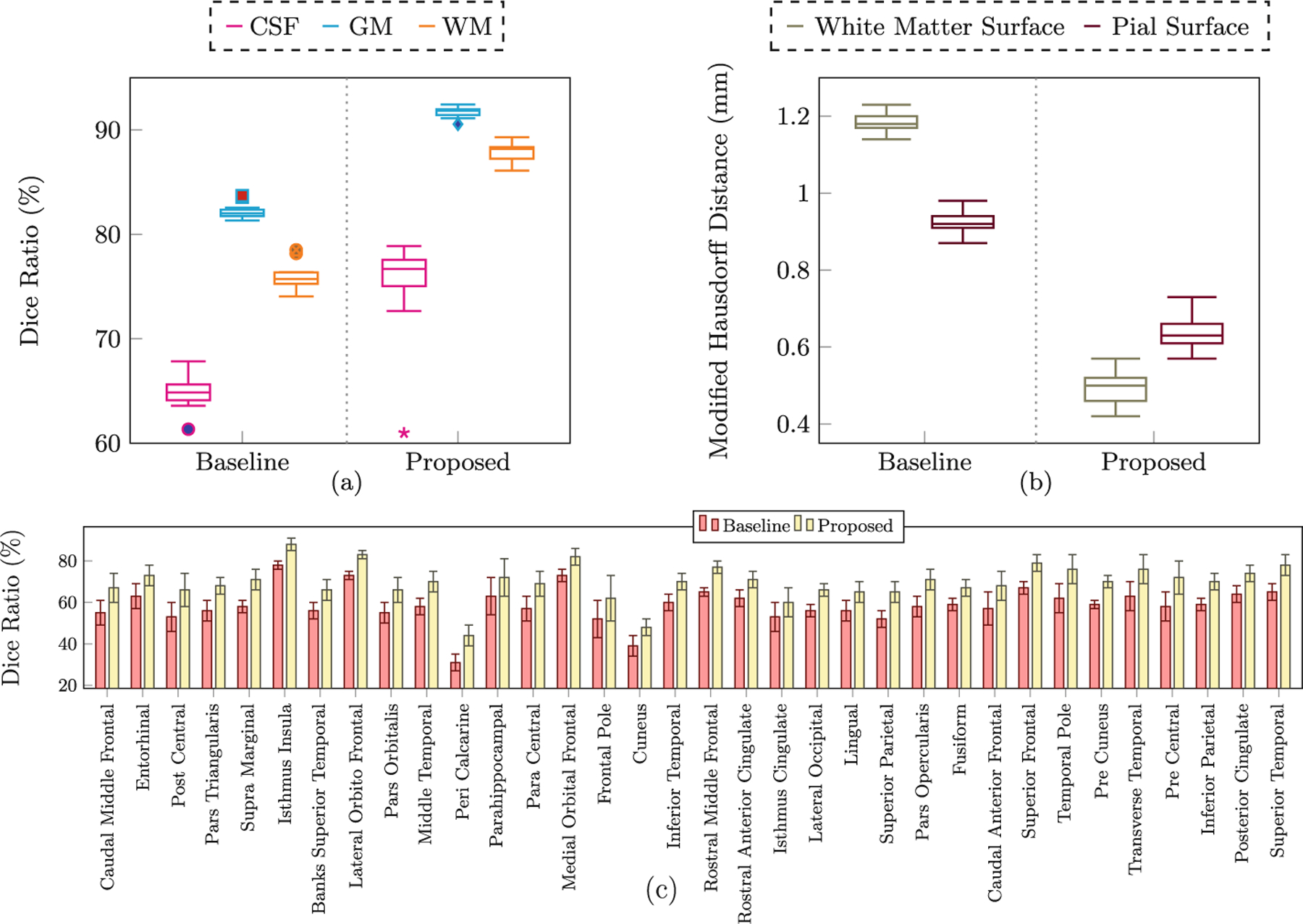
(a) Dice ratios for different tissue types. (b) Modified Hausdorff distance (mm) for the cortical surfaces. (c) Dice ratios for cortical ROIs. All results are statistically significant (p < 0.01, paired t-test)

4. Conclusion

In this paper, we proposed a novel method for consistent construction of cortico-volumetric atlases for the infant brain. The results show that the cortical surface and volumetric atlases constructed by our method are consistent and preserve more anatomical details.