Managing treatment-related uncertainties in proton beam radiotherapy for gastrointestinal cancers

Abstract

In recent years, there has been rapid adaption of proton beam radiotherapy (RT) for treatment of various malignancies in the gastrointestinal (GI) tract, with increasing number of institutions implementing intensity modulated proton therapy (IMPT). We review the progress and existing literature regarding the technical aspects of RT planning for IMPT, and the existing tools that can help with the management of uncertainties which may impact the daily delivery of proton therapy. We provide an in-depth discussion regarding range uncertainties, dose calculations, image guidance requirements, organ and body cavity filling consideration, implanted devices and hardware, use of fiducials, breathing motion evaluations and both active and passive motion management methods, interplay effect, general IMPT treatment planning considerations including robustness plan evaluation and optimization, and finally plan monitoring and adaptation. These advances have improved confidence in delivery of IMPT for patients with GI malignancies under various scenarios.

General introduction and scope

Use of proton therapy in the management of gastrointestinal (GI) malignancies has become increasingly common in the past 10 to 15 years. The clinical rationale for using proton therapy has been covered in separate articles in this special JGO issue and will not be reiterated here. Reported benefits of proton therapy in this patient population are mainly related to its ability to spare healthy organs from unnecessarily excessive radiation when compared to X-ray therapy; of particular relevance are the healthy organs in the vicinity, which are prone to acute (short-term) and late (long-term) radiation side effects. In this review article, we will discuss a number of technical aspects in the planning and management of uncertainties that impact the daily application of proton therapy for GI cancers. It should be noted that most of the topics addressed are broadly applicable to other anatomic sites being managed with proton or heavy charged particle therapy.

At the time of this writing, the proton therapy community is experiencing a transition towards a more sophisticated RT delivery technology, namely intensity modulated proton therapy (IMPT), while moving away from passively scattered proton therapy (PSPT). IMPT has distinct advantages over PSPT, in particular the capability of creating conformal dose distributions both proximally and distally along the beam path from the prescribed target volumes. However, IMPT suffers from increased delivery complexity, thereby increasing the set of uncertainties that can impact plan quality; most notably “breathing motion management” becomes a more important aspect of IMPT compared to PSPT. For these reasons, this report will largely focus on proton therapy uncertainties with IMPT.

Introduction to uncertainties in proton therapy for GI cancers

Range uncertainty and the importance of Monte-Carlo dose calculations

Uncertainty in proton range (i.e., uncertainty in the depth in material or tissue where protons of a given energy will effectively come to rest) remains one of the significant uncertainties affecting all sites of disease and proton therapy delivery modalities. Range uncertainty stems, in part, from the fact that computed tomography (CT) scans are used to define the patient representation for treatment planning, i.e., the 3D geometry identifying the tumor and neighboring critical structures enabling 3D dose calculation. CT images are voxelized (or gridded) samples of Hounsfield Unit (HU), which is directly related to the X-ray linear attention coefficient of a given material, and derived directly from first principles of X-ray attenuation physics as part of CT image reconstruction algorithms. However, this quantity (HU) has a non-linear and potentially degenerate relationship with proton relative stopping power (RSP, relative to water) in the context of various material types and tissues relevant for proton dosimetry. The “stoichiometric method” (1) is the adopted standard in CT HU-to-RSP calibration and is used to reduce overall systematic HU-to-RSP uncertainties. It has been shown that use of dual energy CT (CT scanners performing two simultaneous or serial scans with different X-ray energy spectra) as part of the HU-RSP calibration process can reduce RSP uncertainties (2,3), however, these methods have not seen widespread adoption.

Deficiency in dose calculation accuracy can also manifest as inaccuracy in predicted proton beam range. Monte Carlo (MC) dose calculation algorithms, which involve step-wise and event-by-event calculation of energy and dose deposition from first-principle descriptions of particle and photon interactions, are considered the gold standard in dose calculation accuracy. Historically, non-MC, so-called analytical dose calculation approaches, have been adopted by the community due to practical advantages of reduced computational speed and improved practice efficiency. These approaches assume that the experimental observations made when proton beams impinge on water can be effectively scaled by RSP. Such an approach struggles from deficiencies in the context of tissue/material heterogeneities, partly due to improper modeling of proton scattering (4,5). Improvements in hardware and computing technology have yielded faster MC calculations now feasible for routine clinical use (6,7).

Historically, proton centers have adopted a range uncertainty planning margin of approximately 3.5% + 1 mm expansion along the beam direction (8). Schuemann et al. showed that this margin may be too generous in the context of the liver, as there is less tissue heterogeneity compared with other sites involving more bone-tissue, bone-air, or tissue-lung interfaces. For lung tumors, the range uncertainty margin may need to be 6.3% + 1.2 mm unless MC dose calculation is employed, which improves uncertainty margin to 2.4% + 1.2 mm (5). Treatment of esophagus near the GE junction invariably involves lung-tissue interfaces; as such one can anticipate an increase in the required range uncertainty margin.

Targeting uncertainty; image guidance in proton therapy

Modern radiotherapy is typically delivered using daily image guidance (IGRT). IGRT aims to reduce overall tumor targeting uncertainty. Proton therapy suffers insofar as its IGRT technologies are not as mature compared with X-ray therapy (9). This is likely rooted in proton therapy being a relatively small niche in the broader community, with a different set of active vendors not having the same technologic experience and foundation in image-guidance technology—in particular, concerning software and workflow. The implication is that the IGRT decision-making process may not be optimally efficient, leading indirectly to targeting inaccuracies.

For both proton and X-ray therapies, a geometric margin is typically used to accommodate daily variation in tumor/target position as related to initial positioning error and intrinsic target motion, or other changes which may occur during the daily radiation treatment. IGRT tends to greatly reduce the former (initial positioning) but does not necessarily address the latter (motion during treatment). In X-ray therapy, these sources of targeting “setup error” are accommodated using a planning target volume (PTV) which is derived from a 3D geometric expansion of the clinical target volume (CTV); this PTV is used for all treatment fields. However, in proton therapy, because of the combined uncertainties of both patient/tumor positioning and proton range, construction of a beam-specific PTV is more appropriate—whether this is done a priori, or indirectly via the process of “robust optimization” (to be discussed below).

Organ filling or variation

Accuracy of the proton range prediction is directly related to changes in water-equivalent “thickness” (WET) along the beam path. Such extreme WET sensitivity is absent in the context of X-ray RT. Therefore, for GI sites being managed with proton therapy, changes in stomach, small bowel and large bowel filling (with food, liquid, stool, air or gas) pose unique challenges; these challenges are not addressed with use of daily IGRT but, rather, must be addressed with a combination of robust treatment planning techniques and, potentially, more restrictive dietary instructions for the patient, such as meal timing.

Devices and hardware

Stents

GI or biliary tract stents are commonly used in management of patients with GI malignancies. Non-metallic stents typically pose less of a concern for proton treatment planning due to their relatively small size and their construction from water-like (e.g., plastic) wall material, which typically includes a dopant to provide radiographic contrast. On the other hand, metallic stents such as self-expanding metallic stents (SEMS) require additional consideration due to their high-Z elemental composition. MC dose calculation is theoretically advantageous due to proper handling of the physics of proton interactions in these materials. However, this advantage is deteriorated by a severe practical limitation on accurate SEM modeling in the context of routine CT “simulation” scanning for treatment planning, which does not provide adequate spatial resolution and is subject to streaking and photon starvation artifacts caused by the metal.

Experimental measurement is arguably the best method to evaluate the potential impact of SEMS on proton plan quality. Dose perturbations caused by SEMS for X-ray therapy have been experimentally evaluated for simple single-field treatment plan geometries; dose perturbations range from 0–15%, with effects being more significant proximally due to electron backscatter (10,11). Figure 1 shows planar proton dose perturbations caused by SEMS using a “worst-case” proton radiographic technique [re-analyzed dataset from (12)]. Dose perturbations ranging from very minimal to approximately 30% were observed, depending on the wire mesh-density and gauge, and measurement depth behind the stent. Such dose perturbations are likely moderated by realistic “spread-out Bragg peak” (SOBP) beams (13); use of two or more proton beams would tend to further mitigate the problem since existing hot or cold spots from a single beam direction would tend to be dampened when irradiating from multiple directions.

Figure 1.

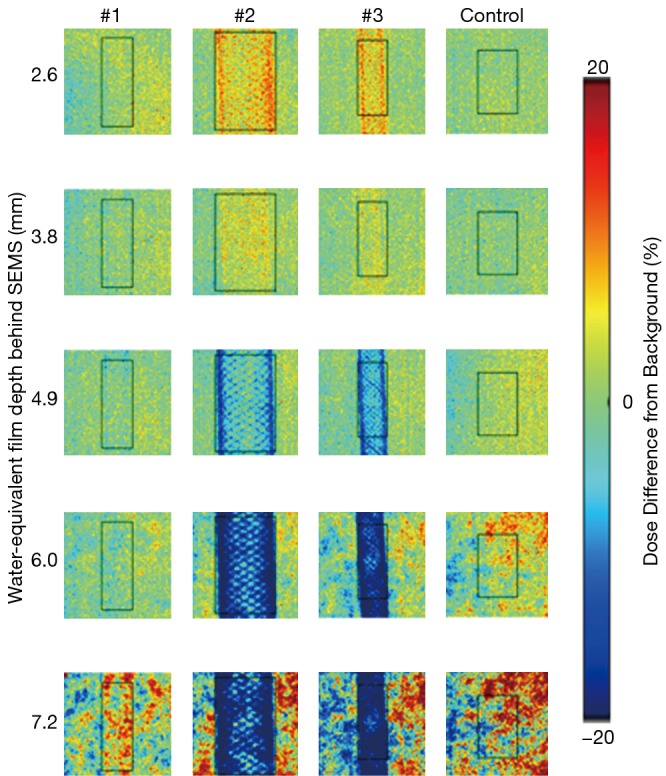
Dose perturbations (dose differences) at depths along a single-energy proton Bragg peak (in % of nominal) caused by self-expanding metallic stent (SEM) placed immediately upstream of the Bragg peak location. The given depths (mm) are measured behind the SEM location. A uniform proton fluence (generated from an IMPT spot pattern) irradiated the SEMs with a single proton energy (119.7 MeV). Gafchromic EBT3 films (Ashland Global Holdings, Inc., Covington KY, USA) were used to measure planar doses. Numbered samples correspond to [1: Flexxus (CONMED, Utica, NY, USA) biliary; 2: Wallflex (Boston Scientific, Marlborough, MA, USA) luminal; 3: Evolution (Cook Medical, Bloomington, IN, USA) biliary; Control: no SEM].

Fiducials

In some GI malignancies, (most commonly pancreas and liver) fiducial markers or other implanted surgical clips are commonly used as radiographic contrast objects to be referenced in CT-based treatment planning and IGRT. Similar to SEMS, fiducials and clips are metallic and small in size, limiting ability to predict their dosimetric impact in “routine” MC-based treatment planning. However, their construction (typically cylindrical) tends to be amenable to specialized modeling and MC-based proton dose calculation; such calculations can help in evaluating differences between different fiducial sizes, geometries, and compositions (14). Similar to the SEMS context, experimental measurement can again provide practical information; this information is simpler to obtain and is potentially less error prone.

Gold cylinders with diameters of approximately 1 mm and lengths between 3–5 mm have typically been used for fiducial markers. Such high-Z markers provide excellent radiographic contrast for imaging but may cause dose perturbations for proton therapy. Fiducials made from lower-Z materials such as titanium, or composite materials such carbon-coated zirconium dioxide, may provide more acceptable proton dosimetry (14-17). The magnitude of proton dose perturbations from gold fiducials can be reduced by decreasing fiducial diameters and lengths (15,17), or by using a thin-wire coil (or “helical”) design (16), at the potential expense of radiographic visibility. Wire gauge used in helical fiducials has direct bearing on proton dose perturbations, which can be significant (18). Notably, biodegradable liquid fiducial markers have recently been introduced; such material could be advantageous considering proton dosimetry (19).

Breathing motion, 4D-CT and the interplay effect

For most GI sites being managed with proton therapy, normal (free-breathing) tumor motion amplitude and variation can be significant. This motion must be evaluated at time of CT simulation and accommodated during treatment planning. Respiration-correlated CT (20), commonly known as “4D-CT,” has become the de facto gold standard for motion evaluation and treatment planning in the context of mobile tumors. 4D-CT is typically rendered as 10 individual 3D CT volumes each representing 1/10 of the breathing cycle. It is generated by measuring a motion surrogate synchronized with the CT scanner during acquisition of an oversampled set of CT projections. Retrospectively, these reconstructed CT projections can be assigned to a “phase” of breathing based on the respiratory surrogate.

Typical tumor motion in the esophagus, pancreas, and liver can range from 3 to 20 mm; in most scenarios, the primary motion axis is along the superior-inferior direction (21-27). For IMPT, such motion will generally require some form of breathing “motion management.” IMPT involves fast scanning of a “pristine” (i.e., not scattered) proton beam of given energy transversely over an area covering the tumor. The 3D dose distribution is accumulated by scanning the tumor with multiple proton beam energies (“energy layers”). Beam spot scanning is achieved using two dipole-bending magnets in respective X and Y directions. Depending on the control system, the scanning can happen either continuously wherein the beam does not turn off, or discretely wherein the beam is turned off between two neighboring spot positions (with the latter being more common in clinical practice). Once scanning for the given energy is completed, the proton accelerator changes energy, requiring a short pause in beam delivery. The time scale of this per-layer spot scanning delivery process is typically within one order of magnitude of patients’ typical breathing periods, as energy switching may take from approximately ¹/₁₀ second to several seconds. Thus, in general, proton “spots” comprising the treatment plan tend to be distributed unevenly across portions of the breathing cycle, resulting in anatomic regions of proton spot pile-up and, conversely, regions of spot under-coverage. Hence, patterns of constructive and destructive dose interference, termed motion “interplay” effects, arise when considering the total 3D dose distribution from each treatment field to the mobile target. These dose perturbations can be severe if not managed (28-30) and represent a significant source of potential uncertainty for GI cancers treated with IMPT. Of note, interplay effects can also result from motion of contextual anatomy, i.e., of periodicity associated with breathing-motion-induced proton range fluctuations (31), even when the tumor remains in a fixed position.

Management of uncertainties in proton therapy for GI cancers

Motion management considerations

Motion management for mobile tumors is a requirement for IMPT to reduce dosimetric plan degradation. With X-ray therapy, motion management has been used to reduce motion amplitude, thereby reducing the size of the target volume, with a commensurate reduction in healthy tissue being irradiated. Depending on the strategy deployed, motion management with IMPT may both maintain dosimetric plan quality as well as reduce radiation volumes. It should be noted that the situation with PSPT is analogous to X-ray therapy, since proton position and energy scanning are happening quasi-simultaneously by way of a fast range modulator wheel to spread out the energy distribution followed by a beam scattering element enlarging the beam. Thus, PSPT results in an equal distribution of proton spot locations and energies over the breathing cycle, eliminating interplay-effect concerns.

Active motion management

Herein “active” motion management is defined as that requiring a patient’s action, or that involving actions performed on the patient, although this terminology may have previously included actions by the delivery control system. Active motion management commonly includes breath holding (BH) and the use of abdominal compression (AC), both of which have been shown to be effective for reducing breathing motion in GI cancers (32-35). BH requires patient compliance and results in decreased delivery efficiency (36).

Passive motion management

Alternatively, passive” motion management is defined as that involving no actions done by or on patients. Passive motion management strategies increase treatment time due to either beam pausing or delivery redundancy, or both (36). The most common passive management strategy in clinical IMPT practice currently is “rescanning” (also known as “repainting”) which involves delivery redundancy. The ideal goal of rescanning is to evenly distribute proton spots across the breathing cycle. However, such a goal is neither tenable from a delivery time standpoint, nor from the standpoint of the delivery control system, since IMPT systems typically have a limitation on a minimum deliverable number of protons per spot location.

Working under the practical constraints of the IMPT delivery system and considerations for reasonable treatment delivery time, numerous clinical rescanning implementations exist which can be categorized as either “volumetric” (3D) or “layered” (2D) (29). The latter can be further subdivided into “scaled” or “isolayered” rescanning (37). Volumetric rescanning involves subdividing the set of spots in the treatment field into N sub-fields, delivered sequentially, where N has a practical limitation given by the minimum deliverable MU for any spot location. Scaled rescanning is a layer-wise analogy of this concept, wherein each energy layer (l) of a treatment field is delivered N_l times, where N_l can potentially vary per layer owing again to the minimum MU constraint. Isolayered rescanning is achieved by setting some maximum allowable MU per spot location (36-41). This scenario is different from the previous methods since it results in spots being rescanned with variable frequency, with the highest weighted spots being rescanned more often.

Another passive motion management strategy for IMPT is respiratory gating (36,42). Ideally identical to 4D-CT acquisition, a respiratory surrogate is monitored during treatment; the beam is subsequently activated during prescribed portions of the normal breathing cycle. Typically, the goal is to treat during the latent portion of breathing near end-expiration, which is more consistent and reproducible than inspiration, resulting in significant reductions in breathing motion amplitude. Accordingly, the treatment plan must have been developed on a 4D-CT including the subset of respiratory phases applicable to the chosen treatment “duty cycle.” Gating is technically challenging to deploy with IMPT control systems because the beam on/off temporal latencies must be short, ideally on the order of tens to hundreds of milliseconds. The beam-on latency requirement is difficult because this implies that the particle accelerator must be able to hold charge in an extraction-ready state for 5–10 seconds to accommodate a typical patient’s breathing period.

Gating can be combined with rescanning to manage residual respiratory motion not sufficiently constrained by gating alone. However, the treatment time penalties associated with combined gating and rescanning can be significant (30,36,43).

CT simulation and motion management standard operating procedures (SOPs) for triaging

Breathing-motion-related uncertainties are best managed by establishing concise and relatively simple guidelines that can accommodate each potential disease site and motion scenario encountered at the time of CT simulation. Example questions to be addressed by such motion management SOPs include: What are the motion thresholds for consideration of each given motion management technique? Which patients and which disease sites are best suited for each given motion management technique? Gelover et al. show an example decision flow schematic that has been implemented clinically for IMPT for all disease sites exhibiting breathing motion (36).

General IMPT treatment planning considerations

The practice of GI radiation oncology is challenging because of the wide range of clinical knowledge that is required to cover multiple organ sites along the entire alimentary tract. Here we will introduce a number of general considerations for IMPT treatment planning, while keeping in mind that a universal solution may not exist across different organ sites and also different treatment platforms and clinical institutions.

Beam angle selection

With X-ray treatment planning, beam angle selection is mainly driven by avoidance of organs-at-risk (OAR) adjacent to the CTV. For proton therapy, the considerations for beam angle selection are more complex. Geometric OAR beam avoidance is still at play, with the caveat that OARs immediately distal to the target are at particular risk due to both range uncertainty and biologically-effective dose uncertainty. The latter concept is addressed in a separate review in this JGO series from Beltran et al. (44).Range uncertainty in the context of breathing motion is of particular consideration for beam angle selection. Numerous investigators have developed tools that incorporate 4D-CT images to derive WET variation (ΔWET) maps as a function of beam angle (35,45-47). These 2D maps can be distilled into a single parameter describing total or average variation. All other considerations aside, beam angles that result in minimal ΔWET should be selected to develop the most motion-robust plans. It must be noted that ΔWET being small does not imply that target motion has been implicitly managed. Examples include tumors in the pancreas or inferior aspect of the liver where ΔWET may be minimal while target motion amplitude may be large.

Hounsfield unit and materials/density overrides

As previously described, structures subject to variable filling with potentially different materials such as food, liquid/water, stool or gas/air, or medical-devices such as stents or fiducials, are routinely encountered in GI proton treatment planning. Planning systems have an important capability to “override” native CT-derived HU with user-supplied HU. The application of HU overrides in the context of MC dose calculation may often imply material and density specification also. HU overrides are supplied to the treatment planning system by way of contours (segmented 3D objects) with the goal of rendering a more-likely, hence more robust, scenario. This can be a highly subjective process; there are special considerations for plan evaluation in the context of HU overrides.

With respect to organ filling, the most frequent example is that of gas/air being present in the GI tract. Whereas the best solution might be to avoid treating through this region of uncertainty, there are situations where this option is undesirable, or, alternatively, where the gas bubble is distal or lateral to the targeted region. An HU override is supplied to the planning system for the drawn gas contour, where the HU value can be derived from a sampling of neighboring HU within the organ and outside of the gas pocket. Obtaining additional CT simulations for dosimetric verification and replanning (when necessary) can be considered and employed.

Plastic stents are often constructed of a doped material that provides relatively high HU. Because the stent walls are thin relative to the total proton beam range, a typical practice is to generously contour and then override the plastic stent wall as water-like material. Then, whether plastic or metal and potentially depending on the diameter of the stent, a decision can be made in terms of stent filling with water-like material or air.

Metallic objects (fiducials, SEMS, etc.) require careful scrutiny when considering HU overrides. The integrity of the CT scan is typically affected by reconstruction artifacts such as higher-HU streaking and lower-HU shadowing around the object. Also, the objects often appear larger due to these artifacts and partial volume averaging. HU overrides are often needed to remove the streaking artifacts; the decision whether to intervene usually is made on the basis of measurement tools that can determine WET along a given line segment (representative of a beam path). Contouring the objects themselves is typically challenging due to their small size and the resultant artifacts. Two features of modern CT scanners can be taken advantage of, namely, reconstruction with “extended HU” scales and iterative reconstruction techniques (48-50), allowing for improved accuracy in metal object identification and contouring as well as better CT image quality. Iterative CT reconstruction can potentially mitigate the need to address streaking artifacts with manually drawn contours and overrides.

Robust plan evaluation

Because of the added complexity of range uncertainty and sensitivity of protons to WET changes, “robust plan evaluation,” or, re-calculation of the plan under certain hypothetical error scenarios, has been widely adopted as standard-of-practice by the proton therapy community for all treatment sites. As a result, aspects of this methodology have been supported by commercial proton treatment planning systems.

3D robust plan evaluation

3D robust plan evaluation can be generalized as including all methods that involve recalculation of the dose distribution on a given 3D CT image. Most commonly, this refers to the recalculation of treatment plan on its nominal planning CT under the influence of position and range uncertainty (41,51). The former is achieved by moving the plan “isocenter(s),” or beam location(s), along the three Cartesian axes (x,y,z) by some positional offset ±δ mm appropriate for the given IGRT strategy and recalculating dose. In practice, this process is typically distilled to evaluate only unidirectional set-up error, resulting in a more digestible set of six scenarios, [x+δ; x-δ; y+δ; y-δ; z+δ; z-δ]. Robust evaluation of range uncertainty involves systematic scaling of the planning CT-(HU-)inferred RSP (3D RSP patient map) by percentages that are keeping with anticipated range fluctuation, e.g., nominal RSP ×1.03 and nominal RSP ×0.97 as representative of ±3% range uncertainty. It should be noted that this systematic scaling of RSP is not necessarily how range uncertainty would manifest in practice. Given the nature of the CT-HU-RSP calibration process, which seeks to minimize mean error, it is potentially more likely that given ranges of HU values corresponding to a given tissue type, (e.g., bone) might result in predicted RSP that is systematically high, while other ranges of HU (e.g., fat) might result in predicted RSP that is systematically low, or vice versa.

Also included in the 3D category would be potential scenarios generated using HU overrides, as previously discussed. Additional CT images could also be integral to 3D evaluation. Examples of this would include dose recalculation on prior planning CTs in the context of an new plan (i.e., adaptive “re-plan”) that is being generated due to initial plan robustness issues revealed during routine CT surveillance, or dose recalculation on different phases of a 4D-CT scan (45,52,53). Most typically, the latter would involve dose recalculation of the “extreme” motion phases.

4D robust plan evaluation

As previously discussed, the interplay effect can significantly impact the dose distribution for treatment sites affected by respiratory motion. The magnitude of the interplay effect can be estimated by calculating the “4D dynamic dose” (39,41,54-58). In a computer simulation, the timing of individual spots is compared with a simulated breathing trace associated with the 4D-CT image set to determine which proton spots would be delivered to which portion of the breathing cycle, or 4D-CT phase. The doses from the spots assigned to each individual 4D-CT phase are then calculated and then “deformed” to a given reference 4D-CT phase (typically the end-of-exhale) using deformable image registration (DIR) and then summed to derive 4D dynamic dose. The dynamic dose can be calculated for N fractions and evaluation occurs either by summing fractional doses (41) or by looking at the per-fraction dosimetric variance (58). In either scenario, the patient breathing and/or delivery timing parameters can be varied per fraction to simulate inter-fractional variation. It must be emphasized that these dynamic dose calculations in patients result in estimates, subject to inaccuracies associated with 4D-CT limitations (reconstruction artifacts and limited temporal binning/resolution), DIR limitations (59), and assumptions about delivery timing and simulated patient breathing.

Robust optimization

Inverse plan optimization (hereafter referred to as “conventional optimization”) is a method for automated plan development. Conventional optimization is an implicit requirement for IMPT; it was born out of two decades of development in X-ray therapy, where it emerged to harness the complex beam shaping capabilities made available with the introduction of the multi-leaf collimator. With conventional optimization, the user provides 3D dosimetric objectives to be met, each with given importance. Mathematically, this is represented as a cost function comprised of weighted objectives; algorithmically, the goal is to minimize this function. In the IMPT context, the planning system determines the set of proton spot energies, positions, and relative weightings as a best-compromise given the input dosimetric objectives.

3D robust optimization

3D robust optimization (RO) is a recent extension of conventional optimization, developed to incorporate robust error scenarios (described previously) into the optimization cost function, which significantly expands the requirements for computational power. Since these error scenarios incorporate geometric setup error as well as range uncertainty, the need for an explicitly-defined PTV is nullified; instead, RO optimizes dose directly to a CTV, thereby implicitly incorporating robustness while potentially reducing normal tissue exposure compared with conventional optimization (7,60-74).

Among methods, perhaps the most common RO strategy is the so-called “worst-case” approach (60,63,64,68). In essense, a worst-case method simplifies the objective function by considering only the minimum dose over the set of included uncertainty scenarios to each given voxel of the designated targets; likewise, for voxels outside the target(s) only the maximum dose is considered. During the last several years, there has been significant progress in RO methodology translating into commercial platforms (60,68). Notably, Ma et al. have demonstrated that robust optimization using MC dose calculation considering dose to each voxel from all robust scenarios (as opposed to worst-case), is practical (7).

4D robust optimization

The Particle Therapy Co-Operative Group (PTCOG) has recently recommended 4D robust optimization (4D RO) to mitigate the IMPT interplay effects in treatment planning for thoracic tumors (74). Owing to similar motion robustness and management considerations, the same recommendations are also highly relevant in GI cancers (75). 4D RO includes dosimetric objectives defined on the individual phases of the 4D-CT dataset in the cost function. Based on reported 4D optimization methods, the CTV defined on the individual phases of the 4D-CT deliberately receives non-uniform doses, i.e., 4D RO creates hot and cold regions along the target motion direction on these 4D-CT phases (39,46,75). But, also by design, the cumulative dose to the CTV over all 4D-CT phases can result in uniform coverage. It has been reported that compared to 3D RO, 4D RO produces significantly more robust and interplay-resistant plans for targets with comparable dose distributions for normal tissues in thoracic and distal esophageal malignancies (39,46), or generates plans with better sparing of normal tissues in hepatocellular carcinoma (75). A detailed review article recently compared 3D and 4D robust optimization (76).

Dynamic 4D robust optimization

4D RO typically relies on matching the delivered proton spots to a specific target location or 4D-CT phase (77) or on the assumption that the interplay effect will be averaged out over the delivery of many fractions (39). However, matching a specific delivery to specific tumor motion is technically difficult to implement; fraction averaging breaks down for hypo-fractionated treatments [i.e., stereotactic body proton therapy (78,79)], and the 4D dynamic dose (hence the interplay effect) are only potentially evaluated post optimization. Consequently, some investigators have taken the approach to directly include the treatment temporal dependences and optimize on the 4D dynamic dose itself, i.e., dynamic 4D RO (d4D RO). Such an approach has seen incremental advancement. Bernatowicz et al. considered a single delivery simulation on the nominal geometry (i.e., no inclusion of 3D RO scenarios) (80). Engwall et al. considered a limited set of dynamic scenarios by simulating breathing changes (81). Pepin et al. expanded this further to consider more dynamic scenarios related to both patient breathing as well as plan delivery timing changes while also incorporating variation in proton range and patient setup (82). The latter two studies relied on MC dose calculation engines. It is not yet clear how much improvement d4D RO can provide over 4D RO in terms of motion-interplay mitigation; at this point the gains are largely hypothetical in context.

Plan monitoring and adaptation

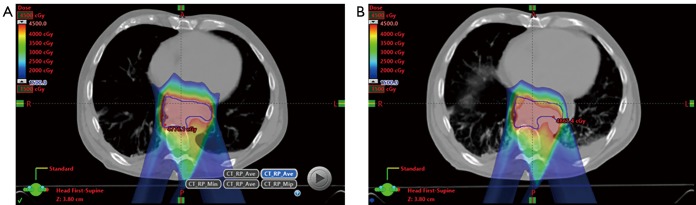
The last concept that will be covered relates to monitoring of plan robustness over the entire course of treatment. This can be accomplished by using new patient anatomic information as provided by a program of repetitive CT scanning. If necessary based on dosimetric criteria, the treatment plans can be “adapted” to accommodate observed imaging changes. In-room CT-on-rails can provide volumetric imaging for both daily IGRT and accurate HU for reliable dose recalculation (83). Alternatively, patients may undergo periodic scans in the CT simulator, as in the example shown in Figure 2 for an esophageal cancer patient treated with IMPT with a pleural effusion. The benefit of CT-on-rails is that the CT images are capturing during actual in-room setup using the same motion management tools to be applied during treatment, where applicable, and are typically obtained more frequently (e.g., daily). The drawback of the former is that CT-based IGRT with an on-rails system typically requires more time in the treatment room than other IGRT methods, thereby potentially decreasing overall practice efficiency. As techniques for cone-beam CT (CBCT) HU reconstruction accuracy continue to evolve, this modality may serve a need for both efficient 3D IGRT as well as plan monitoring and adaptation (84-89). Such methods have not been explored in detail for GI sites, which are particularly challenged by breathing motion-related CBCT artifacts.

Figure 2.

Two posterior-oblique-field esophageal IMPT plan with robustness issue due to progressing pleural effusion: (A) original plan designed to treat the CTV (blue contour) to 4,500 cGy; (B) original plan re-calculated on weekly verification CT scan showing CTV under-coverage due to proton range “undershoot” caused by increasing fluid pocket, in particular for the left-posterior-oblique field.

Mundy et al. evaluated “verification CT” and adaptive replanning frequency data from 708 patients from a contemporary IMPT practice (90). GI sites were represented in this dataset: namely esophagus (N_patients =35; N_{verification scans} =118) and combined liver-pancreas-adrenal (N_patients =18; N_{verif. scans} =46). Adaptive replanning was needed for ~17% and ~22% of patients for these two GI cohorts, respectively. This experience emphasized the importance of establishment of an institution-specific program of adaptive plan surveillance for GI sites managed with IMPT.

Conclusions

The RT community has seen a rapid adaption of proton beam RT for treatment of various malignancies in the GI tract, with an increasing number of institutions implementing IMPT. We reviewed technical aspects of IMPT implementation and relevant uncertainties that impact RT planning and delivery for GI malignancies; we then reviewed existing tools and techniques that can help with the management of these uncertainties. More specifically, we provided a practical and relevant discussion of range uncertainties, dose calculations, image guidance requirements, organ and body cavity filling consideration, implanted devices and hardware, use of fiducials, breathing motion evaluation and both active and passive motion management tools, the interplay effect, general IMPT treatment planning considerations including robustness plan evaluation and optimization, and finally plan monitoring and adaptation. The contemporary state of the art in IMPT has improved our confidence in the application of this modality for patients with GI malignancies.

Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.