Whole Mouse Brain Structural Connectomics using Magnetic Resonance Histology

Abstract

Diffusion tensor histology holds great promise for quantitative characterization of structural connectivity in mouse models of neurological and psychiatric conditions. There has been extensive study in both the clinical and preclinical domains on the complex tradeoffs between the spatial resolution, the number of samples in diffusion q-space, scan time, and the reliability of the resultant data. We describe here a method for accelerating the acquisition of diffusion MRI data to support quantitative connectivity measurements in the whole mouse brain using compressed sensing (CS). The use of CS allows substantial increase in spatial resolution and/or reduction in scan time. Compared to the fully sampled results at the same scan time, the subtle anatomical details of the brain, such as cortical layers, dentate gyrus, and cerebellum were better visualized using CS due to the higher spatial resolution. Compared to the fully sampled results at the same spatial resolution, the scalar diffusion metrics, including fractional anisotropy (FA) and mean diffusivity (MD), showed consistently low error across the whole brain (< 6.0 %) even with 8.0 times acceleration. The node properties of connectivity (strength, cluster coefficient, eigenvector centrality, and local efficiency) demonstrated correlation of better than 95.0% between accelerated and fully sampled connectomes. The acceleration will enable routine application of this technology to a wide range of mouse models of neurologic diseases.

Introduction

Brain connectomes encode information from many sources (synapses, neurons, axons), over many scales (nanometer to millimeter) and have tremendous potential to advance our knowledge of the brain (Oh et al. 2014; Bargmann and Marder 2013; Ragan et al. 2012). Connectomes characterize the structural and functional relationships among the brain’s partitions in health and disease, and the interplay between the structural and functional connectomes is an active area of investigation (Mukai et al. 2015; Pievani et al. 2014; Kingwell 2012; Bozzali et al. 2011; Baldoli et al. 2015). Connectomes derived from magnetic resonance imaging (MRI) provide insight into brain circuits involved in particular behaviors and cognitive tasks, as well as circuits controlled by common gene pathways (Guggisberg et al. 2008; Poirier et al. 2017; Sierra et al. 2015; Sporns and Bullmore 2014; Zingg et al. 2014; Boretius et al. 2009; Pandit et al. 2014). Recent advances in clinical MRI have produced more efficient imaging protocols, novel image processing, and statistical learning algorithms to interrogate and validate functional and structural connectomes using independent, and multiscale approaches (Tuch et al. 2002; Bullmore and Sporns 2009; Yeh et al. 2010; Zhang et al. 2012; Zingg et al. 2014).

Structural connectomes generated in MRI are all derived from tractography (Bozzali et al. 2011; Chen et al. 2015; Hubner et al. 2017; Maier-Hein et al. 2017; Dai et al. 2017; Volz et al. 2018). This method has its own limitation since the characterization of axonal pathways is based on indirect information and numerous assumptions even with high-quality diffusion MRI data and advanced tractography methods (Thomas et al. 2014, Maier-Hein et al. 2017). It has been reported that validation of human connectomes has been limited to “bootstrap” methods and current clinical connectomes generate many more false positives than true positives (Maier-Hein et al. 2017). At the other end of the spatial scale is the use of stereotactic retroviral injections (Oh et al. 2014; Zingg et al. 2014). This approach is considered by most to be the gold standard. But it too has limitations. It is time consuming and expensive. It cannot be extended to the human. And the time and expense limit its widespread use in the rodent.

Magnetic resonance histology (MRH) has recently been used to bridge the gap between MR and retroviral injection by acquiring a meso-scale connectome of the whole mouse brain at spatial resolution more than 12,000 times greater than the resolution used in the best human DTI studies (Calabrese et al. 2015). Using a specially fixed postmortem mouse specimen, we were able to scan the specimen undisturbed in a 9.4T magnet continuously for 10 days. We used a 3D Stesjkal Tanner sequence (Stejskal and Tanner 1965) which allowed us to acquire data with sufficient angular and spatial resolution to reduce many of the limitations encountered in clinical MRI. These data were compared directly against the connectome of Oh et al., which was based on traditional stereotactic injections of fluorescent retro virus (Oh et al. 2014). Our intent in this first MRH mouse connectome was to generate a foundation MR data set that was validated directly against the retroviral method. These data now serve as a reference for comparison against future efforts.

A ten-day scan cannot serve as a routine protocol. In recent years, compressed sensing (CS) has emerged as a new accelerated imaging technique, which enables reconstruction of under sampled data by exploiting image sparsity (Lustig et al. 2007; Liang et al. 2009; Wu et al. 2014; Bilgic et al. 2017; Wang et al. 2018). There are three essential aspects for CS: sparsity, sampling pattern, and reconstruction (Lustig et al. 2007). Most of the complex MRI images may not be sparse in the pixel representation, but they do have a sparse representation in wavelet domain or other transform domains. Various undersampling patterns in k-space have been proposed to generate the incoherent artifacts which can be removed easily with CS reconstruction. Nonlinear reconstruction has been used to enforce both sparsity of the image representation and consistency with the acquired data.

The goal of this paper is a routine scanning protocol using CS that provides connectivity measurements that are ultimately validated against those made with fully sampled data. By modifying the three-dimensional (3D) diffusion-weighted spin-echo pulse sequence for CS acquisition, we evaluated the feasibility of accelerated microscopic-resolution DTI (45 μm³) for the mouse brain using CS with an acceleration factor (AF) up to 8.0. We optimized the k-space sampling strategy for CS diffusion MRI (dMRI) data acquisition, and compared results with the fully sampled dataset as ground truth. The resulting methods allow connectomic studies of the mouse brain with what we believe to be the highest spatial resolution and accuracy yet attained with a cycle time of less than 12 hours. This capability will have enormous application in evaluating mouse models of neurologic disease and the influence of genes and environment on structure in the brain.

Methods

Animal Preparation

Animal experiments were carried out in compliance with the Duke University Institutional Animal Care and Use Committee. Seven wild-type adult (90 ± 2 day) male C57BL/6 mice (Jackson Laboratory, Bar Harbor, ME) were chosen for MR imaging. Brains were perfused using a transcardial perfusion with a 1:10 mixture of ProHance-buffered (Bracco Diagnostics, Princeton, NJ) formalin. Specimens were immersed in buffered formalin for 24 hours and then moved to a 1:200 solution of ProHance/saline to shorten T1 (to about 115 ms) and reduce scan time.

MR images were acquired using a high field MRI (9.4T Oxford 8.9-cm vertical bore magnet with an Agilent VnmrJ 4.0 imaging console) with maximum gradient strength of 2000 mT/m on each axis. We used a modified three-dimensional (3D) diffusion-weighted spin-echo pulse sequence with CS acceleration factor (AF) of 4.0, 5.1 (numerical 5.12), 6.4 and 8.0, with the fully sampled data acquired as the ground truth. The CS scans kept the same experimental parameters as the fully sampled scans (matrix size = 420 × 256 × 256; FOV = 18.9 × 11.52 × 11.52 mm³; TE = 12.7 ms; and TR =100 ms; spatial resolution = 45 μm³ isotropic). The diffusion sampling protocol included 46 unique diffusion directions with a b-value of 4000 s/mm² and 5 non-diffusion-weighted (b0) measurements. Total scan time for the fully sampled dataset was about four days (92.8 hours). Scan time of CS experiments varied from 23.2 hours to 11.6 hours, depending on the acceleration factors (4.0 to 8.0). A fully sampled dataset at spatial resolution of 90 μm³ isotropic was also acquired to demonstrate the improvement in spatial resolution that can be obtained using CS. The singal-to-noise ratio (SNR) values of fully sampled b0 images at 45 μm³ and 90 μm³ spatial resolution are 44.6 and 105.8. Details of the acquisition parameters and reconstruction methods are summarized in Table 1.

Table 1:

The scan parameters of both fully sampled data and the CS data at different acceleration factors.

AF	Resolution (μ m3)	b-value (s/mm2)	Gradient Orientations	TR (ms)	TE (ms)	Matrix Size	Scan time (hours)	Reconstruction Methods
1.0	90	4000	46	100	12.7	210×128×128	23.2	DTI
1.0	45	4000	46	100	12.7	420×256×256	92.8	DTI, GQI
4.0	45	4000	46	100	12.7	420×256×256	23.2	DTI, GQI
5.1*	45	4000	46	100	12.7	420×256×256	18.2	DTI, GQI
6.4	45	4000	46	100	12.7	420×256×256	14.5	DTI, GQI
8.0	45	4000	46	100	12.7	420×256×256	11.6	DTI, GQI

AF: acceleration factor; DTI: diffusion tensor imaging; GQI: generalized Q-sampling Imaging.

^*The accurate AF of 5.1 is 5.12.

CS Sampling

The k-space sampling pattern is generated from a probability density function (PDF) which is derived for each specific level of compression using the expression in equation 1(Adcock et al. 2014; Wang et al. 2018):

$${\text{PDF}}_{\text{k}}=\exp \left(-{\left({\text{p}}_{\text{x}}*\text{k}/\text{n}\right)}^{\text{Py}}\right)$$ (1)

where n is the k-space matrix size (k_max); k = 1, 2, ……, n. The final sampling pattern (SP_k) is generated using Monte Carlo methods to subsample the full PDF yielding the random, sparse sampling which is fundamental to compressed sensing. SP_k was optimized for four different acceleration factors (AF= 4.0, 5.1 ,6.4 and 8.0) by optimizing the selection of p_x and p_y, which was further tested by the point spread function (PSF, Supplemental Figure 2) to measure the incoherence (Lustig et al. 2008). In essence, the k-space points were fully sampled in the center of k-space, with sparser sampling in the high-frequency areas. The optimized k-space sampling pattern was then applied in the fully sampled k-space data to obtain the under sampled k-space data (12.5% ~ 25% of the k-space data). Supplemental Figure 1 shows the PDF and sampling patterns we used for each scan at different acceleration factors.

CS Reconstruction

Reconstruction of the under sampled k-space data was accomplished by minimizing the following function (Lustig et al. 2008; Wang et al. 2018):

$$f(x)=\Vert Fx-y{\Vert }_2^2+{\lambda }_1\Vert \mathit{\text{Ψ}}x{\Vert }_1+{\lambda }_{2}TV(x)$$ (2)

Where x is the image and y is its corresponding k-space, F is the fast Fourier transform (FFT), Ψ is the sparse transform, λ₁ and λ₂ are weighting factors, TV. is the total variation. Four CS acceleration factors (AF = 4.0, 5.1, 6.4 and 8.0) were evaluated. CS saves time on the two phase encoding directions. Thus AF = 8.0 means the acquisition time is 1/8^th the time for a fully sampled image. CS reconstruction in 3D is slightly different than 2D CS reconstruction. Data is under sampled along the two phase encoding directions but fully sampled along the readout direction. The resulting under sampled 3D k-space volume was first Fourier transformed (FFT) along the (fully sampled) readout dimension. Then the CS reconstruction was applied slice-by-slice in two phase dimensions with 200 iterations for each slice. λ₁ equals 0.005 for the sparse solution and λ₂ equals 0.002 for the data consistency. Transforming the data to a series of 2D arrays makes the problem particularly well suited for parallel computation. Our code has been implemented on a Dell high performance cluster.

Whole brain tractography

The tractography of generalized Q-sampling imaging (GQI) was obtained by a modified streamline tracking algorithm implemented in DSI Studio software with maximum two fibers resolved in one voxel (Yeh et al. 2013). Diffusion tensor imaging (DTI) was also used to caluclate the tensor and the scalar indices (AD, RD, FA and MD). The propagation direction was calculated by applying trilinear interpolation on the fiber orientations provided from neighborhood voxels. The next point was then determined by moving in the propagation direction 0.02 mm. The propagation process was repeated until the tracking trajectory exceeded either a turning angle of greater than 65°, or the anisotropy value of the current position was below a predefined threshold. For major white matter tracts, the FA threshold was 0.2 with a minimum fiber length of 5.0 mm, and a total 2,000,000 fibers were generated with whole brain seeding. For whole brain tractography (white matter and gray matter), the FA threshold was 0.075 with a minimum fiber length of 0.5 mm. Five million fibers were generated with whole brain seeding.

Graph theoretical analysis

The whole brain connectome was generated using DSI Studio software with 166 regions of interest (ROIs) parcellation of the whole mouse brain based on previous study (Calabrese et al. 2015). These ROIs are the nodes and their connections are the edges. From these representations, a variety of graph measures can be calculated about the network topology. We used several standard measures to describe the network’s topology using Brain Connectivity Toolbox (Rubinov and Sporns 2010). Node Strength: the sum of weights of links connected to the node (number of fiber tracts to the node); Clustering coefficient: the fraction of triangles around a node. This is equivalent to the fraction of node’s neighbors that are neighbors of each other; Eigenvector centrality: a self-referential measure of centrality: nodes have high eigenvector centrality if they connect to other nodes that have high eigenvector centrality; Local efficiency: the global efficiency computed on the neighborhood of the node, and is related to the clustering coefficient. The parameters were calculated for each individual node.

Results

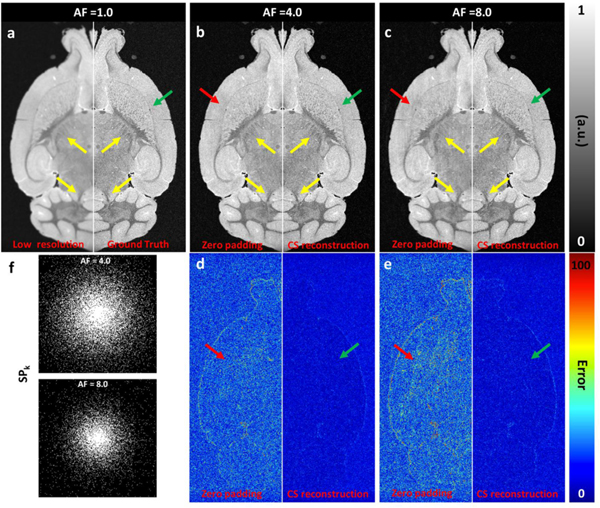
Figure 1 illustrated the value of CS reconstruction in increasing the spatial resolution and reducing the scan time for the protocols in row 1, 2, 3 and 6 in Table 1. Figure 1a shows the fully sampled data at sptatial resolution of 90 μm³ (left) and 45 μm³ (right, as ground truth), where lower resolution is characterized by loss of small structures and subfield bourdaries (yellow and green arrows). The zero-padding images (Fig 1b and Fig 1c, left) show strong incoherent artifacts, while these artifacts are significantly reduced after CS reconstruction at acceleration factor (AF) of 4.0 (Fig 1b, right) and 8.0 (Fig 1c, right). The incoherent artifacts were better visualized in the error mapping images (Fig 1d and Fig 1e, left). The artifacts in the zero padded images were more severe with more aggressive undersampling (Fig 1c and Fig 1e, left) and largely diminished after CS reconstruction even with AF of 8.0 (Fig 1e, right). The optimized SP_k for different AFs (4.0, 5.1, 6.4, 8.0) and the corresponding PDFs are summarized in Supplemental Figure 1 and Supplemental Figure 2.

Figure 1:

The simulation results with CS of a) 1.0; b) 4.0; c) 8.0. The coherence was measured by the point spread function (PSF). CS reconstruction was significantly affected by the sampling pattern (a-e). The fully sampled data was retrospectively downsampled to 4.0 and 8.0, and the CS reconstructed images showed limited error (e). The sampling patterns in k-space with AF =4.0 and 8.0 were also shown (f).

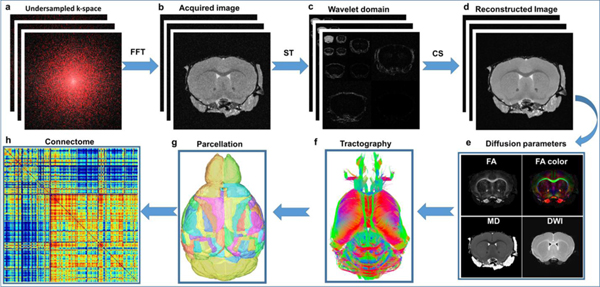
Figure 2 summarizes the methods used in this study, starting from data acquisition to generation of the brain. A set of 46 3D image volumes was acquired with diffusion encoding gradients at equidistant angular spacing on the unit sphere. Five baseline images were acquired interspersed with the diffusion-encoded images. For each of the 51 images, 3D k-space was fully sampled along the readout dimension and partially sampled in the two phase-encoding dimensions. The direct Fourier transform results in incoherent artifacts (b). The artifacts were reduced by transformation into the sparse wavelet domain (c). The final step employed a nonlinear iterative reconstruction using the individual slices (d). The 46 diffusion-weighted arrays were registered to the baseline images to correct for eddy currents yielding a four-dimensional array. Diffusion tensor images were calculated from which the scalar images fractional anisotropy (FA) and mean diffusivity (MD) were derived (e). Whole brain tractography (f) was performed using DSI Studio and the whole mouse brain connectome (h) was generated with priors from an atlas parcellating the brain to 166 regions of interest (ROIs) (Calabrese et al. 2015).

Figure 2:

The CS pipeline from data acquisition to brain connectome. The raw image from under sampled k-space (a) showed incoherent artifacts after direct Fourier transformation (b). The images were much sparser in wavelet domain (c). The images were subsequently reconstructed slice by slice from under sampled data with a nonlinear algorithm (d). The diffusion metrics (FA, MD) were calculated from the reconstructed diffusion images (e). The brain connectome (h) was generated from whole brain tractography (f) and the parcellation of the whole brain (g). FFT: Fast Fourier Transform; ST: Sparsifying Transform; CS: Compressed Sensing; FA: Fractional Anisotropy; MD: Mean Diffusivity

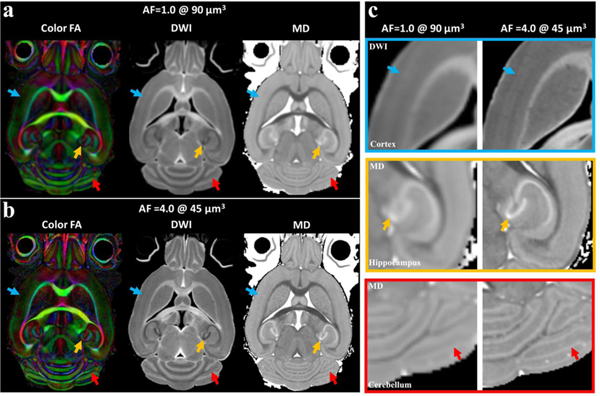
Figure 3 illustrates the color FA, DWI and MD images derived from fully sampled dMRI at 90 μm³ isotropic resolution (matrix size 210 × 128 × 128) and compressed sensing results at 45 μm³ isotropic resolution (matrix size 420 × 256 × 256). The color FA, DWI, and MD images were found to be visually comparable with the fully sampled results, however, CS exhibits significant resolution improvement over the fully sampled images. Note, both scans retained the same angular resolution (46 DWIs and 5 B0 images, table 1), which results in the same scan time (23.2 hours). Compared to the fully sampled results, the subtle anatomical details of the brain, such as cortical layers (green arrows), dentate gyrus in the hippocampus (yellow arrows), and cerebellum (red arrows) were better visualized by CS results (c, enlarged images). The similar results are also shown in striatum region, where the small axonal bundles can be resolved even with AF of 8.0 at 45 μm³ (supplemental figure 4).

Figure 3:

Color FA, FA and MD parametric images derived from fully sampled dMRI at 90³ μm isotropic resolution and compressed sensing results at 45 μm³ isotropic resolution. Note these two scans retained the same scan time and same angular resolution (46 DWI images). Compared to the fully sampled results at the same scan time, the subtle anatomical details of the brain, such as cortex, hippocampus, and cerebellum were better visualized by CS results due to the higher spatial resolution (c).

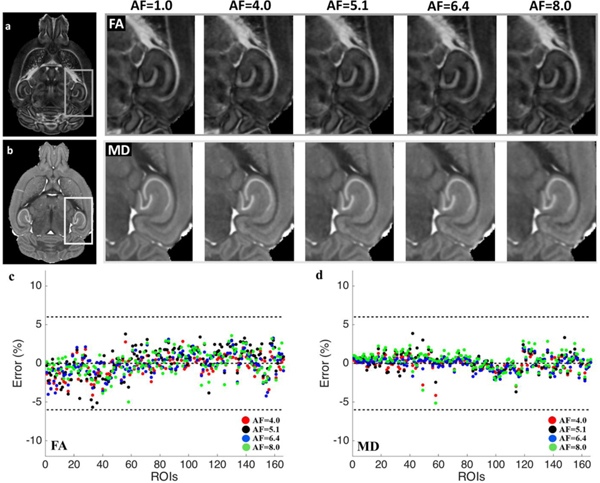
Figure 4 shows ROI-based correlations of two representative scalar indices (FA and MD) as the acceleration factor is increased from 1.0 to 8.0. The error is calculated with respect to ground truth derived from the fully sampled data at 45 μm³ isotropic spatial resolution. The calculated FA and MD images were visually comparable to the references (the fully sampled results) even at AF of 8.0, with major information qualitatively preserved and negligible artifacts. At AF of 8.0, there is some perceptible blurring visible in the mean diffusivity images in the dentate gyrus. Both FA and MD values showed high agreement with the references with limited errors in all the 166 regions of the whole brain (< 6.0 %). FA and MD also showed high correlation (≥ 0.988) to ground truth, up to CS acceleration factor of 8.0 (Supplemental Figure 3).

Figure 4:

FA and MD parametric images appear qualitatively similar up to acceleration factor of 8.0. This is supported by the quantitative agreement, estimated using ROI-based variations of the reconstructed DTI indices (c, d) at varied acceleration factors agree with the respective ground truth values derived from the fully sampled data. The results are from one mouse acquired with various acceleration factors (1.0, 4.0, 5.1, 6.4, 8.0).

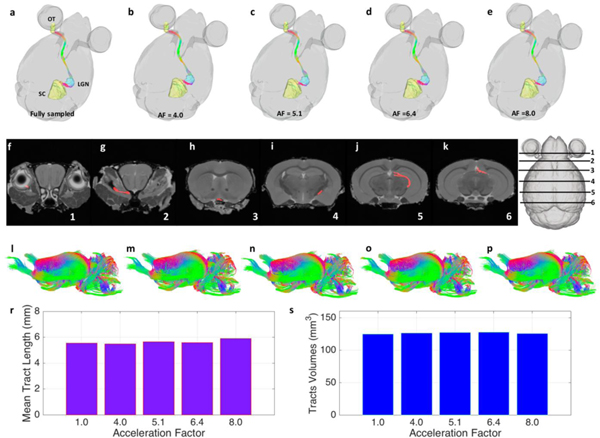
Figure 5 shows the impact of CS acceleration on tractography of white matter. As an example, we focused on the optic pathways/tracts (OT), from the left optic nerve, through the right lateral geniculate nucleus (LGN), and to the right superior colliculus (SC), as shown in Figure 5a–5e. Data displayed as color overlays on six coronal slices of the B0 image (Fig 5f–5k), indicated by the slice diagram. The CS reconstructed results agreed well with the ground truth derived from the fully sampled data. The whole brain white matter tracts are shown in Figure 5i–5p. The maximum variation of mean tract length of the whole white matter tracts was 6.3% at AF of 8.0, and the maximum variation of tracts volume was 2.3% at AF of 6.4.

Figure 5:

Tractography of white matter tracts at different acceleration factors. (a-e) show the specific pathway from left optic tract (OT), through the right lateral geniculate nucleus (LGN), and to the right superior colliculus (SC). Data displayed as color overlays on six coronal slices (f-k), indicated by the slice diagram. (i-p) show the whole brain white matter tracts. The CS reconstructed data agreed well with the fully sampled data, where the maximum variation of mean tract length of the whole white matter tracts was 6.3% at AF of 8.0, and the maximum variation of tracts volume was 2.3% at AF of 6.4 (r-s).

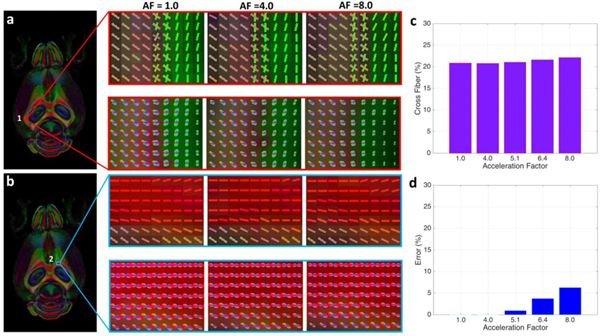
To examine the effect of CS on the resolution of crossing fibers, we focused on two regions through the corpus callosum chosen to represent different levels of fiber complexity. Figure 6 shows these two representative ROIs (positioned at 1: lateral aspect of corpus callosum and alveus; 2: rostral aspect of corpus callosum) with fiber distributions derived from CS data, as well as the fully sampled data. The microstructural organization of white matter tracts in each voxel could be visualized using the orientation distribution function (ODF) map reconstructed from the 46 direction diffusion data. The ODF provides a quantitative estimate of the number of crossing fibers in each region. Region 1 represents a region with a significant number of crossing fibers while region 2 represents a control region with no crossing fibers. The crossing fibers were resolved in the fully sampled data (AF = 1.0) at the interface of corpus callosum and alveus (ROI 1) with virtually no loss of fidelity for CS of 4.0 and 8.0. At AF = 1.0, about 20.90 % percent of the voxels in the whole brain volume showed crossing fibers (QA threshold of 0.1). This was virtually unchanged (< 1% change) at AF = 4.0. The differences increased slightly as AF increased. But even at AF = 8.0, the estimated number of voxels with crossing fibers (~ 22.16 %) is still close to the fully sampled results.

Figure 6:

Two representative ROIs (positioned at 1: lateral aspect of corpus callosum and alveus; 2: rostral aspect corpus callosum) show fiber distributions derived from CS reconstructed data, as well as the fully sampled data. The microstructural organization of white matter tracts in each voxel are visualized using the orientation distribution function (ODF) map reconstructed from the 46-directions diffusion data and the underlying estimated fiber orientations. The crossing fibers were resolved in the fully sampled data (AF = 1.0) at the interface of corpus callosum and alveus (ROI 1), while no cross fibers are shown in the corpus callosum regions (ROI 2). The results at AF = 4.0 agreed well with the fully sampled data with about 1.0% variation, while the difference gradually increased with higher AF. The estimate of the number of crossing fibers in ROI 1 at AF=8.0 differed from the fully sampled data by < 7.0 %.

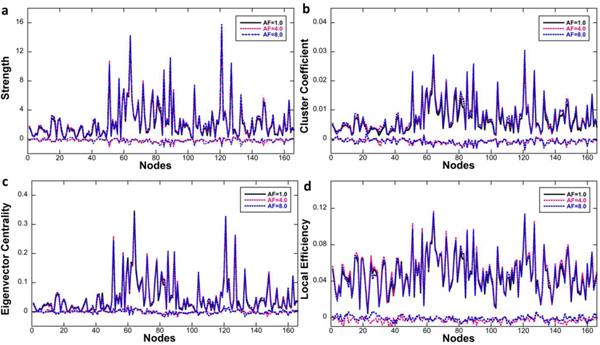
To evaluate the effect of CS on the connectome properties we chose four graph theoretic analysis metrics, and evaluated them for all 166 nodes. In addition to this fine-grained approach, the hierarchical structure of the atlas was used to construct and compare connectomes at a coarser resolution level, for seven major brain subdivisions. Figure 7 illustrates the connectome of the whole brain generated from fully sampled and CS reconstructed data. The connection strengths at AF of 4.0 and 8.0 among seven major parts of the whole brain (isocortex, midbrain, hindbrain, pallium, subpallium, diencephalon, and white matter tracts) were virtually identical to the fully sampled data. The strength, cluster coefficient, eigenvector centrality, and local efficiency of individual nodes at AF of 4.0 and 8.0 did not differ measurably from the fully sampled data as demonstrated in Figure 8. The correlation coefficients of the strength, cluster coefficient, eigenvector centrality, and local efficiency were 0.9908, 0.9798, 0.9951, and 0.9553, respectively, regardless of the acceleration factors. The maximum difference in the strength was 7.95% at AF =8.0.

Figure 7:

Visualization of the connectivity between the seven major parts of the whole brain (isocortex, midbrain, hindbrain, pallium, subpallium, diencephalon, and white matter tracts) generated from the fully sampled data (a) and CS reconstructed data (b-c).

Figure 8:

The strength, cluster coefficient, eigenvector centrality, and local efficiency of individual 166 nodes from CS data showed consistent results with the fully sampled data (d-g). The correlation coefficients of the strength, cluster coefficient, eigenvector centrality, and local efficiency were higher than 0.9908, 0.9798, 0.9951, and 0.9553, respectively, regardless of the acceleration factors. The differences between fully sampled results and CS results are also shown (flat curves at the bottom in each figure).

Discussion

Diffusion MRH offers a noninvasive method for quantitative characterization of brain structural connections in neurological and psychiatric conditions. However, it requires a long scan time due to the need for both high spatial and high angular resolution (Calabrese et al. 2015; Ugwu et al. 2015; Hubner et al. 2017). Even a single high resolution diffusion MRH currently takes days to complete, preventing any population studies (Tuch et al. 2002; Calabrese et al. 2015). Therefore, any method to accelerate DTI acquisition with subsequent validation of the results is highly desirable. To the best of our knowledge the use of CS to accelerate imaging of the mouse brain connectome has not yet been investigated. In this study, we implemented CS method to reduce the acquisition time of mouse brain DTI scans at 9.4 T by a factor of 8.0 without losing significant accuracy in the FA and MD values, cross-fiber numbers, and connectome of the whole brain.

The resolution index in brain connectome histology

The advantages of high-resolution diffusion tensor imaging (DTI) have been demonstrated in human brain studies (Sotiropoulos et al. 2013; Chang et al. 2015). The in vivo data (0.85 mm³) show that structural connectivity networks of human brains can be mapped more accurately and completely with high-resolution DTI as compared with conventional DTI (2 mm³ isotropic) (Chang et al. 2015). In the human connectome project (HC) results demonstrated that high-spatial resolution datasets (1.25 mm³ isotropic) provided greater specificity and allowed reconstruction of certain tract features that were not observed by the lower resolution datasets (2 mm³ isotropic), even when the latter had higher angular resolution (Sotiropoulos et al. 2013).

Scanning a fixed mouse brain is a considerably different challenge than the human brain. The spatial resolution, number of angular samples, and b values can vary enormously between clinical imaging and MRH (Calabrese et al. 2015). We define the resolution index (RI), a metric to help compare scale across methods, as the number of angular samples divided by the voxel volume. It is essentially the product of the q space and k space samples. We will fix the scale in mm^-3. For reference, the human connectome protocol acquires data at 1.05 mm with 128 unique gradient directions i.e. RI= 111 mm⁻³ (Vu et al. 2015). Several investigators have reported on preclinical connectomic studies (Moldrich et al. 2010; Chen et al. 2015; Hubner et al. 2017). Typical techniques employ spatial resolution 100 μm ×100 μm × 500 μm with 30 different directions at b values ~ 1000 s/mm (Hubner et al. 2017) with RI= 6000 mm^-3. MR histology allows scanning at higher resolution for longer times with increased angular sampling. Chen et al used 62.5 μm³ resolution with 6 angles with RI of 24,576 mm⁻³ (Chen et al. 2015). Moldrich et al scanned at 100 um with 30 angles with RI of 30,000 mm⁻³ (Moldrich et al. 2010). Our protocol at 45 μm³ with 46 directions has an RI of 504,801 mm⁻³, ~ 84 times higher than that of most mouse studies.

In clinical diffusion scans, MRI voxels even at 1 mm³ are too large to enable the resolution of axons, where thousands of neurons coexist in a single imaging voxel (Insel et al. 2013). The whole adult human brain (1508 g) contains about 86 billion neurons, containing ~ 62,732 neurons in 1 mm³ (Herculano-Houzel 2009). The result is comparable to the reports from the NIH BRAIN initiative (Insel et al. 2013). In the mouse brain, there are about 187,740 neurons in 1mm³, ~ 3 times higher than in human (Herculano-Houzel 2009). Considering the high resolution dMRI for preclinical scans, the voxel volume (45 μm³) in our protocol is nearly 11,000 times smaller than the clinical studies, which results in about 17 neurons in a single voxel. In principle, compressed sensing (CS) itself cannot overcome the inherent limitation in determining long-range anatomic projections based on voxel-averaged estimates of local fiber orientation obtained from dMRI. Finding connections by characterizing the axonal pathways from water diffusion is the indirect nature of dMRI (Thomas et al. 2014). However, the significant increase in spatial resolution is likely to improve precision and accuracy of the mapping from diffusion signal to fiber orientation estimates, providing more confidence in the results (Sotiropoulos et al. 2013; Chang et al. 2015).

Tradeoffs between spatial resolution and angular resolution

In previous studies, scanning the specially fixed postmortem specimen undisturbed in a 9.4T magnet continuously for 10 days allowed us to generate a brain-wide tractography connectivity with sufficient angular (120 orientations) and spatial resolution (43 μm³). While the 120 diffusion orientations meet or exceed recommendations for optimal ex vivo diffusion imaging (Dyrby et al. 2011; Tournier et al. 2013), we acquired 46 diffusion orientations in our current study and kept similar spatial resolution (45 μm³). The connectomes generated with this protocol have been compared directly to the foundation set (235 hours). Supplemental Figure 5 shows connectomes for the fully sampled (235 hours) protocol, the fully sampled protocol with reduced angular sampling (46 angles), and the protocol with reduced (46 angle) sampling and compressed sensing with AF = 8.0. The fully sampled and the accelerated protocols showed good agreement with high correlation coefficient (0.9695). The male adult mice used in this study were at age P90 from Jackson Laboratory; the male adult mice used in Calabrese et al. study were at age P78 from Charles River Laboratory; the adult mice used in Oh et al. study were at age P56 from Jackson Laboratory. The difference of genetic heterogeneity, and developmental stage may also contribute to the connectome variations (Calabrese et al. 2015; Oh et al. 2014). The total scan time for a fully sampled data (46 diffusion angles) is about four days, while using CS with AF of 8.0 reduces the scan time to about 11 hours. The extremely long scan time for fully sampled data limits the application of diffusion tensor histology for large group studies with high spatial resolution. The streamlined protocol in this work allows us to acquire data with good fidelity and considerably reduced scan time, representing a significant advance because it now enables population studies based on DWI-MRI at unprecedented resolution (Supplemental Figure 6).

Neuronal tracer methods which generate comprehensive and quantitative databases of inter-areal and cell-type-specific projections are the gold standard (Oh et al. 2014; Zingg et al. 2014). However, the use of these stereotactic injections requires a prior hypothesis of the affected pathway, is not ideal for studying multiple pathways within the same brain, and is expensive and time consuming. In contrast, high-quality diffusion tractography provides a sensitive, whole brain coverage, and a nondestructive way to explore fiber tracking and connectivity estimation (Calabrese et al. 2015). Reports indicate that DWI connectome reconstructions, acquired with rigorous attention to the known limitations, represented fairly realistic estimates of the strength of white matter projections compared to the tract-tracing-based measurements in macaque brain (Thomas et al. 2014), and DWI is a valid methodology for robust description and interpretation of brain connectivity (Calabrese et al. 2015; Chen et al. 2015). With careful attention to the acquisition protocol, and a long acquisition time (10 days), DTI was used to produce reliable fiber pathways and a large-scale connectome in a single mouse brain, that agrees well with that derived from the much more time consuming (~2 years) study with hundreds of animals required (Oh et al. 2014). We suggest that the two methods should be complementary.

Acceleration methods for dMRI

The most popular sequence employed for DWI in clinical domain is the single-shot EPI sequence. It offers fast acquisition speed, but also suffered from low SNR and spatial resolution. Multi-shot EPI sequence offers excellence SNR compared to single-shot EPI with the drawback of longer acquisition time (Chang et al. 2015). Parallel imaging techniques like GRAPPA and SENSE merged with EPI are another stratagey employed to reduce the scan time (Deshmane et al. 2012). Recently, simultaneous multislice acquisition using parallel imaging reconstruction has become a routine imaging technique, yielding an acceleration equal to the number of simultaneously excited slices (Barth et al. 2016). In general, EPI is susceptible to numbers of artifacts, including eddy current artifacts, imaging blurring, mangnetic field inhomogeneity, and chemical shift artifacts. In contrast, the 3D Stejskal-Tanner spin echo diffusion-weighted imaging sequence is the preferred imaging technique for ex vivo high-field (9.4 Tesla) rodent brain MRI due to its immunity to magnetic susceptibility and its the inherent signal averaging to increase the signal-to-noise ratio. This sequence, however, is time consuming and allows a limited number of diffusion encoding directions within a reasonable scan time. CS has been used to accelerate acquisition at high magnetic field (9.4 Tesla), to provide a higher spatial resolution and/or reduce acquisition time. The 3D pulse sequence is particularly attractive for CS because it is time-consuming and undersampling two phase encoding dimentions in 3D Cartesian imaging helps achieve the high degree of 2D incoherence assumed in CS reconstruction (Wang et al. 2018). The significant scan time reduction by undersampling both phase dimensions would be extremely beneficial to any ex vivo 3D MRI study of rodent brains. However, the acquisition time is still too long for in vivo human brain imaging even with AF of 8.0. While CS has been used effecitviely in clinical imaging, translating almost any protocol from the preclinical to the clinical environment is fraught since the underlying challenges are fundamentally different.

One limitation of our study is our use of single b value (single-shell). However, CS can potentially enable multi-shell diffusion MRH acquisition by significant reduction of scan time. Multi-shell may give better estimation of the fiber orientation distribution function and more accurate structural tractography (Sotiropoulos et al. 2013). Another limitation of our study is that CS was only applied in undersampling k-space. CS may also be applied on q-space, or k-space and q-space simulataneous to further accelerate the scan in the future. These advances will allow to estimate neurite orientation dispersion and density imaging (NODDI) and enable new opportunities to relate diffusion-weighted signals directly to the underlying cellular microstructure using biophysical models of brain tissue (Zhang et al. 2012). Furthermore, a cloud approach pipeline is under developing for sharing and analyzing brain imaging data for interested researchers. In addition, only healthy mice were used to validate the proposed method, detecting brain connectivity alterations in disease models are warranted in further studies.